Human Scalp Potentials Reflect a Mixture of Decision-Related Signals during Perceptual Choices

Abstract

Single-unit animal studies have consistently reported decision-related activity mirroring a process of temporal accumulation of sensory evidence to a fixed internal decision boundary. To date, our understanding of how response patterns seen in single-unit data manifest themselves at the macroscopic level of brain activity obtained from human neuroimaging data remains limited. Here, we use single-trial analysis of human electroencephalography data to show that population responses on the scalp can capture choice-predictive activity that builds up gradually over time with a rate proportional to the amount of sensory evidence, consistent with the properties of a drift-diffusion-like process as characterized by computational modeling. Interestingly, at time of choice, scalp potentials continue to appear parametrically modulated by the amount of sensory evidence rather than converging to a fixed decision boundary as predicted by our model. We show that trial-to-trial fluctuations in these response-locked signals exert independent leverage on behavior compared with the rate of evidence accumulation earlier in the trial. These results suggest that in addition to accumulator signals, population responses on the scalp reflect the influence of other decision-related signals that continue to covary with the amount of evidence at time of choice.

Introduction

In recent years, the study of the computational and neurobiological basis of perceptual decision making has received considerable attention (Bogacz et al., 2006; Gold and Shadlen, 2007; Heekeren et al., 2008; Ratcliff and McKoon, 2008; Sajda et al., 2009; Purcell et al., 2010; Gold and Heekeren, 2013; Shadlen and Kiani, 2013). Current computational accounts posit that perceptual decisions involve an integrative mechanism in which sensory evidence supporting different decision alternatives accumulates over time to a preset internal decision boundary (Ratcliff, 1978; Usher and McClelland, 2001; Ratcliff and Smith, 2004; Palmer et al., 2005). Correspondingly, several non-human primate (NHP) neurophysiology studies have revealed patterns of single-unit activity that are in agreement with this integrative mechanism in sensorimotor areas guiding choice, such as the lateral intraparietal area (LIP), the frontal eye fields (FEFs), and the superior colliculus (SC; Horwitz and Newsome, 1999; Kim and Shadlen, 1999; Shadlen and Newsome, 2001; Gold and Shadlen, 2007). Specifically, firing rates of a subset of neurons in these areas build up over time with a rate proportional to the amount of sensory evidence (i.e., difficulty of the task) and eventually converge to a common firing level (decision boundary) as the animal commits to a choice.

Although these NHP findings have motivated several human electrophysiology studies to look for neural correlates of similar decision-related activity (Philiastides and Sajda, 2006; Philiastides et al., 2006; Donner et al., 2009; Ratcliff et al., 2009; de Lange et al., 2010; O'Connell et al., 2012; Wyart et al., 2012; van Vugt et al., 2012; Cheadle et al., 2014; Polanía et al., 2014), our understanding of how response patterns seen in single-unit data manifest themselves at the level of scalp activity obtained from a population of neurons remains limited. Major limiting factors include the heterogeneity of neuronal responses in the areas from which individual neurons are selected (Ding and Gold, 2010, 2012b; Meister et al., 2013), the constraints imposed by the selection procedure itself, which often requires neurons to exhibit persistent and choice-predictive activity (Gnadt and Andersen, 1988), and crucially the influence of a wider network of regions that can simultaneously encode other decision-related variables such as choice certainty, expected reward, or embodied decision signals (Kiani and Shadlen, 2009; Ding and Gold, 2010, 2012a,b, 2013; Nomoto et al., 2010; Meister et al., 2013).

Here we used a visual decision-making task and human electroencephalography (EEG) coupled with computational modeling to investigate the extent to which population responses as captured by scalp potentials resemble the pattern of activity reported previously in single-unit experiments. Our findings suggest that, similar to NHP neurophysiology, EEG responses exhibit a gradual build-up of activity, the slope of which is proportional to the amount of sensory evidence in the stimulus. Unlike single-unit activity from choice-selective neurons and computational modeling predictions of a “common boundary” at time of choice, however, scalp potentials appear to reflect the additional influence of other quantities correlating with decision difficulty and therefore continue to appear as being parametrically modulated by the amount of sensory evidence.

Materials and Methods

Participants.

Twenty-five right-handed volunteers participated in the study (13 female; mean age, 26.5 years; range, 21–35 years). All had normal or corrected-to-normal vision and reported no history of neurological problems. Informed consent was obtained according to procedures approved by the local ethics committee of the Charité, University Medicine Berlin.

Stimuli and task.

We used a set of 30 face and 30 car grayscale images (size 500 × 500 pixels, 8 bits/pixel). Face images were obtained from a database provided by the Max Planck Institute or Biological Cybernetics in Tübingen, Germany (Troje and Bülthoff, 1996; http://faces.kyb.tuebingen.mpg.de/). Car images were sourced from the web. We ensured that spatial frequency, luminance, and contrast were equalized across all images. The magnitude spectrum of each image was adjusted to the average magnitude spectrum of all images in the database. The phase spectrum was manipulated so that noisy images characterized by their percentage phase coherence were generated (Dakin et al., 2002). We used a total of four different phase coherence values (22, 24.5, 27, and 29.5%), chosen based on behavioral pilot experiments such that the overall behavioral performance spanned psychophysical threshold. At each of the four phase coherence levels we generated multiple frames for every image.

Participants performed a visual face-versus-car categorization task (Philiastides et al., 2011) by discriminating dynamically updating sequences of either face or car images (Fig. 1A). Image sequences were presented in rapid serial visual presentation (RSVP) fashion at a frame rate of 30 frames per second (i.e., 33.3 ms per frame without gaps). Each trial consisted of a single sequence with a series of images from the same stimulus class (i.e., either a face or a car) at one of the four possible phase coherence levels. Importantly, within each phase coherence level, the overall amount of noise remained unchanged, whereas the spatial distribution of the noise varied across individual frames such that different parts of the underlying image could be revealed sequentially.

Figure 1.

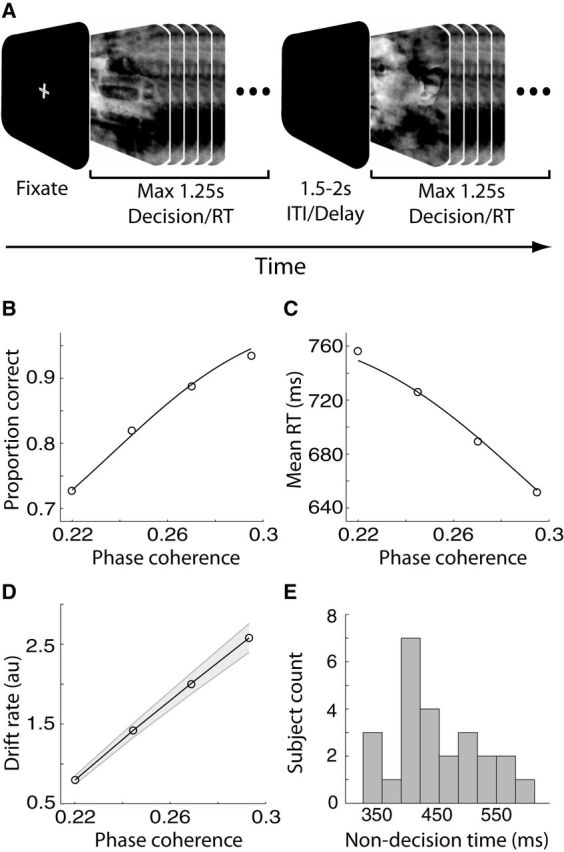
Experimental design, behavioral, and computational modeling results. A, Schematic representation of our behavioral paradigm. For each trial, a noisy and rapidly updating (every 33.3 ms) dynamic stimulus of either a face or a car image, at one of four possible phase coherence levels, was presented for a maximum of 1.25 s. Within this time subjects had to indicate their choice by pressing a button. The dynamic stimulus was interrupted upon subjects' response and it was followed by a variable delay lasting between 1.5 and 2 s. ITI, Intertrial interval. B, Average proportion of correct choices, across subjects, as a function of the phase coherence of our stimuli. Performance improved as phase coherence increased. C, Average RT, across subjects, as a function of the phase coherence of our stimuli. Mean RT decreased as phase coherence increased. In B and C curves are average model fits to the behavioral data using the diffusion model of Palmer et al. (2005). D, Average DDM drift rates as a function of the phase coherence of our stimuli. Drift rates increased as phase coherence increased. Shaded region represents SEs across subjects. E, DDM non-decision time distribution across participants indicating a sizeable between-subject variability.

A Dell Precision 360 Workstation with nVidia Quadro FX500/FX600 graphics card and Presentation software (Neurobehavioral Systems) controlled the stimulus presentation. We presented stimuli at a distance of 1.5 m to the subject on a Dell 2001 FP TFT display (resolution, 1600 × 1200 pixels; refresh rate, 60 Hz). Each image subtended 4.76° × 4.76° of visual angle. We instructed subjects to fixate in the center of the monitor and respond as accurately and as quickly as possible by pressing one of two buttons—left for faces and right for cars—using their right index and middle fingers, respectively. As soon as a response was made, the RSVP sequence was interrupted and it was followed by an intertrial interval, which varied randomly in the range 1500–2000 ms (increments of 100 ms). The RSVP sequence was allowed to remain on the screen for a maximum of 1.25 s. If subjects failed to respond within the 1.25 s period the trial was marked as a no-choice trial and was excluded from further analysis. We used a total of 480 trials (i.e., 60 trials per perceptual category and phase coherence level) during the course of the experiment. We presented trials in four blocks of 120 trials to allow subjects to rest briefly between blocks.

EEG data acquisition.

We acquired EEG data in a dark, electrically and acoustically shielded cabin (Industrial Acoustics Company) using BrainAmp DC amplifiers (Brain Products GmbH) from 74 Ag/AgCl scalp electrodes placed according to the 10–10 system (EasyCap GmbH). In addition, we collected eye movement data from three periocular electrodes placed below the left eye and at the left and right outer canthi. We referenced all electrodes to the left mastoid with a chin ground. Electrode impedances were kept <20 kΩ.

Data were sampled at 1000 Hz and filtered on-line with an analog bandpass filter of 0.1–250 Hz. We used a software-based 0.5 Hz high-pass filter to remove DC drifts and 50 and 100 Hz notch filters to minimize line noise artifacts. These filters were applied noncausally (using MATLAB filtfilt) to avoid phase-related distortions. We also re-referenced data to the average of all channels. To obtain accurate stimulus event and response onset times we collected these signals on two external channels on the EEG amplifiers to ensure synchronization with the EEG data.

Eye-movement artifact removal.

Before the main experiment, we asked subjects to complete an eye movement calibration experiment during which they were instructed to blink repeatedly upon the appearance of a white fixation cross in the center of the screen and then to make several horizontal and vertical saccades according to the position of the fixation cross. The fixation cross subtended 0.6° × 0.6° of visual angle. Horizontal saccades subtended 20° and vertical saccades subtended 15°. We used this procedure to determine linear components associated with eye blinks and saccades (using principal component analysis) and to later project these artifacts out of the EEG data collected for the main experiment (Parra et al., 2003). Additional trials with strong eye movement or other movement artifacts were manually removed by inspection.

Drift diffusion modeling.

We fit our behavioral data [accuracy and response time (RT)] with the power-rate drift diffusion model (DDM) introduced by Palmer et al. (2005) which, in a manner similar to other versions of the diffusion model (Bogacz et al., 2006), assumes a stochastic accumulation of sensory evidence over time, toward one of two decision boundaries corresponding to the two choices. The model returns estimates of internal components of processing such as the rate of evidence accumulation (drift rate), the distance between decision boundaries controlling the amount of evidence required for a decision (decision boundary), and the duration of non-decision processes (non-decision time), which include stimulus encoding and response production. In short, the model tries to simultaneously fit the proportion of correct choices (i.e., psychometric function), P_c(s), and the mean reaction time profile (chronometric function), RT(s), by assuming that the drift rate, μ, is a power function of the stimulus strength, s:

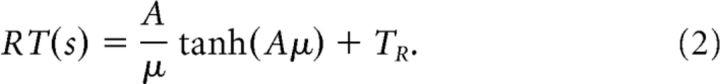P_c(s) is estimated using a logistic function (Eq. 1), where μ = (ks)^β, with the sensitivity parameter k, the decision boundary A, and the power scaling exponent β as free parameters. The mean response time RT(s) is a rescaled version of the original logistic function with an additive time constant T_R representing non-decision time (the fourth free parameter of the model).

For each subject, the free parameters were iteratively adjusted to maximize the summed log likelihood of the predicted mean response time and accuracy (see Palmer et al., 2005, their Eqs. 3–5). For a more detailed interpretation of the model and its parameters, refer to Palmer et al. (2005). For completion, we compared the fits of this model with those of the simpler proportional-rate (linear) model, by the same authors, and found that the power-rate diffusion model we used here provided a better fit to the behavioral data (mean χ² = 2.5 vs 7.8 for the linear model with 7 df).

Crucially, this version of DDM predicts a common decision boundary across the different levels of sensory evidence. To validate this further, we also fit the data with the full Ratcliff DDM and allowed the decision boundaries to change as a function of stimulus evidence (Ratcliff, 1978)—including a variant in which the boundaries were additionally allowed to decay as a function of time to account for the urgency to make a response in more difficult trials (Milosavljevic et al., 2010). To fit the DDM we used the diffusion model analysis toolbox (DMAT, http://ppw.kuleuven.be/okp/dmatoolbox/; Vandekerckhove and Tuerlinckx, 2007). We used the same model-fitting procedures we described earlier (Philiastides et al., 2011). The model that best fit behavior in the most parsimonious way was one in which drift rate was the only parameter varying with task difficulty. We viewed this as additional evidence that decision boundaries remained unchanged across the different levels of sensory evidence. Crucially, repeating all relevant analyses using model estimates obtained from this analysis (rather than those from Palmer et al., 2005) yielded virtually identical results.

Single-trial EEG analysis.

We used a multivariate linear discriminant analysis to discriminate between the highest (29.5% phase coherence) and lowest (22% phase coherence) levels of sensory evidence, locked either to the onset of the stimulus or to the subjects' response (stimulus- and response-locked analysis, respectively). Unlike conventional, univariate, trial-average event-related potential analysis techniques, multivariate algorithms are designed to spatially integrate information across the multidimensional sensor space, rather than across trials, to increase signal-to-noise ratio (SNR). Specifically, our method tried to identify a projection in the multidimensional EEG data, denoted as x(t), that maximally discriminated between the two conditions of interest. A weighting vector w (spatial filter) was used to generate a one-dimensional projection y(t) from D channels in the EEG data:

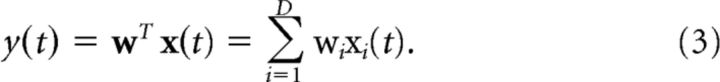Our method learned the spatial weighting vector w that led to the maximal separation (discrimination) between the two groups of trials along the projection y(t) using a regularized Fisher discriminant (Duda et al., 2001; Blankertz et al., 2011). Specifically, the projection vector w is defined as w = S_c (m₂ − m₁), where m_i is the estimated mean of condition i and S_c = 1/2(S₁ + S₂) is the estimated common covariance matrix (i.e., the average of the condition-wise empirical covariance matrices, S_i = 1/(n−1)∑_j=1ⁿ(x_j − m_i)(x_j − m_i)^T, with n = number of trials). To treat potential estimation errors we replaced the condition-wise covariance matrices with regularized versions of these matrices: Ş_i = (1 − λ)S_i + λvI, with λ ∈ [0, 1] being the regularization term and v the average eigenvalue of the original S_i (i.e., trace(S_i)/D, with D being the dimensionality of our EEG space). Note that λ = 0 yields unregularized estimation and λ = 1 assumes spherical covariance matrices. Here, we optimized λ using leave-one-out cross validation (λ values, mean ± SD: 0.098 ± 0.159 and 0.118 ± 0.153 for stimulus- and response-locked analysis, respectively).

The analysis was repeated separately for each subject. We used this approach to learn w for different windows (of duration = 50 ms) centered at various latencies relative to the onset of the stimulus (−100 before to 1000 ms after the stimulus, in increments of 10 ms) and the subjects' response (−600 ms before to 500 ms after the response, in increments of 10 ms). Note that y(t) is an aggregate representation of the data over all sensors and, compared with individual channel data, is assumed to be a better estimator of the underlying neural activity and is often thought to have better SNR and reduced interference from sources that do not contribute to the discrimination (Parra et al., 2005).

We quantified the performance of the classifier for each time window of interest by using the area under a receiver operator characteristic (ROC) curve (Green and Swets, 1966), referred to as A_z, with a leave-one-out cross-validation approach (Duda et al., 2001). To assess the significance of the resultant discriminating component we used a bootstrapping technique in which we performed the leave-one-out test after randomizing the truth labels of our trials. We repeated this randomization procedure 1000 times to produce a probability distribution for A_z and estimate the A_z leading to a significance level of p < 0.01.

To visualize the profile of the discriminating components across individual trials, we constructed discriminant component maps (as seen in Figs. 2E and, later, 4E). To do so we applied the spatial filter w of the window that resulted in the highest discrimination performance across a more extended time range of the data. Each row of one such discriminant component map represents a single trial across time. In addition we sorted trials (i.e., the rows of these maps) based on the amplitude of the discriminating component in the time window of maximum discrimination. We also used this approach to compute the temporal profile of the discriminating component, y(t), as a function of the sensory evidence dimension (as seen in Figs. 2C,D and, later, 4C,D). In the stimulus-locked analysis we used the resulting temporal profiles to look for evidence of a gradual build-up of activity leading up to the point of maximum discrimination and to extract single-trial build-up rates of this accumulating activity. Build-up rates (slopes) were computed using linear regression between onset and peak time of the accumulating activity extracted from individual participants. We extracted subject-specific accumulation onset times by selecting (through visual inspection) the time point at which the discriminating activity began to rise in a monotonic fashion after an initial dip in the data following any early (nondiscriminative) evoked responses present in the data (as seen in Fig. 2C,D).

Figure 2.

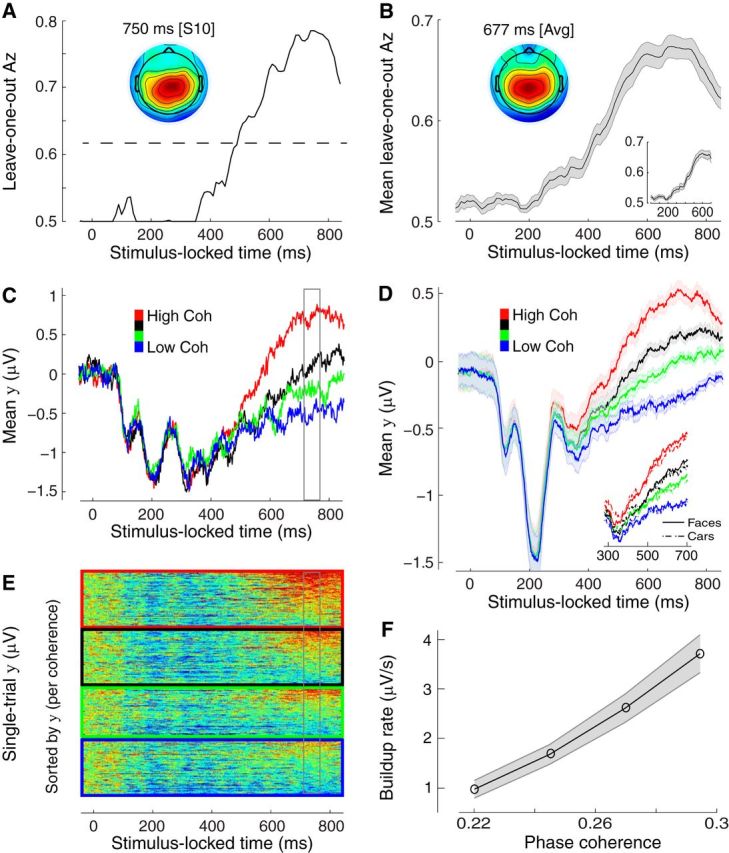
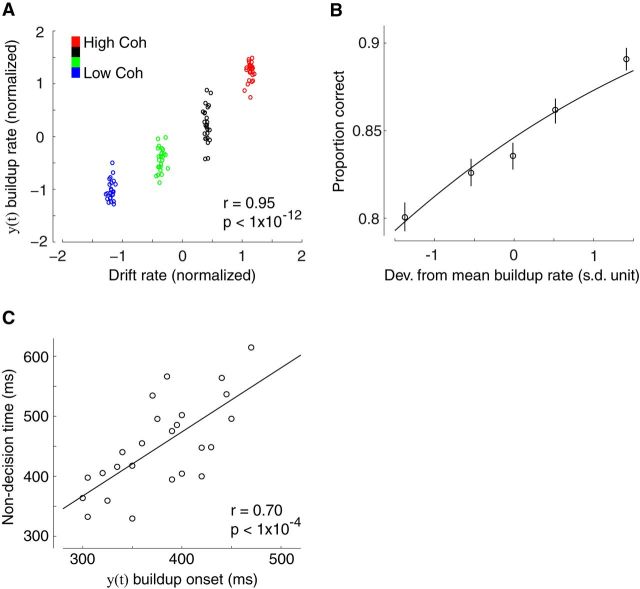
Stimulus-locked discriminating activity. A, Classifier performance (A_z) during high-vs-low sensory evidence discrimination of stimulus-locked data for a representative subject. The dashed line represents the subject-specific A_z value leading to a significance level of p = 0.01, estimated using a bootstrap test. The scalp topography is associated with the discriminating component estimated at time of maximum discrimination. B, Mean classifier performance and scalp topography across subjects (N = 25). Shaded region represents SE across subjects. C, The temporal profile of the discriminating component activity averaged across trials (for the same participant as in A) for each level of sensory evidence, obtained by applying the subject-specific spatial projections estimated at the time of maximum discrimination (gray window) for an extended time window relative to the onset of the stimulus (−50 to 850 ms poststimulus). Note the gradual build-up of component activity, the slope of which is modulated by the amount of sensory evidence. D, The mean temporal profile of the discriminating component across subjects for each level of sensory evidence. Same convention as in C. Shaded region represents SE across subjects. Inset, Same data broken down by stimulus category (face and cars). E, Single-trial discriminant component maps for the same data shown in C. Each row in these maps represents discriminant component amplitudes, y(t), for a single trial across time. The panels, from top to bottom, are sorted by the amount of sensory evidence (high to low). We sorted the trials within each panel by the mean component amplitude (y) in the window of maximum discrimination (shown in gray). Note single-trial variability within each level of sensory evidence. F, The mean build-up rate of the accumulating activity across subjects was positively correlated with the amount of sensory evidence. Build-up rates were estimated by linear fits through the data based on subject-specific onset and peak accumulation times (see Materials and Methods). Shaded region represents SEs across subjects.

Figure 4.

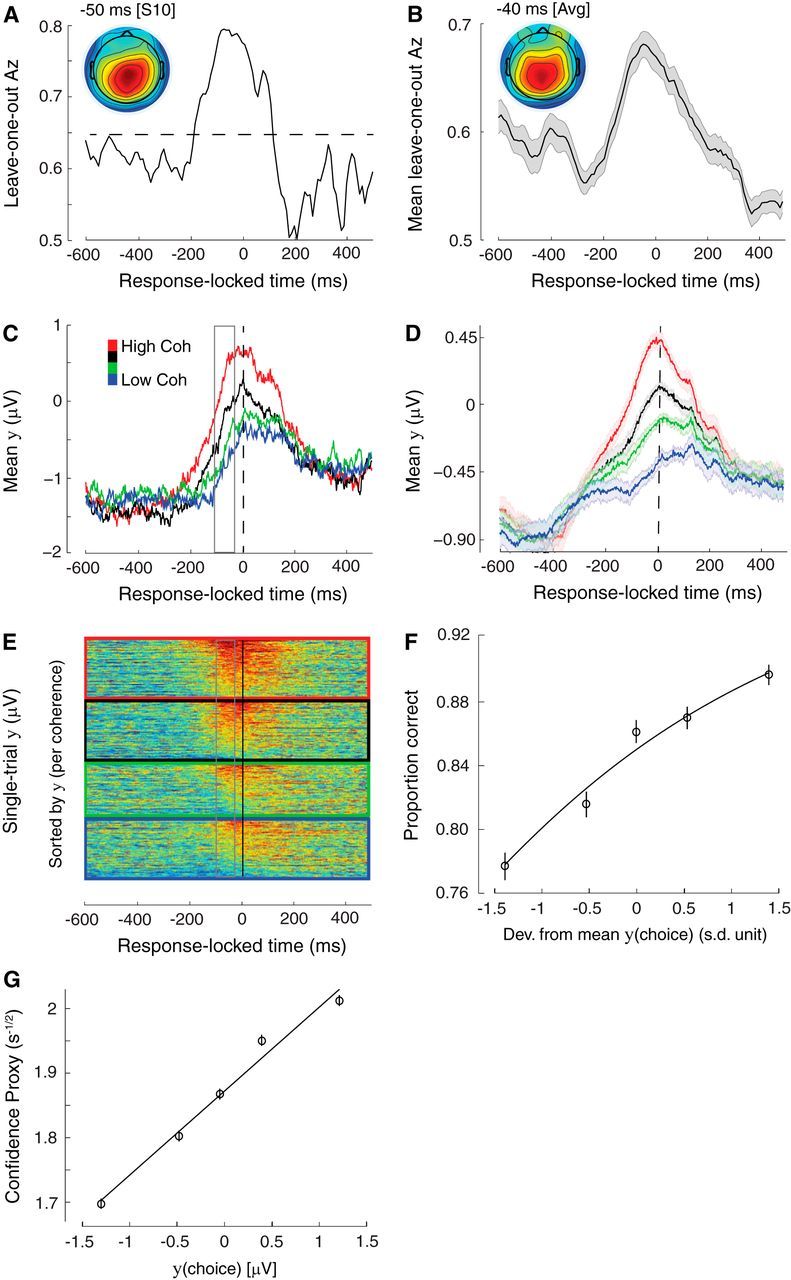
Response-locked discriminating activity. A, Classifier performance (A_z) during high-vs-low sensory evidence discrimination of response-locked data for a representative subject. The dashed line represents the subject-specific A_z value leading to a significance level of p = 0.01, estimated using a bootstrap test. The scalp topography is associated with the discriminating component estimated at time of maximum discrimination. B, Mean classifier performance and scalp topography across subjects (N = 25). Shaded region represents SE across subjects. C, The temporal profile of the discriminating component activity averaged across trials (for the same participant as in A) for each level of sensory evidence, obtained by applying the subject-specific spatial projections estimated at the time of maximum discrimination (gray window) for an extended time window around the subjects' response (−600 to 500 ms around the response). Note that the traces at time of choice (vertical dashed line) appear to be parametrically modulated by the amount of sensory evidence, rather than converging to a common “threshold.” D, The mean temporal profile of the discriminating component across subjects for each level of sensory evidence. Same convention as in C. Shaded region represents SE across subjects. E, Single-trial discriminant component maps for the same data shown in C. Each row in these maps represents discriminant component amplitudes, y(t), for a single trial across time. The panels, from top to bottom, are sorted by the amount of sensory evidence (high to low). We sorted the trials within each panel by the mean component amplitude (y) in the window of maximum discrimination (shown in gray). Note single-trial variability within each level of sensory evidence. F, Trial-by-trial fluctuations in component amplitude at time of choice were positively correlated with the probability of making a correct response (Eq. 7). To visualize this association the data points were computed by grouping trials into five bins based on the deviations in component amplitude. Importantly, the curve is a fit of Equation 7 to individual trials. Error bars represent SEs across subjects. G, Trial-by-trial deviations from the mean component amplitude at time of choice were positively correlated with a DDM-derived proxy of decision confidence, which in turn is inversely proportional to the square root of decision time (DT; see text for details). The data points were obtained following the same procedure as in F. Importantly, the curve is a linear fit to individual trials. Error bars represent SEs across subjects.

Given the linearity of our model, we also computed scalp topographies of the discriminating components resulting from Equation 3 by estimating a forward model for each component:

where the EEG data and discriminating components are now in a matrix and vector notation, respectively, for convenience (i.e., time is now a dimension of X and y). This forward model (Eq. 4) is a normalized correlation between the discriminating component y and the activity in X and it describes the electrical coupling between them. Strong coupling indicates low attenuation of the component and can be visualized as the intensity of vector a. We used these scalp projections as a means of localizing the underlying neuronal sources (see next section).

Distributed source reconstruction.

To spatially localize the resultant discriminating component activity associated with stimulus- and response-locked discriminating components, we used a distributed source reconstruction approach based on empirical Bayes (Phillips et al., 2005; Friston et al., 2006, 2008) as implemented in SPM8 (http://www.fil.ion.ucl.ac.uk/spm/). The method allows for an automatic selection of multiple cortical sources with compact spatial support that are specified in terms of empirical priors, while the inversion scheme allows for a sparse solution for distributed sources (for details, see Phillips et al., 2005; Friston et al., 2006, 2008). We used a three-sphere head model, which comprised three concentric meshes corresponding to the scalp, the skull, and the cortex. The electrode locations were coregistered to the meshes using fiducials in both spaces and the head shape of the average MNI brain.

To compute the electrode activity to be projected onto these locations we applied Equation 4 to extract the temporal evolution of scalp activity that was correlated with the stimulus- and response-locked components yielding peak discrimination performance. More specifically, we computed a forward model indexed by time, a(t), in 1 ms increments in the range 350–750 ms after the stimulus and 200 ms before until 100 ms after the response, respectively.

Single-trial logistic regression analyses.

We used logistic regression to examine how neural activity associated with the accumulation build-up rate (extracted from the stimulus-locked analysis from individual subject data) and the component amplitude at time of choice (extracted from the response-locked analysis from individual subject data) correlated with participants' behavioral performance. To factor out the effect of task difficulty in our analyses we first z-scored at each level of sensory evidence, separately, both the single-trial build-up rates and the EEG component amplitudes at time of choice. Subsequently, we proceeded to perform different regression analyses on these trial-to-trial residual fluctuations. Regression analyses were performed separately for each subject.

To assess how the fluctuations in the build-up rate of stimulus-locked activity influenced participants' probability of making a correct choice, we performed the following regression analysis:

Further, to confirm that these fluctuations in the build-up rate provide more explanatory power than can already be explained away by RTs, we included RTs as an additional predictor in the following regression analysis:

To assess how the fluctuations in the amplitude of response-locked activity influenced participants' probability of making a correct choice, we performed the following regression analysis:

In all cases we tested whether the regression coefficients resulting across subjects (β₁ values in Eqs. 5–7) came from a distribution with mean different from zero (using separate two-tailed t test).

Finally, to assess whether the component amplitudes at time of choice provided more explanatory power for the probability of a correct response than what was already conferred by the build-up rate of the accumulating activity earlier in the trial, we included both measures as predictors in a third regression analysis:

As before, we performed a two-tailed t test to assess whether regression coefficients for the component amplitude at time of choice (β₂ values in Eq. 8) came from a distribution with mean different from zero.

Spectral analysis.

To compute spectral estimates of EEG activity in the beta band (13–30 Hz), we used a multitaper method as described by Mitra and Pesaran (1999). To generate power spectral density estimates over rolandic cortex (sensors C1/C3/C5, CP1/CP3/CP5) at time of choice, we applied a multitaper window Fourier transform centered on the motor response (400 ms window, 8 Hz spectral smoothing), to individual trials across the four levels of sensory evidence. The results were magnitude-squared and averaged across tapers, trials, and sensors. To quantify the strength of the responses we converted the resulting power estimates P(β) into units of percentage change from prestimulus baseline, according to:

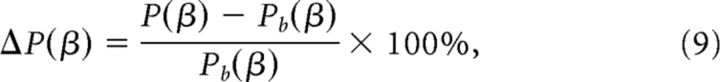where P_b(β) denotes the average power spectral density in the prestimulus period (starting 500 ms before stimulus onset).

Results

Behavioral and modeling performance

Our behavioral data indicated that the level of sensory evidence in the stimulus had a strong effect on subjects' choices. Specifically, the amount of sensory evidence was positively correlated with accuracy (t₍₉₈₎ = 14.19, p < 0.001; Fig. 1B) and negatively correlated with RT (t₍₉₈₎ = −5.78, p < 0.001; Fig. 1C). We also fit this accuracy and RT data with a power-rate DDM (Palmer et al., 2005). The model fit our subjects' psychometric and chronometric functions well (Eqs. 1, 2; all R² > 0.8) revealing a systematic increase in the rate of evidence accumulation (drift rate) as a function of the amount of sensory evidence (F_(3,72) = 130.11, p < 0.001; Fig. 1D).

Crucially, our DDM predicts a common decision boundary across the different levels of sensory evidence. To validate this further we also fit the data with the full Ratcliff DDM and allowed the decision boundaries to change as a function of stimulus evidence (Ratcliff, 1978)—including a variant in which the boundaries were additionally allowed to decay as a function of time to account for the urgency to make a response in more difficult trials (Milosavljevic et al., 2010). We found that whereas drift rate was changing as a function of task difficulty, the decision boundaries remained unchanged, endorsing the notion of a common boundary across levels of sensory evidence.

Stimulus-locked EEG analysis

In analyzing the EEG data we were initially interested in identifying signals exhibiting a gradual build-up of activity consistent with a process of sensory evidence integration. We hypothesize that if such signals exist we should observe a ramp-like activity later in the trial with a build-up rate proportional to the amount of stimulus evidence and drift rate estimates from the DDM. Furthermore, we hypothesize that trial-by-trial changes in the build-up rate of such activity should be predictive of behavioral performance even within nominally identical stimuli (i.e., after factoring out overall task difficulty effects).

To test these hypotheses we used a multivariate linear classifier designed to spatially integrate information across the multidimensional sensor space (Materials and Methods, Eq. 3) such that trial-to-trial variability was preserved. To obtain robust signatures of the relevant EEG activity (quantity “y” in Eq. 3) we first discriminated between the highest and lowest phase coherence trials. We used the area under a ROC curve (i.e., A_z value) with a leave-one-out cross validation approach to quantify the classifier's performance at various time windows locked to the onset of the stimulus. Persistent accumulating activity with a build-up rate proportional to the amount of sensory evidence should result in a gradual increase in the classifier's performance while the traces for easy and more difficult trials diverge as a function of elapsed time.

Indeed, we observed that the classifier's performance began to increase gradually after 300 ms and peaked around 700 ms poststimulus, on average. This pattern was clearly visible in individual (Fig. 2A) as well as in the group results (Fig. 2B). Importantly, we found that individual discriminator performance peaked before each participant's mean response time suggesting that differences in motor preparation across levels of sensory evidence are unlikely to have contributed to classifier performance. To further mitigate this concern we repeated the discrimination analysis making sure that the data from the last 100 ms before the response were excluded from the training of the classifier. We found that the gradual build-up and overall discrimination performance remained unchanged (Fig. 2B, inset).

Having identified subject-specific spatial projections in the data for the time window yielding maximum discrimination between the highest and lowest levels of sensory evidence we applied these projections (using Eq. 3) to an extended time window as well as to trials from the remaining levels of sensory evidence. This exercise can be thought of as subjecting the relevant data through the same neural generators responsible for discriminating between the two extreme levels of sensory evidence and was designed to serve two main purposes.

First, we characterized the temporal profile of the resulting discriminating component beyond the point of maximum discrimination and we demonstrated that there exists a postsensory, gradual, build-up of activity (see Fig. 2C for individual and Fig. 2D for group results). At the same time we extracted onset times and build-up rates (slopes) for these accumulating signals. In line with the temporal evolution of the classifier's performance, neural activity began to rise gradually around 350 ms poststimulus, on average (Fig. 2D). Second, we treated the trials from the two intermediate levels of sensory evidence as “unseen” data (independent of those used to train the classifier), to more convincingly test for a true parametric effect on the build-up rate associated with the different levels of sensory evidence (i.e., build-up rate 22 < 24.5 < 27 < 29.5% phase coherence).

Using this approach we demonstrated that the build-up rates from the two intermediate levels were in fact situated between the two extreme conditions used to originally train the classifier, thereby establishing a systematic effect across the four levels of incoming evidence (F_(3,72) = 56,07, p < 0.001, post hoc paired t tests, all p values <0.001; Fig. 2F). Correspondingly, we also found a significant correlation between the build-up rates and the drift rate estimates resulting from the DDM (r = 0.95, p < 0.001, Fig. 3A), linking the ramp-like activity in our data with a drift diffusion-like process of evidence accumulation, in line with NHP neurophysiology reports (Horwitz and Newsome, 1999; Kim and Shadlen, 1999; Shadlen and Newsome, 2001; Gold and Shadlen, 2007).

Figure 3.

Correlating build-up activity with behavioral and modeling parameters. A, The build-up rate of accumulating activity in y(t) was positively correlated with DDM estimates of drift rate. Each data point represents a participant at one of the four possible levels of sensory evidence. B, Trial-by-trial deviations from the mean build-up rate in y(t) were positively correlated with the probability of making a correct response (Eq. 5). To visualize this association the data points were computed by grouping trials into five bins based on the deviations in build-up rate. Importantly, the curve is a fit of Equation 5 to individual trials. Error bars represent SEs across subjects. C, The onset time of accumulating activity in y(t) was positively correlated with DDM estimates of non-decision time across participants, indicating that the decision process moved later in time for participants with longer non-decision times. Each data point represents a single participant.

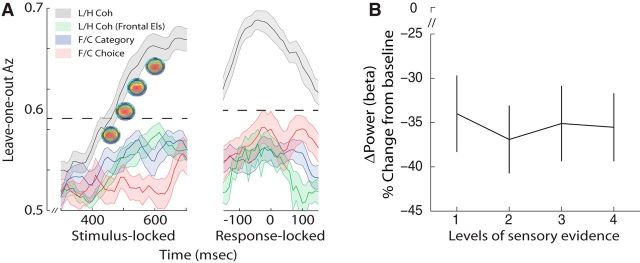
To test whether these effects are driven primarily by one of the image categories we looked at the ramp-like activity separately for faces and cars. We found no significant difference in the average slope of the two perceptual categories across subjects (two-tailed, paired t test, p > 0.1; Fig. 2D, inset), consistent with a general-purpose accumulation of decision evidence. Moreover, to test whether there are additional discriminating components specific to image category or choice, we trained two separate classifiers to discriminate directly along these dimensions (i.e., face-vs-car images over all levels of sensory evidence and face-vs-car choices at the lowest level of sensory evidence to exploit error trials). Discrimination performance was not statistically reliable along these dimensions during the gradual build-up of activity observed above (see Fig. 5A). Any activity discriminating category or choice on the scalp (rather than sensory evidence) could arise only if the generators for each category (or choice) are spatially separable. The absence of these effects suggests that during decision formation in higher-level brain areas, pools of neurons with different category and choice selectivity operate within the same area(s) and, as such, their individual contributions cannot be separated on the scalp.

Figure 5.

Control analyses. A, Mean classifier performance (A_z) during high-vs-low sensory evidence discrimination along with representative scalp topographies at different time windows during the decision phase (gray), high-vs-low sensory evidence discrimination using only far-frontal sensors (green), face-vs-car category discrimination (blue), and face-vs-car choice discrimination (red) of stimulus- and response-locked data. The dashed line represents the mean A_z value leading to a significance level of p = 0.01, estimated using a bootstrap test. Shaded region represents SE across subjects. B, Beta power (18–30 Hz) estimates during a window centered at time of choice, expressed as percentage signal change from prestimulus baseline across the four levels of sensory evidence. Error bars represent SE across subjects.

Thus far we focused our analysis on mean estimates of the build-up rate of the accumulating activity obtained from our data. Our multivariate EEG analysis, however, offered an opportunity to additionally exploit the trial-by-trial variability in the data in establishing a concrete association between neural activity and behavioral outcome. As expected, our individual subject data revealed significant neuronal variability across trials during the period of evidence accumulation, a finding that was clearly visible even for trials within the same level of sensory evidence (Fig. 2E). If this trial-by-trial variability in the build-up rate of the EEG activity embodies intertrial differences in the quality of the evidence accumulation itself, then trials with higher build-up rates should lead to more accurate decisions.

To test this prediction formally, we performed a separate single-trial regression analysis whereby the single-trial slopes extracted during the build-up of activity from individual subjects were used to predict the probability of a correct choice (Eq. 5). Importantly, we designed this analysis to address potentially confounding stimulus effects, such as the level of stimulus difficulty/salience. As stimulus difficulty could be reflected in the slope of EEG activity (e.g., overall higher build-up rates for easier, compared with more difficult, trials) and because accuracy, on average, was greater for easy than difficult trials (Fig. 1B), it seemed possible that a correlation could arise artifactually.

To address this issue we first separated trials into the four different levels of sensory evidence and for each of them we computed the trial-to-trial deviations around the mean build-up rate. We then performed the single-trial regression analysis using only these residual fluctuations, effectively exposing correlations across trials within the same level of sensory evidence. Crucially, we found that the trial-by-trial perturbations in the build-up rate of our accumulating activity were a significant predictor of our subjects' accuracy on individual trials (p < 0.001; Fig. 3B). Additionally, we confirmed that these trial-by-trial fluctuations exerted independent influence on the likelihood of a correct response compared with response times (Eq. 6, p < 0.001). This is consistent with previous findings showing that single-trial estimates of drift rate are only partially correlated with response time, due to the high degree of variability in decision processing (Ratcliff et al., 2009; here, mean correlation between build-up rate and RTs, r = 0.36).

To provide further support that the onset time of the ramp-like activity in the EEG corresponds to the start of the decision process itself, we exploited the substantial variability we observed across subjects in the non-decision time parameter of the DDM (minimum: 329 ms, maximum: 615 ms; Fig. 1E). Non-decision time represents the time spent in early sensory processing (i.e., predecision sensory events) as well as in programming a motor response (after committing to a choice). The extent of the variability in this parameter coupled with the nature of our task, which required participants to make speeded responses (thereby minimizing variance in motor execution; Müller-Gethmann et al., 2003; Klein-Flügge et al., 2013), suggests that this variance is largely due to interindividual differences in the events preceding the decision process (i.e., early sensory component of non-decision time). According to this interpretation, individual decision onset times should shift in time by a corresponding amount. Consistent with this prediction we found a significant, across-subject, correlation between non-decision times from the DDM and accumulation onset times extracted from our neural data (r = 0.70, p < 0.001; Fig. 3C).

Finally, despite requiring our subjects to maintain fixation during the stimulus presentation, we wanted to unequivocally rule out the potentially confounding influences of eye movements on the observed effects (e.g., more eye movements in difficult compared with easier trials). To this end we repeated all discrimination analyses using only the far frontal electrodes (Fp1, Fpz, Fp2)—which are affected the most by eye movements—and showed that our classifier's performance was significantly reduced (see Fig. 5A), suggesting that eye movements were not the primary driver of the observed effects.

Response-locked EEG analysis

As highlighted earlier, our behavioral and modeling results suggest that at the conclusion of the decision process (i.e., as one commits to a choice) the observed build-up of activity should, on average, converge to a common level regardless of the amount of sensory evidence. This common boundary response profile has been traced repeatedly in individual neurons in areas of the parietal and prefrontal cortex of monkeys (Horwitz and Newsome, 1999; Kim and Shadlen, 1999; Shadlen and Newsome, 2001; Gold and Shadlen, 2007), but it remains unclear whether a corresponding effect exists at the level of population responses recorded on the surface of the scalp in humans.

To test this formally we aligned our data to the onset of subjects' responses and trained a classifier to discriminate between high- and low-sensory evidence trials (in the same way we performed our analysis on stimulus-locked data earlier). A common boundary response profile should hamper our classifier's ability to discriminate between the two conditions in a systematic way, with the poorest performance nearer the time of response. In contrast, if additional quantities that covary with the amount of decision evidence (e.g., choice certainty, expected reward, etc.), are superimposed onto the signal recorded on the scalp, our analysis should yield the opposite result, with classifier performance increasing around the time of choice.

These predictions stem from the fact that our classifier is designed to return activity from processes that help maximize the difference across the two conditions of interest while minimizing the effect of processes common to both conditions. Activity related to the process of evidence accumulation leading to a common decision boundary at time of choice would no longer contribute to the discrimination across conditions and would therefore be “unmixed” from other decision-related signals ultimately responsible for driving discriminator performance.

Our findings were consistent with the latter interpretation. Specifically, our classifier's performance peaked shortly before subjects' choice (40 ms before the response, on average) and this pattern was clearly visible in individual (Fig. 4A) as well as in the group results (Fig. 4B). Similar to our stimulus-locked analysis, we applied subject-specific spatial discriminating projections to an extended time window as well as to trials from the remaining levels of sensory evidence (those excluded from classifier training). Rather than a convergence to a common amplitude at time of choice, the temporal profile of the resulting discriminating component revealed, on average, a systematic amplitude modulation as a function of sensory evidence, clearly discernible in individual (Fig. 4C) as well as in the group results (F_(3,72) = 108.93, p < 0.001, post hoc paired t tests, all p values <0.001; Fig. 4D).

To test whether this activity is choice predictive, we performed a separate regression analysis whereby we used the trial-by-trial discriminator component amplitudes (Fig. 4E) to predict the probability of a correct response (Eq. 7). Importantly, we first factored out the influence of task difficulty (as in the stimulus-locked analysis) and used only the residual trial-by-trial component amplitudes as predictors to expose correlations within each of the levels of sensory evidence. We found that these trial-by-trial amplitude fluctuations were a significant predictor of subjects' accuracy (p < 0.001; Fig. 4F). Crucially, although these amplitude fluctuations were weakly correlated with the build-up rate of accumulation we computed earlier (r = 0.16, p < 0.001), they exerted independent leverage on the likelihood of a correct response (Eq. 8, p < 0.001). This finding confirms that EEG amplitudes at time of choice are not a mere manifestation of the process of evidence accumulation but, rather, embody the additional influence of other postsensory, decision-related signals.

To further rule out the possibility that differences in motor preparation (i.e., vigor) contributed to the observed effects, we looked at beta-band desynchronization, which can be used as an index of the vigor and intention to initiate a motor response (Pfurtscheller and Neuper, 1997; Schnitzler et al., 1997; Formaggio et al., 2008). Specifically, if participants were responding with a more forceful button press during easier trials, one would expect a systematic decrease in beta power as the level of sensory evidence increases (i.e., a negative correlation), primarily over perirolandic cortex. We tested this formally by computing beta power (13–30 Hz) within a window centered on the response (Eq. 9). Although there was a clear power reduction in the beta band as expected, this reduction was not modulated by the level of sensory evidence (F_(3,72) = 1.36, p = 0.26; Fig. 5B).

One signal likely contributing to the amplitude effects around the time of response is choice certainty (i.e., confidence). Though our task was not designed to capture confidence directly (e.g., through post-decision confidence reports), we used a DDM-inspired proxy of decision confidence to test the extent to which our discriminating activity correlates with such quantity. This exploratory analysis was motivated by recent neurophysiology reports (Ding and Gold, 2010, 2012b; Nomoto et al., 2010; Fetsch et al., 2014) proposing that choice confidence (a form of reward-predicting signal) can be computed continuously as the decision process unfolds, culminating shortly before a response. In the context of the DDM used here, confidence can be estimated as the SNR in the amount of accumulated evidence (Ding and Gold, 2013), with more confident trials arising due to higher SNR. More specifically, as evidence is sampled (independently) from a normal distribution in infinitesimal time steps, the overall amount of accumulated evidence (i.e., signal) can be computed as the product of the drift rate (slope of accumulation) and elapsed time. Similarly, the SD in the accumulated evidence (i.e., noise) resulting from a drift diffusion process increases proportionally to the square root of elapsed time (Ross, 1996).

As our DDM predicted a common decision boundary (i.e., same amount of accumulated evidence, on average) across levels of task difficulty at time of choice, our measure of confidence simply becomes inversely proportional to the square root of the total decision time (DT = time of choice − build-up onset time). We made use of this prediction to formally test whether discriminating activity at time of choice is indeed related to a DDM-inspired measure of decision confidence. Specifically, we performed a single-trial linear regression analysis and demonstrated that the discriminator component amplitude at time of choice was a reliable predictor of our confidence proxy (i.e., 1/$\sqrt{\left(\text{DT}\right)}$ on each trial (p < 0.001; Fig. 4G).

Exploratory source reconstruction

Taking advantage of the linearity of our multivariate model, we also computed scalp projections (i.e., estimated a forward model; Eq. 4) of the discriminating activity as a means of interpreting the neuroanatomical significance of both the stimulus-locked and response-locked component activity. The scalp topographies for the time point of peak discrimination in the two analyses can be seen in Figures 2 and 3, top (individual and group results). To test the reliability of the scalp topographies over the gradual build-up of discriminating activity (in the stimulus-locked analysis) we looked at the spatial weights (w in Eq. 3) for each window along the decision phase and found they were very highly correlated (mean r > 0.9), suggesting the same set of generators operates during this period. Correspondingly, the forward models associated with these windows were very similar (see Fig. 5A). Interestingly, the scalp topographies for the stimulus- and response-locked discriminating activity were also qualitatively very similar, suggesting that evidence accumulation and other decision-related signals at time of choice might be encoded in partially overlapping networks, consistent with recent reports from NHP neurophysiology (Kiani and Shadlen, 2009; Ding and Gold, 2013).

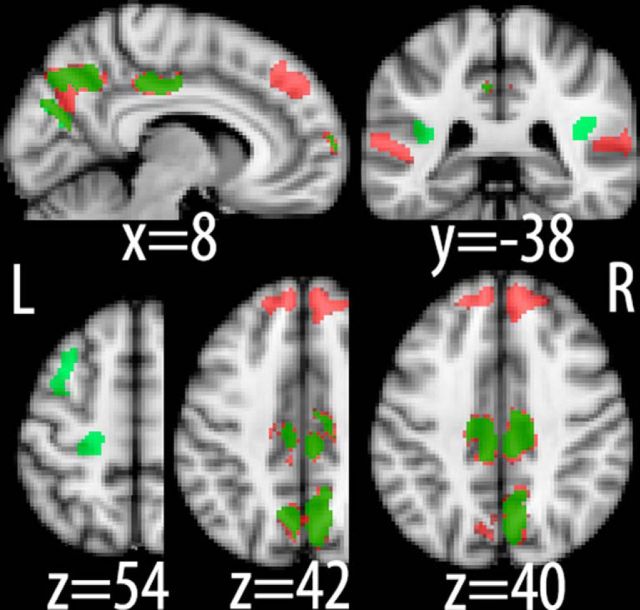
To test this formally we used these scalp projections as a means of localizing the underlying neural generators for our stimulus- and response-locked components using a Bayesian distributed source reconstruction technique as implemented in SPM8 (Friston et al., 2008; see Materials and Methods). This technique was able to account for >98% of the variance in our data in both cases. More specifically, activity associated with stimulus-locked activity was identified in regions of the prefrontal (inferior frontal gyrus) and parietal (medial intraparietal sulcus, posterior cingulate cortex) cortices (Fig. 6; red), areas that have previously been implicated in decision making and evidence accumulation (Heekeren et al., 2004; Ploran et al., 2007; Tosoni et al., 2008; Filimon et al., 2013). Interestingly, our source reconstruction also revealed bilateral clusters in superior temporal sulcus, suggesting that higher-level sensory areas encoding object categories might also exhibit decision-related build-up of activity.

Figure 6.

Neuronal source reconstruction. Source localization linked to stimulus-locked (red) and response-locked (green) discriminating activity, respectively. Note the distributed nature of the identified network as well as the overlap between the two analyses in posterior parietal cortex. Slice coordinates are given in millimeters in MNI space.

Noteworthy is that discriminating activity at time of choice (Fig. 6; green) was identified in the same regions of the parietal cortex found to be associated with evidence accumulation above, lending support to the notion that quantities such as choice confidence might also be represented in the process of evidence accumulation itself. Additionally, we identified bilateral clusters of activity in parietal operculum that were extending into insular cortex as well as in the superior frontal sulcus. Finally, there was an additional activation in motor cortex indicating that decision variables might also be encoded in regions controlling the motor effectors used to indicate the choice, in line with recent reports on the embodiment of decision making (Donner et al., 2009; Sherwin and Sajda, 2013).

Discussion

The neural basis of perceptual decision making has often been viewed as a window into the fundamental processes of cognition (Shadlen and Kiani, 2013). Pioneered in awake behaving animal studies, notably in NHPs, these efforts originally focused on identifying single-unit activity, or activity arising from small neuronal populations, which could explain variance or predict aspects of the stimulus or behavior. More recently there has been substantial effort to identify neural correlates of perceptual decision-making processing in humans using neuroimaging, such as fMRI, EEG, and MEG (Donner et al., 2007; Philiastides and Sajda, 2007; Ploran et al., 2007; Heekeren et al., 2008; Tosoni et al., 2008; Sajda et al., 2009; Noppeney et al., 2010; Philiastides et al., 2011; Siegel et al., 2011; Wyart et al., 2012; Filimon et al., 2013).

In this paper we used a dynamic stimulus paradigm, while analyzing the trial-to-trial variability in the evoked EEG within the context of sequential sampling models, to show that at the macroscopic scale of EEG, multiple neural correlates reflecting different aspects of the decision-making processes are superimposed, both in space and time. Here we demonstrated that a careful analysis, which tracks trial-to-trial variability as a function of time in the trial, relative to the stimulus presentation and/or the response, could be used to tease them apart. More specifically, we showed that stimulus-locked signatures of evidence appearing as early as 300 ms poststimulus could be disentangled from other choice-predictive signals, which continue, on average, to covary positively with the amount of sensory evidence near the time of choice. We also showed that a DDM-inspired proxy of choice confidence could potentially account (in part) for these late response-locked signals.

Recent NHP (Kiani and Shadlen, 2009; Fetsch et al., 2014) and human EEG (De Martino et al., 2013; Zizlsperger et al., 2014) studies using more direct measures of confidence reported that such quantities emerge from the same generators involved in stimulus evidence accumulation. Consistent with this interpretation, our distributed source analysis revealed that the network correlates of stimulus- and response-locked signals partially overlap in topology. Nonetheless, they each also showed unique cortical generators that ultimately help to further differentiate them from one another. One of the generators uniquely associated with response-locked signals was found in an area of the premotor/motor apparatus, providing support that (at least for RT tasks) decisions can also be implemented in the areas that guide subsequent actions (Donner et al., 2009; Sherwin and Sajda, 2013) while emphasizing that multiple signals could be encoded in parallel near the time of choice.

It is clear from our work that a spatially distributed view of the perceptual decision-making process can yield insight that would not be seen if recordings were made from a single area, or at the level of single neurons or small populations. Although understanding the microcircuitry of processes underlying decision making will continue to require recordings at the single-unit and/or small-population level of activity, particularly in NHPs, it is also clear that macro-scale networks are only observable if one takes the entire brain into account. In fact, one would not expect a one-to-one correspondence between activity generated at the micro-scale and that observed at the macro-scale.

For example, even though single-unit recordings in NHPs have consistently reported neural activity from choice-selective neurons (i.e., from a “winning decision pool”) in SC and LIP to converge to a common firing level (Horwitz and Newsome, 1999; Shadlen and Newsome, 2001; Roitman and Shadlen, 2002), decision-related neurons that are selective for an action other than the chosen one do not converge to a common activity level at time of choice (for an example, see Roitman and Shadlen, 2002, their Fig. 7A). Because the EEG signal reflects population responses, it is reasonable to assume that scalp activity would, instead, represent the absolute difference in activity between the two response profiles described above. This is because, mechanistically, the difference signal likely comes about through mutual inhibition between the competing pools of integrator neurons (Larsen and Bogacz, 2010). In this context, increased inhibition on one group releases inhibition on the other, thereby producing a positive potential on the scalp. As such, the observed scalp activity would not converge to a common decision boundary at time of choice but, rather, would appear stronger (more positive) for higher levels of sensory evidence.

Recent reports showing that spatial derivatives of human scalp EEG yield activity profiles that match what is seen in single-unit activity in NHPs, in terms of accumulation of stimulus evidence to a common boundary (Kelly and O'Connell, 2013), are in fact surprising given the distributed nature of the EEG recordings and the spatial averaging that naturally results from ohmic conduction and low-pass filtering of the CSF and the skull (Nunez and Srinivasan, 2005). We performed a similar current source density analysis (Perrin et al., 1989) on our data and found no such convergence to a common boundary, suggesting that their observation may be specific to their experimental paradigm (e.g., where changes in sensory evidence must first be detected in background noise and then accumulated to form a decision).

More specifically, in the study by Kelly and O'Connell (2013), the direction discrimination task was designed such that the dynamic motion stimulus was continuously active, whereby long periods of pure noise were interleaved with periods of partially coherent motion based on which choice was made. As such, the design included both a detection and a discrimination component. Though the task is attractive, as it eliminates early evoked responses associated with transient visual responses, it is markedly different from most perceptual decision-making tasks that study evidence accumulation, because detection is usually not included as an additional component. It is noteworthy that RTs described by Kelly and O'Connell (2013) are long relative to other comparable two-alternative forced-choice RT tasks, suggesting that perhaps the combined detection and discrimination task taps on additional cognitive processes, thereby leading to a common boundary. For example, the temporal expectation that coherent motion would appear (caused by the long interstimulus intervals), together with the added time required to detect the stimulus at different motion strengths, could lead to persistent increases in amplitude and latency shifts of P300-like signals (Gerson et al., 2005; Rohenkohl and Nobre, 2011), which mix on the scalp with accumulator signals related to discrimination, causing the curves to seemly match at time of choice.

In addition, recent evidence points to a substantial heterogeneity in the responses of individual neurons in LIP, FEFs, and SC in terms of their reflecting evidence accumulation to a common boundary as well as in encoding other decision variables that are parametrically modulated by the amount of sensory evidence near the time of choice (Ding and Gold, 2010, 2012b, 2013; Nomoto et al., 2010; Meister et al., 2013). Importantly, this heterogeneity is seen both at the level of local neuronal populations and in areas across the brain. We would expect such heterogeneity to obscure any activity representing accumulation of evidence to a common boundary, at least when measured with scalp EEG. It is important to consider whether findings at the macroscopic level of EEG truly reflect the same underlying processes of accumulation of evidence to a common boundary or are instead explainable by differences and idiosyncrasies in the stimulus/task design, relative to those used in NHP studies.

Ultimately, identifying the constituent, mechanistic processes underlying perceptual decision making will require both microscopic and macroscopic approaches that leverage advantages of performing experiments in NHPs and/or human subjects. Although the goal is to integrate the results into a common view of perceptual decision making, our study suggests that caution is required when designing human neuroimaging studies based on direct translation of single-unit patterns of activity because the resolution of the measured neural activity is substantially different.

Intriguingly, our results can form the foundation upon which future studies using macroscopic approaches can continue to interrogate the neural systems underlying human decision making. Similarly, being able to noninvasively exploit different decision-related variables on a trial-by-trial basis can be used in the development of cognitive interfaces that help inform a diverse set of socioeconomic problems. These may range from brain–computer-interface design for augmenting decision making, particularly in problems relying on inconclusive or ambiguous evidence (e.g., image analysis; Sajda et al., 2007; Parra et al., 2008), to identifying psychopathological precursors to behavioral changes resulting from cognitive decline and major neuropsychiatric disorders (e.g., schizophrenia; Lesh et al., 2011).