Modeling Scalable Pattern Generation in DNA Reaction Networks

Abstract

We have developed a theoretical framework for developing patterns in multiple dimensions using controllable diffusion and designed reactions implemented in DNA. This includes so-called strand displacement reactions in which one single-stranded DNA hybridizes to a hemi-duplex DNA and displaces another single-stranded DNA, reversibly or irreversibly. These reactions can be designed to proceed with designed rate and molecular specificity. By also controlling diffusion by partial complementarity to a stationary, cross-linked DNA, we can generate predictable patterns. We demonstrate this with several simulations showing deterministic, predictable shapes in space.

1. Introduction

Pattern formation is biologically and technologically important. Biomimetic methods for moving from top-down to bottom-up formation of designed patterns and materials have the potential to revolutionize manufacturing by dramatically reducing costs. These approaches include biomimetic molecular recognition (Chen et al. 2011) leading to self-assembled, folded structures made from block-copolymers, (Murnen et al.) biopolymers (Rothemund 2006) or patterned microparticles. Yet none of these techniques has recapitulated the “algorithmic” assembly used by complex organisms to create macroscopic structures (Peter and Davidson 2009). Very precise submicroscopic structures have been generated using deterministic DNA assembly in so-called DNA Origami, but this is at or near the molecules’ own size scale and is not scalable to cellular or larger length scales (Rothemund 2006). Longer-range ordering has been accomplished with DNA-assembled nanoparticle crystals, but the definition of the pattern is so far limited to repetitive patterns (Macfarlane et al. 2011). Meso- and nano-structured materials formed by self-assembly are finding applications in photonics (Fan et al. 2011), microelectronics, micro electromechanical systems (MEMS), and analytical devices (Fernandez and Khademhosseini 2010). We also feel that programmed self-assembly may have applications in tissue engineering (Nichol and Khademhosseini 2009).

Biological patterns are often an outgrowth of the behavior of reaction-diffusion networks, as first described by Alan Turing (Turing 1952). Mathematical models of reaction-diffusion networks have been shown to be capable of generating complex and beautiful patterns resembling everything from leopards’ spots to variegated pigmentation in sea shells. That said, the first actual demonstration of a biological Turing mechanism occurred almost 40 years after the theoretical description, (Castets et al. 1990) illustrating how difficult these systems are to study, let alone engineer.

One of the aims of synthetic biology is to standardize the engineering of biology. Being able to rationally program spatio-temporal organization would be a great accomplishment, but requires the ability to algorithmically set down biological molecules and superstructures in specific times and places. While no scalable, programmable pattern formation system has yet been demonstrated, we now describe a potential approach that should allow for nearly arbitrary pattern formation from bottom-up principles. Our approach appropriately rests on having programmable chemical reaction networks (CRNs) unfold in time and space.

While complex chemical reaction diffusion systems (e.g., the well known B-Z reaction) are known (Vanag and Epstein 2001), they are far from programmable. We will instead rely upon implementing CRNs with programmable DNA circuits (Yin et al. 2008, Phillips and Cardelli 2009). Arbitrary CRNs can be implemented in DNA, (Soloveichik et al. 2010) and the function of at least one modeled circuit has been verified in vitro (Zhang and Winfree 2009). However, previous work focused on the implementation of DNA CRNs in time, rather than in space. We now hope to design DNA CRNs that are inhomogeneous in space. We will initially focus on small, modular DNA reaction networks that can be treated as building blocks, meaning that the basic reaction can be duplicated, modified, and linked together to run in parallel. These primitives are then shown to be the basis for more complex CRNs that act as algorithmic, spatial pattern generators.

2. DNA-based programmable chemical reaction networks

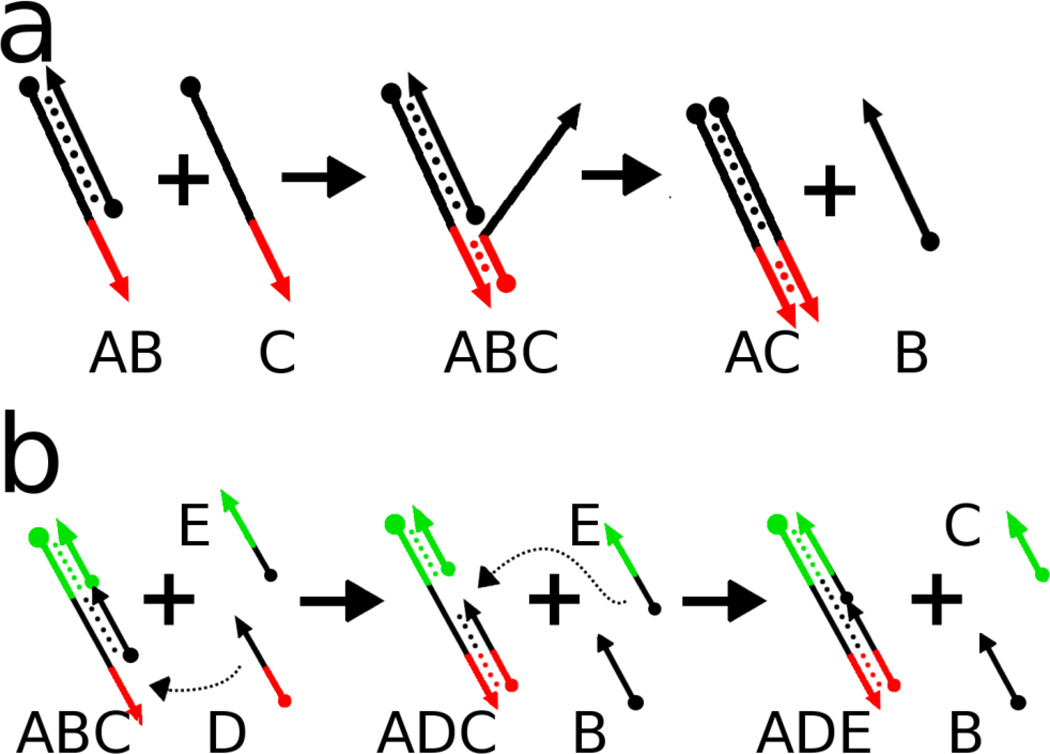
Reaction networks that can be programmed to interact with one another should also prove capable of pattern formation. DNA strand displacement reactions represent a class of reactions that have programmable inputs and outputs, and predictable kinetics (Zhang and Winfree 2009). In strand displacement reactions, a single-stranded DNA molecule binds to a hemi-duplex DNA molecule via specific Watson-Crick pairings (the so-called 'toehold'). Hybridization proceeds from the toehold via strand displacement to form a longer, more stable DNA duplex, with concomitant release of the originally paired strand (Figure 1a). Because progression of the reaction is only favorable for complementary DNA strands, parallel reactions occurring concurrently in solution can be designed to be chemically “orthogonal,” as eloquently described by Phillips and Cardelli (Phillips and Cardelli 2009). Orthogonal strand displacement reactions can be coupled in arbitrary networks, (Soloveichik et al. 2010) where single-stranded outputs from one reaction can serve as the inputs of additional strand displacement reactions. DNA-based chemical reaction networks (CRNs) are completely programmable, unlike (for instance) a Zhabotinski reaction. In this system, the predetermined location of the feature and operational parameters of the reaction are programmed into the base sequence (i.e. the pattern is generated deterministically according to the DNA hybridization rules).

Figure 1.

DNA-DNA reactions including. (A) shows a strand displacement and (B) strand displacement chain

3. Simulation of DNA CRNs

In order to simulate DNA CRNs, we needed to be able to solve equations relating diffusion and bimolecular kinetics, in either 1D or 2D. To this end, we used MATLAB’s ODE45 solver or a simple Euler method solver. We include MATLAB code with demonstrations of all simulations performed in this paper in the Supporting Material online.

4. Controlling diffusion via hybridization

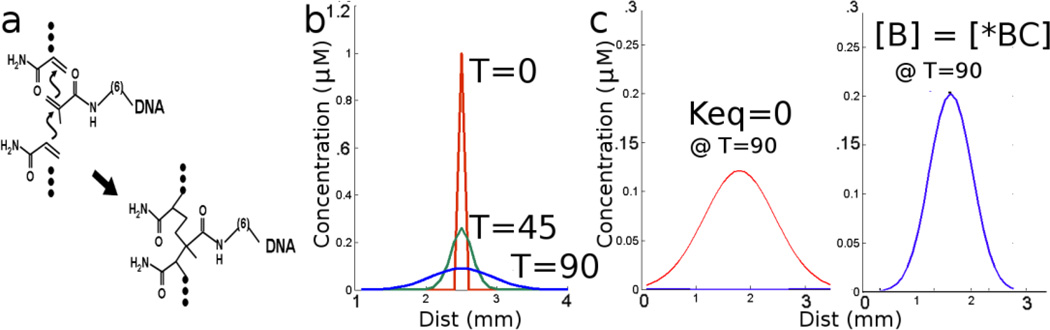
In order to create patterns with a reaction-diffusion system, we must be able to control both diffusion and reactivity. While there are many examples of how designed DNA circuits control reactivity, there are virtually no examples of programmable diffusion. We realized that we could slow the diffusion of any given component of a programmable DNA CRN by incorporating antisense oligonucleotides into the matrix where diffusion was occurring, in this instance a hydrogel. Figure 2a shows how the DNA may be anchored by co-polymerizing antisense molecules terminating with an acrylic moiety, an acrydite, into the hydrogel superstructure. Because of the complete control over sequence that is afforded by DNA CRNs, different DNAs in the network can have zero, partial, or complete complementarity to the immobilized antisense strand. This will in turn lead to variable (and programmable) diffusion through the hydrogel, since the diffusion parameters for any given DNA can be altered from complete fixed to fully diffusible depending on the number and strength of the base-pairs formed.

Figure 2.

The effect of decorated acrylamide on diffusion. (a) A DNA oligonucleotide terminated with an acrydite moiety is incorporated into a growing acrylamide polymer. (b) Starting from a narrow distribution, DNA spreads through a gel by free diffusion. In (c) free diffusion (left, Keq=0) is compared to a species that interacts significantly with the immobile DNA (right, Keq=2×10⁶mol⁻¹D=), which diffuses more slowly.

We first wanted to simulate the execution of DNA CRNs in which there was differential diffusion due to hybridization. We examined mobile DNA species A and B which were presumed to have equal diffusion coefficients (D=0.1×10⁻⁸ cm²sec⁻¹) in an unmodified gel. We then compare the predicted diffusion of A and B in the presence of an immobilized, complementary species C*. We further assume that species A has no significant interactions with C*, but that B does. Both C* and BC* have zero diffusion because C* is covalently linked to the gel (denoted by asterisk). This slows the effective diffusion of B relative to A. We assume an equilibrium constant of Keq=1×10⁻⁶mol⁻¹ such that [B] = [BC*] when all reagents are present at a concentration of 2 µM. This could be readily achieved by designing about 9 base-pairs of complementarity between B and C*. We further assume that the rate of binding/unbinding is fast relative to diffusion. Figure 2c shows that A and B have very different concentration profiles at the same time point due to their interactions with the fixed, complementary oligonucleotide.

Beyond this simple simulation, the diffusion of an oligonucleotide is influenced by its size and conformation, and manipulation of these variables provides opportunities to engineer a given DNA strand's diffusion.

5. Generating a simple pattern based on diffusion and strand displacement CRNs

We will initially show how we might implement a spatially-controlled reaction by controlling the reactivity and the diffusion of a set of properly designed DNA constructs. Two DNA molecules that are diffusing towards one another will react to form a local, immobilized fluorescent product. From a historical perspective, this is similar to Ouchterlony double-diffusion experiments (Ouchterlony 1958). In these experiments an antigen and a mixture of antibodies were allowed to diffuse toward each other through a gel matrix. Depending on the diffusion constants of the antigen and antibody, a region of visible immuno-precipitation occurred at some location between the starting locations.

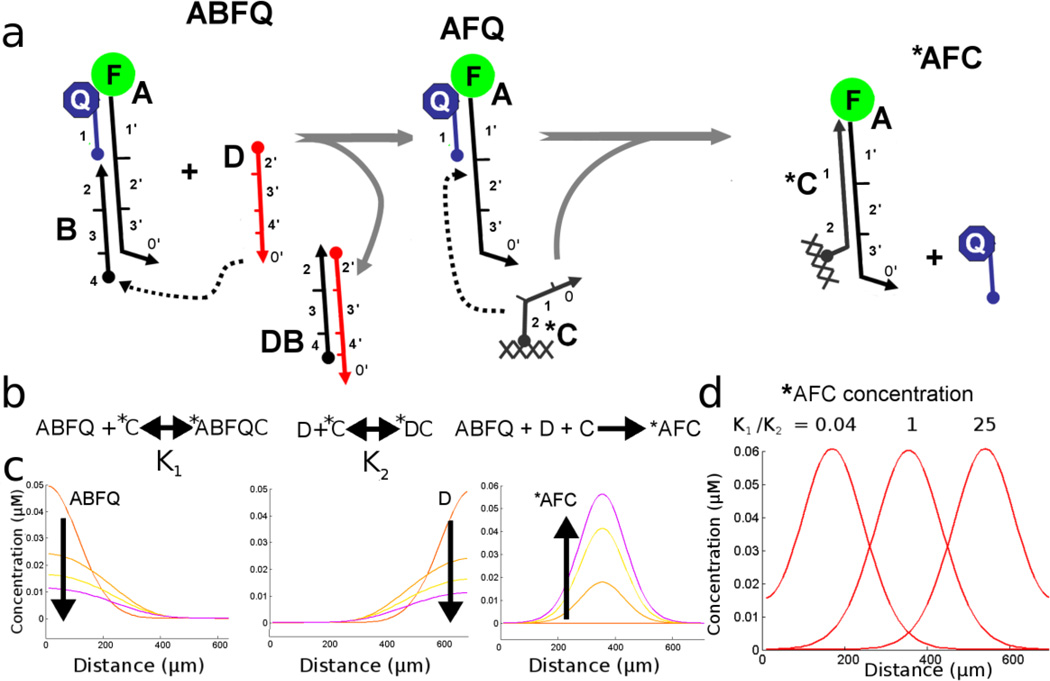
The strategy for implementing this simple reaction with DNA is shown in Figure 3A. We set up a simulation modeling two diffusing DNA substrates, a diffusible complex called ABFQ and a second diffusible reactant D. As above, ABFQ and D can partially hybridize to an immobilized oligonucleotide, C* (through short domain 0). Interactions between ABFQ and C* or between D and C* slow their diffusion by a predictable degree, as demonstrated above. The equilibration between mobile strands (A and B) and the immobile strand C* is described by K₁ and K₂ as shown in Figure 3b.

Figure 3.

(a) Schematic shows the reaction governing the formation of the final, fluorescent product AFC. DNA sub sequences are numbered with their complementary sub-sequences denoted with an apostrophe. (b) The three reactions occur simultaneously; ABFQ and D are in fast equilibrium with *C to form immobile products (denoted by asterisks) with equilibrium constants K₁ and K₂. ABFQ and D form an immobile product *AFC when they are co-localized. (c) Concentration plots show the reactants ABFQ, and D through time as well as the evolution of *AFC. (d) Concentration plot shows the final distribution of product *AFC as a function of the ratio of the two equilibrium constants K₁ and K₂.

In order to readily see where and how strand displacement reactions are taking place, the complex denoted ABFQ is composed of a common backbone (A) which is modified with a fluorophore (F), a blocker strand (B), and quencher-modified oligonucleotide (Q). Upon interaction with displacer (D), the blocker is displaced and the complex is converted to an intermediate, AFQ. Our simulation treats the nonfluorescent intermediate, AFQ, as mobile with an equivalent diffusion coefficient to ABFQ. Upon interaction with the immobilized oligonucleotide C*, this intermediate undergoes a further strand displacement reaction that releases the quencher Q. The fluorescent product AFC* is also immobilized by hybridization to C*. Thus, an immobile fluorescent band should indicate where the strand displacement reactions have taken place in the gel.

6. Modifying pattern formation by modifying diffusivity

Since adjusting the energy of interactions with the immobile phase can change the effective diffusion of a mobile DNA, it should also be able to change the pattern generated by reactive DNA species. For example, by adjusting the length and base pair content of domain 0’ on ABFQ we can change its interaction with domain 0 on C* and arbitrarily adjust the reaction equilibrium constant K₁ (See Figure 3b). In our simulation, we start, as above, with micromolar concentrations and a Keq=1×10⁻⁶mol⁻¹ for both complex ABFQ diffusing from the left and displacer oligonucleotide D diffusing from the right. Figure 3c shows the cross-section of the concentration patterns that would be generated in a gel when both species diffuse at equal rates; fluorescent product (AFC*) evolution occurs in the center. By altering the diffusion coefficients of the substrates, we can control the location where the fluorescent product is produced. Figure 3d shows three cases where the ratio of the equilibrium constants (K₁/K₂) is varied. We start by assuming that the unmodified diffusion constants of ABFQ and D are equal. If species ABFQ has an equilibrium constant five times higher (K₁=5×10⁻⁶mol⁻¹; for example, by decreasing the number of base-pairs between A and C*) and species D is decreased by a factor of five (K₂=0.5×10⁻⁶mol⁻¹ by increasing the length of domain 0’ on D) then the ratio K₁/K₂ is increased from 1 to 25 and this creates a line shifted to the right; the opposite changes produce a K₁/K₂ ratio of 0.04 and shift the line to the left. It should be noted that although the position of fluorescent product AFC* is only affected by the ratio of K₁ to K₂ rather than the absolute values of K₁ and K₂, these absolute values affect the time required for the pattern to develop. We chose to perform simulations at conditions that approximate our observations of DNA in a gel medium of ~5% w/v acrylamide. The same patterns could be generated in a different density of gel by adjusting the length of interactions with X or by simulating over a different timescale.

7. Analytically representing diffusivity via complementarity

It is computationally expensive to model equilibrium between fixed and mobile states for each species in the CRN. To simplify and speed up the simulation, we implement an effective diffusion coefficient D_eff for each species depending on its designed complementarity to the fixed DNA. Fast equilibrium with a fixed, immobile state constitutes a time-average of the diffusion at normal rate (corresponding to diffusion coefficient D) and zero. The native diffusion rate D without DNA interactions is determined by the medium (e.g. polyacrylamide gel). While different hydrogel densities will affect the global diffusion coefficients, the relative diffusivities among the components arising from interactions with immobile DNA can be treated an independent variable. The quantity of DNA co-polymerized into the gel is independent of the quantity of acrylamide and the type of buffer used to generate the hydrogel matrix. From the concentrations and standard free energy of the DNA-DNA reaction (Nakano et al. 1999), we can calculate K_eq, the standard equilibrium constant for the reaction and in turn derive the fraction of time spent in the fixed state BC*.

First, we calculate the dissociation constant and the concentration of the reactants from their initial concentrations, B₀ and C₀.

$${\mathrm{K}}_{\mathrm{d}}=1/{\mathrm{K}}_{\mathrm{e}\mathrm{q}}$$ (1)

$$[\mathrm{B}]={\mathrm{B}}_0-[\mathrm{B}\mathrm{C}]$$ (2)

$$[\mathrm{C}]={\mathrm{C}}_0-[\mathrm{B}\mathrm{C}]$$ (3)

Taking the definition of the equilibrium constant:

$${\mathrm{K}}_{\mathrm{e}\mathrm{q}}=[\mathrm{B}\mathrm{C}]/[\mathrm{B}][\mathrm{C}]$$ (4)

And defining the fraction of B bound at any given time as follows:

$${\mathrm{F}}_{\text{bound}}=[\mathrm{B}\mathrm{C}]/{\mathrm{B}}_0$$ (5)

We can substitute and simplify using the quadratic equation to express the F_bound of BC in terms of B₀, C₀ and K_d:

$${\mathrm{F}}_{\text{bound}}=\frac{({\mathrm{B}}_0+{\mathrm{C}}_0+{\mathrm{K}}_{\mathrm{d}})-\sqrt{{({\mathrm{B}}_0+{\mathrm{C}}_0+{\mathrm{K}}_{\mathrm{d}})}^2-4{\mathrm{B}}_0{\mathrm{C}}_0}}{2{\mathrm{B}}_0}$$ (6)

We can therefore express the effective diffusion coefficient with the following relationship:

$${\mathrm{D}}_{\text{eff}}=(1-{\mathrm{F}}_{\text{bound}})\times \mathrm{D}$$ (7)

For complex simulations, we will use D_eff in lieu of modeling equilibrium between a mobile and immobile state. To predict the diffusion from sequence, we use an estimated K_eq of B + C* ↔ BC* based on calculated ΔG values from widely used and empirically validated base-pair stacking energies (Breslauer et al. 1986). This approximation breaks down without fast equilibrium or if all B sites are occupied. As B₀ approaches saturation, the diffusion in that saturated region will approach the native diffusion rate. If this is to be avoided in practice, the concentration of B₀ should be considerably greater than the species it is designed to interact with.

8. Specifying a pattern in two dimensions

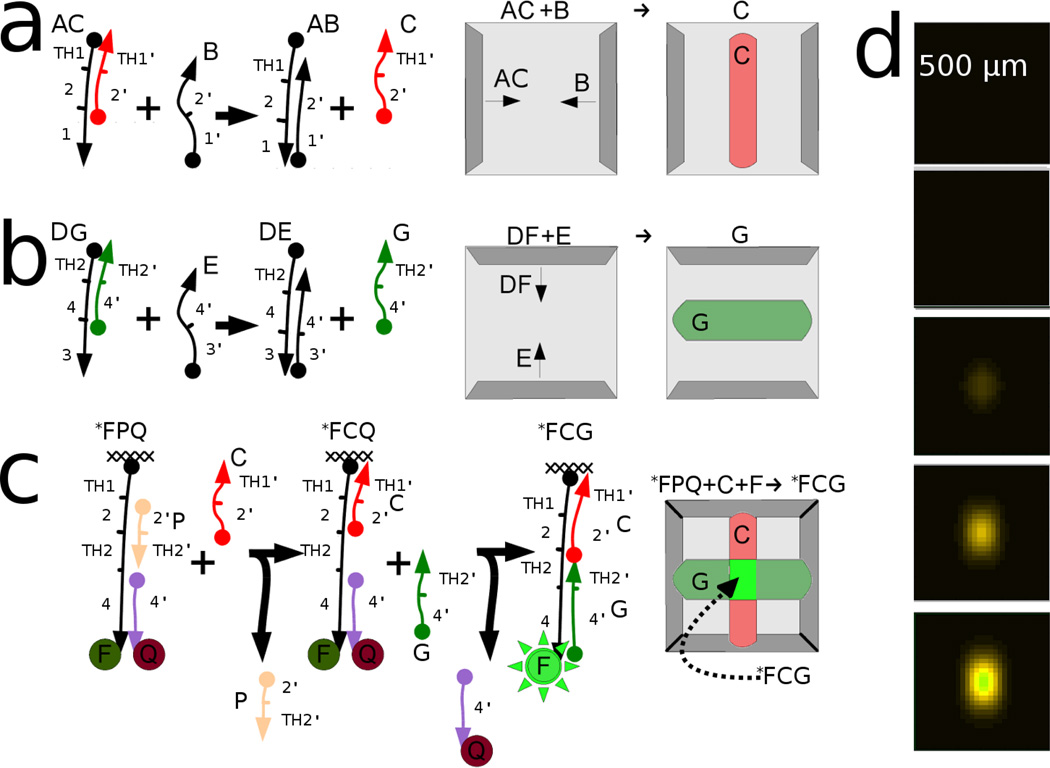
The ability to specify the location of a reaction product can be extended into additional dimensions. The products of two otherwise orthogonal reactions can create a third product. In other words, two Ouchterlony-like line generators can be designed and aligned such that only at their intersection will a final product be generated. For example, in Figure 4a species AC and B diffuse horizontally and meet to produce species C in a vertical line, while the orthogonal reaction in Figure 4b produces a horizontal line (species G). At the intersection of these two lines, C and G react with the immobilized fluorogenic construct FQP* to form a central fluorescent spot, rather than a line.

Figure 4.

a) Schematic shows a strand displacement that results in product C located in the vertical line. (b) Schematic of a second strand displacement with a different toe-hold that results in product G located in a horizontal line. (c) Schematic shows the fluorogenic strand displacement in which immobilized FPQ becomes immobilized fluorescent product FCG only after reacting with both C and G. This produces a single fluorescent region located in the center of the gel. (d) Images from our simulator showing the evolution of product FCG over time; time points are evenly spaced from 10 to 30 hours. The simulation uses the D_eff approximation from equation 7; Fixed species (noted with *) are presumed to have D_eff = 0 and all other species have D_eff = 0.15e-8 cm²/sec

Figure 4d shows a simulation of this system. This simulation involved the simplifying assumption that the effective diffusion constants (according to equation 7) should accurately model diffusivity, thus alleviating the need for additional terms to account for transiently bound species. The slight asymmetry in the final frame of Figure 4d is due to the sequential reaction of FQP* with C, then G; a delay introduced by requiring the first reaction to be complete allows for more progress in the AC+B reaction and, thus, a wider horizontal line (and a taller final spot in the vertical direction). It is also worth noting that the sharpness of the generated spot is limited by the forward reaction rates, as we will discuss below.

We set out to show how patterns might be developed in multiple dimensions by autonomous DNA-DNA interactions. The results of our simulations indicate that a feature could be deterministically developed at a specific location within a reduced diffusion medium based solely on its sequence. In essence, positional information can be directly encoded into sequence. In principle, these interactions can occur with both fixed and mobile elements and produce more complex effects by contingently interacting with the fixed strands.

9. Composite patterns based on orthogonal strand displacement CRNs

Because DNA:DNA interactions can be designed to be very specific, it is possible to build reaction networks where each reaction is chemically orthogonal; the reactions will not randomly or aberrantly interact with one another. For example, expansion of the 'point generation' program described above with orthogonal, DNA-based CRNs should allow the generation of arbitrary, complex patterns.

We present an example in which we selectively de-quench immobilized fluorophores in multiple, spatially-confined regions based on the lateral and vertical overlap of diffusing, orthogonal, DNA-based CRNs. Each system, lateral (row) and vertical (column), has a pair of reagents with defined sequences and diffusivities that determine the final position of a fluorescent feature. The fluorescent feature can be thought of as a “pixel” or dot at an arbitrary position.

In greater detail, the seven strand-displacement reactions (Figure 5a through g) are designed, independent line generators, similar to the system described above. Two of the reactions produce vertical lines and three produce horizontal lines as shown in Figure 5a. For example, line generator A produces a vertical line, while line generator C produces a horizontal line. The overlap of those two lines produces a fluorescent dot. Dot formation can occur because the gel contains two immobilized fluorophore-quencher pair species, F_aQP_a and F_bQP_b, with specific 8 base-pair toeholds (shown as TH1 and TH2 in Figure 4c). In the case of the overlap of line generator A and line generator C, the reaction cascade ultimately produced single-stranded nucleic acid species that specifically interacted with toehold TH1_a then TH2_a to create a fluorescent dot in the upper left of the gel. An example of the progression of events is as follows. Overall, three different pixels are created using vertical line generator A. Line generator A produces a product in a specific vertical region. Immobilized construct F_aQP_a uses a version of TH1_a that responds specifically to this product. In the vertical line from line generator A, TH2_a is opened to make a “primed” region, as shown in Figure 5a. In this primed vertical line, the specific toehold (TH2_a on product F_aQP_a) is ready to interact with the products of horizontal line generator C, which is responsive to TH2_a and completes the cascade of strand exchange reactions, resulting in dequenching of F_aQP_a and forming fluorescent dot A∩C. It should be noted that programming the reactions with specific toeholds also avoids the initiation of undesired reaction cascades; the intersection of vertical line B with horizontal line E does not activate the substrate.

Figure 5.

a) Images from our simulator show the regions activated by the reaction systems described in Table 1. The labeled regions indicate intended location the products of reaction systems A-H should appear. (b) A simulation of the same system shows a ‘C’ pattern. (a) In the same simulation with a larger space (all else remaining constant) the pattern scales with the space.

Table 1 describes the complete inter-reactivity of the 7 line generators. Table 1 also gives two effective diffusion coefficients for each generator, corresponding to the diffusion of the components from two sides. Ultimately, the seven lines develop in parallel to produce five immobilized spots that differentially interact with the two reporters to produce the crescent shape, and a simulation that takes into account diffusion is shown in Figure 5b.

Table 1.

shows diffusion coefficients of a set of constructs which produce an simple 2D figure.

Name	Position	Reacts with	Deff,1 (cm2sec−1)	Deff, 2 (cm2sec−1)
A	L/R	Xa TH1	.22	1.1
B	L/R	Xb TH1	.6	.6
C	U/D	Xa TH2	.22	1.1
D	U/D	Xb TH2	.22	1.1
E	U/D	Xa TH2	.65	.65
F	U/D	Xa TH2	1.1	.22
G	U/D	Xb TH2	1.1	.22

10. Scalability and resolution limits

This system is scalable in an unintuitive way. The topology of the pattern will be generated without regard to the dimensions of the gel slab (although the time and material necessary to achieve the result will increase with the size of the gel). This is shown in Figure 5c where a simulation was run with all parameters consistent with those used for the generation of Figure 5b, with the exception that the size of the simulated region was enlarged.

The minimal size of the features generated by this system also scales with the overall size of the gel in which the reactions are occurring. The narrowest possible features are generated when reactants diffuse only a short distance into each others’ territory before reacting. Sharp features are obtained if the effective diffusion rate does not greatly exceed the effective reaction rate. Whether a given reaction is diffusion- or reaction-limited can be characterized in terms of the Thiele modulus. Reeves et al. conclude that for effective patterning using diffusing signal molecules, the Thiele modulus must be approximately 1, at which point the influences of reaction and diffusion are balanced (Reeves et al. 2006). Because we directly link sequence design to reactivity and diffusivity, we in turn exert direct control over the Thiele modulus of the system.

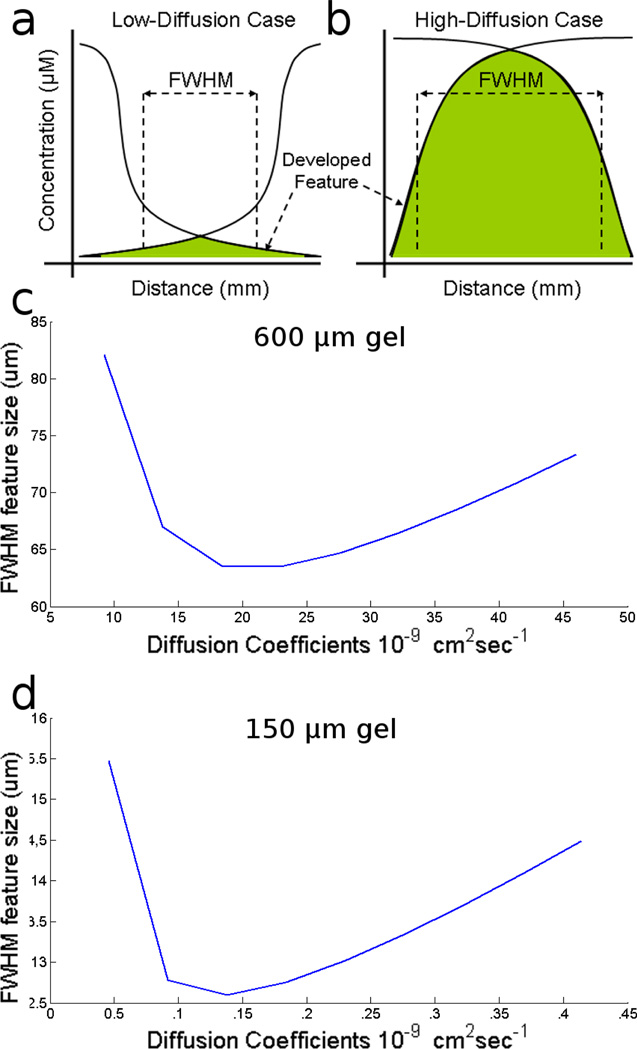
The existence of such an optimum diffusion coefficient can be best illustrated with a thought experiment. We can take a gel of width 600 µm and embed a reaction where two DNA molecules are diffusing towards one another (as shown above in Figure 3) and will react with a rate coefficient of 10₆ mol⁻¹ sec⁻¹ Soloveichik et al. 2010). If we imagine a case in which diffusion rate is extremely slow, the advance edges of the DNA samples will yield a low, broad concentration profile and a correspondingly broad feature (see Figure 6a). In the opposite extreme, if we consider a diffusion rate that is very fast, such that the molecules diffuse across the entire gel before they find a partner and react, then this should also produce a broad feature (see Figure 6b).

Figure 6.

A thought experiment illustration shows that in both the high-diffusion extreme (a) and the low-diffusion extreme (b), the resulting feature is broad. (c) Graph shows the relationship between the diffusion coefficients of reagents and the final full-width half-max size of the generated feature in the case with a gel of 600 µm in width. The same relationship is shown in (d) for a gel 150 µm in width. It shows that there is an optimal diffusion coefficient for a given size gel which produces a feature of approximately 10% of the full width of the gel.

In order to find an optimal diffusion coefficient that will produce narrow lines we used a numerical simulation. A typical DNA substrate has a native diffusion rate of 4.6 10⁻⁸ cm²sec⁻¹ in a 5% acrylamide gel (experimental estimate, data not shown), a value that can be further modified by interactions with oligonucleotides embedded in the gel. Using these reasonable estimates of the values of diffusion and reaction coefficients above, we estimate that the smallest full-width, half-max (FWHM) feature that can be generated in a 600 µm gel is approximately 63 µm or ~11% of the width of the gel (Figure 6c). This in turn corresponds to a hybridization length of 10 residues between substrate and gel, which reduces diffusion by 58% to ca. 2×10⁻⁸ cm²sec⁻¹.

As we discussed above, the topology (and hence the resolution) of the feature size should scale with the outer dimensions of the gel. If we decrease the width of the gel to 150 µm, Figure 6d shows that the optimized diffusion coefficient produces a feature of width ~13 µm (again ~9% of the width), corresponding to ~11 bases of hybridization.

In principle, so long as diffusion can be limited to match the overall size of the gel, there is no limit to the smallest feature size that can be generated. With optimal conditions, a feature as small as ~10% of the width of the gel itself can be generated in any gel that can be fabricated. Indeed, during Drosophila development, the spatial reproducibility of the bicoid signal is limited to about 10% of the length of the embryo (Gregor et al. 2007). This insight suggests the interesting hypothesis that Drosophila may tune its diffusive environment. Astoundingly, for some signaling molecules, it seems that the Drosophila embryo may have indeed evolved to control diffusivity (Yan and Lin 2009). Removing heparan sulfate proteoglycans markedly decreased the distance over which the morphogen Hedgehog could act in developing Drosophila. It is not necessarily clear if this is due to a decreased or increased diffusion coefficient (Lander 2007). From a practical, experimental standpoint, this implies that to be able to make very small features, one must be able to manipulate increasingly smaller samples. In addition, there will be a breakdown of the relationship between increased hybridization and lower D_eff as a given interaction becomes strong enough to affix DNA strands semi-permanently, so that lateral motion cannot be modeled by simple diffusion. If the k_off is too slow, our implicit assumption of local equilibrium will not be valid. This breakpoint occurs at a k_off of ca. 10⁻² sec⁻¹ at room temperature, or approximately 15 base-pairs of interaction between substrate and gel (Robelek et al. 2006). This practical limitation sets the minimal, controllable feature size at about 10 µm for the types of reagents and timescales described here.

11. Reaction diffusion systems can generate complex spatial patterns

The above are simple systems with deterministic results. Feedback and amplification can create more complex, dynamic patterns. Periodic systems, for instance, can be generated by a system that comprises both amplification and inhibition at different time scales. This was described for a spatially homogenous system (Soloveichik et al. 2010) that developed a periodic reaction in time and is similar to some predator prey systems (Fujii and Rondelez 2013). The ideal case can be realized by three reactions: two competing self-amplifiers and a pull-down. The simplified reactions are described as:

$$\begin{array}{cc}\mathrm{A}+\mathrm{B}\to 2\mathrm{A}\hfill & \mathrm{k}=1.5{\mathrm{M}}^{-1}{\text{sec}}^{-1}\hfill \\ \mathrm{B}\to 2\mathrm{B}\hfill & \mathrm{k}=1{\text{sec}}^{-1}\hfill \\ \mathrm{B}\to \mathrm{C}\hfill & \mathrm{k}=1{\text{sec}}^{-1}\hfill \end{array}$$

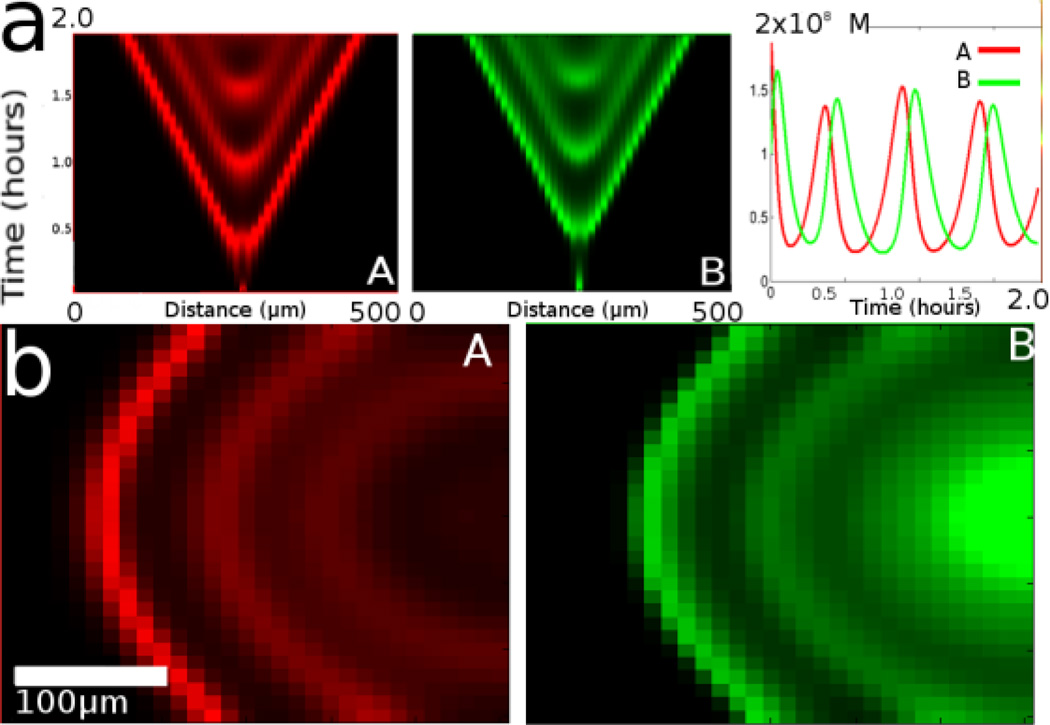
These three net reactions can be treated as modules and implemented by a collection of DNA strand displacement reactions (Soloveichik et al. 2010). The modules involve 3–7 DNA species, including ‘fuel’ species that are initially at relatively large concentrations and unreactive ‘waste’ species that are generated as the reaction continues. When the rates for the reaction are correctly balanced, the concentrations of reagents A and B will oscillate. Figure 7a shows the concentration of A and B in a 1-D simulation of the full, 15-equation reaction-diffusion system described by Soloveichik et al. The simulated time was 2 hours. The result is presented as an intensity chart. Time is depicted on the Y-axis, distance on the X-axis and the color intensity represents the concentration. At any given point along the X-axis, the reporters are phase-separated oscillators in time. This is shown as a line graph at right that represents the intensities of the two reporters at the central point of the 1-D simulation. A complete description of the CRN and the simulator are given in Supporting Material online.

Figure 7.

Periodic patterns created by an amplifier/inhibitor system. (a) Intensity vs location vs. time plot shows the complete 15 species model of the DNA system in time and space with two species X1 and X2 plus their 2-color overlay pattern where X1 is red and X2 is green. (b) A simplified simulation of the system in 2 dimensions at one time point; the waves of production of species X1 and X2 move from right to left in time (see Supporting Material online).

A periodic pattern is also generated in space. The waves of transient A and B spread out from the initial small concentration of species A. Spatial periodicity is clearly observed in a modeled 2-D intensity image (Figure 7b, a single frame at ~1.5 simulated hours of the three-equation reaction scheme described above). The images in Figure 7b show the distribution of concentration of reporters A and B in space in both directions along the X and Y axis. Ripples move out from a point of initial excitation concentration of A. The initial conditions include uniform, mobile reagents and a small quantity of ‘trigger’ species in one small zone at the center of the active region. The experiment presented in Figure 7 is an expansion of the reaction diffusion system presented in Figure 4 in the following sense: output species are fixed and some intermediates are mobile with a consistent diffusion coefficient of 0.1×10⁻⁸ cm²sec⁻¹. In the oscillating case, mechanisms are in place to regenerate the mobile species. This could be physically accomplished in a similar approach to our experimental work presented elsewhere (Chen et al. 2011).

12. Controlling diffusivity to control chemical reactions

Diffusion control leading to spatial organization can potentially be used to also control chemical reactivity. For example, oligonucleotides linked to small, reactive organic compounds can be organized by templating, which in turn helps to control the order and regiospecificity of the reactions that the small molecules undergo (Kleiner et al. 2010, Li and Liu 2004). By implementing such templated reactions in the context of CRNs it should be possible to add new levels of spatial and temporal control to compound synthesis.

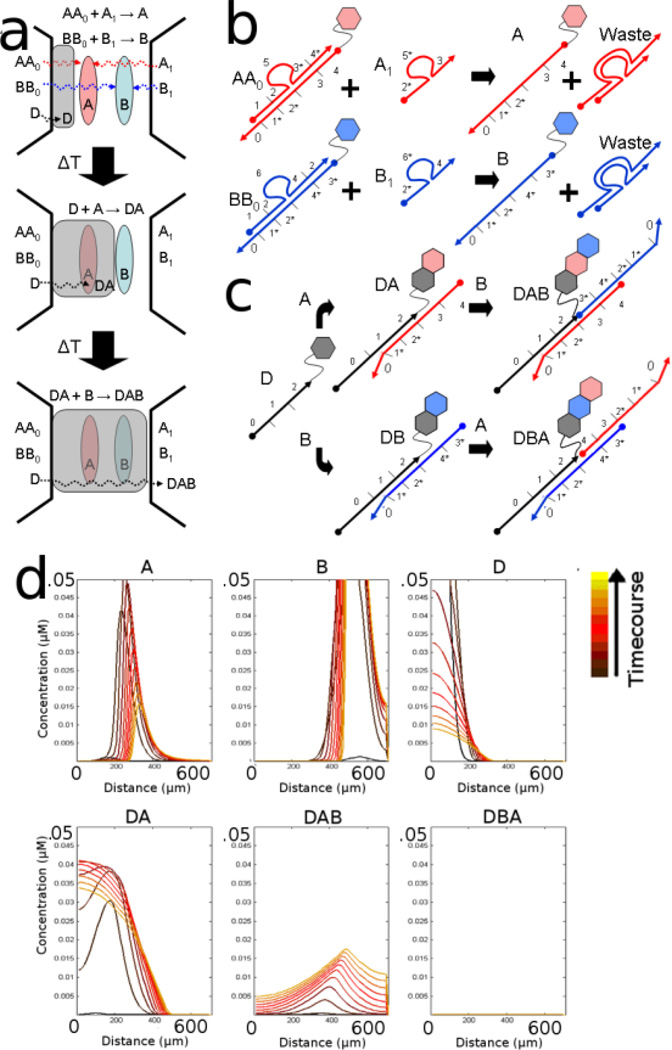
First, control over diffusion can direct the creation of a specific product. Two oligonucleotides carrying reactive chemical species (A and B) can be formed into lines in a gel using procedures those described above (see Figure 8a). In this example, the diffusion of precursors AA₀ and BB₀ are controlled by partial hybridization of an immobilized oligonucleotide to domain 0 on the chimeric oligonucleotide strands A and B. Upon meeting a counter-diffusing strand, strand displacement reactions 'activate' AA₀ and BB₀ to become immobile substrates A and B (through reactions shown in Figure 8b). The diffusivity of a third reactant, DNA species D, is similarly adjusted by varying complementarity to domain 0. If species D diffuses slowly it can react with already immobilized, activated A and B, forming either DA or DB. However, since reactive species D diffuses through the activated lines of A and B sequentially this also establishes an order of reaction. Only one of the two possible products shown in Figure 8c, DAB, should be generated. We simulate the relative production of DAB relative to DBA in Figure 8d.

Figure 8.

a) Two lines (of species A and B) are developed. (b) A scheme for developing these species are shown. For instance AA₀ meets A₁ and develops A. (c) Reactive species D diffuses slowly through them and react to form a complex that depends on the order of operations. (d) The concentration of each species develops over time and is highly selective for product DAB.

Similar ordered reactions have been performed by programmed DNA nanorobots (Yurke 2007. However, as with many aspects of the amorphous computations described herein, the scalability of 'classic' DNA nanotechnology may prove difficult, especially for the production of chemicals in bulk. Gel-based separations are already common, and thus the concept of controlled, gel-based reactions is more amenable to scaling. Moreover, the process of chemical assembly could occur continuously in the gel, with new reactants constantly diffusing, being activated, and assembling in an ordered fashion.

The system is modular and eminently programmable, and changing the immobilized DNA sequence would change the order and kinetics of compound activation, which would in turn alter both the nature and efficiency of production of a final chemical product. Simplistically, depending on the sequences of the chimeras, DBA rather than DAB could be produced with high specificity. More importantly, though, should a given reaction prove inefficient, the width of the reaction zones for the self-assembled DNA bands could be increased by simply altering hybridization and thus diffusivity, allowing more time for the reaction to occur. It is reasonable to suggest that such a system could be combined with programmable nucleic acid reactions (Soloveichik et al. 2010) to realize a fully programmable, algorithmic system for chemical construction.

13. Discussion

The diverse forms of self-organization in living systems develop from ostensibly simple homogeneity. This aspect of biology has fascinated humans since antiquity (Aristotle 2004. From a more modern point of view, we were inspired by the biological insights presented in Alan Turing’s seminal paper (Turing 1952), which formulated a set of conditions for pattern formation, including plausible kinetic equations that had symmetry-breaking properties. These systems have been extensively explored since then (Koch and Meinhardt 1994). Turing speculated that such reaction-diffusion systems could be the basis of embryonic morphogenesis. His work made it clear that specific properties of reactivity and diffusivity were necessary conditions for generating self-organized patterns. However, while biology excels at this feat, the methods by which it is accomplished are idiosyncratic and not as amenable to engineering as the programmable CRNs that we have imagined herein. The development of complex reaction networks is only realistic if the design can be made rational and generalized. There must be explicit, computable relationships between sequence and inter-reactivity and between sequence and diffusivity. The thermodynamic properties of nucleic acid hybridization are well known (Nakano et al. 1999). Linear strands with specific energies of hybridization to an immobile strand can thus be computationally designed to specify diffusion. We envision that the species in such circuits (including amplifiers, thresholds and logic gates) will dynamically modulate diffusivity by alternately exposing or hiding diffusion-modifying sequences to the fixed medium. By developing concepts for programming diffusivity and reactivity using nucleic acid sequence information, we provide a path forward for both better understanding the CRNs that underlie biology and for creating new CRNs with new applications. While computer simulation is generally adequate to prove that such systems can produce biological patterns, a physical system could reveal how simulation and theory might differ. Eventually, reaction diffusion systems like those presented here could direct the behavior of synthetic biological systems that mimic life-like behavior.

With respect to understanding biology, biological reaction-diffusion systems like those proposed by Turing are a hypothetical general model for the formation of complex patterns (Maini and Othmer 2001). In the most classic example, the use of diffusing, interacting molecules to generate a pattern compares quite directly to axis formation in Drosophila. In the case of the anterior-posterior axis, bicoid protein induces the expression of hunchback on only one side of the embryo. Maternal cells apply the bicoid mRNA to the anterior side of the embryo. This initial maternal polarity allows formation of more complex patterns downstream in development (Okabe-Oho et al. 2009). Drosophila development uses the positional information encoded into the diffusion gradient to determine the anterior-posterior location of key features. This is similar the patterns that emerge from our system where DNA species diffuse from opposite sides of a gel. A similar approach based on our technique could be used to set up initial order in an otherwise stochastic, self-organizing system. While we focused on patterns with predetermined outcomes, the control over reaction and diffusion is equally applicable to stochastic systems more typical of Turing patterns.

Our exploration of programmable CRNs has already yielded insights relevant to biological pattern formation. Our analysis indicated a resolution limit to pattern formation by passive diffusion. We attempted to optimize the conditions for minimal feature size, and found that, a feature as small as ~10% of the width of the gel could be generated. We can consider the feature width in our system to be the probability distribution of many individual molecular interactions. This implies that in a stochastic system with few molecular events, the best possible embryo-to-embryo variability would be 10% of the width of the system. In Drosophila development this is indeed the observed value (Gregor et al. 2007).

We also explored the scalability of topology with our pattern generation system. In our simulations, a reaction-diffusion system within a gel produces features. The size and topography of those features scale with the outer dimensions of the gel. This is also reflected in the many examples of scaled patterns in biology. For example, across several varieties of Drosophila, the bicoid-generated features scale with the embryo size. The requirements for scale invariance of biological morphogenesis include an excess of binding sites to slow the morphogens’ diffusion and that the total number of binding sites should stay constant even as the size increases (Umulis 2009. Our analysis anticipates these findings in an intuitive way: a constant number of immobile DNA molecules in a larger volume yields a lower concentration. A lower concentration of immobilized DNA produces a higher effective diffusion rate. Higher diffusion over a larger sized gel maintains the Thiele modulus condition for optimal feature size.

In contrast to the work on Drosophila morphogenesis, many other studies have focused on either a basic understanding of natural pattern-formation systems or theoretical possibilities to generate stochastic patterns. By developing a programmable system for deterministic and non-linear CRNs it may prove possible to reimagine the mechanisms underlying many biological phenomena. For example, visibly patterned phenomena such as skin pigmentation may be developed from a reaction-diffusion type Turing mechanism (Nakamasu et al. 2009), and could be demonstrated using our system.

Programmed self-organization may also be an innovation that has great utility outside of biology. Most famously, chemical reaction networks have been substantiated in what is now known as the Belousov-Zhabotinsky reaction. This reaction, like Turing's hypothetical reactions, has specific diffusion rates that affect the appearance of patterns (Field and Noyes 1974). Our system offers the possibility of developing much more complex patterns and behaviors. Indeed, given the advances that have been made in DNA computation, it may be possible to engineer very complex chemical reaction networks such as those pioneered by Qian and Winfree (2011), and to then use these CRNs for pattern formation at a variety of length scales. New deterministic and algorithmic patterns could potentially lead to the generation of “smart” materials whose bulk architectures are structured down to the nanoscale. For example, Janus particles, whose surfaces are two differentially patterned hemispheres, can be used to generate complex topologies (Chen et al. 2011). It stands to reason that particles with more complex surfaces generated by internal reaction-diffusion systems could generate more complex, patterned associations. Additionally, a reaction-diffusion system might allow for a macroscopic positioning of other DNA structures, such as DNA origami (Rothemund 2006. A meso-scale pattern might be etched into a medium by selectively melting a polymer gel cross-linked by self-assembled DNA helices (Zhu et al. 2010).

Ultimately, modularity, abstraction and encoding should prove very important in engineering self-organizing systems. By analogy to computer science, the implementation of modular CRNs should be like a high-level computer language. A computer programmer need not know the deepest workings of the hardware (e.g., register shifts, memory addresses, etc.) in order to write useful software. The work presented herein is a step toward such a CRN language and compiler.

Supplementary Material

11047_2013_9392_MOESM1_ESM. Supporting Material.

MATLAB program showing each simulation figure and its derivation is included online as allen_simulation_supplement.m.