Assessing the heterogeneity of treatment effects via potential outcomes of individual patients

Summary

There is growing interest in understanding the heterogeneity of treatment effects (HTE), which has important implications in treatment evaluation and selection. The standard approach to assessing HTE (i.e. subgroup analyses based on known effect modifiers) is informative about the heterogeneity between subpopulations but not within. It is arguably more informative to assess HTE in terms of individual treatment effects, which can be defined by using potential outcomes. However, estimation of HTE based on potential outcomes is challenged by the lack of complete identifiability. The paper proposes methods to deal with the identifiability problem by using relevant information in baseline covariates and repeated measurements. If a set of covariates is sufficient for explaining the dependence between potential outcomes, the joint distribution of potential outcomes and hence all measures of HTE will then be identified under a conditional independence assumption. Possible violations of this assumption can be addressed by including a random effect to account for residual dependence or by specifying the conditional dependence structure directly. The methods proposed are shown to reduce effectively the uncertainty about HTE in a trial of human immunodeficiency virus.

1. Introduction

It is well recognized that treatment effects can be heterogeneous, i.e. that the same treatment can have different effects on different patients. Understanding the heterogeneity of treatment effects (HTE) is of increasing importance in treatment evaluation and selection. The standard approach to assessing HTE is subgroup analyses (or, more generally, regression analyses) based on known effect modifiers, which may be demographic variables, disease aetiology, certain baseline measurements and genetic markers (e.g. Peto (1982), Gail and Simon (1985), Russek-Cohen and Simon (1997) and Pocock et al. (2002)). A subgroup analysis comparing treatment effects on different subpopulations is informative about the HTE between subpopulations but not within. In fact, one could think of an individual patient's treatment outcomes as determined by a large set of prognostic factors and effect modifiers. Ideally, with all relevant information available and used correctly, one would be able to predict precisely the outcome of an individual patient under a given treatment. In reality, however, some effect modifiers may be unknown to the scientific community, resulting in residual HTE that cannot be explained by known effect modifiers.

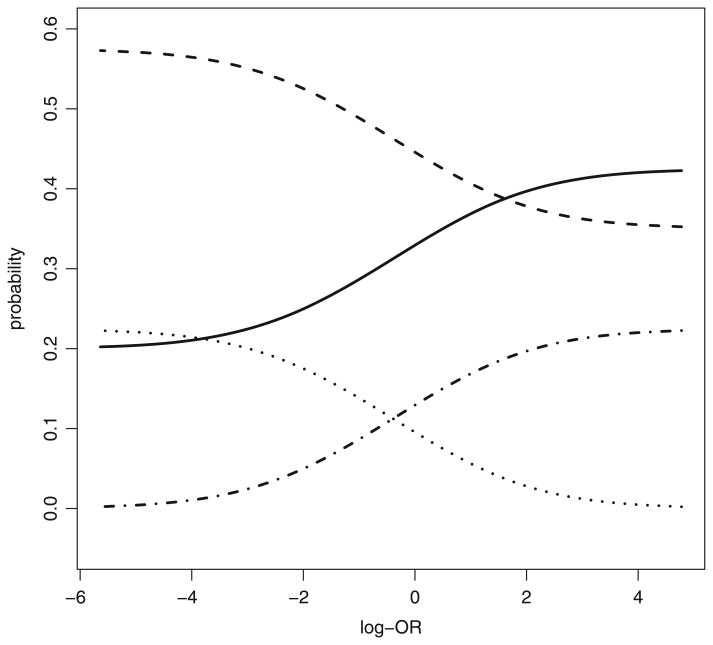
It is perhaps more natural to think of HTE in terms of individual potential outcomes (Gadbury and Iyer, 2000; Gadbury et al., 2001, 2004; Poulson et al., 2012). Under the causal model of Rubin (1974), each patient has a potential outcome under each possible treatment, and the effect of an experimental treatment relative to a control can be assessed on each individual patient by comparing the corresponding potential outcomes. Consider, for example, a randomized, double-blinded, placebo-controlled, confirmatory clinical trial known as ‘MOTIVATE’ (maraviroc versus optimized therapy in viraemic antiretroviral treatment-experienced patients; Gulick et al. (2008)). Maraviroc is a CC chemokine receptor 5 antagonist and a new antiretroviral drug for treating human immunodeficiency virus type 1 (HIV-1). The MOTIVATE trial compares maraviroc with placebo, each combined with optimized background therapy (OBT), with respect to a success rate (virologic response at week 48 of treatment; see Section 4 for details). Because the outcome is binary, patients can be classified into four categories according to their potential outcomes under the two treatments, as shown in Table 1. The observed success rates are 57.5% and 22.5% for maraviroc and placebo respectively. Because the difference is highly significant, statistically and clinically, it is clear that the use of maraviroc can lead to improved outcomes on the population level. Moreover, the positive effect of maraviroc appears quite consistent across subpopulations (Fatkenheuer et al., 2008). However, these findings do not imply that every patient would fare better with maraviroc and OBT than with OBT alone. Assuming that the observed success rates are the true rates, Fig. 1 shows possible values of the four cell probabilities in Table 1 as functions of an odds ratio. In particular, π₁₀, the proportion of patients who would fare better with OBT alone than with maraviroc plus OBT, varies over a wide range (0–22.5%). These are the patients who would be harmed if maraviroc were to be applied to the entire population in addition to OBT. In this situation, it seems natural to characterize HTE in terms of the cell probabilities in Table 1.

Table 1. Contingency table for binary potential outcomes in HIV-1 patients treated with placebo or maraviroc (in addition to optimized background therapy).

Placebo	Maraviroc		Row sum
	Failure	Success
Failure	π00	π01	π0+
Success	π10	π11	π1+
Column sum	π+0	π+1	1

Fig. 1.

Possible values of the cell probabilities in Table 1 as functions of the log-odds ratio, log{π₁₁π₀₀/(π₀₁π₁₀)} for fixed marginal probabilities π₁₊ = 0.225 and π₊₁ = 0.575 as estimated from the MOTIVATE study (see Section 4 for details): , π₀₀;— — —, π₀₁; · · · · · ·, π₁₀; · — · —, π₁₁

The objective of this paper is to develop methods for estimating HTE on the basis of potential outcomes, either in the entire population or in a subpopulation defined by known effect modifiers. This objective is directly relevant to treatment evaluation in regulatory settings and is potentially helpful in discovering new effect modifiers. An analysis of HTE based on potential outcomes may be complementary to a standard subgroup analysis based on known effect modifiers. The latter approach can be useful in medical practice by informing treatment selection. However, with limited knowledge of effect modifiers, it is usually impossible to identify subpopulations that are completely homogeneous with respect to the potential outcomes. Thus, for treatment evaluation, the need remains to understand the residual HTE in a subpopulation defined with the best available knowledge of effect modifiers. Moreover, a large amount of unexplained HTE, suggested by an analysis based on potential outcomes, may motivate scientists to search for new effect modifiers. Although scientists would naturally like to discover all kinds of biomarkers, a data-based motivation could be an important consideration in allocating limited resources. Further implications of individual level HTE are discussed by Poulson et al. (2012).

Previous work in this area includes derivation of bounds (Gadbury and Iyer, 2000; Gadbury et al., 2004) and a sensitivity analysis approach (Gadbury et al., 2001). Gadbury and co-workers recognized that the observed data are insufficient to identify all aspects of HTE, which depend on the joint distribution of potential outcomes under different treatments. Randomization in a clinical trial allows us to identify empirically the marginal distribution of each potential outcome but not their joint distribution, which is also known as the fundamental problem of causal inference (Holland, 1986). Our first step in dealing with this identifiability problem is to adjust for covariates. If the set of covariates is sufficient for explaining the (usually positive) dependence between potential outcomes (for different treatments applied to the same patient), the joint distribution of potential outcomes and hence all measures of HTE will then be identified by assuming conditional independence between potential outcomes given observed covariates. Possible violations of this assumption can be addressed by including a random effect to account for residual dependence or by specifying the conditional dependence structure directly. The latter approach is a considerable generalization of the sensitivity analysis approach that was proposed by Gadbury et al. (2001).

In the next section, we set up the notation and give a general rationale for the methods proposed. We then describe some specific methods for estimating HTE in Section 3 and apply them in Section 4 to real data from the HIV trial mentioned earlier. The paper ends with a discussion in Section 5.

The programs that were used to analyse the data can be obtained from http://www.blackwellpublishing.com/rss

2. Notation and rationale

Suppose that a randomized clinical trial is conducted to compare an experimental treatment (e.g. maraviroc) with a control treatment, which may be placebo or a standard treatment, with respect to a clinical outcome of interest. To fix ideas, we focus on a binary outcome (1 for success; 0 for failure) in most of this paper; extension to a continuous outcome is considered in Appendix C. The success criterion for an individual patient often has important implications on the study design. For example, the primary end point in the MOTIVATE trial implies a longitudinal study that follows patients for at least 48 weeks. For ease of presentation, we shall be concerned with a general binary outcome, which may or may not be time dependent, until it becomes necessary to consider specific features of the study design. For a generic patient in the target population, let Y(t) denote the potential outcome that will realize if the patient receives treatment t (0 for control; 1 for experimental). Note that the Y(t), t = 0, 1, cannot both be observed on the same subject except in crossover trials under certain conditions, which we do not consider until Section 5. Let T denote the treatment assigned randomly to a study subject; thus T is a Bernoulli variable independent of all baseline variables. Without considering non-compliance, we assume that T is also the actual treatment given to the subject, and we write Y = Y(T) for the actual outcome.

As indicated earlier, it is important in treatment evaluation to assess HTE in terms of the joint probabilities

$${\pi }_{\text{jk}}=P\{Y(0)=j,Y(1)=k\},j,k=0,1.$$

These probabilities are not empirically identifiable. Owing to randomization, it is straightforward to identify and estimate the marginal probabilities

$$\begin{array}{c}{\pi }_{1+}={\pi }_{10}+{\pi }_{11}=P\{Y(0)=1\}=P(Y=1|T=0),\\ {\pi }_{+1}={\pi }_{01}+{\pi }_{11}=P\{Y(1)=1\}=P(Y=1|T=0).\end{array}$$

Gadbury et al. (2004) showed that π₁₀, the proportion of patients who would be harmed by the new treatment relative to the control, is constrained by the marginal probabilities:

$$max(0,{\pi }_{1+}-{\pi }_{+1})\le {\pi }_{10}\le min(1-{\pi }_{+1},{\pi }_{1+}).$$ (1)

Together with the marginal probabilities (π₁₊ and π₊₁), the value of π₁₀ (or any other cell probability), either assumed or identified under suitable assumptions, is sufficient to determine the other cell probabilities, which are subject to similar bounds. The lower bound in inequality (1) corresponds to maximal positive dependence between Y(0) and Y(1), and the upper bound corresponds to maximal negative dependence. If π₁₊ < π₊₁, then maximal positive dependence means that Y(0) ≤ Y(1) with probability 1. Although this may be plausible in some settings (e.g. Huang et al. (2012)), the use of OBT for all patients in the MOTIVATE trial makes it quite implausible to assume a priori that Y(0) ≤ Y(1). Another special case, which is interesting though admittedly unrealistic, arises when Y(0) is independent of Y(1), in which case we have π₁₀ = π₁₊(1 − π₊₁).

Of course, the potential outcomes Y(0) and Y(1) generally depend on each other because they arise from the same patient; in that sense they resemble repeated measurements, except that they cannot both be observed. Our first step in accounting for the dependence between Y(0) and Y(1) is to condition on relevant covariates that are associated with both outcomes. Let X denote a vector of such covariates measured at baseline, which may include both prognostic factors (with only ‘main effects’) and effect modifiers (which interact with treatment). The distinction between prognostic factors and effect modifiers depends on the link function and therefore is not always clear cut for a binary outcome. In the MOTIVATE trial, X may include baseline measurements of HIV ribonucleic acid (RNA) and CD4 cells as well as genotypic and phenotypic sensitivity. Without considering specific methods yet, we note that X can be used to sharpen the bounds on the π_jk. Specifically, by applying inequality (1) to each stratum defined by X, we obtain

$$max\{0,{\pi }_{1+|X}(\mathbf{X})-{\pi }_{+1|X}(\mathbf{X})\}\le {\pi }_{10|X}(\mathbf{X})\le min\{1-{\pi }_{+1|X}(\mathbf{X}),{\pi }_{1+|X}(\mathbf{X})\},$$ (2)

where π_jk|X(X) = P{Y(0) = j, Y(1) = k|X} (j, k = 0, 1), and π_1+|X(X) and π_+1|X(X) are defined similarly. The lower bound in inequality (2) corresponds to maximal positive dependence of Y(0) and Y(1) given X, whereas the upper bound corresponds to maximal negative dependence. Taking expectations over X in inequality (2) leads to

$$E[max\{0,{\pi }_{1+|X}(\mathbf{X})-{\pi }_{+1|X}(\mathbf{X})\}]\le {\pi }_{10}\le E[min\{1-{\pi }_{+1|X}(\mathbf{X}),{\pi }_{1+|X}(\mathbf{X})\}].$$ (3)

It is elementary to show that the lower bound in inequality (3) is generally higher than that in inequality (1), and they coincide when π_1+|X.(X) − π_+1|X (X) is always positive or always negative (i.e. when there is no qualitative interaction between T and X). Similarly, the upper bound in inequality (3) is generally lower than that in inequality (1). Analogous results hold for the other cell probabilities. Thus, conditioning on X may be a good starting point in understanding the π_jk.

In general, we propose to estimate π_jk = E{π_jk|X(X)} by averaging over X an estimate of π_jk|X(X). Note that π_jk|X(X) is generally dependent on X because X is chosen to be associated with the potential outcomes. This is not a problem with estimating π_jk and can actually be helpful in sharpening the bounds, as shown in the preceding paragraph. However, when X contains strong effect modifiers, it may be necessary to consider restricted use of the new treatment to a subpopulation of patients with a favourable benefit–risk profile. If such a subpopulation is predefined, that subpopulation can be taken to be the entire population without loss of generality, and the methodology proposed remains applicable. Without a predefined subpopulation, we would have to use the data to identify a favourable subpopulation. Although not designed for that purpose, the methodology proposed can help the search for a favourable subpopulation, as we discuss in Section 4.

Estimates of π_jk|X(X) may be obtained by using three different approaches, which are outlined below and further developed in Section 3.

2.1. Covariate adjustment based on conditional independence

If X is sufficient for explaining the dependence between Y(0) and Y(1), then we can expect that

$$Y(0)\perp Y(1)|\mathbf{X},$$ (4)

i.e. that Y(0) and Y(1) are conditionally independent given X. This assumption is similar in spirit to the missingness at random assumption for missing data (Rubin, 1976) and the assumption of strongly ignorable treatment assignment in causal inference (Rosenbaum and Rubin, 1983); they all attempt to reduce a stochastic dependence of concern by conditioning on relevant covariates. Like the latter two assumptions, assumption (4) cannot be verified with the observed data and must be based on external information such as expert opinions. Methods based on assumption (4) are described in Section 3.1.

2.2. Sensitivity analysis based on a random-effect model

We might question the validity of assumption (4) because X may not explain all the dependence between Y(0) and Y(1). We therefore relax assumption (4) in Section 3.2 by including a latent variable to account for any residual dependence between Y(0) and Y(1). The relaxed assumption can be written as

$$Y(0)\perp Y(1)|(\mathbf{X},U),$$ (5)

where U is a subject-specific random effect that is independent of X. In the MOTIVATE trial, U can be a suitable combination of all relevant characteristics of a patient that are predictive of the outcome and that are unmeasured in the study or yet unknown to the scientific community. In other words, U represents what is missing from X that makes assumption (4) break down. The assumption that U is independent of X is not as stringent as it may seem, because a candidate U could be orthogonalized with respect to X. Under assumption (5), assumption (4) corresponds to the special case that U is a constant. In general, the distribution of U is not identifiable if we observe only a random sample of (T, X, Y). We therefore propose in Section 3.2 a sensitivity analysis approach based on a range of assumptions about the variability of U. We also show how to gauge the variability of U from longitudinal data and thus narrow the range of the sensitivity analysis.

2.3. Sensitivity analysis based on an odds ratio

The inclusion of a random effect imposes a particular positive dependence structure for Y(0) and Y(1) given X. Although this structure may be plausible in some situations, it is not guaranteed to hold. To accommodate negative dependence as well as different forms of positive dependence between Y(0) and Y(1) given X, we also propose another sensitivity analysis approach based on the odds ratio

$$\rho (\mathbf{X})=\frac{{\pi }_{11|X}(\mathbf{X}){\pi }_{00|X}(\mathbf{X})}{{\pi }_{01|X}(\mathbf{X}){\pi }_{10|X}(\mathbf{X})}.$$ (6)

Note that ρ(X) captures the entire dependence structure for Y(0) and Y(1) given X and is not constrained by the conditional probabilities π_1+|X(X) and π_+1|X(X). This approach is described in Section 3.3.

3. Methodology

This section presents methods for estimating the joint probabilities π_jk from a random sample of subjects, with individual subjects denoted by the subscript i=1,…,n (attached to random variables). Our methodological discussion will be focused on point estimation and sensitivity analysis. For the methods proposed, asymptotic normality is usually immediate from standard M-estimation theory (e.g. van der Vaart (1998) and Stefanski and Boos (2002)), and asymptotic variance formulae are straightforward to derive though cumbersome to present. For ease of implementation, we recommend non-parametric bootstrap standard errors and confidence intervals for inference.

3.1. Covariate adjustment based on conditional independence

Under the conditional independence assumption (4), the cell probabilities can be identified as

$$\begin{array}{lll}{\pi }_{\text{jk}}\hfill & =\hfill & E[P\{Y(0)=j,Y(1)=k\left|\mathbf{X}\right\}]\hfill \\ \hfill & =\hfill & E[P\{Y(0)=j\left|\mathbf{X}\right\}P\{Y(1)=k|\mathbf{X}\}]\hfill \\ \hfill & =\hfill & E\{P(Y=j|T=0,\mathbf{X})P(Y=k|T=1,\mathbf{X})\},\hfill \end{array}$$ (7)

where the last step follows from randomization.

Assume first that X is discrete, taking values in {x₁,…, x_L}, say. Write S_tl = {i: T_i = t, X_i = x_l} and n_tl = |S_tl|, where |·| denotes the size of a set. Then the conditional probability p(y|t, x) = P(Y = y|T = t, X = x) can be estimated empirically by

$$\widehat{p}(y|t,{\mathbf{x}}_l)=\frac{1}{n_{\text{tl}}}\sum _{i\in S_{\text{tl}}}I(Y_i=y),$$

and the corresponding estimate of π_jk is given by

$$\frac{1}{n}\sum _{l=1}^L{n}_{+l}\widehat{p}(j|0,{\mathbf{x}}_l)\widehat{p}(k|1,{\mathbf{x}}_l),$$

where n_+l = n_0l + n_1l.

For a general covariate vector X, one could specify a regression model for p(y|t, x), such as the generalized linear model (GLM)

$$p(1|t,\mathbf{x};\theta )=1-p(0|t,\mathbf{x};\theta )=\psi \{{\theta }_1+{\theta }_{T}t+{\theta }_X^{\prime }\mathbf{x}+{\mathit{\theta }}_{\mathit{\text{TX}}}^{\prime }(t\mathbf{x})\},$$ (8)

where ψ is an inverse link function. The exact form of model (8) is not important; for example, the interaction term can be omitted if X does not include effect modifiers. The regression parameter θ can be estimated by maximizing the likelihood ${\Pi }_{i=1}^{n}p(Y_i|T_i,{\mathbf{X}}_i;\theta )$ and the resulting estimate will be denoted by θ̂. Now equation (7) can be used to estimate π_jk by

$$\frac{1}{n}\sum _{i=1}^{n}p(j|0,{\mathbf{X}}_i;\widehat{\theta })p(k|1,{\mathbf{X}}_i;\widehat{\theta }).$$ (9)

3.2. Sensitivity analysis based on a random-effect model

Under assumption (5), it can be shown as in equation (7) that

$$\begin{array}{lll}{\pi }_{\mathit{\text{jk}}}\hfill & =\hfill & E\{P(Y=j|T=0,\mathbf{X},U)P(Y=k|T=1,\mathbf{X},U)\}\hfill \\ \hfill & =\hfill & \mathit{\int }\mathit{\int }{p}^{\ast }(j|0,\mathbf{x},u)p^{\ast }(k|1,\mathbf{x},u)\mathrm{d}{F}_U(u)\mathrm{d}{F}_X(\mathbf{x}),\hfill \end{array}$$ (10)

where p*(y|t, x, u) = P(Y = y|T = t, X = x, U = u). Here and in what follows, F denotes a (conditional) distribution function with the subscript indicating the random variable(s) concerned. To fix ideas, consider the generalized linear mixed model (GLMM)

$$p^{\ast }(1|t,\mathbf{x},u;{\mathit{\theta }}^{\ast })=1-p^{\ast }(0|t,\mathbf{x},u;{\mathit{\theta }}^{\ast })=\psi \{{\theta }_1^{\ast }+{\theta }_T^{\ast }t+{\mathit{\theta }}_{\mathbf{X}}^{\mathbf{\ast }\mathbf{\prime }}\mathbf{x}+{\mathit{\theta }}_{\mathit{\text{TX}}}^{\ast \prime }(t\mathbf{x})+u\},$$ (11)

with $U\sim N(0,{\sigma }_U^2)$. Then equation (10) suggests that π_jk may be estimated by

$$\frac{1}{n}\sum _{i=1}^n{\int }_{-\infty }^{\infty }{p}^{\ast }(j|0,{\mathbf{X}}_i,u;{\mathit{\theta }}^{\ast })p^{\ast }(k|1,{\mathbf{X}}_i,u;{\mathit{\theta }}^{\ast })\varphi (u;0,{\sigma }_U^2)\mathrm{d}u,$$ (12)

where ϕ(·; μ, σ²) is the density function of N(μ, σ²), with $({\mathit{\theta }}^{\ast },{\sigma }_U^2)$ replaced by estimates or plausible values (as in a sensitivity analysis). The question is how to obtain such values. In general, the parameters $({\mathit{\theta }}^{\ast },{\sigma }_U^2)$ are not completely identifiable from the (T_i, X_i, Y_i), i= 1,…, n; this is essentially fitting a GLMM to cross-sectional data. However, some relevant information may be available from repeated measurements, which are typically available at baseline and follow-up visits. In the MOTIVATE trial, for example, repeated measurements of virologic response are available at 11 time points from baseline to week 48 of treatment. In the rest of this subsection, we consider estimation of θ* and π_jk with ${\sigma }_U^2$ fixed, discuss how the resulting inference depends on ${\sigma }_U^2$ and then suggest ways to extract information about ${\sigma }_U^2$ from longitudinal data.

For a given value of ${\sigma }_U^2$, θ* can be estimated by maximizing the likelihood

$${\mathit{\theta }}^{\ast }\mapsto \prod _{i=1}^n{\int }_{-\infty }^{\infty }{p}^{\ast }(Y_i|T_i,{\mathbf{X}}_i,u;{\mathit{\theta }}^{\ast })\varphi (u;0,{\sigma }_U^2)\mathrm{d}u.$$ (13)

Although this may appear complicated, it can be simplified for common link functions. In Appendix A, we show that, under the GLMM (11), the GLM (8) is correct with $\mathit{\theta }={(1+{\sigma }_U^2)}^{-1/2}\mathit{\theta }\ast$ for the probit link, and approximately correct with $\mathit{\theta }={(1+{\sigma }_U^2/c^2)}^{-1/2}\mathit{\theta }\ast$, where c ≈ 1.70, for the logit link. This suggests that we can fit model (8) by using standard GLM software and then recover θ* as ${(1+{\sigma }_U^2)}^{1/2}\mathit{\theta }$ for the probit link or as ${(1+{\sigma }_U^2/c^2)}^{1/2}\mathit{\theta }$ (approximately) for the logit link. The resulting estimate of θ* can then be substituted into expression (12) together with the given value of ${\sigma }_U^2$.

Given a GLM estimate of θ, θ* in expression (12) varies as a function of ${\sigma }_U^2\in (0,\infty )$. When ${\sigma }_U^2$ approaches 0, θ* approaches θ and expression (12) approaches the estimate (9) based on conditional independence. When ${\sigma }_U^2\to \infty$, expression (12) approaches a limit that corresponds to maximal positive dependence between Y(0) and Y(1) given X, as shown in Appendix B. For the case of π₁₀, Appendix B also shows that the limit of expression (12) when n and ${\sigma }_U^2$ both approach ∞ is just the lower limit in inequality (3), which is analogous to but generally higher than the lower limit in inequality (1). Thus, a sensitivity analysis based on ${\sigma }_U^2\in (0,\infty )$ can account for any and all positive dependence between Y(0) and Y(1) given X.

Such a sensitivity analysis can be sharpened by using reliable information about ${\sigma }_U^2$, which may be available from longitudinal data. Suppose that we have longitudinal measurements of the same outcome following an expanded GLMM:

$$P(Y_{\mathit{\text{im}}}=1|T_i,{\mathbf{X}}_i,U_{\mathit{\text{im}}})=\psi \{{\theta }_{1m}^{\ast }+{\theta }_{\mathit{\text{Tm}}}^{\ast }{T}_i+{\mathit{\theta }}_{\mathit{\text{Xm}}}^{\ast \prime }{\mathbf{X}}_i+{\mathit{\theta }}_{\mathit{\text{TXm}}}^{\ast \prime }(T_i{\mathbf{X}}_i)+U_{\mathit{\text{im}}}\},$$ (14)

where the subscript m denotes the mth measurement. We let m = 1,…, M with M corresponding to the outcome of primary interest. The original Y_i, U_i and θ* are now known as Y_im, U_im and ${\mathit{\theta }}_M^{\ast }$ respectively. Although ${\mathit{\theta }}_m^{\ast }={({\theta }_{1m}^{\ast },{\theta }_{\mathit{\text{Tm}}}^{\ast },{\mathit{\theta }}_{\mathit{\text{Xm}}}^{\ast \prime },{\mathit{\theta }}_{\mathit{\text{TXm}}}^{\ast \prime })}^{\prime }$ is allowed to depend on m in an arbitrary fashion, some components may be assumed constant in m if this is scientifically plausible. Suppose that U_im = V_i + W_im, where V_i is characteristic of a subject and W_im represents random fluctuation within a subject. The essence of this assumption is that, within a subject, the contemporaneous correlation (between potential outcomes at the same time point) is stronger than the non-contemporaneous correlation (between two outcomes at different time points). Suppose that the V_i and the W_im are independent of each other and of the (T_i, X_i). If $V_i\sim N(0,{\sigma }_V^2)$ and $W_{im}\sim N(0,{\sigma }_W^2)$ (i = 1,…,n; m = 1,…, M), then ${\sigma }_U^2={\sigma }_V^2+{\sigma }_W^2$. This requires var(U_im) to be constant over time, at least within a suitable time window containing the primary end point (to be discussed later). Using the arguments of Appendix A, we can integrate the W_im-component of U_i out of GLMM (14) and obtain

$$P(Y_{\mathit{\text{im}}}=1|T_i,{\mathbf{X}}_i,V_i)=\psi \{{\theta }_{1m}^{\ast \ast }+{\theta }_{\mathit{\text{Tm}}}^{\ast \ast }{T}_i+{\mathit{\theta }}_{\mathit{\text{Xm}}}^{\ast \ast \prime }{\mathbf{X}}_i+{\mathit{\theta }}_{\mathit{\text{TXm}}}^{\ast \ast \prime }(T_i{\mathbf{X}}_i)+r{V}_i\},$$ (15)

exactly for the probit link and approximately for the logit link. Here,

$${\mathit{\theta }}_m^{\ast \ast }={({\theta }_{1m}^{\ast \ast },{\theta }_{\mathit{\text{Tm}}}^{\ast \ast },{\mathit{\theta }}_{\mathit{\text{Xm}}}^{\ast \ast \prime },{\mathit{\theta }}_{\mathit{\text{TXm}}}^{\ast \ast \prime })}^{\prime }={r\mathit{\theta }}_m^{\ast },$$

$r={(1+{\sigma }_W^2)}^{-1/2}$ for the probit link and $r={(1+{\sigma }_W^2/c^2)}^{-1/2}$ for the logit link. Note that r ≤ 1 with equality holding if and only if ${\sigma }_W^2=0$. Because model (15) is a standard GLMM, $var({\text{rV}}_i)=r^2{\sigma }_V^2$ is directly estimable by using standard GLMM software. If we assume that ${\sigma }_W^2=0$, so that W_im≡0, then ${\sigma }_U^2={\sigma }_V^2=var(r{V}_i)$ becomes identifiable and estimable. Otherwise, noting that $var(r{V}_i)\le {\sigma }_V^2\le {\sigma }_U^2$, var(rV_i) may serve as a lower bound for ${\sigma }_U^2$ in a sensitivity analysis. To implement this analysis based on model (15), one should choose a set of repeated measurements containing the outcome of primary interest as well as some adjacent measurements within a suitable time window. The choice of the time window represents a bias–variance trade-off, with wider windows affording better precision at the expense of potential bias due to model misspecification.

In addition to a lower bound for ${\sigma }_U^2$, one could recover θ* from model (15) as ${\mathit{\theta }}_M^{\ast }={(1+{\sigma }_W^2)}^{1/2}{\mathit{\theta }}_M^{\ast \ast }$ for the probit link or as ${\mathit{\theta }}_M^{\ast }={(1+{\sigma }_W^2/c^2)}^{1/2}{\mathit{\theta }}_M^{\ast \ast }$ for the logit link, if one is confident about model (15). The resulting estimate of θ* (based on a given value of ${\sigma }_W^2$) may be more efficient than the estimate that maximizes likelihood (13) (based on a given value of ${\sigma }_U^2$), especially when the ${\mathit{\theta }}_m^{\ast }$ (m = 1,…, M) are closely related to each other. However, this approach relies heavily on correct specification of model (15) and is thus more susceptible to misspecification bias.

3.3. Sensitivity analysis based on an odds ratio

To accommodate alternative dependence structures (e.g. negative dependence) for Y(0) and Y(1) given X, we now propose a sensitivity analysis approach based on the odds ratio given by equation (6). Note that assumption (4) corresponds to ρ(X) ≡ 1. In general, we could specify a model for the odds ratio such as $\rho (\mathbf{X};\beta )=exp({\beta }_1+{\beta }_X^{\prime }\mathbf{X})$, where $\beta ={({\beta }_1,{\beta }_X^{\prime })}^{\prime }$. Specification of the model and plausible parameter values must be based on substantive knowledge, because the observed data provide no information about ρ(X). When the dimension of β is high, it can be difficult to cover a wide range of β-values in obtaining and presenting estimates of the π_jk as functions of β. Therefore, without reliable and concrete information about ρ(X), it does not seem advantageous to perform a sensitivity analysis based on a covariate-dependent odds ratio. In the rest of this subsection, we shall work with a fixed odds ratio, ρ(X) ≡ ρ ∈ (0,∞), for ease of interpretation, implementation and presentation, although the methodology extends easily to a more general model for ρ(X).

In a 2×2 contingency table with cell probabilities q = (q₀₀, q₀₁, q₁₀, q₁₁)′, q₁₁ can be determined from the odds ratio ρ and the marginal probabilities q₁₊ = q₁₀ + q₁₁ and q₊₁ = q₀₁ + q₁₁ as

$$q_{11}=\frac{1+(q_{1+}+q_{+1})(\rho -1)-\omega }{2(\rho -1)},$$

where

$$\omega =\surd [{\{1+(q_{1+}+q_{+1})(\rho -1)\}}^2+4\rho (1-\rho )q_{1+}{q}_{+1}].$$

The rest of q can then be obtained as q₁₀ = q₁₊ − q₁₁, q₀₁ =q₊₁ − q₁₁ and q₀₀ = 1 − q₁₁ − q₁₀ − q₀₁. Let Q denote the map (q₁₊, q₊₁, ρ) ↦ q for recovering cell probabilities. Then we can write

$$\begin{array}{lll}\pi \hfill & =\hfill & {({\pi }_{00},{\pi }_{01},{\pi }_{10},{\pi }_{11})}^{\prime }\hfill \\ \hfill & =\hfill & E\{{({\pi }_{00|X}(\mathbf{X}),{\pi }_{01|X}(\mathbf{X}),{\pi }_{10|X}(\mathbf{X}),{\pi }_{11|X}(\mathbf{X}))}^{\prime }\}\hfill \\ \hfill & =\hfill & E[\mathbf{Q}\{{\pi }_{1+|X}(\mathbf{X}),{\pi }_{+1|X}(\mathbf{X}),\rho \}].\hfill \end{array}$$

Now let p̂(y|t, X) be an estimate of p(y|t, x) = P(Y = y|T = t, X = x) from Section 3.1, which may be obtained non-parametrically through stratification or parametrically under a regression model. Because of randomization, p̂(1|0, x) estimates π_1+|X(x) and p̂(1|t, x) estimates π_+1|X(x). It follows that π, the vector of joint probabilities, is estimated by

$$\frac{1}{n}\sum _{i=1}^n\mathbf{Q}\{\widehat{p}(1|0,{\mathbf{X}}_i),\widehat{p}(1|1,{\mathbf{X}}_i),\rho \}.$$

It is easy to see that, when n and ρ both approach ∞, the estimate of π₁₀ given above converges to the lower bound in inequality (3) corresponding to maximal positive dependence (conditional on X). Analogous results hold for ρ → − ∞ and for the other cell probabilities. Thus, stringent as it may seem, the assumption of a constant odds ratio does not exclude any possible value of the π_jk.

3.4. Summarizing remarks

We have presented three methods that are roughly increasing in generality, except for some modelling assumptions (GLMMs in Section 3.2; a constant odds ratio in Section 3.3). The method of Section 3.1 assumes conditional independence of Y(0) and Y(1) given X, the method of Section 3.2 assumes positive conditional dependence (of a particular structure), and the method of Section 3.3 accommodates both positive and negative conditional dependence. The first method is simpler though perhaps less credible than the other two. The second method is probably the most demanding in terms of data, modelling assumptions and possibly computation, but it also can be the most informative, because it provides a data-driven lower bound on the extent of positive dependence. The last method can be restricted to positive dependence by forcing ρ > 1, but further restriction would require substantive knowledge.

4. Application

We now apply the methods of Section 3 to the MOTIVATE trial that was introduced in Section 1, a randomized, double-blinded, placebo-controlled, confirmatory clinical trial comparing maraviroc plus OBT with placebo plus OBT for treating HIV-1. The MOTIVATE study consists of two substudies that were identically designed and conducted (albeit in different countries), produced similar results and are therefore combined in our analysis. The study enrolled a total of 1049 patients with R5 HIV-1 who had been treated with or had resistance to three antiretroviral drug classes and had HIV-1 RNA levels of more than 5000 copies ml⁻¹. The patients were randomized in a 2:2:1 ratio to receive one of three antiretroviral regimens (maraviroc once daily, maraviroc twice daily and placebo), each of which also included OBT based on treatment history and drug resistance testing. Our analysis is focused on comparing the maraviroc twice daily group with the placebo group, as the two maraviroc groups produced similar results.

The outcome of interest to us is virologic response (defined as HIV RNA level below 400 copies ml⁻¹) at week 48 of treatment. As mentioned earlier, the observed virologic response rates are 57.5% and 22.5% in the maraviroc twice daily and placebo groups respectively, and the difference between the two groups (35.0%; 95% confidence interval 27.7−42.4%) is highly significant (p < 0.0001). Fig. 1 shows that the cell probabilities π_jk (j, k = 0, 1) vary widely as functions of the marginal log-odds ratio, log{π₀₀π₁₁/(π₀₁π₁₀)}, which is not identifiable from the data. Without prior information about the marginal log-odds ratio, a sensitivity analysis based on Fig. 1 would not be very informative. Using the methods proposed, we now show that the ranges of the π_jk can be narrowed by borrowing information from relevant covariates and repeated measurements.

The covariates that were included in our analysis are age, RNA (the logarithm of the baseline level of HIV RNA), CD4 (the logarithm of the baseline count of CD4 cells), and GSS and PSS (genotypic and phenotypic sensitivity scores, defined as the number of antiretroviral drugs used concomitantly to which a patient's HIV was fully susceptible, as determined by genotypic and phenotypic resistance testing at baseline). GSS and PSS take integer values from 0 to 3. The regression model for covariate adjustment is a logistic regression model given by equation (8), where X consists of the five covariates just defined. An estimate of (π₀₀, π₀₁, π₁₀, π₁₁) is obtained as (0.359, 0.432, 0.062, 0.147) by using the method of Section 3.1, with respective standard errors (0.0092, 0.0061, 0.0021, 0.0069). Throughout this section, we base inference on 400 non-parametric bootstrap samples obtained by sampling with replacement from the original subjects, without changing the observed data within a subject. Standard errors are obtained as empirical standard deviations, and confidence intervals as 2.5th and 97.5th empirical percentiles, across the 400 bootstrap samples.

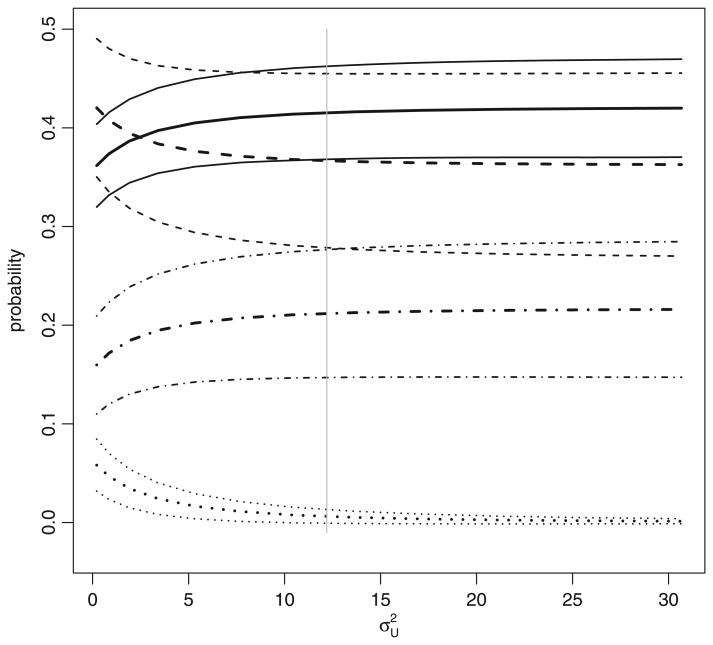
The data are also analysed by using the method of Section 3.2 under the random-effect model given by equation (11), with a logit link and the same covariate vector X as in the previous analysis. For a given value of ${\sigma }_U^2$, we estimate θ* as ${(1+{\sigma }_U^2/c^2)}^{1/2}\mathit{\theta }$ and the π_jk by using expression (12). The results (point estimates and confidence intervals of cell probabilities) are plotted in Fig. 2 as functions of ${\sigma }_U^2$. As ${\sigma }_U^2\to 0$, the results converge to those reported in the preceding paragraph (based on conditional independence), as expected. With increasing ${\sigma }_U^2$, the estimated probabilities tend to increase for concordant pairs (π₀₀, π₁₁) and to decrease for discordant pairs (π₀₁, π₁₀). To gauge the magnitude of ${\sigma }_U^2$, a GLMM analysis based on model (15) is performed on repeated measurements at 24, 32, 40 and 48 weeks. Although earlier measurements (from baseline to 20 weeks) are also available, we restrict our analysis to the later measurements in an attempt to reduce misspecification bias. Indeed, Fig. 2A of Gulick et al. (2008) shows that virologic response rates first rise in a non-linear fashion and then decline in a slow, steady and apparently linear fashion. An analysis of all repeated measurements would require a complex model for the mean structure and possibly additional random effects for the correlation structure. The resulting inference would be more susceptible to bias and of questionable relevance to our goal of understanding ${\sigma }_U^2$. Our restricted analysis of later measurements is carried out with ${\theta }_{1m}^{\ast \ast }$ depending on m freely and the rest of ${\mathit{\theta }}_m^{\ast \ast }$ independent of m; this amounts to adding an indicator for the follow-up visit as a categorical covariate. From this analysis, var(rV_i) is estimated to be 20.2 (95% confidence interval 12.2−30.2). Because ${\sigma }_U^2\ge var(r{V}_i)$, a conservative 97.5% lower confidence bound for ${\sigma }_U^2$ is given by 12.2, the lower confidence bound for var(rV_i). This suggests that interpretation of Fig. 2 should be focused on later portions of the curves, which happen to be flatter than the earlier portions and have narrower ranges. In particular, the range of π₁₀, the proportion of patients who would be harmed by maraviroc, is much narrower in Fig. 2 than in Fig. 1. The argument of Berger and Boos (1994) can be used to conclude that, with ${\sigma }_U^2$ treated as an unknown nuisance parameter, a 95% upper confidence bound for π₁₀ is below 4%; this is obtained by evaluating the upper confidence bound curve for π₁₀ at the lower confidence bound for ${\sigma }_U^2$. In contrast, a 97.5% lower confidence bound for π₀₁, the proportion of patients who would benefit from maraviroc, is clearly above 25%; the Berger−Boos argument is not needed here because we are taking the infimum of the lower confidence bound curve.

Fig. 2.

Sensitivity analysis for the MOTIVATE study of Section 4 based on a random-effect model (|, conservative 97.5% lower confidence bound for ${\sigma }_U^2$, which is obtained as 12.2 from a GLMM analysis (see Section 4 for details)): point estimates ( , — — —, · — · —, · · · · · · ·) and 95% confidence intervals ( , — — —, · — · —, · · · · · · ·) for π₀₀ ( ),π₀₁(— — —),π₁₀(· · · · · · ·) and π₁₁ (· — · —)

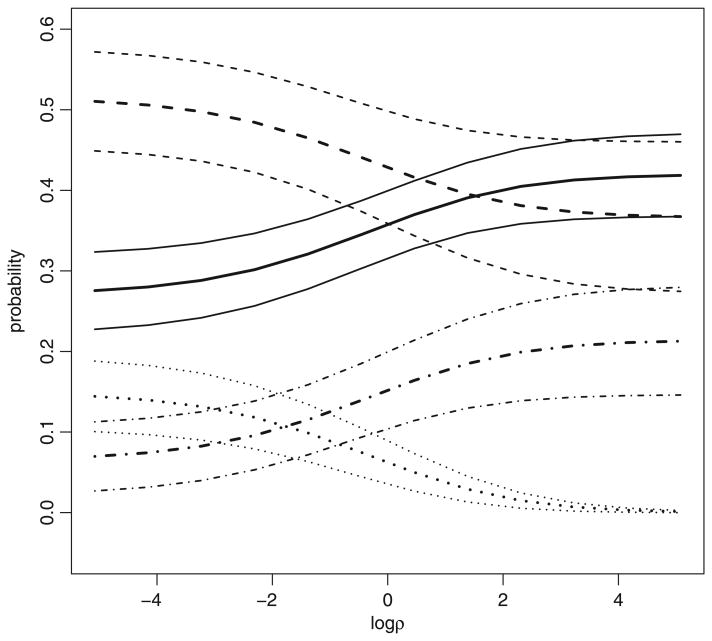
Fig. 3 shows another sensitivity analysis based on ρ(X) ≡ ρ, as described in Section 3.3. It includes negative conditional dependence (i.e. ρ < 1) for completeness, although there is no reason to expect a negative dependence between Y(0) and Y(1) given X in this situation. Even without prior information about ρ, the curves in Fig. 3 are notably more constrained than those in Fig. 1. The extra information obviously comes from the covariates as well as the regression model (8). The results at ρ= 1 correspond to those based on conditional independence as well as those in Fig. 2 with ${\sigma }_U^2\to 0$. If we restrict attention to positive conditional dependence (i.e. ρ > 1), then this analysis yields the same range of point estimates for each joint probability π_jk as in Fig. 2.

Fig. 3.

Sensitivity analysis for the MOTIVATE study of Section 4 based on the conditional odds ratio ρ(X) defined by equation (6): point estimates ( , — — —, · — · —, · · · · · · ·) and 95% confidence intervals ( , — — —, ·— · —, ·· · · · ·) for π₀₀ ( ), π₀₁ (— — —), π₁₀ (· · · · · · ·) and π₁₁ (· — · —), as functions of ρ(X) ≡ ρ

The above results should be weighed according to the plausibility of the underlying assumptions for the different methods. Because the GLMM analysis indicates a high level of within-subject correlation (after adjusting for X), the conditional independence assumption (4) is seriously in doubt, and the resulting analysis is not as credible as the two sensitivity analyses. Although based on different assumptions, both sensitivity analyses can cover the full range between conditional independence and maximal positive conditional dependence of Y(0) and Y(1) given X. In addition, the random-effect-based approach, under the assumptions of Section 3.2, also provides a lower bound on the extent of positive conditional dependence, which can be used to narrow the spectrum of the sensitivity analysis. The key assumption for the lower bound, that the contemporaneous correlation is stronger than the non-contemporaneous correlation, seems quite plausible in the present situation, and we therefore place more emphasis on the random-effect-based analysis than on the odds-ratio-based analysis.

The random-effect-based analysis suggests that it is fairly unlikely for maraviroc to affect adversely the virologic response (at week 48) of a patient who already receives OBT. This finding adds considerable assurance to the current knowledge of maraviroc (Gulick et al., 2008; Fatkenheuer et al., 2008). If this were not so (i.e. if the analysis showed that a large proportion of patients could be harmed by the addition of maraviroc to OBT), it might be necessary to consider restricting the use of maraviroc to a subpopulation of patients with a more favourable benefit–risk profile. The search for such a subpopulation could be facilitated by intermediate results in the preceding analyses. For example, potential effect modifiers could be identified by examining the regression coefficients in models (8) and (15), and the various estimates of π_jk|X(X) could be used to develop a candidate subpopulation. To contain the adverse effect of maraviroc, it makes sense to look for patients with small estimates of π_10|X(X). Once a candidate subpopulation has been identified, the methods proposed can then be applied to the target subpopulation to re-estimate the π_jk, presumably by using a cross-validation approach to avoid overfitting. If no subpopulation based on X can be found with a satisfactory benefit–risk profile, the scientific community may then be motivated to search for new and more informative biomarkers.

5. Discussion

This paper adds to the literature on HTE assessment, which is currently dominated by subgroup analyses and multiplicity adjustments, with a different approach based on potential outcomes of individual patients. Gadbury and colleagues have previously studied HTE in terms of potential outcomes. This paper builds on their work by developing new and practical methods that incorporate relevant information in covariates and repeated measurements in assessing HTE. To address the inherent identifiability issue, we propose a covariate adjustment method based on conditional independence as well as two sensitivity analysis methods, one of which extends the work of Gadbury et al. (2001). The HIV example in Section 4 shows that relevant covariates and repeated measurements can indeed help to reduce the uncertainty about HTE. Originally developed for a binary outcome, the methods are extended to a continuous outcome in Appendix C.

In practice, the choice between the three methods proposed should be based on the available information and the plausibility of the underlying assumptions. The first method (Section 3.1), which is conceptually simple and easy to implement, could serve as a starting point. It would not be the final analysis, though, unless one is fairly confident about the conditional independence assumption. In situations like the MOTIVATE study, where longitudinal data are available, the second method (Section 3.2) could be used to assess the effect of positive conditional dependence and also to estimate a lower bound for that dependence, under a suitable GLMM framework. The last method (Section 3.3), which is even more general though perhaps less informative than the second method, could nonetheless be used as a safety net when reliable information is unavailable about the dependence structure of Y(0) and Y(1) given X.

As alluded to earlier, a promising approach to understanding HTE may be the crossover design, where potential outcomes for different treatments are actually observed on the same subject, albeit in different time periods. However, the crossover design has its own issues, as noted by Poulson et al. (2012). Depending on the disease being studied and the treatments being compared, a crossover design may be infeasible or seriously compromised by a substantial carry-over effect. Even without these problems, evaluation of HTE in a crossover study could be complicated by an individual period effect. Poulson et al. (2012) show in a two-period two-treatment setting that the sample variance of the observed individual treatment difference overestimates the true variance of the individual treatment effect. Nonetheless, the crossover design can still be a valuable tool for studying HTE. It will be of interest to see whether the methods that are developed here can be extended to the crossover design and combined with the results of Poulson et al. (2012) to yield further insights into HTE.

Although developed for randomized clinical trials, our methods can certainly be extended to observational studies. The main issue in such extensions is to ensure adequate control for confounding. For this, all potential confounders need to be measured and included in X to meet the condition of strongly ignorable treatment assignment (Rosenbaum and Rubin, 1983).

Appendix A: Relationship between θ and (θ, ${\sigma }_U^2$) in Section 3.2

For the probit link, model (11) implies that model (8) holds with $\mathit{\theta }={(1+{\sigma }_U^2)}^{-1/2}{\mathit{\theta }}^{\ast }$. This observation, which was noted previously by Carroll et al. (1984), can be argued as follows. With ψ = Φ, the standard normal distribution function, we have

$$\begin{array}{ccc}p(1|t,\mathbf{x})& =& \int p(1|t,\mathbf{x},u){\mathrm{d}F}_{U|T,X}(u|t,\mathbf{x})\\ & =& \int \mathrm{\Phi }\{(1,t,{\mathbf{x}}^{\prime },{t\mathbf{x}}^{\prime }){\mathit{\theta }}^{\ast }+u\}\varphi (u;0,{\sigma }_U^2)\mathrm{d}u\\ & =& \int P\{Z<(1,t,{\mathbf{x}}^{\prime },{t\mathbf{x}}^{\prime }){\mathit{\theta }}^{\ast }+u\}\varphi (u;0,{\sigma }_U^2)\mathrm{d}u,\end{array}$$

where Z is a standard normal variable independent of U. The second step in this expression makes use of the assumed independence between U and (T, X), and the last step follows from the definition of Φ. Now we can write p(1|t, x) as the marginal probability

$$\begin{array}{ccc}P\{Z<(1,t,{\mathbf{x}}^{\prime },t{\mathbf{x}}^{\prime }){\mathit{\theta }}^{\ast }+U\}& =& P\{Z-U<(1,t,{\mathbf{x}}^{\prime },t{\mathbf{x}}^{\prime }){\mathit{\theta }}^{\ast }\}\hfill \\ & =& P\left\{\frac{Z-U}{\surd (1+{\sigma }_U^2)}<\frac{(1,t,{\mathbf{x}}^{\prime },t{\mathbf{x}}^{\prime }){\mathit{\theta }}^{\ast }}{\surd (1+{\sigma }_U^2)}\right\}\hfill \\ & =& \mathrm{\Phi }\left\{\frac{(1,t,{\mathbf{x}}^{\prime },t{\mathbf{x}}^{\prime }){\mathit{\theta }}^{\ast }}{\surd (1+{\sigma }_U^2)}\right\},\hfill \end{array}$$

which leads to the result claimed.

For the logit link, we can approximate ψ(a) = exp(a)/{1 + exp(a)} by Φ(a/c), where c= 15π/(16√3)≈ 1.70 (e.g. Johnson and Kotz (1970), Zeger et al. (1988) and Liang and Liu (1991)). This allows us to write

$$\begin{array}{lll}p(1|t,\mathbf{x})\hfill & =\hfill & \int \psi \{(1,t,{\mathbf{x}}^{\prime },t{\mathbf{x}}^{\prime }){\mathit{\theta }}^{\ast }+u\}\varphi (u;0,{\sigma }_U^2)\mathrm{d}u\hfill \\ \hfill & \approx \hfill & \int \mathrm{\Phi }\left\{\frac{(1,t,{\mathbf{x}}^{\prime },t{\mathbf{x}}^{\prime }){\mathit{\theta }}^{\ast }+u}{c}\right\}\varphi (u;0,{\sigma }_U^2)\mathrm{d}u\hfill \\ \hfill & =\hfill & \mathrm{\Phi }\left\{\frac{(1,t,{\mathbf{x}}^{\prime },t{\mathbf{x}}^{\prime }){\mathit{\theta }}^{\ast }}{c\surd (1+{\sigma }_U^2/c^2)}\right\}\hfill \\ \hfill & \approx \hfill & \psi \left\{\frac{(1,t,{\mathbf{x}}^{\prime },t{\mathbf{x}}^{\prime }){\mathit{\theta }}^{\ast }}{\surd (1+{\sigma }_U^2/c^2)}\right\}.\hfill \end{array}$$

In this case, model (11) implies that model (8) holds approximately with $\mathit{\theta }={(1+{\sigma }_U^2/c^2)}^{-1/2}{\mathit{\theta }}^{\ast }$.

Appendix B: Limit of expression (12) as ${\sigma }_U^2\to \infty$

We fix θ and consider θ* as a function of ${\sigma }_U^2:{\mathit{\theta }}^{\ast }({\sigma }_U^2)={(1+{\sigma }_U^2)}^{1/2}\mathit{\theta }$ for the probit link and ${\mathit{\theta }}^{\ast }({\sigma }_U^2)={(1+{\sigma }_U^2/c^2)}^{1/2}\mathit{\theta }$ for the logit link. To fix ideas, we focus on estimating π₁₀, i.e. the case that j = 1 and k = 0 in expression (12); the other cases can be treated with the same argument. Let us define

$$\begin{array}{lll}h(\mathbf{x},{\sigma }_U^2)\hfill & =\hfill & P\{Y(0)=1,Y(1)=0|\mathbf{X}=\mathbf{x};{\mathit{\theta }}^{\ast }({\sigma }_U^2),{\sigma }_U^2\}\hfill \\ \hfill & =\hfill & {\int }_{-\infty }^{\infty }{p}^{\ast }\{1|0,\mathbf{x},u;{\mathit{\theta }}^{\ast }({\sigma }_U^2)\}{p}^{\ast }\{0|1,\mathbf{x},u;{\mathit{\theta }}^{\ast }({\sigma }_U^2)\}\varphi (u;0,{\sigma }_U^2)\mathrm{d}u\hfill \\ \hfill & =\hfill & {\int }_0^1\psi \{{\mathit{\theta }}^{\ast }{({\sigma }_U^2)}^{\prime }\mathbf{b}(0,\mathbf{x})+{\sigma }_U{z}_q\}[1-\psi \{{\mathit{\theta }}^{\ast }{({\sigma }_U^2)}^{\prime }b(1,x)+{\sigma }_U{z}_q\}]\mathrm{d}q,\hfill \end{array}$$ (16)

where b(t, x) = (1, t, x′, tx′)′, z_q is the qth quantile of the standard normal distribution and a change of variables is used in the last step. Now expression (12) can be rewritten as $n^{-1}{\sum }_{i=1}^{n}h({\mathbf{X}}_i,{\sigma }_U^2)$.

Let us focus on the probit link for the moment. As ${\sigma }_U^2\to \infty$, we have, for t = 0, 1,

$$\psi \{{\mathit{\theta }}^{\ast }{({\sigma }_U^2)}^{\prime }\mathbf{b}(t,\mathbf{x})+{\sigma }_U{z}_q\}=\psi \{{(1+{\sigma }_U^2)}^{1/2}{\mathit{\theta }}^{\prime }\mathbf{b}(t,\mathbf{x})+{\sigma }_U{z}_q\}\to \{\begin{array}{c}1\text{if}{\mathit{\theta }}^{\prime }\mathbf{b}(t,\mathbf{x})+z_q>0,\\ 0\text{if}{\mathit{\theta }}^{\prime }\mathbf{b}(t,\mathbf{x})+z_q<0.\end{array}$$

The case that θ′ b(t, x) + z_q = 0 is irrelevant for our purpose. The above expression implies that the integrand in equation (16) converges to

$$I\{{\mathit{\theta }}^{\prime }\mathbf{b}(0,\mathbf{x})+z_q>0,{\mathit{\theta }}^{\prime }\mathbf{b}(1,\mathbf{x})+z_q<0\}=I\{-{\mathit{\theta }}^{\prime }\mathbf{b}(0,\mathbf{x})<z_q<-{\mathit{\theta }}^{\prime }\mathbf{b}(1,\mathbf{x})\},$$

where I is the indicator function, for almost every q (write respect to Lebesgue measure). By the dominated convergence theorem,

$$h(\mathbf{x},{\sigma }_U^2)\to max[0,\mathrm{\Phi }\{{\mathit{\theta }}^{\prime }\mathbf{b}(0,\mathbf{x})\}-\mathrm{\Phi }\{{\mathit{\theta }}^{\prime }\mathbf{b}(1,\mathbf{x})]=max\{0,{\pi }_{1+|X}(\mathbf{x})-{\pi }_{+1|X}(\mathbf{x})\}=:h(\mathbf{x},\infty ).$$

Note that the above limit is simply the lower limit for π_10|X(x) given in inequality (2), which is attained under maximal positive dependence between Y(0) and Y(1) given X = x. Applying the dominated convergence theorem once again (with respect to x), we see that expression (12) converges to $n^{-1}{\sum }_{i=1}^{n}h({\mathbf{X}}_i,\infty )$ as ${\sigma }_U^2\to \infty$. Furthermore, the population counterpart of expression (12), with the sample average replaced by expectation (with respect to X), converges to E{h(X, ∞)}. Note that

$$\begin{array}{lll}E\{h(\mathbf{X},\infty )\}\hfill & =\hfill & \int max\{0,{\pi }_{1+|X}(\mathbf{x})-{\pi }_{+1|X}(\mathbf{x})\}\mathrm{d}{F}_X(\mathbf{x})\hfill \\ \hfill & \ge \hfill & max\left[0,\int \{{\pi }_{1+|X}(\mathbf{x})-{\pi }_{+1|X}(\mathbf{x})\}\mathrm{d}{F}_X(\mathbf{x})\right]\hfill \\ \hfill & =\hfill & max(0,{\pi }_{1+}-{\pi }_{+1}).\hfill \end{array}$$

Thus, the limit E{h(X, ∞)}, which is also the lower limit in inequality (3), is indeed higher (i.e. sharper) than the lower limit in inequality (1), which does not involve any covariate information.

With minimal modifications, the result in the above paragraph remains valid (approximately) for the logit link.

Appendix C: Extension to continuous outcomes

The joint distribution, F(y₀, y₁) = P{Y(0) ≤y₀, Y(1)≤y₁}, contains all relevant information about HTE for an arbitrary outcome variable. This joint distribution is itself a succinct summary of HTE for a binary outcome and categorical outcomes with more than two levels, to which the methods of Section 3 extend readily. This appendix is therefore focused on a continuous or quantitative outcome, for which there may be more succinct summaries of HTE than the joint distribution of potential outcomes. For example, the difference D = Y(1) − Y(0) can be used to represent the effect of the experimental treatment relative to the control on an individual patient, and one might be interested in estimating ${\sigma }_D^2=var(D)$, which measures the overall extent of HTE, or more generally the distribution function F_D. From F_D one could further derive important quantities such as selected quantiles of D or the proportion of patients who would benefit from, or be harmed by, the new treatment. These quantities are functionals of the joint distribution F which are not determined by the marginal distributions F_t(y) = P{Y(t) ≤ y}, t = 0, 1.

Under assumption (4), F(y₀, y₁) = E{F_{Y|T, X} (y₀|0, X) F_{Y|T, X} (y₁|1, X)} can be estimated by substituting an estimate of F_{Y|T, X}, which may be parametric or non-parametric, and replacing expectation with sample average (over the X_i). From this it is straightforward to derive estimates of HTE-related quantities. For example, suppose that F_{Y|T, X} follows a normal linear model given by

$$Y={\theta }_1+{\theta }_{T}T+{\mathit{\theta }}_X^{\prime }\mathbf{X}+{\mathit{\theta }}_{\mathit{\text{TX}}}^{\prime }(T\mathbf{X})+\varepsilon ,$$ (17)

where $\varepsilon \sim N(0,{\sigma }_{\varepsilon }^2)$, independently of (T, X). Then assumption (4) implies that

$$F_D(d)=E\left\{\mathrm{\Phi }\left(\frac{d-{\theta }_T-{\mathit{\theta }}_{\mathit{\text{TX}}}^{\prime }\mathbf{X}}{{\sigma }_{\varepsilon }\surd 2}\right)\right\}.$$

When assumption (4) is in doubt, the random-effect-based approach of Section 3.2 extends easily to any outcome for which a GLMM is appropriate. Suppose, for example, that F_{Y|T, X, U} follows the linear mixed model

$$Y={\theta }_1^{\ast }+{\theta }_T^{\ast }T+{\theta }_X^{\ast \prime }\mathbf{X}+{\theta }_{\mathit{\text{TX}}}^{\ast \prime }(T\mathbf{X})+U+\varepsilon \ast ,$$ (18)

where $U\sim N(0,{\sigma }_U^2)$ and ${\varepsilon }^{\ast }\sim N(0,{\sigma }_{\varepsilon \ast }^2)$, independently of each other and of (T, X). Then assumption (5) implies that

$$F_D(d)=E\left\{\mathrm{\Phi }\left(\frac{d-{\theta }_T^{\ast }-{\mathit{\theta }}_{\mathit{\text{TX}}}^{\ast \prime }\mathbf{X}}{{\sigma }_{\varepsilon \ast }\surd 2}\right)\right\}.$$ (19)

The parameters in model (18) may be (partially) estimable from longitudinal data under suitable assumptions (see Section 3.2). In any case, we note that model (18) implies model (17) with θ = θ* and ${\sigma }_{\varepsilon }^2={\sigma }_U^2+{\sigma }_{\varepsilon \ast }^2$, so that θ* is directly estimable from a linear regression analysis based on model (17), and ${\sigma }_{\varepsilon \ast }^2$ can be recovered as ${\sigma }_{\varepsilon }^2-{\sigma }_U^2$ for a specified value of ${\sigma }_U^2$.

The odds-ratio-based approach of Section 3.3 can be extended to general outcomes by using copulas (Nelsen, 1999). A copula is a multivariate distribution function with uniform (0, 1) marginals. It captures the dependence structure in a multivariate distribution without being constrained by the marginal distributions. In the present context, it allows us to represent the joint distribution of Y(0) and Y(1) given X as

$$P\{Y(0)\le y_0,Y(1)\le y_1|\mathbf{X}=\mathbf{x}\}=C\{F_{Y|T,X}(y_0|0,\mathbf{x}),F_{Y|T,X}(y_1|1,\mathbf{x})\},$$

where C is the copula. Instead of conditional independence, we now assume that, given X, the conditional dependence of Y(0) and Y(1) is described by the copula C(·, ·; ρ), where C is taken from a parametric family of copulas and ρ is a parameter that represents the strength of the dependence. Note that the copula could be allowed to depend on X if necessary. Now F(y₀, y₁) can be identified and estimated as E[C{F_{Y|T, X} (y₀|0, X), F_{Y|T, X} (y₁|1, X); ρ}]. In particular, if F_{Y|T, X} follows model (17) and C(·, ·; ρ) is a normal copula with correlation coefficient ρ, we then have

$$F_D(d)=E\left(\mathrm{\Phi }\left[\frac{d-{\theta }_T-{\theta }_{\mathit{\text{TX}}}^{\prime }\mathbf{X}}{{\sigma }_{\varepsilon }\surd \{2(1-\rho )\}}\right]\right).$$ (20)

A sensitivity analysis based on equation (20) is similar to an analysis based on equation (19) but perhaps more general in that it accommodates negative dependence between Y(0) and Y(1) given X.