The Cellular Origins of the Outer Retinal Bands in Optical Coherence Tomography Images

Abstract

Purpose.

To test the recently proposed hypothesis that the second outer retinal band, observed in clinical OCT images, originates from the inner segment ellipsoid, by measuring: (1) the thickness of this band within single cone photoreceptors, and (2) its respective distance from the putative external limiting membrane (band 1) and cone outer segment tips (band 3).

Methods.

Adaptive optics-optical coherence tomography images were acquired from four subjects without known retinal disease. Images were obtained at foveal (2°) and perifoveal (5°) locations. Cone photoreceptors (n = 9593) were identified and segmented in three dimensions using custom software. Features corresponding to bands 1, 2, and 3 were automatically identified. The thickness of band 2 was assessed in each cell by fitting the longitudinal reflectance profile of the band with a Gaussian function. Distances between bands 1 and 2, and between 2 and 3, respectively, were also measured in each cell. Two independent calibration techniques were employed to determine the depth scale (physical length per pixel) of the imaging system.

Results.

When resolved within single cells, the thickness of band 2 is a factor of three to four times narrower than in corresponding clinical OCT images. The distribution of band 2 thickness across subjects and eccentricities had a modal value of 4.7 μm, with 48% of the cones falling between 4.1 and 5.2 μm. No significant differences were found between cells in the fovea and perifovea. The distance separating bands 1 and 2 was found to be larger than the distance between bands 2 and 3, across subjects and eccentricities, with a significantly larger difference at 5° than 2°.

Conclusions.

On the basis of these findings, we suggest that ascription of the outer retinal band 2 to the inner segment ellipsoid is unjustified, because the ellipsoid is both too thick and proximally located to produce the band.

Resolved in single cones, typical thickness of the second outer retinal band is 4.7 μm, and the band is located closer to outer segment tips than external limiting membrane. These findings suggest the band does not originate from the inner segment ellipsoid.

Introduction

In the two decades since the emergence of optical coherence tomography (OCT) as a retinal imaging modality, it has grown to become a standard of ophthalmic care.¹ Optical coherence tomography permits cross-sectional imaging of the retina,² and a distinctive feature of the retinal OCT cross-sectional image (B-scan) is the striated pattern that follows the laminar structure of the retina. Many of the quantitative clinical norms established for OCT-based ophthalmic diagnosis depend upon identification and quantification of the B-scan bands. Such methods are commonly applied to the diagnosis and assessment of diseases of the retina and optic nerve, including glaucoma,^3–6 AMD,^7,8 and diabetic macular edema.^9–11

Figure 1.

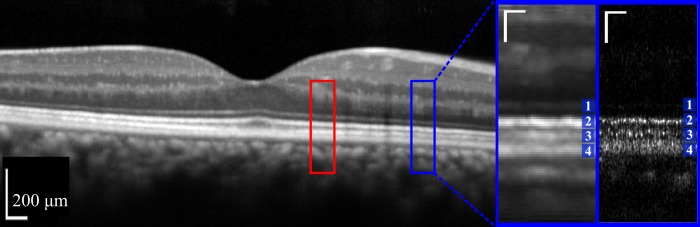
Comparison of conventional OCT with AO-OCT. Horizontal wide-field Spectralis B-scan centered on the fovea of one of the study's subjects (left). Image is displayed as the instrument displays it, in logarithmic scale. Red and blue boxes indicate locations, 2.0° nasal and 5.0° nasal, used for AO-OCT imaging. Magnified view (near right) of a portion of the Spectralis image containing outer retinal layers at 5.0° nasal, in linear scale. Corresponding AO-OCT image (far right) from the same location in the same subject, also shown in linear scale. In both inset images, the outer retinal layers 1 through 4 are labeled. Bands 1, 3, and 4 correspond to putative ELM, COST, and RPE, respectively. The controversy surrounding the origin of band 2 is the subject of the present investigation. For the Spectralis, linearizing required use of the instrument's reported dynamic range (43 dB). All of the qualitative and quantitative observations presented in this paper were performed using linear intensity for both Spectralis and AO-OCT images. The Spectralis was operated in ‘ART' mode, and the resulting image is an average of 100 frames. The AO-OCT image shown is a single frame. In magnified views, scale bars (white) indicate 50 μm in lateral and axial dimensions.

During OCT's first decade of use in clinical and research applications, three bands were identified in B-scans of the outer retina, the portion of the retina external to the outer nuclear layer. The first was attributed to the external (or outer) limiting membrane (ELM),^12–14 and the third was attributed to the RPE.¹³ The second band was usually attributed to the junction between the inner and outer segments (IS/OS),^13,15–17 although some investigators attributed it to the inner segment ellipsoid (ISe), the mitochondria-dense, distal-most portion of the IS.^18,19

While early time-domain and spectral-domain (SD) OCT systems proved capable of resolving the most prominent laminar structures of the retina, they lacked sufficient lateral resolution for resolving the single cells constituting the layers. The advent of adaptive optics (AO) OCT^20,21 combined the cellular depth resolution of OCT with cellular lateral resolution as well, an approach which led to the first laterally- and axially-resolved images of cone photoreceptors.²² This approach revealed that the third band, previously attributed to RPE, consisted of two neighboring bands.²³ Analysis of the resulting volumetric images revealed that the more anterior (proximal) of these was highly correlated with the second band, suggesting a common cellular origin, and it was referred to as the cone outer segment tips (COST),²⁴ while the name RPE was maintained for the more posterior (distal) fourth band (see Fig. 1).

Figure 2.

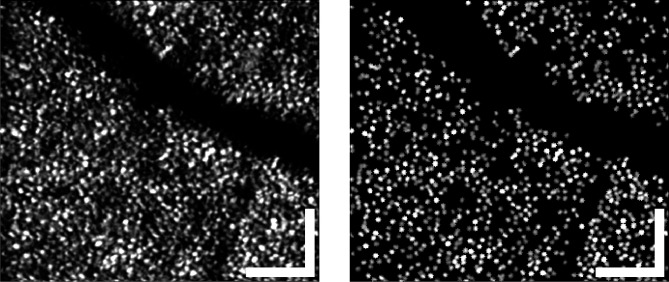
In SD-OCT, a point source is scanned over the retina, acquiring one axial scan (A-scan) per retinal location. If the point source is scanned in a line across the retina, a 2D, cross-sectional image of the retina (B-scan) is created. If the point source is raster scanned, in two dimensions, a 3D, volumetric image may be generated. From the latter, areal (or en face) projections of the retinal layers at specific depths (C-scans) may be extracted. C-scans from the depths of bands 2 and 3 are shown (right). Both reveal regular mosaics of the overlapping bright spots²⁴ whose spacing agrees with histologic measurements of cone photoreceptors.⁷⁸ At both layers, reflected light appears to be confined, laterally, to the interior of the cell.

Continued improvements in sensitivity, resolution, and speed of conventional (non-AO) SD-OCT permitted better differentiation of layers in single B-scans, and was consistent with the current trend of naming at least four outer retinal layers in the macula,²⁵ as well as a fifth (the rod OS tips) in the peripheral retina, where it becomes sufficiently displaced from RPE to form a distinct layer.²⁶

A recent review of the existing nomenclature²⁷ challenged the attribution of band 2 to the IS/OS junction. The authors compared anatomical models of foveal and perifoveal (6°) cone photoreceptors, based on an extensive, quantitative review of outer retinal histology literature, with Spectralis OCT B-scans acquired at the same locations. They posed two key challenges to the attribution of band 2 to IS/OS, both based on analysis of the axial, laminar structure of the retina:

1. The IS/OS junction should produce a thin reflection, but band 2 is thick; and

2. Inner segments and outer segments should be of similar length, but band 2 is much closer to ELM than the RPE (which, using standard clinical OCT systems, is axially indistinguishable from COST in the fovea).

In contrast to IS/OS, ISe is thick (16–20 μm) and closer to ELM than COST/RPE in the fovea. Moreover, when OCT B-scans were aligned to the histology-based model of the cones, the peak of band 2 aligned with ISe. On these grounds, the authors recommended attribution of band 2 to ISe. Their findings were affirmed during an international OCT nomenclature meeting, whose official recommendation was to refer to band 2 as the “ellipsoid zone” (EZ).²⁸ These recommendations were based on analysis of the laminar structure of the retina, but not on cellular structure, because commercial OCT systems lack sufficient resolution for measuring cells or subcellular structures. The OCT bands follow the laminar structure of the retina, but these bands consist of images of cellular and subcellular structures, laterally integrated by blur and/or low contrast. To resolve band structure at this scale requires not only the micron resolution in the axial dimension afforded by OCT, but also micron resolution in the two lateral dimensions. The addition of AO to OCT provides these additional dimensions, improving lateral resolution to 2 to 3 μm. The purpose of the present investigation is to use the high 3D resolution of AO-OCT to characterize the outer retinal OCT bands at the cellular scale. Although in volumetric images of the retina (as opposed to two dimensional [2D], cross-sectional B-scans), it is more correct to regard the bands as surfaces, with narrow thickness compared with their lateral extents, we opted to use the term “band” in order to be consistent with the literature. Also, while significant controversy surrounds the origins of band 3 as well,^27,28 we have opted sometimes to use the term COST, in order to avoid confusion of the two distinct controversies.

We hypothesize that band 2, when characterized at the cellular level, will be substantially thinner than it appears in clinical OCT images, and that it will lie approximately equidistant from bands 1 and 3. The methods and results presented here are an outgrowth of preliminary work (Jonnal RJ, et al. IOVS 2012;53:ARVO E-Abstract 5601 and Zawadzki RJ, et al. IOVS 2012;53:ISIE E-Abstract 12). There, we used AO-OCT to measure the thickness of band 2 within single cells and observed thicknesses ranging from 4 to 10 μm, measured in a small number of cells (<500). Another AO-OCT study of a comparably small number of cells (100)²⁹ corroborated our initial findings. Our present hypotheses are based on these preliminary findings, and the present study is designed to test these hypotheses by: (1) incorporating metrological calibration of the OCT instrument, (2) measuring larger numbers of cells in order to better describe the statistical distributions of their properties, (3) developing a quantitative approach for measuring band thickness and a physically justified method for deducing object thickness, and (4) performing measurements on multiple healthy volunteers to test intersubject variability of the measures.

Methods

The Second Generation UC Davis AO-OCT Instrument

The OCT system consisted of a light source (λ = 840 nm, Δλ = 112 nm; Broadlighter, Superlum Inc., Carrigtwohill, Co. Cork, Ireland), and a Michelson interferometer consisting of a 90/10 fiber beam splitter that sent 90% and 10% of the source's output, respectively, to the reference and sample arms. The sample arm contained x- and y-direction galvanometers for scanning the beam over the retina, a custom achromatizing lens to cancel longitudinal chromatic aberration due to the eye,³⁰ and the components of the AO system. The reference channel consisted of a planar mirror and a water cuvette designed to match chromatic dispersion induced by the eye. Reflected and back-scattered light from the two interferometer arms was combined again in the fiber coupler and sent to the spectrometer, consisting of a fiber collimator, transmissive holographic diffraction grating, F-theta lens, and a CMOS linescan detector (4096 pixel ×2 lines [2048 × 2 used]; Sprint spL4096-140 km; Basler AG, Ahrensburg, Germany). The OCT system acquired 125,000 lines/sec. The theoretical axial resolution was 2.8 μm in air and 2.0 μm in the eye (n = 1.38).

The AO system incorporated a Shack-Hartmann wavefront sensor (SHWS) consisting of a lenslet array (D_array = 10  mm, D_lenslet = 0.5  mm, f = 30  mm; Northrop Grumman Corp., Falls Church, VA, USA) and sCMOS detector (2048x2048 pixel; Ace acA2040-180 km; Basler AG), and a high-speed, high-stroke deformable mirror (DM; DM-97-15; ALPAO SAS, Montbonnot, France). The AO system was limited by centroid computation time, and ran at 25 Hz using the full 4 megapixel spots image. The pupil diameter was 6.75, 13.5, and 10 mm at the eye, DM, and SHWS, respectively. Diffraction-limited imaging (σ_Zernike ≤ 60 nm) was achieved for all subjects, corresponding to a theoretical lateral resolution (R_x) of 2.5 μm in the retina (3.4 μm in air, validated using a 1951 United States Air Force resolution test chart).

Custom software was developed for both instrumentation systems. The OCT software was written in C++, with specialized graphics processing unit (GPU)-based OCT post processing, which permitted MHz-rate A-scan computation and real-time volume display.³¹ The AO software was written in Python/NumPy, and implemented a novel pupil scaling technique and a far-field camera, which provided real-time images of the double-pass lateral point spread function (PSF). The AO system provided real-time wavefront reconstruction and residual error feedback, informing operators when the correction was diffraction limited. The AO system also provided a method for dynamically adding positive or negative defocus, by modifying the SHWS reference coordinates. As such, it was capable of shifting the plane of best focus in the retina.

The sample channel of the system was designed to correct for beam distortions and astigmatism that accumulate as the imaging light is relayed by the multiple off-axis spherical mirrors in the sample channel. The out-of-plane design of the new system is described in detail elsewhere.³²

Because the hypotheses investigated in this study involve measurement of axial morphology, it was critical to calibrate the depth scale of the OCT. We performed two independent calibration procedures, one in the spectral domain and one in the spatial domain (see Appendix for details). From these calibration steps we determined that the depth scale of the OCT was 2.55 μm/pixel in air and 1.85 μm in the retina. Morphometric measurements presented here employ this depth scale.

Data Acquisition and Post Processing

Four healthy subjects (referred to as S1, S2, S3, and S4) without known retinal disease were imaged. This research followed the tenets of the Declaration of Helsinki and was approved by the institutional review board of the University of California, Davis Medical Center (Sacramento, CA, USA). Each subject was imaged using AO-OCT at two nasal retinal eccentricities along the horizontal meridian, in the fovea (2.0° nasal) and perifovea (5.0° nasal), loci chosen to facilitate comparison with similar measurements conducted using clinical OCT.²⁷ Focus was shifted using the AO system to maximize the intensity of the outer retinal bands, by less than 0.05 diopters (D) for all subjects, corresponding to displacements of the AO correction plane by ±19 μm. Generally, image quality was optimum when the focus shift was 0 D. Stability of the AO correction was optimized by dynamically adjusting the pupil position in the x- and y-directions. One subject (S1) required scaling down of the AO correction pupil to 6.1 mm in order to achieve a stable closed-loop correction, yielding a theoretical lateral resolution of 2.8 μm, still sufficient for resolving cones at both eccentricities. Illumination power, measured at the cornea, was 350 μW. A single volume series required up to 30 seconds of continual exposure to acquire, including time to fine-tune alignment of the eye and close the AO loop. For a 30-second exposure, the incident power at the cornea is a factor of 10 below the maximum permissible exposure (MPE) limits set by ANSI.^33,34

At each eccentricity, a series of five volumetric images was acquired. Each volume subtended 0.7° (~210 μm) in each lateral dimension, and consisted of 300 × 300 samples, acquired in a raster scanned pattern. From these, the single best volume (highest cone mosaic contrast and fewest eye motion artifacts) was selected for analysis.

In one subject, S3, B-scans were acquired using a Spectralis HRA+OCT (Heidelberg Engineering, Heidelberg, Germany), to compare a commercial device with AO-OCT in the same subject. We selected this instrument because it was used in previous investigations of the same questions.^27,28 We sought to replicate those initial observations, but our proposed method for testing our hypotheses did not require Spectralis images; our hypotheses were tested by AO-OCT imaging alone, and the Spectralis comparison is presented just to provide context for the AO-OCT results.

The Spectralis instrument reported the dynamic range of each acquired log-scale image, in decibels. We used this value to convert the log-scale image to a linear intensity image in order to facilitate comparison with the AO-OCT images, all of which were acquired, viewed, and quantified in linear scale. Letting Î represent the log (dB) image, digitized with arbitrary bit depth, and D represent the reported dynamic range of the image, in decibels, conversion to linear intensity (I) was done using the following equation:

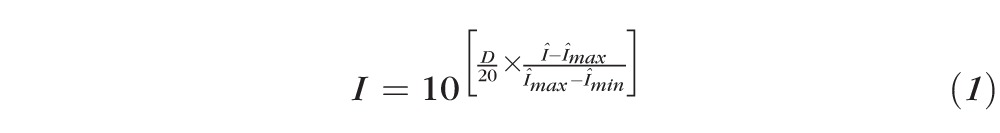This equation maps the instrument's decibel values, linearly, into the intensity range (0,1], which effectively amounts to a linear scaling of the original intensity image, which preserves all relevant structural information (e.g., full-width half-maximum [FWHM] of peaks, σ of Gaussian fits, etc.), notwithstanding minor differences owing to 8-bit digitization of the (presumably) higher bit-depth acquired images.

In SD-OCT, a spectrometer is used to image the spectrum of the source, modulated by interference between the sample and reference mirror, at each sampling location in the raster scan; see Figure 2 for a description of how the volumetric OCT image is built up. These modulated spectra must be processed in order to recover depth information at each sampling location. First, the DC component of the spectrum, estimated by averaging all the spectra in the volume, was subtracted from each acquired spectrum. Next, the spectra were mapped from wavelength (λ) into wave number (k = 2 π/λ) by linear interpolation. Then, the effects of residual dispersion mismatch were compensated using an automated, numerical approach (see Appendix). Finally, A-lines were generated by Fourier transformation of the spectra and assembled into 3D volumetric images, which were subjected to 3D segmentation as follows:

Each A-scan was automatically searched for retinal features, using a model-based classifier. For the purposes of this investigation, the classifier was used to identify features corresponding to bands 1 through 3 in the outer retina. Classifying features in single A-scans was motivated by the goal of confining morphometric analysis to single cells. Without a priori knowledge of the cellular structure of the tissue, A-scans cannot safely be grouped for analysis without risk of conflating features from multiple cells. On the other hand, not every A-scan contains each feature. In order to assemble the topographic maps, where a feature was missing (e.g., in the space between cones or in especially noisy A-scans), the location was interpolated from surrounding A-scans. This step produces areal topographies for each of the bands, showing where in depth each band lies. High-pass filtering of these topographies, to remove relief due to axial eye motion and retinal curvature (real or virtual), permitted quantitative characterization of the local roughness of each layer. The high-pass filter was implemented by fitting a third-order polynomial surface to the original topography image and subtracting the fit from the original image.

Using the areal topography, each band was visualized by extracting the classified pixels from each A-scan and assembling them into a 2D, areal projection. Figures 2 and 3 depict the areal projections of reflective bands from the retina (C-scans).

Figure 3.

Typical areal projection of band 2, from S3 at 5°, the same portion of retina shown in Figure 4. The full mosaic is shown on the left, and the cones automatically identified and segmented for analysis on the right. A number of cones were clearly missed by the algorithm, which was intentionally tuned to favor a low false-positive rate over a low miss rate. In spite of the misses, more than a thousand cones were found, on average, in a volumetric image. Scale bars: 50 μm.

As has been demonstrated previously,²⁴ C-scans of bands 2 and 3 have a periodic appearance consistent with images of the cone mosaic acquired using other AO imaging modalities.³⁵ Using one of these (or the sum of both), a custom, 2D gradient search algorithm was applied to identify and localize the cone photoreceptors (see Appendix). This algorithm was tuned to have high specificity (0% false positives) at the expense of low sensitivity (10%–20% miss rate), since the negative consequences of false positives for statistical analysis were thought to outweigh the benefit of improved statistical power. No manual correction was employed.

The band segmentation described in steps 1 and 2, combined with the cone identification in step 3, provided 3D volumetric images of the cones. The cone images were then subjected to a variety of quantitative analyses in order to test our hypotheses (band 2 thickness and position).

Quantitative Analysis

Testing the first hypothesis required measurement of the FWHM thickness of a reflective band, localized to a single cell. To directly measure the FWHM, one must know the maximum intensity of the reflection, but this is only known when this peak is centered upon one pixel of the A-scan, which is almost never the case. Generally direct measurement will result in underestimation of peak intensity and subsequent overestimation of the width. We addressed this issue by measuring the width of a fit to the peak, rather than the width of the peak itself. In so doing, we avoided the assumption that the peak was centered upon a single pixel.

Following extraction of cone sub-volumes, band 2 thickness was assessed as follows:

1. The 3D linear intensity image of the cone was averaged in both lateral dimensions, yielding a single axial reflectance profile of the cone;

2. Five A-scan pixels containing the peak corresponding to band 2 were extracted. Five pixels (corresponding to 9.25 μm) were selected because it was the largest number of pixels observed never to contain more than one peak, in a small random sample of (~100) cones;

3. These five pixels were used to perform a least-squares fit to a one-dimensional Gaussian function 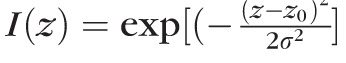. From the fit, the value of σ was determined; and

4. Finally, thickness of band 2, 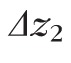(defined as the FWHM of the Gaussian fit), was calculated using the relation .

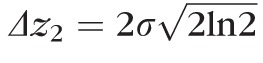To address the second hypothesis, about the relative separations of band 2 from bands 1 and 3, we identified these peaks in the axial reflectance profile of the cone, and measured the distances between them. For this step, no subpixel localization of peaks was performed, all separations are given as multiples of the axial sampling interval (S_z), with accordingly limited precision. Noise associated with whole-pixel localization is a form of discretization noise, and its SD is given by 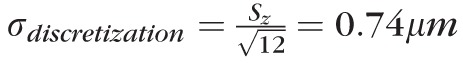. We did not perform subpixel localization because we predicted that this source of variance would be swamped by variance in OS length, a prediction confirmed by the results below.

We performed two kinds of measurements on the data, thickness of individual reflections (designated 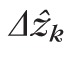for band k) and separations between reflections (designated 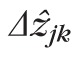for the distance between bands j and k). We use the hat (^) symbol to distinguish an image measurement from the underlying physical thickness (Δz_k) or length (Δz_jk).

Results

Intensity Projections and Topography of Band 2

After segmenting and labeling each A-scan, layers of interest, such as that corresponding to band 2, can be extracted and visualized. Such an areal projection of band 2, extracted from a volume at 5° from S3, is shown in Figure 3 (left). Using this surface projection, the cones can be readily identified (Fig. 3, right), and segmented in three dimensions.

While the intensities of the detected features can be assembled into areal projections of the cone mosaic, the locations, in depth, of those features can be assembled into topographical maps of the bands. Figure 4 shows such a map of the same retinal area shown in Figure 3. Figure 4 (left) shows the topography of the band in the raw acquired volumetric image. Broadly speaking, two sources of relief can be observed: low spatial frequency variations due to macroscopic curvature of the retina and axial eye movements, and high spatial frequency variations due to axial displacements of surface 2 among neighboring cells. By high-pass filtering layer topographies, we were able to extract the cellular variations, shown in Figure 4 (right). The local roughness of the surface, σ_z2 was quantified by computing the SD of the high-pass filtered topography. For surface 2, average roughness 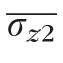was 1.6 μm  ± 0.3 μm over all subjects and eccentricities, with statistically significant dependence on neither subject (P = 0.63) nor eccentricity (P = 0.40). For surface 3, was 3.9 μm at 5° and 5.1 μm at 2°, with a significant difference between the two (P < 0.01). Assuming that band 3 originates from the distal tips of the OS, its relative roughness suggests that variation in OS length is due more to differences among distal-ward OS extent.

Figure 4.

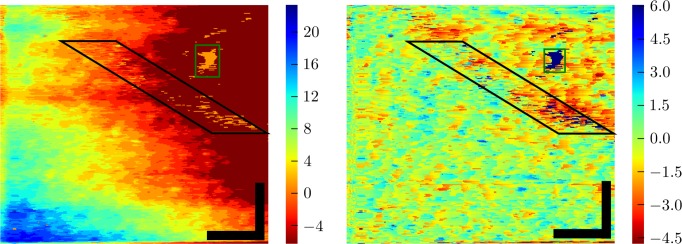
Topography (in μm) of band 2, from S3 at 5°, the same portion of retina shown in Figures 3 and 5. Our custom model-based classification algorithm located the depth of band 2 in the retina automatically (see Appendix). The resulting topography (left) revealed a wide spectrum of height variation. Low frequency variation was due to gross curvature of the retina and axial eye movements. High frequency variation was due to axial displacements among neighboring cone cells, which are more evident after high-pass filtering the topographic image (right). The boxes denote areas with numerous segmentation errors. Those in the black box fall under an intervening blood vessel (visible in Fig. 3), and result from the relatively low reflectance of the underlying cones. Those in the green box are due to a 20-μm region in which cone visibility is poor for an unknown reason (also visible in Fig. 3). Roughness of the high-pass filtered surface was quantified by computing the depth variance along fast scans in the corrected image and taking the square root of the average of those variances. The resulting roughness was 1.6 ± 0.3 μm. Scale bars: 50 μm.

Thickness of Band 2 at the Cellular Level

The cone coordinates and band topographic maps shown in Figures 3 and 4 were used to segment individual cones in 3D. The resulting subvolumes extended axially from ELM to COST, thereby containing the cellular structures responsible for bands 1, 2, and 3. 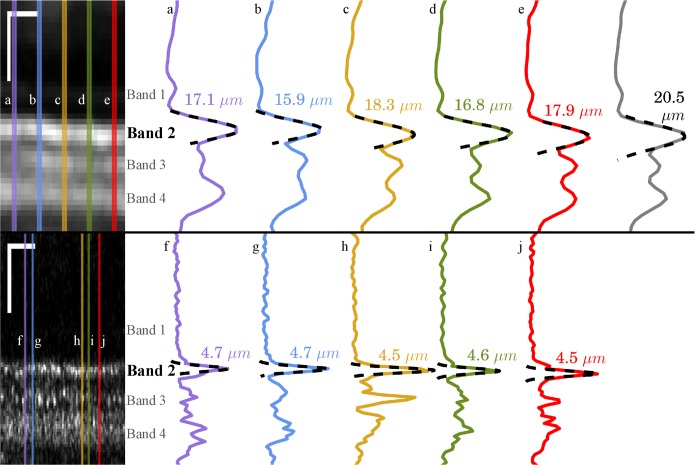For each cell, the thickness of band 2 was quantified by averaging the cell's A-scans together, fitting the band 2 peak with a Gaussian function, and computing the FWHM thickness of the image band 2 ( ) from the resulting smoothed signal. For one subject at the 5.0° eccentricity, we acquired comparable images using a clinical OCT system and estimated band 2 thickness using an identical approach. Figure 5 shows the resulting thickness estimates from both systems. From the small number of profiles shown, it appears that thickness measured with clinical OCT is three to four times greater than that measured using AO-OCT. The thickness estimate from the clinical system is even larger when 10 A-scans (corresponding to 56 μm on the retina) are averaged, as shown by the gray plot shown in the upper right part of Figure 5.

Figure 5.

Band thickness measured with Spectralis OCT and AO-OCT. A 210-μm wide section of a Spectralis B-scan (top left), acquired from S3 at 5.0° and converted to linear intensity scale. The Spectralis instrument permits saving of log-intensity data only; in order to convert to a linear scale, the system's reported dynamic range (43 dB) was used. The overlaid lines indicate the locations of the five A-scans plotted at (top right), labeled a-e. The sixth (gray) plot represents the average of 10 A-scans (56 μm), equal to the size of regions analyzed by other investigators.²⁷ Overlaid on each plot is a least-squares Gaussian fit (dashed line), from which the FWHM of the peak can be readily calculated, indicated for each plotted A-scan. A comparable AO-OCT B-scan (bottom left) from the same subject and eccentricity, also shown in linear scale. Locations for the plotted A-scans (bottom right), labeled f-j, were selected by identifying bright cones in the image. Full-width half maximum values, calculated the same way, were considerably smaller. Note that in both OCT and AO-OCT, averaging over multiple cells leads to an overestimate of layer thickness, due to axial displacements of the reflections. Scale bars: 50 μm.

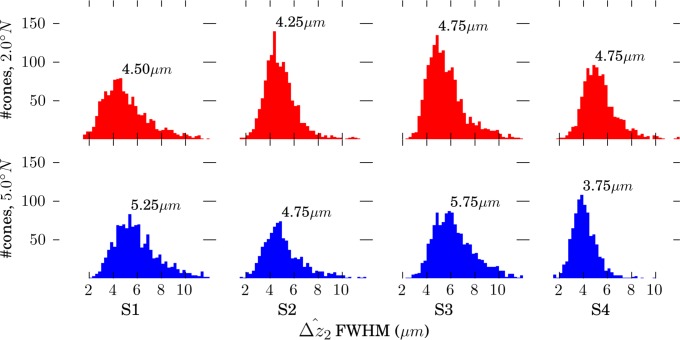
Figure 6 shows measured band 2 thickness ( ) for each of the 9593 cones we studied. Distributions from individual volumes, as well as the overall distribution, were highly positively skewed (γ₁ > 9), with a mode of 4.7 μm, and with 48% of the cones falling between 4.1 and 5.2 μm. No significant difference was found between cells in the fovea and perifovea. In Figure 5, we intentionally selected a representative AO-OCT B-scan, one with 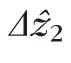values close to the aggregate mode across subjects. As is evident from the distributions in Figure 6, many cones were imaged with smaller 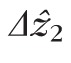, and many others with larger .

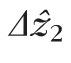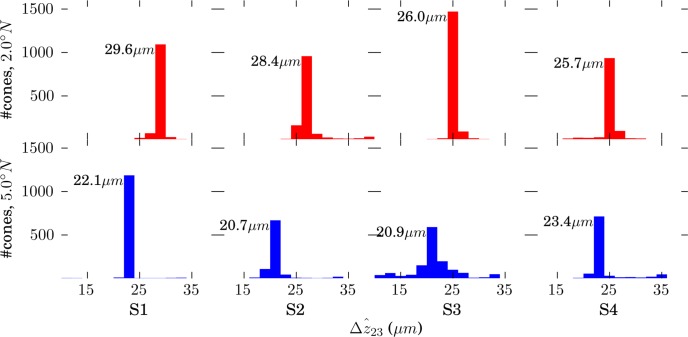
Figure 6.

Distributions of band 2 thickness in four subjects, measured at two retinal eccentricities. Each distribution was binned at 0.25-μm intervals, and mode (fullest bin) thickness is shown for each plot. Mean thickness was 0.5 to 1.5-μm larger than the mode.

Separations of Bands 1, 2, and 3 at the Cellular Level

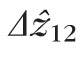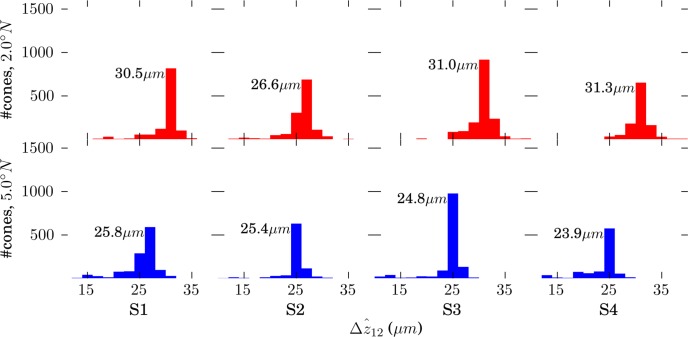
For each cell, the distances between bands 1 and 2 ( ) and between bands 2 and 3 ( 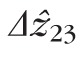) were computed. The resulting lengths for all cones are shown in Figures 7 and 8. Across subjects, average values for 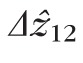and 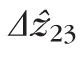were 29.9 and 27.4 μm, respectively, in the fovea, and 25.0 and 21.7 μm, respectively, in the perifovea. In all subjects, a significant eccentricity dependence was found for both 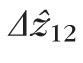and 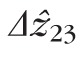, with both being larger at 2.0° than 5.0°. 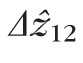was significantly greater than 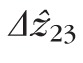, by 2.5 and 3.3 μm at 2.0° and 5.0°, respectively, as shown in Figure 9.

Figure 7.

Distributions of 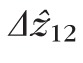, defined by the distance between peak of the band 1 (ELM) reflection and the peak of the band 2 reflection. Because no subpixel fitting of peaks was employed, precision was limited by the 0.74 μm (RMS) axial quantization error.

Figure 8.

Distributions of 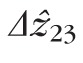, defined by the distance between peak of the band 2 reflection and the peak of the band 3 reflection. Because no subpixel fitting of peaks was employed, precision was limited by the 0.74 μm (RMS) axial quantization error.

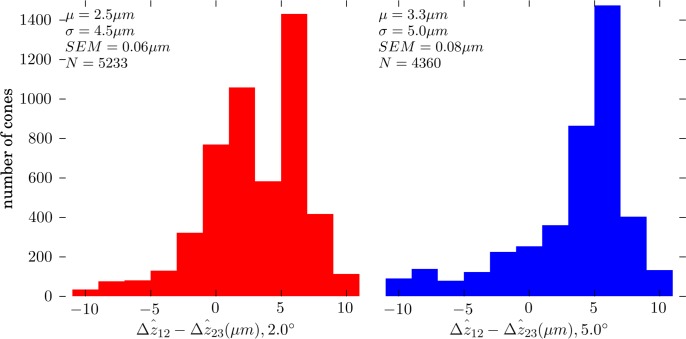
Figure 9.

Distributions of 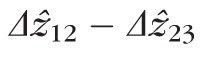at 2.0° (left) and 5.0° (right), for all four subjects. At both eccentricities 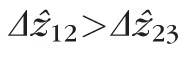for most cones, with average differentials of + 2.5 and + 3.3 μm at 2.0° and 5.0°, respectively. Thus, band 2 lies approximately between band 1 (ELM) and band 3, but slightly closer to the latter.

Discussion

We have presented measurements of several features found in three dimensional AO-OCT images of the cone IS and OS in several thousand cells from each of four healthy volunteers. Our goal has been to study these features at the cellular scale, in order to quantify the cellular contributions to the OCT image. To facilitate interpretation of our findings, we will first summarize what is known about these structures from histologic studies. Second, we will interpret our measurements of band 2 thickness and describe sources of imprecision and noise that may play a role in the observed measurements. Third, we will interpret our measurements of the location of band 2. Finally, we will discuss several other characteristics of the images and outline some paths for future research.

Histology of the Ellipsoid and IS/OS Junction

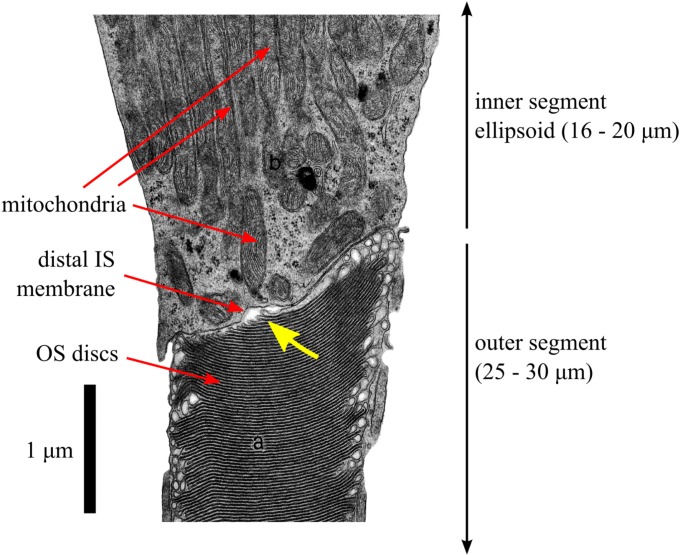
To our knowledge, the proposal²⁷ that ISe is responsible for band 2 represented the first serious, quantitative attempt to determine the band's origin. Prior to that study, it had most often been referred to as the IS/OS junction, but no detailed account had been given of how the structures involved in that junction generate the band. Figure 10 is a high-magnification electron micrograph of the relevant portion of a human cone photoreceptor. This image is consistent with similar images produced by other investigators.^36,37 The region containing distal IS and proximal OS reveals several features. In the fovea and perifovea, the ISe stretches 20 and 16 μm, respectively,²⁷ between the central IS and the distal IS membrane. Due to the sequential addition and extension of membrane on the proximal edge of the OS, the newest discs span a small fraction of the approximately 2-μm OS diameter, and the full diameter of the OS is not reached until the 10th to 15th disc. The resulting surface is optically rough, consisting of approximately 140 nm (~λ/6) steps in double-pass optical path change. This image, and others like it, reveal a thin (50–200 nm) pocket of what may be interstitial fluid between the distal IS membrane and proximal OS tapered disc stack. However, it is not known whether this extracellular space exists in vivo or it is an artifact of electron microscopy preparation and/or imaging.

Figure 10.

An electron micrograph of a partial human cone photoreceptor (reprinted with permission from Hogan MJ, Alvarado JA, Weddell JE. Histology of the Human Eye: An Atlas and Textbook. Philadelphia: Saunders; 1971. Copyright Elsevier; annotations modified).⁸⁰ The image shows portions of the cone IS (top) and OS (bottom). The portion of IS shown is a part of the IS ellipsoid (ISe), densely packed with mitochondria (each ~3-μm long), arranged with their long axes parallel to the optical axis of the cone. In the OS, the stacked discs (~50-nm spacing) are clearly visible. Only a small portion of the ISe and OS fall within the micrograph; at this scale, the segments would each span the entirety of this page. Also visible is the distal membrane of the IS, seen here (and in comparable micrographs from other sources, see text) to lie at an angle to the cell's optical axis. The newest 10 to 15 discs, at the proximal edge of the OS, are narrower than mature discs. The slope of the distal IS membrane is similar to the slope of the proximal edge of the OS. In this image, and others like it, a narrow (50–200 nm) gap is visible between the distal IS membrane and proximal discs of the OS (yellow arrow). It is not known whether this gap is an artifact of tissue preparation for electron microscopy or whether it corresponds to a region of interstitial fluid that separates the IS and OS.

Interpretation of Band 2 Thickness

We found that the thickness of band 2, when measured within cones, the putative origin of the band, was typically 4.7 μm at the eccentricities we studied, as shown in Figure 6. This thickness is inconsistent with attribution of the band to the ISe, known from histology to span 16 to 20 μm at these eccentricities.

Our findings may lend support to alternative hypotheses, but we must first demarcate some valid hypothetical ground. We will begin by describing briefly how the OCT image is formed, then enumerate what we believe to be the main potential sources of error, and finally discuss the resulting bounds placed on physical properties of band 2.

In SD-OCT, an image is formed when light reflected from a surface (i.e., formed by an interface between refractive index-mismatched materials) interferes with light reflected from the reference mirror, generating a single-frequency modulation of the detected k-spectrum and a consequent single peak in the Fourier transform of that spectrum; an image of a complex object is treated as the sum of multiple so-formed images.^38–42 For the sake of clarity here we ignore the presence of speckle, additional structure in the image caused by interference between closely-spaced scatterers within the sample.

The SD-OCT image can be considered a convolution of the OCT system's axial PSF (APSF) and the series of one or more reflectors comprising the object. While the claim²⁷ that the band resulting from imaging a series of reflectors in the retina has a width equal to the square root of the summed squares of the APSF width (R_z) and the axial extent of the series (Δz_ab) is true under certain circumstances (when the reflectors themselves have a Gaussian reflectance distribution with depth or when either R_z or Δz_ab approach zero), it is not generally true. In fact, as Δz_ab increases, 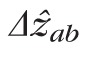approaches Δz_ab + R_z, but as the number of reflectors N_a…b increases, 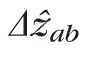approaches Δz_ab. Nevertheless, the quadratic sum approach is a conservative estimate; we may safely state that 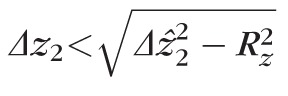. In addition to being a conservative estimate of object extent, this approach also facilitates direct comparison between our results and others.²⁷ Next, we describe a number of potential sources of error in our measurements, and describe how these may further constrain the hypothetical ground.

While the coherence function of the light source and the APSF are related, the latter may be broadened by uncorrected dispersion mismatch between the reference and sample channels of the interferometer. In real retinal OCT systems these are not perfectly matched because the eye, containing dispersive media, is only present in the sample channel. We employed a water vial in the reference channel to create dispersion comparable with that of the eye, but the subject's eye length never matches the vial's length perfectly, and also the dispersion coefficient of water is likely different from those of the various ocular media.⁴³ We corrected residual dispersion mismatch with an automated, numerical algorithm, which resulted in visually better images with higher contrast, but it is not known to what extent residual uncorrected dispersion mismatch contributed to broadening of the system's axial resolution.

A second possible factor is blur. The theoretical lateral resolution (R_x) of our system was 2.5 μm. While this is sufficient for resolving the cones, it is not sufficient for optically isolating them, since the spaces between cells are smaller than R_x. Furthermore, although the AO system indicated diffraction-limited imaging on all subjects, the true optical resolution may have been larger than R_x. A number of factors can cause this discrepancy: delays (inherent in all AO systems) between wavefront error measurement and mirror control; noncommon path aberrations between the sample channel's OCT and SHWS arms; and imperfect focusing. In addition to optical blur, eye movements during fixation may cause motion blur. Blur is an important consideration because in neighboring cells with axially displaced bands 2, blur would broaden the peaks associated with each band. Effectively, in the presence of optical and motion blur, band 2 roughness (σ_z2) makes a contribution to 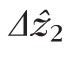. The thicker (≥15.9 μm; Fig. 5) appearance of band 2 in clinical OCT images is likely due, in part, to blurring together of axially displaced features (Fig. 4), compounded by averaging of large numbers of imperfectly registered B-scans.

A third possible factor is discretization error. Because the A-scans attributed to individual cones were averaged prior to Gaussian fitting of the band 2 peak, subpixel variation in the location of band 2 among A-scans makes a contribution to the breadth of the peak. We initially attempted to avoid this error by performing Gaussian fits to individual segmented A-scans, but found that this approach led to unacceptably large residual fitting errors and subsequently high variance in thickness measurements, presumably due to speckle and shot noise.

The potential sources of error described above all lead to overestimates of Δz₂. To our knowledge, the only source of error that could cause an underestimate is calibration error. Our calibration procedure and empirical validation (see Appendix) suggest that miscalibration was not a significant source of error, resulting in no more than 17 nm of uncertainty per 2.55-μm pixel (0.67%). Thus, we believe that our measurements are more likely to lead to overestimates of Δz₂, rather than underestimates. To describe the central tendency of 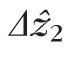, we reported the modal value of its distribution, 4.7 μm. The mode of the distribution was clearly visible, owing to the large number of cells studied. If, however, the sources of error are all positive (tending to increase measured values), and if the variance of the distributions of 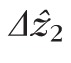is due to noise rather than structural variance, the smallest values we observed (2–2.5 μm in most volumes) might be better representative of .

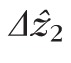The bright, specular reflection observed in the center of the fovea is sometimes used to estimate the OCT system's true axial PSF,^44,45 since it includes the effects of dispersion mismatch. This approach typically yields values 25% to 50% higher than what is expected theoretically. We measured the foveal reflex, in one subject, to have a FWHM width of 3.1 μm, 50% higher than expected. The factors above may have contributed to the difference between this value and the theoretical value of R_z. If we use this measured estimate of the system's axial PSF, and perform the quadratic subtraction described above, the resulting axial extent of band 2's constituent interfaces is 3.5 μm, strongly suggesting that the band does not originate from ISe. In fact, in the 9593 cells we imaged, none had a band 2 broad enough to have originated from the entire ISe.

Finally, we may conclude that band 2 is generated by one or more interfaces typically spanning a distance of 3.5 μm, and that this estimate itself may be inflated by (1) broadening of the APSF by dispersion mismatch, (2) smearing of the peak by optical blur and surface roughness, (3) smearing of the peak by subpixel motion of the surface, and (4) applying a conservative method of reconstructing object thickness. From histologic images of the IS and OS, it appears that the only two distinct interfaces separated by less than 3.5 μm are the distal IS membrane and the proximal OS membrane.

Phase-sensitive measurements of OS length have shown that the SD of OS length (the distance from band 2 to band 3) among A-scans of a single cone is 45 nm.⁴⁶ This variation could be due to roughness of the two bands of the OS, or to phase noise (the manifestation of shot noise in the phase domain). Phase noise can be estimated from the signal-to-noise ratio (SNR) of the intensity image.⁴⁷ We reanalyzed some data from an earlier study⁴⁶ in order to estimate the SNR from a subset of the originally analyzed cells and found an average SNR of 6.9, giving a predicted phase noise of approximately 31-nm RMS in each reflection. If we assume both surfaces of the OS contribute equally to the noise, the total noise is expected to be 44 nm, nearly equal to the 45 nm that was observed. This suggests that a negligible amount of the phase variance originated from axial extent or roughness of the surfaces, which in turn suggests that they are thin reflectors or interfaces.

The proximal surface of OS is rough, owing to the stepped, comb-like projections of OS discs (Fig. 10, between the yellow arrow's tip and the left edge of the OS). This rough surface is likely to generate more phase variance than the relatively flat distal surface of IS, which suggests that the latter is more likely the origin of the reflection than the former.

Interpretation of Band 2 Position

From histologic images it is known that the IS and OS of cones in the fovea are approximately equal (34 and 35 μm, respectively²⁷). Given the expected 20-μm axial extent of the ellipsoid region, we would expect to see a signal originating from that structure substantially (20 μm) closer to band 1 (ELM) than band 3 (COST). This is not what we observed. Figures 7, 8, and 9 show that in the fovea, band 2 is closer to band 3 than band 1, and that this difference becomes larger in the perifovea. Thus, the relative location of band 2, when resolved within single cells, is inconsistent with the inner segment ellipsoid. By contrast, it is consistent with the junction between IS and OS, which lies slightly closer to COST than ELM at 2° and grows relatively closer to COST with increasing retinal eccentricity, as OSs become shorter.²⁶

Other Objections to the IS/OS Attribution

Another argument²⁷ made against the IS/OS attribution is that a reflection as apparently bright as that of band 2 could not arise from the refractive index mismatch between IS and OS (n_IS = 1.394, n_OS = 1.39, Δn = 0.004), which would result in a reflectivity of 0.00021%. A structure with reflectivity of 0.00021% requires 57 dB of sensitivity to observe, a number well within the theoretical and measured sensitivities of SD-OCT systems.^40,42 A comparable SD-OCT system was measured to have a sensitivity of 98.4 dB,⁴⁸ sufficient for detecting reflections more than 14,000 times less reflective than IS/OS. In addition, this calculation depends on precise knowledge of the aforementioned refractive indices, as well as the possible role played by interstitial fluid (n ≈ 1.33) or interphotoreceptor matrix⁴⁹ between the IS and OS, none of which have been measured in the intact, living retina.

If we consider the junction between the IS and OS to be analogous to the coupling of two optical fibers with different geometric and optical properties, we may also consider the possibility that some of the reflected light may be due to fiber transmission mode mismatch,⁵⁰ reflection of light from IS that fails to couple into OS. This would occur, for instance, if the IS supports multiple waveguide modes while the OS supports just one. Such mode mismatch, if it exists, would serve to further brighten the reflection from IS/OS. This is an admittedly speculative idea, and also begs the question of the anatomical origin of the reflection by assuming it originates at IS/OS, but may nevertheless be of interest to future investigators.

Characteristics of Other Outer Retinal Bands

The purpose of this investigation was to present a novel characterization of the axial (or longitudinal) structure of the outer retina, based on measuring this structure within individual cells. While the original results presented here bear, for the most part, on characteristics of band 2, they are closely related to characteristics of bands 1 and 3 as well. Here, we will briefly review some of the relevant studies of the microscopic structure of these bands, in order to provide an overview of the role played by photoreceptors in generating the OCT outer retinal bands.

Band 1.

As described in the Introduction, the first bright outer retinal band was initially attributed to the external limiting membrane (ELM). The ELM consists of a network of adherens junctions among Müller cells and photoreceptors. These junctions are themselves complex, consisting of cytoskeletal, transmembrane, and extracellular components, which together connect the membranes of adjacent cells. They are thought to form bands (zonulae adherens) around the photoreceptors and Müller cells,⁵¹ providing nearly continuous anchoring between the cells. While the ELM is not a true membrane, it has been shown to block diffusion of large (>3.6 nm) molecules.⁵²

A distinct first outer retinal band was initially visualized using ultrahigh resolution OCT,¹³ and thereafter attributed to ELM.¹⁴ Commercial SD-OCT systems now have sufficient resolution and sensitivity for visualizing ELM, and ELM changes have been associated with a number of retinal pathologies: AMD,^53,54 geographic atrophy,⁵⁵ macular hole,⁵⁶ and edema subsequent to diabetic retinopathy.⁵⁷ As with the other outer retinal bands, little work has been done to confirm the anatomical origin of the band, though some anecdotal findings have been shown. Using AO-OCT in two human subjects, the en face projection of ELM was shown to be inversely correlated with the en face projections of IS/OS and COST (Jonnal RJ, et al. IOVS 2012;53:ARVO E-Abstract 5601), which is consistent with the interpretation that light is scattered from the junctional complexes at the perimeters of the ISs but transmits through their cores. Also using AO-OCT, in one subject, at 6° in the temporal retina, the ELM was clearly shown to consist of two distinct reflective bands, separated in depth by no more than a few microns (Zawadzki RJ, et al. IOVS 2012; 53:ISIE E-Abstract 12). The bands were not distinguishable using a commercial device.

Band 3.

As with band 2, there is some disagreement over the origin of band 3, variously attributed to OS tips,²⁴ contact cylinders,²⁷ and interdigitation zone (IZ).²⁸ Investigators using AO-OCT initially identified the band²³ and showed it to have, in en face view, a periodic, quasi-hexagonally tiled structure highly correlated with the mosaic originating from IS/OS,²⁴ as is clearly visible in the en face projections of bands 2 and 3 in Figure 2. This finding suggests a common cellular (or subcellular) origin for bands 2 and 3.

The OS, consisting of a stack of regularly-spaced membranous disks, is optically homogeneous. Thus, without positing an additional reflective surface located somewhere between the IS/OS junction and the OS tips, the most proximal plausible source of band 3 is COST. A small minority of cones, however, do exhibit extra reflections between bands 2 and 3, and these are observed to move distally as the OS discs renew.⁵⁸

Conventional (non-AO) OCT has been used to show that the Stiles-Crawford directionality (ρ) of the band 3 reflection is greater than that of band 2, and that both are significantly wave guided,⁵⁹ which suggests that light responsible for band 3 passes through the OS and not, for instance, between the OSs of neighboring cells. Some investigators have speculated that band 3 might originate from light scattered from melanin in the RPE, but OCT images of subjects with albinism^60–62 show the presence of band 3, which suggests that melanin may not play an important role in its genesis.

These findings lead to a pair of hypothetical origins for band 3. It may (1) originate at the posterior tip of the OS, or (2) originate more distally (in the RPE, for instance) but consist of light that is scattered from distal tissue and recoupled into the OS waveguide. These hypotheses are consistent with the observation (Fig. 2) that light from bands 2 and 3 is largely confined, laterally, to the interior of the cones. Thus, while ‘contact cylinder' and ‘IZ' may correctly name the axial region of the band 3's origin, those terms are misleading as to the lateral origin, which appears to be intracellular.

Two additional observations implicate the tips of the OSs as the origin of band 3. First, the small RMS (45 nm) in phase difference between bands 2 and 3⁴⁶ suggests that the surface responsible for band 3 is flat (e.g., a single interface or reflector). Second, the observation that this phase difference changes as the OS continually renews dics⁶³ suggests that the band 3 reflection originates at something that moves smoothly away from band 2, such as the end of the OS.

Conclusions

On the basis of the present findings, we suggest that the proposed ascription of band 2 to the ISe is unwarranted. In addition, because of the reinterpretation of outer retinal structure implied by the term “ellipsoid,” we suggest that the recent nomenclatural shift to “EZ” is unjustified. The thickness and location of the band, as measured within single cells, support the hypothesis that the band originates from one or more reflectors constituting some aspect of the IS/OS junction. The axial extents of the structures immediately adjacent to IS/OS (ISe and OS) are both significantly larger than the observed thickness of the band, demonstrating that neither of those, in its entirety, is responsible for it. The present findings are consistent with nomenclature designating any intracellular structures that span no more than 3.5 μm and lie slightly closer to the COST than ELM (e.g., “IS/OS junction,” “IS tips,” “connecting cilium,” “proximal OS margin,” etc.).

Thus far, some investigators adopting the new nomenclature have acknowledged the current state of uncertainty.⁶⁴ However, continued use of the terms ISe and EZ may cause future investigators to ascribe disruptions in it to mitochondrial atrophy or dysfunction, which could be profoundly misleading. This is not to say that ellipsoid changes could not manifest as visible disruptions in band 2, by, for instance, altering ellipsoid refractive index or the morphology of the distal IS membrane, but rather that such disruptions do not necessarily implicate changes in the ellipsoid.

The choice of terminology also significantly impacts interpretation of past work. Ascription of band 2 to ISe would require serious revision (or rejection) of a number of findings: in vivo functional imaging of the retina,^65–68 measurements of OS disc renewal,^46,63 morphological characterization of the outer retina,²⁶ and numerous studies of outer retinal disease.^69–77

Numerous fertile areas of investigation remain. The quantitative characterization of band 2 presented here narrows the scope of hypotheses as to the band's origin, but the question is not completely settled. Additional studies, perhaps consisting of further comparisons of histology and OCT images, would be necessary to determine with certainty the band's origin. Another facet of the question concerns the differences between AO-OCT images and commercial OCT images. Both bands 2 and 3 are substantially broader in clinical OCT images. This difference may be partly due to the longer coherence length of the commercial systems, but there may be other factors as well, such as spectral shaping, filtering, and image averaging, the effects of which are not completely understood. A better understanding of the causes of difference would permit more accurate interpretation of commercial OCT images, which would serve the clinical and research communities well. Adaptive optics SD-OCT offers better lateral resolution than SD-OCT, which permits study of retinal structure (and function) at the cellular scale. The latter, however, is much more widely used, deployed in thousands of clinical and research settings, and permits more rapid and comprehensive screening of greater numbers of patients and experimental subjects. As such, accurate interpretation of commercial SD-OCT images is of utmost importance.

Appendix: Data Processing and Instrument Calibration

Numerical Dispersion Compensation in OCT

While a water cuvette in the reference channel compensated for the bulk of chromatic dispersion due to the eye, variations among eye lengths made this compensation imperfect. Residual dispersion was compensated numerically. First, the Hilbert transformation of the spectrum was computed, giving a zero-phase phasor A(k)e⁰. Next, a unity-amplitude phasor was generated, e^−iθ, with θ = ak³ + bk². The coefficients a and b were automatically chosen using optimization of an objective function on image quality, which depends upon residual dispersion mismatch. The product of these two functions, A(k)e^−iθ was the dispersion-corrected, k-space spectrum.

Calibration

The main goals of this paper, measurement of the axial extent of band 2 and its relative proximity to bands 1 and 3, depend upon careful calibration of the OCT system's axial scale (i.e., the factor S_z relating pixel spacing in the A-scan with optical path lengths in the eye). This factor can be theoretically determined from characteristics of the spectrometer, as follows.

Let N be the number of pixels on the detector, with λ₁ and λ_N representing the wavelengths present on the first and N^th pixels of the detector, respectively. Note that λ₁ and λ_N are functions of just the spectrometer optics, diffraction grating, and sensor, and are independent of the source's actual spectrum. The corresponding wave numbers, in units of m⁻¹ are given by k₁ = 1/λ₁ and k_N = 1/λ_N. We can calculate the wavelength sampling interval δλ = [λ_N − λ₁]/N, and the wave number sampling interval δk = [k₁ − k_N]/N. From the definitions of k₁ and k_N, it follows that the wave number sampling interval is given by 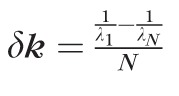, in units of m⁻¹pixel⁻¹.

Let F[S(k)] be the discrete Fourier transformation of S(k) and F[S(k)][j] represent the j^th bin of the transformation. For an N-point signal in k-space, S(k), sampled at intervals of δk (or with a sampling frequency of 1/δk), the j^th bin of F[S(k)] contains the signal's power at a frequency of (j/N)(1/δk). Thus, for signals in k-space, F[S(k)] has units of physical length, m; since the A-scan is the DFT of the k-mapped spectrum, its pixels correspond to depths in the sample.

Considering the doubling of optical path length due to the double pass of the OCT beam through the sample, as well as the refractive index n of the sample, the physical length corresponding to a single pixel is described by:

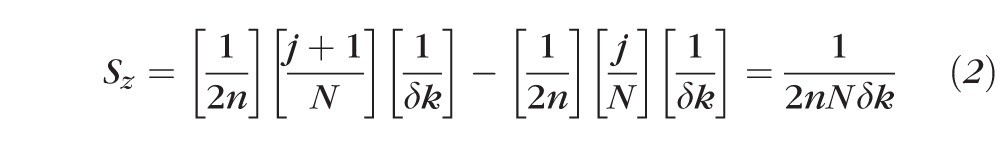Substituting our definition of δk into this equation, we get

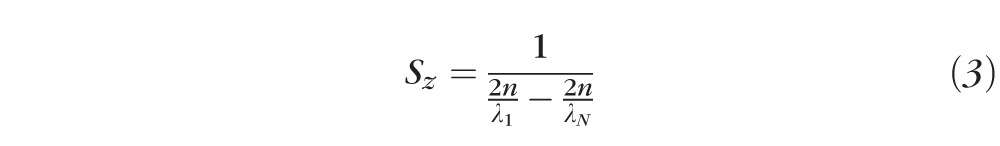where n is the refractive index of the tissue and [λ₁, λ_N] is the spectral range interrogated by the spectrometer. The equation for S_z has some interesting consequences. For instance, the depth corresponding to a single pixel is independent of the number of pixels in the spectrometer. Also, because λ₁ and λ_N are independent of the source spectrum, S_z is as well. Thus, S_z is distinct from the coherence length of the system given by 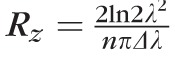. R_z is equivalent to the coherence function FWHM, or axial PSF. S_z depends only on characteristics of the spectrometer, whereas R_z depends only on characteristics of the light source. Both depend on the refractive index of the retina n, which is assumed here to be 1.38

We performed two independent calibration procedures for the depth scale of the OCT system, one in the spectral domain and another in the spatial domain. First, we coupled a mercury-argon calibration lamp (HG-1, Ocean Optics, Inc., Dunedin, FL, USA) into the spectrometer channel. The source has five peaks at known wavelengths. By determining the location (on the detector) of each of these peaks, we were able to fit a linear function to those wavelengths. Spectrometers, in general, are not linear; because we employed an F-theta lens in our spectrometer, linear approximation was sufficient. Using the linear fit we were able to extrapolate the values of λ₁ and λ_N, 775 and 913 nm, respectively, and a wavelength function on pixel number x of λ(x) = 6.8 × 10⁻¹¹x + 775 × 10⁻⁹. The experimental value of δλ, described above, can be seen in this equation (6.8 × 10^− 11m). Calculating S_z from experimentally determined values of λ₁ and λ_N yielded a value of 2.55 μm in air, or 1.85 μm in the retina.

The precision of this estimate is limited by the number of calibration lines produced by the source and the precision with which these can be localized on the detector. The five peaks generated by the calibration lamp had FWHM widths of 30 pixels, at most, corresponding to 2-nm FWHM of spectral bandwidth. If, conservatively, we assume peak localization error equal to the peak width (σ_peak = 2 nm), error propagation through the equation for S_z gives an axial scale uncertainty σ_Sz = 17 nm, less than 1% of S_z. This value was calculated and confirmed using a Monte Carlo simulation.

To confirm the value of S_z in the spatial domain, we placed a mirror in the sample channel and systematically varied the optical path difference between it and the reference mirror, using a calibrated micrometer stage. We observed that physical displacements of 2.63 μm corresponded to single pixel displacements in the OCT B-scan of the mirror. Thus, an error of less than 3% was found between the two calibration approaches. In the second calibration method the sources of error (precision and accuracy of the micrometer translation stage, dispersion mismatch between sample and reference arms, roughness of the glass slide) were more numerous and more difficult to characterize. As such, we preferred the result of the lamp calibration step, S_z = 2.55 μm, which corresponds to 1.85 μm in the eye. This is the value we use throughout the present analysis.

Cone Identification and Segmentation

Automated identification of cones started with bandpass filtering of the en face cone mosaic projection. The passband of the filter was based on published reports of cone spacing⁷⁸ as well as the observed density in acquired images. After filtering the image, horizontal and vertical gradients were computed and the negative-slope zero crossings were identified in both gradients. The intersection of the horizontal zero-crossings and vertical zero-crossings represent the coordinates of the cones. The only free parameter in the algorithm was the width of the passband. Increasing and decreasing its width improves detection sensitivity and specificity, respectively. We chose a relatively narrow initial passband (±10% of the expected cone row-row spacing, 57 and 42 cyc/deg, respectively, at 2° and 5°), narrowing it further until the resulting cone count corresponded to less than or equal to 80% of the expected cone density. This approach was motivated by our goal of achieving high specificity for cones, but it did not rule out spurious inclusion of rods (blurred together by the filter). It has been shown that the outer segment tips of cones and rods lie at different depths in the outer retina, and that COST and ROST are not visible in the same en face slices of AO-OCT volumes.^32,79 We used this axial displacement by checking the automatically identified cone locations in the COST projection of one volume (S3, 5°, shown in Fig. 3), verifying that all of the identified cones were located on the bright cone outer segment tips, and not in the intervening dark areas (where the ROS passes the COST), providing further evidence that rods were not confounding the cone identification algorithm, and that the algorithm was sufficiently specific.

Once the center of the cone was identified, surrounding pixels were assigned to the cone on the bases of their proximity and intensity. On average, a 10.8-μm² area (22 pixels) was included per cone. Once the cone's A-scans were identified, these were labeled using a model-based classifier. In short, a model of each retinal eccentricity was developed by aligning and averaging all the A-scans in a given volume and using an attribute tree to identify and label the outer retinal layers. Individual A-scans were cross-correlated with the labeled model, and the regions of the cone profile corresponding to each label were searched for statistically significant peaks. If all four outer retinal bands were located, the A-scan was used in the analysis. Fewer than 20% of the A-scans were excluded on this basis--a number made small, perhaps, by the specificity-tuned identification algorithm. The labeled, aligned A-scans constituting a single cone were then averaged and submitted to further quantitative analysis, described in the Methods section.