Using instrumental variables to estimate a Cox's proportional hazards regression subject to additive confounding

Abstract

The estimation of treatment effects is one of the primary goals of statistics in medicine. Estimation based on observational studies is subject to confounding. Statistical methods for controlling bias due to confounding include regression adjustment, propensity scores and inverse probability weighted estimators. These methods require that all confounders are recorded in the data. The method of instrumental variables (IVs) can eliminate bias in observational studies even in the absence of information on confounders. We propose a method for integrating IVs within the framework of Cox's proportional hazards model and demonstrate the conditions under which it recovers the causal effect of treatment. The methodology is based on the approximate orthogonality of an instrument with unobserved confounders among those at risk. We derive an estimator as the solution to an estimating equation that resembles the score equation of the partial likelihood in much the same way as the traditional IV estimator resembles the normal equations. To justify this IV estimator for a Cox model we perform simulations to evaluate its operating characteristics. Finally, we apply the estimator to an observational study of the effect of coronary catheterization on survival.

1 Introduction

Observational studies are subject to confounding by variables that have nonzero effects on both the treatment and the endpoint. The presence of confounding is one of the major reasons for biased estimates of the effects of treatments. This bias may be removed or ameliorated by accounting for the confounding variables in an appropriate statistical model, a process known as “adjustment”, or by using various forms of propensity score analysis (e.g., stratifying, matching, weighting). Nevertheless, bias reduction by adjustment, propensity scores or inverse probability weighting (Curtis et al. 2007; Hernan and Robins 2006; Hirano and Imbens 2001) is only possible for confounders that are known and recorded. Omitted confounders will bias estimation.

Instrumental variable (IV) methodology is an approach developed in the econometrics and statistics literature that has been used increasingly in health services research, outcomes research, and epidemiology over the past two decades (Greenland 2000; Hernan and Robins 2006; Newhouse and McClellan 1998; Stukel et al. 2007; Wooldridge 2002). If a genotype is used as an IV, the method is referred to as Mendelian randomization (Thanassoulis and O'Donnell 2009). The IV approach can yield unbiased estimates of the association of treatments and outcomes despite the presence of omitted confounding variables.

The method of IVs was demonstrated and contrasted to the methods of adjustment and propensity scores by Stukel et al. (2007) in a paper exploring the effect of invasive management following acute myocardial infarction on survival by using a dataset that linked Medicare claims data to a chart review of 122,124 patients. They found using IVs that invasive cardiac management reduced the mortality rate by 16 %, whereas adjustment (by Cox's model) and propensity scores yielded estimates of 49 and 46 %, respectively. Stukel et al.'s (2007) IV based estimate of mortality reduction was much closer to the estimates obtained in randomized clinical studies of 8–21 %. An unsatisfactory feature of the analysis performed in Stukel et al. (2007) is that the hazard rate was not directly modeled, which led to the use of ad hoc transformations, and begs the question of whether an IV procedure can be formulated for hazard ratios or more generally for estimation of a Cox survival model.

The use of IVs in generalized linear models is described by Wooldridge (2002, p. 427). Two distinct approaches have been taken to incorporating instruments into logistic regression models: 1, two stage methods and 2, orthogonality of the instrument and the residuals. The former is an extension of two stage least squares from the linear model setting (Vansteelandt et al. 2011). The first stage is the linear regression of the treatment onto the instrument, from which the predicted values are saved. The second step is the logistic regression of the dependent variable on this predicted value, and possibly the residuals from the previous linear regression (Vansteelandt et al. 2011). The second approach to incorporating instruments into logistic regression consists of estimating equations that assume orthogonality of the instrument with the difference between the observed and expected value of the binary dependent variable. That is, it solves the zero of the sum of the product obtained by multiplying the instrument by the difference of the dependent variable with its expected value. This method has been proposed by Foster (1997), Johnston et al. (2008) and Rassen et al. (2009). These latter approaches yield consistent estimates if the omitted covariates have additive effects on the expected value of the endpoint. In contrast, the non-omitted covariates are modelled using the link function (e.g. logit).

In Stukel et al. (2007), an ad hoc approach to IVs was used in which the endpoint was defined as death by a fixed time point (they considered both 1 and 4 years). The effect of the treatment on this binary endpoint was estimated using IVs for linear models. The resulting risk difference estimate was transformed to approximate the hazard ratio using a formula to relate risk differences to risk ratios. A two stage approach is used to estimate a hazard ratio in Carslake et al. (2012). Brannas (2001) has proposed IV estimation of the parameters of the Buckley-James regression model (Buckley and James 1979). Bijwaard (2008) has proposed an approach to using IVs in both proportional hazards models with piecewise constant baseline hazards and accelerated failure time models based on linear rank statistics and applied this method in Bijwaard and Ridder (2005). Related work dealing with estimation of the causal effect in randomized studies has been done by Robins and Tsiatis (1991) and Baker (1998).

In survival analysis, the overwhelmingly most prevalent regression technique is Cox's model. Yet none of the above IV approaches are designed for the Cox model. Therefore, in this paper we propose a method for estimating the hazard ratio without parameterizing the baseline hazard, as with Cox's model, using an IV. The method we develop extends the approach of instrument-residual orthogonality to the hazard ratio setting to obtain estimating equations that resemble the partial likelihood score equations. The method is approximate and limited to a particular causal model. However, it performs very well in simulations and outperforms the standard Cox model when the model does not hold, thus demonstrating robustness. The method is illustrated in an example estimating the effect of coronary catheterization on survival.

2 The setting

Let T̃ denote the time-to-event (survival time), and let X denote the assigned treatment (or treatments) of interest for an individual. For the purpose of specifying causal models and effects, we let T̃(x) denote the potential survival time that would have been observed in the absence of censoring had (possibly contrary to fact) the treatment been x, where x is a possible value of X, and with all other variables held fixed. In practice, we observe T = T(X) = min(T̃(X), C) and Δ = Δ(X) = 1(T̃(X) ≤ C), where C is the potential censoring time.

2.1 A treatment and covariate model that integrates to Cox's proportional hazards model for the treatment

Suppose U is a covariate on which T(x) depends. We first suppose that the data generating process or causal model is coherent with the Cox model except for an additive departure from proportional hazards. Specifically, the causal model is given by

$$Pr[\stackrel{\sim }{T}(x)=t|\stackrel{\sim }{T}(x)\ge t,U=u]=\lambda (t;x|u)={\lambda }_0(t)exp(\beta \prime x)+h(u,t),$$ (1)

where the additive part h(U, t) is subject to the constraint E[h(U, t)|T̃(x) ≥ t]=0 for all x. This model has the following desirable property: If the treatment X is applied independently of the covariate U then the conditional distribution of T(X) given X = x is a proportional hazards model. In other words, the marginal distribution of T(x) (obtained by integrating with respect to the U) is a proportional hazards model

$$Pr[\stackrel{\sim }{T}(x)=t|\stackrel{\sim }{T}(x)\ge t]=\lambda (t;x)={\lambda }_0(t)exp(\beta \prime x).$$ (2)

Therefore the parameter β in model (1) can be interpreted as the log of the population average hazard ratio corresponding to a unit change in x. The challenge addressed in this paper is the estimation of β when the variable U is not measured.

2.2 Omitted covariates

If a covariate U is unobserved we refer to it as an omitted covariate. If the treatment X is applied independently of U then it is possible to estimate the parameter β in (1) consistently using the maximum partial likelihood estimator (MPLE, Cox, 1972). If U is a cause of both X and T̃(x) for any x, it is called an omitted confounder. MPLE will not be consistent if omitted confounders are present.

2.3 IV assumptions

To facilitate causal inference about β we introduce an IV, W, defined as follows:

Assumption 1 The instrument W affects X.

Assumption 2 The instrument W has no effect on T except through its effect on X. In particular, (a) W and T are independent conditional on X and (b) W is independent of U or any other variable that affects T.

Because censoring is a component of time-to-event studies, we need one more assumption:

Assumption 3 The censoring time, C, satisfies E[Wh(U, t)|T(X) ≥ t, C ≥ t] = E[Wh(U, t)|T(X) ≥ t]. A sufficient condition is the independence of C with ({T(x)}_x∈R(X), U, W), where R(X) is the set of potential treatments and {T(x)}_x∈R(X) is the set of potential event times (survival or censoring) for an individual.

2.4 Key property

Our construction of an IV estimator for the marginal hazard ratio relies on the assumption that the omitted covariate has an additive effect as specified in Model (1), as will become evident in the next section. Moreover the additive term is assumed to satisfy the property E[h(U, t)|T̃(x) ≥ t]=0. This mean-zero property guarantees that the marginal distribution of T̃(x) with respect to x is a proportional hazards model with hazard ratio exp(β), as shown in the Appendix 1. The Appendix 1 also proves that one choice for h(U, t) is A(t)U + ln mgf_U[−A(t)], for any function A(t) where mgf_U is the moment generating function of U.

An important practical consideration is that if E[h(U, t)|T̃(x) ≥ t]=0 then it is not necessary to specify h(U, t). Therefore, the availability of a valid IV allows the Cox model to only have to hold up to an additive (mean-zero) function of an omitted confounder and time in order for a causal estimator of the effect of treatment to be available.

3 Estimating equation

In this section we derive an estimating equation for the parameter β of (1) and (2) based on n independent and identically distributed observations ${\{T_i,{\Delta }_i,X_i,W_i\}}_{i=1}^n$ that we argue is approximately consistent even if there is omitted confounding. We now define Y_i{t) = 1(T_i ≥ t) and N_i(t) = 1(T_i ≤ t, Δ_i = 1).

The estimating equation we shall derive closely resembles the score equation based on the partial likelihood for Cox's proportional hazards model.

3.1 Motivation of the estimating equation using risk sets

We use the risk set paradigm to motivate our estimator, as used in Cox (1972). Suppose there is an event at time t. Consider all subjects at risk just before time t; i.e., all those for whom Y_j(t) = 1. According to our model the hazard of an event at time t for such an individual is exp[βx_j] + h(U_j, t). Given that an event occurs at time t the probability that it occurs in a particular subject, i, is that individual's hazard divided by the sum of the hazard of all subjects at risk at time t

$$\begin{array}{ll}{p}_i(t)\hfill & =\frac{{\lambda }_0(t)exp(\beta \prime X_i)+h(U_i,t)}{{\sum }_{Y_j(t)=1}{\lambda }_0(t)exp(\beta \prime X_j)+h(U_j,t)}\hfill \\ \hfill & =\frac{{\lambda }_0(t)exp(\beta \prime X_i)+h(U_i,t)}{{\sum }_{Y_j(t)=1}{\lambda }_0(t)exp(\beta \prime X_j)+{\sum }_{Y_j(t)=1}h(U_j,t)}\hfill \end{array}$$

The second term in the denominator ${\sum }_{Y_j(t)=1}h(U_j,t)$ is o(1) because of Assumption 1 and therefore neglible compared to ${\sum }_{Y_j(t)=1}{\lambda }_0(t)exp(\beta \prime X_j)$, which is o(n). It follows that

$$p_i(t)\approx \frac{{\lambda }_0(t)exp(\beta \prime X_i)+h(U_i,t)}{{\sum }_{Y_j(t)=1}{\lambda }_0(t)exp(\beta \prime X_j)}=\frac{exp(\beta \prime X_i)+h(U_i,t)/{\lambda }_0(t)}{{\sum }_{Y_j(t)=1}exp(\beta \prime X_j)}.$$ (3)

The expected value of W in the subject incurring an event at time t given those at risk just before time t is ${\sum }_{Y_j(t)=1}{W}_j{p}_j(t)$. Using (3) this expression is approximately equal to

$$\sum _{Y_j(t)=1}{W}_i\frac{exp(\beta \prime X_i)+h(U_i,t)/{\lambda }_0(t)}{{\sum }_{Y_j(t)=1}exp(\beta \prime X_j)}=\frac{{\sum }_{Y_j(t)=1}{W}_{i}exp(\beta \prime X_i)}{{\sum }_{Y_j(t)=1}exp(\beta \prime X_j)}+\frac{{\sum }_{Y_j(t)=1}{W}_{i}h(U_i,t)}{{\lambda }_0(t){\sum }_{Y_j(t)=1}exp(\beta \prime X_j)}$$

The numerator of the second term on the right has expected value E[Wh(U, t)| T(X) ≥ t, C ≥ t] which by Assumption 3 is equal to

$$\begin{array}{l}\mathrm{E}[\mathit{\text{Wh}}(U,t)|T(X)\ge t]\hfill \\ =\text{Cov}[W,h(U,t)|T(X)\ge t]+\mathrm{E}[W|T(X)\ge t]\mathrm{E}[h(U,t)|T(X)\ge t]\hfill \\ =\text{Cov}[W,h(U,t)|T(X)\ge t].\hfill \end{array}$$ (4)

The latter equation uses the mean-zero property E[h(U, t)|T(X) ≥ t]=0 assumed as part of model (1).

By Assumption 2, the instrument W and the omitted covariate U are independent, implying that Cov[W, h(U, t)] = 0. It is not the case that the last term of (4), Cov[W, h(U, t)|T(X) ≥ t], is necessarily equal to zero. Because X is affected by W and U conditioning on the event T(X) ≥ t induces lack of independence between W and U (Hernan et al. 2004; Cole et al. 2010). However, we propose that this covariance is approximately zero especially for smaller values of t (e.g. independence at t = 0). Therefore, it follows that the expected value of the IV in the subject having an event at time t given those at risk at time t is approximately $\frac{{\sum }_{Y_j(t)=1}{W}_{i}exp(\beta \prime X_i)}{{\sum }_{Y_j(t)=1}exp(\beta \prime X_j)}$. If we let t₍₁₎ ≤ t₍₂₎, …, t_(n) be the sorted values of the observed event or censoring times it follows that

$$g(\beta )\approx \sum _{i=1}^n{\delta }_{(i)}[W_{(i)}-\frac{{\sum }_{j\varepsilon R_{(i)}}{W}_{j}exp(\beta \prime X_j)}{{\sum }_{j\varepsilon R_{(i)}}exp(\beta \prime X_j)}]$$ (5)

is approximately zero. Using counting process notation the proposed estimating equation is given by

$$g(\beta )\approx \sum _{i=1}^n\underset{0}{\overset{\tau }{\int }}[W_i-\frac{{\sum }_{j=1}^n{W}_j{Y}_j(t)exp(\beta \prime X_j)}{{\sum }_{j=1}^n{Y}_j(t)exp(\beta \prime X_j)}]{\mathit{\text{dN}}}_i(t).$$ (6)

Therefore, we propose that the estimation equation, g(β) = 0, be solved with respect to β to obtain an estimator, β̂, of the log-hazard ratio.

It is worth noting that this estimating equation is identical in form to the score equation of the partial likelihood for Cox's model relating the time-to-event to the treatment X, with the exception that W replaces X in two places (as occurs in the case of the IV estimator for a linear model).

3.2 Covariance and standard error

An estimator of the variance of β̂ is the sandwich estimator (i.e., White-Huber estimator) B⁻¹ AB⁻¹ where B equals the matrix of partial derivatives $\frac{\partial }{\partial \beta }g(\beta ){|}_{\beta =\widehat{\beta }}$ and A is the covariance matrix of g(β). Let $S_k(t;\beta )={\sum }_{j=1}^n{W}_j^k{Y}_j(t)exp(\beta X_j)$. Using results for integrals of counting processes with respect to predictable processes [16], the term A can be estimated by

$$\sum _{i=1}^n\underset{0}{\overset{\tau }{\int }}{[W_i-\frac{S_1(t;\beta )}{S_0(t;\beta )}]}^2{\mathit{\text{dN}}}_i(t).$$

The denominator (B) of the sandwich estimator of the variance is a term that resembles the correlation of the treatment variable and the instrumental variables. Consequently the variance will be large if the instrument is weakly associated with the treatment. If there is no association, the expected value of the variance is infinity. If there is a weak association, the denominator of the expression may be close to zero, resulting in a highly variable estimator of the standard error.

4 Simulations

4.1 Simulation methods

We conducted simulations to evaluate the behavior of the estimating equations (6). To simulate the setting of a Cox model subject to confounding bias we introduce an omitted covariate of the survival time that is also a cause of the observed treatment X. We conducted these simulations under two scenarios for the effect of the omitted covariate. In the first scenario, the omitted covariate, U affects the time-to-event as in model (1). In the second scenario, the covariate has a multiplicative effect on the hazard; the conditional hazard given X and U is λ₀(t) exp(βX + θU).

We considered over a thousand scenarios, over which we varied the censoring rate (25, 50 or 75 %), the strength of the instrument (weak, modest, moderate, strong), the strength of the effect of the omitted covariate on the treatment (null, moderate, strong), the strength of omitted covariate on the time-to-event (null, moderate, strong) and β, the true log hazard ratio of interest.

We randomly generated the IV, W from a standard normal distribution. For scenarios in which the omitted covariate had an additive effect, U was generated from a uniform distribution independent of W. The treatment X is binary and generated to have an association with W and U using a logistic regression model. We considered two situations for the strength of the association of the instrument and treatment. For the strong instrument, the odds ratio relating the binary treatment to a unit change in the instrument is 10, whereas the odds ratio is 5, 2, and 1.2 for moderate, modest and weak instruments, respectively. For the weak instrument the average F-statistic for the test of the association of the instrument and the treatment is 9 which matches the criteria for defining an instrument as weak (Staiger and Stock 1997). We considered four conditions for confounding by the omitted covariate: none, moderate and strong. The odds ratio relating the binary treatment to the omitted covariate is 2 for the case of moderate confounding, and 5 and 10 for the case of strong confounding (both strong scenarios examined).

For scenarios in which the omitted covariate has an additive effect on the hazard the time-to-event was generated based on X and U according to model (1) in which the λ₀(t) was set to one, and h(u, t) = At + B(t) where A ranged from 0 to 1 depending on the scenario and B(t) is calculated based on A as shown in the Appendix 1. For scenarios in which multiplicative hazards hold for the effect of the omitted covariate we generated the time-to-event using the conditional hazard λ(t; x, u) = exp(β_xx + β_uu) where β_u ranged from 0 to ln(5).

The number of events for all scenarios was 500. For each scenario 1,000 datasets were generated. For each dataset the IV point and interval estimator we propose were calculated using the R code found in the Appendix 2 and the MPLE was calculated using the function coxph() of the library survival in R 3.0.2.

4.2 Simulation results

4.2.1 Simulation results for omitted covariates with additive effect on the hazard

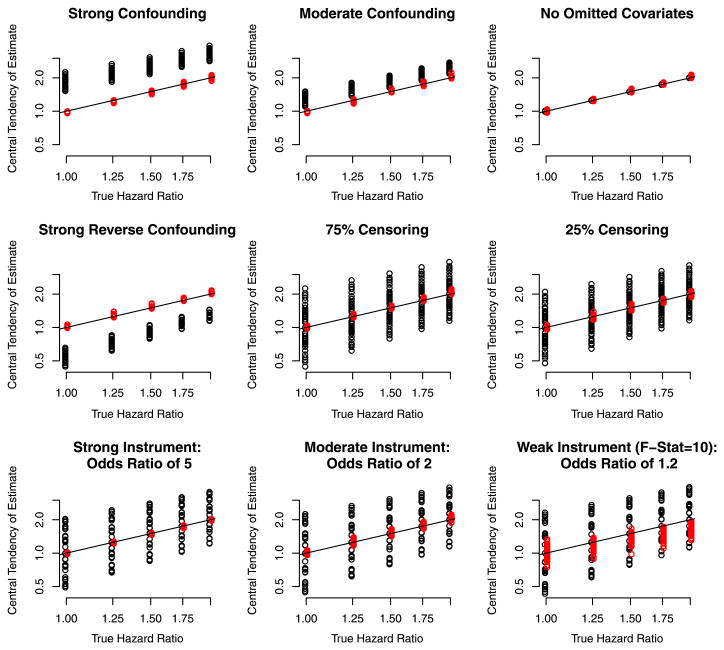
Figure 1 depicts the results of the simulations for an omitted covariate with an additive effect on the hazard. Each panel compares the central tendency of the IV estimator (red) we proposed, and the Cox MPLE (black) to the causal estimand. Each point is the geometric mean of the 1,000 hazard ratio estimates based on 1,000 randomly generated datasets for a particular scenario. Note that the geometric mean is the exponentiated mean of the of estimated log hazard ratios (the coefficient from Coxs model). The scenarios vary with respect to the settings for the association of the event and treatment, for the association of the treatment and the omitted covariates, for the association of the instrument and the treatment and the frequency of censoring, as described in the previous section. The straight diagonal line in the figure is the line of symmetry.

Fig. 1.

Depiction of the central tendency of the IV estimator (red) and the MPLE estimator (black) for scenarios in which the omitted confounder has an additive effect on the hazard. In the each panel, each point represents the geometric mean of the estimate based on 1,000 randomly generated datasets each of which has 500 events. Note The variability depicted is not the variance of the estimator, but the variability of the bias depending on the confounding scenario (Color figure online)

In Fig. 1 the top left panel shows the results of the simulations in which there was strong confounding by the omitted covariate (which combines the scenarios of of an odds ratio of 5 or 10 relating the treatment to the omitted covariate, and the specification of A = 1 in the omitted covariate mode 1 as described in the previous subsection), but over which other aspects of the simulation varied (strength of the instrument, and censoring percentage). The bias of the instrumental variable estimator was neglible (e.g. red dots all on line of symmetry) and not sensitive to variation in the scenarios (e.g. the red points overlap so much it is not difficult to discern that for each value for the true hazard ratio there is 24 different points, that represent 24 scenarios over which the association of the treatment and instrument varied, the censoring frequency varied and the instrument strength varied). It clearly outperformed the Cox MPLE, whose bias depends on how strongly the treatment and omitted covariate are related). The panel labelled moderate confounding shows that under moderate confounding by the omitted covariate, the IV etimator is relatively unbiased while the Cox MPLE is not. The results when there is no confounding by an omitted covariate confirm that the MPLE is optimal in this situation. The other 6 panels show the results according to various characteristics of the simulation.

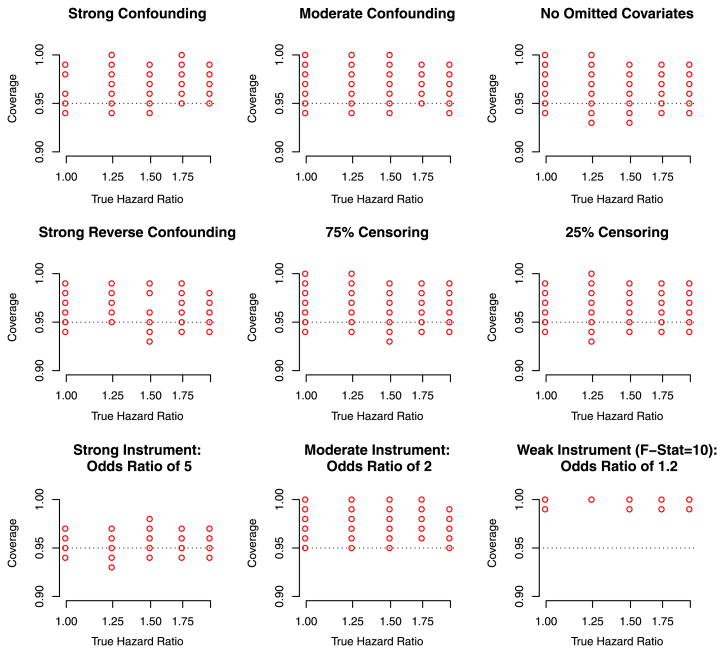
Figure 2 depicts the empirical coverage of the IV interval estimator (based on the asypmototic variance specified in Sect. 3.2). The empirical coverage of the IV based nominal 95 % confidence interval was close to 95 % for scenarios in which the instrument was strong but biased considerably above 95 % if the instrument was weak. The empirical coverage of the MPLE (data not shown) was close to zero except for the scenarios in which there was no confounding.

Fig. 2.

Depiction of the coverage of the IV estimator for scenarios in which the omitted confounder has an additive effect on the hazard. In the each panel, each point represents the empirical coverage based on 1,000 randomly generated datasets each of which has 500 events. The coverage of the MPLE is not represented here which in the vast majority of scenarios had an empirical coverage close to zero, with the exception of the scenario in which there was no confounding

4.2.2 Simulation results for omitted covariates with multiplicative effect on the hazard

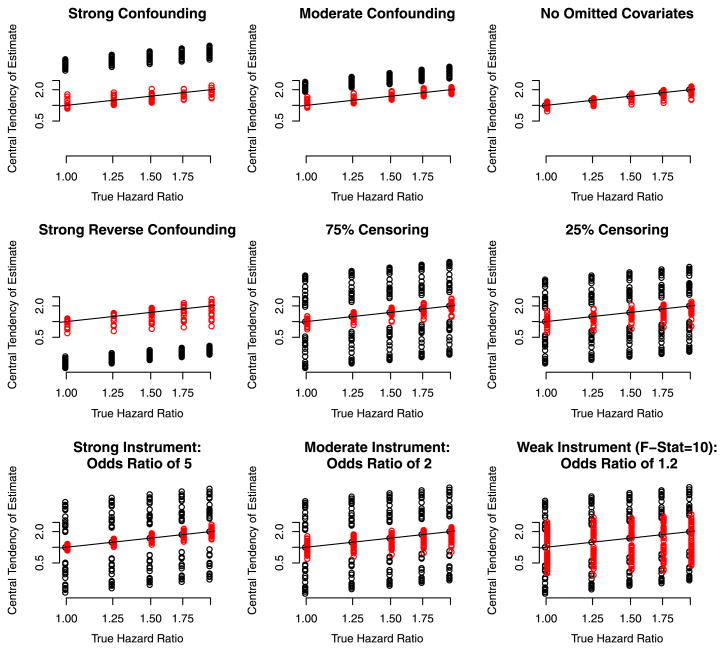
Figure 3 reports the simulation results for omitted covariates with multiplicative effects. The pattern of results are similar to those reported above for omitted covariates with additive effects, but the IV estimator is more biased than in the additive setting under which it is developed, especially evident in the panel titled “Strong Reverse Confounding”. On the other hand, except in the scenario of no omitted covariates the MPLE is considerably more biased.

Fig. 3.

Depiction of the central tendency of the IV estimator (red) and the MPLE estimator (black) for scenarios in which the omitted confounder has a multiplicative effect on the hazard as in Fig. 1 separately by the characteristics of the scenarios (Color figure online)

5 Example

IVs were used by Stukel et al. (2007) to evaluate the effect of invasive cardiac management on survival. The authors merged baseline chart data from a national cohort of 122,124 subjects with acute myocardial infarction with Medicare claims. The claims data were used to determine if the patients had invasive cardiac management, defined as catheterization within 30 days of hospitalization.

Stukel et al. (2007) analyzed the data using Cox's multiple regression model for adjustment, propensity score matching, and IV estimation. The IV used was the incidence rate of cardiac catheterization in the residential area. A justification of geographic rates as instrumental variables can be found in Newhouse and McClellan (1998). In addition to these variables, a rich array of possible confounding covariates was available. Median follow-up in the cohort was 2.6 years with a maximum of 4 years.

Stukel et al. (2007) used IVs for linear models to estimate the effect of invasive cardiac management on survival as no methods for right censored data were known to exist. The model in (1) is comparable in the sense that the involvement of the omitted confounders is additive. As endpoints the authors selected (i) death during follow-up within 1 year, and (ii) death during follow-up within 4 years. These endpoints underestimate actual mortality. For instance, the 1 year endpoint will be 1 for a patient who dies during follow-up at 6 months, but 0 for a patient who died at 6 months but after the end of follow-up. The mean value of the 4 year endpoint was 0.45, whereas the Kaplan–Meier estimator of mortality by 4 years (for the entire cohort) was 0.50. The longest follow-up in the study was 4 years.

Using IVs for linear models, Stukel et al. (2007) estimated that invasive cardiac management decreased death during follow-up at 1 year by 0.054 (95 % CI 0.024–0.084). The decrease in death during follow-up at 4 years was estimated to be 0.097 (95 % CI 0.066–0.129).

These point-in-time survival effects were transformed to hazard ratios using a formula to transform a risk difference to a risk ratio (risk ratio equals one plus the quotient of risk difference to risk in control group). Stukel et al. (2007) estimated the hazard ratio to be 0.86 (0.78–0.94) based on the 1 year endpoint, and 0.84 (0.79–0.90) based on the 4 year endpoint. Assuming proportionality of hazards, the risk difference at time t is δ = S₀(t)^HR − S₀(t), where S₀ is the survival curve in the untreated. Therefore the hazard ratio satisfies HR = ln(S₀(t) + δ)/ln S₀(t). Using this transformation of the risk difference into a relative risk, Stukel et al estimated the hazard ratios as 0.84 (0.79–0.90) at 1 year and 0.76 (0.69– 0.83) at 4 years. In addition to the method of IVs, the authors reported the estimates of the hazard ratio by Cox's regression model and propensity scores.

We applied our approach with the same covariates used by Stukel et al. (2007). Because the treatment is defined as catheterization within 31 days, we restricted the analysis to follow-up after 31 days, otherwise the estimator would incur an immortal time bias (Suissa 2008).

Our estimate of the hazard ratio is 0.70. This value is further from the null than that reported by Stukel et al. (2007), 0.84, based on the 4 year endpoint. On the other hand, it is not too distant from the 0.76 we calculated based on Stukel et al's analysis of the 4 year endpoint that uses the transformation based on proportionality of hazards as described above. Our estimator is considerably less extreme than the hazard ratios estimated by Cox's adjustment model and by propensity scores. A hazard ratio of 0.70 is not in the range of 0.80–0.92, reported by randomized studies of the effect of catheterization. Nevertheless, some of those estimates might have been biased toward the null because of use of intention-to-treat analysis.

As we discovered in our simulations and reported in Sect. 4.2, the standard error is imprecisely estimated for weak instruments. We obtained a bootstrap standard error. The standard error based on the bootstrap was 2.5 times smaller than the standard error based on the sandwich variance. Based on 1,000 bootstraps, the resulting 95 % confidence interval was 0.60–0.82.

We also conducted analyses within separate time windows. When data were restricted to the first year (minus first 31 days), the HR estimator was 0.72 (0.56–0.84). When restricted to the interval from 1 year to 4 years, it was 0.68 (0.56–0.80).

Clearly, the confidence interval for our IV estimator is many times wider than the confidence interval of the hazard ratio estimator by Cox's model or by propensity scores. This is because the variance of the IV estimator is inversely proportional to the strength of association between the treatment and the IV. The geographically derived instrument used in this catheterization study has a small correlation, 0.17, with the treatment. Although the dataset has more than 13,000 deaths in both the exposed and unexposed groups, the resulting IV estimator has the variance of an effect estimate that could be achieved by a randomized study that allocated 1,200 subjects in equal proportions to catheterization or not.

6 Discussion

We have proposed a causal estimator of the hazard ratio of a Cox regression model from right censored data using IVs. We evaluated the estimator in simulations and demonstrated its application using a large health services dataset. Our results are promising. Our estimator is much less biased than the estimator based on Cox's proportional hazard model that ignores omitted confounding, including when the underlying causal model upon which the estimator was developed does not hold.

Our estimator is consistent if the IV and omitted covariates are independent, as for standard IV analysis. However, an additional (non-IV) assumption that restricts the form of any omitted confounders to be additive on the scale of the hazard ratio and to be centered (i.e., have 0 mean) was needed in order for the resulting estimator to be theoretically valid. This raised concerns about the generalizability of the method. However, we also performed simulations in which the omitted covariate had a multiplicative effect. The results suggest that our estimator is considerably less biased than the estimator based on the Cox model. In future work we hope to develop an IV procedure to recover causal estimates when the omitted confounder has a multiplicative effect on the hazard.

The supposition of additive effects of omitted covariates resembles an approach using IV in logistic regression (Foster 1997; Johnston et al. 2008; Rassen et al. 2009). Those methods define the instrument to be uncorrelated with the difference of the endpoint with its expected value based on the logistic model.

The method we propose is only useful to the extent that instrumental variables exist. The identification and validation of IVs is an area requiring development. It may be that the method of instrumental variables never realizes its promise because they either do not exist, are hard to identify, or cannot be justified. Hernan and Robins (2006) speak of IVs as exchanging the assumption of no omitted covariates with the IV assumption. It is not possible to conclusively validate empirically that a variable is an instrument. The asumption of no effect on an endpoint except through its effect on the treatment is an untestable assumption. However, when multiple IVs are available some procedures have been proposed in the econometric literature to help address validity.

In our example taken from Stukel et al. (2007) we employed a geographic rate as an IV. The use of geographically based variables as instruments is common in health services research and health economics (McClellan et al. 1994; Newhouse and McClellan 1998; Landrum and Ayanian 2001). It is possible that the geographic rate of catheterization is associated with omitted covariates that modify the risk of mortality, invalidating it as an instrument. Other types of variables investigated as IVs are clinician utilization rates, and clinician's last selected treatment in a similar patient. Further work is needed to develop methods for proposing and vetting IVs.

IVs are also used to correct for treatment measurement error. The connection between IVs and measurement error in logistic regression has been discussed by Buzas and Stefanski (1996, 2005). A special case of the IVs is if W₁, W₂ are error-prone replicate measurements of a continuous treatment, then each is essentially an IV for the other. Huang and Wang (2000) developed a methodology for using replicates to estimate the hazard ratio of Cox's model. The estimating equations we propose for IVs are similar to those proposed by Huang and Wang for replicates in the measurement error problem. Despite this seemingly close connection it is important to note that the measurement error problem is more akin to an omitted covariate problem than an omitted confounder problem. Therefore, the concern is effect attenuation (a form of bias in which the effect is pulled too far towards 0 but the sign is unchanged) as opposed to the case considered here in which a naive analysis can be completely incorrect (i.e., have the wrong sign).

In conclusion, we propose that the method of IVs we have derived be used as an alternative to adjusted (regression) models, propensity score models and inverse probability weighting whenever a plausible IV exists and if any omitted confounders can be considered to have additive effects.

Appendix 1: The marginal is Cox proportional hazards model

Here we show that if the treatment X is applied independently of U in model (1) that the marginal distribution of the time-to-event with respect to X is proportional hazards. This is relevant because it shows that parameter β of that model has an intepretation as the logarithm of the hazard ratio comparing the potential outcome if a subject recieves X = 1 to the potential outcome if a subject recieves X = 0 and U is unknown (i.e. not conditioned on).

The survival curve corresponding to model (1), S(t; x|U) = Pr[T̃(x) ≥ t|U] is

$$exp[-\underset{0}{\overset{t}{\int }}\{{\lambda }_{01}(t)exp(\beta \prime x)+h(u,t)\}\mathit{\text{dt}}]=exp[-{\Lambda }_{01}(t)exp(\beta \prime x)]exp[-H(u,t)]$$

where $H(u,t)={\int }_0^{t}h(u,t\prime )\mathit{\text{dt}}\prime$. If X is applied independently of U then the marginal causal model for the survival curve, obtained by integrating over U equals

$$\begin{array}{ll}S(t;x)\hfill & =\int S(t;x|u){\mathit{\text{dF}}}_U=\int exp[-{\Lambda }_{01}(t)exp(\beta \prime x)]exp[-H(u,t)]{\mathit{\text{dF}}}_U(u)\hfill \\ \hfill & =exp[-{\Lambda }_{01}(t)exp(\beta \prime x)]\int exp[-H(u,t)]{\mathit{\text{dF}}}_U(u).\hfill \end{array}$$ (7)

Suppose H(u, t) = A(t)u + B(t). Then (7) becomes

$$S(t;x)=exp[-{\Lambda }_{01}(t)exp(\beta \prime x)]exp[-B(t)]\int exp[-A(t)u]{\mathit{\text{dF}}}_U(u)$$ (8)

$$=exp[-{\Lambda }_{01}(t)exp(\beta \prime x)]exp[-B(t)]{\text{mgf}}_U[-A(t)].$$ (9)

Therefore if we take B(t) = ln mgf_U[−A(t)] the marginal causal survival curve is S(t; x) = exp[−Λ₀₁(t) exp(β′x)] which is a Cox proportional hazards model.

This particular causal conditional model has the property that E[h(u, t)|T̃(x) ≥ t] equals zero as demonstrated below:

$$\begin{array}{ll}\mathrm{E}[h(U,t)|\stackrel{\sim }{T}(x)\ge t]\hfill & =\int h(u,t)dPr[U\le u|\stackrel{\sim }{T}(x)\ge t]\hfill \\ \hfill & =\int h(u,t)Pr[\stackrel{\sim }{T}(x)\ge t|U=u]{\mathit{\text{dF}}}_U(u)/S(t;x)\hfill \\ \hfill & =\int h(u,t)exp[-exp(\beta \prime x){\Lambda }_0(t)-H(u,t)]{\mathit{\text{dF}}}_U(u)/S(t;x)\hfill \\ \hfill & =exp[-exp(\beta \prime x){\Lambda }_0(t)]\int h(u,t)exp[-H(u,t)]{\mathit{\text{dF}}}_U(u)/S(t;x)\hfill \\ \hfill & =S(t;x)\int h(u,t)exp[-H(u,t)]{\mathit{\text{dF}}}_U(u)/S(t;x)\hfill \\ \hfill & =\frac{d}{\mathit{\text{dt}}}\{-\int exp[-A(t)u-B(t)]{\mathit{\text{dF}}}_U(u)\}\hfill \\ \hfill & =-\frac{d}{\mathit{\text{dt}}}\{exp[-B(t)]{\text{mgf}}_U(-A(t))\}\hfill \\ \hfill & =0,\hfill \end{array}$$ (10)

when B(t) = ln mgf_U[−A(t)].

Appendix 2: R code for implementing the estimating equation

library (rootSolve)
IVHR <– function (Time, Status, X, W) {
  # Status is 1 if event occurred , 0 for censored
  # Time is time–to–event Status=l, and time of censoring otherwise
  # X is treatment or exposure of interest
  # W is the instrument
  n <– length (Time)
  ord <– order(–Time)
  Time <– Time [ord]
  Status <– Status[ord]
  X <– X[ord]
  W<– W[ord]
  Est.Equat <– function (beta) {
    HR <– exp(beta *X)
    S.0 <– cumsum(HR)
    S.W1 <– cumsum(W*HR)
    sum(Status * (W – S.W1/S.0))
  }
out.solution <– multiroot (Est.Equat, start=0)
beta.hat <– ifelse (out.solution\$estim.precis < 0.00001, out.solution\$root , NA)
HR <– exp(beta.hat *X)
S.0 <– cumsum(HR)
S.W1 <– cumsum(W*HR)
S.X1 <– cumsum(X*HR)
S.W1X1 <– cumsum(W*X*HR)
Var.E.E <– sum(Status * (W – S.W1/S.0)ˆ2)
Deriv <– –sum(Status * (S.W1X1/S.0 – (S.W1*S.X1)/S.0ˆ2))
SE <– sqrt(Var.E.E/Deriv ˆ 2)
list (Est.log.HR=beta.hat , SE=SE, SE.2=SE.2)
}