ESTIMATING THE DURATION OF SPECIATION FROM PHYLOGENIES

Abstract

Speciation is not instantaneous but takes time. The protracted birth–death diversification model incorporates this fact and predicts the often observed slowdown of lineage accumulation toward the present. The mathematical complexity of the protracted speciation model has barred estimation of its parameters until recently a method to compute the likelihood of phylogenetic branching times under this model was outlined (Lambert et al. 2014). Here, we implement this method and study using simulated phylogenies of extant species how well we can estimate the model parameters (rate of initiation of speciation, rate of extinction of incipient and good species, and rate of completion of speciation) as well as the duration of speciation, which is a combination of the aforementioned parameters. We illustrate our approach by applying it to a primate phylogeny. The simulations show that phylogenies often do not contain enough information to provide unbiased estimates of the speciation-initiation rate and the extinction rate, but the duration of speciation can be estimated without much bias. The estimate of the duration of speciation for the primate clade is consistent with literature estimates. We conclude that phylogenies combined with the protracted speciation model provide a promising way to estimate the duration of speciation.

Speciation takes time. Both detailed speciation models and fossil data support this (Avise 1999; Gavrilets 2004; Norris and Hull 2012). Only in the case of speciation by polyploidy can speciation happen in a single generation (McCarthy et al. 1995), but this constitutes only 15–31% of all speciation events in plants (Wood et al. 2009). Regardless of the underlying mechanism of speciation, it is intriguing then to ask how long it takes for a new species to form and what factors affect this duration. This question has been identified as one of the key open questions by the Marie Curie Speciation Network (2012). Here, we focus on the first part of the question: how do we quantify the duration of speciation?

The answer may perhaps be found by studying fossil data, but the incompleteness of the fossil record, apart from a few exceptional cases (e.g., Ezard et al. 2011), limits this approach. Even when there is much fossil data, estimates based on these data will be biased because short-lived, young species are often not recognized (Norris and Hull 2012). Molecular phylogenies provide an alternative route that may shine light on this question. Since the pioneering work of Avise and colleagues (Avise and Walker 1998; Avise et al. 1998), little progress has been made in the last decade, until recently, Etienne and Rosindell (2012) studied a lineage diversification model assuming that, following ideas of Purvis et al. (2009) and Rosindell et al. (2010), speciation is a gradual, protracted process. There is continual formation of incipient species that undergo the speciation process and become good species upon completion of this process. Both good and incipient species can produce new incipient species. A species thus consists of a complex of all lineages that are not separated by a speciation-completion event. The model predicts the often observed slowdown of lineage accumulation toward the present (Etienne and Rosindell 2012, see also Purvis et al. 2009) because incipient species that are currently in the process of formation are not yet identified as good species. The protracted speciation model may therefore also be viewed as a model of species recognition, that is, of the observer's ability to distinguish different species (Purvis et al. 2009), but evidently the probability of species recognition depends strongly on the progress in the speciation process, that is, the accumulation of a sufficient number of differences or (reproductive) incompatibilities to attract taxonomic attention (Purvis et al. 2009; Etienne and Rosindell 2012). Whether species are considered to be good or not depends crucially on one's species concept. We deliberately do not single out any particular species concept because the protracted speciation model is conceptually independent of the species concept; only the interpretation of the rate of speciation-completion will vary with different approaches to species delineation.

The protracted speciation model provides a prediction for the duration of completed speciation events for a given set of model parameters (Etienne and Rosindell 2012). Etienne and Rosindell (2012) developed a likelihood approach for the protracted speciation model to estimate the model parameters from the phylogeny of extant species, in the absence of extinction, and to compare model performance with that of other models. Lambert et al. (2014) developed a new mathematical framework that allows the computation of the likelihood of the protracted model given the phylogeny also for the case that extinction is nonzero. This approach is based on a coalescent point process representation (Popovic 2004; Lambert 2010; Lambert and Stadler 2013). Here, we implement this method in an R package, called Protracted Birth-Death (PBD). Furthermore, we present various properties of the duration of speciation, also incorporated in PBD. We study on simulated data how well the model parameters (rate of initiation of speciation, rate of extinction of incipient and good species, and rate of completion of speciation) as well as the expected duration of speciation can be estimated. We find that although the model parameters cannot be reliably estimated, the duration of speciation, which is a function of these model parameters, can be reliably estimated. We illustrate our method with a primates phylogeny from Fabre et al. (2009). Our estimate of the duration of speciation for this clade is plausible in the light of the literature (Curnoe et al. 2006), lending further support to the utility of the protracted speciation model.

Methods

MODEL

Here, we outline the protracted speciation model which is schematically represented in Figure1A. The protracted speciation model assumes that there are speciation-initiation events at which incipient species are formed. These incipient species may become good species, and when they eventually become good, speciation is said to be completed. Both incipient and good species are subject to extinction and both are able to give rise to incipient species. Thus, a species consists of a good (or representative, see below) species and all its extant incipient descendants (or relatives): speciation-completion events separate different species, but these events are not recorded in the phylogeny, because it is the speciation-initiation event that marks the time of divergence.

Figure 1.

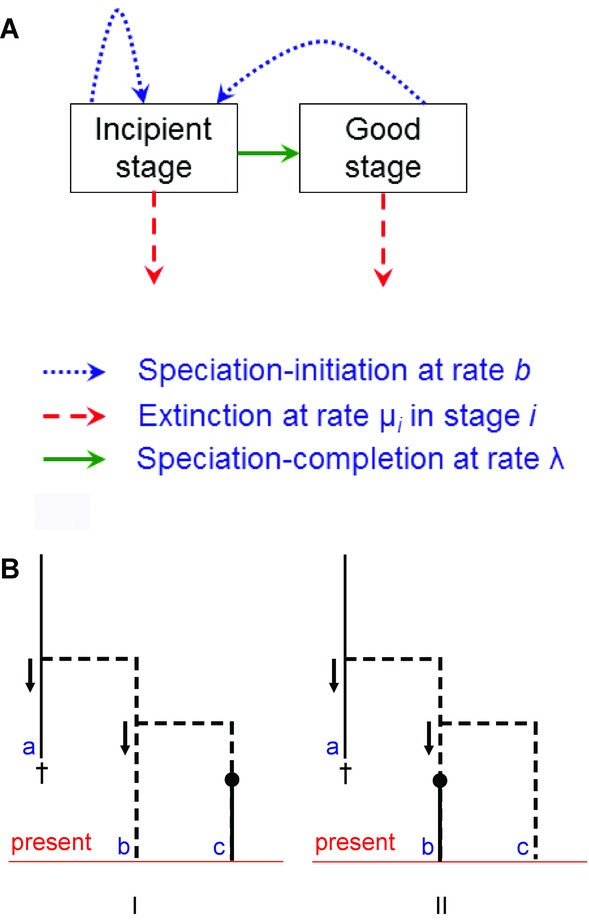
The protracted speciation model. (A) Schematic overview of transitions. Incipient species and good species produce incipient species at rate b. Each stage has its own extinction rate μ_i and incipient species become good at rate λ. (B) Illustration of the problem of identifying good species and the first-order correction we make, following Lambert et al. (2014). Solid lines denote good species, dashed lines denote incipient species, filled circles denote speciation-completion events, arrows indicate the parent species and lowercase letters denote different taxa. Taxon a is a good yet extinct species that gave rise to taxon b, which in turn produced taxon c that underwent speciation-completion in panel I, whereas in panel II taxon b underwent speciation-completion. Biologically, there are two good (representative) species in both panels: in panel I taxon b is representative of species a and taxon c is a different species, whereas in panel II taxon c is representative of species a and taxon b is a different species. The approach of Lambert et al. (2014) is an approximation, in that it recognizes two good extant species in panel I but only one good extant species in panel II, as taxon c is not considered to represent species a, but an incipient species of species b.

We will focus here on the time-homogeneous Markov version of the model, that is, the rate parameters are independent of time, implying that all waiting times are exponentially distributed, but we note that time-dependence of the parameters can be easily taken into account (see Lambert et al. 2014). We use the following notation: by i we denote the stage of the species where i = 1 for the incipient stage and i= 2 for the good stage; b_i is the speciation-initiation rate, that is, the rate at which species in stage i produce incipient species; μ_i is the extinction rate of species in stage i and λ is the speciation-completion rate, that is, the rate at which incipient species become good. For analytical tractability (see below), we must assume that all rates of speciation-initiation are equal: b₁ = b₂ = b. This assumption implies that all topologies are equally likely as in the constant-rate birth–death model (Lambert et al. 2014); if this assumption is relaxed, we can obtain more balanced or more unbalanced trees than in the constant-rate birth–death model (Etienne and Rosindell 2012). To keep the number of parameters manageable, we also assume that incipient and good species become extinct at the same rate.μ₁ = μ₂ = μ (but this is not a technical necessity). We note that the protracted speciation model as introduced by Etienne and Rosindell (2012) thus covers the three principal controls of speciation rate identified by Dynesius and Jansson (2014): (1) splitting control, that is, rate of speciation-initiation; (2) persistence control, that is, rate of extinction of incipient species; (3) duration control, that is, the speciation-completion rate.

There is a biologically complicating factor: an incipient species with a good but extinct species as ancestor should be regarded as a representative of this ancestor, and therefore a good species (see Etienne and Rosindell 2012; Lambert et al. 2014), but only allowing species to be good if they have experienced the transition from incipient to good species ignores this. Lambert et al. (2014) developed a first-order correction of this: it distinguishes incipient and representative species; the latter are either true good species or the first descendant from a good (but extinct) species (in some natural ordering of all its extant descendants). We expect this correction to be a good approximation if the rate of speciation-initiation is not too large. From hereon, we will use this model of Lambert et al. (2014) and call these representative species good species. We refer to Etienne and Rosindell (2012) and Lambert et al. (2014) for more details on the protracted speciation model.

LIKELIHOOD

Lambert et al. (2014) derived the likelihood of the branching times 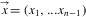—where x_n-1 = T, the crown age of a phylogeny of n extant and m missing species (that are all good or representative of an extinct good species)—conditional on a speciation event at the crown age and the survival of the two crown lineages. Assuming that the missing species arise from n-sampling (Etienne et al. 2012; Lambert and Stadler 2013; Lambert et al. 2014) rather than ρ-sampling (binomial sampling), the likelihood is given by Lambert et al.'s equation (7):

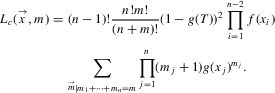(1)

Here we used the convention, x_n = x_{n– 1} = T; the factorial (n – 1)! can be dropped when calculating the likelihood of the phylogeny (oriented tree) rather than the branching times, and replaced by 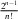when calculating the likelihood of labeled trees (Stadler 2013). The functions 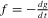and g can be found by solving a system of four ordinary differential equations, that is, Lambert et al.'s equations (10), (11), (25), (26) and their very last, unnumbered, equation (for g_r). These equations read, dropping Lambert et al.'s superscripts to simplify notation,

(2a)

(2b)

(2c)

(2d)

with

(3)

Here, p₁ is the probability that a species in the incipient stage at time t (measured in My before the present) has no good descending species that have extant descendants at the present (t = 0). q_j denotes the probability that a species in stage j at time t has no extant descendants at the present, that is, that the lineage is extinct; q₂ is thus the probability that a species in the good stage at time t has no extant descendants at the present. Equations (2c)) and (2d) are similar to equations (7a) and (7b) in the BiSSE model (Maddison et al. 2007); indeed, all these equations describe the dynamics of extinction probabilities depending on the state of the lineage. However, they crucially differ because (1) in BiSSE transitions between states happen in both directions, whereas in the protracted model there is no transition from good to incipient, and (2) in BiSSE at speciation, the daughter species inherit the state of the parent, whereas in the protracted model good species give rise to incipient species.

To obtain the likelihood, we have to integrate this set of equations numerically and evaluate its solution at the branching times 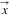. This likelihood can be used to estimate parameters by likelihood optimization. We provide the R package PBD to compute and maximize the likelihood. This package also allows time-dependent rates of speciation-initiation, speciation-completion, and extinction.

ROBUSTNESS OF MAXIMUM LIKELIHOOD (ML)

To assess the robustness (particularly bias) of the ML approach in yielding the correct parameter values, we simulated 1000 phylogenetic trees under the protracted speciation model for various sets of parameters (b = 0.5, λ = 0.1, 0.3, 1, μ₁ = μ₂ = μ = 0, 0.1, 0.2), and a fixed crown age of 5, 10, or 15 My, conditional on the realized tree retaining the initial root (i.e., survival of both original crown lineages). We used the function pbd_sim_cpp to perform these simulations. This function uses the coalescent process to efficiently simulate branching times (see Lambert et al. 2014). We then estimated the parameters using ML. For each set of estimated parameters, we evaluated the mean or expected duration of speciation τ (from hereon simply duration of speciation), which is defined as the time it takes for an incipient species to become good or to have a descendant become good. An expression for the expected duration of speciation is given by Etienne and Rosindell (2012):

(4)

where

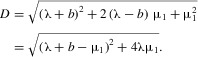(5)

The duration of speciation differs from the speciation-completion time in that the latter is the waiting time until a single incipient lineage completes the speciation process if extinction was zero, whereas the former is the time needed for an incipient species or one of its descendants to complete speciation, conditional on the fact that speciation completes, that is, this is the time taken by any species that succeeded in speciating completely.

To evaluate the potential bias introduced when fitting the standard birth–death model to phylogenies, ignoring the effect of protracted speciation, we fitted the standard, unprotracted, birth–death model to the simulated data as well.

EMPIRICAL EXAMPLE

To illustrate our approach, we applied it to a clade that satisfied two conditions: (1) a reasonably sized and sampled phylogeny is available, and (2) some independent estimates of the duration of speciation are known from the literature. Because literature on this topic is scarce, the second condition is the most stringent. One study that meets this condition is a relatively recent and in-depth paper by Curnoe et al. (2006) on the duration of speciation in primates. The first condition is also satisfied for primates because Fabre et al. (2009) provide a primate phylogeny with 273 tips and 103 missing species. The data we used are deposited in Dryad (datadryad.org/resource/doi:10.5061/dryad.8492,particularly da-tadryad.org/bitstream/handle/10255/dryad.8494/PRIMATES-C-hronogram_273_taxa.tre?sequence = 1). To check for robus-tness, we compared the results to the four timetrees provided by Springer et al. (2012), available as Supporting Information, Text S2, Newick timetrees 1–4 (doi:10.1371/journal.pone.0049521.s008). These timetrees differ in the relaxed clock model used (autocorrelated or independent evolutionary rates with hard-bounded or soft-bounded constraints).

We estimated the parameters of the protracted speciation model for this clade, including the missing species using the n-sampling likelihood approach outlined above, and computed the duration of speciation. Here, we not only computed the expected duration but also the full probability density. This density can be computed, using the same considerations as in Etienne and Rosindell (2012), and yields:

(6)

where

(7)

This probability density attains a maximum at

(8)

The density, mode and any quantile, or moment (including the mean) can be computed with the package PBD, available on CRAN and on Dryad (datadryad.org/resource/doi: 10.5061/dryad.js88n), together with the simulated data and R code.

With the estimated parameter values, we ran 1000 simulations to obtain a bootstrap estimate of the error in our estimated mean duration of speciation. It also provided a way to assess the goodness-of-fit of the model by comparing simulated lineage-through-time plots with the observed one.

Results and Discussion

In our test of the protracted speciation model on phylogenies with known parameter values, we found that for the simulations for small crown ages, the ML optimization often did not converge, indicating a very flat likelihood surface and hence very limited information in the data. Indeed, clade sizes were often small, less than 10 species, and often only two, the minimum produced by the simulations as they were conditioned on survival of the crown lineages. With three parameters to be estimated, small clades simply leave too few degrees of freedom to allow reliable parameter estimation. We therefore restricted further analysis to a crown age of 15 My to get reasonably sized clades for all parameter combinations considered. We found that the parameter estimates of the speciation-initiation rate and the extinction rate are often biased and highly variable, particularly for low speciation-completion rates and high extinction rates (Fig.2A and B). However, the estimates for the incipient diversification rate (speciation-initiation rate minus extinction rate), the speciation-completion rate, and particularly the duration of speciation contain little bias and relatively little variation (Fig.2C–E), and thus this seems a promising new approach for estimating temporal characteristics of the speciation process. Although clade size has a substantial effect on how well individual parameters (i.e., extinction) are estimated, it scarcely has an effect on the quality of the estimation of the duration of speciation (Fig. S1).

Figure 2.

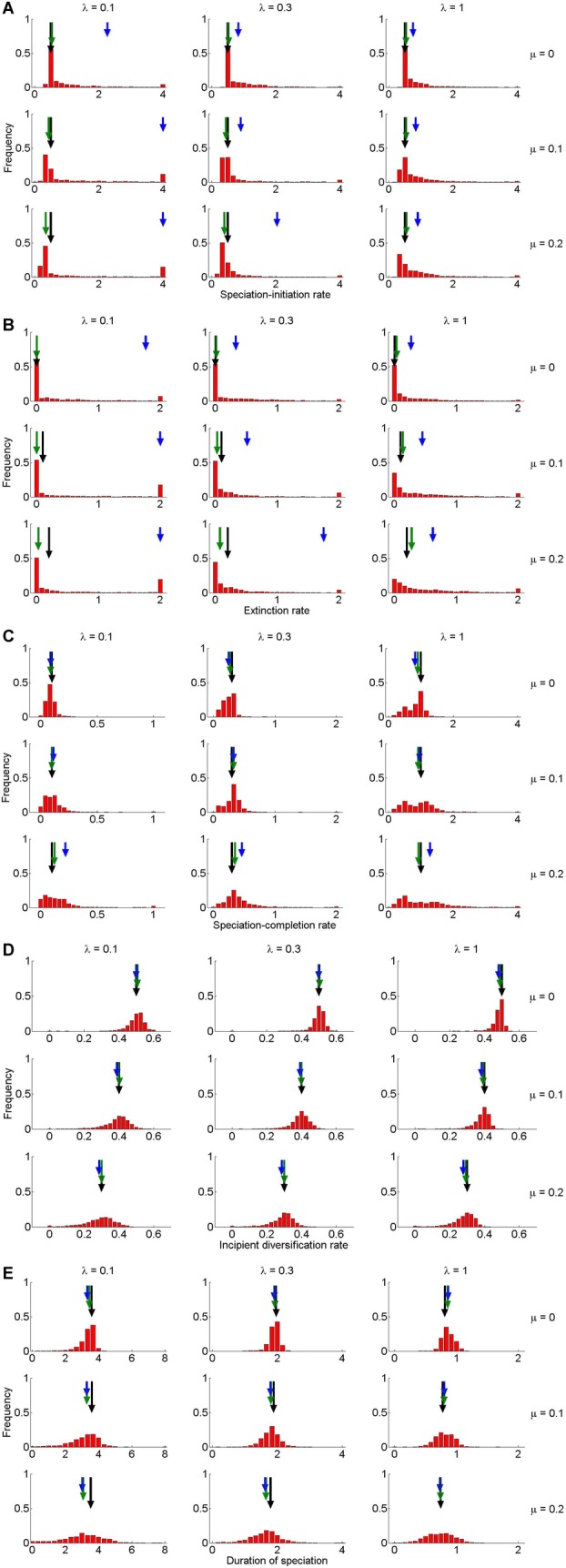
Distribution of the estimated parameters. (A) Speciation-initiation rate, (B) extinction rate, (C) incipient diversification rate (speciation-initiation rate minus extinction rate), (D) speciation-completion rate, (E) duration of speciation in species that complete the speciation process (a composite of the speciation-initiation rate, the speciation-completion rate, and the extinction rate, eq. 4). The distribution represents the estimates for 1000 replicate simulations (red bars), their mean value (shortest, blue, arrow), the median (medium-sized, green, arrow), and the true simulation value (longest, black, arrow) for various simulation parameter sets: speciation initiation rate is 0.5 (all panels), the extinction rate μ takes the values 0, 0.1, and 0.2 (rows), and the speciation completion rate λ takes the values 0.1, 0.3, and 1 (columns). The simulated trees all had a crown age of 15 My. The last bar in the histograms contains all simulations with a value equal or larger than the corresponding value on the x-axis.

When fitting the standard, unprotracted, birth–death model to the simulation data, we found that the estimated speciation rate largely underestimated the speciation-initiation rate and increased with increasing speciation-completion rate (Fig. S2A). The latter is the expected behavior because the number of species decreases. However, we observed no clear relationship between the estimated speciation rate and the parameters controlling speciation in the protracted model. Hence, fitting the standard birth–death model in cases when speciation is protracted may be highly misleading.

When we applied our approach to the primate clade of Fabre et al. (2009), we found that the speciation-initiation rate and the extinction rate produce a likelihood ridge in the b – μ -plane, whereas the speciation-completion rate is orthogonal to the other parameters (Fig.3A). This is reminiscent of the well-known property of the constant-rate birth–death model that the net diversification rate can be estimated reliably, but the ratio of speciation and extinction rates cannot (Paradis 2004; Rabosky 2010; Aldous et al. 2011; Etienne et al. 2012; Stadler 2013), which was confirmed in our simulations. The expected duration of speciation, calculated from the ML estimates, is around 0.61 My, whereas the median is 0.45 My. The bootstrap values range between 0.02 and 1.12 My and have a mean and median of 0.61 My (so extremely close to our ML estimate indicating there is no bias) and a standard deviation of 0.14 My (Fig.3B), which can be used as an estimate of the error in the expected duration of speciation. Allowing different rates of extinction for good or incipient species changes the model parameters substantially (with incipient species going extinct at a higher rate than good species), but not the duration of speciation. For the four timetrees of Springer et al. (2012), we obtained expected durations of speciation of 0.66 (autocorrelated rates with hard-bounded constraints), 0.65 (autocorrelated rates with soft-bounded constraints), 0.51 (independent rates with hard-bounded constraints), and 0.43 (independent rates with soft-bounded constraints).

Figure 3.

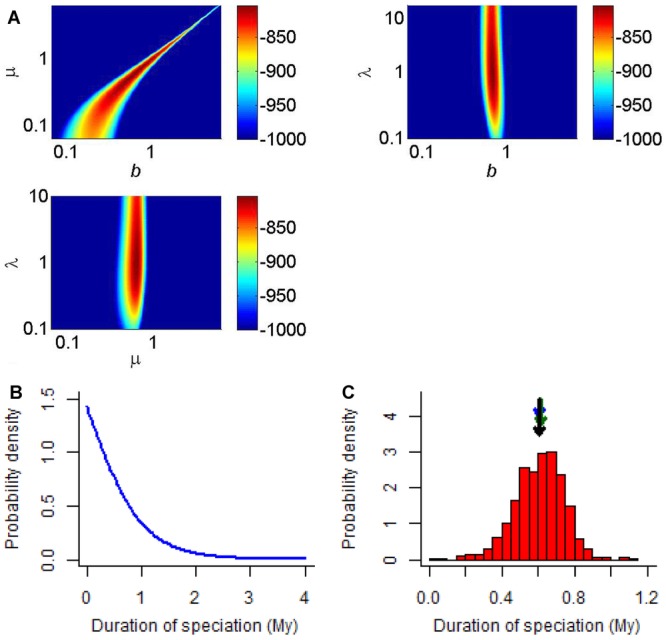
Application of the protracted speciation model to the primate clade. (A) Projections of the log-likelihood surface around the likelihood optimum for the primate clade; the third parameter is always kept at its maximum likelihood (ML) value. All log-likelihood values lower than −1000 are in dark blue (black on black-and-white version). (B) Probability density distribution of the duration of speciation at the ML parameter estimates. This provides insight in the variation across the clade: although the mode predicts that most speciation events will be short, there is a substantial tail of the distribution at long durations. (C) Bootstrap distribution of the duration of speciation for the ML parameter estimates. This provides insight in the bias and uncertainty of the expected duration of speciation: the longest (black) arrow indicates the expected duration at the ML estimates (see also panel A), whereas the medium (green) and shortest (blue) arrows indicate the median and mean of the bootstrap values, respectively.

Our estimates are in line with those of Curnoe et al. (2006) who suggested a maximum duration of speciation of around 1 million years based on the difference between divergence times of sister species and interphylogroup divergence times. Curnoe et al. (2006) argued that this is not the same as the time needed for full reproductive isolation, which in their opinion can be much larger (up to 4 My). For our analysis, strict adherence to this biological species concept would mean that many of the tips in the phylogeny should still be considered incipient species. We would arrive at a smaller tree with longer branching times, giving rise to a larger duration of speciation. Thus, estimates of the duration of speciation are always directly related to the taxonomy used: species in the tree are assumed to be good species that have completed the speciation process according to our species concept.

The values for the inverse of the speciation-completion rate and the duration of speciation may be very different because the latter is also affected by the speciation-initiation rate and the extinction rate as equation (4) shows. We may expect very high values of b with very low values of λ: very frequent speciation-initiation, with only an occasional completion of the speciation process. This idea was already coined by Mayr (1963) and Stanley (1978) who called the unsuccessful species “aborted species” as they indeed prematurely become extinct. Rosenblum et al. (2012) proposed a model for the idea, the ephemeral speciation model, which is a special case of the protracted speciation model where rates of speciation-initiation are high but rates of speciation-completion are low. Recent support comes from Phillimore et al. (2007) who found subspeciation rates to be much higher than speciation rates, and from Levin (2012) in his discussion of the long time for hybrid sterility to arise in flowering plants.

The lineage-based protracted speciation model has been introduced phenomenologically (Etienne and Rosindell 2012), but has a mechanistic basis in the simplest null model of the family of Bateson-Dobzhansky-Muller speciation models (Gavrilets 2004, p. 131). This null model starts with a two-loci, two-allele haploid population with haplotype ab fixed where alleles a and B are assumed to be incompatible. It produces incipient species by (irreversible) mutation of the first allele from a to A. This incipient species, with haplotype Ab, is assumed to be spatially isolated from the mother species (no migration). Speciation completes when the second allele mutates (irreversibly) from b to B, resulting in a population of haplotype AB. The daughter species and the parent species are incompatible because one carries the a-allele and the other the B-allele. There are many possible extensions of this null model of mutation and drift, considering the divergence of two rather than one populations (i.e., not only the daughter species undergoes mutation), migration, local adaptation, and reversibility of mutations, but all two-loci two-allele models in Gavrilets (2004) that require only one incompatibility for speciation to be complete, have a speciation-completion time that is exponentially distributed. This is the crucial feature that is incorporated in the protracted speciation model as described above.

There are also multidimensional versions of the BDM model where a certain number of incompatibilities are required for speciation to complete (Orr 1995; Gavrilets 2004; Wang et al. 2013). In such cases, the speciation-completion time is no longer exponentially distributed. Etienne and Rosindell (2012) proposed that such models can be mimicked by the protracted speciation model with multiple incipient stages. The probability density of the speciation-completion time is a convolution of exponential distributions. For instance, in the special case that the transition rates are all the same, the speciation-completion time has a Gamma distribution. Lambert et al. (2014) provided a likelihood formula for this model (where transition rates are allowed to be different), and it seems that our method can thus be readily extended to more realistic versions of the BDM model, and that comparison of the performance of these models on phylogenetic trees would allow us to infer how hybrid incompatibilities build up over time. However, not only does the computation of the duration of speciation become problematic in this case because the mathematical machinery that Etienne and Rosindell (2012) employed to derive an expression for the duration of speciation is no longer applicable, the model itself needs reconsidering. Imagine, for example, that in a model with three incipient stages, we have an incipient species in the third incipient stage. It produces a new incipient species (at rate b). Then what incipient stage does this new incipient species have? With respect to its parent incipient species, it has stage 1, but with respect to the grandparent species, it is also in stage 3 as it has accumulated the same number of incompatibilities with the grandparent as the parent (and perhaps even one more, depending on how we view its difference from the parent). Because of these considerations, we argue that a more detailed analysis of the build-up of incompatibilities is needed to make inferences on which BDM model is most likely (see Wang et al. 2013 for a promising direction). Outside of the BDM framework, matters get even trickier (see, e.g., Chevin et al. 2014).

Although we thus caution against overinterpreting and extending the lineage-based model of protracted speciation and welcome new models of protracted speciation with fewer limitations, the protracted speciation model with a single incipient stage is still a coherent model that can act as a proper null model of macroevolution that accounts for the fact that speciation takes time. Every model is a simplification of reality, and the art of modeling consists in incorporating the key elements. We argue that incorporating the fact that speciation takes time is such a key element leading to a new perspective and a major improvement compared to the constant-rate birth–death model, whereas incorporating a more realistic distribution for the waiting time to speciation-completion is the obvious next step.

The rate of speciation-completion in the protracted speciation model is linked to the more commonly known rate at which populations acquire reproductive isolation. Rabosky and Matute (2013) found that the macroevolutionary speciation rates, as estimated from phylogenies, are decoupled from rates of acquisition of reproductive isolation in birds and Drosophila. At first sight, this may seem to be at odds with the basic prediction from the protracted speciation model that longer time to speciation-completion leads to lower species diversity (because incipient species may go extinct before speciation-completion) and hence an overall smaller rate of speciation. To explore this paradox further, we estimated the speciation rate with the constant-rate birth–death model (as Rabosky and Matute 2013 did) and the speciation-completion rate with the protracted speciation model from the phylogenetic branching times for 80 bird clades (there are no complete phylogenies available for Drosophila). We observed that the correlation between the two rates was in fact weak for low speciation-completion rates (Fig. S3). In our simulations, we also found only slight variation in the estimated speciation rates with one order of magnitude variation in the rate of speciation-completion (Fig. S2). Hence, this agrees with Rabosky and Matute's (2013) findings of apparent decoupling between speciation rate and reproductive isolation. The paradox can be resolved by recognizing that the speciation rate estimated using a constant-rate birth–death model is meaningless if speciation is considerably protracted, and hence conclusions on decoupling of these rates are premature.

The protracted speciation model can explain slowdowns in lineage accumulation through time, but it is not the only model that can do this (see reviews by Morlon 2014 and Moen and Morlon 2014). Time-dependence (Nee et al. 1992, 1994; Morlon et al. 2011; Stadler 2011) and diversity-dependence (Valentine 1973; Nee et al. 1992; Rabosky and Lovette 2008; Phillimore and Price 2008; Rabosky 2009; Etienne et al. 2012) of speciation and extinction rates have similar effects (Moen and Morlon 2014). The availability of the likelihood for the protracted speciation model now allows explicit comparisons of model performance on the wealth of currently available phylogenies. Although such a meta-analysis is interesting, we argue that its conclusions are limited to the precise mathematical formulation of the time-dependence, diversity-dependence, or protractedness of speciation. For instance, several mathematical formulations of diversity-dependence have been proposed, such as a linearly or an exponentially declining speciation rate, or increasing extinction rate. Similarly, the choice of functions in time-dependent speciation and extinction is endless, and our discussion on the BDM model suggests a multitude of alternative protracted speciation models. We expect that phylogenetic branching times alone will not contain sufficient information to single out any of these models: the likelihoods will be quite similar, or can be made similar by choosing a different function of time or diversity, or a different waiting time distribution for speciation-completion. We base this expectation on the results of Purvis et al. (2009) who found decisive support for diversity-dependence in only one (Dendroica) out of 14 avian clades, and on a pilot study we conducted ourselves on the 45 avian clades of Phillimore and Price (2008). Choosing between these alternative models should therefore involve other types of data. Because the diversity-dependent model predicts a different historical diversity than time-dependence or protracted speciation, fossil data will be crucial for model selection. Topological features of phylogenies may also be informative: the protracted speciation, with differential speciation-initiation rates (good and incipient species produce new incipient species at different rates), naturally allows for imbalanced phylogenies (Etienne and Rosindell 2012), whereas time-dependence and diversity-dependence cannot do so without rate heterogeneity between lineages (but see Etienne and Haegeman 2012 for a particular extension of the diversity-dependent model that does produce imbalanced phylogenies without rate heterogeneity). There are also more philosophical argument to prefer one model over the other. Time-dependence may seem an ad hoc explanation as it requires external forcing, but in the presence of such external forcing, it becomes the most obvious explanation. Diversity-dependence relies on the assumption that ecological limits are inhibiting diversification just at the present day, but not in the past (but see Etienne and Haegeman 2012 for a possible resolution of this paradox), whereas slowdowns in lineage accumulation near the present arises naturally, without additional assumptions, under the protracted speciation model. This feature works in favor of the protracted speciation model, even if a particular implementation of it is outperformed quantitatively by an alternative model.

We estimated the duration of speciation for the primate tree using a consensus tree. Currently, phylogenetic trees are usually built using a standard, nonprotracted birth–death model, or even a simple Yule model as the prior for the species tree. Ideally, the protracted speciation model should be implemented as a species tree prior in phylogenetic reconstruction software package such as BEAST (Drummond and Rambaut 2007), MrBayes (Huelsenbeck and Ronquist 2001; Ronquist and Huelsenbeck 2003), or RevBayes (Höhna et al. 2013), and protracted speciation parameter values can then be directly taken from the Bayesian posterior distribution of these parameters when reconstructing the phylogeny from sequence alignments. This implementation is not trivial, however, because considering that speciation is protracted not just affects the species tree prior, but also the probability distribution of the gene tree when we have multiple samples per species.

We see a fruitful future for applying the methods developed in this article to detect changes in the duration of speciation along environmental gradients. For instance, it allows studying how the duration of speciation changes with latitude or across biogeographic realms, and how it depends on species’ traits, for example, body size. We hope that this article will stimulate these research areas to deepen our understanding of macroevolution.

DATA ARCHIVING

The doi for our data is 10.5061/dryad.js88n.

Supporting Information

Additional Supporting Information may be found in the online version of this article at the publisher's website

Figure S1

The (relative) error in estimating the parameters as a function of clade size (A) speciation-initiation rate, (B) extinction rate, (C) incipient diversification rate (speciation-initiation rate minus extinction rate), (D) speciation-completion rate, (E) duration of speciation in species that complete the speciation process (a composite of the speciation-initiation rate, the speciation-completion rate, and the extinction rate, eq. 4).

Figure S2. Speciation rates estimated with a constant-rate birth–death model from phylogenies simulated with the protracted speciation model.

Figure S3. Speciation rate, estimated using the constant-rate birth–death model, versus the speciation-completion rate, estimated using the protracted speciation model, for 80 avian clades.