DYNAMICS AND STAGNATION IN THE MALTHUSIAN EPOCH

Abstract

This paper examines the central hypothesis of the influential Malthusian theory, according to which improvements in the technological environment during the pre-industrial era had generated only temporary gains in income per capita, eventually leading to a larger, but not significantly richer, population. Exploiting exogenous sources of cross-country variations in land productivity and the level of technological advancement the analysis demonstrates that, in accordance with the theory, technological superiority and higher land productivity had significant positive effects on population density but insignificant effects on the standard of living, during the time period 1–1500 CE.

1 Introduction

The transition from an epoch of stagnation to an era of sustained economic growth has marked the onset of one of the most remarkable transformations in the course of human history. While living standards in the world economy stagnated during the millennia preceding the Industrial Revolution, income per capita has encountered an unprecedented ten-fold increase in the past two centuries, profoundly altering the level and the distribution of education, health and wealth across the globe.¹

The Malthusian theory has been a central pillar in the interpretation of the process of development during the pre-industrial era and in the exploration of the forces that brought about the transition from stagnation to growth. Nevertheless, the underlying premise of the theory, that technological progress and resource expansion during this epoch had contributed primarily to the size of the population leaving income per capita relatively unaffected in the long run, has not been tested.²

The Malthusian theory, inspired by Thomas R. Malthus (1798), suggests that the worldwide stagnation in income per capita during the pre-industrial epoch reflected the counterbalancing effect of population growth on the expansion of resources, in an environment characterized by the positive effect of the standard of living on population growth along with diminishing labor productivity. Periods marked by the absence of changes in the level of technology or in the availability of land, were characterized by a stable population size as well as a constant income per capita, whereas periods characterized by improvements in the technological environment or in the availability of land generated only temporary gains in income per capita, eventually leading to a larger but not richer population. Technologically superior economies ultimately had denser populations but their standard of living did not reflect their technological advancement.

This research conducts a cross-country empirical analysis of the predictions of the influential Malthusian theory.³ It exploits exogenous sources of cross-country variation in land productivity and technological levels to examine their hypothesized differential effects on population density versus income per capita during the time period 1–1500 CE.

In light of the potential endogeneity of population and technological progress (Boserup, 1965), this research develops a novel identification strategy to examine the hypothesized effects of technological advancement on population density and income per capita. It establishes that the onset of the Neolithic Revolution that marked the transition of societies from hunting and gathering to agriculture, as early as 10,000 years ago, triggered a sequence of technological advancements that had a significant effect on the level of technology in the Middle Ages. As argued by Jared Diamond (1997), an earlier onset of the Neolithic Revolution has been associated with a developmental head start that enabled the rise of a non-food-producing class whose members were essential for the advancement of written language, science and technology, and for the formation of cities, technology-based military powers and nation states. Thus, variations in favorable biogeographical factors (i.e., prehistoric domesticable species of wild plants and animals) that led to an earlier onset of the Neolithic Revolution across the globe are exploited as exogenous sources of variation in the onset of the Neolithic Revolution and, consequently, in the level of technological advancement during the time period 1–1500 CE.

Consistent with Malthusian predictions, the analysis uncovers statistically significant positive effects of land productivity and the technological level on population density in the years 1 CE, 1000 CE, and 1500 CE. In contrast, the effects of land productivity and technology on income per capita in these periods are not significantly different from zero. Moreover, the estimated elasticities of income per capita with respect to these two channels are about an order of magnitude smaller than the corresponding elasticities of population density.

Importantly, the qualitative results remain robust to controls for the confounding effects of a large number of geographical factors, including absolute latitude, access to waterways, distance to the technological frontier, and the share of land in tropical versus temperate climatic zones, which may have had an impact on aggregate productivity either directly, by affecting the productivity of land, or indirectly via the prevalence of trade and the diffusion of technologies. Furthermore, the results are also qualitatively unaffected when a direct measure of technological sophistication, rather than the timing of the Neolithic Revolution, is employed as an indicator of the level of aggregate productivity. Finally, the study establishes that the results are not driven by unobserved time-invariant country fixed effects. In particular, it demonstrates that, while the change in the level of technology between 1000 BCE and 1 CE was indeed associated with a significant change in population density over the 1–1000 CE time horizon, the level of income per capita during this time period was relatively unaffected, as suggested by the Malthusian theory.

2 The Malthusian Model

2.1 The Basic Structure of the Model

Consider an overlapping-generations economy in which activity extends over infinite discrete time. In every period, the economy produces a single homogeneous good using land and labor as inputs. The supply of land is exogenous and fixed over time whereas the evolution of labor supply is governed by households’ decisions in the preceding period regarding the number of their children.

2.1.1 Production

Production occurs according to a constant-returns-to-scale technology. The output produced at time t, Y_t, is:

$$Y_t={(AX)}^{\alpha }{L}_t^{1-\alpha };\alpha \in (0,1),$$ (1)

where L_t and X are, respectively, labor and land employed in production in period t, and A measures the technological level.⁴ The technological level may capture the percentage of arable land, soil quality, climate, cultivation and irrigation methods, as well as the knowledge required for engagement in agriculture (i.e., domestication of plants and animals). Thus, AX captures the effective resources used in production.

Output per worker produced at time t, y_t ≡ Y_t/L_t, is therefore:

$$y_t={(AX/L_t)}^{\alpha }.$$ (2)

2.1.2 Preferences and Budget Constraints

In each period t, a generation consisting of L_t identical individuals joins the workforce. Each individual has a single parent. Members of generation t live for two periods. In the first period of life (childhood), t − 1, they are supported by their parents. In the second period of life (parenthood), t, they inelastically supply their labor, generating an income that is equal to the output per worker, y_t, which they allocate between their own consumption and that of their children.

Individuals generate utility from consumption and the number of their (surviving) children:⁵

$$u^t={(c_t)}^{1-\gamma }{(n_t)}^{\gamma };\gamma \in (0,1),$$ (3)

where c_t is the consumption and n_t is the number of children of an individual of generation t.

Members of generation t allocate their income between their consumption, c_t, and expenditure on children, ρn_t, where ρ is the cost of raising a child.⁶ Hence, the budget constraint for a member of generation t (in the second period of life) is:

$$\rho n_t+c_t\le y_t.$$ (4)

2.1.3 Optimization

Members of generation t allocate their income optimally between consumption and child rearing, so as to maximize their intertemporal utility function (3) subject to the budget constraint (4). Hence, individuals devote a fraction (1 − γ) to consumption and a fraction γ of their income to child rearing:

$$\begin{array}{l}{c}_t=(1-\gamma )y_t;\\ n_t=\gamma y_t/\rho .\end{array}$$ (5)

Thus, in accordance with the Malthusian paradigm, income has a positive effect on the number of surviving children.

2.2 The Evolution of the Economy

2.2.1 Population Dynamics

The evolution of the working population is determined by the initial size of the working population, L₀ > 0, and the number of (surviving) children per adult, n_t. Specifically, the size of the working population in period t + 1, L_t+1, is:

$$L_{t+1}=n_t{L}_t.$$ (6)

where L_t is the size of the working population in period t, and L₀ > 0 is given.

Substituting (2) and (5) into (6), the time path of the working population is governed by the first-order difference equation:

$$L_{t+1}=(\gamma /\rho ){(AX)}^{\alpha }{L}_t^{1-\alpha }\equiv \phi (L_t;A),$$ (7)

where, as depicted in Figure 1, φ_L(L_t; A) > 0 and φ_LL(L_t; A) < 0 so φ(L_t; A) is strictly concave in L_t, and φ(0; A) = 0, lim_Lt→0 φ_L(L_t; A) = ∞ and lim_{Lt→ ∞} φ_L (L_t; A) = 0.

Figure 1.

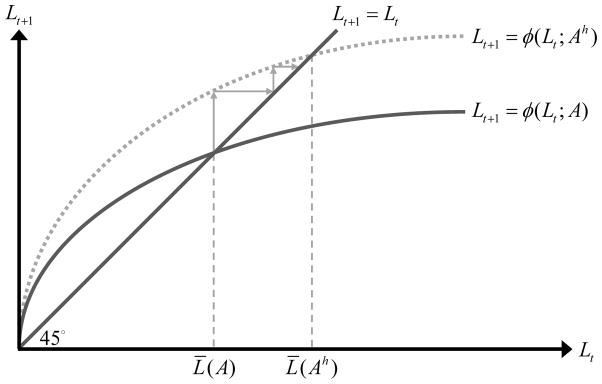
The Evolution of Population Size

Hence, for a given level of technology, A, noting that L₀ > 0, there exists a unique, stable steady-state level of the adult population, L̄:⁷

$$\overline{L}={(\gamma /\rho )}^{1/\alpha }(AX)\equiv \overline{L}(A),$$ (8)

and population density, P̄_d:

$${\overline{P}}_d\equiv \overline{L}/X={(\gamma /\rho )}^{1/\alpha }A\equiv {\overline{P}}_d(A).$$ (9)

Importantly, as is evident from (8) and (9), an improvement in the technological environment, A, increases the steady-state levels of the adult population, L̄, and population density, P̄_d:

$$\frac{\partial \overline{L}}{\partial A}>0\text{and}\frac{\partial {\overline{P}}_d}{\partial A}>0.$$ (10)

As depicted in Figure 1, if the economy is in a steady-state equilibrium, an increase in the technological level from A to A^h generates a transition process in which population gradually increases from its initial steady-state level, L̄, to a higher one, L̄^h. Similarly, a decline in the population due to an epidemic such as the Black Death (1348–1350 CE) would temporarily reduce population, while temporarily increasing income per capita. The rise in income per capita, however, will generate a gradual increase in population back to the initial steady-state level, L̄.

2.2.2 The Time Path of Income per Worker

The evolution of income per worker is determined by the initial level of income per worker and the number of (surviving) children per adult. Specifically, income per worker in period t + 1, y_t+1, noting (2) and (6), is:

$$y_{t+1}={[(AX)/L_{t+1}]}^{\alpha }={[(AX)/n_t{L}_t]}^{\alpha }=y_t/n_t^{\alpha }.$$ (11)

Substituting (5) into (11), the time path of income per worker is governed by the first-order difference equation:

$$y_{t+1}={(\rho /\gamma )}^{\alpha }{y}_t^{1-\alpha }\equiv \psi (y_t),$$ (12)

where, as depicted in Figure 2, ψ′(y_t) > 0 and ψ″(y_t) < 0 so ψ(y_t) is strictly concave, and ψ(0) = 0, lim_yt→0 ψ′(y_t) = ∞ and lim_{yt→ ∞} ψ′(y_t) = 0.

Figure 2.

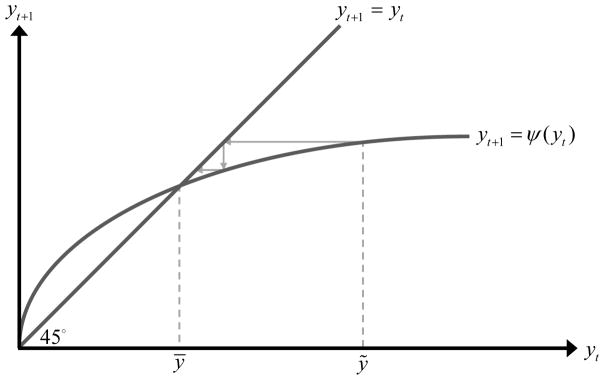
The Evolution of Income per Worker

Hence, given y₀ > 0, there exists a unique, stable steady-state level of income per worker, ȳ:⁸

$$\overline{y}=(\rho /\gamma ).$$ (13)

Importantly, as is evident from (2) and (13), while an advancement in the level of technology, A, increases the level of income per worker in the short-run, y_t, it does not affect the steady-state level of income per worker, ȳ:

$$\frac{\partial y_t}{\partial A}>0\text{and}\frac{\partial \overline{y}}{\partial A}=0.$$ (14)

As depicted in Figures 1 and 2, if the economy is in a steady-state equilibrium, an increase in the technological level from A^l to A^h generates a transition process in which income per worker initially increases to a higher level, ỹ, reflecting higher labor productivity in the absence of population adjustment. However, as population increases, income per worker gradually declines to the initial steady-state equilibrium, ȳ. Similarly, a decline in the population due to an epidemic such as the Black Death (1348–1350 CE) would temporarily reduce population to L̃, while temporarily increasing income per capita to ỹ. The rise in income per worker will generate a gradual increase in population back to the steady-state level, L̄, and thus a gradual decline in income per worker back to ȳ.

2.3 Testable Predictions

The Malthusian theory generates the following testable predictions:

1. Within a country, an increase in productivity would lead in the long run to a larger population, without altering the long-run level of income per capita.

2. Across countries, those characterized by superior land productivity or a superior level of technology would have, all else equal, higher population densities in the long run, but their standards of living would not reflect the degree of their technological advancement.

These predictions emerge from a Malthusian model as long as the model is based upon two fundamental features: (a) a positive effect of the standard of living on population growth, and (b) decreasing returns to labor due to the presence of a fixed factor of production – land.⁹

3 Empirical Framework

3.1 Empirical Strategy

The empirical examination of the central hypothesis of the Malthusian theory exploits exogenous sources of cross-country variation in land productivity and technological levels to examine their hypothesized differential effects on population density and income per capita during the time period 1–1500 CE.

In light of the potential endogeneity of population and technological progress, this research develops a novel identification strategy to examine the hypothesized effects of technological advancement on population density and income per capita. First, it establishes that the onset of the Neolithic Revolution, which marked the transition of societies from hunting and gathering to agriculture as early as 10,000 years ago, triggered a sequence of technological advancements that had a significant effect on the level of technology in the Middle Ages. As argued by Diamond (1997), an earlier onset of the Neolithic Revolution has been associated with a developmental head start that enabled the rise of a non-food-producing class whose members were essential for the advancement of written language, science and technology, and for the formation of cities, technology-based military powers and nation states.¹⁰ Thus, variation in the onset of the Neolithic Revolution across the globe is exploited as a proxy for variation in the level of technological advancement during the time period 1–1500 CE.

In addition, to address the possibility that the relationship between the timing of the Neolithic transition and population density in the Common Era may itself be spurious, being perhaps co-determined by an unobserved channel such as human capital, the analysis appeals to the role of prehistoric biogeographical endowments in determining the timing of the Neolithic Revolution. Importantly, the productivity of land for agriculture in the Common Era is largely independent of the initial geographical and biogeographical endowments that were conducive for the onset of the Neolithic Revolution. While agriculture originated in regions of the world to which the most valuable domesticable wild plant and animal species were native, other regions proved more fertile and climatically favorable once the diffusion of agricultural practices brought the domesticated varieties to them (Diamond, 1997). Thus, the analysis adopts an instrumental variables strategy, exploiting variation in the numbers of prehistoric domesticable species of plants and animals that were native to a region prior to the onset of sedentary agricultural practices as exogenous sources of variation for the number of years elapsed since the Neolithic Revolution to demonstrate its causal effect on population density in the Common Era.¹¹

Moreover, a direct, period-specific measure of technological sophistication is also employed as an alternative metric of the level of aggregate productivity to demonstrate the qualitative robustness of the baseline results for the years 1000 CE and 1 CE.¹² Once again, the link running from the exogenous prehistoric biogeographical endowments to the level of technological advancement in the Common Era, via the timing of the Neolithic transition, enables the analysis to exploit the aforementioned biogeographical variables as instruments for the indices of technological sophistication in the years 1000 CE and 1 CE to establish their causal effects on population density in these periods.

Finally, in order to ensure that the results from the level regressions are not driven by unobserved time-invariant country fixed effects, this research also employs a first-difference estimation strategy with a lagged explanatory variable. In particular, the robustness analysis exploits cross-country variation in the change in the level of technological sophistication between the years 1000 BCE and 1 CE to explain the cross-country variations in the change in population density and the change in income per capita over the 1–1000 CE time horizon.

3.2 The Data

The most comprehensive worldwide cross-country historical estimates of population and income per capita since the year 1 CE have been assembled by Colin McEvedy and Richard Jones (1978) and Angus Maddison (2003) respectively.¹³ Indeed, despite inherent problems of measurement associated with historical data, these sources remain unparalleled in providing comparable estimates across countries in the last 2000 years and have, therefore, widely been regarded as standard sources for such data in the long-run growth literature.¹⁴ For the purposes of the current analysis, the population density of a country for a given year is computed as population in that year, as reported by McEvedy and Jones (1978), divided by total land area.

The measure of land productivity employed is the first principal component of the percentage of arable land and an index reflecting the overall suitability of land for agriculture, based on geospatial soil quality and temperature data, as reported by Navin Ramankutty et al. (2002) and aggregated to the country level by Stelios Michalopoulos (2008).¹⁵ The variable for the timing of the Neolithic Revolution, constructed by Louis Putterman (2008), measures the number of thousand years elapsed, relative to the year 2000 CE, since the majority of the population residing within a country’s modern national borders began practicing sedentary agriculture as the primary mode of subsistence.

The index of technological sophistication is constructed based on historical cross-cultural technology data, reported with global coverage in Peregrine’s (2003) Atlas of Cultural Evolution. In particular, for a given time period and for a given culture in the archaeological record, the Atlas of Cultural Evolution draws on various anthropological and historical sources to report the level of technological advancement, on a 3-point scale, in each of four sectors of the economy, including communications, industry (i.e., ceramics and metallurgy), transportation, and agriculture. The index of technological sophistication is constructed following the aggregation methodology of Diego Comin, William Easterly, and Erick Gong (2008).¹⁶

3.3 The Neolithic Revolution and Technological Advancement

This section establishes that the Neolithic Revolution triggered a cumulative process of economic development, conferring a developmental head start to societies that experienced the agricultural transition earlier. In line with this assertion, Table 1 reveals preliminary results indicating that an earlier onset of the Neolithic Revolution is indeed positively and significantly correlated with the level of technological sophistication in non-agricultural sectors of the economy in the years 1000 CE and 1 CE. For instance, the coefficient estimates for the year 1000 CE, all of which are statistically significant at the 1 percent level, indicate that a 1 percent increase in the number of years elapsed since the onset of the Neolithic Revolution is associated with an increase in the level of technological advancement in the communications, industrial, and transportation sectors by 0.37, 0.07, and 0.38 percent respectively.

Table 1.

The Neolithic Revolution as a proxy for Technological Advancement

	(1)	(2)	(3)	(4)	(5)	(6)
	OLS	OLS	OLS	OLS	OLS	OLS
	Dependent Variable is Level of:
	Log Communications Technology in:		Log Industrial Technology in:		Log Transportation Technology in:
	1000 CE	1 CE	1000 CE	1 CE	1000 CE	1 CE
Log Years since Neolithic Transition	0.368*** (0.028)	0.283*** (0.030)	0.074*** (0.014)	0.068*** (0.015)	0.380*** (0.029)	0.367*** (0.031)
Observations	143	143	143	143	143	143
R-squared	0.48	0.26	0.17	0.12	0.52	0.51

Summary – This table demonstrates that the timing of the Neolithic Revolution is positively and significantly correlated with the level of technology in multiple non-agricultural sectors of an economy in the years 1000 CE and 1 CE.

Notes – (i) the level of technology in communications is indexed according to the absence of both true writing and mnemonic or non-written records, the presence of only mnemonic or non-written records, or the presence of both; (ii) the level of technology in industry is indexed according to the absence of both metalworks and pottery, the presence of only pottery, or the presence of both; (iii) the level of technology in transportation is indexed according to the absence of both vehicles and pack or draft animals, the presence of only pack or draft animals, or the presence of both; (vi) robust standard error estimates are reported in parentheses; (v) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.

These findings lend credence to the empirical strategy employed by this research to test the Malthusian theory. Specifically, they provide evidence justifying the use of the exogenous source of cross-country variation in the timing of the Neolithic Revolution as a proxy for the variation in the level of technological advancement across countries during the agricultural stage of development. Moreover, they serve as an internal consistency check between the cross-country Neolithic transition-timing variable and those on historical levels of technological sophistication, all of which are relatively new in terms of their application in the empirical literature on long-run development.

3.4 The Basic Regression Model

Formally, the baseline specifications adopted to test the Malthusian predictions regarding the effects of land productivity and the level of technological advancement on population density and income per capita are:

$$ln{P}_{i,t}={\alpha }_{0,t}+{\alpha }_{1,t}ln{T}_i+{\alpha }_{2,t}ln{X}_i+{\mathit{\alpha }}_{\mathbf{3},\mathit{t}}^{\prime }{\mathbf{\Gamma }}_{\mathit{i}}+{\mathit{\alpha }}_{\mathbf{4},\mathit{t}}^{\prime }{\mathit{D}}_{\mathit{i}}+{\delta }_{i,t},$$ (15)

$$ln{y}_{i,t}={\beta }_{0,t}+{\beta }_{1,t}ln{T}_i+{\beta }_{2,t}ln{X}_i+{\mathit{\beta }}_{3,\mathrm{t}}^{\prime }{\mathbf{\Gamma }}_{\mathit{i}}+{\mathit{\beta }}_{\mathbf{4},\mathit{t}}^{\prime }{\mathit{D}}_{\mathit{i}}+{\epsilon }_{i,t},$$ (16)

where P_i,t is the population density of country i in year t; y_i,t is country i’s income per capita in year t; T_i is the number of years elapsed since the onset of agriculture in country i; X_i is a measure of land productivity for country i, based on the percentage of arable land and an index of agricultural suitability; Γ_i is a vector of geographical controls for country i, including absolute latitude and variables gauging access to waterways; D_i is a vector of continental dummies; and, δ_i,t and ε_i,t are country-specific disturbance terms for population density and income per capita, respectively, in year t.

4 Cross-Country Evidence

Consistent with the predictions of the Malthusian theory, the results demonstrate highly statistically significant positive effects of land productivity and the number of years elapsed since the Neolithic Revolution on population density in the years 1500 CE, 1000 CE and 1 CE. The effects of these explanatory channels on income per capita in the corresponding periods, however, are not significantly different from zero, a result that fully complies with Malthusian priors. These results are shown to be robust to controls for other geographical factors, including absolute latitude, access to waterways, distance to the nearest technological frontier, the percentage of land in tropical versus temperate climatic zones, and small island and landlocked dummies, all of which may have had an impact on aggregate productivity either directly, by affecting the productivity of land, or indirectly by affecting trade and the diffusion of technologies.¹⁷ Moreover, as foreshadowed by the initial findings in Table 1, the results are qualitatively unaffected when the index of technological sophistication, rather than the number of years elapsed since the Neolithic Revolution, is employed as a proxy for the level of aggregate productivity.

4.1 Population Density in 1500 CE

This section establishes the significant positive effects of land productivity and the level of technological advancement, as proxied by the timing of the Neolithic Revolution, on population density in the year 1500 CE. The results from regressions explaining log population density in the year 1500 CE are presented in Table 2. In particular, a number of specifications comprising different subsets of the explanatory variables in equation (15) are estimated to examine the independent and combined effects of the transition-timing and land-productivity channels, while controlling for other geographical factors and continental fixed effects.

Table 2.

Explaining Population Density in 1500 CE

	(1)	(2)	(3)	(4)	(5)	(6)
	OLS	OLS	OLS	OLS	OLS	IV
	Dependent Variable is Log Population Density in 1500 CE
Log Years since Neolithic Transition	0.833*** (0.298)		1.025*** (0.223)	1.087*** (0.184)	1.389*** (0.224)	2.077*** (0.391)
Log Land Productivity		0.587*** (0.071)	0.641*** (0.059)	0.576*** (0.052)	0.573*** (0.095)	0.571*** (0.082)
Log Absolute Latitude		−0.425*** (0.124)	−0.353*** (0.104)	−0.314*** (0.103)	−0.278** (0.131)	−0.248** (0.117)
Mean Distance to Nearest Coast or River				−0.392*** (0.142)	0.220 (0.346)	0.250 (0.333)
Percentage of Land within 100 km of Coast or River				0.899*** (0.282)	1.185*** (0.377)	1.350*** (0.380)
Continent Dummies	Yes	Yes	Yes	Yes	Yes	Yes
Observations	147	147	147	147	96	96
R-squared	0.40	0.60	0.66	0.73	0.73	0.70
First-stage F-statistic	–	–	–	–	–	14.65
Overid. p-value	–	–	–	–	–	0.440

Summary – This table establishes, consistently with Malthusian predictions, the significant positive effects of land productivity and the level of technological advancement, as proxied by the timing of the Neolithic Revolution, on population density in the year 1500 CE, while controlling for access to navigable waterways, absolute latitude, and unobserved continental fixed effects.

Notes – (i) log land productivity is the first principal component of the log of the percentage of arable land and the log of an agricultural suitability index; (ii) the IV regression employs the numbers of prehistoric domesticable species of plants and animals as instruments for log transition timing; (iii) the statistic for the first-stage F-test of these instruments is significant at the 1 percent level; (iv) the p-value for the overidentifying restrictions test corresponds to Hansen’s J statistic, distributed in this case as chi-square with one degree of freedom; (v) a single continent dummy is used to represent the Americas, which is natural given the historical period examined; (vi) regressions (5)-(6) do not employ the Oceania dummy due to a single observation for this continent in the IV data-restricted sample; (vii) robust standard error estimates are reported in parentheses; (viii) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.

Consistent with Malthusian predictions, Column 1 reveals the positive relationship between log years since transition and log population density in the year 1500 CE, while controlling for continental fixed effects.¹⁸ Specifically, the estimated OLS coefficient implies that a 1 percent increase in the number of years elapsed since the Neolithic transition increases population density in 1500 CE by 0.83 percent, an effect that is statistically significant at the 1 percent level.¹⁹ Moreover, based on the R-squared of the regression, the transition-timing channel appears to explain 40 percent of the variation in log population density in 1500 CE along with the dummies capturing unobserved continental characteristics.

The effect of the land-productivity channel, controlling for absolute latitude and continental fixed effects, is reported in Column 2. In line with theoretical predictions, a 1 percent increase in land productivity raises population density in 1500 CE by 0.59 percent, an effect that is also significant at the 1 percent level. Interestingly, in contrast to the relationship between absolute latitude and contemporary income per capita, the estimated elasticity of population density in 1500 CE with respect to absolute latitude suggests that economic development during this period was on average higher at latitudinal bands closer to the equator.²⁰ Thus, while proximity to the equator was beneficial in the agricultural stage of development, it appears detrimental in the industrial stage. The R-squared of the regression indicates that, along with continental fixed effects and absolute latitude, the land-productivity channel explains 60 percent of the cross-country variation in log population density in 1500 CE.

Column 3 presents the results from examining the combined explanatory power of the previous two regressions. The estimated coefficients on the transition-timing and land-productivity variables remain highly statistically significant and continue to retain their expected signs, while increasing slightly in magnitude in comparison to their estimates in earlier columns. Furthermore, transition timing and land productivity together explain 66 percent of the variation in log population density in 1500 CE, along with absolute latitude and continental fixed effects.

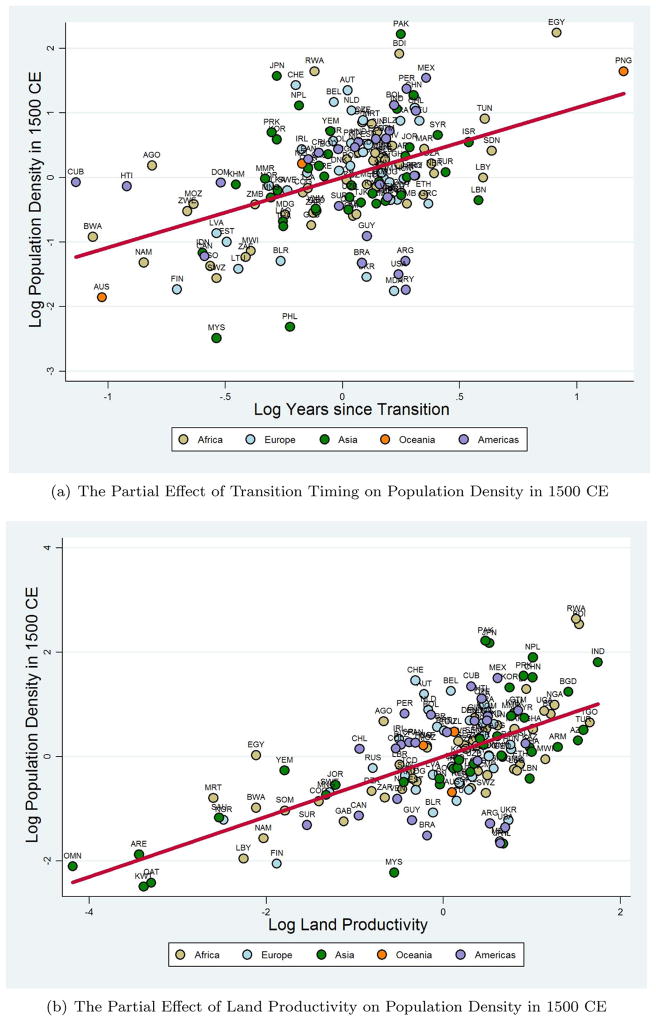
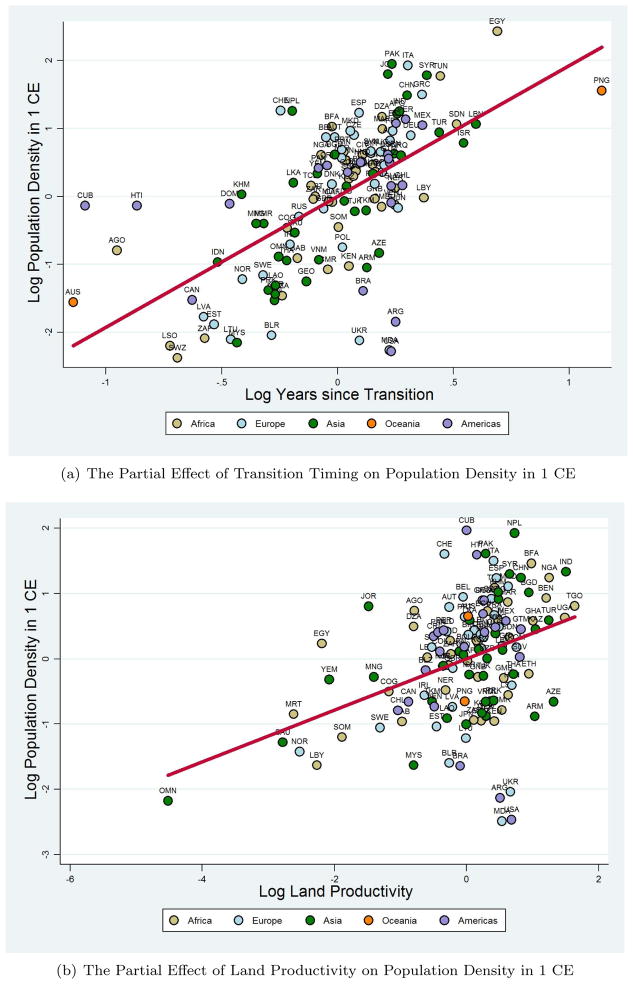
The explanatory power of the regression in Column 3 improves by an additional 7 percentage points once controls for access to waterways are accounted for in Column 4, which constitutes the baseline regression specification for population density in 1500 CE. In comparison to the estimates reported in Column 3, the effects of the transition-timing and land-productivity variables remain reassuringly stable in both magnitude and statistical significance when subjected to the additional geographical controls. Moreover, the estimated coefficients on the additional geographical controls indicate significant effects consistent with the assertion that better access to waterways has been historically beneficial for economic development by fostering urbanization, international trade and technology diffusion. To interpret the baseline effects of the variables of interest, a 1 percent increase in the number of years elapsed since the Neolithic Revolution raises population density in 1500 CE by 1.09 percent, conditional on land productivity, absolute latitude, waterway access and continental fixed effects. Similarly, a 1 percent increase in land productivity generates, ceteris paribus, a 0.58 percent increase in population density in 1500 CE.²¹ These conditional effects of the transition-timing and land-productivity channels from the baseline specification are depicted as partial regression lines on the scatter plots in Figures 3(a) and 3(b) respectively.

Figure 3.

Transition Timing, Land Productivity, and Population Density in 1500 CE

Summary – This figure depicts the partial regression line for the effect of transition timing (land productivity) on population density in the year 1500 CE, while controlling for the influence of land productivity (transition timing), absolute latitude, access to waterways, and continental fixed effects. Thus, the x- and y-axes plot the residuals obtained from regressing transition timing (land productivity) and population density, respectively, on the aforementioned set of covariates.

The analysis now turns to address issues regarding causality, particularly with respect to the transition-timing variable. Specifically, while variations in land productivity and other geographical characteristics are inarguably exogenous to the cross-country variation in population density, the onset of the Neolithic Revolution and the outcome variable of interest may in fact be endogenously determined. Specifically, although reverse causality is not a source of concern, given that the vast majority of countries underwent the Neolithic transition prior to the Common Era, the OLS estimates of the effect of the time elapsed since the transition to agriculture may suffer from omitted variable bias, reflecting spurious correlations with the outcome variable being examined.

To establish the causal effect of the timing of the Neolithic transition on population density in the Common Era, the investigation appeals to Diamond’s (1997) hypothesis on the role of exogenous geographical and biogeographical endowments in determining the timing of the Neolithic Revolution. Accordingly, the emergence and subsequent diffusion of agricultural practices were primarily driven by geographical conditions such as climate, continental size and orientation, as well as the availability of wild plant and animal species amenable to domestication. However, while geographical factors certainly continued to play a direct role in economic development after the onset of agriculture, it is postulated that the availability of prehistoric domesticable wild plant and animal species did not influence population density in the Common Era other than through the timing of the Neolithic Revolution. The analysis consequently adopts the numbers of prehistoric domesticable species of wild plants and animals, obtained from the dataset of Olsson and Hibbs (2005), as instruments to establish the causal effect of the timing of the Neolithic transition on population density.

The final two columns in Table 2 report the results associated with a subsample of countries for which data on the biogeographical instruments are available. To allow meaningful comparisons between IV and OLS coefficient estimates, Column 5 repeats the baseline OLS regression analysis on this particular subsample of countries, revealing that the coefficients on the explanatory variables of interest remain largely stable in terms of both magnitude and significance compared to those estimated using the baseline sample. This is a reassuring indicator that any additional sampling bias introduced by the restricted sample, particularly with respect to the transition-timing and land-productivity variables, is negligible. Consistent with this assertion, the explanatory powers of the baseline and restricted sample regressions are nearly identical.

Column 6 presents the IV regression results from estimating the baseline specification with log years since transition instrumented by the numbers of prehistoric domesticable species of plants and animals.²² The estimated causal effect of the timing of the Neolithic transition on population density not only retains statistical significance at the 1 percent level but is substantially stronger in comparison to the estimate in Column 5. This pattern is consistent with attenuation bias afflicting the OLS coefficient as a result of measurement error in the transition-timing variable. To interpret the causal impact of the timing of the Neolithic Revolution, a 1 percent increase in years elapsed since the onset of agriculture causes, ceteris paribus, a 2.08 percent increase in population density in the year 1500 CE.

The coefficient on land productivity, which maintains stability in both magnitude and statistical significance across the OLS and IV regressions, indicates that a 1 percent increase in land productivity raises population density by 0.57 percent, conditional on the timing of the Neolithic transition, other geographical factors and continental fixed effects. Finally, the rather strong F-statistic from the first-stage regression provides verification for the significance and explanatory power of the biogeographical instruments employed for the timing of the Neolithic Revolution, while the high p-value associated with the test for overidentifying restrictions is supportive of the claim that these instruments do not exert any independent influence on population density in 1500 CE other than through the transition-timing channel.

4.2 Population Density in Earlier Historical Periods

This section demonstrates the significant positive effects of land productivity and the level of technological advancement, as proxied by the timing of the Neolithic Revolution, on population density in the years 1000 CE and 1 CE. The results from regressions explaining log population density in the years 1000 CE and 1 CE are presented in Tables 3 and 4 respectively. As before, the independent and combined explanatory powers of the transition-timing and land-productivity channels are examined while controlling for other geographical factors and unobserved continental characteristics.

Table 3.

Explaining Population Density in 1000 CE

	(1)	(2)	(3)	(4)	(5)	(6)
	OLS	OLS	OLS	OLS	OLS	IV
	Dependent Variable is Log Population Density in 1000 CE
Log Years since Neolithic Transition	1.232*** (0.293)		1.435*** (0.243)	1.480*** (0.205)	1.803*** (0.251)	2.933*** (0.504)
Log Land Productivity		0.470*** (0.081)	0.555*** (0.065)	0.497*** (0.056)	0.535*** (0.098)	0.549*** (0.092)
Log Absolute Latitude		−0.377** (0.148)	−0.283** (0.116)	−0.229** (0.111)	−0.147 (0.127)	−0.095 (0.116)
Mean Distance to Nearest Coast or River				−0.528*** (0.153)	0.147 (0.338)	0.225 (0.354)
Percentage of Land within 100 km of Coast or River				0.716** (0.323)	1.050** (0.421)	1.358*** (0.465)
Continent Dummies	Yes	Yes	Yes	Yes	Yes	Yes
Observations	142	142	142	142	94	94
R-squared	0.38	0.46	0.59	0.67	0.69	0.62
First-stage F-statistic	–	–	–	–	–	15.10
Overid. p-value	–	–	–	–	–	0.281

Summary – This table establishes, consistently with Malthusian predictions, the significant positive effects of land productivity and the level of technological advancement, as proxied by the timing of the Neolithic Revolution, on population density in the year 1000 CE, while controlling for access to navigable waterways, absolute latitude, and unobserved continental fixed effects.

Notes – (i) log land productivity is the first principal component of the log of the percentage of arable land and the log of an agricultural suitability index; (ii) the IV regression employs the numbers of prehistoric domesticable species of plants and animals as instruments for log transition timing; (iii) the statistic for the first-stage F-test of these instruments is significant at the 1 percent level; (iv) the p-value for the overidentifying restrictions test corresponds to Hansen’s J statistic, distributed in this case as chi-square with one degree of freedom; (v) a single continent dummy is used to represent the Americas, which is natural given the historical period examined; (vi) regressions (5)-(6) do not employ the Oceania dummy due to a single observation for this continent in the IV data-restricted sample; (vii) robust standard error estimates are reported in parentheses; (viii) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.

Table 4.

Explaining Population Density in 1 CE

	(1)	(2)	(3)	(4)	(5)	(6)
	OLS	OLS	OLS	OLS	OLS	IV
	Dependent Variable is Log Population Density in 1 CE
Log Years since Neolithic Transition	1.560*** (0.326)		1.903*** (0.312)	1.930*** (0.272)	2.561*** (0.369)	3.459*** (0.437)
Log Land Productivity		0.404*** (0.106)	0.556*** (0.081)	0.394*** (0.067)	0.421*** (0.094)	0.479*** (0.089)
Log Absolute Latitude		−0.080 (0.161)	−0.030 (0.120)	0.057 (0.101)	0.116 (0.121)	0.113 (0.113)
Mean Distance to Nearest Coast or River				−0.685*** (0.155)	−0.418 (0.273)	−0.320 (0.306)
Percentage of Land within 100 km of Coast or River				0.857** (0.351)	1.108*** (0.412)	1.360*** (0.488)
Continent Dummies	Yes	Yes	Yes	Yes	Yes	Yes
Observations	128	128	128	128	83	83
R-squared	0.47	0.41	0.59	0.69	0.75	0.72
First-stage F-statistic	–	–	–	–	–	10.85
Overid. p-value	–	–	–	–	–	0.590

Summary – This table establishes, consistently with Malthusian predictions, the significant positive effects of land productivity and the level of technological advancement, as proxied by the timing of the Neolithic Revolution, on population density in the year 1 CE, while controlling for access to navigable waterways, absolute latitude, and unobserved continental fixed effects.

Notes – (i) log land productivity is the first principal component of the log of the percentage of arable land and the log of an agricultural suitability index; (ii) the IV regression employs the numbers of prehistoric domesticable species of plants and animals as instruments for log transition timing; (iii) the statistic for the first-stage F-test of these instruments is significant at the 1 percent level; (iv) the p-value for the overidentifying restrictions test corresponds to Hansen’s J statistic, distributed in this case as chi-square with one degree of freedom; (v) a single continent dummy is used to represent the Americas, which is natural given the historical period examined; (vi) regressions (5)-(6) do not employ the Oceania dummy due to a single observation for this continent in the IV data-restricted sample; (vii) robust standard error estimates are reported in parentheses; (viii) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.

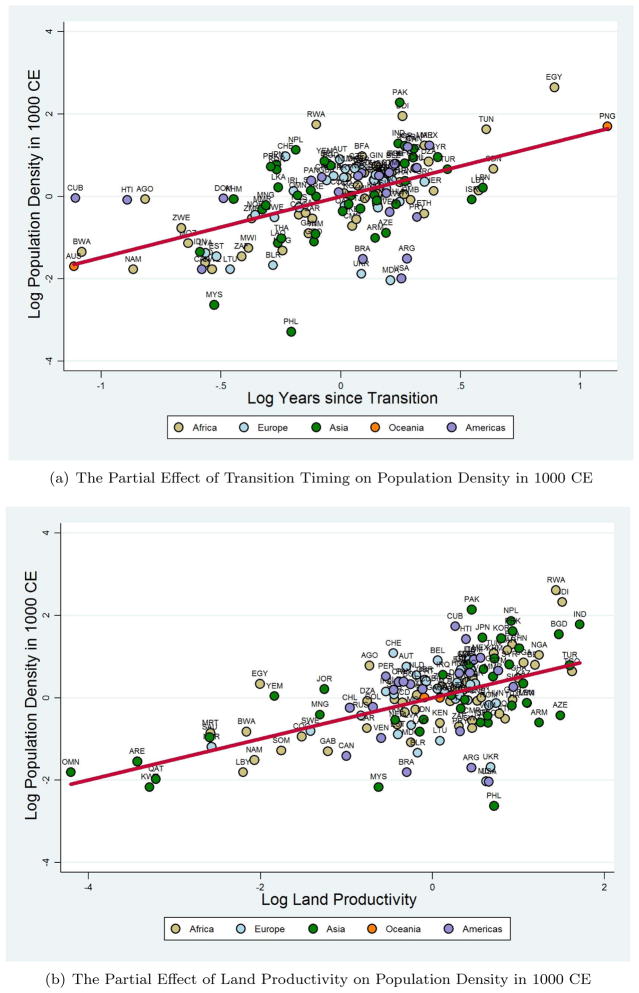
In line with the empirical predictions of the Malthusian theory, the findings reveal highly statistically significant positive effects of land productivity and an earlier transition to agriculture on population density in these earlier historical periods as well. Moreover, the positive impact on economic development of geographical factors capturing better access to waterways is also confirmed for these earlier periods.²³

The stability patterns exhibited by the magnitude and significance of the coefficients on the explanatory variables of interest in Tables 3–4 are strikingly similar to those observed in the 1500 CE analysis. Thus, for instance, while statistical significance remains unaffected across specifications, the independent effects of Neolithic transition timing and land productivity from the first two columns in each table increase slightly in magnitude when both channels are examined concurrently in Column 3, and remain stable thereafter when subjected to the additional geographical controls in the baseline regression specification of the fourth column. This is a reassuring indicator that the variance-covariance characteristics of the regression samples employed for the different periods are not fundamentally different from one another, despite differences in sample size due to the greater unavailability of population density data in the earlier historical periods. The qualitative similarity of the results across periods also suggests that the empirical findings are indeed more plausibly associated with the Malthusian theory as opposed to being consistently generated by spurious correlations between population density and the explanatory variables of interest across the different historical periods.

To interpret the baseline effects of interest from Column 4 of the analysis for each historical period, a 1 percent increase in the number of years elapsed since the onset of the Neolithic Revolution raises population density in the years 1000 CE and 1 CE by 1.48 and 1.93 percent respectively, conditional on the productivity of land, absolute latitude, access to waterways and continental fixed effects.²⁴ Similarly, a 1 percent increase in land productivity is associated with, ceteris paribus, a 0.50 percent increase in population density in 1000 CE and a 0.39 percent increase in population density in 1 CE.²⁵

For the 1000 CE analysis, the additional sampling bias introduced on OLS estimates by moving to the IV-restricted subsample in Column 5 is similar to that observed earlier in Table 2, whereas the bias appears somewhat larger for the analysis in 1 CE. This is partly attributable to the smaller size of the subsample in the latter analysis. The IV regressions in Column 6, however, once again reflect the pattern that the causal effect of transition timing on population density in each period is stronger than its corresponding reduced-form effect, while the effect of land productivity remains rather stable across the OLS and IV specifications. In addition, the strength and credibility of the numbers of domesticable plant and animal species as instruments continue to be supported by their explanatory power in the first-stage regressions and by the results of the overidentifying restrictions tests. The similarity of these findings with those obtained in the 1500 CE analysis reinforces the validity of these instruments and, thereby, lends further credence to the causal effect of the timing of the Neolithic transition on population density.

Finally, turning attention to the differences in coefficient estimates obtained for the three periods, it is interesting to note that, while the positive effect of land productivity on population density remains rather stable, that of the number of years elapsed since the onset of agriculture declines over time. For instance, comparing the IV coefficient estimates on the transition-timing variable across Tables 2–4, the positive causal impact of the Neolithic Revolution on population density diminishes by 0.53 percentage points over the 1–1000 CE time horizon and by 0.85 percentage points over the subsequent 500-year period. This pattern is consistently reflected by all regression specifications examining the effect of the transition-timing variable, lending support to the assertion that the process of development initiated by the technological breakthrough of the Neolithic Revolution conferred social gains characterized by diminishing returns over time.²⁶

4.3 Income per Capita versus Population Density

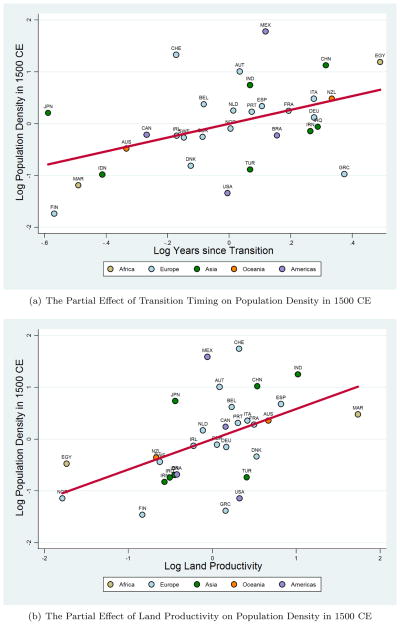
This section examines the Malthusian prediction regarding the neutrality of the standard of living with respect to land productivity and the level of technological advancement, as proxied by the timing of the Neolithic Revolution. Table 5 presents the results from estimating the baseline empirical model, as specified in equation (16), for income per capita in the years 1500 CE, 1000 CE and 1 CE. Since historical income per capita data are available for a relatively smaller set of countries, the analysis at hand also conducts corresponding tests for population density using the income per capita data-restricted samples for the three historical periods. This permits an impartial assessment of whether higher land productivity and an earlier onset of the Neolithic Revolution are manifested mostly in terms of higher population density, as opposed to higher income per capita, as the Malthusian theory would predict.

Table 5.

Effects on Income per Capita versus Population Density

	(1)	(2)	(3)	(4)	(5)	(6)
	OLS	OLS	OLS	OLS	OLS	OLS
	Dependent Variable is:
	Log Income per Capita in:			Log Population Density in:
	1500 CE	1000 CE	1 CE	1500 CE	1000 CE	1 CE
Log Years since Neolithic Transition	0.159 (0.136)	0.073 (0.045)	0.109 (0.072)	1.337** (0.594)	0.832** (0.363)	1.006** (0.481)
Log Land Productivity	0.041 (0.025)	−0.021 (0.025)	−0.001 (0.027)	0.584*** (0.159)	0.364*** (0.110)	0.681** (0.255)
Log Absolute Latitude	−0.041 (0.073)	0.060 (0.147)	−0.175 (0.175)	0.050 (0.463)	−2.140** (0.801)	−2.163** (0.979)
Mean Distance to Nearest Coast or River	0.215 (0.198)	−0.111 (0.138)	0.043 (0.159)	−0.429 (1.237)	−0.237 (0.751)	0.118 (0.883)
Percentage of Land within 100 km of Coast or River	0.124 (0.145)	−0.150 (0.121)	0.042 (0.127)	1.855** (0.820)	1.326** (0.615)	0.228 (0.919)
Continent Dummies	Yes	Yes	Yes	Yes	Yes	Yes
Observations	31	26	29	31	26	29
R-squared	0.66	0.68	0.33	0.88	0.95	0.89

Summary – This table establishes, consistently with Malthusian predictions, the relatively small effects of land productivity and the level of technological advancement, as proxied by the timing of the Neolithic Revolution, on income per capita in the years 1500 CE, 1000 CE and 1 CE, but their significantly larger effects on population density in the same time periods, while controlling for access to navigable waterways, absolute latitude, and unobserved continental fixed effects.

Notes – (i) log land productivity is the first principal component of the log of the percentage of arable land and the log of an agricultural suitability index; (ii) a single continent dummy is used to represent the Americas, which is natural given the historical period examined; (iii) regressions (2)–(3) and (5)–(6) do not employ the Oceania dummy due to a single observation for this continent in the corresponding regression samples, restricted by the availability of income per capita data; (iv) robust standard error estimates are reported in parentheses; (v) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.

Columns 1–3 reveal that income per capita in each historical period is effectively neutral to variations in the timing of the Neolithic Revolution, the agricultural productivity of land, and other productivity-enhancing geographical factors, conditional on continental fixed effects.²⁷ In particular, the effects of transition timing and land productivity on income per capita are not only substantially smaller than those on population density, they are also not statistically different from zero at conventional levels of significance.²⁸ Moreover, the other geographical factors, which, arguably, had facilitated trade and technology diffusion, do not appear to significantly affect income per capita.

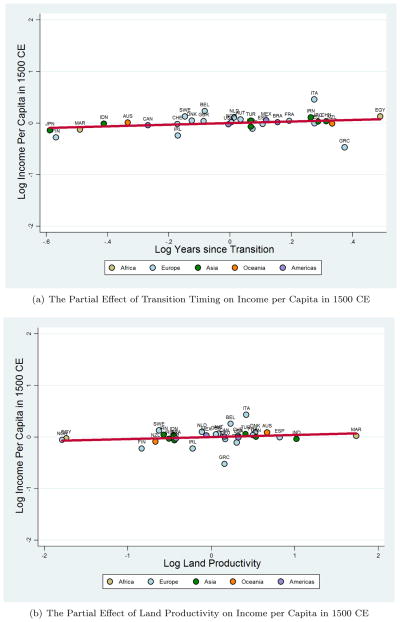
In contrast, the regressions in Columns 4–6 reveal, exploiting the same variation in explanatory variables as in the preceding income per capita regressions, that the elasticities of population density in each period with respect to Neolithic transition timing and land productivity are not only highly statistically significant, but are also larger by about an order of magnitude than the corresponding elasticities of income per capita. Thus, for the year 1500 CE, a 1 percent increase in the number of years elapsed since the Neolithic Revolution raises population density by 1.34 percent but income per capita by only 0.16 percent, conditional on land productivity, geographical factors and continental fixed effects. Similarly, a 1 percent increase in land productivity is associated, ceteris paribus, with a 0.58 percent increase in population density in 1500 CE but only a 0.04 percent increase in income per capita in the same time period. The conditional effects of Neolithic transition timing and land productivity on income per capita versus population density in the year 1500 CE are depicted as partial regression lines on the scatter plots in Figures 4(a) and 4(b) for income per capita, and in Figures 5(a) and 5(b) for population density.

Figure 4.

Transition Timing, Land Productivity, and Income per Capita in 1500 CE

Summary – This figure depicts the partial regression line for the effect of transition timing (land productivity) on income per capita in the year 1500 CE, while controlling for the influence of land productivity (transition timing), absolute latitude, access to waterways, and continental fixed effects. Thus, the x- and y-axes plot the residuals obtained from regressing transition timing (land productivity) and income per capita, respectively, on the aforementioned set of covariates.

Figure 5.

Transition Timing, Land Productivity, and Population Density in 1500 CE

Summary – This figure depicts, using the income per capita data-restricted sample, the partial regression line for the effect of transition timing (land productivity) on population density in the year 1500 CE, while controlling for the influence of land productivity (transition timing), absolute latitude, access to waterways, and continental fixed effects. Thus, the x- and y-axes plot the residuals obtained from regressing transition timing (land productivity) and population density, respectively, on the aforementioned set of covariates.

While the results revealing the cross-country neutrality of income per capita, despite differences in aggregate productivity, are fully consistent with Malthusian predictions, there may exist potential concerns regarding the quality of the income per capita data employed by the current analysis. In particular, contrary to Maddison’s (2008) implicit assertion, if the historical income per capita estimates were in part imputed under the Malthusian prior regarding similarities in the standard of living across countries, then applying these data to test the Malthusian theory itself would clearly be invalid.²⁹

The current investigation therefore performs a rigorous robustness analysis of the baseline results with respect to the aforementioned data quality concerns. In particular, Columns 1–3 in Table 6 reveal the results from estimating the baseline specification for income per capita in the three historical periods, using regressions where each observation is weighted down according to the number of observations in the sample reported to possess the same level of income per capita as the observation in question.³⁰ To the extent that the potential lack of variability in subsets of Maddison’s income per data may have biased the baseline results in favor of the Malthusian theory, this methodology alleviates such bias in the regression by reducing the relative importance of clusters of the data where observed variation is lacking.

Table 6.

Robustness to Income per Capita Data Quality Concerns

	(1)	(2)	(3)	(4)	(5)	(6)
	Weighted OLS	Weighted OLS	Weighted OLS	Weighted OLS	Weighted OLS	Weighted OLS
	Observations Weighted According to:
	Income Data Frequency			Total Population Size
	Dependent Variable is Log Income per Capita in:
	1500 CE	1000 CE	1 CE	1500 CE	1000 CE	1 CE
Log Years since Neolithic Transition	0.173 (0.162)	0.122* (0.063)	0.189 (0.121)	0.278 (0.171)	0.143* (0.068)	0.289 (0.175)
Log Land Productivity	0.039 (0.023)	−0.045* (0.022)	0.008 (0.031)	−0.005 (0.026)	−0.062* (0.030)	−0.011 (0.027)
Log Absolute Latitude	−0.042 (0.080)	0.205* (0.108)	−0.442 (0.362)	−0.089 (0.052)	0.298*** (0.031)	0.080 (0.089)
Mean Distance to Nearest Coast or River	0.219 (0.202)	−0.370** (0.148)	0.139 (0.298)	0.332** (0.148)	−0.592*** (0.108)	−0.180 (0.189)
Percentage of Land within 100 km of Coast or River	0.153 (0.169)	−0.228 (0.137)	0.159 (0.257)	0.329 (0.227)	−0.477*** (0.122)	0.003 (0.277)
Continent Dummies	Yes	Yes	Yes	Yes	Yes	Yes
Observations	31	26	29	31	26	29
R-squared	0.54	0.79	0.29	0.74	0.83	0.45

Summary – This table demonstrates that the relatively small effects of land productivity and the level of technological advancement, as proxied by the timing of the Neolithic Revolution, on income per capita in the years 1500 CE, 1000 CE and 1 CE remain robust under two different weighted regression methodologies, designed to dispel concerns regarding the quality of the historical income per capita data series.

Notes – (i) log land productivity is the first principal component of the log of the percentage of arable land and the log of an agricultural suitability index; (ii) the weight of country i in regressions (1)–(3) is inversely proportional to the frequency with which i’s income per capita occurs in the corresponding samples, i.e., $w_i=n_i^{-1}/{\sum }_i{n}_i^{-1}$, where n_i is the number of countries with income per capita identical to i; (iii) the weight of country i in regressions (4)–(6) is directly proportional to the population size of i in the corresponding samples, i.e., w_i = p_i/Σ_i p_i, where p_i is the size of the population of i; (iv) a single continent dummy is used to represent the Americas, which is natural given the historical period examined; (v) regressions (2)–(3) and (5)–(6) do not employ the Oceania dummy due to a single observation for this continent in the corresponding regression samples, restricted by the availability of income per capita data; (vi) robust standard error estimates are reported in parentheses; (vii) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.

A comparison of each of the first three columns between Tables 5 and 6 indicates that the baseline results remain both quantitatively and qualitatively robust with respect to the aforementioned weighting procedure. The quantitative robustness of the results are verified by the fact that, despite the statistical significance of some of the effects in the year 1000 CE under the weighted methodology, the transition-timing and land-productivity channels continue to remain economically non-substantial for income per capita in all three periods, as reflected by estimated elasticities that are still about an order of magnitude smaller than those of population density in the corresponding periods.

Reassuringly, a similar robustness pattern of the baseline results for income per capita is observed with respect to Columns 4–6 of Table 6 where an alternative sample weighting procedure is employed, with individual observations weighted up according to their respective population densities. To the extent that the sample variation in income per capita may have been artificially introduced under the premise that technologically advanced societies, as reflected by their higher population densities, also enjoyed marginally higher standards of living, this weighting procedure would a priori amplify the manifestation of technological differences as differences in income per capita, and thus bias the results against Malthusian predictions. Nevertheless, despite exacerbating any systematic bias in favor of rejecting the theory, the results obtained under this weighting procedure continue to demonstrate the insignificance of the land-productivity and transition-timing channels for income per capita in all three historical periods.

To summarize the main findings of the analysis thus far, the results indicate that more productive societies sustained higher population densities, as opposed to higher standards of living, during the time period 1–1500 CE. These findings are entirely consistent with the Malthusian prediction that in pre-industrial economies, resources temporarily generated by more productive technological environments were ultimately channeled into population growth, with negligible long-run effects on income per capita.

4.4 Technological Sophistication

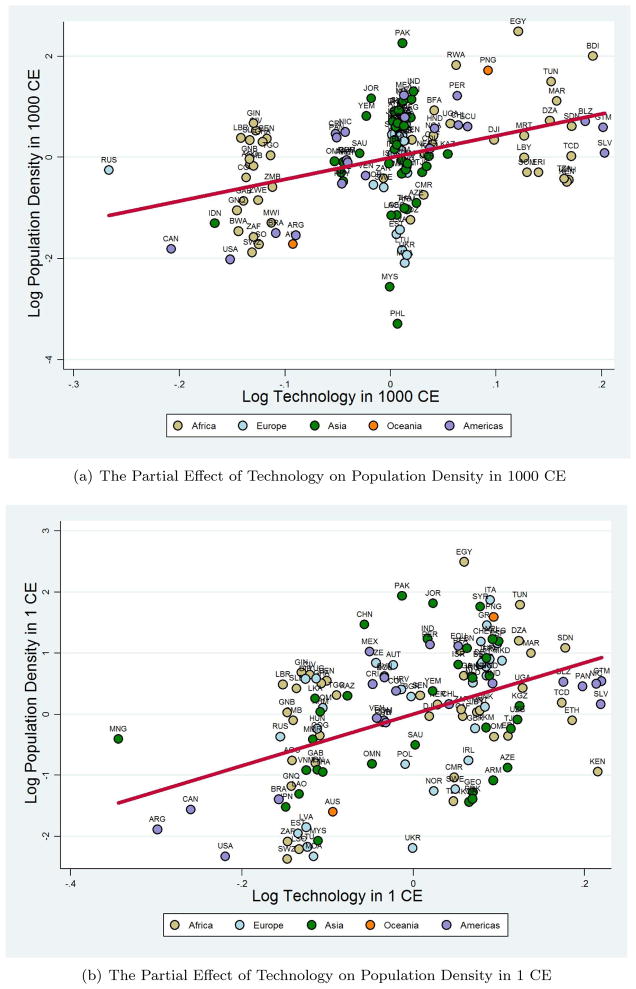
This section demonstrates the qualitative robustness of the results, regarding the significant positive effect of technology, as proxied by the timing of the Neolithic Revolution, on population density, but its neutrality for income per capita, under direct measures of technological advancement. In particular, Table 7 presents the findings from estimating the baseline specification for population density and income per capita in the years 1000 CE and 1 CE, employing the index of technological sophistication corresponding to these periods, in lieu of the number of years elapsed since the Neolithic Revolution, as an indicator of the level of aggregate productivity.

Table 7.

Robustness to Direct Measures of Technological Sophistication

	(1)	(2)	(3)	(4)	(5)	(6)
	OLS	OLS	OLS	OLS	OLS	OLS
	Full Sample	Full Sample	Income Sample	Income Sample	Income Sample	Income Sample
	Dependent Variable is:
	Log Population Density in:		Log Income per Capita in:		Log Population Density in:
	1000 CE	1 CE	1000 CE	1 CE	1000 CE	1 CE
Log Technology Index in Relevant Period	4.315*** (0.850)	4.216*** (0.745)	0.064 (0.230)	0.678 (0.432)	12.762*** (0.918)	7.461** (3.181)
Log Land Productivity	0.449*** (0.056)	0.379*** (0.082)	−0.016 (0.030)	0.004 (0.033)	0.429** (0.182)	0.725** (0.303)
Log Absolute Latitude	−0.283** (0.120)	−0.051 (0.127)	0.036 (0.161)	−0.198 (0.176)	−1.919*** (0.576)	−2.350*** (0.784)
Mean Distance to Nearest Coast or River	−0.638*** (0.188)	−0.782*** (0.198)	−0.092 (0.144)	0.114 (0.164)	0.609 (0.469)	0.886 (0.904)
Percentage of Land within 100 km of Coast or River	0.385 (0.313)	0.237 (0.329)	−0.156 (0.139)	0.092 (0.136)	1.265** (0.555)	0.788 (0.934)
Continent Dummies	Yes	Yes	Yes	Yes	Yes	Yes
Observations	140	129	26	29	26	29
R-squared	0.61	0.62	0.64	0.30	0.97	0.88

Summary – This table demonstrates that the relatively small effect of the level of technological advancement on income per capita in the years 1000 CE and 1 CE, but its significantly larger effect on population density in the same time periods, remains qualitatively robust when direct measures of technological sophistication for the corresponding years are used in lieu of the timing of the Neolithic Revolution.

Notes – (i) the technology index for a given time period reflects the average degree of technological sophistication across communications, transportation, industrial, and agricultural sectors in that period; (ii) the almost perfect collinearity between the degree of technological sophistication in the agricultural sector and the timing of the Neolithic transition does not permit the use of the latter as a covariate in these regressions; (iii) log land productivity is the first principal component of the log of the percentage of arable land and the log of an agricultural suitability index; (iv) a single continent dummy is used to represent the Americas, which is natural given the historical period examined; (v) regressions (3)–(6) do not employ the Oceania dummy due to a single observation for this continent in the corresponding regression samples, restricted by the availability of income per capita data; (vi) robust standard error estimates are reported in parentheses; (vii) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.

As mentioned previously, the index of technological sophistication in each period is based on cross-cultural, sector-specific technology data from Peregrine (2003), aggregated up to the country level by averaging across sectors and cultures within a country, following the aggregation methodology of Comin, Easterly, and Gong (2008). Specifically, the index not only captures the level of technological advancement in communications, transportation, and industry, but also incorporates information on the prevalence of sedentary agricultural practices relative to hunting and gathering.³¹ Since the timing of the Neolithic transition is a priori expected to be highly correlated with the prevalence of agriculture across countries in both 1000 CE and 1 CE, its inclusion as an explanatory variable in the current analysis would constitute the exploitation of redundant information and potentially obfuscate the results of the analysis. The regressions in Table 7 therefore omit the timing of the Neolithic Revolution as an explanatory variable for both population density and income per capita in the two periods examined.³²

Foreshadowing the qualitative robustness of the findings from previous sections, the logged indices of technology in the years 1000 CE and 1 CE are indeed highly correlated with the logged transition-timing variable. For instance, in the full cross-country samples employed by the population density regressions in Section 4.2, the logged Neolithic transition-timing variable possesses correlation coefficients of 0.73 and 0.62 with the logged indices of technology in the years 1000 CE and 1 CE respectively. Similarly, in the income per capita data-restricted samples employed in Section 4.3, the corresponding correlation coefficients are 0.82 and 0.74.

Columns 1–2 reveal the full-sample regression results for population density in the years 1000 CE and 1 CE. Consistent with Malthusian predictions, the regressions indicate highly statistically significant positive relationships between technological sophistication and population density in the two time periods. To interpret the coefficients of interest, a 1 percent increase in the level of technological sophistication in the years 1000 CE and 1 CE corresponds to a rise in population density in the respective time periods by 4.32 and 4.22 percent, conditional on the productivity of land, geographical factors, and continental fixed effects.³³ In addition, Columns 1–2 also indicate that the effects of the land-productivity channel on population density remain largely stable in comparison to previous estimates presented in Tables 3–4.

The results from replicating the 1000 CE and 1 CE analyses of Section 4.3, using the period-specific indices of technology as opposed to the timing of the Neolithic transition, are presented in Columns 3–6. For each time period examined, the regressions for income per capita and population density reveal, exploiting identical variations in explanatory variables, that the estimated elasticity of population density with respect to the degree of technological sophistication is not only highly statistically significant, but at least an order of magnitude larger than the corresponding elasticity of income per capita. Indeed, the conditional correlation between technology and income per capita is not statistically different from zero at conventional levels of significance. A similar pattern also emerges for the estimated elasticities of population density and income per capita in each period with respect to the land-productivity channel. These findings therefore confirm the Malthusian prior that, in pre-industrial times, variations in the level of technological advancement were ultimately manifested as variations in population density as opposed to variations in the standard of living across regions.

The remainder of the analysis in this section is concerned with establishing the causal effect of technology on population density in the years 1000 CE and 1 CE. Since the measures of technology employed by the preceding analysis are contemporaneous to population density in the two periods examined, the issue of endogeneity is perhaps more germane in this case than it was when examining the effect of the timing of the Neolithic Revolution on population density under the OLS estimator. In particular, the estimated coefficients associated with the period-specific technology indices in Columns 1–2 of Table 7 may, in part, be capturing reverse causality, due to the potential scale effect of population on technological progress, as well as the latent influence of unobserved country-specific characteristics that are correlated with both technology and population density. To address these issues, the analysis to follow appeals to Diamond’s (1997) argument, regarding the Neolithic transition to agriculture as a triggering event for subsequent technological progress, to exploit the exogenous component of cross-country variation in technology during the first millennium CE, as determined by the variation in the prehistoric biogeographical endowments that led to the differential timing of the Neolithic Revolution itself.³⁴

The analysis proceeds by first establishing the causal effect of the Neolithic Revolution on subsequent technological progress. Given the high correlation between the prevalence of sedentary agricultural practices in Peregrine’s (2003) dataset and the timing of the Neolithic transition, the current analysis exploits, for each period examined, an alternative index of technological sophistication that is based only on the levels of technological advancement in communications, transportation, and industry, but otherwise identical in its underlying aggregation methodology to the index employed thus far. This permits a more transparent assessment of the argument that the Neolithic Revolution triggered a cumulative process of development, fueled by the emergence and propagation of a non-food producing class within agricultural societies that enabled sociocultural and technological advancements over and above subsistence activities.

Table 8 presents the results of regressions examining the impact of the timing of the Neolithic Revolution on the level of non-agricultural technological sophistication in the years 1000 CE and 1 CE, while controlling for land productivity, absolute latitude, access to waterways, and continental fixed effects. In line with priors, the regressions in Columns 1 and 4 establish a highly statistically significant positive relationship between the timing of the Neolithic Revolution and the level of non-agricultural technological sophistication in each period, exploiting variation across the full sample of countries. To allow fair comparisons with the results from subsequent IV regressions, Columns 2 and 5 repeat the preceding OLS analyses but on the subsample of countries for which data on the biogeographical instruments for the timing of the Neolithic Revolution are available. The results indicate that the OLS coefficients of interest from the preceding full-sample analyses remain robust to this change in the regression sample. Finally, Columns 3 and 6 establish the causal effect of the Neolithic Revolution on the level of non-agricultural technological sophistication in the two time periods, employing the prehistoric availability of domesticable species of plants and animals as instruments for the timing of the Neolithic transition. Not surprisingly, as observed with earlier IV regressions, the causal impact of the Neolithic transition is, in each case, larger relative to its impact obtained under the OLS estimator, a pattern that is consistent with measurement error in the transition-timing variable and the resultant attenuation bias afflicting OLS coefficient estimates.

Table 8.

The Causal Effect of the Neolithic Revolution on Technological Sophistication

	(1)	(2)	(3)	(4)	(5)	(6)
	OLS	OLS	IV	OLS	OLS	IV
	Full Sample	Restricted Sample	Restricted Sample	Full Sample	Restricted Sample	Restricted Sample
	Dependent Variable is Log Non-Agricultural Technology in:
	1000 CE			1 CE
Log Years since Neolithic Transition	0.115*** (0.024)	0.146*** (0.030)	0.279*** (0.073)	0.152*** (0.027)	0.174*** (0.029)	0.339*** (0.074)
Log Land Productivity	−0.006 (0.008)	−0.012 (0.015)	−0.009 (0.014)	−0.024*** (0.008)	−0.027* (0.016)	−0.023 (0.019)
Log Absolute Latitude	0.012 (0.014)	0.000 (0.019)	0.005 (0.018)	0.039** (0.016)	0.026 (0.022)	0.032 (0.020)
Mean Distance to Nearest Coast or River	0.008 (0.033)	0.117** (0.053)	0.129** (0.051)	0.007 (0.035)	0.050 (0.084)	0.066 (0.078)
Percentage of Land within 100 km of Coast or River	0.024 (0.038)	0.080 (0.052)	0.112* (0.058)	0.047 (0.048)	0.110 (0.070)	0.149** (0.076)
Continent Dummies	Yes	Yes	Yes	Yes	Yes	Yes
Observations	143	93	93	143	93	93
R-squared	0.76	0.72	0.67	0.59	0.55	0.47
First-stage F-statistic	–	–	13.47	–	–	13.47
Overid. p-value	–	–	0.256	–	–	0.166

Summary – This table presents the causal effect of the timing of the Neolithic Revolution on the level of technology in non-agricultural sectors in the years 1000 CE and 1 CE, while controlling for land productivity, access to navigable waterways, absolute latitude, and unobserved continental fixed effects.

Notes – (i) unlike the regular technology index, the index of non-agricultural technology for a given time period reflects the average degree of technological sophistication across only communications, transportation, and industrial sectors in that period; (ii) log land productivity is the first principal component of the log of the percentage of arable land and the log of an agricultural suitability index; (iii) the IV regressions employ the numbers of prehistoric domesticable species of plants and animals as instruments for log transition timing; (iv) the statistic for the first-stage F-test of these instruments is significant at the 1 percent level; (v) the p-values for the overidentifying restrictions tests correspond to Hansen’s J statistic, distributed in both instances as chi-square with one degree of freedom; (vi) a single continent dummy is used to represent the Americas, which is natural given the historical period examined; (vii) regressions (2)–(3) and (5)–(6) do not employ the Oceania dummy due to a single observation for this continent in the IV data-restricted sample; (viii) robust standard error estimates are reported in parentheses; (ix) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.

In light of the causal link between the timing of the Neolithic transition and the level of technological advancement in the first millennium CE, the analysis may now establish the causal impact of technology on population density in the two time periods examined. This is accomplished by exploiting exogenous variation in the level of technological advancement generated ultimately by differences in prehistoric biogeographical endowments that led to the differential timing of the transition to agriculture across countries. Table 9 reveals the results of this analysis where, as in Table 7, the measure of technology employed is the overall index that incorporates information on the prevalence of sedentary agriculture along with the level of advancement in non-agricultural technologies.

Table 9.

The Causal Effect of Technological Sophistication on Population Density

	(1)	(2)	(3)	(4)	(5)	(6)
	OLS	OLS	IV	OLS	OLS	IV
	Full Sample	Restricted Sample	Restricted Sample	Full Sample	Restricted Sample	Restricted Sample
	Dependent Variable is Log Population Density in:
	1000 CE			1 CE
Log Technology Index in Relevant Period	4.315*** (0.850)	4.198*** (1.164)	14.530*** (4.437)	4.216*** (0.745)	3.947*** (0.983)	10.798*** (2.857)
Log Land Productivity	0.449*** (0.056)	0.498*** (0.139)	0.572*** (0.148)	0.379*** (0.082)	0.350** (0.172)	0.464** (0.182)
Log Absolute Latitude	−0.283** (0.120)	−0.185 (0.151)	−0.209 (0.209)	−0.051 (0.127)	0.083 (0.170)	−0.052 (0.214)
Mean Distance to Nearest Coast or River	−0.638*** (0.188)	−0.363 (0.426)	−1.155* (0.640)	−0.782*** (0.198)	−0.625 (0.434)	−0.616 (0.834)
Percentage of Land within 100 km of Coast or River	0.385 (0.313)	0.442 (0.422)	0.153 (0.606)	0.237 (0.329)	0.146 (0.424)	−0.172 (0.642)
Continent Dummies	Yes	Yes	Yes	Yes	Yes	Yes
Observations	140	92	92	129	83	83
R-squared	0.61	0.55	0.13	0.62	0.58	0.32
First-stage F-statistic	–	–	12.52	–	–	12.00
Overid. p-value	–	–	0.941	–	–	0.160

Summary – This table presents the causal effect of direct measures of technological sophistication in the years 1000 CE and 1 CE, as determined by exogenous factors governing the timing of the Neolithic Revolution, on population density in the same time periods, while controlling for land productivity, access to navigable waterways, absolute latitude, and unobserved continental fixed effects.

Notes – (i) the technology index for a given time period reflects the average degree of technological sophistication across communications, transportation, industrial, and agricultural sectors in that period; (ii) the almost perfect collinearity between the degree of technological sophistication in the agricultural sector and the timing of the Neolithic transition does not permit the use of the latter as a covariate in these regressions; (iii) log land productivity is the first principal component of the log of the percentage of arable land and the log of an agricultural suitability index; (iv) the IV regressions employ the numbers of prehistoric domesticable species of plants and animals as instruments for the log of the technology index in each of the two periods; (v) in both cases, the statistic for the first-stage F-test of these instruments is significant at the 1 percent level; (vi) the p-values for the overidentifying restrictions tests correspond to Hansen’s J statistic, distributed in both instances as chi-square with one degree of freedom; (vii) a single continent dummy is used to represent the Americas, which is natural given the historical period examined; (viii) regressions (2)–(3) and (5)–(6) do not employ the Oceania dummy due to a single observation for this continent in the IV data-restricted sample; (ix) robust standard error estimates are reported in parentheses; (x) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.

To facilitate comparisons of results obtained under the OLS and IV estimators, the full-sample OLS results from Table 7 for the years 1000 CE and 1 CE are again presented in Columns 1 and 4 of Table 9, while Columns 2 and 5 present the same regressions conducted on the IV-restricted subsample of countries. The causal effects of the level of technological advancement in the years 1000 CE and 1 CE, instrumented by the prehistoric availability of domesticable plant and animal species, on population density in the corresponding periods are revealed in Columns 3 and 6. The estimated IV coefficients indicate a much larger causal impact of technology on population density, with a 1 percent increase in the level of technological sophistication in 1000 CE and 1 CE raising population density in the respective time periods by 14.53 and 10.80 percent, conditional on the productivity of land, absolute latitude, access to waterways, and continental fixed effects. Thus, in line with the predictions of the Malthusian theory, the results indicate that, during the agricultural stage of development, temporary gains due to improvements in the technological environment were indeed channeled into population growth, thereby leading more technologically advanced societies to sustain higher population densities.

4.5 Robustness to Technology Diffusion and Geographical Factors

This section establishes the robustness of the results for population density and income per capita in the year 1500 CE with respect to the spatial influence of technological frontiers, as well as other geographical factors such as climate and small island and landlocked dummies, all of which may have had an effect on aggregate productivity either directly, by affecting the productivity of land, or indirectly, by affecting the prevalence of trade and technology diffusion. Specifically, the technology-diffusion hypothesis suggests that spatial proximity to societies at the world technology frontier confers a beneficial effect on development by facilitating the diffusion of new technologies from the frontier through trade as well as sociocultural and geopolitical influences. In particular, the diffusion channel implies that, ceteris paribus, the greater the geographical distance from the technological leaders in a given period, the lower the level of economic development amongst the followers in that period.

To account for the technology-diffusion channel, the current analysis employs as a control variable the great-circle distance from the capital city of a country to the closest of eight worldwide regional technological frontiers. These centers of technology diffusion are derived by Ashraf and Galor (2010), who employ historical urbanization estimates provided by Tertius Chandler (1987) and George Modelski (2003) to identify frontiers based on the size of urban populations. Specifically, for a given time period, their procedure selects from each continent the two largest cities in that period, belonging to distinct sociopolitical entities. Thus, the set of regional technological frontiers identified for the year 1500 CE comprises London and Paris in Europe, Fez and Cairo in Africa, Constantinople and Peking in Asia, and Tenochtitlan and Cuzco in the Americas.

Column 1 of Table 10 reveals the qualitative robustness of the full-sample regression results for population density in the year 1500 CE under controls for distance to the closest regional frontier as well as small island and landlocked dummies. To the extent that the gains from trade and technology diffusion are manifested primarily in terms of population size, as the Malthusian theory would predict, distance to the frontier has a highly statistically significant negative impact on population density. Nevertheless, the regression coefficients associated with the Neolithic transition-timing and land-productivity channels remain largely stable, albeit somewhat less so for the former, in comparison to their baseline estimates from Column 4 in Table 2. Indeed, the lower magnitude of the coefficient associated with the transition-timing channel is attributable to the fact that several frontiers in the year 1500 CE, including Egypt, China, and Mexico, were also centers of diffusion of agricultural practices during the Neolithic Revolution and, as such, distance to the frontier in 1500 CE is partly capturing the effect of the differential timing of the Neolithic transition itself.

Table 10.

Additional Robustness Checks

	(1)	(2)	(3)	(4)	(5)	(6)
	OLS	OLS	OLS	OLS	OLS	OLS
	Full Sample	Full Sample	Income Sample	Income Sample	Income Sample	Income Sample
	Dependent Variable is:
	Log Population Density in 1500 CE		Log Income per Capita in 1500 CE		Log Population Density in 1500 CE
Log Years since Neolithic Transition	0.828*** (0.208)	0.877*** (0.214)	0.117 (0.221)	0.103 (0.214)	1.498** (0.546)	1.478** (0.556)
Log Land Productivity	0.559*** (0.048)	0.545*** (0.063)	0.036 (0.032)	0.047 (0.037)	0.596*** (0.123)	0.691*** (0.122)
Log Absolute Latitude	−0.400*** (0.108)	−0.301** (0.129)	−0.020 (0.110)	0.028 (0.247)	−0.354 (0.392)	0.668 (0.783)
Mean Distance to Nearest Coast or River	−0.403*** (0.152)	−0.388*** (0.144)	0.175 (0.286)	0.202 (0.309)	0.394 (0.994)	0.594 (0.844)
Percentage of Land within 100 km of Coast or River	0.870*** (0.272)	0.837*** (0.280)	0.160 (0.153)	0.245 (0.208)	1.766*** (0.511)	2.491*** (0.754)
Log Distance to Frontier	−0.186*** (0.035)	−0.191*** (0.036)	−0.005 (0.011)	−0.001 (0.013)	−0.130* (0.066)	−0.108* (0.055)
Small Island Dummy	0.067 (0.582)	0.086 (0.626)	−0.118 (0.216)	−0.046 (0.198)	1.962** (0.709)	2.720*** (0.699)
Landlocked Dummy	0.131 (0.209)	0.119 (0.203)	0.056 (0.084)	0.024 (0.101)	1.490*** (0.293)	1.269*** (0.282)
Percentage of Land in Temperate Zones		−0.196 (0.513)		−0.192 (0.180)		−1.624* (0.917)
Percentage of Land in (Sub)Tropical Zones		0.269 (0.307)		−0.025 (0.308)		1.153 (1.288)
Continent Dummies	Yes	Yes	Yes	Yes	Yes	Yes
Observations	147	147	31	31	31	31
R-squared	0.76	0.76	0.67	0.67	0.94	0.96

Summary – This table demonstrates that the relatively small effects of land productivity and the level of technological advancement, as proxied by the timing of the Neolithic Revolution, on income per capita in the year 1500 CE, but their significantly larger effects on population density in the same time period, remain robust under additional controls for technology diffusion and climatic factors.

Notes – (i) log land productivity is the first principal component of the log of the percentage of arable land and the log of an agricultural suitability index; (ii) a single continent dummy is used to represent the Americas, which is natural given the historical period examined; (iii) robust standard error estimates are reported in parentheses; (iv) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.

The regression in Column 2 extends the robustness analysis of Column 1 by adding controls for the percentage of land in temperate and tropical zones. The findings demonstrate that the effects of the Neolithic transition-timing, land-productivity, and spatial technology-diffusion channels on population density are indeed not spuriously driven by these additional climatological factors.

Columns 3–6 reveal the robustness of the results for income per capita as well as population density in the income per capita data-restricted sample, under controls for the technology-diffusion channel and additional geographical factors. In comparison to the relevant baseline regressions presented in Columns 1 and 4 of Table 5, the coefficients associated with the transition-timing and land-productivity channels remain both qualitatively and quantitatively stable. In particular, the estimated elasticities of population density with respect to these channels are about an order of magnitude larger than the corresponding elasticities of income per capita regardless of the set of additional controls included in the specification.

With regard to the influence of technology diffusion, the qualitative pattern of the effects on population density versus income per capita is similar to those associated with the transition-timing and land-productivity channels. The finding that the negative elasticity of income per capita with respect to distance to the frontier is not only statistically insignificant but also at least an order of magnitude smaller than that of population density confirms Malthusian priors that the gains from trade and technology diffusion were primarily channeled into population growth rather than to improvements in living standards during pre-industrial times.³⁵ While this finding may also be consistent with a non-Malthusian migration-driven theory of population movements against a spatial productivity gradient, the results uncovered by the first-difference estimation strategy pursued in the next section provide evidence in favor of the proposed Malthusian interpretation.

4.6 Robustness to Alternative Theories and Country Fixed Effects

This section examines the robustness of the empirical findings to alternative theories and time-invariant country fixed effects. Specifically, the level regression results may be explained by the following non-Malthusian theory. In a world where labor is perfectly mobile, regions with higher aggregate productivity would experience labor inflows until regional wage rates were equalized, implying that, in levels, technology should be positively associated with population density but should not be correlated with income per capita across regions. Such a theory would also imply, however, that increases in the level of technology in any given region should generate increases in the standard of living in all regions. This runs contrary to the Malthusian prediction that increases in the level of technology in a given region should ultimately translate into increases in population density in that region, leaving income per capita constant at the subsistence level in all regions. Thus, examining the effect of a change in technology on changes in population density versus income per capita, as opposed to the impact of the level of technology on the levels of population density versus income per capita, constitutes a more discriminatory test of the Malthusian model.

Moreover, the level regressions in Table 7, indicating the significant positive relationship between the level of technology and population density but the absence of a systematic relationship with income per capita, could potentially reflect spurious correlations between technology and one or more unobserved time-invariant country fixed effects. By investigating the effect of changes on changes, however, one may “difference out” time-invariant country fixed effects, thereby ensuring that the coefficients of interest in the regression will not be afflicted by any such omitted variable bias. In addition, while the relationship between contemporaneous changes in technology and population density or income per capita could reflect reverse causality, this endogeneity issue may be alleviated somewhat by examining the impact of the lagged change in technology on changes in population density versus income per capita.

The current investigation thus examines the effect of the change in the level of technology between the years 1000 BCE and 1 CE on the change in population density, versus its effect on the change in income per capita, over the 1–1000 CE time horizon. In particular, the analysis compares the results from estimating the following empirical models:

$$\mathrm{\Delta }ln{P}_{i,t}={\mu }_0+{\mu }_1\mathrm{\Delta }ln{A}_{i,t-1}+{\phi }_{i,t},$$ (17)

$$\mathrm{\Delta }ln{y}_{i,t}={\nu }_0+{\nu }_1\mathrm{\Delta }ln{A}_{i,t-1}+{\psi }_{i,t},$$ (18)

where Δln P_i,t ≡ ln P_i,t+1 − ln P_i,t (i.e., the difference in log population density in country i between 1 CE and 1000 CE); Δln y_i,t ≡ ln y_i,t+1 − ln y_i,t (i.e., the difference in log income per capita of country i between 1 CE and 1000 CE); Δln A_i,t−1 ≡ ln A_i,t − ln A_i,t−1 (i.e., the difference in log technology of country i between 1000 BCE and 1 CE); and, φ_i,t and ψ_i,t are country-specific disturbance terms for the changes in log population density and log income per capita. In addition, the intercept terms, μ₀ and ν₀, capture the average trend growth rates of population density and income per capita respectively over the 1–1000 CE time horizon. These models are the first-difference counterparts of (15) and (16), given that (i) ln A_i,t−1 is used in lieu of ln T_i, and (ii) the fixed effects of land productivity and the other geographical controls, including continental dummies, are time-invariant in those specifications.³⁶

As discussed earlier, the alternative migration-driven theory predicts that an increase in technology in a given region will not differentially increase income per capita in that region due to the cross-regional equalization of wage rates, but will increase income per capita in all regions. In light of the specifications defined above, this theory would therefore imply that ν₁ = 0 and ν₀ > 0. According to the Malthusian theory, on the other hand, not only will the long-run level of income per capita remain unaffected in the region undergoing technological advancement, it will remain unaffected in all regions as well. The Malthusian theory thus implies that both ν₁ = 0 and ν₀ = 0.

Table 11 presents the results from estimating equations (17) and (18). As predicted by the Malthusian theory, the slope coefficients in Columns 1 and 2 indicate that the change in the level of technology between the years 1000 BCE and 1 CE has a positive and statistically significant effect on the change in population density over the 1–1000 CE time horizon. In contrast, Column 3 reveals that the corresponding effect on the change in income per capita over the time period 1–1000 CE is relatively marginal and not statistically significantly different from zero. Moreover, the intercept coefficient in Column 3 suggests that the standard of living in 1000 CE was not significantly different from that in 1 CE, a finding that accords well with the Malthusian viewpoint. Overall, the results from the first-difference estimation strategy pursued in this section lend further credence to the Malthusian interpretation of the level regression results presented in earlier sections.

Table 11.

Robustness to Alternative Theories and Time-Invariant Country Fixed Effects

	(1)	(2)	(3)
	OLS	OLS	OLS
	Full Sample	Income Sample	Income Sample
	Dependent Variable is Diff. in:
	Log Population Density between 1 CE and 1000 CE		Log Income per Capita between 1 CE and 1000 CE
Diff. in Log Technology Index between 1000 BCE and 1 CE	1.747*** (0.429)	3.133* (1.550)	0.073 (0.265)
Constant	0.451*** (0.053)	−0.026 (0.204)	−0.040 (0.064)
Observations	126	26	26
R-squared	0.17	0.34	0.00

Summary – This table establishes that the change in the level of technological sophistication that occurred between the years 1000 BCE and 1 CE was primarily associated with a change in population density as opposed to a change in income per capita over the 1–1000 CE time horizon, and also reveals that there was no trend growth in income per capita during this period, thereby demonstrating robustness to time-invariant country fixed effects and dispelling an alternative migration-driven theory that is consistent with the level regression results.

Notes – (i) the technology index for a given time period reflects the average degree of technological sophistication across communications, transportation, industrial, and agricultural sectors in that period; (ii) the absence of controls from both regressions is justified by the removal of time-invariant country fixed effects through the application of the first-difference methodology; (iii) robust standard error estimates are reported in parentheses; (iv) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.

5 Concluding Remarks

This paper examines the central hypothesis of the influential Malthusian theory, according to which improvements in the technological environment during the pre-industrial era had generated only temporary gains in income per capita, eventually leading to a larger, but not significantly richer, population. It exploits exogenous sources of cross-country variation in land productivity and technological levels to examine their hypothesized differential effects on population density versus income per capita during the time period 1–1500 CE.

Consistent with Malthusian predictions, the analysis uncovers statistically significant positive effects of land productivity and the technological level on population density in the years 1500 CE, 1000 CE and 1 CE. In contrast, the effects of land productivity and technology on income per capita in these periods are not significantly different from zero. Moreover, the estimated elasticities of income per capita with respect to these two channels are about an order of magnitude smaller than the corresponding elasticities of population density. Importantly, the qualitative results remain robust to controls for the confounding effects of a large number of geographical factors, including absolute latitude, access to waterways, distance to the technological frontier, and the share of land in tropical versus temperate climatic zones, which may have had an impact on aggregate productivity either directly, by affecting the productivity of land, or indirectly via the prevalence of trade and the diffusion of technologies. Furthermore, the results are also qualitatively unaffected when a direct measure of technological sophistication, rather than the timing of the Neolithic Revolution, is employed as an indicator of the level of aggregate productivity. Finally, the study establishes that the results are not driven by unobserved time-invariant country fixed effects.

The analysis also dispels a non-Malthusian theory that may appear consistent with the level regression results. Specifically, in a world with perfect labor mobility, regions with higher aggregate productivity would have experienced labor inflows until regional wage rates were equalized, implying that technology should be positively associated with population density but should not be correlated with income per capita. However, labor inflows in response to technological improvements in a given region would result in higher income per capita in all regions, implying that changes in the level of technology should be positively associated with changes in the standard of living. On the contrary, using a first-difference estimation strategy with a lagged explanatory variable, the analysis demonstrates that, while changes in the level of technology between 1000 BCE and 1 CE were indeed associated with significant changes in population density over the 1–1000 CE time horizon, the level of income per capita across regions during this period was, in fact, largely unaffected, as suggested by the Malthusian theory.

In the course of the analysis, the paper generates three additional findings. First, in contrast to the positive relationship between absolute latitude and contemporary income per capita, population density in pre-industrial times was on average higher at latitudinal bands closer to the equator. Thus, while proximity to the equator has been found to be detrimental in the industrial stage of development, it appears to have been beneficial during the agricultural stage. Second, the paper also establishes the importance of technological diffusion in the pre-industrial world. To the extent that the gains from trade and technology diffusion are manifested primarily in terms of population size, as the Malthusian theory would predict, distance to the frontier has a highly statistically significant negative impact on population density. Finally, the analysis provides the first test of Diamond’s (1997) influential hypothesis in the context of pre-industrial societies, establishing that, indeed, an earlier onset of the Neolithic Revolution contributed to the level of technological sophistication and thus population density in the pre-modern world.

Interestingly, the epoch of Malthusian stagnation in income per capita masked a dynamism that may have ultimately brought about the phase transition that was associated with the take-off from the Malthusian regime. Although the growth of income per capita was minuscule over the Malthusian epoch, in the course of the Malthusian interaction between technology and population, technological progress intensified and world population significantly increased in size – a dynamism that was instrumental for the emergence of economies from the Malthusian trap.

Appendix A First-Stage Regressions

Table A.1.

First-Stage Regressions

	(1)	(2)	(3)	(4)	(5)	(6)
	OLS	OLS	OLS	OLS	OLS	OLS
	Second-Stage Dependent Variable is:
	Log of Population Density in 1500 CE	Log of Population Density in 1000 CE	Log of Population Density in 1 CE	Log of Technology Index in 1/1000 CE	Log of Population Density in 1000 CE	Log of Population Density in 1 CE
	Endogenous Variable is:
					Log Technology Index in:
	Log Years since Neolithic Transition				1000 CE	1 CE
Excluded Instruments:
Domesticable Plants	0.012** (0.005)	0.013** (0.005)	0.012** (0.006)	0.012** (0.005)	0.001 (0.001)	0.007*** (0.002)
Domesticable Animals	0.067** (0.029)	0.064** (0.028)	0.048* (0.029)	0.063** (0.028)	0.020*** (0.006)	−0.002 (0.008)
Second-Stage Controls:
Log Land Productivity	0.040 (0.049)	0.025 (0.049)	−0.011 (0.037)	0.023 (0.049)	0.002 (0.014)	−0.003 (0.017)
Log Absolute Latitude	−0.127*** (0.042)	−0.130*** (0.043)	−0.083* (0.044)	−0.120*** (0.044)	−0.015 (0.014)	−0.005 (0.019)
Mean Distance to Nearest Coast or River	0.127 (0.141)	0.103 (0.140)	0.094 (0.156)	0.079 (0.143)	0.112** (0.044)	0.055 (0.093)
Percentage of Land within 100 km of Coast or River	−0.165 (0.137)	−0.190 (0.136)	−0.227* (0.136)	−0.171 (0.137)	0.044 (0.036)	0.061 (0.063)
Continent Dummies	Yes	Yes	Yes	Yes	Yes	Yes
Observations	96	94	83	93	92	83
R-squared	0.68	0.70	0.71	0.67	0.71	0.51
Partial R-squared	0.27	0.28	0.25	0.26	0.17	0.16
F-statistic	14.65	15.10	10.85	13.47	12.52	12.00

Summary – This table collects the first-stage regression results for all IV regressions examined in the text. Specifically, regressions (1), (2), and (3) represent, respectively, the first stage of regression (6) in Tables 2, 3, and 4. Regression (4) corresponds to the first stage of both regressions (3) and (6) in Table 8. Finally, regressions (5) and (6) represent the first stage of regressions (3) and (6), respectively, in Table 9.

Notes – (i) log land productivity is the first principal component of the log of the percentage of arable land and the log of an agricultural suitability index; (ii) the partial R-squared reported is for the excluded instruments only; (iii) the F-statistic is from the test of excluded instruments and is always significant at the 1 percent level; (iv) a single continent dummy is used to represent the Americas, which is natural given the historical period examined; (v) the dummy for Oceania is not employed due to the presence of a single observation for this continent in the corresponding regression samples; (vi) robust standard error estimates are reported in parentheses; (vii) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.

Appendix B Variable Definitions and Sources

Population Density in 1 CE, 1000 CE, and 1500 CE

Population density in a given year is calculated as population in that year, as reported by Colin McEvedy and Richard Jones (1978), divided by land area today, as reported by the World Bank’s World Development Indicators. The cross-sectional unit of observation in McEvedy and Jones’ dataset is a region delineated by its international borders in 1975. Historical population estimates are provided for regions corresponding to either individual countries or, in some cases, to sets comprised of 2–3 neighboring countries (e.g., India, Pakistan and Bangladesh). In the latter case, a set-specific population density figure is calculated based on total land area and the figure is then assigned to each of the component countries in the set. The same methodology is also employed to obtain population density for countries that exist today but were part of a larger political unit (e.g., the former Yugoslavia) in 1975. The population data reported by the authors are based on a wide variety of country and region-specific historical sources, the enumeration of which would be impractical for this appendix. The interested reader is therefore referred to McEvedy and Jones (1978) for more details on the original data sources cited therein.

Income per Capita in 1 CE, 1000 CE, and 1500 CE

The level of income per capita, as reported by Angus Maddison (2003), for a given year. Additional details are available on the author’s website. The interested reader is also referred to www.ggdc.net/maddison/other%5Fbooks/HS-8%5F2003.pdf for a discussion of the data by the author.

Years since Neolithic Transition

The number of thousand years elapsed, until the year 2000, since the majority of the population residing within a country’s modern national borders began practicing sedentary agriculture as the primary mode of subsistence. This measure, reported by Louis Putterman (2008), is compiled using a wide variety of both regional and country-specific archaeological studies as well as more general encyclopedic works on the transition from hunting and gathering to agriculture during the Neolithic. The reader is referred to www.econ.brown.edu/fac/Louis%5FPutterman/agricultural%20data%20page.htm for a detailed description of the primary and secondary data sources employed by the author in the construction of this variable.

Plants and Animals (used as instrumental variables)

The number of domesticable species of plants and animals, respectively, that were prehistorically native to the continent or landmass to which a country belongs. These variables are obtained from the dataset of Ola Olsson and Douglas A. Hibbs, Jr. (2005).

Land Productivity

This measure is composed of (1) the percentage of arable land, as reported by the World Development Indicators, and (2) an index of the suitability of land for agriculture, based on geospatial soil pH and temperature data, as reported by Navin Ramankutty et al. (2002) and aggregated to the country level by Stelios Michalopoulos (2008). In particular, log land productivity is the first principal component of the logs of these variables, capturing 83 percent of their combined variation.

Absolute Latitude

The absolute value of the latitude of a country’s approximate geodesic centroid, as reported by The World Factbook, an online resource maintained by Central Intelligence Agency (CIA), accessible at https://www.cia.gov/library/publications/the-world-factbook/.

Mean Distance to Nearest Coast or River

The distance, in thousands of kilometers, from a GIS grid cell to the nearest ice-free coastline or sea-navigable river, averaged across the grid cells of a country. This variable is part of Harvard University’s Center for International Development (CID) Research Datasets on General Measures of Geography, available online at http://www.cid.harvard.edu/ciddata/geographydata.htm.

Percentage of Land within 100 km of Coast or River

The percentage of a country’s total land area that is located within 100 kilometers of an ice-free coastline or sea-navigable river, as reported by the CID Research Datasets on General Measures of Geography.

Technology Index in 1000 BCE, 1 CE, and 1000 CE

The index of technology for a given year is constructed using worldwide historical cross-cultural data on sector-specific levels of technology, reported on a 3-point scale by the Atlas of Cultural Evolution (Peter N. Peregrine, 2003). Following the aggregation methodology adopted by Diego Comin, William Easterly, and Erick Gong (2008), the index employs technology data on four sectors, including communications, industry (i.e., ceramics and metallurgy), transportation, and agriculture.

The level of technology in each sector is indexed as follows. In the communications sector, the index is assigned a value of 0 under the absence of both true writing and mnemonic or non-written records, a value of 1 under the presence of only mnemonic or non-written records, and a value of 2 under the presence of both. In the industrial sector, the index is assigned a value of 0 under the absence of both metalworks and pottery, a value of 1 under the presence of only pottery, and a value of 2 under the presence of both. In the transportation sector, the index is assigned a value of 0 under the absence of both vehicles and pack or draft animals, a value of 1 under the presence of only pack or draft animals, and a value of 2 under the presence of both. Finally, in the agricultural sector, the index is assigned a value of 0 under the absence of sedentary agriculture, a value of 1 when agriculture is practiced but only as a secondary mode of subsistence, and a value of 2 when agriculture is practiced as the primary mode of subsistence. In all cases, the sector-specific indices are normalized to assume values in the [0, 1]-interval. The technology index for a given culture is thus the unweighted average across sectors of the sector-specific indices for that culture.

Given that the cross-sectional unit of observation in Peregrine’s dataset is an archaeological tradition or culture, specific to a given region on the global map, and since spatial delineations in Peregrine’s dataset do not necessarily correspond to contemporary international borders, the culture-specific technology index in a given year is aggregated to the country level by averaging across those cultures from Peregrine’s map that appear within the modern borders of a given country. For more details on the underlying data and the aggregation methodology employed to construct this index, the reader is referred to Peregrine (2003) and Comin, Easterly, and Gong (2008).

Non-agricultural Technology Index in 1000 BCE, 1 CE, and 1000 CE

The index of non-agricultural technology for a given year is based on the same underlying data and aggregation methodology discussed above for the overall technology index. However, unlike the overall index, the non-agricultural counterpart incorporates data on the sector-specific technology indices for only the communications, industrial (i.e., ceramics and metallurgy), and transportation sectors.

Distance to Frontier in 1500 CE

The distance, in thousands of kilometers, from a country’s modern capital city to the closest regional technological frontier in the year 1500 CE, as reported by Quamrul Ashraf and Oded Galor (2010). Specifically, the authors employ historical urbanization estimates from Tertius Chandler (1987) and George Modelski (2003) to identify frontiers based on the size of urban populations, selecting the two largest cities from each continent that belong to different sociopolitical entities. Thus, in the year 1500 CE, the set of regional frontiers comprises London (UK), Paris (France), Cairo (Egypt), Fez (Morocco), Constantinople (Turkey), Peking (China), Tenochtitlan (Mexico), and Cuzco (Peru). For additional details, the reader is referred to Ashraf and Galor (2010).

Percentage of Land in Temperate Zones

The percentage of a country’s total land area in Köppen-Geiger temperate zones (including zones classified as Cf, Cs, Df, and Dw), as reported by the CID Research Datasets on General Measures of Geography.

Percentage of Land in Tropical and Subtropical Zones

The percentage of a country’s total land area in Köppen-Geiger tropical and subtropical zones (including zones classified as Af, Am, Aw, and Cw), as reported by the CID Research Datasets on General Measures of Geography.

Small Island and Landlocked Dummies

0/1-indicators for whether or not a country is a small island nation, and whether or not it possesses a coastline. These variables are constructed by the authors based on information reported by the CIA in The World Factbook online resource.

Appendix C Descriptive Statistics

Table C.1.

Descriptive Statistics – Means and Standard Deviations

	Obs.	Mean	S.D.	Min.	Max.
Log Population Density in 1500 CE	184	0.883	1.424	−3.817	4.135
Log Population Density in 1000 CE	177	0.449	1.366	−4.510	3.442
Log Population Density in 1 CE	155	−0.163	1.455	−4.510	3.170
Log Income per Capita in 1500 CE	31	6.343	0.260	5.991	7.003
Log Income per Capita in 1000 CE	28	6.084	0.141	5.991	6.477
Log Income per Capita in 1 CE	30	6.129	0.163	5.991	6.696
Log Years since Neolithic Transition	164	8.313	0.642	5.892	9.259
Log Technology Index in 1000 CE	149	0.573	0.160	0.118	0.693
Log Technology Index in 1 CE	149	0.529	0.163	0.061	0.693
Log Land Productivity	158	0.000	1.293	−4.815	1.657
Log Absolute Latitude	205	2.913	0.967	−0.693	4.277
Mean Distance to Nearest Coast or River	160	0.342	0.471	0.008	2.386
Percentage of Land within 100 km of Coast or River	160	0.463	0.375	0.000	1.000
Log Distance to Frontier	207	7.499	1.435	0.000	9.288
Percentage of Land in Temperate Zones	160	0.297	0.420	0.000	1.000
Percentage of Land in (Sub)Tropical Zones	160	0.364	0.433	0.000	1.000

Table C.2.

Descriptive Statistics – Pairwise Correlations

	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)	(15)
Log Population Density in 1500 CE	1.000 (184)
Log Population Density in 1000 CE	0.965 (177)	1.000 (177)
Log Population Density in 1 CE	0.881 (155)	0.940 (155)	1.000 (155)
Log Income per Capita in 1500 CE	0.726 (31)	0.641 (29)	0.670 (29)	1.000 (31)
Log Income per Capita in 1000 CE	0.128 (28)	0.238 (26)	0.253 (26)	0.106 (28)	1.000 (28)
Log Income per Capita in 1 CE	0.225 (30)	0.323 (29)	0.453 (29)	0.337 (27)	0.485 (27)	1.000 (30)
Log Years since Neolithic Transition	0.498 (158)	0.571 (152)	0.638 (135)	0.561 (31)	0.463 (28)	0.415 (30)	1.000 (164)
Log Technology Index in 1000 CE	0.584 (148)	0.562 (143)	0.565 (131)	0.646 (31)	0.303 (28)	0.329 (30)	0.715 (146)	1.000 (149)
Log Technology Index in 1 CE	0.495 (148)	0.524 (144)	0.554 (132)	0.635 (30)	0.283 (27)	0.380 (30)	0.597 (146)	0.827 (148)	1.000 (149)
Log Land Productivity	0.509 (152)	0.433 (147)	0.397 (131)	0.408 (31)	−0.115 (28)	−0.051 (30)	−0.002 (151)	−0.011 (146)	−0.126 (146)	1.000 (158)
Log Absolute Latitude	0.139 (184)	0.147 (177)	0.347 (155)	0.320 (31)	−0.363 (28)	−0.302 (30)	0.304 (163)	0.325 (149)	0.279 (149)	0.120 (158)	1.000 (205)
Mean Distance to Nearest Coast or River	−0.302 (157)	−0.326 (152)	−0.358 (136)	−0.387 (31)	0.173 (28)	−0.123 (30)	−0.020 (154)	0.003 (148)	−0.042 (148)	−0.167 (153)	−0.014 (160)	1.000 (160)
Percentage of Land within 100 km of Coast or River	0.367 (157)	0.343 (152)	0.365 (136)	0.452 (31)	−0.417 (28)	0.002 (30)	0.091 (154)	0.086 (148)	0.095 (148)	0.215 (153)	0.212 (160)	−0.670 (160)	1.000 (160)
Log Distance to Frontier	−0.351 (184)	−0.363 (177)	−0.429 (155)	−0.168 (31)	−0.025 (28)	−0.055 (30)	−0.396 (164)	−0.271 (149)	−0.258 (149)	−0.121 (158)	−0.369 (205)	0.156 (160)	−0.195 (160)	1.000 (207)
Percentage of Land in Temperate Zones	0.355 (157)	0.347 (152)	0.372 (136)	0.420 (31)	−0.544 (28)	−0.188 (30)	0.273 (154)	0.258 (148)	0.168 (148)	0.326 (153)	0.605 (160)	−0.263 (160)	0.422 (160)	−0.327 (160)	1.000 (160)
Percentage of Land in (Sub)Tropical Zones	−0.071 (157)	−0.094 (152)	−0.225 (136)	−0.226 (31)	−0.007 (28)	−0.093 (30)	−0.436 (154)	−0.476 (148)	−0.461 (148)	0.160 (153)	−0.710 (160)	−0.136 (160)	0.024 (160)	0.334 (160)	−0.577 (160)

Notes – Number of observations in parentheses.

Appendix D Supplementary Results

This appendix section collects some supplementary figures referred to in the text, and presents some additional findings demonstrating the robustness of the main results.

Figures D.1(a) and D.1(b) depict the partial regression lines associated with the transition-timing and land-productivity channels, respectively, in the baseline regression for population density in 1000 CE, whereas Figures D.2(a) and D.2(b) perform the same for population density in 1 CE. Moreover, Figures D.3 and D.4 illustrate the extent of cross-sectional and intertemporal variation prevalent across Maddison’s (2003) historical income per capita estimates. Finally, the partial regression lines associated with the period-specific indices of technology in the baseline regressions for population density in 1000 CE and 1 CE are depicted in Figures D.5(a) and D.5(b) respectively.

With respect to additional results demonstrating robustness, Table D.1 establishes that the results for population density and income per capita in 1500 CE are robust under two alternative specifications that relax potential constraints imposed by the baseline regression models, including (i) the treatment of the Americas as a single entity in accounting for continental fixed effects, and (ii) the employment of only the common variation in (the logs of) the percentage of arable land and the index of agricultural suitability when accounting for the effect of the land-productivity channel by way of the first principal component of these two variables.

Given that historical population estimates are also available from Maddison (2003), albeit for a smaller set of countries than McEvedy and Jones (1978), Table D.2 demonstrates that the baseline results for population density in the three historical periods, obtained using data from McEvedy and Jones, are indeed qualitatively unchanged under Maddison’s alternative population estimates. Finally, given the possibility that the disturbance terms in the baseline regression models may be non-spherical in nature, particularly since economic development has been spatially clustered in certain regions of the world, Tables D.3 and D.4 repeat the baseline analyses for population density and income per capita in the three historical periods (i.e., the years 1500 CE, 1000 CE, and 1 CE), with the standard errors of the point estimates corrected for spatial autocorrelation following the methodology of Timothy G. Conley (1999).

Figure D.1.

Transition Timing, Land Productivity, and Population Density in 1000 CE

Summary – This figure depicts the partial regression line for the effect of transition timing (land productivity) on population density in the year 1000 CE, while controlling for the influence of land productivity (transition timing), absolute latitude, access to waterways, and continental fixed effects. Thus, the x- and y-axes plot the residuals obtained from regressing transition timing (land productivity) and population density, respectively, on the aforementioned set of covariates.

Figure D.2.

Transition Timing, Land Productivity, and Population Density in 1 CE

Summary – This figure depicts the partial regression line for the effect of transition timing (land productivity) on population density in the year 1 CE, while controlling for the influence of land productivity (transition timing), absolute latitude, access to waterways, and continental fixed effects. Thus, the x- and y-axes plot the residuals obtained from regressing transition timing (land productivity) and population density, respectively, on the aforementioned set of covariates.

Figure D.3.

The Cross-Sectional Variability of Income per Capita in 1500 CE

Summary – This figure depicts the cross-sectional variability of Maddison’s (2003) income per capita estimates for the year 1500 CE. The x-axis plots the cumulative fraction of the data corresponding to each observation (in ascending order), and the y-axis plots the quantiles of the uniform distribution of log income per capita in 1500 CE. The closer the observations are to the 45-degree line, the more uniformly distributed is the data and, hence, the larger is the cross-sectional variability.

Figure D.4.

The Intertemporal Variability of Income per Capita, 1000–1500 CE

Summary – This figure depicts the intertemporal variability of Maddison’s (2003) income per capita estimates over the time period 1000–1500 CE. The x- and y-axes plot income per capita in the years 1000 CE and 1500 CE respectively. The farther the observations are from the 45-degree line, the greater is the intertemporal variability.

Figure D.5.

Technological Sophistication and Population Density in 1000 CE and 1 CE

Summary – This figure depicts the partial regression lines for the effect of technological sophistication on population density in the years 1000 CE and 1 CE, respectively, while controlling for the influence of land productivity, absolute latitude, access to waterways, and continental fixed effects. Thus, for a given year, the x- and y-axes plot the residuals obtained from regressing the technology index and population density, respectively, for that year on the aforementioned set of covariates.

Table D.1.

Robustness to Alternative Specifications

	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
	Standard OLS	Standard OLS	Standard OLS	Weighted OLS	Standard OLS	Standard OLS	Standard OLS	Weighted OLS
	Full Sample	Income Sample	Income Sample	Income Sample	Full Sample	Income Sample	Income Sample	Income Sample
	Alternative Specification Includes:
	Both North and South America Dummies				Both Components of Land Productivity
	Dependent Variable is:
	Log Population Density in 1500 CE		Log Income per Capita in 1500 CE		Log Population Density in 1500 CE		Log Income per Capita in 1500 CE
Log Years since Neolithic Transition	1.169*** (0.183)	1.390** (0.649)	0.160 (0.143)	0.174 (0.166)	1.079*** (0.183)	1.536** (0.596)	0.145 (0.163)	0.151 (0.208)
Log Land Productivity	0.562*** (0.052)	0.562*** (0.157)	0.040 (0.025)	0.039 (0.023)
Log Absolute Latitude	−0.341*** (0.104)	−0.091 (0.554)	−0.045 (0.086)	−0.043 (0.084)	−0.325*** (0.108)	0.124 (0.423)	−0.046 (0.067)	−0.046 (0.071)
Mean Distance to Nearest Coast or River	−0.477*** (0.142)	−0.501 (1.300)	0.213 (0.198)	0.219 (0.206)	−0.390*** (0.142)	−0.248 (1.102)	0.203 (0.226)	0.187 (0.267)
Percentage of Land within 100 km of Coast or River	0.703** (0.302)	1.803* (0.865)	0.122 (0.147)	0.153 (0.173)	0.900*** (0.284)	1.693** (0.723)	0.135 (0.135)	0.153 (0.178)
Log Arable Percentage of Land					0.343*** (0.095)	−0.315 (0.504)	0.064 (0.085)	0.079 (0.117)
Log Suitability Index for Agriculture					0.270*** (0.086)	0.736* (0.356)	−0.008 (0.067)	−0.017 (0.084)
Continent Dummies	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Observations	147	31	31	31	147	31	31	31
R-squared	0.74	0.89	0.66	0.54	0.73	0.90	0.66	0.54

Notes – (i) log land productivity in regressions (1)–(4) is the first principal component of the log of the percentage of arable land and the log of the agricultural suitability index that are used in regressions (5)–(8); (ii) the weight of country i in regressions (4) and (8) is inversely proportional to the frequency with which i’s income per capita occurs in the corresponding samples, i.e., $w_i=n_i^{-1}/{\sum }_i{n}_i^{-1}$, where n_i is the number of countries with income per capita identical to i; (iii) a single continent dummy is used to represent the Americas in regressions (5)–(8); (iv) robust standard error estimates are reported in parentheses; (v) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.

Table D.2.

Robustness to Population Data from Maddison’s Historical Statistics

	(1)	(2)	(3)	(4)	(5)	(6)
	OLS	OLS	OLS	OLS	OLS	OLS
	Full Sample	Income Sample	Full Sample	Income Sample	Full Sample	Income Sample
	Dependent Variable is Log Population Density based on Maddison’s Estimates for:
	1500 CE		1000 CE		1 CE
Log Years since Neolithic Transition	1.190*** (0.287)	0.984* (0.498)	1.845*** (0.360)	0.809*** (0.273)	1.865*** (0.576)	0.824*** (0.277)
Log Land Productivity	0.481*** (0.115)	0.625*** (0.184)	0.489*** (0.137)	0.348*** (0.104)	0.474*** (0.163)	0.582** (0.219)
Log Absolute Latitude	−0.102 (0.293)	0.109 (0.401)	0.012 (0.297)	−1.838** (0.635)	0.092 (0.265)	−2.207*** (0.638)
Mean Distance to Nearest Coast or River	−0.983* (0.551)	−0.844 (1.066)	−0.941* (0.535)	−0.616 (0.606)	−1.128 (0.707)	−0.501 (0.601)
Percentage of Land within 100 km of Coast or River	1.546** (0.583)	1.492** (0.688)	0.954 (0.725)	1.446** (0.630)	1.182 (0.773)	1.119 (0.733)
Continent Dummies	Yes	Yes	Yes	Yes	Yes	Yes
Observations	48	31	47	26	43	29
R-squared	0.85	0.88	0.84	0.95	0.81	0.92

Notes – (i) log land productivity is the first principal component of the log of the percentage of arable land and the log of an agricultural suitability index; (ii) a single continent dummy is used to represent the Americas, which is natural given the historical period examined; (iii) regressions (4)–(6) do not employ the Oceania dummy due to a single observation for this continent in the corresponding regression samples; (iv) robust standard error estimates are reported in parentheses; (v) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.

Table D.3.

Robustness to Corrections for Spatial Autocorrelation

	(1)	(2)	(3)	(4)	(5)	(6)
	Corrected OLS	Spatial GMM	Corrected OLS	Spatial GMM	Corrected OLS	Spatial GMM
	Full Sample	Restricted Sample	Full Sample	Restricted Sample	Full Sample	Restricted Sample
	Dependent Variable is Log Population Density in:
	1500 CE		1000 CE		1 CE
Log Years since Neolithic Transition	1.087*** [0.184]	2.038*** [0.387]	1.480*** [0.213]	2.713*** [0.498]	1.930*** [0.316]	3.322*** [0.404]
Log Land Productivity	0.576*** [0.053]	0.583*** [0.092]	0.497*** [0.066]	0.575*** [0.095]	0.394*** [0.076]	0.448*** [0.093]
Log Absolute Latitude	−0.314*** [0.108]	−0.257* [0.141]	−0.229* [0.123]	−0.117 [0.138]	0.057 [0.101]	0.124 [0.115]
Mean Distance to Nearest Coast or River	−0.392** [0.195]	0.318 [0.351]	−0.528** [0.207]	0.373 [0.370]	−0.685*** [0.168]	−0.423 [0.294]
Percentage of Land within 100 km of Coast or River	0.899*** [0.319]	1.395*** [0.417]	0.716** [0.351]	1.550*** [0.409]	0.857** [0.371]	1.143** [0.461]
Continent Dummies	Yes	Yes	Yes	Yes	Yes	Yes
Observations	147	96	142	94	128	83
R-squared	0.73	0.70	0.67	0.62	0.69	0.72

Notes – (i) log land productivity is the first principal component of the log of the percentage of arable land and the log of an agricultural suitability index; (ii) the spatial GMM regressions employ the numbers of prehistoric domesticable species of plants and animals as instruments for log transition timing; (iii) a single continent dummy is used to represent the Americas, which is natural given the historical period examined; (iv) the spatial GMM regressions do not employ the Oceania dummy due to a single observation for this continent in the corresponding regression samples; (v) standard errors corrected for spatial autocorrelation are reported in square brackets; (vi) the spatial distribution of countries in ℜ² is specified using aerial distances between geodesic centroids; (vii) the spatial autocorrelation in error terms is modelled as declining linearly along a 4,000 km radius from each observation; (viii) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.

Table D.4.

Additional Robustness to Corrections for Spatial Autocorrelation

	(1)	(2)	(3)	(4)	(5)	(6)
	Corrected OLS	Corrected OLS	Corrected OLS	Corrected OLS	Corrected OLS	Corrected OLS
	Dependent Variable is:
	Log Income per Capita in:			Log Population Density in:
	1500 CE	1000 CE	1 CE	1500 CE	1000 CE	1 CE
Log Years since Neolithic Transition	0.159** [0.064]	0.073* [0.038]	0.109 [0.069]	1.337*** [0.437]	0.832*** [0.263]	1.006*** [0.376]
Log Land Productivity	0.041** [0.016]	−0.021 [0.023]	−0.001 [0.020]	0.584*** [0.125]	0.364*** [0.098]	0.681*** [0.147]
Log Absolute Latitude	−0.041 [0.043]	0.060 [0.108]	−0.175 [0.123]	0.050 [0.343]	−2.140*** [0.704]	−2.163*** [0.838]
Mean Distance to Nearest Coast or River	0.215** [0.100]	−0.111 [0.125]	0.043 [0.116]	−0.429 [0.893]	−0.237 [0.656]	0.118 [0.859]
Percentage of Land within 100 km of Coast or River	0.124* [0.075]	−0.150 [0.110]	0.042 [0.082]	1.855*** [0.620]	1.326** [0.524]	0.228 [0.605]
Continent Dummies	Yes	Yes	Yes	Yes	Yes	Yes
Observations	31	26	29	31	26	29
R-squared	0.66	0.68	0.33	0.88	0.95	0.89

Notes – (i) log land productivity is the first principal component of the log of the percentage of arable land and the log of an agricultural suitability index; (ii) a single continent dummy is used to represent the Americas, which is natural given the historical period examined; (iii) regressions (2)–(3) and (5)–(6) do not employ the Oceania dummy due to a single observation for this continent in the corresponding regression samples; (iv) standard errors corrected for spatial autocorrelation are reported in square brackets; (v) the spatial distribution of countries in ℜ² is specified using aerial distances between geodesic centroids; (vi) the spatial autocorrelation in error terms is modelled as declining linearly along a 4,000 km radius from each observation; (vii) *** denotes statistical significance at the 1 percent level, ** at the 5 percent level, and * at the 10 percent level, all for two-sided hypothesis tests.