Abstract
The early stage of drug discovery is often based on selecting the highest affinity lead compound. To this end the structural and energetic characterization of the binding reaction is important. The binding energetics can be resolved into enthalpic and entropic contributions to the binding Gibbs free energy. Most compound binding reactions are coupled to the absorption or release of protons by the protein or the compound. A distinction between the observed and intrinsic parameters of the binding energetics requires the dissection of the protonation/deprotonation processes. Since only the intrinsic parameters can be correlated with molecular structural perturbations associated with complex formation, it is these parameters that are required for rational drug design. Carbonic anhydrase (CA) isoforms are important therapeutic targets to treat a range of disorders including glaucoma, obesity, epilepsy, and cancer. For effective treatment isoform-specific inhibitors are needed. In this work we investigated the binding and protonation energetics of sixteen [(2-pyrimidinylthio)acetyl]benzenesulfonamide CA inhibitors using isothermal titration calorimetry and fluorescent thermal shift assay. The compounds were built by combining four sulfonamide headgroups with four tailgroups yielding 16 compounds. Their intrinsic binding thermodynamics showed the limitations of the functional group energetic additivity approach used in fragment-based drug design, especially at the level of enthalpies and entropies of binding. Combined with high resolution crystal structural data correlations were drawn between the chemical functional groups on selected inhibitors and intrinsic thermodynamic parameters of CA-inhibitor complex formation.
Introduction
Significant effort has been devoted to develop drugs that bind to their targets with high affinity and sufficient selectivity [1], [2]. The binding affinity, i.e. the change in Gibbs free energy of binding (ΔG), is the sum of the changes in enthalpic and entropic contributions (ΔH and TΔS respectively) that often compensate each other [3]. Optimization of the enthalpic and entropic contributions to binding is fundamental to improving the affinity of small molecule inhibitors in drug development. However, our capabilities to do this routinely are limited by our understanding of structure-thermodynamic correlations [4]–[9]. Thermodynamic measurement of the energetic contributions to protein-compound complex formation is not straightforward in the presence of additional contributions from solvent effects such as protonation/deprotonation of the interacting moieties, i.e. ΔH is the sum of the contributions from the ΔH of binding (intrinsic) and ΔH of protonation.
Thermodynamics has found increasing use in drug design and development when targeting the inhibition of carbonic anhydrases (CAs). CAs are zinc metal containing enzymes that catalyze the reversible hydration of CO2 and dehydration of bicarbonate. CAs perform important physiological functions in all kingdoms of life [10], [11]. There are 12 catalytically active CA isoforms in humans. CAs are involved in many physiological and pathological processes including pH and CO2 homeostasis, respiration and transport of bicarbonate and CO2 in various metabolizing tissues and lungs, electrolyte secretion, CO2 fixation and biosynthetic reactions, bone resorption, calcification and tumorigenicity [11]–[15]. Abnormal activities of CAs are often associated with different human diseases, such as glaucoma, epilepsy, Alzheimer’s and Parkinson’s diseases, obesity, and cancer [15]–[18]. Therefore CAs are important therapeutic targets and some inhibitors are clinically approved drugs [19]. The most studied class of CA inhibitors is aromatic sulfonamides [12], [20], [21]. Although about 30 CA inhibitors are currently used as drugs, the challenge of developing compounds that are selective for a specific isoform still remains [22], [23].
In this study the structure-thermodynamic profile of CA inhibitor binding was investigated. The underlying contributions of ΔH and TΔS to the ΔG have been shown to be important parameters to integrate into rational drug design programs targeted at CAs [24], however, the directly measured values of these terms are non-intrinsic since they include the energetic contributions from protonation events that accompany the binding reaction between a CA and its compound [25], [26]. It is important to note that only the deprotonated form of the sulfonamide binds to the CA active site. Furthermore, the active site Zn-coordinated hydroxide must be protonated before it can be replaced by the amino group of the sulfonamide [27]. Therefore, the observed parameters depend on the conditions of the experiment, such as pH and buffer composition [28] and, therefore it is important to dissect the protonation-deprotonation contributions to the thermodynamic parameters of binding. Since the modification of functional groups is the basis of medicinal chemistry in rational drug development and is essential to optimization of a promising lead candidates, it is of fundamental importance to calculate the intrinsic parameters that can be used to estimate the effect of the addition or replacement of functional groups [29], [30].
Detailed investigation of the compound structure-activity relationships (SAR) is required in order to rationally design new compounds with desired properties [28], [31], [32]. Here we analyzed both the intrinsic thermodynamics of binding in terms of the compound chemical structure and also the structures of protein-ligand crystallographic complexes leading to a more-in-depth understanding of the binding reaction itself and the changes in binding profile as chemical modifications in drug-like molecules are made. Analysis of previously published structures of compounds bound to several CA isoforms [33], together with four newly solved crystal structures of CA II with compounds 1d, 2c, 4c, and CA XIII with 4c, revealed that all compounds bound to CAs in a similar mode but with significant differences that may be correlated to differences in the thermodynamics of binding. The series of 16 closely related compounds were analyzed and mapped in the direction of incrementally changing chemical functional groups to correlate with the increments in the intrinsic thermodynamic parameters. By determining the intrinsic thermodynamic binding parameters we are able to assess the important contributions to affinity and suggest routes to novel therapeutically useful compound development.
Results and Discussion
Observed thermodynamics of inhibitor binding to CA
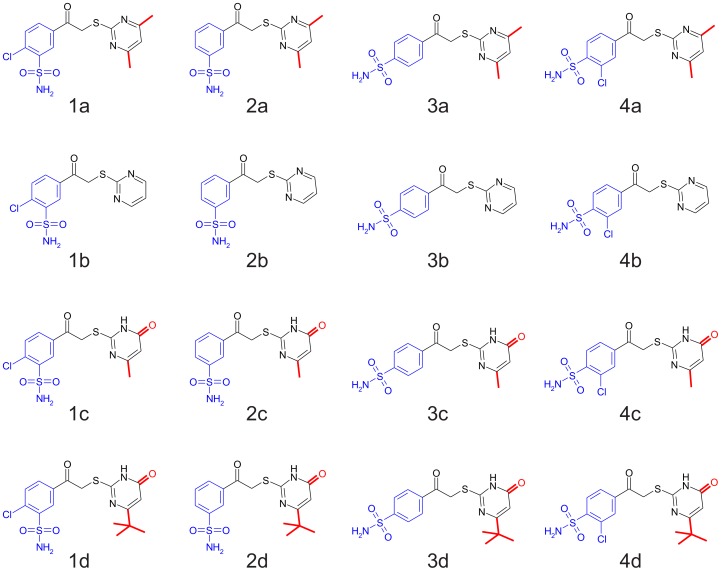
Sixteen compounds (1a, 2a, …, 4d, Fig. 1) made by combining four different aromatic sulfonamide headgroups (1, 2, 3, and 4) with four modified pyrimidine tailgroups (a, b, c, and d) were chosen to study the correlations of compound chemical structure with the thermodynamics of binding. Furthermore, the energetic additivity of these head and tail-groups was investigated by comparing whether the addition of a particular tailgroup to different headgroups will contribute the same increment in thermodynamics of binding.
Figure 1. The structures of S-alkylated pyrimidine derivative compounds used in this study.
Compounds are grouped according to 4 sulfonamide headgroups (1–4) and 4 tailgroups (a–d) totaling 16 compounds.
The observed binding affinities (ΔbGobs) of the compounds were previously measured using fluorescent thermal shift assay (FTSA) as described by Čapkauskaite et al. [12], [33]. In this work, the binding of 16 inhibitors to five CA isoforms (CA I, CA II, CA VII, CA XII, and CA XIII) was analyzed using ITC which provided the observed enthalpy (ΔbHobs) and entropy (ΔbSobs) in addition to the ΔbGobs. The observed affinities determined by ITC essentially confirmed our previous FTSA results (Table 1). Furthermore, stopped-flow CO2 hydration assay (SFA) was used as control in order to confirm inhibition constants of compound 1b binding to five isoforms of recombinant human carbonic anhydrases. The observed dissociation constants spanned the range from 0.25 nM to 10 µM. Figs. 2, 3 and 4 show typical experimental data of FTSA, ITC and SFA measurements. The observed enthalpies and entropies of binding, determined by ITC, are listed in Table 1.
Table 1. Experimentally measured observed dissociation constants (determined by FTSA and ITC), averaged Gibbs free energies, and the enthalpies and entropies (determined by ITC) of the compound binding to five isoforms of human recombinant CAs.
| CA I | 1a | 1b | 1c | 1d | 2a | 2b | 2c | 2d | 3a | 3b | 3c | 3d | 4a | 4b | 4c | 4d | |
| Kd_ITC | 850 | 2300 | 2000 | 240 | 100 | 1500 | 1900 | 230 | 85 | 110 | 180 | 23 | 19 | 49 | 90 | 7.0 | |
| Kd_FTSA | 1000 | 3100 | 830 | 100 | 370 | 770 | 830 | 100 | 22 | 67 | 67 | 1.4 | 5.0 | 10 | 4.0 | 0.25 | |
| ΔG | −35.8 | −33.1 | −35.0 | −40.4 | −36.9 | −35.4 | −35.0 | −40.5 | −43.7 | −41.9 | −41.3 | −49.0 | −47.6 | −45.5 | −45.9 | −52.7 | |
| ΔH | −18.1 | −16.6 | −18.3 | −26.0 | −33.2 | −31.7 | −24.3 | −26.2 | −31.3 | −27.9 | −23.3 | −37.4 | −29.2 | −28.6 | −20.8 | −28.1 | |
| TΔS | 17.7 | 16.5 | 16.7 | 14.4 | 3.7 | 3.7 | 10.7 | 14.3 | 12.4 | 14.0 | 18.0 | 11.6 | 18.4 | 16.9 | 25.1 | 24.6 | |
| CA II | Kd_ITC | 150 | 430 | 130 | 100 | 570 | 730 | 1100 | 740 | 64 | 12 | 49 | 27 | 14 | 38 | 20 | 90 |
| Kd_FTSA | 220 | 330 | 200 | 50 | 1000 | 1100 | 1300 | 500 | 33 | 17 | 67 | 45 | 17 | 11 | 21 | 40 | |
| ΔG | −40.0 | −38.1 | −40.4 | −42.4 | −36.4 | −35.9 | −35.2 | −36.9 | −43.6 | −46.6 | −43.0 | −44.2 | −46.4 | −45.6 | −45.6 | −42.9 | |
| ΔH | −14.0 | −23.3 | −19.4 | −22.9 | −22.6 | −30.1 | −14.2 | −12.3 | −33.2 | −46.8 | −22,6 | −19.5 | −31.4 | −37.9 | −19.4 | −12.4 | |
| TΔS | 26.0 | 14.8 | 21.0 | 19.5 | 13.8 | 5.8 | 21.0 | 24.6 | 10.4 | −0.2 | 20.4 | 24.7 | 15.0 | 7.7 | 26.2 | 30.5 | |
| CA VII | Kd_ITC | 460 | 660 | 320 | 92 | 10000 | 1600 | 12000 | 3500 | 260 | 82 | 630 | 340 | 61 | 89 | 68 | 230 |
| Kd_FTSA | 330 | 710 | 130 | 40 | 6700 | 4000 | 4000 | 500 | 130 | 67 | 170 | 33 | 13 | 5,0 | 36 | 11 | |
| ΔG | −38.0 | −36.6 | −39.7 | −42.9 | −30.2 | −33.2 | −30.7 | −30.7 | −40.1 | −42.3 | −38.5 | −41.4 | −44.9 | −45.6 | −43.4 | −43.3 | |
| ΔH | −23.6 | −44.7 | −17.0 | −23.7 | −10.4 | −10.2 | −10.6 | −4.6 | −54.3 | −50.7 | −54.3 | −27.4 | −19.4 | −31.6 | −14.6 | −15.7 | |
| TΔS | 14.4 | −8.1 | 22.7 | 19.2 | 19.8 | 23.0 | 20.1 | 26.1 | −14.2 | −8.4 | −15.8 | 14.0 | 25.5 | 14.0 | 28.8 | 27.6 | |
| CA XII | Kd_ITC | 1400 | 370 | 550 | 84 | 7900 | 620 | 2800 | 940 | 230 | 370 | 330 | 29 | 460 | 450 | 500 | NA |
| Kd_FTSA | 1400 | 1300 | 500 | 43 | 3300 | 3300 | 3700 | 1300 | 910 | 560 | 560 | 140 | 910 | 830 | 330 | 330 | |
| ΔG | −34.8 | −36.6 | −37.3 | −42.9 | −31.4 | −34.7 | −32.6 | −35.4 | −37.6 | −37.7 | −37.8 | −42.7 | −36.7 | −36.9 | −38.5 | −38.5 | |
| ΔH | −18.2 | −19.4 | −10.8 | −9.0 | −28.4 | −15.5 | −12.6 | −13.4 | −23.4 | −30.7 | −11.8 | −10.8 | −29.1 | −24.7 | −24.7 | NA | |
| TΔS | 16.6 | 17.2 | 26.5 | 33.9 | 3.0 | 19.2 | 20.0 | 22.0 | 14.2 | 7.0 | 26.0 | 31.9 | 7.6 | 12.2 | 13.8 | NA | |
| CA XIII | Kd_ITC | 300 | 270 | 88 | 62 | 23000 | 700 | 3500 | 2100 | 130 | 77 | 1500 | 50 | 25 | 44 | 144 | 5.6 |
| Kd_FTSA | 330 | 330 | 200 | 25 | 1000 | 1300 | 1500 | 170 | 83 | 130 | 360 | 5.0 | 10 | 17 | 33 | 5.0 | |
| ΔG | −38.6 | −38.7 | −40.8 | −44.0 | −31.6 | −35.7 | −33.4 | −37.0 | −41.4 | −41.6 | −36.4 | −46.3 | −46.3 | −44.9 | −42.5 | −49.2 | |
| ΔH | −11.9 | −15.4 | −16.5 | −20.9 | −27.9 | −16.0 | −14.8 | −27.7 | −35.9 | −33.9 | −29.1 | −24.9 | −33.9 | −37.1 | −23.8 | −26.9 | |
| TΔS | 26.7 | 23.3 | 24.3 | 23.1 | 3.7 | 19.7 | 18.6 | 9.3 | 5.5 | 7.7 | 7.3 | 21.4 | 12.4 | 7.8 | 18.7 | 22.3 |
Experimental results are for 37°C, pH 7.0. Intrinsic binding parameters were calculated from these data using Eq. (1–4) and are listed in table 3.
NA – not determined by ITC due to poor solubility of the compound and relatively high concentration due to weak binding as compared to other CA isoforms.
Figure 2. Fluorescent thermal shift assay data for selected compound 1a and 4a binding to CA I and CA XIII.
Top graphs show raw protein denaturation curves and the bottom graphs show the compound dosing curves. Datapoints are the experimental midpoints of the denaturation curves while the lines are drawn according to the model [39].
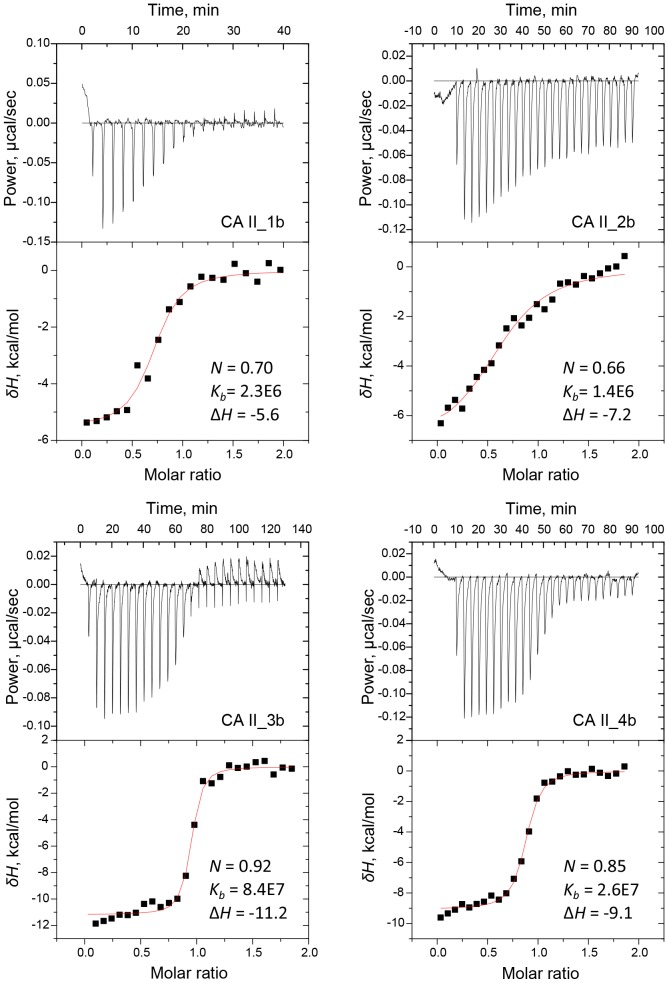
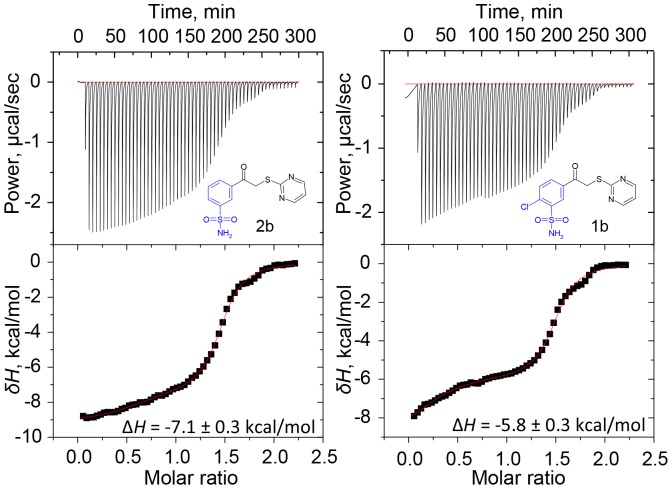
Figure 3. ITC data for compound (1–4)b binding to CA II.
Upper graphs are power compensation curves while the lower graphs are the integrated ITC binding curves determined at 37°C.
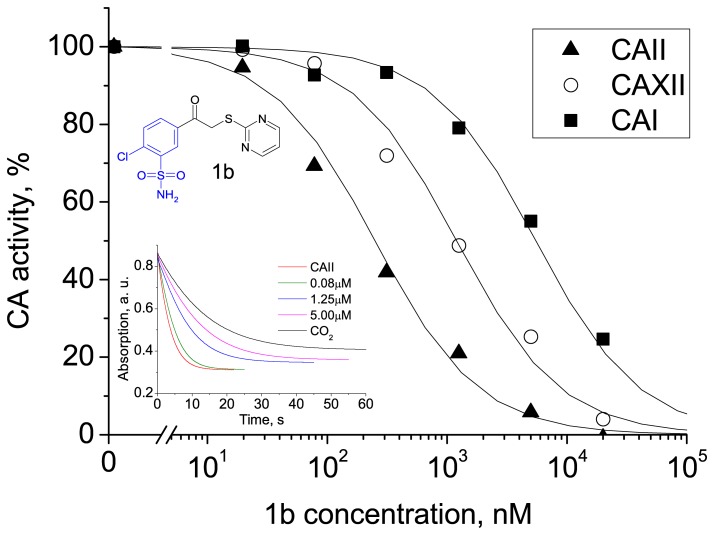
Figure 4. SFA data for inhibition of CA I, CA II and CA XII by compound 1b determined at 25°C.
The inset shows the curves of pH drop monitored by indicator spectrophotometry for CA II.
Thermodynamics of protonation of the inhibitor and zinc-bound hydroxide anion
The sulfonamide group of the inhibitor must be deprotonated in order to bind to CA [27]. For calculations of intrinsic parameters, it is important to know the enthalpy of deprotonation of sulfonamide (ΔHprot) and its pKa value. The pKa was calculated and measured experimentally. For compounds containing chlorine (1(a–d) and 4(a–d)), the calculated pKa values were equal to 8.7 (Table 2). For inhibitors without chlorine (2(a–d) and 3(a–d)), the calculated pKa values were equal to 9.7. The difference between the calculated values of compounds a, b, c, and d did not exceed ±0.2.
Table 2. pKa values and ΔHprot of compounds (1–4)b and the pKa values and ΔHprot of H2O bound to Zn in the active site of human recombinant CAs at 37°C.
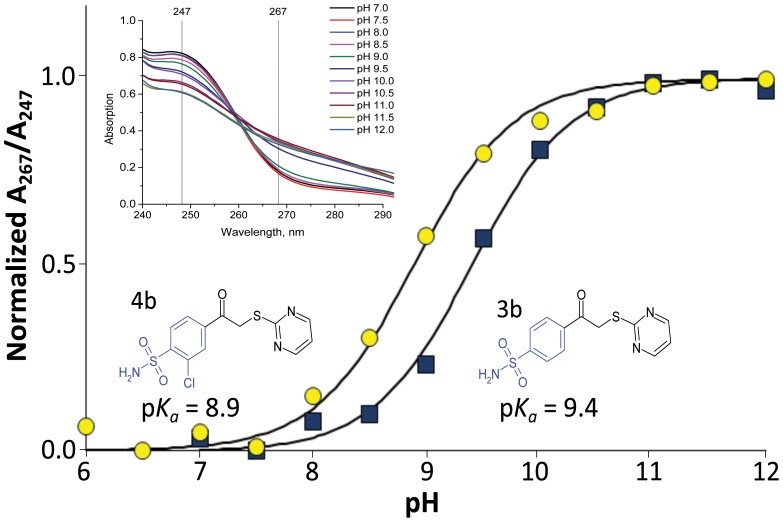
The pKa values were also determined spectrophotometrically for compounds (1–4)b according to [34] as described in materials and methods. The absorbance spectra of the four compounds were taken at various pH (Fig. 5). The ratio of absorbance at two wavelengths where the pH effect is large (10 nm above and below isosbestic point) was normalized and plotted as a function of pH yielding the pKa of the sulfonamide headgroup. For compounds 1(a–d) and 4(a–d) containing Cl in the benzene ring, the experimental pKa was 8.9±0.2 and for compounds 2(a–d) and 3(a–d) the experimental pKa was 9.4±0.2. These values are similar to the calculated values. Since compound a, c, and d solubility at high pH prevented accurate pKa determination, and as confirmed by calculation, we assumed that compounds a, c, and d would have the same pKas and therefore these values were later used in calculations of intrinsic parameters (Table 3).
Figure 5. Spectrophotometric determination of the sulfonamide group deprotonation pKa for 3b and 4b.
The inset shows the absorption spectra of compound 3b in solutions at various pH.
Table 3. Intrinsic dissociation constants, Gibbs free energies, enthalpies, and entropies of the compound binding to five isoforms of human recombinant CAs.
| 1a | 1b | 1c | 1d | 2a | 2b | 2c | 2d | 3a | 3b | 3c | 3d | 4a | 4b | 4c | 4d | ||
| CA I | Kd | 11 | 31 | 15 | 1.8 | 2.2 | 4.0 | 4.7 | 0.55 | 0.16 | 0.32 | 0.41 | 0.021 | 0.11 | 0.26 | 0.015 | 0.22 |
| Δ G | −47.3 | −44.6 | −46.5 | −51.9 | −51.4 | −49.9 | −49.5 | −55.0 | −58.2 | −56.4 | −55.8 | −63.4 | −59.1 | −57.0 | −64.3 | −57.4 | |
| Δ H | −36.6 | −35.1 | −36.8 | −44.5 | −57.3 | −55.8 | −48.4 | −50.3 | −55.4 | −52.0 | −47.4 | −61.5 | −47.7 | −47.2 | −46.7 | −39.4 | |
| T Δ S | 10.7 | 9.5 | 9.7 | 7.4 | −5.9 | −5.9 | 1.1 | 4.7 | 2.8 | 4.4 | 8.4 | 1.9 | 11.4 | 9.8 | 17.6 | 18.0 | |
| CA II | Kd | 1.0 | 2.1 | 0.88 | 0.40 | 1.3 | 1.6 | 2.1 | 1.1 | 0.08 | 0.025 | 0.10 | 0.062 | 0.085 | 0.11 | 0.11 | 0.33 |
| Δ G | −53.5 | −51.6 | −53.8 | −55.8 | −52.7 | −52.3 | −51.6 | −53.3 | −59.9 | −63.0 | −59.4 | −60.6 | −59.8 | −59.0 | −59.0 | −56.3 | |
| Δ H | −23.7 | −33.0 | −29.1 | −32.6 | −37.8 | −45.3 | −29.5 | −27.5 | −48.4 | −62.0 | −37.8 | −34.7 | −41.1 | −47.6 | −29.0 | −22.0 | |
| T Δ S | 29.8 | 18.6 | 24.7 | 23.2 | 14.9 | 7.0 | 22.1 | 25.8 | 11.5 | 1.0 | 21.6 | 25.9 | 18.7 | 11.4 | 30.0 | 34.3 | |
| CA VII | Kd | 1.9 | 3.3 | 1.0 | 0.29 | 12 | 3.9 | 10 | 2.0 | 0.27 | 0.11 | 0.50 | 0.16 | 0.13 | 0.10 | 0.24 | 0.24 |
| Δ G | −51.8 | −50.4 | −53.4 | −56.6 | −46.9 | −49.9 | −47.4 | −45.5 | −56.8 | −59.0 | −55.2 | −58.1 | −58.7 | −59.3 | −57.2 | −57.1 | |
| Δ H | −27.8 | −48.9 | −21.2 | −27.9 | −20.2 | −19.9 | −20.4 | −14.4 | −67.3 | −60.4 | −64.1 | −37.2 | −23.6 | −35.8 | −18.8 | −19.9 | |
| T Δ S | 24.0 | 1.5 | 32.3 | 28.7 | 26.7 | 30.0 | 27.0 | 31.1 | −10.5 | −1.4 | −8.9 | 20.9 | 35.1 | 23.5 | 38.4 | 37.2 | |
| CA XII | Kd | 6.7 | 3.3 | 32 | 0.29 | 7.8 | 2.2 | 4.9 | 1.7 | 0.71 | 0.70 | 0.65 | 0.10 | 3.1 | 3.0 | 2.0 | 1.6 |
| Δ G | −48.5 | −50.4 | −51.0 | −56.6 | −48.1 | −51.4 | −49.3 | −52.1 | −54.3 | −54.4 | −54.5 | −59.4 | −50.5 | −50.6 | −51.7 | −52.2 | |
| Δ H | −25.5 | −26.7 | −18.1 | −16.3 | −41.3 | −28.3 | −25.4 | −26.2 | −36.3 | −43.5 | −24.6 | −23.6 | −36.4 | −32.0 | −19.1 | NA | |
| T Δ S | 23.0 | 23.7 | 32.9 | 40.3 | 6.8 | 23.1 | 23.9 | 25.9 | 18.0 | 10.9 | 29.9 | 35.8 | 14.1 | 18.6 | 32.6 | NA | |
| CA XIII | Kd | 3.6 | 3.4 | 1.5 | 0.44 | 17 | 3.5 | 8.4 | 2.2 | 0.38 | 0.35 | 2.6 | 0.057 | 0.18 | 0.31 | 0.78 | 0.060 |
| Δ G | −50.2 | −50.3 | −52.4 | −55.5 | −46.1 | −50.2 | −47.9 | −51.5 | −56.0 | −56.1 | −51.0 | −60.8 | −57.9 | −56.5 | −54.1 | −60.7 | |
| Δ H | −29.5 | −33.0 | −34.1 | −38.6 | −51.1 | −39.3 | −38.0 | −50.9 | −59.1 | −57.1 | −52.3 | −48.1 | −51.6 | −54.8 | −41.4 | −44.5 | |
| T Δ S | 20.7 | 17.3 | 18.3 | 16.9 | −5.0 | 10.9 | 9.9 | 0.6 | −3.1 | −1.0 | −1.3 | 12.7 | 6.3 | 1.7 | 12.7 | 16.2 |
NA – not determined by ITC due to poor solubility of the compound and relatively high concentration due to weak binding as compared to other CA isoforms.
The ΔHprot of sulfonamide group for compounds (1–4)b was determined using ITC (Table 2). First, the inhibitor was deprotonated by applying 1.5 equivalent NaOH to reach the pH at least one unit above the pKa. Then the deprotonated inhibitor solution was titrated with acid by ITC. Titration curves of 1b and 2b are shown in Fig. 6. The first transition represents the titration of excess NaOH, the second transition represents the titration of inhibitor. The inhibitors with chlorine (1b and 4b) had protonation enthalpy of −5.8±0.3 kcal/mol (−24.3 kJ/mol) while the inhibitors without chlorine (2b and 3b) exhibited the enthalpies of protonation −7.1±0.3 kcal/mol (−29.7 kJ/mol) (Table 2). The effect of modifications in pyrimidine ring for ΔHprot values was below the standard error of the measurement.
Figure 6. Determination of the enthalpy of protonation for 1b and 2b by ITC.
Compounds were deprotonated by adding 1.5 equivalent NaOH and titrating with HNO3.
The Zn-bound hydroxy ion in the active site of CA must be protonated for the binding reaction to occur. Thermodynamic parameters of protonation of the hydroxide in the five CA isoforms were previously determined using ITC for 25°C [31], [35]–[37]. In Table 2, the pKa and ΔHprot values for all investigated CA isoforms were calculated for 37°C. CA I has similar pKa and ΔHprot values to CA XIII, CA II has similar pKa value to CA VII and CA XII, and similar ΔHprot value to CA XII. Some of these similarities can be explained by comparing amino acids in the active site of CA isoforms.
Intrinsic thermodynamics of inhibitor binding
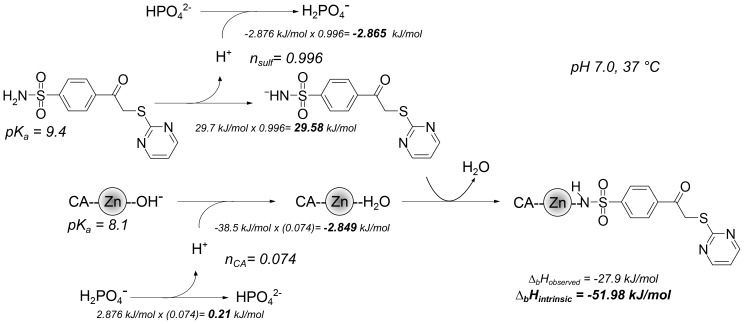
Fig. 7 shows a scheme of the processes linked to the binding of 3b to CA I. The pKa of CA I is 8.1 and Δb_proton_CAH value is −38.5 kJ/mol. The pKa value of 3b is 9.4 and Δb_proton_sulf H value is −29.7 kJ/mol. The enthalpy of phosphate buffer protonation Δb_proton_buf H = −2.9 kJ/mol. fCA = 0.926, fsulf = 0.004. nsulf = 1 − fsulf = 0.996, nCA = 1 − fCA = 0.074 and nbuf = nsulf+nCA. From equation 4 (materials and methods), the intrinsic enthalpy is ΔbH = −52.0 kJ/mol. All compounds binding intrinsic parameters are listed in Table 3.
Figure 7. The processes linked to the binding of 3b to CA I.
The two left-central reactions show the binding-linked deprotonation of the inhibitor sulfonamide and the protonation of the zinc-bound hydroxide, respectively. Top and bottom lines show linked phosphate buffer (de)protonation reactions. The numbers give estimates of the enthalpies for each process multiplied by the number of linked protons (n) yielding the observed enthalpic contribution of each reaction at pH 7.0, 37°C. The intrinsic enthalpy of binding, shown by the rightmost arrow, is equal to −51.98 kJ/mol. The observed enthalpy, estimated for phosphate buffer at pH 7.0, is equal to −27.90 kJ/mol. Zinc atom is shown as grey shaded sphere and the carbonic anhydrase protein is shown as CA.
Compound structure correlations with binding thermodynamics
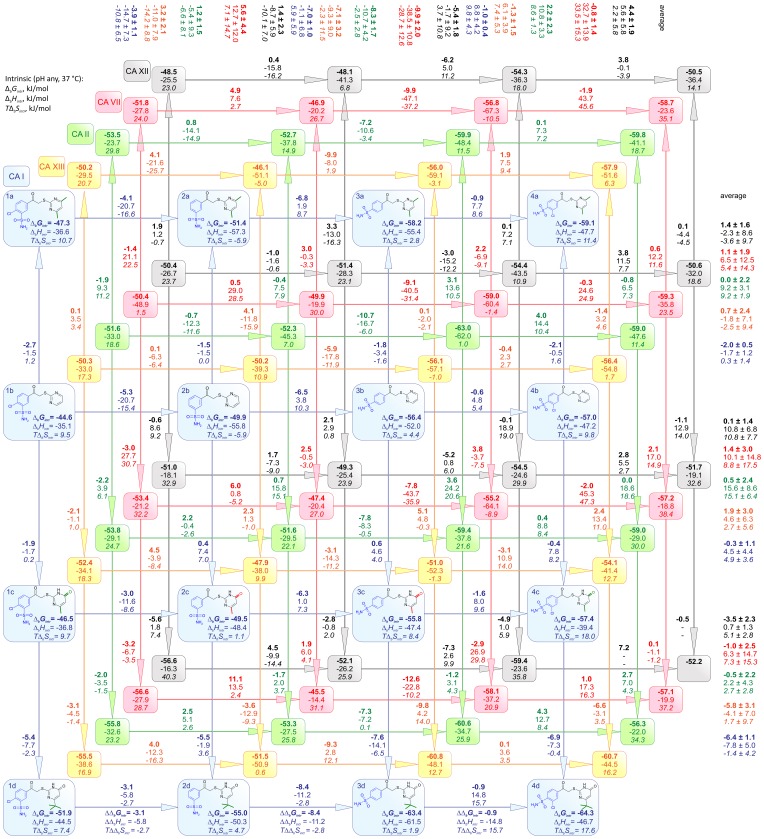
The intrinsic thermodynamic parameters 16 compounds binding to five CA isoforms are shown in Fig. 8. The map shows inhibitor structure correlations with the thermodynamics of binding. The most similar compounds are arranged next to each other and the arrows show which compounds are being compared. The intrinsic ΔbG (top number, bold), ΔbH (middle number), and TΔbS (bottom number, itallic) values for binding are listed within the shapes and the values next to the arrows show the incremental differences in thermodynamic values between the two compounds. The incremental differences show how much energy is gained or lost when adding or removing a chemical group of the compound.
Figure 8. Inhibitor structure correlations with the thermodynamics of binding.
Intrinsic parameters of compound binding to five investigated CA isoforms are given within the shapes. Different colors represent different CA isoforms. Numbers next to arrows show the Gibbs free energy (top number, bold), enthalpy (middle number), and entropy (TΔbS, bottom number) of binding differences between two neighboring compounds (in kJ/mol at 37°C). Numbers to the top and right of the map are averages between same heads and tails of the compounds. The standard deviations indicate the presence and absence of the energetic additivity of compound functional groups.
Different colors on the map represent different CA isoforms, blue – CA I, yellow – CA XIII, green – CA II, red – CA VII, and black – CA XII. The order of the isozymes is shown not according to the numbering of CAs, but according to the similarities of the active site of the protein. To determine the similarity between the active sites, the following amino acids were considered to be important (numbers of CA II in UniProt database): 62, 64, 65, 67, 91, 121, 130, 134, 140, 197, 199, 201, and 203. These amino acids were compared among the five CAs and it was determined that the similarity between CA I and CA II is 30.8% while the similarity between CA I and CA XIII is 46.2%. CA XIII is quite similar to CA II (61.5%). The arrangement of CAs is according to the similarity of the active site, but it is quite arbitrary because it depends on which amino acids are considered important for the recognition of the compound.
The intrinsic ΔbG of CA I binding is more negative in the direction 1 → 2 → 3 → 4. Therefore, the para position for the sulfonamide is better than meta in terms of affinity. Comparing 3 → 4, the affinity changes slightly (1 kJ/mol), but ΔbH and ΔbS contributions change significantly more. For the inhibitors of group 3, the binding to CA is driven by enthalpy. When chlorine is incorporated (group 4), ΔbH favorable contribution decreases by 8.8 kJ/mol, while TΔbS favorable contribution increases by 9.8 kJ/mol. However, when compound structure changes in direction 2 → 1 (incorporation of chlorine in the para position), the binding affinity increases by 3.9 kJ/mol, but the ΔbH contribution becomes less favorable by 14.7 kJ/mol and TΔbS contribution increases by 10.8 kJ/mol. The incorporation of chlorine both in meta and para substituted compounds makes entropy more favorable while the enthalpy less favorable. It can be explained by the hydrophobicity of the chlorine. Comparing 2 → 3 (change in the position of sulfonamide headgroup from meta to para), ΔbG becomes more favorable by 7 kJ/mol. In groups a, b, and c, the change occurs due to more favorable entropy (6.5 kJ/mol), while in group d, the enthalpic contribution is greater than entropic. For all inhibitors in groups 2 and 3, the binding to CA I is enthalpy driven (entropy is negative in some cases). The ΔbG of compound binding to CA I is more negative in the direction a → b → c → d, though ΔbG of b → c modification has a value of approximately zero, thus the incorporation of oxo and methyl groups did not affect the binding affinity. The strongest binders for CA I are 3d and 4d.
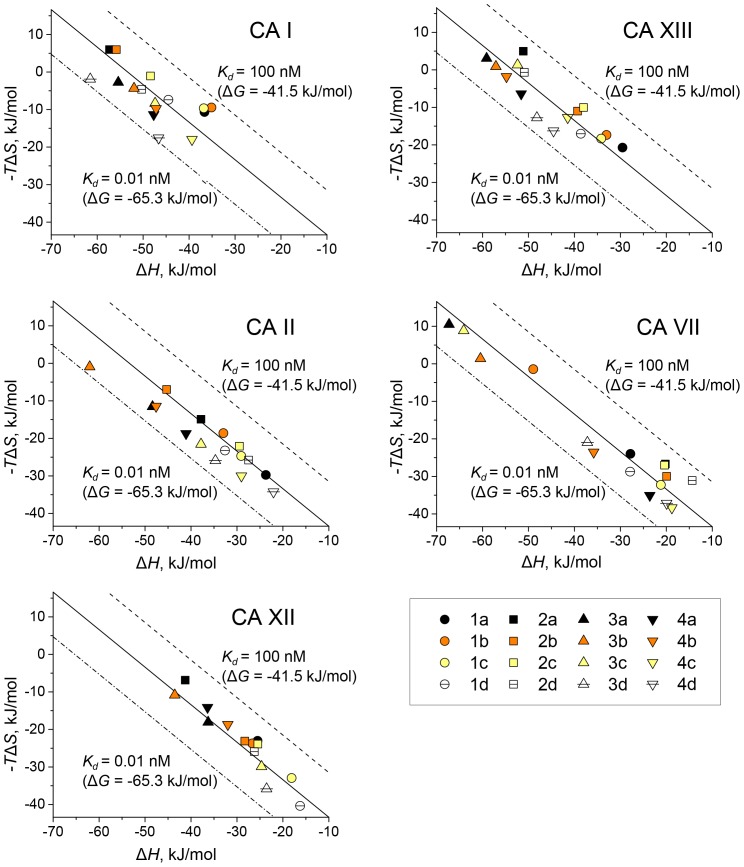
Fig. 9 shows the enthalpy – entropy compensation graphs for the 16 compounds binding to the five CAs. Affinities of the compounds (ΔbG) span relatively narrow range as compared to the range of enthalpies and entropies. Some compounds exhibit strongly enthalpy-driven binding, while others of very similar chemical structure have significant entropic contribution to binding.
Figure 9. The intrinsic enthalpy – entropy compensation graphs for the 16 studied compound binding to five CA isoforms.
Diagonal central line represents the dissociation constant of 1.0 nM (ΔbG = −53.4 kJ/mol at 37°C) while adjacent dashed lines show extremely tight binding of 10 pM or lower affinity at 100 nM. The compounds exhibit the range of affinities between 0.01 and 10 nM (ΔbG between −65.3 and −47.5 kJ/mol) while the enthalpies varied to a greater extent between −14 and −68 kJ/mol. The entropies (TΔbS) also span the wide range between 11 and −41 kJ/mol.
The compound binding affinities to CA XIII (Figs. 8 and 9) increase in the direction 2 → 1 and 2 → 3 → 4. The ΔbG change in the direction 3 → 4 (incorporation of chlorine) is relatively small, but the enthalpy becomes less favorable while the entropy – more favorable. The same energetic changes happen when chlorine is incorporated in meta substituted inhibitors. In direction 2 → 3 (change in the position of sulfonamide headgroup from meta to para), the ΔbG decreases by 7.1 kJ/mol. The 2 → 3 change in groups a, b, and c has more favorable enthalpy (13.4 kJ/mol more negative) and in group d, contribution of enthalpy decreases. The binding entropy of 3a, 3b, and 3c to CA XIII is unfavorable and it is enthalpy-driven. Incorporation of oxo and methyl or dimethyl groups does not affect the binding affinity, but modification of tert-butyl in pyrimidine ring changes ΔbG to more negative by 5.8 kJ/mol. The strongest binders for CA XIII are inhibitors 3d and 4d and similarly to CA I, the reaction is enthalpy-driven.
For CA II, the binding affinity increases in the direction 2 → 3 (8.3 kJ/mol), but for 1 → 2 and 3 → 4 it slightly decreases. Though ΔbG changes are small, for the changes 2 → 1 and 3 → 4, the entropy becomes more favorable while the enthalpy – less favorable. However, for 2 → 3, the enthalpy becomes more favorable with a minor change in entropy. For modifications 3b → 3c and 4b→ 4c, the entropy increases on average by 19.6 kJ/mol. This can be explained by a higher residual mobility of group c compounds in active site of CA II.
The modifications 3b → 3a and 4b → 4a also increase the entropy of binding, but not so strongly (8.9 kJ/mol). Similar to CA I and CA XIII, the incorporation of oxo and methyl or dimethyl groups does not affect the binding affinity to CA II. However, differently from CA I and CA XIII, the incorporation of tert-butyl in pyrimidine ring does not change the binding affinity to CA II. The strongest binders for CA II are inhibitors 3b and 3d and they are also enthalpy-driven.
For CA VII, the binding affinity increases in the direction of 2 → 3 (9.9 kJ/mol). In 1 → 2, the binding affinity decreases while in 3 → 4, there are no visible changes. For 3 → 4, the enthalpy becomes less favorable (by 32.7 kJ/mol) while the entropy – more favorable (by 33.5 kJ/mol). Here we can see nicely visible entropy – enthalpy compensation phenomenon. In contrast from CA I, CA II, and CA XIII, here for 2 → 1, the enthalpy becomes more favorable but entropy – less favorable. For 2 → 3, the contribution of enthalpy is very high (change of 38.5 kJ/mol), while b → a and b → c → d has no effect on the binding affinity. CA VII exhibits high affinity with all inhibitors 3 and 4, where the strongest binders are 3b and 4b. Binding of 3b and 4b is enthalpy-driven, but there are compounds that exhibit greater portion of entropy driven binding with CA VII.
For CA XII, the binding affinity increases only in direction 2 → 3 (by 5.4 kJ/mol). In 1 → 2 and 3 → 4, it slightly decreases. Although ΔbG changes are small, for 1 → 2 and 3 → 4, the entropy becomes more while enthalpy – less favorable. Incorporation of oxo and methyl or dimethyl groups does not affect the binding affinity, but incorporation of tert-butyl in the pyrimidine ring changes ΔbG to more negative by 3.5 kJ/mol. The strongest binders for CA XII are 1d and 3d and they exhibit greater portion of entropy driven binding.
S1 Figure shows the compound chemical structure correlation map with the intrinsic and observed binding affinities (Kd). For structure – thermodynamics considerations, it is important to have intrinsic binding values. However, in order to know the affinities that are observed in practice and have the contributions of real fractions at pH 7.0, one may use the observed affinities at pH 7.0, that were determined both by FTSA and ITC, and the experimental values are listed in Table 1.
Protein-compound crystallographic structure correlations with binding thermodynamics
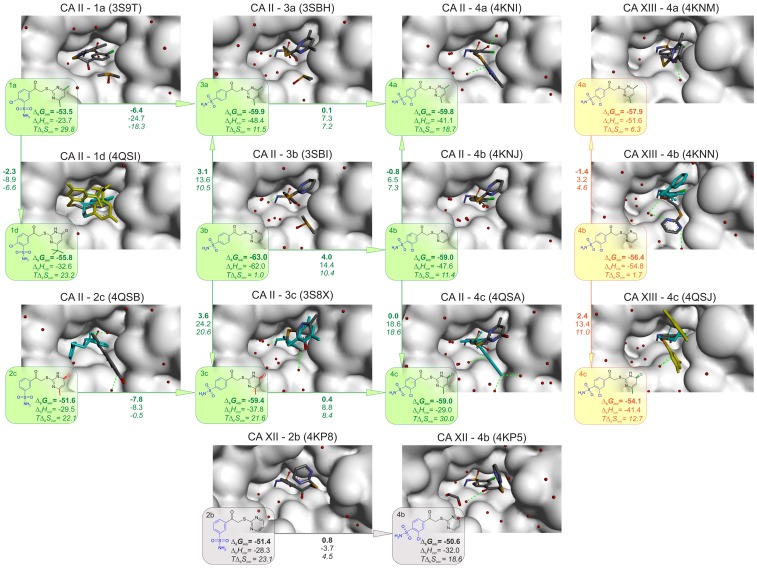
Fig. 10 shows the 14 CA-compound complex crystal structures that were solved with this series of compounds. Nine structures are available for CA II, 3– for CA XIII, and 2– for CA XII. The PDB IDs and the thermodynamic values of binding are shown next to the structurally aligned protein surface views showing the main mode of compound binding and the position of water and cosolvent molecules. All compounds bound to CA by making a coordination bond between the sulfonamide nitrogen and protein Zn atom. The benzene ring containing the sulfonamide headgroup is clearly visible in the electron density of all structures. However, the second ring is partially or mostly flexible and poorly visible in some structures. Two possible orientations of the second ring are visible in some structures.
Figure 10. Compound chemical structure and the thermodynamics of binding correlations with the crystal structures of some compound binding mode in the active site of CAs (1a, 1d, 3a, 3b, 3c, 4a, 4b, and 4c with CAII; 4a, 4b, and 4c with CA XIII; 2b and 4b with CA XII).
The thermodynamic parameters of binding and the colors of the shapes are same as in Figure 8 and indicate the CA isoform. Colors in the crystal structures are: yellow shows the pyrimidine ring that is not fixed in the crystal structure and has multiple conformations with low occupancies; blue shows the alternative conformation of the pyrimidine ring when both conformations are visible in the electron density maps.
Comparison of the crystal structures of 1a and 1d bound to CA II (Fig. 10, 3S9T and 4QSI, respectively) shows that the Cl-benzene ring in both cases is positioned similarly, with the Cl in the hydrophobic pocket. The first ring of 1d - CA II is well defined in the crystal structure, but the electron density of the acetylthio linker could not be interpreted unambiguously and therefore two alternative positions of the linker are modeled placing sulfur atoms into the electron density blobs. There is no electron density for the pyrimidine rings, their positions are deduced from the positions of linkers (see also S2 Figure, A). Therefore, the pyrimidine ring is not fixed in the crystal structure and has multiple conformations with low occupancies. However, entire structure of the inhibitor 1a (3S9T, Fig. 10) could be fit to the electron density.
Inhibitors 3a, 3b, and 3c in the active center of CA II (3SBH, 3SBI, and 3S8X) are bound in a similar way and differ only in the conformations of linkers between the pyrimidine and benzene rings. The same situation was observed while comparing 4a, 4b, and 4c bound to CA II (4KNI, 4KNJ, and 4QSA). Despite different location of the Cl-benzene (4(a–c)), which is found in two alternative conformations in these structures, and benzene (3(a–c)) rings, the pyrimidine moiety is located in the same position between Phe131 and Pro202, except for 4c and 4a, where it is found on the other side relative to the Phe131. Compound 4c in CA II is found in alternative conformations (S2 Figure, C). The pyrimidine rings are located on both sides of Phe131 and Cl-benzene is also in two orientations.
Compounds of group a are well visualized in the crystal structures of 1a, 3a, and 4a in the active centers of CA II (3S9T, 3SBH, and 4KNI) and 4a bound in CA XIII (4KNM). The position of the Cl-benzene ring in crystal structures of groups 1 and 4 is more variable (Cl atom positions in these structures coincide except for CA II –4c, the planes of the rings vary by up to 2.1 Å). In contrast, the benzene rings of para-substituted group 3 (3SBH, 3SBI, and 3S8X) nearly coincide with each other. Pyrimidine rings also coincide within this group. Meta-substituted group 2 in the active center of CA II is represented by 2c (4QSB, S2 Figure, B). The benzene ring in the crystal structure is found in two alternative conformations, shifted with respect to the position of the benzene ring of group 3. A possible explanation could be a clash of the meta-substituent of group 2 either with Phe131, or with Pro202. The pyrimidine rings are found in two positions (S2 Figure, B) and neither is similar to group 3, poorly resolved in the crystal structure. It is interesting to compare the binding of 2c in CA II with the crystal structure of 2b in CA XII (4KP8). In the active center of CA XII, the benzene as well as pyrimidine rings are found in similar positions to 3 compounds in CA II, where the differences between meta and para position of pyrimidine are compensated by linker conformation. The absence of Phe131 in CA XII makes such orientation of the linker possible.
Crystal structures of CA XII with 4b and 2b exhibit different orientations of the headgroup benzene rings. The pyrimidine rings are positioned similarly, but the plane orientation is different. There are no steric hindrance issues for the meta-substituted 2b in CA XII, as it would be expected for CA II due to the absence of Phe131. For 2b → 4b, the formation of a hydrogen bond between inhibitor and water molecule in the active site of CA XII is a likely reason for the decrease in entropy of the system.
There are three crystal structures of CA XIII with 4a, 4b, and 4c (Fig. 10). The 4c structure shows the formation of one hydrogen bond with a water molecule while 4b – with three. This change may be the reason that causes the increase in the entropy as methyl and oxo groups are introduced in the pyrimidine ring.
It is difficult to make unambiguous correlations between the crystal structures and the thermodynamics of binding. However, several trends are clear. First, CA II structures with 3a, 3b, and 4b, exhibit relatively small entropic contribution to binding (1.0 to 11.5 kJ/mol), while all remaining 6 compounds exhibit relatively large entropic contribution to binding (18.7 to 30.0 kJ/mol). This correlates with the fact that in three former structures, the second ring is in the same orientation and well represented by the electron density, while the latter 6 structures exhibit a different orientation of the second ring and are mostly poorly represented by the electron density. The latter 6 structures are less ordered and therefore there is larger portion of the entropic drive to the binding reaction.
Conclusions
It is important to distinguish the observed thermodynamic parameters from intrinsic. Only the intrinsic parameters could be correlated with the structure. The intrinsic parameters of CA binding show that the incorporation of chlorine both in meta and para substituted compounds, increases the favorable entropic and decreases the favorable enthalpic contribution to the binding affinity (except in CA VII with meta substituted compounds). The para substituted compounds exhibit stronger affinities than meta. The addition of tert-butyl group, increases the affinity for CA I and CA XIII, but not for CA II, CA VII, and CA XII. All 16 tested compounds showed only partial additivity of thermodynamic parameters. All 16 compounds exhibited enthalpically-driven binding with a relatively small but variable entropic contribution. At least two independent methods that measure binding, such as FTSA and ITC, are required to accurately measure the observed affinities. Enthalpies are important for the determination of intrinsic thermodynamic parameters. The use of non-intrinsic observed parameters would lead to incomplete or inaccurate determination of the underlying forces and energetic reasons of binding needed for drug design.
Crystallographic data shows that substitutions in the pyrimidine ring considered in the present work do not influence the location of inhibitors in CA II. However, the differences in the position of substituents in the headgroup ring influence the position of inhibitor binding. The Cl atom in most cases is directed into the hydrophobic pocket. Para-substituted compounds 4, despite variations in the position of the Cl-benzene, have two fixed conformations of the pyrimidine moiety regardless of the pyrimidine-substituents. The meta-substituted 1, due to the steric clashes with the protein moiety, show variations in the positions of pyrimidine rings. Same trend is observed comparing the binding of 2 and 3 in CA II: para-substituted compounds have a similar way of binding, regardless of pyrimidine decorations, while meta-substituted compounds position pyrimidine rings in a different way due to steric clashes. Detailed correlation between the crystal structures and the enthalpies and entropies of binding largely confirm that enthalpic binders make tighter contacts and are more ordered in crystal structures, while compounds that are partially disordered in crystal structures have greater entropy contribution to the binding energetics. Therefore, enthalpy-driven compounds are better leads for drug design than entropy drive-compounds.
Materials and Methods
Chemistry
The synthesis, chemical structural characterization, and purity of the 16 compounds used in this study has been previously described by Čapkauskaitė et al. [12], [33]. Instant JChem was used for structure database management, search and prediction, Instant JChem 6.1.3, 2013, ChemAxon (http://www.chemaxon.com).
Protein preparation
Expression and purification of human CA I, CA II, CA VII, CA XII, and CA XIII has been previously described: CA I by Baranauskienė et al. [38], CAII by Cimmperman et al. [39], CA VII and CA XIII by Sūdžius et al. [40], and CA XII by Jogaitė et al. [35].
Fluorescent thermal shift assay (FTSA)
The binding parameters of 16 sulfonamide inhibitors were determined by the fluorescent thermal shift assay (FTSA). This method is used for rapid screening of protein and compound interactions[41]–[43]. FTSA measurements were performed in a Corbett Rotor-Gene 6000 (QIAGEN Rotor-Gene Q) instrument using the blue channel (excitation 365±20, detection 460±15 nm). Samples contained 5 µM protein, 0–200 µM compound, 50 µM solvatochromic dye ANS (8-anilino-1-naphthalene sulfonate) in 50 mM phosphate buffer (pH 7.0) containing 100 mM NaCl and the final DMSO concentration 2%. The applied heating rate was 1°C/min. Data analysis was performed as previously described by Baranauskiene et al. [38].
Isothermal titration calorimetry (ITC)
Isothermal titration calorimetry (ITC) measurements of inhibitor binding to proteins were performed using VP-ITC instrument (Microcal, Inc., Northampton, USA) with 6–20 µM protein solution in the cell and 60–200 µM of the compound solution in the syringe. ITC instrument measures the heat evolution during the titration and can be used to determine the ΔG, ΔH, and ΔS of a reaction [44], [45]. A typical experiment consisted of 25 injections (10 µl each) added at 3 min intervals. Experiments were performed at 37°C in 50 mM phosphate buffer containing 100 mM NaCl at pH 7.0, with a final DMSO concentration of 2%, equal in the syringe and the cell. All experiments were repeated at least twice.
The enthalpy of inhibitor deprotonation was also measured using VP-ITC instrument. Inhibitor solution (0.25 mM) was deprotonated by adding 1.5 equivalent of NaOH and titrated with 2.5 mM nitric acid. A typical experiment consisted of 58 injections (5 µl each) added at 3 min intervals. Experiments were performed at 37°C with final DMSO concentration of 0.5%, equal in the syringe and the sample cell. All experiments were repeated at least three times.
Stopped-flow kinetic CO2 hydration assay (SFA)
Enzyme inhibition experiments were performed using Applied Photophysics SX.18MV-R stopped-flow spectrometer at 25°C. Stopped-flow kinetic CO2 hydration assay is used for direct determination of carbonic anhydrase activity and inhibitory properties of compounds [46], [47]. Reaction velocities were measured by recording the absorbance of bromthymol blue indicator (50 µM, 615 nm). The sample consisted of 100–500 nM CA I, 20 nM CA II, 50 nM CA VII, 100 nM CA XII or 200–500 nM CA XIII, 0–10 µM 1b inhibitor (in ≤0.2% DMSO) and MOPS buffer containing 100 mM NaCl, pH 7.0. Saturated CO2 solution was prepared by bubbling the CO2 gas in Milli-Q water at 25°C for 1 hour. A single exponential model was used to fit raw curves and the IC50 was determined using sigmoidal dose-response model with the Hill slope of 1. The observed IC50 of compound 1b determined by SFA are compared with Kd obtained by FTSA, ITC in Table 4.
Table 4. Comparison of Kd (determined by ITC, FTSA) and IC50 (determined by SFA) of the compound 1b binding to five isoforms of human recombinant CAs.
| Kd, nM (ITC) | Kd, nM (TSA) | IC50, nM (SFA) | |
| CAI | 2300 | 3100 | 5550 |
| CAII | 430 | 330 | 220 |
| CAVII | 660 | 710 | 830 |
| CAXII | 370 | 1300 | 1100 |
| CAXIII | 270 | 330 | 450 |
All three methods provided the same values within the error margin.
Measurement of pKa of the sulfonamide group of the compounds
The pKa of the sulfonamide group of the compounds was measured with the spectrophotometer “Agilent 89090A” as previously described by Snyder et al. [34]. Ultraviolet spectra (λ = 200–380 nm) were collected at each pH between 6.0 and 12.0 at intervals of 0.5 pH units. The ratio of absorbances at two wavelengths (10 nm above and below isosbestic point) was plotted as a function of pH. The pKa value was determined as a midpoint of the curve. The pKa values were also calculated using Marvin Sketch software and confirmed by ACD/Labs online calculator I-Lab 2.0.
Intrinsic thermodynamics
The observed binding constants and observed enthalpies are dependent on buffer components and pH. Observed parameters were experimentally measured in phosphate buffer at pH 7.0, 37°C. The intrinsic binding constant Kb is equal to observed binding constant Kb_obs divided by the available fractions of deprotonated inhibitor and protonated zinc hydroxide anion:
| (1) |
The fractions of deprotonated inhibitor and CA with the protonated water molecule bound to zinc in the active site can be calculated if both pKa values are known:
| (2) |
| (3) |
The observed enthalpy is the sum of all protonation events and the binding reaction. Linked reactions that have to be subtracted are the protonation/deprotonation of buffer, deprotonation of sulfonamide, and protonation of the hydroxide anion bound to active site zinc:
| (4) |
where the intrinsic binding enthalpy is ΔbH, the observed binding enthalpy is ΔbHobs, enthalpy of inhibitor protonation – Δb_proton_sulf H, enthalpy of CA protonation – Δb_proton_CA H, the buffer protonation enthalpy – Δb_proton_buf H, nsulf = 1 − fsulf, nCA = 1 − fCA and nbuf = nsulf+nCA. nsulf is the number of protons released during the deprotonation of sulfonamide, nCA is the number protonated hydroxide ions bound to the active site Zn and nbuf is the number of protons taken or released by the buffer.
Crystallization
Human CA II and CA XIII in 20 mM NaHepes, pH 7.5 and 50 mM NaCl were concentrated to the concentration 20–50 mg/ml. Crystals were grown by sitting drop vapor diffusion method by mixing equal volumes of protein solution and crystallization buffer at 20°C. Buffers used for crystallization are presented in Table 5. Co-crystals of CA with inhibitors were prepared by soaking with 0.5 mM solution of inhibitor in crystallization buffer. Soaking solutions were prepared by mixing of 50 mM stock solution of inhibitor in DMSO with crystallization solution from reservoir. Soaking was performed several days before data collection.
Table 5. X-ray crystallographic data collection and refinement statistics.
| Isoform-compound | CA II-4c | CA II-2c | CA II-1d | CA XIII-4c |
| PDB ID | 4QSA | 4QSB | 4QSI | 4QSJ |
| Crystallization buffer | 2M sodium malonate (pH 7.5) | 2.2M sodium malonate (pH 7.5) | 0.1M sodium BICINE (pH 9.0) and 3.1M sodium malonate (pH 7.0) | 0.1M sodium citrate (pH 5.5), 0.2M sodium acetate (pH 4.5) and 28% PEG4000 |
| Spacegroup | P21 | P21 | P21 | P212121 |
| Unit cell (Å) | a = 42.12, b = 40.99, c = 71.64, α = γ = 90°, β = 104.06° | a = 42.25, b = 40.98, c = 71.48, α = γ = 90°, β = 104.04° | a = 42.06, b = 40.92, c = 71.59, α = γ = 90°, β = 104.01° | a = 56.51, b = 57.68, c = 159.88, α = β = γ = 90.0° |
| Resolution (Å) | 23.31–1.50 | 18.75–1.40 | 24.36–1.95 | 39.10–1.70 |
| Nref (unique) | 38075 | 46809 | 16250 | 57690 |
| Rmerge, (outer shell) | 0.065 (0.119) | 0.099 (0.390) | 0.048 (0.263) | 0.060 (0.377) |
| I/σ (outer shell) | 17.3 (8.5) | 16.8 (2.5) | 28.1 (6.3) | 18.1 (3.8) |
| Multiplicity (outer shell) | 7.0 (5.5) | 5.0 (5.0) | 6.8 (6.5) | 5.2 (5.2) |
| Completeness (%) (outer shell) | 99.2 (94.7) | 99.7 (99.9) | 93.6 (89.1) | 99.2 (99.3) |
| Natoms | 2475 | 2374 | 2292 | 4942 |
| Rwork | 0.166 | 0.188 | 0.157 | 0.166 |
| Rfree | 0.205 | 0.220 | 0.209 | 0.202 |
| Baverage | 15.138 | 16.507 | 19.510 | 17.382 |
| RMSbonds | 0.024 | 0.025 | 0.018 | 0.022 |
| RMSangles | 2.289 | 2.392 | 1.892 | 2.163 |
All datasets were collected at 100 K, test set size was 10%.
Data collection and structure determination
All datasets except 4QSI were collected at the EMBL beam line X13 at the DORIS storage ring (DESY, Hamburg). 4QSI dataset was collected using X-ray diffractometer MicroMax 007 HF (Rigaku, Japan) equipped with RaxisIV++ detector at the Institute of Biotechnology (Vilnius, Lithuania). Datasets were processed using CCP4 program suite [48]: MOSFLM [49], TRUNCATE [50] and SCALA [51]. Structures were solved by molecular replacement using MOLREP [52]. The protein chain from the PDB entry 3HLJ was used as a starting model for CA II structures and PDB entry 2NN0 for CA XIII. Models were refined with REFMAC [53] and manually corrected in COOT [54]. Atomic coordinates of compounds were generated using molecular editor Avogadro [55]. Descriptions of compound geometry for model refinement were generated using LIBREFMAC [56]. The data collection and refinement statistics of PDB entries are presented in Table 4. ACCESSION NUMBERS: Coordinates and structure factors have been deposited in the Protein Data Bank with accession numbers 4QSA, 4QSB, 4QSI, and 4QSJ.
Supporting Information
Inhibitor structure correlations with the observed and intrinsic affinity. Observed and intrinsic (in the brackets) ΔbG and Kd values of compound binding to five investigated CA isoforms are given within the shapes. Different colors represent different CA isoforms. Numbers next to arrows show the Gibbs free energy (top number) and Kd (bottom number) of binding differences between two neighboring compounds (ΔbG in kJ/mol at 37°C). Numbers to the top and right of the map are averages between same heads and tails of the compounds. The standard deviations indicate the presence or absence of the energetic additivity of compound functional groups. Note that observed and intrinsic affinities often differ by more than 100 fold.
(TIF)
Electron densities of compounds 1d, 2c, and 4c in the active centers of CA II and CA XIII. Electron density maps |Fobs-Fcalc| were calculated in the absence of compound. Alternative conformations of compounds are shown in different colors. Zn atoms are shown as blue spheres. A, Electron density map of 1d bound to CA II and contoured at 2.8σ. B, Two conformations of 2c modeled in the active center of CA II. Electron density map contoured at 2.3 σ. C, Two alternative positions of the second ring of 4c modeled in CA II. Electron density map contoured at 2.5σ. D, Compound 4c in the active center of CA XIII, protein chain B. Electron density map contoured at 2.7σ. E, Compound 4c in the active center of CA XIII, protein chain A. Electron density map contoured at 2.6σ.
(TIF)
Data Availability
The authors confirm that all data underlying the findings are fully available without restriction. All relevant data are within the paper and its Supporting Information files.
Funding Statement
This research was funded by a grant from the Research Council of Lithuania (LIG-09/2012). Authors thank FP7-REGPOT-2009-1 grant “MoBiLi” agreement No.: 245721, and the COST projects TD0905 and CM0804. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Reynolds CH. Holloway MK (2011) Thermodynamics of Ligand Binding and Efficiency. Medicinal Chemistry Letters 2:433–437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Ruben AJ, Kiso Y, Freire E (2006) Overcoming roadblocks in lead optimization: a thermodynamic perspective. Chem Biol Drug Des 67:2–4. [DOI] [PubMed] [Google Scholar]
- 3. Chodera JD, Mobley DL (2013) Entropy-enthalpy compensation: role and ramifications in biomolecular ligand recognition and design. Annu Rev Biophys 42:121–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Biela A, Betz M, Heine A, Klebe G (2012) Water makes the difference: rearrangement of water solvation layer triggers non-additivity of functional group contributions in protein-ligand binding. ChemMedChem 7:1423–1434. [DOI] [PubMed] [Google Scholar]
- 5. Chaires JB (2008) Calorimetry and thermodynamics in drug design. Annu Rev Biophys 37:135–151. [DOI] [PubMed] [Google Scholar]
- 6. Freire E (2008) Do enthalpy and entropy distinguish first in class from best in class? Drug Discov Today 13:869–874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Garbett NC, Chaires JB (2012) Thermodynamic studies for drug design and screening. Expert Opin Drug Discov 7:299–314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Olsson TSG, Ladbury JE, Pitt WR, Williams MA (2011) Extent of enthalpy-entropy compensation in protein-ligand interactions. Protein Sci 20:1607–1618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Olsson TSG, Williams MA, Pitt WR, Ladbury JE (2008) The thermodynamics of protein-ligand interaction and solvation: insights for ligand design. J Mol Biol 384:1002–1017. [DOI] [PubMed] [Google Scholar]
- 10. Domsic JF, Avvaru BS, Kim CU, Gruner SM, Agbandje-McKenna M, et al. (2008) Entrapment of carbon dioxide in the active site of carbonic anhydrase II. J Biol Chem 283:30766–30771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Hassan M, Shajee B, Waheed A, Ahmad F, Sly W (2013) Structure, function and applications of carbonic anhydrase isozymes. Bioorg Med Chem 21:1570–1582. [DOI] [PubMed] [Google Scholar]
- 12. Čapkauskaitė E, Zubrienė A, Baranauskienė L, Tamulaitienė G, Manakova E, et al. (2012) Design of [(2-pyrimidinylthio)acetyl]benzenesulfonamides as inhibitors of human carbonic anhydrases. Eur J Med Chem 51:259–270. [DOI] [PubMed] [Google Scholar]
- 13. Pastorekova S, Parkkila S, Zavada J (2006) Tumor-associated carbonic anhydrases and their clinical significance. Adv Clin Chem 42:167–216. [PubMed] [Google Scholar]
- 14. Supuran CT (2010) Carbonic anhydrase inhibitors. Bioorg Med Chem Lett 20:3467–3474. [DOI] [PubMed] [Google Scholar]
- 15. Supuran CT (2008) Carbonic anhydrases: novel therapeutic applications for inhibitors and activators. Nat Rev Drug Discov 7:168–181. [DOI] [PubMed] [Google Scholar]
- 16. Aggarwal M, Boone CD, Kondeti B, McKenna R (2013) Structural annotation of human carbonic anhydrases. J Enzyme Inhib Med Chem 28:267–277. [DOI] [PubMed] [Google Scholar]
- 17. Alterio V, Di Fiore A, D’Ambrosio K, Supuran CT, De Simone G (2012) Multiple binding modes of inhibitors to carbonic anhydrases: how to design specific drugs targeting 15 different isoforms? Chem Rev 112:4421–4468. [DOI] [PubMed] [Google Scholar]
- 18. Lopez M, Bornaghi LF, Innocenti A, Vullo D, Charman SA, et al. (2010) Sulfonamide linked neoglycoconjugates-a new class of inhibitors for cancer-associated carbonic anhydrases. J Med Chem 53:2913–2926. [DOI] [PubMed] [Google Scholar]
- 19. Rogez-Florent T, Duhamel L, Goossens L, Six P, Drucbert AS, et al. (2014) Label-free characterization of carbonic anhydrase-novel inhibitor interactions using surface plasmon resonance, isothermal titration calorimetry and fluorescence-based thermal shift assays. J Mol Recognit 27:46–56. [DOI] [PubMed] [Google Scholar]
- 20. Klinger AL, McComsey DF, Smith-Swintosky V, Shank RP, Maryanoff BE (2006) Inhibition of carbonic anhydrase-II by sulfamate and sulfamide groups: an investigation involving direct thermodynamic binding measurements. J Med Chem 49:3496–3500. [DOI] [PubMed] [Google Scholar]
- 21. Supuran CT (2008) Carbonic anhydrases-an overview. Curr Pharm Des 14:603–614. [DOI] [PubMed] [Google Scholar]
- 22. Gitto R, Agnello S, Ferro S, De Luca L, Vullo D, et al. (2010) Identification of 3,4-dihydroisoquinoline-2(1H)-sulfonamides as potent carbonic anhydrase inhibitors: synthesis, biological evaluation, and enzyme–ligand X-ray studies. J Med Chem 53:2401–2408. [DOI] [PubMed] [Google Scholar]
- 23. Zubrienė A, Čapkauskaitė E, Gylytė J, Kišonaitė M, Tumkevičius S, et al. (2014) Benzenesulfonamides with benzimidazole moieties as inhibitors of carbonic anhydrases I, II, VII, XII and XIII. J Enzyme Inhib Med Chem 29:124–131. [DOI] [PubMed] [Google Scholar]
- 24. Whitesides GM, Krishnamurthy VM (2005) Designing ligands to bind proteins. Q Rev Biophys 38:385–395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Holdgate GA (2001) Making cool drugs hot: isothermal titration calorimetry as a tool to study binding energetics. Biotechniques 31:164–184. [PubMed] [Google Scholar]
- 26. Leavitt S, Freire E (2001) Direct measurement of protein binding energetics by isothermal titration calorimetry. Curr Opin Struct Biol 11:560–566. [DOI] [PubMed] [Google Scholar]
- 27. Khalifah RG, Zhang F, Parr JS, Rowe ES (1993) Thermodynamics of binding of the CO2-competitive inhibitor imidazole and related compounds to human carbonic anhydrase I: an isothermal titration calorimetry approach to studying weak binding by displacement with strong inhibitors. Biochemistry 32:3058–3066. [DOI] [PubMed] [Google Scholar]
- 28. Baker BM, Murphy KP (1996) Evaluation of linked protonation effects in protein binding reactions using isothermal titration calorimetry. Biophys J 71:2049–2055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Baum B, Muley L, Smolinski M, Heine A, Hangauer D, et al. (2010) Non-additivity of functional group contributions in protein-ligand binding: a comprehensive study by crystallography and isothermal titration calorimetry. J Mol Biol 397:1042–1054. [DOI] [PubMed] [Google Scholar]
- 30. Ladbury JE, Klebe G, Freire E (2010) Adding calorimetric data to decision making in lead discovery: a hot tip. Nat Rev Drug Discov 9:23–27. [DOI] [PubMed] [Google Scholar]
- 31. Baranauskienė L, Matulis D (2012) Intrinsic thermodynamics of ethoxzolamide inhibitor binding to human carbonic anhydrase XIII. BMC Biophys 5:12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Krishnamurthy VM, Kaufman GK, Urbach AR, Gitlin I, Gudiksen KL, et al. (2008) Carbonic anhydrase as a model for biophysical and physical-organic studies of proteins and protein-ligand binding. Chem Rev 108:946–1051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Čapkauskaitė E, Zubrienė A, Smirnov A, Torresan J, Kišonaitė M, et al. (2013) Benzenesulfonamides with pyrimidine moiety as inhibitors of human carbonic anhydrases I, II, VI, VII, XII, and XIII. Bioorg Med Chem 21:6937–6947. [DOI] [PubMed] [Google Scholar]
- 34. Snyder PW, Mecinovic J, Moustakas DT, Thomas SW 3rd, Harder M, et al. (2011) Mechanism of the hydrophobic effect in the biomolecular recognition of arylsulfonamides by carbonic anhydrase. Proc Natl Acad Sci U S A 108:17889–17894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Jogaitė V, Zubrienė A, Michailovienė V, Gylytė J, Morkūnaitė V, et al. (2013) Characterization of human carbonic anhydrase XII stability and inhibitor binding. Bioorg Med Chem 21:1431–1436. [DOI] [PubMed] [Google Scholar]
- 36. Pilipuitytė V, Matulis D (2014) Intrinsic thermodynamics of trifluoromethanesulfonamide and ethoxzolamide binding to human carbonic anhydrase VII. J Mol Recognit. 10.1002/jmr.2404 [DOI] [PubMed] [Google Scholar]
- 37. Morkūnaitė V, Gylytė J, Zubrienė A, Baranauskienė L, Kišonaitė M, et al. (2014) Intrinsic thermodynamics of sulfonamide inhibitor binding to human carbonic anhydrases I and II. J Enzyme Inhib Med Chem. 10.3109/14756366.2014.908291 [DOI] [PubMed] [Google Scholar]
- 38. Baranauskienė L, Hilvo M, Matulienė J, Golovenko D, Manakova E, et al. (2010) Inhibition and binding studies of carbonic anhydrase isozymes I, II and IX with benzimidazo[1,2-c][1,2,3]thiadiazole-7-sulphonamides. J Enzyme Inhib Med Chem 25:863–870. [DOI] [PubMed] [Google Scholar]
- 39. Cimmperman P, Baranauskienė L, Jachimovičiūtė S, Jachno J, Torresan J, et al. (2008) A quantitative model of thermal stabilization and destabilization of proteins by ligands. Biophys J 95:3222–3231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Sūdžius J, Baranauskienė L, Golovenko D, Matulienė J, Michailovien V, et al. (2010) 4-[N-(substituted 4-pyrimidinyl)amino]benzenesulfonamides as inhibitors of carbonic anhydrase isozymes I, II, VII, and XIII. Bioorg Med Chem 18:7413–7421. [DOI] [PubMed] [Google Scholar]
- 41. Cummings MD, Farnum MA, Nelen MI (2006) Universal screening methods and applications of ThermoFluor. J Biomol Screen 11:854–863. [DOI] [PubMed] [Google Scholar]
- 42. Kemp MM, Weïwer M, Koehler AN (2012) Unbiased binding assays for discovering small-molecule probes and drugs. Bioorg Med Chem 20:1979–1989. [DOI] [PubMed] [Google Scholar]
- 43. Niesen FH, Berglund H, Vedadi M (2007) The use of differential scanning fluorimetry to detect ligand interactions that promote protein stability. Nat Protoc 2:2212–2221. [DOI] [PubMed] [Google Scholar]
- 44. Ladbury JE (2004) Application of isothermal titration calorimetry in the biological sciences: things are heating up! Biotechniques. 37:885–887. [DOI] [PubMed] [Google Scholar]
- 45. Wiseman T, Williston S, Brandts JF, Lin LN (1989) Rapid measurement of binding constants and heats of binding using a new titration calorimeter. Anal Biochem 179:131–137. [DOI] [PubMed] [Google Scholar]
- 46. Khalifah RG (1971) The carbon dioxide hydration activity of carbonic anhydrase. I. Stop-flow kinetic studies on the native human isoenzymes B and C. J Biol Chem 246:2561–73. [PubMed] [Google Scholar]
- 47. Supuran CT (2008) Carbonic anhydrases: novel therapeutic applications for inhibitors and activators. Nat Rev Drug Discov 7:168–181. [DOI] [PubMed] [Google Scholar]
- 48. Collaborative Computational Project N 4 (1994) The CCP4 suite: programs for protein crystallography. Acta Cryst D 50:760–763. [DOI] [PubMed] [Google Scholar]
- 49. Leslie AGW (2006) The integration of macromolecular diffraction data. Acta Crystallogr D Biol Crystallogr 62:48–57. [DOI] [PubMed] [Google Scholar]
- 50. French S, Wilson K (1978) On the Treatment of Negative Intensity Observations. Acta Cryst A 34:517–525. [Google Scholar]
- 51. Evans P (2006) Scaling and assessment of data quality. Acta Cryst D62:72–82 10.1107/S0907444905036693 [DOI] [PubMed] [Google Scholar]
- 52. Vagin A, Teplyakov A (1997) MOLREP: an Automated Program for Molecular Replacement. J Appl Cryst 30:1022–1025. [Google Scholar]
- 53. Murshudov GN, Vagin AA, Dodson EJ (1997) Refinement of macromolecular structures by the maximum-likelihood method. Acta Crystallogr D Biol Crystallogr 53:240–55. [DOI] [PubMed] [Google Scholar]
- 54. Emsley P, Cowtan K (2004) Coot: model-building tools for molecular graphics. Acta Crystallogr D Biol Crystallogr 60:2126–32. [DOI] [PubMed] [Google Scholar]
- 55. Hanwell MD, Curtis DE, Lonie DC, Vandermeersch T, Zurek E, et al. (2012) Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J Cheminform 4:17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Vagin AA, Steiner RA, Lebedev AA, Potterton L, McNicholas S, et al. (2004) REFMAC5 dictionary: organization of prior chemical knowledge and guidelines for its use. Acta Crystallogr D Biol Crystallogr 60:2184–95. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Inhibitor structure correlations with the observed and intrinsic affinity. Observed and intrinsic (in the brackets) ΔbG and Kd values of compound binding to five investigated CA isoforms are given within the shapes. Different colors represent different CA isoforms. Numbers next to arrows show the Gibbs free energy (top number) and Kd (bottom number) of binding differences between two neighboring compounds (ΔbG in kJ/mol at 37°C). Numbers to the top and right of the map are averages between same heads and tails of the compounds. The standard deviations indicate the presence or absence of the energetic additivity of compound functional groups. Note that observed and intrinsic affinities often differ by more than 100 fold.
(TIF)
Electron densities of compounds 1d, 2c, and 4c in the active centers of CA II and CA XIII. Electron density maps |Fobs-Fcalc| were calculated in the absence of compound. Alternative conformations of compounds are shown in different colors. Zn atoms are shown as blue spheres. A, Electron density map of 1d bound to CA II and contoured at 2.8σ. B, Two conformations of 2c modeled in the active center of CA II. Electron density map contoured at 2.3 σ. C, Two alternative positions of the second ring of 4c modeled in CA II. Electron density map contoured at 2.5σ. D, Compound 4c in the active center of CA XIII, protein chain B. Electron density map contoured at 2.7σ. E, Compound 4c in the active center of CA XIII, protein chain A. Electron density map contoured at 2.6σ.
(TIF)
Data Availability Statement
The authors confirm that all data underlying the findings are fully available without restriction. All relevant data are within the paper and its Supporting Information files.