Abstract
Given the availability of genomic data, there have been emerging interests in integrating multi-platform data. Here, we propose to model genetics (single nucleotide polymorphism (SNP)), epigenetics (DNA methylation), and gene expression data as a biological process to delineate phenotypic traits under the framework of causal mediation modeling. We propose a regression model for the joint effect of SNPs, methylation, gene expression, and their nonlinear interactions on the outcome and develop a variance component score test for any arbitrary set of regression coefficients. The test statistic under the null follows a mixture of chi-square distributions, which can be approximated using a characteristic function inversion method or a perturbation procedure. We construct tests for candidate models determined by different combinations of SNPs, DNA methylation, gene expression, and interactions and further propose an omnibus test to accommodate different models. We then study three path-specific effects: the direct effect of SNPs on the outcome, the effect mediated through expression, and the effect through methylation. We characterize correspondences between the three path-specific effects and coefficients in the regression model, which are influenced by causal relations among SNPs, DNA methylation, and gene expression. We illustrate the utility of our method in two genomic studies and numerical simulation studies.
Keywords: causal inference, epigenetics, genetic association studies, path-specific effect, SNP-set analysis, variance component test
1. Introduction
Single-platform genomic studies have constituted a popular approach to reveal the mechanisms behind various clinical outcomes. Some results have been translated into clinical applications such as gefitinib for non-small cell lung cancer harboring EGFR mutation [1]. Despite the success of single-platform approach, significant amount of genomic information is lost if one focuses only on a single platform. Thus, a new hypothesis has been advocated that diseases consist of multiple types of genetic and epigenetic alterations, and each platform provides a different and complementary view of the whole disease.
One of the most popular single-platform genomic analyses is genome-wide association studies (GWAS), which have been a standard approach for assessing the association of single nucleotide polymorphisms (SNPs) with various phenotypic traits such as disease status. In addition to disease status, epigenetic DNA methylation and gene expression can also be construed as molecular phenotypic traits. Genetic association studies focusing on expression-quantitative and methylation-quantitative trait loci, respectively, are so-called eQTL and mQTL studies. As both GWAS and QTL studies become a standard practice in genetic research, considerable interest is emerging in integrating the two, including GWAS in asthma [2,3], osteoporosis [4], type 2 diabetes [5], skin cancer [6], glioblastoma, and Crohn’s disease [7]. These studies consider SNP-disease and SNP-molecular quantitative trait associations separately. For example, the most commonly used two-stage approach is to identify the top GWAS SNPs that are also QTL SNPs. Although the two-stage approach is supported by the findings that disease-associated SNPs are more likely to be QTL [8, 9], and thus decreases false positives, whether the association of those QTL SNPs with methylation/expression can be translated to be a contribution to the disease risk is rarely addressed.
This article is motivated by an asthma GWAS, in which the association between SNPs in the ORMDL3 gene and risk of childhood asthma was discovered and validated [2]. It was also reported that 10 SNPs in the ORMDL3 gene are highly associated with its expression value in an eQTL study [2, 10]. We will focus on the ORMDL3 gene because it has been well validated across different studies, and instead of analyzing individual SNPs, we perform a joint analysis of the 10 SNPs at ORMDL3. Such a multi-SNP approach has been advocated to combine multiple related SNPs in a gene [11, 12] and shown to have better performance in breast cancer GWAS than the single-SNP approach [12]. In addition to the evidence on the relations among SNPs and gene expression of ORMDL3 and asthma risk, there is also a molecular study of the joint effect of SNPs and DNA methylation on regulation of ORMDL3 expression [13]. Thus, we propose a method to analyze the influence of SNPs, DNA methylation, and gene expression jointly on disease risk.
We present in this article an analytic framework of integrating multiple genomic data using causal mediation modeling [14–16]. We have developed a statistical method for GWAS that integrates the gene expression data [17]. However, the current method focuses on the overall effect of SNP and gene expression and is not able to investigate the mechanistic effect among multiple genomic data. Here, by jointly modeling an SNP set within a gene, its DNA methylation and expression and the outcome as a biological process, we propose to study path-specific effects [18] (Figure 1). We develop an efficient testing procedure for the three path-specific effects. We focus on hypothesis testing because p-values serve as a nice summary statistic to efficiently scan through the entire genome, which is an important and critical step when conducting genome-wide studies.
Figure 1.
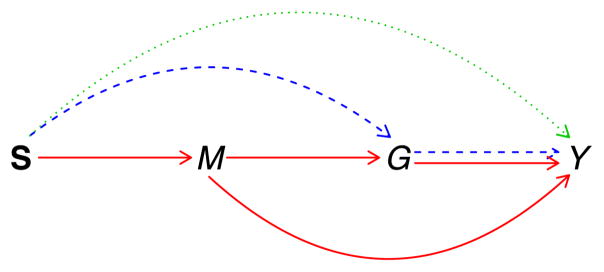
Causal diagram of SNPs (S), DNA methylation (M), gene expression (G), and outcome of interest (Y). Three path-specific effects are in different types of lines: ΔS→Y direct effect of SNPs on outcome is in dotted line; ΔS→G→Y, indirect effect mediated through gene expression but not through methylation is in dashed lines; ΔS→MY, indirect effect mediated through methylation is in solid lines.
The rest of the paper is organized as follows. In Section 2, we introduce the joint model for SNPs, DNA methylation and gene expression on disease risk, and QTL models for methylation and expression. In Section 3, we propose a variance component score test for any arbitrary set of regression coefficients, and we also construct an omnibus test using a perturbation procedure to accommodate different underlying disease models. In Section 4, we introduce three path-specific effects under the framework of causal mediation modeling. In Section 5, we study how different relationships among SNPs, DNA methylation, and gene expression can affect the correspondence between the three path-specific effects and coefficients in the joint model for disease. In Section 6, we illustrate the utility of our methods with two data applications. One is to analyze the prognosis of glioblastoma multiforme collected from The Cancer Genome Atlas by integrating 12 methylation loci and expression data of GRB10 gene as well as miR-633 micro-RNA expression. The other application is to reanalyze the 10 SNPs at ORMDL3 gene to investigate the direct effect on asthma risk as well as the indirect effect mediated through ORMDL3 expression. In Section 7, we conduct numerical studies for ORMDL3 gene that integrate SNP, DNA methylation, and gene expression data in genetic association studies to evaluate the three path-specific effects. We conclude with discussion in Section 8.
2. The model
For subject i, i = 1, …, n, the joint model of Y is determined by covariates Xi, an SNP-set Si containing p SNPs, one DNA methylation Mi, one mRNA gene expression Gi, and all possible cross-product interactions among SNPs, methylation, and expression:
| (1) |
where
 (·) is a differentiable and strictly increasing transformation function with strictly increasing inverse function
(·) is a differentiable and strictly increasing transformation function with strictly increasing inverse function
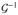 (·). When the outcome of interest Yi is dichotomous and
(·). When the outcome of interest Yi is dichotomous and
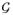 is the logistic link, it becomes a logistic model [19]. Note that we start from a very general model, but later, we will accommodate other nested parsimonious models. As DNA methylation can be affected by SNPs [13, 20] and gene expression can be affected by SNPs and methylation [13], we further consider the following QTL regression models for DNA methylation M and gene expression G:
is the logistic link, it becomes a logistic model [19]. Note that we start from a very general model, but later, we will accommodate other nested parsimonious models. As DNA methylation can be affected by SNPs [13, 20] and gene expression can be affected by SNPs and methylation [13], we further consider the following QTL regression models for DNA methylation M and gene expression G:
| (2) |
| (3) |
where , FM and FG|M can be any arbitrary distributions, μMi = E(Mi|Xi, Si), and μG|Mi = E(Gi|Xi, Si, Mi).
3. The testing procedure for any subset of parameters in the outcome model
In this section, we develop a testing procedure for an arbitrary set of regression coefficients in model (1). To illustrate the development, we focus on testing H0 : βG = βMG = 0, βSG = βSMG = 0, but tests for any other sets of regression coefficients can be developed following the same development. For simplicity, we consider the model for Y that follows the generalized linear model [21], and
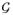 (·) is a canonical link function.
(·) is a canonical link function.
3.1. Derivation of the test statistic for H0 : βG = βMG = 0, βSG = βSMG = 0
A classical approach such as likelihood ratio test (LRT) or Wald test may work well if a single SNP is of interest. However, the conventional approach is subject to power loss or bias if the number of SNPs (p) is large [17]. Moreover, the correlation among SNPs due to the linkage disequilibrium can lead to numerical difficulties in fitting model (1).
To overcome this problem, we assume that the effects βSGj and βSMGj(j = 1, …, p) are independent and follow arbitrary distributions with mean 0 and variances τSG and τSMG, respectively. The resulting model for the outcome Y hence becomes a generalized linear mixed model (GLMM) [22]. The problem for testing the null H0 : βG = βMG = 0, βSG = βSMG = 0 becomes jointly testing for the variance components (τSG = τSMG = 0) and two scalar regression coefficients for fixed effects of gene expression and methylation-by-expression interaction (βG = βMG = 0) in the induced GLMM: H0 : τSG = τSMG = 0 and βG = βMG = 0.
The model (1) can be expressed in matrix notations as follows:
| (4) |
where μT = (μ1, …, μn), μi = E(Yi|Xi, Si, Mi, Gi), XT = (X1, …, Xn), ST = (S1, …, Sn), MT = (M1, …, Mn), GT = (G1, …, Gn), and , X̃ = (X, M, S, CSM), V = (G, CMG, CSG, CSMG), and . One can easily show that the scores for τSG, τSMG, βG, and βMG under the induced GLMM are as follows:
where μ0 is the mean of Y under the null model:
| (5) |
A classic score test has several numerical challenges [17], so we develop a test statistic by taking the weighted sum of UτSG, UτSMG, , and :
| (6) |
By combining the scores of parameters of interest, the test statistic has a nice quadratic function of Y and is closely related to the variance component score test [23].
A challenge remains in estimating α as its dimension is large (q + 1 + 2p). We use a ridge regression to stabilize the estimation by introducing an L2 penalty on the coefficients. The penalized log-likelihood under the null model (5) is
, where li is the log of the density of Yi under the null model (5) and λ is a tuning parameter. The estimation of α can be achieved by solving the estimating equation X̃(Y−μ0)−λI2α = 0 where I2 is (q+1+2p)×(q+1+2p) block diagonal matrix with the top (q+1)×(q+1) block diagonal matrix being 0 and the bottom 2p×2p diagonal matrix being I2p×2p. For selection of the tuning parameter λ, we use generalized cross-validation (GCV) [24] to estimate λ as the minimizer of the GCV function
, where
, Δ0 = diag{
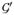 (μ0i)}, μ0i is the ith element of μ0, and λ is searched within a range of
to ensure
, an assumption that we later use to derive the asymptotic distribution of Q.
(μ0i)}, μ0i is the ith element of μ0, and λ is searched within a range of
to ensure
, an assumption that we later use to derive the asymptotic distribution of Q.
Different weighting schemes (a1 − a4) can be implemented to reflect the prior knowledge regarding the genetic effects. If no such knowledge is available, we propose to weight each term using the inverse of standard deviation. The corresponding variance for UτSG, UτSMG,
, and
follows the form 1T(
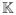 · H ·
· H ·
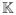 )1 with
, GGT, and
, respectively, where A · B denotes the component-wise multiplication of conformable matrices A and B, 1 denotes a vector of ones, the diagonal and off-diagonal elements of H are
and hii′ = 2[μ0i(1−μ0i)] [μ0i′(1−μ0i′)].
)1 with
, GGT, and
, respectively, where A · B denotes the component-wise multiplication of conformable matrices A and B, 1 denotes a vector of ones, the diagonal and off-diagonal elements of H are
and hii′ = 2[μ0i(1−μ0i)] [μ0i′(1−μ0i′)].
The asymptotic distribution of Q̂ under the null can be derived by accounting for the fact that Q̂ = Q(α̂λ̂) is a function of α̂λ̂ depending on the tuning parameter λ̂. Define , where and . We show in Appendix C the asymptotic distribution of the test statistic under the null
where and ε is a random vector following N(0, D). It follows that the null distribution of Q̂ converges in distribution to , where dv is the vth eigenvalue of B = D1/2ATAD1/2 and are iid χ2 random variables with 1 degree of freedom. The p-value of the test statistic Q can then be obtained using the characteristic function inversion method [25].
3.2. The omnibus test
So far, the test statistic Q in (6) is derived under the outcome model specified in (1), which assumes all possible two-way and three-way interactions. In this section, we denote the test statistic (6) as Q4. Suppose that the outcome Y does not depend on the three-way interaction (βSMG = 0), or it does not depend on the three-way interaction, SNP-by-methylation, or the SNP-by-expression interaction (βSMG = βSM = βSG = 0), or it depends only on the main effect of gene expression (βSMG = βSM = βSG = 0 and βMG = 0), then it is more powerful to test for the path-specific effect ΔS→G→Y using the test statistics , and Q1 = n−1(Y − μ0)T (a1GGT)(Y − μ0), respectively. Q1–Q4 all provide valid tests under the null. Under those more parsimonious models, the test statistic Q4 loses power as it tests for unnecessary parameters. However, if the outcome model is truly determined by all two-way and three-way interactions as (1), Q1–Q3 will lose power compared with Q4. In reality, we do not know the underlying true outcome model, and it is almost impossible that all genetic loci across the genome unanimously follow the same outcome model. Hence, it is desirable to develop a test that can accommodate different models to optimize statistical power. To this end, we further propose an omnibus test that can capture the strongest evidence among the four candidate models corresponding to Q1–Q4. Specifically, we compute the minimum p-value of four models and compare the observed minimum p-value to its null distribution, approximated by a resampling perturbation procedure.
As shown in Section 3.1, Q̂ converges in distribution to Q(0) = ||Aε||2. The empirical distribution of Q(0) can be estimated using perturbation [26, 27]. Set
, where Ui is the ith row of U,
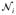 ’s are independent N(0, 1). By generating independent
’s are independent N(0, 1). By generating independent
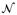 = (
= (
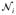 , …,
, …,
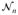 ) repeatedly, the perturbed realization of Q(0) can be obtained, denoted by {Q̂(0)(b), b = 1, …, B}, where B is the number of perturbations. The p-value can be approximated as the tail probability by comparing {Q̂(0)(b)} with the observed Q. Hence, one can calculate the p-values of the four candidate models by inputting Ui with different combinations of Gi, MiGi, SiGi, and SiMiGi, generating their perturbed realizations of the null counterpart for the candidate model k as {Q̂k(0)(b)} and comparing them with corresponding observed values Qk(k = 1, …, 4). Note that for each perturbation b, the random normal perturbation variable
) repeatedly, the perturbed realization of Q(0) can be obtained, denoted by {Q̂(0)(b), b = 1, …, B}, where B is the number of perturbations. The p-value can be approximated as the tail probability by comparing {Q̂(0)(b)} with the observed Q. Hence, one can calculate the p-values of the four candidate models by inputting Ui with different combinations of Gi, MiGi, SiGi, and SiMiGi, generating their perturbed realizations of the null counterpart for the candidate model k as {Q̂k(0)(b)} and comparing them with corresponding observed values Qk(k = 1, …, 4). Note that for each perturbation b, the random normal perturbation variable
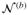 is the same across the four tests. Let P̂k =
is the same across the four tests. Let P̂k =
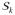 (Qk) be the p-value for the candidate model k, where
(Qk) be the p-value for the candidate model k, where
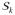 (q) = pr{Q̂k(0)(b) > q}. The null distribution of the minimum p-value, P̂min = mink P̂k can be approximated by
. The p-value of the omnibus test hence can be calculated by comparing P̂min with
.
(q) = pr{Q̂k(0)(b) > q}. The null distribution of the minimum p-value, P̂min = mink P̂k can be approximated by
. The p-value of the omnibus test hence can be calculated by comparing P̂min with
.
4. The path-specific effect
Here, we would like to introduce the path-specific effect under the causal mediation model and to show its correspondence to the regression coefficients in model (1) in the next section, in order to build the mechanistic interpretation of the testing procedure developed in Section 3. As shown in Figure 1, we are able to decompose the overall genetic effect into path-specific effects, studying the mechanistic contribution of genetic effect through epigenetic DNA methylation and gene transcription. In addition to shedding light on the mechanism of disease etiology, the path-specific effect may have translational utility. Unlike genetic alterations, epigenetic alterations or gene expression are potentially reversible. The reversibility of DNA methylation has been harnessed for therapeutic reasons in myelodysplastic syndromes and myelogenous leukemia, for which the Food and Drug Administration has already approved the use of drugs that prevent re-methylation [28–30]. Therefore, understanding the genetic contribution through path-specific effects may address the limitation of current GWAS where very little therapeutic devices can be developed.
Path-specific effects were first proposed by Avin [18] and have also been proposed to address confounding in mediation analysis [31]. We define three path-specific effects in the context of genetic studies: ΔS→Y denotes the direct effect of SNPs on the outcome, not through the DNA methylation or the expression (the green and dotted path in Figure 1); ΔS→G→Y denotes the indirect effect of SNPs on the outcome that is mediated through the gene expression but not through the DNA methylation (the blue and dashed path); and ΔS→MY denotes another indirect effect of SNPs that is mediated through the DNA methylation (the red and solid path). The three path-specific effects can be formally defined using the counterfactual notations defined in Appendix A:
With the assumptions of no-unmeasured confounding detailed in Appendix A, one can show that E[Yi(sa, M(sc), G(sb, M(sc)))|X] = ∫∫ E(Yi|X, sa, m, g)dFG|M(g|X, m, sb)dFM(m|X, sc). Given covariates X, the effects ΔS→Y, ΔS→G→Y and ΔS→MY can be expressed as integration of the joint model with respect to DNA methylation and gene expression based on the observed values:
5. Correspondence of no path-specific effects and regression coefficients in the outcome model
In this section, we would like to show how the null hypotheses for each path-specific effect are related to the regression coefficients in the joint model (1), and the results have been summarized in Table I. To better understand the six conditions in Table I, we further study them, again under the causal mediation framework. With the no-unmeasured confounding assumptions (Appendix B) and by the results of VanderWeele and Vansteelandt [15], the natural direct effect (DE) and indirect effect (IE) of SNPs on expression mediated through methylation can be expressed as follows:
| (7) |
| (8) |
Table I.
The correspondence between no path-specific effect and regression coefficients in the joint model of the outcome by different SNP–methylation–expression relationships.
| S–M–G relationship | Effect = 0 | Corresponding βs = 0 | |
|---|---|---|---|
|
|
δS ≠ 0 and αM αS ≠ 0 | ΔS→Y | βS, βSM, βSG, βSMG |
| ΔS→G→Y | βG, βMG, βSG, βSMG | ||
| ΔS→MY | βM, βMG, βSM, βSMG, βG, βSG | ||
|
| |||
|
|
δS αM ≠ 0 and αS = αSM = 0 | ΔS→Y | βS, βSM, βSG, βSMG |
| ΔS→G→Y | |||
| ΔS→MY | βM, βMG, βSM, βSMG, βG, βSG | ||
|
| |||
|
|
, αM = 0 and αSM = 0 | ΔS→Y | βS, βSM, βSG, βSMG |
| ΔS→G→Y | βG, βMG, βSG, βSMG | ||
| ΔS→MY | βM, βMG, βSM, βSMG | ||
|
| |||
|
|
αS = αSM = 0, αM = 0 and δS ≠ 0 | ΔS→Y | βS, βSM, βSG, βSMG |
| ΔS→G→Y | |||
| ΔS→MY | βM, βMG, βSM, βSMG | ||
|
| |||
|
|
δS = 0 and αS ≠ 0 | ΔS→Y | βS, βSM, βSG, βSMG |
| ΔS→G→Y | βG, βMG, βSG, βSMG | ||
| ΔS→MY | |||
|
| |||
|
|
δS = αS = αSM = 0 | ΔS→Y | βS, βSM, βSG, βSMG |
| ΔS→G→Y | |||
| ΔS→MY | |||
Using these two expressions, we can show how the six S–M–G relationships on the right in Table I can be illustrated as causal diagrams on the left. First, condition 1 represents the situation where all possible causal effects among S, M, and G exist, including DE (αS ≠ 0), IE (αM ≠ 0), and effect of the SNPs on the methylation (δS ≠ 0). In condition 2, δS ≠ 0 indicates an effect of the SNPs on the methylation, and αM ≠ 0 and αS = αSM = 0 indicate an indirect effect of the SNPs on the gene expression but no direct effect. In condition 3, δS ≠ 0 indicates an effect of the SNPs on the methylation, and αS ≠ 0 and αM = 0, αSM = 0 indicates a direct effect of the SNPs on the gene expression but no indirect effect mediated through methylation. Condition 4 indicates an effect of the SNPs on the methylation (δS ≠ 0) but neither a direct nor an indirect effect on the gene expression (αS = αSM = 0, αM = 0). In condition 5, δS = 0 indicates no effect of the SNPs on the methylation and αS ≠ 0 indicates a direct effect of the SNPs on the gene expression, whereas the effect of the methylation on gene expression may or may not exist. In condition 6, δS = 0 indicates no effect from the SNPs to the methylation, and αS = αSM = 0 indicates no direct effect of the SNPs on the gene expression, whereas the effect of the methylation on the gene expression may or may not exist.
We show in the Supporting information how no path-specific effect is related to the model (1) and summarize the results in Table I. For the results in Table I to hold, we assume that if there are two or more elements in β not equal to zero, there does not exist a combination of the nonzero elements for all S such that Δ = 0, to exclude the possibility of cancelation by chance. The direct effect ΔS→Y corresponds to βS, βSM, βSG, and βSMG, which is not influenced by the relationship among SNPs, methylation, and expression. The indirect effect of SNPs mediated through expression ΔS→G→Y is affected by the S–M–G relationship. Specifically, if there does not exist a direct effect of SNPs on gene expression (the second, fourth, and sixth conditions), ΔS→G→Y is zero; otherwise, it corresponds to βG, βMG, βSG, and βSMG. The result is intuitive because if the direct effect from SNPs to expression does not exist, the path-specific effect from SNPs to expression to outcome cannot even be initiated (the blue and dashed path in Figure 1). The indirect effect of SNPs mediated through methylation ΔS→MY is also affected by the relationships among the genomic feature. Similarly, the path would not be initiated if no effect from SNPs to methylation (the fifth and sixth conditions), and thus, ΔS→MY is zero and does not correspond to any parameters (the red and solid path in Figure 1). Otherwise, ΔS→MY corresponds to all parameters related to methylation (βM, βMG, βSM, βSMG), and it also corresponds to the parameters related to expression (βG and βSG) if methylation modulates gene expression (the first and second conditions).
Note that the assumptions in Appendix B help us translate the six conditions in Table I into causal diagrams, which provide intuitive interpretation how S–M–G relationships affect path-specific effects. However, the correspondence results shown in Table I or the tests developed in Section 3 do not require the assumptions.
5.1. The test for H0 : Δ S→G→Y = 0
With the results shown in Table I, we are able to provide a mechanistic explanation of the testing procedure in Section 3 for the null hypothesis H0 : βG = βMG = 0, βSG = βSMG = 0. From Table I, we know that under the causal structure where S, M, and G are all causally linked, that is, the first condition,
Therefore, the testing procedure in Section 3 corresponds to a test for the effect of the SNPs S on the outcome Y mediated through the gene expression G. Actually, under the first, third, and fifth conditions in Table I, the path-specific effect Δ S→G→Y corresponds to the same set of parameters.
5.2. The test for H0 : ΔS→Y = 0 and H0 : ΔS→MY = 0
Similarly, the test statistic for H0 : ΔS→Y = 0 can be constructed as Q = n−1(Y − μ0)T K(Y − μ0) where , and for H0 : ΔS→MY = 0, for the first and second conditions in Table I and for the third and fourth conditions. Following similar development to Sections 3.1 and 3.2, their corresponding asymptotic distributions and omnibus tests can also be derived.
5.3. Selection for model structure of genomic data, S, M, and G
To implement the testing procedure for the path-specific effects, we have to determine the causal structure of the genomic data, SNPs S, DNA methylation M, and gene expression G. Once the structure is determined, one can identify the set of parameters to be tested by looking up Table I. There are multiple ways to determine the structure of S, M, and G. The best way to understand their causal structure is from literature or existing biological evidence. If such prior knowledge is not available, we may rely on statistical analyses. For example, one may estimate the three arrows among S, M, and G: the direct and indirect effects of S on G with respect to M using (7) and (8). Alternatively, one may perform model selection of the six candidate models illustrated in Table I using selection criteria such as Akaike information criterion [32] or Bayesian information criterion [33]. The association among the genomic predictors is presumably orthogonal to the test of path-specific effects on phenotypic outcome, and thus, the model selection should not result in inflation of type I error for the tests.
6. Data applications
6.1. GRB10 gene and mortality of glioblastoma multiforme
Although the method is motivated by GWAS, here, instead of investigating genetic variants, we focus on the effect of epigenetic methylation. Glioblastoma multiforme (GBM) is the most common malignant brain tumor that is rapidly fatal with median survival rate between 12.1 and 14.6 months depending on the types of treatment [34]. Because of its poor prognosis, it is important to identify genes that may be responsible for the survival of GBM patients. Multiple sets of genomic data on GBM as well as its survival information have been archived in The Cancer Genome Atlas, a research project to map the genomes of many types of cancer. We exploit the multi-platform genome data in The Cancer Genome Atlas to investigate the epigenetic effect on GBM mortality. Specifically, we will integrate epigenetic DNA methylation, micro-RNA expression, and gene expression data to jointly model the overall survival of GBM. There are 271 patients with complete level 3 data on methylation, micro-RNA, and gene expression arrays. The survival is dichotomized into less than 390 days (the median survival) and greater than or equal to 390 days.
According to our analyses of epigenetic methylation and gene expression, we have found that the GRB10 gene is significantly associated with overall survival of GBM [35]. Here, we combine 12 methylation loci at GRB10 from Illumina 27K array and its expression value on Agilent G4502A expression array (Agilent Technologies, Santa Clara, CA) to perform a gene-based analysis supported by the evidence that GRB10 expression is regulated by its methylation [36]. We further add a third component, the expression of micro-RNA, miR-633. We have found that two methylation sites of GRB10 are associated with the expression of miR-633 with p = 0.024 and 0.060, and the expression of miR-633 is also highly associated with expression of GRB10 with p = 0.0031 from Wald-type hypothesis tests for least square estimators. Furthermore, it has also been shown that GRB10 gene is the target of miR-633 [37] and micro-RNA expression can be regulated by methylation [38]. Therefore, according to our statistical analyses and literature, we set up a model as Figure 1 based on the first condition in Table I with S, M, G, and Y being 12 methylation loci of GRB10, miR-633 expression, GRB10 expression, and GBM mortality, respectively.
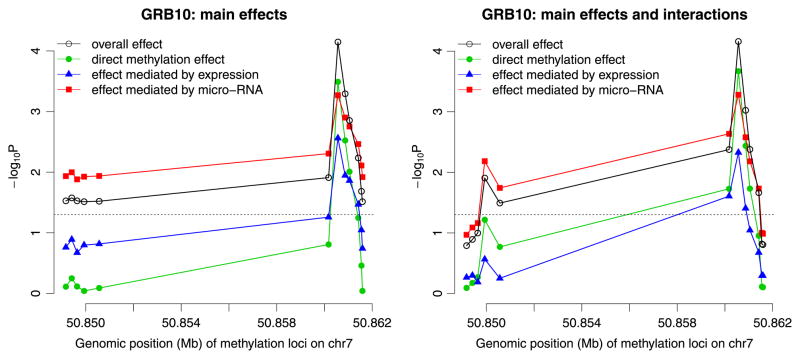
We first study the effect of GRB10 methylation using single-locus LRT. We analyze the three path-specific effects focusing on one methylation locus at a time. Two possible models were investigated. One is the model with only the main effect of methylation, miR-633 and GRB10 expressions, and the other considers the main effects as well as all possible cross-product interactions. The results are shown in Figure 2. It is obvious that the most significant is the effect mediated through miR-633 expression although the other two path-specific effects also have a few loci with significant or marginally significant p-values.
Figure 2.
The p-values from single-locus analyses of 12 methylation loci at GRB10 gene with glioblastoma multiforme survival using likelihood ratios tests. The dashed line indicates p = 0.05.
The results of multi-locus analyses for the 12 methylation loci at GRB10 are provided in Table II. The three path-specific effects on survival are statistically significant from the omnibus tests (Table II). Consistent with the single-locus analyses, the effect of methylation mediated through miR-633 expression is more prominent, compared with the other two path-specific effects. This mediation effect is most significant in the main effect model (p-value = 0.0060), and the omnibus test provides very similar p-value (0.0040) (Table II). In addition to investigating three path-specific effects, we test the overall effect by testing the union set of the parameters from the three effects. The overall effect is again most significant in the main effect model and approximated well by the omnibus test (p-value = 0.020). Compared with our proposed method, conventional LRT provides similar results but with larger p-values for the effect mediated through miR-633 expression and the direct effect. Our approach can have more significant results than LRT in these two tests probably because there are more parameters to be tested in these two tests. We conclude that GRB10 methylation has a significant effect on overall survival of GBM, which is most likely mediated through miR-633 expression and possibly through GRB10 expression.
Table II.
The p-values from analyses of 12 methylation loci at GRB10 gene and survival (<390 versus ≥ 390 days) of glioblastoma multiforme.
| ΔS→Y | ΔS→G→Y | ΔS→MY | Overall | |
|---|---|---|---|---|
| Omnibus (Q1–Q4) | 0.024 | 0.042 | 0.004 | 0.020 |
| Q4: all βs | 0.030 | 0.034 | 0.042 | 0.155 |
| Q3: main effects and two-way interactions | 0.026 | 0.034 | 0.034 | 0.115 |
| Q2: main and mRNA-by-micro-RNA effects | 0.020 | 0.040 | 0.010 | 0.050 |
| Q1: main effects | 0.022 | 0.040 | 0.006 | 0.020 |
| Likelihood ratio test, all βs | 0.045 | 0.038 | 0.014 | 0.017 |
ΔS→Y, the direct effect of methylation on survival; ΔS→G→Y, the effect of methylation on survival mediated through gene expression but not through micro-RNA expression; ΔS→MY, the effect of methylation on survival mediated through micro-RNA expression; Overall, the overall effect of methylation on survival, no matter through which paths.
6.2. ORMDL3 gene and asthma risk
We reanalyze the 10 SNPs at ORMDL3 genes and its expression to study the path-specific and joint effects on the risk of developing asthma using the Medical Research Council Asthma (MRCA) data [2, 10]. Because there is only one mediator, ORMDL3 expression, the path-specific effect can be simplified to one direct effect, the effect of SNPs on the risk of asthma independent of gene expression, and one indirect effect, the effect of SNPs on asthma mediated through gene expression. The MRCA (Medical Research Council Asthma) data contain 108 asthma cases and 50 controls. The genotype data were collected with the Illumina 300K chip, and the gene expression was collected using the Affymetrix U133 Plus 2.0 (Affymetrix, Inc., Santa Clara, CA). The data were analyzed using both additive and dominant models where genotype was coded as the number of the minor allele (0, 1, 2) and the presence of the minor allele (0, 1), respectively. To link the data to the variables in model (1), Y, asthma status (yes versus no), S, 10 SNPs of ORMDL3, and G = M, ORMDL3 expression.
There are strong associations between the SNPs and the gene expression (eight out of 10 with p-value < 0.05), i.e., the SNPs are eQTL. For additive models, direct, indirect, and overall effects are all statistically significant (omnibus p-value = 0.021, 0.030, and 0.0015, respectively). However, the analyses assuming dominant models suggest a nonsignificant indirect effect (omnibus p-value = 0.39) albeit the direct and overall effects are even more significant (omnibus p-value = 0.0065 and 0.0010, respectively). Unlike the GRB10 gene for GBM survival, here, the model with main effects and interactions provides more significant signals than the model with only main effects (Table III).
Table III.
The p-values from reanalyses of 10 single nucleotide polymorphisms (SNPs) at ORMDL3 gene and asthma risk.
| Additive
|
Dominant
|
|||||
|---|---|---|---|---|---|---|
| Direct | Indirect | Overall | Direct | Indirect | Overall | |
| Omnibus | 0.021 | 0.030 | 0.002 | 0.007 | 0.386 | 0.001 |
| Main and interaction effects | 0.015 | 0.022 | 0.002 | 0.006 | 0.449 | 0.002 |
| Main effects | 0.104 | 0.245 | 0.031 | 0.007 | 0.309 | 0.003 |
| Likelihood ratio test, main effects | 0.067 | 0.319 | 0.053 | 0.009 | 0.416 | 0.007 |
Direct, the direct effect of SNPs on asthma risk; Indirect, the effect of SNPs on asthma mediated through gene expression; Overall, the overall effect of SNPs on asthma, no matter through direct or indirect effect.
In this example, we compare our method for multi-SNP analyses with LRT for the model with only main effects (i.e., 10 SNPs and one gene expression) because the model that includes interactions does not converge, which exemplifies the limitation of LRT for multi-locus analyses. In general, our approach provides more significant results than LRT in both additive and dominant models. It can be explained by the large degrees of freedom in these tests. Another explanation may be that LRT can only afford to evaluate the suboptimal model with only main effects, while the optimal model in this study is the one that includes SNP-by-expression interactions, as discussed earlier.
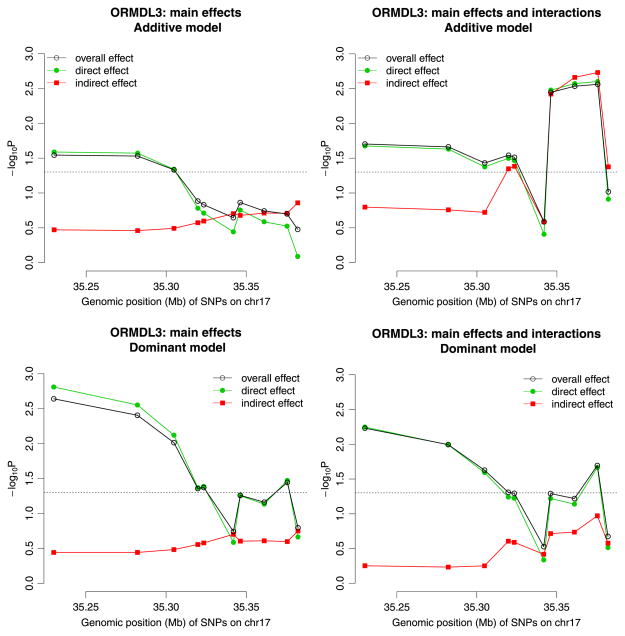
We also perform single-SNP analyses using LRT in both main effect and interaction models where SNPs are coded in additive and dominant modes (Figure 3). The results for main effect model are consistent with the multi-locus analyses in Table III. For additive, there are three SNPs that are highly significant in direct, indirect, and overall effects in the model assuming interaction effects (Figure 3b). The three SNPs are not very significant under the dominant mode, and in contrast, there are another three upstream SNPs that have significant direct and overall effects but very nonsignificant indirect effects (Figures 3c, d).
Figure 3.
The p-values from single-locus analyses of 10 SNPs at ORMDL3 gene with asthma risk using likelihood ratios tests. The dashed line indicates p = 0.05.
7. Simulation
We have demonstrated the utility of our method in joint analyses of SNP and expression in the asthma study and of methylation, micro-RNA expression, and gene expression in the study of glioblastoma multiforme survival. However, to our knowledge, there is no publicly available data on SNP, DNA methylation, and expression data for the appropriate target tissue in GWAS. Thus, we resort to numerical studies to evaluate the performance of our method.
7.1. Settings
To mimic the motivating data example of the asthma genetic study, we simulated the data focusing on the ORMDL3 gene. We simulated 99 HapMap SNPs at the region where the ORMDL3 gene is located using HAPGEN [39]. Ten out of the 99 HapMap SNPs are available in the Illumina HumanHap 300K array (i.e., 10 typed SNPs). The 10 typed SNPs were found to be highly associated with the risk of childhood asthma [2]. We assumed rs7359623 to be causal SNP Scausal. The DNA methylation, gene expression, and disease outcome were generated using the causal SNP, but the analyses were based on the 10 typed SNPs. The DNA methylation is generated by the model: Mi = 0 + Scausal,iδS + εM,i, where εM,i follows a beta(α = 2, β = 5) distribution that is further standardized to have mean zero and variance 1. The gene expression is generated by the following model: Gi = 0 + Scausal,iαS + MiαM + MiScausal,iαSM + εG|M,i, where εG|M,i ~ N(0, sd = 0.4)+ 0.5 × U(−0.3, 0.3), U denotes a uniform distribution. The outcome Y was generated by a logistic regression model: logit[P(Yi = 1|Scausal,i, Mi, Gi)] = −1.2 + Scausal,iβS + MiβM + GiβG + MiScausal,iβSM + GiScausal,iβSG + MiGiβMG + MiGiScausal,iβSMG. Note that G and M follow arbitrary distributions to illustrate the flexibility of the proposed method. In the setting without measurement error, Mobserved,i = Mi and Gobserved,i = Gi. We also investigated the influence of measurement error on the performance of the test for three path-specific effects where we introduced additional errors to the DNA methylation and gene expression values: Mobserved,i = Mi + εerror,i and Gobserved,i = Gi + εerror,i with εerror ~ N(0, sd = 0.5).
For each simulation, we generated a cohort with 1000 subjects, from which we selected 150 cases and 150 controls for the genetic association study of disease Y. For the 150 cases and 150 controls, we have complete data on the 10 SNPs, methylation and expression of ORMDL3 gene as well as their case/control status. We investigated the performance of our methods using the 10 typed SNPs and the DNA methylation and gene expression in case–control data. By setting different configurations of δs and αs, we were able to generate data according to different SNP-methylation–expression relationships illustrated in Table I. But here, we will focus on the first condition in Table I: δS ≠ 0 and αMαS ≠ 0 (i.e., SNPs are both mQTL and eQTL) because the testing procedures under other conditions are the same or just special cases. We studied the performance of tests under various configurations of βs. The empirical size is estimated from 2000 simulations, and the power is estimated from 1000 simulations.
7.2. Size and power of ΔS→Y
The empirical size and power of testing H0 : ΔS→Y = 0 are presented in Table IV. In general, the results using Davies’s characteristic function inversion method are very similar to the perturbation method. Empirical sizes are correct under different null models: all βs are zero, all βs are zero except βM (=0.3), all βs are zero except βG (=0.3). For settings under the alternatives, the test that assumes the correct model has the optimal power, and our proposed omnibus test can almost reach the optimal power across different settings. For example, under the setting with only SNP effect (βS = 0.3), the perturbation test focusing on main effects has the optimal power 62.4%; under the setting with main effects and two-way interactions (βS = βM = βG = 0.3, βMG = 0.4, βSM = βSG = 0.5, βSMG = 0), the test focusing on main effects plus all two-way interactions has the optimal power 95.6%; and the omnibus tests are very close to the two optimal tests (61.4% and 93.0%, respectively) (Table IV).
Table IV.
Empirical size and power (%) of ΔS→Y.
| True βs | βS | 0 | 0.3 | 0 | 0 | 0.3 | 0.3 | 0.2 | 0.3 | 0.3 | 0.3 | 0 |
| βM | 0 | 0 | 0.3 | 0 | 0.3 | 0.3 | 0.2 | 0.3 | 0.3 | 0.3 | 0 | |
| βG | 0 | 0 | 0 | 0.3 | 0.3 | 0.45 | 0.3 | 0 | 0.3 | 0.3 | 0 | |
| βMG | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.3 | 0 | 0.4 | 0 | |
| βSM | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0 | |
| βSG | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0 | |
| βSMG | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.5 | |
| Perturbation | Omnibus (Q1–Q4) | 4.75 | 61.4 | 5.60 | 4.80 | 60.8 | 57.6 | 31.2 | 60.6 | 95.8 | 93.0 | 99.6 |
| Q4: all | 4.25 | 58.2 | 5.80 | 5.40 | 59.8 | 56.0 | 29.8 | 59.2 | 96.0 | 94.4 | 100.0 | |
| Q3: two-way | 4.35 | 60.8 | 5.40 | 5.20 | 59.8 | 56.2 | 31.0 | 59.0 | 96.6 | 95.6 | 11.4 | |
| Q2: main + βMG | 4.60 | 61.4 | 5.60 | 5.60 | 62.0 | 59.2 | 34.0 | 61.2 | 44.4 | 34.6 | 12.2 | |
| Q1: main | 4.70 | 62.4 | 5.40 | 5.40 | 61.8 | 59.4 | 31.6 | 61.2 | 45.2 | 30.6 | 12.0 | |
| Davies | Q4: all | 4.45 | 58.5 | 5.20 | 4.50 | 56.4 | 54.6 | 29.1 | 57.0 | 97.3 | 95.7 | 99.8 |
| Q3: two-way | 4.50 | 60.7 | 4.70 | 4.80 | 58.0 | 56.0 | 30.7 | 57.0 | 98.0 | 96.8 | 12.9 | |
| Q2: main + βMG | 4.60 | 62.8 | 5.10 | 4.90 | 60.0 | 59.2 | 32.6 | 59.2 | 45.1 | 35.2 | 12.0 | |
| Q1: main | 4.80 | 63.0 | 4.90 | 4.90 | 59.7 | 58.9 | 31.2 | 57.2 | 44.7 | 32.3 | 11.8 | |
| Likelihood ratio test, main | 6.10 | 42.5 | 5.00 | 4.70 | 38.1 | 38.5 | 18.2 | 35.4 | 26.6 | 19.9 | 8.80 | |
Q4, the test for the model with all β parameters in model (1); Q3, the test for the model with all parameters except βSMG; Q2, the test for the model with βS, βM, βG, and βMG; Q1, the test for the model with βS, βM, and βG; Omnibus, the omnibus test for the previous four tests.
We also compare our methods with conventional LRTs. The major limitation of LRT is that it cannot afford cross-product interactions here because of their colinearity with the main effects. Under the null, the main effect LRT has correct sizes. However, LRT loses power under the alternatives, compared with our variance component tests (VCT), even under the setting with only main effects. The power loss may result from the high correlation among the SNPs due to linkage disequilibrium and the large degrees of freedom.
7.3. Size and power of ΔS→G→Y
The empirical size and power of testing H0 : ΔS→G→Y = 0 are presented in Table V. Similar to the results of ΔS→Y, Davies’s method and perturbation have similar results. Empirical sizes are correct under different null: all βs are zero, all βs are zero except βS (=0.3), all βs are zero except βM (=0.3). Under the alternatives, tests assuming the correct models perform the best, and the omnibus test can almost reach the optimal power with limited power loss. For example, under the setting with βS = 0.2, βM = 0.2, βG = 0.3, βMG = 0.3 and all other βs to be zero, the test includes main effects, and βMG performs the best with power 81.8%, and the omnibus test has power 80.2%.
Table V.
Empirical size and power (%) of ΔS→G→Y.
| True βs | βS | 0 | 0.3 | 0 | 0 | 0.3 | 0.3 | 0.2 | 0.3 | 0.3 | 0.3 | 0 |
| βM | 0 | 0 | 0.3 | 0 | 0.3 | 0.3 | 0.2 | 0.3 | 0.3 | 0.3 | 0 | |
| βG | 0 | 0 | 0 | 0.3 | 0.3 | 0.45 | 0.3 | 0 | 0.3 | 0.3 | 0 | |
| βMG | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.3 | 0 | 0.4 | 0 | |
| βSM | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0 | |
| βSG | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0 | |
| βSMG | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.5 | |
| Perturbation | Omnibus (Q1–Q4) | 5.55 | 4.80 | 6.80 | 62.4 | 58.8 | 91.4 | 80.2 | 49.6 | 64.6 | 95.0 | 51.0 |
| Q4: all | 4.30 | 5.20 | 4.80 | 53.2 | 52.6 | 89.0 | 79.0 | 50.2 | 62.0 | 92.2 | 66.8 | |
| Q3: to-way | 4.60 | 4.80 | 5.80 | 60.8 | 59.4 | 91.6 | 76.2 | 34.0 | 69.4 | 91.0 | 9.60 | |
| Q2: main + βMG | 4.90 | 4.60 | 5.80 | 53.4 | 53.6 | 88.6 | 81.8 | 56.2 | 52.2 | 96.0 | 9.80 | |
| Q1: main | 5.00 | 4.80 | 5.40 | 66.0 | 64.6 | 93.8 | 62.0 | 4.40 | 46.2 | 34.6 | 11.6 | |
| Davies | Q4: all | 3.85 | 4.40 | 4.50 | 53.6 | 52.3 | 88.6 | 77.7 | 47.7 | 60.9 | 91.5 | 64.3 |
| Q3: two-way | 4.85 | 4.80 | 5.10 | 62.0 | 60.3 | 92.3 | 75.8 | 32.0 | 70.7 | 90.5 | 9.60 | |
| Q2: main + βMG | 5.05 | 5.30 | 5.60 | 55.1 | 53.7 | 88.8 | 81.9 | 55.3 | 51.1 | 96.2 | 10.3 | |
| Q1: main | 5.10 | 4.60 | 4.90 | 67.1 | 66.5 | 94.5 | 62.8 | 4.20 | 48.5 | 36.6 | 12.5 | |
| Likelihood ratio test, main | 5.95 | 4.90 | 5.80 | 68.5 | 67.8 | 94.6 | 64.0 | 4.90 | 50.8 | 37.6 | 13.6 | |
Notations are the same as Table IV.
The sizes of LRT are correct, and its power is very similar to the VCT that only focus on main effects because the only parameter to be tested βG is a scalar. LRT is subject to power loss when higher-order interactions are involved in the underlying true model. The difference between LRT and our VCT focusing on main effects is that the parameters under the null βS are estimated with ridge regression in VCT.
7.4. Size and power of ΔS→MY
The empirical size and power of testing H0 : ΔS→MY = 0 are presented in Table VI. Similar to the previous results, empirical sizes are correct under the null: all βs are zero, all βs are zero except βS (=0.3). Under the alternatives, tests assuming the correct models perform optimally, and the omnibus test can reach the optimal power across different settings. Similar to the results of ΔS→G→Y, size and power of LRT are very similar to our VCT focusing on main effects because the parameters to be tested are two scalars βM and βG. And, LRT is less statistically powerful than VCT when true models contain cross-product interactions.
Table VI.
Empirical size and power (%) of ΔS→MY.
| True βs | βS | 0 | 0.3 | 0 | 0 | 0.3 | 0.3 | 0.2 | 0.3 | 0.3 | 0.3 | 0 |
| βM | 0 | 0 | 0.3 | 0 | 0.3 | 0.3 | 0.2 | 0.3 | 0.3 | 0.3 | 0 | |
| βG | 0 | 0 | 0 | 0.3 | 0.3 | 0.45 | 0.3 | 0 | 0.3 | 0.3 | 0 | |
| βMG | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.3 | 0 | 0.4 | 0 | |
| βSM | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0 | |
| βSG | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0 | |
| βSMG | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.5 | |
| Perturbation | Omnibus (Q1–Q4) | 5.45 | 4.80 | 58.6 | 54.6 | 92.4 | 99.0 | 93.4 | 85.8 | 98.0 | 100.0 | 70.4 |
| Q4: all | 5.00 | 5.00 | 52.6 | 45.4 | 89.4 | 98.4 | 94.4 | 87.0 | 98.0 | 100.0 | 79.8 | |
| Q3: two-way | 5.40 | 4.80 | 59.4 | 53.0 | 91.8 | 98.8 | 93.2 | 82.4 | 98.8 | 100.0 | 31.6 | |
| Q2: main + βMG | 4.95 | 5.20 | 54.2 | 47.4 | 91.0 | 98.8 | 93.8 | 87.4 | 81.8 | 97.8 | 28.8 | |
| Q1: main | 5.55 | 4.20 | 61.8 | 58.2 | 93.2 | 98.8 | 85.2 | 63.6 | 77.6 | 71.6 | 33.8 | |
| Davies | Q4: all | 4.80 | 4.90 | 51.9 | 46.9 | 90.7 | 98.8 | 94.2 | 86.2 | 97.5 | 99.9 | 77.0 |
| Q3: two-way | 5.20 | 4.20 | 56.7 | 53.6 | 93.4 | 99.4 | 93.6 | 82.3 | 98.4 | 99.9 | 32.0 | |
| Q2: main + βMG | 5.10 | 4.50 | 52.4 | 49.3 | 92.0 | 99.1 | 94.4 | 86.9 | 82.5 | 98.5 | 28.6 | |
| Q1: main | 5.35 | 4.30 | 61.0 | 58.4 | 94.6 | 99.4 | 85.9 | 63.2 | 79.5 | 72.4 | 34.1 | |
| Likelihood ratio test, main | 6.20 | 5.10 | 6.35 | 60.9 | 93.5 | 99.3 | 84.5 | 63.7 | 77.7 | 69.6 | 33.9 | |
Notations are the same as Table IV.
7.5. Other SNP-methylation–expression relationships
We also perform simulations under different SNP-methylation–expression relationships (data not shown). The performance is very similar to what is presented here because the testing procedure is the same as or simply a special case of what is presented earlier. As shown in Table I, the test for ΔS→Y is the same across different SNP-methylation–expression relationships; the test for ΔS→G→Y is also the same if it is not zero; the test for ΔS→MY focuses on βM, βMG, βSM, βSMG as well as βG, βSG under the first and second conditions but only on βM, βMG, βSM, βSMG for the third and fourth conditions, and ΔS→MY is zero under the last two conditions.
7.6. Measurement error of DNA methylation and gene expression
The corresponding results for ΔS→Y, ΔS→G→Y and ΔS→MY with measurement error in M and G are presented in Tables S1–S3, respectively. Compared with those without measurement error (Tables V and VI), the path-specific effects mediated through M or G, ΔS→G→Y and ΔS→MY lose power because of the noisy measurement of M and G (Tables S2 and S3). However, when there is no SNP-by-methylation or SNP-by-expression interactions, the power for the test of ΔS→Y seems inflated because of insufficient adjustment of the effect from M and G (Table S1). For the three path-specific effects, the type I errors are all well-protected under the null. The insufficient adjustment of the effect from M and G does not introduce bias to the S–Y direct effect under the null (the third and fourth columns in Table S1) but may give undue inflation to the effect ΔS→Y under the alternative (the fifth to eighth columns in Table S1).
8. Discussion
To formulate biological hypotheses using a mediation diagram is intuitive and provides an attractive analytic strategy to integrate biology into statistical models. The major contributions of what we present here are as follows: (1) to build a general framework that is able to integrate multi-platform genomic data and to characterize the biological process among multiple molecular features as path-specific effects; (2) to accommodate various candidate models; and (3) to allow for multi-locus analyses. The method developed here is ‘gene-centric’, and the proposed testing procedure can be used to scan through all the genes in the genome. R codes for the proposed testing procedures are available upon request. Furthermore, the models (1)–(3) can be easily generalized to incorporate gene sets, biological pathways, or a molecular network. For example, one may obtain a test statistic for a gene set by taking weighted sum of the gene-centric statistics (6) where flexible weights may be incorporated to account for the correlation among genes.
Although studies that substantiate the notion of mediation modeling in two-platform genomic data or univariate analyses have been reported, here, we propose a novel path-specific approach to investigate biological mechanisms. Wang et al. [40] proposed a Bayesian approach to model overall survival of GBM by gene expression and classified the expression into those regulated by DNA methylation and those not [40]. We had also proposed to model the overall effect of SNP on the risk of asthma by exploiting expression data [17]. Liu et al. [41] used a conventional single-mediator mediation model with single locus to discriminate the causal relationships among SNPs, methylation, and the risk of rheumatoid arthritis [41]. However, despite borrowing information from another genomic data, these studies still focus more on a single platform, and none of these works are able to tackle the path-specific effects.
The event that SNPs regulate methylation and gene expression occurs within a cell. Thus, it is plausible to assume that no phenotypic covariates exert undue influence on SNP-methylation and SNP-expression relationships (Assumption (3) in Appendix A) and that it is unlikely that downstream factors of SNPs should confound methylation-disease and expression-disease relations (Assumption (4) in Appendix A). Based on the same reasoning, the confounders that we collect and adjust for to ensure the causal interpretation for SNP-disease association (Assumption (1) in Appendix A) should be very similar to those for methylation-disease and expression-disease associations (Assumption (2) in Appendix A). However, if we focus on a partial set of genetic factors of a multigenetic disease, the remaining causal genetic factors that have been left out from the analyses may violate the assumptions. Thus, in addition to controlling for phenotypic confounding covariates, we need to assume that the complex genetic architecture does not violate our assumptions or to analyze all causal genetic factors.
Kraft et al. propose to study genetic association of disease when gene–environment interaction may exist [42]. Their method has a close relation to one of our path-specific effects. They test for the effect of SNP and gene–environment cross-product interactive effect in a joint model of genetic and environment factors. As environmental factors such as the habit of cigarette smoking may be influenced by genetic factors [43], the test for the main effect of SNPs as well as their interaction with the environmental factor corresponds to the direct effect, the effect of SNPs on the outcome not mediated through environment. If the environment factor is independent of the genetic factor, then their test is not only for the direct effect but also for the joint effect.
The genomic markers, S, M, and G need to be selected prior to putting them into the model. There are several practical considerations to be aware of. One has to decide how to group the set of S, M, and G in model (1). A natural choice would be to select those that belong to the same gene, that is, SNPs, methylation loci, and gene expression value for a gene. Alternatively, statistical analyses may help identify such a set and determine its causal structure. For selecting the number of markers in S, one may include as many markers as possible to increase the likelihood of covering the causal marker, which, on the other hand, may introduce unnecessary noise if some markers are independent of the causal one. As the statistical power depends on unknown correlation structure between the causal marker and the typed markers [17], it is challenging to recommend an optimal number of markers to be analyzed. One may group the markers within a gene as we did for the GBM data or combine those reported in the previous literature as we did for the asthma data. As discussed in Sections 5.3 and 7.6, one also needs to be cautious about determining the structure of the genomic data and the influence of measurement error on the performance of the method.
Supplementary Material
Acknowledgments
Funding statements:
The author would like to thank the referees for their helpful comments. The work is supported by the National Institute of Health (R03 CA182937-2) and Richard B. Salomon Award Fund, Brown University.
Appendix A: Counterfactual notations and assumptions for identifying three path-specific effects
To study path-specific effects based on the causal theory, we first need to define counterfactual notations. Let Y(s, m, g) be the potential outcome that would have been observed if SNPs (S), DNA methylation (M), and gene expression (G) had been set to s, m, and g, respectively, G(s, m) be the potential outcome of gene expression, had the SNPs (S) and DNA methylation (M) been set to s and m, respectively, and M(s) be the potential outcome of DNA methylation, had the SNPs (S) been set to s. The notation without parenthesis (M, G, Y) denotes the observed value. Note that Y(s, m, g), M(s), and G(s, m) may or may not be observed. They are equivalent to observed values when their determinants are set to the observed values: Yi(s = Si, m = Mi, g = Gi) = Yi, Mi(s = Si) = Mi and Gi(s = Si, m = Mi) = Gi.
We use A ⊥ B|C to denote that A is independent of B conditioning on C. In order to identify the path-specific effect using the data, we make the following four assumptions: after controlling for the covariates (X), (1) Y(s, m, g) ⊥ S|X: no-unmeasured confounding for the effect of SNPs (S) on the outcome (Y); (2) Y(s, m, g) ⊥ (M, G)|S, X: no-unmeasured confounding for the effect of DNA methylation and gene expression ((M, G)) on the outcome (Y) after controlling for SNPs (S); (3) (M(s), G(s)) ⊥ S|X: no-unmeasured confounding for the effect of SNPs (S) on DNA methylation and gene expression ((M, G)); (4) Y(s, m, g) ⊥ (M(s*), G(s*))|X: there are no SNPs (S)-induced factors that can confound the DNA methylation-outcome and gene expression-outcome joint relation.
Appendix B: Assumptions for interpreting S–M–G relationships with causal mediation model
We make the following assumptions of no-unmeasured confounding: after controlling for the covariates (X), (1) G(s, m) ⊥ S|X: no-unmeasured confounding for the effect of SNPs (S) on the gene expression (G); (2) G(s, m) ⊥ M|S, X: no-unmeasured confounding for the effect of DNA methylation (M) on the gene expression (G) after controlling for SNPs (S); (3) M(s) ⊥ S|X: no-unmeasured confounding for the effect of SNPs (S) on DNA methylation (M); (4) G(s, m) ⊥ M(s*)|X: no SNPs (S)-induced DNA methylation-gene expression confounder.
Appendix C: Asymptotic distribution of Q̂
First note that test statistic Q̂ can be rewritten as ||n−1/2Va (Y − μ̂0)||2. We denote the scores for the model (1) in the main text as SU = n−1/2UT (Y − μ(α0)). Using the result that the ridge estimator α̂λ̂ is a -consistent estimator of α0 with [44], it has been shown that n−1/2Va (Y − μ̂0) can be expressed as [45]. A simple calculation can show that
By the central limit theorem, in distribution as n → ∞, where ε follows N(0, D). From the previous result and the Slutsky theorem, we have . Finally, it follows from the continuous mapping theorem,
Footnotes
Additional supporting information may be found in the online version of this article at the publisher’s web site.
References
- 1.Lynch TJ, Bell DW, Sordella R, Gurubhagavatula S, Okimoto RA, Brannigan BW, Harris PL, Haserlat SM, Supko JG, Haluska FG, Louis DN, Christiani DC, Settleman J, Haber DA. Activating mutations in the epidermal growth factor receptor underlying responsiveness of non-small-cell lung cancer to gefitinib. New England Journal of Medicine. 2004;350(21):2129–2139. doi: 10.1056/NEJMoa040938. [DOI] [PubMed] [Google Scholar]
- 2.Moffatt M, Kabesch M, Liang L, Dixon A, Strachan D, Heath S, Depner M, von Berg A, Bufe A, Rietschel E, Heinzmann A, Simma B, Frischer T, Willis-Owen SA, Wong KC, Illig T, Vogelberg C, Weiland SK, von Mutius E, Abecasis GR, Farrall M, Gut IG, Lathrop GM, Cookson WO. Genetic variants regulating ORMDL3 expression contribute to the risk of childhood asthma. Nature. 2007;448(7152):470–473. doi: 10.1038/nature06014. [DOI] [PubMed] [Google Scholar]
- 3.Cusanovich DA, Billstrand C, Zhou X, Chavarria C, De Leon S, Michelini K, Pai AA, Ober C, Gilad Y. The combination of a genome-wide association study of lymphocyte count and analysis of gene expression data reveals novel asthma candidate genes. Human Molecular Genetics. 2012;21(9):2111–2123. doi: 10.1093/hmg/dds021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hsu YH, Zillikens MC, Wilson SG, Farber CR, Demissie S, Soranzo N, Bianchi EN, Grundberg E, Liang L, Richards JB, Estrada K, Zhou Y, van Nas A, Moffatt MF, Zhai G, Hofman A, van Meurs JB, Pols HA, Price RI, Nilsson O, Pastinen T, Cupples LA, Lusis AJ, Schadt EE, Ferrari S, Uitterlinden AG, Rivadeneira F, Spector TD, Karasik D, Kiel DP. An integration of genome-wide association study and gene expression profiling to prioritize the discovery of novel susceptibility loci for osteoporosis-related traits. PLoS Genetics. 2010;6(6):e1000977. doi: 10.1371/journal.pgen.1000977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhong H, Beaulaurier J, Lum PY, Molony C, Yang X, MacNeil DJ, Weingarth DT, Zhang B, Greenawalt D, Dobrin R, Hao K, Woo S, Fabre-Suver C, Qian S, Tota MR, Keller MP, Kendziorski CM, Yandell BS, Castro V, Attie AD, Kaplan LM, Schadt EE. Liver and adipose expression associated SNPs are enriched for association to type 2 diabetes. PLoS Genetics. 2010;6(5):e1000932. doi: 10.1371/journal.pgen. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhang M, Liang L, Morar N, Dixon AL, Lathrop GM, Ding J, Moffatt MF, Cookson WO, Kraft P, Qureshi AA, Han J. Integrating pathway analysis and genetics of gene expression for genome-wide association study of basal cell carcinoma. Human Genetics. 2012;131(4):615–623. doi: 10.1007/s00439-011-1107-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Xiong Q, Ancona N, Hauser ER, Mukherjee S, Furey TS. Integrating genetic and gene expression evidence into genome-wide association analysis of gene sets. Genome Research. 2012;22(2):386–397. doi: 10.1101/gr.124370.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Nicolae DL, Gamazon E, Zhang W, Duan S, Dolan ME, Cox NJ. Trait-associated SNPs are more likely to be eQTLSs: annotation to enhance discovery from GWAS. PLoS Genetics. 2010;6(4):e1000888. doi: 10.1371/journal.pgen.1000888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gamazon ER, Badner JA, Cheng L, Zhang C, Zhang D, Cox NJ, Gershon ES, Kelsoe JR, Greenwood TA, Nievergelt CM, Chen C, McKinney R, Shilling PD, Schork NJ, Smith EN, Bloss CS, Nurnberger JI, Edenberg HJ, Foroud T, Koller DL, Scheftner WA, Coryell W, Rice J, Lawson WB, Nwulia EA, Hipolito M, Byerley W, McMahon FJ, Schulze TG, Berrettini WH, Potash JB, Zandi PP, Mahon PB, McInnis MG, Zollner S, Zhang P, Craig DW, Szelinger S, Barrett TB, Liu C. Enrichment of cis-regulatory gene expression SNPs and methylation quantitative trait loci among bipolar disorder susceptibility variants. Molecular Psychiatry. 2012;18(3):340–346. doi: 10.1038/mp.2011.174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dixon A, Liang L, Moffatt MF, Chen W, Heath S, Wong KC, Taylor J, Burnett E, Gut I, Farrall M, Lathrop GM, Abecasis GR, Cookson WO. A genome-wide association study of global gene expression. Nature Genetics. 2007;39(10):1202–1207. doi: 10.1038/ng2109. [DOI] [PubMed] [Google Scholar]
- 11.Kwee L, Liu D, Lin X, Ghosh D, Epstein M. A powerful and flexible multilocus association test for quantitative traits. The American Journal of Human Genetics. 2008;82(2):386–397. doi: 10.1016/j.ajhg.2007.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wu M, Kraft P, Epstein M, Taylor D, Chanock S, Hunter D, Lin X. Powerful SNP set analysis for case-control genomewide association studies. American Journal of Human Genetics. 2010;86(6):929–942. doi: 10.1016/j.ajhg.2010.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Berlivet S, Moussette S, Ouimet M, Verlaan DJ, Koka V, Tuwaijrl AA, Kwan T, Sinnett D, Pastinen T, Naumova AK. Interaction between genetic and epigenetic variation defines gene expression patterns at the asthma-associated locus 17q12-q21 in lymphoblastoid cell lines. Human Genetics. 2012;131(7):1161–1171. doi: 10.1007/s00439-012-1142-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.MacKinnon D. Introduction to Statistical Mediation Analysis. NY: Taylor & Francis; 2008. [Google Scholar]
- 15.VanderWeele TJ, Vansteelandt S. Conceptual issues concerning mediation, intervention and composition. Statistics and its Interface. 2009;2:457–468. [Google Scholar]
- 16.Imai K, Keele L, Yamamoto T. Identification, inference and sensitivity analysis for causal mediation effects. Statistical Science. 2010;25(1):51–71. [Google Scholar]
- 17.Huang YT, VanderWeele TJ, Lin X. Joint analysis of SNP and expression data in genetic association studies of complex diseases. Annals of Applied Statistics. 2014;8(1):352–376. doi: 10.1214/13-AOAS690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Avin C, Shpitser I, Pearl J. Identifiability of path-specific effects. Proceedings of the International Joint Conferences on Artificial Intelligence; Edinburgh, Scotland, UK. 2005. pp. 357–363. [Google Scholar]
- 19.Prentice RL, Pyke R. Logistic disease incidence models and case-control studies. Biometrika. 1979;66(3):403–411. [Google Scholar]
- 20.Gibbs JR, van der Brug MP, Hernandez DG, Traynor BJ, Nalls MA, Lai SL, Arepalli S, Dillman A, Rafferty IP, Tron-coso J, Johnson R, Zielke HR, Ferrucci L, Longo DL, Cookson MR, Singleton AB. Abundant quantitative trait loci exist for DNA methylation and gene expression in human brain. PLoS Genetics. 2010;6(5):e1000952. doi: 10.1371/journal.pgen.1000952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.McCullagh P, Nelder JA. Generalized Linear Models. Chapman & Hall/CRC; London: 1989. [Google Scholar]
- 22.Breslow NE, Clayton DG. Approximate inference in generalized linear mixed models. Journal of the American Statistical Association. 1993;88(421):9–25. [Google Scholar]
- 23.Lin X. Variance component test in generalised linear models with random effects. Biometrika. 1997;84(2):309–326. [Google Scholar]
- 24.O’Sullivan F, Yandell BS, Raynor WJ. Automatic smoothing of regression functions in generalized linear models. Journal of the American Statistical Association. 1986;81(393):96–103. [Google Scholar]
- 25.Davies RB. Algorithm AS 155: the distribution of a linear combination of chi-square random variables. Applied Statistics. 1980;29(3):323–333. [Google Scholar]
- 26.Parzen M, Wei LJ, Ying Z. A resampling method based on pivotal estimating functions. Biometrika. 1994;81(2):341–350. [Google Scholar]
- 27.Cai T, Wei LJ, Wilcox M. Semiparametric regression analysis for clustered failure time data. Biometrika. 2000;87(4):867–878. [Google Scholar]
- 28.Issa JP, Gharibyan V, Cortes J, Jelinek J, Morris G, Verstovsek S, Talpaz M, Garcia-Manero G, Kantarjian HM. Phase II study of low-dose decitabine in patients with chronic myelogenous leukemia resistant to imatinib mesylate. Journal of Clinical Oncology. 2005;23(17):3948–3956. doi: 10.1200/JCO.2005.11.981. [DOI] [PubMed] [Google Scholar]
- 29.Garcia-Manero G, Kantarjian HM, Sanchez-Gonzalez B, Yang H, Rosner G, Verstovsek S, Rytting M, Wierda WG, Ravandi F, Koller C, Xiao L, Faderl S, Estrov Z, Cortes J, O’Brien S, Estey E, Bueso-Ramos C, Fiorentino J, Jabbour E, Issa JP. Phase 1/2 study of the combination of 5-aza-2′-deoxycytidine with valproic acid in patients with leukemia. Blood. 2006;108(10):3271–3279. doi: 10.1182/blood-2006-03-009142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kaminskas E, Farrell A, Abraham S, Baird A, Hsieh LS, Lee SL, Leighton JK, Patel H, Rahman A, Sridhara R, Wang YC, Pazdur R. Approval summary: azacitidine for treatment of myelodysplastic syndrome subtypes. Clinical Cancer Research. 2005;11(10):3604–3608. doi: 10.1158/1078-0432.CCR-04-2135. [DOI] [PubMed] [Google Scholar]
- 31.VanderWeele TJ, Vansteelandt S, Robins JM. Effect decomposition in the presence of an exposure-induced mediator-outcome confounder. Epidemiology. 2014;25(2):300–306. doi: 10.1097/EDE.0000000000000034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Akaike H. A new look at the statistical model identification. IEEE Transactions on Automatic Control. 1974;19(6):716–723. [Google Scholar]
- 33.Schwarz GE. Estimating the dimension of a model. Annals of Statistics. 1978;6(2):461–464. [Google Scholar]
- 34.Stupp R, Mason WP, van den Bent MJ, Weller M, Fisher B, Taphoorn MJ, Belanger K, Brandes AA, Marosi C, Bogdahn U, Curschmann J, Janzer RC, Ludwin SK, Gorlia T, Allgeier A, Lacombe D, Cairncross JG, Eisenhauer E, Mirimanoff RO European Organisation for Treatment of Cancer Brain Tumor and Radiotherapy Groups and National Cancer Institute of Canada Clinical Trials Group. Radiotherapy plus concomitant and adjuvant temozolomide for glioblastoma. New England Journal of Medicine. 2005;352(10):987–996. doi: 10.1056/NEJMoa043330. [DOI] [PubMed] [Google Scholar]
- 35.Smith AA, Huang YT, Eliot M, Houseman EA, Marsit CJ, Wiencke JK, Kelsey KT. A novel approach to the discovery of survival biomarkers in glioblastoma using a joint analysis of DNA methylation and gene expression. Epigenetics. 2014;9:873–883. doi: 10.4161/epi.28571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Turan N, Ghalwash MF, Katari S, Coutifaris C, Obradovic Z, Sapienza C. DNA methylation differences at growth related genes correlate with birth weight: a molecular signature linked to developmental origins of adult disease? BMC Medical Genomics. 2012;5:10. doi: 10.1186/1755-8794-5-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jia P, Sun J, Guo AY, Zhao Z. SZGR: a comprehensive schizophrenia gene resource. Molecular Psychiatry. 2010;15(5):453–462. doi: 10.1038/mp.2009.93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Suzuki H, Maruyama R, Yamamoto E, Kai M. DNA methylation and microRNA dysregulation in cancer. Molecular Oncology. 2012;6(6):567–578. doi: 10.1016/j.molonc.2012.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Marchini J, Howie B, Myers S, McVean G, Donnelly P. A new multipoint method for genome-wide association studies via imputation of genotypes. Nature Genetics. 2007;39(7):906–913. doi: 10.1038/ng2088. [DOI] [PubMed] [Google Scholar]
- 40.Wang W, Baladandayuthapani V, Morris JS, Boom BM, Manyam G, Do KA. iBAG: integrative Bayesian analysis of high-dimensional multiplatform genomics data. Bioinformatics. 2013;29(2):149–159. doi: 10.1093/bioinformatics/bts655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Liu Y, Aryee MJ, Padyukov L, Fallin MD, Hesselberg E, Runarsson A, Reinius L, Acevedo N, Taub M, Ronninger M, Shchetynsky K, Scheynius A, Kere J, Alfredsson L, Klareskog L, Ekstrom TJ, Feinberg AP. Epigenome-wide association data implicate DNA methylation as an intermediary of genetic risk in rheumatoid arthritis. Nature Biotechnology. 2013;31(2):142–147. doi: 10.1038/nbt.2487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kraft P, Yen YC, Stram DO, Morrison J, Gauderman WJ. Exploiting gene-environment interaction to detect genetic associations. Human Heredity. 2007;63(2):111–119. doi: 10.1159/000099183. [DOI] [PubMed] [Google Scholar]
- 43.VanderWeele TJ, Asomaning K, Tchetgen Tchetgen EJ, Han Y, Spitz M, Shete S, Wu X, Gaborieau V, Wang Y, McLaugh-lin J, Hung RJ, Brennan P, Amos CI, Christiani DC, Lin X. Genetic variants on 15q25. 1, smoking and lung cancer: as assessment of mediation and interaction. American Journal of Epidemiology. 2012;175(10):1013–1020. doi: 10.1093/aje/kwr467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Knight K, Fu W. Asymptotics for lasso-type estimators. The Annals of Statistics. 2000;28(5):1356–1378. [Google Scholar]
- 45.Lin X, Lee S, Christiani DC, Lin X. Test for interactions between a genetic marker set and environment in generalized linear models. Biostatistics. 2013;14(4):667–681. doi: 10.1093/biostatistics/kxt006. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.