Summary
We consider rules for discarding predictors in lasso regression and related problems, for computational efficiency. El Ghaoui and his colleagues have propose ‘SAFE’ rules, based on univariate inner products between each predictor and the outcome, which guarantee that a coefficient will be 0 in the solution vector. This provides a reduction in the number of variables that need to be entered into the optimization. We propose strong rules that are very simple and yet screen out far more predictors than the SAFE rules. This great practical improvement comes at a price: the strong rules are not foolproof and can mistakenly discard active predictors, i.e. predictors that have non-zero coefficients in the solution. We therefore combine them with simple checks of the Karush–Kuhn–Tucker conditions to ensure that the exact solution to the convex problem is delivered. Of course, any (approximate) screening method can be combined with the Karush–Kuhn–Tucker, conditions to ensure the exact solution; the strength of the strong rules lies in the fact that, in practice, they discard a very large number of the inactive predictors and almost never commit mistakes. We also derive conditions under which they are foolproof. Strong rules provide substantial savings in computational time for a variety of statistical optimization problems.
1. Introduction
Our focus here is statistical models fitted by using l1-penalization, starting with penalized linear regression. Consider a problem with N observations and p predictors. Let y denote the N-vector of outcomes, and X be the N × p matrix of predictors, with ith row xi and jth column xj. For a set of indices
 ={j1,…,jk}, we write X
={j1,…,jk}, we write X to denote the N × k submatrix X
to denote the N × k submatrix X =(xj1,…,xjk), and we write b
=(xj1,…,xjk), and we write b =(bj1,…,bjk) for a vector b. We assume that the predictors and outcome have been centred, so that we can omit an intercept term from the model. The lasso (Tibshirani, 1996); Chen et al., 1998)) optimization problem is
=(bj1,…,bjk) for a vector b. We assume that the predictors and outcome have been centred, so that we can omit an intercept term from the model. The lasso (Tibshirani, 1996); Chen et al., 1998)) optimization problem is
| (1) |
where λ≥ 0 is a tuning parameter.
There has been considerable work in the past few years deriving fast algorithms for this problem, especially for large values of N and p. A main reason for using the lasso is that the l1 -penalty tends to set some entries of β̂ to exactly 0, and therefore it performs a kind of variable selection. Now suppose that we knew, a priori to solving problem (1), that a subset of the variables
 ⊆ {1,…p} will be inactive at the solution, i.e. they will have zero coefficients: β
⊆ {1,…p} will be inactive at the solution, i.e. they will have zero coefficients: β = 0. (If X does not have full column rank, which is necessarily the case when p>N, then there may not be a unique lasso solution; we do not pay special attention to this case and will write ‘the solution’ when we really mean ‘a solution’.) Then we could discard the variables in
= 0. (If X does not have full column rank, which is necessarily the case when p>N, then there may not be a unique lasso solution; we do not pay special attention to this case and will write ‘the solution’ when we really mean ‘a solution’.) Then we could discard the variables in
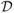 from the optimization, replacing the design matrix in problem (1) by X
from the optimization, replacing the design matrix in problem (1) by X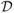 c,
c,
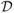 c = {1,…p}\
c = {1,…p}\
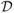 , and just solve for the remaining coefficients β̂
, and just solve for the remaining coefficients β̂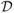 c. For a relatively large set
c. For a relatively large set
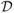 , this would result in substantial computational savings.
, this would result in substantial computational savings.
El Ghaoui et al. (2010) constructed such a set of discarded variables by looking at the univariate inner products of each predictor with the response. Namely, their ‘SAFE’ rule discards the jth variable if
| (2) |
where is the smallest tuning parameter value for which all coefficients in the solution are 0. In deriving this rule, El Ghaoui et al. (2010) proved that any predictor satisfying condition (2) must be inactive at the solution; said differently, condition (2) implies that β̂j = 0. (Their proof relies on the dual of problem (1); it has nothing to do with the rest of this paper, but we summarize it in Appendix A because we find it interesting.) They then showed that applying the SAFE rule (2) to discard predictors can save both time and memory in the overall computation, and they also derived analogous rules for l1 -penalized logistic regression and l1 -penalized support vector machines.
The existence of any such rule is surprising (at least to us), and the work presented here was inspired by the SAFE work. In this paper, we propose strong rules for discarding predictors in the lasso and other problems that involve lasso-type penalties. The basic strong rule for the lasso looks like a modification of condition (2), with ‖xj‖2‖y‖2/λmax replaced by 1: it discards the jth variable if
| (3) |
The strong rule (3) tends to discard more predictors than the SAFE rule (2). For standardized predictors (‖xj‖2=1 for all j), this will always be so, as ‖y‖2/λmax≥1 by the Cauchy-Schwartz inequality. However, the strong rule (3) can erroneously discard active predictors, ones that have non-zero coefficients in the solution. Therefore we rely on the Karush–Kuhn–Tucker (KKT) conditions to ensure that we are indeed computing the correct coefficients in the end. A simple strategy would be to add the variables that fail a KKT check back into the optimization. We discuss more sophisticated implementation techniques, specifically in the context of our glmnet algorithm, in Section 7 at the end of the paper.
The most important contribution of this paper is a version of the strong rules that can be used when solving the lasso and lasso-type problems over a grid of tuning parameter values λ1 ≥ λ2 ≥…≥ λm. We call these the sequential strong rules. For the lasso, having already computed the solution β̂(λk−1) at λk−1, the sequential strong rule discards the jth predictor from the optimization problem at λk if
| (4) |
The sequential rule (4) performs much better than both the basic rule (3) and the SAFE rule (2), as we demonstrate in Section 2. El Ghaoui et al. (2011) also propose a version of the SAFE rule that can be used when considering multiple tuning parameter values, which is called ‘recursive SAFE’, but it also is clearly outperformed by the sequential strong rule. Like its basic counterpart, the sequential strong rule can mistakenly discard active predictors, so it must be combined with a check of the KKT conditions (see Section 7 for details).
At this point, the reader may wonder: any approximate or non-exact rule for discarding predictors can be combined with a check of the KKT conditions to ensure the exact solution—so what makes the sequential strong rule worthwhile? Our answer is twofold.
In practice, the sequential strong rule can discard a very large proportion of inactive predictors and rarely commits mistakes by discarding active predictors. In other words, it serves as a very effective heuristic.
The motivating arguments behind the sequential strong rule are quite simple and the same logic can be used to derive rules for l1-penalized logistic regression, the graphical lasso, the group lasso and others.
The mistakes that were mentioned in (a) are so rare that for a while a group of us were trying to prove that the sequential strong rule for the lasso was foolproof, while others were trying to find counterexamples (hence the large number of coauthors!). We finally did find some counterexamples of the sequential strong rule and one such counterexample is given in Section 3, along with some analysis of rule violations in the lasso case. Furthermore, despite the similarities in appearance of the basic strong rule (3) to the SAFE rule (2), the arguments motivating the strong rules (3) and (4) are entirely different, and rely on a simple underlying principle. In Section 4 we derive analogous rules for the elastic net, and in Section 5 we derive rules for l1-penalized logistic regression. We give a version for more general convex problems in Section 6, covering the graphical lasso and group lasso as examples.
Finally, we mention some related work. Wu et al. (2009) studied l1-penalized logistic regression and built a screened set
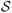 based on the inner products between the outcome and each feature. As with the strong rules, their construction does not guarantee that the variables in
based on the inner products between the outcome and each feature. As with the strong rules, their construction does not guarantee that the variables in
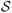 actually have zero coefficients in the solution and so, after fitting on XSc, they checked the KKT optimality conditions for violations. In the case of violations, they weakened their set
actually have zero coefficients in the solution and so, after fitting on XSc, they checked the KKT optimality conditions for violations. In the case of violations, they weakened their set
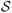 and repeated this process. Also, Fan and Lv (2008) studied the screening of variables based on their inner products in the lasso and related problems, but not from an optimization point of view; their screening rules may again set coefficients to 0 that are non-zero in the solution; however, they argued that under certain situations this can lead to better performance in terms of estimation risk.
and repeated this process. Also, Fan and Lv (2008) studied the screening of variables based on their inner products in the lasso and related problems, but not from an optimization point of view; their screening rules may again set coefficients to 0 that are non-zero in the solution; however, they argued that under certain situations this can lead to better performance in terms of estimation risk.
2. Strong rules for the lasso
2.1. Definitions and simulation studies
As defined in Section 1, the basic strong rule for the lasso discards the jth predictor from the optimization problem if
| (5) |
where is the smallest tuning parameter value such that β̂(λmax)= 0. If we are interested in the solution at many values λ1 ≥…≥ λm, then, having computed the solution β̂(λk−1) at λk−1, the sequential strong rule discards the jth predictor from the optimization problem at λk if
| (6) |
Here we take λ0=λmax. As β̂(λmax)=0, the basic strong rule (5) is a special case of the sequential rule (6).
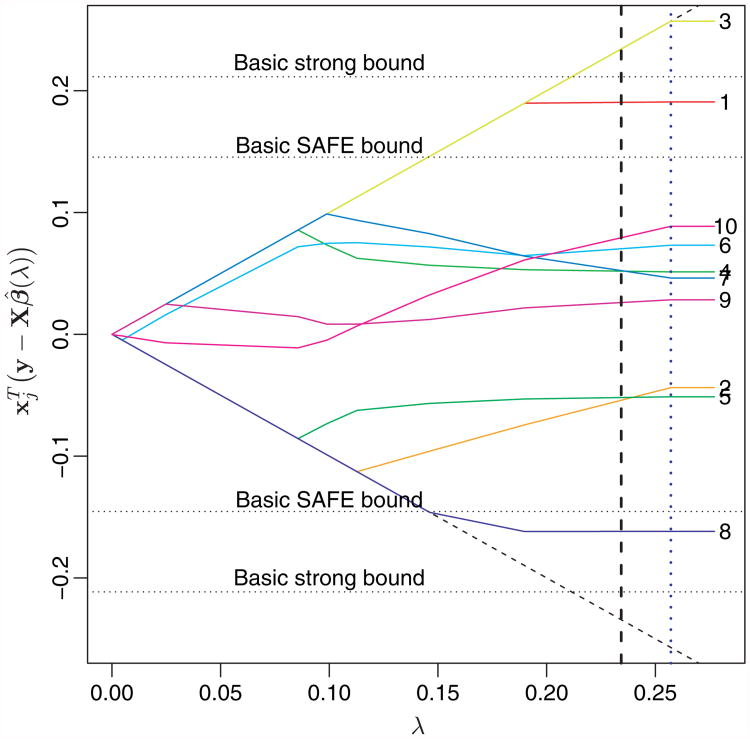
First of all, how does the basic strong rule compare with the basic SAFE rule (2)? When the predictors are standardized (meaning that ‖xi‖2=1 for every i), it is easy to see that the basic strong bound is always larger than the basic SAFE bound, because ‖y‖2/λmax ≥ 1 by the Cauchy-Schwartz inequality. When the predictors are not standardized, the ordering between the two bounds is not as clear, but in practice the basic strong rule still tends to discard more predictors unless the marginal variances of the predictors are wildly different (by factors of say 10 or more). Fig. 1 demonstrates the bounds for a simple example.
Fig. 1.
Basic SAFE and basic strong bounds in a simple example with 10 predictors, labelled at the right-hand side: inner product of each predictor with the current residual, as a function of λ; the predictors that are in the model are those with maximal (absolute) inner product, equal to ± λ; The dotted vertical line is drawn at λmax; the broken vertical line is drawn at some value λ = λ′ at which we want to discard predictors; the basic strong rule keeps only predictor number 3, whereas the basic SAFE rule keeps predictors 8 and 1 as well
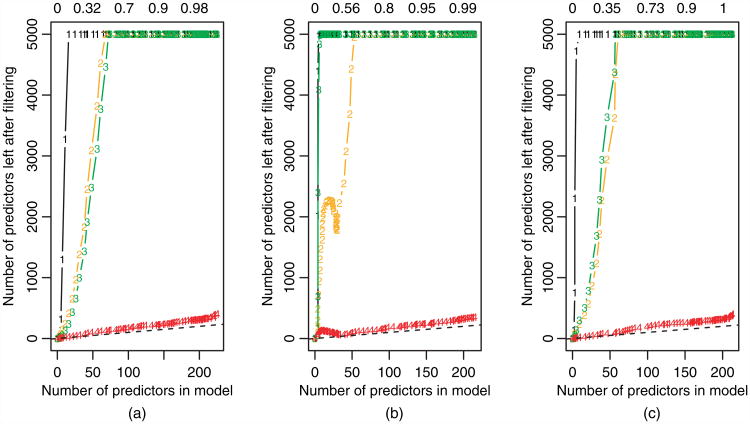
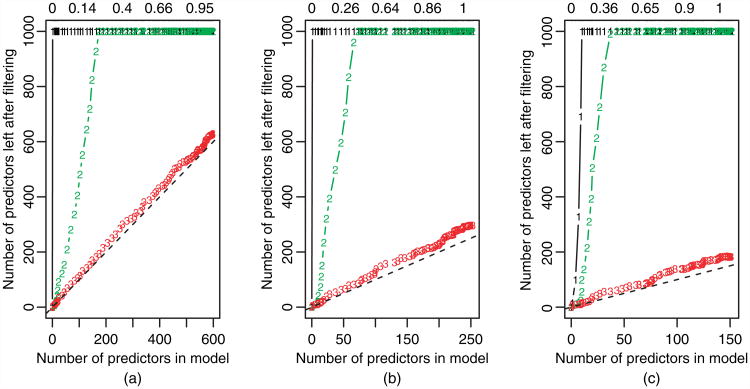
More importantly, how do the rules perform in practice? Figs 2 and 3 attempt to answer this question by examining several simulated data sets. (A few real data sets are considered later in Sections 3.2.) In Fig. 2, we compare the performance of the basic SAFE rule, recursive SAFE rule, basic strong rule and sequential strong rule in discarding predictors for the lasso problem along a sequence of 100 tuning parameter values, equally spaced on the log-scale. The three panels correspond to different scenarios for the model matrix X; in each we plot the number of active predictors in the lasso solution on the x-axis, and the number of predictors left after filtering with the proposed rules (i.e. after discarding variables) on the y-axis. The basic SAFE rule is denoted by 1s, the recursive SAFE rule by 2s the basic strong rule by 3s and the sequential strong rule by 4s. The details of the data generation are given in the caption of the figure. The sequential strong rule is remarkably effective.
Fig. 2.
Lasso regression: results of different rules applied to three different scenarios with various values of N and p, (a) no correlation, (b) positive correlation and (c) negative correlation (1, SAFE rule; 2, recursive SAFE rule; 3, basis strong rule; 4, sequential strong rule); number of predictors left after screening at each stage, plotted against the number of predictors in the model for a given value of λ (decreasing from left to right; in (a) and (b) the X-matrix entries are independent identically distributed standard Gaussian with pairwise correlation 0 and 0.5; in (c), a quarter of the pairs of features (chosen at random) had correlation −0.8; in the plots, we are fitting along a path of 100 decreasing λ-values equally spaced on the log-scale; a broken line with unit slope is added for reference; the proportion of variance explained by the model is shown along the top of the plot; there were no violations of either of the strong rules any of the three scenarios
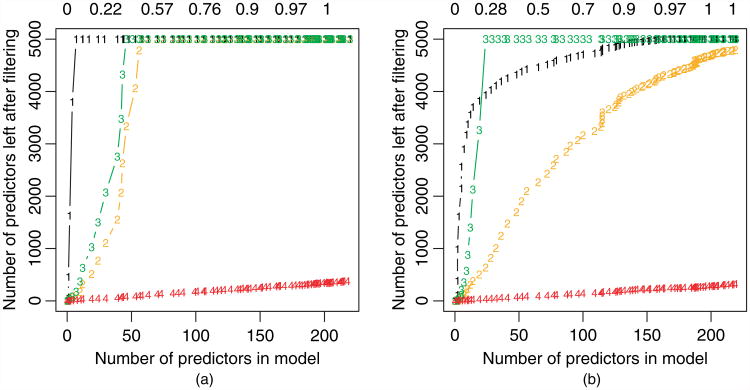
Fig. 3.
Lasso regression: results of different rules when the predictors are not standardized (1, SAFE rule; 2, recursive SAFE rule; 3, basis strong rule; 4, sequential strong rule); the scenario in (a) (equal population variance) is the same as in Fig. 2(a), except that the features are not standardized before fitting the lasso; in the data generation for (b)(unequal population variance), each feature is scaled by a random factor between 1 and 50, and again, no standardization is done
It is common practice to standardize the predictors before applying the lasso, so that the penalty term makes sense. This is what was done in the examples of Fig. 2. But, in some instances, we might not want to standardize the predictors, and so in Fig. 3 we investigate the performance of the rules in this case. In Fig. 3(a) the population variance of each predictor is the same; in Fig. 3(b) it varies by a factor of 50. We see that in the latter case the SAFE rules outperform the basic strong rule, but the sequential strong rule is still the clear winner. There were no violations of either of the strong rules in either panel.
After seeing the performance of the sequential strong rule, it might seem like a good idea to combine the basic SAFE rule with the sequential strategy; this yields the sequential SAFE rule, which discards the jth predictor at the parameter value λk if
| (7) |
We believe that this rule is not foolproof, in the same way that the sequential strong rule is not foolproof, but have not yet found an example in which it fails. In addition, although rule (7) outperforms the basic and recursive SAFE rules, we have found that it is not nearly as effective as the sequential strong rule at discarding predictors and hence we do not consider it further.
2.2. Motivation for the strong rules
We now give some motivation for the sequential strong rule (6). The same motivation also applies to the basic strong rule (5), recalling that the basic rule corresponds to the special case λ0=λmax and β̂(λmax)=0.
We start with the KKT conditions for the lasso problem (1). These are
| (8) |
where γj is the jth component of the subgradient of ‖β̂‖1:
| (9) |
Let , where we emphasize the dependence on λ. The key idea behind the strong rules is to assume that each cj(λ) is non-expansive in λ, i.e.
| (10) |
This condition is equivalent to cj(λ) being differentiable almost everywhere, and satisfying |c′j (λ)|≤1 wherever this derivative exists, for j=1,…, p. Hence we call condition (10) the ‘unit slope’ bound.
Using condition (10), if we have |cj(λk−1)| < 2 λk − λk−1, then
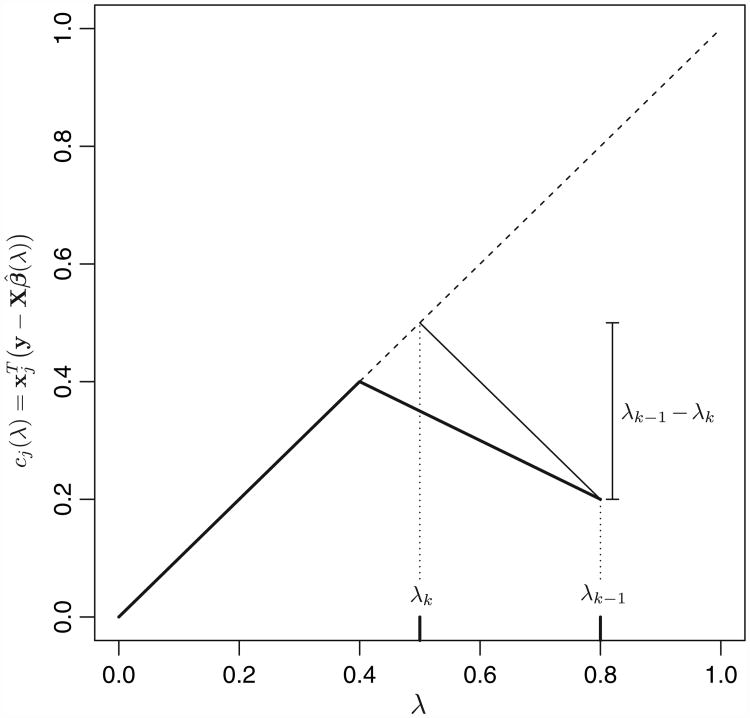
which implies that β̂j(λk)=0 by the KKT conditions (8) and (9). But this is exactly the sequential strong rule (6), because . In words: assuming that we can bound the amount that cj(λ) changes as we move from λk−1 to λk, if the initial inner product cj(λk−1) is too small, then it cannot ‘catch up’ in time. An illustration is given in Fig. 4.
Fig. 4.
Illustration of the slope bound (10) leading to the strong rules (5) and (6): The inner product (
 ) cj is plotted in as a function of λ, restricted to only one predictor for simplicity. the slope of cj between λk−1 and λk is bounded in absolute value by 1, so the most it can rise over this interval is λk−1 − λk; therefore, if it starts below λk−(λk−1−λk) =2λk−λk−1, it cannot possibly reach the critical level by λk
) cj is plotted in as a function of λ, restricted to only one predictor for simplicity. the slope of cj between λk−1 and λk is bounded in absolute value by 1, so the most it can rise over this interval is λk−1 − λk; therefore, if it starts below λk−(λk−1−λk) =2λk−λk−1, it cannot possibly reach the critical level by λk
The arguments until this point do not really depend on the Gaussian lasso problem in any critical way, and similar arguments can be made to derive strong rules for l1-penalized logistic regression and more general convex problems. But, in the specific context of the lasso, the strong rules, and especially the unit slope assumption (10), can be explained more concretely. For simplicity, the arguments that are provided here assume that rank(X)=p, so that necessarily p ≤ N, although similar arguments can be used motivate the p>N case. Let
 denote the set of active variables in the lasso solution,
denote the set of active variables in the lasso solution,
Also let s=sign(β̂ ). Note that
). Note that
 and s are implicitly functions of λ. It turns out that we can express the lasso solution entirely in terms of
and s are implicitly functions of λ. It turns out that we can express the lasso solution entirely in terms of
 and s:
and s:
| (11) |
| (12) |
where we write
to mean. (X )T. On an interval of λ in which the active set does not change, the solution (11)–(12) is just linear in λ. Also, the solution (11)–(12) is continuous at all values of λ at which the active set does change. (For a reference, see Efron et al. (2004).) Therefore the lasso solution is a continuous, piecewise linear function of λ, as is
. The critical points, or changes in slope, occur whenever a variable enters or leaves the active set. Each cj(λ) is differentiable at all values of λ that are not critical points, which means that it is differentiable almost everywhere (since the set of critical points is countable and hence has measure zero). Further, c′j(λ) is just the slope of the piecewise linear path at λ, and hence condition (10) is really just a slope bound. By expanding equation (11) and (12) in the definition of cj(λ), it is not difficult to see that the slope at λ is
)T. On an interval of λ in which the active set does not change, the solution (11)–(12) is just linear in λ. Also, the solution (11)–(12) is continuous at all values of λ at which the active set does change. (For a reference, see Efron et al. (2004).) Therefore the lasso solution is a continuous, piecewise linear function of λ, as is
. The critical points, or changes in slope, occur whenever a variable enters or leaves the active set. Each cj(λ) is differentiable at all values of λ that are not critical points, which means that it is differentiable almost everywhere (since the set of critical points is countable and hence has measure zero). Further, c′j(λ) is just the slope of the piecewise linear path at λ, and hence condition (10) is really just a slope bound. By expanding equation (11) and (12) in the definition of cj(λ), it is not difficult to see that the slope at λ is
| (13) |
Therefore the slope condition |c′j(λ)|≤ 1 is satisfied for all active variables j ∊
 . For inactive variables it can fail but is unlikely to fail if the correlation between the variables in
. For inactive variables it can fail but is unlikely to fail if the correlation between the variables in
 and
and
 c is small (thinking of standardized variables). From expression (13), we can rewrite the slope bound (10) as
c is small (thinking of standardized variables). From expression (13), we can rewrite the slope bound (10) as
| (14) |
In this form, the condition looks like the well-known ‘irrepresentable condition’, which we discuss in the next section.
2.3. Connection to the irrepresentable condition
A common condition appearing in work about model selection properties of the lasso is the ‘irrepresentable condition’ (Zhao and Yu, 2006; Wainwright, 2009; Candes and Plan, 2009), which is closely related to the concept of ‘mutual incoherence’ (Fuchs, 2005; Tropp 2006; Meinhausen and Buhlmann, 2006) If
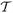 is the set of variables present in the true (underlying) linear model, i.e.
is the set of variables present in the true (underlying) linear model, i.e.
where β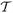 ∊ℝ|
∊ℝ|
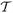 | is the true coefficient vector and z∊ℝn is noise, then the irrepresentable condition is that
| is the true coefficient vector and z∊ℝn is noise, then the irrepresentable condition is that
| (15) |
for some 0 < ε ≤ 1.
The conditions (15) and (14) appear extremely similar, but a key difference between the two is that the former pertains to the true coefficients generating the data, whereas the latter pertains to those found by the lasso optimization problem. Because
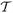 is associated with the true model, we can put a probability distribution on it and a probability distribution on sgn(β
is associated with the true model, we can put a probability distribution on it and a probability distribution on sgn(β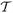 ), and then show that, with high probability, certain design matrices X satisfy condition (15). For example, Candes and Plan (2009) showed that, if |
), and then show that, with high probability, certain design matrices X satisfy condition (15). For example, Candes and Plan (2009) showed that, if |
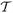 | is small,
| is small,
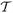 is drawn from the uniform distribution on |
is drawn from the uniform distribution on |
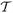 |-sized subsets of {1,…,p}, and each entry of sgn(β
|-sized subsets of {1,…,p}, and each entry of sgn(β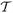 ) is equal to ±1 with equal probability, then designs X with
satisfy the irrepresentable condition (15) with very high probability. Unfortunately the same types of argument cannot be applied directly to condition (14). A distribution on
) is equal to ±1 with equal probability, then designs X with
satisfy the irrepresentable condition (15) with very high probability. Unfortunately the same types of argument cannot be applied directly to condition (14). A distribution on
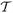 and sgn (β
and sgn (β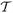 ) induces a different distribution on
) induces a different distribution on
 and sgn (β
and sgn (β ), via the lasso optimization procedure. Even if the distributions of
), via the lasso optimization procedure. Even if the distributions of
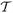 and sgn(β
and sgn(β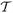 ) are very simple, the distributions of
) are very simple, the distributions of
 and sgn(β̂
and sgn(β̂ ) are likely to be complicated.
) are likely to be complicated.
Under the same assumptions as those described above, and an additional assumption that the signal-to-noise ratio is high, Candes and Plan (2009) proveed that for λ = 2 √{2 log p} the lasso solution satisfies
with high probability. In this event, conditions (14) and (15) are identical; therefore the work of Candes and Plan (2009) proves that condition (14) also holds with high probability, under the stated assumptions and only when λ = 2 √ {2 log(p)}. For our purposes, this is not very useful because we want the slope bound to hold along the entire path, i.e. for all λ. But, still, it seems reasonable that confidence in condition (15) should translate to some amount of confidence in condition (14). And, luckily for us, we do not need the slope bound (14) to hold exactly or with any specified level of probability, because we are using it as a computational tool and revert to checking the KKT conditions when it fails.
3. Violations of the strong rules
3.1. Simple counterexample
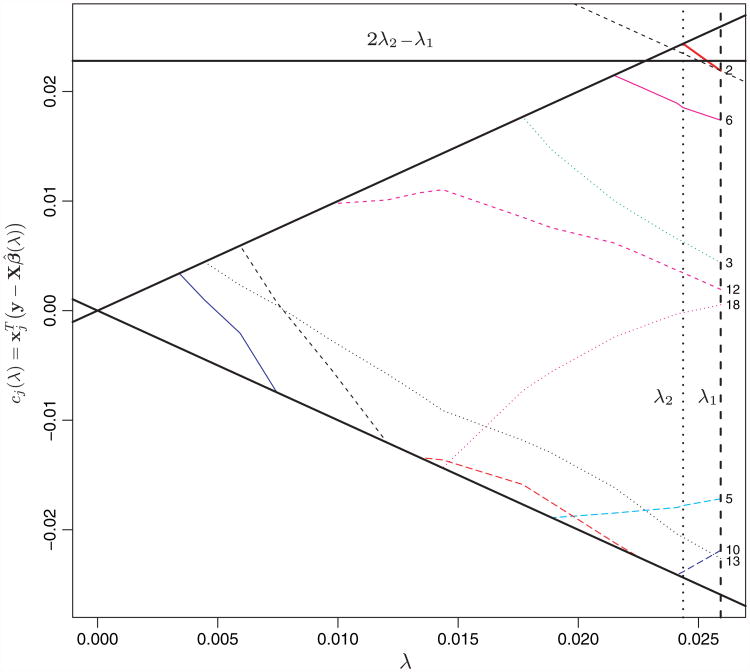
Here we demonstrate a counterexample of both the slope bound (10) and the sequential strong rule (6). We chose N = 50 and p = 30, with the entries of y and X drawn independently from a standard normal distribution. Then we centred y and the columns of X, and scaled the columns of X to have unit norm. As Fig. 5 shows, for predictor j = 2, the slope of is c′j(λ)=‒1.586 for all λ ∊ [λ2, λ1], where λ2 = 0.0244 and λ = 0.0259. Moreover, if we were to use the solution at λ1 to eliminate predictors for the fit at λ2, then we would eliminate the second predictor based on the bound (6). But this is clearly a problem, because the second predictor enters the model at λ2. By continuity, we can choose λ2 in an interval around 0.0244 and λ1 in an interval around 0.0259, and still break the sequential strong rule (6).
Fig. 5.
Example of a violation of the slope bound (10), which breaks the sequential strong rule (6): the entries of y and X were generated as independent, standard normal random variables with N = 50 and p = 30. (hence there is no underlying signal); the lines with slopes ±λ are the envelopes of maximal inner products achieved by predictors in the model for each λ; for clarity we only show a short stretch of the solution path; the right-hand broken vertical line is drawn at λ1, and we are considering the the solution at a new value λ2 < λ1, the broken vertical line to its left; the dotted horizontal line is the bound (6); in the top right-hand part of the plot, the inner product path for the predictor j = 2 is drawn and starts below the bound, but enters the model at λ2; the slope of the segment between λ1 and λ2 is −1.586; a line of slope −1 is drawn beside the segment for reference; the plot contains other examples of large slopes leading to rule violations, e.g. around λ = 0.007
We believe that a counterexample of the basic strong rule (5) can also be constructed, but we have not yet found one. Such an example is somewhat more difficult to construct because it would require that the average slope exceed 1 from λmax to λ, rather than exceeding 1 for short stretches of λ-values.
3.2. Numerical investigation of violations
We generated Gaussian data with N = 100, and the number predictors p varying over the set {20,50,100,500,1000}. The predictors had pairwise correlation 0.5. (With zero pairwise correlation, XTX would be orthogonal in the population and hence ‘close to’ orthogonal in the sample, making it easier for the strong rules to hold—see the next section. Therefore we chose pairwise correlation 0.5 to challenge the rules.) For each value of p, we chose a quarter of variables uniformly at random, assigned them coefficient values equal to ±2 with equal probability and added Gaussian noise to the true signal to generate y. Then we standardized y and the columns of X. We ran the R package glmnet version 1.5, which uses a path of 100 values of λ spanning the entire operating range, equally spaced on a log-scale. This was used to determine the exact solutions, and then we recorded the number of violations of the sequential strong rule.
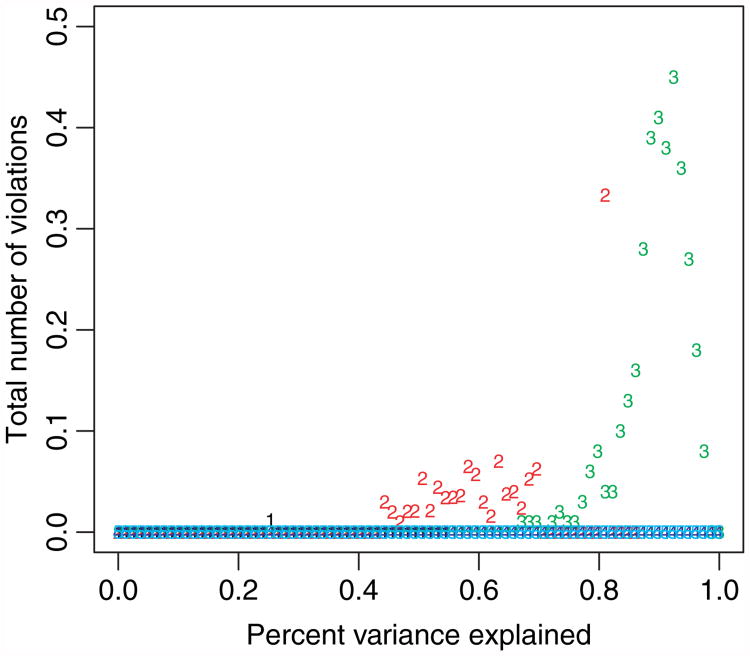
Fig. 6 shows the results averaged over 100 draws of the simulated data. We plot the percentage variance explained on the x-axis (instead of λ, since the former is more meaningful), and the total number of violations (out of p predictors) on the y-axis. We see that violations are quite rare, in general never averaging more than 0.3 erroneously discarded predictors! They are more common at the unregularized (small λ) end of the path and also tend to occur when p is fairly close to N. (When p = N, the model can produce a saturated fit, but only ‘just’. So, for this scenario, the coefficient paths are somewhat erratic near the end of the path.) When p ≫ N (p = 500 or p= 1000 here), there were no violations in any of 100 the simulated data sets. It is perhaps not surprisingly, then, that there were no violations in the examples shown in Figs 2 and 3 since there we had p ≫ N as well.
Fig. 6.
Total number of violations (out of predictors) of the sequential strong rule, for simulated data with N =100 and different values of p (1, p=20; 2, p= 50; 3, p= 100; 4, p=500; 5, p =1000): a sequence of models is fitted, over 100 decreasing values of λ from left to right; the features are drawn from a Gaussian distribution with pairwise correlation 0.5; the results are averages over 100 draws of the simulated data
In Table 1 we applied the strong rules to three large data sets from the University of California, Irvine, machine learning repository, and a standard microarray data set. As before, we applied glmnet along a path of about 100 values of λ. There were no violations of the rule in any of the solution paths, and a large fraction of the predictors were successfully discarded. We investigate the computational savings that result from the strong rule in Section 7.
Table 1. Results for sequential strong rule on three large classification data sets from the University of California, Irvine, machine learning repository and a standard microarray data set†.
| Data set | Model | N | p | Average number remaining after screening | Number of violations |
|---|---|---|---|---|---|
| Arcene | Gaussian | 100 | 10000 | 189.8 | 0 |
| Logistic | 153.4 | 0 | |||
| Dorothea | Gaussian | 800 | 100000 | 292.4 | 0 |
| Logistic | 162.0 | 0 | |||
| Gisette | Gaussian | 6000 | 5000 | 1987.3 | 0 |
| Logistic | 622.5 | 0 | |||
| Golub | Logistic | 38 | 7129 | 60.8 | 0 |
| Logistic | 125.5 | 0 |
glmnet was run with the default path of 100 λ-values, in both regression and classification mode. Shown are the average number of predictors left after screening by the strong rule (averaged over the path of λ-values). There were no violations of the screening rule in any of the runs.
3.3. Sufficient condition for the slope bound
Tibshirani and Taylor (2011) prove a general result that can be used to give the following sufficient condition for the unit slope bound (10). Under this condition, both basic and sequential strong rules will never discard active predictors. Recall that an m × m matrix A is diagonally dominant if |Aii| ≥ Σj≠i |Aij| for all i= 1,…,m. Their result gives us the following theorem.
Theorem 1. Suppose that X has full column rank, i.e. rank.(X) = p. If
| (16) |
then the slope bound (10) holds, and hence the strong rules (5), (6) never produce violations.
Proof. Tibshirani and Taylor (2011) consider a problem
| (17) |
where D is a general m × n penalty matrix. They derive the dual problem corresponding to problem (17), which has a dual solution û(λ) relating to the primal solution α̂(λ) by
In the proof of their ‘boundary lemma’, lemma 1, they show that, if DDT is diagonally dominant, then the dual solution satisfies
| (18) |
Now we show that, when rank(X) = p, we can transform the lasso problem (1) into a problem of the form (17), and we apply this lemma to obtain the desired result. First, we let α = Xβ and D = (XTX)−1XT. Then the lasso problem (1) can be solved by instead solving
| (19) |
and taking β̂ = (XTX)−1XTα̂. For the original lasso problem (1), we may assume without a loss of a generality that y ∊ col(X), because otherwise we can replace y by y′, its projection onto col(X), and the loss term decouples: . Therefore we can drop the constraint α ∊col(X) in problem (19), because, by writing α = α′ + α″ for α′ ∊ col(X) and α″┴ col(X), we see that the loss term is minimized when α″ = 0 and the penalty term is unaffected by α″, as Dα″ = (XTX)−1XTα ″ = 0. Hence we have shown that the lasso problem (1) can be solved by solving problem (17) with D = (XTX)−1XT (and taking β̂ =(XTX)−1XTα̂).
Now, the solution û(λ) of the dual problem corresponding to problem (17) satisfies
and so
Thus we have exactly ûj(λ) = cj(λ) for j = 1,…,p, and applying the boundary lemma (18) completes the proof.
We note a similarity between condition (16) and the positive cone condition that was used in Efron et al. (2004). It is not difficult to see that the positive cone condition implies condition (16), and actually condition (16) is easier to verify because it does not require looking at every possible subset of columns.
A simple model in which diagonal dominance holds is when the columns of X are orthonormal, because then XTX = I. But the diagonal dominance condition (16) certainly holds outside the orthonormal design case. We finish this section by giving two such examples below.
-
Equi-correlation model: suppose that ‖xj‖2 = 1 for all j = 1,…,p, and for all j≠k. Then the inverse of XTX is
where 1 ∊ ℝp is the vector of all 1s. This is diagonally dominant as long as τ ≥ 0.
-
Haar basis model: suppose that
(20) the lower triangular matrix of 1s. Then (XTX)−1 is diagonally dominant. This arises, for example, in the one-dimensional fused lasso where we solve
If we transform this problem to the parameters α1 = 1 and αi = βi − βi−1 for i = 2,…,N, then we obtain a lasso with design X as in eqaution (20).
4. Strong rules for the elastic net
In the elastic net (Zou and Hastie, 2005) we solve the problem
| (21) |
(This is the original form of the ‘naive’ elastic net that was proposed in Zou and Hastie (2005), with additional the factors of , just for notational convenience.) Letting
we can rewrite problem (21) as
| (22) |
In this (standard lasso) form we can apply SAFE and strong rules to discard predictors. Note that , and ‖ỹ‖2 = ‖y‖2. Hence the basic SAFE rule for discarding predictor j is
The glmnet package uses the parameterization (αλ, (1 − α)λ) instead of (λ1, λ2) With this parameterization the basic SAFE rule has the form
| (23) |
The strong screening rules have a simple form under the glmnet parameterization for the elastic net. The basic strong rule for discarding predictor j is
| (24) |
while the sequential strong rule is
| (25) |
Fig. 7 shows results for the elastic net with standard independent Gaussian data with N = 100 and p= 1000, for three values of α. There were no violations in any of these figures, i.e. no predictor was discarded that had a non-zero coefficient at the actual solution. Again we see that the strong sequential rule performs extremely well, leaving only a small number of excess predictors at each stage.
Fig. 7.
Elastic net: results for the different screening rules (23), (24) and (25) for three different values of the mixing parameter α (a) 0.1, (b) 0.5 and (c) 0.9 (1, SAFE rule; 2, strong global rule; 3, strong sequential rule); in the plots, we are fitting along a path of decreasing λ values and the plots show the number of predictors left after screening at each stage; the proportion of variance explained by the model is shown along the top of the plots; there were no violations of any of the rules in the three scenarios
5. Strong rules for logistic regression
In this setting, we have a binary response yi ∊ {0,1} and we assume the logistic model
Letting pi = Pr(Y = 1|xi), we seek the coefficient vector β̂ that minimizes the penalized (negative) log-likelihood,
| (26) |
(We typically do not penalize the intercept β̂0.) El Ghaoui et al. (2010) derived a SAFE rule for discarding predictors in this problem, based on the inner products between y and each predictor, and derived by using similar arguments to those given in the Gaussian case.
Here we investigate the analogue of the strong rules (5) and (6). The KKT conditions for problem (26) are
| (27) |
where γj is the jth component of the subgradient of ‖β̂‖1, the same as in expression (9). Immediately we can see the similarity between expressions (8) and (9). Now we define , and again we assume condition (10). This leads to the basic strong rule, which discards predictor j if
| (28) |
where p̄ = 1ȳ and . It also leads to the sequential strong rule, which starts with the fit p{β̂0(λk−1), β(λk−1} at λk−1, and discards predictor j if
| (29) |
Fig. 8 shows the result of applying these rules to the newsgroup document classification problem (Lang, 1995). We used the training that was set cultured from these data by Koh et al. (2007). The response is binary and indicates a subclass of topics; the predictors are binary and indicate the presence of particular trigram sequences. The predictor matrix has 0:05% non-zero values. Results are shown for the basic strong rule (28) and the sequential strong rule (29). We could not compute the basic SAFE rule for penalized logistic regression for this example, as this had a very long computation time, using our R language implementation. But in smaller examples it performed much like the basic SAFE rule in the Gaussian case. Again we see that the sequential strong rule (29), after computing the inner product of the residuals with all predictors at each stage, allows us to discard the vast majority of the predictors before fitting. There were no violations of either rule in this example.
Fig. 8.
Penalized logistic regression: results for newsgroup example, using the basic strong rule (28) (1) and the strong sequential strong rule (29) (2) (-------, 1–1 line, drawn on the log-scale)
Some approaches to penalized logistic regression such as the glmnet package use a weighted least squares iteration within a Newton step. For these algorithms, an alternative approach to discarding predictors would be to apply one of the Gaussian rules within the weighted least squares iteration. However, we have found rule (29) to be more effective for glmnet.
Finally, it is interesting to note a connection to the work of Wu et al. (2009), who used to screen predictors (single nucleotide polymorphisms in genomewide association studies, where the number of variables can exceed a million. Since they only expected models with say k≤15 terms, they selected a small multiple, say 10k, of single nucleotide polymorphisms and computed the lasso solution path to k terms. All the screened single nucleotide polymorphisms could then be checked for violations to verify that the solution found was global.
6. Strong rules for general problems
Suppose that we are interested in a convex problem of the form
| (30) |
Here f is a convex and differentiable function, and β = (β1, β2,…,βr) with each βj being a scalar or a vector. Also λ ≥ 0, and cj ≥ 0, pj ≥ 1 for each j=1,…,r. The KKT conditions for problem (30) are
| (31) |
where ∇jf(β̂)= (∂f(β̂)/∂βj1,…,∂f(β̂)/∂(βjm) if βj = (βj1,…,βjm) (and is simply the jth partial derivative if βj is a scalar). Above, θj is a subgradient of ‖βj‖pj and satisfies ‖θj‖qj ≤ 1, where 1/pj+ 1/qj= 1. In other words, ‖·‖pj and ‖·‖qj are dual norms. Furthermore, ‖θj‖qj < 1 implies that β̂j = 0.
The strong rules can be derived by starting with the assumption that each ∇jf{β̂(λ)} is a Lipschitz function of λ with respect to the lqj-norm, i.e.
| (32) |
Now the sequential strong rule can be derived just as before: suppose that we know the solution β̂(λk−1) at λk−1 and are interested in discarding predictors for the optimization problem (30) at λk < λk−1 Observe that for each j, by the triangle inequality,
| (33) |
the second line following from assumption (32). The sequential strong rule for discarding predictor j is therefore
| (34) |
Why?: using inequality (33), the above inequality implies that
hence ‖θj‖qj < 1, and β̂j = 0. The basic strong rule follows from inequality (34) by taking λk−1 = λmax =maxi{‖∇if(0)‖qi/ci}, the smallest value of the tuning parameter for which the solution is exactly 0.
Rule (34) has many potential applications. For example, in the graphical lasso for sparse inverse covariance estimation (Friedman et al., 2007), we observe N multivariate normal observations of dimension p, with mean 0 and covariance Σ. Let S be the observed empirical covariance matrix, and Θ = Σ−1. The problem is to minimize the penalized (negative) log-likelihood over non-negative definite matrices Θ,
| (35) |
The penalty ‖Θ‖1 sums the absolute values of the entries of Θ; we assume that the diagonal is not penalized. The KKT conditions for equation (35) can be written in matrix form as
| (36) |
where Γij is the (i, j) th component of the subgradient of ‖Θ‖1. Depending on how we choose to make conditions (36) fit into the general KKT conditions framework (31), we can obtain different sequential strong rules from rule (34). For example, by treating everything elementwise we obtain the rule |Sij − Σ̂ij(λk−1)| < 2λk – λk−1, and this would be useful for an optimization method that operates elementwise. However, the graphical lasso algorithm proceeds in a block-wise fashion, optimizing over one whole row and column at a time. In this case, it is more effective to discard entire rows and columns at once. For a row i, let s12, σ12 and Γ12 denote Si,−i, Σi,−i and Γi,−i respectively. Then the KKT conditions for one row can be written as
| (37) |
Now given two values λk <λk−1, and the solution Σ̂(λk−1) at λk−1,wehave the sequential strong rule
| (38) |
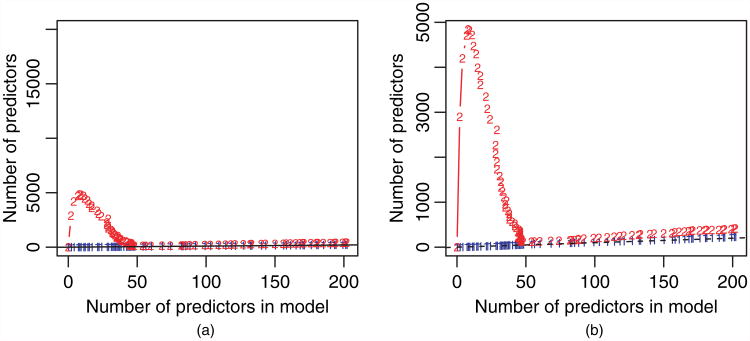
If this rule is satisfied, then we discard the entire ith row and column of Θ, and hence set them to 0 (but retain the ith diagonal element). Fig. 9 shows an example with N =100 and p=300, and standard independent Gaussian variates. No violations of the rule occurred.
Fig. 9.
Graphical lasso: results for applying the basic (1) and sequential strong rule (38) (2) (
 , unit slopeline for reference)
, unit slopeline for reference)
A better screening rule for the graphical lasso was found by Witten and Friedman (2011), after this paper had been completed. It has the simple form
| (39) |
In other words, we discard a row and column if all elements in that row and column are less than λ. This simple rule is safe: it never discards predictors erroneously.
As another example, the group lasso (Yuan and Lin, 2006) solves the optimization problem
| (40) |
where Xg is the N ×ng data matrix for the gth group. The KKT conditions for problem (40) are
where θg is a subgradient of ‖βg‖2. Hence, given the solution β̂(λk−1 )at λk−1, and considering a tuning parameter value λk< λk−1, the sequential strong rule discards the gth group of coefficients entirely (i.e. it sets βg(λk)=0) if
7. Implementation and numerical studies
The strong sequential rule (34) can be used to provide potential speed improvements in convex optimization problems. Generically, given a solution β̂(λ0) and considering a new value λ<λ0, let
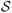 (λ0) be the indices of the predictors that survive the screening rule (34): we call this the strong set. Denote by ε the eligible set of predictors. Then a useful strategy would be as follows.
(λ0) be the indices of the predictors that survive the screening rule (34): we call this the strong set. Denote by ε the eligible set of predictors. Then a useful strategy would be as follows.
Set ε =
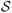 (λ).
(λ).Solve the problem at value λ by using only the predictors in ε.
Check the KKT conditions at this solution for all predictors. If there are no violations, we are done. Otherwise add the predictors that violate the KKT conditions to the set ε, and repeat steps (b) and (c).
Depending on how the optimization is done in step (b), this could be quite effective.
First we consider a generalized gradient procedure for fitting the lasso. The basic iteration is
where Stλ(x) = sgn(x)(|x|− tλ)+ is the soft threshold operator, and t is a step size. When p>N, the strong rule reduces the Np operations per iteration to approximately N2. As an example, we applied the generalized gradient algorithm with approximate backtracking to the lasso with N = 100, over a path of 100 values of λ spanning the entire relevant range. The results in Table 2 show the potential for a significant speed up.
Table 2. Timings for the generalized gradient procedure for solving the lasso (Gaussian case)†.
| p | Time (s) without strong rule | Time (s) with strong rule |
|---|---|---|
| 200 | 10.37 (0.38) | 5.50 (0.26) |
| 500 | 23.21 (0.69) | 7.38 (0.28) |
| 1000 | 43.34 (0.85) | 8.94 (0.22) |
| 2000 | 88.58 (2.73) | 12.02 (0.39) |
N =100 samples are generated in each case, with all entries N(0,1) and no signal (regression coefficients are 0). A path of 100 λ-values is used, spanning the entire operating range. Values shown are the mean and standard deviation of the mean, over 20 simulations. The times are somewhat large, because the programs were written in the R language, which is much slower than C or Fortran. However the relative timings are informative.
Next we consider the
glmnet procedure, in which co-ordinate descent is used, with warm starts over a grid of decreasing values of λ. In addition, an ‘ever-active’ set of predictors
 (λ) is maintained, consisting of the indices of all predictors that have had a non-zero coefficient for some λ′ greater than the current value λ under consideration. The solution is first found for this set; then the KKT conditions are checked for all predictors. If there are no violations, then we have the solution at λ; otherwise we add the violators into the active set and repeat.
(λ) is maintained, consisting of the indices of all predictors that have had a non-zero coefficient for some λ′ greater than the current value λ under consideration. The solution is first found for this set; then the KKT conditions are checked for all predictors. If there are no violations, then we have the solution at λ; otherwise we add the violators into the active set and repeat.
The existing
glmnet strategy and the strategy that was outlined above are very similar, with one using the ever-active set
 (λ) and the other using the strong set
(λ) and the other using the strong set
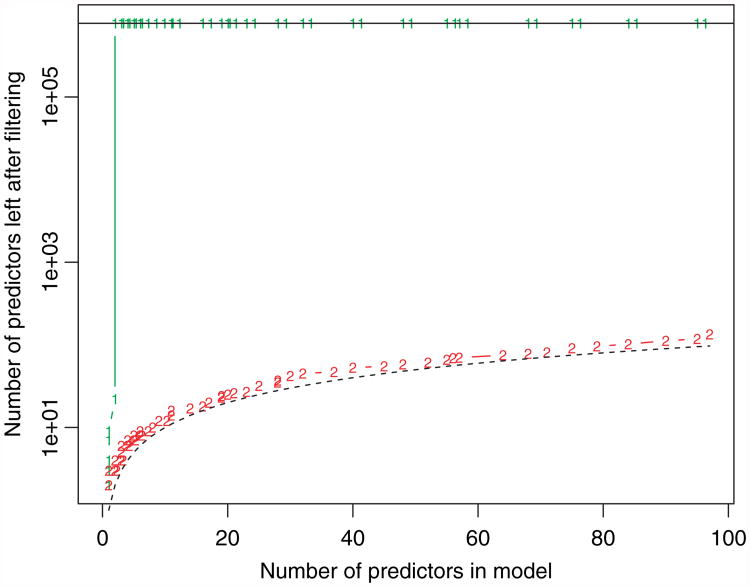
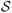 (λ). Fig. 10 shows the active and strong sets for an example. Although the strong rule greatly reduces the total number of predictors, it contains more predictors than the ever-active set; accordingly, the ever-active set incorrectly excludes predictors more often than does the strong set. This effect is due to the high correlation between features and the fact that the signal variables have coefficients of the same sign. It also occurs with logistic regression with lower correlations, say 0.2.
(λ). Fig. 10 shows the active and strong sets for an example. Although the strong rule greatly reduces the total number of predictors, it contains more predictors than the ever-active set; accordingly, the ever-active set incorrectly excludes predictors more often than does the strong set. This effect is due to the high correlation between features and the fact that the signal variables have coefficients of the same sign. It also occurs with logistic regression with lower correlations, say 0.2.
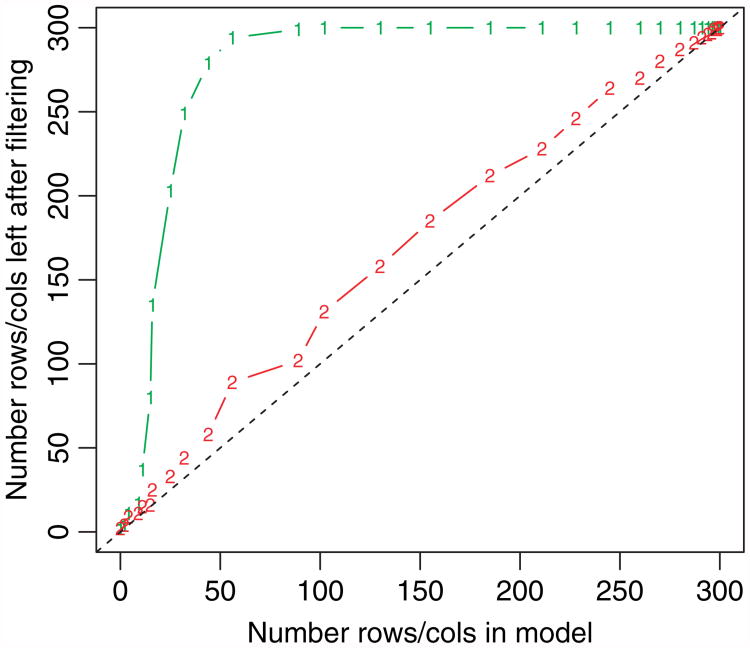
Fig. 10.
Gaussian lasso setting, N = 200, p =20000, pairwise correlation between features of 0.7 (the first 50 predictors have positive, decreasing coefficients): Shown are the number of predictors left after applying the strong sequential rule (6)(2) and the number that have ever been active (1) (i.e. had a non-zero coefficient in the solution) for values of λ larger than the current value (
 , unit slope line for reference); (b) is a zoomed version of the full scale plot (a)
, unit slope line for reference); (b) is a zoomed version of the full scale plot (a)
In light of this, we find that using both
 (λ) and
(λ) and
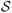 (λ) can be advantageous. For glmnet we adopt the following combined strategy.
(λ) can be advantageous. For glmnet we adopt the following combined strategy.
Set ε =
 (λ)
(λ)Solve the problem at value λ by using only the predictors in ε.
Check the KKT conditions at this solution for all predictors in
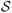 (λ). If there are vilations, add these predictors into ε, and go back to step (a) using the current solution as a warm start.
(λ). If there are vilations, add these predictors into ε, and go back to step (a) using the current solution as a warm start.Check the KKT conditions for all predictors. If there are no violations, we are done. Otherwise add these violators into
 (λ), recompute
(λ), recompute
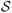 (λ) and go back to step (a) using the current solution as a warm start.
(λ) and go back to step (a) using the current solution as a warm start.
Note that violations in step (c) are fairly common, whereas those in step (d) are rare. Hence the fact that the size of
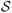 (λ) is very much less than p makes this an effective strategy.
(λ) is very much less than p makes this an effective strategy.
We implemented this strategy and compare it with the standard glmnet algorithm in a variety of problems, shown in Tables 3 and 4. We see that the new strategy offers a speed-up factor of 20 or more in some cases and never seems to slow the computations substantially.
Table 3. glmnet timings for the data sets of Table 1.
| Data set | N | p | Model | Time (s) without strong rule | Time (s) with strong rule |
|---|---|---|---|---|---|
| Arcene | 100 | 10000 | Gaussian | 0.32 | 0.25 |
| Binomial | 0.84 | 0.31 | |||
| Gisette | 6000 | 5000 | Gaussian | 129.88 | 132.38 |
| Binomial | 70.91 | 69.72 | |||
| Dorothea | 800 | 100000 | Gaussian | 24.58 | 11.14 |
| Binomial | 55.00 | 11.39 | |||
| Golub | 38 | 7129 | Gaussian | 0.09 | 0.08 |
| Binomial | 0.23 | 0.35 |
Table 4. glmnet timings for fitting a lasso problem in various settings†.
| Setting | Correlation | Time (s) without strong rule | Time (s) with strong rule |
|---|---|---|---|
| Gaussian | 0 | 0.99 (0.02) | 1.04 (0.02) |
| 0.4 | 2.87 (0.08) | 1.29 (0.01) | |
| Binomial | 0 | 3.04 (0.11) | 1.24 (0.01) |
| 0.4 | 3.25 (0.12) | 1.23 (0.02) | |
| Cox | 0 | 178.74 (5.97) | 7.90 (0.13) |
| 0.4 | 120.32 (3.61) | 8.09 (0.19) | |
| Poisson | 0 | 142.10 (6.67) | 4.19 (0.17) |
| 0.4 | 74.20 (3.10) | 1.74 (0.07) |
There are p=20000 predictors and N =200 observations. Values shown are the mean and standard error of the mean over 20 simulations. For the Gaussian model the data were generated as standard Gaussian with pairwise correlation 0 or 0.4, and the first 20 regression coefficients equalled to 20, 19,…,1 (the rest being 0). Gaussian noise was added to the linear predictor so that the signal-to-noise ratio was about 3.0. For the logistic model, the outcome variable y was generated as above, and then transformed to {sgn(y) + 1}/2. For the survival model, the survival time was taken to be the outcome y from the Gaussian model above and all observations were considered to be uncensored.
The strong sequential rules also have the potential for space savings. With a large data set, one could compute the inner products with the residual off line to determine the strong set of predictors, and then carry out the intensive optimization steps in memory by using just this subset of the predictors.
The newest versions of the glmnet package, available on the Comprehensive R Archive Network, incorporate the strong rules that were discussed in this paper. In addition, R language scripts for the examples in this paper will be made freely available from http://www-stat.stanford.edu/∼tibs/strong.
8. Discussion
The global strong rule (3) and especially the sequential strong rule (4) are extremely useful heuristics for discarding predictors in lasso-type problems. In this paper we have shown how to combine these rules with simple checks of the KKT conditions to ensure that the exact solution to the convex problem is delivered, while providing a substantial reduction in computation time. We have also derived more general forms of these rules for logistic regression, the elastic net, group lasso graphical lasso and general p-norm regularization. In future work it would be important to understand why these rules work so well (rarely make errors) when p≫N.
Acknowledgments
We thank Stephen Boyd for his comments, and Laurent El Ghaoui and his co-authors for sharing their paper with us before publication and for their helpful feedback on their work. We also thank the referees and editors for constructive suggestions that substantially improved this work. Robert Tibshirani was supported by National Science Foundation grant DMS-9971405 and National Institutes of Health contract N01-HV-28183. Jonathan Taylor and Ryan Tibshirani were supported by National Science Foundation grant DMS-0906801.
Appendix A: Derivation of the SAFE rule
The basic SAFE rule of El Ghaoui et al. (2010) for the lasso is defined as follows: fitting at λ, we discard predictor j if
| (41) |
where is the smallest λ for which all coefficients are 0. El Ghaoui et al. (2010) derived this bound by looking at a dual of the lasso problem (1). This dual has the following form. Let . Then the dual problem is
| (42) |
The relationship between the primal and dual solutions is θ̂ = Xβ̂ − y, and
| (43) |
for each j=1,…,p.
Here is the argument that leads to condition (41). Suppose that we have a dual feasible point θ0, i.e. for j=1,2,…,p. Below we discuss specific choices for θ0. Let γ = G(θ0) Hence γ represents a lower bound for the value of G at the solution θ̂. Therefore we can add the constraint G(θ)≥ γ to the dual problem (42) and problem is changed. Then, for each predictor j, we find
| (44) |
If mj < λ (note the strict inequality), then we know that at the solution , which implies that β̂ = 0 by expression (43). In other words, if the inner product never reaches the level λ over the feasible set G(θ)≥ γ, then the coefficient β̂j must equal 0.
Now, for a given lower bound γ, problem (44) can be solved explicitly, and this gives . Then the rule mj < λ is equivalent to
| (45) |
To make this usable in practice, we need to find a dual feasible point θ0 and substitute the resulting lower bound γ = G(θ0) into expression (45). A simple dual feasible point is θ0 = y λ/λ max and this yields ; substituting into expression (45) gives the basic SAFE rule (41).
A better feasible point θ0 (i.e. giving a higher lower bound) will yield a rule in expression (45) that discards more predictors. For example, the recursive SAFE rule starts with a solution β̂(λ0) for some λ0 >λ and the corresponding dual point θ0 =X β̂(λ0)−y. Then θ0 is scaled by the factor λ/λ0 to make it dual feasible and this leads to the recursive SAFE rule of the form
| (46) |
where c is a function of y, λ, λ0 and θ0. Although the recursive SAFE rule has the same flavour as the sequential strong rule, it is interesting that it involves the inner products rather than , with r being the residual y−X β̂(λ0). Perhaps as a result, it discards far fewer predictors than the sequential strong rule.
References
- Candes EJ, Plan Y. Near-ideal model selection by l1 minimization. Ann Statist. 2009;37:2145–2177. [Google Scholar]
- Chen S, Donoho D, Saunders M. Atomic decomposition for basis pursuit. SIAM J Scient Comput. 1998;20:33–61. [Google Scholar]
- Efron B, Hastie T, Johnstone I, Tibshirani R. Least angle regression. Ann Statist. 2004;32:407–499. [Google Scholar]
- El Ghaoui L, Viallon V, Rabbani T. Technical Report UC/EECS-2010-126. EECS Deptartment, University of California at Berkeley; Berkeley: 2010. Safe feature elimination in sparse supervised learning. [Google Scholar]
- El Ghaoui L, Viallon V, Rabbani T. Safe feature elimination for the lasso and sparse supervised learning. 2011 To be published. [Google Scholar]
- Fan J, Lv J. Sure independence screening for ultrahigh dimensional feature space (with discussion) J R Statist Soc B. 2008;70:849–911. doi: 10.1111/j.1467-9868.2008.00674.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J, Hastie T, Hoefling H, Tibshirani R. Pathwise coordinate optimization. Ann Appl Statist. 2007;2:302–332. [Google Scholar]
- Fuchs J. Recovery of exact sparse representations in the presense of noise. IEEE Trans Inform Theor. 2005;51:3601–3608. [Google Scholar]
- Koh K, Kim SJ, Boyd S. An interior-point method for large-scale l1-regularized logistic regression. J Mach Learn Res. 2007;8:1519–1555. [Google Scholar]
- Lang K. Newsweeder: learning to filter netnews. Proc 21st Int Conf Machine Learning. 1995:331–339. Available from http://www-stat.stanford.edu/hastie/glmnet.
- Meinhausen N, Buhlmann P. High-dimensional graphs and variable selection with the lasso. Ann Statist. 2006;34:1436–1462. [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. J R Statist Soc B. 1996;58:267–288. [Google Scholar]
- Tibshirani R, Taylor J. The solution path of the generalized lasso. Ann Statist. 2011;39:1335–1371. [Google Scholar]
- Tropp J. Just relax: convex programming methods for identifying sparse signals in noise. IEEE Trans Inform Theor. 2006;3:1030–1051. [Google Scholar]
- Wainwright MJ. Sharp thresholds for high-dimensional and noisy sparsity recovery using l1-constrained quadratic programming (lasso) IEEE Trans Inform Theor. 2009;55:2183–2202. [Google Scholar]
- Witten D, Friedman J. A fast screening rule for the graphical lasso. J Computnl Graph Statist. 2011 to be published. [Google Scholar]
- Wu TT, Chen YF, Hastie T, Sobel E, Lange K. Genomewide association analysis by lasso penalized logistic regression. Bioinformatics. 2009;25:714–721. doi: 10.1093/bioinformatics/btp041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. J R Statist Soc B. 2006;68:49–67. [Google Scholar]
- Zhao P, Yu B. On model selection consistency of the lasso. J Mach Learn Res. 2006;7:2541–2563. [Google Scholar]
- Zou H, Hastie T. Regularization and variable selection via the elastic net. J R Statist Soc B. 2005;67:301–320. [Google Scholar]