Abstract
The functional magnetic resonance (fMRI) baseline is known to drift over the course of an experiment and is often attributed to hardware instability. These ultraslow fMRI fluctuations are inseparable from blood oxygenation level dependent (BOLD) changes in standard single echo fMRI and they are therefore typically removed before further analysis in both resting-state and task paradigms. However, some part of these fluctuations may be of neuronal origin, as neural activity can indeed fluctuate at the scale of several minutes or even longer, such as after the administration of drugs or during the ultradian rhythms. Here, we show that it is possible to separate the slow BOLD and non-BOLD drifts automatically using multi-echo fMRI and multi-echo independent components analysis (ME-ICA) denoising by demonstrating the detection of a visual signal evoked from a flickering checkerboard with slowly changing contrast.
Keywords: fMRI, Multi-echo, Denoising, Slow drift, Non-BOLD, BOLD
Introduction
The functional magnetic resonance imaging (fMRI) baseline is known to drift over the course of an experiment (Aguirre et al., 1997; Zarahn et al., 1997). These drifts are nonlinear, vary by voxel, and are difficult to distinguish from slow changes in brain response to pharmaceutical drugs (Wise et al., 2004) or spontaneous fluctuations in the resting state (Biswal et al., 1995). They are attributed to scanner instability (Smith et al., 1999), pooling of blood in veins (Lee et al., 1995), subject motion and incomplete motion correction (Bandettini et al., 1993), and brain physiology changes (Yan et al., 2009). In standard single echo blood oxygen level dependent (BOLD) fMRI, the non-BOLD drifts are inseparable from the data making the detection of slow BOLD related change difficult. We show that it is possible to do this with multi-echo (ME) fMRI.
Common approaches to remove drift in preprocessing of single echo fMRI data have involved using linear, low-order polynomial or spline models (Bandettini et al., 1993; Liu et al., 2001; Kay et al., 2008), high pass filtering (Lund et al., 2006), or ICA component removal (Thomas et al., 2002). Improper modeling and removal of drifts affects the sensitivity of the statistical results (Lowe and Russell, 1999) and also limits the task or frequencies which can be measured in these experiments. For task paradigms the strategy has been to use box-car and repetitive event designs using frequencies that exceed scanner drift frequencies (Birn et al., 2002). For resting state scans, the data are typically band-pass filtered to remove frequencies that are deemed unlikely to be functionally relevant (Cordes et al., 2001). However, these approaches do not work in the case of an experiment that has only one transition (e.g. bolus injection of a drug) or very slow changes (sleep, circadian rhythms, transcranial magnetic stimulation (TMS)). In these cases it is particularly important to properly model the baseline changes in order to accurately measure the desired BOLD responses, which is complicated by long run lengths and potentially coupled subject motion.
There are several dual-echo techniques that have been proposed that attempt to capture baseline drift in a very short echo acquired in the space before the standard echo (Talagala et al., 1999; Bright and Murphy, 2013; Ing and Schwarzbauer, 2012). However, there will always be some BOLD weighting in the measured short echo time series due to the long acquisition window required to obtain the images, which increases the effective echo time (TE). Speck and Hennig (1998) used an eight echo acquisition to simultaneously map both and spin density or inflow effects over a few slices in the brain. The ability to calculate both of these parameters at every time point comes at the cost of reduced brain coverage and increased repetition time due to the large number of echoes required to obtain good simultaneous parameter estimates. This makes the method difficult to extend to cognitive studies, which typically require whole brain coverage. An alternate MRI functional imaging technique that intrinsically measures a quantitative baseline is arterial spin labeling (ASL) (Aguirre and Detre, 2012). ASL time series do not exhibit signal drifts owing to the subtraction of the control and tag images to generate flow images. Wang et al. (2003) demonstrated the benefits of using ASL for long task block lengths and runs separated in time by over 2 min in length. Notably, the BOLD data in this study was high-pass filtered and inherently limited their ability to detect the longer block tasks. However, the reduced coverage, slower measurement times, and lower signal-to-noise ratio (SNR) of ASL, as compared to BOLD fMRI, remain problematic for applications to many studies (Wang et al., 2011). Furthermore, the insensitivity of ASL to slow motion and drifts is at the expense of enhanced motion sensitivity to short-term motion on the time scale of the TR arising from the pairwise image subtractions.
Improvements in imaging acquisition have made it possible to trade high resolution single echo images for coarser resolution at multiple echo times per repetition with minimal sacrifice in repetition time (TR) and spatial coverage for fMRI (TEs: 14,30, 46 ms, 2 s TR, 28 slices with cubic resolution of 3.5 mm, for example). Multi-echo acquisition enables the measurement of TE-dependence of the signal (Peltier and Noll, 2002) but is still more frequently used in quantitative T2* measurements than in fMRI (Gowland and Bowtell, 2007). In the context of fMRI, the acquired echoes are typically combined to improve the overall image SNR and recover signal dropout (Posse et al., 1999; Poser et al., 2006). The recently developed multi-echo independent components analysis (ME-ICA) denoising method (Kundu et al., 2013) uses TE-dependence throughout the analysis pipeline to separate the data into primarily BOLD and non-BOLD subspaces in an automatic, data driven way that is based on the principles of BOLD contrast. ME-ICA differs from other automated ICA component selection methods in that no restrictions are placed on the time-frequency or anatomical localization characteristics of the components in the selection process. Therefore, it has the potential to separate artifactual, hardware-related drifts, which would fall into the non-BOLD subspace, from hemodynamic signal changes that are likely of neuronal relevance. Importantly, this enables study of low-frequency BOLD components that would ordinarily be discarded in the band-pass filtering step that is conventionally applied during preprocessing.
In this study, we use a visual task with slowly changing contrast over 5 min as an example of a slow BOLD change and we compare conventional preprocessing to ME-ICA denoising. As well, we investigate the temporal, amplitude properties of the time series and the sensitivity of the methods in differentiating two slow slope changes. We demonstrate the ability to separate the sigmoid task response from baseline drifts using ME-ICA denoising in a case where the task is undetectable in conventionally preprocessed data.
Methods
Subjects
Fifteen healthy volunteers (aged 21–39, 8 males) participated in this study. Informed consent was obtained for each subject in accordance with the Combined Neuroscience Institutional Review Board of the National Institutes of Health. Subjects were instructed to remain awake, lie still and fixate on the cross in the center of the screen during all visual tasks. The entire experiment had a duration of an hour and a half of imaging, which consisted of one anatomical and seven functional scans.
MR Image acquisition
Scanning was performed on a 3T Skyra (Siemens GmBH, Germany) using a 32 channel head coil. A whole brain 3D T1 MPRAGE anatomical scan was performed with a cubic resolution of 1 mm (TR: 2.5 s, TI: 1.1 s, TE: 5.4 ms, flip angle: 7°), matrix 256 × 256 × 256, field-of-view 25.6 cm, 6 min, followed by a 10 minute resting state scan and 7.5 minute multi-echo EPI fMRI visual tasks with scan parameters of TE: 13, 30, 43 ms, TR: 2 s, at a cubic resolution of 3.5 mm with GRAPPA acceleration factor 2 over 28 slices covering the whole brain (flip angle 90°, matrix 64 × 64, field-of-view 22.4 cm, interleaved slice acquisition). Four dummy scans preceded each run to ensure steady-state equilibration for the saved data. Respiratory and cardiac traces were recorded using respiratory bellows and pulse oximeter with AcqKnowledge software (BIOPAC Systems Inc., Goleta, CA).
Visual contrast tasks
The visual stimuli consisted of a full visual field checkerboard reversing from black to white at a rate of 7.5 Hz. The timing and amplitude of the stimuli are illustrated in Fig. 1 and consist of a) a contrast localization run with 15 s blocks of one of four different contrast levels: 2.5%, 5%, 20%, and 100%, alternating with a fixation cross (0% contrast), there are a total of 16 contrast blocks or four repetitions of each contrast b) a long block of 80 s at 20% contrast followed by 80 s of fixation (0% contrast) c) a long block of 80 s at 5% contrast followed by 80 s of fixation d) a shorter block of 60 s at 20% contrast followed by 100 s of fixation e) a sigmoid ramp (at slope of −1/40) from 20% to 0% contrast over the course of 2 min and f) a sigmoid ramp (at a slope of −1/60) from 16% to 0% contrast transition over the course of 5 min. Instructions to fixate on the cross in the middle of the checkerboard were reiterated between scans to ensure the subject remained awake and on task for the duration of the experiment. The flanking pairs of 15 s blocks at 80% in each task served as an embedded vigilance check for task compliance and are not explicitly considered further.
Fig. 1.
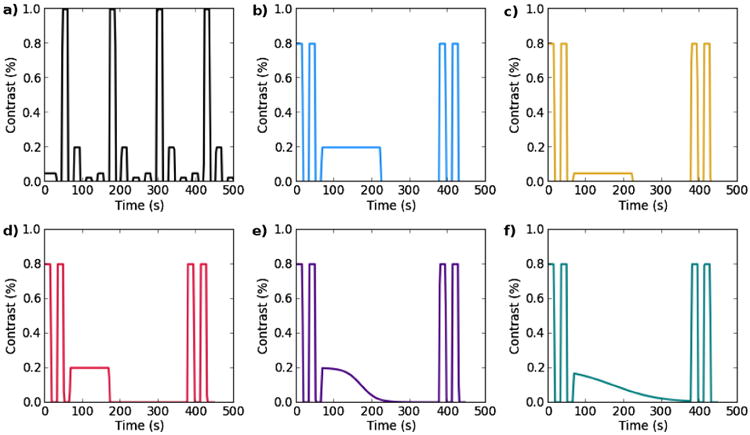
Tasks. a) contrast localizer block task b) long 20% contrast block c) 5% contrast block d) short 20% contrast block, e and f) sigmoid ramp tasks.
Preprocessing
Processing of the fMRI data was performed using AFNI (Cox, 1996), compile date: 17 Dec, 2013. Each echo was pre-processed separately as described below prior to ME-ICA denoising.
Single echo
The anatomical image was first skull-stripped and then warped to Talairach coordinates (auto_tlrc, TT_N27 template). The anatomical image was then registered to the first frame of the middle echo (30 ms) data and 12 parameter affine coregistration was computed using the local Pearson correlation (LPC) cost function (Saad et al., 2009) with the gray matter segment of the EPI base image (3dSeg) as the LPC weight mask. Motion correction (3dvolreg) for all echoes was performed using the first frame of the middle echo as reference. The estimated six-parameter rigid body motion parameters were combined with the anatomical-functional coregistration parameters into a single alignment matrix. The images from each TE were slice-time corrected (3dTshift) and subsequently simultaneously motion corrected and spatially aligned (3dvolreg) using the combined alignment matrix.
Optimal echo combination
The optimal echo time for imaging the BOLD effect is where TE equals , However, varies across the brain and as such, single echo images are not optimally sensitive to this variation. The acquisition of multiple echoes enables the calculation of an “optimal” weighted average of echoes that recovers signal in drop-out areas and improves contrast-to-noise (CNR) ratio throughout the brain (Posse et al., 1999; Poser et al., 2006). The optimal echo combination (OC) as found in Poser et al. (2006) used here is described below.
The signal at an echo, n, varies as a function of the initial signal intensity So and transverse susceptibility and is given by the mono-exponential decay:
| (1) |
which can be linearized to simplify estimation of and So as the slope and intercept of a line by least squares fitting:
| (2a) |
| (2b) |
The normalized data weighting that maximizes BOLD CNR for a set of N echoes is given by
| (3) |
Where is the transverse relaxation time estimated for each voxel using Eq. (2b) above.
The OC time series are used in the results and in certain steps of the ME-ICA pipeline as described below. The OC time series summed using these weights are more comparable to the denoised data output from the ME-ICA pipeline, which are calculated from the OC data, while being preprocessed the same way as single echo data.
Multi-echo ICA denoising
A summary of the ME-ICA denoising method is found here, for full details please see Kundu et al. (2013).
Theory
TE-dependence analysis determines the BOLD or non-BOLD origin of fMRI signal changes in a component based on how the component's value scales with TE. A component is, for example, a beta weight from general linear model fitting of each echo, or a component from ICA or principal components analysis (PCA).
Estimation of both So and simultaneously from Eq. (1) is noisy (Gowland and Bowtell, 2007), however, for small changes in So and , Eq. (2b) can approximated as
| (4) |
which is specially separable into two sub-models where one depends only on So (Eq. (5a)) and the other only on (Eq. (5b)) as follows:
| (5a) |
or
| (5b) |
These sub-models are separately fit to the data on a voxelwise basis and goodness of fit F-statistic are calculated for each model. Note that precise values of and So cannot be calculated using this approach as some physiological or motion artifacts may produce coupled and So changes (Wu and Li, 2005) but that it is sufficient to classify a signal fluctuation as primarily change and not an So change (Kundu et al., 2012).
The F-statistics generated from the voxelwise fit coefficients can be used together with the normalized voxel (v) component (c) values zc,v to create two summary statistics κ, and ρ representing BOLD, or , and non-BOLD, or So, component weighting respectively, as follows:
| (6) |
| (7) |
where the weighting by attenuates the effect of random fit error in brain regions where the component is not prominent. Values of the exponent p > 2 generate similar results (Kundu et al., 2013) and increase weight values of F where the amplitude z is high. In this model it is expected that high κ and low ρ indicate a weighted and likely functionally related BOLD component (Kundu et al., 2012).
Components were split into primarily BOLD and non-BOLD sets after sorting based on their values of κ and ρ. Sorted values of κ and ρ produce spectra with clear elbows and a threshold is determined using an elbow finding algorithm. Components with κ above the κ threshold and ρ below the ρ threshold are selected as functionally related “high κ” multi-echo denoised (me-dn) BOLD components, and the remainder are identified as “low ρ” non-BOLD components. Additionally, me-dn BOLD selected components with relatively low ρ but with outlier values of percent variance explained and percent signal change (at the 90th percentile of voxelwise percent signal change) are excluded from the me-dn BOLD set because they localize to the sagittal sinus and draining veins Kundu et al. (2012). The component selection algorithm is designed to be conservative and prevent the incorrect assignment of components containing BOLD signal and as such, imperfect separation is possible.
Implementation
After preprocessing, ME datasets were optimally combined and dimensionally reduced by TE-dependence based principal components analysis (ME-PCA) Kundu et al. (2013). Dimensionality estimation was based on the κ and ρ spectra of the PCA components, which have clear elbows where a threshold can be determined. Components with κ above the κ threshold and ρ below the ρ threshold were kept as were components explaining high variance. The dimensionally reduced ME data were then decomposed with FastICA (implemented in Python MDP) producing a mixing matrix which was variance normalized in the time dimension. This mixing matrix was fit to the (full rank) OC data to compute values of κ and ρ for each component as defined above. The component amplitude maps and time series obtained by regressing the optimally combined ME time series on the full ICA mixing matrix were used as the basis for producing denoised time series. Specifically, multiplying the subset of BOLD high κ component signal amplitude maps with their respective time series produced the me-dn BOLD high κ time series dataset. Similarly, multiplying the subset of low ρ high κ and outlier variance component signal amplitude maps with their respective time series produced the low ρ non-BOLD time series dataset.
Analysis
Individual general linear model analysis with the task regressors defined in Fig. 1 was applied to each of four datasets derived from the preprocessed data above using 3dDeconvolve: single echo data (single) taken as the middle echo of the multi-echo acquisition, OC data, me-dn BOLD, and non-BOLD components resulting from the ME-ICA preprocessing of the multi-echo data. Linear polynomial detrending was used in the regression baseline for the OC and single echo data where indicated. No higher order detrending was applied for the me-dn BOLD or non-BOLD components. Group maps were created for each task type (3dttest).
Results
First, a comparison of the group contrast scaling response in the contrast localizer task is shown for the single echo, OC, and denoised time series. Next, the temporal response to the slow block and ramp tasks is shown illustrating the benefit of using denoised BOLD time series in comparison to conventional preprocessing. Finally, the spatial specificity of the BOLD component response for these tasks is demonstrated along with a comparison of all the tasks.
Contrast localization/response
The contrast localization task is an example of a standard fMRI task design. It is used here to illustrate the equivalence of the results of me-dn BOLD in terms of percent change response with improvements in the resolution of the contrast levels. The group average temporal and amplitude response for each of the contrast levels along with the standard error are shown in the Fig. 2 for me-dn BOLD, non-BOLD, OC, and single-echo data. The timecourse averages were taken over the V1 ROI and across the repetitions of the contrast in the localizer task and then averaged across subject. The me-dn BOLD timecourses clearly show an increase in percent change as a function of contrast, which is reflected in the amplitude plot (part e of the Figure). Both the OC and single-echo also show this same increase and response curves however, the 5% and 20% time series appear very close in amplitude and in fact appear reversed in comparison to the me-dn BOLD components. The median values of the individual peak differences still increase as a function of contrast as indicated in the amplitude boxplots. The me-dn BOLD component timecourses appear to be less noisy as compared to the single echo, some of this is due to the inclusion of the three echoes in combination, as can be seen in the improved profile in the OC panel. The timecourses of the me-dn BOLD components all start from the same intercept value as the jitter is taken up in the non-BOLD components. In the following analyses OC rather than single echo time series will be used because it is more comparable to the me-dn BOLD data.
Fig. 2.
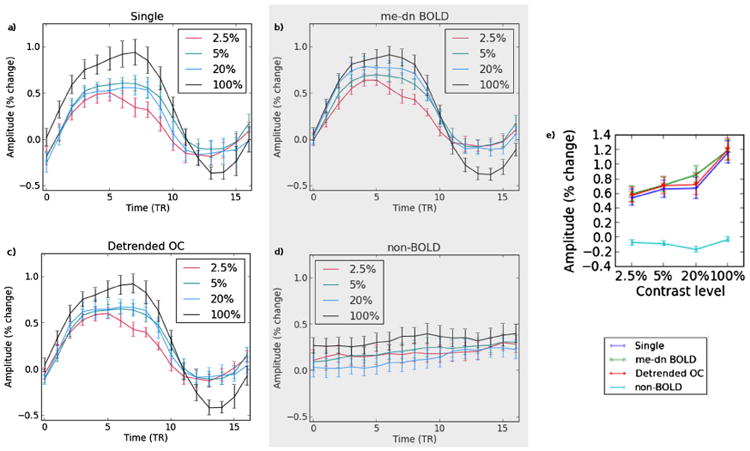
The contrast response curves are shown for a) single echo, b) me-dn BOLD, c) optimally combined (OC), and d) non-BOLD time series for the 2.5%, 5%, 20% and 100% contrast levels. Part e) shows the magnitude of the difference between the maximum and baseline for all time series types.
Temporal response
Fig. 3 contains group average time series over voxels in the visual cortex for the 20% block (left) and ramp (right) contrast tasks for me-dn BOLD component, optimally combined (OC) echo, and non-BOLD time series, the shading is the standard error about the mean (thick line). The visual cortex region of interest (ROI) was identified from a group map (thresholded at p < 0.05 family wise error (FWE)) using the contrast localization task. For the OC time series, the block task response is visible but shows a positive trend, which is removed after detrending. In the ramp task the response is relatively flat with some positive trend that is completely removed after detrending. In the me-dn BOLD time series the response to the block stimulus is clearly visible and there is a plausible negative trend for the ramp task. Note that the shape of the block response differs slightly between the detrended OC and the me-dn BOLD data, particularly in the period after the stimulus. The non-BOLD component time series suggests that the positive trend found in the OC time series is artifactual and obscures the ramp task. The massive averaging, over all the voxels in V1 and over all subjects, of the non-BOLD time series reveals the likely scanner specific trend is mostly linear, but obscures the higher order baseline variations seen on a voxel-wise basis as discussed in A.
Fig. 3.
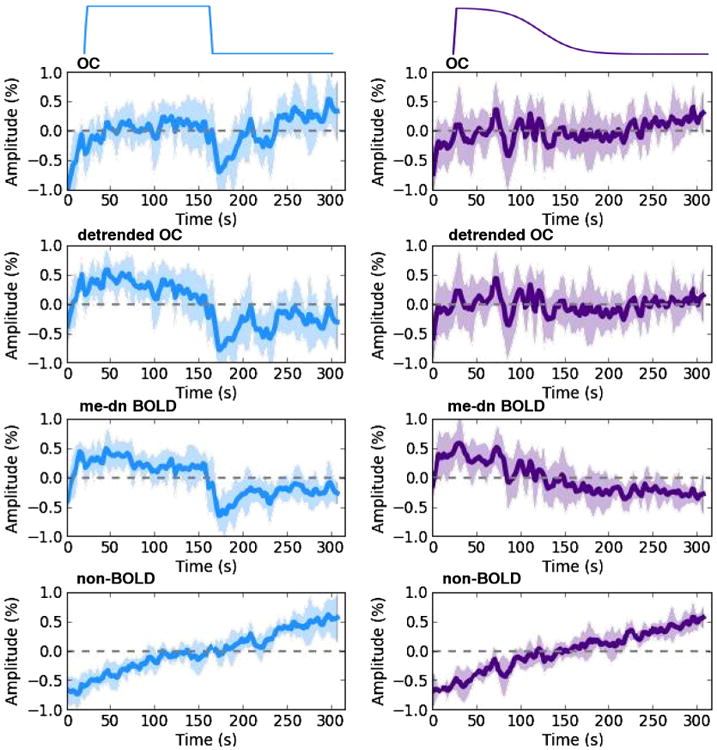
Group average time series taken over voxels in V1 for the 20% block and ramp tasks for the OC, detrended OC, me-dn BOLD, and non-BOLD components where the thick line is the mean and the shading is the standard error, the data are demeaned.
Spatial localization
Each row in Fig. 4 represents a group average of the individual correlation maps over all the subjects for the 20% block (left) and ramp (right) contrast tasks for the OC, detrended, me-dn BOLD components, and non-BOLD component time series. The maps are thresholded at p < 0.05, FWE corrected. Only the task regressor was used in the model to create the individual correlation maps. The me-dn BOLD component maps show clear localization to the visual cortex of the response in both tasks. The OC data show a weak response in the visual cortex which becomes statistically significant after detrending for the block task but not for the ramp task. The non-BOLD component time series shows no supra-threshold voxels, but does show non-specific response pattern at lower thresholds (shown in Supplementary materials).
Fig. 4.
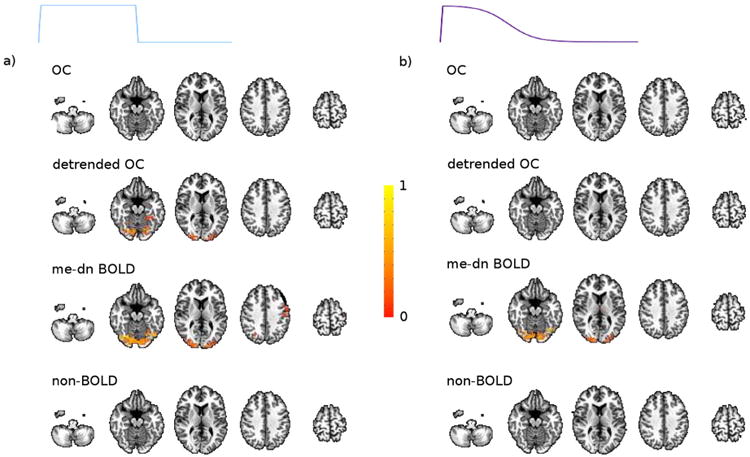
The spatial response to the a) 20% block and b) ramp tasks for the OC, me-dn BOLD, detrended, and non-BOLD time series.
Temporal, amplitude and slope differentiation
Fig. 5 shows group averaged time series over V1 for pairs of tasks to compare the amplitude, temporal, and slope differentiation properties of the OC, detrended, and me-dn BOLD data. Part a) shows the two amplitude (20%, 5%) tasks where the adaptation rate is seen clearly in the denoised data. The percent change amplitude difference taken from the equilibrium segments of this averaged time series show a change of 0.25% for the 20% case and 0.25% for the 5% case in the me-dn data. Part b) of the Figure shows the long and short 20% block tasks with matched adaptation rate and baseline in the denoised data, which is seen in the detrended data with higher variance, but not in the conventional data. Part c) shows the two ramp tasks both with negative trends following the task in the denoised data, which is not reflected in the OC or detrended data. Linear fits to the slopes show the ability to identify the two slope tasks in the me-dn data whereas the slope in the OC is positive. The fits to each slope are insignificantly different from one another. Fitting a line to the detrended time series, yields a zero slope. The slope values for each of the fits and individual voxel counts for both slope tasks are shown in the Supplementary materials.
Fig. 5.
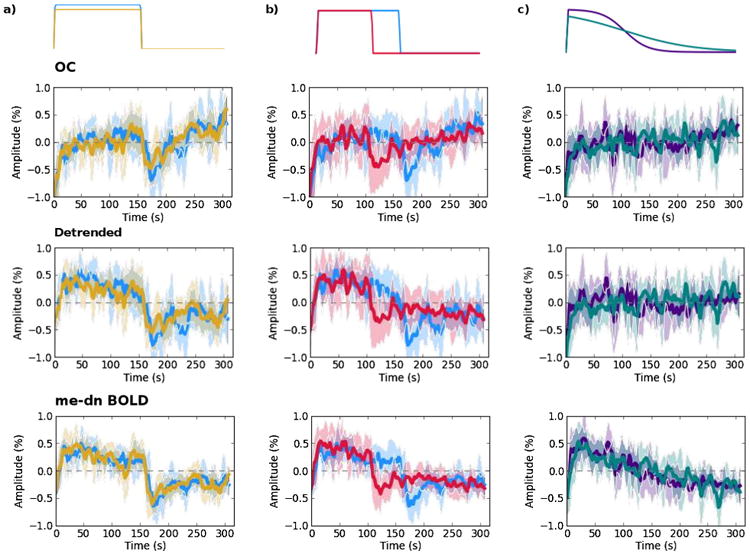
Pairs of tasks are shown for the OC, detrended, and me-dn BOLD time series for comparison a) 20% and 5% blocks b) 20% long and short blocks and c) both ramp tasks.
Discussion
We have shown that ME-ICA denoising of multi-echo fMRI data can directly separate ultraslow BOLD from non-BOLD drifts based on an analysis of TE-dependence. The resulting me-dn dataset contains a faithful temporal representation of the low frequency task and is also spatially localized in the expected visual regions. This denoising process was equally valuable for standard block designs, as exemplified by the contrast localization task, where it ties the blocks to the same baseline and improves the differentiation of contrast levels.
The BOLD signal contrast changes measured in the block design task from all preprocessing methods reflect a comparable monotonic increase with contrast level in V1. These results are in agreement with prior reports of contrast dependent BOLD responses (Chiacchiaretta et al., 2013; Kastner et al., 2004; Tootell et al., 1995). The short duration of the block task with small number of block repeats (15 s × 4 repeats) for each contrast gives this task low contrast to noise ratio and reduces its ability to distinguish between the contrast levels in comparison to other studies. Despite this, the me-dn BOLD data show clearly the expected stratification of amplitude for the contrast levels. In comparison, the optimally combined time series from the same data has almost identical amplitudes for each level except at 20% contrast where there is a substantial dip, which is explained by a dip in the non-BOLD components (Fig. 2e). A separate study using similar contrast levels (Chiacchiaretta et al., 2013) found contrast level stratification using spin echo instead of gradient echo contrast. However, in their results the undershoot was not different between the two image types and here there seems to be a greater undershoot for the 100% contrast block. The larger undershoot in our study could be a function of task duration or due to using interleaved contrast levels in the task rather than a single contrast level per run where the neural demand may reach steady state. We did explicitly randomize contrast block level order for a subset of the subjects to account for this effect, but the order did not make a difference as seen by Kastner et al. (2004).
The contrast adaptation in the long stimulus blocks (Figs. 1b, c) is similar to that found by (Gardner et al., 2005) at similar contrast levels. They used high pass filtering at 0.004 Hz to control for slow drifts which they stated did accentuate the decay at the beginning of their adaption period. The current results do not suffer from such distortion. The lack of amplitude difference between the 20% and 5% contrast levels in the long blocks (see Fig. 5a) is in disagreement with the different amplitude levels found by Gardner et al. (2005). The response difference that was found in the contrast localization task was small (−0.1%) and non-significant but a larger significant difference was found between 20% and 2.5% (see Fig. 2b). One potential explanation for the difference between our experiments and that of others is an absolute calibration difference between the projector contrast levels as viewed in the scanner bore, which we did not explicitly quantify.
The group map for the 20% stimulus block shows what could be a motor response in addition to the visual response in the visual cortex, which is not present in the ramp task (see Fig. 4, row 3 slice 4). This cluster is potentially related to a task correlated effect between checkerboard and fixation conditions. In the ramp task, the checkerboard is constantly there, which may explain the lack of this cluster in this task, which is potentially an argument towards the benefit of slowly varying tasks to reduce task correlated artifacts.
As a new result, we show the ability to differentiate task slopes using me-dn data (see Fig. 5c). Slope responses are also expected from learning tasks, which have not generally been extensively measured using fMRI. In a simultaneous ASL/BOLD experiment using a sequence motor learning task over 20 min, (Olson et al., 2006) showed brain areas with reduction in blood flow correlated with the reduction in response time as the task was learned over the scan. However, they could not find a similar result in their BOLD data, but could find regions involved in error making. For our scanner, the hardware drift in the consolidated non-BOLD components is approximately a 1% change over 5 min (0.003%/s) therefore any task slope responses below this would not be able to be resolved using standard methods.
ASL has previously been shown to have better noise stability across the frequency spectrum than BOLD and to be more sensitive to tasks longer than 60 s blocks (Aguirre et al., 2002; Wang et al., 2003), but here the long block stimulus is easily detected after denoising. Multi-echo fMRI with ME-ICA denoising therefore provides an alternative functional imaging method for these types of task and applications like pharmaceutical fMRI where ASL has been suggested as potential imaging marker of drug action (Wang et al., 2011), but with greater spatial and temporal coverages and sensitivity than ASL. While the non-BOLD components are largely removed in ME-ICA denoising, any BOLD baseline drifts or changes in neurovascular coupling are still not accounted for. This yields an opportunity to more closely study these possibly artifactual BOLD changes in combination with other types of imaging contrasts such as ASL, spin echo, or diffusion weighting. Additionally, a multi-contrast approach would aid in the investigation of the effects of inflow and any changes in intra and extra vascular BOLD weighting that may occur over the echoes on the denoising process.
The tasks used in this study have simple known models, in particular both ramp tasks are effectively linear and have a similar percent change increase to the opposing hardware gradient drift. Arguably, the addition of a period of baseline preceding the task or simply using a more complicated contrast variation pattern would improve detection after linear detrending. In other studies, the exact brain response model will not be known and the detrending model estimate could impact the measured response shape. The use of higher order detrending, more typical of runs of this length, does not improve the results in the detrended data in either the block or ramp tasks and may remove useful or interesting slow BOLD effects.
In this experiment, the expected effects occur over several minutes and should not be affected by local variations in the heart or respiratory rate (Birn et al., 2009). An investigation of the recorded cardiac and respiratory signals indicated that there was not a general slowing of both heart and respiratory rates as the subject relaxes in the scanner, which could have potentially been seen in the BOLD components (see Supplementary materials). The extent to which the denoised BOLD components correlate with the neural signal could be investigated with simultaneous EEG for example. Until it is known how much of the respiratory and cardiac effects remain in the denoised BOLD components it is advisable to continue to record these physiological parameters.
This work provides an important step forward in the detection of low frequency baseline BOLD changes such as those found after the administration of pharmaceuticals, in ultraradian rhythms or learning paradigms. Experiments to measure these changes must be longer than a standard fMRI scan to capture their full characteristics thereby incurring greater amounts of non-BOLD hardware drifts in addition to an increased likelihood of contamination from subject motion.
ME-ICA is a principled approach that can directly separate slowly varying artifacts from the desired BOLD response. It is more stable than methods that simultaneously fit for BOLD and spin density changes at each voxel as it uses aggregated fit statistics over the entire volume. Other ICA methods applied at the individual subject level without the multi-echo acquisition require the use of circular reasoning in the form of prior spatial or temporal assumption to find effects of interest in those same domains. ME-ICA also uses the third domain of TE-dependence for dimensionality estimation, which enables a stable-high dimensional decomposition of the data that does not require high pass pre filtering. Additionally, the component selection process is fully independent of anatomical templates. Both of these features ultimately make the ME-ICA approach straightforward and reliable. Many studies already exist in the literature that could benefit from using this technique as a clean way to separate out BOLD specific signal. The ability of multi-echo fMRI and ME-ICA denoising to remove the non-BOLD baseline opens the possibilities of using novel continuous paradigms and resolve complicated brain responses.
Supplementary Material
Highlights.
Successful separation of slow task signal from slow non-BOLD baseline drifts using ME-ICA
ME-ICA resolves tasks responses more faithfully than standard preprocessing.
ME-ICA enables the study of low-frequency BOLD activity and the use of slower task paradigms.
Appendix A. Baseline drift in a single subject
The time series plots shown above are averaged over all subjects and V1 and smooth out the trends that are seen at the voxel level. A 3 × 3 grid of time series from voxels from the visual cortex of a single subject is shown in Fig. A.6 for the 20% long block task illustrating these baseline variations. The me-dn BOLD (red), non-BOLD (black) and OC (blue) time series are shown overlayed. Voxel a shows an excellent agreement between the me-dn BOLD and OC time series and a principally linear positive trendin the non-BOLD component (which can be seen to influence the OC at the beginning and end of the task). Voxels b, c, d, e, and f show the ability of me-dn to pull out the task signal from very noisy voxels to a better extent than OC. Voxels g, h, and i show a very nonlinear non-BOLD baseline, which translates to a similar OC time series, however me-dn BOLD shows a completely flat trace, indicating no task response was likely present in this voxel.
In particular, note that the OC time series follows the non-BOLD components in many voxels. Additionally, the non-BOLD trend in each of these voxels is generally positive, however the baseline in each voxel has its own particular signature. Some of the non-BOLD fluctuations are reminiscent of possible task patterns (e.g. voxel f) but are successfully automatically removed using the ME-ICA denoising procedure revealing the true task response. This demonstrates a strength of ME-ICA denoising at the single subject and single voxel level.
Fig. A.6.
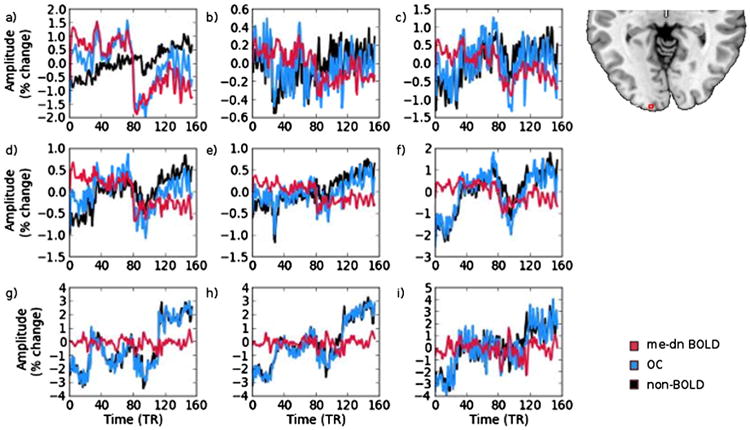
A set of voxels taken from the visual cortex of a single subject for the 20% block task (‘on’ for the first half of the time shown). The time courses shown are me-dn BOLD (red), non-BOLD (black) and OC (blue).
Appendix B. Supplementary data
Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.neuroimage.2014.10.051.
References
- Aguirre GK, Detre JA. The development and future of perfusion fMRI for dynamic imaging of human brain activity. Neuroimage. 2012;62:1279–1285. doi: 10.1016/j.neuroimage.2009.05.030. http://dx.doi.org/10.1016/j.neuroimage.2012.04.039. [DOI] [PubMed] [Google Scholar]
- Aguirre GK, Zarahn E, D'Esposito M. Empirical analyses of bold fMRI statistics. II. Spatially smoothed data collected under null-hypothesis and experimental conditions. Neuroimage. 1997;5:199–212. doi: 10.1006/nimg.1997.0264. [DOI] [PubMed] [Google Scholar]
- Aguirre GK, Detre JA, Zarahn E, Alsop DC. Experimental design and the relative sensitivity of bold and perfusion fMRI. Neuroimage. 2002;15:488–500. doi: 10.1006/nimg.2001.0990. http://dx.doi.org/10.1006/nimg.2001.0990. [DOI] [PubMed] [Google Scholar]
- Bandettini PA, Jesmanowicz A, Wong EC, Hyde JS. Processing strategies for time-course data sets in functional MRI of the human brain. Magn Reson Med. 1993;30:161–173. doi: 10.1002/mrm.1910300204. [DOI] [PubMed] [Google Scholar]
- Birn RM, Cox RW, Bandettini PA. Detection versus estimation in event-related fMRI: choosing the optimal stimulus timing. Neuroimage. 2002;15:252–264. doi: 10.1006/nimg.2001.0964. http://dx.doi.org/10.1006/nimg.2001.0964. [DOI] [PubMed] [Google Scholar]
- Birn RM, Murphy K, Handwerker DA, Bandettini PA. fMRI in the presence of task-correlated breathing variations. Neuroimage. 2009;47:1092–1104. doi: 10.1016/j.neuroimage.2009.05.030. http://dx.doi.org/10.1016/j.neuroimage.2009.05.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med. 1995;34:537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Bright MG, Murphy K. Removing motion and physiological artifacts from intrinsic bold fluctuations using short echo data. Neuroimage. 2013;64:526–537. doi: 10.1016/j.neuroimage.2012.09.043. http://dx.doi.org/10.1016/j.neuroimage.2012.09.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiacchiaretta P, Romani GL, Ferretti A. Sensitivity of bold response to increasing visual contrast: spin echo versus gradient echo epi. Neuroimage. 2013;82C:35–43. doi: 10.1016/j.neuroimage.2013.05.069. http://dx.doi.org/10.1016/j.neuroimage.2013.05.069. [DOI] [PubMed] [Google Scholar]
- Cordes D, Haughton VM, Arfanakis K, Carew JD, Turski PA, Moritz CH, Quigley MA, Meyerand ME. Frequencies contributing to functional connectivity in the cerebral cortex in “resting-state data”. AJNR Am J Neuroradiol. 2001;22:1326–1333. [PMC free article] [PubMed] [Google Scholar]
- Cox RW. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res. 1996;29:162–173. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- Gardner JL, Sun P, Waggoner RA, Ueno K, Tanaka K, Cheng K. Contrast adaptation and representation in human early visual cortex. Neuron. 2005;47:607–620. doi: 10.1016/j.neuron.2005.07.016. http://dx.doi.org/10.1016/j.neuron.2005.07.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gowland PA, Bowtell R. Theoretical optimization of multi-echo fMRI data acquisition. Phys Med Biol. 2007;52:1801–1813. doi: 10.1088/0031-9155/52/7/003. http://dx.doi.org/10.1088/0031-9155/52/7/003. [DOI] [PubMed] [Google Scholar]
- Ing A, Schwarzbauer C. A dual echo approach to motion correction for functional connectivity studies. Neuroimage. 2012;63:1487–1497. doi: 10.1016/j.neuroimage.2012.07.042. http://dx.doi.org/10.1016/j.neuroimage.2012.07.042. [DOI] [PubMed] [Google Scholar]
- Kastner S, O'Connor DH, Fukui MM, Fehd HM, Herwig U, Pinsk MA. Functional imaging of the human lateral geniculate nucleus and pulvinar. J Neurophysiol. 2004;91:438–448. doi: 10.1152/jn.00553.2003. http://dx.doi.org/10.1152/jn.00553.2003. [DOI] [PubMed] [Google Scholar]
- Kay KN, David SV, Prenger RJ, Hansen KA, Gallant JL. Modeling low-frequency fluctuation and hemodynamic response timecourse in event-related fMRI. Hum Brain Mapp. 2008;29:142–156. doi: 10.1002/hbm20379. http://dx.doi.org/10.1002/hbm.20379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundu P, Inati SJ, Evans JW, Luh WM, Bandettini PA. Differentiating bold and non-bold signals in fMRI time series using multi-echo epi. Neuroimage. 2012;60:1759–1770. doi: 10.1016/j.neuroimage.2011.12.028.. http://dx.doi.org/10.1016/j.neuroimage.2011.12.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundu P, Brenowitz ND, Voon V, Worbe Y, Vrtes PE, Inati SJ, Saad ZS, Bandettini PA, Bullmore ET. Integrated strategy for improving functional connectivity mapping using multiecho fMRI. Proc Natl Acad Sci U S A. 2013;110:16187–16192. doi: 10.1073/pnas.1301725110. http://dx.doi.org/10.1073/pnas.1301725110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee AT, Glover GH, Meyer CH. Discrimination of large venous vessels in time-course spiral blood-oxygen-level-dependent magnetic-resonance functional neuro-imaging. Magn Reson Med. 1995;33:745–754. doi: 10.1002/mrm.1910330602. [DOI] [PubMed] [Google Scholar]
- Liu TT, Frank LR, Wong EC, Buxton RB. Detection power, estimation efficiency, and predictability in event-related fMRI. Neuroimage. 2001;13:759–773. doi: 10.1006/nimg.2000.0728. http://dx.doi.org/10.1006/nimg.2000.0728. [DOI] [PubMed] [Google Scholar]
- Lowe MJ, Russell DP. Treatment of baseline drifts in fMRI time series analysis. J Comput Assist Tomogr. 1999;23:463–473. doi: 10.1097/00004728-199905000-00025. [DOI] [PubMed] [Google Scholar]
- Lund TE, Madsen KH, Sidaros K, Luo WL, Nichols TE. Non-white noise in fMRI: does modelling have an impact? Neuroimage. 2006;29:54–66. doi: 10.1016/j.neuroimage.2005.07.005. http://dx.doi.org/10.1016/j.neuroimage.2005.07.005. [DOI] [PubMed] [Google Scholar]
- Olson IR, Rao H, Moore KS, Wang J, Detre JA, Aguirre GK. Using perfusion fMRI to measure continuous changes in neural activity with learning. Brain Cogn. 2006;60:262–271. doi: 10.1016/j.bandc.2005.11.010. http://dx.doi.org/10.1016/j.bandc.2005.11.010. [DOI] [PubMed] [Google Scholar]
- Peltier SJ, Noll DC. T(2)(*) dependence of low frequency functional connectivity. Neuroimage. 2002;16:985–992. doi: 10.1006/nimg.2002.1141. [DOI] [PubMed] [Google Scholar]
- Poser BA, Versluis MJ, Hoogduin JM, Norris DG. Bold contrast sensitivity enhancement and artifact reduction with multiecho epi: parallel-acquired inhomogeneity-desensitized fMRI. Magn Reson Med. 2006;55:1227–1235. doi: 10.1002/mrm.20900. http://dx.doi.org/10.1002/mrm.20900. [DOI] [PubMed] [Google Scholar]
- Posse S, Wiese S, Gembris D, Mathiak K, Kessler C, Grosse-Ruyken ML, Elghahwagi B, Richards T, Dager SR, Kiselev VG. Enhancement of bold-contrast sensitivity by single-shot multi-echo functional mr imaging. Magn Reson Med. 1999;42:87–97. doi: 10.1002/(sici)1522-2594(199907)42:1<87::aid-mrm13>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- Saad ZS, Glen DR, Chen G, Beauchamp MS, Desai R, Cox RW. A new method for improving functional-to-structural mri alignment using local Pearson correlation. Neuroimage. 2009;44:839–848. doi: 10.1016/j.neuroimage.2008.09.037. http://dx.doi.org/10.1016/j.neuroimage.2008.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith AM, Lewis BK, Ruttimann UE, Ye FQ, Sinnwell TM, Yang Y, Duyn JH, Frank JA. Investigation of low frequency drift in fMRI signal. Neuroimage. 1999;9:526–533. doi: 10.1006/nimg.1999.0435. http://dx.doi.org/10.1006/nimg.1999.0435. [DOI] [PubMed] [Google Scholar]
- Speck O, Hennig J. Functional imaging by I0- and T2*-parameter mapping using multi-image epi. Magn Reson Med. 1998;40:243–248. doi: 10.1002/mrm.1910400210. [DOI] [PubMed] [Google Scholar]
- Talagala S, Peltier SJ, Voyvodic JT. Correction for signal drift in fMRI: use of interleaved acquisition of bold sensitive and insensitive images. ISMRM international conference. 1999;7:1669. [Google Scholar]
- Thomas CG, Harshman RA, Menon RS. Noise reduction in bold-based fMRI using component analysis. Neuroimage. 2002;17:1521–1537. doi: 10.1006/nimg.2002.1200. [DOI] [PubMed] [Google Scholar]
- Tootell RB, Reppas JB, Kwong KK, Malach R, Born RT, Brady TJ, Rosen BR, Belliveau JW. Functional analysis of human mt and related visual cortical areas using magnetic resonance imaging. J Neurosci. 1995;15:3215–3230. doi: 10.1523/JNEUROSCI.15-04-03215.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Aguirre GK, Kimberg DY, Roc AC, Li L, Detre JA. Arterial spin labeling perfusion fMRI with very low task frequency. Magn Reson Med. 2003;49:796–802. doi: 10.1124/jpet.110.172577. http://dx.doi.org/10.1002/mrm.10437. [DOI] [PubMed] [Google Scholar]
- Wang DJJ, Chen Y, Fernndez-Seara MA, Detre JA. Potentials and challenges for arterial spin labeling in pharmacological magnetic resonance imaging. J Pharmacol Exp Ther. 2011;337:359–366. doi: 10.1002/mrm.10437. http://dx.doi.org/10.1124/jpet.110.172577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wise RG, Williams P, Tracey I. Using fmri to quantify the time dependence of remifentanil analgesia in the human brain. Neuropsychopharmacology. 2004;29:626–635. doi: 10.1038/sj.npp.1300364. http://dx.doi.org/10.1038/sj.npp.1300364. [DOI] [PubMed] [Google Scholar]
- Wu G, Li SJ. Theoretical noise model for oxygenation-sensitive magnetic resonance imaging. Magn Reson Med. 2005;53:1046–1054. doi: 10.1002/mrm20451. http://dx.doi.org/10.1002/mrm.20451. [DOI] [PubMed] [Google Scholar]
- Yan L, Zhuo Y, Ye Y, Xie SX, An J, Aguirre GK, Wang J. Physiological origin of low-frequency drift in blood oxygen level dependent (bold) functional magnetic resonance imaging (fMRI) Magn Reson Med. 2009;61:819–827. doi: 10.1002/mrm.21902. http://dx.doi.org/10.1002/mrm.21902. [DOI] [PubMed] [Google Scholar]
- Zarahn E, Aguirre GK, D'Esposito M. Empirical analyses of bold fMRI statistics. I. Spatially unsmoothed data collected under null-hypothesis conditions. Neuroimage. 1997;5:179–197. doi: 10.1006/nimg.1997.0263. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


