On high heels and short muscles: A multiscale model for sarcomere loss in the gastrocnemius muscle

Abstract

High heels are a major source of chronic lower limb pain. Yet, more than one third of all women compromise health for looks and wear high heels on a daily basis. Changing from flat footwear to high heels induces chronic muscle shortening associated with discomfort, fatigue, reduced shock absorption, and increased injury risk. However, the long-term effects of high-heeled footwear on the musculoskeletal kinematics of the lower extremities remain poorly understood. Here we create a multiscale computational model for chronic muscle adaptation to characterize the acute and chronic effects of global muscle shortening on local sarcomere lengths. We perform a case study of a healthy female subject and show that raising the heel by 13 cm shortens the gastrocnemius muscle by 5% while the Achilles tendon remains virtually unaffected. Our computational simulation indicates that muscle shortening displays significant regional variations with extreme values of 22% in the central gastrocnemius. Our model suggests that the muscle gradually adjusts to its new functional length by a chronic loss of sarcomeres in series. Sarcomere loss varies significantly across the muscle with an average loss of 9%, virtually no loss at the proximal and distal ends, and a maximum loss of 39% in the central region. These changes reposition the remaining sarcomeres back into their optimal operating regime. Computational modeling of chronic muscle shortening provides a valuable tool to shape our understanding of the underlying mechanisms of muscle adaptation. Our study could open new avenues in orthopedic surgery and enhance treatment for patients with muscle contracture caused by other conditions than high heel wear such as paralysis, muscular atrophy, and muscular dystrophy.

1. Motivation

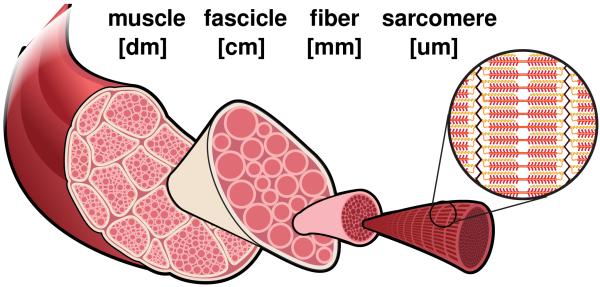
More than two thirds of all American women frequently dress in high-heeled shoes [3], 40% wear their high heels on a daily basis, 10% even more than eight hours per day [45]. High heels are a major contributor to foot problems and lower limb pain, associated with chronic conditions such as hallux vagus, corns, callusses, metatarsalgia, Achilles tendon tightness, planar fasciitis, and Haglund’s deformity [12]. In the United States alone, the annual health care cost attributed to high-fashion footwear is estimated to exceed $3 billion [41]. High-heeled footwear forces the foot into a plantarflexed position associated with shortening of the calf muscle-tendon unit [11]. Short-term, this position is energetically inefficient: It causes excessive actin-myosin overlap and forces muscle fibers into a non-optimal operating range [14]. Long-term, our calf muscles adapt to their new position: They shorten to reposition the actin-myosin overlap into back its optimal regime [12]. Figure 1 summarizes the spatial scales involved in chronic muscle adaptation [44].

Figure 1.

Chronic muscle adaptation across the scales. Muscle shortening spans from the whole muscle level via the fascicle level and fiber level all the way down to the sarcomere level and bridges five orders of magnitude in length.

On the muscle level, frequent high heel wear affects primarily in the gastrocnemuius muscle, while the lengths of the soleus muscle and the Achilles tendon remain virtually unchanged [21]. On the fascicle level, frequent high heel use shortens the average fascicle length of the medial gastrocnemius muscle by 12% [10]. Not surprisingly, these functional and structural changes affect the active range of motion of the ankle joint and cause a noticeable shift towards the supinated position [12]. This reduced range of motion decreases efficient shock absorption and increases the risk of ligament sprains [21]. In addition, habitual high heel wearers compromise muscle efficiency, suffer from discomfort and muscle fatigue, and increase the risk of strain injuries [11]. Yet, switching back to flat footwear can be extremely painful [22]; it overstretches the triceps surae and may trigger planar fasciitis [32], the most common cause of heel pain [40].

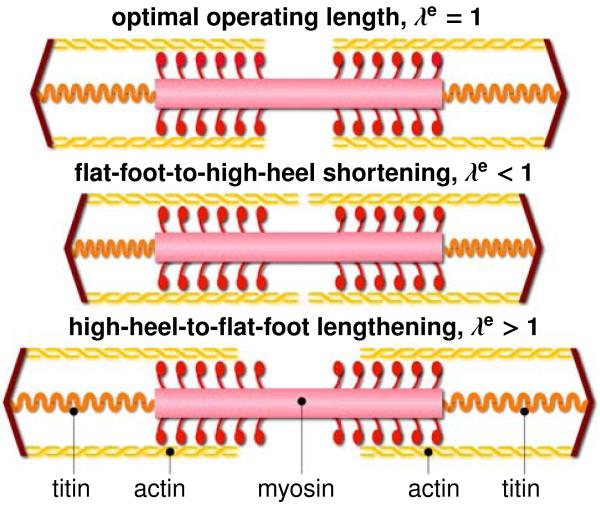
The smallest functional unit involved in chronic muscle adaptation is a sarcomere. Sarcomeres are 3um long assemblies of thick filaments of myosin sliding along thin filaments of actin [25]. On the sarcomere level, an optimal overlap of actin and myosin filaments is critical to maximum force generation [30]. Not surprisingly, the sarcomere length is tightly regulated [20]. Figure 2 illustrates a sarcomere unit at its optimal operating length, and in non-optimal shortened and lengthened positions. To always maintain each sarcomere within its optimal operating range, skeletal muscle responds to a chronic reduction in functional length through the active removal of sarcomeres in series [37]. Almost half a century ago, controlled immobilization experiments in mice [43] and cat [37] have demonstrated the chronic loss of sarcomeres in series by fixing a muscle in a shortened position. Recent studies suggest that frequent high heel use has similar effects: It reduces the fascicle length, which may trigger the controlled removal of sarcomeres in an attempt to reposition the muscle in its optional operating regime [10]. Taken together, the above studies provide valuable insight into chronic muscle shortening at the individual scales. Yet, the interaction of the underlying mechanisms across the scales remains poorly understood [44]. Here we present a continuum model for chronic muscle adaptation, in which changes in whole muscle length are treated as emergent properties of local changes in sarcomere number, muscle fiber length, and fascicle length. Continuum modeling is a valuable tool to reveal the mechanisms behind skeletal muscle adaptation [44]. Combined with the theory of finite growth [2], the nonlinear field theories of mechanics provide high-resolution insight into local stretch concentrations in response to altered muscle kinematics [5]. Multiscale models of finite growth correlate the global elastic stretch along the muscle fiber direction with the local sarcomere length [6]. To maintain this length within its physiologically optimal regime, the local sarcomere number undergoes dynamic change, which translates globally into an inelastic stretch or growth [17]. Previous models for cardiac muscle, the extensor digitorum, and the biceps brachii have successfully applied this concept to model positive growth associated with chronic muscle lengthening in dilated cardiomyopathy [18], limb lengthening, and tendon tear [47]. Here we adopt the same paradigm to model negative growth associated with chronic muscle shortening in frequent high heel wear.

Figure 2.

Chronic muscle adaptation on the sarcomere scale. Sarcomeres are 3um long assemblies of thick filaments of myosin sliding along thin filaments of actin. An optimal overlap of actin and myosin is critical to maximum force generation. To maintain sarcomeres within their optimal operating range, skeletal muscle responds to chronic shortening by removing sarcomeres in series.

2. Methods

To simulate the short- and long-term effects of high-heeled footwear, we create a subject-specific model of the lower limb using magnetic resonance images in flat foot and high heel positions. We perform a finite element analysis of acute and chronic muscle shortening using the continuum theory of finite growth.

2.1. Continuum model

To represent large muscle deformations, we adopt the kinematics of finite growth, and introduce the deformation map φ(X, t) mapping particles X from the initial configuration to particles x = φ(X, t) in the new configuration. We multiplicatively decompose its gradient F = ∇_Xφ into an elastic contribution F^e and an inelastic contribution F^g [35], which we associate with chronic muscle adaptation [47],

$$\mathit{F}={\nabla }_{X\phi }={\mathit{F}}^{\mathrm{e}}{\mathit{F}}^{\mathrm{g}}.$$ (1)

The Jacobian J = det(F) defines the change in muscle volume,

$$J=\det \left(\mathit{F}\right)=J^{\mathrm{e}}{J}^{\mathrm{g}},$$ (2)

which we decompose into an elastic volume change J^e = det(F^e) and an inelastic volume change J^g = det(F^g) attributed to muscle adaptation. Similar to the deformation gradient and the Jacobian, we interpret the total stretch λ along the fiber direction of the initial configuration n₀ as the product of the elastic stretch λ^e and the inelastic stretch λ^g associated with chronic changes in muscle length [29],

$$\lambda ={\left[{\mathit{n}}_0{\mathit{F}}^{\mathrm{t}}\mathit{F}{\mathit{n}}_0\right]}^{1∕2}={\lambda }^{\mathrm{e}}{\lambda }^{\mathrm{g}}.$$ (3)

We model chronic muscle shortening as the removal of sarcomeres in series. This implies that we can express the muscle adaptation tensor F^g as rank-one update of the identity tensor I [47],

$${\mathit{F}}^{\mathrm{g}}=\mathit{I}+[\vartheta -1]{\mathit{n}}_0\otimes {\mathit{n}}_0,$$ (4)

where ϑ is the relative serial sarcomere number. Values of ϑ < 1 represent the removal of sarcomeres in series associated with chronic muscle shortening; values of ϑ > 1 represent the addition of sarcomeres in series associated with chronic muscle lengthening [23]. As a consequence of the specific format of the adaptation tensor F^g, the serial sarcomere number ϑ not only represents the local muscle fiber shortening λ^g, but also to the volume change in response to sarcomere loss J^g,

$$\vartheta ={\lambda }^{\mathrm{g}}=\det \left({\mathit{F}}^{\mathrm{g}}\right)=J^{\mathrm{g}}.$$ (5)

We use the Sherman-Morrison formula to calculate the inverse of the adaptation tensor, F^g−1 = I +[1−ϑ] / ϑ n₀ ⊗ n₀. With the muscle fiber direction in the current configuration n = F n₀ and the inverse F^g−1 we find an explicit expression for the elastic tensor,

$${\mathit{F}}^{\mathrm{e}}=\mathit{F}{\mathit{F}}^{\mathrm{g}-1}=\mathit{F}+\frac{1-\vartheta }{\vartheta }\mathit{n}\otimes {\mathit{n}}_0.$$ (6)

We can then express the Finger tensor in terms of the serial sarcomere number ϑ,

$${\mathit{b}}^{\mathrm{e}}={\mathit{F}}^{\mathrm{e}}{\mathit{F}}^{\mathrm{et}}=\mathit{F}{\mathit{F}}^{\mathrm{t}}+\frac{1-{\vartheta }^2}{{\vartheta }^2}\mathit{n}\otimes \mathit{n}.$$ (7)

To focus on chronic muscle shortening, for simplicity, we assume homogeneously distributed isotropic material properties for the passive muscle tissue and adopt a strain energy function of Neo-Hookean type,

$$\psi =\frac{1}{2}L{\ln }^2\left(J^{\mathrm{e}}\right)+\frac{1}{2}G[{\mathit{b}}^{\mathrm{e}}:\mathit{i}-3-2\ln (J^{\mathrm{e}}\left)\right],$$ (8)

where L and G are the Lamé constants and i is the spatial identity tensor. We assume that the overall muscle microstructure, stiffness, and density are preserved upon adaptation [31], and derive the corresponding Kirchhoff stress tensor from the second law of thermodynamics,

$$\tau =2\frac{\partial \psi }{\partial {\mathit{b}}^{\mathrm{e}}}{\mathit{b}}^{\mathrm{e}}=\left[L\ln \right(J^{\mathrm{e}})-G]\mathit{i}+G{\mathit{b}}^{\mathrm{e}}.$$ (9)

At the subcellular level, we model the evolution of the serial sarcomere number ϑ as a strain-driven process [38]. We adopt the following evolution equation [48],

$$\vartheta =k\left(\vartheta \right)\varphi \left({\lambda }^{\mathrm{e}}\right),$$ (10)

where k is the adaptation function [26],

$$k=-\frac{1}{\tau }{\left[\frac{\vartheta -{\vartheta }^{\min }}{1-{\vartheta }^{\min }}\right]}^{\gamma },$$ (11)

parameterized in terms of the adaptation speed τ, the shape parameter for the adaptation function γ, and the minimum serial sarcomere number ϑ^min, and φ is the adpatation criterion,

$$\varphi =\langle {\lambda }^{\mathrm{crit}}-{\lambda }^{\mathrm{e}}\rangle .$$ (12)

Similar to the yield criterion in plasticity, the adaptation criterion φ activates sarcomere removal only if the elastic stretch is lower than the critical stretch as 〈λ^crit−λ^e〉 = λ^crit λ^e and deactivates sarcomere changes for elastic stretches above the critical stretch as 〈λ^crit − λ^e〉 = 0.

2.2. Computational model

To solve the nonlinear finite element equations of for chronic muscle adaptation, we implement our model as a user subroutine into the implicit commercial finite element solver Abaqus/Standard Version 6.13 (Simulia, Providence, RI) [1]. We introduce the relative serial sarcomere number ϑ as an internal variable, and solve its evolution equation (10) locally at the integration point level [17]. At each discrete time step t, we determine the current sarcomere number ϑ for a given current deformation state F and a given sarcomere number ϑ_n from the previous time step t_n using a finite difference approximation,

$$\vartheta =\frac{\vartheta -{\vartheta }_{\mathrm{n}}}{\Delta t},$$ (13)

where ∆t = t − t_n denotes the current time increment. We adopt an implicit time integration scheme and reformulate the evolution equation (10) with the help of equation (13), to introduce the discrete residual R in terms of the unknown sarcomere number,

$$\mathrm{R}=\vartheta -{\vartheta }_{\mathrm{n}}+k\varphi \Delta t\stackrel{.}{=}0.$$ (14)

We solve this nonlinear equation using a local Newton iteration [18]. Within each iteration step, we calculate the linearization of the residual R with respect to the serial sarcomere number ϑ,

$$\mathrm{K}=\frac{\partial \mathrm{R}}{\partial \vartheta }=1-\left[\frac{\partial k}{\partial \vartheta }\varphi +k\frac{\partial \varphi }{\partial \vartheta }\right]\Delta t.$$ (15)

Here, ∂k / ∂ϑ = −γ k / [ϑ − ϑ^min] and ∂φ / ∂ϑ = λ / ϑ² denote the linearizations of the adaptation function (11) and of the adaptation criterion (12). Within each Newton iteration, we update the unknown sarcomere number,

$$\vartheta \leftarrow \vartheta -\mathrm{R}∕\mathrm{K},$$ (16)

until we achieve local convergence, i.e., until the absolute value of the sarcomere update ∆ϑ = −R / K reaches a user-defined threshold value, here we choose 10⁻⁸. After determining the current sarcomere number ϑ, we can successively determine the adaptation tensor F^g from equation (4), the elastic tensor F^e = F←F^g−1 from equation (6), the elastic left Cauchy-Green tensor b^e = F^e ←F^{e t} from equation (7), the Kirchhoff stress τ from equation (9), and, finally, the fourth-order tensor of the Eulerian constitutive moduli,

$$\mathbf{c}=4{\mathit{b}}^{\mathrm{e}}\leftarrow \frac{{\partial }^2\psi }{\partial {\mathit{b}}^{\mathrm{e}}\otimes {\mathit{b}}^{\mathrm{e}}}\leftarrow {\mathit{b}}^{\mathrm{e}}={\mathbf{c}}^{\mathrm{e}}+{\mathbf{c}}^{\mathrm{g}}.$$ (17)

The first term, the Hessian of the free energy function at constant growth F^g, defines the elastic constitutive moduli,

$${\mathbf{c}}^{\mathrm{e}}=L\mathit{i}\otimes \mathit{i}+[G-L\ln (J^{\mathrm{e}}\left)\right][\mathit{i}\overline{\otimes }\mathit{i}+\mathit{i}\underset{¯}{\otimes }\mathit{i}],$$ (18)

with the common abbreviations, ${\left\{•\overline{\otimes }\mathrm{o}\right\}}_{ijkl}={\left\{•\right\}}_{ik}{\left\{\mathrm{o}\right\}}_{jl}$ and ${\left\{•\underset{¯}{\otimes }\mathrm{o}\right\}}_{ijkl}={\left\{•\right\}}_{il}{\left\{\mathrm{o}\right\}}_{jk}$, for the non-standard fourth order products. The second term, the Hessian of the free energy function at constant deformation F, defines the correction of the constitutive moduli due to muscle adaptation [47],

$${\mathbf{c}}^{\mathrm{g}}=-\frac{k}{\lambda \vartheta \mathrm{K}}[L\mathit{I}+2G∕{\vartheta }^2\mathit{n}\otimes \mathit{n}]\otimes [\mathit{n}\otimes \mathit{n}]\Delta t.$$ (19)

Instead of the Kirchhoff stress (9) and the constitutive moduli (17), the user-defined subroutine in Abaqus/Standard utilizes the Cauchy or true stress, σ = τ/J,

$${\sigma }^{\text{abaqus}}=\left[\right[L\ln \left(J^{\mathrm{e}}\right)-G]\mathit{i}+G{\mathit{b}}^{\mathrm{e}}]∕J,$$ (20)

and the Jauman rate of the Kirchhoff stress divided by the Jacobian, which requires the following modification of the tangent moduli [49],

$${\mathbf{c}}^{\text{abaqus}}=[\mathbf{c}+\frac{1}{2}[\tau \overline{\otimes }\mathit{i}+\mathit{i}\overline{\otimes }\tau +\tau \underset{¯}{\otimes }\mathit{i}+\mathit{i}\underset{¯}{\otimes }\tau \left]\right]∕J.$$ (21)

The local stress σ^abaqus of equation (20) and the local tangent moduli c^abaqus of equation (21) enter the righthand side vector and the iteration matrix of the global Newton iteration. Upon its convergence, we store the relative serial sarcomere number ϑ locally at the integration point level.

2.3. Magnetic Resonance Imaging

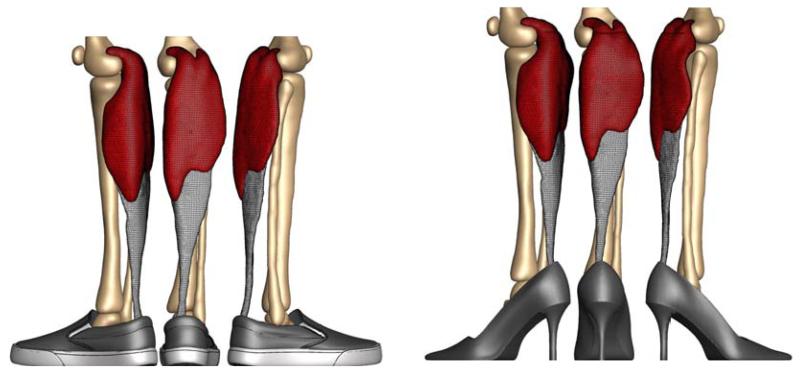
To create a finite element model of the lower limb, we collect magnetic resonance images of a healthy 20-year old female subject [4]. We acquire two sets of axial images, in flat foot and in high heel positions, using a product fat water separation gradient echo sequence with parallel imaging using IDEAL (GE Healthcare, Waukesha, WI) [34] and a 3T MRI system using Discovery MR750 (GE Healthcare, Waukesha, WI). To control the foot position during the high heel scan, we build a cardboard shoe model with a well-defined heel height of 13 cm.

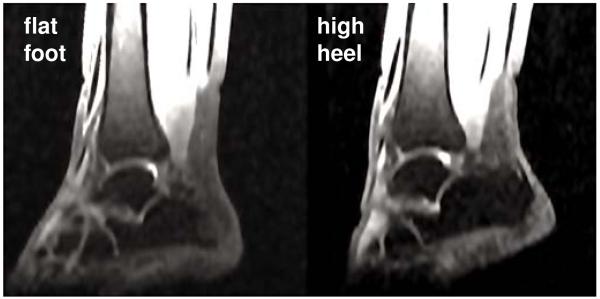
Figure 3 shows the resulting magnetic resonance images of the right lower limb in flat foot and high heel positions. Images have an in-plane resolution of 0.62 mm 0.62 mm and a slice thickness of 3mm. The magnetic resonance images provide the basis for the the finite element model and define the boundary conditions when changing from flat foot to high heel position. Figure 4 illustrates the workflow to generate a finite element model from magnetic resonance images. Using the medical image viewer OsiriX [36], we manually identify the individual muscles, bones, and tendons as regions of interest in a slice-by-slice manner. We then export binary masks from these regions to create a mesh for every component using the Computational Geometry Algorithms Library CGAL [16]. Finally, we filter the preliminary mesh to create a final mesh with smooth surfaces [39].

Figure 3.

Sagittal magnetic resonance images of the right lower limb of a healthy 20-year old female subject. Images show the ankle joint in flat foot position, right, and in high heel position at a heel hight of 13 cm, left. The scans provide the basis for the the finite element model and define the boundary conditions when changing from flat foot to high heel position.

Figure 4.

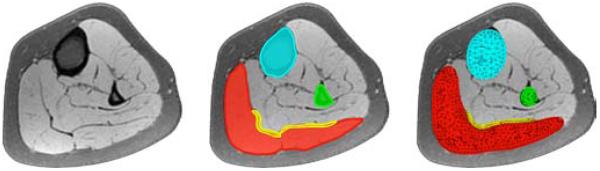
Generation of finite element model from magnetic resonance images of the lower limb. We manually segment the image slices and identify the muscles, bones, and tendons as regions of interest in the medical image viewer OsiriX [36], left. To create a mesh for each component, we convert the individual regions into binary masks and process them with CGAL [16], middle. Finally, we filter the preliminary mesh to create smooth surfaces [39], right.

2.4. Finite element model

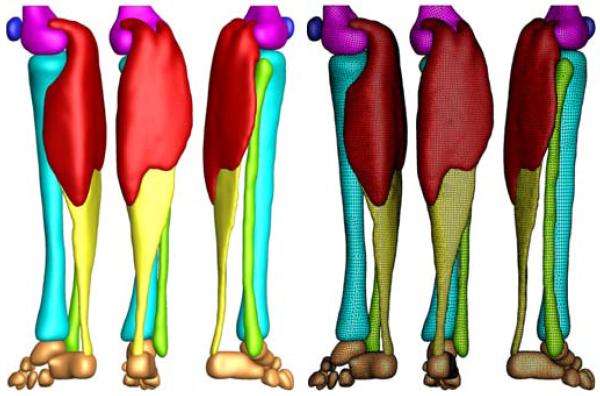
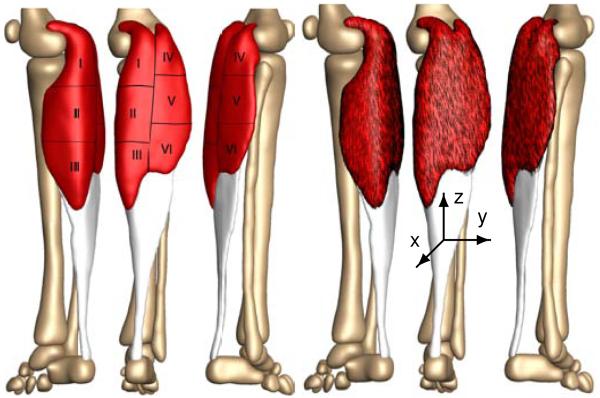
Figure 5 shows the final finite element model of the lower limb, which contains 81,146 nodes and 377,034 linear tetrahedral and pyramid elements. We choose a combination of tetrahedral and pyramid elements because of their ease of use when meshing complex geometries from clinical images. We note, however, that linear tetrahedral elements are known to be overly stiff, and that using either quadratic tetrahedra or hexahedral elements would fix this issue. Our model consists of the femur with 22,838 elements, shown in magenta, the patella with 8,987 elements, shown in blue, the gastrocnemius muscle with 165,820 elements, shown in red, the tibia with 48,369 elements, shown in cyan, the fibula with 22,086 elements, shown in green, the Achilles tendon with 55,945 elements, shown in yellow, and the tarsal bones with 52,989 elements, shown in orange.

Figure 5.

Finite element model of the lower limb. The model consists of 81,146 nodes and 377,034 linear tetrahedral and pyramid elements. The proximal end of the gastrocnemius muscle (165,820 elements, red) is fixed next to the femur while the distal end is connected to the Achilles tendon (55,945 elements, yellow). The femur (22,838 elements, magenta), patella (8,987 elements, blue), tibia (48,369 elements, cyan), fibula (22,086 elements, green), and the tarsal bones (52,989 elements, orange) are modeled as rigid bodies.

We model the gastrocnemius muscle as Neo-Hookean elastic with Lamé constants L = 0.714 N/mm² and G = 0.179 N/mm². Once the elastic fiber stretch falls below the threshold of λ^crit =1.0, we gradually remove sarcomeres towards a minimum sarcomere number of ϑ^min = 0.0 with an adaptation speed τ = 1.0 days and a shape parameter γ = 1.0. This implies that here, we drive muscle loss through non-tensile loading, while physiological muscle loss could generally occur in response to a variety of other environmental changes [44]. For computational efficiency, we assume that the bones and the Achilles tendon are significantly stiffer than the gastrocnemius muscle and model them as rigid bodies [27, 46].

Table 1 summarizes the dimensions of the muscle tendon unit in flat foot and high heel positions extracted from our magnetic resonance images. When changing from the flat footwear to high heels, the gastrocnemius medialis shortens by 12 mm while the Achilles tendon maintains its length. These measurements support our model assumption of a rigid tendon. To fix the muscle-tendon unit in space, we apply homogeneous Dirichlet boundary conditions at the medial and lateral heads of the gastrocnemius muscle where they attach to the condyle of the femur. To move the model from flat foot to high heel position and vice versa, we apply inhomogeneous Dirichlet boundary conditions at the distal nodes of the Achilles tendon and prescribe a gradual upward and downward displacement of 12 mm.

Table 1.

Dimensions of muscle tendon unit in flat foot and high heel positions. Wearing footwear with a heel height of 13 cm shortens the gastrocnemius medialis by 12mm while the Achilles tendon remains unaffected. These changes in length define the inhomogeneous Dirichlet boundary conditions of our finite element simulation.

	muscle- tendon unit [mm]	gastrocnemius medialis [mm]	achilles tendon [mm]
flat foot	396	225	171
high heel	384	213	171
difference	−12	−12	0

2.5. Muscle fiber model

As the foot is moved into the high heel position, we gradually allow the gastrocnemius muscle to remove sarcomeres in series to reposition the remaining sarcomeres at their optimal operating length. As a bipennate muscle, the gastrocnemius muscle consists of two rows of oblique muscle fibers, which face in opposite diagonal directions and converge jointly in the Achilles tendon. To account for these regionally varying fiber orientations, we divide the muscle into six regions of interest and assign each region an individual fiber orientation [33].

Figure 6 illustrates our muscle fiber orientation model of the gastrocnemius muscle. Table 2 summarizes the fiber orientations n₀ associated with six discrete regions of interest [33].

Figure 6.

Muscle fiber orientation model of the gastrocnemius muscle. The gastrocnemius muscle (red) is a bipennate muscle. It consists of two rows of oblique muscle fibers, which face in opposite diagonal directions and converge in a joined tendon (grey). Table 2 summarizes the six characteristic regions of interest with their six discrete fiber orientations n₀ [33].

Table 2.

Muscle fiber orientations in the gastrocnemius muscle. The gastrocnemius muscle is a bipennate muscle. It consists of two rows of oblique muscle fibers, which face in opposite diagonal directions and converge in the Achilles tendon. Figure 6 illustrates six characteristic regions of interest with the six fiber orientations n₀ [33].

region	location	n 0x	n0y	n0z
I	medial-proximal	0.014	−0.197	0.980
II	medial-central	0.025	−0.242	0.970
III	medial-distal	0.075	−0.317	0.946
IV	lateral-proximal	0.021	−0.193	0.981
V	lateral-central	0.024	−0.208	0.978
VI	lateral-distal	0.040	−0.247	0.968

2.6. Boundary conditions

To explore the acute and chronic effects of global muscle shortening on local sarcomere lengths, we simulate three scenarios: (i) acute effects when changing from flat foot to high heel position, (ii) chronic effects when maintaining the high heel position, and (iii) acute effects when changing back from high heel to flat foot position.

Figure 7 illustrates our finite element model of the lower limb. The left model shows the baseline state created from magnetic resonance images in flat foot position. The right model shows the shortened state created from images in high heel position. First, we move the model from flat foot to high heel position by prescribing an upward displacement on the distal nodes of the Achilles tendon. Then, we keep the foot in this position and allow the gastrocnemius to shorten and adapt to its new physiological length. Last, after the muscle has adapted, we move the foot back into the flat foot position.

Figure 7.

Finite element model of muscle shortening in response to frequent high heel use. The left model shows the baseline state created from magnetic resonance images in flat foot position. The right model shows the shortened state created from images in high heel position. To move the flat foot into the high heel position, we apply inhomogeneous Dirichlet boundary conditions by prescribing a 12 mm upward displacement of the distal end of the Achilles tendon. Then we maintain the foot in this position to allow the muscle to adapt to its new physiological length.

3. Results

All three simulations run robustly, converge quadratically, and generate conceptually feasible results, which we discuss in detail in the following three subsections.

3.1. Acute effects when switching from flat foot to high heel

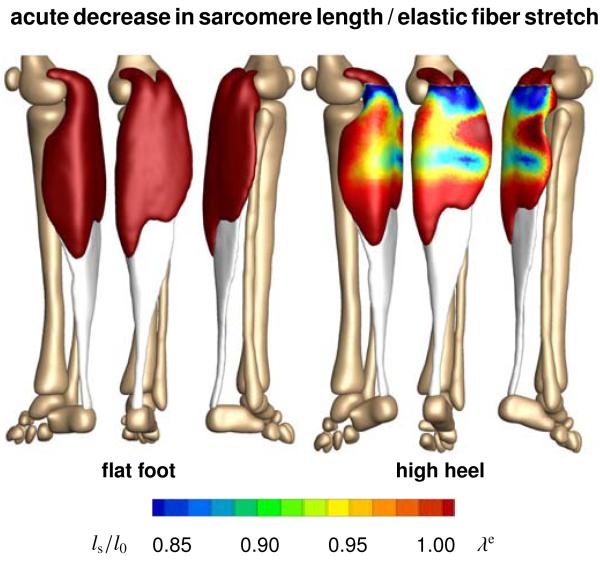
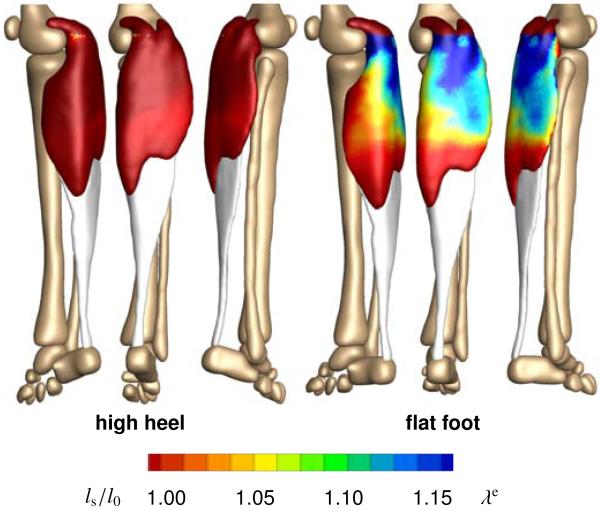
Figure 8 illustrates the acute change in sarcomere length when switching from flat footwear to high heels. Wearing shoes with a heel height of 13 cm induces a muscle shortening of 12 mm. In response to acute muscle shortening, the sarcomere length decreases. A decrease in length places the sarcomeres into a non-optimal operating regime at λ^e < 1.0 and the whole muscle into an energetically unfavorable working range. Sarcomere lengths display significant regional variations with an extreme shortening of l_s/l₀ = 0.78 in the central gastrocnemius.

Figure 8.

Acute decrease in sarcomere length when switching from flat footwear to high heels. In response to acute muscle shortening, the sarcomere length decreases. Sarcomere lengths display significant regional variations with extreme values of l_s/l₀ = 0.78 in the central gastrocnemius. The relative sarcomere length l_s/l₀ is a measure for the elastic fiber stretch λ^e.

3.2. Chronic effects when switching from flat foot to high heel

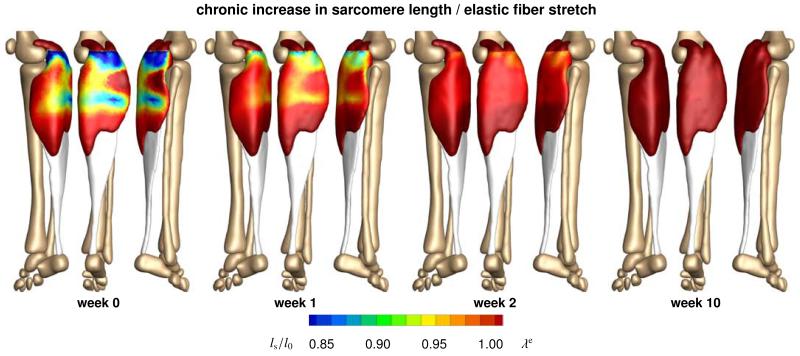
Figure 9 illustrates the chronic change in sarcomere length in frequent high heel wearers. In response to chronic muscle shortening, the initially shortened sarcomere length increases gradually as the muscle remains in its shortened position. This repositions the sarcomeres back into their optimal operating regime at λ^e = 1.0. Initially, sarcomere lengths display significant regional variations with extreme values of l_s/l₀ = 0.78 located in the central gastrocnemius. Over time, these variations disappear. As the muscle adapts to its new physiological length, the sarcomere lengths converge towards a homogeneous distribution at their initial length l₀.

Figure 9.

Chronic increase in sarcomere length when frequently wearing high-heeled footwear. In response to chronic muscle shortening, the sarcomere length increases gradually as the muscle remains in its shortened position. Sarcomere lengths display significant regional variations with extreme values of l_s/l₀ = 0.78 located in the central gastrocnemius. The relative sarcomere length l_s/l₀ is a measure for the elastic fiber stretch λ^e.

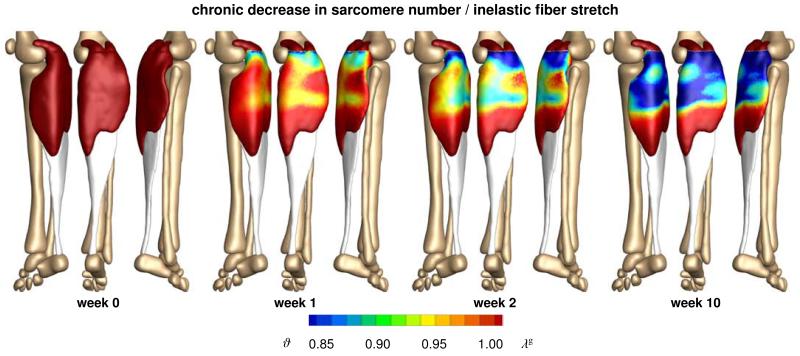
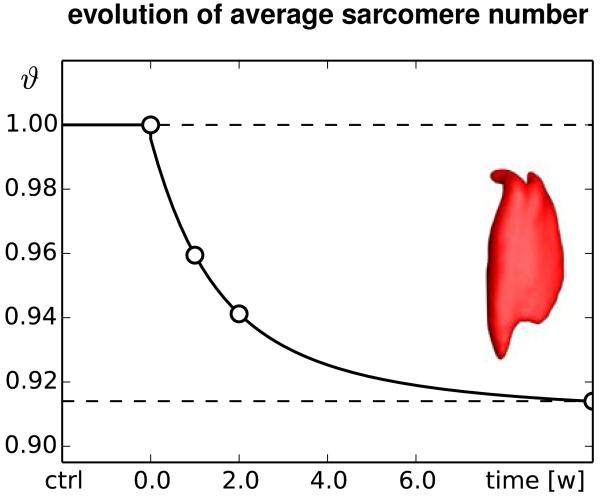
Figure 10 illustrates the chronic change in sarcomere number in frequent high heel wearers. In response to chronic muscle shortening, the sarcomere number decreases gradually as the muscle remains in its shortened position. The average weighted sarcomere number gradually decreases from ϑ = 1.00 to 0.96 after one week and 0.94 after two weeks until it converges to 0.91 after ten weeks of frequent high heel use. At this point, each sarcomere is repositioned back in its optimal operating regime.

Figure 10.

Chronic decrease in sarcomere number when frequently wearing high-heeled footwear. In response to chronic muscle shortening, the sarcomere number decreases gradually as the muscle remains in its shortened position. Sarcomere loss displays significant regional variations with extreme values of ϑ = 0.61 located in the central gastrocnemius. The relative sarcomere number ϑ is a measure for the inelastic fiber stretch λ^g.

The side-by-side comparison of Figures 9 and 10 illustrates the interplay between the elastic and inelastic fiber stretches λ^e and λ^g: Initially, changing from flat footwear to high heels compresses the muscle and the elastic fiber stretch drops significantly below its baseline value of one. On the sarcomere level, this implies significant sarcomere shortening and an increase in actin and myosin overlap. Over time, the relative serial sarcomere number decreases below its baseline value of one, while, at the same time, the sarcomere length returns to its initial value. The solution converges towards a state at which the elastic fiber stretch has returned to one throughout the entire muscle and the inelastic fiber stretch has taken up all the deformation.

Figures 9 and 10 indicate that the sarcomere loss is highly heterogeneous. At the proximal end of the gastrocnemius, where the medial and lateral heads attach to the rigid condyle of the femur, the muscle does not sense the kinematic change associated with wearing high heels. At its distal end, where the compliant muscle smoothly blends into the stiff Achilles tendon, relative kinematic changes are suppressed by the structural support of the tendon. Sarcomere loss is localized between these two regions with extreme values of ϑ = 0.61 corresponding to a chronic local fiber shortening 39%.

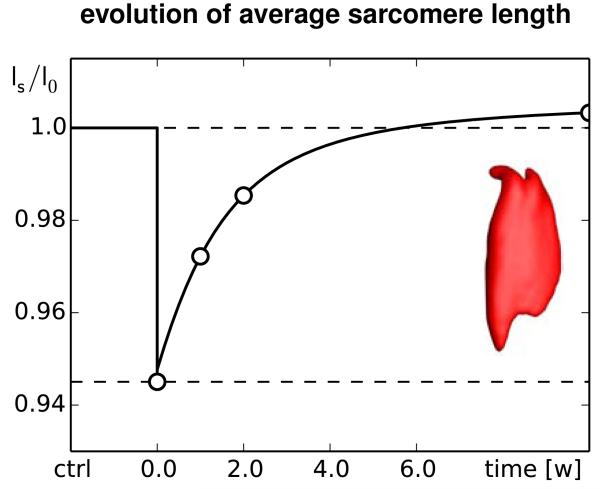
Figures 11 and 12 summarize the dynamic changes in sarcomere length and sarcomere number. Both graphs reflect the interplay between elastic and inelastic fiber stretch with a gradual transition from acute sarcomere shortening with λ^e < 1 at λ^g = 1 to chronic sarcomere loss with λ^g < 1 at λ^e = 1. Since the graphs contain the averaged values across the entire muscle, the minimum average sarcomere length and average sarcomere number of 0.94 and 0.91 are less pronounced than the local extreme values of 0.78 and 0.61 of the contour plots in Figures 9 and 10.

Figure 11.

Chronic increase in sarcomere length when switching from flat footwear to high heels. In response to muscle shortening of 12 mm, the sarcomere length in the gastrocnemius muscle decreases acutely from l_s/l₀ = 1.0 to 0.95 and then returns chronically to its initial length. The marked time points correspond to the contour plots in Figure 9.

Figure 12.

Chronic decrease in sarcomere number when switching from flat footwear to high heels. In response to muscle shortening of 12 mm, the sarcomere number in the gastrocnemius muscle decreases chronically from ϑ = 1.0 to 0.96 after one week and 0.94 after two weeks until it converges at 0.91 after ten weeks. The marked time points correspond to the contour plots in Figure 10.

3.3. Acute effects when switching from high heel to flat foot

Figure 13 illustrates the acute change in sarcomere length when switching back to flat foot position after a period of extended high heel wearing. In response to acute muscle lengthening, the sarcomere length increases. An increase in length places the sarcomeres into a non-optimal operating regime at λ^e > 1.0. Sarcomere lengths display significant regional variations with an extreme lengthening of l_s/l₀ = 1.29 in the central gastrocnemius.

Figure 13.

Acute increase in sarcomere length when switching from high heels to flat footwear. In response to acute muscle lengthening, the sarcomere length increases. Sarcomere lengths display significant regional variations with extreme values of l_s/l₀ = 1.29 located in the central gastrocnemius. The relative sarcomere length l_s/l₀ is a measure for the elastic fiber stretch λ^e.

4. Discussion

Even though high heels are known to be a major source of chronic lower limb pain, more than one third of American women wear high heels on a daily basis. To characterize the effects of high-heeled footwear on muscle adaptation in the lower limb, we created a multiscale computational model for chronic muscle shortening. To calibrate the model, we performed a case study of a healthy female subject and created two lower limb models using magnetic resonance images, one in flat foot and one in high heel position. Surprisingly, when moving the foot from flat position to a heel height of 13 cm, the length of the calf muscle-tendon unit changes only marginally from 396 mm to 384 mm corresponding to a stretch of λ = 0.97. However, a closer look reveals two essential characteristics: The Achilles tendon remains at a constant length of 171 mm with λ = 1.00, while the gastrocnemius experiences the entire length change of 12 mm from 225 mm to 213 mm corresponding to a stretch of λ = 0.95. More importantly, the finite element simulation suggests that this stretch is not distributed homogeneously across the gastrocnemius muscle: In the proximal and distal regions, where the muscle is structurally supported by the stiffer femur and Achilles tendon, the muscle experience virtually no stretch; in the central muscle region, local stretches take extreme values of λ = 0.78.

Acutely, switching from flat footwear to high heels causes excessive actin-myosin overlap and forces the muscle to operate in a non-optimal operating regime [11], see Figure 2. When moving from the flat to the high heel position, our simulations predict an acute average reduction in sarcomere length by 5%, see Figure 11, with local extrema of sarcomere shortening of 22% in the central gastrocnemius, see Figure 9. These values are in excellent agreement with recent studies, which have reported a fascicle length difference of 12% in the medial gastrocnemius muscle, with lengths of 56.0±7.7mm in the flat foot group compared to 49.6±5.7mm in the high heel group [10]. In the same study, in agreement with our measurements and simulations, the length of the Achilles tendon was almost identical in both groups with 18.69 cm in the flat foot group and 18.91 cm in the high heel group [10].

Chronically, skeletal muscle adapts to its new physiological length by removing sarcomeres in series to reposition its sarcomeres back into their optimal regime [42], see Figure 2. When maintaining the foot in the high heel position, our simulations predict a chronic average reduction in serial sarcomere number by 9%, see Figure 12, with local maxima of sarcomere loss of 31% in the central gastrocnemius, see Figure 10. These values lie within the range of the reported sarcomere loss during immobilization experiments in mice, where the serial sarcomere number decreased by 10% from 2,200 to 1,975 in the soleus after four weeks of immobilization [43] and by 9% from 3,200 to 2,900 in the tibialis anterior after two weeks of immobilization [7]. These values are slightly lower than the reported sarcomere loss in cat, where the serial sarcomere number decreased by 40% from 13,844 to 8,258 in the soleus after four weeks of immobilization [37]. Undoubtably, these immobilization experiments impose a more drastic kinematic constraint than frequent high heel wearing [13]. Nonetheless, the chronic sarcomere loss reported upon immobilization represents a valuable upper limit for the sarcomere loss we can expect in women who frequently wear high-heeled shoes.

Acutely, switching back from frequent high heel use to flat footwear causes a drastic reduction in actin-myosin overlap and forces the muscle to operate in a non-optimal operating regime [20], see Figure 2. When moving from the foot from high heel to flat, our simulations predict an acute sarcomere lengthening with local extrema of 29% in the central gastrocnemius, see Figure 13. Our large regional variations in sarcomere length are in agreement with previous studies, which have reported significant regional variations in fascicle lengths and sarcomere lengths in the stretched cat biceps femoris muscle [8]. Our sarcomere lengths agree with common observation that switching back from high heels to flat footwear induces muscle overstretch associated with muscle pain [22] and increased risk of strain injuries [11].

While our study provides valuable insight into the mechanisms of chronic muscle shortening on the muscle and sarcomere levels, our current model has a few limitations: First, to illustrate the conceptual feasibility of our method, we have only prototyped the study for a single heel height and a single study subject. It would be interesting to explore the dimensions of the muscle-tendon unit in Table 1 for flat foot and high heel positions with varying heel heights in different study subjects [14]. Second, for simplicity, in equation (8), we have modeled skeletal muscle as isotropic Neo-Hookean material. While an isotropic model might be a sufficient approximation under compressive loading when switching from flat foot to high heel, a more sophisticated anisotropic model that takes into account strain stiffening might be more appropriate under tensile loading when switching from high heel to flat foot [5, 19]. Since we have only reported strains and stretches, here, sophisticated constitutive modeling might not be critical; yet, it would be worth considering in future studies, especially when addressing chronic force alterations in muscle [21] and tendon [15, 28]. Third, the model presented here only accounts for sarcomere removal upon chronic understretch. To add sarcomeres in series upon chronic overstretch [44], we would need to modify the adaptation function in equation (11) to k = [[ϑ^max − ϑ]/[ϑ^max − 1]]^γ/τ and activate it through the modified adaptation criterion in equation (12) as φ = 〈 λ^e λ^crit〉 using the generic approach [26] adopted for skeletal muscle - [47]. Last, until now, we have only compared our model qualitatively against animal immobilization models in mice [43] and cat [37]. Recent developments in microendoscopy now enable the non-invasive sarcomere imaging in vivo [24]. We have designed our model with these new technologies in mind [9]. We are currently in the process of measuring sarcomere lengths in flat foot and high heel positions in different regions of the gastrocnemius muscle to validate our model with in vivo human data.

What can we learn from this study? First and foremost, we have seen that we can interpret chronic changes in whole muscle length as emergent properties of local changes in sarcomere number, muscle fiber length, and fascicle length. This has allowed us to create multiscale computational models, which strongly support the hypothesis that frequent high-heel use alters the natural position of the calf muscle-tendon complex. Our results suggest that this change could initiate a chain reaction of negative effects [12]: Acutely, it creates excessive actin-myosin overlap associated with energetically inefficient muscle use [14]. Chronically, it initiates an adaptation process associated with the loss of sarcomeres and significant muscle shortening [10]. A major concern is that these changes are chronic. Changing back to flat footwear does not provide immediate cure; quite the contrary: For most frequent high heel wearers, switching to the flat foot position can be extremely painful. It overstretched the triceps surae [22], which might cause muscle pain and planar fasciitis [32]. To ensure comfort and reduce risk of injury [11], recent recommendations suggest limiting the heel hight to 5 cm or less [14]. To maintain muscle fiber lengths and ankle range of motion [22], recent studies recommend intensive passive stretching exercise with long frequent stretching times in dorsiflexion direction [21]. Our study strongly supports these recommendations.

5. Concluding remarks

We have created a computational model of the lower limb to study the acute and chronic effects of high-heeled footwear on the kinematics of the calf muscle-tendon unit. Through the case study of a healthy female subject, we have shown that raising the heel by 13 cm reduces the length of the muscle-tendon unit by 12 mm or 3%. Notably, this change affects almost exclusively the gastrocnemius muscle, which experiences an average shortening of 5%, while the length of the Achilles tendon remains virtually unchanged. Our computational simulations indicate that muscle shortening displays significant regional variations with extreme values of 22% in the central gastrocnemius. Our model suggests that the muscle gradually adjusts to its new functional length by a chronic loss of sarcomeres in series. Sarcomere loss varies regionally with virtually no loss at the proximal and distal ends and a maximum loss of 39% in the central muscle region. Collectively, these changes result in chronic muscle shortening associated with discomfort, compromised muscle efficiency, increased fatigue, reduced shock absorption, and increased risk of strain injuries. Computational modeling of chronic muscle shortening provides a valuable tool to shape our understanding of the interacting mechanisms in skeletal muscle adaptation. Our study could open new avenues in orthopedic surgery and enhance treatment in patients with muscle contracture caused by other conditions than high heel wear such as paralysis, muscular atrophy, and muscular dystrophy.