Abstract
Giant chiroptical responses routinely occur in three dimensional chiral metamaterials (MMs), but their resonance elements with complex subwavelength chiral shapes are challenging to fabricate in the optical region. Here, we propose a new paradigm for obtaining strong circular conversion dichroism (CCD) based on extrinsic 2D chirality in multilayer achiral MMs, showing that giant chiroptical response can be alternatively attained without complex structures. Our structure consists of an array of thin Au squares separated from a continuous Au film by a GaAs dielectric layer, where the Au squares occupy the sites of a rectangular lattice. This structure gives rise to a pronounced extrinsically 2D-chiral effect (CCD) in the mid-infrared (M-IR) region under an oblique incidence, where the 2D-chiral effect is due to the mutual orientation of the Au squares array and the incident light propagation direction; the large magnitude of CCD due to the large difference between left-to-left and right-to-right circularly polarized reflectance conversion efficiencies.
Chirality is an intrinsic feature of chiral molecules, which cannot be superposed on their mirror image called enantiometers1. This is an ubiquitous property in the organic world, found in proteins, DNA, sugar molecules, viruses, amino acids and cholesteric liquid crystals2. Consequently, the analysis of intrinsically 3D-chiral effects has been widely used in the fields of spectroscopy of chemical and biomolecular substances3, compact thin-film optical diodes4 and circular polarized emission5. Meanwhile, 2D intrinsic chirality is also found in natural planar chiral systems such as the surface of Au monocrystal and the surface of a metal-metal eutectic6. However, 2D- and 3D- chiroptical responses in natural chiral materials are usually very weak7. They can only be observed once the material exhibits a macroscopic path length of light. This limitation has been lifted by recent advances in both chiral metamaterials (MMs)7,8,9,10 and non-chiral planar MMs11,12,13,14,15, which have opened new routes towards significant circular dichroism11 and optical activity12 -3D chirality as well as pronounced circular conversion dichroism16 and asymmetric transmission-2D chirality17,18,19,20,21,22, surpassing those of natural chiral materials.
Chiral MMs, such as helical structures23,24, dual-layer twisted-arc MMs2, twisted U shape split ring MMs25, single-layered gold sawtooth gratings26 and multilayer gammadion MMs27 are likely to possess strong chiroptical response. However, periodic arrays with ultrasmall chiral figures and precise alignment are complicated to achieve in the optical region28. Therefore, a more challenging task is to achieve chiral effects using intrinsically achiral MMs. This can be obtained by tilting the non-chiral MMs out of their symmetry axes with respect to the incident light11. This response is termed extrinsic chirality owing to the non-chiral nature of the structures12. Such effects are later demonstrated in various kinds of planar achiral MMs under oblique incident light, such as periodically repeating metallic spheres29, asymmetrical split rings30, nanorings31 or circular nanoholes32. Compared with chiral MMs, planar MMs consisting of nonchiral resonators have simpler patterns and are thus easier to realize33. Recently, some remarkable research demonstrates that the extrinsic chirality from the planar MMs consisting of non-chiral meta-molecules may lead to strong optical activity11, circular dichroism (CD)12 and circular conversion dichroism (CCD)1. It shows that planar achiral MMs can be used to achieve pronounced extrinsically 3D- and 2D- chiral effects that are identical to those produced by 3D- and 2D-chiral systems. Following these significant works, very recently the concept of extrinsic chirality has been put forward, showing that, achiral MMs based on coupling in a multilayer structure also have a potential to provide a strong chiroptical response. This is because the strong magnetic response caused by the antisymmetric oscillation modes of the two coupled layers can enhance circular polarization difference and circular polarization conversion effects. Therefore, multilayer nonchiral MMs have appealing properties and have drawn much interest. For example, Zhang et al. numerically demonstrate a giant circular polarization conversion using layer-by-layer nonchiral MMs34, but this multilayer structure only operates in the GHz region. Zhao et al. show that a giant and broadband circular polarization can be achieved in multilayer twisted arrays of metasurfaces28, whereas the efficiency of the circular polarization selectivity in such structures is strongly dependent on the number of layers, namely the more layers of the structure, the better chiroptical response; this structure with many layers may complicate the fabrication scheme. Thus, an effective method for obtaining the nonchiral MMs with much simpler geometry as well as stronger chiroptical effect in the optical spectral region is desirable and necessary for practical applications.
It has been shown that metamaterial perfect absorbers (MPAs) consisting of two metallic layers spaced apart by a dielectric spacer have extraordinary large absorbance resonances across much of the electromagnetic spectra35,36,37,38. This phenomenon is attributed to the ability to engineer materials with specified permittivity and permeability responses, allowing for matching the impedance of the MPAs to that of free space hence leading to perfect absorbance39. Drawing on insights from this interesting phenomenon, we wondered whether it would be possible to use MPAs for realizing giant extrinsically 2D-chiral effect in the optical regime under off-normal incidence. Our intuitive picture was that a large chiral effect should occur if structures support strong electric and magnetic resonances. It is because the chirality is characterized by electric and magnetic dipolar moments and enhancing chirality spectroscopy entails manipulation of both electric and magnetic fields of light40,41,42. With this idea in mind, we propose an array of thin gold (Au) squares separated from a continuous Au film by a GaAs dielectric layer, where the Au squares occupy the sites of a rectangular lattice. A rectangular periodic square array is a 2D anisotropic system that possesses different polarization modes along the two orthogonal lattice vectors. Such an achiral MM that interacts with an oblique incident light can obtain an extrinsically 2D chirality if it is tilted around any in-plane axis that does not coincide with one of the array's lines of mirror symmetry of the MM pattern.
In this work a CCD effect has been investigated to characterize the extrinsic 2D chirality of the structure. Under oblique incidence, our structure gives rise to a giant CCD response in the mid- infrared (M-IR) region if only the two principle axes of the structure are not contained in the plane of incidence. The large magnitude of CCD is due to the large difference between the left-to-left and right-to-right circularly polarized reflectance conversion efficiencies. Our goal is to show that, by introducing a rectangular geometry in the lattice of MPAs based on metal-dielectric-metal (MDM) multilayers, one can obtain a giant 2D-chiral effect analogous to 2D-chiral MMs in the optical region, while having much simpler patterns that are easier to implement. Moreover, this achiral structure is ultrathin that may be integrated within today's nanophotonic systems. It may be useful for chiral sensing as well as possible applications in circular polarization transformers and waveplates.
Results
Metamaterials design and simulation method
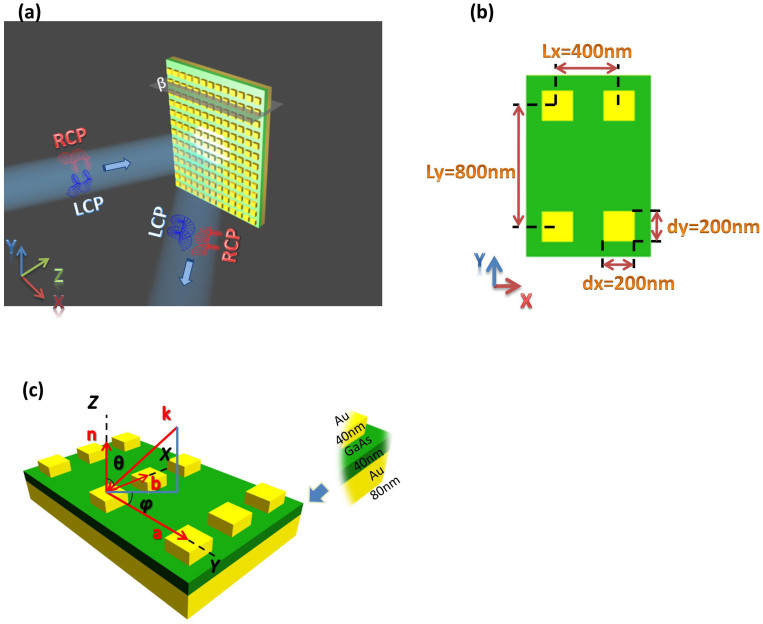
Figure 1(a) shows the schematic image of the proposed nonchiral MMs, which consists of two gold layers spaced by a 40 nm thick GaAs dielectric interlayer. The physical origin of high absorbance is the localization of magnetic and electric resonance moments in the metal-dielectric-metal structure. The top Au layer is a 40 nm thick square gold nanodisk array, where Lx = 400 nm denotes the short side of the rectangular lattice, Ly = 800 nm presents the long side of the rectangular lattice and the side length of the Au square is d = 200 nm. The bottom gold layer has a thickness of 80 nm, which is larger than the penetration depth of light in the optical regime. It will prevent incident light transmitting through the top two layers thus resulting in a nearly zero transmittance. Moreover, by pairing upper squares with a metal ground layer, strong electric and magnetic dipolar resonances are created to couple the incident light into the structure43. Therefore, it can be predicted that the difference in the absorbance (reflectance) for right-handed circularly polarized (RCP) and left-handed circularly polarized (LCP) incident waves may be large under off-normal incidence. The top view of the unit cell is shown in Fig. 1(b), while Fig. 1(c) shows the incident wavevector k, the vector normal to the surface n, and the two primitive lattice vectors (a and b) in red. The incident angle θ is measured between the wavevector k and the vector n. φ is the rotation angle between the parallel (to the x–y plane) component of the wavevector and the x axis. The z-axis is normal to the MM surface and the x-y plane is parallel to the surface. The structure is suspended in a vacuum and the Au squares are periodically extended along the x and y axes. Au is selected as the metal due to its stability and low ohmic loss. We use a finite difference time domain (FDTD) simulator from commercial software ‘3D EM Explorer Studio' to model the structure. The dielectric properties of Au as given by Johnson & Christy are used44. A plane wave is incident onto the structure at an oblique angle θ, as described in Fig. 1(c). Periodic boundary conditions were used in the x and y directions. The FDTD mesh size was 2 nm to provide an accurate calculation on the plasmonic effect. In 3D EM Explorer Studio, we can specify the phases for the Ep and Es components, where Ep is p polarization of the incident E-field and Es is s polarization of the incident E - field. The phase difference between Ep and Es is 90° for RCP and −90° for LCP incident light. The Ep and Es amplitudes are the same for both LCP and RCP.
Figure 1.
(a) Schematic of the MDM-MPAs. A plane wave is incident on the surface of the Au square array. The thicknesses of the Au squares, GaAs spacer, and Au mirror are 40, 40, and 80 nm, respectively. The whole structure is suspended in air. β is a cross-section through the structure along the x-z plane. (b) Illustration of absorber's rectangular lattice pattern, where the lattice constant in x direction is Lx = 400 nm and in y direction is Ly = 800 nm and the square dimension is dx = dy = 200 nm. (c) Demonstration of the wavevector (k), the vector normal to the surface (n), the two primitive lattice vectors (a or b) and the rotation angle φ in x–y plane, the components are marked in red.
Large circular conversion dichroism from a metal-dielectric-metal square array
The complex circular transmission and reflection matrices are defined as 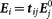 and
and 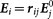 , where ‘i' and ‘j' are symbols for RCP (+) and LCP (−) components14. The intensities of the corresponding transmitted, reflected, and converted components for RCP and LCP incident light are denoted by
, where ‘i' and ‘j' are symbols for RCP (+) and LCP (−) components14. The intensities of the corresponding transmitted, reflected, and converted components for RCP and LCP incident light are denoted by 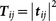 and
and 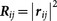 . It has been shown that total transmittance and reflectance through the planar MMs, defined as Tj
=
Tjj
+
Tij and Rj
=
Rjj
+
Rij may be different for circularly polarized waves of either opposite handedness or opposite incident directions11,12,13,14,15,16,17,18. However, in our proposed MDM-MPAs the bottom Au layer prevents incident light transmitting through the top two layers hence leading to a nearly zero transmittance. Therefore, here we are mainly focusing on the absolute difference in absorbance of RCP and LCP calculated as ΔA = A+ − A− where A± = 1 − T± − R±, as well as the efficiencies of conversion in reflectance (CCD
=
R−−
−
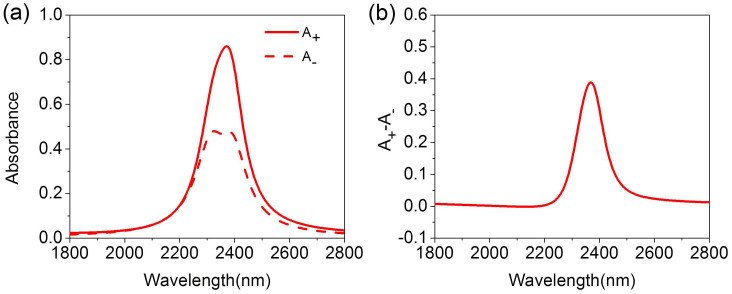
R++) for the circular polarized light incident on the upper square array. Figure 2(a) shows the absorbance for RCP (red solid line) and LCP (red dashed line) incident waves with θ = φ = 45°, Lx = 400 nm and Ly = 800 nm. Both RCP and LCP curves possess one main absorbance band. In particular, a near perfect absorbance for RCP incident light (A+ = 0.86) is achieved around the resonance wavelength of 2370 nm, whereas the highest absorbance deceases to A− = 0.47 for LCP light. The absorbance peaks stem from the electric and magnetic resonances in the MDM-MPAs, which can in turn contribute to the strong absorbance difference (ΔA) as large as 0.39 at 2370 nm shown in Fig. 2(b). Note that, here ΔA is due to the fact that the 2D extrinsic chirality arises from the mutual orientation of non-chiral unit cells and the direction of the light propagation1. Therefore, the absorbance of the proposed structure is strongly dependent on the state of circular polarization of the incident light.
. It has been shown that total transmittance and reflectance through the planar MMs, defined as Tj
=
Tjj
+
Tij and Rj
=
Rjj
+
Rij may be different for circularly polarized waves of either opposite handedness or opposite incident directions11,12,13,14,15,16,17,18. However, in our proposed MDM-MPAs the bottom Au layer prevents incident light transmitting through the top two layers hence leading to a nearly zero transmittance. Therefore, here we are mainly focusing on the absolute difference in absorbance of RCP and LCP calculated as ΔA = A+ − A− where A± = 1 − T± − R±, as well as the efficiencies of conversion in reflectance (CCD
=
R−−
−
R++) for the circular polarized light incident on the upper square array. Figure 2(a) shows the absorbance for RCP (red solid line) and LCP (red dashed line) incident waves with θ = φ = 45°, Lx = 400 nm and Ly = 800 nm. Both RCP and LCP curves possess one main absorbance band. In particular, a near perfect absorbance for RCP incident light (A+ = 0.86) is achieved around the resonance wavelength of 2370 nm, whereas the highest absorbance deceases to A− = 0.47 for LCP light. The absorbance peaks stem from the electric and magnetic resonances in the MDM-MPAs, which can in turn contribute to the strong absorbance difference (ΔA) as large as 0.39 at 2370 nm shown in Fig. 2(b). Note that, here ΔA is due to the fact that the 2D extrinsic chirality arises from the mutual orientation of non-chiral unit cells and the direction of the light propagation1. Therefore, the absorbance of the proposed structure is strongly dependent on the state of circular polarization of the incident light.
Figure 2. Spectra for right and left circularly polarized light incident at angle θ = φ = 45° (a) the absorbance of MDM-MPAs with Lx = 400 nm and Ly = 800 nm; (b) ΔA = A+ − A− for MDM-MPAs with Lx = 400 nm and Ly = 800 nm at θ = φ = 45°.
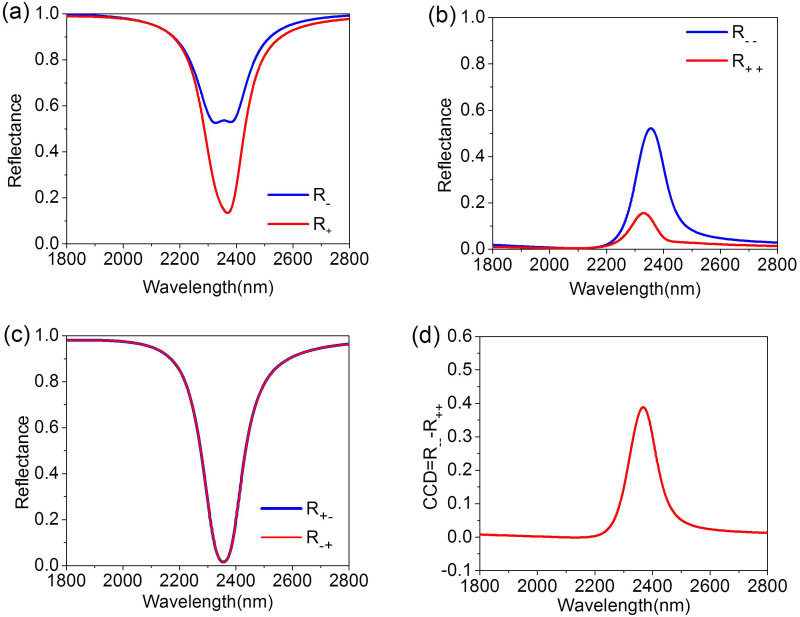
Although our proposed MDM-MPA exhibits a near zero transmittance, one could alternatively take advantage of the reflectance spectra for the possible applications of the chiroptical response since the difference of the reflectance of the structure ΔR = R+ − R− is also large for the different circular polarized incident light, where R+ = R++ + R−+ and R− = R−− + R+−. Here, R++, R−−, R−+, R+− correspond to right-to-right, left-to-left, left-to-right and right-to-left polarized reflectance conversion efficiencies. Figure 3(a) shows that the reflectance at 2370 nm is R+ = 0.14 for the RCP and R− = 0.53 for the LCP incident light. Nevertheless, ΔR cannot distinguish between extrinsic 3D chirality (circular dichroism) and 2D chirality (circular conversion dichroism). In order to resolve this problem, we further look at R++, R−−, R+− and R−+. As can be seen in Fig. 3(b), the diagonal elements R−− and R++ are not identical indicating that our structure exhibits an extrinsically 2D-chiral reflectance effect, where the circular conversion dichroism is expressed by the difference between the magnitudes of the diagonal elements CCD = R−− − R++ shown in Fig. 3(d). Figure 3(c) shows that the off-diagonal elements of the matrix R−+ and R+− are equal showing the absence of an extrinsic 3D chirality namely a circular dichroism, which is expressed as CD = R−+ − R+−. However, the MDM-MPA does not show the asymmetric transmission phenomenon due to the effect of zero transmission.
Figure 3. Spectra for right and left circularly polarized light incident at angle θ = φ = 45° (a) the spectra of R− and R+; (b) the spectra of R−− and R++; (c) the spectra of R+− and R−+; (d) the spectra of CCD = R−− − R++ of MDM-MPAs with Lx = 400 nm and Ly = 800 nm.
The giant CCD results from the coupling between the MDM multilayers, which gives rise to a strong magnetic response. Such a strong magnetic dipolar moment is connected to an antisymmetric charge-oscillation eigenmode, providing the combined plasmon mode a twist in the propagation direction of the wave to imitate 2D chirality45. To shed more light on the origin of the large 2D-chiroptical response, we then look at the electromagnetic field distribution in the MDM-MPAs induced by the off-normal incident light. The distributions of total electric field intensity 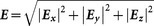 , total magnetic field intensity
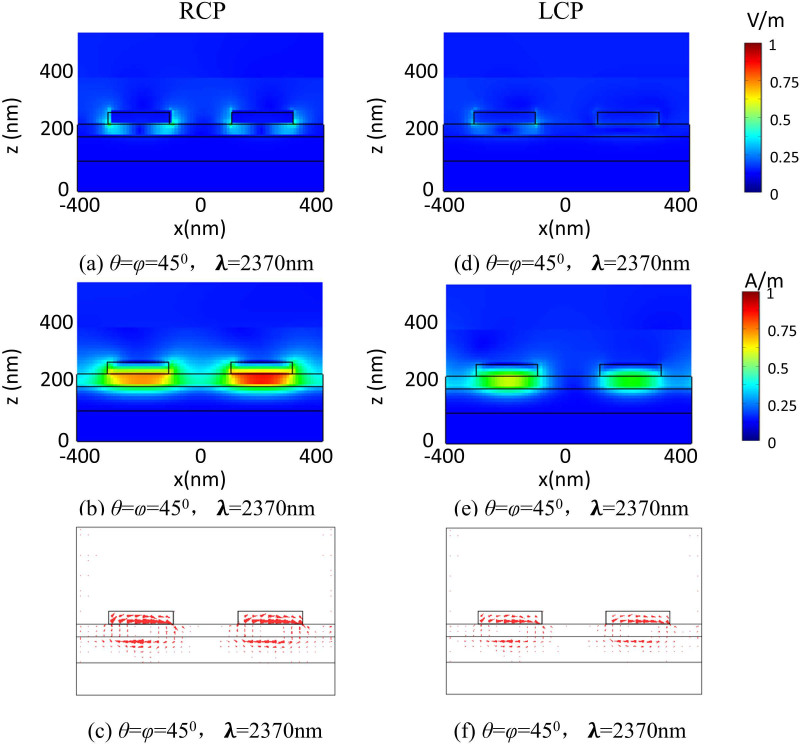
, total magnetic field intensity 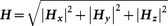 and displacement current (JD) along β plane associated with A+ = 0.86 at λ = 2370 nm for the RCP incident light at θ = φ = 45° are shown in Fig. 4(a)–4(c). In the field maps of Fig. 4, the arrows show JD whereas the color shows the magnitude of the electric field and magnetic field. Figure 4(a) shows that the E field can be localized in both the aperture between the Au squares and the GaAs dielectric interlayer. Meanwhile, as can be seen in Fig. 4(b) the H field is efficiently confined in the GaAs layer between the Au layers. This is due to the formation of the JD loops shown in Fig. 4(c) and a concomitant coupling between surface plasmons counterpropagating on the two closely spaced interfaces46. Therefore, this structure provides a simultaneous excitation of an electric and magnetic resonance moment to enhance the localized electromagnetic fields. Correspondingly, the structure exhibits a near perfect absorbance for the RCP incident light. Figure 4(d)–4(f) show E, H and JD respectively, associated with A− = 0.47 at λ = 2370 nm for the LCP incident light at θ = φ = 45°. It shows that the patterns of E and H field distribution are similar with the ones for the RCP incident wave, which indicates that the electric and magnetic dipolar resonances are also simultaneously excited to lead to a main peak in the absorbance spectra. However, both E and H field intensities are weaker, which is consistent with the much lower absorbance shown in Fig. 2(a).
and displacement current (JD) along β plane associated with A+ = 0.86 at λ = 2370 nm for the RCP incident light at θ = φ = 45° are shown in Fig. 4(a)–4(c). In the field maps of Fig. 4, the arrows show JD whereas the color shows the magnitude of the electric field and magnetic field. Figure 4(a) shows that the E field can be localized in both the aperture between the Au squares and the GaAs dielectric interlayer. Meanwhile, as can be seen in Fig. 4(b) the H field is efficiently confined in the GaAs layer between the Au layers. This is due to the formation of the JD loops shown in Fig. 4(c) and a concomitant coupling between surface plasmons counterpropagating on the two closely spaced interfaces46. Therefore, this structure provides a simultaneous excitation of an electric and magnetic resonance moment to enhance the localized electromagnetic fields. Correspondingly, the structure exhibits a near perfect absorbance for the RCP incident light. Figure 4(d)–4(f) show E, H and JD respectively, associated with A− = 0.47 at λ = 2370 nm for the LCP incident light at θ = φ = 45°. It shows that the patterns of E and H field distribution are similar with the ones for the RCP incident wave, which indicates that the electric and magnetic dipolar resonances are also simultaneously excited to lead to a main peak in the absorbance spectra. However, both E and H field intensities are weaker, which is consistent with the much lower absorbance shown in Fig. 2(a).
Figure 4.
3D-FDTD simulation of (a) total electric field intensity distribution, (b) total magnetic field intensity distribution, and (c) displacement current (JD) distribution for the RCP incident light at θ = φ = 45° where λ = 2370 nm. Simulation of (d) total electric field intensity distribution, (e) total magnetic field intensity distribution, and (f) displacement current (JD) distribution for the LCP incident light at θ = φ = 45° where λ = 2370 nm.
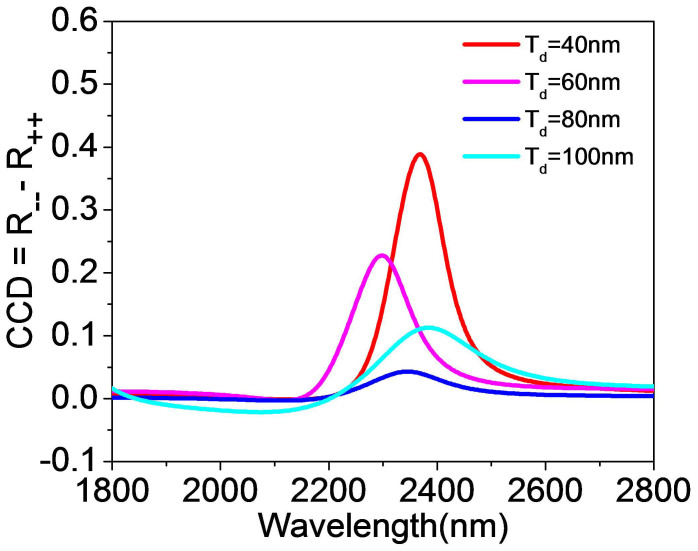
The thickness of the dielectric layer is important since it affects the dipole resonance, i.e. the resonance effect is diminished and the absorbance is reduced (reflectance is increased) with increasing thickness43. A comparison of CCD response at angle θ = φ = 45° for the different thicknesses of GaAs dielectric interlayer Td = 40 nm, 60 nm, 80 nm and 100 nm is presented in Fig. 5. It can be seen that the various thicknesses of the dielectric interlayer have a significant effect on the value and frequency band of the CCD curve: the maximum CCD is decreased and the spectra of the CCD is shifted as the thickness of GaAs layer is increased. It is because the frequency of the magnetic resonant dipole in the MDM-MPAs is shifted once we change the dielectric layer thickness, thus the magnetic moment needs to be relocated by means of redesigning the geometry of the Au squares to obtain the impedance match to a vacuum47. As a result, the best performance of the 2D-chiral effect may appear at diverse angles of oblique incident wave for the various Td.
Figure 5. Circular conversion dichroism for φ = θ = 45° with different thicknesses of GaAs dielectric interlayer in MDM-MPAs.
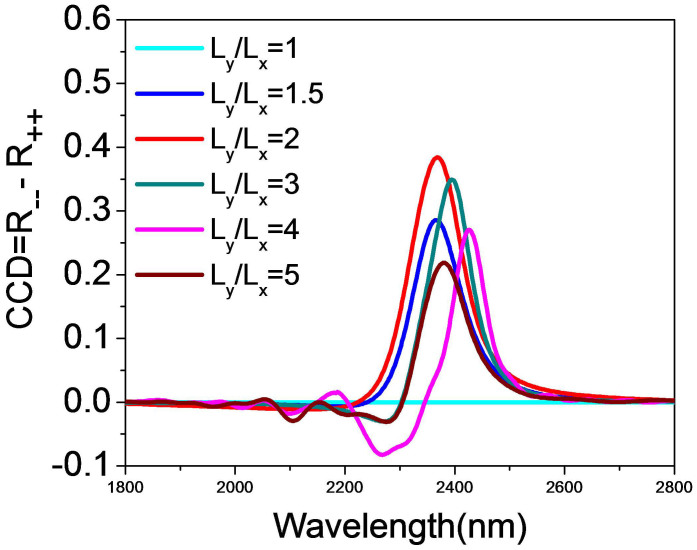
To show how the CCD spectra evolve when changing the ratios of the sides of the rectangular lattice (Ly/Lx), we show in Fig. 6 the CCD evolution for fixed Lx = 400 nm and θ = φ = 45° as the values of the Ly of the rectangular lattice are varied. It appears that we are unable to obtain a 2D-chiral response (CCD = 0) for a square array of the Au squares (Lx = Ly = 400 nm) at φ = 45° as the plane of incidence falls on a line of mirror symmetry of the structure. By increasing the ratio of Ly/Lx, the value of CCD is gradually increased. However, for larger ratio values of Ly/Lx, the CCD response is suppressed. This is most likely due to the fact that the coupling of neighboring Au squares along the y direction is reduced by increasing the value of Ly, since the rectangular lattice becomes dilute.
Figure 6. Circular conversion dichroism for φ = θ = 45° with different ratios of Ly/Lx in the MDM-MPAs.
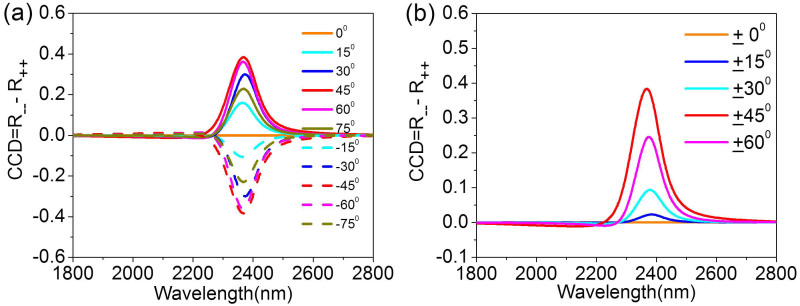
Figure 7(a) presents the CCD spectra for different values of rotation angle φ at a fixed incident angle θ = 45°. The spectral band and shape of the CCD spectra depend weakly on φ. The maximum value of CCD increases with φ, whereas it starts being reduced when φ becomes larger than 45°. We note that the circular difference effects vanishes for the structure orientation φ = 0° and 90°, in which case the anisotropic axis of the structure is in the incident plane hence leading to a mirror plane of the experimental geometry48. Importantly, the CCD spectra reverse the sign for opposite values of φ, which corresponds to two enantiomeric arrangements. This will certainly eliminate various problems with the fabrication of exact mirror image left- and right- intrinsically chiral structures. In Fig. 7(b), we also study the θ effect on the CCD spectra by fixing φ = 45°. As expected, there is no chiroptical response at normal incidence (θ = 0°). Particularly, the CCD response increases with θ, it can be significantly enhanced for θ > 30° and obtains the maximum value of 0.39 at 2370 nm for θ = 45°. Therefore, in our simulation the 2D-chiroptical response is optimized at φ = θ = 45°. Particularly, opposite signs of incidence lead to the same chiroptical effect. Namely, the spectra of CCD shown in Fig. 7(b) do not reverse for opposite angles of incidence13, which satisfies the definition of extrinsic 2D chirality.
Figure 7. Circular conversion dichroism for (a) θ = 45° incidence with different values of φ; (b) φ = 45° incidence with different values of θ.
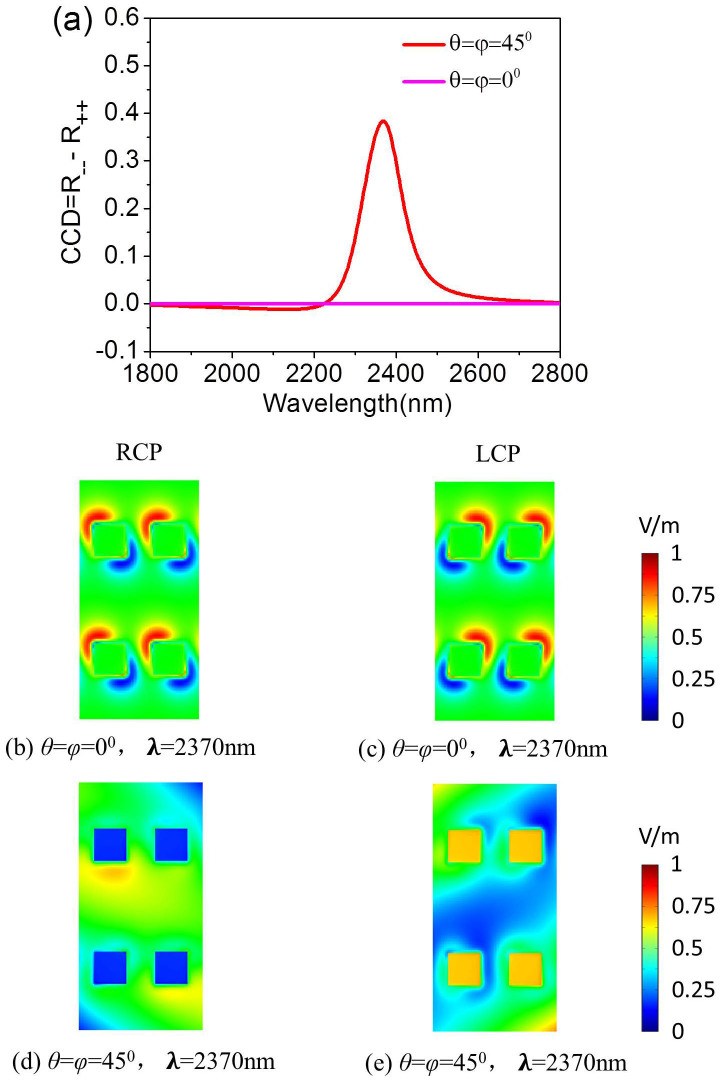
In Fig. 8(a), we present two CCD spectra for normal (θ = φ = 0°) incidence where 2D chirality is absent, and for oblique (θ = φ = 45°) incidence where a substantial 2D-chiroptical response exists. Figure 8(b)–8(c) show the snapshots of the E field distributions at λ = 2370 nm on the Au square array-air interface with RCP and LCP incident waves under normal incidence (θ = φ = 0°), it shows that the field patterns for the two circular polarization are exact mirror images of each other. The difference of these field patterns cancels out hence leading to a zero CCD. Figure 8(d)–8(e) show that on tilting the structure i.e. θ = φ = 45°, the field patterns are very different between the different circularly polarized waves and a clear asymmetry appears in the snapshots, which is due to the fact that a various, asymmetric plasmon modes are excited by the RCP and LCP waves. Moreover, the E field is not distributed uniformly over the square array under the off-normal incidence. It is because that the time of the pulse propagating through different regions of the structure is unequal. Different circularly polarized light gives rise to the phase of the various resonance modes that cause constructive or deconstructive interferences of the modes at the squares. This results in a significant difference in the reflectance and absorbance of the structure between the RCP and LCP waves.
Figure 8.
(a) FDTD simulation of the circular conversion dichroism spectra of the MDM-MPA at normal (θ = φ = 0°) and oblique (θ = φ = 45°) incidences. (b) Snapshots of normalized electric field distribution at the Au square array-air during light propagation through the MDM-MPA with θ = φ = 0° at λ = 2370 nm for RCP incident light. (c) Snapshots of normalized electric field distribution at the Au square array-air during light propagation through the MDM-MPA with θ = φ = 0° at λ = 2370 nm for LCP incident light. (d) Snapshots of normalized electric field distribution at the Au square array-air during light propagation through the MDM-MPA with θ = φ = 45° at λ = 2370 nm for RCP incident light. (e) Snapshots of normalized electric field distribution at the Au square array-air during light propagation through the MDM-MPA with θ = φ = 45° at λ = 2370 nm for LCP incident light.
Discussion
In conclusion, we have demonstrated that a large extrinsically 2D-chiroptical response in the M-IR region can be observed in highly symmetric plasmonic square arrays based on MDM multilayers, where the Au squares occupy the sites of a rectangular lattice. This extrinsic 2D chirality results from the mutual orientation of the MDM-MPAs and the oblique incident wave. It is thought that the giant CCD is related to the strong magnetic dipole moment. Furthermore, our structure can obtain the two “enantiomers” from the same array by tilting at opposite angles of in-plane rotation (φ), which will avoid the problems with the fabrication of exact mirror image left- and right- intrinsically chiral structures. Our structure may be directly integrated into nanophotonic devices owing to its ultrathin profile. Its simple geometry is very amenable to large area advanced nanofabrication techniques and could thus become an important enabling technology in numerous photonics applications. Our proposed concept may be easily scaled down to the shorter wavelength region for a variety of exciting applications in the visible regime.
Methods
For the numerical calculations, we used the finite difference time domain (FDTD) Method by means of commercial software ‘3D EM Explorer Studio'. The scheme of the nonchiral MMs is shown in Fig. 1(a), the top view of the unit cell is shown in Fig. 1(b), while Fig. 1(c) shows the incident wavevector k, the vector normal to the surface n, and the two primitive lattice vectors (a and b) in red. The incident light is incident onto the structure at an oblique angle θ in order to achieve the extrinsic 2D chirality. To account for the periodic nature of the MM, the model boundary at 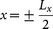 and
and 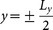 is set to periodic boundary conditions, respectively. Perfect matched layer is applied in the z direction. The optical constant of gold is taken from the data of Johnson and Christy41. The FDTD mesh size was 2 nm to provide an accurate calculation on the plasmonic effect. In 3D EM Explorer Studio, we can specify the phases for the Ep and Es components, where Ep is p polarization of the incident E-field and Es is s polarization of the incident E - field. The phase difference between Ep and Es is 90° for RCP and −90° for LCP incident light. The Ep and Es amplitudes are the same for both LCP and RCP.
is set to periodic boundary conditions, respectively. Perfect matched layer is applied in the z direction. The optical constant of gold is taken from the data of Johnson and Christy41. The FDTD mesh size was 2 nm to provide an accurate calculation on the plasmonic effect. In 3D EM Explorer Studio, we can specify the phases for the Ep and Es components, where Ep is p polarization of the incident E-field and Es is s polarization of the incident E - field. The phase difference between Ep and Es is 90° for RCP and −90° for LCP incident light. The Ep and Es amplitudes are the same for both LCP and RCP.
Author Contributions
T.C. conceived the idea of using plasmonic nanorods array based on MDM multilayers, where the Au squares occupy the sites of a rectangular lattice, for obtaining a large extrinsically 2D-chiral response in the M-IR region. T.C. designed the metamaterial and performed numerical analysis. C.W.W. and L.B.M. carried out the simulations, Y.L. prepared the figures. T.C. supervised the research and wrote the manuscript.
Acknowledgments
We acknowledge the financial support from National Natural Science Foundation of China (Grant No. 61172059 and 51302026), Ph.D Programs Foundation of Ministry of Education of China (Grant No. 20110041120015), Postdoctoral Gathering Project of Liaoning Province (Grant No. 2011921008), and The Fundamental Research for the Central University (Grant No. DUT14YQ109).
References
- Plum E., Fedotov V. A. & Zheludev N. I. Extrinsic electromagnetic chirality in metamaterials. J. Opt. A: Pure Appl. Opt. 11, 074009 (2009). [Google Scholar]
- Cui Y., Kang L., Lan S., Rodrigues S. & Cai W. Giant Chiral Optical Response from a Twisted-Arc Metamaterial. Nano Lett. 14, 1021–1025 (2014). [DOI] [PubMed] [Google Scholar]
- Ranjbar B. & Gill P. Circular Dichroism Techniques: Biomolecular and Nanostructural Analyses- A Review. Chem. Biol. Drug Des. 74, 101–120 (2009). [DOI] [PubMed] [Google Scholar]
- Hwang J. et al. Electro-tunable optical diode based on photonic bandgap liquid-crystal heterojunctions. Nat. Mater. 4, 383–387 (2005). [DOI] [PubMed] [Google Scholar]
- Kopp V. I., Fan B., Vithana H. K. M. & Genack A. Z. Low-threshold lasing at the edge of a photonic stop band in cholesteric liquid crystals. Opt. Lett. 23, 1707–1709 (1998). [DOI] [PubMed] [Google Scholar]
- Fullman R. L. & Wood D. L. Origin of spiral eutectic structures L'origine des structures eutectiques, spiraliformes Der ursprung der eutektischen spiralstrukturen. Acta Metall. 2, 188 (1954). [Google Scholar]
- Ziolkowski R. W. & Engheta N. [INTRODUCTION, HISTORY, AND SELECTED TOPICS IN FUNDAMENTAL THEORIES OF METAMATERIALS]. Metamaterials: Physics and Engineering Explorations [Engheta, N. & Ziolkowski, R. W.(ed.)] [5–37] (John Wiley & Sons & IEEE Press, New Jersey, 2006). [Google Scholar]
- Liu Y. & Zhang X. Metamaterials: a new frontier of science and technology. Chem. Soc. Rev. 40, 2494–2507 (2011). [DOI] [PubMed] [Google Scholar]
- Plum E., Fedotov V. A., Schwanecke A. S., Zheludev N. I. & Chen Y. Giant optical gyrotropy due to electromagnetic coupling. Appl. Phys. Lett. 90, 223113 (2007). [Google Scholar]
- Plum E. et al. Metamaterial with negative index due to chirality. Phys. Rev. B 79, 035407 (2009). [Google Scholar]
- Plum E. et al. Metamaterials: optical activity without chirality. Phys. Rev. Lett. 102, 113902 (2009). [DOI] [PubMed] [Google Scholar]
- Plum E., Fedotov V. A. & Zheludev N. I. Optical activity in extrinsically chiral metamaterial. Appl. Phys. Lett. 93, 191911 (2008). [Google Scholar]
- Plum E., Fedotov V. A. & Zheludev N. I. Asymmetric transmission: a generic property of two-dimensional periodic patterns. J. Opt. 13, 024006 (2011). [Google Scholar]
- Plum E., Fedotov V. A. & Zheludev N. I. Planar metamaterial with transmission and reflection that depend on the direction of incidence. Appl. Phys. Lett. 94, 131901 (2009). [Google Scholar]
- Singh R., Plum E., Zhang W. & Zheludev N. I. Highly tunable optical activity in planar achiral terahertz metamaterials. Opt. Express 18, 13425–13430 (2010). [DOI] [PubMed] [Google Scholar]
- Schwanecke A. S. et al. Nanostructured Metal Film with Asymmetric Optical Transmission. Nano Lett. 8, 2940–2943 (2008). [DOI] [PubMed] [Google Scholar]
- Fedotov V. A., Schwanecke A. S. & Zheludev N. I. Asymmetric Transmission of Light and Enantiomerically Sensitive Plasmon Resonance in Planar Chiral Nanostructures. Nano Lett. 7, 1996–1999 (2007). [Google Scholar]
- Fedotov V. A. et al. Asymmetric Propagation of Electromagnetic Waves through a Planar Chiral Structure. Phys. Rev. Lett. 97, 167401 (2006). [DOI] [PubMed] [Google Scholar]
- Menzel C. et al. Asymmetric Transmission of Linearly Polarized Light at Optical Metamaterials. Phys. Rev. Lett. 104, 253902 (2010). [DOI] [PubMed] [Google Scholar]
- Shi J. H. et al. Dual-band asymmetric transmission of linear polarization in bilayered chiral metamaterial. Appl. Phys. Lett. 102, 191905 (2013). [Google Scholar]
- Shi J. H. et al. Broadband chirality and asymmetric transmission in ultrathin 90°-twisted Babinet-inverted metasurfaces. Phys. Rev. B 89, 165128 (2014). [Google Scholar]
- Xu Y. Q., Shi Q. C., Zhu Z. & Shi J. H. Mutual conversion and asymmetric transmission of linearly polarized light in bilayered chiral metamaterial. Opt. Express 22, 25679–25688 (2014). [DOI] [PubMed] [Google Scholar]
- Gansel J. K. et al. Gold helix photonic metamaterial as broadband circular polarizer. Science 325, 1513–1515 (2009). [DOI] [PubMed] [Google Scholar]
- Christofi A., Stefanou N., Gantzounis G. & Papanikolaou N. Giant Optical Activity of Helical Architectures of Plasmonic Nanorods. J. Phys. Chem. C. 116, 16674–16679 (2012). [Google Scholar]
- Mutlu M., Akosman A. E., Serebryannikov A. E. & Ozbay E. Asymmetric chiral metamaterial circular polarizer based on four U-shaped split ring resonators. Opt. Lett. 36, 1653–1655 (2011). [DOI] [PubMed] [Google Scholar]
- Gao W. et al. Circular dichroism in single-layered gold sawtooth gratings. J. Opt. Soc. Am. B. 29, 3021–3026 (2012). [Google Scholar]
- Cao T. et al. Strongly tunable circular dichroism in gammadion chiral phase-change metamaterials. Opt. Express. 21, 27841–27851 (2013). [DOI] [PubMed] [Google Scholar]
- Zhao Y., Belkin M. A. & Alù A. Twisted optical metamaterials for planarized ultrathin broadband circular polarizers. Nat. Commun. 3, 870 (2012). [DOI] [PubMed] [Google Scholar]
- Yannopapas V. Circular dichroism in planar nonchiral plasmonic metamaterials. Opt. Lett. 34, 632–634 (2009). [DOI] [PubMed] [Google Scholar]
- Shi J. H. et al. Tunable symmetric and asymmetric resonances in an asymmetrical split-ring metamatrial. J. Appl. Phys. 112, 073522 (2012). [Google Scholar]
- Feng C., Wang Z. B., Lee S., Jiao J. & Li L. Giant circular dichroism in extrinsic chiral metamaterials excited by off-normal incident laser beams. Opt. Commun. 285, 2750–2754 (2012). [Google Scholar]
- Maoz B. M., Moshe A. B., Vestler D., Bar-Elli O. & Markovich G. Chiroptical Effects in Planar Achiral Plasmonic Oriented Nanohole Arrays. Nano Lett. 12, 2357–2361 (2012). [DOI] [PubMed] [Google Scholar]
- Volkov S. N. et al. Optical activity in diffraction from a planar array of achiral nanoparticles. Phys. Rev. A. 79, 043819 (2009). [Google Scholar]
- Zhang P. et al. Giant circular polarization conversion in layer-by-layer nonchiral metamaterial. J. Opt. Soc. Am. A. 30, 1714–1718 (2013). [DOI] [PubMed] [Google Scholar]
- Landy N. I., Sajuyigbe S., Mock J. J., Smith D. R. & Padilla W. J. Perfect Metamaterial Absorber. Phys. Rev. Lett. 100, 207402 (2008). [DOI] [PubMed] [Google Scholar]
- Feng Q., Pu M., Hu C. & Luo X. Engineering the dispersion of metamaterial surface for broadband infrared absorption. Opt. Lett. 37, 2133–2135 (2012). [DOI] [PubMed] [Google Scholar]
- Wang J. et al. Tunable broad-band perfect absorber by exciting of multiple plasmon resonances at optical frequency. Opt. Express. 20, 14871–14878 (2012). [DOI] [PubMed] [Google Scholar]
- Fedotov V. A., Mladyonov P. L., Prosvirnin S. L. & Zheludev N. I. Planar electromagnetic metamaterial with a fish scale structure. Phys. Rev. E 72, 056613 (2005). [DOI] [PubMed] [Google Scholar]
- Shrekenhamer D., Chen W. & Padilla W. J. Liquid Crystal Tunable Metamaterial Absorber. Phys. Rev. Lett. 110, 177403 (2013). [DOI] [PubMed] [Google Scholar]
- García-Etxarri A. & Dionne J. A. Surface-enhanced circular dichroism spectroscopy mediated by nonchiral nanoantennas. Phys. Rev. B 87, 235409 (2013). [Google Scholar]
- Tang Y. & Cohen A. E. Optical Chirality and Its Interaction with Matter. Phys. Rev. Lett. 104, 163901 (2010). [DOI] [PubMed] [Google Scholar]
- Tang Y. & Cohen A. E. Enhanced Enantioselectivity in Excitation of Chiral Molecules by Superchiral Light. Science 332, 333–336 (2011). [DOI] [PubMed] [Google Scholar]
- Zhang B. et al. Polarization-independent dual-band infrared perfect absorber based on a metal-dielectric-metal elliptical nanodisk array. Opt.Express. 19, 15221–15228 (2011). [DOI] [PubMed] [Google Scholar]
- Johnson P. B. & Christy R. W. Optical constants of the noble metals. Phys. Rev. B. 6, 4370–4379 (1972). [Google Scholar]
- Decker M., Klein M. W., Wegener M. & Linden S. Circular dichroism of planar chiral magnetic metamaterials. Opt. Lett. 32, 856–858 (2007). [DOI] [PubMed] [Google Scholar]
- Dayal G. & Ramakrishna S. A. Design of highly absorbing metamaterials for Infrared frequencies. Opt. Express 20, 17503–17508 (2012). [DOI] [PubMed] [Google Scholar]
- García-Meca C. et al. Double-negative polarization independent fishnet metamaterial in the visible spectrum. Opt. Lett. 34, 1603–1605 (2009). [DOI] [PubMed] [Google Scholar]
- Verbiest T., Kauranen M., Persoons A. & Persoons A. Optical activity of anisotropic achiral surfaces. Phys. Rev. Lett. 77, 1456–1459 (1996). [DOI] [PubMed] [Google Scholar]