On the failure load and mechanism of polycrystalline graphene by nanoindentation

Abstract

Nanoindentation has been recently used to measure the mechanical properties of polycrystalline graphene. However, the measured failure loads are found to be scattered widely and vary from lab to lab. We perform molecular dynamics simulations of nanoindentation on polycrystalline graphene at different sites including grain center, grain boundary (GB), GB triple junction, and holes. Depending on the relative position between the indenter tip and defects, significant scattering in failure load is observed. This scattering is found to arise from a combination of the non-uniform stress state, varied and weakened strengths of different defects, and the relative location between the indenter tip and the defects in polycrystalline graphene. Consequently, the failure behavior of polycrystalline graphene by nanoindentation is critically dependent on the indentation site, and is thus distinct from uniaxial tensile loading. Our work highlights the importance of the interaction between the indentation tip and defects, and the need to explicitly consider the defect characteristics at and near the indentation site in polycrystalline graphene during nanoindentation.

Large-area, monolayer graphene grown by chemical vapor deposition (CVD) is often polycrystalline in nature and therefore contains internal grain boundaries (GBs) as well as GB junctions¹,²,³,⁴,⁵,⁶,⁷,⁸. The effect of GBs on the mechanical properties of polycrystalline graphene has attracted great attention as defects often dictate its strength. Several groups have carried out experiment and modeling to study the strength of polycrystalline graphene and report the correlations between GBs and mechanical properties⁹,¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶. In Grantab et al.'s molecular dynamics (MD) simulations⁹, a bicrystalline graphene with specific arrangement of pentagons and heptagons along straight GBs was modeled. It was reported that GBs with large tilt angles can achieve near-intrinsic strength of graphene in its pristine form. Recently, Rasool et al.'s experiment¹⁷ on bicrystal graphene membrane prepared by CVD supported Grantab et al.'s finding.

In reality, there must be GB junctions in the polycrystalline graphene¹⁴. In addition, atomic force microscopy (AFM) nanoindentation has been used to measure the mechanical properties of polycrystalline graphene in experiment¹²,¹⁸,¹⁹. Some of these studies¹⁰,¹³ showed that GBs severely weaken the failure load of polycrystalline graphene, while other studies, for example, Lee et al.¹² and Rasool et al.¹⁷ reported that the failure load is only slightly reduced despite the presence of GBs. The measured failure loads of polycrystalline graphene in these AFM nanoindentations are found to be widely scattered and vary not only from lab to lab, but also from one indentation to another within the same lab. Furthermore, it is worth mentioning that it remains a challenge to experimentally observe the atomic-scale rupture process in the nanoindentation of polycrystalline graphene due to the buried contact between two bodies²⁰, making it difficult to understand the failure load scattering observed in experiment. Clearly an in-depth understanding of the origin of this scattering and the failure process of polycrystalline graphene under nanoindentation is of both scientific interest and technological significance.

In this paper, we perform a series of large-scale MD simulations of nanoindentation on polycrystalline graphene by varying indentation locations, including the center of grain, GB, GB triple junction, and hole, to answer the following questions: (1) What is the correlation between the scattering of the failure loads and the different defect types and indentation locations? (2) What is the physical origin of this failure load scattering? (3) What is the atomic-scale failure mechanism of polycrystalline graphene by nanoindentation? And (4) What is the difference in the rupture process between nanoindentation and uniaxial tensile loading? Our present study reveals that depending on the relative position between the indenter tip and defects, significant scattering in failure load is observed. This scattering is found to arise from a combination of the non-uniform stress state in the polycrystalline graphene, varied strengths for different types of defects, and the relative position between the indenter tip and the defects. Our work also shows that the rupture of polycrystalline graphene starts directly from a defect when the defect is right beneath the indentation tip, while the rupture of polycrystalline graphene starts from a nearby GB when the indentation site is at the center of grain. This failure process by nanoindentation is in contrast to that by uniaxial tensile loading, in which rupture starts preferentially at a GB junction. Our study shows that the measured mechanical properties of polycrystalline graphene by nanoindentation, such as the failure loads and the failure mechanism, are strongly dependent on the indentation location.

Results

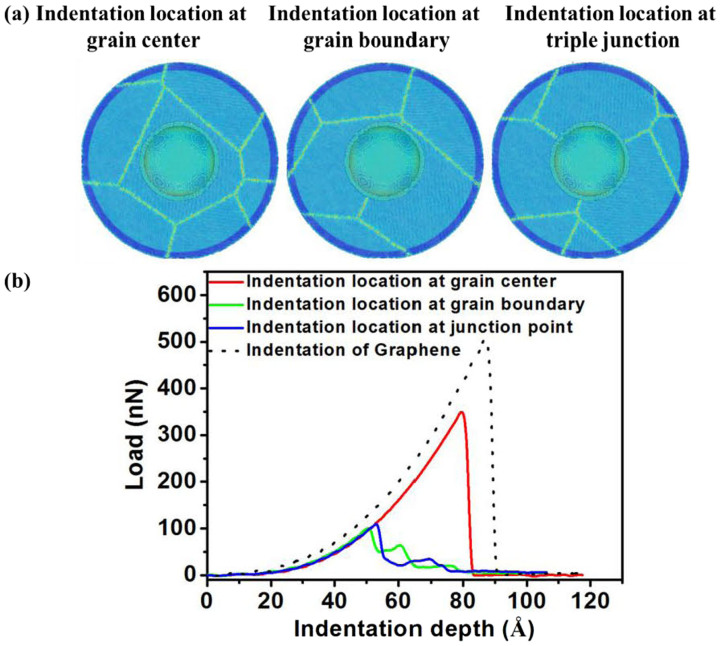
Figure 1(a) shows the top views of three different indentation locations, with the indenter tip placed directly on top of the grain center, GB, and GB triple junction, respectively. The normal load vs. indentation depth (d) curves for these three different indentation locations are shown in Fig. 1(b). The single-crystal graphene indentation result is also plotted for comparison. Our results show that the failure loads of polycrystalline graphene are lower than that of single-crystal graphene. Meanwhile, the failure loads of polycrystalline graphene are found to be widely scattered. On the one hand, the failure load for the indenter tip on top of the grain center is 30% smaller than but still at least comparable to that for single-crystal graphene. On the other hand, the failure loads for the indenter tip on top of GB and GB triple junction are 80% smaller than that for single-crystal graphene. Hence, our results in Fig. 1 clearly reveal the significant failure load scattering caused by different indentation locations. Besides, it should be noted that the failure load is not the same as the failure strength. It was found that although the failure loads measured by nanoindentation may have a wide distribution, the distribution in fracture strength is actually quite narrow¹²,¹⁹.

Figure 1. Failure measurements of the polycrystalline graphene indented at three different locations.

(a) The top views of indentation location at the grain center (left panel), GB (middle panel), and GB triple junction (right panel). Atoms are colored according to their von Mises stress. (b) The normal load vs. indentation depth (d) curves for three different indentation locations. The single-crystal graphene indentation result is plotted for comparison. Significant scattering in the failure load is observed for indentation on different locations.

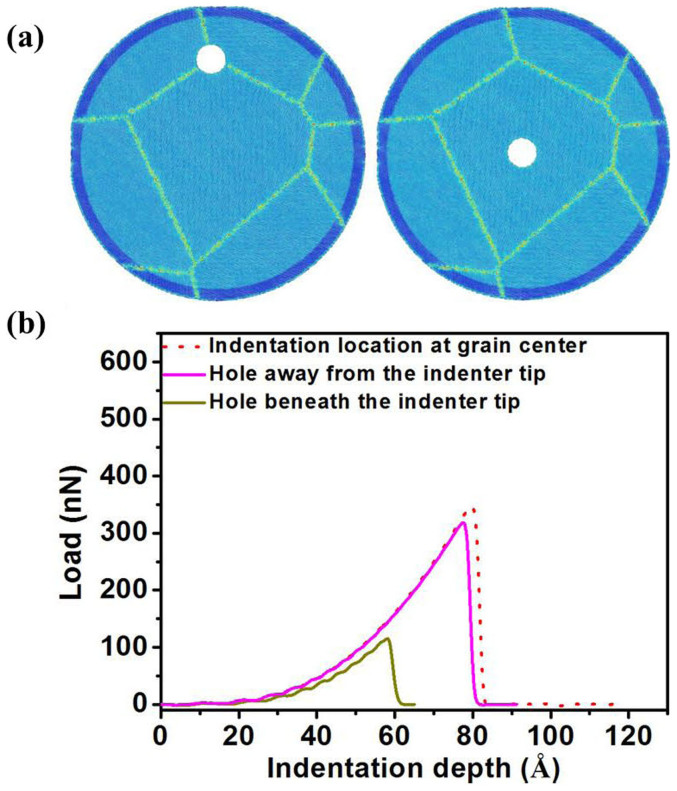
Some other defects, such as hole, are inevitable either because of the production process or because of the environmental and operating conditions²¹,²²,²³,²⁴. In our indentation tests, a hole with a radius of 2.5 nm is placed both under and a distance away from the indenter tip. Figure 2(a) displays these two scenarios: a hole is positioned right beneath the indenter tip and a hole is a distance away from the indenter tip which is positioned right on top of a grain center. The corresponding normal load vs. indentation depth curves are shown in Fig. 2(b). Apparently, the relative position between the indenter tip and hole gives rise to a large difference in failure load. It is seen that the failure load is not related to the defect hole provided that the hole is away from the indenter tip. However, the failure load is significantly decreased when the hole is placed under the indenter tip. This is consistent with a recent experiment, in which a significant drop in the mechanical properties of graphene containing vacancy defects was observed²³. Hence, our results in Fig. 2 clearly reveal another possible scattering in failure load, which originates from the interaction between the indenter tip and hole. In our MD simulations, we only consider two extreme cases, as shown in Fig. 2, that is, the hole is placed right beneath the indenter tip and the hole is placed at a distance away from the indenter tip. For the former, the failure load is significantly decreased; while for the latter, the change in the failure load is insignificant. In real experiments, if the hole and the tip are misaligned, the change of the failure load is expected to fall in between the two extremes.

Figure 2. Failure measurements of the polycrystalline graphene in the presence of a hole.

(a) A hole exists right beneath the indenter tip (right panel) and at a GB junction (left panel) away from the indenter tip which is positioned on top of a grain center. The color indicates the von Mises stress. (b) The normal load vs. indentation depth curves. The dotted line represents the indentation result without a hole. It is seen that the relative position between the indenter tip and the hole gives rise to the large difference in failure load.

Our MD simulation results in Figs. 1 and 2 clearly demonstrate the high sensitivity of the measured failure load to the relative position between the indenter tip and defects, and the significant scattering in failure load with varying indentation locations, such as the grain center, GB, GB triple junction, and hole. To further understand the origin of this failure load scattering, the single-crystal graphene indentation is also investigated (See Supplementary Fig. S3). For single-crystal graphene without any defects, a non-uniform stress distribution is clearly observed around the indenter tip. The contact point has the highest stress and the stress decreases inversely with distance from the indenter tip. But in polycrystalline graphene, there are defects, such as GBs and GB junctions. It is known that the strengths of GBs and GB junctions are weaker than that of the pristine crystalline grain²¹. As a result, the measured failure load in principle should be significantly scattered and is dependent on the relative position between the defects and the indenter tip. For example, if the indenter tip is far away from any defects, the failure load should be close to that of the single-crystal graphene. But if the GB or GB junction is right beneath the indenter tip, the failure load should be significantly lower because of the high stress state and also the weak strength of GB or GB junction. In the presence of a hole, the failure load of polycrystalline graphene should not depend on the presence of the hole as long as the hole is sufficiently far away from the indenter tip. However, if the hole is right beneath the indenter tip, the failure load should decrease as the material strength in the contact area is weaken by the hole and the localized stress there is high. Hence, the present work demonstrates that the failure load scattering arises from a combination of the non-uniform stress state in the polycrystalline graphene, varied and also weakened strengths for different types of defects, and the relative location between the indenter tip and the defects.

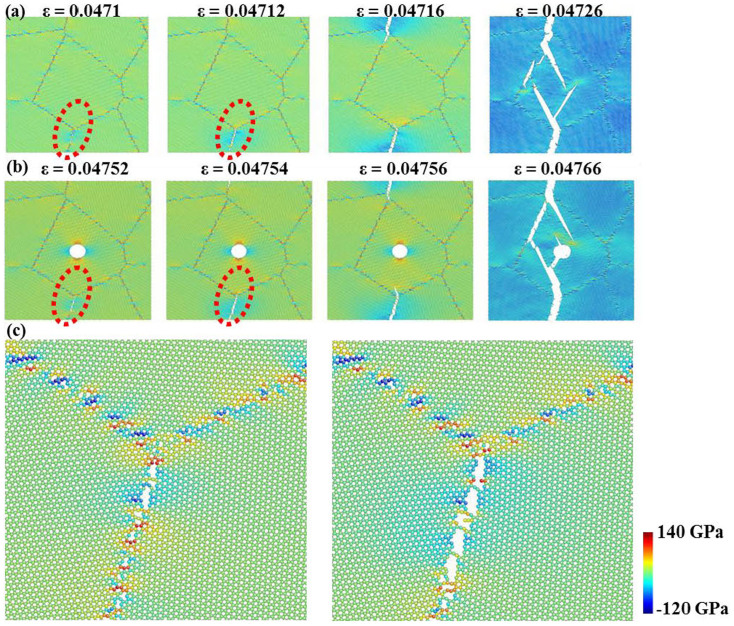
It is well-known that with AFM nanoindentation, it is difficult to capture the atomic-level rupture process of polycrystalline graphene in situ due to the hidden nature of the contact between two bodies. But with the advantage of MD simulations, we can examine the rupture process of polycrystalline graphene at the atomic scale in detail, which in turn will provide useful revelation on the failure load scattering. Figure 3 demonstrates the rupture processes of polycrystalline graphene under indentation at the different locations. When the indenter tip is positioned at a grain center (See Fig. 3(a)), it is found that the initial crack starts from GB rather than from grain interior. This is due to the non-uniform atomic stress distribution arising from imperfect GB atomic structure (see Supplementary Fig. S4) and also its weak strength compared to the grain interior. In addition, in the presence of a hole which is away from the indenter tip (See Fig. 3(b)), the initial crack also starts from a GB which is connected with the hole, highlighting the importance of the interaction between GB and hole. However, when the indenter tip is positioned on the defects, such as GB, GB junction, and hole, as shown in Fig. 3(c–e), the crack always starts directly from the defect due to the high local atomic stress caused by the contact and the weakened strength at these defect sites.

Figure 3. The rupture processes of polycrystalline graphene for the different indentation locations.

The indenter tip is positioned on (a) grain center, (b) the same as (a) but with a hole at a GB junction, (c) GB, (d) GB junction, and (e) hole, respectively. The dotted circles indicate the initial crack formation. The close-up views of these crack formations are shown in the right panels. For clarity, the indenter tip is not shown. The rupture of polycrystalline graphene starts from a GB when the indenter tip is positioned on the center of grain, while the rupture of polycrystalline graphene starts directly from a defect when the indenter tip is positioned on the defect. Evidently, the failure behavior of polycrystalline graphene is dependent on the indentation location.

We further examine the deformation process of polycrystalline graphene with and without a hole under uniaxial tensile loading. Typical failure processes are shown in Fig. 4. We first notice that the failure process of polycrystalline graphene is not affected by the hole located in the grain center. We further notice that the crack preferentially starts from a GB junction wherein one of the connecting GBs is perpendicular or nearly perpendicular to the loading direction, as reported in recent MD simulations²¹,²⁵,²⁶. After crack initiation, the crack propagates along this connecting GB, and then branches out either along connecting GBs or across grain interior along armchair or zigzag paths²⁷. The close-up views of crack formation and propagation at a GB junction are shown in Fig. 4(c). Our work shows that the failure behavior of polycrystalline graphene by nanoindentation can be very different from that by uniaxial tensile loading. Upon indentation, the rupture of polycrystalline graphene starts directly from defects when the indenter tip is positioned right on top of the defects, while the rupture of polycrystalline graphene starts from a GB when the indenter tip is positioned on top of grain center. Experimental measurements can therefore be widely scattered depending on the location of the indenter tip. However, the rupture process of polycrystalline graphene by uniaxial tensile loading starts preferentially from a GB junction, and measurements are therefore more predictable.

Figure 4. The deformation and failure processes of polycrystalline graphene with and without a hole under uniaxial tensile loading.

(a)–(b) A sequence of snapshots that capture the crack initiation and propagation of polycrystalline graphene with and without a hole, respectively. The dotted circles indicate the initial crack formation. (c) The close-up views of crack formation and propagation at a GB junction. It is seen that the rupture process of polycrystalline graphene by uniaxial tensile loading preferentially starts at a GB junction.

Discussion

Currently, it is still a challenge to use MD method to simulate a polycrystalline graphene with a grain size comparable to that grown by CVD due to the limited computing capacity. It should be noted that, in general, the size of grain should not affect our main conclusion. However, for a polycrystalline graphene with a larger grain size, a larger scattering range in failure load is expected. This is because when the indenter tip is placed at the center of a larger grain, a higher load is needed to initiate the failure; whereas when the intenter tip is placed at a GB or a GB triple junction, a similar failure load to that with a smaller grain is expected. Besides, it should be mentioned that the varying indentation location in our work is not the only factor that can lead to the scattering of failure load. Other factors, such as experimental AFM set-up, tip size and shape, sample quality, grain size, GB atomic structures, and alignment between the tip center and the defect, can also cause the scattering of failure load¹²,¹³,¹⁷,²³.

We have performed MD simulations of nanoindentation on polycrystalline graphene to investigate the origin of the significant scattering in failure load and to reveal the underlying failure mechanism, focusing on the effect of indentation locations, including the center of grain, GB, GB triple junction, and hole. Our key finding is that the measured failure load as well as the failure mechanism of polycrystalline graphene by nanoindentation are strongly dependent on the indentation location. Depending on the relative position between the indenter tip and the defects, significant scattering in failure load is observed. This scattering arises from a combination of the non-uniform stress state in polycrystalline graphene, the varied and weakened strengths for different types of defects, and the relative position between the indenter tip and the defects. Consequently, the failure behavior of polycrystalline graphene by nanoindentation is dependent on the indentation location and is different from that by uniaxial tensile loading. During indentation, the rupture of polycrystalline graphene starts directly from a defect when the indenter tip is positioned on top of the defect, while the rupture of polycrystalline graphene starts from a GB when the indenter tip is positioned on top of the center of a grain. In contrast, the rupture process of polycrystalline graphene by uniaxial tensile loading starts preferentially from a GB junction. The present work provides useful insights into the significant scattering in the failure load and reveals the underlying failure mechanism of polycrystalline graphene during nanoindentation.

Methods

The square polycrystalline graphene sample is generated using the Voronoi tessellation method²⁸,²⁹,³⁰. The sample has a length of 50 nm, width of 50 nm, and contains four randomly oriented grains of various shapes and sizes. The grain positions are randomly distributed within the simulation sheet. The created polycrystalline graphene sample is annealed to eliminate low or high-density regions near the GBs and junctions. We first anneal the sample at 3000 K for 50 ps after which the sample is quenched to 300 K during a 10 ps run allowing the sample to obtain its equilibrium size (pressure driven to zero)¹¹. A grain, GB, or GB triple junction is shifted to the whole sample center, and then it is cut to be a circular sample for indentation.

Our MD simulations are performed using Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)³¹. We use the hemispherical diamond tip that is allowed to deform together with the circular polycrystalline graphene (see Supplementary Fig. S1). The interatomic interaction for the tip and polycrystalline graphene is described by the adaptive intermolecular reactive empirical bond order (AIREBO) potential³². And the interatomic interaction between tip and polycrystalline graphene is described by the long-range van der Waals interactions. A constant integration time step of 0.5 fs is used in all the simulations. The simulations are performed at the temperature of 300 K. The atomic configurations are visualized with the AtomEye package³³.

From the indentation simulations, the normal load vs. indentation depth relation can be obtained. To do so, the tip is driven towards the polycrystalline graphene at 0.25 Å/ps. The curves of normal load vs. indentation depth are independent of the loading speeds ranging from 0.25 to 1.0 Å/ps (see Supplementary Fig. S2). The normal load is calculated as the average force in the normal direction exerted on the tip by the polycrystalline graphene. The indentation depth is defined as the difference between the lowest point of the tip and the initial position of the polycrystalline graphene sheet. Periodic boundary conditions are applied in the lateral directions. The uniaxial tensile fracture behavior of the polycrystalline graphene is investigated under a constant strain rate of 4 × 10⁷ s⁻¹ in the x direction. The pressure in the y direction is adjusted to 0 GPa to satisfy the zero-stress boundary condition, and periodic boundary conditions are applied in all directions. The stress is calculated from the normal tensor component along the loading direction of the virial stress.

Author Contributions

Z.S.L., Y.W.Z. and V.B.S. initiated and guided the project. Z.D.S. and Q.W. performed the MD simulations, analyzed the data and prepared the figures and the manuscript. S.S.Q. generated the atomic structure of polycrystalline graphene. Q.X.P. advised on the simulation and the interpretation of the results. All the authors contributed to the research work.

Supplementary Material

Supplementary Information

Supplementary Information