Still No Evidence for the Encoding Variability Hypothesis: A Reply to ^and

Abstract

Koen and Yonelinas (2010) contrasted the recollection and encoding variability accounts of the finding that old items are associated with more variable memory strength than new items. The study indicated that (a) increasing encoding variability did not lead to increased measures of old item variance, and (b) old item variance was directly related to the contribution of recollection. Jang, Mickes, and Wixted (2012) and Starns, Rotello, and Ratcliff (2012) wrote responses that, on the surface, appear to challenge those results. However, the issues raised about our first finding turn out to have no theoretical or empirical support. In addition, although Jang et al. replicated our second finding, they contested our conclusions on the basis of a perceived problem with the analyses (i.e., we used 5 rather than 2 points to calculate predicted zROC slopes). However, their concern was misplaced because the pattern of results is the same regardless of the number of points used in the analysis. They also conducted a simulation that, at first glance, appeared to suggest that our second finding was biased to favor the recollection account of the dual process model. We show that this conclusion arose because Jang et al. mistakenly built the contested correlation pattern into the simulated data. Overall, the 2 response articles serve to strengthen the main conclusions of our initial article by reiterating that there is no evidence in support of the encoding variability account, and the replication study by Jang et al. adds to the evidence favoring the recollection account.

In studies of human recognition memory, considerable debate has been centered on determining whether the dual process signal-detection (DPSD) model or the unequal-variance signal-detection (UVSD) model provides a better account of memory performance. At the heart of this debate is how to account for the ubiquitous finding that old items have more variable strengths than new items (Egan, 1958; Ratcliff, Sheu, & Gronlund, 1992; Wixted, 2007; Yonelinas & Parks, 2007), a finding referred to as the old item variance effect. While both the DPSD and UVSD models are able to mathematically account for this effect, the theoretical explanations they provide are quite different.

In a recent report, we (Koen & Yonelinas, 2010) examined the recollection and encoding variability accounts of the old item variance effect, and we concluded that our results supported the recollection account rather than the encoding variability account. However, the commentaries by Jang, Mickes, and Wixted (2012) and Starns, Rotello, and Ratcliff (2012) suggested that our results had no bearing on the encoding variability account. Furthermore, Jang and colleagues concluded that our test examining the recollection account was “not informative” (p. 521). In the current article, we point out that their arguments are largely tangential to the main point of the original article. In fact, a careful reading of their articles indicates that they provide more support for our original conclusions by including empirical replications of the initial results and by suggesting that the encoding variability account may be even more impoverished as an explanation than the empirical data had suggested. Before assessing the arguments made in those commentaries, it is necessary to briefly discuss how the recollection account of the DPSD model and the encoding variability account of the UVSD model explain the old item variance effect as well as describe the logic of our previous study, because there appears to be some misunderstanding about these points.

The DPSD model proposes that recognition memory can be based on recollection of qualitative details about a studied event or on assessments of familiarity (Yonelinas, 1994, 1999; for review, see Yonelinas, 2001a, 2002; Yonelinas, Aly, Wang, & Koen, 2010). Recollection is assumed to be a threshold process, which means that some items are recollected, whereas others are not recollected (i.e., they can fall below the memory threshold). In contrast, familiarity is represented as an equal-variance signal detection process, which means that all items are familiar but that studied items are generally more familiar than new items (Yonelinas & Parks, 2007). The contribution of recollection to recognition memory causes the old items to be more variable than the new items because both recollection and familiarity contribute to recognition of studied items (i.e., the old items contain a mixture of two classes of items), whereas only familiarity contributes to recognition of new items. Note that there may be cases in which subjects do falsely recollect a large proportion of new items (e.g., Roediger & McDermott, 1995; Lampinen, Watkins, & Odegard, 2006), but recollection is more likely to occur for studied compared with new items under standard test conditions.

Another way of describing the old item variance effect is based on the UVSD model, which proposes that old items are both stronger and more variable than new items (Egan, 1958; Green & Swets, 1988; Wixted, 2007). However, since its rise to prominence as a model of recognition memory, its critical shortcoming has been that it does not provide a theoretical explanation for why the strength of old items is more variable than the strength of new items. This was highlighted early on, when Green and Swets (1988) stated,

The justification for the Gaussian model with unequal-variance is, we believe, not to be made on theoretical but rather on practical grounds. It is a simple, convenient way to summarize the empirical data with the addition of a single parameter. (p. 79)

One way of addressing this shortcoming is to adopt the encoding variability account of the old item variance effect such as that proposed by Ratcliff et al. (1992) and, more recently, by Wixted (2007). To quote Wixted,

An equal-variance model would result if each item on the list had the exact same amount of strength added during study. However, if the amount of strength that is added differs across items, which surely must be the case, then both strength and variability would be added, and an unequal-variance model would apply. (p. 154)

While the encoding variability account of the old item variance effect could represent a significant step forward as a theoretical explanation of the UVSD model, it is an idea that had never actually been directly tested. Given the widespread application of the UVSD model to recognition memory, and given that the unequal variance assumption is such a critical component of the model, this omission is rather surprising.

The aim of the Koen and Yonelinas (2010) study was to contrast the encoding variability account of the UVSD model and the recollection account of the DPSD model. That is, our goal was to determine if the encoding variability and recollection accounts were sufficient to account for the increase in old item variance observed on recognition tests. To do so, participants in this experiment completed two study-test phases. In the pure study-test phase, participants studied 160 words each presented for 2.5 s. In the mixed study-test phase, we increased the amount of encoding variability by having participants study 160 words, with half presented for 1 s and the other half presented for 4 s. It was expected that there would be encoding variability in the pure list condition because not all items would be encoded equally well, but most important, there should be more encoding variability in the mixed list condition because some items were presented 4 times longer than others. Thus, to the extent that encoding variability produces the old item variance effect, old item variance should be greater in the mixed list than in the pure list because old item variance is assumed to be due to the fact that “the amount of strength that is added differs across items” (Wixted, 2007). In both test phases, participants provided a recognition confidence response using a 6-point scale followed by a modified remember/know (RK) judgment (Tulving, 1985; Yonelinas, 2001b). Because participants sometimes confuse RK responses with confidence responses (Yonelinas, 2001b; Yonelinas et al., 2010) the instructions were designed to ensure that the participants made a remember response only when they could retrieve a specific detail about the study event (for additional results showing the effects of using these different types of test instructions, see Rotello, Macmillan, Reeder, & Wong, 2005). In contrast, if they thought the item was studied but they could not recollect any specific details they should respond “know,” and if the item was new they should respond “new.”

An examination of the confidence responses indicated that increasing encoding variability did not increase old item variance. This was measured by examining the slope of the z-transformed receiver operating characteristic (zROC) derived by plotting the confidence responses. The zROC slope will be equal to 1.0 when the old and new distributions have equal variance and a slope of less than 1.0 when the old item variance is greater than that of the new item distribution. The results indicated that increasing encoding variability led to a slight decrease, rather than the expected increase, in old item variance (i.e., the zROC slope was numerically, but not significantly, larger in the mixed list). Thus, the results provided no support for the encoding variability hypothesis. In contrast, the old item variance effect was found to be due almost entirely to the inclusion of recollected items to the old item distributions. That is, when the remembered items were removed, the old item distribution was no longer more variable than the new item distribution. Moreover, estimates of recollection and familiarity derived from the RK reports accurately predicted the amount of old item variance that was observed in the confidence ROC. Both of these results provide direct support for the a priori predictions of the recollection account. We argued that more dramatic manipulations of encoding variability might affect old item variance—perhaps it is necessary to use much larger differences in encoding than increasing the study duration by a factor of 4—but that it was clear that the large old item variance effects that were observed in item recognition could be attributed to recollection rather than encoding variability.

There were three main questions raised by Jang and colleagues (2012) and Starns, Rotello, and Ratcliff (2012) about our study, and we discuss each of them below.

1. Does Including Two Different Presentation Durations Mean That Our Results Have No Bearing on Encoding Variability? Absolutely Not

First, Jang et al. (2012) and Starns, Rotello, and Ratcliff (2012) argued that we did not examine the encoding variability account of the UVSD model in our experiment because we had two distinct classes of items in our mixed list (i.e., 1 s and 4 s). Their argument is that when you have two different types of items in a test list then the old item strength distribution will reflect a mixture of two different types of items. Thus, the resulting old item distribution will no longer be Gaussian even if the strength distributions for the two different types of items were themselves Gaussian. For example, in an extreme case in which the two types of items have very different levels of memory strength, the mixture distribution could be bimodal such that there is a lower peak for the weak items and a higher peak for the strong items, rather than a single Gaussian distribution. The commenters argue that it is inappropriate to even try to account for memory in this type of experiment using a standard UVSD model because it presupposes perfectly Gaussian distributions. They are certainly correct in the sense that mixing distributions could lead to non-Gaussian distributions. However, it turns out that in practice, and certainly in the current study, there is virtually no impact of mixing on the results. Thus, the mixing argument that they adopt in order to avoid having to account for the observed results is inadequate.

First, by the logic of the commentators, one would never be able to use the standard UVSD model because, invariably, test lists always contain mixtures of different types of items (e.g., trial-to-trial variation in how long a participant studies an item, mixtures of concrete and abstract words, etc.). Thus, mixing occurs in virtually all item recognition memory experiments, and yet the resulting ROCs are typically found to be in good agreement with the Gaussian assumption. One might argue that there is something peculiar that happens when you mix only two classes of items together as in our mixed lists. However, we did not have just two distinct classes of items; rather we had an indeterminate number of different types of items being mixed together (e.g., some 1 s items are encoded more weakly and some more strongly, and some 4 s items are encoded more weakly and some more strongly; concrete and abstract words). Thus, the type of mixing that occurred in our mixed list occurs all the time, so it would not be expected to fundamentally alter the type of Gaussian-shaped old item distributions that have typically been observed in item recognition.

Second, even if we had managed to somehow mix only two distributions, this type of mixing is not expected to have any sizable impact on the Gaussian assumption of the old item distribution. To verify this, we conducted a series of simulations in which we generated strong and weak confidence data with a mixture UVSD model, mixed (i.e., added) the like confidence bins of the weak and strong items together, and fit the resultant data with a standard UVSD model to see if mixing violates the Gaussian assumption. To simulate the data, the strength and variance of the weak distribution was set to .4 and 1.25, respectively, and the variance of the strong distribution was also set to 1.25. The strength of the strong distribution was varied from 0.4 to 3.0 in intervals of 0.2 to create monotonically increasing levels of strength differences (i.e., the strength difference ranged from 0.0 to 2.6). We incorporated a wide and realistic range of different response criteria by using the observed criterion locations from each of the 32 participants in our study because extreme conservative and liberal response biases can increase the influence of mixing (Starns, Rotello, and Ratcliff, 2012). Eighty trials from the strong distribution, 80 trials from the weak distribution, and 160 trials from the new item distribution were randomly selected using a parametric bootstrap method given the mean and variance of the weak and strong distributions in conjunction with the criterion locations.

For each level of difference in strength between the weak and strong distributions, each “participant” was simulated 20 times, resulting in 20 “experiments” for each strength difference. The dependent measure was the average of the sum of the G² value for the 32 participants across the 20 experiments at each level of the strength difference. These data are plotted in Figure 1, and the results show that the effect of mixing is miniscule, even with very large differences in strength between weak and strong items. The deviation from Gaussian (i.e., indicated by higher G² values) does not even approach significance (the dotted line) until the difference in strong and weak item strength is very large (e.g., d′ difference of greater than 2.4). Importantly, even at the large strength difference plotted, the average G² value was not statistically significant, which indicates that a Gaussian model still provides an adequate account of the data. It is important to note that the 95% confidence interval began to encompass the critical G² value at strength differences greater than 2.4. The difference in strength seen in our experiment (Koen & Yonelinas, 2010) was less than 1 and did not even approach the most extreme value that is plotted. On the basis of these simulations, the concern that something may have happened in the mixed list that invalidates the use of the standard UVSD model is entirely unfounded.

Figure 1.

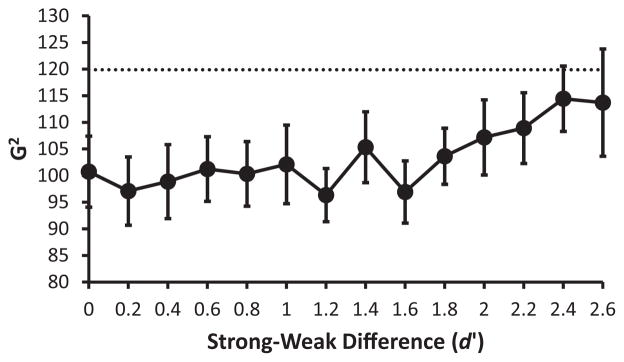
The effects of mixing on the Gaussian assumption. Model fit (G²) is plotted across levels of strength difference between weak and strong distributions. The dotted line indicates when mixing strong and weak items violates the Gaussian assumption of the standard UVSD model (i.e., the standard Gaussian UVSD model would be rejected). Across the range of strength differences, the G² value never reaches significance and only approaches significance at highest strength differences. The average G² values were determined by averaging the sum of G² values for 32 participants across 20 simulated experiments. Error bars represent 95% confidence intervals.

Third, probably more important than these theoretical arguments, however, is that there was no indication in the empirical data that the Gaussian shape of the old item distribution in the mixed list was any different from that in the pure list conditions. That is, mixing will lead the zROCs to become nonlinear, but as is almost always the case in item recognition, the zROCs were linear—and this was true in both the mixed and the pure conditions. This is important because it shows that there was no evidence for rejecting the standard UVSD model in favor of the mixture-UVSD model as proposed by Jang et al. (2012) and Starns, Rotello, and Ratcliff (2012). The fact remains that increasing encoding variability did not lead to an increase in old item variance as predicted by the encoding variability hypothesis. It would be a simple mistake to ignore these results on the basis that mixing led to a violation of the Gaussian assumption because there is no theoretical or empirical evidence to substantiate this claim.

Nonetheless, Jang et al. (2012) went on to suggest how we should have designed our study to overcome the apparent conceptual problem with our design. This is an important step to take because otherwise one wonders whether the encoding variability account is falsifiable at all. Jang and colleagues argued that

To test the encoding variability hypothesis, one might attempt to add variable amounts of memory strength to half of the study items on a list (e.g., by using a wide range of normally distributed study times) and to add less variable amounts of memory strength to the other half (e.g., by using a constant study duration). (p. 514)

Unfortunately, the experiment that they suggest is even less likely to provide evidence for the encoding variability account than our original experiment. Presumably, by avoiding two discrete classes of items the Gaussian assumption would no longer be violated, and thus the results may reveal evidence for encoding variability. As shown above there was no evidence that mixing items violated the Gaussian assumption in the first place. Even if there had been, their proposed experiment is unlikely to be useful because, by increasing amount of different study durations, one would necessarily reduce the average difference in the strengths of the strong and weakly encoded items, compared with the case in which one used two discrete study durations. Thus, its effects would be smaller than what one would expect in the design we had used.¹

2. How Much of the Variance Does “Encoding Variability” Account for? Little to None

Jang et al. (2012) and Starns, Rotello, and Ratcliff (2012) pointed out that inducing encoding differences by increasing study time by a factor of 4, as we did, is not expected to have much of an effect on old item variance. We are in complete agreement with the commenters on this point. In fact, this is a point we thought we had made quite clearly in the original article. For example, we devoted an entire section of the analysis to examine subjects with the largest strength effects. Moreover, in the discussion we stated,

It remains to be determined, however, whether more extreme manipulations of encoding strength (e.g., a study time ratio of greater than 4:1) might begin to impact old item variability (see Norman & O’Reilly, 2003). The important point is that relative to the increase in old item variance produced by mixing recollected and familiar items, the effect of encoding variability appears to be negligible. (p. 1541)

The simulations/calculations described by Jang et al. (2012) and Starns, Rotello, and Ratcliff (2012) are useful in strengthening the conclusion that the effects of encoding variability, if they exist at all, are extremely subtle. Yet, one should be cautious in determining how large of a strength difference is needed to see differences in old item variance, because, as Starns, Rotello, and Ratcliff correctly pointed out, the effect will be larger at extreme levels of response bias. That is, we could expect the required strength difference to produce an effect on old item variance to be smaller when participants have very conservative/liberal response biases. This is essentially the point Jang et al. (2012) and Starns, Rotello, and Ratcliff (2012) made about one of our auxiliary analyses that examined a wide range of response criteria. Having said this, however, we do want to reiterate that one should not conclude that encoding variability does not happen or that it can never have any effect on old item variance, just that it appears to be negligible compared with the effect of recollection.

While it is true that encoding variability could, in principal, cause old item variance to increase, the results from Koen and Yonelinas (2010) as well as the replication study from Jang and colleagues (2012) suggest that, in practice, increasing encoding variability does not have a noticeable effect on old item variance. However, should it not at least have some effect? One possibility is that it actually does have a small impact on old item variance, but the effect is simply so small that it is not detectable in a standard recognition memory experiment. Another possibility is that encoding variability really does not affect old item variance. As we pointed out in our original article (Koen & Yonelinas, 2010), computational memory models such as TODAM2 (Murdock, 1993) and CLS (Norman & O’Reilly, 2003) indicate that equal variance old and new item familiarity distributions can arise even when each studied item is strengthened by a different amount because old and new items are assessed in exactly the same way. That is, the test item is matched to all items stored in memory, so the amount of encoding variability will influence what is stored in memory and how well both old and new items match the information stored in memory.

3. Why Does Recollection Account for the Old Item Variance Effect, Whereas the UVSD Model Fails to Account for This Relationship? Because the UVSD Model Is Insufficient

In addition to the two arguments discussed above, Jang and colleagues (2012) challenged the results we reported that were in support of the recollection account. The recollection account makes two predictions regarding the relationship between RK judgments and confidence ROCs. First, the account predicts that the old item variance effect will be eliminated if the contribution of recollection is removed. Confirming this hypothesis, the zROC slope, our estimate of the old item variance effect, was no different from 1.0 after the contribution of recollection, as estimated from the RK data, was removed from the confidence ROC (also see Yonelinas, 2001b). Thus, the first prediction of the recollection account was confirmed because zROC slopes equal to one indicate that old items have the same strength variability as new items. Because neither reply contested this finding, we will not discuss it further.

The second prediction of the recollection account, which was targeted by Jang et al. (2012), is that one should be able to predict the amount of old item variance observed in recognition on the basis of estimates of recollection and familiarity from the RK data. In line with this prediction, estimates of old item variance derived from RK recollection and familiarity estimates showed a significant positive correlation with the amount of old item variance observed in the confidence ROC. To determine if this finding was specific to the recollection account of the DPSD model, we also examined the RK data from the perspective of the UVSD model. Estimates of old item variability derived from fitting the UVSD model to the RK responses failed to predict the amount of old item variability observed in the confidence data. Thus, examining the data from the perspective of the DPSD model revealed a systematic relationship between the shape of the recognition confidence ROCs and RK judgments, whereas the UVSD model was unable to relate the two types of recognition tasks in this way. Note that the same was true for both the pure and mixed lists, so one cannot ignore these results on the basis of the mixture argument discussed earlier.

Jang and colleagues (2012) first replicated our experiment and found exactly the same pattern of results, attesting to the robust nature of these effects. Namely, the DPSD model, with the recollection account, accurately predicted the old item variance observed in the confidence data on the basis of the RK responses, whereas the UVSD failed to account for this relationship. However, Jang and colleagues suggested that this result occurred because we used the 5 observed false alarm rates from the confidence ROC to predict zROC slope in the analysis of the DPSD model, whereas we used only the 2 false alarm rates from the RK data to predict zROC slope in the analysis of the UVSD model. We initially did this because, from the perspective of the UVSD model, the zROC has to be linear, and so it makes no difference whether one uses 2 or 5 points to estimate zROC slope.

Jang et al.’s (2012) point is well taken, and we agree that it is possible that the UVSD model performed poorly relative to the DPSD model because we did not assess the two models in exactly the same way. However, if one actually looks to see whether using 2 or 5 ROC points makes any difference, it is quite clear that this concern is misled because the conclusions are exactly the same with both methods. To address this concern, we calculated the RK old item variance estimate for the DPSD model described above with only the 2 false alarm points in the RK data (in contrast to the 5 confidence false alarm points reported in Koen & Yonelinas, 2010). In this way, the assessment of the DPSD model and the UVSD model relied on exactly the same number of points. Table 1 shows the correlations for the UVSD model based on 2 points as well as the estimates from the DPSD model based on the original 5 points and with 2 points. As is apparent, the pattern of correlations was the same for the 2- and 5-point methods, indicating that the advantage of the recollection account of the DPSD model over the UVSD model was not due to the different numbers of false alarm points used in the old item variance estimates. Regardless of the number of points used in the estimation of the RK data, the relationship between confidence and RK data was revealed only when viewing the data through the lens of the DPSD model. While the correlations were slightly smaller when using 2 points compared with 5, they were clearly significant in both cases. Thus, the reanalysis verifies the initial findings in showing that the recollection account of the DPSD model, but not the UVSD model, can account for the correspondence between confidence and RK data.

Table 1.

Correlations Between the Observed z-Receiver Operating Characteristic (zROC) Slope and the z-Slopes That Are Predicted by the Dual Process Signal-Detection (DPSD) and Unequal-Variance Signal-Detection (UVSD) Models

Model	N	Pure list		Mixed list
		Pearson’s r	p	Pearson’s r	p
DPSD 5-points	31	.50	.004	.56	.001
DPSD 2-points	31	.39	.032	.51	.004
UVSD 2-points	30	.09	.645	.17	.363

Note. The DPSD 5-point and the UVSD 2-point results were reported in Koen and Yonelinas (2010), and the DPSD 2-point is new. One participant was excluded from the analysis because he or she did not provide any “know” judgments. Another participant was excluded from the UVSD correlation because his or her estimated z-slope was greater than five standard deviations from the mean and caused the UVSD correlation to look worse than it was.

Jang and colleagues (2012) also described a simulation that led them to suggest that, despite the fact that the DPSD model accurately predicted the observed old item variance effect and the UVSD model did not, “this result does not weigh in favor of the DPSD model” (p. 521), because the prediction was “preordained to favor the DPSD model” (p. 520). Their simulation appeared to show that the DPSD model would be able to account for the relationship between old item variance and RK judgments better than the UVSD model could, even when the data had been generated entirely by the UVSD model.

How could a simulation lead them to such an apparently nonsensical conclusion? An examination of what they did in their simulation reveals that they mistakenly embedded the observed correlation between the RK and confidence judgments that was predicted by the DPSD model into their simulated data. That is, to create simulated data, the authors started by taking the observed RK and confidence responses from each participant, and from this they then derived two pairs of memory parameters from the UVSD model for each participant (i.e., d′ and V_o values were estimated by fitting the confidence data with the UVSD model and a different set of d′ and V_o values were obtained by fitting the RK data with a saturated UVSD model). They then created simulated data based on those sets of UVSD parameters by adding sampling noise to each simulated participant and then examined the correlations between the simulated ROC data and the simulated RK data using the same method that had been used to examine the observed data.

Critically, the confidence and RK responses that were used to generate the parameters that formed the basis of the simulation were related to one another because they came from the same participants. In fact, we know that they were statistically related in the sense that the RK data could be used to accurately predict the confidence data using the DPSD model, but not using the UVSD model (Jang et al., 2012; Koen & Yonelinas, 2010). Thus, the data that they used in the first step of their simulation contained the critical relationship between the RK and confidence data. This relationship was in no way predicted or generated by the UVSD model; rather, it was a relationship that was provided by the empirical data. It is no surprise, then, that the results from the simulated data behaved just like the original data because the original data were used as a basis for the simulated data.

From the perspective of the UVSD model, the finding that there was no correlation in the simulated data between RK and confidence is expected given that the old item variance (i.e., zROC slope) parameters were not correlated across the confidence and RK methods in the observed data. Thus, there was no reason to expect the UVSD model to show any relationship between the simulated confidence and RK data, even though the UVSD model generated the data, because the simulated data were generated from a set of parameters that were uncorrelated to begin with.

Although it may not be obvious, from the perspective of the DPSD model the results of their simulation also make sense. That is, the data used to generate the simulations were consistent with the DPSD model in the sense that the data contained the critical relationship between the RK and confidence data. Importantly, the DPSD model can account for the exact same RK data as a UVSD model because both models are saturated, and saturated models provide perfect fits to the data. That is, although the UVSD model generated the simulated RK data, the DPSD could also simulate exactly the same data. Thus, the RK part of their simulation was equally consistent with both the UVSD the DPSD models.

Moreover, the two models produce ROCs for item recognition that are virtually identical across the typically observed range of response criterion points (Yonelinas, 1999; Yonelinas & Parks, 2007), so they do not differ appreciably with respect to what the simulated confidence ROCs would look like either, at least in regard to item recognition ROCs. Thus, the zROC slope produced by examining the simulated RK data with the DPSD model would not be expected to produce any appreciable differences compared with what was observed in the original data, and thus the correlation would remain unchanged. The same holds true for the simulated confidence data, in that the zROC slope in the simulated data would not be expected to appreciably differ from what was observed in our initial analysis.

The important point is that the relationship between RK and ROC data (see Table 1) was included in the method used to generate the simulated data, so one should not be surprised that it was also seen in the simulated data. Thus, the simulation was not based solely on the UVSD model, but rather was based on the observed correlation structure of the original data. If one wanted to generate data that were based solely on the UVSD model, one could have selected parameter values (i.e., d′ and V_o) for each participant and generated both the confidence and RK data from the same set of parameters. But that is not what they did; rather they started with the correlation that was known to be consistent with the DPSD model and inconsistent with the UVSD model. Effectively, all Jang et al. (2012) did was to add some noise to the original confidence and RK data, then redo the original correlation analysis, which led to the same conclusions as were apparent in the original data.

Why does the UVSD model fail to account for the observed relationship between old item variance and recollection, and can it be fixed? One possible account is that the UVSD model is correct, but it is just that it is not valid to apply it to RK data and expect it to produce meaningful parameter estimates. For example, one suggestion has been that there may be more variability in the participant’s response criteria in a RK test than in a confidence task (e.g., Wixted & Stretch, 2004; Dunn, 2008; Rotello, Macmillan, & Reeder, 2004). Although this is an interesting post hoc account, as far as we know it has never been directly tested. In any case, in order to account for ROC and RK data it would be necessary to postulate an additional parameter to incorporate criterion variability in addition to the existing d′ and V_o constructs thought to underlie recognition memory. Alternatively, one could argue that RK responses are based on fundamentally different underlying memory signals than are confidence judgments. Aside from being a rather nonparsimonious explanation, it seems particularly difficult to believe that this argument is correct given that participants were making both confidence and RK judgments as each test item was presented. In either case, one would need to modify the existing UVSD model in order to account for the data.

Is There Any Other Empirical Evidence That Speaks Directly to Both the Recollection and the Encoding Variability Accounts?

A recent recognition study designed to test a novel prediction of the recollection account of the DPSD model (Aly & Yonelinas, 2012) provides additional support for the recollection account. The logic of that study was as follows. If the old item variance effect (i.e., the finding that old items are more variable in strength than the new items) is really due to the fact that recollection contributes more to the old items than to the new items, then the old item variance effect should be reversed if one could design a recognition test where recollection supports memory only for new items. That is, if recollection supports memory for new rather than old items, then old items should be less variable in memory strength than the new items. In such a case, the ROC should become asymmetrical in the opposite way to what has always been seen in tests of item recognition (i.e., the zROC slope should now be greater than 1.0 rather than less than 1.0; for reviews see Wixted, 2007; Yonelinas & Parks, 2007). Given that this pattern has never been reported in the literature as far as we are aware, it is a very strong prediction of the recollection account of the DPSD model. In addition, it is particularly relevant in the current context because such a pattern of data would appear to be inconsistent with the encoding variability account. Encoding variability can only increase old item variance because it adds variability; it can never decrease variability (DeCarlo, 2010). If old item variance is determined solely by encoding variability, then recognition zROCs are constrained to be less than or equal to 1.0, never greater than 1.0.

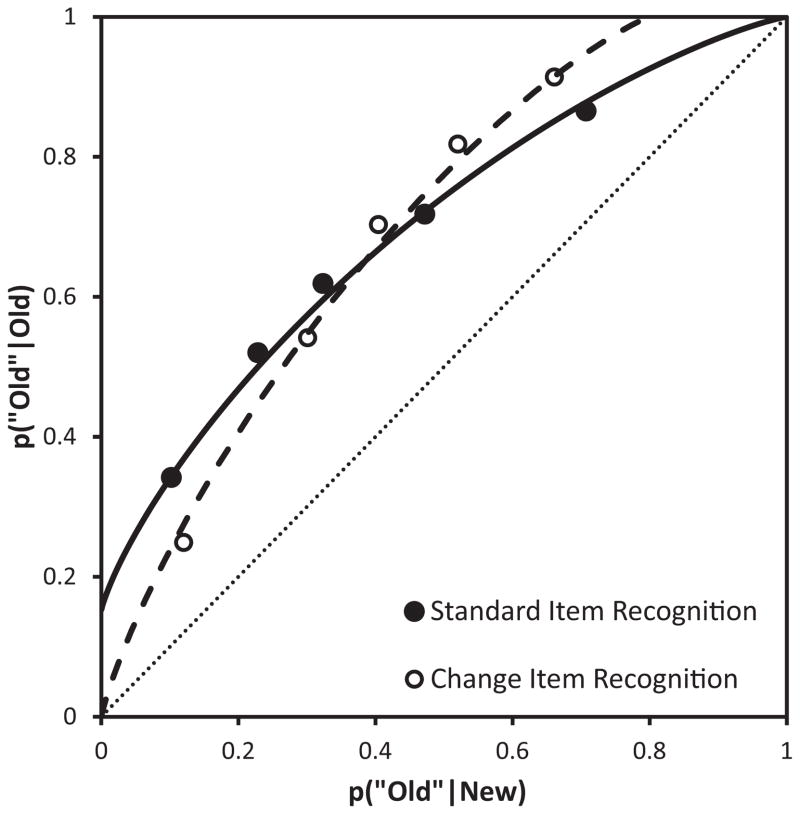
Under what conditions would recollection be useful in rejecting new items as new, but not be useful in accepting old items as old? Well, take a minute to look around your desk. If your desks are anything like ours, they are cluttered with different objects. Now, imagine that we were to subsequently present you with a picture and ask if it was an identical photo of your desk or if it was a photo in which we had removed or added something from the desk. How would you respond? Under these conditions, recollection can help you reject new items (e.g., “There is always a coffee mug next to my keyboard, and it’s not there, so this must be a new photo.”), but recollection is not useful in allowing you to accept an old item as old (e.g., “My coffee mug is where it should be, but that does not help me very much because those guys could have changed any one of a number of different objects.”). On the basis of this type of real world example, Aly and Yonelinas (2012) had participants study a series of scenes and required them to discriminate between scenes that remained unchanged from the study phase (i.e., old scenes) and those where some aspects of the scene were changed (i.e., new scenes). The resulting ROCs from this experiment were asymmetrical “the wrong way,” exactly as predicted by the recollection account (see Figure 2). This was contrasted to a performance matched standard recognition memory test in which old and new items were very different from one another.

Figure 2.

Aggregate ROCs from a standard item recognition test and from a change item recognition test reported in Experiment 8 of Aly and Yonelinas (2012). The solid and dashed lines are the best fitting DPSD function for the standard and change item recognition tests, respectively. The dotted line represents chance performance.

Although such results do not falsify the UVSD model, they do demonstrate that encoding variability is not sufficient to account for old item variance. Something else appears to be generating the old item variance effect, and we contend that this something is recollection. There may well be other ways of explaining the results from Aly and Yonelinas (2012) that do not rely on the DPSD model, but the results clearly indicate that the encoding variability account is insufficient.

Moving Forward With the DPSD Model

The UVSD model is still widely used in studies of recognition memory. Given that the model assumes there are two functionally independent memory components underlying performance (d′ and old item variance), one would imagine that there should be some psychological explanation for these underlying components. Unfortunately, up until recently, there has been little effort to provide and test psychological explanations for these mathematical constructs. The current debate is encouraging in the sense that there is now at least some consideration of how one could test different accounts of the critical components underlying the UVSD model. Even if one were to take all of the arguments of Jang et al. (2012) and Starns, Rotello, and Ratcliff (2012) at face value, we can all agree that currently, there is no evidence at all to suggest that the variance parameter reflects encoding variability. We have argued that it seems to be well explained as being due to the contribution of recollection (also see Koen & Yonelinas, 2011; Aly & Yonelinas, 2012). Whether other theoretical explanations of the UVSD model will be proposed and tested is an important question for future research. But at the very least, the results suggest that one should be very cautious about assessing recognition memory using the UVSD model, as we have no idea what one of its two components is actually measuring (i.e., the model has no construct validity).

At the same time, the shortcomings of the DPSD model should not be overlooked. For example, as correctly pointed out by Starns, Rotello, and Ratcliff (2012), neither the DPSD nor the UVSD model directly speaks to response time (RT) data. To the extent that one considers RT data in these paradigms (e.g., 6-point confidence or RK responses) to be directly interpretable, one would like a model to account for both accuracy and RT. Ratcliff and Starns (2009) have made important progress in modeling response times in 6-point confidence data by assuming that there is a separate information accumulation process for each of the six confidence bins (i.e., one memory accumulation process per finger), and Starns, Ratcliff, and McKoon (2012) have developed a similar model that can account for RTs in response bias studies. Although these models do not provide an explanation of old item variance effect, perhaps this type of accumulation process could be incorporated into the dual process model. For example, rather than stipulating that there are six information accumulators, as Ratcliff and Starns did, one might start by assuming there are two—one for recollection and one for familiarity. The next logical step would be to conduct studies to try to determine the rate of information accrual for each process.

To assess the contribution of recollection and familiarity as a function of retrieval time, we examined recognition ROCs under speeded and self-paced conditions (Koen & Yonelinas, 2011). Importantly, one cannot just examine standard response confidence ROCs because any changes in ROC shape could arise because the speed manipulation influences the information that is retrieved from memory (i.e., the shapes of the memory strength distributions) or because it disrupts a participant’s ability to convert the memory information into one of the six different types of responses (i.e., confidence response). Thus, the shapes of the observed ROCs are not expected to be particularly meaningful (but see Ratcliff & Starns, 2009). To avoid this type of confound, we used response bias manipulations to plot ROCs, so for a given response bias condition participants made only simple yes/no responses in the speeded or self-paced conditions, thus reducing concerns about affecting decision processes. We found that speeding led to a decrease in recollection with little or no influence on familiarity. This joins a large body of literature indicating the item familiarity is available earlier than is recollection in both humans (e.g., Gronlund & Ratcliff, 1989; McElree, Dolan, & Jacoby, 1999; Yonelinas & Jacoby, 1994; but see Starns, Ratcliff, & McKoon, 2012) and rodents (Sauvage, Beer, & Eichenbaum, 2010).

Thus, the results generally suggest that the information accrual function is more rapid for familiarity than for recollection. However, additional studies will be needed to make precise claims about the shape of the information accrual functions. Hopefully, armed with this type of knowledge of the availability of recollection and familiarity, one can begin to construct models of recognition accuracy and RT.

Conclusions

We disagree with the commentaries on a number of important issues; however, it is important to emphasize that we all now agree that there is absolutely no empirical evidence that encoding variability produces the old item variance effect. As intuitively appealing as it may seem, encoding some items more strongly than others does not increase the old item variance relative to conditions in which there is less encoding variability. If it has any effect at all, it appears to be so small as to be negligible. Beyond this point of agreement, the commentaries wish to argue that our original experiment did not provide a particularly good test of the encoding variability account because we mixed only two classes of items together and we should have mixed more different types of items. We believe that we have demonstrated that their proposed study is even less likely to provide relevant evidence than our original study, and that there is no evidence that mixing had any noticeable effects on the outcome of our study. In contrast, the results of our original study, as well as the replication reported by Jang et al. (2012), showed that the old item variance effect arose because of the contribution of recollection as measured by RK judgments, thus verifying the a priori predictions of the recollection account. Jang et al. (2012) claimed that these results possibly arose because we used 5 rather than 2 false alarm points in our analysis, but we showed that the conclusion held regardless of the number of points used in the estimation. Based on a simulation, they further suggested that the DPSD model was preordained to outperform the UVSD model because the simulated data, which were supposedly generated by the UVSD model, also showed that recollection accurately predicted old item variance and the UVSD model did not. However, we showed that this arose because they had mistakenly incorporated the predicted correlation structure into their simulated data.

Nonetheless, it is important that we reiterate what we can and cannot conclude from the Koen and Yonelinas (2010) results. First, we cannot conclude that encoding variability does not occur, nor can we conclude that it has no effect on old item variance. The results show only that encoding variability is an insufficient explanation of the old item variance effect, whereas the recollection account can explain this effect. The results also do not show that the UVSD model is unable to fit the ROC data. As has been shown many times before, both the UVSD and DPSD models account for the observed shapes of the ROCs seen in item recognition tests very well (for review see Yonelinas & Parks, 2007), and this was the case in our study as well (see Table 3 in Jang et al., 2012). The UVSD model does fail to account for the shape of the ROCs in tests thought to rely more on recollection, such as tests of associative and source memory (e.g., Kelley & Wixted, 2001; Yonelinas, 1997), but that is not what was examined in Koen and Yonelinas (2010). The results show only that the encoding variability account is not a sufficient explanation of the old item variance effect, but there may be other as yet unspecified mechanisms, such as the introduction of additional memory processes, which might be postulated to account for the high levels of old item variance that are typically observed. One aspect of the study, however, does directly challenge the UVSD model, and that is the finding that the old item variance effect could be accurately predicted by examining recollection and familiarity using RK judgments. It was only when examined using the DPSD model that that relationship was revealed. The UVSD model was blind to this relationship because, we contend, it is wrong. Although it may provide a convenient way of mathematically describing the ROC data, it fails to capture the fundamental relationship between these two different tests of recognition memory.

We do, however, believe that more research is needed to directly test the predictions of the theoretical accounts of the different signal-detection models, as well as explore the shortcomings of such models (e.g., Ratcliff & Starns, 2009). To our knowledge, our study (Koen & Yonelinas, 2010) was the first to directly test the encoding variability account. Yet, this study provides only one case in which the evidence did not favor the encoding variability account, and there may yet be other situations in which the data will support the encoding variability account (and possibly not the recollection account). Until such studies show otherwise, however, the recollection account of the DPSD model appears to provide the best account of the old item variance effect in recognition memory across a wide range of conditions (e.g., Aly & Yonelinas, 2012). Importantly, unlike the UVSD model, the initial advancement of the DPSD model was made on both practical and theoretical grounds (Yonelinas, 1994). The addition of a single parameter to the familiarity process (i.e., recollection) not only provides a simple way to mathematically account for the data, but it also provides a psychological construct that can be tested and validated by the extant literature.