Abstract
This research argues that deep-rooted factors, determined tens of thousands of years ago, had a significant effect on the course of economic development from the dawn of human civilization to the contemporary era. It advances and empirically establishes the hypothesis that, in the course of the exodus of Homo sapiens out of Africa, variation in migratory distance from the cradle of humankind to various settlements across the globe affected genetic diversity and has had a long-lasting effect on the pattern of comparative economic development that is not captured by geographical, institutional, and cultural factors. In particular, the level of genetic diversity within a society is found to have a hump-shaped effect on development outcomes in both the pre-colonial and the modern era, reflecting the trade-off between the beneficial and the detrimental effects of diversity on productivity. While the intermediate level of genetic diversity prevalent among Asian and European populations has been conducive for development, the high degree of diversity among African populations and the low degree of diversity among Native American populations have been a detrimental force in the development of these regions.
1 Introduction
Existing theories of comparative development highlight a variety of proximate and ultimate factors underlying some of the vast inequities in living standards across the globe. The importance of geographical, cultural and institutional factors, human capital formation, ethnic, linguistic, and religious fractionalization, colonialism and globalization has been at the center of a debate regarding the origins of the differential timing of transitions from stagnation to growth and the remarkable transformation of the world income distribution in the last two centuries. While theoretical and empirical research has typically focused on the effects of such factors in giving rise to and sustaining the Great Divergence in income per capita in the pre-industrial era, attention has recently been drawn towards some deep-rooted factors that have been argued to affect the course of comparative economic development.
This paper argues that deep-rooted factors, determined tens of thousands of years ago, have had a significant effect on the course of economic development from the dawn of human civilization to the contemporary era. It advances and empirically establishes the hypothesis that, in the course of the exodus of Homo sapiens out of Africa, variation in migratory distance from the cradle of humankind in East Africa to various settlements across the globe affected genetic diversity and has had a long-lasting hump-shaped effect on the pattern of comparative economic development that is not captured by geographical, institutional, and cultural factors.
Consistent with the predictions of the theory, the empirical analysis finds that the level of genetic diversity within a society has a hump-shaped effect on development outcomes in the pre-colonial as well as in the modern era, reflecting the trade-off between the beneficial and the detrimental effects of diversity on productivity. While the intermediate level of genetic diversity prevalent among the Asian and European populations has been conducive for development, the high degree of diversity among African populations and the low degree of diversity among Native American populations have been a detrimental force in the development of these regions. This paper thus highlights one of the deepest channels in comparative development, pertaining not to factors associated with the dawn of complex agricultural societies as in Diamond’s (1997) influential hypothesis, but to conditions innately related to the very dawn of mankind itself.
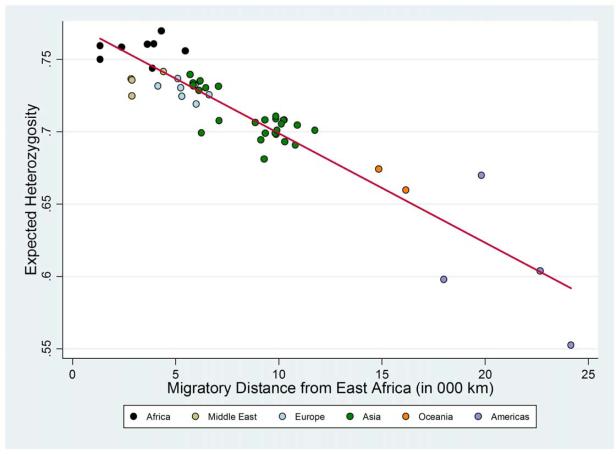
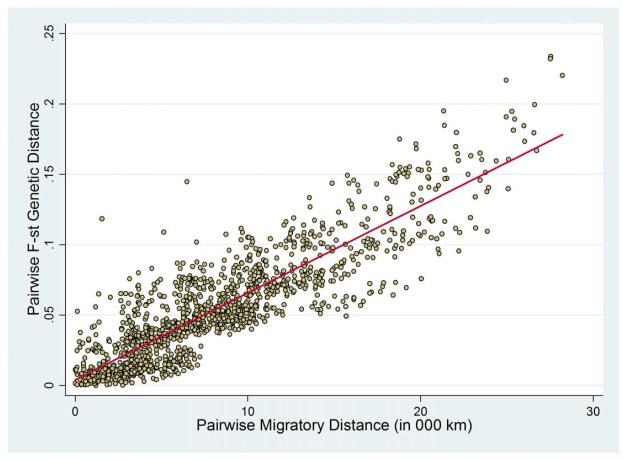
The hypothesis rests upon two fundamental building blocks. First, migratory distance from the cradle of humankind in East Africa had an adverse effect on the degree of genetic diversity within ancient indigenous settlements across the globe. Following the prevailing hypothesis, commonly known as the serial-founder effect, it is postulated that, in the course of human expansion over planet Earth, as subgroups of the populations of parental colonies left to establish new settlements further away, they carried with them only a subset of the overall genetic diversity of their parental colonies. Indeed, as depicted in Figure 1, migratory distance from East Africa has an adverse effect on genetic diversity in the 53 ethnic groups across the globe that constitute the Human Genome Diversity Cell Line Panel.
Figure 1.
Expected Heterozygosity and Migratory Distance in the HGDP-CEPH Sample
Second, there exists an optimal level of diversity for economic development, reflecting the interplay between the conflicting effects of diversity on the development process. The adverse effect pertains to the detrimental impact of diversity on the efficiency of the aggregate production process of an economy. Heterogeneity increases the likelihood of mis-coordination and distrust, reducing cooperation and disrupting the socioeconomic order. Greater population diversity is therefore associated with the social cost of a lower total factor productivity, which inhibits the ability of society to operate efficiently with respect to its production possibility frontier.
The beneficial effect of diversity, on the other hand, concerns the positive role of diversity in the expansion of society’s production possibility frontier. A wider spectrum of traits is more likely to be complementary to the development and successful implementation of advanced technological paradigms.1 Greater heterogeneity therefore fosters the ability of a society to incorporate more sophisticated and efficient modes of production, expanding the economy’s production possibility frontier and conferring the benefits of increased total factor productivity.
Higher diversity in a society’s population can therefore have conflicting effects on the level of its total factor productivity. Aggregate productivity is enhanced on the one hand by an increased capacity for technological advancement, while simultaneously diminished on the other by reduced cooperation and efficiency.2 However, if the beneficial effects of population diversity dominate at lower levels of diversity and the detrimental effects dominate at higher levels (i.e., if there are diminishing marginal returns to both diversity and homogeneity), the theory would predict an inverted-U relationship between genetic diversity and development outcomes over the course of the development process.
In estimating the impact on economic development of migratory distance from East Africa via its effect on genetic diversity, this research overcomes limitations and potential concerns that are presented by the existing data on genetic diversity across the globe (i.e., measurement error, data limitations, and potential endogeneity). Population geneticists typically measure the extent of diversity in genetic material across individuals within a given population (such as an ethnic group) using an index called expected heterozygosity. Like most other measures of diversity, this index may be interpreted simply as the probability that two individuals, selected at random from the relevant population, are genetically different from one another. Specifically, the expected heterozygosity measure for a given population is constructed by geneticists using sample data on allelic frequencies, i.e., the frequency with which a “gene variant” or allele (e.g., the brown vs. blue variant for the eye color gene) occurs in the population sample. Given allelic frequencies for a particular gene or DNA locus, it is possible to compute a gene-specific heterozygosity statistic (i.e., the probability that two randomly selected individuals differ with respect to the gene in question), which when averaged over multiple genes or DNA loci yields the overall expected heterozygosity for the relevant population.
The most reliable and consistent data for genetic diversity among indigenous populations across the globe consists, however, of only 53 ethnic groups from the Human Genome Diversity Cell Line Panel. According to anthropologists, these groups are not only historically native to their current geographical location but have also been isolated from genetic flows from other ethnic groups. Empirical evidence provided by population geneticists (e.g., Ramachandran et al., 2005) for these 53 ethnic groups suggest that, indeed, migratory distance from East Africa has an adverse linear effect on genetic diversity as depicted in Figure 1. Migratory distance from East Africa for each of the 53 ethnic groups was computed using the great circle (or geodesic) distances from Addis Ababa (Ethiopia) to the contemporary geographic coordinates of these ethnic groups, subject to five obligatory intermediate waypoints (i.e., Cairo (Egypt), Istanbul (Turkey), Phnom Penh (Cambodia), Anadyr (Russia) and Prince Rupert (Canada)), that capture paleontological and genetic evidence on prehistorical human migration patterns.
Nonetheless, while the existing data on genetic diversity pertain only to ethnic groups, data for examining comparative development are typically available at the country level. Moreover, many national populations today are composed of multiple ethnicities, some of which may not be indigenous to their current geographical locations. This raises two complex tasks. First, one needs to construct of a measure of genetic diversity for national populations, based on genetic diversity data at the ethnic group level, accounting for diversity not only within each component group but for diversity due to differences between ethnic groups as well. Second, it is necessary to account for the potential inducement for members of distinct ethnic groups to relocate to relatively more lucrative geographical locations.
To tackle these difficulties, this study adopts two distinct strategies. The first restricts attention to development outcomes in the pre-colonial era when, arguably, regional populations were indigenous to their current geographical location and largely homogenous in terms of their ethnic compositions, with the presence of multiple indigenous ethnicities in a given region having a negligible effect on the diversity of the regional population. The second, more complex strategy involves the construction of an index of genetic diversity for contemporary national populations that accounts for the expected heterozygosity within each sub-national group as well as the additional component of diversity at the country level that arises from the genetic distances between its pre-colonial ancestral populations. The examination of comparative development under this second strategy would have to additionally account for the potential inducement for members of distinct ethnic groups to relocate to relatively more lucrative geographical locations.
The examination of comparative development in the pre-colonial era, when societies were in their agricultural stage of development, requires the interpretation of outcomes from a Malthusian equilibrium point of view. Improvements in the technological environment during the Malthusian epoch generated only temporary gains in income per capita, eventually leading to a larger, but not richer, population (Ashraf and Galor, 2010). Thus the relevant variable gauging comparative economic development during this era is population density as opposed to income per capita. In light of this argument, this study employs cross-country historical data on population density as the outcome variable of interest in the historical analysis and examines the hypothesized effect of human genetic diversity within societies on their population densities in the year 1500 CE.3
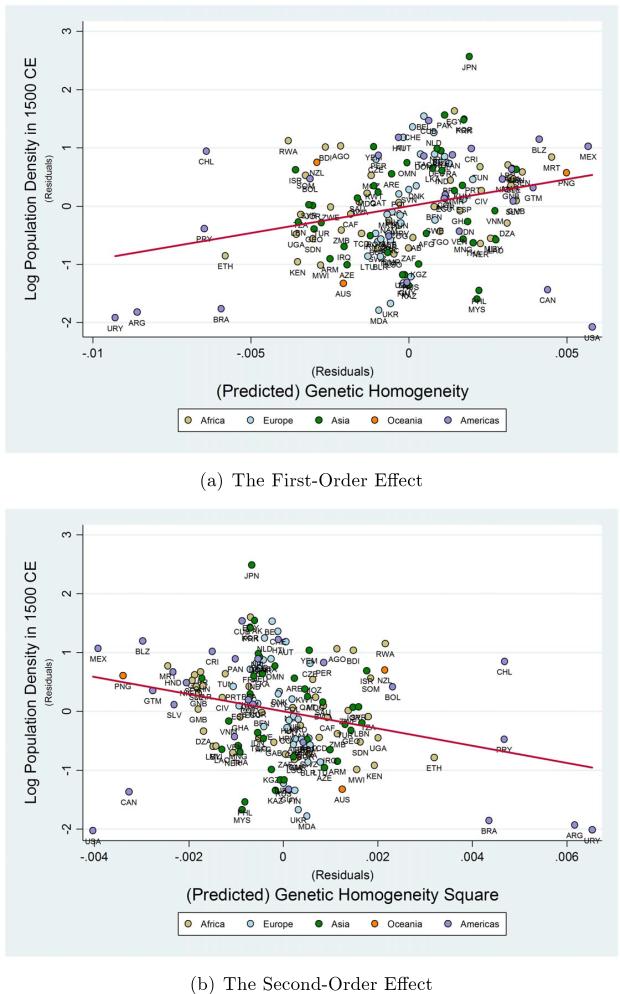
Using data on genetic diversity observed at the ethnic group level, the historical analysis reveals, consistently with the proposed hypothesis, a highly significant hump-shaped effect of genetic diversity on log population density in the year 1500 CE. In particular, accounting for the influence of the timing of the Neolithic Revolution, the natural productivity of land for agriculture, as well as other geographical characteristics that may affect population density in the pre-industrial era, the estimated linear and quadratic coefficients associated with genetic diversity imply that a 1 percentage point increase in diversity for the least diverse society in the regression sample would raise its population density by 58%, whereas a 1 percentage point decrease in diversity for the most diverse society would raise its population density by 23%. Despite the statistical significance and robustness of these effects, however, the analysis is subsequently expanded upon to lend further credence to these findings by alleviating concerns regarding sample size limitations and potential endogeneity bias.
The issue of data limitations encountered by the analysis stems from the fact that diversity data at the ethnic group level currently spans only a modest subset of the sample of countries for which historical population estimates are available. The potential endogeneity issue, on the other hand, arises from the possibility that genetic diversity within populations could partly reflect historical processes such as interregional migrations that were, in turn, determined by historical patterns of comparative development. Furthermore, the direction of the potential endogeneity bias is a priori ambiguous. For example, while historically better developed regions may have been attractive destinations to potential migrants, serving to increase genetic diversity in relatively wealthier societies, the more advanced technologies in these societies may also have conferred the necessary military prowess to prevent or minimize foreign invasions, thereby reducing the likelihood of greater genetic diversity in their populations.4
In surmounting the aforementioned data limitations and potential endogeneity issues, this research appeals to the “out of Africa” theory regarding the origins of Homo sapiens. According to this well-established hypothesis, the human species, having evolved to its modern form in East Africa some 150,000 years ago, thereafter embarked on populating the entire globe in a stepwise migration process beginning about 70,000–90,000 BP.5 Using archeological data combined with mitochondrial and Y-chromosomal DNA analysis to identify the most recent common ancestors of contemporary human populations, geneticists are able to not only offer evidence supporting the origin of humans in East Africa but also trace the prehistorical migration routes of the subsequent human expansion into the rest of the world. In addition, population geneticists studying human genetic diversity have argued that the contemporary distribution of diversity across populations should reflect a serial-founder effect originating in East Africa. Accordingly, since the populating of the world occurred in a series of stages where subgroups left initial colonies to create new colonies further away, carrying with them only a portion of the overall genetic diversity of their parental colonies, contemporary genetic diversity in human populations should be expected to decrease with increasing distance along prehistorical migratory paths from East Africa.6 Indeed, several studies in population genetics (e.g., Prugnolle et al., 2005; Ramachandran et al., 2005; Wang et al., 2007) have found strong empirical evidence in support of this prediction.
The present study exploits the explanatory power of migratory distance from East Africa for genetic diversity within ethnic groups in order to overcome the data limitations and potential endogeneity issues encountered by the initial analysis discussed above. In particular, the strong ability of prehistorical migratory distance from East Africa in explaining observed genetic diversity permits the analysis to generate predicted values of genetic diversity using migratory distance for countries for which diversity data are currently unavailable. This enables a subsequent analysis to estimate the effects of genetic diversity, as predicted by migratory distance from East Africa, in a much larger sample of countries. Moreover, given the obvious exogeneity of migratory distance from East Africa with respect to development outcomes in the Common Era, the use of migratory distance to project genetic diversity alleviates concerns regarding the potential endogeneity between observed genetic diversity and economic development.
The main results from the historical analysis, employing predicted genetic diversity in the extended sample of countries, indicate that, controlling for the influence of land productivity, the timing of the Neolithic Revolution, and continental fixed effects, a 1 percentage point increase in diversity for the most homogenous society in the sample would raise its population density in 1500 CE by 36%, whereas a 1 percentage point decrease in diversity for the most diverse society would raise its population density by 29%. Further, a 1 percentage point change in diversity in either direction at the predicted optimum of 0.683 would lower population density by 1.5%.7
Moving to the contemporary period, the analysis, as discussed earlier, constructs an index of genetic diversity at the country level that not only incorporates the expected heterozygosities of the pre-Columbian ancestral populations of contemporary sub-national groups, as predicted by the migratory distances of the ancestral populations from East Africa, but also incorporates the pairwise genetic distances between these ancestral populations, as predicted by their pairwise migratory distances. Indeed, the serial-founder effect studied by population geneticists not only predicts that expected heterozygosity declines with increasing distance along migratory paths from East Africa, but also that the genetic distance between any two populations will be larger the greater the migratory distance between them.
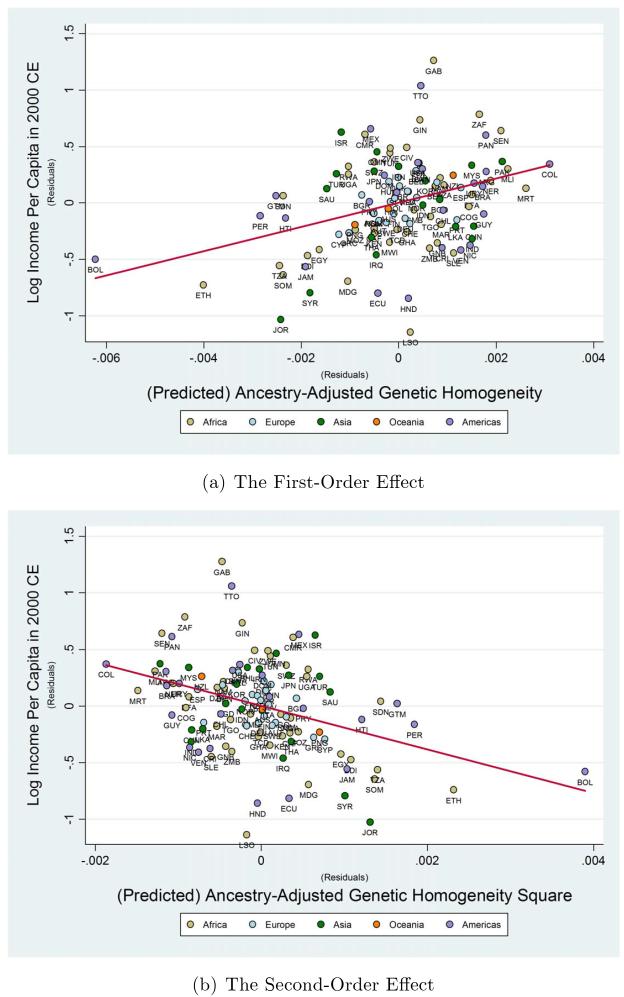
The baseline results from the contemporary analysis indicate that the genetic diversity of contemporary national populations has an economically and statistically significant hump-shaped effect on income per capita. This hump-shaped impact of diversity on income per capita is robust to continental fixed effects, and to controls for ethnic fractionalization and various measures of institutional quality, including social infrastructure, an index gauging the extent of democracy, constraints on the power of chief executives, legal origins, major religion shares, and the share of the population of European descent, as well as to controls for years of schooling, disease environments, and other geographical factors that have received attention in the literature on cross-country comparative development.
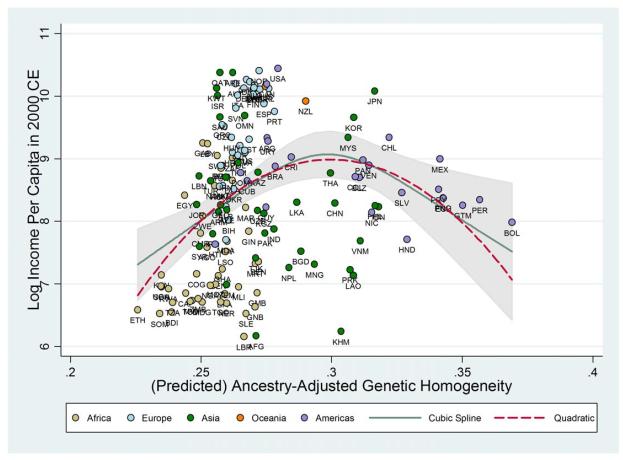
The direct effect of genetic diversity on contemporary income per capita, once institutional, cultural, and geographical factors are accounted for, indicates that: (i) increasing the diversity of the most homogenous country in the sample (Bolivia) by 1 percentage point would raise its income per capita in the year 2000 CE by 39%, (ii) decreasing the diversity of the most diverse country in the sample (Ethiopia) by 1 percentage point would raise its income per capita by 21%, (iii) a 1 percentage point change in genetic diversity (in either direction) at the optimum level of 0.721 (that most closely resembles the diversity level of the U.S.) would lower income per capita by 1.9%, (iv) increasing Bolivia’s diversity to the optimum level prevalent in the U.S. would increase Bolivia’s per capita income by a factor of 4.7, closing the income gap between the U.S. and Bolivia from 12:1 to 2.5:1, and (v) decreasing Ethiopia’s diversity to the optimum level of the U.S. would increase Ethiopia’s per capita income by a factor of 1.7 and, thus, close the income gap between the U.S. and Ethiopia from 47:1 to 27:1.
Reassuringly, the highly significant and stable hump-shaped effect of genetic diversity on income per capita in the year 2000 CE is not an artifact of post-colonial migrations towards prosperous countries and the concomitant increase in ethnic diversity in these economies. The hump-shaped effect of genetic diversity remains highly significant and the optimal diversity estimate remains virtually intact if the regression sample is restricted to (a) non-OECD economies (i.e., economies that were less attractive to migrants), (b) non Neo-European countries (i.e., excluding the U.S., Canada, New Zealand and Australia), (c) non-Latin American countries, (d) non Sub-Saharan African countries, and perhaps most importantly (e) to countries whose indigenous population is larger than 97% of the entire population (i.e., under conditions that virtually eliminate the role of migration in the creation of diversity).
The remainder of the paper is organized as follows: Section 2 briefly reviews some related literature. Section 3 presents a basic model that predicts a hump-shaped effect of diversity on economic development. Section 4 covers the historical analysis, discussing the empirical strategy as well as the relevant data and data sources before presenting the empirical findings. Section 5 does the same for the contemporary analysis, and, finally, Section 6 concludes.
2 Related Literature
The existing literature on comparative development has emphasized a variety of factors underlying some of the vast differences in living standards across the globe. The influence of geography, for instance, has been stressed from a historical perspective by Jones (1981), Diamond (1997), and Pomeranz (2000), and is highlighted empirically by Gallup et al. (1999) and Olsson and Hibbs (2005), amongst others. Institutions, on the other hand, are given historical precedence by North and Thomas (1973), Mokyr (1990), and Greif (1993), and are emphasized empirically by Hall and Jones (1999), La Porta et al. (1999), Rodrik et al. (2004), and Acemoglu et al. (2005). In related strands of the literature on institutions, Engerman and Sokoloff (2000) and Acemoglu et al. (2005) have stressed the role of colonialism, while the effects of ethno-linguistic fractionalization are examined by Easterly and Levine (1997), Alesina et al. (2003), and others. Meanwhile, the historical impact of sociocultural factors has been highlighted by Weber (1905) and Landes (1998), with empirical support coming from Barro and McCleary (2003), Tabellini (2008), as well as Guiso et al. (2009). Finally, the importance of human capital formation has been underlined in unified growth theory (e.g., Galor, 2010), and has been demonstrated empirically by Glaeser et al. (2004).8
This research is the first to argue that the variation in prehistorical migratory distance from the cradle of humankind to various settlements across the globe has had a persistent effect on the process of development and on the contemporary variation in income per capita across the globe. The paper is also unique in its attempt to establish the role of genetic (rather than ethnic) diversity within a society as a significant determinant of its development path and, thus, its comparative economic performance across space and time.
The employment of data and empirical results from the field of population genetics places this research in the neighborhood of a recent insightful paper in the economic literature by Spolaore and Wacziarg (2009) who have appealed to data on genetic distance between human populations to proxy for the effect of sociocultural differences between societies on the diffusion of economic development.9 Specifically, the authors argue that genetic distance between populations, which captures their divergence in biological and cultural characteristics over time, has been a barrier to the horizontal diffusion of technological innovations across populations. They show that Fst genetic distance, a measure that reflects the time elapsed since two populations shared a common ancestor, confers a statistically significant positive effect on both historical and contemporary pairwise income differences. In contrast, the genetic diversity metric within populations exploited by this paper facilitates the analysis of the effect of the variation in traits across individuals within a society on its development process.
Unlike Spolaore and Wacziarg (2009) where genetic distance between populations diminishes the rate of technological diffusion and reduces productivity, the hypothesis advanced and tested in this paper suggests that genetic diversity within a population confers both social costs, in the form of lower social capital arising from differences amongst individual members, and social benefits in the form of diversity-driven knowledge accumulation. Hence, the overall effect of genetic diversity on developmental outcomes would be hump-shaped, rather than monotonically negative. The results of the empirical analysis conducted in this study suggest that the previously unexamined beneficial effect of genetic differences is indeed a significant factor in the overall influence of the genetic channel on comparative development.
The examination of the effects of genetic diversity along with the influence of the timing of agricultural transitions also places this paper in an emerging strand of the literature that has focused on empirically testing Diamond’s (1997) assertion regarding the long-standing impact of the Neolithic Revolution.10 Diamond (1997) has stressed the role of biogeographical factors in determining the timing of the Neolithic Revolution, which conferred a developmental head-start to societies that experienced an earlier transition from primitive hunting and gathering techniques to the more technologically advanced agricultural mode of production. According to this hypothesis, the luck of being dealt a favorable hand thousands of years ago with respect to biogeographic endowments, particularly exogenous factors contributing to the emergence of agriculture and facilitating the subsequent diffusion of agricultural techniques, is the single most important driving force behind the divergent development paths of societies throughout history that ultimately led to the contemporary global differences in standards of living. Specifically, an earlier transition to agriculture due to favorable environmental conditions gave some societies an early advantage by conferring the benefits of a production technology that generated resource surpluses and enabled the rise of a non-food-producing class whose members were crucial for the development of written language and science, and for the formation of cities, technology-based military powers and nation states. The early technological dominance of these societies subsequently persisted throughout history, being further sustained by the subjugation of less-developed societies through exploitative geopolitical and historical processes such as colonization.
While the long-standing influence of the Neolithic Revolution on comparative development remains a compelling argument, this research demonstrates that, contrary to Diamond’s (1997) unicausal hypothesis, the composition of human populations with respect to their genetic diversity has been an significant and persistent factor that affected the course of economic development from the dawn of human civilization to the present. In estimating the economic impact of human genetic diversity while controlling for the channel emphasized by Diamond (1997), the current research additionally establishes the historical significance of the timing of agricultural transitions for pre-colonial population density, which, as already argued, is the relevant variable capturing comparative economic development during the Malthusian epoch of stagnation in income per capita.11
3 Diversity and Productivity: A Basic Model
Consider an economy where the level of productivity is affected by the degree of genetic diversity in society. Specifically, genetic diversity generates conflicting effects on productivity. A wider spectrum of traits is complementary to the adoption or implementation of new technologies. It enhances knowledge creation and fosters technological progress, thereby expanding the economy’s production possibility frontier. However, a wider spectrum of traits also reduces the likelihood of cooperative or trustful behavior, generating inefficiencies in the operation of the economy relative to its production possibility frontier.
Suppose that the degree of genetic diversity, ω ∈ [0, 1], has a positive but diminishing effect on the level of technology that is available for production. Specifically, the level of technology, A, and thus the economy’s production possibility frontier, is determined by a vector of institutional, geographical, and human capital factors, z, as well as by the degree of diversity, ω.12
| (1) |
where A(z, ω) > 0, Aω(z, ω) > 0, and Aωω(z, ω) < 0 for all ω ∈ [0, 1], and limω→0 Aω(z, ω) = ∞ and limω→1 Aω(z, ω) = 0.
Suppose further that the position of the economy relative to its production possibly frontier is adversely affected by the degree of genetic diversity. In particular, a fraction, αω, of the economy’s potential productivity, A(z, ω), is lost due to lack of cooperation and resultant inefficiencies in the production process.
Output per worker is therefore determined by the level of employment of factors of production, x, the level of productivity, A(z, ω), and the degree of inefficiency in production, α ∈ (0, 1).
| (2) |
where x is a vector of factor inputs per worker, and αω is the extent of erosion in productivity due to inefficiencies in the production process.13 Hence, as follows from (2), y(ω) is a strictly concave hump-shaped function of ω. Specifically,
| (3) |
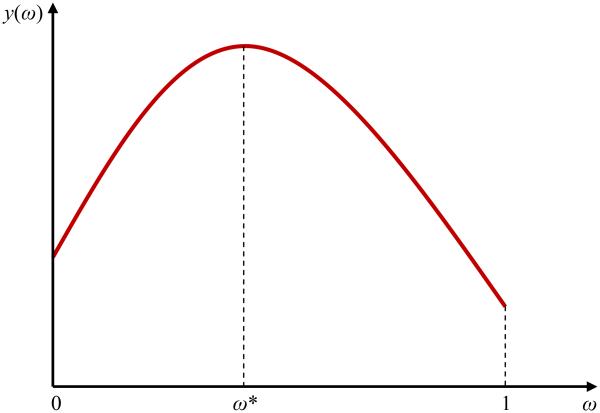
Thus, as depicted in Figure 2, there exists an intermediate level of diversity, ω* ∈ (0, 1), that maximizes the level of output per worker. In particular, ω* satisfies
| (4) |
Figure 2.
The Hump-Shaped Effect of Diversity on Development
4 The Historical Analysis
4.1 Data and Empirical Strategy
This section discusses the data and empirical strategy employed to examine the impact of genetic diversity on comparative development in the pre-colonial era.
4.1.1 Dependent Variable: Historical Population Density
As argued previously, the relevant variable reflecting comparative development across countries in the pre-colonial Malthusian era is population density. The empirical examination of the proposed genetic hypothesis therefore aims to employ cross-country variation in observed genetic diversity and in that predicted by migratory distance from East Africa to explain cross-country variation in historical population density. Data on historical population density are obtained from McEvedy and Jones (1978) who provide figures at the country level, i.e., for regions defined by contemporary national borders, over the period 400 BCE–1975 CE.14 However, given the greater unreliability (and less availability in terms of observations) of population data for earlier historical periods, the baseline regression specification adopts population density in 1500 CE as the preferred outcome variable to examine. The analysis in Appendix A additionally examines population density in 1000 CE and 1 CE to demonstrate the robustness of the genetic channel for earlier time periods.
4.1.2 Independent Variable: Genetic Diversity
The most reliable and consistent data for genetic diversity among indigenous populations across the globe consists of 53 ethnic groups from the Human Genome Diversity Cell Line Panel, compiled by the Human Genome Diversity Project-Centre d’Etudes du Polymorphisme Humain (HGDPCEPH).15 According to anthropologists, these 53 ethnic groups are not only historically native to their current geographical location but have also been isolated from genetic flows from other ethnic groups. Population geneticists typically measure the extent of diversity in genetic material across individuals within a given population (such as an ethnic group) using an index called expected heterozygosity. Like most other measures of diversity, this index may be interpreted simply as the probability that two individuals, selected at random from the relevant population, are genetically different from one another. Specifically, the expected heterozygosity measure for a given population is constructed by geneticists using sample data on allelic frequencies, i.e., the frequency with which a “gene variant” or allele occurs in the population sample. Given allelic frequencies for a particular gene or DNA locus, it is possible to compute a gene-specific heterozygosity statistic (i.e., the probability that two randomly selected individuals differ with respect to a given gene), which when averaged over multiple genes or DNA loci yields the overall expected heterozygosity for the relevant population.
Consider a single gene or locus l with k observed variants or alleles in the population and let pi denote the frequency of the i-th allele. Then, the expected heterozygosity of the population with respect to locus l, , is:
| (5) |
Given allelic frequencies for each of m different genes or loci, the average across these loci then yields an aggregate expected heterozygosity measure of overall genetic diversity, Hexp, as:
| (6) |
where kl is the number of observed variants in locus l.
Empirical evidence uncovered by Ramachandran et al. (2005) for the 53 ethnic groups from the Human Genome Diversity Cell Line Panel suggests that migratory distance from East Africa has an adverse linear effect on genetic diversity.16 They interpret this finding as providing support for a serial-founder effect originating in East Africa, reflecting a process where the populating of the world occurred in a series of discrete steps involving subgroups leaving initial settlements to establish new settlements further away and carrying with them only a subset of the overall genetic diversity of their parental colonies.
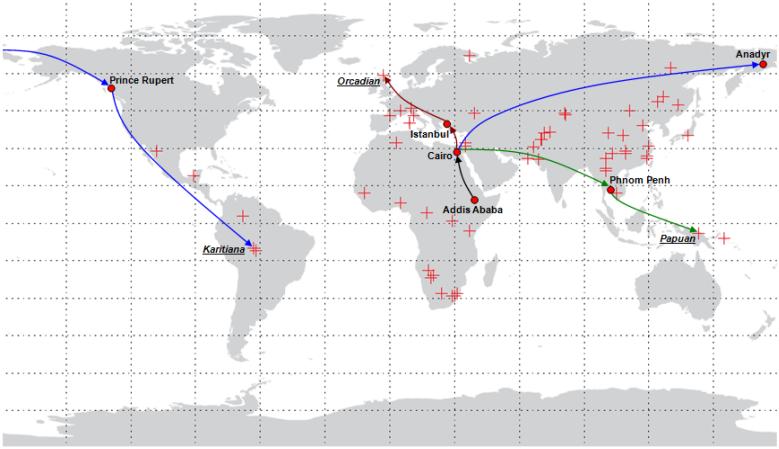
In estimating the migratory distance from East Africa for each of the 53 ethnic groups in their data set, Ramachandran et al. (2005) calculate great circle (or geodesic) distances using Addis Ababa (Ethiopia) as the point of common origin and the contemporary geographic coordinates of the sampled groups as the destinations. Moreover, these distance estimates incorporate five obligatory intermediate waypoints, used to more accurately capture paleontological and genetic evidence on prehistorical human migration patterns that are consistent with the widely-held hypothesis that, in the course of their exodus from Africa, humans did not cross large bodies of water. The intermediate waypoints, depicted on the world map in Figure 3 along with the spatial distribution of the ethnic groups from the HGDP-CEPH sample, are: Cairo (Egypt), Istanbul (Turkey), Phnom Penh (Cambodia), Anadyr (Russia) and Prince Rupert (Canada). For instance, as illustrated in Figure 3, the migration path from Addis Ababa to the Papuan ethnic group in modern-day New Guinea makes use of Cairo and Phnom Penh whereas that to the Karitiana population in Brazil incorporates Cairo, Anadyr and Prince Rupert as intermediate waypoints.17 The migratory distance between endpoints (i.e., Addis Ababa and the location of a group) is therefore the sum of the great circle distances between these endpoints and the waypoint(s) in the path connecting them, and the distance(s) between waypoints if two or more such points are required.
Figure 3.
The 53 HGDP-CEPH Ethnic Groups and Migratory Paths from East Africa
The empirical analysis of Ramachandran et al. (2005) establishes migratory distance from East Africa as a strong negative predictor of genetic diversity at the ethnic group level. Based on the R-squared of their regression, migratory distance alone explains almost 86% of the cross-group variation in within-group diversity.18 In addition, the estimated OLS coefficient is highly statistically significant, possessing a t-statistic = −9.770 (P-value < 10−4), and suggests that predicted expected heterozygosity falls by 0.076 percentage points for every 10,000 km increase in migratory distance from Addis Ababa.19 This is the relationship depicted earlier on the scatter plot in Figure 1.
The present study exploits the explanatory power of migratory distance from East Africa for the cross-sectional variation in ethnic group expected heterozygosity in order to advance the empirical analysis of the effect of diversity on development in two dimensions. First, given the potential endogeneity between observed genetic diversity and economic development as discussed earlier, the use of genetic diversity values predicted by migratory distance from East Africa alleviates concerns regarding endogeneity bias. Specifically, the identifying assumption being employed here is that distances along prehistorical human migration routes from Africa have no direct effect on economic development during the Common Era. Second, the strong capacity of migratory distance in predicting genetic diversity implies that the empirical analysis of the genetic hypothesis proposed in this study need not be restricted to the 53 HGDP-CEPH ethnic groups that span only 21 countries, especially since data on the outcome variable of interest (i.e., population density in the year 1500 CE) are available for a much larger set of countries.
To further elaborate, the current analysis tests the proposed genetic hypothesis both using observed genetic diversity in a limited sample of 21 countries, spanned by the 53 ethnic groups in the HGDP-CEPH data set, and using genetic diversity predicted by migratory distance from East Africa in an extended sample of 145 countries. In the 21-country sample, genetic diversity and migratory distance are aggregated up to the country level by averaging across the set of ethnic groups located within a given country.20 For the extended sample, however, the distance calculation methodology of Ramachandran et al. (2005) is adopted to first construct migratory distance from East Africa for each country, using Addis Ababa as the origin and the country’s modern capital city as the destination along with the aforementioned waypoints for restricting the migration route to landmasses as much as possible.21 This constructed distance variable is then applied to obtain a predicted value of genetic diversity for each country based on the coefficient on migratory distance in Ramachandran et al.’s (2005) regression across the 53 HGDP-CEPH ethnic groups. Hence, it is this predicted genetic diversity at the country level that is employed as the explanatory variable of interest in the extended sample of countries.22
4.1.3 Control Variables: Neolithic Transition Timing and Land Productivity
Diamond’s (1997) hypothesis has identified the timing of the Neolithic Revolution as a proximate determinant of economic development, designating initial geographic and biogeographic conditions that governed the emergence and adoption of agricultural practices in prehistorical hunter-gatherer societies as the ultimate determinants in this channel. Some of these geographic and biogeographic factors, highlighted in the empirical analysis of Olsson and Hibbs (2005), include the size of the continent or landmass, the orientation of the major continental axis, type of climate, and the number of prehistorical plant and animal species amenable for domestication.23
The current analysis controls for the ultimate and proximate determinants of development in the Diamond channel using cross-country data on the aforementioned geographic and biogeographic variables as well as on the timing of the Neolithic Revolution.24 However, given the empirical link between the ultimate and proximate factors in Diamond’s hypothesis, the baseline specification focuses on the timing of the Neolithic transition to agriculture as the relevant control variable for this channel. The results from an extended specification that incorporates initial geographic and biogeographic factors as controls are presented in Appendix A to demonstrate robustness.
The focus of the historical analysis on economic development in the pre-colonial Malthusian era also necessitates controls for the natural productivity of land for agriculture. Given that in a Malthusian environment resource surpluses are primarily channeled into population growth with per capita incomes largely remaining at or near subsistence, regions characterized by natural factors generating higher agricultural crop yields should, ceteris paribus, also exhibit higher population densities (Ashraf and Galor, 2010).25 If diversity in a society influences its development through total factor productivity (comprised of both social capital and technological know-how), then controlling for the natural productivity of land would constitute a more accurate test of the effect of diversity on the Malthusian development outcome – i.e., population density.
In controlling for the agricultural productivity of land, this study employs measurements of three geographic variables at the country level including (i) the percentage of arable land, (ii) absolute latitude, and (iii) an index gauging the overall suitability of land for agriculture based on ecological indicators of climate suitability for cultivation, such as growing degree days and the ratio of actual to potential evapotranspiration, as well as ecological indicators of soil suitability for cultivation, such as soil carbon density and soil pH.26
4.1.4 The Baseline Regression Specifications
In light of the proposed genetic diversity hypothesis as well as the roles of the Neolithic transition timing and land productivity channels in agricultural development, the following specification is adopted to examine the influence of observed genetic diversity on economic development in the limited sample of 21 countries:
| (7) |
where Pit is the population density of country i in a given year t, Gi is the average genetic diversity of the subset of HGDP-CEPH ethnic groups that are located in country i, Ti is the time in years elapsed since country i’s transition to agriculture, Xi is a vector of land productivity controls, △i is a vector of continental dummies, and εit is a country-year specific disturbance term.27
Moreover, considering the remarkably strong predictive power of migratory distance from East Africa for genetic diversity, the baseline regression specification employed to test the proposed genetic channel in the extended cross-country sample is given by:
| (8) |
where Ĝi is the genetic diversity predicted by migratory distance from East Africa for country i using the methodology discussed in Section 4.1.2. Indeed, it is this regression specification that is estimated to obtain the main empirical findings.28
Before proceeding, it is important to note that the regression specifications in (7) and (8) above constitute reduced-form empirical analyses of the genetic diversity channel in Malthusian economic development. Specifically, according to the proposed hypothesis, genetic diversity has a non-monotonic impact on society’s level of development through two opposing effects on the level of its total factor productivity: a detrimental effect on social capital and a beneficial effect on the knowledge frontier. However, given the absence of measurements for the proximate determinants of development in the genetic diversity channel, a more discriminatory test of the hypothesis is infeasible. Nonetheless, the results to follow are entirely consistent with the theoretical prediction that, in the presence of diminishing marginal effects of genetic diversity on total factor productivity in a Malthusian economy, the overall reduced-form effect of genetic diversity on cross-country population density should be hump-shaped – i.e., that β1t > 0 and β2t < 0. Moreover, as will become evident, the unconditional hump-shaped relationship between genetic diversity and development outcomes does not differ significantly between the adopted quadratic and alternative non-parametric specifications.
4.2 Empirical Findings
This section presents the results from empirically investigating the relationship between genetic diversity and log population density in the pre-colonial Malthusian era. Results for observed diversity in the limited 21-country sample are examined in Section 4.2.1. Section 4.2.2 discusses the baseline results associated with examining the effect of predicted diversity on log population density in 1500 CE in the extended sample of 145 countries. The robustness of the diversity channel with respect to alternative concepts of distance, including the aerial distance from East Africa as well as migratory distances from several “placebo” points of origin across the globe, are presented in Section 4.2.3.
The analysis is subsequently expanded upon in Appendix A to demonstrate the robustness of the diversity channel with respect to (i) explaining comparative development in earlier historical periods, specifically log population density in 1000 CE and 1 CE, (ii) the technology diffusion hypothesis that postulates a beneficial effect on development arising from spatial proximity to regional technological frontiers, (iii) controls for microgeographic factors including the degree of variation in terrain and access to waterways, and finally, (iv) controls for the exogenous geographic and biogeographic factors favoring an earlier onset of agriculture in the Diamond channel.
4.2.1 Results from the Limited Sample
The initial investigation of the proposed genetic diversity hypothesis using the limited sample of countries is of fundamental importance for the subsequent empirical analyses, performed using the extended sample, in three critical dimensions. First, since the limited sample contains observed values of genetic diversity whereas the extended sample comprises values predicted by migratory distance from East Africa, similarity in the results obtained from the two samples would lend credence to the main empirical findings associated with predicted genetic diversity in the extended sample of countries. Second, the fact that migratory distance from East Africa and observed genetic diversity are not perfectly correlated with each other makes it possible to test, using the limited sample of countries, the assertion that migratory distance affects economic development through genetic diversity only and is, therefore, appropriate for generating predicted genetic diversity in the extended sample of countries.29 Finally, having verified the above assertion, the limited sample permits an instrumental variables regression analysis of the proposed hypothesis with migratory distance employed as an instrument for genetic diversity. This then constitutes a more direct and accurate test of the genetic diversity channel given possible concerns regarding the endogeneity between genetic diversity and economic development. As will become evident, the results obtained from the limited sample are reassuring on all three aforementioned fronts.
Explaining Comparative Development in 1500 CE
Table 1 presents the limited sample results from regressions explaining log population density in 1500 CE.30 In particular, a number of specifications comprising different subsets of the explanatory variables in equation (3) are estimated to examine the independent and combined effects of the genetic diversity, transition timing, and land productivity channels.
Table 1.
Observed Diversity and Economic Development in 1500 CE
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
| Dependent Variable is Log
Population Density in 1500 CE |
|||||
| Observed Diversity | 413.504*** (97.320) |
225.440*** (73.781) |
203.814* (97.637) |
||
| Observed Diversity Sqr. | −302.647*** (73.344) |
−161.158** (56.155) |
−145.717* (80.414) |
||
| Log Transition Timing | 2.396*** (0.272) |
1.214*** (0.373) |
1.135 (0.658) |
||
| Log % of Arable Land | 0.730** (0.281) |
0.516*** (0.165) |
0.545* (0.262) |
||
| Log Absolute Latitude | 0.145 (0.178) |
−0.162 (0.130) |
−0.129 (0.174) |
||
| Log Land Suitability | 0.734* (0.381) |
0.571* (0.294) |
0.587 (0.328) |
||
|
| |||||
| Optimal Diversity | 0.683*** (0.008) |
0.699*** (0.015) |
0.699*** (0.055) |
||
|
| |||||
| Continent Dummies | No | No | No | No | Yes |
| Observations | 21 | 21 | 21 | 21 | 21 |
| R-squared | 0.42 | 0.54 | 0.57 | 0.89 | 0.90 |
Note: Heteroskedasticity robust standard errors are reported in parentheses.
Significant at 1%
Significant at 5%
Significant at 10%.
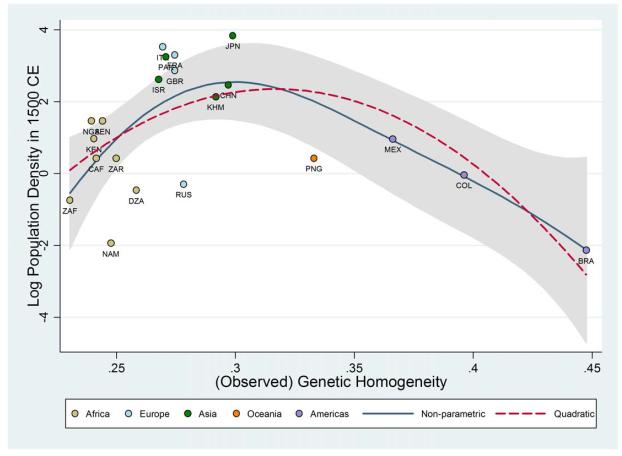
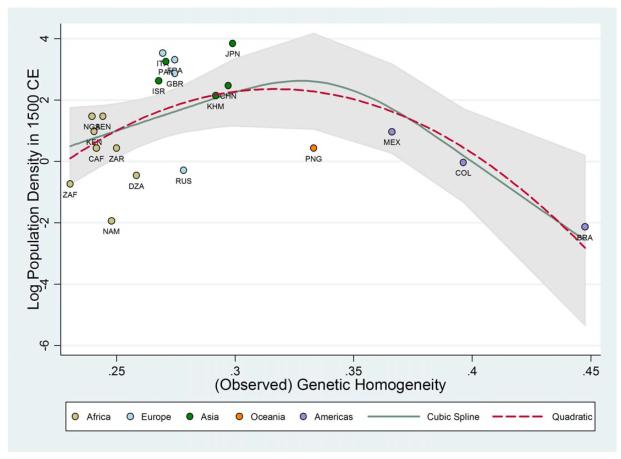
Consistent with the predictions of the proposed diversity hypothesis, Column 1 reveals the unconditional cross-country hump-shaped relationship between genetic diversity and log population density in 1500 CE. Specifically, the estimated linear and quadratic coefficients, both statistically significant at the 1% level, imply that a 1 percentage point increase in genetic diversity for the most homogenous society in the regression sample would raise its population density in 1500 CE by 114%, whereas a 1 percentage point decrease in diversity for the most diverse society would raise its population density by 64%. In addition, the coefficients also indicate that a 1 percentage point change in diversity in either direction at the predicted optimum of 0.683 would lower population density by 3%.31 Furthermore, based on the R-squared coefficient of the regression, the genetic diversity channel appears to explain 42% of the variation in log population density in 1500 CE across the limited sample of countries. The quadratic relationship implied by the OLS coefficients reported in Column 1 is depicted together with a non-parametric local polynomial regression line on the scatter plot in Figure 4.32 Reassuringly, as illustrated therein, the estimated quadratic falls within the 95% confidence interval band of the non-parametric relationship.33
Figure 4.
Observed Genetic Diversity and Population Density in 1500 CE – The Unconditional Relationship
The unconditional effects of the Neolithic transition timing and land productivity channels are reported in Columns 2 and 3 respectively. In line with the Diamond hypothesis, a 1% increase in the number of years elapsed since the transition to agriculture increases population density in 1500 CE by 2.4%, an effect that is also significant at the 1% level. Similarly, consistent with the predictions of the land productivity channel, population density in 1500 CE possesses statistically significant positive elasticities with respect to both the percentage of arable land as well as the index gauging the suitability of land for agriculture. Moreover, the agricultural transition timing and land productivity channels independently explain 54% and 57% of the limited cross-country sample variation in log population density in 1500 CE.
Column 4 presents the results obtained from exploiting the combined explanatory power of all three channels for log population density in the year 1500 CE. Not surprisingly, given the small sample size as well as the pairwise correlations between covariates reported in Table G.2 in Appendix G, the estimated conditional effects are sizeably reduced in magnitude in comparison to their unconditional estimates presented in earlier columns. Nonetheless, the OLS coefficients associated with all channels retain their expected signs and continue to remain highly statistically significant. To interpret the conditional effects of the genetic diversity channel, the estimated linear and quadratic coefficients associated with genetic diversity imply that, accounting for the influence of the transition timing and land productivity channels, a 1 percentage point increase in genetic diversity for the most homogenous society in the regression sample would raise its population density in 1500 CE by 58%, whereas a 1 percentage point decrease in diversity for the most diverse society would raise its population density by 23%. Further, a 1 percentage point change in diversity in either direction at the predicted optimum of 0.699 would lower population density by 1.6%. Additionally, by exploiting the combined explanatory power of all three channels, the estimated model explains an impressive 89% of the limited sample cross-country variation in log population density.
Table G.2.
Pairwise Correlations for the 21-Country Historical Sample
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | ||
|---|---|---|---|---|---|---|---|---|
| (1) | Log Population Density in 1500 CE | 1.000 | ||||||
| (2) | Observed Genetic Diversity | 0.244 | 1.000 | |||||
| (3) | Migratory Distance from Addis Ababa | −0.226 | −0.968 | 1.000 | ||||
| (4) | Human Mobility Index | −0.273 | −0.955 | 0.987 | 1.000 | |||
| (5) | Log Neolithic Transition Timing | 0.735 | −0.117 | 0.024 | 0.011 | 1.000 | ||
| (6) | Log % of Arable Land | 0.670 | 0.172 | −0.183 | −0.032 | 0.521 | 1.000 | |
| (7) | Log Absolute Latitude | 0.336 | 0.055 | −0.012 | 0.044 | 0.392 | 0.453 | 1.000 |
| (8) | Log Land Suitability for Agriculture | 0.561 | −0.218 | 0.282 | 0.245 | 0.299 | 0.376 | 0.049 |
Finally, the results from estimating the regression model in equation (3) are reported in Column 5, which indicates that the results from previous columns were not simply reflecting the possible influence of some unobserved continent-specific attributes. In spite of the sample size limitations and the smaller variability of covariates within continents in comparison to that across continents, genetic diversity continues to exert significant influence in a manner consistent with theoretical predictions. Reassuringly, the estimated average within-continent effects of the diversity channel are very similar to the cross-continent effects reported in Column 4 and the implied optimal level of diversity remains intact, lending credence to the assertion that these effects are indeed due to genetic diversity as opposed to unobserved continental characteristics.34
To summarize, the limited sample results presented in Table 1 demonstrate that genetic diversity has a statistically significant hump-shaped relationship with log population density in the year 1500 CE. The analysis, however, also reveals significant effects associated with the Neolithic transition timing and land productivity channels. Indeed, the non-monotonic effect of diversity on log population density prevails under controls for these other explanatory channels, and remains remarkably stable in magnitude regardless of whether the cross-country variations exploited by the analysis are within or across continents. While, given the obvious limitations of the sample employed, these results may initially appear to be more illustrative rather than conclusive, they are in fact reassuringly similar to those obtained in the extended sample of countries, as will become evident in Section 4.2.2 below. This similarity provides further assurance regarding the validity of the inferences made with the main empirical findings that are associated with predicted as opposed to observed values of genetic diversity.
Establishing the Exogeneity of Migratory Distance
As already mentioned, the fact that the limited cross-country sample comprises observed genetic diversity, which is strongly but not perfectly correlated with migratory distance from East Africa, permits a formal examination of whether migratory distance influences population density solely via the serial-founder effect on genetic diversity. This is a particularly important test since, if migratory distance from East Africa actually affects economic development either directly or via some other unobserved channels, then the main empirical analysis conducted using predicted values of diversity would be attributing this latent influence to the genetic diversity channel.35
To implement the aforementioned test, the current analysis examines a specification that includes migratory distance from East Africa rather than genetic diversity to explain the cross-country variation in log population density in 1500 CE. The associated results are then compared with those obtained from estimating an alternative specification including both migratory distance and genetic diversity as covariates. Unless migratory distance and genetic diversity are ultimate and proximate determinants within the same channel, then genetic diversity, when included in the regression, should not capture most of the explanatory power otherwise attributed to migratory distance. However, while Column 1 of Table 2 reveals a highly statistically significant unconditional hump-shaped effect of migratory distance from East Africa on log population density, this effect not only becomes insignificant but also drops considerably in magnitude once genetic diversity is accounted for in Column 2. Further, although the linear and quadratic coefficients associated with the effect of genetic diversity, conditional on migratory distance from East Africa, are admittedly somewhat weaker in magnitude when compared to their unconditional estimates in Table 1, they continue to remain statistically significant at conventional levels of significance.
Table 2.
Migratory Distance from East Africa and Economic Development in 1500 CE
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
|
| ||||||
| OLS | OLS | OLS | OLS | 2SLS | 2SLS | |
| Dependent Variable is Log
Population Density in 1500 CE |
||||||
| Observed Diversity | 255.219** (100.586) |
361.421** (121.429) |
285.190*** (88.064) |
243.110*** (63.880) |
||
| Observed Diversity Sqr. | −209.808** (73.814) |
−268.514*** (87.342) |
−206.576*** (66.852) |
−179.581*** (52.038) |
||
| Migratory Distance | 0.505*** (0.148) |
0.070 (0.184) |
||||
| Migratory Distance Sqr. | −0.023*** (0.006) |
−0.014 (0.009) |
||||
| Mobility Index | 0.353** (0.127) |
0.051 (0.154) |
||||
| Mobility Index Sqr. | −0.012*** (0.004) |
−0.003 (0.006) |
||||
| Log Transition Timing | 1.014*** (0.361) |
1.119** (0.487) |
||||
| Log % of Arable Land | 0.608*** (0.188) |
0.634*** (0.211) |
||||
| Log Absolute Latitude | −0.209* (0.121) |
−0.133 (0.127) |
||||
| Log Land Suitability | 0.494** (0.233) |
0.549** (0.253) |
||||
|
| ||||||
| Continent Dummies | No | No | No | No | No | Yes |
| Observations | 21 | 21 | 18 | 18 | 21 | 21 |
| R-squared | 0.34 | 0.46 | 0.30 | 0.43 | – | – |
|
| ||||||
| P-value for: | ||||||
| Joint Sig. of Diversity and its Sqr. | 0.023 | 0.027 | ||||
| Joint Sig. of Distance and its Sqr. | 0.235 | |||||
| Joint Sig. of Mobility and its Sqr. | 0.905 | |||||
Note: Heteroskedasticity robust standard errors are reported in parentheses.
Significant at 1%
Significant at 5%
Significant at 10%.
The results of the “horse race” regression in Column 2 are perhaps even more striking given the prior that genetic diversity, as opposed to migratory distance, is likely to be afflicted by larger measurement errors. Nevertheless, since migratory distance is measured as the sum of aerial distances between intercontinental waypoints, it may also be viewed as a noisy proxy of the distance along actual migration routes taken by prehistorical humans during their exodus out of Africa. In order to test whether genetic diversity survives a “horse race” with a less noisy measure of migratory distance from East Africa, Columns 3–4 repeat the preceding analysis using migratory distance based on the index of human mobility employed previously by Ashraf et al. (2010). This index captures the average distance from Addis Ababa to the HGDP ethnic groups located within a given country, along “optimal” land-restricted routes that minimize the time cost of movement on the surface of the Earth in the absence of steam-powered transportation technologies. The index thus accounts for natural impediments to human mobility, including various meteorological and topographical conditions, and incorporates information on the time cost of travelling under such conditions. Reassuringly, as revealed in Columns 3–4, while distance from East Africa based on the mobility index possesses a significant hump-shaped correlation with log population density, this unconditional relationship virtually disappears once genetic diversity is accounted for by the analysis, lending further support to the claim that distance along prehistorical human migration routes from East Africa confers an effect on development outcomes through genetic diversity alone.36
The analysis now turns to address concerns regarding the fact that diversity and economic development may be endogenously determined. In particular, Column 5 presents the results from estimating the preferred regression specification, with genetic diversity instrumented by migratory distance.37 The results from a similar analysis that also accounts for continental fixed effects are reported in Column 6. Interestingly, in comparison to their OLS counterparts in Table 1, the estimated 2SLS coefficients associated with the diversity channel remain relatively stable in magnitude, suggesting that the potential endogeneity between genetic diversity and economic development need not be a source of concern, conditional on controls for the transition timing and land productivity channels. Overall, the results uncovered here provide support for the inferences made with predicted genetic diversity in the main empirical analysis to follow.
4.2.2 The Baseline Results from the Extended Sample
This section establishes the hump-shaped impact of genetic diversity, predicted by migratory distance from East Africa, on log population density in 1500 CE, using the extended sample of 145 countries. To reveal the independent and combined effects of the genetic diversity, transition timing, and land productivity channels, Table 3 presents the results from estimating a number of specifications spanning relevant subsets of the explanatory variables in equation (8).
Table 3.
Predicted Diversity and Economic Development in 1500 CE
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Dependent Variable is Log
Population Density in 1500 CE |
||||||
| Predicted Diversity | 250.986*** (66.314) |
213.537*** (61.739) |
203.017*** (60.085) |
195.416*** (55.916) |
199.727** (80.281) |
|
| Predicted Diversity Sqr. | −177.399*** (48.847) |
−152.107*** (45.414) |
−141.980*** (44.157) |
−137.977*** (40.773) |
−146.167*** (56.251) |
|
| Log Transition Timing | 1.287*** (0.170) |
1.047*** (0.188) |
1.160*** (0.143) |
1.235*** (0.243) |
||
| Log % of Arable Land | 0.523*** (0.117) |
0.401*** (0.096) |
0.393*** (0.103) |
|||
| Log Absolute Latitude | −0.167* (0.093) |
−0.342*** (0.096) |
−0.417*** (0.124) |
|||
| Log Land Suitability | 0.189 (0.124) |
0.305*** (0.094) |
0.257*** (0.096) |
|||
|
| ||||||
| Optimal Diversity | 0.707*** (0.021) |
0.702*** (0.025) |
0.715*** (0.110) |
0.708*** (0.051) |
0.683*** (0.110) |
|
|
| ||||||
| Continent Dummies | No | No | No | No | No | Yes |
| Observations | 145 | 145 | 145 | 145 | 145 | 145 |
| R-squared | 0.22 | 0.26 | 0.38 | 0.50 | 0.67 | 0.69 |
Note: Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses.
Significant at 1%
Significant at 5%
Significant at 10%.
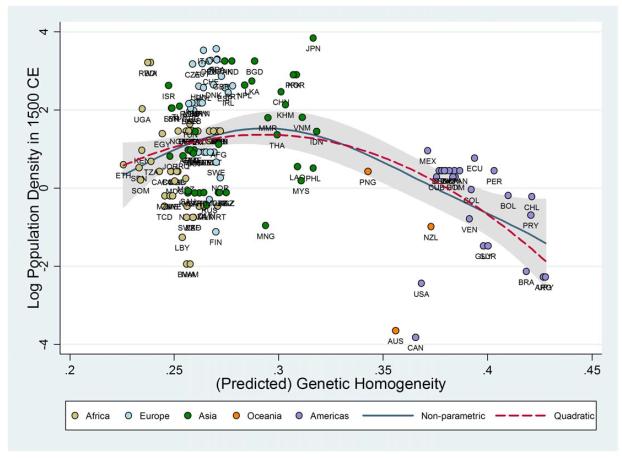
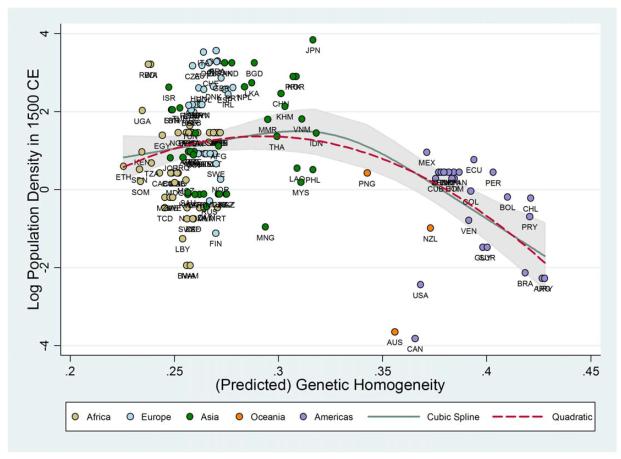
The unconditional hump-shaped relationship between genetic diversity and log population density in 1500 CE is reported in Column 1. In particular, the estimated linear and quadratic coefficients, both statistically significant at the 1% level, imply that a 1 percentage point increase in genetic diversity for the least diverse society in the regression sample would raise its population density by 59%, whereas a 1 percentage point decrease in genetic diversity for the most diverse society would raise its population density by 25%.38 Further, population density in 1500 CE is unconditionally predicted by the regression to be maximized at an expected heterozygosity value of about 0.707, which roughly corresponds to that predicted for southern China by migratory distance from East Africa. Indeed, a 1 percentage point change in genetic diversity in either direction at the predicted optimum lowers population density by 1.8%. Moreover, based on the R-squared of the regression, the cross-country variation in genetic diversity alone explains 22% of the cross-country variation in population density. The quadratic relationship implied by the OLS coefficients reported in Column 1 is depicted together with a non-parametric local polynomial regression line on the scatter plot in Figure 5. As before, the estimated quadratic falls within the 95% confidence interval band of the non-parametric relationship and, moreover, approximates the non-parametric regression line rather well.
Figure 5.
Predicted Genetic Diversity and Population Density in 1500 CE – The Unconditional Relationship
Column 2 reports the unconditional effect of the timing of the agricultural transition on population density in 1500 CE. In line with the Diamond hypothesis, a 1% increase in the number of years elapsed since the Neolithic transition to agriculture is associated with a 1.3% increase in population density, an effect that is also statistically significant at the 1% level. Furthermore, 26% of the cross-country variation in population density is explained by the cross-country variation in the timing of the agricultural transition alone. Perhaps unsurprisingly, as foreshadowed by the sample correlations in Table G.4 in Appendix G, the unconditional effects of both the genetic diversity and agricultural transition timing channels are somewhat weakened in magnitude once they are simultaneously taken into account in Column 3, which reduces the omitted variable bias afflicting the coefficient estimates reported in earlier columns. The coefficients on both channels, however, retain their expected signs and continue to remain statistically significant at the 1% level with the combined cross-country variation in genetic diversity and transition timing explaining 38% of the cross-country variation in population density.
Table G.4.
Pairwise Correlations for the 145-Country Historical Sample
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) | (14) | (15) | (16) | (17) | (18) | (19) | (20) | (21) | (22) | (23) | (24) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | Log Population Density in 1500 CE | 1.000 | |||||||||||||||||||||||
| (2) | Log Population Density in 1000 CE | 0.963 | 1.000 | ||||||||||||||||||||||
| (3) | Log Population Density in 1 CE | 0.876 | 0.936 | 1.000 | |||||||||||||||||||||
| (4) | Predicted Genetic Diversity | 0.391 | 0.312 | 0.341 | 1.000 | ||||||||||||||||||||
| (5) | Log Neolithic Transition Timing | 0.511 | 0.567 | 0.645 | 0.275 | 1.000 | |||||||||||||||||||
| (6) | Log % of Arable Land | 0.582 | 0.501 | 0.455 | 0.132 | 0.157 | 1.000 | ||||||||||||||||||
| (7) | Log Absolute Latitude | 0.101 | 0.090 | 0.284 | 0.106 | 0.322 | 0.272 | 1.000 | |||||||||||||||||
| (8) | Log Land Suitability for Agriculture | 0.364 | 0.302 | 0.248 | −0.251 | −0.133 | 0.649 | −0.044 | 1.000 | ||||||||||||||||
| (9) | Log Distance to Frontier in 1500 CE | −0.360 | −0.367 | −0.401 | −0.021 | −0.396 | −0.188 | −0.318 | −0.012 | 1.000 | |||||||||||||||
| (10) | Log Distance to Frontier in 1000 CE | −0.243 | −0.328 | −0.389 | −0.084 | −0.522 | −0.101 | −0.307 | 0.175 | 0.606 | 1.000 | ||||||||||||||
| (11 | Log Distance to Frontier in 1 CE | −0.326 | −0.390 | −0.503 | −0.082 | −0.521 | −0.177 | −0.341 | −0.002 | 0.457 | 0.703 | 1.000 | |||||||||||||
| (12) | Mean Elevation | −0.028 | −0.046 | −0.047 | 0.106 | 0.069 | −0.051 | −0.026 | 0.018 | 0.018 | 0.033 | 0.028 | 1.000 | ||||||||||||
| (13) | Terrain Roughness | 0.197 | 0.199 | 0.218 | −0.161 | 0.215 | 0.126 | 0.068 | 0.287 | −0.060 | −0.110 | −0.229 | 0.626 | 1.000 | |||||||||||
| (14) | Mean Distance to Nearest Waterway | −0.305 | −0.331 | −0.366 | 0.195 | −0.017 | −0.178 | −0.014 | −0.230 | 0.155 | 0.118 | 0.170 | 0.429 | −0.002 | 1.000 | ||||||||||
| (15) | % of Land within 100 km of Waterway | 0.383 | 0.362 | 0.391 | −0.192 | 0.110 | 0.294 | 0.244 | 0.290 | −0.210 | −0.084 | −0.219 | −0.526 | 0.039 | −0.665 | 1.000 | |||||||||
| (16) | Climate | 0.527 | 0.567 | 0.633 | 0.080 | 0.621 | 0.438 | 0.563 | 0.101 | −0.414 | −0.456 | −0.460 | −0.178 | 0.147 | −0.497 | 0.431 | 1.000 | ||||||||
| (17) | Orientation of Continental Axis | 0.479 | 0.500 | 0.573 | 0.159 | 0.644 | 0.302 | 0.453 | 0.066 | −0.202 | −0.241 | −0.336 | −0.019 | 0.260 | −0.236 | 0.285 | 0.482 | 1.000 | |||||||
| (18) | Size of Continent | 0.308 | 0.339 | 0.408 | 0.465 | 0.454 | 0.244 | 0.327 | −0.159 | −0.125 | −0.218 | −0.267 | 0.148 | −0.079 | 0.104 | −0.170 | 0.327 | 0.668 | 1.000 | ||||||
| (19) | Domesticable Plants | 0.510 | 0.538 | 0.663 | 0.346 | 0.636 | 0.371 | 0.642 | −0.112 | −0.439 | −0.507 | −0.502 | −0.197 | 0.074 | −0.333 | 0.334 | 0.817 | 0.613 | 0.487 | 1.000 | |||||
| (20) | Domesticable Animals | 0.580 | 0.615 | 0.699 | 0.249 | 0.768 | 0.366 | 0.640 | −0.055 | −0.427 | −0.467 | −0.461 | −0.124 | 0.132 | −0.322 | 0.349 | 0.778 | 0.743 | 0.516 | 0.878 | 1.000 | ||||
| (21) | Migratory Distance from Addis Ababa | −0.391 | −0.312 | −0.341 | −1.000 | −0.275 | −0.132 | −0.106 | 0.251 | 0.021 | 0.084 | 0.082 | −0.106 | 0.161 | −0.195 | 0.192 | −0.080 | −0.159 | −0.465 | −0.346 | −0.249 | 1.000 | |||
| (22) | Aerial Distance from Addis Ababa | −0.287 | −0.238 | −0.283 | −0.934 | −0.331 | −0.044 | −0.017 | 0.334 | −0.053 | 0.079 | 0.073 | −0.153 | 0.170 | −0.220 | 0.292 | −0.074 | −0.058 | −0.429 | −0.281 | −0.191 | 0.934 | 1.000 | ||
| (23) | Migratory Distance from London | −0.537 | −0.473 | −0.518 | −0.899 | −0.497 | −0.271 | −0.385 | 0.176 | 0.215 | 0.224 | 0.256 | 0.001 | 0.088 | −0.081 | −0.042 | −0.407 | −0.455 | −0.569 | −0.683 | −0.612 | 0.899 | 0.800 | 1.000 | |
| (24) | Migratory Distance from Tokyo | −0.420 | −0.403 | −0.353 | −0.266 | −0.559 | −0.187 | −0.316 | 0.056 | 0.164 | 0.227 | 0.224 | −0.122 | −0.264 | −0.128 | −0.118 | −0.220 | −0.672 | −0.310 | −0.309 | −0.626 | 0.266 | 0.172 | 0.418 | 1.000 |
| (25) | Migratory Distance from Mexico City | 0.198 | 0.128 | 0.167 | 0.822 | −0.034 | 0.009 | −0.006 | −0.210 | 0.169 | 0.189 | 0.180 | 0.002 | −0.284 | 0.094 | −0.194 | −0.014 | −0.035 | 0.268 | 0.148 | 0.075 | −0.822 | −0.759 | −0.675 | −0.025 |
The results of examining the combined explanatory power of the genetic diversity and land productivity channels are reported in Column 4.39 Once again, given the sample correlations, the linear and quadratic coefficients associated with genetic diversity are naturally somewhat weaker when compared to their unconditional estimates of Column 1. More importantly, the coefficients remain highly statistically significant and also rather stable in magnitude relative to those estimated while controlling for the timing of the Neolithic transition. In addition, the overall significance of the land productivity channel is also confirmed, particularly by the estimated coefficients on the log percentage of arable land and log absolute latitude variables, which indeed appear to possess their expected signs.40 Nonetheless, these estimates continue to reflect some amount of omitted variable bias resulting from the exclusion of the transition timing channel. For instance, the fact that log agricultural transition timing has a sample correlation of 0.28 with genetic diversity and one of 0.32 with log absolute latitude implies that the estimated effects of these variables on log population density in Column 4 may be partially capturing the latent influence of the excluded Neolithic transition timing channel.
Column 5 presents the results from exploiting the explanatory power of all three identified channels for log population density in 1500 CE. In line with the theoretical predictions of each hypothesis, the coefficient estimates possess their expected signs and are all statistically significant at the 1% level. Moreover, in comparison to their estimates in Columns 3 and 4, the linear and quadratic coefficients associated with the diversity channel remain largely stable. In particular, the estimated coefficients of interest imply that, controlling for the influence of land productivity and the timing of the Neolithic Revolution, a 1 percentage point increase in genetic diversity for the least diverse society in the sample would raise its population density in 1500 CE by 44%, whereas a 1 percentage point decrease in diversity for the most diverse society would raise its population density by 18%. Further, population density in 1500 CE is predicted to be maximized at an expected heterozygosity value of 0.708, where a 1 percentage point change in diversity in either direction would lower population density by 1.4%. Overall, based on the R-squared of the regression, the cross-country variations in genetic diversity, agricultural transition timing, and land productivity together explain 67% of the cross-country variation in population density in 1500 CE.
Finally, Column 6 reports the results from estimating the baseline regression model, specified in equation (8), which allows the analysis to capture unobserved continent-specific attributes that could potentially have an influence on population density. Despite the more modest cross-country variation in genetic diversity within continents as opposed to that across continents, the coefficients associated with diversity remain rather stable, increasing slightly in magnitude with the inclusion of continental dummies, although the statistical significance of the linear coefficient drops to the 5% level.41 Specifically, the coefficients associated with the diversity channel indicate that, controlling for the influence of land productivity, the timing of the Neolithic Revolution, and continental fixed effects, a 1 percentage point increase in diversity for the most homogenous society in the sample would raise its population density in 1500 CE by 36%, whereas a 1 percentage point decrease in diversity for the most diverse society would raise its population density by 29%. In addition, a 1 percentage point change in genetic diversity in either direction at the predicted optimum diversity level of 0.683, which roughly corresponds to that predicted for Japan by migratory distance from East Africa, would lower population density by 1.5%. Reassuringly, the optimal level of predicted diversity in the extended sample is quite similar to that obtained for observed diversity in the limited 21-country sample.
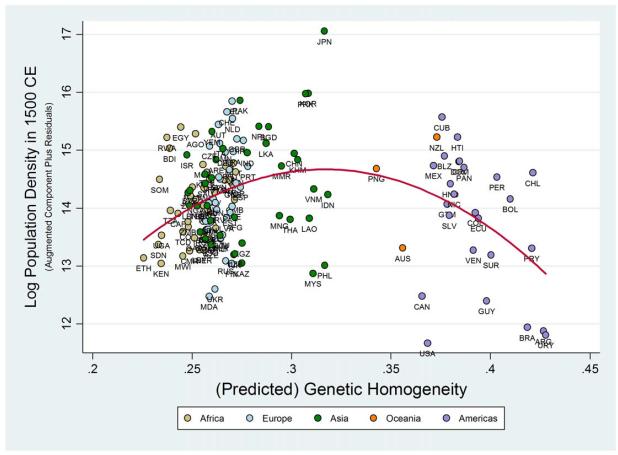
To place the worldwide effect of the diversity channel into perspective, the coefficients reported in Column 6 imply that increasing the expected heterozygosity of the most homogenous native South American populations by 11.1 percentage points to the predicted optimum would have raised their population density in 1500 CE by a factor of 6.07. On the other hand, decreasing the expected heterozygosity of the most heterogenous East African populations by 9.1 percentage points to the optimum would have raised their population density by a factor of 3.36. The hump-shaped effect of genetic diversity on log population density in 1500 CE, conditional on the timing of the Neolithic, land productivity, and continental fixed effects, is depicted on the scatter plot in Figure 6.42
Figure 6.
Predicted Genetic Diversity and Population Density in 1500 CE – Conditional on Transition Timing, Land Productivity, and Continental Fixed Effects
To summarize the results reported in Table 3, genetic diversity as predicted by migratory distance from East Africa is found to have a highly statistically significant non-monotonic effect on population density in 1500 CE. This finding is entirely consistent with the theoretical prediction of the proposed genetic diversity channel that comprises both an adverse effect of diversity on Malthusian economic development, via diminished social capital, and a favorable effect arising from increased technological creativity. The analysis also confirms the significant beneficial effects of an earlier Neolithic transition to agriculture as well as geographical factors conducive to higher agricultural yields. Nevertheless, controlling for these additional explanatory channels hardly affects the hump-shaped relationship between genetic diversity and population density, a finding that remains robust to the inclusion of continental dummies as well.
4.2.3 Robustness to Aerial Distance and Migratory Distances from “Placebo” Points of Origin Across the Globe
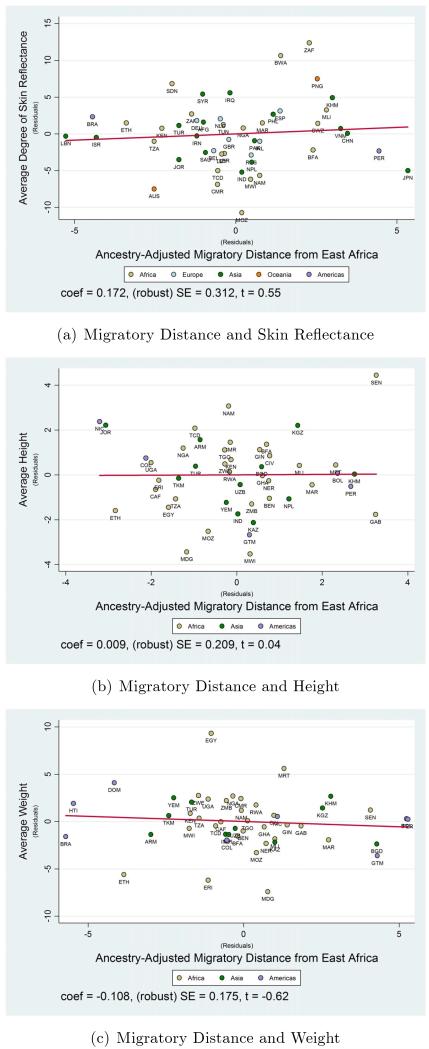
The results from the limited sample analysis discussed earlier demonstrate that the cross-country variation in migratory distance from East Africa has a significant non-monotonic influence on comparative development in 1500 CE and that this impact runs exclusively via the serial-founder effect on genetic diversity. This finding, however, does not preclude the possibility that alternative measures of distance, potentially correlated with migratory distance from East Africa, may also explain the historical cross-country variation in economic development in a similar non-monotonic fashion. Indeed, if this is the case, then the role previously ascribed to the “out of Africa” migration of Homo sapiens as a deep determinant of comparative development becomes suspect, undermining the credibility of the proposed genetic diversity channel. Nonetheless, alternative distances, as will become evident, do not impart any significant influence, similar to that associated with migratory distance from East Africa, on log population density in 1500 CE.
The current analysis compares regression results obtained using migratory distance from Addis Ababa in the baseline specification with those obtained under several alternative concepts of distance. The alternative concepts of distance considered by the analysis include the aerial or “as the crow flies” distance from Addis Ababa as well as migratory distances from “placebo” points of origin in other continents across the globe, namely London, Tokyo, and Mexico City, computed using the same waypoints employed in constructing migratory distance from Addis Ababa.43 As revealed in Table G.4 in Appendix G, with the exception of migratory distance from Tokyo, these other distances are rather strongly correlated with migratory distance from Addis Ababa. Despite some of these high correlations, however, the results presented in Table 4 indicate that migratory distance from Addis Ababa is the only concept of distance that confers a significant non-monotonic effect on log population density.
Table 4.
Robustness to Alternative Distances
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
|
| |||||
| Distance from: | Addis Ababa | Addis Ababa | London | Tokyo | Mexico City |
| Dependent Variable is Log
Population Density in 1500 CE |
|||||
| Migratory Distance | 0.138** (0.061) |
−0.040 (0.063) |
0.052 (0.145) |
−0.063 (0.099) |
|
| Migratory Distance Sqr. | −0.008*** (0.002) |
−0.002 (0.002) |
−0.006 (0.007) |
0.005 (0.004) |
|
| Aerial Distance | −0.008 (0.106) |
||||
| Aerial Distance Sqr. | −0.005 (0.006) |
||||
| Log Transition Timing | 1.160*** (0.144) |
1.158*** (0.138) |
1.003*** (0.164) |
1.047*** (0.225) |
1.619*** (0.277) |
| Log % of Arable Land | 0.401*** (0.091) |
0.488*** (0.102) |
0.357*** (0.092) |
0.532*** (0.089) |
0.493*** (0.094) |
| Log Absolute Latitude | −0.342*** (0.091) |
−0.263*** (0.097) |
−0.358*** (0.112) |
−0.334*** (0.099) |
−0.239*** (0.083) |
| Log Land Suitability | 0.305*** (0.091) |
0.254** (0.102) |
0.344*** (0.092) |
0.178** (0.080) |
0.261*** (0.092) |
|
| |||||
| Observations | 145 | 145 | 145 | 145 | 145 |
| R-squared | 0.67 | 0.59 | 0.67 | 0.59 | 0.63 |
|
| |||||
Note: Heteroskedasticity robust standard errors are reported in parentheses.
Significant at 1%
Significant at 5%
Significant at 10%.
Specifically, consistent with the proposed diversity hypothesis, Column 1 reveals a highly statistically significant hump-shaped relationship between migratory distance from Addis Ababa and log population density in 1500 CE, conditional on controls for the Neolithic transition timing and land productivity channels. In contrast, the linear and quadratic effects of aerial distance from Addis Ababa, reported in Column 2, are not statistically different from zero at conventional levels of significance. Similarly, as shown in Columns 3–5, the migratory distances from “placebo” points of origin do not impart any statistically discernible effect, linear or otherwise, on log population density in the year 1500 CE.
These results strengthen the assertion that conditions innately related to the prehistorical migration of humans out of Africa have had a lasting impact on comparative development. Given the high correlations between migratory distance from Addis Ababa and some of these alternative distance concepts, the fact that these other distances fail to reveal any significant effects makes the argument in favor of the “out of Africa” hypothesis even stronger. Together with earlier findings establishing migratory distance from Addis Ababa and genetic diversity as ultimate and proximate determinants in the same channel, the findings from these “placebo” tests of distance lend further credence to the proposed diversity hypothesis.
5 The Contemporary Analysis
5.1 Data and Empirical Strategy
This section discusses the data and empirical strategy employed to examine the impact of genetic diversity on contemporary comparative development.
5.1.1 The Index of Contemporary National Population Diversity
The construction of the index of genetic diversity for contemporary national populations is partly based on their ethnic compositions resulting from population flows amongst countries in the post-Columbian era. Specifically, given the genetic diversity of the ancestral populations of the source countries, data on post-Columbian population flows can be used to construct a weighted average expected heterozygosity measure for the national population of each country in the contemporary period.44 This measure alone, however, would not capture the full extent of genetic diversity in contemporary national populations as it would fail to account for the diversity arising from differences between sub-national ethnic groups.
To additionally incorporate the between-group component of diversity in contemporary national populations, the index makes use of the concept of Fst genetic distance from field of population genetics. Details regarding the construction of this ancestry-adjusted measure of genetic diversity, that also accounts for the diversity arising from differences between sub-national ethnic groups, are presented in Appendix B.
Reassuringly, the ancestry-adjusted measure of genetic diversity dominates the unadjusted measure in predicting economic development in the contemporary period. In line with the diversity hypothesis, Column 1 in Table 5 reveals a significant unconditional hump-shaped relationship between the adjusted measure of diversity and income per capita in the year 2000 CE. This relationship is depicted together with a non-parametric local polynomial regression line on the scatter plot in Figure 7. As in the historical analysis, the estimated quadratic fit falls within the 95% confidence interval band of the non-parametric relationship.
Table 5.
Adjusted versus Unadjusted Diversity
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Dependent Variable is Log Income
Per Capita in 2000 CE |
||||||
| Predicted Diversity (Ancestry Adjusted) |
556.439*** (129.697) |
254.906*** (88.619) |
533.983*** (164.216) |
387.314** (188.300) |
||
| Predicted Diversity Sqr.
(Ancestry Adjusted) |
−397.224*** (90.784) |
−176.907*** (62.730) |
−377.365*** (117.645) |
−273.925** (136.442) |
||
| Predicted Diversity
(Unadjusted) |
140.903*** (51.614) |
10.152 (52.732) |
1.670 (69.101) |
−64.226 (81.419) |
||
| Predicted Diversity Sqr.
(Unadjusted) |
−107.686*** (38.133) |
−7.418 (38.000) |
−4.057 (52.990) |
51.016 (64.295) |
||
|
| ||||||
| Continent Dummies | No | Yes | No | Yes | No | Yes |
| Observations | 143 | 143 | 143 | 143 | 143 | 143 |
| R-squared | 0.13 | 0.47 | 0.08 | 0.45 | 0.14 | 0.48 |
|
| ||||||
| P-value for: | ||||||
| Joint Sig. of Adjusted Diversity and its Sqr. | 0.009 | 0.038 | ||||
| Joint Sig. of Unadjusted Diversity and its Sqr. | 0.399 | 0.741 | ||||
Note: Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses.
Significant at 1%
Significant at 5%
Significant at 10%.
Figure 7.
Adjusted Genetic Diversity and Income Per Capita in 2000 CE – The Unconditional Relationship
Column 2 establishes that the unconditional quadratic relationship from Column 1 remains qualitatively intact when conditioned for the impact of continent fixed effects. As revealed in Columns 3 and 4, however, while the unadjusted measure also possesses a significant unconditional hump-shaped relationship with income per capita across countries, the relationship disappears once the regression is augmented to account for continental dummies. Moreover, examining jointly the explanatory powers of the ancestry-adjusted and unadjusted measures of genetic diversity for income per capita, Columns 5 and 6 demonstrate the superior relative performance of the adjusted measure, regardless of whether continent fixed effects are accounted for by the analysis, lending further credence ex post to the methodology employed in constructing the index of contemporary population diversity.45
5.1.2 The Empirical Model
Maintaining symmetry with the earlier historical analysis, a regression specification similar to that employed for the historical regressions is adopted initially to examine the contemporary impact of genetic diversity along with the transition timing and land productivity channels. The current specification, however, is further augmented with controls for institutional, cultural, and additional geographical factors that have received attention in the literature. This permits the examination of the direct impact of the diversity channel, as opposed to its overall impact that additionally captures indirect effects potentially correlated with these other determinants.
Formally, the following specification is adopted as a baseline to examine the direct influence of contemporary population diversity on the modern world income distribution:
| (9) |
where yi is the income per capita of country i in the year 2000 CE; Ĝi is the index of contemporary population diversity for country i, as discussed above; Ti and Xi are the Neolithic transition timing and land productivity controls for country i; Λi is a vector of institutional and cultural controls for country i; Γi is a vector of additional geographical controls for country i; and, finally, ηi is a country specific disturbance term.46
5.2 Empirical Findings
5.2.1 Results for Comparative Development
The empirical findings indicate that the highly significant hump-shaped effect of genetic diversity on macroeconomic outcomes in the pre-industrial period is present in the contemporary period as well. Furthermore, the persistent hump-shaped impact of genetic diversity on the pattern of comparative economic development is a direct effect that is not captured by contemporary geographical, institutional, and cultural factors.47
Using a sample of 143 countries for which data are available for the entire set of control variables used in the baseline regression for the year 1500 CE, Column 1 of Table 6 reveals a significant hump-shaped effect of genetic diversity on income per capita in 2000 CE, accounting for the set of baseline controls employed in the historical analysis – i.e., the logs of the timing of the Neolithic transition, the percentage of arable land, absolute latitude and the suitability of land for agriculture, as well as continental fixed effects.48 Further, consistent with the notion that the optimal level of diversity increased in the process of industrialization, as the beneficial forces associated with greater diversity became intensified in an environment characterized by more rapid technological progress, the findings indicate that the optimal level of diversity with respect to the modern world income distribution is indeed higher than that obtained with respect to population density in the pre-colonial Malthusian era. Specifically, while the estimate for the optimal level in 1500 CE is 0.683 (Column 4), the estimated optimum in 2000 CE, under the same specification, is 0.713.
Table 6.
Diversity and Economic Development in 2000 CE and 1500 CE
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Dependent Variable is: | ||||
| Log Income Per Capita in 2000 CE |
Log Population Density in 1500 CE |
|||
| Predicted Diversity (Ancestry Adjusted) |
204.610** (86.385) |
237.238*** (85.031) |
244.960*** (83.379) |
|
| Predicted Diversity Sqr.
(Ancestry Adjusted) |
−143.437** (61.088) |
−166.507*** (60.474) |
−171.364*** (59.386) |
|
| Predicted Diversity
(Unadjusted) |
198.587** (79.225) |
|||
| Predicted Diversity Sqr.
(Unadjusted) |
−145.320*** (55.438) |
|||
| Log Transition Timing
(Ancestry Adjusted) |
0.061 (0.262) |
0.002 (0.305) |
||
| Log Transition Timing
(Unadjusted) |
−0.151 (0.186) |
1.238*** (0.241) |
||
| Log % of Arable Land | −0.110 (0.100) |
−0.119 (0.107) |
−0.137 (0.111) |
0.378*** (0.108) |
| Log Absolute Latitude | 0.164 (0.125) |
0.172 (0.119) |
0.192 (0.143) |
−0.423*** (0.122) |
| Log Land Suitability | −0.193** (0.095) |
−0.177* (0.102) |
−0.189* (0.102) |
0.264*** (0.095) |
| Log Population Density in 1500 CE |
0.047 (0.097) |
|||
|
| ||||
| Optimal Diversity | 0.713*** (0.100) |
0.712*** (0.036) |
0.715*** (0.118) |
0.683*** (0.095) |
|
| ||||
| Continent Dummies | Yes | Yes | Yes | Yes |
| Observations | 143 | 143 | 143 | 143 |
| R-squared | 0.57 | 0.57 | 0.57 | 0.68 |
Note: Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses.
Significant at 1%
Significant at 5%
Significant at 10%.
Column 2 shows that the hump-shaped effect of diversity on income per capita remains virtually intact when the control for the Neolithic transition is adjusted to capture the average time elapsed since the pre-Columbian ancestral populations of each country today experienced the transition to agriculture (i.e., traits that are embodied in the country’s population today, rather than the country’s geographical attributes). In particular, the estimated linear and quadratic coefficients on genetic diversity are both statistically significant at the 1% level. They imply that increasing the diversity of the most genetically homogenous country in the sample (Bolivia) by 1 percentage point would raise its income per capita in 2000 CE by 29%, whereas decreasing the diversity of the most genetically diverse country in the sample (Ethiopia) by 1 percentage point would raise its income per capita by 21%. Further, a 1 percentage point change in diversity (in either direction) at the optimum level of 0.712 would lower income per capita by 1.7%.49
Importantly, the hump-shaped effect of genetic diversity on income per capita in 2000 CE does not reflect an inertia originating from its effect on technology and, thus, population density in 1500 CE. As established in Column 3, the results are essentially unchanged if the regression accounts for the potentially cofounding effect of population density in 1500 CE. Namely, the effect of genetic diversity on income per capita in 2000 CE does not operate though its impact on population density in the year 1500 CE.
The findings uncovered by the analysis thus far suggest that genetic diversity has a highly significant hump-shaped effect on income per capita in the year 2000 CE. Moreover, as established by the analysis to follow, this overall effect comprises a direct impact that does not operate through institutional, cultural and other geographical factors.
Using a sample of 109 countries for which data are available for the institutional and cultural controls that are employed in the examination, Column 1 of Table 7 demonstrates that genetic diversity has a hump-shaped effect on income per capita in the year 2000 CE, accounting for the set of baseline controls employed in the historical analysis –i.e., the logs of the weighted timing of the Neolithic transition, the percentage of arable land, and absolute latitude, as well as continental fixed effects.50 The estimated linear and quadratic coefficients associated with the diversity channel are both statistically significant at the 1% level and the estimate for the optimal level of diversity is 0.713. The regression in Column 2 examines the robustness of the results to the inclusion of a measure of institutional quality, as captured by the social infrastructure index of Hall and Jones (1999). The estimated hump-shaped effect of genetic diversity remains highly statistically significant and rather stable, while the optimal level of diversity increases to 0.725.51
Table 7.
Diversity and Other Determinants of Economic Development in 2000 CE
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| Full Sample |
Full Sample |
Full Sample |
Full Sample |
Full Sample |
Full Sample |
Schooling Sample |
Schooling Sample |
|
| Dependent Variable is Log Income
Per Capita in 2000 CE |
||||||||
| Predicted Diversity (Ancestry Adjusted) |
315.282*** (85.309) |
225.858*** (67.857) |
219.453*** (67.261) |
245.377*** (69.200) |
277.342*** (69.452) |
272.274*** (83.202) |
271.249*** (73.818) |
215.675*** (67.984) |
| Predicted Diversity Sqr.
(Ancestry Adjusted) |
−220.980*** (60.304) |
−155.826*** (48.011) |
−151.489*** (47.512) |
−170.036*** (48.737) |
−192.386*** (49.056) |
−188.868*** (58.239) |
−188.899*** (52.806) |
−150.871*** (48.295) |
| Log Transition Timing
(Ancestry Adjusted) |
−0.273 (0.269) |
−0.092 (0.200) |
0.032 (0.189) |
0.352 (0.242) |
0.396* (0.233) |
0.383 (0.242) |
0.112 (0.234) |
−0.046 (0.208) |
| Log % of Arable Land | −0.218*** (0.061) |
−0.159*** (0.049) |
−0 171*** (0.049) |
−0.211*** (0.047) |
−0.183*** (0.051) |
−0.183*** (0.051) |
−0.084 (0.056) |
−0.084 (0.056) |
| Log Absolute Latitude | 0.123 (0.122) |
0.083 (0.100) |
0.038 (0.103) |
0.119 (0.097) |
0.009 (0.108) |
0.007 (0.108) |
0.007 (0.099) |
−0.006 (0.087) |
| Social Infrastructure | 2.359*** (0.269) |
2.389*** (0.257) |
2.072*** (0.375) |
1.826*** (0.417) |
1.810*** (0.436) |
1.470*** (0.426) |
0.880** (0.418) |
|
| Ethnic Fractionalization | −0.684** (0.277) |
−0.505 (0.319) |
−0.333 (0.280) |
−0.336 (0.291) |
0.051 (0.280) |
−0.122 (0.265) |
||
| % of Population at Risk of
Contracting Malaria |
−0.502 (0.351) |
−0.495 (0.380) |
−0.734* (0.389) |
−0.723** (0.353) |
||||
| % of Population Living in
Tropical Zones |
−0.319 (0.204) |
−0.312 (0.212) |
−0.411* (0.214) |
−0.185 (0.199) |
||||
| Mean Distance to Nearest
Waterway |
−0.368** (0.186) |
−0.367* (0.190) |
−0.179 (0.216) |
−0.062 (0.188) |
||||
| % of Population of European
Descent |
0.061 (0.621) |
|||||||
| Years of Schooling | 0.134*** (0.042) |
|||||||
|
| ||||||||
| Optimal Diversity | 0.713*** (0.014) |
0.725*** (0.032) |
0.724*** (0.049) |
0.722*** (0.014) |
0.721*** (0.068) |
0.721*** (0.089) |
0.718*** (0.052) |
0.715*** (0.073) |
|
| ||||||||
| OPEC Dummy | No | No | No | No | Yes | Yes | Yes | Yes |
| Legal Origin Dummies | No | No | No | Yes | Yes | Yes | Yes | Yes |
| Major Religion Shares | No | No | No | Yes | Yes | Yes | Yes | Yes |
|
| ||||||||
| Observations | 109 | 109 | 109 | 109 | 109 | 109 | 94 | 94 |
| R-squared | 0.74 | 0.84 | 0.85 | 0.87 | 0.90 | 0.90 | 0.91 | 0.93 |
Note: Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses. All regressions include sub-Saharan Africa and continent dummies.
Significant at 1%
Significant at 5%
Significant at 10%.
The regression in Column 3 is designed to examine whether the effect of genetic diversity operates via ethnic fractionalization. It demonstrates that the effect of genetic diversity is virtually unaffected by the potentially confounding impact of ethnic fractionalization.52 While, as established earlier in the literature, ethnic fractionalization does indeed confer a significant adverse effect on income per capita in the year 2000 CE, the hump-shaped impact of genetic diversity remains highly statistically significant. Moreover, the estimate for the optimal level of diversity, 0.724, is effectively unchanged in comparison to earlier columns.
Column 4 demonstrates the robustness of the hump-shaped effect of genetic diversity to the inclusion of additional cultural and institutional controls (i.e., legal origins and the fraction of the population affiliated with major religious). The coefficients associated with genetic diversity remain highly significant statistically and rather stable in magnitude, while the estimated optimal level of diversity, 0.722, remains virtually intact.
Column 5 establishes the robustness of the results to the inclusion of controls for the health environment (i.e., percentage of the population at risk of contracting malaria, and percentage of the population in tropical zones), additional geographical controls gauging access to waterways, and an OPEC dummy. The results in this column, which reflects the baseline specification for examining the impact of diversity on development in the modern world, therefore reveal the direct effect of genetic diversity, once institutional, cultural, and geographical factors are accounted for.53 The direct hump-shaped impact of genetic diversity on log income per capita in 2000 CE, as established in Column 5, is depicted on the scatter plot in Figure 8.54
Figure 8.
Adjusted Genetic Diversity and Income Per Capita in 2000 CE – Conditional on Transition Timing, Land Productivity, Institutional and Geographical Determinants, and Continental Fixed Effects
The coefficients associated with the diversity channel in Column 5 imply that: (i) increasing the diversity of the most homogenous country in the sample (Bolivia) by 1 percentage point would raise its income per capita in the year 2000 CE by 39%, (ii) decreasing the diversity of the most diverse country in the sample (Ethiopia) by 1 percentage point would raise its income per capita by 21%, (iii) a 1 percentage point change in genetic diversity (in either direction) at the optimum level of 0.721 (that most closely resembles the diversity level of the U.S.) would lower income per capita by 1.9%, (iv) increasing the diversity of Bolivia to the level prevalent in the U.S. would increase Bolivia’s per capita income by a factor of 4.7, closing the income gap between the two countries from 12:1 to 2.5:1, and (v) decreasing the diversity of Ethiopia to the level prevalent in the U.S. would increase Ethiopia’s per capita income by a factor of 1.7 and thus close the income gap between the two countries from 47:1 to 27:1.
The regression in Column 6 examines the robustness of the baseline results to the inclusion of the share of the population of European descent as an additional control variable. The results indicate that the coefficients associated with genetic diversity remain highly statistically significant and reassuringly stable in magnitude, while the estimated optimal level of diversity is virtually unaffected.55
Moreover, as reported in Column 8, even if one accounts for the contribution of human capital formation over the time period 1960–2000, the hump-shaped effect of genetic diversity on income per capita in 2000 CE remains highly statistically significant. Further, the estimate for the optimal level of diversity drops only moderately from 0.718 (as presented in Column 7, that accounts for the smaller sample of 94 countries for which data on education and all other variables are available) to 0.715.
Reassuringly, the highly significant and stable hump-shaped effect of genetic diversity on income per capita in 2000 CE is not an artifact of post-colonial migration towards prosperous countries and the concomitant increase in ethnic diversity in these economies. Importantly, for the sample of countries whose national population is largely indigenous to their current geographical location, the hump-shaped effect of genetic diversity on contemporary income per capita is highly significant and virtually identical to the one observed in the entire sample. Thus, since genetic diversity in these populations is the level of diversity predicted by migratory distance from East Africa, rather than the actual one, the potential concern about endogeneity between genetic diversity and income per capita in the modern world is alleviated.
In particular, as established in Table 8, the hump-shaped effect of genetic diversity remains highly significant and the optimal diversity estimate remains virtually intact if the sample is restricted to (a) non-OECD economies (i.e., economies that were less attractive to migrants) in Column 2, (b) non Neo-European countries (i.e., excluding USA, Canada, New Zealand and Australia) in Column 3, (c) non-Latin American countries in Column 4, (d) non Sub-Saharan African countries in Column 5, and (e) countries whose indigenous population is larger than 97% of the entire population (i.e., under conditions that virtually eliminate the role of migration in the creation of diversity over the last 500 years) in Column 6.56
Table 8.
Addressing Endogenous Post-Columbian Migrations
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
|
| ||||||
| Full Sample |
Non OECD |
w/o Neo Europes |
w/o Latin America |
w/o Sub Saharan |
>0.97 Indigenous |
|
| Dependent Variable is Log Income
Per Capita in 2000 CE |
||||||
| Predicted Diversity (Ancestry Adjusted) |
277.342*** (69.452) |
271.979*** (84.232) |
261.367*** (69.946) |
412.222*** (148.781) |
264.805** (107.492) |
304.735** (111.588) |
| Predicted Diversity Sqr.
(Ancestry Adjusted) |
−192.386*** (49.056) |
−188.974*** (59.200) |
−181.811*** (49.261) |
−287.067*** (102.021) |
−183.863** (77.684) |
−213.389** (77.255) |
| Log Transition Timing
(Ancestry Adjusted) |
0.396* (0.233) |
0.390 (0.281) |
0.355 (0.231) |
0.518* (0.298) |
0.068 (0.442) |
0.448* (0.254) |
| Log % of Arable Land | −0.183*** (0.051) |
−0.236*** (0.060) |
−0.201*** (0.055) |
−0.189*** (0.050) |
−0.211** (0.097) |
−0.104 (0.061) |
| Log Absolute Latitude | 0.009 (0.108) |
−0.021 (0.119) |
−0.025 (0.111) |
−0.139 (0.126) |
0.218 (0.242) |
−0.074 (0.130) |
| Social Infrastructure | 1.826*** (0.417) |
1.313** (0.579) |
1.416*** (0.507) |
2.044*** (0.545) |
1.585*** (0.486) |
1.311* (0.716) |
| Ethnic Fractionalization | −0.333 (0.280) |
−0.437 (0.375) |
−0.390 (0.300) |
−0.752** (0.348) |
0.104 (0.408) |
−0.044 (0.412) |
| % of Population at Risk of Contracting Malaria |
−0.502 (0.351) |
−0.605 (0.381) |
−0.591 (0.370) |
−0.308 (0.486) |
−0.425 (0.581) |
−0.153 (0.434) |
| % of Population Living in Tropical Zones |
−0.319 (0.204) |
−0.196 (0.239) |
−0.302 (0.219) |
−0.520** (0.252) |
−0.528 (0.341) |
−0.339 (0.312) |
| Mean Distance to Nearest Waterway |
−0.368** (0.186) |
−0.387* (0.222) |
−0.452** (0.210) |
−0.494*** (0.186) |
−0.743 (0.469) |
−0.367* (0.201) |
|
| ||||||
| Optimal Diversity | 0.721*** (0.068) |
0.720*** (0.085) |
0.719*** (0.015) |
0.718*** (0.023) |
0.720*** (0.180) |
0.714*** (0.012) |
|
| ||||||
| Observations | 109 | 83 | 105 | 87 | 71 | 37 |
| R-squared | 0.90 | 0.82 | 0.89 | 0.93 | 0.86 | 0.98 |
Note: Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses. All regressions include controls for major religion shares as well as OPEC, legal origin, sub-Saharan Africa and continent dummies.
Significant at 1%
Significant at 5%
Significant at 10%.
5.2.2 The Costs and Benefits of Genetic Diversity
This section presents empirical evidence on some of the channels through which genetic diversity confers a hump-shaped effect on income per capita across countries in the modern world. In line with the theory that diversity should be expected to confer costs on productivity, in the form of lower social capital, and benefits, in the form of more rapid knowledge creation, it establishes that countries with greater diversity are also characterized, on average, by a lower prevalence of interpersonal trust and a higher intensity of scientific knowledge creation. Specifically, exploiting cross-country variations in the degree of interpersonal trust and the annual average number of scientific articles per capita in the 1981–2000 time period, the analysis demonstrates that genetic diversity has a statistically significant negative relationship with the prevalence of trust but a positive one with scientific productivity, conditional on a similar set of baseline controls employed in the preceding analysis of contemporary comparative development.57
Using a sample of 58 countries for which trust data as well as data on all baseline controls employed by the analysis are available, Column 1 of Table 9 shows that genetic diversity has a statistically significant negative effect on the prevalence of trust, accounting for the Neolithic transition timing and land productivity channels, as well as contemporary cultural, geographical, and institutional factors. The coefficient corresponding to the diversity channel indicates that a 1 percentage point increase in genetic diversity is associated with a 0.02 percentage point decrease in the prevalence of trust. Moreover, as demonstrated in Column 2, this adverse impact of diversity on trust remains intact when the regression specification is augmented to account for the effect of average years of schooling in the population.
Table 9.
The Costs and Benefits of Diversity
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
|
| ||||||
| Full Sample |
Full Sample |
Common Sample |
Full Sample |
Full Sample |
Common Sample |
|
| Dependent Variable is: | ||||||
| Degree of Interpersonal Trust |
Scientific Articles per Capita per Year 1981-2000 |
|||||
| Predicted Diversity (Ancestry Adjusted) |
−1.855** (0.861) |
−2.193** (0.873) |
−1.901** (0.937) |
2.371*** (0.558) |
1 761*** (0.530) |
2.816** (1.233) |
| Log Transition Timing
(Ancestry Adjusted) |
0.069 (0.068) |
0.079 (0.067) |
0.083 (0.063) |
−0.087* (0.046) |
−0.080* (0.045) |
−0.180** (0.086) |
| Log % of Arable Land | 0.002 (0.020) |
−0.004 (0.018) |
−0.017 (0.018) |
0.009 (0.016) |
0.006 (0.015) |
−0.004 (0.037) |
| Log Absolute Latitude | −0.006 (0.029) |
0.017 (0.029) |
0.009 (0.030) |
0.046* (0.024) |
0.055** (0.023) |
0.078 (0.072) |
| Social Infrastructure | 0.201*** (0.070) |
0.108 (0.085) |
0.102 (0.083) |
0.697*** (0.109) |
0.542*** (0.124) |
0.627*** (0.200) |
| Ethnic Fractionalization | 0.056 (0.071) |
0.053 (0.066) |
0.062 (0.070) |
0.093 (0.095) |
0.075 (0.094) |
0.089 (0.156) |
| % of Population at Risk of Contracting Malaria |
−0.062 (0.090) |
−0.022 (0.088) |
−0.038 (0.093) |
0.095* (0.054) |
0.136*** (0.048) |
0.026 (0.121) |
| % of Population Living in Tropical Zones |
−0.076 (0.055) |
0.002 (0.064) |
0.006 (0.063) |
0.016 (0.058) |
0.049 (0.055) |
0.108 (0.181) |
| Mean Distance to Nearest Waterway |
0.093 (0.061) |
0.115* (0.059) |
0.096* (0.055) |
0.106*** (0.038) |
0.117*** (0.034) |
0.159** (0.067) |
| Years of Schooling | 0.021* (0.012) |
0.027** (0.011) |
0.031*** (0.008) |
0.021 (0.023) |
||
|
| ||||||
| Observations | 58 | 58 | 56 | 93 | 93 | 56 |
| R-squared | 0.79 | 0.80 | 0.82 | 0.80 | 0.82 | 0.81 |
Note: Bootstrapped standard errors, accounting for the use of a generated regressor, are reported in parentheses. All regressions include additional geographical controls for terrain characteristics, as well as OPEC, legal origin, sub-Saharan Africa and continent dummies.
Significant at 1%
Significant at 5%
Significant at 10%.
In contrast, using a sample of 93 countries for which data on scientific productivity as well as data on the full set of baseline controls are available, Column 4 shows that genetic diversity has a statistically significant positive effect on the average annual number of published scientific articles per capita. Specifically, the coefficient of interest indicates that a 1 percentage point increase in genetic diversity is associated with an increase in the annual number of scientific articles per capita of about 0.02, conditional on the influence of Neolithic transition timing, land productivity, and contemporary cultural, geographical, and institutional factors. In addition, as established by Column 5, accounting for the effect of average years of schooling in the population does not qualitatively alter the beneficial impact of diversity on scientific productivity in the 1981–2000 time period.
Finally, Columns 3 and 6 demonstrate that the conditional detrimental effect of genetic diversity on trust as well as its beneficial effect on scientific productivity both remain fully intact when the relevant regressions are performed on a common sample of countries, thereby lending further support to the theoretical assertion that diversity confers conflicting effects on productivity, generating inefficiencies in the production process while, at the same time, fostering the expansion of society’s production possibility frontier.
6 Concluding Remarks
This paper argues that deep-rooted factors, determined tens of thousands of years ago, had a significant effect on the course of economic development from the dawn of human civilization to the contemporary era. It advances and empirically establishes the hypothesis that, in the course of the exodus of Homo sapiens out of Africa, variation in migratory distance from the cradle of humankind to various settlements across the globe affected genetic diversity, and has had a long-lasting effect on the pattern of comparative economic development that is not captured by geographical, institutional, and cultural factors.
The level of genetic diversity within a society is found to have a hump-shaped effect on development outcomes in the pre-colonial era, reflecting the trade-off between the beneficial and the detrimental effects of diversity on productivity. Moreover, the level of genetic diversity in each country today (as determined by the genetic diversities and genetic distances amongst its ancestral populations), has a non-monotonic effect on income per capita in the modern world. While the intermediate level of genetic diversity prevalent among Asian and European populations has been conducive for development, the high degree of diversity among African populations and the low degree of diversity among Native American populations have been a detrimental force in the development of these regions.
Figure A.1.
Predicted Genetic Diversity and Population Density in 1000 CE – Conditional on Transition Timing, Land Productivity, and Continental Fixed Effects
Figure A.2.
Predicted Genetic Diversity and Population Density in 1 CE – Conditional on Transition Timing, Land Productivity, and Continental Fixed Effects
Figure C.1.
Observed Genetic Diversity and Population Density in 1500 CE – Cubic Spline vs. Quadratic Fit
Figure C.2.
Predicted Genetic Diversity and Population Density in 1500 CE – Cubic Spline vs. Quadratic Fit
Figure C.3.
The First- and Second-Order Partial Effects of Predicted Diversity on Population Density in 1500 CE – Conditional on Transition Timing, Land Productivity, and Continental Fixed Effects
Figure C.4.
Adjusted Genetic Diversity and Income Per Capita in 2000 CE – Cubic Spline vs. Quadratic Fit
Figure C.5.
The First- and Second-Order Partial Effects of Adjusted Diversity on Income Per Capita in 2000 CE – Conditional on Transition Timing, Land Productivity, Institutional and Geographical Determinants, and Continental Fixed Effects
Figure C.6.
Ancestry-Adjusted Migratory Distance and Some Mean Physiological Characteristics of Contemporary National Populations
Table D.1.
Robustness of the Role of Migratory Distance in the Serial-Founder Effect
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Dependent Variable is Observed
Genetic Diversity |
||||||
| Migratory Distance | −0.799*** (0.054) |
−0.825*** (0.062) |
−0.798*** (0.067) |
−0.796*** (0.072) |
−0.799*** (0.091) |
−0.689*** (0.148) |
| Absolute Latitude | −0.015 (0.015) |
−0.002 (0.017) |
−0.003 (0.015) |
−0.002 (0.022) |
0.075 (0.044) |
|
| % of Arable Land | −0.014 (0.026) |
−0.013 (0.031) |
−0.009 (0.028) |
−0.012 (0.040) |
0.002 (0.045) |
|
| Mean Land Suitability | 1.883 (1.515) |
−1.702 (5.575) |
−1.347 (5.019) |
−1.563 (6.466) |
1.353 (5.404) |
|
| Range of Land Suitability | −0.932 (4.643) |
−1.332 (4.393) |
−1.104 (5.829) |
−2.026 (5.722) |
||
| Land Suitability Gini | −4.124 (4.936) |
−4.273 (4.628) |
−4.350 (5.030) |
−4.121 (4.194) |
||
| Mean Elevation | 0.877 (2.355) |
0.839 (2.394) |
−2.459 (1.572) |
|||
| Std. Dev. of Elevation | −0.060 (2.285) |
−0.026 (2.284) |
3.416 (2.134) |
|||
| Mean Distance to Nearest
Waterway |
−0.084 (1.148) |
0.502 (0.986) |
||||
|
| ||||||
| Continent Dummies | No | No | No | No | No | Yes |
| Observations | 21 | 21 | 21 | 21 | 21 | 21 |
| R-squared | 0.94 | 0.95 | 0.95 | 0.96 | 0.96 | 0.98 |
| Partial R2 of Mig. Dist. | 0.94 | 0.93 | 0.93 | 0.90 | 0.81 | |
Note: Heteroskedasticity robust standard errors are reported in parentheses.
Significant at 1%
Significant at 5%
Significant at 10%.
Table D.2.
Results of Table 1 with Correction for Spatial Dependence in Errors
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
| Dependent Variable is Log
Population Density in 1500 CE |
|||||
| Observed Diversity | 413.504*** [85.389] |
225.440*** [55.428] |
203.814*** [65.681] |
||
| Observed Diversity Sqr. | −302.647*** [64.267] |
−161.158*** [42.211] |
−145.717*** [53.562] |
||
| Log Transition Timing | 2.396*** [0.249] |
1 214*** [0.271] |
1.135*** [0.367] |
||
| Log % of Arable Land | 0.730*** [0.263] |
0.516*** [0.132] |
0.545*** [0.178] |
||
| Log Absolute Latitude | 0.145 [0.180] |
−0.162* [0.084] |
−0.129 [0.101] |
||
| Log Land Suitability | 0.734* [0.376] |
0.571** [0.240] |
0.587** [0.233] |
||
|
| |||||
| Continent Dummies | No | No | No | No | Yes |
| Observations | 21 | 21 | 21 | 21 | 21 |
| R-squared | 0.42 | 0.54 | 0.57 | 0.89 | 0.90 |
Note: Standard errors corrected for spatial autocorrelation, following Conley (1999), are reported in brackets. To perform this correction, the spatial distribution of observations was specified on the Euclidean plane using aerial distances between all pairs in the sample, and the autocorrelation was modelled as declining linearly away from each location upto a threshold of 5,000 km. This threshold excludes spatial interactions between the Old World and the New World, which is appropriate given the historical period being considered.
Significant at 1%
Significant at 5%
Significant at 10%.
Table D.3.
Results of Table 2 with Correction for Spatial Dependence in Errors
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
|
| ||||||
| OLS | OLS | OLS | OLS | Spatial GMM |
Spatial GMM |
|
| Dependent Variable is Log
Population Density in 1500 CE |
||||||
| Observed Diversity | 255.219*** [77.933] |
361.420*** [108.692] |
285.191*** [81.538] |
243.108*** [55.325] |
||
| Observed Diversity Sqr. | −209.808*** [58.315] |
−268.514*** [77.740] |
−206.577*** [61.906] |
−179.579*** [44.271] |
||
| Migratory Distance | 0.505*** [0.110] |
0.070 [0.138] |
||||
| Migratory Distance Sqr. | −0.023*** [0.004] |
−0.014* [0.008] |
||||
| Mobility Index | 0.353*** [0.108] |
0.051 [0.125] |
||||
| Mobility Index Sqr. | −0.012*** [0.003] |
−0.003 [0.005] |
||||
| Log Transition Timing | 1.014*** [0.356] |
1.119*** [0.370] |
||||
| Log % of Arable Land | 0.608*** [0.187] |
0.634*** [0.202] |
||||
| Log Absolute Latitude | −0.209** [0.107] |
−0.133 [0.099] |
||||
| Log Land Suitability | 0.494** [0.227] |
0.549** [0.242] |
||||
|
| ||||||
| Continent Dummies | No | No | No | No | No | Yes |
| Observations | 21 | 21 | 18 | 18 | 21 | 21 |
| R-squared | 0.34 | 0.46 | 0.30 | 0.43 | – | – |
Note: Standard errors corrected for spatial autocorrelation, following Conley (1999), are reported in brackets. To perform this correction, the spatial distribution of observations was specified on the Euclidean plane using aerial distances between all pairs in the sample, and the autocorrelation was modelled as declining linearly away from each location upto a threshold of 5,000 km. This threshold effectively excludes spatial interactions between the Old World and the New World, which is appropriate given the historical period being considered. Columns 5–6 present the results from estimating the corresponding 2SLS specifications in Table 2 using Conley’s (1999) spatial GMM estimation procedure.
Significant at 1%
Significant at 5%
Significant at 10%.
Table D.4.
Robustness to Log-Log Specifications
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Limited Sample
Historical |
Full Sample Historical |
Contemporary |
||||
| Dependent Variable is: | ||||||
| Log Population Density in 1500 CE |
Log Population Density in 1500 CE |
Log Population Density in 1000 CE |
Log Population Density in 1 CE |
Log Income per Capita in 2000 CE |
||
| Log Diversity | 451.066** (151.797) |
415.864* (190.651) |
423.298** (170.963) |
420.595** (199.565) |
481.771** (239.630) |
516.776*** (187.998) |
| Squared Log Diversity | −425.579** (150.883) |
−396.906* (204.655) |
−407.990** (159.515) |
−402.344** (185.258) |
−458.413** (222.306) |
−480.727*** (176.526) |
| Log Transition Timing | 1 249*** (0.370) |
1.177* (0.618) |
1 241*** (0.232) |
1.606*** (0.265) |
2.132*** (0.425) |
0.061 (0.258) |
| Log % of Arable Land | 0.510*** (0.164) |
0.417* (0.221) |
0.392*** (0.105) |
0.370*** (0.116) |
0.348*** (0.133) |
−0.119 (0.103) |
| Log Absolute Latitude | −0.155 (0.131) |
−0.123 (0.170) |
−0.413*** (0.124) |
−0.368*** (0.127) |
−0.110 (0.137) |
0.174 (0.125) |
| Log Land Suitability | 0.571* (0.296) |
0.674 (0.407) |
0.256*** (0.099) |
0.189* (0.108) |
0.209 (0.129) |
−0.177* (0.098) |
|
| ||||||
| Continent Dummies | No | Yes | Yes | Yes | Yes | Yes |
| Observations | 21 | 21 | 145 | 140 | 126 | 143 |
| R-squared | 0.89 | 0.91 | 0.69 | 0.62 | 0.62 | 0.57 |
Note: The relevant measures of diversity employed are observed diversity in Columns (1)-(2), predicted diversity in Columns (3)-(5), and ancestry-adjusted predicted diversity in Column (6). The transition timing measure used in Column (6) is ancestry adjusted. Heteroskedasticity robust standard errors are reported in parentheses in Columns (1)-(2). Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses in Columns (3)-(6).
Significant at 1%
Significant at 5%
Significant at 10%.
Table D.6.
Zeroth- and First-Stage Results of 2SLS Regressions
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Column 5, Table 2 |
Column 6, Table 2 |
|||||
| 0th-Stage |
1st-Stage |
0th-Stage |
1st-Stage |
|||
| Dependent Variable is: | Dependent Variable is: | |||||
| Observed Diversity |
Observed Diversity |
Observed Diversity Squared |
Observed Diversity |
Observed Diversity |
Observed Diversity Squared |
|
| 2nd-Stage Excluded Instr. : |
||||||
| Migratory Distance | −0.814*** (0.064) |
−5.143*** (0.686) |
−5.841*** (0.959) |
−0.657*** (0.196) |
−3.992*** (0.850) |
−4.234*** (1.053) |
| Predicted Diversity Sqr.
(from 0th-Stage) |
– | −3.937*** (0.628) |
−4.327*** (0.880) |
– | −3.699*** (0.916) |
−3.752*** (1.145) |
| 2nd-Stage Controls : |
||||||
| Log Transition Timing | −0.017** (0.006) |
−0.119*** (0.016) |
−0.139*** (0.023) |
−0.013** (0.004) |
−0.082*** (0.017) |
−0.088*** (0.021) |
| Log % of Arable Land | 0.000 (0.003) |
0.004** (0.002) |
0.007** (0.003) |
0.002 (0.004) |
0.015*** (0.003) |
0.017*** (0.005) |
| Log Absolute Latitude | 0.003* (0.002) |
0.018*** (0.002) |
0.020*** (0.003) |
0.005* (0.002) |
0.027*** (0.006) |
0.028*** (0.007) |
| Log Land Suitability | 0.005 (0.005) |
0.032*** (0.004) |
0.035*** (0.006) |
0.005 (0.005) |
0.031*** (0.007) |
0.032*** (0.009) |
|
| ||||||
| Continent Dummies | No | No | No | Yes | Yes | Yes |
| Observations | 21 | 21 | 21 | 21 | 21 | 21 |
| R-squared | 0.96 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 |
Note: Heteroskedasticity robust standard errors are reported in parentheses.
Significant at 1%
Significant at 5%
Significant at 10%.
Table D.7.
Robustness to the Ecological Components of Land Productivity
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Limited Sample
Historical |
Full Sample Historical |
Contemporary |
||||
| Dependent Variable is: | ||||||
| Log Population Density in 1500 CE |
Log Population Density in 1500 CE |
Log Population Density in 1000 CE |
Log Population Density in 1 CE |
Log Income per Capita in 2000 CE |
||
| Diversity | 236.192** (97.554) |
242.583** (92.470) |
171.881** (77.885) |
181.681** (88.465) |
195.610** (98.917) |
276.208*** (97.567) |
| Diversity Squared | −166.679** (73.114) |
−171.668** (74.712) |
−122.687** (55.168) |
−129.288** (62.044) |
−137.814** (69.331) |
−195.003*** (69.311) |
| Log Transition Timing | 1.565*** (0.378) |
1.689* (0.866) |
1 214*** (0.225) | 1.526*** (0.244) |
1.839*** (0.357) |
−0.027 (0.284) |
| Log % of Arable Land | 0.547** (0.192) |
0.539 (0.313) |
0.382*** (0.091) |
0.338*** (0.093) |
0.199* (0.104) |
−0.134 (0.089) |
| Log Absolute Latitude | 0.183 (0.160) |
0.221 (0.289) |
−0.137 (0.166) |
−0.124 (0.170) |
0.292* (0.150) |
0.069 (0.164) |
| Log Temperature | 1.520** (0.591) |
1.423 (0.993) |
1.508*** (0.535) |
1.971*** (0.558) |
3.092*** (0.580) |
−0.274 (0.458) |
| Log Precipitation | 0.714*** (0.224) |
0.767* (0.372) |
0.358** (0.153) |
0.197 (0.163) |
0.176 (0.182) |
−0.236 (0.155) |
| Log Soil Fertility | 0.162 (0.554) |
0.171 (0.579) |
0.473 (0.303) |
0.541 (0.329) |
0.772** (0.359) |
−0.258 (0.297) |
|
| ||||||
| Continent Dummies | No | Yes | Yes | Yes | Yes | Yes |
| Observations | 21 | 21 | 145 | 140 | 126 | 143 |
| R-squared | 0.93 | 0.93 | 0.72 | 0.67 | 0.72 | 0.57 |
Note: The relevant measures of diversity employed are observed diversity in Columns (1)-(2), predicted diversity in Columns (3)-(5), and ancestry-adjusted predicted diversity in Column (6). The transition timing measure used in Column (6) is ancestry adjusted. The measures for temperature and precipitation represent their respective intertemporal averages during the time period 1961–1990 and are computed using the gridded dataset of New et al. (2002). The measure for soil fertility incoporates soil carbon density and soil pH, and is obtained from the gridded dataset of Ramankutty et al. (2002). All three measures are aggregated to the country level by averaging across the grid cells within a country. Heteroskedasticity robust standard errors are reported in parentheses in Columns (1)-(2). Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses in Columns (3)-(6).
Significant at 1%
Significant at 5%
Significant at 10%.
Table D.8.
Robustness to the Subsistence Mode Prevalent in 1000 CE
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Limited Sample 1500 CE |
Full Sample 1500 CE |
Full Sample 1000 CE |
||||
| Baseline |
w/ Sub. Mode |
Baseline |
w/ Sub. Mode |
Baseline |
w/ Sub. Mode |
|
| Dependent Variable is: | ||||||
| Log Population Density in 1500 CE |
Log Population Density in 1500 CE |
Log Population Density in 1000 CE |
||||
| Diversity | 186.515** (67.317) |
180.340*** (51.275) |
194.141** (76.265) |
196.984*** (56.215) |
200.006** (96.042) |
241.019*** (60.902) |
| Diversity Squared | −131.922** (51.717) |
−129.882*** (39.681) |
−142.349*** (53.585) |
−144.055*** (40.161) |
−145.722** (66.585) |
−173.861*** (42.845) |
| Log Transition Timing | 1.401 (0.826) |
0.867 (0.849) |
1 107*** (0.254) |
1.013*** (0.210) |
1.549*** (0.320) |
1.388*** (0.252) |
| Log Subsistence Mode | 1.678*** (0.465) |
2.030*** (0.730) |
2.543** (0.996) |
|||
| Log % of Arable Land | 0.504** (0.191) |
0.453** (0.150) |
0.421*** (0.101) |
0.458*** (0.097) |
0.384*** (0.123) |
0.447*** (0.114) |
| Log Absolute Latitude | −0.172 (0.150) |
−0.158 (0.155) |
−0.420*** (0.128) |
−0.332*** (0.115) |
−0.369*** (0.141) |
−0.288** (0.121) |
| Log Land Suitability | 0.706** (0.298) |
0.413 (0.269) |
0.226** (0.098) |
0.162* (0.094) |
0.173 (0.111) |
0.067 (0.100) |
|
| ||||||
| Continent Dummies | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 20 | 20 | 140 | 140 | 135 | 135 |
| R-squared | 0.90 | 0.92 | 0.67 | 0.72 | 0.58 | 0.67 |
Note: The relevant measures of genetic diversity employed are observed diversity in Columns (1)-(2), and predicted diversity in Columns (3)-(6). Subsistence mode is a categorical measure reported at the level of a cultural group by Peregrine (2003). Specifically, the measure assumes a value of 0 in the absence of sedentary agriculture, a value of 1/2 when agriculture is practiced but only as a secondary mode of subsistence, and a value of 1 when agriculture is practiced as the primary mode of subsistence. The measure is aggregated to the country level by averaging across the cultural groups that, in the year 1000 CE, resided in regions within the modern national borders of a country. Heteroskedasticity robust standard errors are reported in parentheses in Columns (1)-(2). Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses in Columns (3)-(6).
Significant at 1%
Significant at 5%
Significant at 10%.
Table D.9.
Adjusted Migratory Distance vs. Alternative Distances
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Dependent Variable is Log Income Per Capita in 2000 CE |
||||
| Migratory Distance (Ancestry Adjusted) |
0.601*** (0.073) |
0.499*** (0.124) |
0.532*** (0.160) |
0.564** (0.235) |
| Migratory Distance Sqr.
(Ancestry Adjusted) |
−0.030*** (0.004) |
−0.026*** (0.006) |
−0.027*** (0.008) |
−0.029*** (0.010) |
| Migratory Distance
(Unadjusted) |
0.078 (0.084) |
|||
| Migratory Distance Sqr.
(Unadjusted) |
−0.002 (0.003) |
|||
| Aerial Distance
(Unadjusted) |
0.064 (0.201) |
|||
| Aerial Distance Sqr.
(Unadjusted) |
−0.002 (0.011) |
|||
| Aerial Distance (Ancestry Adjusted) |
0.043 (0.330) |
|||
| Aerial Distance Sqr. (Ancestry Adjusted) |
−0.001 (0.018) |
|||
|
| ||||
| Observations | 109 | 109 | 109 | 109 |
| R-squared | 0.28 | 0.29 | 0.29 | 0.29 |
Note: Heteroskedasticity robust standard errors are reported in parentheses.
Significant at 1%
Significant at 5%
Significant at 10%.
Table D.10.
Robustness to Fst Genetic Distances
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Limited Sample
Historical |
Full Sample Historical |
Contemporary |
||||
| Baseline |
w/ Gen. Dist. |
Baseline |
w/ Gen. Dist. |
Baseline |
w/ Gen. Dist. |
|
| Dependent Variable is: | ||||||
| Log Population Density in 1500 CE |
Log Population Density in 1500 CE |
Log Income per Capita in 2000 CE |
||||
| Diversity | 184.672** (63.338) |
201.230** (65.970) |
194.681** (81.638) |
194.743** (85.603) |
185.512** (86.160) |
212.380** (99.759) |
| Diversity Squared | −130.466** (48.774) |
−144.435** (50.450) |
−142.204** (57.192) |
−145.347** (60.802) |
−128.045** (61.150) |
−150.435** (71.184) |
| Log Transition Timing | 1.150* (0.634) |
1.044 (0.915) |
1.236*** (0.242) |
1.025*** (0.312) |
−0.218 (0.285) |
−0.122 (0.347) |
| Log % of Arable Land | 0.433** (0.172) |
0.314 (0.396) |
0.392*** (0.099) |
0.362*** (0.107) |
−0.155 (0.100) |
−0.136 (0.102) |
| Log Absolute Latitude | −0.138 (0.150) |
−0.160 (0.184) |
−0.419*** (0.122) |
−0.477*** (0.128) |
0.068 (0.117) |
0.077 (0.124) |
| Log Land Suitability | 0.636* (0.294) |
0.778 (0.559) |
0.259*** (0.095) |
0.324*** (0.097) |
−0.147 (0.093) |
−0.148 (0.092) |
| Genetic Distance to the U.K.
(1500 match) |
−0.014 (0.049) |
−0.027 (0.027) |
||||
| Genetic Distance to Ethiopia
(1500 match) |
−0.047 (0.084) |
−0.069 (0.043) |
||||
| Genetic Distance to the U.S.
(weighted) |
0.030 (0.037) |
|||||
| Genetic Distance to Ethiopia
(weighted) |
−0.075* (0.043) |
|||||
|
| ||||||
| Continent Dummies | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 20 | 20 | 142 | 142 | 139 | 139 |
| R-squared | 0.91 | 0.91 | 0.69 | 0.71 | 0.61 | 0.62 |
Note: The relevant measures of diversity employed are observed diversity in Columns (1)-(2), predicted diversity in Columns (3)-(4), and ancestry-adjusted predicted diversity in Columns (5)-(6). The transition timing measure used in Columns (5)-(6) is ancestry adjusted as well. Heteroskedasticity robust standard errors are reported in parentheses in Columns (1)-(2). Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses in Columns (3)-(6).
Significant at 1%
Significant at 5%
Significant at 10%.
Table D.11.
Robustness to Regional Fixed Effects and Sub-Sampling on Regional Clusters
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
|
| |||||
| Full Sample |
w/out SSA |
w/out LAC |
w/out SSA & LAC |
only SSA & LAC |
|
| Dependent Variable is Log Income
Per Capita in 2000 CE |
|||||
| Predicted Diversity (Ancestry Adjusted) |
299.370*** (63.294) |
285.108*** (89.612) |
492.169*** (141.359) |
597.082*** (194.662) |
250.578*** (86.422) |
| Predicted Diversity Sqr.
(Ancestry Adjusted) |
−209.044*** (45.538) |
−199.109*** (65.355) |
−342.630*** (98.352) |
−415.660*** (137.757) |
−175.074*** (62.321) |
| Log Transition Timing
(Ancestry Adjusted) |
0.293* (0.173) |
0.023 (0.236) |
0.352* (0.208) |
−0.033 (0.269) |
0.359 (0.271) |
| Log % of Arable Land | −0.188*** (0.048) |
−0.195*** (0.071) |
−0.192*** (0.043) |
−0.152** (0.067) |
−0.173** (0.070) |
| Log Absolute Latitude | −0.044 (0.090) |
0.131 (0.120) |
−0.189 (0.114) |
−0.173 (0.153) |
−0.037 (0.111) |
| Social Infrastructure | 1.156** (0.465) |
0.790* (0.433) |
1.525** (0.601) |
0.868 (0.609) |
0.413 (0.920) |
| Ethnic Fractionalization | −0.338 (0.257) |
0.147 (0.283) |
−0.739** (0.284) |
−0.511* (0.296) |
−0.282 (0.450) |
| % of Population at Risk of
Contracting Malaria |
−0.671** (0.301) |
−0.561** (0.267) |
−0.426 (0.416) |
0.121 (0.320) |
−1.135** (0.425) |
| % of Population Living in
Tropical Zones |
−0.307 (0.190) |
−0.557*** (0.192) |
−0.469** (0.219) |
−0.976*** (0.265) |
−0.129 (0.223) |
| Mean Distance to Nearest
Waterway |
−0.384** (0.180) |
−0.797*** (0.246) |
−0.416*** (0.149) |
−0.665** (0.247) |
−0.275 (0.240) |
|
| |||||
| Optimal Diversity | 0.716*** (0.008) |
0.716*** (0.011) |
0.718*** (0.006) |
0.718*** (0.007) |
0.716*** (0.013) |
|
| |||||
| Observations | 109 | 71 | 87 | 49 | 60 |
| R-squared | 0.90 | 0.89 | 0.93 | 0.94 | 0.80 |
Note: Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses. All regressions include controls for an OPEC dummy, legal origin dummies, and major religion shares, as well as regional dummies for (i) Sub-Saharan Africa (except Columns (2) and (4)), (ii) Middle East and North Africa, (iii) Europe and Central Asia, (iv) South Asia, (v) East Asia and Pacific, and (vi) Latin America and Caribbean (except Columns (3)-(5)).
Significant at 1%
Significant at 5%
Significant at 10%.
Table D.12.
Robustness to Percentage of the Population of European Descent
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| Full Sample |
Full Sample |
Non OECD |
Non OECD |
w/o Neo Europes |
w/o Neo Europes |
Non European |
Non European |
|
| Dependent Variable is Log Income
Per Capita in 2000 CE |
||||||||
| Predicted Diversity (Ancestry Adjusted) |
277.342*** (69.452) |
272.274*** (83.202) |
271.979*** (84.232) |
263.805** (115.923) |
261.367*** (69.946) |
272.904*** (89.295) |
280.902*** (76.868) |
280.957** (111.552) |
| Predicted Diversity Sqr.
(Ancestry Adjusted) |
−192.386*** (49.056) |
−188.868*** (58.239) |
−188.974*** (59.200) |
−183.258** (80.816) |
−181.811*** (49.261) |
−189.886*** (62.495) |
−195.093*** (54.133) |
−195.132** (77.587) |
| Log Transition Timing
(Ancestry Adjusted) |
0.396* (0.233) |
0.383 (0.242) |
0.390 (0.281) |
0.373 (0.302) |
0.355 (0.231) |
0.386 (0.249) |
0.480* (0.278) |
0.480 (0.299) |
| Log % of Arable Land | −0.183*** (0.051) |
−0.183*** (0.051) |
−0.236*** (0.060) |
−0.235*** (0.060) |
−0.201*** (0.055) |
−0.202*** (0.055) |
−0.198*** (0.055) |
−0.198*** (0.055) |
| Log Absolute Latitude | 0.009 (0.108) |
0.007 (0.108) |
−0.021 (0.119) |
−0.022 (0.122) |
−0.025 (0.111) |
−0.024 (0.112) |
0.016 (0.112) |
0.016 (0.115) |
| Social Infrastructure | 1.826*** (0.417) |
1.810*** (0.436) |
1.313** (0.579) |
1.304** (0.615) |
1.416*** (0.507) |
1.426*** (0.517) |
1.790*** (0.464) |
1.790*** (0.547) |
| Ethnic Fractionalization | −0.333 (0.280) |
−0.336 (0.291) |
−0.437 (0.375) |
−0.446 (0.402) |
−0.390 (0.300) |
−0.386 (0.302) |
−0.384 (0.359) |
−0.384 (0.374) |
| % of Population at Risk of
Contracting Malaria |
−0.502 (0.351) |
−0.495 (0.380) |
−0.605 (0.381) |
−0.591 (0.443) |
−0.591 (0.370) |
−0.612 (0.408) |
−0.511 (0.380) |
−0.511 (0.433) |
| % of Population Living in
Tropical Zones |
−0.319 (0.204) |
−0.312 (0.212) |
−0.196 (0.239) |
−0.184 (0.257) |
−0.302 (0.219) |
−0.318 (0.228) |
−0.276 (0.232) |
−0.276 (0.254) |
| Mean Distance to Nearest
Waterway |
−0.368** (0.186) |
−0.367* (0.190) |
−0.387* (0.222) |
−0.382* (0.229) |
−0.452** (0.210) |
−0.461** (0.215) |
−0.315 (0.206) |
−0.315 (0.208) |
| % of Population of European
Descent |
0.061 (0.621) |
0.095 (0.902) |
−0.157 (0.700) |
−0.001 (0.891) |
||||
|
| ||||||||
| Optimal Diversity | 0.721*** (0.068) |
0.721*** (0.089) |
0.720*** (0.085) |
0.720*** (0.195) |
0.719*** (0.015) |
0.719*** (0.022) |
0.720*** (0.021) |
0.720*** (0.036) |
|
| ||||||||
| Observations | 109 | 109 | 83 | 83 | 105 | 105 | 88 | 88 |
| R-squared | 0.90 | 0.90 | 0.82 | 0.82 | 0.89 | 0.89 | 0.84 | 0.84 |
Note: Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses. All regressions include controls for major religion shares as well as OPEC, legal origin, sub-Saharan Africa and continent dummies.
Significant at 1%
Significant at 5%
Significant at 10%.
Table D.13.
Standardized Betas and Partial R-squares in the Baseline Regressions
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Limited Sample
Historical |
Full Sample Historical |
Contemporary |
||||
| Tbl. 1, Col. 4 |
Tbl. 1, Col. 5 |
Tbl. 3, Col. 6 |
Tbl. A1, Col. 6 |
Tbl. A.2, Col. 6 |
Tbl. 6, Col. 2 |
|
| Dependent Variable is: | ||||||
| Log Population Density in 1500 CE |
Log Population Density in 1500 CE |
Log Population Density in 1000 CE |
Log Population Density in 1 CE |
Log Income per Capita in 2000 CE |
||
| Diversity | 7.203 [0.32] |
6.512 [0.21] |
7.008 [0.07] |
6.955 [0.06] |
7.540 [0.06] |
5.510 [0.03] |
| Diversity Squared | −6.913 [0.30] |
−6.251 [0.18] |
−6.936 [0.07] |
−6.838 [0.06] |
−7.364 [0.06] |
−5.485 [0.03] |
| Log Transition Timing | 0.372 [0.35] |
0.348 [0.24] |
0.490 [0.20] |
0.653 [0.28] |
0.765 [0.34] |
0.024 [0.00] |
| Log % of Arable Land | 0.343 [0.29] |
0.363 [0.24] |
0.315 [0.11] |
0.304 [0.08] |
0.256 [0.06] |
−0.120 [0.01] |
| Log Absolute Latitude | −0.109 [0.06] |
−0.086 [0.03] |
−0.257 [0.10] |
−0.236 [0.07] |
−0.069 [0.01] |
0.136 [0.02] |
| Log Land Suitability | 0.291 [0.32] |
0.299 [0.32] |
0.225 [0.06] |
0.173 [0.03] |
0.163 [0.03] |
−0.201 [0.03] |
|
| ||||||
| Continent Dummies | No | Yes | Yes | Yes | Yes | Yes |
| Observations | 21 | 21 | 145 | 140 | 126 | 143 |
| R-squared | 0.89 | 0.90 | 0.69 | 0.62 | 0.61 | 0.57 |
Note: The relevant measures of diversity employed are observed diversity in Columns (1)-(2), predicted diversity in Columns (3)-(5), and ancestry-adjusted predicted diversity in Column (6). The transition timing measure used in Column (6) is ancestry adjusted. Partial R-squares are reported in square brackets. The standardized betas are reported in units of a standard deviation in the dependent variable.
| Ethnic Group | Migratory Distance (in km) |
Country | Region |
|---|---|---|---|
| Bantu (Kenya) | 1,338.94 | Kenya | Africa |
| Bantu (Southeast) | 4,306.19 | South Africa | Africa |
| Bantu (Southwest) | 3,946.44 | Namibia | Africa |
| Biaka Pygmy | 2,384.86 | Central African Republic | Africa |
| Mandenka | 5,469.91 | Senegal | Africa |
| Mbuti Pygmy | 1,335.50 | Zaire | Africa |
| San | 3,872.42 | Namibia | Africa |
| Yoruba | 3,629.65 | Nigeria | Africa |
|
| |||
| Bedouin | 2,844.95 | Israel | Middle East |
| Druze | 2,887.25 | Israel | Middle East |
| Mozabite | 4,418.17 | Algeria | Middle East |
| Palestinian | 2,887.25 | Israel | Middle East |
|
| |||
| Adygei | 4,155.03 | Russia | Europe |
| Basque | 6,012.26 | France | Europe |
| French | 5,857.48 | France | Europe |
| Italian | 5,249.04 | Italy | Europe |
| Orcadian | 6,636.69 | United Kingdom | Europe |
| Russian | 5,956.40 | Russia | Europe |
| Sardinian | 5,305.81 | Italy | Europe |
| Tuscan | 5,118.37 | Italy | Europe |
|
| |||
| Balochi | 5,842.06 | Pakistan | Asia |
| Brahui | 5,842.06 | Pakistan | Asia |
| Burusho | 6,475.60 | Pakistan | Asia |
| Cambodian | 10,260.55 | Cambodia | Asia |
| Dai | 9,343.96 | China | Asia |
| Daur | 10,213.13 | China | Asia |
| Han | 10,123.19 | China | Asia |
| Han (North China) | 9,854.75 | China | Asia |
| Hazara | 6,132.57 | Pakistan | Asia |
| Hezhen | 10,896.21 | China | Asia |
| Japanese | 11,762.11 | Japan | Asia |
| Kalash | 6,253.62 | Pakistan | Asia |
| Lahu | 9,299.63 | China | Asia |
| Makrani | 5,705.00 | Pakistan | Asia |
| Miao | 9,875.32 | China | Asia |
| Mongola | 9,869.85 | China | Asia |
| Naxi | 9,131.37 | China | Asia |
| Oroqen | 10,290.53 | China | Asia |
| Pathan | 6,178.76 | Pakistan | Asia |
| She | 10,817.81 | China | Asia |
| Sindhi | 6,201.70 | Pakistan | Asia |
| Tu | 8,868.14 | China | Asia |
| Tujia | 9,832.50 | China | Asia |
| Uygur | 7,071.97 | China | Asia |
| Xibo | 7,110.29 | China | Asia |
| Yakut | 9,919.11 | Russia (Siberia) | Asia |
| Yi | 9,328.79 | China | Asia |
|
| |||
| Melanesian | 16,168.51 | Papua New Guinea | Oceania |
| Papuan | 14,843.12 | Papua New Guinea | Oceania |
|
| |||
| Colombian | 22,662.78 | Colombia | Americas |
| Karitiana | 24,177.34 | Brazil | Americas |
| Maya | 19,825.71 | Mexico | Americas |
| Pima | 18,015.79 | Mexico | Americas |
Table G.1.
Summary Statistics for the 21-Country Historical Sample
| Obs. | Mean | S.D. | Min. | Max. | |
|---|---|---|---|---|---|
| Log Population Density in 1500 CE | 21 | 1.169 | 1.756 | −2.135 | 3.842 |
| Observed Genetic Diversity | 21 | 0.713 | 0.056 | 0.552 | 0.770 |
| Migratory Distance from Addis Ababa | 21 | 8.238 | 6.735 | 1.335 | 24.177 |
| Human Mobility Index | 18 | 10.965 | 8.124 | 2.405 | 31.360 |
| Log Neolithic Transition Timing | 21 | 8.342 | 0.539 | 7.131 | 9.259 |
| Log % of Arable Land | 21 | 2.141 | 1.168 | −0.799 | 3.512 |
| Log Absolute Latitude | 21 | 2.739 | 1.178 | 0.000 | 4.094 |
| Log Land Suitability for Agriculture | 21 | −1.391 | 0.895 | −3.219 | −0.288 |
Table G.3.
Summary Statistics for the 145-Country Historical Sample
| Obs. | Mean | S.D. | Min. | Max. | |
|---|---|---|---|---|---|
| Log Population Density in 1500 CE | 145 | 0.881 | 1.500 | −3.817 | 3.842 |
| Log Population Density in 1000 CE | 140 | 0.463 | 1.445 | −4.510 | 2.989 |
| Log Population Density in 1 CE | 126 | −0.070 | 1.535 | −4.510 | 3.170 |
| Predicted Genetic Diversity | 145 | 0.711 | 0.053 | 0.572 | 0.774 |
| Log Neolithic Transition Timing | 145 | 8.343 | 0.595 | 5.991 | 9.259 |
| Log % of Arable Land | 145 | 2.232 | 1.203 | −2.120 | 4.129 |
| Log Absolute Latitude | 145 | 3.003 | 0.924 | 0.000 | 4.159 |
| Log Land Suitability for Agriculture | 145 | −1.409 | 1.313 | −5.857 | −0.041 |
| Log Distance to Frontier in 1500 CE | 145 | 7.309 | 1.587 | 0.000 | 9.288 |
| Log Distance to Frontier in 1000 CE | 145 | 7.406 | 1.215 | 0.000 | 9.258 |
| Log Distance to Frontier in 1 CE | 145 | 7.389 | 1.307 | 0.000 | 9.261 |
| Mean Elevation | 145 | 0.555 | 0.481 | 0.024 | 2.674 |
| Terrain Roughness | 145 | 0.178 | 0.135 | 0.013 | 0.602 |
| Mean Distance to Nearest Waterway | 145 | 0.350 | 0.456 | 0.014 | 2.386 |
| % of Land within 100 km of Waterway | 145 | 0.437 | 0.368 | 0.000 | 1.000 |
| Climate | 96 | 1.531 | 1.046 | 0.000 | 3.000 |
| Orientation of Continental Axis | 96 | 1.521 | 0.685 | 0.500 | 3.000 |
| Size of Continent | 96 | 30.608 | 13.605 | 0.065 | 44.614 |
| Domesticable Plants | 96 | 13.260 | 13.416 | 2.000 | 33.000 |
| Domesticable Animals | 96 | 3.771 | 4.136 | 0.000 | 9.000 |
| Migratory Distance from Addis Ababa | 145 | 8.399 | 6.970 | 0.000 | 26.771 |
| Aerial Distance from Addis Ababa | 145 | 6.003 | 3.558 | 0.000 | 14.420 |
| Migratory Distance from London | 145 | 8.884 | 7.104 | 0.000 | 26.860 |
| Migratory Distance from Tokyo | 145 | 11.076 | 3.785 | 0.000 | 19.310 |
| Migratory Distance from Mexico City | 145 | 15.681 | 6.185 | 0.000 | 25.020 |
Table G.5.
Summary Statistics for the 143-Country Contemporary Sample
| Obs. | Mean | S.D. | Min. | Max. | |
|---|---|---|---|---|---|
| Log Income Per Capita in 2000 CE | 143 | 8.416 | 1.165 | 6.158 | 10.445 |
| Log Population Density in 1500 CE | 143 | 0.891 | 1.496 | −3.817 | 3.842 |
| Predicted Genetic Diversity (Unadjusted) | 143 | 0.712 | 0.052 | 0.572 | 0.774 |
| Predicted Genetic Diversity (Ancestry Adjusted) | 143 | 0.727 | 0.027 | 0.631 | 0.774 |
| Log Neolithic Transition Timing (Unadjusted) | 143 | 8.343 | 0.599 | 5.991 | 9.259 |
| Log Neolithic Transition Timing (Ancestry Adjusted) | 143 | 8.498 | 0.455 | 7.213 | 9.250 |
| Log % of Arable Land | 143 | 2.251 | 1.180 | −2.120 | 4.129 |
| Log Absolute Latitude | 143 | 3.014 | 0.921 | 0.000 | 4.159 |
| Log Land Suitability for Agriculture | 143 | −1.416 | 1.321 | −5.857 | −0.041 |
Table D.6.
Pairwise Correlations for the 143-Country Contemporary Sample
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | ||
|---|---|---|---|---|---|---|---|---|---|
| (1) | Log Income Per Capita in 2000 CE | 1.000 | |||||||
| (2) | Log Population Density in 1500 CE | −0.011 | 1.000 | ||||||
| (3) | Predicted Genetic Diversity (Unadjusted) | −0.212 | 0.378 | 1.000 | |||||
| (4) | Predicted Genetic Diversity (Ancestry Adjusted) | −0.157 | 0.058 | 0.759 | 1.000 | ||||
| (5) | Log Neolithic Transition Timing (Unadjusted) | 0.191 | 0.512 | 0.276 | 0.006 | 1.000 | |||
| (6) | Log Neolithic Transition Timing (Ancestry Adjusted) | 0.440 | 0.241 | −0.165 | −0.161 | 0.756 | 1.000 | ||
| (7) | Log % of Arable Land | −0.008 | 0.571 | 0.097 | 0.078 | 0.156 | 0.153 | 1.000 | |
| (8) | Log Absolute Latitude | 0.502 | 0.083 | 0.082 | 0.035 | 0.322 | 0.411 | 0.248 | 1.000 |
| (9) | Log Land Suitability for Agriculture | −0.105 | 0.369 | −0.251 | −0.240 | −0.133 | −0.078 | 0.670 | −0.041 |
Table D.7.
Summary Statistics for the 109-Country Contemporary Sample
| Obs. | Mean | S.D. | Min. | Max. | |
|---|---|---|---|---|---|
| Log Income Per Capita in 2000 CE | 109 | 8.455 | 1.189 | 6.524 | 10.445 |
| Predicted Genetic Diversity (Ancestry Adjusted) | 109 | 0.727 | 0.029 | 0.631 | 0.774 |
| Log Neolithic Transition Timing (Ancestry Adjusted) | 109 | 8.422 | 0.480 | 7.213 | 9.250 |
| Log % of Arable Land | 109 | 2.248 | 1.145 | −2.120 | 4.129 |
| Log Absolute Latitude | 109 | 2.841 | 0.960 | 0.000 | 4.159 |
| Social Infrastructure | 109 | 0.453 | 0.243 | 0.113 | 1.000 |
| Ethnic Fractionalization | 109 | 0.460 | 0.271 | 0.002 | 0.930 |
| % of Population at Risk of Contracting Malaria | 109 | 0.369 | 0.438 | 0.000 | 1.000 |
| % of Population Living in Tropical Zones | 109 | 0.361 | 0.419 | 0.000 | 1.000 |
| Mean Distance to Nearest Waterway | 109 | 0.298 | 0.323 | 0.008 | 1.467 |
| % of Population of European Descent | 109 | 0.318 | 0.407 | 0.000 | 1.000 |
| Average Years of Schooling | 94 | 4.527 | 2.776 | 0.409 | 10.862 |
| Migratory Distance from Addis Ababa (Unadjusted) | 109 | 9.081 | 7.715 | 0.000 | 26.771 |
| Migratory Distance from Addis Ababa (Ancestry Adjusted) | 109 | 6.322 | 3.897 | 0.000 | 18.989 |
| Aerial Distance from Addis Ababa (Unadjusted) | 109 | 6.332 | 3.861 | 0.000 | 14.420 |
| Aerial Distance from Addis Ababa (Ancestry Adjusted) | 109 | 5.161 | 2.425 | 0.000 | 12.180 |
Table D.8.
Pairwise Correlations for the 109-Country Contemporary Sample
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) | (14) | (15) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | Log Income Per Capita in 2000 CE | 1.000 | ||||||||||||||
| (2) | Predicted Genetic Diversity (Ancestry Adjusted) | −0.261 | 1.000 | |||||||||||||
| (3) | Log Neolithic Transition Timing (Ancestry Adjusted) | 0.535 | −0.241 | 1.000 | ||||||||||||
| (4) | Log % of Arable Land | 0.050 | 0.087 | 0.214 | 1.000 | |||||||||||
| (5) | Log Absolute Latitude | 0.563 | −0.014 | 0.367 | 0.242 | 1.000 | ||||||||||
| (6) | Social Infrastructure | 0.808 | −0.219 | 0.363 | 0.119 | 0.476 | 1.000 | |||||||||
| (7) | Ethnic Fractionalization | −0.644 | 0.195 | −0.406 | −0.255 | −0.590 | −0.468 | 1.000 | ||||||||
| (8) | % of Population at Risk of Contracting Malaria | −0.784 | 0.406 | −0.628 | −0.204 | −0.599 | −0.593 | 0.672 | 1.000 | |||||||
| (9) | % of Population Living in Tropical Zones | −0.418 | −0.167 | −0.256 | −0.001 | −0.723 | −0.380 | 0.396 | 0.414 | 1.000 | ||||||
| (10) | Mean Distance to Nearest Waterway | −0.444 | 0.331 | −0.280 | −0.189 | −0.238 | −0.309 | 0.417 | 0.443 | −0.079 | 1.000 | |||||
| (11) | % of Population of European Descent | 0.729 | −0.162 | 0.469 | 0.248 | 0.537 | 0.671 | −0.531 | −0.633 | −0.369 | −0.350 | 1.000 | ||||
| (12) | Average Years of Schooling | 0.866 | −0.138 | 0.426 | 0.138 | 0.556 | 0.758 | −0.478 | −0.665 | −0.436 | −0.360 | 0.767 | 1.000 | |||
| (13) | Migratory Distance from Addis Ababa (Unadjusted) | 0.284 | −0.734 | 0.253 | −0.099 | −0.015 | 0.099 | −0.168 | −0.424 | 0.267 | −0.279 | 0.273 | 0.191 | 1.000 | ||
| (14) | Migratory Distance from Addis Ababa (Ancestry Adjusted) | 0.261 | −1.000 | 0.241 | −0.087 | 0.014 | 0.219 | −0.195 | −0.406 | 0.167 | −0.331 | 0.162 | 0.138 | 0.734 | 1.000 | |
| (15) | Aerial Distance from Addis Ababa (Unadjusted) | 0.335 | −0.804 | 0.203 | −0.047 | 0.064 | 0.195 | −0.229 | −0.443 | 0.239 | −0.338 | 0.304 | 0.261 | 0.939 | 0.804 | 1.000 |
| (16) | Aerial Distance from Addis Ababa (Ancestry Adjusted) | 0.328 | −0.943 | 0.173 | −0.021 | 0.131 | 0.297 | −0.261 | −0.406 | 0.108 | −0.365 | 0.231 | 0.233 | 0.665 | 0.943 | 0.819 |
Acknowledgments
This work was supported by NSF grant SES-0921573. The views expressed herein are those of the authors and do not necessarily reflect the views of the National Bureau of Economic Research.
Appendices
A Additional Robustness Checks
A.1 Results for Earlier Historical Periods
This section examines the effects of genetic diversity on economic development in earlier historical periods of the Common Era and, in particular, establishes a hump-shaped relationship between genetic diversity, predicted by migratory distance from East Africa, and log population density in the years 1000 CE and 1 CE. In so doing, the analysis demonstrates the persistence of the diversity channel over a long expanse of time and indicates that the hump-shaped manner in which genetic diversity influences development, along with the optimal level of diversity, did not fundamentally change during the agricultural stage of development.
The results from replicating the analysis of the previous section to explain log population density in 1000 CE and 1 CE are presented in Tables A.1 and A.2 respectively. As before, the individual and combined explanatory powers of the genetic diversity, transition timing, and land productivity channels are examined empirically. The relevant samples, determined by the availability of data on the dependent variable of interest as well as all identified explanatory channels, are comprised of 140 countries for the 1000 CE regressions and 126 countries for the analysis in 1 CE. Despite the more constrained sample sizes, however, the empirical findings once again reveal a highly statistically significant hump-shaped relationship between genetic diversity, predicted by migratory distance from East Africa, and log population density in these earlier historical periods. Additionally, the magnitude and significance of the coefficients associated with the diversity channel in these earlier periods remain rather stable, albeit less so in comparison to the analysis for 1500 CE, when the regression specification is augmented with controls for the transition timing and land productivity channels as well as dummy variables capturing continental fixed effects.
Table A.1.
Predicted Diversity and Economic Development in 1000 CE
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Dependent Variable is Log
Population Density in 1000 CE |
||||||
| Predicted Diversity | 219.722*** (68.108) |
158.631** (63.604) |
179.523*** (65.981) |
154.913** (61.467) |
201.239** (97.612) |
|
| Predicted Diversity Sqr. | −155.442*** (50.379) |
−113.110** (46.858) |
−126.147*** (48.643) |
−109.806** (44.967) |
−145.894** (68.252) |
|
| Log Transition Timing | 1.393*** (0.170) |
1.228*** (0.180) |
1.374*** (0.151) |
1.603*** (0.259) |
||
| Log % of Arable Land | 0.546*** (0.140) |
0.371*** (0.106) |
0.370*** (0.114) |
|||
| Log Absolute Latitude | −0.151 (0.103) |
−0.380*** (0.110) |
−0.373*** (0.137) |
|||
| Log Land Suitability | 0.043 (0.135) |
0.211** (0.104) |
0.190* (0.106) |
|||
|
| ||||||
| Optimal Diversity | 0.707*** (0.039) |
0.701*** (0.127) |
0.712*** (0.146) |
0.705** (0.108) |
0.690** (0.293) |
|
|
| ||||||
| Continent Dummies | No | No | No | No | No | Yes |
| Observations | 140 | 140 | 140 | 140 | 140 | 140 |
| R-squared | 0.15 | 0.32 | 0.38 | 0.36 | 0.61 | 0.62 |
Note: Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses.
Significant at 1%
Significant at 5%
Significant at 10%.
Table A.2.
Predicted Diversity and Economic Development in 1 CE
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Dependent Variable is Log
Population Density in 1 CE |
||||||
| Predicted Diversity | 227.826*** (72.281) |
183.142*** (57.772) |
129.180* (66.952) |
134.767** (59.772) |
231.689** (113.162) |
|
| Predicted Diversity Sqr. | −160.351*** (53.169) |
−132.373*** (42.177) |
−88.040* (49.519) |
−96.253** (43.718) |
−166.859** (79.175) |
|
| Log Transition Timing | 1.793*** (0.217) |
1.636*** (0.207) |
1.662*** (0.209) |
2.127*** (0.430) |
||
| Log % of Arable Land | 0.377** (0.158) |
0.314** (0.125) |
0.348*** (0.134) |
|||
| Log Absolute Latitude | 0.190 (0.125) |
−0.121 (0.119) |
−0.115 (0.135) |
|||
| Log Land Suitability | 0.160 (0.173) |
0.238* (0.124) |
0.210* (0.125) |
|||
|
| ||||||
| Optimal Diversity | 0.710*** (0.052) |
0.692*** (0.027) |
0.734** (0.347) |
0.700*** (0.188) |
0.694*** (0.194) |
|
|
| ||||||
| Continent Dummies | No | No | No | No | No | Yes |
| Observations | 126 | 126 | 126 | 126 | 126 | 126 |
| R-squared | 0.16 | 0.42 | 0.46 | 0.32 | 0.59 | 0.61 |
Note: Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses.
Significant at 1%
Significant at 5%
Significant at 10%.
In a pattern similar to that observed in Table 3, the unconditional effects of genetic diversity in Tables A.1 and A.2 decrease slightly in magnitude when subjected to controls for either the Neolithic transition timing or the land productivity channels, both of which appear to confer their expected effects on population density in earlier historical periods. However, as argued previously, these estimates certainly reflect some amount of omitted variable bias resulting from the exclusion of one or more of the identified explanatory channels in Malthusian economic development. On the other hand, unlike the pattern in Table 3, the coefficients of the diversity channel also weaken moderately in statistical significance, dropping to the 5% level when controlling for transition timing in the 1000 CE analysis and to the 10% level under controls for the land productivity channel in the 1 CE analysis. Nonetheless, this reduction in significance is not entirely surprising when one accounts for the greater imprecision with which population density is recorded for these earlier periods, given that mismeasurement in the dependent variable of an OLS regression typically causes the resulting coefficient estimates to possess larger standard errors.
Column 5 in Tables A.1 and A.2 reveals the results from exploiting the combined explanatory power of the genetic diversity, transition timing, and land productivity channels for log population density in 1000 CE and 1 CE. Interestingly, in each case, the linear and quadratic coefficients associated with diversity remain rather stable when compared to the corresponding estimates obtained under a partial set of controls in earlier columns. In comparison to the corresponding results for population density in 1500 CE from Table 3, the coefficients of the diversity channel uncovered here are statistically significant at the 5% as opposed to the 1% level, a by-product of relatively larger standard errors that again may be partly attributed to the higher measurement error afflicting population density estimates reported for earlier historical periods.
Finally, the last column in each table augments the analysis with controls for continental fixed effects, demonstrating that the coefficients of the genetic diversity channel in each historical period maintain significance in spite of the lower degree of cross-country variation in diversity within each continent as compared to that observed worldwide. Moreover, the magnitudes of the diversity coefficients remain rather stable, particularly in the 1000 CE analysis, and increase somewhat for population density in 1 CE despite the smaller sample size and, hence, even lower within-continent variation in diversity exploited by the latter regression. Further, the estimated optimal levels of diversity in the two periods are relatively stable in comparison to that obtained under the baseline regression for the year 1500 CE. The coefficients associated with diversity from the 1000 CE analysis suggest that, accounting for both land productivity and the timing of the Neolithic transition, a 1 percentage point increase in genetic diversity for the least diverse society in the sample would raise its population density by 38%, whereas a 1 percentage point decrease in diversity for the most diverse society would raise its population density by 26%. On the other hand, for the 1 CE analysis, a similar increase in genetic diversity for the least diverse society would raise its population density by 47%, whereas a similar decrease in diversity for the most diverse society would raise its population density by 28%.A.1 The hump-shaped relationships, based on these coefficients, between genetic diversity and log population density in the years 1000 CE and 1 CE are depicted on the scatter plots in Figures A.1 and A.2.A.2
In sum, the results presented in Tables A.1 and A.2 suggest that, consistent with the predictions of the proposed diversity channel, genetic diversity has indeed been a significant determinant of Malthusian economic development in earlier historical periods as well. The overall non-monotonic effect of diversity on population density in the years 1000 CE and 1 CE is robust, in terms of both magnitude and statistical significance, to controls for the timing of the agricultural transition, the natural productivity of land for agriculture and other unobserved continent-specific geographical and socioeconomic characteristics. More fundamentally, the analysis demonstrates the persistence of the diversity channel, along with the optimal level of diversity, over a long expanse of time during the agricultural stage of development.
A.2 Robustness to the Technology Diffusion Hypothesis
The technology diffusion hypothesis, as mentioned earlier, suggests that spatial proximity to global and regional technological frontiers confers a beneficial effect on the development of less advanced societies by facilitating the diffusion of new technologies from more advanced societies through trade as well as sociocultural and geopolitical influences. In particular, the technology diffusion channel implies that, ceteris paribus, the greater the geographic distance from the global and regional technological “leaders” in a given period, the lower the level of economic development amongst the “followers” in that period. Indeed, several studies in international trade and economic geography have uncovered strong empirical support for this hypothesis in explaining comparative economic development in the contemporary era. This section examines the robustness of the effects of genetic diversity on economic development during the pre-colonial era to controls for this additional hypothesis.
The purpose of the current investigation is to ensure that the preceding analyses were not ascribing to genetic diversity the predictive power that should otherwise have been attributed to the technology diffusion channel. To be specific, one may identify some of the waypoints employed to construct the prehistorical migratory routes from East Africa (such as Cairo and Istanbul) as origins of spatial technology diffusion during the pre-colonial era. This, coupled with the fact that genetic diversity decreases with increasing migratory distance from East Africa, raises the concern that what has so far been interpreted as evidence consistent with the beneficial effect of higher diversity may, in reality, simply be capturing the latent effect of the omitted technology diffusion channel in preceding regression specifications. As will become evident, however, while technology diffusion is indeed found to have been a significant determinant of comparative development in the pre-colonial era, the baseline findings for genetic diversity remain robust to controls for this additional influential hypothesis.
To account for the technology diffusion channel, the current analysis constructs, for each historical period examined, a control variable measuring the great circle distance from the closest regional technological frontier in that period. Following the well-accepted notion that the process of pre-industrial urban development was typically more pronounced in societies that enjoyed higher agricultural surpluses, the analysis adopts historical city population size as an appropriate metric to identify the period-specific sets of regional technological frontiers. Specifically, based on historical urban population data from Chandler (1987) and Modelski (2003), the procedure commences with assembling, for each period, a set of regional frontiers comprising the two largest cities, belonging to different civilizations or disparate sociopolitical entities, from each of Africa, Europe, Asia and the Americas.A.3 The effectiveness of this procedure in yielding an outcome that is consistent with what one might expect from a general familiarity with world history is evident in the regional frontiers obtained for each period as shown in Table A.3.A.4 In constructing the variable measuring distance to the closest regional frontier for a given historical period, the analysis then selects, for each country in the corresponding regression sample, the smallest of the great circle distances from the regional frontiers to the country’s capital city.
Table A.3.
The Regional Frontiers Identified for each Historical Period
| City and Modern Location | Continent | Sociopolitical Entity | Relevant Period |
|---|---|---|---|
| Cairo, Egypt | Africa | Mamluk Sultanate | 1500 CE |
| Fez, Morocco | Africa | Marinid Kingdom of Fez | 1500 CE |
| London, UK | Europe | Tudor Dynasty | 1500 CE |
| Paris, France | Europe | Valois-Orléans Dynasty | 1500 CE |
| Constantinople, Turkey | Asia | Ottoman Empire | 1500 CE |
| Peking, China | Asia | Ming Dynasty | 1500 CE |
| Tenochtitlan, Mexico | Americas | Aztec Civilization | 1500 CE |
| Cuzco, Peru | Americas | Inca Civilization | 1500 CE |
|
| |||
| Cairo, Egypt | Africa | Fatimid Caliphate | 1000 CE |
| Kairwan, Tunisia | Africa | Berber Zirite Dynasty | 1000 CE |
| Constantinople, Turkey | Europe | Byzantine Empire | 1000 CE |
| Cordoba, Spain | Europe | Caliphate of Cordoba | 1000 CE |
| Baghdad, Iraq | Asia | Abbasid Caliphate | 1000 CE |
| Kaifeng, China | Asia | Song Dynasty | 1000 CE |
| Tollan, Mexico | Americas | Classic Maya Civilization | 1000 CE |
| Huari, Peru | Americas | Huari Culture | 1000 CE |
|
| |||
| Alexandria, Egypt | Africa | Roman Empire | 1 CE |
| Carthage, Tunisia | Africa | Roman Empire | 1 CE |
| Athens, Greece | Europe | Roman Empire | 1 CE |
| Rome, Italy | Europe | Roman Empire | 1 CE |
| Luoyang, China | Asia | Han Dynasty | 1 CE |
| Seleucia, Iraq | Asia | Seleucid Dynasty | 1 CE |
| Teotihuacán, Mexico | Americas | Pre-classic Maya Civilization | 1 CE |
| Cahuachi, Peru | Americas | Nazca Culture | 1 CE |
To anticipate the robustness of the baseline results for predicted diversity to controls for the technology diffusion hypothesis, it may be noted that migratory distance from East Africa possesses a correlation coefficient of only 0.02 with the great circle distance from the closest regional frontier in the 1500 CE sample. Furthermore, for the 1000 CE and 1 CE regression samples, migratory distance is again weakly correlated with distance from the closest regional technological frontier in each period, with the respective correlation coefficients being −0.04 and 0.03.A.5 These encouragingly low sample correlations are indicative of the fact that the earlier regression specifications estimated by the analysis were indeed not simply attributing to genetic diversity the effects possibly arising from the technology diffusion channel.
Column 1 of Table A.4 reports the results from estimating the baseline specification for log population density in 1500 CE, while controlling for technology diffusion as originating from the regional frontiers identified for this period. In comparison to the baseline estimates revealed in Column 6 of Table 3, the regression coefficients associated with the genetic diversity channel remain relatively stable, decreasing only moderately in magnitude and statistical significance. Some similar robustness characteristics may be noted for the transition timing and land productivity channels as well. Importantly, however, the estimate for the optimal level of diversity remains virtually unchanged and highly statistically significant. Interestingly, the results also establish the technology diffusion channel as a significant determinant of comparative development in the pre-colonial Malthusian era. In particular, a 1% increase in distance from the closest regional frontier is associated with a decrease in population density by 0.2%, an effect that is statistically significant at the 1% level.
Table A.4.
Robustness to the Technology Diffusion Hypothesis
| (1) | (2) | (3) | |
|---|---|---|---|
| Dependent Variable is Log Population Density in: |
|||
| 1500 CE | 1000 CE | 1 CE | |
|
|
|||
| Predicted Diversity | 156.736** (75.572) |
183.771** (88.577) |
215.858** (105.286) |
| Predicted Diversity Sqr. | −114.626** (52.904) |
−134.609** (61.718) |
−157.724** (73.681) |
| Log Transition Timing | 0.909*** (0.254) |
1.253*** (0.339) |
1.676*** (0.434) |
| Log % of Arable Land | 0.363*** (0.104) |
0.323*** (0.121) |
0.342*** (0.131) |
| Log Absolute Latitude | −0.492*** (0.134) |
−0.454*** (0.149) |
−0.212 (0.142) |
| Log Land Suitability | 0.275*** (0.090) |
0.239** (0.105) |
0.191 (0.120) |
| Log Distance to Frontier in 1500 CE |
−0.187*** (0.070) |
||
| Log Distance to Frontier in 1000 CE |
−0.230* (0.121) |
||
| Log Distance to Frontier in 1 CE |
−0.297*** (0.102) |
||
|
| |||
| Optimal Diversity | 0.684*** (0.169) |
0.683*** (0.218) |
0.684** (0.266) |
|
| |||
| Continent Dummies | Yes | Yes | Yes |
| Observations | 145 | 140 | 126 |
| R-squared | 0.72 | 0.64 | 0.66 |
Note: Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses.
Significant at 1%
Significant at 5%
Significant at 10%.
Columns 2–3 establish the robustness of the diversity channel in 1000 CE and 1 CE to controls for technology diffusion arising from the technological frontiers identified for these earlier historical periods. Specifically, comparing Column 2 with the relevant baseline (i.e., Column 6 in Table A.1), the linear and quadratic coefficients of genetic diversity for the 1000 CE regressions remain largely stable under controls for technology diffusion, decreasing slightly in magnitude but maintaining statistical significance. A similar stability pattern also emerges for the coefficients capturing the influence of the diversity channel in the 1 CE regressions. Indeed, the estimates for optimal diversity in these earlier periods remain rather stable relative to their respective baselines in Tables A.1 and A.2. Finally, in line with the predictions of the technology diffusion hypothesis, a statistically significant negative effect of distance from the closest regional frontier on economic development is observed for these earlier historical periods as well.
The results uncovered herein demonstrate the persistence of the significant non-monotonic effect of diversity on comparative development over the period 1–1500 CE, despite controls for the clearly influential role of technology diffusion from technological frontiers that were relevant during this period of world history. Indeed, these findings lend further credence to the proposed genetic diversity channel by demonstrating that the empirical analyses thus far have not been ascribing to genetic diversity the explanatory power that should otherwise have been attributed to the impact of spatial technology diffusion.
A.3 Robustness to Microgeographic Factors
This section addresses concerns regarding the possibility that the baseline results for predicted genetic diversity could in fact be reflecting the latent impact of microgeographic factors, such as the degree of variation in terrain and proximity to waterways, if these variables happen to be correlated with migratory distance from East Africa. There are several conceivable channels through which such factors could affect a society’s aggregate productivity and thus its population density in the Malthusian stage of development. For instance, the degree of terrain variation within a region can directly affect its agricultural productivity by influencing the arability of land. Moreover, terrain ruggedness may also have led to the spatial concentration of economic activity, which has been linked with increasing returns to scale and higher aggregate productivity through agglomeration by the new economic geography literature. On the other hand, by geographically isolating population subgroups, a rugged landscape could also have nurtured their ethnic differentiation over time (Michalopoulos, 2008), and may thus confer an adverse effect on society’s aggregate productivity via the increased likelihood of ethnic conflict. Similarly, while proximity to waterways can directly affect crop yields by making beneficial practices such as irrigation possible, it may also have augmented productivity indirectly by lowering transportation costs and, thereby, fostering urban development, trade and technology diffusion.A.6
To ensure that the significant effects of genetic diversity in the baseline regressions are not simply reflecting the latent influence of microgeographic factors, the current analysis examines variants of the baseline specification augmented with controls for terrain quality and proximity to waterways. In particular, the terrain controls are derived from the G-ECON data set compiled by Nordhaus (2006) and include mean elevation and a measure of surface roughness, aggregated up to the country level from grid-level data at a granularity of 1° latitude × 1° longitude. In light of the possibility that the impact of terrain undulation could be non-monotonic, the specifications examined also control for the squared term of the roughness index. The control variables gauging access to waterways, obtained from the Gallup et al. (1999) data set, include the expected distance from any point within a country to the nearest coast or sea-navigable river as well as the percentage of a country’s land area located within 100 km of a coast or sea-navigable river.A.7 Foreshadowing the robustness of the baseline results, mean elevation, roughness and roughness square possess only moderate correlation coefficients of −0.11, 0.16 and 0.09, respectively, with migratory distance from East Africa. Moreover, migratory distance is also only moderately correlated with the measures of proximity to waterways, possessing sample correlations of −0.20 and 0.19 with the distance and land area variables described above.
The results from estimating augmented regression specifications for log population density in 1500 CE, incorporating controls for either terrain quality or access to waterways, are shown in Columns 1 and 2 of Table A.5. In each case, the coefficients associated with the diversity channel remain statistically significant and relatively stable, experiencing only a moderate decrease in magnitude, when compared to the baseline results from Table 3. Interestingly, the control variables for terrain quality in Column 1 and those gauging access to waterways in Column 2 appear to confer statistically significant effects on population density in 1500 CE, and mostly in directions consistent with priors. The results suggest that terrain roughness does indeed have a non-monotonic impact on aggregate productivity, with the beneficial effects dominating at relatively lower levels of terrain roughness and the detrimental effects dominating at higher levels. Further, regions with greater access to waterways are found to support higher population densities.
Table A.5.
Robustness to Microgeographic Factors
| (1) | (2) | (3) | |
|---|---|---|---|
| Dependent Variable is Log Population Density in 1500 CE |
|||
| Predicted Diversity | 160.346** (78.958) |
157.073** (79.071) |
157.059** (69.876) |
| Predicted Diversity Sqr. | −118.716** (55.345) |
−112.780** (55.694) |
−114.994** (48.981) |
| Log Transition Timing | 1.131*** (0.225) |
1.211*** (0.201) |
1.215*** (0.197) |
| Log % of Arable Land | 0.397*** (0.099) |
0.348*** (0.099) |
0.374*** (0.087) |
| Log Absolute Latitude | −0.358*** (0.124) |
−0.354*** (0.132) |
−0.352*** (0.122) |
| Log Land Suitability | 0.188* (0.101) |
0.248*** (0.082) |
0.160** (0.081) |
| Mean Elevation | −0.404 (0.251) |
0.502* (0.273) |
|
| Terrain Roughness | 5.938*** (1.870) |
4.076** (1.840) |
|
| Terrain Roughness Sqr. | −7.332** (2.922) |
−7.627*** (2.906) |
|
| Mean Distance to Nearest
Waterway |
−0.437** (0.178) |
−0.390** (0.181) |
|
| % of Land within 100 km of Waterway |
0.731** (0.310) |
1.175*** (0.294) |
|
|
| |||
| Optimal Diversity | 0.675*** (0.224) |
0.696*** (0.188) |
0.683*** (0.083) |
|
| |||
| Continent Dummies | Yes | Yes | Yes |
| Observations | 145 | 145 | 145 |
| R-squared | 0.72 | 0.75 | 0.78 |
Note: Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses.
Significant at 1%
Significant at 5%
Significant at 10%.
The final column of Table A.5 examines the influence of the genetic diversity channel when subjected to controls for both terrain quality and access to waterways. As anticipated by the robustness of the results from preceding columns, genetic diversity continues to exert a significant non-monotonic effect on population density in 1500 CE, without exhibiting any drastic reductions in the magnitude of its impact. Moreover, the estimate for the optimal level of diversity remains fully intact in comparison to the baseline estimate from Column 6 in Table 3. The results of this section therefore suggest that the significant non-monotonic impact of genetic diversity on population density in 1500 CE is indeed not a spurious relationship arising from the omission of microgeographic factors in the baseline regression specification.
A.4 Robustness to Exogenous Factors in the Diamond Hypothesis
This section demonstrates the robustness of the effects of genetic diversity to additional controls for the Neolithic transition timing channel. In particular, the analysis is intended to alleviate concerns that the significant effects of genetic diversity presented in Section 4.2.2, although estimated while controlling for the timing of the Neolithic Revolution, may still capture some latent influence of this other explanatory channel if spurious correlations exist between migratory distance from East Africa and exogenous factors governing the timing of the Neolithic transition. The results from estimating some extended specifications, constructed by augmenting equation (8) with controls for the ultimate determinants in the Diamond hypothesis, for log population density in 1500 CE are presented in Table A.6.
Table A.6.
Robustness to Ultimate Determinants in the Diamond Hypothesis
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
| Dependent Variable is Log
Population Density in 1500 CE |
|||||
| Predicted Diversity | 216.847*** (62.764) |
252.076*** (71.098) |
174.414*** (62.505) |
212.123*** (70.247) |
274.916*** (73.197) |
| Predicted Diversity Sqr. | −154.750*** (45.680) |
−180.650*** (52.120) |
−125.137*** (45.568) |
−151.579*** (51.463) |
−197.120*** (53.186) |
| Log Transition Timing | 1.300*** (0.153) |
1.160*** (0.298) |
|||
| Log % of Arable Land | 0.437*** (0.116) |
0.431*** (0.119) |
0.441*** (0.111) |
0.411*** (0.116) |
0.365*** (0.112) |
| Log Absolute Latitude | −0.212** (0.102) |
−0.426*** (0.131) |
−0.496*** (0.154) |
−0.487*** (0.163) |
−0.332** (0.145) |
| Log Land Suitability | 0.288** (0.135) |
0.184 (0.143) |
0.297** (0.146) |
0.242* (0.146) |
0.280** (0.122) |
| Climate | 0.622*** (0.137) |
0.419 (0.268) |
0.374* (0.225) |
||
| Orientation of Axis | 0.281 (0.332) |
0.040 (0.294) |
−0.169 (0.255) |
||
| Size of Continent | −0.007 (0.015) |
−0.005 (0.013) |
−0.006 (0.012) |
||
| Domesticable Plants | 0.015 (0.019) |
−0.005 (0.023) |
0.003 (0.021) |
||
| Domesticable Animals | 0.154** (0.063) |
0.121 (0.074) |
−0.013 (0.073) |
||
|
| |||||
| Optimal Diversity | 0.701*** (0.021) |
0.698*** (0.019) |
0.697*** (0.051) |
0.700*** (0.078) |
0.697*** (0.020) |
|
| |||||
| Observations | 96 | 96 | 96 | 96 | 96 |
| R-squared | 0.74 | 0.70 | 0.70 | 0.72 | 0.78 |
Note: Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses.
Significant at 1%
Significant at 5%
Significant at 10%.
Following the discussion in Section 4.1.3 on the geographic and biogeographic determinants in the transition timing channel, the additional control variables employed by the current analysis include: (i) climate, measured as a discrete index with higher integer values assigned to countries in Köppen-Geiger climatic zones that are increasingly favorable to agriculture; (ii) orientation of continental axis, measured as the ratio of the longitudinal distance to the latitudinal distance of the continent or landmass to which a country belongs; (iii) size of continent, measured as the total land area of the country’s continent; (iv) the number of domesticable wild plant species known to have existed in prehistory in the region to which a country belongs; and (v) the number of domesticable wild animal species known to have been native to the region in prehistory, as reported in the data set of Olsson and Hibbs (2005).A.8
To demonstrate the robustness of the baseline effects of genetic diversity across the various extended specifications examined in this section, Column 1 first presents the results from estimating the baseline specification for log population density in 1500 CE using the restricted 96-country sample of Olsson and Hibbs (2005). Reassuringly, the highly significant coefficients associated with diversity, as well as the other explanatory channels, remain rather stable in magnitude relative to their estimates obtained with the unrestricted sample in Column 5 of Table 3, implying that any sampling bias that may have been introduced inadvertently by the use of the restricted sample in the current analysis is indeed negligible.A.9
Columns 2–4 reveal the results from estimating variants of the baseline specification where the Diamond channel is controlled for not by its proximate determinant but by one or more of its ultimate determinants – i.e., either the set of geographical factors or the set of biogeographical factors or both. The results indicate that the coefficients associated with diversity continue to remain highly significant and relatively stable in magnitude in comparison to their baseline estimates of Column 1. Interestingly, when controlling for only the geographical determinants of the Diamond channel in Column 2, climate alone is significant amongst the additional factors and likewise, when only the biogeographical determinants are controlled for in Column 3, the number of domesticable animal species, rather than plants, appears to be important. In addition, none of the ultimate factors in the Diamond channel appear to possess statistical significance when both geographic and biogeographic determinants are controlled for in Column 4, a result that possibly reflects the high correlations amongst these control variables. Regardless of these tangential issues, however, genetic diversity, as already mentioned, continues to exert significant influence in a manner consistent with theoretical predictions.
The final column in Table A.6 establishes the robustness of the effects of genetic diversity on Malthusian development in 1500 CE to controls for both the proximate and ultimate determinants in the Diamond channel. Perhaps unsurprisingly, the Neolithic transition timing variable, being the proximate factor in this channel, captures most of the explanatory power of the ultimate exogenous determinants of comparative development in the Diamond hypothesis. More importantly, the linear and quadratic coefficients of the diversity channel maintain relative stability, increasing slightly in magnitude when compared to their baseline estimates, but remaining highly statistically significant in their expected directions. Overall, the results in Table A.6 suggest that the baseline estimates of the impact of genetic diversity presented in Section 4.2.2 earlier are indeed not simply reflecting some latent effects of the influential agricultural transition timing channel.
B The Index of Contemporary Population Diversity
This section discusses the methodology applied to construct the index of genetic diversity for contemporary national populations such that it additionally accounts for the between-group component of diversity. To this effect, the index makes use of the concept of Fst genetic distance from field of population genetics.
Specifically, for any sub-population pair, the Fst genetic distance between the two sub-populations captures the proportion of their combined genetic diversity that is unexplained by the weighted average of their respective genetic diversities. Consider, for instance, a population comprised of two ethnic groups or sub-populations, A and B. The Fst genetic distance between A and B would then be defined as:
| (B.1) |
where θA and θB are the shares of groups A and B, respectively, in the combined population; and are their respective expected heterozygosities; and is the expected heterozygosity of the combined population. Thus, given (i) genetic distance, , (ii) the expected heterozygosities of the component sub-populations, and , and (iii) their respective shares in the overall population, θA and θB, the overall diversity of the combined population is:
| (B.2) |
In principle, the methodology described above could be applied recursively to arrive at a measure of overall diversity for any contemporary national population comprised of an arbitrary number of ethnic groups, provided sufficient data on the expected heterozygosities of all ethnicities worldwide as well as the genetic distances amongst them are available. In reality, however, the fact that the HGDP-CEPH sample provides such data for only 53 ethnic groups (or pairs thereof) implies that a straightforward application of this methodology would necessarily restrict the calculation of the index of contemporary diversity to a small set of countries. Moreover, unlike the earlier historical analysis, exploiting the predictive power of migratory distance from East Africa for genetic diversity would, by itself, be insufficient since, while this would overcome the problem of data limitations with respect to expected heterozygosities at the ethnic group level, it does not address the problem associated with limited data on genetic distances.
To surmount this issue, the current analysis appeals to a second prediction of the serial-founder effect regarding the genetic differentiation of populations through isolation by geographical distance. Accordingly, in the process of the initial step-wise diffusion of the human species from Africa into the rest of the world, offshoot colonies residing at greater geographical distances from parental ones would also be more genetically differentiated from them. This would arise due to the larger number intervening migration steps, and a concomitantly larger number of genetic diversity sub-sampling events, that are associated with offshoots residing at locations farther away from parental colonies. Indeed, this second prediction of the serial-founder effect is bourne out in the data as well. Based on data from Ramachandran et al. (2005), Figure B.1 shows the strong positive correlation between pairwise migratory distances and pairwise genetic distances across all pairs of ethnic groups in the HGDP-CEPH sample. Specifically, according to the regression, variation in migratory distance explains 78% of the variation in Fst genetic distance across the 1378 ethnic group pairs. Moreover, the estimated OLS coefficient is highly statistically significant, possessing a t-statistic = 53.62, and suggests that predicted Fst genetic distance falls by 0.062 percentage points for every 10,000 km increase in pairwise migratory distance. The construction of the index of diversity for contemporary national populations thus employs Fst genetic distance values predicted by pairwise migratory distances.
Figure B.1.
Pairwise Fst Genetic and Migratory Distances in the HGDP-CEPH Sample
In particular, using the hypothetical example of a contemporary population comprised of two groups whose ancestors originate from countries A and B, the overall diversity of the combined population would be calculated as:
| (B.3) |
where, for i ∈ {A, B}, denotes the expected heterozygosity predicted by the migratory distance, di, of country i from East Africa (i.e., the predicted genetic diversity of country i in the historical analysis); and θi is the contribution of country i, as a result of post-Columbian migrations, to the combined population being considered. Moreover, is the genetic distance predicted by the migratory distance between countries A and B, obtained by applying the coefficients associated with the regression line depicted in Figure B.1. In practice, since contemporary national populations are typically composed of more than two ethnic groups, the procedure outlined in equation (B.3) is applied recursively in order to incorporate a larger number of component ethnic groups in modern populations.
C Supplementary Figures
D Supplementary Results
E The HGDP-CEPH Sample of 53 Ethnic Groups
F Variable Definitions and Sources
Outcome Variables:
Population Density in 1 CE, 1000 CE, and 1500 CE
Population density (in persons per square km) for given year is calculated as population in that year, as reported by McEvedy and Jones (1978), divided by total land area, as reported by the World Bank’s World Development Indicators. The cross-sectional unit of observation in McEvedy and Jones’s (1978) data set is a region delineated by its international borders in 1975. Historical population estimates are provided for regions corresponding to either individual countries or, in some cases, to sets comprised of 2–3 neighboring countries (e.g., India, Pakistan and Bangladesh). In the latter case, a set-specific population density figure is calculated based on total land area and the figure is then assigned to each of the component countries in the set. The same methodology is also employed to obtain population density for countries that exist today but were part of a larger political unit (e.g., the former Yugoslavia) in 1975. The data reported by the authors are based on a wide variety of country and region-specific historical sources, the enumeration of which would be impractical for this appendix. The interested reader is therefore referred to McEvedy and Jones (1978) for more details on the original data sources cited therein.
Income Per Capita in 2000 CE
Real GDP per capita, in constant 2000 international dollars, as reported by the Penn World Table, version 6.2.
Interpersonal Trust
The fraction of total respondents within a given country, from five different waves of the World Values Survey conducted during the time period 1981–2008, that responded with “Most people can be trusted” (as opposed to “Can’t be too careful”) when answering the survey question “Generally speaking, would you say that most people can be trusted or that you can’t be too careful in dealing with people?”
Scientific Articles
The mean, over the period 1981-2000, of the annual number of scientific articles per capita, calculated as the total number of scientific and technical articles published in a given year divided by the total population in that year. The relevant data on the total number of articles and population in a given year are obtained from the World Bank’s World Development Indicators.
Genetic Diversity Variables
Observed Genetic Diversity in the Limited Historical Sample
The average expected heterozygosity across ethnic groups from the Human Genome Diversity Cell Line Panel that are located within a given country. The expected heterozygosities of the ethnic groups are from Ramachandran et al. (2005).
Predicted Genetic Diversity in the Extended Historical Sample
The expected heterozygosity (genetic diversity) of a given country as predicted by (the extended sample definition of) migratory distance from Addis Ababa (Ethiopia). This measure is calculated by applying the regression coefficients obtained from regressing expected heterozygosity on migratory distance at the ethnic group level, using the worldwide sample of 53 ethnic groups from the Human Genome Diversity Cell Line Panel. The expected heterozygosities and geographical coordinates of the ethnic groups are from Ramachandran et al. (2005).
Note that for Table D.5 in Appendix D, the migratory distance concept used to predict the genetic diversity of a country’s population is the human-mobility index, calculated for the journey from Addis Ababa (Ethiopia) to the country’s modern capital city, as opposed to the default waypoints-restricted migratory distance concept used elsewhere. For additional details on how the human-mobility index is calculated, the interested reader is referred to the definition of this variable further below.
Table D.5.
Robustness to Genetic Diversity Predicted by the Mobility Index
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Full Sample Historical |
Contemporary |
|||
| Dependent Variable is: | ||||
| Log Population Density in 1500 CE |
Log Population Density in 1000 CE |
Log Population Density in 1 CE |
Log Income per Capita in 2000 CE |
|
| Diversity | 152.163*** (54.100) |
146.551** (64.082) |
196.145** (80.093) |
176.090*** (67.405) |
| Diversity Squared | −113.298*** (37.707) |
−110.752** (44.392) |
−148.569*** (55.513) |
−120.996** (47.536) |
| Log Transition Timing | 1.553*** (0.255) |
2.052*** (0.265) |
3.242*** (0.349) |
0.047 (0.269) |
| Log % of Arable Land | 0.362*** (0.111) |
0.314** (0.128) |
0.182 (0.126) |
−0.144 (0.110) |
| Log Absolute Latitude | −0.489*** (0.135) |
−0.401*** (0.146) |
−0.087 (0.129) |
0.195 (0.142) |
| Log Land Suitability | 0.256** (0.101) |
0.221* (0.118) |
0.301*** (0.116) |
−0.148 (0.106) |
|
| ||||
| Continent Dummies | Yes | Yes | Yes | Yes |
| Observations | 127 | 123 | 113 | 125 |
| R-squared | 0.71 | 0.66 | 0.69 | 0.55 |
Note: The relevant measures of diversity employed are genetic diversity predicted by the human-mobility index in Columns (1)-(3), and its ancestry-adjusted counterpart in Column (4). The transition timing measure used in Column (4) is ancestry adjusted as well. Bootstrapped standard errors, accounting for the use of generated regressors, are reported in parentheses.
Significant at 1%
Significant at 5%
Significant at 10%.
Predicted Genetic Diversity (Ancestry Adjusted)
The expected heterozygosity (genetic diversity) of a country’s population, predicted by migratory distances from Addis Ababa (Ethiopia) to the year 1500 CE locations of the ancestral populations of the country’s component ethnic groups in 2000 CE, as well as by pairwise migratory distances between these ancestral populations. The source countries of the year 1500 CE ancestral populations are identified from the World Migration Matrix, 1500–2000, discussed in Putterman and Weil (2010), and the modern capital cities of these countries are used to compute the aforementioned migratory distances. The measure of genetic diversity is then calculated by applying (i) the regression coefficients obtained from regressing expected heterozygosity on migratory distance from Addis Ababa at the ethnic group level, using the worldwide sample of 53 ethnic groups from the Human Genome Diversity Cell Line Panel, (ii) the regression coefficients obtained from regressing pairwise Fst genetic distances on pairwise migratory distances between these ethnic groups, and (iii) the ancestry weights representing the fractions of the year 2000 CE population (of the country for which the measure is being computed) that can trace their ancestral origins to different source countries in the year 1500 CE. The construction of this measure is discussed in detail in Appendix B. The expected heterozygosities, geographical coordinates, and pairwise Fst genetic distances of the 53 ethnic groups are from Ramachandran et al. (2005). The ancestry weights are from the World Migration Matrix, 1500–2000.
Note that, in contrast to the default waypoints-restricted migratory distance concept used elsewhere, the migratory distance concept used to predict the ancestry-adjusted genetic diversity of a country’s population for Table D.5 in Appendix D is the human-mobility index, calculated for the journey from Addis Ababa (Ethiopia) to each of the year 1500 CE locations of the ancestral populations of the country’s component ethnic groups in 2000 CE, as well as for the journey between each pair of these ancestral populations. For additional details on how the human-mobility index is calculated, the interested reader is referred to the definition of this variable further below.
Distance Variables
Migratory Distance from Addis Ababa in the Limited Historical Sample
The average migratory distance across ethnic groups from the Human Genome Diversity Cell Line Panel that are located within a given country. The migratory distance of an ethnic group is the great circle distance from Addis Ababa (Ethiopia) to the location of the group, along a land-restricted path forced through one or more of five intercontinental waypoints, including Cairo (Egypt), Istanbul (Turkey), Phnom Penh (Cambodia), Anadyr (Russia) and Prince Rupert (Canada). Distances are calculated using the Haversine formula and are measured in units of 1,000 km. The geographical coordinates of the ethnic groups and the intercontinental waypoints are from Ramachandran et al. (2005).
Migratory Distance from Addis Ababa in the Extended Historical Sample
The great circle distance from Addis Ababa (Ethiopia) to the country’s modern capital city, along a land-restricted path forced through one or more of five aforementioned intercontinental waypoints. Distances are calculated using the Haversine formula and are measured in units of 1,000 km. The geographical coordinates of the intercontinental waypoints are from Ramachandran et al. (2005), while those of the modern capital cities are from the CIA’s World Factbook.
Migratory Distance from Addis Ababa (Ancestry Adjusted)
The cross-country weighted average of (the extended sample definition of) migratory distance from Addis Ababa (Ethiopia), where the weight associated with a given country in the calculation represents the fraction of the year 2000 CE population (of the country for which the measure is being computed) that can trace its ancestral origins to the given country in the year 1500 CE. The ancestry weights are obtained from the World Migration Matrix, 1500–2000 of Putterman and Weil (2010).
Migratory Distance from a “Placebo” Point of Origin
The great circle distance from a “placebo” location (i.e., other than Addis Ababa, Ethiopia) to the country’s modern capital city, along a land-restricted path forced through one or more of five aforementioned intercontinental waypoints. Distances are calculated using the Haversine formula and are measured in units of 1,000 km. The geographical coordinates of the intercontinental waypoints are from Ramachandran et al. (2005), while those of the modern capital cities are from the CIA’s World Factbook. The “placebo” locations for which results are presented in the text include London (UK), Tokyo (Japan), and Mexico City (Mexico).
Aerial Distance from Addis Ababa
The great circle distance “as the crow flies” from Addis Ababa (Ethiopia) to the country’s modern capital city. Distances are calculated using the Haversine formula and are measured in units of 1,000 km. The geographical coordinates of capital cities are from the CIA’s World Factbook.
Aerial Distance from Addis Ababa (Ancestry Adjusted)
The cross-country weighted average of aerial distance from Addis Ababa, where the weight associated with a given country in the calculation represents the fraction of the year 2000 CE population (of the country for which the measure is being computed) that can trace its ancestral origins to the given country in the year 1500 CE. The ancestry weights are from the World Migration Matrix, 1500–2000 of Putterman and Weil (2010).
Distance to Frontier in 1 CE, 1000 CE, and 1500 CE
The great circle distance from a country’s capital city to the closest regional technological frontier for a given year. The year-specific set of regional frontiers comprises the two most populous cities, reported for that year and belonging to different civilizations or sociopolitical entities, from each of Africa, Europe, Asia, and the Americas. Distances are calculated using the Haversine formula and are measured in km. The historical urban population data, used to identify the frontiers, are obtained from Chandler (1987) and Modelski (2003), and the geographical coordinates of ancient urban centers are obtained using Wikipedia.
Human Mobility Index
The average migratory distance across ethnic groups from the Human Genome Diversity Cell Line Panel that are located within a given country. The migratory distance of an ethnic group is the distance from Addis Ababa (Ethiopia) to the location of the group, along an “optimal” land-restricted path that minimizes the time cost of travelling on the surface of the Earth in the absence of steam-powered transportation technologies. The optimality of a path is determined by incorporating information on natural impediments to human spatial mobility such as the meteorological and topographical conditions prevalent along the path, as well as information on the time cost of travelling under such conditions as reported by Hayes (1996). Distances are measured in weeks of travel time. The geographical coordinates of the ethnic groups are from Ramachandran et al. (2005). The methodology underlying the construction of this index is discussed in greater detail by Ashraf et al. (2010) and Özak (2010).
Genetic Distance to the U.K./Ethiopia (1500 Match)
The Fst genetic distance, as reported by Spolaore and Wacziarg (2009), between the year 1500 CE populations of a given country and the U.K. (or Ethiopia), calculated as the genetic distance between the two ethnic groups comprising the largest shares of each country’s population in the year 1500 CE.
Genetic Distance to the U.S./Ethiopia (Weighted)
The Fst genetic distance, as reported by Spolaore and Wacziarg (2009), between the contemporary national populations of a given country and the U.S. (or Ethiopia), calculated as the average pairwise genetic distance across all ethnic group pairs, where each pair comprises two distinct ethnic groups, one from each country, and is weighted by the product of the proportional representations of the two groups in their respective national populations.
Transition Timing and Subsistence Mode Variables
Neolithic Transition Timing
The number of thousand years elapsed, until the year 2000, since the majority of the population residing within a country’s modern national borders began practicing sedentary agriculture as the primary mode of subsistence. This measure, reported by Putterman (2008), is compiled using a wide variety of both regional and country-specific archaeological studies as well as more general encyclopedic works on the transition from hunting and gathering to agriculture during the Neolithic. The reader is referred to the author’s web site for a detailed description of the primary and secondary data sources employed by the author in the construction of this variable.
Neolithic Transition Timing (Ancestry Adjusted)
The cross-country weighted average of Neolithic transition timing, where the weight associated with a given country in the calculation represents the fraction of the year 2000 CE population (of the country for which the measure is being computed) that can trace its ancestral origins to the given country in the year 1500 CE. The ancestry weights are obtained from the World Migration Matrix, 1500–2000 of Putterman and Weil (2010).
Subsistence Mode in 1000 CE
An index in the [0,1]-interval that gauges the extent to which sedentary agriculture was practiced, in the year 1000 CE, within a region delineated by a country’s modern international borders. This index is constructed using data from Peregrine’s (2003) Atlas of Cultural Evolution, which reports, amongst other variables, a measure of the mode of subsistence on a 3-point categorical scale at the level of a cultural group (or “archaeological tradition”) that existed in the year 1000 CE. Specifically, the measure is taken to assume a value of 0 in the absence of sedentary agriculture (i.e., if the cultural group exclusively practiced hunting and gathering), a value of when agriculture was practiced but only as a secondary mode of subsistence, and a value of 1 when agriculture was practiced as the primary mode of subsistence. Given that the cross-sectional unit of observation in Peregrine’s (2003) data set is a cultural group, specific to a given region on the global map, and since spatial delineations of groups, as reported by Peregrine (2003), do not necessarily correspond to contemporary international borders, the measure is aggregated to the country level by averaging across those cultural groups that are reported to appear within the modern borders of a given country. For more details on the underlying data employed to construct this index, the interested reader is referred to Peregrine (2003).
Geographical Variables
Percentage of Arable Land
The fraction of a country’s total land area that is arable, as reported by the World Bank’s World Development Indicators.
Absolute Latitude
The absolute value of the latitude of a country’s approximate geodesic centroid, as reported by the CIA’s World Factbook.
Land Suitability for Agriculture
A geospatial index of the suitability of land for agriculture based on ecological indicators of climate suitability for cultivation, such as growing degree days and the ratio of actual to potential evapotranspiration, as well as ecological indicators of soil suitability for cultivation, such as soil carbon density and soil pH. This index was initially reported at a half-degree resolution by Ramankutty et al. (2002). Formally, Ramankutty et al. (2002) calculate the land suitability index (S) as the product of climate suitability (Sclim) and soil suitability (Ssoil), i.e., S = Sclim × Ssoil. The climate suitability component is estimated to be a function of growing degree days (GDD) and a moisture index ( α) gauging water availability to plants, calculated as the ratio of actual to potential evapotranspiration, i.e., Sclim = f1(GDD)f2(α). The soil suitability component, on the other hand, is estimated to be a function of soil carbon density (Csoil) and soil pH (pHsoil), i.e. Ssoil = g1(Csoil)g2(pHsoil). The functions, f1(GDD), f2(α), g1(Csoil), and g2(pHsoil) are chosen by Ramankutty et al. (2002) by empirically fitting functions to the observed relationships between cropland areas, GDD, α, Csoil, and pHsoil. For more details on the specific functional forms chosen, the interested reader is referred to Ramankutty et al. (2002). Since Ramankutty et al. (2002) report the land suitability index at a half-degree resolution, Michalopoulos (2008) aggregates the index to the country level by averaging land suitability across grid cells within a country. This study employs the country-level aggregate measure reported by Michalopoulos (2008) as the control for land suitability in the baseline regression specifications for both historical population density and contemporary income per capita.
Range of Land Suitability
The difference between the maximum and minimum values of a land suitability index, reported at a half-degree resolution by Ramankutty et al. (2002), across grid cells within a country. This variable is obtained from the data set of Michalopoulos (2008). For additional details on the land suitability index, the interested reader is referred to the definition of the land suitability variable above.
Land Suitability Gini
The Gini coefficient based on the distribution of a land suitability index, reported at a half-degree resolution by Ramankutty et al. (2002), across grid cells within a country. This variable is obtained from the data set of Michalopoulos (2008). For additional details on the land suitability index, the interested reader is referred to the definition of the land suitability variable above.
Soil Fertility
The soil suitability component of an index of land suitability for agriculture, based on soil carbon density and soil pH. The soil suitability data are reported at a half-degree resolution by Ramankutty et al. (2000) and are aggregated to the country level by Michalopoulos (2008) by averaging across grid cells within a country. For additional details on the soil suitability component of the land suitability index, the interested reader is referred to the definition of the land suitability variable above.
Mean Elevation
The mean elevation of a country in km above sea level, calculated using geospatial elevation data reported by the G-ECON project (Nordhaus, 2006) at a 1-degree resolution, which, in turn, is based on similar but more spatially disaggregated data at a 10-minute resolution from New et al. (2002). The measure is thus the average elevation across the grid cells within a country. The interested reader is referred to the G-ECON project web site for additional details.
Standard Deviation of Elevation
The standard deviation of elevation across the grid cells within a country in km above sea level, calculated using geospatial elevation data reported by the G-ECON project (Nordhaus, 2006) at a 1-degree resolution, which, in turn, is based on similar but more spatially disaggregated data at a 10-minute resolution from New et al. (2002). The interested reader is referred to the G-ECON project web site for additional details.
Terrain Roughness
The degree of terrain roughness of a country, calculated using geospatial surface undulation data reported by the G-ECON project (Nordhaus, 2006) at a 1-degree resolution, which is based on more spatially disaggregated elevation data at a 10-minute resolution from New et al. (2002). The measure is thus the average degree of terrain roughness across the grid cells within a country. The interested reader is referred to the G-ECON project web site for additional details.
Temperature
The intertemporal average monthly temperature of a country in degrees Celsius per month over the 1961–1990 time period, calculated using geospatial average monthly temperature data for this period reported by the G-ECON project (Nordhaus, 2006) at a 1-degree resolution, which, in turn, is based on similar but more spatially disaggregated data at a 10-minute resolution from New et al. (2002). The measure is thus the spatial mean of the intertemporal average monthly temperature across the grid cells within a country. The interested reader is referred to the G-ECON project web site for additional details.
Precipitation
The intertemporal average monthly precipitation of a country in mm per month over the 1961–1990 time period, calculated using geospatial average monthly precipitation data for this period reported by the G-ECON project (Nordhaus, 2006) at a 1-degree resolution, which, in turn, is based on similar but more spatially disaggregated data at a 10-minute resolution from New et al. (2002). The measure is thus the spatial mean of the intertemporal average monthly precipitation across the grid cells within a country. The interested reader is referred to the G-ECON project web site for additional details.
Mean Distance to Nearest Waterway
The distance, in thousands of km, from a GIS grid cell to the nearest ice-free coastline or sea-navigable river, averaged across the grid cells of a country. This variable was originally constructed by Gallup et al. (1999) and is part of Harvard University’s CID Research Datasets on General Measures of Geography.
Percentage of Land within 100 km of Waterway
The percentage of a country’s total land area that is located within 100 km of an ice-free coastline or sea-navigable river. This variable was originally constructed by Gallup et al. (1999) and is part of Harvard University’s CID Research Datasets on General Measures of Geography.
Percentage of Population Living in Tropical Zones
The percentage of a country’s population in 1995 that resided in areas classified as tropical by the Köppen-Geiger climate classification system. This variable was originally constructed by Gallup et al. (1999) and is part of Harvard University’s CID Research Datasets on General Measures of Geography.
Percentage of Population at Risk of Contracting Malaria
The percentage of a country’s population in 1994 residing in regions of high malaria risk, multiplied by the proportion of national cases involving the fatal species of the malaria pathogen, P. falciparum (as opposed to other largely non-fatal species). This variable was originally constructed by Gallup and Sachs (2001) and is part of Columbia University’s Earth Institute data set on malaria.
Climate
An index of climatic suitability for agriculture, based on the Köppen-Geiger climate classification system. This variable is obtained from the data set of Olsson and Hibbs (2005).
Orientation of Continental Axis
The orientation of a continent (or landmass) along a North-South or East-West axis. This measure, reported in the data set of Olsson and Hibbs (2005), is calculated as the ratio of the largest longitudinal (East-West) distance to the largest latitudinal (North-South) distance of the continent (or landmass).
Size of Continent
The total land area of a continent (or landmass) as reported in the data set of Olsson and Hibbs (2005).
Domesticable Plants
The number of annual and perennial wild grass species, with a mean kernel weight exceeding 10 mg, that were prehistorically native to the region to which a country belongs. This variable is obtained from the data set of Olsson and Hibbs (2005).
Domesticable Animals
The number of domesticable large mammalian species, weighing in excess of 45 kg, that were prehistorically native to the region to which a country belongs. This variable is obtained from the data set of Olsson and Hibbs (2005).
Institutional, Cultural, and Human Capital Variables
Social Infrastructure
An index, calculated by Hall and Jones (1999), that quantifies the wedge between private and social returns to productive activities. To elaborate, this measure is computed as the average of two separate indices. The first is a government anti-diversion policy (GADP) index, based on data from the International Country Risk Guide, that represents the average across five categories, each measured as the mean over the 1986–1995 time period: (i) law and order, (ii) bureaucratic quality, (iii) corruption, (iv) risk of expropriation, and (v) government repudiation of contracts. The second is an index of openness, based on Sachs and Warner (1995), that represents the fraction of years in the time period 1950–1994 that the economy was open to trade with other countries, where the criteria for being open in a given year includes: (i) non-tariff barriers cover less than 40% of trade, (ii) average tariff rates are less than 40%, (iii) any black market premium was less than 20% during the 1970s and 80s, (iv) the country is not socialist, and (v) the government does not monopolize over major exports.
Democracy
The 1960–2000 mean of an index that quantifies the extent of institutionalized democracy, as reported in the Polity IV data set. The Polity IV democracy index for a given year is an 11-point categorical variable (from 0 to 10) that is additively derived from Polity IV codings on the (i) competitiveness of political participation, (ii) openness of executive recruitment, (iii) competitiveness of executive recruitment, and (iv) constraints on the chief executive.
Executive Constraints
The 1960–2000 mean of an index, reported annually as a 7-point categorical variable (from 1 to 7) by the Polity IV data set, quantifying the extent of institutionalized constraints on the decision-making power of chief executives.
Legal Origins
A set of dummy variables, reported by La Porta et al. (1999), that identifies the legal origin of the Company Law or Commercial Code of a country. The five legal origin possibilities are: (i) English Common Law, (ii) French Commercial Code, (iii) German Commercial Code, (iv) Scandinavian Commercial Code, and (v) Socialist or Communist Laws.
Major Religion Shares
A set of variables, from La Porta et al. (1999), that identifies the percentage of a country’s population belonging to the three most widely spread religions of the world. The religions identified are: (i) Roman Catholic, (ii) Protestant, and (iii) Muslim.
Ethnic Fractionalization
A fractionalization index, constructed by Alesina et al. (2003), that captures the probability that two individuals, selected at random from a country’s population, will belong to different ethnic groups.
Percentage of Population of European Descent
The fraction of the year 2000 CE population (of the country for which the measure is being computed) that can trace its ancestral origins to the European continent due to migrations occurring as early as the year 1500 CE. This variable is constructed using data from the World Migration Matrix, 1500–2000 of Putterman and Weil (2010).
Average Years of Schooling
The mean, over the 1960–2000 time period, of the 5-yearly figure, reported by Barro and Lee (2001), on average years of schooling amongst the population aged 25 and over.
G Descriptive Statistics
H Evidence from Evolutionary Biology
The proposed diversity hypothesis suggests that there exists an aggregate socioeconomic trade-off with respect to genetic diversity within human populations. Specifically, higher diversity generates social benefits by enhancing society’s productivity through efficiency gains via complementarity across different types, by increasing society’s resilience against negative productivity shocks, and by fostering society’s adaptability to a change in the technological environment. Higher diversity also generates social costs, however, by increasing the likelihood of miscoordination and distrust between interacting agents, and by inhibiting the emergence and sustainability of cooperative behavior in society. Indeed, the ideas underlying these channels ensue rather naturally from well-established concepts in evolutionary biology.
The following narrative discusses some of the analogous arguments from the field of evolutionary biology and presents supporting evidence from recent scientific studies. These studies typically focus on organisms, like ants, bees, wasps, and certain species of spiders and birds, that are not only amenable to laboratory experimentation, but also display a relatively high degree of social behavior in nature, such as living in task-directed hierarchical societies, characterized by division of labor, or engaging in cooperative rearing of their young. The motivation behind studying such organisms is often related to the work of sociobiologists, such as Wilson (1978) and Hölldobler and Wilson (1990), who have argued that the application of evolutionary principles in explaining the behavior of social insects lends key insights to the understanding of social behavior in more complex organisms including humans.
H.1 Benefits of Genetic Diversity
The notion that genetic diversity within a given population is beneficial for individual reproductive fitness, and, hence, the adaptability and survivability of the population as a whole, is one of the central tenets of Darwin’s (1859) theory of evolution. In the short term, by reducing the extent of inbreeding, genetic diversity prevents the propagation of potentially deleterious traits in the population over generations (Houle, 1994). In the long term, by permitting the force of natural selection to operate over a wider spectrum of traits, genetic diversity increases the population’s capacity to adapt to changing environmental conditions (Frankham et al., 1999).
To further elaborate, the study by Frankham et al. (1999) provides clear experimental evidence for the beneficial effect of genetic diversity in enhancing the survivability of populations under deleterious changes in the environment. In their experiment, populations of the common fruit fly, Drosophila melanogaster, were subjected to different rates of inbreeding, and their ability to tolerate increasing concentrations of sodium chloride, or common salt, which is harmful for this species of flies, was compared with those of outbred base populations. Indeed, the less diverse inbred populations became extinct at significantly lower concentrations of sodium chloride than the more genetically diverse base populations.
In related studies, Tarpy (2003) and Seeley and Tarpy (2007) employ the honeybee, Apis mellifera, to demonstrate that polyandry, i.e., the practise of mating with multiple male drones by queen bees, may be an adaptive strategy since the resultant increase in genetic diversity increases the colony’s resistance to disease. For instance, having established colonies headed by queens that had been artificially inseminated by either one or ten drones, Seeley and Tarpy inoculated these colonies with spores of Paenibacillus larvae, the bacterium that causes a highly virulent disease of honeybee larvae. The researchers found that, on average, colonies headed by multiple-drone inseminated queens had markedly lower disease intensity and higher colony strength relative to colonies headed by single-drone inseminated queens.
In addition to increasing disease resistance, it has been argued that genetic diversity within honeybee colonies provides them with a system of genetically-based task specialization, enabling them Evidence to respond resiliently to environmental perturbation (Oldroyd and Fewell, 2007). Evidence supporting this viewpoint is provided by the study of Jones et al. (2004). Honeybee colonies need to maintain their brood nest temperature between 32°C and 36°C, and optimally at 35°C, so that the brood develops normally. Workers regulate temperature by fanning hot air out of the nest when the temperature is perceived as being too high and clustering together and generating metabolic heat when the temperature is perceived to be too low. Ideally, a graded rather than precipitous response is required, so that the colony does not constantly oscillate between heating and cooling responses. In their experiment, Jones et al. artificially constructed genetically uniform and diverse honeybee colonies and compared their thermoregulation performances under exposure to ambient temperatures, finding that, over a period of 2 weeks, the within-colony variance in temperatures maintained by the diverse colonies (0.047°C) was less than one-third of the within-colony variance of the uniform ones (0.165°C) and significantly different (F = 3.5, P < 0.001). Figure H.1 illustrates the superior thermoregulation performance of a genetically diverse colony, in comparison to that of a uniform one, in the Jones et al. experiment.
Figure H.1.
Thermoregulation in Genetically Uniform vs. Diverse Honeybee Colonies (Source: Jones et al., 2004)
A popular hypothesis regarding the benefits of diversity, one that appears most analogous to the arguments raised in this paper, suggests that genetically diverse honeybee colonies may operate more efficiently, by performing tasks better as a collective, and thereby gain a fitness advantage over colonies with uniform gene pools (Robinson and Page, 1989). Results from the experimental study of Mattila and Seeley (2007) provide evidence supporting this hypothesis. Since the channel highlighted by this hypothesis is closely related to the idea proposed in the current study, the remainder of this section is devoted to the Mattila and Seeley experiment.
A honeybee colony propagates its genes in two ways: by producing reproductive males (drones) and by producing swarms, when a reproductive female (queen) and several thousand infertile females (workers) leave and establish a new nest. Swarming is costly and perilous; with limited resources and labor, a swarm must construct new comb, build a food reserve, and begin rearing workers to replace the aging work force. In temperate climates, newly founded colonies must operate efficiently because there is limited time to acquire the resources to support these activities. Colony founding is so difficult that only 20% of swarms survive their first year; most do not gather adequate food to fuel the colony throughout the winter and die of starvation. With the challenges of successful colony founding in mind, Mattila and Seeley conducted a long-term study to compare the development characteristics of genetically diverse and genetically uniform colonies after a swarming event. The researchers began by creating genetically diverse colonies, using queens instrumentally inseminated with semen from multiple drones, and genetically uniform ones, using queens inseminated by one drone. They then generated swarms artificially, selecting from each colony the queen and a random subset of her worker offspring, and allowed these swarms to found new colonies. The observations in Mattila and Seeley’s experiment begin on June 11, 2006, when the swarms established their new nest sites. In particular, they document colony development by measuring comb construction, brood rearing, foraging activity, food storage, population size, and mean weight gain at regular intervals.
As depicted in Figure H.2, Mattila and Seeley found that, during the first two weeks of colony development, colonies with genetically diverse worker populations built about 30% more comb than colonies with genetically uniform populations (F = 25.7, P < 0.001). Furthermore, as illustrated in Figure H.3, during the second week of colony founding, genetically diverse colonies maintained foraging rates (measured as the number of workers returning to hive per minute for all workers and for only those carrying pollen) that were between 27% and 78% higher than those of genetically uniform colonies. Consequently, after two weeks of inhabiting their nest sites, genetically diverse colonies stockpiled 39% more food than the uniform ones. The researchers also found that production of new workers and brood rearing by existing workers were both significantly higher in the genetically diverse colonies within the first month of colony development. As a result of these various accumulated productivity gains, the genetically diverse colonies all survived an unusually cold exposure, occurring two months after the establishment of their nest sites, that starved and killed about 50% of the genetically uniform colonies in the Mattila and Seeley experiment. Based on their findings, the authors conclude that collective productivity and fitness in honeybee colonies is indeed enhanced by intracolonial genetic diversity.
Figure H.2.
Comb Area Growth in Genetically Uniform vs. Diverse Honeybee Colonies (Source: Mattila and Seeley, 2007)
Figure H.3.
Foraging Rates in Genetically Uniform vs. Diverse Honeybee Colonies (Source: Mattila and Seeley, 2007)
H.2 Benefits of Genetic Relatedness and Homogeneity
The notion that genetic relatedness between individuals, and genetic homogeneity within a group in general, can be collectively beneficial is highlighted in an extension of Darwinian evolutionary theory known as kin selection theory. In particular, the concept of “survival of the fittest” in standard Darwinian theory implies that, over time, the world should be dominated by selfish behavior since natural selection favors genes that increase an organism’s ability to survive and reproduce. This implication of evolutionary theory remained at odds with the observed prevalence of cooperative behavior in nature until the formalization of kin selection theory by Hamilton (1964) and Maynard Smith (1964). According to this influential theory, the indirect fitness gains of genetic relatives can in some cases more than compensate for the private fitness loss incurred by individuals displaying altruistic or cooperative behavior. Hence, given that relatives are more likely to share common traits, including those responsible for altruism or cooperation, kin selection provides a rationale for the propagation of cooperative behavior in nature.
An immediate implication of kin selection theory is that, when individuals can distinguish relatives from non-relatives (kin recognition), altruists should preferentially direct aid towards their relatives (kin discrimination). The study by Russell and Hatchwell (2001) provides evidence of this phenomenon in a species of cooperatively breeding birds, Aegithalos caudatus, commonly known as the long-tailed tit. In this species, individuals distinguish between relatives and non-relatives on the basis of vocal contact cues (Sharp et al., 2005) and failed breeders become potential helpers in rearing the young of successful breeders in the same social unit. In their research, Russell and Hatchwell designed an experiment to investigate whether the presence of kin within the social unit was necessary for altruistic behavior, and whether kin were preferred to non-kin when given the choice. As depicted in Figure H.4, the researchers found that failed breeders did not actually become helpers when kin were absent from the social unit (panel a), but when both kin and non-kin were present in the same social unit, the majority of failed breeders provided brood-rearing assistance at the nests of kin (panel b).
Figure H.4.
Preferential Bias of Cooperation with Kin in the Long-Tailed Tit (Source: Russell and Hatchwell, 2001)
Kin selection also predicts that the extent of altruism should be positively correlated with genetic relatedness between potential helpers and beneficiaries, and that this correlation should be stronger the greater the indirect fitness benefit from altruism. Empirical support for this prediction comes from the study by Griffin and West (2003) where relevant data from 18 collectively breeding vertebrate species was used to test the relationship between the amount of help in brood rearing and relatedness, and how this correlation varied with the benefit of helping (measured in terms of relatives’ offspring production and survival). Specifically, the study exploited variation across social units, within each species, in genetic relatedness, the amount of help, and the indirect fitness benefit of helping. Consistently with kin selection theory, the researchers found that the average across species in the within-species correlation between the amount of help and genetic relatedness was 0.33 and significantly larger than zero (P < 0.01). Moreover, the study also found that kin discrimination, i.e., the within-species correlation between the amount of help and relatedness, was higher in species where the indirect fitness benefits from altruism were larger. Figure H.5 depicts the relationship between kin discrimination and the benefit from altruistic behavior across species in Griffin and West’s study.
Figure H.5.
Kin Discrimination and the Indirect Fitness Benefit from Cooperation (Source: Griffin and West, 2003)
While the studies discussed thus far provide evidence of the positive correlation between genetic relatedness and altruism, they do not substantiate the effect of relatedness on the other type of social behavior stressed in kin selection theory, that of mutually or collectively beneficial cooperation. This concept is directly associated with the classic problem of public goods provision due to the “tragedy of commons.” In particular, cooperation within groups that exploit a finite resource can be prone to cheating whereby the selfish interests of individuals result in disadvantages for all members of the group. While cooperative behavior can be enforced through mechanisms such as reciprocity or punishment, kin selection provides a natural alternative for the resolution of such social dilemmas. By hoping relatives pass on shared genes to the next generation, cooperation between related individuals can be mutually beneficial. Experimental evidence of the importance of genetic relatedness for cooperative behavior comes from the study by Schneider and Bilde (2008) that; investigates the role of kinship in cooperative feeding amongst the young in Stegodyphus lineatus, a species of spider displaying sociality in juvenile stages.
Schneider and Bilde argue that communally feeding spiders are ideal to investigate the costs and benefits of cooperation because of their mode of feeding. These spiders hunt cooperatively, by building and sharing a common capture web, but they also share large prey items. Since spiders digest externally by first injecting their digestive enzymes and then extracting the liquidized prey content, communal feeding involves everyone spitting into the same carcass and thereby exploiting a common resource that was jointly created. Such a system is especially prone to cheating because each feeder can either invest in the digestion process by contributing enzymes or may cheat by sucking up the fluids with little prior investment. The outcomes of such conflicts in a collective can thus be quantified by measuring feeding efficiency and weight gain. In this case, kin selection theory predicts that groups with higher mean genetic relatedness should outperform others on these biometrics due to a relatively lower prevalence of such conflicts.
To test this prediction, Schneider and Bilde conducted an experiment with three treatment groups of juvenile spiders: genetically related (sibs), genetically and socially unrelated (unfamiliar nonsibs), and genetically unrelated but socially related (familiar nonsibs). Social, as opposed to genetic, relatedness refers to familiarity gained through learned association as a result of being raised by the same mother (either foster or biological) in pre-juvenile stages. The third treatment group therefore allowed the researchers to control for nongenetic learned associations that could erroneously be interpreted as kin-selected effects. In their experiment, Schneider and Bilde followed two group-level outcomes over time. They measured growth as weight gained over a period of eight weeks and measured feeding efficiency of the groups by quantifying the mass extracted from prey in repeated two-hour assays of cooperative feeding. As depicted in Figure H.6, consistently with kin selection, sib groups gained significantly more weight than unrelated groups (both familiar and unfamiliar) over the experimental period of 8 weeks (F = 9.31, P < 0.01), and while nonsib unfamiliar spider groups had a higher start weight than the two other groups, sib groups overtook them by following a significantly steeper growth trajectory. Indeed, as Figure H.7 illustrates, this growth pattern was based on the higher feeding efficiency of sib groups compared with nonsib groups, with kin groups extracting significantly more mass from their prey during a fixed feeding duration (F = 8.91, P < 0.01). Based on these findings, Schneider and Bilde conclude that genetic similarity facilitates cooperation by reducing cheating behavior and, thereby, alleviates the negative social impact of excessive competition.
Figure H.6.
Weight Growth in Kin vs. Non-kin Groups of Cooperatively Feeding Spiders (Source: Schneider and Bilde, 2008)
Figure H.7.
Feeding Efficiency in Kin vs. Non-kin Groups of Cooperatively Feeding Spiders (Source: Schneider and Bilde, 2008)
Footnotes
The following two mechanisms further illustrate this argument. First, in an economy where the labor force is characterized by genetic heterogeneity in a wide array of traits, to the extent that some of these traits lead to specialization in task-oriented activities, higher diversity will increase productivity for society as a whole, given complementarities across different tasks. Second, in an environment in which only individuals with sufficiently high levels of cognitive abilities can contribute to technological innovation, greater variance in the distribution of these traits across the population will lead to higher productivity.
The underlying hypothesis about the costs and benefits of genetic diversity is consistent with experimental evidence from the field of evolutionary biology, reported in Appendix H, based on species that are both amenable to laboratory experimentation and display a relatively high degree of social behavior in nature. In addition, the hypothesis is consistent with evidence provided by social scientists on the costs and benefits associated with intra-population heterogeneity, primarily in the context of ethnic diversity, as reviewed by Alesina and La Ferrara (2005).
Admittedly, historical data on population density is afflicted by measurement error. However, while measurement error in explanatory variables leads to attenuation bias in OLS estimators, mismeasurement of the dependent variable in an OLS regression, as a result of yielding larger standard errors for coefficient estimates, leads to rejecting the null when it is in fact true. As such, if OLS coefficients are precisely estimated, then confidence that the true coefficients are indeed different from zero rises even in the presence of measurement error in the dependent variable.
The history of world civilization is abound with examples of both phenomena. The “Barbarian Invasions” of the Western Roman Empire in the Early Middle Ages is a classic example of hitorical population diffusion occurring along a prosperity gradient, whereas the The Great Wall of China, built and expanded over centuries to minimize invasions by nomadic tribes, serves (literally) as a landmark instance of the latter phenomenon.
An alternative to this “recent African origin” (RAO) model is the “multiregional evolution accompanied by gene flow” hypothesis, according to which early modern hominids evolved independently in different regions of the world and thereafter exchanged genetic material with each other through migrations, ultimately giving rise to a relatively uniform dispersion of modern Homo sapiens throughout the globe. However, in light of surmounting genetic and paleontological evidence against it, the multiregional hypothesis has by now almost completely lost ground to the RAO model of modern human origins (Stringer and Andrews, 1988).
In addition, population geneticists argue that the reduced genetic diversity associated with the founder effect is due not only to the subset sampling of alleles from parental colonies but also to a stronger force of “genetic drift” that operates on the new colonies over time. Genetic drift arises from the fundamental tendency of the frequency of any allele in an inbreeding population to vary randomly across generations as a result of random statistical sampling errors alone (i.e., the chance production of a few more or less progeny carrying the relevant allele). Thus, given the inherent “memoryless” (Markovian) property of allelic frequencies across generations as well as the absence of mutation and natural selection, the process ultimately leads to either a 0% or a 100% representation of the allele in the population (Griffiths et al., 2000). Moreover, since random sampling errors are more prevalent in circumstances where the law of large numbers is less applicable, genetic drift is more pronounced in smaller populations, thereby allowing this phenomenon to play a significant role in the founder effect.
Consistent with the predictions of the proposed hypothesis, the robustness analysis in Appendix A demonstrates that the non-monotonic effect of genetic diversity on development outcomes is prevalent in earlier historical periods as well. Moreover, genetic diversity explains between 15% and 42% of the cross-country variation in log population density, depending on the historical period examined and the control variables included in the regression specification. Indeed, the impact of genetic diversity is robust to various regression specifications such as the inclusion of controls for the spatial influence of regional technological frontiers via trade and the diffusion of technologies, and controls for microgeographic factors gauging terrain quality and proximity to waterways.
See also Dalgaard and Strulik (2010).
See also Desmet et al. (2006) who demonstrate a strong correlation between genetic and cultural distances among European populations to argue that genetic distance can be employed as an appropriate proxy to study the effect of cultural distance on the formation of new political borders in Europe. In addition, Guiso et al. (2009), employ data on genetic distance between European populations as an instrument for measures of trust to estimate its effect on the volume of bilateral trade and foreign direct investment.
The studies by Olsson and Hibbs (2005) and Putterman (2008) have provided empirical support for the Diamond hypothesis in that the timing of the Neolithic revolution has affected the contemporary variation in income per capita across the globe.
Note that, although the genetic diversity channel raised in this study is conceptually independent of the timing of the agricultural transition, an additional genetic channel that interacts with the time elapsed since the Neolithic Revolution has been examined by Galor and Moav (2002, 2007). These studies argue that the Neolithic transition triggered an evolutionary process resulting in the natural selection of certain genetic traits (such as preference for higher quality children and greater longevity) that are complementary to economic development, thereby implying a ceteris paribus positive relationship between the timing of the agricultural transition and the representation of such traits in the population. Indeed, the empirical evidence recently uncovered by Galor and Moav (2007) is consistent with this theoretical prediction. Thus, while the significant reduced-form effect of the Neolithic Revolution observed in this study may be associated with the Diamond hypothesis, it could also be partly capturing the influence of this additional genetic channel. See also Lagerlōf (2007) for a complementary evolutionary theory regarding the dynamics of human body mass in the process of economic development.
If degree of inefficiency is α(ω), the results of the model would remain intact as long as the contribution of homogeneity for efficiency is diminishing (i.e., as long as α(ω) is non-decreasing and weakly convex in ω).
The reader is referred to Appendix F for additional details.
For a more detailed description of the HGDP-CEPH Human Genome Diversity Cell Line Panel data set, the interested reader is referred to Cann et al. (2002). A broad overview of the Human Genome Diversity Project is given by Cavalli-Sforza (2005). The 53 ethnic groups are listed in Appendix E.
Ramachandran et al. (2005) compute expected heterozygosity (i.e., genetic diversity) for these 53 ethnic groups from allelic frequencies associated with 783 chromosomal loci.
Based on mitochondrial DNA analysis, some recent studies (e.g., Macaulay et al., 2005) have proposed a southern exit route out of Africa whereby the initial exodus into Asia occurred not via the Levant but across the mouth of the Red Sea (between modern-day Djibouti and Yemen), thereafter taking a “beachcombing” path along the southern coast of the Arabian Peninsula to India and onward into Southeast Asia. Moreover, a subsequent northern offshoot from the Persian Gulf region ultimately lead to the settlement of the Near East and Europe. This scenario therefore suggests the use of Sana’a (Yemen) and Bandar Abbas (Iran) as intermediate waypoints instead of Cairo. Adopting this alternative route for computing migratory distances, however, does not significantly alter the main results presented in Section 4.2.
These results are similar to those uncovered in an independent study by Prugnolle et al. (2005) that employs a subset of the HGDP-CEPH sample encompassing 51 ethnic groups whose expected heterozygosities are calculated from allelic frequencies for 377 loci. Despite their somewhat smaller sample at both the ethnic group and DNA analysis levels, Prugnolle et al. (2005) find that migratory distance from East Africa explains 85% of the variation in genetic diversity. On the other hand, using an expanded data set comprised of the 53 HGDP-CEPH ethnic groups and an additional 24 Native American populations, Wang et al. (2007) find that migratory distance explains a more modest 74% of the variation in genetic diversity, based on allelic frequencies for 678 loci. The authors attribute their somewhat weaker results to the fact that the additional Native American ethnic groups in their augmented sample were historically subjected to a high degree of gene flow from foreign populations (i.e., European colonizers), which obscured the genetic legacy of a serial-founder effect in these groups.
This effect corresponds to roughly one-third of the full (worldwide) range of expected heterozygosity values observed across the HGDP-CEPH sample of ethnic groups.
A population-weighted averaging method is infeasible in this case due to the current unavailability of population figures for the HGDP-CEPH ethnic groups.
Clearly, there is some amount of measurement error that is introduced by following this methodology since actual migration paths are only approximated due to the use of five major intercontinental waypoints. For instance, using this general method to calculate the migratory distance to Iceland, which was settled in the 9th century CE by a Norwegian population, fails to capture Oslo as an additional case-specific waypoint. The overall sparsity of historical evidence, however, regarding the actual source of initial settlements in many regions makes a more refined analysis infeasible. Nonetheless, it is credibly postulated that the absence of case-specific waypoints from the analysis does not introduce significant mismeasurement at the global scale. The same argument applies in defense of using modern capital cities as destination points for the migratory paths, although historical evidence suggests that, at least for many cases in the “Old World”, modern capitals were also some of the major centers of urbanization throughout the Common Era (see, e.g., Bairoch, 1988; McEvedy and Jones, 1978).
As argued by Pagan (1984) and Murphy and Topel (1985), the OLS estimator for this two-step estimation method yields consistent estimates of the coefficients in the second stage regression, but inconsistent estimates of their standard errors as it fails to account for the presence of a generated regressor. This inadvertently causes naive statistical inferences to be biased in favor of rejecting the null hypothesis. To surmount this issue, the current study employs a two-step bootstrapping algorithm to compute the standard errors in all regressions that use the extended sample containing predicted genetic diversity at the country level. The bootstrap estimates of the standard errors are constructed in the following manner. A random sample with replacement is drawn from the HGDP-CEPH sample of 53 ethnic groups. The first stage regression is estimated on this random sample and the corresponding OLS coefficient on migratory distance is used to compute predicted genetic diversity in the extended sample of countries. The second stage regression is then estimated on a random sample with replacement drawn from the extended cross-country sample and the OLS coefficients are stored. This process of two-step bootstrap sampling and least squares estimation is repeated 1,000 times. The standard deviations in the sample of 1,000 observations of coefficient estimates from the second stage regression are thus the bootstrap standard errors of the point estimates of these coefficients.
See also Weisdorf (2005).
The data source for the aforementioned geographic and biogeographic controls is Olsson and Hibbs (2005) whereas that for the timing of the Neolithic Revolution is Putterman (2008). See Appendix F for the definitions and sources of all primary and control variables employed by the analysis.
It is important to note, in addition, that the type of land productivity being considered here is largely independent of initial geographic and biogeographic endowments in the Diamond channel and, thus, somewhat orthogonal to the timing of agricultural transitions as well. This holds due to the independence of natural factors conducive to domesticated species from those that were beneficial for the wild ancestors of eventual domesticates. As argued by Diamond (2002), while agriculture originated in regions of the world to which the most valuable domesticable wild plant and animal species were native, other regions proved more fertile and climatically favorable once the diffusion of agricultural practices brought the domesticated varieties to them.
The data for these variables are obtained from the World Bank’s World Development Indicators, the CIA’s World Factbook, and Michalopoulos (2008) respectively. The country-level aggregate data on the land suitability index from Michalopoulos (2008) are, in turn, based on more disaggregated geospatial data on this index from the ecological study of Ramankutty et al. (2002). See Appendix F for additional details.
The fact that economic development has been historically clustered in certain regions of the world raises concerns that these disturbances could be non-spherical in nature, thereby confounding statistical inferences based on the OLS estimator. In particular, the disturbance terms may exhibit spatial autocorrelation, i.e., Cov[εi, εj] > 0, within a certain threshold of distance from each observation. Keeping this possibility in mind, the limited sample analyses presented in the text are repeated in Appendix D, where the standard errors of the point estimates are corrected for spatial autocorrelation across disturbance terms, following the methodology of Conley (1999).
Tables G.1-G.2 in Appendix G present the descriptive statistics of the limited 21-country sample employed in estimating equation (7) while Tables G.3-G.4 present those of the extended 145-country sample used to estimate equation (8). As reported therein, the finite-sample moments of the explanatory variables in the limited and extended cross-country samples are remarkably similar. Specifically, the range of values for predicted genetic diversity in the extended sample falls within the range of values for observed diversity in the limited sample. This is particularly reassuring because it demonstrates that the methodology used to generate the predicted genetic diversity variable did not project values beyond what is actually observed, indicating that the HGDP-CEPH collection of ethnic groups is indeed a representative sample for the worldwide variation in within-country genetic diversity. Moreover, the fact that the finite-sample moments of log population density in 1500 CE are not significantly different between the limited and extended cross-country samples foreshadows the encouraging similarity of the regression results that are obtained under observed and predicted values of genetic diversity.
The fact that migratory distance from East Africa may be correlated with other potential geographical determinants of genetic diversity, particularly factors like the dispersion of land suitability for agriculture and the dispersion of elevation that have been shown to give rise to ethnic diversity (Michalopoulos, 2008), raises the possibility that migratory distance may not be the only source of exogenous variation in genetic diversity. However, Table D.1 in Appendix D indicates that these other factors have little or no explanatory power for the cross-country variation in actual genetic diversity beyond that accounted for by migratory distance via the serial-founder effect. Specifically, the OLS coefficient as well as the partial R-squared associated with migratory distance remain both quantitatively and qualitatively robust when the regression is augmented with these geographical controls, all of which are statistically insignificant in explaining genetic diversity. The reader is referred to Appendix F for detailed definitions of the additional control variables used by the analysis in Table D.1.
Corresponding to Tables 1 and 2 in the text, Tables D.2 and D.3 in Appendix D present results with standard errors and 2SLS point estimates corrected for spatial autocorrelation across observations.
The magnitude of these effects can be derived directly from the estimated linear and quadratic coefficients associated with genetic diversity. Specifically, letting and denote the estimated coefficients on genetic diversity and genetic diversity square, equation (7) can be used to show that the proportional effect on population density of a ΔG change in diversity at the specified level Ḡ is given by: .
The non-parametric regression lines depicted in Figures 4, 5, and 7 are all estimated g using local 2nd-degree polynomial smoothing with a Gaussian kernel function and a kernel bandwidth of 0.06. Corresponding to these figures in the text, Figures C.1, C.2, and C.4 in Appendix C compare, in each case, the quadratic fit with a restricted cubic spline regression, estimated using three equally-spaced knots on the relevant domain of genetic diversity values. These appendix figures indicate that, in each case, the quadratic fit falls within the 95% confidence interval band of the cubic spline regression, as it does with respect to the corresponding non-parametric relationship.
For consistency with Figure 1, which depicts the negative effect of increasing migratory distance from East Africa on genetic diversity, the horizontal axes in Figures 4-8 represent genetic homogeneity (i.e., 1 minus genetic diversity) so as to reflect increasing as opposed to decreasing migratory distance from East Africa.
Despite controls for continental dummies, the fact that (i) the hump-shaped relationship between genetic diversity and economic development appears to be, in part, identified by a relatively smaller number of observations from the Americas on the backward-bending side of the relationship, coupled with the fact that (ii) equations (7)-(9) a priori impose a quadratic relationship between genetic diversity and economic development, could potentially raise concerns that the empirical models being estimated in this paper are misspecified in that the true relationship between diversity and development is logarithmic rather than quadratic in nature. If the relationship is indeed logarithmic then, upon re-estimating the baseline specifications using logged diversity and the square of logged diversity, one should not expect the latter quadratic term to survive in the regressions. Table D.4 in Appendix D presents the results from such an analysis, demonstrating that empirical model misspecification need not be a source of concern. In particular, the results indicate that the baseline findings from both the limited- and extended-sample variants of the historical analysis, as well as those from the contemporary analysis, are qualitatively unaltered when quadratic specifications using logged genetic diversity are employed to examine the impact of diversity on development.
Figures C.6(a)-C.6(c) in Appendix C illustrate that, unlike the significant impact of migratory distance from East Africa on genetic diversity, migratory distance has no systematic relationship with a number of observed physiological characteristics of populations, including average skin reflectance, average height, and average weight, conditional on geographical factors such as the intensity of ultraviolet exposure, absolute latitude, the percentage of arable land, the shares of land in tropical and temperate zones, elevation, access to waterways, and continental fixed effects. Since the physiological characteristics examined in Figures C.6(a)-C.6(c) represent their averages for contemporary national populations, the migratory distance measure is adjusted to account for the modern ethnic compositions of these populations resulting from cross-country migrations in the post-Columbian era.
The difference in the number of observations between Columns 1–2 (21 obs.) and Columns 3–4 (18 obs.) arises due to the fact that the mobility index cannot be calculated for countries that can only be accessed from Addis Ababa by crossing at least one body of water. Restricting the sample used in Columns 1–2 to that in Columns 3–4 does not qualitatively alter the findings. In addition, the unavailability of the mobility index measure for several countries (due to the aforementioned strict land-accessibility constraint) makes this measure less suitable, in comparison to the baseline migratory distance measure of Ramachandran et al. (2005), to predict genetic diversity in the extended cross-country sample. Nevertheless, Table D.5 in Appendix D demonstrates that the main findings from both the extended-sample historical analysis and the contemporary analysis remain qualitatively robust to using genetic diversity predicted by the more sophisticated mobility index, rather than by the baseline, waypoints-restricted migratory distance measure of Ramachandran et al. (2005).
Specifically, since the empirical specification is quadratic in the endogenous regressor, it is necessary to instrument for both genetic diversity and its squared term in order for the system to be exactly identified. Thus, following Wooldridge (2010, pp. 267–268), the strategy adopted introduces a zeroth-stage to the analysis where genetic diversity is first regressed on migratory distance and all the second-stage controls to obtain predicted values of diversity. The predicted genetic diversity from the zeroth-stage is squared and this squared term is then used as an excluded instrument in the second stage along with migratory distance. The zeroth- and first-stage results of the 2SLS regressions reported in Columns 5 and 6 of Table 2 are collected in Table D.6 in Appendix D.
Following the earlier discussion regarding the expected heterozygosity index, these effects are therefore associated with a 0.01 change in the probability that two randomly selected individuals from a given population are genetically different from one another. See Footnote 31 for details on how these effects may be computed based on the estimated linear and quadratic coefficients associated with genetic diversity.
The cross-country variation in genetic diversity and in variables capturing the productivity of land for agriculture together explain 50% of the cross-country variation in population density.
To interpret the coefficients associated with the land productivity channel, a 1% increase in the fraction of arable land and in absolute latitude corresponds, respectively, to a 0.5% increase and a 0.2% decrease in population density. While this latter effect may seem unintuitive, given the positive relationship between absolute latitude and contemporary income per capita, it accurately reflects the fact that agricultural productivity in the past has typically been higher at latitudinal bands closer to the equator. In addition, this finding is also consistent with the “reversal of fortune” hypothesis documented by Acemoglu et al. (2005).
Table D.7 in Appendix D demonstrates that the baseline findings for genetic diversity from both the limited- and extended-sample variants of the historical analysis, as well as those from the contemporary analysis, remain qualitatively intact under alternative regression specifications that control for some of the individual ecological components of the land suitability index, including temperature, precipitation, and soil fertility, in lieu of the baseline control for the overall suitability of land for cultivation.
In addition, consistent with the fact that the baseline control for the timing of the Neolithic Revolution should be expected to capture the contemporaneous effect of the mode of subsistence on population density in the pre-colonial Malthusian era, Table D.8 establishes that augmenting the baseline specifications for examining population density in the years 1500 CE and 1000 CE with an explicit control for the mode of subsistence, while diminishing somewhat the explanatory power of the transition timing channel, does not affect the main findings for genetic diversity. Note that, given underlying data availability constraints on constructing a proxy for the mode of subsistence prevalent in the year 1500 CE, coupled with the fact that cross-country subsistence patterns in 1000 CE should be expected to be highly correlated with those existing in 1500 CE, the analysis in Table D.8 controls only for the mode of subsistence prevalent in the year 1000 CE in augmented regressions explaining population density in both time periods. For detailed definitions of additional control variables used by the robustness analyses in Tables D.7 and D.8, the interested reader is referred to Appendix F.
Figure 6 is an “augmented component plus residual” plot and not the typical “added variable” plot of residuals against residuals. In particular, the vertical axis in this figure represents the component of observed log population density that is predicted by genetic homogeneity and its square plus the residuals from the regression. The horizontal axis, on the other hand, simply represents genetic homogeneity rather than the residuals obtained from regressing homogeneity on the covariates. This methodology permits the illustration of the overall non-monotonic effect of the genetic channel in one scatter plot. Plots depicting the partial regression lines associated with the first-order and second-order effects of genetic homogeneity on log population density in 1500 CE are presented in Figures C.3(a)-C.3(b) in Appendix C.
The choice of these alternative points of origin do not reflect any systematic selection process, other than the criterion that they belong to different continents in order to demonstrate, at a global scale, the neutrality of migratory distance from locations outside of East Africa. Indeed, other points of origin in Europe, Asia and the Americas yield qualitatively similar results.
The data on ethnic compositions are obtained from the World Migration Matrix, 1500–2000 of Putterman and Weil (2010) who compile, for each country in their data set, the share of the country’s population in 2000 CE that is descended from the population of every other country in 1500 CE.
Table D.9 in Appendix D establishes that migratory distance from Addis Ababa, adjusted to reflect the weighted average of migratory distances of the pre-Columbian ancestral populations of a country today, is the only distance concept that confers a significant hump-shaped effect on income per capita in 2000 CE. As shown in the table, the other distance concepts, including (i) the unadjusted measure of migratory distance from Addis Ababa (used in the historical analysis), (ii) the aerial distance from Addis Ababa, and (iii) the ancestry-adjusted aerial distance from Addis Ababa, do not confer any systematic non-monotonic effect on income per capita in 2000 CE, given that the ancestry-adjusted migratory distance measure is accounted for by the regression.
The data on income per capita are from the Penn World Table, version 6.2. The institutional and cultural controls include the social infrastructure index of Hall and Jones (1999), the share of the population of European descent based on the World Migration Matrix, 1500–2000 of Putterman and Weil (2010), legal origin dummies and the shares of the population affiliated with major world religions from the data set of La Porta et al. (1999), as well as the ethnic fractionalization index of Alesina et al. (2003). The additional geographical controls include the share of the population at risk of contracting falciparum malaria from Gallup and Sachs (2001), as well as the share of the population living in Köppen-Geiger tropical zones and distance from the nearest coast or sea-navigable river, both from the data set of Gallup et al. (1999). See Appendix F for further details.
Since (i) genetic diversity for contemporary national populations is partly based on the Fst genetic distances between their pre-Columbian ancestral groups, and (ii) Fst genetic distances and relative expected heterozygosities, even amongst populations in the pre-Columbian era, are in part co-determined by migratory distances, it is necessary to ensure that the observed hump-shaped effect of genetic diversity on comparative development, in both the pre-Columbian and contemporary eras, is not reflecting the latent impact of genetic distance to either the cradle of humankind or the world technological frontier, via channels related to the diffusion of development (Spolaore and Wacziarg, 2009). Table D.10 in Appendix D demonstrates that the baseline findings for genetic diversity from both the limited- and extended-sample variants of the historical analysis, as well as those from the contemporary analysis, are virtually unaffected when the regression specifications are augmented to account for appropriate measures of Fst genetic distance to Ethiopia and to the world technology frontier relevant for the time period being examined. For detailed definitions of the various genetic distance controls used by the robustness analysis in Table D.10, the reader is referred to Appendix F.
Tables G.5-G.6 in Appendix G present the relevant descriptive statistics for this 143-country sample.
Table D.13 in Appendix D reports the standardized beta coefficients and partial R-squares associated with each regressor in the baseline regressions for both the historical and contemporary analyses.
The agricultural suitability index was not found to enter significantly in any of the specifications examined in Table 7 and is therefore dropped from the analysis. Tables G.7-G.8 in Appendix G present the relevant descriptive statistics for the 109-country sample employed in Tables 7-8.
The inclusion of measures from the Polity IV data set, reflecting the extent of democracy or the degree of constraints on the power of chief executives, as additional controls for institutional quality do not affect the results for genetic diversity. Moreover, because these measures enter insignificantly in the regression once social infrastructure has been controlled for, they are excluded from the analysis in Table 7.
Results (not shown) from estimating a similar specification that included ethnic fractionalization square as an additional explanatory variable did not reveal any discernible non-monotonic impact of ethnic fractionalization on income per capita in 2000 CE. Importantly, the regression coefficients associated with genetic diversity, as well as the estimate for the optimal level of diversity, were unaffected.
As established by Table D.11 in Appendix D, the baseline results for diversity in the contemporary analysis are qualitatively robust to (i) controls for regional (rather than continental) fixed effects (Column 1), (ii) dropping observations (Columns 2–4) associated with Sub-Saharan Africa and Latin America that, given their laggard development in comparison to other regions, along with their relatively higher and lower levels of genetic diversity respectively, may be considered a priori to be influential for generating the worldwide hump-shaped relationship between diversity and development, and (iii) restricting the regression sample (Column 5) to only countries in the potentially influential Sub-Saharan Africa and Latin America regional clusters. These results demonstrate that the direct hump-shaped effect of genetic diversity on income per capita in the modern world is not simply a reflection of worldwide cross-regional variations in diversity and economic development.
Similar to Figure 6 in the preceding historical analysis, Figure 8 is an “augmented component plus residual” plot described in detail in Footnote 42. Plots depicting the partial regression lines associated with the first-order and second-order effects of genetic homogeneity on log income per capita in 2000 CE are presented in Figures C.5(a)-C.5(b) in Appendix C.
Since the share of the population of European descent is expected to be highly correlated with unobserved fixed effects associated with European countries as well as the Neo-Europes (i.e., USA, Canada, New Zealand, and Australia), Table D.12 in Appendix D repeats the analysis from Columns 5–6 in Table 7 on different cuts of the cross-country sample, focusing primarily on countries where the share of Europeans in the population is not confoundingly close to 1. Importantly, the findings therein suggest that the baseline results are robust to controlling for the share of Europeans in the population even when the sample is restricted to non-OECD countries (Columns 3–4), non Neo-European countries (Columns 5–6), and non-European countries (Columns 7–8).
This result reflects the well-known fact from the field of population genetics that the overwhelming majority of genetic diversity in human populations stems from the diversity within groups, as opposed to the diversity between groups (see, e.g., Barbujani et al., 1997).
For details on the definitions and data sources of the dependent variables employed by the current analysis, the reader is referred to Appendix F.
These effects are calculated directly via the methodology outlined in Footnote 31 earlier, along with the sample minimum and maximum genetic diversity values of 0.573 and 0.774, respectively, in both the 1000 CE and 1 CE regression samples.
Similar to Figure 6, Figures A.1-A.2 are “augmented component plus residual” plots. See Footnote 42 for further details regarding this type of plot. In addition, for consistency with Figure 1, which depicts the negative effect of increasing migratory distance from East Africa on genetic diversity, the horizontal axes in Figures A.1-A.2 represent genetic homogeneity (i.e., 1 minus genetic diversity) so as to reflect increasing as opposed to decreasing migratory distance from East Africa.
The exclusion of Oceania from the list of continents employed is not a methodological restriction but a natural result arising from the fact that evidence of urbanization does not appear in the historical record of this continent until after European colonization. Moreover, the consideration of the Americas as a single unit is consistent with the historical evidence that this landmass only harbored two distinct major civilizational sequences – one in Mesoamerica and the other in the Andean region of South America. Indeed, the imposition of the criteria that the selected cities in each continent (or landmass) should belong to different sociopolitical units is meant to capture the notion that technology diffusion historically occurred due to civilizational influence, broadly ddefined, as opposed to the influence of only major urban centers that were developed by these relatively advanced societies.
Note that for the year 1 CE there are four cities appearing within the territories of the Roman Empire, which at first glance seems to violate the criterion that the regional frontiers selected should belong to different sociopolitical entities. This is simply a by-product of the dominance of the Roman Empire in the Mediterranean basin during that period. In fact, historical evidence suggests that the cities of Athens, Carthage and Alexandria had long been serving as centers of regional diffusion prior to their annexation to the Roman Empire. Moreover, the appearance of Constantinople under Europe in 1000 CE and Asia in 1500 CE is an innocuous classification issue arising from the fact that the city historically fluctuated between the dominions of European and Asian civilizations.
These correlations differ slightly from those presented in Table G.4 in Appendix G, where the correlations are presented for the entire 145-country sample used in the regressions for 1500 CE.
Indeed, a significant positive relationship between proximity to waterways and contemporary population density has been demonstrated by Gallup et al. (1999).
For completeness, specifications controlling for the squared terms of the other microgeographic factors were also examined. The results from these additional regressions, however, did not reveal any significant non-linear effects and are therefore not reported.
While the influence of the number of domesticable species on the likelihood of the emergence of agriculture is evident, the role of the geographic factors requires some elaboration. A larger size of the continent or landmass implied greater biodiversity and, hence, a greater likelihood that at least some species suitable for domestication would exist. In addition, a more pronounced East-West (relative to North-South) orientation of the major continental axis meant an easier diffusion of agricultural practices within the landmass, particularly among regions sharing similar latitudes and, hence, similar environments suitable for agriculture. This orientation factor is argued by Diamond (1997) to have played a pivotal role in comparative economic development by favoring the early rise of complex agricultural civilizations on the Eurasian landmass. Finally, certain climates are known to be more beneficial for agriculture than others. For instance, moderate zones encompassing the Mediterranean and marine west coast subcategories in the Köppen-Geiger climate classification system are particularly amenable for growing annual, heavy grasses whereas humid subtropical, continental and wet tropical climates are less favorable in this regard, with agriculture being almost entirely infeasible in dry and Polar climates. Indeed, the hypothesized influence of these exogenous factors on the Neolithic Revolution has been established empirically by Olsson and Hibbs (2005) and Putterman (2008).
Note that the specifications estimated in the current analysis do not incorporate continental dummies since a sizeable portion of possible continent-specific effects are captured by some of the (bio)geographic variables in the Diamond channel that are measured at either continental or macro-regional levels. Augmenting the specifications with continental dummies, however, does not significantly alter the results for genetic diversity.
Contributor Information
Quamrul Ashraf, Williams College Department of Economics 24 Hopkins Hall Drive Williamstown, MA 01267.
Oded Galor, Department of Economics Brown University Box B Providence, RI 02912 and NBER.
References
- Acemoglu Daron, Johnson Simon, Robinson James A. Institutions as a Fundamental Cause of Long-Run Growth. In: Aghion Philippe, Durlauf Steven N., editors. Handbook of Economic Growth, Vol IA. Elsevier North-Holland; Amsterdam, The Netherlands: 2005. [Google Scholar]
- Alesina Alberto, La Ferrara Eliana. Ethnic Diversity and Economic Performance. Journal of Economic Literature. 2005 Sep;43(3):762–800. [Google Scholar]
- Alesina Alberto, Devleeschauwer Arnaud, Easterly William, Kurlat Sergio, Wacziarg Romain. Fractionalization. Journal of Economic Growth. 2003 Jun;8(2):155–194. [Google Scholar]
- Ashraf Quamrul, Galor Oded. Dynamics and Stagnation in the Malthusian Epoch; Working Paper, Department of Economics, Williams College; 2010. [Google Scholar]
- Ashraf Quamrul, Galor Oded, Özak Ömer. Isolation and Development. Journal of the European Economic Association. 2010 Apr-May;8(2-3):401–412. [Google Scholar]
- Bairoch Paul. In: Cities and Economic Development: From the Dawn of History to the Present. Braider Christopher., editor. The University of Chicago Press; Chicago, IL: 1988. [Google Scholar]
- Barbujani Guido, Magagni Arianna, Minch Eric, Cavalli-Sforza L. Luca. An Apportionment of Human DNA Diversity. Proceedings of the National Academy of Sciences. 1997 Apr;94(9):4516–4519. doi: 10.1073/pnas.94.9.4516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barro Robert J., McCleary Rachel M. Religion and Economic Growth across Countries. American Sociological Review. 2003 Oct;68(5):760–781. [Google Scholar]
- Cann Howard M., de Toma Claudia, Cazes Lucien, Legrand Marie-Fernande, Morel Valerie, Piouffre Laurence, et al. A Human Genome Diversity Cell Line Panel. Science. 2002 Apr;296(5566):261–262. doi: 10.1126/science.296.5566.261b. [DOI] [PubMed] [Google Scholar]
- Cavalli-Sforza L. Luca. The Human Genome Diversity Project: Past, Present and Future. Nature Reviews Genetics. 2005 Apr;6(4):333–340. doi: 10.1038/nrg1596. [DOI] [PubMed] [Google Scholar]
- Conley Timothy G. GMM Estimation with Cross Sectional Dependence. Journal of Econometrics. 1999 Sep;92(1):1–45. [Google Scholar]
- Dalgaard Carl-Johan, Strulik Holger. University of Copenhagen; 2010. The Physiological Foundations of the Wealth of Nations. Discussion Paper No. 10-05. [Google Scholar]
- Desmet Klaus, Le Breton Michel, Ortun̄o-Ortín Ignacio, Weber Shlomo. Nation Formation and Genetic Diversity. 2006 CEPR Discussion Paper No. 5918. [Google Scholar]
- Diamond Jared. Guns, Germs and Steel: The Fates of Human Societies. W. W. Norton & Co.; New York, NY: 1997. [Google Scholar]
- Diamond Jared. Evolution, Consequences and Future of Plant and Animal Domestication. Nature. 2002 Aug;418(6898):700–707. doi: 10.1038/nature01019. [DOI] [PubMed] [Google Scholar]
- Easterly William, Levine Ross. Africa’s Growth Tragedy: Policies and Ethnic Divisions. Quarterly Journal of Economics. 1997 Nov;112(4):1203–1250. [Google Scholar]
- Engerman Stanley L., Sokoloff Kenneth L. History Lessons: Institutions, Factor Endowments, and Paths of Development in the New World. Journal of Economic Perspectives. 2000 Summer;14(3):217–232. [Google Scholar]
- Gallup John L., Sachs Jeffrey D. The Economic Burden of Malaria. The American Journal of Tropical Medicine and Hygiene. 2001 Jan;64(1-2):85–96. doi: 10.4269/ajtmh.2001.64.85. [DOI] [PubMed] [Google Scholar]
- Gallup John L., Sachs Jeffrey D., Mellinger Andrew D. Geography and Economic Development. International Regional Science Review. 1999 Aug;22(2):179–232. [Google Scholar]
- Galor Oded. The 2008 Lawrence R. Klein Lecture–Comparative Economic Development: Insights from Unified Growth Theory. International Economic Review. 2010 Feb;51(1):1–44. [Google Scholar]
- Galor Oded, Moav Omer. Natural Selection and the Origin of Economic Growth. Quarterly Journal of Economics. 2002 Nov;117(4):1133–1191. [Google Scholar]
- Galor Oded, Moav Omer. The Neolithic Revolution and Contemporary Variations in Life Expectancy; Working Paper, Department of Economics, Brown University; 2007. [Google Scholar]
- Glaeser Edward L., La Porta Rafael, Lopez-de-Silanes Florencio, Shleifer Andrei. Do Institutions Cause Growth? Journal of Economic Growth. 2004 Sep;9(3):271–303. [Google Scholar]
- Greif Avner. Contract Enforceability and Economic Institutions in Early Trade: The Maghribi Traders’ Coalition. American Economic Review. 1993 Jun;83(3):525–548. [Google Scholar]
- Griffiths Anthony J. F., Miller Jeffrey H., Suzuki David T., Lewontin Richard C., Gelbart William M. An Introduction to Genetic Analysis. W. H. Freeman & Co.; New York, NY: 2000. [Google Scholar]
- Guiso Luigi, Sapienza Paola, Zingales Luigi. Cultural Biases in Economic Exchange? Quarterly Journal of Economics. 2009 Aug;124(3):1095–1131. [Google Scholar]
- Hall Robert E., Jones Charles I. Why Do Some Countries Produce So Much More Output Per Worker Than Others? Quarterly Journal of Economics. 1999 Feb;114(1):83–116. [Google Scholar]
- Jones Eric L. The European Miracle: Environments, Economies and Geopolitics in the History of Europe and Asia. Cambridge University Press; Cambridge, UK: 1981. [Google Scholar]
- La Porta Rafael, Lopez-de-Silanes Florencio, Shleifer Andrei, Vishny Robert W. The Quality of Government. Journal of Law, Economics, and Organization. 1999 Mar;15(1):222–279. [Google Scholar]
- Lagerlöf Nils-Petter. Long-Run Trends in Human Body Mass. Macroeconomic Dynamics. 2007 Jun;11(3):367–387. [Google Scholar]
- Landes David S. The Wealth and Poverty of Nations: Why Some Are So Rich and Some So Poor. W. W. Norton & Co.; New York, NY: 1998. [Google Scholar]
- Macaulay Vincent, Hill Catherine, Achilli Alessandro, Rengo Chiara, Clarke Douglas, Meehan William, et al. Single, Rapid Coastal Settlement of Asia Revealed by Analysis of Complete Mitochondrial Genomes. Science. 2005 May;308(5724):1034–1036. doi: 10.1126/science.1109792. [DOI] [PubMed] [Google Scholar]
- McEvedy Colin, Jones Richard. Atlas of World Population History. Penguin Books Ltd.; New York, NY: 1978. [Google Scholar]
- Michalopoulos Stelios. The Origins of Ethnolinguistic Diversity: Theory and Evidence. Working Paper, Department of Economics, Tufts University. 2008 [Google Scholar]
- Mokyr Joel. The Lever of Riches: Technological Creativity and Economic Progress. Oxford University Press; New York, NY: 1990. [Google Scholar]
- Murphy Kevin M., Topel Robert H. Estimation and Inference in Two-Step Econometric Models. Journal of Business and Economic Statistics. 1985 Oct;3(4):370–379. [Google Scholar]
- North Douglass C., Thomas Robert P. The Rise of the Western World: A New Economic History. Cambridge University Press; Cambridge, UK: 1973. [Google Scholar]
- Olsson Ola, Hibbs Douglas A., Jr. Biogeography and Long-Run Economic Development. European Economic Review. 2005 May;49(4):909–938. [Google Scholar]
- Pagan Adrian. Econometric Issues in the Analysis of Regressions with Generated Regressors. International Economic Review. 1984 Feb;25(1):221–247. [Google Scholar]
- Pomeranz Kenneth. The Great Divergence: Europe, China and the Making of the Modern World Economy. Princeton University Press; Princeton, NJ: 2000. [Google Scholar]
- Prugnolle Franck, Manica Andrea, Balloux François. Geography Predicts Neutral Genetic Diversity of Human Populations. Current Biology. 2005 Mar;15(5):R159–R160. doi: 10.1016/j.cub.2005.02.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Putterman Louis. Agriculture, Diffusion, and Development: Ripple Effects of the Neolithic Revolution. Economica. 2008 Nov;75(300):729–748. [Google Scholar]
- Putterman Louis, Weil David N. Post-1500 Population Flows and the Long Run Determinants of Economic Growth and Inequality. Quarterly Journal of Economics. 2010 Nov;125(4):1627–1682. doi: 10.1162/qjec.2010.125.4.1627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramachandran Sohini, Deshpande Omkar, Roseman Charles C., Rosenberg Noah A., Feldman Marcus W., Cavalli-Sforza L. Luca. Support from the Relationship of Genetic and Geographic Distance in Human Populations for a Serial Founder Effect Originating in Africa. Proceedings of the National Academy of Sciences. 2005 Nov;102(44):15942–15947. doi: 10.1073/pnas.0507611102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramankutty Navin, Foley Jonathan A., Norman John, McSweeney Kevin. The Global Distribution of Cultivable Lands: Current Patterns and Sensitivity to Possible Climate Change. Global Ecology and Biogeography. 2002 Sep;11(5):377–392. [Google Scholar]
- Rodrik Dani, Subramanian Arvind, Trebbi Francesco. Institutions Rule: The Primacy of Institutions Over Geography and Integration in Economic Development. Journal of Economic Growth. 2004 Jun;9(2):131–165. [Google Scholar]
- Spolaore Enrico, Wacziarg Romain. The Diffusion of Development. Quarterly Journal of Economics. 2009 May;124(2):469–529. [Google Scholar]
- Stringer Chris B., Andrews Peter. Genetic and Fossil Evidence for the Origin of Modern Humans. Science. 1988 Mar;239(4845):1263–1268. doi: 10.1126/science.3125610. [DOI] [PubMed] [Google Scholar]
- Tabellini Guido. Institutions and Culture. Journal of the European Economic Association. 2008 Apr-May;6(2-3):255–294. [Google Scholar]
- Wang Sijia, Lewis Cecil M., Jr., Jakobsson Mattias, Ramachandran Sohini, Ray Nicolas, Bedoya Gabriel, et al. Genetic Variation and Population Structure in Native Americans. PLoS Genetics. 2007 Nov;3(11):2049–2067. doi: 10.1371/journal.pgen.0030185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber Max. In: The Protestant Ethic and the Spirit of Capitalism. Parsons Talcott, Giddens Anthony., editors. Allen & Unwin; London, UK: 1930. 1905. [Google Scholar]
- Weisdorf Jacob L. From Foraging to Farming: Explaining the Neolithic Revolution. Journal of Economic Surveys. 2005 Sep;19(4):561–586. [Google Scholar]
- Wooldridge Jeffrey M. Econometric Analysis of Cross Section and Panel Data. 2 The MIT Press; Cambridge, MA: 2010. [Google Scholar]
Additional Works Cited
- Barro Robert J., Lee Jong-Wha. International Data on Educational Attainment: Updates and Implications. Oxford Economic Papers. 2001 Jul;53(3):541–563. [Google Scholar]
- Chandler Tertius. Four Thousand Years of Urban Growth: An Historical Census. The Edwin Mellen Press; Lewiston, NY: 1987. [Google Scholar]
- Darwin Charles. On the Origin of Species by Means of Natural Selection. John Murray; London, UK: 1859. [Google Scholar]
- Frankham Richard, Lees Kelly, Montgomery Margaret E., England Phillip R., Lowe Edwin H., Briscoe David A. Do Population Size Bottlenecks Reduce Evolutionary Potential? Animal Conservation. 1999 Nov;2(4):255–260. [Google Scholar]
- Griffin Ashleigh S., West Stuart A. Kin Discrimination and the Benefit of Helping in Cooperatively Breeding Vertebrates. Science. 2003 Oct;302(5645):634–636. doi: 10.1126/science.1089402. [DOI] [PubMed] [Google Scholar]
- Hamilton William D. The Genetical Evolution of Social Behaviour I and II. Journal of Theoretical Biology. 1964 Jul;7(1):1–52. doi: 10.1016/0022-5193(64)90038-4. [DOI] [PubMed] [Google Scholar]
- Hayes Theodore R. Dismounted Infantry Movement Rate Study; Technical Report, U.S. Army Research Institute of Environmental Medicine; 1996. [Google Scholar]
- Hölldobler Bert, Wilson Edward O. The Ants. The Belknap Press of Harvard University Press; Cambridge, MA: 1990. [Google Scholar]
- Houle David. Adaptive Distance and the Genetic Basis of Heterosis. Evolution. 1994 Aug;48(4):1410–1417. doi: 10.1111/j.1558-5646.1994.tb05326.x. [DOI] [PubMed] [Google Scholar]
- Jones Julia C., Myerscough Mary R., Graham Sonia, Oldroyd Benjamin P. Honey Bee Nest Thermoregulation: Diversity Promotes Stability. Science. 2004 Jul;305(5682):402–404. doi: 10.1126/science.1096340. [DOI] [PubMed] [Google Scholar]
- Mattila Heather R., Seeley Thomas D. Genetic Diversity in Honey Bee Colonies Enhances Productivity and Fitness. Science. 2007 Jul;317(5836):362–364. doi: 10.1126/science.1143046. [DOI] [PubMed] [Google Scholar]
- Maynard Smith John. Group Selection and Kin Selection. Nature. 1964 Mar;201(4924):1145–1147. [Google Scholar]
- Modelski George. World Cities: -3000 to 2000. FAROS 2000; Washington, DC: 2003. [Google Scholar]
- New Mark, Lister David, Hulme Mike, Makin Ian. A High-Resolution Data Set of Surface Climate Over Global Land Areas. Climate Research. 2002 May;21(1):1–25. [Google Scholar]
- Nordhaus William D. Geography and Macroeconomics: New Data and New Findings. Proceedings of the National Academy of Sciences. 2006 Mar;103(10):3510–3517. doi: 10.1073/pnas.0509842103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oldroyd Benjamin P., Fewell Jennifer H. Genetic Diversity Promotes Homeostasis in Insect Colonies. Trends in Ecology and Evolution. 2007 Aug;22(8):408–413. doi: 10.1016/j.tree.2007.06.001. [DOI] [PubMed] [Google Scholar]
- Özak Ömer. Mimeo, Brown University; 2010. The Voyage of Homo-Oeconomicus: Some Economic Measures of Distance. [Google Scholar]
- Peregrine Peter N. Atlas of Cultural Evolution. World Cultures: Journal of Comparative and Cross-Cultural Research. 2003 Fall;14(1):1–75. [Google Scholar]
- Robinson Gene E., Page Robert E., Jr. The Genetic Basis of Division of Labor in an Insect Society. In: Breed Michael D., Page Robert E., Jr., editors. The Genetics of Social Evolution. Westview Press; Boulder, CO: 1989. [Google Scholar]
- Russell Andrew F., Hatchwell Ben J. Experimental Evidence for Kin-Biased Helping in a Cooperatively Breeding Vertebrate. Proceedings of the Royal Society: Biological Sciences. 2001 Oct;268(1481):2169–2174. doi: 10.1098/rspb.2001.1790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sachs Jeffrey D., Warner Andrew. Economic Reform and the Process of Global Integration. Brookings Papers on Economic Activity. 1995 Spring;26(1):1–118. [Google Scholar]
- Schneider Jutta M., Bilde Trine. Benefits of Cooperation with Genetic Kin in a Subsocial Spider. Proceedings of the National Academy of Sciences. 2008 Aug;105(31):10843–10846. doi: 10.1073/pnas.0804126105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seeley Thomas D., Tarpy David R. Queen Promiscuity Lowers Disease within Honeybee Colonies. Proceedings of the Royal Society: Biological Sciences. 2007 Jan;274(1606):67–72. doi: 10.1098/rspb.2006.3702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp Stuart P., McGowan Andrew, Wood Matthew J., Hatchwell Ben J. Learned Kin Recognition Cues in a Social Bird. Nature. 2005 Apr;434(7037):1127–1130. doi: 10.1038/nature03522. [DOI] [PubMed] [Google Scholar]
- Tarpy David R. Genetic Diversity within Honeybee Colonies Prevents Severe Infections and Promotes Colony Growth. Proceedings of the Royal Society: Biological Sciences. 2003 Jan;270(1510):99–103. doi: 10.1098/rspb.2002.2199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson Edward O. On Human Nature. Harvard University Press; Cambridge, MA: 1978. [Google Scholar]