Abstract
This paper studies the urban land market in China in 2003—2007. In China, all urban land is owned by the state. Leasehold use rights for land for (re)development are sold by city governments and are a key source of city revenue. Leasehold sales are viewed as a major venue for corruption, prompting a number of reforms over the years. Reforms now require all leasehold rights be sold at public auction. There are two main types of auction: regular English auction and an unusual type which we call a “two stage auction”. The latter type of auction seems more subject to corruption, and to side deals between potential bidders and the auctioneer. Absent corruption, theory suggests that two stage auctions would most likely maximize sales revenue for properties which are likely to have relatively few bidders, or are “cold”, which would suggest negative selection on property unobservables into such auctions. However, if such auctions are more corruptible, that could involve positive selection as city officials divert hotter properties to a more corruptible auction form. The paper finds that, overall, sales prices are lower for two stage auctions, and there is strong evidence of positive selection. The price difference is explained primarily by the fact that two stage auctions typically have just one bidder, or no competition despite the vibrant land market in Chinese cities.
This paper studies the urban land market in China in 2003-2007. Urban land is owned “by the people” and its allocation done by the state.1 In most cities, the local land bureau is responsible for the vast majority of allocations of land, allocated through auction sales of leasehold rights.2 In China, land markets have been viewed as very corrupt, prompting a number of reforms over the years. We will provide some institutional context below but a couple of quotes illustrate that corruption is an on-going issue. In 2004, the China Daily wrote
“China’s Ministry of Lands and Resources announced new measures to crack down on corruption and inefficiency in the land sector. The new rules forbid officials to receive personal benefits from parties under their administration [italics added]. It is estimated that in 2003, the country faced 168,000 violations of its Land Law.”
Yet in June 2008, the Asian Times reported
“Chinese government efforts to clean up land sales, a major source of official corruption…, face a rethink.
…Illegal transfers, corruption in land deals,…are rampant in major cities, according to an investigation published by the National Audit Office (NAO) last week.
…Governments in the 11 cities [studied by the NAO], including Beijing and Shanghai, were also found to have misused 8.4 billion yuan from land-grant fees, Zhai Aicai, of the NAO, said in the report.
….Some cities have given a flexible interpretation to the rules and the auction system has often existed in name only, resulting in a lack of competition among developers and the winning developer being able to secure the land at below its true market value.”
Today, after considerable reform, leaseholds are, in principle, all sold at public auction. There are two main types of auction in most cities: regular English auction and an unusual type of auction which we call a “two stage auction.” The raw data suggest that leaseholds sold at two stage auctions sell at steep price discounts, relative to English auctions. Why are there such sales price differentials; and, related, how do city officials choose auction type for any particular property? Absent corruption, in terms of maximizing expected sales revenue, the paper argues that two stage auctions would be best for properties which are likely to have relatively few bidders, or are “cold.” Allocating cold properties to two stage auctions would suggest negative selection on property unobservables, and would be one possible explanation for the price differential between the auction types. However estimation suggests that selection on unobservables into two stage auctions is in fact positive. The paper argues that two stage auctions are more corruptible, which would explain positive selection, as city officials divert “hot” properties to the more corruptible auction form. Consistent with how we think the corruption process works, much of the price differential between auction types seems to be explained by the fact that two stage auctions are much more likely to have just one bidder, or no competition, despite their benefiting from positive selection on unobservables and despite the vibrant land market in Chinese cities.
The paper is organized as follows. We start with essential background information on Chinese land markets and especially the two auction formats. We then present a conceptual framework to model the key differences between the auction formats. In section 3, we discuss the data and patterns in the data. Section 4 estimates a reduced form model of price differences between the two auction types, and discusses instruments for auction type used to estimate selection into auction type. In Sections 5 and 6 we split the analysis of price differences into its two key components, accounting for joint selection into auction type and competition: whether a property is likely to sell competitively or not depending on auction type; and whether there are price differences across auction types, conditional on a property selling competitively.
1. Background
In the Maoist era and in the early reform years after 1978, land allocations were done by the state, with no market mechanisms involved. Starting in 1986, land administration changed with major reforms over the years (Ding and Knapp 2005, Valetta 2005). The first change was to charge new users for development rights and some incumbent users for use rights. After 1988, use rights for vacant land in the city were allocated through leaseholds, where, for a fixed sum, users obtained a long lease for a specified use (e.g., 70 years for residential land), subject to restrictions on intensity of development. In the 1990’s, many of these allocations were done by “negotiation” in a hidden process, where reportedly leaseholds were often sold for a tiny fraction of market value. This had two consequences.
First, leasehold sales are a major source of revenue for many cities, in essence potentially being a full Henry George tax, allocating all “surplus” land rents to the city. For example, in 2004 and 2005 for Chengdu, Suzhou and Chongqing, leasehold sales revenues ranged from 2.6% to 5% of local GDP. Cities have an expenditure budget and on-the-book revenue sources. On-the-book revenues account for about 70% of total expenditures. Leasehold sales revenues are mostly off-the-book revenues, which are used to effectively close the on-the-book deficit. Negotiated sales at well below market prices deprived cities of major revenues.
Second, negotiated sales were reportedly inherently corrupt, resulting in some indictments of corrupt officials and a variety of reforms, one of which in 2004 was quoted above. Another reform in 2002 banned the secondary market for “land development rights,” which had allowed large traditional holders (e.g., state owned enterprises) to, in effect, privately sell off their own land use rights (Zhu, 2004, 2005). Today the local land bureau is supposed to be in charge of almost all allocations of land for (re)development. Finally and most critically for this paper, a third recent reform was a 2002 law which banned negotiated sales by the land bureau, with the last date for any negotiated sales being August 31, 2004. For the last 4 years at least, all urban land leasehold sales are to be done through public auctions, with details of all transactions posted to the public on the internet.
How does the land market work? Local land use planning is done by an independent committee (albeit with 1-2 representatives from the land bureau on the committee). Given the overall land use plan for the city, at the beginning of each year, annual allocations are planned, based on existing urban land and converted rural land which should be ready for redevelopment during that year. Each plot of land is large with, in our sample, a median area of 22,300 square meters and a median sales price of USD $7 – 8 million. The committee decides the use and other constraints (like floor-area ratio) of each plot to be sold. Once the land becomes available during the year, the committee sets the reserve price, using a formula based on the appraised value submitted by, in principle, independent appraisal companies. Then the land is turned over to the land bureau which prepares it for sale (land for redevelopment in principle should be cleared), and chooses an auction type.
There are three types of auction used in China’s land market. About 97% of sales in major cities are accounted for by two auction types, with the third type generally appearing only in Beijing and Shanghai. We ignore this third type of auction and our econometric specifications exclude Beijing and Shanghai.3 The two main types are guapai auction which we call two stage auction and paimai which is an English auction. English auctions are standard ascending auctions, usually publicly announced 20 working days before the auction. At announcement, basic details (e.g., use restrictions, reserve price, location) are publicized; and potential bidders for a small fee can obtain more detailed information, as well as inspect the site. Participation requires a cash deposit, usually about 10% of the reserve price, which is a non-trivial requirement given the large sizes and sales prices of such properties. English auctions are quite public, often video-taped with the press present. Winning bidders in principle must develop the land themselves.
As with English auctions, two stage auctions are announced about 20 working days in advance; details of the plot are made public; and a deposit is required upon participation in the auction. A key difference is the auction format. With this type of auction, there are two stages. The first stage normally lasts 10 working days after the auction starts. In the second stage, at the end of the 10 working days, if more than one bidder is competing for the property, the auction ends on the spot with an English auction where only active bidders in the first stage are allowed to participate. If there is an ending English auction, it is generally less public than regular English auctions. In the first stage during the 10 working days between the starting date of the auction and the potential ending English auction, after obtaining qualification, people may submit ascending bids in person or on-line. Bids as they arrive are immediately posted on the trading board of the land bureau, as well as typically on the internet, although the identity of bidders is not posted. If, at the end of 10 working days, there is only one remaining bidder, that bidder is assigned the property at his bid price (but not less than the reserve price). Otherwise, with competition, the auction is converted to an English auction.
We will argue this first stage of a two stage auction allows for signaling of valuations for purposes of entry deterrence in non-corrupt contexts and for signaling in a potentially corrupt context, where the auction will be dominated by a corrupt bidder (in league with the land bureau).4 There are two fuzzy parts to the two stage auction format which we will argue are consistent with signaling, especially under corruption. While the auction is announced about 20 working days in advance, the exact date of the start of the first stage of the auction may not be announced at that time, but rather at an unspecified later date. Second, while bidders can apply during the announcement period before the first stage starts, it appears that approvals to participate can be delayed until after the first stage is under way.
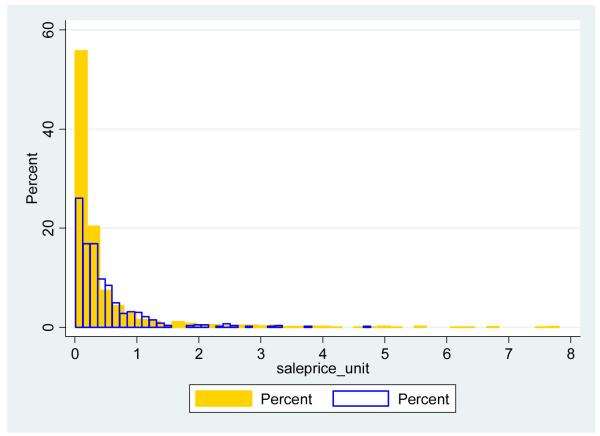
As detailed below, we use data on 2302 auction transactions from 2003 to 2007 in 15 cities, which use both auction types (as opposed to having only two stage auctions). In these cities English auctions account for 28% of auctions. In Figures 1 and 2 we present the indications from raw data that properties sell at a higher price under English as opposed to two stage auctions, and that English auctions are much more likely to be competitive. Figure 1 shows the distribution of unit sales price (price per sq. meter), by auction type for the sample; and Figure 2 shows the distribution of the ratio of sales to reserve prices. The raw data suggest that the distribution of unit sales prices for English auctions is shifted to the right of that for two stage auctions. Of course, the distribution of raw unit sales prices does not condition on property and market characteristics. While differentials in property characteristics could explain price differentials across auction types, below we show that will turn out not to be the case.
Figure 1.
Distribution of unit sales prices by auction type Orange (solid) is two stage auction; white (blank) is English auction
Figure 2.
Distribution of bid-reserve price ratio by auction type Orange (solid) is two stage auction; white (blank) is English auction
In Figure 2, two stage auctions tend to be massed much more around 1.0 for “spread”, which is the ratio of sales to reserve prices. Both conceptually and in a particular sub-sample analyzed below where we know the number of bidders, a ratio of 1 implies that there is just one bidder and thus no competition. Ratios larger than 1 in the sub-sample imply multiple bidders and what we term a competitive auction. Of course, whether there is competition or not is influenced by reserve price; so, if there are differentials in setting reserve prices across auction types, that might explain the differential pattern by auction type in Figure 2. However, reserve prices are set by the outside committee before the choice of auction type by the land bureau; and, as we will see below in Table 4, reserve prices do not seem to affect the choice of auction type.5 Assuming that reserve prices are some fraction of an assessor’s estimate of true market value, a lack of competition is very surprising on its own. In these cities, auctions occur in a setting of rapid urban growth, with per capita urban incomes growing at about 10% a year and local population at 3-4 % a year. Given national restrictions on conversion of rural to urban land at the city fringes, this suggests there should be a high demand for land for new development.
Table 4.
Two stage auction, or not1
| Probit: marginal effects |
Probit: marginal effects |
|
|---|---|---|
| Ln (reserve price) | −.040 (.031) |
−.041 (.030) |
| Dummy: Residential use | −.255** (.058) |
−.250** (.055) |
| Dummy: Mixed use | −.245** (.064) |
−.241** (.062) |
| Ln (dist. To CBD) | −.044 (.038) |
−.044 (.037) |
| Ln (area) | −.0015 (.013) |
−.0037 (.013) |
| Dummy: railway within 2.5 kms. | .055* (.028) |
.057* (.030) |
| Dummy: highway within 2.5 kms. | −.066** (.021) |
−.069** (.022) |
| Lagged change in fiscal strain | −.544** (.236) |
|
|
Xinhua corruption report, 2 month
lead from listing |
−.016 (.016) |
|
|
Xinhua corruption report, 1 month
lead |
.021* (.012) |
|
|
Party secretary turnover, 1 month
lead |
−.300** (.127) |
−.314** (.131) |
|
Party secretary turnover, 1 month
lag |
.157** (.022) |
.162** (.018) |
|
Google report, Land corruption case,
3 month lead |
−.212* (.136) |
−.207* (.129) |
|
Google report, Land corruption case,
2 month lead |
.183* (.040) |
.186** (.037) |
| Season, year, city dummies | Yes | Yes |
| N | 2302 | 2302 |
| Pseudo Rsq | .37 | .36 |
|
Implied F-Stat: adding bottom panel
instruments |
8.1 | 6.6 |
significant at 10% level
significant at 5% or higher level.
All standard errors are robust clustered by city-code.
In the next section we outline a simple conceptual framework, which discusses our empirical hypotheses and the framework behind them. In the following sections, we turn to the econometric formulation looking at auction choices, sales prices, and the degree of competition. We document and explore the price differences between English and two stage auctions. As already noted a key issue concerns selection of properties into auction type and whether properties with better unobservables are more (positive selection) or less (negative selection) likely to sold by two stage auctions.
2. Conceptual framework
We have not fully solved a theoretical model which covers all key aspects, for reasons that will become apparent. Rather we discuss the elements that are relevant and try to draw reasonable conjectures. We start with a discussion of how the two auction formats might be modeled in a world without corruption and how the choice of format affects outcomes. Then we ask how corruption possibilities might have differential implications for the two formats. Finally we discuss the land bureau’s choice of auction format.
Assume for a leasehold auction there are N potential bidders, of which some endogenous number n pay an entry fee, C, and become active bidders.6 A key issue is how the choice of auction format may influence n. We assume auctions are independent private valuation. Specifically, a potential bidder i ’s valuation is Vi = v0 + vi, where v0 is the (expected) common value that is the same for every bidder (based on property characteristics and local market conditions) and vi is the private value component only known to bidder i. vi ’s are i.i.d. 7
We make the standard assumption that all bidders are risk neutral and maximize their expected payoff. Let Vi ∝ F(V) on be the distribution function of the bidder i’s valuation, and let f(V) be the associated density function. A bidder’s payoff when winning the auction with a bid Bi is Ui = Vi – Bi – C.
2.1 English auction
Since an English auction is outcome-equivalent to a second price Vickery auction, our setting is equivalent to that of Tan and Yilankaya (2006), who analyze a simultaneous move entry game in a second price auction with independent price valuations and participation costs. In a symmetric equilibrium of such a model a bidder will decide to enter the auction if and only if his valuation is above a certain value , where r is the reserve price and C is the entry cost. For a bidder with valuation exactly equal to , the only way he can get positive rent from entering the auction is if he is the lone bidder in the auction, in which case he gets a rent of . This case happens with probability , such that all other potential bidders have valuations below . Therefore, the valuation threshold for entry must satisfy
| (1) |
From equation (1), we can solve for the valuation threshold for entry in equilibrium that depends on . Clearly, is increasing in r, C, N.
The probability of selling at the reserve price is . Other possible outcomes in the auction are (1) that there are no bidders, which occurs with probability ; and (2) that there are two or more bidders, so the auction is competitive with the winner being the highest valuation participant, j, who pays the second highest valuation and makes an ex post rent . One can derive expected rents of entrants and expected revenue from the auction8.
2.2 Two stage auction
The two stage auction adds a first stage in which bidders in arbitrary pre-determined sequence (say, the time at which they learn of the auction) decide whether to enter the auction with a bid. Absent of entry fee (so every potential bidder will enter), there is no benefit of bidding early (e.g., see the last minute bidding literature such as Ockenfels and Roth, 2002). With entry fee, the advantage of bidding early is that a bidder can potentially signal that she drew a relatively high private valuation; we will suggest that the bid will signal her actual valuation. The point of the signal is to discourage future potential entrants who might have drawn somewhat higher valuations from entering the auction. For future bidders with somewhat higher valuations, they now know that, if they enter, the prior signaler is prepared to bid up to her valuation. That inferred valuation then defines the minimum price they have to pay. So their expected rent is based on the likelihood that they will win (no future entrants will have an even higher bid) and on the ex post rent (their valuation minus the current signaler’s valuation). Solving the general case with endogenous first stage entry sequence is daunting—whether an early entrant signals with what bid function, whether later entrants with higher valuations enter or not, and the complicated interactions between early and later signalers.
Example
We illustrate the setting with a simple example. Suppose only one randomly selected person has the option to bid early and we consider a possible separating signaling equilibrium. Suppose bidder 1 chooses to enter in stage 1 by using a strictly increasing bidding schedule B(V1) when her valuation is . For , bidder 1 will choose to not enter the auction.
Suppose her valuation is exactly . Based on the Riley argument in the signaling literature, bidder 1 should use the lowest possible signal, the reserve price r. Moreover, in order for bidder 1 not to choose this signal when her valuation is just below , her expected payoff from entering and signaling must be zero. Once bidder 1 reveals that her valuation is , other potential bidders will enter only if their valuation is above , the solution to equation (1) with replacing r and N – 2 replacing N –1. Other potential bidders understand that to win they must outbid bidder 1; but since bidder 1 has committed to enter the auction, she is willing to bid all the way to V1. Thus, for the other potential bidders, the effective reserve price increases to V1. Bidder 1 can win the auction only if no other potential bidders enter the auction, which happens with probability of . Therefore, we must have
| (2) |
Note that since , comparing (2) and (1) reveals that is significantly smaller than .
In the bidding game if bidder 1 does not enter in the first stage, the other N –1 potential bidders play the same game as in an English auction: they first decide on whether to enter in the second stage simultaneously, and then the active bidders bid in the English auction. Exactly as above, we can solve for the valuation threshold for entry, denoted by . Note that is increasing in N, thus , which is the equilibrium entry threshold in the case of an English auction with N potential bidders.
In the Appendix, we show that if bidder 1 has valuation , he has a bidding function that is strictly increasing in V1 and truthfully reveals his valuation. Such a bidding function satisfies the single crossing property, so it isn’t beneficial for lower valuation bidders to pretend to be higher types.
Comparison: English versus two stage auction
Since and , the probability of no sale is lower in a two stage auction than in an English auction. Since bidder 1 can discourage entry by other potential bidders with his early bid, he is more likely to enter in a two stage auction than in an English auction. And when bidder 1 does not enter, other bidders still are more likely to enter a two stage auction than an English auction. The intuition is that the simultaneous entry game in an English auction suffers from coordination failure: one bidder’s entry creates a negative externality for others. Thus, bidders may not enter the auction even when their valuation is significantly higher than the reserve price plus entry cost, for fear of being outbid by others. In contrast, bidder 1 in the sequential entry game of a two stage auction does not suffer from negative externalities from other bidders, thus having a stronger incentive to enter the auction. The flip side of this is that the probability of competitive bidding (two or more active bidders) is lower in a two stage auction than in an English auction, because the early entrant may deter later entrants.
In terms of expected revenue, the comparison between two stage and English auctions is ambiguous in general. The intuition is that while a two stage auction has a higher probability of sale, the likelihood of competitive bidding is smaller than in an English auction. Thus, depending on parameter values, the expected revenue of the two stage auction can be greater or smaller than that of an English auction.
In the Appendix, we show in a numerical example that the expected revenue of a two stage auction is greater than that of an English auction when is low, and vice versa. We conjecture that when land is “cold,” in the sense that the valuation is likely to be low ( e.g., low ) or the potential demand ( N ) is small, a sale and some revenue is more likely under a two stage auction. We note N is unobserved in our data (as is ). With cold properties which in an English auction might generate no active bidders, a two stage auction may generally be a better choice of auction for a revenue-maximizing land bureau, since the threshold valuations for entry are lower. If land is “hot” so an English auction is likely to attract many bidders, English auctions will tend to generate more revenue since two stage auctions may lead to entry deterrence. Thus we might expect a revenue-maximizing land bureau to steer hot properties towards English auctions. Thus overall, there would be negative selection on unobservables into two stage auctions.
2.3 Effect of corruption
Suppose corruption arises in the following way. Under a corrupt sale, a government official reaches an implicit agreement with a particular developer, say, developer 1, so that if he wins the land auction, she will provide special help (which could include weaker enforcement of development constraints or greater government investment in relevant infrastructure), in exchange for a bribery payment. Let Q be the value of the government official’s help to developer 1, and let q ≤ Q be the bribery payment developer 1 makes to the government official, if he wins the auction. Define κ ≡ Q – q as the net benefit to developer 1 from having an under-the-table deal with the government official.
Assume the corrupt government official’s payoff function is given by ER + λq, where ER is the expected revenue from the land auction (that goes to the city coffers) and λ measures how corrupt the government official is. When λ = 0, the government official is non-corrupt, as in the situation we discussed above. When λ becomes larger, the government official cares more about her own bribery income and less about the city’s fiscal revenue. Assume the government official is corrupt with probability of p. This depends on the likelihood the government official in charge of the land is intrinsically corrupt and the likelihood that she has a “partner” developer who is interested in the land and they trust each other. If the government official is corrupt, only she and her partner developer know about their implicit agreement; no other potential bidders know about it. The only thing the other potential bidders know is that with probability p the government official and a developer have an under-the-table deal. What might be the impact of such corruption under the two auction formats?
English auction
Under an English auction, all potential bidders make entry decisions simultaneously in the entry stage and then the active bidders make bidding decisions in the auction stage. Let bidder 1 be the potential partner developer with the government official, so with probability of p her total valuation is V1 + κ, and with probability of 1 – p her valuation is V1. Let be the valuation threshold for entry for bidder 1, and let be the valuation threshold for entry for all other bidders.
With the possibility that bidder 1 is corrupt, bidders make entry decisions in an asymmetric bidding game. Similar to what we had before, must satisfy the following equation:
| (3) |
where the bracketed expression on the left hand side represents a non-corrupt bidder’s expected rent (conditional on there being no other active non-corrupt bidder) in each of three cases: (1) he outbids the corrupt bidder 1; (2) the corrupt bidder 1 does not enter; and (3) bidder 1 is not corrupt and does not enter. Note that the above equation assumes that if bidder 1 is not corrupt, he acts like any other bidder by using the same entry strategy.9 The corrupt bidder 1’s valuation threshold for entry satisfies
| (4) |
where wq is bidder 1’s expected rent when his valuation is and there are q other bidders whose valuations are above but less than .
It can be shown that in equilibrium, , where is the entry threshold we solved in the previous section.10 The reason is as follows. Thanks to the favor from the government official, the corrupt developer 1 can afford bidding more aggressively and thus has a better chance of winning the auction. So she is more likely to enter. Facing the possibility that bidder 1 may be favored, the other potential bidders are less likely to win and thus are less likely to enter.
Two stage auction
In the two stage auction, if the government official is corrupt and has reached an implicit agreement with her partner developer, bidder 1, he should know about the auction beforehand and can act right after it is started. Since both would like to let all other potential bidders know that this land is “claimed,” a simple and natural way to send that signal is for bidder 1 to obtain qualification quickly (potentially with the government official’s help) and make a bid right after the auction is started, before other potential bidders are granted qualification to bid, and perhaps even before they know that the auction has actually started. Since bidder 1 is only signaling that he has the agreement with the government official, bidder 1 only needs to signal that, by bidding just the reserve price (to increase the rent from winning the auction). When κ is relatively large, such signaling by bidder 1, if believed by other bidders, will seriously deter entry by other bidders since they see little hope of outbidding bidder 1.
If a bid at the reserve price submitted right after the auction start date is perceived as a signal of having an insider agreement, a bidder without such an agreement may be tempted to mimic such behavior to scare away other bidders. However, this snapping strategy is not likely to work, even if the snapper knows the time when the auction starts and is granted qualification in advance. If the snapper manages to make a bid at the reserve price before the true corrupt developer, the latter is likely to make a higher bid in order to reclaim the land as long as p is close to one and κ is relatively large. In such a case, the snapper will lose the auction and waste his entry cost. In the Appendix, we illustrate this argument in a simple example.11
We consider the following equilibrium. Let be the minimum threshold in which bidder 1 will send a signal by bidding the reserve price. If seeing that bidder 1 bids at the reserve price right after the auction is announced, all the other potential bidders understand that bidder 1’s valuation is V1 + κ, where . Then they decide simultaneously whether to enter. Let be the valuation threshold for all other potential bidders. Then it must satisfy12
| (5) |
And must satisfy an equation similar to equation (4) with replacing and replacing . Below we argue that this entry threshold for other bidders in a two stage auction, , is greater than that under an English auction.
When no one bids at the reserve price right after the auction is announced, then bidders understand that the government official is not corrupt. In this case our previous analysis of the two stage auction under no corruption is valid.
Comparison of English and two stage auctions under corruption
It can be verified that upon seeing a first day bid at the reserve price, all other potential bidders’ valuation threshold for entry in a two stage auction will be significantly greater than the threshold in the case of an English auction, .13 This occurs because in the case of an English auction, the other potential bidders do not know whether bidder 1 is corrupt. They only know that he is corrupt with probability p. However, in the two stage auction, the other potential bidders know for sure whether bidder 1 is corrupt or not. When he is corrupt, the other potential bidders have a much smaller chance of winning the auction since bidder 1 has substantial advantages from having a higher expected valuation from government help and having made the first bid. This greatly reduces the incentives to enter for other potential bidders.
It can also be shown that the corrupt bidder is more likely to enter a two stage auction than an English auction, that is, is smaller than . Because other potential bidders are less likely to enter the two stage auction, the corrupt bidder sees less risk of losing the auction and thus is more motivated to enter a two stage auction (by posting a bid at the reserve price right after the auction starts) than an English auction.
That the corrupt bidder is more likely but other potential bidders are less likely to enter a two stage auction implies that the corrupt bidder has a much better chance to win the land in a two stage auction than in an English auction. Since the corrupt government official can get the bribery income only if the corrupt developer wins, she would favor a two stage auction if she cares about her corruption income sufficiently.14 Therefore, if the government official is more corrupt, then she is more likely to choose a two stage auction. If she cares more about the fiscal revenue of the city, she is more likely to choose an English auction. Such “caring” of course will not in general be exogenous. One could consider the probability of corruption being detected and punished by government auditing and a penalty function, which may also depend on the tolerance of the local government for lost revenue. In such a context, English auctions are much more visible in the media and may be subject to greater scrutiny.
With corruption, the role of hot versus cold properties also changes. Note that the probability of not having a non-corrupt bidder enter is in an English auction and in a two stage auction. Since , the greater the number of potential bidders, N, the larger the difference in the likelihood that the corrupt bidder wins between the two auctions. Thus, motivated by helping her partner bidder win the auction, a corrupt government official prefers two stage auctions for hotter properties. Moreover, if the bribes which corrupt developers are willing to pay are related to their profits, corrupt government officials have additional incentives to assign hot properties to two stage auctions. Therefore, our analysis suggests positive selection on unobservables into two stage auctions under corruption.
Other auction choice considerations
In an auction setting like ours, collusion among bidders (a group of developer forming a bidding ring) is quite plausible. In the existing literature, scholars have studied collusion in other auction settings (e.g., McAfee and McMillian, 1992, Bajari and Ye, 2003, and Athey, Levin and Seira, 2008). While in China, a group of developers may be attempted to rig an auction, there are several reasons we don’t focus on it in this setting. First, the government’s focus on corruption in land markets has not been on collusive bidding, but rather on corruption among officials. In China it may be less appealing (more dangerous) for individuals to collude against the state per se, as opposed to involving local officials. Also in our context, there seems to be no reason why collusion among bidders would be more successful in a two stage auction than in an English auction, so collusion among bidders would not explain the substantial difference in the likelihood of non-competitive bidding between the two stage and English auctions observed in our data. Thus, it is unclear how the concern about collusion among bidders would affect the land bureau’s choice of auction format. As we show later, our instrumental variables that are related to corruption and city budget needs are strongly correlated with the choice of auction format and there is positive selection on unobservables into two stage auctions. It seems land bureau corruption is at the heart of any explanation of the positive selection. For these reasons we focus on corruption in this paper, and ignore the issue of bidder collusion.
Another factor that may affect the comparison between English and two stage auctions is the riskiness of the land to be auctioned. For different properties, the variance of the private value components across bidders could differ. For a given reserve price, absent corruption, the land bureau might want to assign high variance properties to two stage auctions. The reason is that, when there is a fat left tail of the distribution of Vi, the solution to equation (1) may be quite large, resulting in a low chance of a sale in the English auction. Thus revenue-maximizing officials would choose two stage auctions for risky lands. This would suggest that two stage auctions are associated with a higher probability of no sales; we observe the opposite in the data. Nevertheless, below we control for a number of observables which could be related to variance of valuations such as property type, size, and distance from the city center.
One additional issue we choose to ignore is the sequence of land sales in a city. Our decision is based on the following considerations. First, while it is certainly true that developers can always bid on the next available land, land auctions differ from on-line auctions of staple goods in that land available for development in a particular city within a particular period of time is limited. Considering the heterogeneity of land and the heterogeneity of developers, a developer may not easily find many perfectly substitutable pieces of land and thus has to treat each auction seriously. Second, it does not seem to us that the issue of the sequence of land sales would fundamentally change our arguments about auction choices with or without corruption. Thirdly, a formal modeling of the sequence of land auctions is clearly not tractable in our current framework.
What we see in the data concerning potential signaling
In our data, in general, we know only sales and reserve prices and nothing about the bidding process itself—sequence of bids and number of bidders. However for Beijing we have a sample of 195 two stage auctions, where we know the number of bidders as well as the date when the first bid is submitted. From that data we learn several things. First, and most critically from Table 1, bidders do not signal valuations. In all auctions with just one bidder, almost all bids are within 0.5% of reserve price. This is consistent with our corruption story, but inconsistent with the separating equilibrium of the two stage auction without corruption. Once we have 2 or more bidders then a spread develops. This is the basis for later defining whether an auction is competitive (has more than one bidder) or not, based on spread. Note auctions can be highly contested: in 26 of the cases with 3 or more bidders, there are reported to be over 65 bids in each of the auctions.
Table 1.
Beijing two stage auctions
| Number of bidders | Number of cases: Sales- reserve price ratio ≤ 1.005 |
Number of cases: Sales- reserve price ratio > 1.005 |
|---|---|---|
| 1 | 104 | 1 |
| 2 | 3 | 6 |
| 3 or more | 0 | 75 |
Columns 1 and 2 of Table 2 show that, conditional on property characteristics, having a first day bidder reduces the number of bidders, despite the positive bias (having a first day bid, given 10 days to bid, should mechanically raise the expected number of bidders). Similarly, in columns 3 and 4, having a first day bidder makes it more likely that the auction will be non-competitive. Again this is consistent with the corruption story. But the effects in columns 3 and 4 are weak. It turns out that in Beijing sometimes properties are sold which, contrary to national policy on auctions, have not been cleared for redevelopment; and, in Beijing, we have good data on clearance or not. Not being cleared reduces the number of bidders and increases the chances of non-competition. Controlling for this variable with a sample size of 155, sharpens the first day bidder variable in both formulations, with t-statistics in columns 3 and 4 on the variable rising to 1.99 and 1.83 respectively.
Table 2.
Beijing count and spread estimations
| Poisson: Number of bidders (robust s.e.’s) |
Probit: Sales/reserve price ratio ≤ 1.005 (marg. effects) |
|||
|---|---|---|---|---|
|
Bidder on first day, or not
(167 of 195) |
−.731** (.344) |
−.638* (.338) |
.142 (.103) |
.144 (.111) |
| Residential use | 1.19** (.356) |
−.284** (.097) |
||
| Mixed use | .827* (.421) |
−.216 (.095) |
||
| Ln (area) | .205** (.092) |
.0039 (.028) |
||
| Ln (distance to CBD) | −.631** (.252) |
.171** (.070) |
||
| Ln (reserve price) | −.247 (.173) |
.0016 (.048) |
||
| N | 195 | 181 | 189 | 181 |
| Pseudo Rsq | .030 | .200 | .007 | .101 |
significant at 10% level
significant at 5% level or higher
3. The data and basic patterns
For our econometric analysis, we have data for 15 cities from 2003-2007,15 from the Land Bureau of China (or its branches at the city-level).16 For each auction, the land bureau provides detailed information and posts it on its official website www.landlist.cn. Information includes: the address, the area (in square meters), the use restriction (business, residential, mixed), the type of auction, the reserve price, the sales price if the sale is complete, the post date which is the first date bids are accepted, the sale date, and the buyer’s identity. Sometimes additional information is given, such as the maximum floor-to-area ratio, the building-density, the green coverage rate, and whether the property is cleared or not. For some items including the last, explicit information is only provided in a limited number of cases.
We also obtained the geo-economic characteristics of each piece of land for sale through bendi.google.com. Specifically, we locate each piece of land in the digital map of bendi.google.com using its street address. We then measure the line distance between the land and the CBD of the city where it is in. For the Chinese cities in the sample, we have no difficulty in identifying one central business district. We also create some dummy variables to indicate, whether within a 2.5 km. radius of the center of the property for sale, there is railway (including light rail and subway) or highway.
Our base data consists of 4016 listings, where a listing is a property put up for auction whether the auction is completed and results in a sale, or not. Our 4016 listings exclude industrial use land (about 7% of total listings). As in the USA, industrial land use has a low and highly variable unit price; regressions using USA data which examine the determinants of sales prices for industrial land have low explanatory power (DiPasquale and Wheaton, 1996). More critically in China, such properties are often sufficiently far from the city center stretching into peri-urban areas, that we couldn’t get location characteristics from bendi.google.com.
Of the 4016 listings, 607 remain unsold. Another 1107, while sold, do not have information on either reserve price or sales price, or both. We focus on the remaining 2302 which are completed auctions with full price information. In the Appendix we explore the effect of focusing just on this sample. Here we note some key findings from the Appendix. First, for properties that sell, those with full versus deficient price information have similar unit and reserve sales prices where information does exist on one or the other and only differ in observables in two minor ways: properties without full price information tend to be older listings and nearer the city center. The differences in samples for sales with full versus limited price information seem to be “innocent.” However, unsold properties compared to our working sample of 2302 show distinct differences. For example, unsold properties are more likely to have been offered at English auction potentially evidence of positive selection into two stage auctions; and, not surprisingly, to have been listed more recently. In terms of sales dates, we suspect unsold properties (i.e., those which didn’t sell 10 days after posting) are eventually removed from public listing on the internet, perhaps rebundled, and then relisted, which makes statistical analysis of sale versus no sale difficult, since we don’t know which properties are being offered for the first versus second time.
Differences across auction types
Table 3 is summary of basic statistics about the data, for completed transactions by auction type. In Part a, compared to English auctions, two stage auctions have significantly lower mean unit sales prices and are significantly less likely to sell competitively (have a spread greater than 1.005). However they have no significant difference in unit sales price, conditional on a competitive sale. This suggests that the main effect of two stage auctions is to affect price by deterring entry and competition.
Table 3.
Data on auctions
| a) Two stage vs. English auctions | ||||
|---|---|---|---|---|
| Two stage auction: Mean (N=1661) |
English auction: mean (N=641) |
Difference | t-stat. | |
|
Unit sales price (in
10,000 yuan) |
.47 | 1.0 | −.53 | −2.64 |
|
Proportion non-
competitive |
.574 | .178 | .396 | −20.4 |
|
Unit price if
competitive (in 10, 000 yuan) |
.73 (n =708) | 1.13 (n = 527) | −.40 | −1.62 |
| Area (in sq. meter) | 55289.96 | 53751.1 | 1538.86 | .30 |
|
Distance to CBD (in
km) |
19.9 | 17.8 | 2.1 | 1.86 |
| Commercial use | .38 | .14 | .24 | 13.3 |
| b) Commercial vs. residential and mixed use properties | ||||
|---|---|---|---|---|
| Commercial: mean (N=716) |
Residential and mixed use: Mean (N= 1586) |
Difference | t-stat. | |
|
Unit sales price (in
10, 000 yuan) |
.617 | .615 | .002 | .026 |
|
Unit price if
competitive (in 10, 000 yuan) |
.98 (n=289) | .88 (n=946) | .09 | .55 |
| Area (in sq. meter) | 31354.72 | 65473.59 | −34118.87 | −8.52 |
|
Distance to CBD (in
km) |
18.47 | 19.67 | −1.20 | −1.03 |
|
Proportion two stage
auction |
.88 | .65 | .23 | 13.17 |
|
Proportion non-
competitive |
.596 | .403 | .193 | 8.72 |
We note two stage auctions have a greater proportion of commercial properties. However, we decided that whether a property was designated as commercial was not an element on which we wanted to focus. As Part b of the table reveals, commercial relative to residential and mixed use (which are fairly similar) properties are more likely to be sold through two stage auction and without competition (60% sold non-competitively versus 40% for residential and mixed use). However unit sales prices across uses are similar, both for those that are sold competitively and for those that are not.
4. Baseline effect of auction type on sales prices
In this section we explore the overall effect of auction type on unit sales prices. As we will see in Sections 5 and 6, we are in essence estimating a reduced form price equation. Based on the conceptual section, consider the specification
| (6) |
This specification follows the notion that there is a common value component to any bidders’ valuation. Given this common value, ex ante sales price then depends on the number of potential bidders and potentially the auction format, with the ex post sales price dependent on the actual drawings of private valuations (which encapsulates). In the data, the potential number of bidders and certain determinants of the potential number of bidders (e.g. certain property characteristics) are unobserved. Choice of auction format may be related to these unobservables in one of two ways, which we hope to distinguish. In the absence of corruption, the land bureau might choose to sell “cold” properties by two stage auction, since, relative to an English auction, they may be more likely to draw in at least one bidder. This implies negative selection on properties sold by two stage auction. However two stage auctions may be more corruptible, and part of that may involve positive selection— setting aside the most “delectable morsels” for corrupt participants.
In equation (6), we assume reserve price is proportional to common value, with an added error component that is unrelated to any particulars of the sale (“evaluator error” in ). As noted above, reserve price is set by an outside committee, using a formula based upon the valuation of the land parcel carried out by an independent private land appraiser. In that sense reserve price is an exogenous valuation of property based on observed and unobserved (to us) aspects of the property and general local market conditions. For the same common values to two different properties, the number of potential bidders will vary with the city in question (number of active land developers, controlled below by city and time fixed effects) and aspects of the property. For example, the potential number of bidders may differ for certain types of uses or properties near or further from the city center.
We implement equation (6) with
| (7) |
for property i in city j which is sold at time t. ’s are observed property characteristics such as use restriction, area, and distance to the city center. Auction type, dijt, is whether the land bureau chooses a two stage auction (=1) or not (=0), so that D is the effect of auction type on sales price, which we would like to identify. The dummy terms uj and δt capture city and yearn fixed effects. The arguments in εijt are unobserved time-varying city conditions or property characteristics, which controlling for common value (reserve price), may increase the number of potential bidders. These conditions may affect auction choice. The land bureau’s selection of properties into two stage auctions may involve either negative or positive selection, as noted above.
4.1 Selection problem and instruments
To deal with the auction selection issue, for our baseline results, we estimate a Heckman (1978) endogenous dummy variable model, with a selection control function based on the inverse Mill’s ratio of a probit on auction type,17 as well as the MLE version of that. Also we do IV estimation. We experimented with adding interactions of auction type with covariates to the IV specification, allowing auction effects to vary with covariates but the effects are not instructive, especially given we already have a reduced form specification.18 Instrumental, or control function variables are ones which we think affect selection of auction type by the land bureau, but not sales values conditional on our covariates.
We have several instruments which appear to influence choice of auction type. We generally use two sets of two instruments each. Most arise from a pattern in the data which is illustrated for the first set, as follows. In the month before a new party secretary takes office in a city, the land bureau switches more to using English auctions and then a month later it switches back, in fact switching away from English auctions (in effect, catching-up to its usual mix). We view this as the land bureau being cautious: “cleaning-up” temporarily in the face of uncertainty about the new party secretary’s views on land market corruption; and then returning to business as usual. The same phenomenon occurs with the second set, land corruption cases, although the timing is different.
We have the number of cases per month that relate to real estate corruption in any city j, reported on Google China. Such cases could involve the removal of a major local government official, the indictment of officials, the execution of officials, or a criminal investigation on land transactions. During this month when a case occurs, officials are more careful and schedule more English auctions. A month later they again revert and catch-up to business as usual. A few months after the case, a sanitized report on the case (the average is about .03 reports per city per month) is announced on state run news agencies and picked up by Google China. The announcements on Google China appear to occur 3 months after the case, in the sense that 3 months earlier English auctions jump up, followed in the next month by a drop down.
We have two other types of instruments as well and use them in some robustness experiments. We have a source on corruption investigations more generally, which is the number of news reports per month by the main news agency in China, Xinhua, on corruption in any city j. Xinhua is a state run news agency. Our hypothesized scenario is the city government, the local party, or the National Audit Office conducts an enquiry into local corruption, of which the local land bureau is fully aware. Again, during this month, officials are more careful and schedule more English auctions. A month later they again revert and catch-up to business as usual. A couple of months after the investigation, Xinhua reports on the investigation (the average is about .9 reports per city per month). Thus English auctions increase 2 months before the month of the news report and decrease the next month. This timing of the pattern of one month up followed by one month down is found by experimentation in the data, but it is a clear pattern in all three situations—new party secretary, real estate corruption cases, and corruption investigations.
Finally, we have a measure of the pressure on the land bureau to raise more money through land sales, coming from the city government. We measure the gap between budgetary expenditures of the city E and on-the books revenue R. An instrument would be the lagged growth in the relative deficit: (Ejt–1 – Rjt–1) / Rjt–1 – (Ejt–2 – Rjt–2) / Rjt–2. With city fixed effects we would effectively be instrumenting with the lagged rate of change in this gap and are treating this growth rate as somewhat idiosyncratic and not connected to city demand conditions that would affect the current and future housing market (given city and year fixed effects). Higher lagged deficit growth rates induce more English auctions.
In summary, in the tables in the paper, we use just the first two sets of instruments: party secretary change and real estate corruptions cases. Thus our vector of instruments Z consists of dummy variables for any listing which occurs when a new party secretary takes office (one month lead and one month lag) and dummy variables for any listing which occurs when Google reports a land use corruption case (three months lead and two months lead). These are the strongest instruments; and the Google reporting of corruption is directly connected to real estate corruption. Growth in the relative city fiscal on-the-books deficit in the year before the listing is also a strong instrument at times but is potentially objectionable with only annual variation over 2003-2007 and the potential to be related to real estate prices. We will report (the almost identical) results for key situations, using all 7 instruments. And for few experiments using sub-samples in the paper which are reported just in the text, we use all 7 instruments in order to have sufficient variations within sub-sample cities and time periods for instruments to have some strength. Next we examine the strength of the instruments and later we report results on tests of their validity.
Choice of auction type
Before turning to the sales price estimation we examine the choice of auction type, both to see the role of the instruments and to examine the choice itself. Results are in Table 4, for the situation where we include 4 instruments and where we include all 7. The effect of reserve price on auction type is essentially zero, which is consistent with the idea that reserve price setting is independent of auction choice. Choice of auction type is significantly influenced by land use, where the base case, commercial land, is much more likely to be sold in two stage auction, consistent with Table 3. Commercial land consists of smaller plots, which may be of more interest to specialized neighborhood developers within the city and may have fewer potential bidders. Also, more likely to be sold at two stage auction is land near rails (probably land urbanized in the Maoist era) but not near highways (land urbanized more recently).
Of particular interest is how instruments influence auction choice. In column 1, the variables for the change in party secretary and for announcements of land corruption cases have the hypothesized patterns and are generally significant. In column 2 the other three instruments have the hypothesized effects as well. For four instruments the F-statistic based on the change in the value of the LLF from adding instruments to the probit is 8.1. This is not as high as one would like, but it is reasonable in a context where we have city fixed effects. Going to seven instruments lowers the 1st stage F-statistic, one reason for settling on four instruments.
4.2 Sales Price Results
Sales price results are in Table 5. In all specifications, a 1% increase in reserve price raises sales price by just over 0.9%. Why is the elasticity less than 1? A higher reserve price also contains an effect to discourage entry of potential bidders (where we assume appraisers set a reserve price that is common value plus an idiosyncratic error component). Property characteristics are interpreted to affect the number of potential bidders, conditional on reserve price. Sales prices are distinctly lower for larger plots which may be less manageable, or have fewer experienced developers who would try to utilize them.
Table 5.
Baseline Case: Unite Sales Prices [ln(sales price/area)]
| OLS | Heckman | IV | ||
|---|---|---|---|---|
| 2-step | MLE | LIML | ||
|
Dummy: two stage
auction [2SLS] |
−.170** (.037) |
−.410** (.122) |
−.707** (.217) |
−.428** [−.428*] (.112) [(.225)] |
| Ln (reserve price) | .923** (.028) |
.916** (.012) |
.907** (.025) |
.915** (.015) |
|
Dummy: Residential
use |
.023 (.049) |
−.018 (.033) |
−.068 (.078) |
−.021 (.036) |
| Dummy: Mixed use | .078** (.034) |
.039 (.032) |
−.0091 (.059) |
.036 (.034) |
| Ln (dist. To CBD) | .0083 (.037) |
−.000064 (.014) |
−.010 (.037) |
−.00069 (.017) |
| Ln (area) | −.069** (.011) |
−.069** (.0075) |
−.070** (.013) |
−.069** (.011) |
|
Dummy: railway within
2.5 kms. |
−.025 (.035) |
−.015 (.026) |
−.0034 (.035) |
−.015 (.025) |
|
Dummy: highway
within 2.5 kms. |
−.067 (.038) |
−.077** (.023) |
−.089* (.046) |
−.077** (.023) |
|
Season, year, city
dummies |
Yes | yes | yes | yes |
| N | 2302 | 2302 | 2302 | 2302 |
| Rsq | .85 | .84 | ||
|
Lambda [rho] {Sargan
p-value; 4 instruments} |
.140** (.069) |
[.641** (.235)] |
{.15} | |
significant at 10% level
significant at 5% level or higher. All standard errors (except in Heckman 2-step estimation and IV LIML) are robust clustered by city-code.
The key variable concerns choice of auction type. In OLS estimation, prices are lower for two stage auctions by 17%, as an assumed average effect. With correction for selection, the coefficient has a much larger negative value. The Heckman MLE estimate is about −0.70, about 4 times larger in absolute value. The IV coefficient (standard error) when the first stage simply uses the 4 instruments (i.e., linear probability) is similar, −.646 (.267) for LIML. Coefficients are fairly precisely estimated. While the Heckman MLE is the preferred specification, we note the result is sensitive to some alternatives: the 2-step Heckman estimate which is less efficient and the LIML estimate with predicted probabilities from a first stage Probit as instruments yield coefficients that are smaller in magnitude: −.40. These are still at least twice the OLS estimate.19
In terms of issues of selection, the fact that the treatment effect coefficients are significantly larger than under OLS suggests positive selection: not accounting for selection understates the size of the treatment effect. Correspondingly, for direct evidence on selection, the correlation coefficient in the MLE results is positive and significant, as is the 2-step Heckman estimate of the Mills’ ratio coefficient. The theory section suggested positive selection would be a marker of corruption, and the results indicate that positive selection into two stage auctions is a significant force.
We also examined the validity of instruments to the extent any tests are persuasive. A Sargan p-value of .15 while acceptable is low. We believe this is due to model specification error (see next) rather than unsuitability of instruments per se. If we add to column 1 (the OLS specification) our 4 instruments as covariates, the coefficient on auction type goes from −.1697 to −.1624, a tiny change. If instruments were correlated with unobservables affecting sale prices, assuming that auction type is correlated with unobservables, the added instruments should absorb some of the correlation of unobservables with auction type, affecting its coefficient. That the coefficient is unchanged and instruments are definitely correlated with auction type suggests that the instruments are orthogonal to unobservables.
Finally, we note if we drop the reserve price variable and use property characteristics (and city and time fixed effects) to represent both common value and demand considerations, all coefficients become much more negative.20 For example, the OLS coefficient goes from −.17 (with a reserve price control) to −.34 (without a reserve price control); the Heckman 2-step and MLE rise in absolute value to −.81 and −.92 respectively; and the LIML coefficient goes to −.80. The lambda in the Heckman 2-step rises to .27, while the rho in the Heckman MLE falls to .37. Thus, the results without a reserve price control also suggest positive selection.
4.4 The problem with the baseline approach: “Kink/discontinuity” in the price equation
We speculate that if multiple entrants emerge in the second stage of a two stage auction, the outcomes for English and two stage auctions for that property will be similar. In both cases once into the English auction portion, the sales price will simply be the valuation of the second highest valuation bidder. Corruption more likely takes the form of inducing non-corrupt entrants to stay out of the two stage auction, with the result that sales are at reserve prices. Of the 2302 auctions upon which estimation is based, only 1235 are ex post competitive, or have more than one bidder as inferred from the degree of spread. A non-competitive auction means sales price equals reserve price, so reserve price tells us sales price. We already saw in Table 3 from the raw data that the significant overall unit price differences between English and two stage auctions for the overall sample become insignificant once we look just at auctions which are competitive.
To explore these issues, we examine the two components. How does auction type affect the probability that an auction will be competitive or not? Second, if auctions are competitive does the choice of auction format still affect sales price? The answers to these questions will help us study the revenue losses from use of two stage auctions.
5. The effect of auction type on competition
What is the effect of auction type, on whether an auction will be competitive or not, defined as whether there appears to be more than one bidder because spread exceeds 1.005? A simple probit of competitive or not with auction type as a potentially endogenous dummy variable faces the same selection problem as in the sales price estimation. Properties may be negatively or positively selected into two stage auctions, and such selection itself will affect the potential for competition. The literature handles this in different ways. We use the bivariate recursive probit (Greene, 1998, Evans and Schwab, 1995), as an MLE solution. As a robustness check we also performed regular IV estimation in a linear probability model (Angrist, 1999), where we instrument for auction type with Z’s. Here, the marginal 2-stage auction effects are even stronger than we will report below—reducing the probability of competition by .75.21
The bivariate recursive probit is a two equation MLE model where we model action type as a dummy endogenous variable which is a function of X and Z, with auction type affecting the event: competition or not. That is,
| (8) |
| (9) |
with
| (10) |
| (11) |
where dijt denotes whether an auction is two-stage (1), or not (0), and sijt denotes whether an auction is competitive (1) or not (0). The X’s include city fixed effects, time dummies, seasonal dummies, and ln(ask price) in all equations (cf, equation 7). The recursive structure allows identification in a standard bivariate probit framework (Greene, 1998). In the next section we will add a continuous equation, for sales price in competitive auctions; at that point we will offer more details on estimation.
Results are in Table 6. For the bivariate recursive probit, we show marginal direct and indirect effects. For the variable of interest, two stage auction, there is only a direct auction effect. In the ordinary probit, the marginal effect of two stage auction on the probability of being competitive is −.34, consistent with the raw data in Table 3. In the bivariate recursive formulation that marginal effect is 26% stronger, at −.43.22 This is again suggestive of positive selection into two stage auctions: the two stage auction’s negative effect on competition is understated because properties with better unobservables are selected into two stage auctions. Consistent with this, the rho measuring the degree of correlation between the error terms is positive (.38), and significant. Properties with better unobservables are more likely to be competitive, and more likely to be assigned to two stage auction.
Table 6.
Probability sale is competitive:
| Ordinary probit |
Bivariate recursive probit MLE |
||
|---|---|---|---|
| Marginal effects |
Marginal indirect effects |
Marginal direct effects |
|
|
Dummy: two stage
auction |
−.338** (.079) |
n.a. | −.427** (.085) |
| Ln (reserve price) | .−016 (.027) |
.085 (.067) |
−.023 (.024) |
|
Dummy: Residential
use |
.216** (.055) |
.405** (.131) |
.172** (.062) |
| Dummy: Mixed use | .205** (.049) |
.405** (.156) |
.161** (.069) |
| Ln (dist. To CBD) | −.028 (.021) |
.094 (.085) |
−.035* (.022) |
| Ln (area) | .−045** (.012) |
.002 (.028) |
−.045** (.011) |
|
Dummy: rail within
2.5 kms. |
.013 (.036) |
−.123* (.076) |
.023 (.039) |
|
Dummy: highway
within 2.5 kms. |
−.019 (.029) |
.137** (.067) |
−.028 (.029) |
|
Season, year, city
dummies |
Yes | Yes | Yes |
| N | 2297 | 2297 | |
| Rho | .383** (.157) |
||
| Rsq | .22 | ||
significant at 10% level
significant at 5% level or higher. All standard errors are robust clustered by city-code.
In terms of other variables, relative to the base case of commercial use, sales of residential and mixed use land are likely to be more competitive, while large properties away from the city center are less likely to have competitive bidding. Total marginal effects on competition or not include direct effects23 and then indirect effects24 through the effect of covariates on auction type and hence competition. Indirect effects seem strongest for land use variables, reinforcing the fact that commercial use properties face fewer takers and are less likely to be competitive. Removal of reserve price as a covariate in both equations has little effect on results, consistent with the fact that its coefficient is insignificant in Table 6.
6. Effect of auction format on sales prices, for competitive sales
If properties sell competitively, is there a remaining effect of auction type on sales price? A naive way of looking at this is to ask, conditional on a property selling competitively, ex post does auction type affect price for such properties? That is interesting information. If we examine the sample of 1235 properties for which spread exceeds 1.005, OLS results in column 1 of Table 8 below show no effect of auction type, a coefficient of −.03. This OLS estimate of auction effect on price faces two problems. First there is the auction selection problem discussed earlier, but now there is a second selection issue. Being competitive is endogenous, and there is selection on unobservables into competition that are surely correlated with price. Such selection is mediated by the auction process, so it is not the standard problem in Lee, Maddala and Trost (1980), but rather one modeled in the labor literature (Fraker and Moffitt 1988, Goux and Maurin, 2000) and more recently in firm growth models (Reize, 2001).
Table 8.
Sales prices: “Competitive” sales only
| All sales where spread > 1.0005 | ||
|---|---|---|
| OLS |
MLE (selection on auction
type and competition) (eqs. 7a – 11) |
|
| Dummy: two stage auction | −.031 (.071) |
−.137 (.414) |
| Ln (reserve price) | .870** (.041) |
.867** (.051) |
| Dummy: Residential use | −.157* (.075) |
−.162 (.103) |
| Dummy: Mixed use | −.061 (.042) |
−.065 (.068) |
| Ln (dist. To CBD) | .025 (.048) |
.020 (.047) |
| Ln (area) | −.097** (.027) |
−.098** (.032) |
|
Dummy: there is railway
within 2.5 kms. |
−.049 (.052) |
−.049 (.053) |
|
Dummy: there is highway
within 2.5 kms. |
−.102 (.064) |
−.110 (.077) |
| Season, year, city dummies | Yes | Yes |
| N | 1235 | 1235 |
| σ ε | .510** (.060) |
|
| ρ uε | .114 (.437) |
|
| ρ ν ε | .088 (.212) |
|
| ρ uν | .374** (.186) |
|
| Rsq | .82 | |
Significant at 10% level
significant at 5% level or higher. OLS s.e.’s are robust, city clustered.
We tackle the problem in two ways. First, as a less parametric approach, we utilize the ideas from the literature on identification-at-infinity (Heckman, 1990), by examining auction effects for samples where the predicted probability of a non-competitive sale is small. This isolates a sample where, ex ante, we expect sales to be competitive regardless of auction type; and asks whether, for this sample, there is an effect on sales price of two stage auctions. The main issue with moving to such samples is that, especially when we want to still correct for selection into auction type, we start to run out of cities which have competitive sales in both auction formats.
6.1 Selection into being competitive
Identification-at-infinity
Similar to Mulligan and Rubinstein (2007), for each auction type separately, we estimate the probability that an auction is competitive; specifically that the spread (ratio of sales to reserve price) is greater than 1.005. The covariates are the X’s including reserve price and city fixed effects, but not the instruments (which don’t affect competition per se). We then created different samples: for example all properties where the probability of competition ex ante is predicted to be greater than 0.5, 0.6, 0.7, and so on. Patterns in the raw data are most instructive in terms of how the samples, mix of competitive to non-competitive auctions, and price differences change across auction types as we move to more and more competitive margins.
Table 7 shows the patterns. In Table 7 we distinguish 7 samples, all observations and then 6 samples distinguished by increasing degrees of predicted competitiveness of the auctions. We have three sets of columns. In the first we show that as the degree of predicted competitiveness increases, the ratio of (remaining) two-stage to English auctions declines precipitously. For the full sample the ratio is 2.6; for the most competitive it is 0.06. The result suggests that finding a sufficient sample of two stage auctions that are very likely to be competitive is not easy. The second set of columns shows that as we increase the margin on being competitive, the percentage of auctions with spread rises and converges for the two auction types. This of course follows from the nature of the exercise (creating samples by how competitive they are predicted to be); but it shows the exercise is working.
Table 7.
Auction price differences under competition: data
| Samples | Number | Percent: spread > 1.005 |
Median of spread | |||||
|---|---|---|---|---|---|---|---|---|
| Two Stage . |
Eng . |
Two Stage |
Eng. | Two Stag e |
Eng. | Med diff. Eng. > T.S. Chi2 p-value |
Rank diff. WMW: p-value |
|
| all | 1661 | 641 | .43 | .82 | 1.0 | 1.49 | .000 | .000 |
| Prob. comp. >0.5 | 590 | 574 | .69 | .85 | 1.17 | 1.51 | .000 | .000 |
| Prob. comp. >0.6 | 377 | 535 | .74 | .88 | 1.25 | 1.54 | .000 | .000 |
| Prob. comp. >0.7 | 212 | 503 | .77 | .90 | 1.39 | 1.56 | .029 | .017 |
| Prob. comp. >0.8 | 89 | 406 | .78 | .92 | 1.47 | 1.65 | .360 | .140 |
| Prob. comp.> 0.85 | 49 | 328 | .84 | .93 | 1.91 | 1.68 | .348 | .245 |
| Prob. comp.> 0.9 | 14 | 240 | 1 | .95 | 1.84 | 1.83 | .783 | .991 |
The third set of columns in Table 7 contains the key results. It examines the pattern of spread (sales to reserve price) for English versus two stage auctions. Significant differences in both median and ranks of spread exist at low levels of competition between the two auction types, but diminish as competition increases and disappear by a predicted probability of competition in excess of 0.7. Typically, for identification-at-infinity, a margin of .8 or greater is used. The raw data suggest that at such margins, English and two stage auctions yield similar outcomes.
We then attempted to implement this idea econometrically, by looking at sales which ex ante are “almost certain” to be competitive. The difficulty is that as we make the margin of competition more intensive, we get fewer and fewer two stage auctions in the sample, so there are fewer and fewer cities left in the sample which use both auction types. Second our instruments loose their power and degree of variation as the sample shrinks and what we report is the best case—use of all 7 instruments. So, for example, even if we cut at the probability of being competitive at a relatively low level such as 0.7, the first stage probit drops all but 3 instruments (lack of variation in instruments under city and time fixed effects). And rather than a sample of 715 for sales where the probability of competition exceeds .7 (Table 7), we must work with a sample of 541 in terms of cities which still use both auction types. The improvement in the LLF from adding these instruments has a χ2 - statistic of 2.09 which falls far short of the critical value of 7.8 with 3 degrees of freedom, and the corresponding F-statistic is tiny. If we cut finer in terms of increased degree of competition, we loose most variation in instruments and the problem is worse.
The best we can do is cut at the margin of the probability of competition exceeding .6, which definitely falls short of identification-at-infinity. For these sales we have a sample 792 (out of possible 912 from Table 7) where 9 cities still have both auction types. While all 7 instruments have variability in the sample, the improvement in the LLF for the first stage probit on auction type of adding the instruments is now significant ( χ2 - statistic of 28.5) but the implied F- statistic indicates weak instruments. For this sample, in the same type of price equation as used in Table 5, the coefficient on auction type under MLE Heckman estimation is −.31 and significant. There is no evidence of selection into auction type: rho equals .028 (and is insignificant) and the OLS coefficient is close to the Heckman one at −.29. The effect of auction type is now much smaller than the −.70 in Table 5, but it is not zero. Unfortunately we can’t use this approach to tease out the effect when we are at the margin of properties which are “almost certain” to sell competitively, to see if the effect goes to zero. Thus we turn to the more traditional parametric approach.
6.2 MLE estimation of the bivariate selection into competitive, two-stage auctions
To the model in equations (8) – (11), we now add a third equation for price
| (7a) |
where yijt is sales price in logs. The structure imposes a trivariate normal error
| (12) |
so as to estimate the parameter set Θ = (β D α θ γ σε ρεu ρεν ρuν). The LLF is footnoted and uses results in Genz (2004).25
We estimate the model by MLE, which yields more efficient estimates than a two step approach that adds two control functions to the price equation to deal with the two dimensions of selection; the two-step approach also has a cumbersome standard error calculation (Reize, 2001).26 In Table 8, column 2, we present the results for the price equation, along with the covariance structure. Estimates for the discrete choice part are in the three-equation MLE Appendix. For comparison in the Appendix, we also report the corresponding bivariate recursive probit estimates from which Section 5 and Table 6’s marginal effects are calculated. The two sets of coefficients are very close.
Results on the price equation in Table 8, column 2 are similar to the OLS estimates without any sample corrections. The coefficient for the auction type effect on price in competitive auctions is fairly close to zero and insignificant, as hypothesized.27 In the covariance structure, as before, there is strong positive selection into two-stage auctions. The error term on the price equation has low correlation with the error terms on the discrete events.
Summary
Whether we approach the problem as a parametric one with strong assumptions or use a more non-parametric approach (identification at infinity on raw price data or in a price equation with auction selection), it seems that, once auctions become competitive, price is not affected by auction format. Auction format matters at the margin of whether auctions are competitive or not, all consistent with the corruption signaling hypothesis associated with two stage auctions
6.3 Review gains from switching to English auctions
What are the revenue gains if one was to require properties sold at two-stage auction to be sold at English auction, assuming that would solve the problem of potential corruption between the auctioneer and partner bidders. In our data the actual revenue from properties sold at two-stage auctions is 239.6 billion Yuan or about $34.2 billion. This is modestly higher than the expected revenue for these properties which is predicted from the estimated model, indicating the issue with mediating unit sales price predictions by lot sizes to get sales revenue per property. This predicted revenue if these properties are still sold at two-stage auction is 227.7 billion Yuan, about 5% lower than the actual. The unit sales price calculation is based on the predicted probability of selling competitively if sold at two-stage auction ( prob(⟨sijt = 1|dijt =1⟩) times the predicted price if sold competitively, plus the predicted probability of selling non-competitively at two-stage auction times the reserve price. The predicted price if sold competitively is calculated from the usual price equation adjusted for the two selection terms as footnoted (using parameters from the MLE estimation).28
We compare the revenue from selling properties by two stage auctions with the predicted revenue obtained if all properties sold by two stage auctions in the data were sold at English auctions. This is the predicted probability of these properties selling competitively if switched to English auction times the predicted price when sold competitively, plus the predicted probability of not selling competitively if switched to English auction times the reserve price. The predicted probability of selling competitively is enhanced by the treatment effect of English auction on competition.29 The predicted revenue is 299.6 billion Yuan. This is 25% higher than the actual revenue and 32% higher than the model predicted revenue if sold by two-stage auction. Thus, use of two-stage auction with the associated reduction in degree of competition (through potentially signaling a corrupt sale) deprives cities of significant revenues.
This gain in revenue is illustrated in Figure 3, which for two-stage auctions compares the predicted unit price in the model if sold by two-stage auction, with that if sold by English auction. The 45° line is for model predicted prices if sold still at two-stage auction, while the scatter plot of points is for the predicted prices if these properties were sold by English auction. The difference reflects both the increase in probability of selling competitively for any property, as well as the fact that these properties have relatively good unobservables which enhances their competitive price.
Figure 3.
For 2-stage auction sales: predicted unit price if sold by 2-stage (45° line) versus switching to English auction
7. Summary
To the best of our knowledge, this paper is the first to investigate empirically corruption in auctions beyond simple price-fixing among bidders, to allow corrupt auctioneers and signaling activity. This complements the recent increased interest in the theoretical literature on corruption in auctions (see, e.g., Burguet and Che, 2004, Compte, O., A. Lambert-Mogiliansky and T. Verdier, 2005, Menezes and P. K. Monteiro, 2006). But our paper differs also from this theoretical literature. Corruption in our context takes the form of auction choice, while these theoretical papers consider corruption in a given auction format. Another difference is that both English and two stage auctions are open (that is, all bids are observable to all participants), while the existing literature considers first price sealed bid auctions (so that the corrupt auctioneer can manipulate bids).
In this setting, we show that after controlling for observable land characteristics (and location and time trends), two stage auctions lead to less competitive bidding and thus substantially smaller revenue than English auction in China’s land market. We further demonstrate that land bureau officials in Chinese cities divert hotter properties to two stage auctions that are more corruptible. Since urban land in large Chinese cities is hugely valuable and revenue from land auctions accounts for a large portion of city fiscal revenue, such corruption activities result in large losses of potential public funds. And the losses from this type of corruption are not merely transfers from city coffers to the corrupt officials and developers. This type of corruption also leads to misallocations, as honest developers with higher valuations are deprived of the chances to develop the land.
Acknowledgments
The authors thank Yona Rubinstein for helpful comments and advice, as well as workshop participants at Brown University and Hong Kong University. The views expressed herein are those of the author(s) and do not necessarily reflect the views of the National Bureau of Economic Research.
NBER working papers are circulated for discussion and comment purposes. They have not been peer-reviewed or been subject to the review by the NBER Board of Directors that accompanies official NBER publications.
Appendices
Theory appendix
1. Characterizing a separating equilibrium of a two stage auction without corruption
First we argue that bidder 1 with will not enter the auction at all. Consider a bidder 1 whose valuation is just below but very close to . In equilibrium he does not enter and all other potential bidders understand that his valuation is below . So other bidders enter the English auction if their valuation is above y. Thus, if this bidder 1 deviates from the equilibrium and enters the English auction at the end, his expected payoff will be no more than , which will be less than zero by Equation (2) since .
Now we consider the case when . If bidder 1 enters in stage 1 with a bid B1, the other potential bidders can infer bidder 1’s valuation V1 > B1 + C ≥ r+C from his bidding schedule B(V1 ). Except for this, the same game is played by the other N –1 potential bidders as in the case of an English auction. Exactly as before, the valuation threshold for entry in this case can be solved as . Since V1 > r, we have . The difference between these entry threshold valuations reflects the entry deterrence effect of bidder 1’s signaling.
For , if bidder 1 makes a bid of B and is believed by the other potential bidders as having a valuation of , his expected payoff is
Clearly this payoff function is increasing in bidder 1’s true valuation V1 and the belief of the other potential bidders , but decreasing in his bid B.
In equilibrium, bidder 1 should “tell the truth” by bidding his equilibrium bid B(V1 ), which reveals to the other potential bidders that his true type is V1. For a strictly monotonic bidding schedule to satisfy this truth-telling constraint (or incentive compatibility constraint), bidder 1’s above expected payoff function must satisfy the single crossing condition, so lower valued bidders have no incentive to misrepresent their valuations. It can be checked that this condition is indeed satisfied, because the slope of the indifference curve
is clearly increasing in V1.
From the truth-telling constraint, we can derive the differential equation that characterizes the strictly increasing bidding schedule as follows:
| (a) |
From equation (1) and , we can usethe implicit function theorem to derive
Together with the boundary condition that (the lowest type uses the lowest possible signal), the equation (a) characterizes the strictly increasing signaling schedule.
2. Comparing the English and two stage auctions without corruption: a numerical example
Because a general comparison of the expected revenue between English and two stage auctions is too difficult, we use a simple numerical example to show that the expected revenue is higher for an English auction than for a two stage auction when the land is “hot,” and vice versa. We normalize parameters by setting v0 = 0, C=1. Let r=2. Consider the case of N = 2, and each bidder’s valuation is uniform on [0, ], where . A cold property occurs when is relatively small, while the property is hot when is relatively large.
For an English auction, from equation (1) it can be shown that the entry threshold valuation is . The probability of no entry (hence no sale) is ; the probability of only one bidder entering is , in which case the land will be sold at the reserve price. The probability of competitive bidding is , in which case the expected revenue is the expected lower valuation of the two bidders (by revenue equivalence with the second price auction).
For the two stage auction, we have two scenarios: low valuation scenario and high valuation scenario. The low valuation scenario occurs when ; then bidder 2 will not enter at all as long as bidder 1 has entered. So bidder 1’s entry threshold valuation is , and if he does not enter, bidder 2 will enter if his valuation is above r + C. In this scenario, the probability of no entry (no sale) is ; the probability of only one bidder entering is , in which case the sales price is the reserve price. Note that in this low valuation scenario there will be no competitive bidding.
In the high valuation scenario of the two stage auction (), if bidder 1 does not enter, then bidder 2 should enter with a bid at the reserve price when . If bidder 1 enters with a signaling bid, bidder 2 will enter only if his valuation . From equation (2), it can be shown that bidder 1’s entry threshold valuation is given by . In this scenario, the probability of no entry (no sale) is . There are two cases that result in only one bidder entering: (i) bidder 1 enters with a signaling bid and bidder 2 does not enter, which happens with probability of and with a sales price equal to bidder 1’s signaling bid; and (ii) bidder 1 does not enter and bidder 2 enters with a bid at the reserve price, which happens with probability of . The remainder of the probability goes to the case of competitive bidding.
To see that a revenue maximizing auctioneer prefers a two stage auction over an English auction for cold properties, consider first the low valuation scenario when is close to r + 2C. In our numerical example, this means that . Then in an English auction the entry threshold is , the probability of no sale is about 0.656, the probability of one bidder entering is about 0.308 and that of competitive bidding is less than 0.04. Since the sales price in competitive bidding is less than 4, the expected revenue is no more than 0.776. For a two stage auction, the probability of no sales is 0.563, and the probability of having one bidder enter is 0.438. Thus, the expected revenue of a two stage auction is 0.875, higher than that of an English auction. Because the expected revenue is continuous in , we conclude that for cold properties a two stage auction generates greater expected revenue than an English auction.
Now consider the other extreme case in which is large, e.g., = 24. Then in an English auction the entry threshold is = 6, the probability of no sale is 0.0625, the probability of one bidder entering is 0.375 and that of competitive bidding is 0.563. It can be shown that the total expected revenue of an English auction is 7.5. For a two stage auction, the threshold valuation for bidder 1 is 5.62 and the probability of no sale is about 0.03. The probability of only bidder 2 entering is about 0.205, generating an expected revenue of 0.41. From the preceding Appendix, bidder 1’s signaling bidding function is starting at B = r = 2 when V1 = = 5.62. It can be checked that the event of only bidder 1 entering generates an expected revenue of about 3.88, and the event of competitive bidding generates an expected revenue of 2.99. Thus, the total expected revenue of a two stage auction is 7.28, which is less than that of an English auction.
3. The snapping strategy by a non-corrupt developer does not work: an example
We continue with the example of uniform distribution on [0, ]. Suppose κ is sufficiently large so that other bidders will not enter if they see a bid at the reserve price at the start of the auction. Suppose a non-corrupt bidder plays the snapping strategy by mimicking the corrupt bidder when his valuation is above . We consider the bidder with the threshold valuation. A corrupt bidder will outbid him if , which happens with probability of . With the remainder probability, he succeeds and obtains a payoff of . Thus, playing the snapping strategy yields an expected payoff of . If he plays the equilibrium strategy of waiting to see whether there is a corrupt developer who submits a bid at reserve price at the start of the auction, a non-corrupt bidder with valuation obtains an expected payoff of , where is his expected payoff in the two stage auction without corruption. Note that when p is close to one and κ is large, p* is close to one. Then the snapping strategy will give a non-corrupt bidder too low an expected payoff.
Data appendix
Comparing the estimating sample with samples of unsold properties and properties with incomplete information
| I. Base sample N = 2302 |
II. Unsold N = 607 |
III. Sold: missing price data. N= 1107 |
IV. Unsold Diff (t-stat.) I-II |
V. Missing price data Diff (t-stat) I-III |
|
|---|---|---|---|---|---|
|
Two
stage auction |
.72 | .61 | .69 | 5.11 | 1.66 |
| Area (sq. m.) | 54861 | 54113 | 53831 | −.09 | .25 |
| Distance (km.) | 19.3 | 46.4 | 13.4 | −13.6 | 7.68 |
|
Unit sale
price (10,000 Y) |
.62 | n.a | .58 (n=824) | n.a. | .53 |
|
Unit
reserve price (10, 000 Y) |
.37 | .21 | .31 (n=200) | 5.01 | .50 |
| Mixed use | .38 | .52 | .39 | −6.03 | −.54 |
| Commercial use | .31 | .27 | .28 | 1.99 | 1.76 |
| Residential use | .31 | .21 | .33 | 4.99 | −1.14 |
|
No.
quarters since listing till Dec. 2007 |
8.17 | 4.74 | 9.31 | 19.8 | −6.25 |
significant at 10% level
significant at 5% level or higher
The table above explores the differences in means of variables for the estimating sample versus other listings. A comparison of columns I and II (with tests of differences given in column IV) suggests unsold properties are more distant from the CBD with a lower reserve price; and are more likely to have been offered at English auction. A probit of auction type on sold or not, with controls for property characteristics including reserve price and city and year fixed effects, suggests two stage auctions have a .076 higher probability of a sale. A comparison of columns I and III (with tests of differences given in column V) suggests sales with missing sale or reserve price data are similar to those in our estimating sample. They have similar auction type and use proportions and when data is available have similar reserve and sales unit prices.
MLE appendix
Discrete choice results. 3-equation MLE compared with 2-equation bivariate probit (Non-marginal effects)
|
Competition
equation (3-eq. model) [Competition or not] (eqs 8 & 11) |
Competition equation (2- eq. model) |
Auction
equation (3-eq. model) [2 stage auction or not (eqs. 7 & 10)] |
Auction equation (2-eq. mod) |
|
|---|---|---|---|---|
| Two stage auction | −1.54** (.316) |
−.55** (.311) |
n.a. | n.a. |
| Ln (reserve price) | −.057 (.061) |
−.058 (.061) |
−.137 (.110) |
−.137 (.109) |
|
Dummy: Residential use |
.444** (.148) |
.440** (.158) |
−.811** (.185) |
−.809** (.183) |
| Dummy: Mixed use | .415** (.179) |
.411** (.177) |
−.808** (.208) |
−.806** (.207) |
| Ln (dist. To CBD) | −.089 (.057) |
−.089 (.055) |
−.156 (.139) |
−.153 (.137) |
| Ln (area) | −.112** (.028) |
−.112** (.028) |
−.0040 (.052) |
−.0035 (.045) |
|
Dummy:
rail within 2.5 kms. |
.057 (.098) |
.057 (.097) |
.197* (.113) |
.203* (.115) |
|
Dummy:
highway within 2.5 kms. |
−.070 (.071) |
−.071 (.073) |
−.227** (.079) |
−.224** (.081) |
|
Party
secretary turnover, 1 mont lead |
n.a. | n.a. | −.837** (.321) |
−.815** (.290) |
|
Party
secretary turnover, 1 month lag |
n.a. | n.a. | .803** (.191) |
.800** (.187) |
|
Google
report, Land corruption case, 3 month lead |
n.a. | n.a. | −.670** (.336) |
−.678* (.367) |
|
Google
report, Land corruption case, 2 month lead |
n.a. | n.a. | .974* (.525) |
.959** (.515) |
|
Season, year,
city dummies |
Yes | Yes | Yes | Yes |
| N | 2297 | 2297 | 2297 | 2297 |
Footnotes
Rural land is owned by the village and allocations done by the village leadership.
The central government (national asset committee) and the military may control portions of city land in particular cases, as for example the national capital Beijing.
The third type is sealed bid, or zhaobiao auction. There, bidders submit sealed bids to the land bureau, which decides the winner according to a complicated score function, in which the submitted bid usually accounts for only 20-30% in weight. The remaining 70-80% of the weight goes to the credibility of the bidder and how much social responsibility the bidder is willing to take. Credibility is mainly reflected in two aspects: one is the quality and reputation of the projects the bidder has developed in the past; the other is the bidder’s financial capacity. As for social responsibility, this arises from Beijing’s recent attempt to curb rising housing prices. If a bidder is willing to commit to an upper bound on the housing price of the future development on this piece of land, then this bidder will get a higher score in terms of social responsibility. In a logit framework in looking at auction choices, we did an early test on the validity of the IIA assumption that dropping this third auction type does not affect the analysis of the choice between English and two stage auctions (Hausman-test of coefficient differences, when zhaobiao is added as a choice versus excluded). We could not reject the validity of the IIA assumption.
We conducted surveys of the land bureau officials of 20 cities covered in our sample. In our survey, we asked questions regarding the differences in the mechanism between the two auction formats, in addition to differences in the pattern of bidding behaviors. We also asked how the land bureau chooses between the two auction formats for each piece of land for sale. Our theory conjectures in the next section are informed by our survey findings.
As further evidence that reserve prices are set independently of auction type, in a MLE Heckman selection model where we allow auction type to be a determinant of reserve price, controlling for selection effects of auction type yields an insignificant rho, suggesting no correlation between those unobservables affecting auction choice and those affecting reserve price.
The entry fee consists of (i) cost of making cash deposit to qualify, (ii) cost of preparing documents to meet the qualification requirements, (iii) other transaction costs (e.g., time, consulting fee).
Note that we assume the (expected) common value is common knowledge to all participants, thus the auction is treated as one with independent private valuation.
In the bidding stage, each active bidder’s valuation has the truncated density function of on . Let the associated distribution function be G(V). Then the expected rent for active bidder i from the bidding game is , where G(V−i) denotes the joint distribution of other n –1 active bidders over the domain of . In the entry stage, bidder i with valuation expects that the number of active bidders (including himself) is n = 1, 2,…, N with probability of , where denotes the combination of N – n out of N –1. Thus, the total expected rent for bidder i with valuation from entering the auction is . Expected revenue is .
This assumption holds when ex ante no one knows the identity of the potentially corrupt bidder, so that all potential bidders are symmetric if the government official is not corrupt. If everyone knows that bidder 1 is the only possible developer who can have a deal with government official, he is more likely to enter than other bidders (having a lower threshold) even when in fact he does not have a deal. This is because only bidder 1 knows that no one else is corrupt and all other bidders are worried that bidder 1 is corrupt. This latter case is not that realistic and the analysis will not change much if we allow for this possibility.
Clearly by comparing equations (3) and (4) we must have . if , then equation (4) implies that (note that all wq ’s are zero). If , then equation (3) implies that (note that the first term in the bracket is zero). Comparing equations (1) and (4) reveals that if , then .
Even if a non-corrupt bidder will try the snapping strategy, he will do so only when his valuation is very high for fear of being outbid by a corrupt bidder. It is possible that in equilibrium, a non-corrupt bidder with very high valuation and a corrupt bidder are pooled in using the same strategy of bidding at the reserve price at the start of the auction (whoever manages to be the first is immaterial). In such an equilibrium, a corrupt bidder who does not get the chance to submit a first bid will try to outbid the non-corrupt bidder only when he also has a quite high valuation. What is important, however, is that in such a pooling equilibrium, other bidders are seriously discouraged to enter, either by a very high valuation non-corrupt bidder or by a corrupt bidder.
This assumes that, when their valuations are sufficiently high, other non-corrupt bidders may still enter the auction after seeing that corrupt bidder 1 has entered. Otherwise, the corrupt bidder 1’s signaling can completely prevent entry by other bidders, and the difference between the English and two stage auctions in terms of entry will be larger.
Since in both auctions equation (4) must hold, thus if then , and vice versa. Suppose (counterfactually) , then it can be shown that the left hand of equation (5) is less than that of equation (3), which yields a contradiction (since the right hands of two equations are the same).
Moreover, if the bribery payment to the government official increases with the partner developer’s net profit, then they both are more likely to favor a two stage auction, since the price the corrupt developer pays is likely to be lower.
These are Xiamen, Guangzhou, Shenzhen, Nanning, Changchun, Suzhou, Wuxi, Nanchang, Shenyang, Taiyuan, Chengdu, Tianjin, Hangzhou, Ningbo, and Chongqing.
We exclude Shanghai, Beijing and Nanjing. Shanghai has no English auctions; Beijing has 1; and Nanjing 3 (which are a tiny fraction of sales). In all specifications we utilize city fixed effects, so within city variation in the data (in particular in auction formats which is our focus) is essential.
The selection terms are respectively and where zijt, are the covariates and estimated parameters from the probit on auction type.
We experimented with allowing treatment effects to vary with observables, by adding variables for auction type interacted with the deviation of property characteristics from their means. In OLS the interactions are not significant. In the IV (2SLS) results, the interactions are somewhat statistically stronger and the average treatment effect rises from −.53 (with 7 instruments) to −.81. However there is little variation in treatment responses as covariates go from low to high values.
With use of all 7 instruments, the MLE and 2-step Heckman results are almost the same (−.69 and −.46 respectively). The LIML estimates are higher in absolute value when using either a first stage probit or linear probability model (−.526 and −.893 respectively). All coefficients are significant.
These reported results are for 7 instruments.
These results are based on use of 7 instruments, under LIML estimation.
Use of 7 instruments further increases the strength of the negative effect to −.49.
Marginal direct effects are calculated based on the estimated coefficients in the second equation of the bivariate recursive probit, as well as the predicted probability of being competitive at the mean level of covariates, i.e., P=0.4817. For a continuous variable, its marginal effect is equal to the product of the density of normal distribution at P=0.4817 and its estimated coefficient. For a discrete variable, its marginal effect is equal to Φ(arg Φ(0.4817) + θ) – 0.4817, where Φ(·) (or arg Φ(·)) is the cdf (or inverse of cdf ) of the normal distribution and θ is the estimated coefficient.
The marginal indirect effect of each covariate is obtained from the product of the estimated coefficient of 2-stage auction in the second equation of the biprobit regression and the estimated coefficient of this covariate on auction type in the first equation. We calculate the standard errors using the delta method approach. The variance-covariance matrix is obtained through post-estimation of the biprobit model.
We thank Frank Reize for access to his STATA code on MLE estimation of the model, to check ex post against our STATA code, although in the end we reprogrammed the model in MATLAB. There seems to be a minor error in Reize (2001) in specification of the LLF.
The results are the same if we use 7 instruments.
Let us denote the probability of selling competitively under the switch as prob[sijt =1|dijt =1, d’ijt =0]. Then .
Contributor Information
Hongbin Cai, Guanghua School of Management and IEPR Peking University Beijing 100871 China hbcai@gsm.pku.edu.cn.
J. Vernon Henderson, Department of Economics Box B Brown University Providence, RI 02912 and NBER j_henderson@brown.edu.
Qinghua Zhang, Guanghua School of Management Peking University Beijing 100871 China zhangq@gsm.pku.edu.cn.
References
- Angrist JD. Estimation of Limited Dependent Variable models with Dummy Endogenous Regressors. Journal of Business Economics and Statistics. 1999;19:2–16. [Google Scholar]
- Athey S, Levin J, Seira E. Comparing Open and Sealed Bid Auctions: Evidence from Timber Auctions. Stanford University; 2008. Working Paper. [Google Scholar]
- Bajari P, Ye L. Deciding between Competition and Collusion. Review of Economics and Statistics. 2003;85:971–989. [Google Scholar]
- Burguet R, Che Y-K. Competitive Procurement with Corruption. Rand Journal of Economics. 2004;35:50–68. [Google Scholar]
- Compte O, Lambert-Mogiliansky A, Verdier T. Corruption and Competition in Procurement Auctions. Rand Journal of Economics. 2005;36:1–15. [Google Scholar]
- Ding C, Knaap G. Urban Land Policy Reforming China’s Transitional Economy. In: Ding, Song, editors. Emerging Land and Housing Markets in China. 2005. [Google Scholar]
- DiPasquale D, Wheaton WC. Urban Economics and Real Estate Markets. Prentice Hall; 1996. [Google Scholar]
- Evans WN, Schwab RM. Finishing High School and Starting College. Quarterly Journal of Economics. 1995;110:941–974. [Google Scholar]
- Fraker T, Moffitt R. The Effects of Food Stamps on Labor Supply: a Bivariate Selection Model. Journal of Public Economics. 1988;35:25–56. [Google Scholar]
- Genz A. Numerical Computation of Rectangular Bivariate and Trivariate Normal and t Probabilities. Statistics and Computing. 2004;14:151–160. [Google Scholar]
- Goux D, Maurin E. Returns to Firm-Provided Training: Evidence from Worker-Firm Matched Data. Labour Economics. 2000;7:1–19. [Google Scholar]
- Greene WH. Gender Economics Courses in Liberal Arts Colleges: Further Results. Research in Economic Education. 1998:291–299. [Google Scholar]
- Heckman JJ. Dummy Endogenous Variable in a Simultaneous Equations System. Econometrica. 1978;46:931–970. [Google Scholar]
- Heckman JJ. Varieties of Selection Bias. Papers and Proceedings of the American Economic Association. 1990;80:313–318. [Google Scholar]
- Heckman JJ. Instrumental variables: A Study of Implicit Behavioral Assumptions Used in Making Program Evaluations. Journal of Human Resources. 1997;32:441–462. [Google Scholar]
- Lee L-F, Maddala GS, Trost RP. Asymptotic Covariance Matrices of Two-Stage Probit and Two-Stage Tobit Methods for Simultaneous Equations Models with Selectivity. Econometrica. 1980;48:491–512. [Google Scholar]
- McAfee RP. Bidding Rings. American Economic Review. 1992;82:579–599. [Google Scholar]
- Milgrom PR, Weber R. A Theory of Auctions and Competitive Bidding. Econometrica. 1982;50:1089–1122. [Google Scholar]
- Menezes FM, Monteiro PK. Corruption and Auctions. Journal of Mathematical Economics. 2006;42:97–108. [Google Scholar]
- Mulligan CB, Rubinstein Y. Selection, Investment, and Women’s Relative Wages Over Time. Quarterly Journal of Economics. 2008:1061–1110. [Google Scholar]
- Ockenfels A, Roth A. Last-Minute Bidding and the Rules for Ending Second-Price Auctions: Evidence from eBay and Amazon Auctions on the Internet. American Economic Review. 2002;92:1093–1103. [Google Scholar]
- Pashigian P, Bowen B. What are Products on Sale?: Explanation of Pricing Regularities. Quarterly Journal of Economics. 1991;106:1015–1038. [Google Scholar]
- Reize F. FIML Estimation of a Bivariate Probit Selection Rule—an Application on Firm Growth and Subsidisation. 2001 ZEW Discussion paper No. 01-13. [Google Scholar]
- Shapiro JM. Is There a Daily Discount Rate: Evidence from Food Stamp Nutrition Cycle. Journal of Public Economics. 2005;89:303–325. [Google Scholar]
- Tan G, Yilankaya O. Equilibria in Second Price Auctions with Participation Costs. Journal of Economic Theory. 2006;130:153–169. [Google Scholar]
- Valleta W. The Land Administration Law of 1978. In: Ding, Song, editors. Emerging Land and Housing Market in China. 2005. [Google Scholar]
- Vella M, Verbeek Estimating and interpreting Models with Endogenous Treatment Effects. Journal of Business Economics and Statistics. 1999 [Google Scholar]
- Wooldridge JM. Econometric Analysis of Cross Section and Panel Data. MIT press; 2002. [Google Scholar]
- Wooldridge JM. Instrumental Variables estimation of the Average Treatment Effect in the Correlated Random Coefficient Model. Michigan State University mimeo; 2007. [Google Scholar]
- Zhu J. From Land Use Right to Land Development Right. Urban Studies. 2004;4(2004):1249–1269. [Google Scholar]
- Zhu J. Transitional Institution for the Emerging Land Market in China. Urban Studies. 2005;42:1369–1390. [Google Scholar]