Abstract
Recent research in neuroimaging has focused on assessing associations between genetic variants that are measured on a genomewide scale and brain imaging phenotypes. A large number of works in the area apply massively univariate analyses on a genomewide basis to find single nucleotide polymorphisms that influence brain structure. In this paper, we propose using various dimensionality reduction methods on both brain structural MRI scans and genomic data, motivated by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) study. We also consider a new multiple testing adjustment method and compare it with two existing false discovery rate (FDR) adjustment methods. The simulation results suggest an increase in power for the proposed method. The real-data analysis suggests that the proposed procedure is able to find associations between genetic variants and brain volume differences that offer potentially new biological insights.
Keywords: Distance covariance, Genomewide association studies, Local false discovery rate, Multivariate analysis, Neuroimaging analysis, Positive false discovery rate
1. Introduction
Advanced automated image processing techniques have allowed the assessment of the genetic association with brain phenotypes for complex diseases, such as schizophrenia (Potkin and others, 2009), and Alzheimer’s disease (AD) (Furney and others, 2010). In this work, we consider data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) project (ADNI, 2003) consisting of genetic variants encoded as single nucleotide polymorphisms (SNPs) across whole genome, and brain volume size measured by tensor-based morphometry (TBM) based on structural magnetic resonance imaging (MRI) scans. Specifically, TBM computes the volume of a local brain region in a given subjects’ MRI relative to an average template image based on healthy subjects. Since a signature of AD is the thinning of cortical gray matter and an increase of cerebral spinal fluid volume (particularly in the ventricles), TBM is sensitive to AD-related changes through decreases in volume of the cortex, and increases in volume of the ventricles. Therefore, the goal of this work is to find the genetic variants that result in change of brain volumes.
Stein and others (2010a) conducted a voxelwide and genomewide study using TBM maps from each subject, where each voxel is evaluated with a regression at each SNP based on the SNP’s minor allele count, and using demographic variables as features with quantitative trait as responses. In their experiment, no significant loci were found after a false discovery rate (FDR) based on the multiple testing adjustment procedure at level 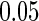 . In a later study, Stein and others (2010b) performed a genomewide search on two brain phenotypes (temporal lobe and hippocampal volume) based on the prior results from the literature. To investigate the associations, they collected an independent sample for each phenotype and performed adjusted regression analysis on the baseline population. Overall, two significantly associated SNPs were identified:
. In a later study, Stein and others (2010b) performed a genomewide search on two brain phenotypes (temporal lobe and hippocampal volume) based on the prior results from the literature. To investigate the associations, they collected an independent sample for each phenotype and performed adjusted regression analysis on the baseline population. Overall, two significantly associated SNPs were identified: 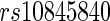 , located on chromosome 12 within an intron of the
, located on chromosome 12 within an intron of the 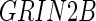 gene, and
gene, and 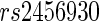 , which is in an intergenic region of chromosome 15. Both SNPs were significantly associated with bilateral temporal lobe volume, while no significant SNPs were found to have associations with hippocampal phenotype.
, which is in an intergenic region of chromosome 15. Both SNPs were significantly associated with bilateral temporal lobe volume, while no significant SNPs were found to have associations with hippocampal phenotype.
For any univariate approach to analysis, multiple testing procedures should be employed as there are many statistical tests being considered simultaneously. A recent error quantity called FDR was proposed for the multiple comparisons problem by Benjamini and Hochberg (1995). Later, Storey (2002, 2003) defined the positive false discovery rate (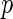 FDR) that is the conditional expectation of false-positive findings given at least one positive identifications has occurred, and also proposed a
FDR) that is the conditional expectation of false-positive findings given at least one positive identifications has occurred, and also proposed a 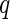 -value algorithm to control the
-value algorithm to control the 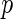 FDR. Efron and others (2001b) defined a local false discovery rate (locfdr), a Bayesian version of FDR. For its estimation, they fit a mixture model to a Gaussian transformation of the inverse cumulative distribution of the
FDR. Efron and others (2001b) defined a local false discovery rate (locfdr), a Bayesian version of FDR. For its estimation, they fit a mixture model to a Gaussian transformation of the inverse cumulative distribution of the 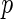 -values. To relate the frequentist and Bayesian versions of FDR, Efron and others (2001b), Efron and others (2001a) and Storey (2002) proved that the FDR controlled by the Benjamini and Hochberg procedure is equivalent to empirical Bayesian FDR given the rejection regions. Furthermore, Newton and others (2003) proposed a hierarchical mixture of Gammas for the multiple comparisons problem and Muralidharan (2010) showed that the locfdr estimation controls FDR/
-values. To relate the frequentist and Bayesian versions of FDR, Efron and others (2001b), Efron and others (2001a) and Storey (2002) proved that the FDR controlled by the Benjamini and Hochberg procedure is equivalent to empirical Bayesian FDR given the rejection regions. Furthermore, Newton and others (2003) proposed a hierarchical mixture of Gammas for the multiple comparisons problem and Muralidharan (2010) showed that the locfdr estimation controls FDR/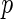 FDR over the entire exponential distribution family.
FDR over the entire exponential distribution family.
The previously published ADNI analyses were able to find associated SNPs or genes that are likely to be related to some specific voxels of the brain scans. However, neighboring structures of the brain were not being considered, and this information could play an important role in associations with disease risk. In this work, this issue is addressed by combining the neighboring voxels into 119 regions based on the GSK CIC atlas (Tziortzi and others, 2011), and then the effects on the regions are simultaneously assessed using the distance covariance statistic (Szekely and others, 2007), which allows for inference on the relationship between a 119-dimensional multivariate phenotype and a single SNP predictor across the entire genome.
We make two contributions to the analysis of the ADNI neuroimaging genomewide study. First, we utilize distance covariance for the analysis of genomewide association study. This framework is able to establish the relationships between genomic variants and brain structural MRI where the entire brain is a multivariate response. By considering a multivariate response variable, we reduce the number of tests being done relative to an approach such as in Stein and others (2010a), which results in more powerful inference. Second, we propose a local fdr modeling algorithm to address the multiplicity which is to fit a two-component mixture of Gammas on the distance covariance statistics. One probabilistic output of this model is the local fdr. This leads to a decision-theoretic rule for selecting significant SNPs that is related to the approach of Newton and others (2003). In the multiple testing step, we also evaluate two existing methods for comparison. Based on our simulation studies and real data analysis using ADNI, experiments show that the proposed method is able to control FDR at different 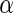 levels as well as provide more powerful findings than Stein and others (2010a)’s work. In addition, we also present the pathway analysis based on our significant findings in the supplementary material available at Biostatistics online, and show that the significant SNPs survived from our procedures provide signal enrichment functions through pathway to AD from the database for annotation, visualization and integrated discovery (DAVID).
levels as well as provide more powerful findings than Stein and others (2010a)’s work. In addition, we also present the pathway analysis based on our significant findings in the supplementary material available at Biostatistics online, and show that the significant SNPs survived from our procedures provide signal enrichment functions through pathway to AD from the database for annotation, visualization and integrated discovery (DAVID).
2. Materials
Data used in the preparation of this article were obtained from the ADNI study (ADNI, 2003). The SNP data and the TBM data from the ADNI study are processed by Paul Thompson’s group, which are the same as those used in the previous studies (Stein and others, 2010a). For the sake of completeness, we describe the genetic and imaging data preprocessing in the following section.
2.1. ADNI study
The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a 60 million, 5-year public–private partnership. The primary goal of ADNI has been to test whether serial MRI, positron emission tomography, other biological markers and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early AD. Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. The principal investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California San Francisco. ADNI is the result of efforts of many co-investigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the United States of America and Canada. The initial goal of ADNI was to recruit 800 subjects, but ADNI has been followed by ADNI-GO and ADNI-2. To date these three protocols have recruited over 1500 adults, ages 55 to 90, to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow-up duration of each group is specified in the protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org.
Of the 852 total subjects released by the ADNI dataset, the availabilities of both brain structural MRI and genetics records were found in 741 subjects. The data for these subjects are used for our experiments, where the volumetric brain differences are assessed in 206 normal older controls, 358 MCI subjects and 177 AD patients.
2.2. Genetic analysis
ADNI released 620901 SNPs using the Illumina 610 Quad array. SNPs that did not fulfil the following quality control criteria were excluded: genotype call rate smaller than 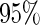 , significant deviation from the Hardy–Weinberg equilibrium where
, significant deviation from the Hardy–Weinberg equilibrium where 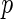 -value
-value 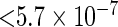 , allele frequency smaller than 0.10, and a quality control score of smaller than 0.15. After applying this list of quality criteria, we obtain a total of 448244 SNPs for the analysis. The number of SNPs measured on each chromosome is in Table 1 in our supplementary material available at Biostatistics online.
, allele frequency smaller than 0.10, and a quality control score of smaller than 0.15. After applying this list of quality criteria, we obtain a total of 448244 SNPs for the analysis. The number of SNPs measured on each chromosome is in Table 1 in our supplementary material available at Biostatistics online.
Table 1.
Summary of the possible outcomes for all 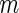 hypotheses
hypotheses
| Accept null hypothesis | Reject null hypothesis | Total | |
|---|---|---|---|
| Null true | 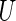 |
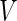 |
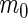 |
| Alternative true | 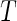 |
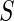 |
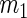 |
 |
 |
 |
2.3. Brain MRI scans
Three-dimensional 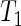 -weighted baseline MRI scans were analyzed using TBM: a method for representing structural differences between local brain regions and a template brain into a deformation field (Friston and others, 2004). The deformation field contains the information on relative positions of different brain scans, while the local shapes (such as volumes, lengths and areas) are encoded in the Jacobian matrix. Therefore, TBM can be used to recognize the local shape of brain differences. The MRI scans were acquired at 58 different ADNI sites, all with 1.5T MRI scanners using a sagittal 3D MP-RAGE sequence for across-site consistency (Jack and others, 2008). All images were calibrated with phantom-based geometric corrections. The scans were linearly registered with nine parameters to the International Consortium for Brain Image template (Mazziotta and others, 2001) to adjust for differences in brain position and scaling. Each subject’s MRI scan was registered against a template scan which is the average of all the healthy subjects (minimal deformation template), using a non-linear inverse-consistent elastic intensity-based registration method (Leow and others, 2005). Furthermore, voxel size variation from registration is represented as the voxel intensity, which is the volumetric difference between the subject and the reference template, calculated from taking the determinant of the Jacobian matrix of the deformation fields. Finally, each brain scan volume is down-sampled to
-weighted baseline MRI scans were analyzed using TBM: a method for representing structural differences between local brain regions and a template brain into a deformation field (Friston and others, 2004). The deformation field contains the information on relative positions of different brain scans, while the local shapes (such as volumes, lengths and areas) are encoded in the Jacobian matrix. Therefore, TBM can be used to recognize the local shape of brain differences. The MRI scans were acquired at 58 different ADNI sites, all with 1.5T MRI scanners using a sagittal 3D MP-RAGE sequence for across-site consistency (Jack and others, 2008). All images were calibrated with phantom-based geometric corrections. The scans were linearly registered with nine parameters to the International Consortium for Brain Image template (Mazziotta and others, 2001) to adjust for differences in brain position and scaling. Each subject’s MRI scan was registered against a template scan which is the average of all the healthy subjects (minimal deformation template), using a non-linear inverse-consistent elastic intensity-based registration method (Leow and others, 2005). Furthermore, voxel size variation from registration is represented as the voxel intensity, which is the volumetric difference between the subject and the reference template, calculated from taking the determinant of the Jacobian matrix of the deformation fields. Finally, each brain scan volume is down-sampled to 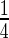 of its original size (using trilinear interpolation to
of its original size (using trilinear interpolation to 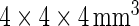 ), which results into
), which results into 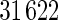 total voxels per scan for faster experimental processing. Similar to Stein and others (2010a), we use the volumetric difference representation of MRI as the quantitative measure of brain tissue volume difference for the genomewide association analysis.
total voxels per scan for faster experimental processing. Similar to Stein and others (2010a), we use the volumetric difference representation of MRI as the quantitative measure of brain tissue volume difference for the genomewide association analysis.
We explore genomewide associations with brain volume difference in terms of voxels; we also perform the same analysis based on groups of voxels, which is the focus of this work. This region of interests (ROIs) approach is a type of dimensionality reduction method that allows for information on local neighborhoods of voxels to be pooled, and reduces possible noise that associates with performing analysis using the entire brain voxels, we denote this as the region-wide study. To conduct the experiment using 119 ROIs, we extracted voxels from each brain region, and computed the average Jacobian scores (per region) that make up the 119 different brain regions from the GSK CIC Atlas as shown in Figure 1, which is based on the Harvard–Oxford atlas with a six-level hierarchy. To extract the corresponding voxels from each brain region in the atlas, we used the FLIRT linear registration tool from FSL (Jenkinson and Smith, 2001; Jenkinson and others, 2002; Smith and others, 2004; Woolrich and others, 2009) in order to register the brain atlas to our template scan. This allows us to extract voxels of different brain regions from the subject’s scan and the registered atlas by direct comparison. We then used the average per-region Jacobian scores from each of the 119 ROIs as the response into genomewide association.
Fig. 1.
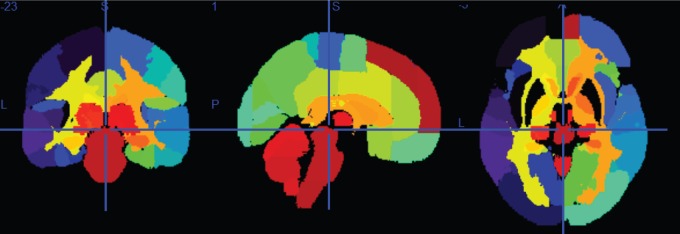
Plots showing from left to right: coronal, sagittal and axial views of GSK CIC Atlas, color coded by the 119 ROIs.
3. Methods
3.1. Distance covariance
The work of distance covariance in Szekely and others (2007) and Szekely and Rizzo (2009) is discussed here. Let 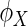 and
and 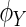 be the characteristic functions of
be the characteristic functions of 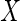 and
and 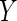 , where
, where 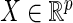 and
and 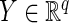 are two random vectors from two arbitrary dimensions
are two random vectors from two arbitrary dimensions 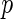 and
and 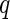 , respectively. The distance covariance
, respectively. The distance covariance 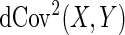 between random vectors
between random vectors 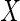 and
and 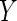 is a non-negative value with finite first moments
is a non-negative value with finite first moments
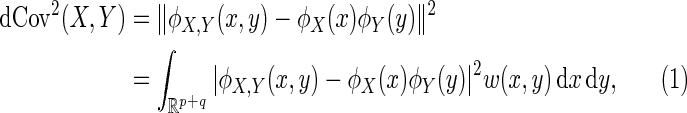 |
(3.1) |
where 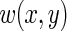 is a positive weight function for which the integral in (3.1) exists.
is a positive weight function for which the integral in (3.1) exists.
The sample distance covariance estimator from Szekely and others (2007) and Szekely and Rizzo (2009) requires that there be no missing values among observations 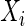 ’s and
’s and 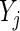 ’s for
’s for  . To relax this requirement, we propose a modified version by assuming the data is missing completely at random (MCAR, Heitjan and Basu, 1996). Here,
. To relax this requirement, we propose a modified version by assuming the data is missing completely at random (MCAR, Heitjan and Basu, 1996). Here, 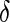 is defined as an indicator which indicates if a variable is missing or present
is defined as an indicator which indicates if a variable is missing or present
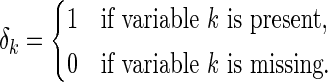 |
(3.2) |
Adjusting the indicator  for observations
for observations 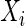 ’s and
’s and 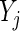 ’s puts larger weights on observations with no missing values and zero weight on observations with missing values. For
’s puts larger weights on observations with no missing values and zero weight on observations with missing values. For 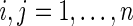 , Our modified preliminary statistics according to Szekely and others (2007) as
, Our modified preliminary statistics according to Szekely and others (2007) as 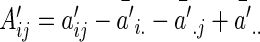 , where
, where
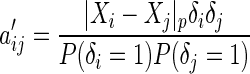 |
(3.3) |
and
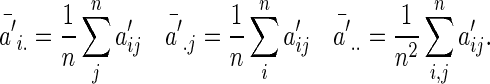 |
Similarly, we define 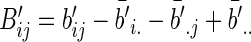 with its elements taking the same form as
with its elements taking the same form as 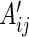 .
.
The modified sample distance covariance 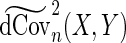 is then given by
is then given by 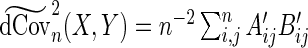 . Having proposed a modified empirical distance covariance for situations where missing values are present, we can study its asymptotic property under the independent assumption. The expectation of
. Having proposed a modified empirical distance covariance for situations where missing values are present, we can study its asymptotic property under the independent assumption. The expectation of 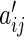 in (3.3) is
in (3.3) is
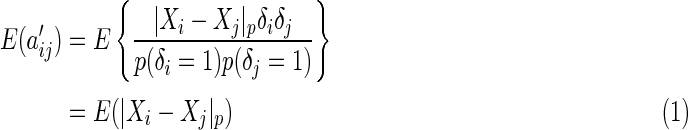 |
(3.4) |
and similarly, 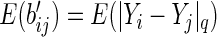 . Arguing as in Szekely and others (2007), we have that if
. Arguing as in Szekely and others (2007), we have that if 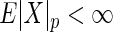 and
and 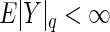 , then
, then 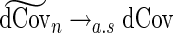 . Consequently, it can be shown that
. Consequently, it can be shown that
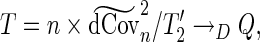 |
(3.5) |
where 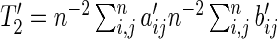 and
and 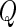 is a positive semidefinite quadratic form of centered Gaussian random variables with
is a positive semidefinite quadratic form of centered Gaussian random variables with 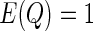 . Szekely and others (2007) proposed a permutation test for hypothesis testing. However, the permutation scheme is extremely computationally expensive when dealing with large scale data such as our genomewide association study. In terms of obtaining
. Szekely and others (2007) proposed a permutation test for hypothesis testing. However, the permutation scheme is extremely computationally expensive when dealing with large scale data such as our genomewide association study. In terms of obtaining 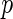 -values, we apply a Gamma approximation for inference on the distance covariance statistics (Gretton and others, 2008), which is discussed in Section 3.2.
-values, we apply a Gamma approximation for inference on the distance covariance statistics (Gretton and others, 2008), which is discussed in Section 3.2.
For comparison purposes, we also investigate the case of missing at random (MAR) for imputing the missing values using a publicly available software PLINK (PLINK, 2007). The results from the genotype imputation are addressed in Section 5.
3.2. Multiple testing procedure
We now review the multiple testing problem and define FDR. Assume that there are 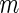 tests for the study, the goal is to identify the significant SNPs at a certain
tests for the study, the goal is to identify the significant SNPs at a certain 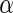 level. Table 1 shows the possible outcomes of conducting
level. Table 1 shows the possible outcomes of conducting  tests simultaneously, for which the null hypothesis is true in
tests simultaneously, for which the null hypothesis is true in 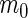 of them. Of the
of them. Of the 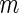 tests of hypotheses,
tests of hypotheses, 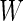 hypotheses are failed to be rejected and
hypotheses are failed to be rejected and 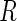 rejected the null hypothesis.
rejected the null hypothesis.
Benjamini and Hochberg (1995) introduced a new measure called FDR, defined as
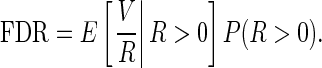 |
(3.6) |
Storey (2002, 2003) proposed another measure, 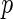 FDR, which is the expected false-positive rate conditioned on positive finding (
FDR, which is the expected false-positive rate conditioned on positive finding (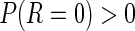 ). The
). The 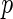 FDR takes the following form:
FDR takes the following form:
 |
(3.7) |
Our aim is to control 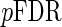 , and we present three algorithms to achieve this goal for the remainder of this section.
, and we present three algorithms to achieve this goal for the remainder of this section.
The first algorithm is the 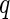 -value algorithm, which was first presented by Storey (2002).
-value algorithm, which was first presented by Storey (2002). 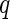 -value requires that the prior knowledge of the null distribution of the test is known, such that the
-value requires that the prior knowledge of the null distribution of the test is known, such that the 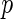 -values can be computed under the null density. In the case of distance covariance, Gretton and others (2008) proposed to fit a Gamma distribution as the null density, with the following parameters:
-values can be computed under the null density. In the case of distance covariance, Gretton and others (2008) proposed to fit a Gamma distribution as the null density, with the following parameters:
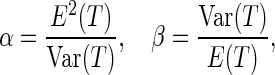 |
(3.8) |
where 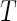 is defined as (3.5). Hence, the parameters in (3.8) can be estimated by the distance covariance statistics, and the
is defined as (3.5). Hence, the parameters in (3.8) can be estimated by the distance covariance statistics, and the 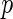 -values are able to be computed from the Gamma approximation for the
-values are able to be computed from the Gamma approximation for the 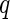 -value method. The algorithm for the
-value method. The algorithm for the 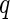 -value method is as follows: first, for each
-value method is as follows: first, for each 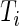 , we compute the
, we compute the 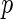 -value
-value 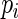 under the Gamma approximation; we then compute
under the Gamma approximation; we then compute 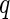 -values
-values 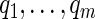 for each test using the method of Storey (2003); by defining
for each test using the method of Storey (2003); by defining 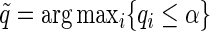 , we reject all tests with
, we reject all tests with 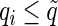 . Storey (2002, 2003) have showed that the
. Storey (2002, 2003) have showed that the 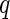 -value algorithm controls FDR under the desired
-value algorithm controls FDR under the desired 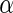 level, which is referred to as Algorithm 1 hereafter. Note that step 2 of the above algorithm is computed using the publicly available R-package qvalue.
level, which is referred to as Algorithm 1 hereafter. Note that step 2 of the above algorithm is computed using the publicly available R-package qvalue.
The second algorithm uses local fdr ((5.1) in Efron and others (2001b)) to control 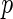 FDR. In Efron and others (2001b)’s work, the null distribution is assumed either known or collected by permutation. Here, we chose to use a Gamma approximation with empirical estimations of (3.8) as the null density candidate for distance covariance statistics, and the detailed derivations are presented in Section 2 of the supplementary material available at Biostatistics online. The following is a summary of Efron and others (2001b)’s work.
FDR. In Efron and others (2001b)’s work, the null distribution is assumed either known or collected by permutation. Here, we chose to use a Gamma approximation with empirical estimations of (3.8) as the null density candidate for distance covariance statistics, and the detailed derivations are presented in Section 2 of the supplementary material available at Biostatistics online. The following is a summary of Efron and others (2001b)’s work.
We now propose a new algorithm (denoted as local fdr modeling) for multiple testing adjustment. The traditional multiple correction methods are based on 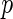 -values (e.g. Algorithms 1 and 2), while our proposed method models the test statistics directly. The algorithm for the local fdr modeling is similar to Algorithm 2, but skipping the second step. This rule is similar to the one proposed by Newton and others (2003) in a different genomics setting, where more powerful inference can be obtained by not mapping the test statistics from
-values (e.g. Algorithms 1 and 2), while our proposed method models the test statistics directly. The algorithm for the local fdr modeling is similar to Algorithm 2, but skipping the second step. This rule is similar to the one proposed by Newton and others (2003) in a different genomics setting, where more powerful inference can be obtained by not mapping the test statistics from  ’s to
’s to 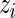 ’s.
’s.
 |
 |
4. Simulation study and real-data analysis
We have implemented distance covariance in Matlab for our experiments. The R packages qvalue, mixfdr and mixtools were used for the multiple testing procedures. All the analyses were accomplished by using the university high performance computing cluster, which consists of 128 Intel Xeon E5450 nodes, each with 8 cores and 32 GB of memory.
4.1. Simulation design
To evaluate the methods described in Section 3, we simulated the data to examine the FDRs and power estimates by controlling 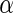 at desired levels, and the settings of the simulation study were to mimic the structure of the genotypes and the phenotypes of the ADNI study. We considered two types of correlations (i.e. the pure linear correlation, and the mixed linear and non-linear correlations) and the impact of univariate and multivariate effects into three simulation settings. For each setting, the samples were generated from a null and an alternative population, and 1000 genotypes were generated for multiple testing. Then, we examined the association one genotype at a time across the 1000 genotypes for the following three settings. In this first case, we generated 50 paired samples: each pair included a single genotype and a phenotype, and followed a bivariate Normal distribution, where the correlation coefficient
at desired levels, and the settings of the simulation study were to mimic the structure of the genotypes and the phenotypes of the ADNI study. We considered two types of correlations (i.e. the pure linear correlation, and the mixed linear and non-linear correlations) and the impact of univariate and multivariate effects into three simulation settings. For each setting, the samples were generated from a null and an alternative population, and 1000 genotypes were generated for multiple testing. Then, we examined the association one genotype at a time across the 1000 genotypes for the following three settings. In this first case, we generated 50 paired samples: each pair included a single genotype and a phenotype, and followed a bivariate Normal distribution, where the correlation coefficient 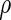 was
was 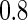 under the alternative or around zero under the null. For the second and the third case, the sample size was 100, and the univariate genotype was generated from
under the alternative or around zero under the null. For the second and the third case, the sample size was 100, and the univariate genotype was generated from 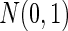 while the dimensions of phenotype were enlarged to 30. The
while the dimensions of phenotype were enlarged to 30. The 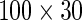 phenotype data formed the mixed association effects between phenotypes and the genotypes under the alternative, where the mixed associations were linear, exponential and quadratic transformations (i.e. 10 duplicated copies of 100 genotypes; 10 exponential transformations of 100 genotypes and 10 quadratic forms of 100 genotypes). For the null population, the single genotype again was generated from
phenotype data formed the mixed association effects between phenotypes and the genotypes under the alternative, where the mixed associations were linear, exponential and quadratic transformations (i.e. 10 duplicated copies of 100 genotypes; 10 exponential transformations of 100 genotypes and 10 quadratic forms of 100 genotypes). For the null population, the single genotype again was generated from 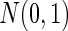 and the 30-dimensional phenotypes followed a multivariate Normal with mean 0 and covariance matrix
and the 30-dimensional phenotypes followed a multivariate Normal with mean 0 and covariance matrix 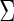 , where
, where 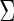 was independent in the second simulation design and positive dependent (diagonal terms are one and off diagonal terms are 0.5) on third case. The ratio between the null and alternative population was 19:1, and a total of 1000 runs were repeated for each setting to assess the FDRs and power performances.
was independent in the second simulation design and positive dependent (diagonal terms are one and off diagonal terms are 0.5) on third case. The ratio between the null and alternative population was 19:1, and a total of 1000 runs were repeated for each setting to assess the FDRs and power performances.
4.2. Simulation results
Three FDR procedures were presented in Section 3.2, which we summarize again in the following:
Algorithm 1:
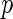 -values (from Gamma approximation) +
-values (from Gamma approximation) + 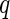 -value method (Storey 2003).
-value method (Storey 2003).Algorithm 2:
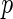 -values (from Gamma approximation) + local fdr method (Efron and others, 2001a).
-values (from Gamma approximation) + local fdr method (Efron and others, 2001a).Algorithm 3: local fdr modeling proposed in Section 3.2.
Before the discussion of the FDRs and power estimates of three algorithms, we performed size analysis to evaluate whether a Gamma approximation (Gretton and others, 2008) is a proper null density for Algorithms 1 and 2. We generated 1000 (genotypes vs phenotypes) samples for the size analysis, where the associations were all from the null population for the three simulation settings; 50 runs were repeated to calculate the size. Table 2 reports the size estimates according to nominal values from 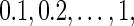 and the size estimates are very close to their corresponding nominal values for all three simulations. Therefore, we concluded that the Gamma approximation is an appropriate null distribution for the distance covariance statistic.
and the size estimates are very close to their corresponding nominal values for all three simulations. Therefore, we concluded that the Gamma approximation is an appropriate null distribution for the distance covariance statistic.
Table 2.
The empirical size results from the three simulations for the size analysis
| Size | Simulation 1 | Simulation 2 | Simulation 3 |
|---|---|---|---|
| 0.1 | 0.115 | 0.110 | 0.110 |
| 0.2 | 0.219 | 0.221 | 0.224 |
| 0.3 | 0.309 | 0.324 | 0.326 |
| 0.4 | 0.392 | 0.415 | 0.416 |
| 0.5 | 0.472 | 0.498 | 0.499 |
| 0.6 | 0.556 | 0.576 | 0.578 |
| 0.7 | 0.653 | 0.656 | 0.658 |
| 0.8 | 0.775 | 0.746 | 0.748 |
| 0.9 | 0.940 | 0.878 | 0.877 |
| 1.0 | 1.000 | 1.000 | 1.000 |
Table 3 shows the average FDRs, the average powers, and their standard errors at nominal 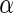 levels 0.05, 0.1, 0.15 and 0.2 for the three simulations. The results show that the average FDRs are all close or lower to the desired
levels 0.05, 0.1, 0.15 and 0.2 for the three simulations. The results show that the average FDRs are all close or lower to the desired 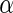 values. The powers of Algorithm 2 and 3 outperform Algorithm 1 for all
values. The powers of Algorithm 2 and 3 outperform Algorithm 1 for all 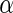 values; this implies the algorithms which utilize the local fdr method result in powerful inference. In addition, the average estimated power of simulation 3 is smaller but close to the power of simulation 2 at each level. This shows that the results of all multiple testing adjusted algorithms are slightly affected by the noise of the dependent covariance structure, but the overall performances are robust. Furthermore, the results of Algorithms 2 and 3 are similar in our simulation studies, and this suggests that Algorithm 3 controls FDR well.
values; this implies the algorithms which utilize the local fdr method result in powerful inference. In addition, the average estimated power of simulation 3 is smaller but close to the power of simulation 2 at each level. This shows that the results of all multiple testing adjusted algorithms are slightly affected by the noise of the dependent covariance structure, but the overall performances are robust. Furthermore, the results of Algorithms 2 and 3 are similar in our simulation studies, and this suggests that Algorithm 3 controls FDR well.
Table 3.
Simulation results of the average FDR estimates 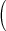 with standard error
with standard error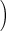 and the average power estimates
and the average power estimates 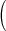 with standard error
with standard error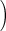 of the three algorithms described in Section 3.2.
of the three algorithms described in Section 3.2.
 |
Algorithm 1: 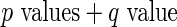 |
Algorithm 2: 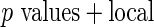 fdr fdr |
Algorithm 3: local fdr modeling |
||||
|---|---|---|---|---|---|---|---|
| FDR (s.e.) | power (s.e.) | FDR (s.e.) | power (s.e.) | FDR (s.e.) | power (s.e.) | ||
| Simulation 1 | 0.05 | 0.000 (0.000) | 0.000 (0.000) | 0.019 (0.026) | 0.882 (0.065) | 0.039 (0.121) | 0.904 (0.068) |
| 0.10 | 0.006 (0.011) | 0.691 (0.114) | 0.063 (0.050) | 0.964 (0.032) | 0.080 (0.122) | 0.965 (0.033) | |
| 0.15 | 0.007 (0.012) | 0.777 (0.142) | 0.121 (0.068) | 0.985 (0.019) | 0.128 (0.127) | 0.984 (0.020) | |
| 0.20 | 0.028 (0.076) | 0.900 (0.085) | 0.186 (0.080) | 0.993 (0.013) | 0.184 (0.126) | 0.990 (0.029) | |
| Simulation 2 | 0.05 | 0.000 (0.000) | 0.000 (0.000) | 0.020 (0.026) | 0.801 (0.106) | 0.035 (0.044) | 0.882 (0.087) |
| 0.10 | 0.000 (0.000) | 0.035 (0.026) | 0.071 (0.051) | 0.916 (0.085) | 0.088 (0.061) | 0.934 (0.038) | |
| 0.15 | 0.002 (0.007) | 0.467 (0.175) | 0.134 (0.070) | 0.950 (0.064) | 0.150 (0.075) | 0.959 (0.025) | |
| 0.20 | 0.008 (0.016) | 0.665 (0.159) | 0.194 (0.080) | 0.964 (0.048) | 0.212 (0.082) | 0.970 (0.016) | |
| Simulation 3 | 0.05 | 0.000 (0.000) | 0.000 (0.000) | 0.017 (0.024) | 0.758 (0.095) | 0.030 (0.033) | 0.844 (0.066) |
| 0.10 | 0.000 (0.000) | 0.020 (0.000) | 0.064 (0.051) | 0.899 (0.059) | 0.084 (0.070) | 0.918 (0.045) | |
| 0.15 | 0.002 (0.007) | 0.418 (0.179) | 0.126 (0.070) | 0.944 (0.036) | 0.145 (0.091) | 0.951 (0.029) | |
| 0.20 | 0.004 (0.011) | 0.572 (0.159) | 0.194 (0.084) | 0.963 (0.024) | 0.208 (0.103) | 0.965 (0.029) | |
Simulation  is based on linear correlation
is based on linear correlation simulation
simulation 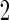 is based on mixed correlations with independent covariance matrix and simulation
is based on mixed correlations with independent covariance matrix and simulation  is based on mixed correlations with dependent covariance matrix in Section 4.1.
is based on mixed correlations with dependent covariance matrix in Section 4.1.
4.3. Application to ADNI data sets
We evaluated the three algorithms using the ADNI dataset. For each test, the independent variable is a single SNP across the whole genome (448244 SNPs). The multivariate response is a 119 dimensional vector (i.e. 119 ROIs), with each value corresponding to the average voxel value for such brain region, based on the GSK CIC Atlas. We also considered the entire brain imaging voxels (31 622 voxels) as another multivariate response for ADNI study, and the results are shown in supplementary material available at Biostatistics online. In addition to the three algorithms described in Section 3.2, we also implemented a modified version of Stein and others (2010a)’s work, in which they originally considered simple linear regression (slr) as the association test between a single SNP and brain a voxel, with our modification being a single SNP and a brain region. For this method, we selected the brain region with the highest  -value at each SNP, then use the local fdr method to perform multiple testing adjustment. This procedure is denoted as Algorithm 4 (
-value at each SNP, then use the local fdr method to perform multiple testing adjustment. This procedure is denoted as Algorithm 4 (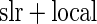 fdr method).
fdr method).
Table 4 displays the number of significant SNPs controlled by the 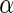 values from each algorithm. Note that there were 1180 significant SNPs with
values from each algorithm. Note that there were 1180 significant SNPs with 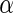 at 0.5 in Algorithm 4 (Stein and others, 2010a), while Algorithms 2 and 3 resulted in
at 0.5 in Algorithm 4 (Stein and others, 2010a), while Algorithms 2 and 3 resulted in 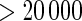 findings, with Algorithm 1 yielded slightly above 5000 SNPs at
findings, with Algorithm 1 yielded slightly above 5000 SNPs at 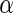 level 0.05. To compare the inference information of the significant SNPs in Table 4, the top 1180 SNPs were selected from each of the algorithm as the input variables for disease status classification. Specifically, we performed binary disease status classification (206 normal patients against 177 ADs) due to the fact that AD is the definitive form of the illness with much higher severity than MCI. We used LIBSVM (Chang and Lin, 2011) for binary classification with leave-one-out to compute the prediction accuracy. The majority count was 53.786%, and the prediction accuracy of top 1180 SNPs from Algorithm 1–3 were all 57.441%, as the top 1180 SNPs from the three algorithms were exactly the same. The prediction accuracy of Algorithm 4 was the same as the majority count. In addition, Algorithms 1–3 at
level 0.05. To compare the inference information of the significant SNPs in Table 4, the top 1180 SNPs were selected from each of the algorithm as the input variables for disease status classification. Specifically, we performed binary disease status classification (206 normal patients against 177 ADs) due to the fact that AD is the definitive form of the illness with much higher severity than MCI. We used LIBSVM (Chang and Lin, 2011) for binary classification with leave-one-out to compute the prediction accuracy. The majority count was 53.786%, and the prediction accuracy of top 1180 SNPs from Algorithm 1–3 were all 57.441%, as the top 1180 SNPs from the three algorithms were exactly the same. The prediction accuracy of Algorithm 4 was the same as the majority count. In addition, Algorithms 1–3 at 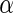 level 0.05 found 5388, 27965 and 23128 significant SNPs (Table 4), and these SNPs yielded 57.964%, 62.141% and 62.402% prediction accuracies, respectively. We have also performed the functional annotation clustering analysis using DAVID v6.7 (DAVID, 2003). Table 5 lists the top eight clusters enrichment scores and the total enrichment scores. Since the top 1180 SNPs from algorithms 1, 2 and 3 were identical, the enrichment scores from these three algorithms were also the same, with each having a total score of 10.257 which is greater than the total enrichment score of 5.739 from Algorithm 4.
level 0.05 found 5388, 27965 and 23128 significant SNPs (Table 4), and these SNPs yielded 57.964%, 62.141% and 62.402% prediction accuracies, respectively. We have also performed the functional annotation clustering analysis using DAVID v6.7 (DAVID, 2003). Table 5 lists the top eight clusters enrichment scores and the total enrichment scores. Since the top 1180 SNPs from algorithms 1, 2 and 3 were identical, the enrichment scores from these three algorithms were also the same, with each having a total score of 10.257 which is greater than the total enrichment score of 5.739 from Algorithm 4.
Table 4.
Number of significant SNPs found by the different algorithms with different  levels, under the region-wide study. The ADNI study was used for this experiment
levels, under the region-wide study. The ADNI study was used for this experiment
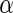 |
Algorithm 1: 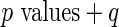 value value |
Algorithm 2: 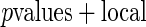 fdr fdr |
Algorithm 3: local fdr modeling | Algorithm 4: 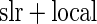 fdr fdr |
|---|---|---|---|---|
| 0.05 | 5388 | 27 965 | 23 128 | 0 |
| 0.10 | 8447 | 34 659 | 29 288 | 18 |
| 0.15 | 11 041 | 39 875 | 34 261 | 38 |
| 0.20 | 13 804 | 44 604 | 38 794 | 95 |
| 0.30 | 19 299 | 53 716 | 47 535 | 275 |
| 0.40 | 25 537 | 63 449 | 56 853 | 612 |
| 0.50 | 448 073 | 75 030 | 68 365 | 1180 |
Table 5.
Enrichment scores for each cluster from DAVID database
| Top 1180 SNPs from each algorithm in Table 4 | ||||
|---|---|---|---|---|
| Annotation cluster | Algorithm 1
|
Algorithm 2
|
Algorithm 3
|
Algorithm 4
|
| 1 | 3.167 | 3.167 | 3.167 | 1.479 |
| 2 | 1.680 | 1.680 | 1.680 | 1.332 |
| 3 | 1.198 | 1.198 | 1.198 | 1.040 |
| 4 | 1.157 | 1.157 | 1.157 | 0.775 |
| 5 | 1.014 | 1.014 | 1.014 | 0.508 |
| 6 | 0.947 | 0.947 | 0.947 | 0.261 |
| 7 | 0.572 | 0.572 | 0.572 | 0.175 |
| 8 | 0.523 | 0.523 | 0.523 | 0.169 |
| Total | 10.257 | 10.257 | 10.257 | 5.739 |
 Top 1180 SNPs were selected from 5388 SNPs in Algorithm 1 at level 0.05.
Top 1180 SNPs were selected from 5388 SNPs in Algorithm 1 at level 0.05.
 Top 1180 SNPs were collected from 27965 SNPs in Algorithm 2 at level 0.05;
Top 1180 SNPs were collected from 27965 SNPs in Algorithm 2 at level 0.05;
 Top 1180 SNPs were collected from 23128 SNPs in Algorithm 3 at level 0.05;
Top 1180 SNPs were collected from 23128 SNPs in Algorithm 3 at level 0.05;
 1180 SNPs found at level 0.5 in Algorithm 4.
1180 SNPs found at level 0.5 in Algorithm 4.
The above analyses imply that Algorithm 4 (Stein and others, 2010a) yields less significant findings even with a higher nominal 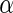 level, and the 1180 SNPs contain less information in both disease status classification and functional annotation clustering analysis. We further investigate the functional enrichment terms of Algorithms 2 and 3 at
level, and the 1180 SNPs contain less information in both disease status classification and functional annotation clustering analysis. We further investigate the functional enrichment terms of Algorithms 2 and 3 at 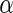 level 0.05 in the region-wide study, and the results are listed in supplementary material available at Biostatistics online.
level 0.05 in the region-wide study, and the results are listed in supplementary material available at Biostatistics online.
5. Discussion and conclusion
In this work, we have performed neuroimaging genomewide association studies using the ADNI dataset. The proposed method using distance covariance is able to identify the dependencies between the SNP variants and the brain volume differences, and utilize brain region interaction effects at the same time. We also proposed a local fdr modeling strategy and compared the performances with two existing multiple testing adjustment methods. The simulation studies showed that 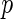 -values computed from Gamma approximation with the local fdr method (Algorithm 2) and local fdr modeling (Algorithm 3) were able to control FDR at the proper levels. In the real-data application, the significant SNPs found by distance covariance contained more information than slr (Stein and others, 2010a) in both disease status classification, and function annotation clustering analysis. This is because slr only captures linear relationship between SNPs and brain MRI scans, while distance covariance is able to model non-linear associations.
-values computed from Gamma approximation with the local fdr method (Algorithm 2) and local fdr modeling (Algorithm 3) were able to control FDR at the proper levels. In the real-data application, the significant SNPs found by distance covariance contained more information than slr (Stein and others, 2010a) in both disease status classification, and function annotation clustering analysis. This is because slr only captures linear relationship between SNPs and brain MRI scans, while distance covariance is able to model non-linear associations.
In addition to the distance covariance statistic in (3.3) that we have proposed for missing data, another option to deal with the missing values is to impute the genotypes by assuming the missing values are MAR. We used PLINK to impute the missing values in the ANDI study under the assumption of MAR, as it is computationally efficient (Li and others, 2009). The PLINK algorithm uses the standard EM algorithm and performs probabilistic estimation for each allele combination based on the relatively small regions of genome for each individual (PLINK, 2007). Based on the results of our PLINK imputation, the non-missing rate of the data increased from 99.61% to 99.67%. Therefore, we work with the original datasets and assume MCAR. Exploring combinations of imputation algorithms with distance covariance measures deserves further investigation, but is beyond the scope of the paper.
There remain many open questions that could lead to important further developments. We utilized distance covariance to measure the relationship between genetic variants and differences in brain volumes in the first stage. This representation can be applied to capture the non-linear dependencies between two sets of vectors with arbitrary dimensions, but it might also suffer a possible bias when the number of dimensionality is much greater than the sample size (Cope, 2009). Therefore, we placed more emphasis of our results on the region-wide study in this work, and we plan to study regularization approaches to the dependency measure to reduce this bias in future work. It would also be desirable to develop distance covariance-type measures that explicitly incorporate the discrete nature of the SNP data.
Supplementary material
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
Acknowledgements
This research is supported in part by National Science Foundation grant DBI-1262538. Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: Abbott; Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Amorfix Life Sciences Ltd.; AstraZeneca; Bayer HealthCare; BioClinica, Inc.; Biogen Idec, Inc.; Bristol-Myers Squibb Company; Eisai, Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; F. Hoffmann-La Roche Ltd. and its affiliated company Genentech, Inc.; GE Healthcare; Innogenetics, N.V.; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research  Development, LLC.; Johnson
Development, LLC.; Johnson  Johnson Pharmaceutical Research
Johnson Pharmaceutical Research  Development LLC.; Medpace, Inc.; Merck
Development LLC.; Medpace, Inc.; Merck  Co., Inc.; Meso Scale Diagnostics, LLC.; Novartis Pharmaceuticals Corporation; Pfizer, Inc.; Servier; Synarc, Inc. and Takeda Pharmaceutical Company. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of California, Los Angeles. This research was also supported by NIH grants P30 AG010129 and K01 AG030514. Conflict of Interest: None declared.
Co., Inc.; Meso Scale Diagnostics, LLC.; Novartis Pharmaceuticals Corporation; Pfizer, Inc.; Servier; Synarc, Inc. and Takeda Pharmaceutical Company. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of California, Los Angeles. This research was also supported by NIH grants P30 AG010129 and K01 AG030514. Conflict of Interest: None declared.
References
- ADNI. Alzheimer’s disease neuroimaging initiative. 2003. http://www.loni.ucla.edu/ADNI/
- Benjamini Y., Hochberg Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society Series B. 1995;57:289–300. [Google Scholar]
- Chang C.-C., Lin C.-J. LIBSVM: A library for support vector machines. ACM Transactions on Intelligent Systems and Technology. 2011;2:1–27:27. [Google Scholar]
- Cope L. Discussion of: Brownian distance covariance. The Annals of Applied Statistics. 2009;3:1279–1281. doi: 10.1214/09-AOAS312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DAVID. The database for annotation, visualization and integrated discovery (david) 2003. http://david.abcc.ncifcrf.gov/ [PubMed]
- Efron B., Storey J. D., Tibshirani R. Microarrays, empirical Bayes methods, and false discovery rates. Genetic Epidemiology. 2001a;23:70–86. doi: 10.1002/gepi.1124. [DOI] [PubMed] [Google Scholar]
- Efron B., Tibshirani R., Storey J. D., Tusher V. Empirical bayes analysis of a microarray experiment. Journal of the American Statistical Association. 2001b;96:1151–1160. [Google Scholar]
- Friston K. J., Frith C. D., Dolan R. J., Price C. J., Zeki S., Ashburner J. T., Penny W. D. Human Brain Function. Academic Press; 2004. [Google Scholar]
- Furney S. J., Simmons A., Breen G., Pedroso I., Lunnon K., Proitsi P., Hodges A., Powell J., Wahlund L.-O., Kioszewaka I. Genome-wide association with MRI atrophy measures as a quantitative trait locus for Alzheimer’s disease. Molecular Psychiatry. 2010;16:1130–1138. doi: 10.1038/mp.2010.123. and others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gretton A., Fukumizu K., Teo C., Song L., Schölkopf B., Smola A. J. A kernel statistical test of independence. Advances in Neural Information Processing Systems. 2008 [Google Scholar]
- Heitjan D. F., Basu S. Distinguishing missing at random and missing completely at random. The American Statistician. 1996;50(3):207–213. [Google Scholar]
- Jack C. R., Bernstein M. A., Fox N. C., Thompson P., Alexander G., Harvey D., Borowski B., Britson P. J., Whitwell J. L., Ward C. The Alzheimer’s disease neuroimaging initiative (ADNI): MRI methods. Journal Magnetic Resonance Imaging. 2008;7:685–691. doi: 10.1002/jmri.21049. and others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M., Bannister P., Brady M., Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage. 2002;17:825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- Jenkinson M., Smith S. M. A global optimisation method for robust affine registration of brain images. Medical Image Analysis. 2001;5:143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- Leow A. D., Huang S.-C., Geng A., Becker J. T., Davis S., Toga A. W., Thompson P. M. Inverse consistent mapping in 3D deformable image registration: its construction and statistical properties. Information Processing in Medical Imaging. 2005;3565:493–503. doi: 10.1007/11505730_41. [DOI] [PubMed] [Google Scholar]
- Li Y., Willer C., Sannaa S., Abecasis G. Genotype imputation. Annual Review of Genomics and Human Genetics. 2009;10:387–406. doi: 10.1146/annurev.genom.9.081307.164242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazziotta J., Toga A., Evans A., Fox P., Lancaster J., Zilles K., Woods R., Paus T., Simpson G., Pike B., Holmes C. A probabilistic atlas and reference system for the human brain: international consortium for brain mapping (ICNM) Philosophical Transactions of the Royal Society of London - Series B, Biological Sciences. 2001;356:1293–1322. doi: 10.1098/rstb.2001.0915. and others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muralidharan O. An empirical Bayes mixture method for effect size and false discovery rate estimation. The Annals of Applied Statistics. 2010;4:422–438. [Google Scholar]
- Newton M. A., Noueiry A., Sarkar D., Ahlquist P. Detecting differential gene expression with a semiparametric hierarchical mixture method. Biostatistics. 2003;5:155–176. doi: 10.1093/biostatistics/5.2.155. [DOI] [PubMed] [Google Scholar]
- PLINK. Plink: a tool set for whole-genome association and population-based linkage analyses. 2007. http://pngu.mgh.harvard.edu/purcell/plink/ [DOI] [PMC free article] [PubMed]
- Potkin S. G., Turner J. A., Guffanti G., Lakatos A., Fallon J. H., Nguyen D. D., Mathalon D., Ford J., Lauriello J., Macciardi F. A genome-wide association study of schizophrenia using brain activation as a quantitative phenotype. Schizophrenia Bulletin. 2009;35:96–108. doi: 10.1093/schbul/sbn155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith S. M., Jenkinson M., Woolrich M. W., Beckmann C. F., Behrens T. E., Berg H. J., Bannister P. R., Luca M. D., Drobnjak I., Flitney D. E. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23:208–219. doi: 10.1016/j.neuroimage.2004.07.051. and others. [DOI] [PubMed] [Google Scholar]
- Stein J. L., Hua X., Lee S., Ho A. J., Leow A. D., Toga A. W., Saykin A. J., Shen L., Foroud T., Pankratz N. Voxelwise genome-wide association study (vgwas) Neuroimage. 2010a;53:1160–1174. doi: 10.1016/j.neuroimage.2010.02.032. and others, and the ADNI. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein J. L., Hua X., Morra J. H., Lee S., Hibar D. P., Ho A. J., Leow A. D., Toga A. W., Sul J. H., Kang H. M. Genome-wide analysis reveals novel genes influencing temporal lobe structure with relevance to neurodegeneration in Alzheimer’s disease. Neuroimage. 2010b;51:542–554. doi: 10.1016/j.neuroimage.2010.02.068. and others, and the ADNI. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey J. D. A direct approach to false discovery rates. Journal of the Royal Statistical Society Series B. 2002;64:479–498. [Google Scholar]
- Storey J. D. The positive false discovery rate: a Bayesian interpretation and the q-value. The Annals of Statistics. 2003;31:2013–2035. [Google Scholar]
- Szekely G. J., Rizzo M. L. Brownian distance covariance. The Annals of Applied Statistics. 2009;3:1236–1265. doi: 10.1214/09-AOAS312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szekely G. J., Rizzo M. L., Bakirov N. K. Measuring and testing dependence by correlation of distances. The Annals of Statistics. 2007;35:2769–2794. [Google Scholar]
- Tziortzi A. C., Searlea G. E., Tzimopouloua S., Salinasa C., Beavera J. D., Jenkinsonb M., Laruelle M., Rabiner E. A., Gunn R. N. Imaging dopamine receptors in humans with [11c]-(+)-phno: dissection of d3 signal and anatomy. Neuroimage. 2011;54:264–277. doi: 10.1016/j.neuroimage.2010.06.044. [DOI] [PubMed] [Google Scholar]
- Woolrich M. W., Jbabdi S., Patenaude B., Chappell M., Makni S., Behrens T., Beckmann C., Jenkinson M., Smith S. M. Bayesian analysis of neuroimaging data in FSL. Neuroimage. 2009;45:173–186. doi: 10.1016/j.neuroimage.2008.10.055. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


