Electrostatic Properties of Complexes along a DNA Glycosylase Damage Search Pathway

Abstract

Human uracil DNA glycosylase (hUNG) follows an extended reaction coordinate for locating rare uracil bases in genomic DNA. This process begins with diffusion-controlled engagement of undamaged DNA, followed by a damage search step in which the enzyme remains loosely associated with the DNA chain (translocation), and finally, a recognition step that allows the enzyme to efficiently bind and excise uracil when it is encountered. At each step along this coordinate, the enzyme must form DNA interactions that are highly specialized for either rapid damage searching or catalysis. Here we make extensive measurements of hUNG activity as a function of salt concentration to dissect the thermodynamic, kinetic, and electrostatic properties of key enzyme states along this reaction coordinate. We find that the interaction of hUNG with undamaged DNA is electrostatically driven at a physiological concentration of potassium ions (ΔG_elect = −3.5 ± 0.5 kcal mol^–1), with only a small nonelectrostatic contribution (ΔG_non = −2.0 ± 0.2 kcal mol^–1). In contrast, the interaction with damaged DNA is dominated by the nonelectrostatic free energy term (ΔG_non = −7.2 ± 0.1 kcal mol^–1), yet retains the nonspecific electrostatic contribution (ΔG_elect = −2.3 ± 0.2 kcal mol^–1). Stopped-flow kinetic experiments established that the salt sensitivity of damaged DNA binding originates from a reduction of k_on, while k_off is weakly dependent on salt. Similar findings were obtained from the salt dependences of the steady-state kinetic parameters, where the diffusion-controlled k_cat/K_m showed a salt dependence similar to k_on, while k_cat (limited by product release) was weakly dependent on salt. Finally, the salt dependence of translocation between two uracil sites separated by 20 bp in the same DNA chain was indistinguishable from that of k_on. This result suggests that the transition-state for translocation over this spacing resembles that for DNA association from bulk solution and that hUNG escapes the DNA ion cloud during translocation. These findings provide key insights into how the ionic environment in cells influences the DNA damage search pathway.

DNA glycosylases initiate the base excision repair pathway by localizing to a specific lesion site and catalytically cleaving the glycosidic bond of a damaged base. Different glycosylases can be highly specialized for the removal of specific lesions that in some cases vary only subtly from native bases.^5,6 Achievement of high enzymatic specificity for damaged sites as well as rapid searching of abundant undamaged DNA sequences requires highly optimized thermodynamic and kinetic interactions with both specific and nonspecific sequences. The basis for this statement is straightforward: if the enzyme binds too tightly to nonspecific DNA sequences, the residence time will be too long to efficiently scan the entire genome before the next replication event, while if interactions are too weak, insufficient time will be spent inspecting individual DNA base pairs, leading to overlooked base lesions.^7,8 Determining the factors that contribute to the molecular recognition of both specific and nonspecific DNA sequences can shed light on how these enzymes have optimized their scan-and-repair mechanisms under solution conditions found in human cells.

It is generally accepted that the DNA glycosylase damage search process involves two major modes: an associativea mode that involves tracking along the DNA using a loosely associated enzyme state (often called “sliding”) and a dissociative mode that involves intermittent dissociation and reassociation of the enzyme with the DNA chain (“hopping”).^4,9−21 Since most studies of the damage search mechanism have used dilute, low-salt solutions,^11,12,22,23 a key unknown is how the individual nonspecific and specific complexes respond to the high salt concentrations encountered in the cell nucleus. A general understanding of such electrostatic effects is important given the generally large impact salt concentration has on the kinetic and thermodynamic properties of many enzyme-DNA complexes.^5,6,24−27

Counterion condensation (CC) theory attributes the electrostatic component of the protein–DNA binding free energy to the cratic entropy of mixing. In this view, during binding to the phosphate backbone the cationic side chains of the protein displace cations from the DNA ion cloud into bulk solution.^7,8,27−29 As the bulk salt concentration is increased, the cratic entropy of mixing becomes less favorable because the ion gradient between the DNA ion cloud and bulk solution is reduced. These effects are described by eq 1,^7,8,27−29 where the term log K_a^non accounts for the nonelectrostatic contribution to the free energy of binding, and the second term reflects the electrostatic component, where N is the total number of counterions displaced during binding.

1

These counterions may be cations released from the DNA (ZΨ) or tightly bound anions (β) that are displaced from cationic side chains of the protein. In this formalism, Z is equal to the number of DNA phosphate groups in contact with the bound protein, and Ψ is the fraction of a cation bound per phosphate group according to polyelectrolyte theory (Ψ ≈ 0.64 for short DNA oligos).³⁰⁻³² A feature of this model is that extrapolation of the binding energy to 1 M salt makes the electrostatic term equal to zero, allowing the nonelectrostatic free energy component to be estimated. This approach, though simplistic in terms of its dissection of the nonelectrostatic and electrostatic terms,^28,33,34 provides useful parameters that describe the driving forces governing the stability of various protein–DNA complexes on the damage recognition pathways of DNA glycosylases. It should be noted that CC theory focuses solely on effects derived from ion displacement and does not explicitly take into account the effect of ion concentration dependent changes in protein and DNA hydration. However, it has previously been established that changes in water activity do not occur with increasing concentrations of typical monovalent salts, and consequently, that electrostatic effects can be probed independently from changes in hydration.³⁵

In this study, we use CC theory to understand how each transient complex on the damage search pathway of human uracil DNA glycosylase (hUNG) responds to changes in salt concentration (Figure 1). We measured the salt concentration dependences of the thermodynamic and kinetic parameters for formation of both nonspecific and specific DNA complexes and the effect of salt on steady-state catalysis by hUNG. Finally, we make the first measurements of how the electrostatic environment of DNA impacts intramolecular DNA translocation by hUNG between uracil sites separated by 20 bp. The results show that an ionic environment approximating that of the cell nucleus enhances the specificity of hUNG but significantly diminishes the efficiency of facilitated diffusion by the dissociative (“hopping”) pathway, but not the associative (“sliding”) pathway. The implications of these findings to the damage search process in human cells are discussed.

Figure 1.

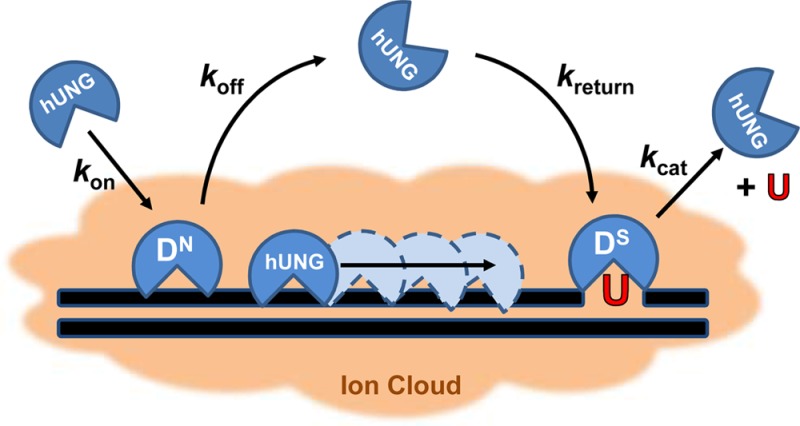
Human UNG (hUNG) DNA search and repair pathway is composed of four transient states: stationary states where the enzyme is engaged with nonspecific (D^N) or specific uracilated sequences (D^S), and two mobile states where the enzyme can translocate along DNA via associative or dissociative pathways of facilitated diffusion. Nonspecific and specific complexes must have distinct interactions that facilitate efficient recognition and repair (see text). The D^N complex is characterized primarily by contacts with the phosphate backbone, while the D^S complex involves additional nonpolar and hydrogen bonding interactions with the uracil base (see Figures 2A and 3A). The overall transfer probability between two uracil lesions is defined as the sum of two pathways: P_trans = P_assoc + P_diss, where P_assoc and P_diss are the probabilities of transfer via the associative and dissociative pathways, respectively. When uracils are spaced far enough apart such that all successful transfers occur via at least one dissociation event, this equation reduces to P_trans = P_diss. Kinetically, P_diss is defined as the product of two probabilities: P_diss = [k_off/(k_assoc + k_off)][k_return/(k_bulk + k_return)]. The first term describes the probability that hUNG will dissociate from a nonspecific DNA site as opposed to making an associative step along the DNA, and the second term gives the likelihood that the enzyme, once dissociated, escapes to the bulk solvent (k_bulk) rather than reassociating with the DNA chain (k_return) to complete transfer by the dissociative pathway.

Experimental Methods

Expression and Purification of hUNG

The catalytic domain of wild-type, N-terminal truncated hUNG (residues 82–304) was cloned into a pET-21a vector and expressed in Bl21-DE3 pLysS Escherichia coli cells. Cells containing the hUNG encoding vector were grown in 2 L of LB medium at 37 °C to an optical density (D₆₀₀) of 0.5, then hUNG expression was induced at 25 °C by the addition of 0.25 mM IPTG, and the cells were grown at 25 °C overnight. The cells were harvested by centrifugation and frozen at −80 °C overnight. Cells were resuspended in lysis buffer (50 mM Tris-acetate pH 7.0, 10 mM NaCl, 5% glycerol, 0.1% Triton-X-100, 1 mM EDTA, 1 mM DTT) followed by addition of lysozyme, 5 mM MgCl₂, and DNase1. The supernatant was then clarified by centrifugation at 40000g for 60 min at 4 °C and directly loaded onto an anion exchange column (UNO-Q12, BioRad) that had been preequilibrated with Buffer A (50 mM Tris-Acetate pH 7.0, 10 mM NaCl, 1 mM DTT). The flow through containing hUNG was loaded onto a Mono-S cation exchange column (GE Healthcare) preequlibrated with Buffer A. hUNG was then purified by gradient elution with Buffer A containing 800 mM NaCl. Fractions containing hUNG were dialyzed and concentrated into 10 mM sodium phosphate pH 7.5, 300 mM NaCl, 1 mM EDTA, 1 mM DTT, 25% glycerol and passed through a gel filtration column using BioRad P-100 resin and eluted in 10 mM sodium phosphate pH 7.5, 150 mM NaCl. The purified protein was then diluted to final buffer conditions of 10 mM sodium phosphate, 110 mM NaCl, 20% glycerol and stored at −80 °C. The concentrations of hUNG stock solutions were determined using the absorbance at 280 nm and an extinction coefficient of 33.68 mM^–1 cm^–1.

Oligonucleotide Preparation

1-[2-Deoxy-5-O-(4,4′-dimethoxytrityl)-2-fluoro-1-β-arabinofuranosyl]uracil was previously synthesized.^4,9−21,36 The specific substrate (D^S) was synthesized using standard phosphoramidite chemistry on an Applied Biosystems 390; however, the coupling time for the addition of the fluorinated uracil nucleoside phosphoramidite was increased to 10 min. The size, purity, and nucleotide composition of D^S were assessed by denaturing polyacrylamide gel electrophoresis with visualization by crystal violet staining and MALDI mass spectrometry. All other oligonucleotides sequences were purchased from either Integrated DNA technologies (http://www.idtdna.com) or Eurofin (http://www.operon.com) and purified in house by denaturing polyacrylamide gel electrophoresis (PAGE). Concentrations of solutions were determined by the absorbance at 260 nm using nearest neighbor extinction coefficients. Characterization of the previously synthesized phosphoramidite and all oligonucleotide sequences used in this study are listed in the Supplementary Methods, Supporting Information.

Experimental Conditions

Most experiments were conducted at 20 °C in Buffer B (20 mM potassium phosphate (pH 7.5), 0.002% Brij 35 detergent (Sigma-Aldrich), 1 mM DTT) unless otherwise stated. The potassium phosphate stock was brought to pH 7.5 using concentrated KOH; this resulted in a final potassium concentration of 36 mM. Site transfer experiments were conducted at 20 °C in Buffer C (20 mM HEPES (pH 7.5), 0.002% Brij 35 detergent (Sigma-Aldrich), 3 mM EDTA (added from a 0.5 M stock at pH 8.0), 1 mM DTT). HEPES stock was brought to pH 7.5 using concentrated KOH; this resulted in a final potassium concentration of 12 mM. Higher potassium concentrations for both buffers were achieved by addition of either KCl, KGlu, or KF.

Dissociation Constants for DNA Binding Using Fluorescence Measurements

Binding of hUNG to nonspecific DNA (D^N) was measured by fluorescence anisotropy with a SPEX Fluoromax 3 spectrofluorometer at 20 °C (excitation wavelength of 494 nm, emission wavelength of 518 nm). Concentrated hUNG in Buffer B was titrated into a cuvette containing 100 nM of fluorescein labeled DNA in Buffer B. After each addition, the solution was allowed to equilibrate for 4 min inside the fluorometer, and three measurements were averaged. For dissociation constants (1/K_a) of >6 μM, values were determined by diluting a solution of concentrated hUNG and 100 nM labeled DNA in Buffer B with a solution of 100 nM labeled DNA only. Potassium concentrations were adjusted by addition of KCl, KGlu, or KF to Buffer B to sample a range of 36–170 mM. Temperature dependence of the nonspecific binding affinity was measured using the same experimental procedure at additional temperatures of 10, 15, and 25 °C in the presence of 36 mM and 150 mM K⁺ using KGlu. All data were then fitted using eq 2, where A₀ and A_f are the minimal and maximal anisotropy values, respectively.

2

Binding of hUNG to specific DNA (D^S) was followed by an increase in the fluorescence of 2-aminopurine (2-AP). Emission was recorded over the wavelength range of 330–500 nm using an excitation wavelength of 310 nm, 0.25 s integration time, and averaging of three scans. Background corrected fluorescence intensity at 370 nm was plotted against hUNG concentration and fitted using eq 2. Similar results were obtained by integrating the entire emission spectrum.

Stopped-Flow Kinetic Measurements

Stopped-flow fluorescence experiments were performed at 20 °C in Buffer B using an Applied Photophysics device in two-syringe mode (dead time = 2 ms). The dissociation and association kinetics for specific DNA (D^S) were followed using 2-AP fluorescence changes using an excitation wavelength of 310 nm and a 360 nm cut-on filter. Ten to fifteen kinetic traces were averaged to produce an acceptable signal-to-noise ratio. All bimolecular association reactions were performed under second-order conditions with equivalent concentrations (400 nM or 600 nM) of both the enzyme and DNA well above the 1/K_a to ensure irreversibility of the binding event. Higher specific DNA concentrations were used at higher salt due to increased background fluorescence of KGlu. Data were then linearized as a function of unbound DNA concentration and fitted using the second order rate equation (eq 3), where A₀ and A_t are the initial and final unbound DNA concentrations, respectively.

3

Dissociation kinetics were measured by mixing a solution containing both D^S and saturating amounts of hUNG with an equal volume of a concentrated solution of duplex DNA containing an abasic site (aDNA) to ensure irreversible trapping of dissociated enzyme molecules. Data were fitted using a single exponential decay expression F_t = ΔF exp(−k_offt) + C, where F_t is the voltage at time t, ΔF is the amplitude of the voltage change, and C is a constant offset. All other relevant specifications for the individual experiments are described in the figure legends and text.

Steady-State Kinetic Measurements

Time-dependent increase in the steady-state fluorescence of DNA containing a uracil lesion adjacent to 2-AP (PUA-30) was followed using a SPEX Fluoromax 3 spectrofluorometer in the time base mode as previously described.³⁷ Emission was observed at 370 nm using an excitation wavelength of 315 nm and a sampling interval of 10 s. Michaelis–Menten parameters were determined from hyperbolic fits of the initial rates as a function of DNA substrate concentration.

Intramolecular Site Transfer Assay

The methods of Schonhoft and Stivers⁴ were followed using a substrate with two uracil sties spaced by 20 bp such that all intramolecular site transfers occurred by the dissociative pathway.⁴ Stock solutions of DNA containing either a 5′ or 3′ ³²P end label were generated by incubation of a DNA strand with [γ³²P]ATP (PerkinElmer) and T4 polynucleotide kinase (New England Biolabs) or [α³²P]ATP (PerkinElmer) and terminal transferase (New England Biolabs), respectively. The 5′- and 3′-labeled strands were hybridized by heating to 95 °C in a heating block for 20 min and allowing the block to cool to room temperature. Unincorporated [γ³²P] and [α³²P]ATP were removed by gel filtration.

Each reaction of the site transfer assay contained 40 nM ³²P-labeled duplex DNA substrate, composed of mixing equal amounts of 5′- and 3′-labeled DNA, in Buffer C. Site transfer experiments were conducted in Buffer C due to the reduced intramolecular site transfer (P_trans) observed when phosphate buffer was used (Buffer B). We attribute this affect to competitive inhibition by phosphate dianion. The reaction was then initiated by the addition of hUNG to a final concentration of 5 pM and incubated at 20 °C. At each time point, an aliquot of the reaction mix was quenched with uracil DNA glycosylase inhibitor (UGI) at a final concentration of 0.1 U (New England Biolabs), which rapidly and efficiently quenched hUNG activity. Following reaction quenching, abasic sites were cleaved by heating each aliquot at 95 °C for 10 min in the presence of 165 mM EDA pH 8.0. The fragments were then separated on a 12% nondenaturing polyacrylamide gel. The gel was dried, exposed overnight to a storage phosphor screen, and imaged with a Typhoon 8600 phosphorimager (GE Healthcare). All gel images were quantified using QuantityOne (Bio-Rad) by the box method. Background correction was accomplished by subtracting the intensity of a portion of the gel directly below each band from the intensity of the corresponding band of interest.

Results

Ion Effects on Nonspecific DNA Binding

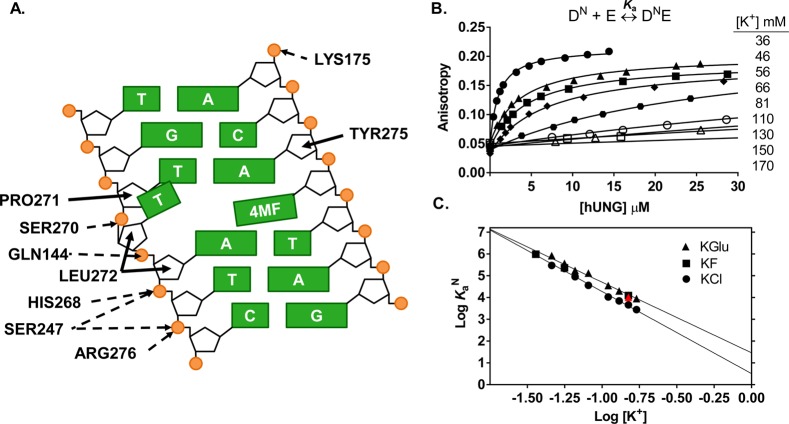
The DNA binding interface of hUNG consists of a well-conserved 27 Å groove with positive electrostatic potential.³⁸ Despite this substantial cleft, close contact (≤3.3 Å) between cationic groups of hUNG and the phosphate backbone are localized to only a few sites shared in both the nonspecific and specific DNA complexes (Figure 2A).³⁸⁻⁴⁰ The relatively sparse ionic contacts between hUNG and DNA leads to the question of the nature of the thermodynamic interactions that stabilize the nonspecific hUNG-DNA complex. To determine if interactions between hUNG and nonspecific DNA were predominantly electrostatic or nonelectrostatic in nature, the salt dependence of the nonspecific equilibrium association constant (K_a^N) was measured at concentrations of potassium ions in the range 36–170 mM using three different counterions (Cl^–, F^–, and Glu^–). Different anions were used to determine whether there was a contribution from anion release from hUNG during formation of the nonspecific complex.³² Plots of the log [salt] against log K_a^N were used to determine the electrostatic (ΔG_elect) and nonelectrostatic (ΔG_non) contributions to the binding free energy, and the number of ions (N) displaced upon hUNG-DNA association according to eq 1.

Figure 2.

Salt dependence of the nonspecific DNA (D^N) equilibrium binding affinity. (A) Schematic of electrostatic interactions implicated in ion release (dashed arrows) and the nonelectrostatic (solid arrows) interactions between hUNG and nonspecific DNA (Protein Data Bank entry 2OXM,⁴⁰ 4MF = 4-methylindole). Using mutagenesis and NMR imino exchange methods, the partially extruded thymine residue and its interactions with the enzyme have been substantiated in solution using an hUNG-nonspecific DNA complex with central T/A base pair.^73,74 These studies showed that normal T/A base pairs (not G/C) undergo enhanced imino proton exchange when bound to hUNG and involve the residues depicted in the graphic. Electrostatic interactions are defined by nitrogen and oxygen atoms <3.3 Å apart from DNA phosphate oxygens, while nonelectrostatic interactions are all carbon–carbon pairs <3.9 Å apart. An additional hydrogen bond between hUNG and the O2 of the partially extruded thymine across from 4MF was omitted in the diagram for clarity.⁴⁰ (B) Changes in fluorescence anisotropy of D^N (100 nM) as a function of hUNG concentration at varying potassium ion concentrations (36–170 mM). Full binding curves for 81–170 mM K⁺ are provided in Supplementary Figure S1, Supporting Information. (C) Dependence of K_a on the concentrations of KGlu (triangles), KCl (circles), KF (squares). Inclusion of 500 μM MgCl₂ at physiological K⁺ (150 mM) had a negligible effect on the observed K_a (red triangle, see text).

Fluorescence anisotropy measurements revealed a strong KCl dependence of hUNG binding to nonspecific DNA (N = −3.8, Table 1). The binding affinity was 300-fold weaker when using 170 mM potassium chloride (1/K_a^N = 360 ± 50 μM) as compared to the 36 mM potassium phosphate reference state (1/K_a^N = 1.3 ± 0.3 μM). The presence of small anion effects was indicated by the observation that the slope of the salt dependence reduced to −3.2 and −3.0 for KGlu and KF (Table 1). For comparison, the binding affinities in the presence of 170 mM of either salt were 3-fold lower than when the same concentration of KCl was used (1/K_a^N = 118 ± 5 μM) (Figure 2B, Figure S1, and Table S1, Supporting Information). The complete binding curves at high salt (81–170 mM K⁺) are shown in Supplementary Figure S1, Supporting Information.

Table 1. Analysis of the Salt Dependences of the Thermodynamic and Kinetic Parameters Using Equation 1^a.

	slope (N)b	Xnonc
KaN	–3.2 ± 0.1	29 ± 3 M–1
	–3.0 ± 0.1d	38 ± 1 M–1d
	–3.8 ± 0.1e	3.2 ± 0.7 M–1e
KaS	–2.1 ± 0.1f	2.29 ± 0.05 × 105 M–1f
	–2.2 ± 0.3d	8.9 ± 0.5 × 104 M–1d
konN,g	–1.5 ± 0.2	6 ± 2 × 106 M–1 s–1
konS	–1.5 ± 0.2	6 ± 2 × 106 M–1 s–1
koffN,h	1.4 ± 0.1	9.5 ± 0.2 × 104 s–1
koffS	0.5 ± 0.1	24 ± 2 s–1
kcat	0.9 ± 0.2	83 ± 12 s–1
1/Km	–2.2 ± 0.2	1.4 ± 0.1 × 10–4 Md
kcat/Km	–1.3 ± 0.2	5.9 ± 0.2 × 105 M–1 s–1
Ptransi	–1.5 ± 0.3	0.00 ± 0.05

^aAll experiments were conducted using KGlu unless otherwise noted.

^bThe slope (N) obtained from nonlinear regression fitting to eq 1.

^cX^non is the extrapolated value of the indicated parameter to the condition of 1 M [K⁺].

^dDetermined from equilibrium binding measurements using KF.

^eDetermined from equilibrium binding measurements using KCl.

^fCalculated from the ratio of the kinetic constants k_on^S/k_off^S.

^gk_on^N is assumed equal to k_on^S.

^hCalculated from the ratio of k_on^N/K_a^N.

ⁱP_trans is defined in terms of the ratio of kinetic constants detailed in the legend to Figure 1.

We also evaluated whether the nonspecific DNA binding affinity was affected by the addition of 500 μM MgCl₂ to the standard buffer containing 150 mM KGlu. (This approximates the concentrations of free potassium and magnesium ions in eukaryotic cells.^41,42) The binding affinity was only slightly weakened with the addition of magnesium [1/K_a^N (MgCl₂) = 97 ± 6 μM, versus 1/K_a^N = 80 ± 5 μM (no MgCl₂)], indicating that monovalent cations dominate over divalent cations under physiological conditions. Accordingly, we performed the remainder of the experiments using monovalent salts.

As expected from CC theory, a linear dependence between log K_a^N and log[KCl] was observed (eq 1, Figure 2C). The absolute value of the slope (N ≈ −4) reflects the total number of ions displaced from the DNA (ZΨ) and hUNG (β) upon binding (N = ZΨ + β). This number of displaced ions is slightly greater than the number of cations that are expected to be released based on the theoretical value of Ψ = 0.64 cations/per DNA phosphate,^27,32 and the observation that hUNG makes ionic contacts with five phosphate groups within the backbone of nonspecific DNA [ZΨ = (5)(0.64) ≈ 3 cations].¹ This result suggested that one anion might also be displaced from hUNG during binding. Consistent with this suggestion, the slope decreased to N ≈ −3 when KGlu and KF were used (Figure 2C, Table 1). Thus, one chloride ion and three potassium ions are likely released from hUNG and nonspecific DNA when KCl is used as the salt.³²

The above behavior of KCl, KF, and KGlu salts is consistent with the fact that small ions of high charge density (such as fluoride and the carboxylate anion) interact more strongly with water than with the ammonium and guanidinium side chain atoms of hUNG. In contrast, the large weakly hydrated chloride anion forms weak interactions with water and binds tightly to these protein side chains.^43,44 Thus, the KCl data reflect the additional displacement of a chloride anion from hUNG to allow DNA phosphate binding. To focus our study on cation effects at the hUNG-DNA interface, we chose to perform all subsequent experiments using KGlu or KF.

Extrapolating the log linear data to a 1 M standard state for KGlu simplifies eq 1 such that only the nonelectrostatic binding component remains (log K_a^non) (Table 1). From this simplification, the nonelectrostatic free energy contribution to the total binding free energy is ΔG_non = −2.0 ± 0.2 kcal mol^–1 (Table 2). If ΔG_non is subtracted from the observed binding free energy at physiological salt (ΔG_bind), the electrostatic contribution can be estimated (i.e., ΔG_elec = ΔG_bind – ΔG_non = −3.5 ± 0.5 kcal mol^–1). This analysis shows that the formation of the nonspecific complex at physiological salt concentration is primarily driven by electrostatic interactions resulting in ion release.

Table 2. Electrostatic (ΔG_elec) and Nonelectrostatic (ΔG_non) Contributions to the Binding Free Energy (ΔG_bind) for Nonspecific (D^N) and Specific (D^S) hUNG Complexes in the Presence of 150 mM K^+a.

	DN	DS,b
ΔGbindc (kcal mol–1)	–5.5 ± 0.3	–9.4 ± 0.1
ΔGelecd (kcal mol–1)	–3.5 ± 0.5	–2.3 ± 0.2
ΔGnone (kcal mol–1)	–2.0 ± 0.2	–7.2 ± 0.1

^aAll values are derived from experiments using KGlu.

^bK_a calculated from the ratio k_on/k_off obtained from stopped-flow fluorescence measurements

^cCalculated ΔG_bind = −RT ln K_a, using K_a at 150 mM [K⁺].

^dΔG_elec = ΔG_bind – ΔG_non. ΔG_elec pertains to the condition of 150 mM K⁺.

^eΔG_non = −RT ln K_a, using the measured K_a at 1 M K⁺.

Ion Effects on the Binding Equilibrium for Specific DNA

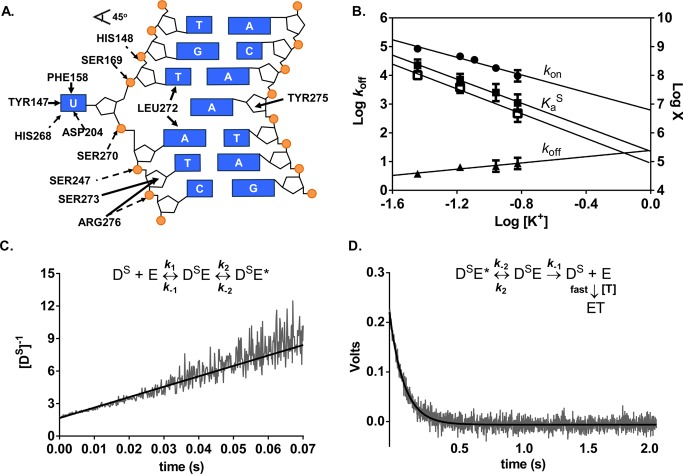
The electrostatic and nonelectrostatic interactions predicted from the crystal structure of a specific complex between hUNG and DNA are depicted in Figure 3A.⁴⁵ In general, this complex appears to retain the electrostatic contributions that were observed in the nonspecific complex (Figure 2A), but gains substantial nonelectrostatic interactions arising from flipping of the uracil base into the active site and the intercalation of a leucine side chain into the base stack. In addition, the DNA is severely bent in this structure leading to compression and expansion of the interphosphate distances typically seen in B DNA.

Figure 3.

Salt dependences of the association and dissociation constants and equilibrium binding affinity for specific DNA (D^S) determined by stopped-flow fluorescence measurements at 20 °C. (A) Schematic of electrostatic interactions implicated in ion release (dashed arrows) and the nonelectrostatic (solid arrows) interactions between hUNG and specific DNA (Protein Data Bank entry 1EMH(45)). Insertion of the side chain of Leu272 into the DNA duplex and movement of uracil into the hUNG active site results in numerous nonelectrostatic contacts not present in the nonspecific complex. (B) Dependence on KGlu concentration of k_on^S (circles), k_off^S (triangles), the calculated K_a^S obtained from the ratio k_off^S/k_on^S (solid squares), and the measured K_a^S from equilibrium fluorescence titrations using KF (open squares). Log k_off^S is plotted on the left y-axis and the remaining parameters are plotted on the right y-axis [X = K_a^S (M^–1) and k_on (M^–1 s^–1)]. (C) Linearized kinetic trace of the second-order association of D^S (600 nM) with hUNG (600 nM) at 150 mM K⁺. Equal volume solutions of D^S and hUNG of equal concentration (400–600 nM) were mixed and the time dependent increase in 2-AP fluorescence was followed (λ_ex= 310 nm). The line is the best-fit to a second-order rate equation. (D) Kinetic trace of the dissociation of hUNG from D^S at 150 mM K⁺. Abasic site-containing DNA (aDNA, 5 μM) was mixed with an equal volume solution containing 0.8 μM hUNG and 0.2 μM D^S and the time dependent decrease in 2-AP fluorescence was followed (λ_ex = 310 nm). The line is the best-fit to a single exponential decay. Controls established that the observed rate was zero-order with respect to DNA trap.

To evaluate the relative importance of these specific interactions, the salt dependence of the binding affinity for the specific substrate (D^S) was measured by monitoring the increase in 2-AP fluorescence as a function of hUNG concentration using various concentrations of potassium fluoride. These experiments used a 19 base pair duplex (D^S) that contained the fluorescent base 2-AP adjacent to U^β. This 2′-fluorinated uracil nucleotide prevents glycosidic bond cleavage during the time frame of the measurements (the fluorine is in the β anomeric configuration in this substrate analogue).³⁶ Upon binding of hUNG, the uracil base is flipped into the active site, unstacking 2-AP and leading to an increase in its fluorescence intensity.³⁶ In these experiments KF was used because high concentrations of KGlu introduced spectral interferences that prevented reproducible fluorescence measurements. This substitution is justified because the salt dependences of nonspecific DNA binding are identical in the presence of both of these salts (Figure 2C).

For the specific substrate, a linear dependence between log K_a^S and the log [KF] was observed (Figure 3B, Figure S4), but a shallower slope was observed than for the nonspecific complex (N = −2.1, Table 1). Although the reduced slope may indicate that fewer ions are displaced, this conclusion is not consistent with the number of ionic contacts observed in the crystal structure (Figure 3A). This apparent discrepancy may arise from the severe bending observed in the specific complex, which is not accounted for by simple polyelectrolyte theory where DNA is considered as a rod with identical phosphate-phosphate distances.^28,29,33 Regardless, Table 2 shows that the specific complex is primarily stabilized by nonelectrostatic interactions at a physiological salt concentration (ΔG_non = −7.2 ± 0.1 kcal mol^–1, ΔG_elec = −2.2 ± 0.2 kcal mol^–1). This is consistent with the structural findings described above where hUNG interacts extensively with the extruded uracil base and Leu272 inserts into the DNA duplex. None of these nonelectrostatic interactions are observed in the nonspecific complex (Figure 2A).

Salt Effects on the Kinetics for Binding and Dissociation from Specific DNA

Association and dissociation kinetics of the specific DNA complex (D^S) was measured by following the changes in 2-AP fluorescence using a stopped–flow rapid kinetic device (Figure 3C,D). To determine the salt sensitivity of k_on, we monitored the increase in 2-AP fluorescence under irreversible second-order conditions, in which both the enzyme and DNA were mixed in equal molar amounts (400 or 600 nM) using increasing concentrations of KGlu (36–150 mM). The large signal-to-noise ratio at these high DNA concentrations significantly decreased the spectral interference from KGlu that was observed in the equilibrium binding assay, where the DNA concentration was 20-fold lower. To ensure that association was essentially irreversible for these measurements, the hUNG and DNA concentrations were kept well above the value for the equilibrium dissociation constant (1/K_a^S) at all salt concentrations. The irreversible conditions at high salt were confirmed by measuring k_on using 400 and 600 nM concentrations of both DNA and enzyme (110 mM KGlu). These conditions resulted in k_on values that were the same within the errors of these measurements (1.0 ± 0.7 × 10⁸ M^–1 s^–1 and 1.8 ± 0.1 × 10⁸ M^–1 s^–1). The irreversible nature of these association reactions was further substantiated by the fact that the same change in voltage was observed at all salt concentrations tested, indicating that the same degree of saturation was reached (Supplementary Figure S2A, Supporting Information). A linearized kinetic trace at 150 mM K⁺ is shown in Figure 3C, which was fitted to eq 3 to obtain the association rate constant [k_on = (9.6 ± 0.4) × 10⁷ M^–1 s^–1]. All additional kinetic traces are shown in Supplementary Figure S2A. This association rate increased by an order of magnitude as the salt concentration was decreased to 36 mM [k_on^S = (8.5 ± 0.1) × 10⁸ M^–1 s^–1] (Table S2, Supporting Information). We note that this represents one of the most rapid macromolecule binding reactions, approaching the extreme of previously reported electrostatically enhanced association rates.⁴⁶

The dissociation rates for specific DNA complexes (k_off^S) were also determined at increasing concentrations of potassium ions (36–150 mM) by monitoring the decrease in 2-AP fluorescence upon dissociation of hUNG from the DNA (Figures 3D and S2B). To ensure that all enzyme molecules dissociated irreversibly, the dissociated enzyme was trapped with an excess of DNA containing an abasic site (aDNA). In contrast with the association rate, the first-order dissociation rate was found to increase only modestly (∼2-fold) when the salt concentration was raised from 36 to 150 mM K⁺ (3.8 ± 0.3 s^–1 to 8.7 ± 0.7 s^–1) (Table S2, Supporting Information). On the basis of comprehensive kinetic measurements with the similarly behaved E. coli enzyme,^36,47,48 it is long-known that the single-exponential dissociation reflects rate-limiting exit of the uracil base from the enzyme active site.^36,47,48 The dissociation of the DNA from the enzyme occurs in an extremely rapid step after the slower internal steps and is not detected in the fluorescence measurements. Thus, the relative salt insensitivity of k_off is fully consistent with a slow internal step being overall rate limiting for dissociation of the specific DNA, while association is influenced by a different salt sensitive step.

The salt dependence of the binding kinetics to nonspecific DNA was not directly addressable due to weak binding and the fast association and dissociation rates. Since nonspecific binding precedes formation of the specific complex, it is reasonable to conclude that the association rates for the nonspecific complex are similarly affected by salt as the specific complex (i.e., k_on^N = k_on^S). Using these assumed values for k_on^N, the dissociation rates for nonspecific DNA at each [K⁺] were calculated from the relationship k_off^N = k_on^N/K_a^N using the measured equilibrium association constants at each salt concentration. The approach indicated a 7-fold increase in k_off^N over the salt range tested [k_off^N (calculated, 36 mM salt) = 1100 ± 300 s^–1, k_off^N (calculated, 150 mM salt) = 7700 ± 500 s^–1], which is similar to the effect on k_on^N and k_on^S. This analysis suggests the same rate-limiting transition state is being followed in the forward and reverse directions for binding and dissociation of nonspecific DNA (i.e., two-state behavior).

Salt Effects on Steady-State Kinetics of hUNG Catalyzed Uracil Excision

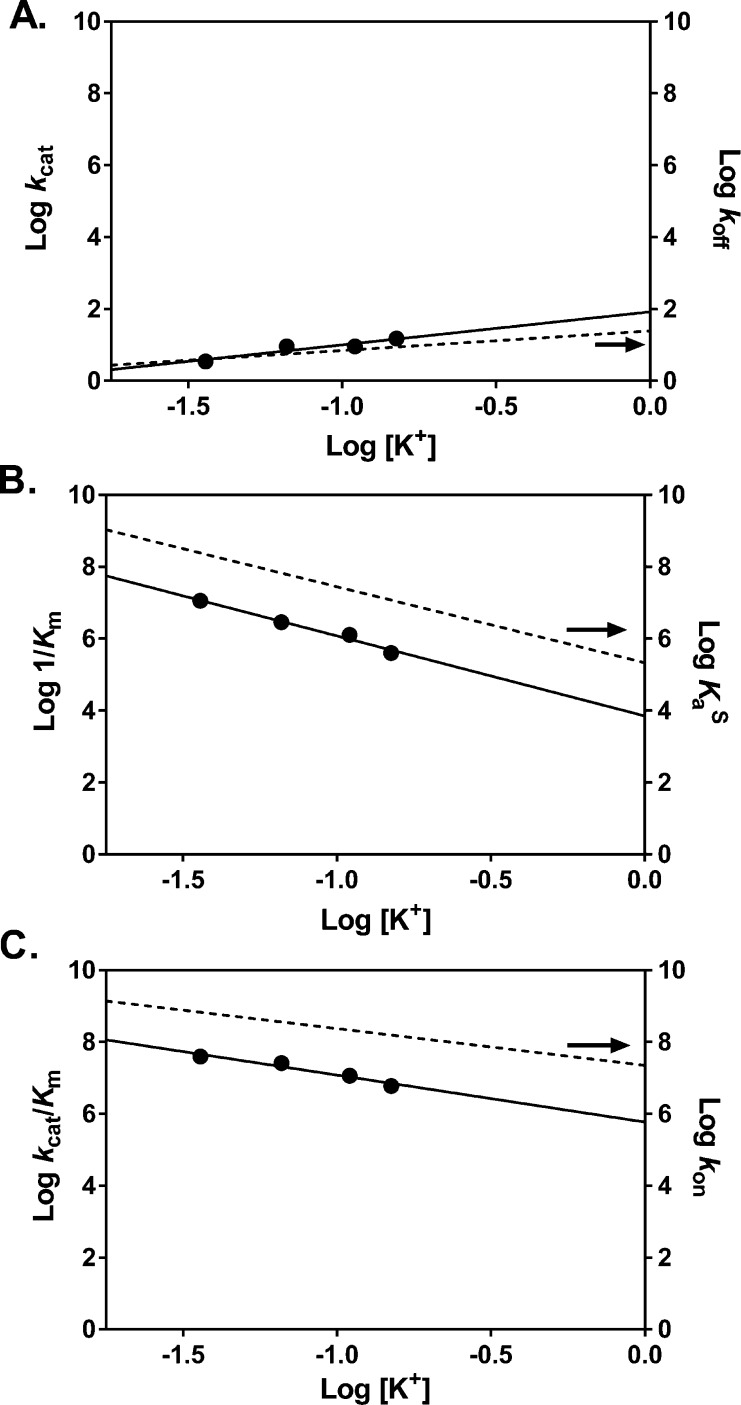
Steady-state kinetic measurements used a continuous fluorescence assay and a 30 base pair oligo (PUA-30) that contained a 2-AP base adjacent to a U-A base pair.³⁷ The initial rate of reaction was determined by monitoring the time-dependent increase in 2-AP fluorescence, which reports on hUNG catalyzed excision of the adjacent uracil base. Nonlinear regression fitting of the data to the Michaelis–Menten equation is shown in Figure S3A–D, from which k_cat, K_m, and k_cat/K_m values were determined (Table S3). As shown in Figure S3, we were able to attain greater than >85% saturation of the enzyme with substrate at salt concentrations between 36 and 110 mM. However, at the highest concentration of 150 mM only 63% saturation was achieved, resulting in a larger uncertainty in k_cat. Nevertheless, even at this salt concentration k_cat/K_m was well-determined because this second-order rate constant is also given by the initial slope of the saturation curve when [S] ≪ K_m (Figure S3D). We attempted to attain greater saturation of the enzyme at 150 mM concentration of salt, but the DNA concentration could not be increased beyond 4 μM due to apparent substrate inhibition or aggregation as the concentration was increased further.

Plots of log k_cat, log 1/K_m, and log k_cat/K_m against log [K⁺] were all linear (Figure 4A–C). The k_cat value increased 4-fold as the salt concentration was increased from 36 to 150 mM K⁺ (3.5 ± 0.3 s^–1 and 15 ± 2 s^–1) (Figure 4A), which is a similar response as k_off. The slopes of the log–log plots for k_cat and k_off were slightly positive, implying ion uptake, with N^kcat = 0.9 ± 0.2 and N^koff = 0.5 ± 0.1 (Table 1). Since k_cat is limited by product release and not chemistry,^49,50 and the product complex is structurally and thermodynamically similar to the substrate complex,⁵⁰ it would appear that the rate-limiting transition states for both substrate and product dissociation do not involve significant ion uptake. In contrast, the 1/K_m and k_cat/K_m values had stronger dependences on the salt concentration, with slopes resembling that of K_a^S and k_on, respectively (N^1/Km = −2.2 and N^kcat/Km = −1.3, compare values in Table 1). The approximately 10-fold greater values of k_on as compared to k_cat/K_m at each salt concentration may arise from the different sequences of these specific substrates, or the presence of additional partially rate-limiting transition states that comprise k_cat/K_m (for instance, uracil excision occurs at a single-turnover rate k_ex = 240 s^–1).⁴ Regardless, these results indicate that diffusion-controlled (or near diffusion-controlled) processes like k_on and k_cat/K_m involve transition-states that necessitate ion release.

Figure 4.

Salt dependences of k_cat, K_m, and k_cat/K_m. (A) The value for k_cat (circles) is limited by product release and is minimally dependent on KGlu concentration. This is similar to the behavior observed for k_off (dashed line). (B) The dependence of 1/K_m (circles) on KGlu concentration is very similar to that observed for specific DNA binding K_a^S (dashed line). (C) The dependence of k_cat/K_m (circles) on KGlu concentration is identical to the dependence observed for k_on (dashed line).

Increased Salt Concentrations Reduce the Probability of Intramolecular Site Transfer

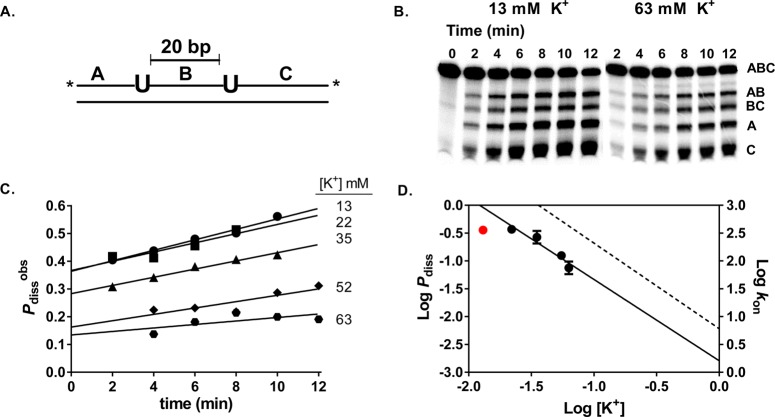
To characterize the salt dependence of the transition state for intramolecular translocation of hUNG between two uracil sites spaced 20 base pairs apart on the same strand in duplex DNA (S20), we used our previously developed assay for measuring facilitated diffusion.^12,51 This site spacing was chosen because all transfer events result from hUNG dissociating and reassociating with the DNA at least once (only the dissociative pathway is operational, P_diss).⁴ After postreaction sample processing (see Methods), the electrophoretically separated DNA fragments produced from uracil from single and double uracil excision events were quantified using phosphorimaging analysis. Intramolecular site transfer results in the production of excess A and C fragments that result from double-excision events, while single site excision produces exactly equal amounts of the A, C, AB, and BC product bands (Figure 5A,B).^21,51 The time independent dissociative site transfer probability (P_diss) can be calculated precisely using eq 4 by linear extrapolation of the observed transfer probabilities (P_diss^obs) to zero time.b

4

Figure 5.

Salt dependence of the intramolecular dissociative transfer probability of hUNG between two uracil sites spaced 20 bp apart (P_diss). (A) Schematic of the substrate (S20) used. The asterisk denotes the location of the ³²P end labels. (B) Phosphorimages of the gel-resolved site transfer products derived from S20 in the presence of 13 mM and 63 mM K⁺. (C) Determination of P_diss at varying K⁺ levels in the range 13–63 mM. The observed site transfer probability (P_diss^obs, eq 3) is calculated at each time point and then linearly extrapolated to time zero to determine the true value (P_diss). (D) Comparison of the dependences of P_diss (circles) and k_on (dashed line) on K⁺ concentration. The P_diss value at 13 mM (red circle) deviated negatively from the linear correlation and was omitted from the linear regression analysis.c

We measured P_diss in the presence of 13–63 mM K⁺ ion, beyond which site transfer by the dissociative pathway was no longer detectable. As shown in Figure 5C, P_diss showed a strong dependence on salt concentration, decreasing 4-fold between 13 mM and 63 mM K⁺ (Table S4). A log linear dependence was observed between 22 mM and 63 mM K⁺ (Figure 5D),c which provided a slope value N = −1.5 ± 0.3. This slope value is identical to the salt dependence of the association rate k_on, which suggests that hUNG molecules undergoing dissociative translocation move outside of the ion cloud, and their reassociation is influenced in the same way by the presence of bulk salt ions (see Discussion).

Discussion

Electrostatic Contribution to Nonspecific DNA Binding is Entropy Driven

The disparate effects of salt ions on the binding of hUNG to undamaged and damaged DNA indicates that distinct thermodynamic interactions are involved in stabilizing these complexes. According to CC theory, weaker binding induced by high salt concentrations originates from a reduction in the entropy of mixing associated with expelling ions from the DNA ion cloud into bulk solution. Therefore, the electrostatic component of the binding energy is purely entropic. We confirmed this entropic expectation for the nonspecific DNA complex by measuring the logarithmic salt dependence of the binding affinities at four temperatures, where the slopes of the log K_a vs log [KGlu] plots were indistinguishable at each of the temperatures (Figure S5, Supporting Information).²⁷ The corresponding analyses for the specific complex could not be performed because of experimental difficulties in making reliable 2-AP fluorescence measurements of equilibrium binding at low DNA concentrations at multiple temperatures.

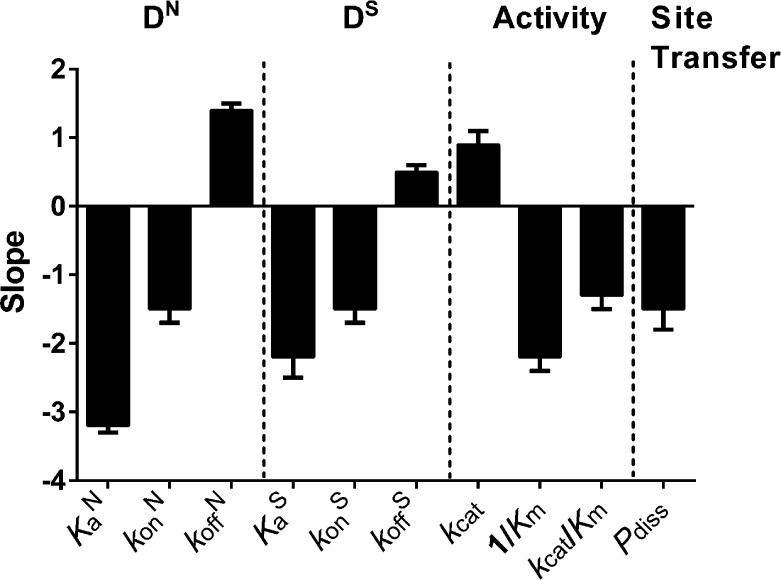
Previous studies have shown that the complex between hUNG and nonspecific DNA is held together by a handful of enzyme contacts with the phosphate backbone, with minimal distortion of the double helix (Figure 2A).⁴⁰ The structural view is in agreement with the present thermodynamic findings, where approximately three monovalent cations are released from the DNA upon binding, and only a small nonelectrostatic contribution to the binding free energy is indicated, suggesting minimal duplex distortion (Figure 6). These data characterize the nonspecific DNA complex as a loosely associated state that is formed by virtue of the entropic effects of cation displacement from the DNA. The weak electrostatic character of the nonspecific complex provides a binding mode for hUNG that is consistent with rapid facilitated diffusion by the previously described dissociative and associative pathways (Figure 1). A binding lifetime on nonspecific DNA in the millisecond to sub-millisecond time regime has the virtue of minimizing the time spent bound to undamaged DNA sequences and provides frequent opportunities for repeated cycles of enzyme dissociation, rapid 3D diffusion and local rebinding of the DNA chain. This type of mechanism, combined with short-range associative transfers where the enzyme remains in contact with the DNA (<10 bp),⁴ provides excellent search coverage at a maximum possible rate that is only bounded by the limits of diffusion.

Figure 6.

Summary of the salt dependences of each measured thermodynamic and kinetic parameter (X) (see Discussion). The dependences are represented as the slopes of the respective log [salt] vs log X plots. Positive slopes indicate dissociation processes resulting in ion condensation, which are facilitated by high ionic strength (k_cat, k_off). Negative slopes result from processes that involve ion displacement and are hindered by high salt concentrations.

Specific DNA Binding is Driven by Nonelectrostatic Interactions

In contrast with nonspecific DNA, the formation of the specific complex with uracilated DNA was driven primarily by nonelectrostatic forces depicted in Figure 3A. Despite the crystallographic evidence that all the ionic interactions present in the nonspecific complex are preserved in the specific complex,^40,52 the stability of the specific hUNG-DNA complex was less dependent on salt (Table 1). Such behavior of a specific and nonspecific protein–DNA complex has been observed in studies of lac Repressor and attributed to structural differences between the two complexes that lead to changes in ion displacement stoichiometry.⁵³⁻⁵⁸ For the case of hUNG, the most striking difference between the nonspecific and specific complexes is the severe distortion of the helical parameters of the DNA in the latter, suggesting that similar effects of duplex deformation may be operative. In general, it is not clear how distortions of the DNA helix that are induced upon protein binding alter the surrounding ion cloud and the observed stoichiometry of ion displacement. If an increase in charge density of the phosphate backbone upon DNA bending promotes the condensation of additional cations, then the net number of ions displaced upon binding would be reduced. This potential contribution to the interpretation of ΔG_elect for the specific complex does not impact the primary finding that a large nonelectrostatic component to the binding free energy is introduced upon formation of this complex.

Another implication of the different contributions of electrostatic and nonelectrostatic binding energy terms for the nonspecific and specific complexes is that binding specificity is enhanced at higher salt concentrations (defined as the ratio K_a^S/K_a^N).³⁵ While this calculation is best performed for sequences of identical length and nearly identical sequence (which is not the case for the specific and nonspecific duplexes used in this study), the relative change in specificity as a function of salt is still informative. At low salt (36 mM), the specificity of hUNG for the specific DNA is 290 ± 90 while at physiological salt (150 mM), the specificity increases approximately 4-fold (1300 ± 200). The greater salt sensitivity of nonspecific DNA binding and the large nonelectrostatic component of the binding energy for the specific complex have the combined effect of minimizing sequestration of the enzyme on bulk undamaged DNA, while allowing the specific complex to persist long enough for efficient catalysis to take place.

Association of hUNG with DNA Is Accelerated by Electrostatics

Long-range electrostatic interactions are known to play a significant role in accelerating the association of proteins with various targets, and the polyanionic nature of DNA makes this effect especially significant in the case of protein–DNA association.^59,60 The acceleration provided by the electrostatic interaction will supply a biasing force that increases the basal rate of association in the absence of such a force (k_on^non).⁴⁶ For modest sized enzymes such as hUNG that exhibit diffusion-controlled binding, an upper limit for k_on^non ≈ 10⁶ M^–1 s^–1 has been estimated from theoretical considerations.⁶¹⁻⁶⁴ This theoretical upper limit has been achieved in some highly efficient systems (the association of barnase with its inhibitor barstar is one well-characterized example).⁶⁵ For hUNG we estimate k_on^non = 6 ± 2 × 10⁶ M^–1 s^–1 from extrapolating the salt dependent association rates to 1 M salt (Table 1). Extrapolation from the 1 M standard state used to estimate k_on^non to a physiologically relevant salt concentration of 150 mM reveals that the association rate is increased by 1 order of magnitude. The electrostatic contribution toward lowering the free energy barrier for association at physiological salt may be calculated using eq 5 (G_elec^‡ = −1.6 ± 0.3 kcal mol^–1).

5

An electrostatic enhancement of the same magnitude is also indicated from the salt dependence of k_cat/K_m (Table 1). This correspondence indicates that the rate-limiting transition state for enzyme-DNA association and steady-state turnover under limiting substrate conditions share similar electrostatic characteristics. It should be noted that G_elec^‡ comprises all net effects arising from electrostatic interactions. This includes an increased contribution from facilitated diffusion as the salt concentration is decreased from 1 to 0.15 M. However, a large contribution from facilitated diffusion would not be expected for the relatively small duplexes used in this study.

Dissociation of the Specific Complex is a Multistep Process

Although dissociation of the nonspecific complex (k_off^N) was enhanced by increasing salt concentrations, the salt effect was reduced for dissociation of both the specific (k_off^S) and abasic product DNA complexes (using k_cat as a surrogate for the product k_off) (Table 1 and Figure 6). These different salt effects on the nonspecific and two specific complexes can be rationalized by the crystallographic finding that extensive nonelectrostatic contacts are formed in the specific complexes, which must be broken prior to dissociation (Figure 3A).^40,45,50 Breaking of these specific contacts must occur in a relatively salt-insensitive rate-limiting transition state that precedes dissociation. This view is consistent with previous rapid kinetic studies with UNG that have elucidated a two-step binding mechanism for formation of specific complexes.⁴⁸ In contrast, the nonspecific complex apparently forms in a salt sensitive single-step reaction, with association and dissociation occurring in the same rate-limiting transition-state. Thus, equal numbers of counterions should be released in the forward binding direction and taken up in the reverse dissociation reaction, which is supported by the similar slopes for the salt dependences of k_on^N and k_off^N in Table 1 and Figure 6.

The Dissociative Facilitated Diffusion Pathway Involves Escape of hUNG from the DNA Ion Cloud

We previously reported that the associative pathway for intramolecular site transfer was salt insensitive, but that the dissociative pathway was salt sensitive over the range that was studied.⁴ The insensitivity of associative pathway was explained by the relatively constant nature of the ion cloud around the DNA over a wide range of salt concentrations,⁶⁶⁻⁶⁸ and the supposition that associative transfers do not lead to net ion displacement. The salt dependence of the dissociative pathway was interpreted to result from enzyme molecules diffusing beyond the ion cloud during short-range dissociation and reassociation events.

The data presented here provide further support for the conclusion that the fundamental distinction between the associative and dissociative pathways is that during dissociative transfers hUNG escapes the ion cloud prior to reassociating at a nearby position on the DNA chain. We utilized a substrate containing a uracil site spacing of 20 base pairs such that all transfers required at least one dissociation event (the associative transfer length of hUNG is only about ∼5 bp).⁴ The finding that P_diss and k_on have indistinguishable dependences on salt (Figure 6), demonstrates that the overall dissociative transfer process involves a salt sensitive step resembling that of enzyme-DNA association from bulk solution. This interpretation is supported by the kinetic definition of the probability of dissociative transfers: P_diss = [k_off/(k_assoc + k_off)][k_return/(k_bulk + k_return)]. The first term describes the probability that hUNG will dissociate from nonspecific DNA (k_off) as opposed to making an associative step along the DNA (k_assoc), and the second term gives the likelihood that the enzyme, once dissociated, escapes to the bulk solvent (k_bulk) rather than reassociating with the DNA chain to complete transfer (k_return = k_on). We have shown here that k_off is salt insensitive and we have previously shown that k_assoc is salt insensitive.⁴ Thus, to a first approximation, the first term remains the same at all salt concentrations. In contrast, the second term contains the constant k_return = k_on, which is salt sensitive based on our measurements, while escape to bulk is reasonably assumed to be salt independent. Taking k_return = k_on and dividing the numerator and denominator in the second term by k_on, gives P_diss = 1/(k_bulk/k_on + 1) at each salt concentration. This equation predicts that P_diss will decrease to zero in a manner that depends on the salt concentration dependence of k_on, which is the basis of our assertion and interpretation.

The above result sheds light on the nature of the transition state of enzyme molecules undergoing dissociative transfer. Since the DNA ion cloud extends only a few nanometers from the DNA chain, enzyme molecules that undergo dissociative transfers must diffuse at least this distance. We have made estimates in the range 3–7 nm for the mean distance that hUNG diffuses from the DNA chain during dissociative transfers using simple Stoke-Einstein diffusion equations.⁴ More recently, we developed a Monte Carlo simulation program for the glycosylase hOGG1 that can be used to further elaborate microscopic aspects of the site transfer mechanism.^4,69−71

The implication of the salt sensitivity of the dissociative pathway is that hUNG molecules undergoing dissociative transfers at physiological salt will suffer a decrease in productive association events. Nevertheless, the dissociated enzyme will still be positionally correlated with the departed DNA chain in both high and low salt conditions. The reduced efficiency at high salt is overcome by multiple rebinding attempts, which may result in productive binding occurring at a position along the DNA chain that is more distant from the initial position of dissociation than at low salt concentrations. When productive binding finally occurs, the salt insensitive associative search begins in the same manner as at low salt. Thus, the fundamental aspects of the transfer mechanism do not change between low and physiological concentrations of salt. What remains to be taken into consideration is the effect of other environmental factors within the nucleus, such as the macromolecular crowding, that could modulate the effects of high ion concentrations and favor the formation of compact hUNG-DNA search complexes as compared to dilute solution.^46,72 Thus, future studies will focus on increasingly realistic experimental models to understand search and repair mechanisms in physiologically relevant contexts and eventually human cells.

Glossary

Abbreviations

hUNG

human uracil DNA glycosylase

hOGG

8-oxoguanine DNA glycosylase

U^β

1-[2-Deoxy-5-O-(4,4‘-dimethoxytrityl)-2-fluoro-1-β-arabinofuranosyl]uracil

2-AP

2-aminopurine

CC

Counterion Condensation

ΔG_bind

binding free energy at physiological salt (150 mM K⁺)

ΔG_elect

electrostatic component of the binding free energy

ΔG_non

nonelectrostatic component of the binding free energy

D^N

15mer nonspecific DNA

D^S

19mer specific DNA containing a U^β-G pair

aDNA

19mer DNA containing an abasic site

PUA-30

30mer DNA containing a single U-A base pair

S20

90mer-DNA with two U-A base pairs separated by 20 bp

Supporting Information Available

Supplemental methods, four supporting tables, and five supporting figures. Nonspecific binding affinities determined under various salt conditions (Table S1); k_on, k_off, and binding affinities determined at all salt concentrations tested for specific DNA (Table S2), steady-state kinetic parameters of hUNG and specific DNA binding at various salt concentrations (Table S3), site transfer probabilities at multiple salt concentrations (Table S4), full nonspecific binding curves for high salt conditions (Figure S1), raw association and dissociation kinetic data (Figure S2), double reciprocal plots for the steady-state kinetic data presented (Figure S3), a comparison of fluorescence titrations used to determine specific DNA binding affinity and stopped-flow data (Figure S4), and the temperature dependence of the nonspecific DNA binding affinity (Figure S5). This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States