Growth Rate Analysis and Efficient Experimental Design for Tumor Xenograft Studies

Abstract

Human tumor xenograft studies are the primary means to evaluate the biological activity of anticancer agents in late-stage preclinical drug discovery. The variability in the growth rate of human tumors established in mice and the small sample sizes make rigorous statistical analysis critical. The most commonly used summary of antitumor activity for these studies is the T/C ratio. However, alternative methods based on growth rate modeling can be used. Here, we describe a summary metric called the rate-based T/C, derived by fitting each animal’s tumor growth to a simple exponential model. The rate-based T/C uses all of the data, in contrast with the traditional T/C, which only uses a single measurement. We compare the rate-based T/C with the traditional T/C and assess their performance through a bootstrap analysis of 219 tumor xenograft studies. We find that the rate-based T/C requires fewer animals to achieve the same power as the traditional T/C. We also compare 14-day studies with 21-day studies and find that 14-day studies are more cost efficient. Finally, we perform a power analysis to determine an appropriate sample size.

Introduction

Human tumor cell lines grown as xenografts in immunocompromised mice have in recent years played an increasingly important role in the late-stage preclinical development of targeted anticancer therapies.^1–5 Identification of compounds and dose regimens with the broadest possible therapeutic window (the range between the maximal efficacy and the minimum allowable toxicity) is a driving goal of late-stage preclinical research. Evaluating the ability of anticancer agents to reduce tumor growth in preclinical xenograft models provides the basis for compound optimization. Preclinical biological activity in xenograft models has been shown to be reasonably well correlated with human clinical outcomes,⁶ particularly when conducted at clinically relevant exposures.⁷

A typical xenograft study involves the comparison of different drug treatments or combinations of drugs in mice bearing xenograft tumors in their flanks. Therapy is typically initiated only after tumors have reached a certain minimum size. During this treatment phase, repeated measurements of the tumor volume are made using digital calipers, and biological activity is quantified via the assessment of changes in tumor volume between treated and control mice.

One common measure of efficacy is the T/C ratio, the ratio of tumor volume in control versus treated mice at a specified time. Another measure that is frequently used is the closely-related Tumor Growth Inhibition index, which is defined as (1 – (mean volume of treated tumors)/(mean volume of control tumors)) × 100%. While these measures are easy to implement and interpret, they have their limitations. In particular, the measures are inefficient, as they do not make use of any data collected before the final day of treatment. Another problem is that the measure is biased because animals are usually sacrificed when the tumor volume exceeds 10% of the body weight or exceeds 2 cm in diameter. If this occurs before the end of the study, these animals will be excluded from the analysis. A second source of bias occurs when tumors in the control group (which are usually larger than those in the treatment group) experience a differential slowing of their growth rate relative to treatment because of nutrient- and oxygen-limiting conditions.

Various researchers have considered alternative methods of analyzing xenograft studies, and several complex models have been proposed that fit all the data.^8–14 Some of the methods are based on non-parametric analysis,^8,9 which may not have sufficient power to handle small sample sizes. Other researchers have used mixed-effects regression models,^10–14 which provide several advantages, including the ability to model missing data, mouse-to-mouse variability in the growth rates, and a correlated noise structure. However, the multiple coefficients of a nonlinear regression model are less interpretable than a single efficacy measure (analogous to a T/C ratio or a Tumor Growth Inhibition index). From an organizational standpoint, these complex models lie outside the domain of off-the-shelf statistical methods, and are complicated to implement and understand from the biologists’ perspective. The sheer volume of xenograft studies in even a mid-sized company may make custom-fit regression models for each study unrealistic.

In this paper, we present a new method of analysis called the rate-based T/C, which is based on fitting each tumor’s growth curve to an exponential model. This approach makes use of all the available data, and it is simple enough to be calculated with an Excel spreadsheet. We verify that the rate-based T/C has better precision than the traditional T/C by applying both methods to data from a large number of in-house studies. By making more efficient use of the data, the rate-based T/C may allow fewer animals to be used in the study while still maintaining sufficient precision.

In addition to the analysis method, we also consider aspects of the experimental design. In particular, we compare the cost effectiveness of 14-day studies with 21-day studies. We also show how historical datasets can be used to recommend a sample size with adequate power for future studies. These findings should allow researchers to reduce study costs and obtain accurate estimates of in vivo biological activity.

Quick Guide to Equations and Assumptions

We assume that the tumor volume for each animal follows an exponential growth pattern. This can be written as

$${\log }_{10}(\text{tumor volume})=a+b\times \text{time}+\text{error}$$ (1)

Here, a and b are parameters that correspond to the log initial volume and growth rate, respectively. These parameters are specific to a given animal. We assume that the error terms are independent and normally distributed with equal variance.

We consider two measures of antitumor activity. The first is the traditional T/C (commonly used), which is defined as

$$\text{traditional}T/C=\frac{\text{mean tumor volume in the treatment group at the final day of treatment}}{\text{mean volume in the control group at the final day of treatment}}$$ (2)

The second measure, proposed by us, is called the rate-based T/C. This is based on the ratio of the fitted growth rates of treated versus control groups, normalized to a study length of 21 days.

$$\text{Rate}-\text{based}T/C={10}^{({\mu }_{\mathrm{T}}-{\mu }_{\mathrm{C}})\times 21\text{days}}$$ (3)

Here, μ_T is the mean of the growth rates for the treatment group, and μ_C is the mean of the growth rates for the control group. The rate-based T/C uses a fixed time (day 21) so that it is less dependent on the choice of the final treatment day. A time of 21 days was chosen so as to be consistent with the most commonly used treatment length at our facility.

To evaluate the precision of the rate-based T/C and the traditional T/C, we compare the Z-scores of the two measures. The Z-score is computed by generating a large number of bootstrap samples¹⁵ from the original data and computing the measures on each sample. For a given measure of antitumor activity, we define the Z-score as¹⁶

$$Z\text{-score}=\frac{\left|\text{mean across the bootstrap samples of the log of the measure}\right|}{\text{standard deviation across the bootstrap samples of the log of the measure}}$$ (4)

A larger Z-score indicates better precision for the measure. This formula assumes that the measure is always positive and that it equals one under the null hypothesis. The Z-score could be used to estimate the power to detect a significant difference between the two groups at a given false positive rate (α). We used the formula¹⁷

$$\begin{array}{l}\text{Power}=\mathbf{\Phi }((Z\text{-score})-{\mathbf{\Phi }}^{-1}(1-\alpha /2))\\ +\mathbf{\Phi }(-(Z\text{-score})-{\mathbf{\Phi }}^{-1}(1-\alpha /2))\end{array}$$ (5)

Here, Φ is the cumulative distribution function of the standard normal distribution. This formula assumes that the distribution of the log of the measure across the bootstrap samples is approximately normal.

Materials and Methods

Xenograft studies

To assess the performance of different measures and experimental designs, we retrospectively analyzed a set of 219 xenograft biological activity studies in mice completed between 2006 and 2012. The studies involved 36 different xenograft models derived from cell lines. Supplementary Table S1 lists the number of studies completed with each of the different models. Thirteen different drug discovery programs spanning a variety of drug targets were used to provide a range of different cell lines and model systems for the exploration of the model-fitting procedures. Although each study is unique, the experimental details for a typical study in our analysis are described by Kupperman et al.¹⁸ Our research made use of data collected for other purposes, and thus no additional animals were needed for our work. Therefore our research did not require IRB approval.

The average number of treatment groups was 4.4 (in addition to the control group), and a majority (76%) of the studies in this dataset had between two and six treatment groups. Most studies (78%) used 10 animals in each treatment group, while a significant minority (7%) used 8 animals per group.

The average study length in this dataset was 21 days (SD = 5). Longer studies included a regrowth phase (following the final day of treatment). All studies were considered only during their treatment phase (some studies included a regrowth phase, which was not used in the analysis). Studies involving primary patient-derived xenografts were not included in the analysis. For the purposes of this analysis, we did not include biological treatments, focusing exclusively on small-molecule treatments. It is worth noting that biological treatments may behave differently in terms of growth kinetics.

Tumor volume measurements

The width and length of the tumors were measured at regular intervals (typically twice weekly) with digital vernier calipers. The volumes were estimated using the formula: volume = (width)² × (length)/2, where the width is the smaller of the two dimensions. For some of the studies, one or more animals had only partial data because they died early or reached a humane endpoint and were removed. The studies involved a total of 1103 control versus treatment comparisons.

Model-fitting and calculation of rate-based T/C measure

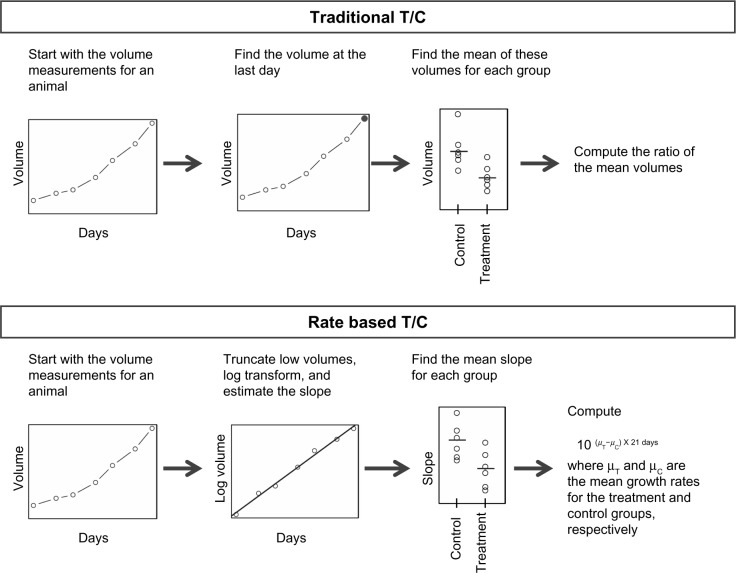
Figure 1 shows how the traditional T/C and rate-based T/C are computed. The rate-based T/C relies on the assumption that the tumor volumes grow exponentially with time. To fit the data into this growth model, the volumes are log transformed, and linear regression is applied using Equation 1. Unfortunately, log transformation can make low volume measurements become extreme; so to prevent this problem, tumor volumes below 50 mm³ were truncated to 50 mm³. Note that the exponential model is able to handle animals with missing data. For our analysis, the exponential growth rates were estimated for any animal with at least two unique measurement times.

Figure 1.

The process for computing the traditional T/C and the rate-based T/C.

To test the assumption of exponential growth, we plotted the log tumor volume versus time for 100 randomly selected animals (Supplementary Fig. S1) and confirmed that the relationship was approximately linear in most cases. We also plotted the corresponding residuals versus the fitted values (Supplementary Fig. S2) and confirmed that the residual values had no apparent systematic pattern. In addition, we computed the R² values for the fits among all the control group animals (Supplementary Fig. S3). The R² values were generally quite high, with an interquartile range of 0.93–0.98.

Although the exponential growth model performed well for most animals, non-exponential growth is still possible. For treatment groups with non-exponential growth (ie, non-constant growth rates), fitting the data into Equation 1 would yield the mean growth rates. Thus, the rate-based T/C could still be useful to detect differences in the mean growth rates between the groups.

Bootstrapping

Different summarization methods and designs will produce different levels of precision in the result. To estimate the level of precision, we used a technique called bootstrapping.¹⁵ Bootstrapping is a standard statistical practice that is used to estimate properties of a measure (such as its mean or variance) by random sampling with replacement from the original dataset. (This assumes that the original dataset is obtained from an independent and identically distributed population.) Bootstrapping thus starts with an original dataset and randomly generates multiple datasets that are similar to the original dataset. By computing the mean and standard deviation for each bootstrapped sample, the precision of the measures can be compared against each other. We used this technique to compare the precision of the different measures and show how changes in the study length and number of animals per group can affect the precision.

We performed a bootstrap analysis as follows (see Supplementary Fig. S4 for a flow chart). For each pair of control versus treatment arms, we generated 30 bootstrap samples of the data for the pair. For each animal in each bootstrap sample, we truncated the low tumor volumes and performed a least-squares fit to Equation 1 to estimate the tumor growth rate. The mean growth rate for each group was used in Equation 3 to compute the rate-based T/C for the bootstrap sample. We also computed the traditional T/C using Equation 2 without any log transformation or truncation.

Comparison of study designs against each other

To quantify the variation across different bootstrap samples, we used Equation 4 to compute the Z-score for each control versus treatment comparison. We then computed the median Z-score across all the comparisons for both the traditional T/C and rate-based T/C. The number of animals per group in the bootstrap samples was varied from 4 to 10 animals, and the Z-score calculations were redone. Two different study lengths were considered by truncating the data at either 14 or 21 days. The impact on the Z-score was then examined.

We were interested in understanding the implications of different study designs on the overall cost. A detailed financial model was constructed by us, based on in-house data, to evaluate each step of a xenograft study in terms of manpower and consumable costs. To compare relative costs of studies against each other, we normalized the studies to the most expensive study, setting the cost of that to 100%.

We also performed power calculations for the rate-based T/C using 14 days of data. The Z-scores computed by bootstrapping were used in Equation 5 to estimate the power of each comparison. Equation 5 assumes that the distribution of the log of the rate-based T/C across the bootstrap samples is approximately normal, so we verified this assumption using normal QQ plots (see Supplementary Fig. S5). Next, among the comparisons for which the rate-based T/C was below 0.4, the power estimates were averaged. The threshold of 0.4 was chosen because it is a common cutoff to determine if the antitumor activity is sufficient to be of practical significance. The result was an estimate of the average power to detect a rate-based T/C below 0.4. The average power was estimated for various sample sizes.

Results

Figure 2 shows examples of the rate-based and traditional T/C computed for two different studies. The calculations were done using the data up to days 7, 14, or 21. The traditional T/C tends to decrease as the study length increases, since the groups become more separated with time. In contrast, the rate-based T/C is normalized to a fixed day, so it is more stable with respect to study length.

Figure 2.

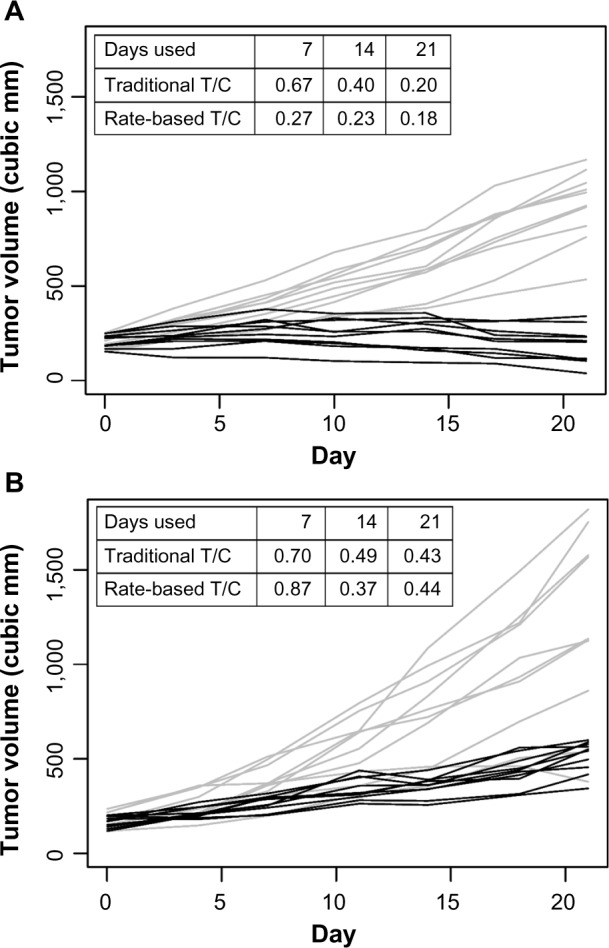
Treatment group (gray lines) and vehicle group (black lines) growth curves for two different studies (panels A and B). The traditional T/C and the rate-based T/C were computed using data up to days 7, 14, or 21.

Table 1 shows the estimated power versus the number of animals per group. For xenograft studies that are being conducted for the purposes of assessing robust biological activity (typically assessed as a T/C below 0.4), the rate-based T/C is powered at between 99% (for 10 animals) and 93% (for 4 animals). While this runs counter to the perception of xenograft studies being noisy, the basic point is one that is familiar to many researchers in the field, namely that robust biological activity in a xenograft study can be quite reliable. To place the power of these studies in context, it is worth noting that a power of 80% is typically considered adequate for hypothesis testing.¹⁹

Table 1.

Mean power versus the number of animals per group.

NUMBER OF ANIMALS		AVERAGE POWER TO DETECT A RATE-BASED T/C VALUE BELOW 0.4
4	0.930
5	0.951
6	0.965
7	0.973
8	0.979
9	0.982
10	0.986

Figure 3 shows the median Z-score versus the study cost for several different scenarios. A Z-score of 1.96 corresponds to a 5% chance of observing a result as a consequence of chance (α = 0.05). It is thus worth noting that a xenograft study run with 10 mice for 21 days provides a Z score of 4.63, corresponding to a 0.0004% chance of observing the result purely by chance (α = 0.000004).

Figure 3.

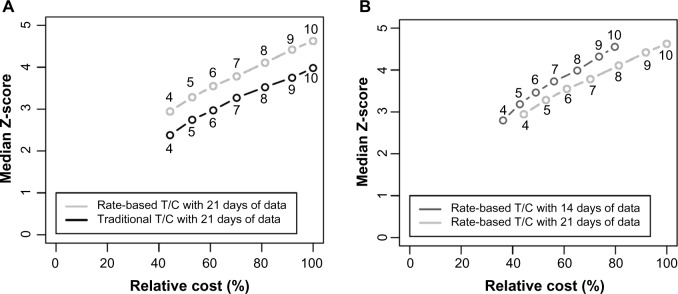
Median Z-score versus study cost. Panel (A) compares the traditional T/C and rate-based T/C, while panel (B) compares 21-day studies with 14-day studies. In both panels, the x-axis shows the cost of the study relative to the cost of a 21-day study with 10 animals per group.

Figure 3A shows that the rate-based T/C has a higher median Z-score and is thus more precise than the traditional T/C for the same group size. While the gain from the rate-based T/C is small, it is statistically significant, with a P-value of 2 × 10⁻¹⁶ found by using the nonparametric sign test to compare the two measures with 10 animals per group. This small change also allows a reduction in study sizes, as switching to the rate-based T/C allows a reduction from 10 animals to 7 animals with no reduction in Z-score. Note that using the rate-based T/C yields a Z-score of 2.95 for a study with four mice at 21 days (α cutoff of 0.003).

Figure 3B shows that for a given sample size, 14-day studies are almost identical in precision to 21-day studies (Z-score of 3.19 for five mice at 14 days versus 3.28 for five mice at 21 days). However, the 14-day studies are less expensive, and also permit a higher study throughput, if that is desired. Supplementary Figure S6 shows the iso-Z curves for a range of study sizes and study lengths (the calculation is described in the Supplementary File). Each line on these plots connects points with the same Z-score. For a Z-score of 3, study lengths of 10–21 days are essentially equivalent in terms of the study size. As the study length is reduced below 10 days, larger group sizes are required to achieve the same Z-score.

We acknowledge that the final choice of sample size is somewhat subjective, as this will also depend on the study objectives in any given situation. Also, the benefit of increased power is hard to quantify in financial terms, so one cannot easily compare with the cost of an increased sample size. In our case, we believe that a sample size of six animals per group, with a power of 0.96, is reasonable for routine compound screening.

Discussion

The rate-based T/C has several advantages over the traditional T/C measure, as listed in Table 2. The rate-based T/C uses all available data, while the traditional T/C uses data from only a single day. Thus, the rate-based T/C is able to account for random differences in the initial volume. In addition, fitting all the data reduces the effect of measurement noise and allows the rate-based T/C estimates to be more precise.

Table 2.

Properties of the traditional T/C and rate-based T/C.

TRADITIONAL T/C	RATE-BASED T/C
Uses data from a single day, leading to reduced precision	Uses all available data
Excludes animals that are removed early (due to death or humane endpoint), leading to bias and reduced precision	Includes all the animals
Strongly depends on study length	Minimal dependence on study length if the growth rates are constant

In addition to making full use of the data, the rate-based T/C has an advantage in that the measure does not strongly depend on the study length. The traditional T/C, however, is sensitive to the study length because longer studies show a greater divergence in the volumes of the groups. As the growth rate of the control arm usually determines the length of a xenograft study for a given model, comparing T/C ratios between xenograft models usually results in comparisons between studies of different lengths. For such experiments, the rate-based T/C would allow a more meaningful comparison, because the analysis could be normalized to the same fixed time, regardless of the actual study lengths.

In xenograft studies, animals are often sacrificed for humane reasons, such as high tumor volume or excessive drug toxicity. As a result, these animals have shorter time series profiles compared with the other animals in the same study. We acknowledge that as with the traditional T/C, the rate-based T/C also suffers from a reduction in precision when animals are removed early. With the rate-based T/C, the growth rates for the sacrificed animals are still estimated and used to calculate the overall effect size. The estimated growth rates for these animals will tend to have less precision compared with animals that were not sacrificed early. Therefore, early animal sacrifices will reduce the precision of the overall rate-based T/C estimate. However, we expect this reduction in precision to be small in most cases because sacrifices usually occur toward the end of the study, when the tumor sizes become large and drug toxicity effects accumulate. In such cases, measurements should be available for most of the time points, so the growth rate for a sacrificed animal can still be estimated accurately. We do not expect early sacrifices to cause substantial bias in the rate-based T/C because the sacrificed animals are still included in the analysis.

Although our data showed that the simple exponential model used for the rate-based T/C worked well in most cases, it is possible for tumors to grow at a non-constant rate in some cases. In particular, larger tumors may have slower growth rates (because of oxygen perfusion and nutrient limitations) or may sometimes cavitate (as the poorly vascularized center of a large tumor turns necrotic and collapses). This could bias the biological activity assessment with both the traditional T/C and rate-based T/C, as the smaller treated tumors do not experience these effects to the same extent. However, we expect the rate-based T/C to be less affected than the traditional T/C because the rate-based analysis includes data from earlier time points, before the growth rate slows. Even when the growth rates vary over time, the rate-based T/C analysis is still meaningful because it measures differences in the average growth rate between groups.

A limitation of the rate-based T/C shares with the traditional T/C in that the scale is not particularly intuitive. In particular, the scale does not have a fixed level that corresponds to stasis. For example, with a slow growing tumor model, a T/C of 0.3 may correspond to tumor regression, but in a fast growing tumor model, a T/C of 0.3 may only correspond to reduced growth. Using the growth rate ratio of treated versus control would eliminate this problem. For example, we could define the growth rate inhibition as a measure of biological activity equal to (1–(growth rate of treatment group)/(growth rate of control group)) × 100%. For this measure, a value of 0% would indicate that the treatment has no effect, a value of 100% would indicate stasis, and a value above 100% would indicate tumor regression.

To help scientists analyze their tumor xenograft data, we created an Excel spreadsheet that computes the rate-based T/C. The spreadsheet is available as a Supplementary File, and its details are described there.

The bootstrap approach presented in this paper allows us to estimate the uncertainty in our efficacy measures in an unbiased manner. In contrast, if we had instead used uncertainty estimates that relied on assumptions specific to each biological activity measure, it would have favored measures that made conservative estimates of the uncertainty. The bootstrap approach is also preferable to simulation studies. In particular, simulation studies require assumptions about the data, so simulation would favor biological activity measures that were based on similar assumptions.

We acknowledge that other research facilities will have different amounts of measurement variability and different cost structures, so the results may be different across sites. However, we expect the rate-based T/C to outperform the traditional T/C regardless of where the data are generated because the rate-based T/C uses the data more efficiently. The recommended study length and sample size may depend on the facility, but the bootstrap approach we presented here should allow other researchers to optimize their own in-house studies. For our studies, as we have pointed out here, the use of 10 animals in 21-day studies resulted in a 99% power to detect a T/C of 0.4 and a Z-score of 4.63 (α = 0.000004). In this context, analysis based on historical data was useful to us as it suggested ways in which to rationally optimize study design without compromising experimental rigor.

Although our analysis focuses on minimizing the cost for a given level of precision, cost is not necessarily the most important factor when designing a preclinical study. Other factors should be considered, such as the simplicity of the experimental design, the total time required to prepare and complete the study, laboratory space constraints, and the likelihood that the preclinical study will be predictive of future clinical results.

While our analysis recommended reducing the study length, we caution the reader that long-term studies are still necessary in some cases. In particular, certain drug side effects may not be observable in shorter studies. Since xenograft studies often have a secondary goal to provide tolerability data, researchers should consider this factor when deciding the study length. In addition, a reduction in the tumor growth rate may not be observable in a shorter trial if the drug has a delayed effect. If we expect a drug to have a delayed effect based on the mechanism of action, then a short study would not be suitable. In practice, shorter studies could be recommended for screening, while longer studies could be used for confirmation.

In summary, our work presents a simple, alternative metric for tumor xenograft studies, based on the growth rates of control and treated tumors. We also demonstrate that this metric is capable of providing equivalent statistical power with fewer animals and shorter study lengths.

Major Findings

The novel measure of antitumor activity proposed here, the rate-based T/C, is more efficient than the traditional T/C, requiring fewer animals to achieve the same power. We also find that 14-day studies are more cost efficient than 21-day studies, and that studies with six animals per group have sufficient power.

Not all research facilities have the same level of variability and operating costs, so the results may differ across sites. However, we expect the rate-based T/C to outperform the traditional T/C regardless of where the study is performed because the rate-based T/C makes more efficient use of the data. The optimal study length and animal number will depend on the variability and cost associated with each site, but our methodology should allow other researchers to optimize their own studies. Overall, our results help investigators reduce the size and duration of xenograft biological activity studies without compromising statistical power.

Supplementary Data

Supplementary Table S1.

Supplementary Figure S1. It shows the log tumor volume versus time for 100 randomly selected animals.

Supplementary Figure S2. It shows the residuals from regressing the log tumor volume on time for 100 randomly selected animals.

Supplementary Figure S3. It shows a histogram of the R² values from regressing the log tumor volume on time for all control group animals.

Supplementary Figure S4. It shows a flow chart describing the bootstrap analysis.

Supplementary Figure S5. It shows a normal QQ plot for the log of the rate-based T/C across the bootstrap samples.

Supplementary Figure S6. It shows the estimated Z-score for a range of sample sizes and study lengths.