DNA Translocations through Solid-State Plasmonic Nanopores

Abstract

Nanopores enable label-free detection and analysis of single biomolecules. Here, we investigate DNA translocations through a novel type of plasmonic nanopore based on a gold bowtie nanoantenna with a solid-state nanopore at the plasmonic hot spot. Plasmonic excitation of the nanopore is found to influence both the sensor signal (nanopore ionic conductance blockade during DNA translocation) and the process that captures DNA into the nanopore, without affecting the duration time of the translocations. Most striking is a strong plasmon-induced enhancement of the rate of DNA translocation events in lithium chloride (LiCl, already 10-fold enhancement at a few mW of laser power). This provides a means to utilize the excellent spatiotemporal resolution of DNA interrogations with nanopores in LiCl buffers, which is known to suffer from low event rates. We propose a mechanism based on plasmon-induced local heating and thermophoresis as explanation of our observations.

Solid-state nanopores have emerged as a versatile concept for label-free detection and investigation of biomolecules at the single-molecule level.¹ In brief, molecules that translocate through a small pore in a thin membrane can be electrically detected one by one, because they temporarily modulate the ionic conductance of the pore. The concept has proven useful for many applications, including molecular size discrimination,² investigation of biomolecular interactions at the single-molecule level,³ and investigation of local structures along elongated molecules, such as protein bound to DNA.⁴

Several variations and extensions of the nanopore concept have recently been explored, to a large extent motivated by a common goal to achieve nanopore-based DNA sequencing. Examples include nanopores systems with integrated tunneling detectors,⁵ and nanopore sensors combined with optics.⁶⁻⁹ Besides direct optical detection,^6,7,9 illuminating a nanopore with light was recently shown to be useful for modulation of the nanopore’s surface charge density, thereby enabling optical control of the electroosmotic flow through the pore.¹⁰ The integration of metal nanostructures close to a nanopore generates additional possibilities, including light-induced local heating, as recently explored for both biological¹¹ and solid-state⁸ nanopores. Such optical heating is a result of the strong interaction of light and metal nanoparticles through excitation of plasmons (collective charge oscillations in the particles).¹²

In addition to heating, plasmonic systems enable control and manipulation of optical fields at the nanoscale. Optical nanoantennas that are made of two closely spaced and optically coupled plasmonic nanoparticles are particularly interesting in this respect. They can be used to focus optical fields to the subdiffraction-limited gap region between the individual structures, typically referred to as the hot spot, where the optical field can be very intense.¹³ A common example is the bowtie antenna, consisting of two metal nanotriangles that face each other, as depicted in Figure 1a.^13,14

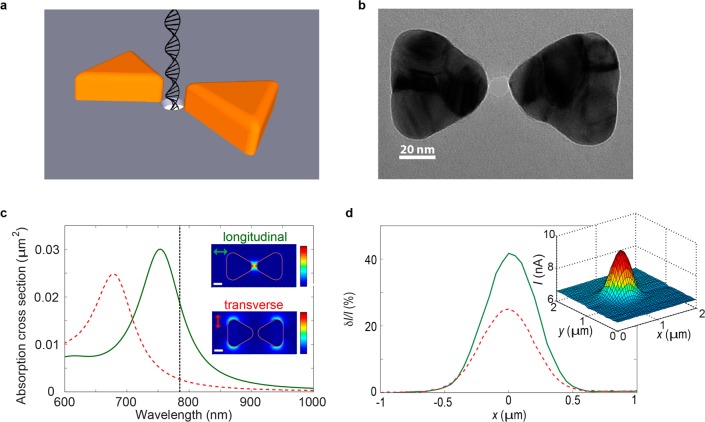
Figure 1.

Plasmonic nanopore concept and basic characteristics. (a) Schematic illustration of a DNA molecule translocating through a plasmonic nanopore that consists of a gold bowtie antenna with a 10 nm nanopore at the gap center (not to scale). (b) TEM top-view image of a plasmonic nanopore device. (c) Simulated absorption cross sections of the plasmonic nanopore in longitudinal (green full line) and transverse (red dashed line) excitation. The black dotted line indicates the laser wavelength of 785 nm that was used in our experiments. The insets show color plots of the simulated electrical field intensity enhancement at 785 nm in the plane of the antenna and through the middle of the gold triangles (color maps from 0 to 1200 and 0 to 65 for longitudinal and transverse mode, respectively). Scale bars are 20 nm. (d) Change in current, δI, relative to the baseline current, I, for line scans of the pore through the laser focus for longitudinal (green full line) and transverse (red dashed line) mode at 0.5 mW. The inset shows a 2D scan of the variation in current along the focal plane (longitudinal mode, 100 mV bias voltage).

Here we demonstrate label-free detection of single DNA molecules with a solid-state plasmonic nanopore. The sensor device is based on a nanopore that is placed right at the hot spot of a gold bowtie nanoantenna.⁸ We explore the effects of plasmon excitation on the essential parameters in nanopore sensing experiments, primarily the sensor signal (changes in the pore conductance due to DNA translocation); the translocation time (the time a DNA molecule occupies the pore during translocation); and the event rate (the number of translocated DNA molecules per unit time). To gain a better understanding of plasmonic effects on DNA nanopore translocations and, in particular, the role of plasmonic heating, we also provide complementary control measurements where the temperature of conventional (nonplasmonic) nanopores was regulated by heating the whole flow cell with a Peltier element (referred to as temperature-control measurements).

Solid-State Plasmonic Nanopore Sensor

Figure 1a depicts the geometry of the solid-state plasmonic nanopore. The bowtie antenna consists of two 30 nm thick equilateral gold triangles (that measure 60 nm from one tip to the opposite flat side), separated by a 10 nm gap. A 1 nm thick titanium layer under the gold ensured good adhesion to the underlying 20 nm thick silicon nitride (SiN) membrane. Right at the gap of the plasmonic antenna, we drill a 10 nm-in-diameter nanopore through the membrane using a transmission electron microscope (TEM). Figure 1b shows a TEM image of a plasmonic nanopore. As mentioned above, the gold bowtie antenna can focus incident light to the small gap region right at the pore mouth. This is illustrated in the upper inset of Figure 1c, which shows a finite-difference time-domain (FDTD) simulation of the enhancement in the electric field intensity (compared with the incident field) when the sensor is excited with 785 nm light polarized along the direction of the antenna (longitudinal excitation, illustrated in the figure). As expected, the optical field is enhanced by many orders of magnitude in a ∼10 nm hot spot in the gap between the two gold triangles. The lower inset instead shows the simulated enhancement in the electric field intensity upon excitation with light polarized in the transverse direction. While the hot spot at the pore mouth is not excited in transverse mode, there is still a considerable amount of light absorption (red dashed line in Figure 1c) and corresponding local heating. As a result, we expect effects related to local heating to appear in both longitudinal mode and in transverse mode, although to a lesser extent for transverse excitation. In contrast, effects that require intense optical fields close to the pore are expected to appear for longitudinal excitation only.

Plasmonic excitation modulates the ionic conductance of the pore,⁸ which enables us to accurately align the plasmonic nanopore with the focal spot of a 785 nm laser in our custom-made microscope setup (see Methods for experimental details). Briefly, the ionic current flowing through the pore is measured at a constant bias voltage (100 mV), while the pore is scanned through the laser focus. Figure 1d shows the relative change in current for a plasmonic pore in 1 M KCl that is scanned across the focal spot, for both longitudinal (full green line) and transverse (red dashed line) excitation, at 0.5 mW. The signal is strongest when the bowtie is excited in the longitudinal mode, as predicted from the FDTD simulations. The observed difference between longitudinal and transverse mode is smaller than predicted, which is likely due to small differences between the actual nanopore-bowtie and the simulated structure. Scanning in all three dimensions provides the coordinates of the laser focus as the position of highest plasmon-induced change in the nanopore conductance, at which the pore is positioned for further experiments. When the nanopore is fixed at a given position, the nanopore current varies linearly with voltage, both with and without laser excitation, as shown in Supporting Information Figure S2.

DNA Sensing with Plasmonic Nanopores

We demonstrate the potential of the plasmonic nanopore for single-molecule sensing using doubled-stranded DNA (dsDNA, 48.5 kilobase pairs). The DNA molecules were added at a concentration of 10 ng/μL in a 1 M KCl buffer on one side of the membrane (opposite from the plasmonic antenna, unless stated otherwise) and pulled through the pore electrophoretically by a 100 mV potential applied across the membrane. The purple curve in Figure 2a shows the ionic nanopore current without plasmonic excitation, before and after adding DNA to the flow cell. Translocation of DNA molecules leads to the downward spikes in the current. The green and orange curves in Figure 2a show the sensor signal during plasmon excitation. The separation of the time traces demonstrates a significant increase in the open nanopore current (baseline) upon laser excitation. This increase varied between different plasmonic nanopores, which likely is due to differences in alignment and the exact nanopore-bowtie geometry. Importantly, the noise level upon plasmon excitation remains sufficiently low to allow for detection of single DNA molecules with high signal-to-noise ratio. Details of two DNA translocation events at 5 mW laser excitation are shown to the right in Figure 2a. The upper panel is an example of a dsDNA molecule translocating in a linear fashion, while the bottom panel corresponds to a partially folded molecule.¹⁵

Figure 2.

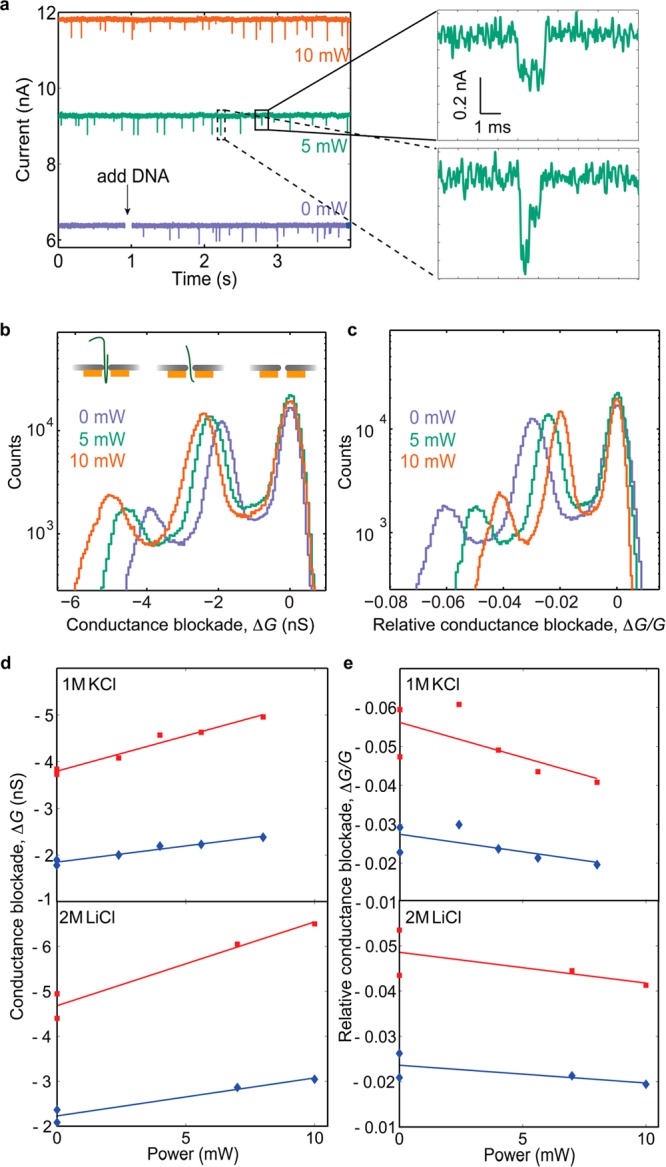
DNA translocations through a plasmonic solid-state nanopore. (a) Examples of current traces in 1 M KCL without (purple) and with (green, orange) plasmon excitation (longitudinal mode). The panels to the right show the details of one linear (top) and one partially folded (bottom) translocation event upon 5 mW laser excitation. (b) Conductance blockade histograms for DNA translocations in 1 M KCl at 0 mW (purple), 5 mW (green), and 10 mW (orange) laser excitation. (c) Same as in (b), but for the relative conductance blockades (blockades normalized with the open pore conductance at each power). (d) Position of the conductance blockade peaks versus power for measurements in 1 M KCl (top) and 2 M LiCl (bottom). Diamonds and squares correspond to the first and the second translocation peak, respectively. (e) Same as in (d), but for the relative conductance blockades. The lower points (lower absolute values) at 0 mW corresponds to the last acquisition during the experiments.

We construct conductance blockade histograms to investigate in detail how plasmonic excitation affects the sensor signal. The histograms in Figure 2b represent the two main conductance blockade levels from more than 700 DNA translocation events. The peaks at 0 nS correspond to the open pore conductance at each laser power. The middle peaks at about −2 nS correspond to one DNA strand blocking the pore, and the peaks near −4 to −5 nS arise from DNA molecules that are partially folded when moving through the pore (i.e., two strands blocking the pore). The results clearly show that the conductance blockade and hence, the sensor signal, increases with plasmonic excitation. Plasmonic excitation sometimes also resulted in an increase in the noise level (e.g., see Figure 4a), which exemplifies that an increase in signal does not always lead to an increase in the signal-to-noise ratio of a sensor. We repeated the measurements using 2 M LiCl as buffer medium, which has similar bulk conductivity as 1 M KCl (see Figure S1 in the Supporting Information) while providing significantly lower translocation speeds.¹⁶ The results are presented in Figure 2d, showing conductance blockades versus laser power for DNA translocations in 1 M KCl (top) and 2 M LiCl (bottom). The trend of increasing conductance blockade with laser excitation is clear at both buffer conditions. These observations can be explained by plasmonic heating of the nanopore. Plasmons in the optical antenna are excited by the laser illumination and decay either through re-emission of photons or through nonradiative absorption.¹² The absorption results in local heating of the nanopore and a corresponding temperature increase of the buffer in and around the nanopore. In turn, an increase in temperature increases the buffer conductivity, thereby enhancing both the open pore conductance and the magnitude of the blockades.¹⁷ A clear increase in the conductance blockades with temperature was indeed confirmed by our temperature-control measurements (see Supporting Information Figure S9a).

Figure 4.

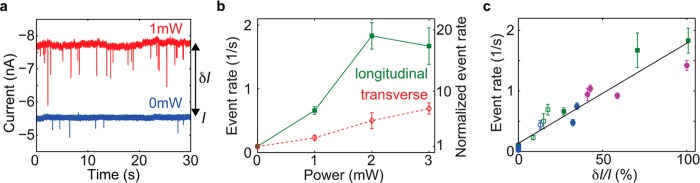
Plasmon-induced event rate enhancement in 2 M LiCl. (a) Examples of current traces at 0 mW (blue) and 1 mW laser excitation in longitudinal mode. The DNA was added to the side of the antenna, thereof the negative currents. (b) Event rate (left y-axis) and event rate normalized with the initial value at 0 mW (right y-axis) versus laser power for the same plasmonic nanopore as in (a), excited in longitudinal mode (green filled squares) and in transverse mode (red open diamonds). The error bars correspond to the statistical error of the mean. (c) Event rate versus relative increase in the open pore current upon laser excitation, δI/I. Different colors correspond to different plasmonic nanopores. Filled and open symbols are for longitudinal and transverse polarization, respectively. Squares and circles correspond to DNA added from the side of the bowtie antenna and the other side, respectively. The black full line is a linear fit to all data. The green markers correspond to the data in (b).

Histograms of the relative conductance blockades, ΔG/G (where G is the open pore conductance at the given laser power and ΔG is the magnitude of the conductance blockade) are shown for different laser powers in Figure 2c for the 1 M KCl experiment. The corresponding peak positions are plotted versus laser power for both 1 M KCl and 2 M LiCl in Figure 2e. The graphs show that the relative conductance blockades decrease slightly with increasing laser power. Interestingly, we see a similar decrease in the relative conductance blockades also upon uniform heating of a nanopore (see Supporting Information Figure S9b). However, we cannot exclude additional effects, other than heating, that could contribute to the observed decrease in relative conductance blockades. For example, light-induced changes in the surface charge density at the pore wall would primarily affect the open pore conductance and not the conductance blockade during DNA translocation.¹⁰ We also note that part of the decrease was often nonreversible (did not go back when the laser excitation was switched off), which is likely caused by small changes in the nanopore geometry during measurements.

The translocation time, Δt, is another essential parameter in nanopore sensing experiments. Interestingly, we find that the translocation time stays approximately constant upon plasmon excitation, both in 1 M KCl and in 2 M LiCl (Figure 3a). This suggests that plasmon excitation in our device is capable of modulating both the open pore conductance and the conductance blockades, as shown above, without significantly affecting the force balance during DNA translocation, which sets the translocation time. This is a nontrivial result, because the force balance and hence, the translocation time, typically depends on the same parameters that affect the nanopore ionic current, including temperature and surface charge. Indeed, our temperature-control measurements show a considerable decrease in the translocation time with increasing temperature (more than 50% shorter translocation time at 45 °C compared to at 10 °C, see Figure 3b). An increase in the negative surface charge density of the nanopore, which was reported for laser-illuminated conventional nanopores,¹⁰ would instead create an electroosmotic flow that opposes the DNA translocation, thereby leading to an increase in the translocation time. Hence, the fact that we do not observe a significant change in the translocation time upon plasmonic excitation may result from a coincidental balance between the competing effects from heating and a change in the surface charge of the nanopore.

Figure 3.

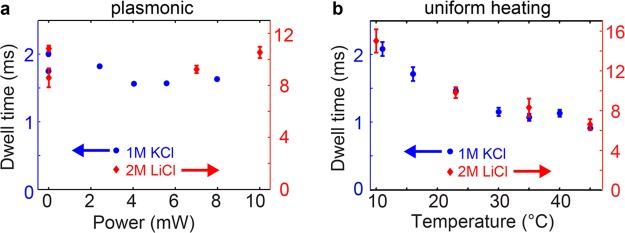
(a) Dwell times for λ-DNA translocations through plasmonic nanopores upon plasmon excitation at different powers (longitudinal) in 1 M KCl (blue circles, left axis) and in 2 M LiCl (red diamonds, right axis). (b) Dwell times at different temperatures for λ-DNA translocations through 10 nm in diameter conventional nanopores in 1 M KCl (blue circles, left axis) and in 2 M LiCl (red diamonds, right axis). All error bars were calculated as the standard error of the mean (and are smaller than the symbols for 1 M KCl in (a)).

However, an alternative, and in our opinion more likely, explanation of the insensitivity of the translocation time to plasmon excitation is based on the fact that plasmonic heating is highly local. The gold bowtie antenna acts as a local nanoscale heat source and causes a temperature increase that is strongest at the gold surface and drops to below half of the maximum value already at a 100 nm distance from the structure (see Figure 5a).¹² Although a local temperature increase and corresponding decrease in buffer viscosity acts to reduce the drag coefficient on the DNA inside the pore, this effect is counteracted by an enhancement of the electroosmotic flow through the pore that opposes the DNA movement (also due to the temperature-induced change in viscosity, a more detailed discussion is provided in section F in Supporting Information).^18,19 As a result, local heating of the nanopore is not expected to significantly affect the translocation time. By contrast, the decrease in translocation time that we observe upon uniform heating is dominated by temperature-induced changes in the viscous drag on the untranslocated part of the DNA that is farther away from the pore (where local heating would be low).²⁰ Hence, plasmon-induced local heating may indeed affect both the open pore conductance and conductance blockades without significantly affecting the translocation time, in agreement with our observations.

Figure 5.

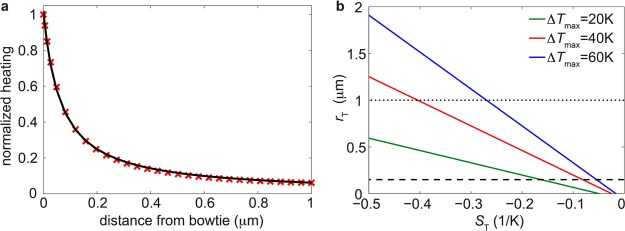
Analysis of thermophoretic effects in plasmonic nanopores. (a) Normalized heating profile away from the antenna in the orthogonal direction to the membrane, starting at the top of the bowtie nanoantenna at the gap center. The red markers are results from the finite-element simulation and the black full curve is a fit to eq 2, using a = 0.06581 μm and b = 0.06425 μm. (b) Estimated thermophoretic capture distance (r_T) versus the Soret coefficient (S_T) for local heating of the nanopore at different temperatures. The dashed and dotted lines correspond to the estimated electrophoretic capture radii in 2 M LiCl and 1 M KCl, respectively.

Plasmon-Induced Enhancement of the Event Rate

The most noticeable effect of plasmon excitation on the DNA translocation behavior through plasmonic nanopores is a dramatic increase in the event rate in LiCl buffers. Figure 4a shows typical consecutive current traces of DNA translocations in 2 M LiCl without (blue) and with (red) laser excitation. The increase in noise that can be observed upon plasmonic excitation was not always present and is also not fully understood at this stage.

The event rate at different laser powers for both longitudinal and transverse excitation is shown in Figure 4b for the same sample. At longitudinal excitation, the enhancement in the event rate exceeds 1 order of magnitude already at 2 mW. The effect is significant also in transverse mode (around 30% of the enhancement in longitudinal mode for the same laser power). This shows that the effect is not exclusively dependent on the optical hot spot at the plasmonic nanopore, because the hot spot is only excited in the longitudinal mode (see Figure 1c). The two data points at 0 mW were acquired between measurements at the different polarizations, demonstrating that the effect is reversible and directly related to plasmon excitation. Interestingly, while also observed for 1 M LiCl (Supporting Information Figure S5), the rate enhancement effect was never observed for DNA in KCl buffer. Instead, for KCl we typically observe a decrease in the event rate upon laser excitation (Supporting Information Figure S3). It should also be noted that the event rate in 2 M LiCl was found to be linearly dependent on the bias voltage (Supporting Information Figure S6), indicating that the event rate is limited by transport of molecules to the nanopore rather than by the barrier involved in the DNA entering the pore.²¹

We performed a systematic study of the event rate in 2 M LiCl at different conditions in order to gain a better understanding of the plasmon-induced enhancement. The main results are presented in Figure 4c (while results from additional experiments can be found in Supporting Information Figure S4). On the x-axis of Figure 4c, we use the relative increase in the open pore current upon laser excitation, δI/I (not to be confused with the relative conductance blockade, ΔG/G). We find δI/I to be a suitable parameter in describing the optical response of the plasmonic nanopore, and particularly useful for comparing results obtained for different plasmonic nanopore chips and results acquired at different polarizations. Each color in Figure 4c corresponds to a different plasmonic nanopore. Filled and open symbols correspond to longitudinal and transverse excitation, respectively. Finally, round markers correspond to DNA being translocated from the opposite side of the bowtie antenna, while squares correspond to DNA added at the same side as the nanoantenna.

Remarkably, the results for all combinations of these different conditions together collapse to display a clear, approximately linear, dependence of the event rate on δI/I. The implications of this are multifold. First, when compared using δI/I instead of laser power, the enhancement in the event rate is of similar strength for both polarizations. This indicates that the strength of plasmon excitation and optical absorption is essential, while the effect does not require excitation of the plasmonic hot spot. We can therefore exclude explanations of the effect that are based on optical forces resulting from the strong field gradients in the hot spot. The independence on translocation direction shows that the effect can neither be ascribed to any vertical asymmetry of the plasmonic nanopore (i.e., from having the plasmonic antenna only on one side of the membrane). Also, the effect is quantitatively the same for different sensor chips, showing that small changes in the plasmonic nanopore geometry do not significantly modulate the effect.

The clear dependence of the event rate on δI/I, and the insensitivity to other experimental conditions like polarization, indicates that the event rate enhancement is caused by plasmon-induced heating, which for a given δI/I is the same for longitudinal and transverse excitation. Our temperature-control measurements show some increase in the event rate with temperature. However, this increase is fairly moderate, from around 0.1 s^–1 at 20 °C to around 0.15 s^–1 at 45 °C, while the plasmon-induced enhancement exceeds 1 order of magnitude already at very low laser powers. In order to enable a direct comparison between the temperature-control measurements and the plasmonic measurements, we convert δI/I to an upper limit of the temperature increase caused by plasmon excitation. This is done using the measured temperature-dependence of the bulk conductivity of our 2 M LiCl buffer (Supporting Information Figure S1) and by assuming that δI/I is caused only by a change in temperature. [At the time of proof reading of this paper, a new measurement of the bulk conductivity of 1 M KCl using a micropore indicated a slightly stronger temperature dependence of the buffer bulk conductivity compared with the results given in Supporting Information Figure S1, that were obtained with the Zetasizer Nano. We note that such potentially stronger temperature dependence would slightly lower the estimated plasmonic heating temperatures, but not affect the main conclusions of the paper.] From this (Supporting Information Figure S10), it is clear that the plasmon-induced enhancement is significantly stronger than expected from uniform heating. Furthermore, the temperature-regulated measurements show enhancements for both 2 M LiCl and 1 M KCl (Supporting Information Figure S11), while the plasmon-induced rate enhancement only appears for LiCl. On the basis of these results, we can exclude a simple increase in temperature as the main cause of the observed plasmon-induced rate enhancement.

Instead, we suggest that the effect is related to the localized nature of plasmonic heating and the associated strong thermal gradients around the plasmonic nanopore. DNA and other biomolecules are known to move along thermal gradients through thermophoresis,²² which has previously been proposed to influence the translocation dynamics of polymers through nanopores.^11,23,24 Thermophoresis is a complex process, and both the magnitude and the direction of thermophoretic forces depend on multiple variables, including temperature, size and charge of the moving molecule, type of salt and ionic strength.²² Interestingly, LiCl is known to result in negative thermophoresis, for which molecules move from cold to warm regions.²⁵⁻²⁷ This was recently demonstrated for DNA at high concentrations of LiCl.²⁸ We propose that negative thermophoresis aid the capture process in our experiments, by moving DNA molecules toward the warm nanopore and into the small region close the pore within which they are electrophoretically captured and translocated (i.e., they are moved to within the electrophoretic capture distance).

We adopt the theoretical model by He et al.²⁴ to evaluate if thermophoretic capture of DNA is consistent with the observed plasmon-enhanced event rate. The thermophoretic capture distance r_T describes the distance from the pore below which thermophoresis start to dominate over diffusion. Whether thermophoretic effects are likely to affect the capture process of DNA can then be evaluated by comparing r_T with the electrophoretic capture distance. We can estimate r_T from²⁴

1

where ΔT(r) is the plasmon-induced temperature increase at distance r from the structure and S_T is the Soret coefficient that describes both direction and magnitude of thermophoresis of lambda-DNA in the buffer medium. To determine r_T for a given S_T, we need the temperature distribution around the illuminated plasmonic nanopore, which was calculated by finite-element simulations (see Methods for details). The normalized temperature profile away from the bowtie antenna along the pore direction is presented in Figure 5a. As expected, the temperature can be accurately fitted as inversely proportional to the distance from the structure¹²

2

where a and b are fit parameters and ΔT_max is the maximum temperature increase close to the pore. Although the plasmonic heating is local, the temperature increase is still significant at distances outside the electrophoretic capture distance, which is very short for 2 M LiCl (∼150 nm at our experimental conditions, see section E in Supporting Information). Combining eq 1 and eq 2 gives

3

Equation 3 predicts that local heating combined with a negative Soret coefficient will result in a positive thermophoretic capture distance. The relation also predicts that r_T, and therefore also the event rate,²¹ increases linearly with the local temperature increase at the nanopore. This is in agreement with the experimental trend shown in Figure 4c and Supporting Information Figure S10.

We plot r_T versus S_T for different values of ΔT_max in order to evaluate if the model can explain the experimentally observed rate enhancements for realistic values of S_T (Figure 5b). For 60 K heating of the nanopore, the estimated thermophoretic capture distance exceeds the electrophoretic capture distance (dashed line in the figure) already for S_T ≈ −0.06 K^–1. Experimentally, 60 K local heating increased the event rate around 16 times (see the linear trend in Supporting Information Figure S10). When the theoretical model is used, this enhancement yields a predicted value of S_T ≈ −0.6 K^–1, for which r_T ≈ 2.4 μm (16 times larger than the estimated electrophoretic capture distance in 2 M LiCl).

To evaluate if S_T ≈ −0.6 K^–1 is a reasonable value for our experimental conditions, we can compare it with the estimated value obtained by extrapolation from reported values of S_T for short single stranded DNA (ssDNA) at high LiCl concentrations (short Debye lengths, r_D).²⁸S_T was reported to be around −0.01 K^–1 for 80 bp ssDNA at LiCl concentrations corresponding to r_D ≈ 1 nm, and the fitted curve in the same report suggests that the magnitude would increase to at least −0.015 K^–1 when increasing the concentration to 2 M LiCl (r_D ≈ 0.2 nm). Using an approximate scaling of S_T as the square root of the DNA length, as reported for dsDNA in low ionic strength KCl,²² we estimate S_T to be on the order of −0.4 K^–1 for 48.5 kbp DNA at 2 M LiCl. Given the many uncertainties involved in order to reach this value, we find it remarkably close to the predicted value of S_T ≈ −0.6 K^–1, for which our thermophoretic model quantitatively agrees with the experimentally observed rate enhancements. On the basis of this analysis, we conclude that thermophoresis can have significant effects on molecules at micrometer distances from a locally heated nanopore and that negative thermophoresis is a plausible mechanism for the observed plasmon-enhanced event rate.

If thermophoresis plays the major role in the event-rate enhancement, the effect should also appear for a locally heated nonplasmonic nanopore. We tested this by positioning a conventional nanopore at the diffraction-limited focal spot of the laser in our setup. While this approach should provide less localized heating than plasmonic heating (and correspondingly lower temperature gradients), we note that eq 1 predicts r_T to be determined by the temperature increase at r_T and not by the temperature gradient at r_T. This, perhaps nonintuitive, prediction is in perfect analogy with the model for electrophoretic capture by Grosberg and Rabin,²¹ which predicts the electrophoretic capture distance to be determined by the electric bias potential and not by the gradient in the potential (the electric field), although the electrophoretic force arise from the latter. Indeed, although a much higher laser power was required (50 mW increased δI/I by around 23%) to get a similar current increase as for the plasmonic nanopores, we observed a significant event rate enhancement in 2 M LiCl also for the locally heated nonplasmonic nanopore (Supporting Information Figure S8).

The small plasmon-induced decrease in event frequency that is observed in 1 M KCl may be related to positive thermophoresis in KCl,^22,28 and a corresponding decrease in the DNA concentration close to the pore. Considering the much larger capture distance in 1 M KCl compared with in 2 M LiCl (∼1 μm, see dotted line in Figure 5b and section E in Supporting Information), this effect is expected to be less pronounced, which is in good agreement with our observations. We finally note that thermophoretic motion of the salt ions in the solution may also play a role by affecting the spatial distribution of the ionic concentration close to the nanopore. While K⁺ ions are thermophobic above room temperature,²⁹ Li⁺ ions are typically thermophilic²⁶ and may thus accumulate around the nanopore. This could affect both the capture process as well as the effective nanopore conductance. However, the magnitude of the Soret coefficient is highly dependent on particle size,²² and it is expected to be very small for the Li⁺ ions (on the order of 10^–3 to 10^–2 K^–1).²⁵ We therefore think such effects at most play a minor role for our observations.

This article presents a systematic investigation of plasmonic effects on DNA translocations through solid-state plasmonic nanopores. We were able to characterize the response of the sensor device to translocating dsDNA molecules by quantifying the most important parameters such as conductance blockades, translocation time, and event rate. All observed plasmonic effects on these parameters are consistent with plasmonic local heating of the nanopore. The most significant plasmonic effect that we observe is a dramatic enhancement of the event rate in LiCl buffer, which is attributed to negative thermophoresis in the strong thermal gradients caused by plasmonic heating. It should be stressed that this plasmon-induced rate enhancement is of high relevance for nanopore sensing, because measurements in LiCl buffers typically suffer from very low event rates at suitable molecular concentrations, but provide other important advantages such as low translocation speeds and a corresponding high spatiotemporal resolution.

Plasmonic excitation and local heating of our solid-state plasmonic nanopore also increased the sensor signal (larger conductance blockades) without a corresponding decrease in the translocation time that one obtains for uniform heating. With respect to sensor signals, we note that the addition of plasmonic functionalities to nanopores also opens up for optical detection schemes, including monitoring shifts in plasmonic resonances,³⁰⁻³⁴ plasmon-enhanced fluorescence,^35,36 and surface-enhanced Raman scattering.⁶ The two latter are based on the strong optical fields around plasmonic nanostructures and are particularly suitable for our system that provides a plasmonic hot spot right at the nanopore. Furthermore, optical forces based on the strong optical field gradients in the plasmonic hot spot may be useful for trapping and controlling the motion of biomolecules through nanopores.^37,38

Methods

Sample Fabrication

Plasmonic nanopore chips were fabricated from prefabricated 4-in. wafers containing multiple (256) individual silicon (Si) chips with freestanding SiN membranes (approximately 40 μm × 40 μm and 20 nm thick). The chips were designed to have a 500 nm insulating silicon dioxide layer between the Si and the nanopore membrane to minimize capacitive noise.^39,40 This layer was removed from membrane regions using a 7 min buffered oxide wet etch. Arrays of plasmonic bowtie nanoantennas were defined on top of the membranes using conventional electron beam lithography, as described in our earlier work.⁸ Finally, a TEM (Philips CM300UT-FEG or FEI Tecnai TF20) was used to drill a single 10 nm-in-diameter pore through the SiN membrane right at the gap position of a suitable optical nanoantenna. The plasmonic nanopore chips were stored in a water–ethanol (1:1) mixture until usage.

DNA Translocations through Plasmonic Nanopores

After a short oxygen plasma treatment, the plasmonic nanopore chip was mounted in a custom-made flow cell such that it separated two compartments containing buffer solution (1 M KCl or 2 M LiCl buffer, each containing 10 mM Tris (tris(hydroxymethyl)aminomethane) and 1 mM EDTA (ethylenediaminetetraacetic acid) at pH 8). The ionic current flowing through the nanopore was monitored using Ag/AgCl electrodes connected to a patch clamp amplifier (Axon Axopatch 200B, Molecular Devices, US) and the measured signals were transferred to a computer via a DAC card (USB-6251, National Instruments, US). A 100 mV bias voltage was used in all experiments unless stated otherwise. We used light from a 785 nm diode laser (Omicron-Laserage Laserprodukte GmbH, Germany) for plasmon excitation. The laser beam was expanded to about 7 mm using two lenses and focused into the flow cell through a water-immersion objective (60×, Olympus, The Netherlands) in a custom-built inverted microscope. A rotatable quarter wave plate was used to control the polarization. A piezo stage (P-545, Physik Instrumente, Germany) enabled accurate control of the position of the plasmonic nanopore with respect to the focused laser beam. Experiments were performed using a custom-designed LabView program (National Instruments) that controlled our instruments. For translocation experiments, unmethylated λ DNA (Promega) was first heat treated at 65 °C for 10 min and then stored on ice before it was added to the flow cell.

Optical FDTD Simulations

FDTD Solutions (Lumerical Solutions, Inc., Canada) was used to model the optical properties of the plasmonic nanopore. The bowtie antenna was modeled as two 30 nm thick and 60 nm long (tip to end) gold triangles separated by a 10 nm gap on a 20 nm thin SiN membrane (refractive index, RI = 2), and with a 10 nm in diameter pore through the membrane at the gap center. The upper corners of the triangles were slightly rounded (15 nm-in-diameter rounding) to better resemble the fabricated structures. The RI of the surrounding medium was set to 1.33. Symmetry was used to reduce the computational time. The plasmonic antennas were excited by a pulse from a total-field scattered-field source with the optical axis perpendicular to the membrane and the polarization in either the longitudinal or the transverse mode. The optical absorption cross section was calculated through the net power flow into a box surrounding the antenna.

Combined Optical and Thermal Simulations

The temperature distribution around a plasmonic nanopore illuminated with 785 nm light was calculated using the finite-element method (Comsol Multiphysics). The same geometry was used as for the FDTD simulations, but with rounded corners only in the plane of the membrane. We also excluded the nanopore to reduce the simulation time. The total simulation region was a cube with a side length of 2 μm. Refractive indices for the membrane, the surrounding medium and the gold antenna were 2, 1.33 and taken from Johnson and Christy,⁴¹ respectively. The thermal conductivity of the SiN membrane was set to 3 W/(m × K)⁴² and we used values from the built-in library for gold and for the surrounding medium (using values for water for the latter). A tetrahedral mesh was used (maximum element size far from the antenna set to 1/10 of the wavelength).

Maxwell’s equations were solved in the wave optics module in Comsol Multiphysics and used to calculate the optical absorption and corresponding heat source of the nanoantenna upon illumination by a plane wave at 785 nm, polarized in the longitudinal direction. Perfectly matched layers were used to avoid back scattering at the outer boundaries. The 2-fold symmetry of the nanoantenna allowed us to calculate only one quadrant of the simulation region by using a perfect electric conductor boundary plane (orthogonal to the polarization and to the membrane) and a perfect magnetic conductor boundary plane (parallel to polarization and orthogonal to the membrane), both going through the center of the antenna.

The steady-state temperature distribution of the system could then be calculated by solving the heat equation (heat transfer module) using the total power dissipation obtained above as the heat source. Newton’s cooling law was imposed on the outer boundaries of the simulation

4

where ϕ is the heat flux over the boundary, κ is the thermal conductivity of the material at the boundary, L = 2 μm is the typical length scale, T is the temperature at the boundary and T_inf is the set temperature of the surrounding environment far away. The Nusselt number (Nu) was set to 1.4 after optimization using simulations for a spherical heat source and comparison with the corresponding known analytical solution. The use of Newton’s cooling law as boundary condition provided significantly more accurate temperature distributions compared with using a fixed temperature at the boundary.

Supporting Information Available

Results on buffer conductivity versus temperature, current–voltage characteristics with and without plasmon excitation, event rate versus bias voltage, plasmonic effects on translocation times in 1 M KCl, event rate results from additional experiments and at different buffer conditions, TEM images of plasmonic nanopores before and after measurements, results from temperature-controlled experiments, discussion on capture distances and on temperature effects on translocation times. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^† Organic Electronics, Department of Science and Technology, Campus Norrköping, Linköping University, SE-60174 Norrköping, Sweden.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States