Interleaved diffusion-weighted EPI improved by adaptive partial-Fourier and multi-band multiplexed sensitivity-encoding reconstruction

Abstract

Purpose

We report a series of techniques to reliably eliminate artifacts in interleaved echo-planar imaging (EPI) based diffusion weighted imaging (DWI).

Methods

First, we integrate the previously reported multiplexed sensitivity encoding (MUSE) algorithm with a new adaptive Homodyne partial-Fourier reconstruction algorithm, so that images reconstructed from interleaved partial-Fourier DWI data are free from artifacts even in the presence of either a) motion-induced k-space energy peak displacement, or b) susceptibility field gradient induced fast phase changes. Second, we generalize the previously reported single-band MUSE framework to multi-band MUSE, so that both through-plane and in-plane aliasing artifacts in multi-band multi-shot interleaved DWI data can be effectively eliminated.

Results

The new adaptive Homodyne-MUSE reconstruction algorithm reliably produces high-quality and high-resolution DWI, eliminating residual artifacts in images reconstructed with previously reported methods. Furthermore, the generalized MUSE algorithm is compatible with multi-band and high-throughput DWI.

Conclusion

The integration of the multi-band and adaptive Homodyne-MUSE algorithms significantly improves the spatial-resolution, image quality, and scan throughput of interleaved DWI. We expect that the reported reconstruction framework will play an important role in enabling high-resolution DWI for both neuroscience research and clinical uses.

Introduction

Multi-shot interleaved echo-planar imaging (EPI) can potentially generate images with reduced geometric distortion, sharper point-spread function (PSF), and higher spatial resolution and fidelity (1,2) than single-shot EPI. Interleaved EPI-based diffusion-weighted imaging (DWI) and diffusion tensor imaging (DTI), however, are highly susceptible to phase inconsistencies among multiple EPI segments because of the increased motion sensitivity in the presence of strong diffusion sensitizing gradients. The inter-segment phase inconsistencies usually result in pronounced in-plane aliasing artifacts, which in turn make the interleaved diffusion-weighted EPI (iDWEPI) data useless unless a proper phase correction is performed.

We have recently shown that it is feasible to generate high-resolution and high-quality DWI data from interleaved EPI scans using a multiplexed sensitivity encoding (MUSE) reconstruction algorithm (3), which is consisted of four steps. First, EPI Nyquist artifacts are corrected using a phase cycled reconstruction algorithm (4). Specifically, the inconsistencies between positive and negative readout gradients were estimated from the baseline non-diffusion-weighted T2 image (4) and the information was used to remove Nyquist artifact in DWI data. Second, a conventional parallel image reconstruction (e.g., the sensitivity encoding (SENSE) method (5)) is used to reconstruct images from each of the Nyquist-corrected EPI segments, using known coil sensitivity profiles; these images are used to estimate shot-to-shot phase variations due to motion. Third, the estimated phase information is spatially smoothed using a 2D low-pass Hanning filter (16×16). Fourth, the smoothed phase information and the Nyquist-corrected EPI data from all segments are included in a mathematical framework that jointly estimates the aliasing-free magnitude proton density maps (assumed to be consistent across multiple EPI segments) using known coil sensitivity profiles as constraints. If the DWI data are acquired with a partial-Fourier scheme, then the missing ky lines in each Nyquist-corrected EPI segment can be estimated from the acquired ky lines with Cuppen’s iterative algorithm (6), which preserves the phase information, prior to the SENSE reconstruction in step 2. Using the MUSE algorithm, aliasing artifacts resulting from inter-segment phase inconsistencies can be eliminated without relying on additional navigator echoes. In comparison to conventional parallel image reconstruction of same full k-space data set (i.e., averaging four SENSE-produced images reconstructed from each of the four EPI segments), the MUSE reconstruction is far less susceptible to undesirable noise amplification because of the improved matrix inversion conditioning of the MUSE framework.

The reported MUSE implementation, however, has a few technical limitations. First, when there exist either significant motion-induced k-space energy displacements along the phase-encoding direction of DWI data or pronounced local susceptibility field gradients, the conventional partial-Fourier phase estimation procedures (e.g., Cuppen’s iterative algorithm (6); Homodyne reconstruction (7)) become inappropriate and the reconstructed partial-Fourier MUSE images may be prone to residual artifacts. Second, as compared with single-shot or single-shot parallel EPI, multi-shot interleaved EPI has a significantly lower imaging throughput. It has been shown that the EPI throughput can be improved using multi-band imaging based on either simultaneous excitation (8–10) or consecutive excitation of multiple slices corresponding to each data acquisition window (10,11), or the combination of simultaneous and consecutive excitation (12). However, the existing MUSE framework cannot be directly applied to interleaved multi-band EPI data since it only considers the shot-to-shot phase variation within a single slice, and the integration of multi-band imaging and iDWEPI has not yet been reported to the best of our knowledge.

To address the above-mentioned limitations and to reliably realize high-resolution and high-throughput DWI, here we report a series of improved techniques. First, an adaptive partial-Fourier reconstruction method suitable for the MUSE framework is developed to eliminate residual artifacts resulting from either motion-induced k-space energy peak displacement or fast phase variations due to strong local susceptibility field gradients. Second, a simultaneous multi-band and multi-shot interleaved EPI pulse sequence, in which the CAIPIRINHA scheme (13) is incorporated to control the aliasing patterns, is implemented to improve the imaging throughput of high-resolution DWI. Finally, the MUSE reconstruction framework with adaptive partial Fourier reconstruction is further generalized to accommodate multi-band and multi-shot interleaved EPI data, simultaneously achieving high-quality, high-resolution and high-throughput DWI.

Theory

Adaptive partial Fourier MUSE reconstruction

In our previously implemented partial-Fourier reconstruction procedure for MUSE, we chose to use Cuppen’s iterative algorithm to calculate absent high-frequency k-space data from the acquired partial-Fourier k-space data while preserving the image-domain phase terms so that subsequent SENSE or MUSE reconstructions could be performed. Instead of using Cuppen’s algorithm, one may alternatively integrate the Homodyne and MUSE reconstruction in the following manner: 1) double the amplitude signals of asymmetrically sampled k-space data (i.e., Homodyne processing); and 2) use the data from step 1 in a subsequent MUSE reconstruction. This integrated Homodyne-MUSE reconstruction procedure is the direct extension of the integrated Homodyne-SENSE procedure originally reported by King and Angelos (14). The phase correction required by partial-Fourier reconstruction is inherently performed in both Cuppen-MUSE and Homodyne-MUSE procedures, and the produced DWI data are of high-quality and high-resolution in most cases.

The above-mentioned Cuppen-MUSE and Homodyne-MUSE procedures, however, are not capable of addressing a challenging issue: the significant k-space energy peak displacement resulting from intra-scan motion during DWI scans (15). It has been shown that the k-energy displacement may result in either signal loss (termed Type I artifact) or artificial signal elevation (termed Type II artifact) in single-shot EPI (15,16). In interleaved EPI, Type I and II artifacts may co-exist and further complicate both Cuppen-MUSE and Homodyne-MUSE reconstruction because the definition of the symmetrically and asymmetrically sampled k-space regions changes from shot to shot due to k-energy peak displacements.

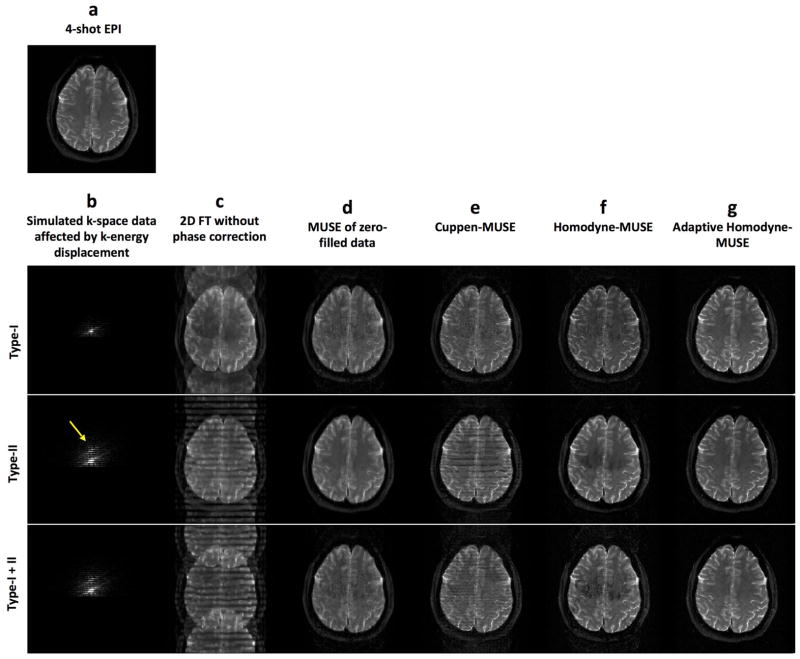
To our knowledge, the artifacts resulting from the k-energy peak displacement in iDWEPI have not yet been systematically evaluated and addressed. Therefore, we performed a mathematical simulation (shown in Figure 1) to illustrate the impact of k-energy peak displacement on iDWEPI. First, a gold-standard magnitude image is used as the input of the simulation (Figure 1a). We then generated three sets of simulated 4-shot interleaved EPI k-space data, affected by Type I artifact (with k-energy of the second segment shifted toward the negative ky direction to the un-acquired k-space area), Type II artifact (with k-energy of the fourth segment shifted toward the positive ky direction), and co-existing Type I and II artifacts (with k-energy of the second and fourth segments shifted toward different directions), respectively (Figure 1b). As expected, images reconstructed by 2D Fourier transform are affected by aliasing artifacts because of the inconsistent phase values among 4 segments (Figure 1c). When the simulated k-space data are simply zero-filled (i.e., without undergoing either Cuppen or Homodyne partial Fourier reconstruction) followed by MUSE phase correction, the reconstructed images (Figure 1d) are free from aliasing artifact but appear blurry. Using either the previously reported Cuppen-MUSE (Figure 1e) or Homodyne-MUSE (Figure 1f) procedures, the reconstructed images appear sharper but are degraded by residual artifacts because of k-energy displacements. Specifically, 1) it can be seen that Type II banding artifacts (Figure 1c) can be reduced by the iterative Cuppen-MUSE reconstruction, but the residual banding signals still degrade the Cuppen-MUSE produced images (Figure 1e); 2) With the Homodyne-MUSE reconstruction, Type II artifacts result in signal loss, rather than banding, in the reconstructed images (Figure 1f). This signal loss in Homodyne-MUSE produced images is mainly due to signal incoherence across four segments, which is the result of applying a fixed ramp weighting function that inappropriately enhances signals from the fourth segment.

Figure 1.

(a) The gold-standard magnitude signal used as the simulation input. (b) Mathematically simulated 4-shot interleaved EPI k-space data affected by Type I artifact (with k-energy of the second segment shifted toward the negative ky direction to the un-acquired k-space area), Type II artifact (with k-energy of the fourth segment shifted toward the positive ky direction), and co-existing Type I and II artifact (with k-energy of the second and fourth segments shifted toward different directions). Images reconstructed by using (c) 2D Fourier transform of the simulated k-space data without phase correction, (d) the zero-filled simulated k-space data followed by MUSE phase correction, (e) the previously reported Cuppen-MUSE procedure, (f) non-adaptive Homodyne-MUSE procedure, and (g) adaptive Homodyne-MUSE reconstruction.

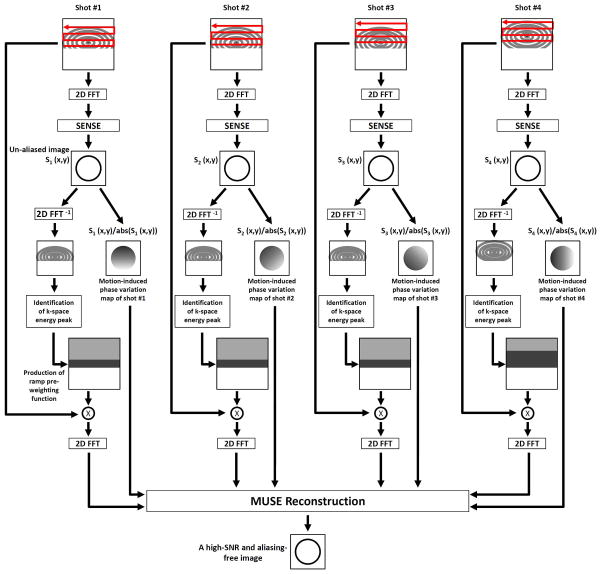
In order to eliminate k-energy displacement related artifacts in partial-Fourier MUSE DWI data, here we report an adaptive Homodyne-MUSE procedure which is schematically illustrated in Figure 2. It can be seen that the conventional SENSE algorithm is first applied to reconstruct an aliasing-free image from each of the EPI segments, providing two types of information. First, the location of k-space energy peak is identified. Second, the motion-induced shot-to-shot variations of image-domain phases are measured. Based on the k-energy peak location the symmetrically and asymmetrically sampled k-space regions can be appropriately defined, and the k-space pre-weighting function used in Homodyne processing can be generated accordingly for each EPI segment. Here we use a ramp pre-weighting function instead of a step pre-weighting function to minimize undesirable Gibbs ripple artifacts. Afterward, the zero-filled k-space data from all segments are multiplied by the corresponding pre-weighting waveforms and then processed by the MUSE phase correction algorithm to produce the final aliasing-free image of high signal-to-noise ratio (SNR). Similar to the original Homodyne-SENSE implementation, only the real parts of the reconstructed images will be kept. Using this procedure outlined in Figure 2, Type II artifact can be corrected. In order to minimize the impact of Type I artifact (i.e., with k-energy peak shifted to the un-acquired k-space area), the k-space energy levels in all EPI segments are compared and the segments with significantly lower energy levels resulting from Type I artifact will be excluded from the MUSE reconstruction.

Figure 2.

The flow chart of adaptive Homodyne-MUSE reconstruction.

Using the adaptive Homodyne-MUSE reconstruction algorithm described above, both Type I and Type II artifacts can be minimized. For example, Figure 1g shows adaptive Homodyne-MUSE images reconstructed from three sets of simulated k-space data. All images have high spatial-resolution and quality, and the residual artifacts are effectively removed as compared with the Cuppen-MUSE and conventional Homodyne-MUSE produced images.

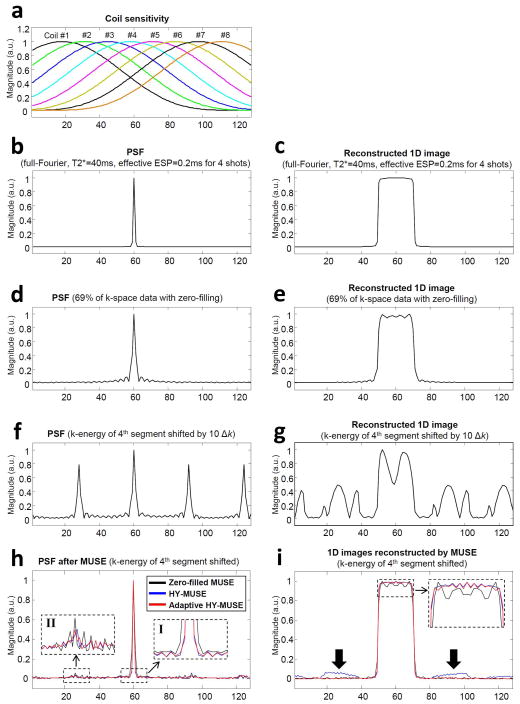
In order to quantitatively compare non-adaptive and adaptive Homodyne-MUSE reconstruction methods, particularly in terms of their PSF and residual artifacts, we further performed a series of 1D numerical simulations using either a single point function or a 1D box waveform as input. Figure 3a shows 1D coil sensitivity profiles used to create multi-channel data sets in our simulation. Figures 3b and 3c show the PSF (using the single point function as input) and a 1D image (using the 1D box waveform as input) reconstructed by Fourier transform of the simulated full k-space data of 4-shot interleaved EPI (with T2* = 40ms and echo-spacing time = 0.2ms), respectively. Figures 3d and 3e show the PSF and 1D image reconstructed by Fourier transform from 69% of k-space data with zero-filling, respectively. Figures 3f and 3g show the PSF and Fourier transform reconstructed 1D image in the presence of Type II artifact (with the k-energy peak displacement by 10Δk in the fourth segment), respectively. Figure 3h compares the PSF corresponding to zero-filled MUSE (black line), Homodyne-MUSE (blue line), and adaptive Homodyne-MUSE (red line) reconstruction. It can be seen that both Homodyne-MUSE and adaptive Homodyne-MUSE have sharper PSF as compared with the zero-filled MUSE reconstruction (dashed box I), although they do not completely eliminate aliasing artifacts (dashed box II). Figure 3i compares the 1D images reconstructed with zero-filled MUSE (black), Homodyne-MUSE (blue), and adaptive Homodyne-MUSE (red), respectively. It can be seen that the residual artifacts (arrows) in the adaptive Homodyne-MUSE produced image are significantly lower than that in the conventional Homodyne-MUSE produced image.

Figure 3.

(a) The simulated coil sensitivity profiles used to create multi-channel MRI data. (b) The point spread function (PSF) and (c) 1D image reconstructed with Fourier transform from full k-space data of 4-shot interleaved EPI. (d) The PSF and (e) 1D image reconstructed with Fourier transform from partial Fourier (69%) k-space data with zero-filling. (f) The PSF and (g) 1D image reconstructed with Fourier transform from partial Fourier k-space data with the fourth EPI segment shifted by 10Δk (Type II artifact). (h) The PSF and (i) 1D images reconstructed from partial-Fourier k-space data, in the presence of Type II artifact in the fourth EPI segment, using zero-filled MUSE (black solid line), non-adaptive Homodyne-MUSE (blue solid line), and adaptive Homodyne-MUSE (red solid line).

Generalization of MUSE algorithm to multi-band interleaved EPI

As described in the Introduction section and shown in Equation 1, the original MUSE framework is designed to calculate the magnitude proton density maps (p_n) that are consistent across multiple EPI segments, using known coil sensitivity profiles ( $S{|}_n^w$) and the SENSE-estimated shot-to-shot phase variations ( $\mathrm{\Theta }{|}_n^k$) as constraints.

$$\left[\begin{array}{c}u{|}_1^w\\ u{|}_2^w\\ ⋮\\ u{|}_N^w\end{array}\right]=\frac{1}{N}\left[\begin{array}{cccc}S{|}_1^w{e}^{i\frac{2\pi }{N}·0·0}& S{|}_2^w{e}^{i\frac{2\pi }{N}·0·1}& \cdots & S{|}_N^w{e}^{i\frac{2\pi }{N}·0·(N-1)}\\ S{|}_1^w{e}^{i\frac{2\pi }{N}·1·0}{e}^{i\mathrm{\Theta }{|}_1^2}& S{|}_2^w{e}^{i\frac{2\pi }{N}·1·1}{e}^{i\mathrm{\Theta }{|}_2^2}& \cdots & S{|}_N^w{e}^{i\frac{2\pi }{N}·1·(N-1)}{e}^{i\mathrm{\Theta }{|}_N^2}\\ ⋮& ⋮& \ddots & ⋮\\ S{|}_1^w{e}^{i\frac{2\pi }{N}·(N-1)·0}{e}^{i\mathrm{\Theta }{|}_1^N}& S{|}_2^w{e}^{i\frac{2\pi }{N}·(N-1)·1}{e}^{i\mathrm{\Theta }{|}_2^N}& \cdots & S{|}_N^w{e}^{i\frac{2\pi }{N}·(N-1)·(N-1)}{e}^{i\mathrm{\Theta }{|}_N^N}\end{array}\right]\left[\begin{array}{c}{p}_1\\ p_2\\ ⋮\\ p_N\end{array}\right]$$ (1)

Here $u{|}_k^w$ represents the aliased image-domain signal (i.e., from a certain voxel in the reduced-FOV image) of the k-th EPI segment (k=1,2,… N; where N is the total number of EPI segments) measured with coil number w (w=1,2,… W; where W is the total number of coils); p_n represents the unaliased full-FOV image signal at location n (n=1… N; separated by $\frac{{\mathit{FOV}}_y}{N}$ along the phase-encoding direction); $S{|}_n^w$ represents the known coil sensitivity profile for coil number w at location n; $\mathrm{\Theta }{|}_n^k$ represents the shot-to-shot phase inconsistency at location n for the k-th EPI segment. Note that Equation 1 is the generalized form of the MUSE reconstruction for N-shot interleaved EPI, and Equations 9 and 10 shown in (3) are for 2-shot interleaved EPI and can be obtained by setting N=2 in Equation 1.

The MUSE algorithm, originally designed for single-band imaging (i.e., Equation 1), can be generalized to accommodate interleaved EPI data acquired with simultaneous multi-band imaging. Similar to the original MUSE method, the multi-band MUSE algorithm comprises four steps. First, EPI Nyquist artifacts resulting from inconsistencies between positive and negative readout gradients are corrected using a phase cycled reconstruction, which is highly effective for interleaved EPI data (4). Second, images free from both in-plane and through-plane aliasing artifacts are reconstructed from each of the multi-band EPI segments using the SENSE algorithm based on known coil sensitivity profiles. Shot-to-shot phase variations due to motion can be estimated from the SENSE-produced images. Third, the estimated phase information is spatially smoothed. Fourth, the smoothed phase information and the Nyquist-corrected EPI data from all segments are included in a generalized mathematical framework that jointly estimates the aliasing-free proton density maps using the known coil sensitivity profiles and SENSE-estimated shot-to-shot phase variations as constraints. This is shown in Equation 2 using two-band interleaved EPI as an example.

$$\left[\begin{array}{c}u{|}_1^w\\ u{|}_2^w\\ ⋮\\ u{|}_N^w\end{array}\right]=\frac{1}{N}\left[\begin{array}{cccccc}S1{|}_1^w{e}^{i\frac{2\pi }{N}·0·0}& \cdots & S1{|}_N^w{e}^{i\frac{2\pi }{N}·0·(N-1)}& S2{|}_1^w{e}^{i\frac{2\pi }{N}·0·0}& \cdots & S2{|}_N^w{e}^{i\frac{2\pi }{N}·0·(N-1)}\\ S1{|}_1^w{e}^{i\frac{2\pi }{N}·1·0}{e}^{i\mathrm{\Theta }1{|}_1^2}& \cdots & S1{|}_N^w{e}^{i\frac{2\pi }{N}·1·(N-1)}{e}^{i\mathrm{\Theta }1{|}_N^2}& S2{|}_1^w{e}^{i\frac{2\pi }{N}·1·0}{e}^{i\mathrm{\Theta }2{|}_1^2}& \cdots & S2{|}_N^w{e}^{i\frac{2\pi }{N}·1·(N-1)}{e}^{i\mathrm{\Theta }2{|}_N^2}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ S1{|}_1^w{e}^{i\frac{2\pi }{N}·(N-1)·0}{e}^{i\mathrm{\Theta }1{|}_1^N}& \cdots & S1{|}_N^w{e}^{i\frac{2\pi }{N}·(N-1)·(N-1)}{e}^{i\mathrm{\Theta }1{|}_N^N}& S2{|}_1^w{e}^{i\frac{2\pi }{N}·(N-1)·0}{e}^{i\mathrm{\Theta }2{|}_1^N}& \cdots & S2{|}_N^w{e}^{i\frac{2\pi }{N}·(N-1)·(N-1)}{e}^{i\mathrm{\Theta }2{|}_N^N}\end{array}\right]\left[\begin{array}{c}p{1}_1\\ p{1}_2\\ ⋮\\ p{1}_N\\ p{2}_1\\ p{2}_2\\ ⋮\\ p{2}_N\end{array}\right]$$ (2)

Here $u{|}_k^w$ represents the aliased and multi-band image-domain signal (i.e., with both in-plane and through-plane aliasing artifacts) of the k-th EPI segment (k=1,2,… N; where N is the total number of EPI segments) measured with coil number w (w=1,2,… W; where W is the total number of coils); p1_n and p2_n represent the unaliased full-FOV image signals at location n (n=1… N; separated by $\frac{{\mathit{FOV}}_y}{N}$ along the phase-encoding direction) in the first and second slice, respectively, of the simultaneously excited slices; $S1{|}_n^w$ and $S2{|}_n^w$ represent the known coil sensitivity profiles for coil number w at location n in the first and second slice, respectively, of the simultaneously excited slices; $\mathrm{\Theta }1{|}_n^k$ and $\mathrm{\Theta }2{|}_n^k$ represent the phase errors due to motion or B₀-drifting at location n for the k-th EPI segment from the first slice and second slice, respectively, of the simultaneously excited slices. Note that the two-band MUSE algorithm shown in Equation 2 can be immediately extended to accommodate multi-band interleaved EPI data with a larger number of simultaneously excited slices.

If multi-band interleaved DWI data are acquired with a partial-Fourier scheme, then the adaptive Homodyne algorithm (Figure 2) and the multi-band MUSE framework can be integrated to produce high-quality and high-resolution images. Specifically, multi-band k-space data in asymmetrically sampled k-space regions (with their extensions varied from shot-to-shot according to the actual location of k-energy peaks: see Figure 2) are doubled and then used to reconstruct images free from both in-plane and through-plane aliasing artifacts, using known coil sensitivity profiles and SENSE-estimated shot-to-shot phase variations as constraints. Similar to the original Homodyne-SENSE implementation, only the real parts of the reconstructed images will be kept. In our implementation, the coil sensitivity profiles are calculated from single-band interleaved T2-weighted EPI data (without diffusion-weighting) with the same number of segments as in multi-band iDWEPI acquisition. The coil sensitivity profiles are not spatially smoothed.

Methods

Imaging data were acquired from a phantom and healthy volunteers on a 3 Tesla MRI scanner (General Electric, Waukesha, WI, USA) using either an 8-channel or a 32-channel phase array coil.

Implementation of multi-band interleaved DWI pulse sequence

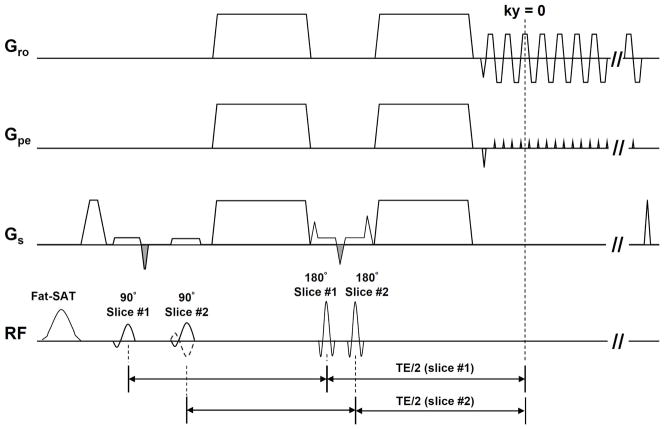
We have implemented 2-band 2-shot and 2-band 4-shot interleaved DWI pulse sequences, with FOV shifted differently between two consecutively excited slices. As shown in Figure 4 (2-band interleaved EPI), two slices are excited within the same TR by two consecutive 90° RF pulses after applying a spectrally-selective fat saturation RF pulse, and then two consecutive 180° RF pulse are used to refocus the two slices. Two fly-back gradients (two negative gradients with gray filled waveforms in G_s) are added to balance the gradient areas between two consecutive RF pulses. The spin echoes of two excited slices are refocused at the same ky line, although with slightly different TE values. For both 2-band 2-shot and 2-band 4-shot interleaved acquisition, the polarity of the second excitation RF pulse alternates between two consecutive TRs (i.e., solid and dash-lines in Figure 4), thereby shifting one of the consecutively excited slices by half the FOV (i.e., controlled aliasing) with the CAIPIRINHA scheme (13). The distance between two consecutively excited slices was 48mm, which was sufficient to perform parallel imaging with our multi-channel coil. It should be noted that the mono-polar diffusion weighted probe gradient scheme should be chosen so that the spin echoes from two consecutively excited slices occur at the same time.

Figure 4.

The simultaneous 2-band interleaved diffusion weighted EPI pulse sequence.

Evaluation of adaptive Homodyne-MUSE in single-band interleaved EPI

We first performed human DWI studies to evaluate the image quality of single-band interleaved DWI data reconstructed with the developed adaptive Homodyne-MUSE algorithm in comparison to the previously reported Cuppen-MUSE algorithm. Two sets of single-band 4-shot interleaved DWI data were acquired from a healthy volunteer using an 8-channel phase array coil with the following parameters: in-plane matrix size = 512 × 512 and 256 × 256, number of overscan ky lines for partial Fourier acquisition = 20, FOV = 24 × 24 cm², axial-plane slice thickness = 8mm (for 512 × 512) and 4 mm (for 256 × 256), number of axial slices = 24, TR = 6 sec, TE = 78.6 msec (for 512 × 512) and 68 msec (for 256 × 256), and b-value = 800 s/mm². Three different approaches were used to reconstruct the acquired DWI data: 1) single-band MUSE processing of zero-filled k-space data without partial Fourier reconstruction, 2) single-band Cuppen-MUSE reconstruction, and 3) single-band adaptive Homodyne-MUSE reconstruction. Images reconstructed with each approach were compared in terms of their anatomic resolvability and artifact level.

Evaluation of adaptive Homodyne-MUSE in multi-band interleaved EPI

We performed a phantom imaging study to evaluate the image quality of multi-band interleaved EPI reconstructed with the developed adaptive Homodyne-MUSE algorithm. Full-Fourier 2-band 2-shot interleaved EPI data were acquired from a phantom using a 32-channel phase array coil with the following parameters: in-plane matrix size = 128 × 128, FOV = 18 × 18 cm², slice thickness = 4mm, and TR = 4 sec. The TE values of two consecutively excited slices were 103.9 and 94.7 msec. With this acquisition scheme, 128 kx ×64 ky lines from a pair of consecutively excited slices were acquired in each shot, and 14 shots (covering 28 axial slices) were performed in each TR. The full-Fourier 2-band 2-shot EPI data were first reconstructed using multi-band MUSE to produce gold standard images for subsequent evaluation of partial Fourier reconstruction. Afterward, 40% of the acquired ky lines were discarded to produce partial-Fourier imaging data, which were then processed with three approaches: 1) multi-band MUSE without partial-Fourier reconstruction, 2) Cuppen’s iterative partial-Fourier reconstruction followed by multi-band MUSE, and 3) the new multi-band adaptive homodyne-MUSE. The reconstructed images were then compared in terms of image quality and residual artifacts.

In addition, a full-Fourier single-band 2-shot interleaved EPI data set was acquired from the same phantom with identical parameters, so that images reconstructed from single-band and multi-band MUSE methods can be further compared.

High-resolution diffusion tensor imaging based on adaptive Homodyne and multi-band MUSE

Two DTI data sets were acquired from two healthy volunteers using a 2-band 4-shot interleaved EPI sequence with a 32-channel phase array coil. Imaging parameters included: in-plane matrix size = 384 × 384, the total number of overscan ky lines = 24 (i.e., 6 ky lines per segment), FOV = 19.2 × 19.2 cm², axial-plane slice thickness = 6mm, TR = 5 sec in one scan and 2.8 sec in the other scan, and b-value = 600 s/mm² at 25 directions. The TE values of two consecutively excited slices were 66.9 and 58.2 msec. With this 2-band and 4-shot acquisition scheme, 384 kx ×54 ky lines from a pair of consecutively excited slices were acquired in each shot, and 8 shots (covering 16 axial slices) were performed in each TR. The multi-band adaptive Homodyne-MUSE algorithm was used to reconstruct images, and fractional anisotropy (FA) maps were then calculated.

Another DTI data set with 2mm³ isotropic voxel size and b-value = 800 s/mm² was acquired from one healthy volunteer using a 2-band 2-shot interleaved EPI sequence with a 32-channel phase array coil. The whole brain was covered by 68 axial slices (corresponding to 34 shots in our 2-band sequence) with 4 sec TR. The imaging throughput of this 2-band 2-shot EPI protocol was 70% higher than that what can be achieved by single-band 2-shot EPI with the same TR, b-value, voxel size, and brain coverage.

Results

Evaluation of adaptive Homodyne-MUSE in single-band interleaved EPI

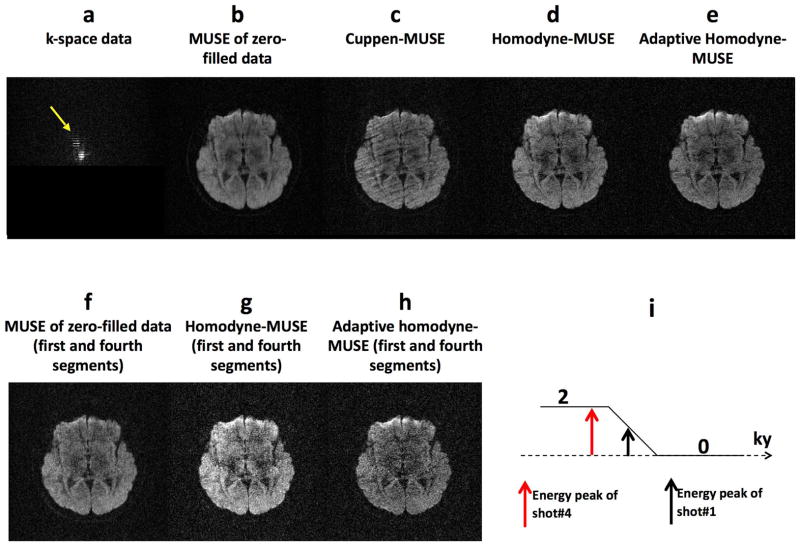
Figure 5a shows a set of single-band 4-shot interleaved DWI k-space data (256 × 256) acquired from a healthy volunteer. It can be seen that the k-space energy corresponding to the fourth EPI segment is shifted toward the positive ky direction (by approximately 20 ky lines: yellow arrow). The MUSE reconstruction of zero-filled k-space data (i.e., without partial-Fourier processing) produces an aliasing-free image but with lower resolvability (Figure 5b). Using the previously reported Cuppen-MUSE procedure, the reconstructed image is degraded by artifacts resulting from k-space energy displacement (Figure 5c), which is not taken into consideration in Cuppen-MUSE. Using the non-adaptive Homodyne-MUSE, the produced image has lower residual artifact but is affected by artificial signal variations resulting from k-energy displacement (Figure 5d). Since only one of the four EPI segments has significant k-energy displacement (i.e., k-energy displacement in 25% of data), the artificial signal variation in Figure 5d is not obvious from visual inspection and will be further examined as shown in the next paragraph. Using the adaptive Homodyne-MUSE reconstruction, the produced image has a low level of artifact is not susceptible to artificial signal elevation (Figure 5e).

Figure 5.

(a) K-space data of a single-band 4-shot interleaved DWI (256 × 256) acquired from a healthy volunteer with k-space energy shifted in fourth segment toward the positive ky direction (by approximately 20 ky lines: yellow arrow). The images reconstructed by using (b) MUSE reconstruction of zero-filled k-space data, (c) the previously reported Cuppen-MUSE procedure, (d) the non-adaptive Homodyne-MUSE, and (e) the adaptive Homodyne-MUSE reconstruction. The images reconstructed from only the first and fourth EPI segments (i.e., with k-energy displacement in 50% of data) by using (f) the MUSE reconstruction of zero-filled k-space data, (g) the non-adaptive Homodyne-MUSE reconstruction, and (h) the adaptive Homodyne-MUSE reconstruction. (i) The k-energy displacement in 50% of the input k-space data.

To better visualize the artificial signal variations in non-adaptive Homodyne-MUSE, we compared the quality of images reconstructed from only the first and fourth EPI segments (i.e., with k-energy displacement in 50% of data). The MUSE reconstruction of zero-filled k-space data produces an aliasing-free but blurry image (Figure 5f: signal intensity = 7051±2690 a.u.). As expected, the image shown in Figure 5f has similar intensities as that in Figure 5b but with higher noise level. The non-adaptive Homodyne-MUSE produces an image with obvious artificial signal elevation (increased by 41.6% compared to Figure 5f) due to Type II artifact (Figure 5g: signal intensity = 9987±4320 a.u.) because of the k-energy displacement in 50% of the input k-space data (Figure 5i). Using the developed adaptive Homodyne-MUSE algorithm, the produced image has the correct signal intensity (reduced by 2.2% compared to Figure 5f) and a low aliasing-artifact level (Figure 5h: signal intensity = 6896±3536 a.u.). The L2 norm of the percentage signal difference between Figures 5f and 5g is 2.52×10⁶ %, and the L2 norm of the difference between Figures 5f and 5h is 1.23×10⁶ %.

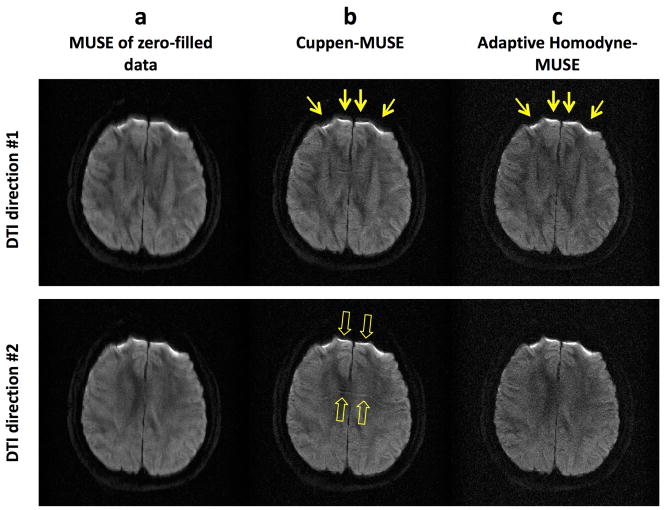
Figure 6 shows that the new adaptive Homodyne-MUSE algorithm is robust even in the presence of fast phase variations due to strong local susceptibility field gradients. As compared with the images reconstructed by MUSE from zero-filled k-space data (Figure 6a), the Cuppen-MUSE produced images (Figure 6b) have higher anatomic resolvability but are degraded by edge broadening (yellow arrows in Figure 6b) and residual aliasing artifact (hollow arrows in Figure 6b) because fast phase variations cannot be properly estimated by Cuppen’s algorithm. Using the adaptive Homodyne-MUSE algorithm, the produced images have higher anatomic resolvability without either edge broadening (yellow arrows in Figure 6c) or residual aliasing artifact.

Figure 6.

The images reconstructed by (a) MUSE from zero-filled k-space data, (b) the Cuppen-MUSE algorithm, and (c) the adaptive Homodyne-MUSE algorithm.

Evaluation of adaptive Homodyne-MUSE in multi-band interleaved EPI

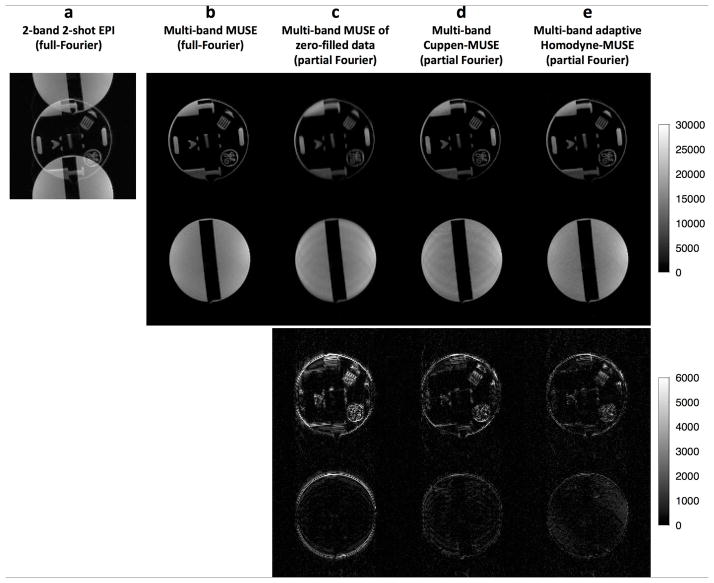
Multi-band interleaved EPI data acquired from a phantom scan are shown in Figure 7. Figure 7a shows a 2-band 2-shot EPI image reconstructed from full-Fourier k-space data (without diffusion sensitizing gradients) using a 2D Fourier transform; it can be seen that there is an overlap of signals from two consecutively excited slices due to the controlled aliasing patterns of the CAIPIRINHA scheme. Figure 7b shows the images from each slice reconstructed from the full-Fourier k-space data using our multi-band MUSE algorithm. These full-Fourier images can be used as the gold standard for evaluating images reconstructed from partial-Fourier k-space data. Images reconstructed from truncated and zero-filled k-space data using multi-band MUSE, multi-band Cuppen-MUSE, and multi-band adaptive Homodyne MUSE are shown in the top two rows of Figures 7c, d, and e, respectively. The differences between the reconstructed partial-Fourier images and the gold standard (Figure 7b) are shown in the bottom two rows of Figures 7c to e. It can be seen that the multi-band adaptive Homodyne-MUSE reconstruction can produce partial-Fourier images with the lowest artifact level and highest resolvability.

Figure 7.

(a) A 2-band 2-shot EPI phantom image reconstructed from full-Fourier k-space data (without diffusion sensitizing gradients) using a 2D Fourier transform, where there is signal overlap from two consecutively excited slices with controlled aliasing. (b) Images reconstructed from full-Fourier k-space data using our multi-band MUSE algorithm. Images reconstructed from truncated and zero-filled k-space data using (c) multi-band MUSE, (d) multi-band Cuppen-MUSE, and (e) multi-band adaptive Homodyne MUSE are shown in the top two rows of 6c to e. The differences between the reconstructed partial-Fourier images and the gold standard (Figure 6b) are shown in the bottom two rows of 6c to e.

Figure 8 compares interleaved EPI data generated by different acquisition and reconstruction schemes, including a) single-band acquisition and conventional Homodyne reconstruction; b) single-band acquisition and Homodyne-SENSE reconstruction (i.e., averaging multiple images reconstructed from individual EPI segments using the Homodyne-SENSE method); c) single-band acquisition and adaptive Homodyne-MUSE reconstruction; d) multi-band acquisition and multi-band Homodyne-SENSE reconstruction (i.e., averaging multiple images reconstructed from individual EPI segments using the non-adaptive multi-band Homodyne-SENSE method); e) multi-band acquisition and adaptive multi-band Homodyne-MUSE reconstruction. The SNR was calculated by taking the ratio of the mean signal intensity to the signal variation within the region-of-interest (i.e., red areas in Figure 8a). It can be seen that the adaptive Homodyne-MUSE reconstruction produces images with higher SNR than the Homodyne-SENSE produced images, for both single-band and multi-band acquisition. These data also show that the SNR penalty resulting from the multi-band scheme (using single-band data set as a reference) is insignificant (e.g., 7% and 6% for the two chosen slices).

Figure 8.

(a) Single-band interleaved EPI reconstructed with the Homodyne algorithm. (b) Single-band interleaved EPI reconstructed with the Homodyne-SENSE algorithm. (c) Single-band interleaved EPI reconstructed with the adaptive Homodyne-MUSE method. (d) Multi-band interleaved EPI reconstructed with the non-adaptive Homodyne-SENSE algorithm. (e) Multi-band interleaved EPI reconstructed with the adaptive multi-band Homodyne-MUSE algorithm.

High-resolution diffusion tensor imaging based on adaptive Homodyne and multi-band MUSE

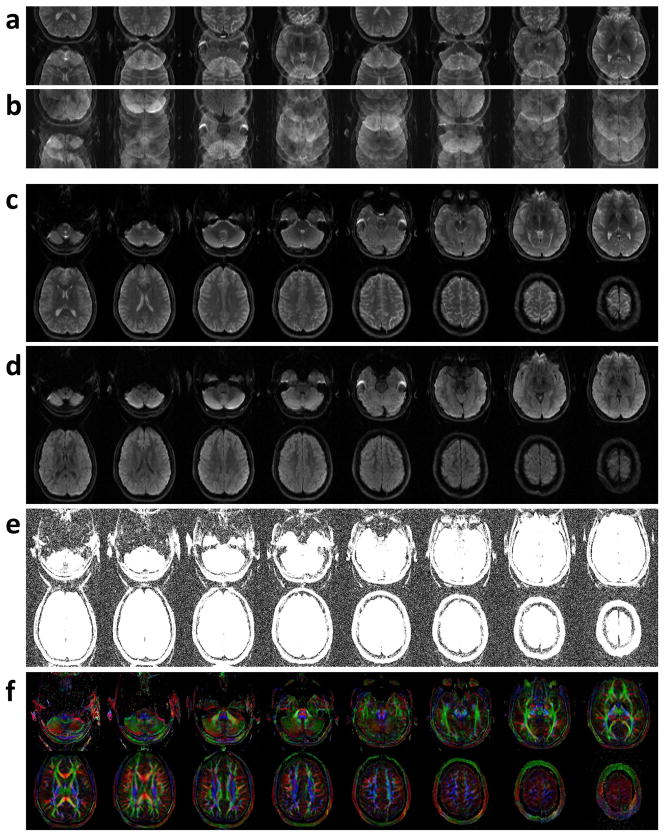
T2-weighted and diffusion-weighted images reconstructed from the acquired 2-band 4-shot EPI data using a 2D Fourier transform are shown in Figures 9a and b, respectively. It can be seen that signals from two simultaneously excited slices overlap in the T2-weighted images (Figure 9a), and additional aliasing artifacts due to shot-to-shot phase variations further degrade the quality of the DWI images (Figure 9b). Using the developed multi-band adaptive Homodyne-MUSE algorithm, T2-weighted and diffusion-weighted images free of in-plane and through-plane aliasing artifacts can be reconstructed, as shown in Figures 9c and d, respectively. Figure 9e shows the same images as in Figure 9d but with a display scale adjusted to show background signals. It can be seen that aliasing artifacts (in Figures 9a and 9b) can be effectively removed using the developed method. The calculated color-coded FA maps of high-quality and high in-plane resolution (0.5 × 0.5 × 6 mm³) are shown in Figure 9f.

Figure 9.

(a) T2-weighted and (b) diffusion-weighted images reconstructed from the acquired 2-band 4-shot EPI data using a 2D Fourier transform. (c) T2-weighted and (d) diffusion-weighted images free of in-plane and through-plane aliasing artifacts reconstructed by using the developed multi-band adaptive Homodyne-MUSE algorithm. (e) The diffusion-weighted images shown in Figure 9d were scaled thus the background signals free of aliasing artifacts can be seen. (f) The calculated color-coded FA maps of high-quality and high in-plane resolution (0.5 × 0.5 × 6 mm³).

Consistent with our findings from numerical simulation and phantom studies, we found that human images reconstructed with the developed multi-band adaptive Homodyne-MUSE method (e.g., Figure 9d) have higher quality than images reconstructed with the conventional parallel MRI (i.e., 2D Fourier transform for in-plane reconstruction, followed by SENSE processing along the slice-direction for unfolding multi-band signals). For example, the gray-white matter contrast-to-noise ratio in images shown in Figure 9d is 6.59, and the gray-white matter contrast-to-noise ratio in images obtained with the conventional parallel MRI, which is susceptible to aliasing artifacts due to shot-to-shot phase variations, is only 4.86 (images not shown). We also found that, since the developed multi-band adaptive Homodyne-MUSE method is less susceptible to undesirable noise amplification as compared with the multi-band Homodyne-SENSE (i.e., averaging four images reconstructed from each of the four EPI segments using multi-band Homodyne-SENSE), the resultant gray-white matter contrast-to-noise ratio is higher (6.59 in adaptive Homodyne-MUSE produced images; and 5.76 in Homodyne-SENSE produced images: not shown).

Discussion

Although single-shot DWEPI is less susceptible to motion-related artifacts, it is difficult to achieve high spatial-resolution using routine single-shot EPI protocols (17,18). In comparison to single-shot EPI, interleaved EPI can produce DWI data of significantly higher in-plane spatial-resolution. However, interleaved DWI data may be easily degraded by aliasing artifacts resulting from shot-to-shot phase variations. Our experimental data suggest that the improved MUSE algorithm presented in this paper is a reliable approach to eliminate aliasing artifacts in interleaved EPI, thereby enabling DWI of high resolution and high quality. Since the MUSE algorithm is capable of estimating shot-to-shot phase errors directly from the acquired DWI data without relying on a navigator echo, the imaging throughput of our DWI protocol is higher as compared with the previously reported interleaved DWI protocols that either include navigator echoes (1,19–21) or use variable sampling density in k-space (22–24) in which the scan throughput is reduced. As demonstrated in this paper, the imaging throughput of interleaved DWI scans can further be improved when simultaneous multi-band imaging is incorporated, and both in-plane and through-plane aliasing artifacts in multi-band multi-shot DWI can be effectively eliminated by the generalized multi-band MUSE algorithm.

Because of the inherently shorter TE and higher SNR the partial-Fourier acquisition scheme is superior to the full-Fourier scheme for DWI scans based on either single-shot or interleaved EPI pulse sequences. In order to perform the MUSE reconstruction that requires complex partial Fourier imaging data as inputs, we previously chose to first apply Cuppen’s iterative algorithm to preserve the phase information in partial Fourier images (i.e., Cuppen-MUSE). Alternatively, one may integrate the Homodyne partial-Fourier and MUSE reconstruction (i.e., Homodyne-MUSE) through multiplying the input k-space data with a filter waveform (similar to the Homodyne-SENSE technique reported by King and Angelos (14)) to produce high-resolution DWI data. The Cuppen-MUSE and Homodyne-MUSE methods, however, do not take the motion induced k-energy displacement into consideration. When the k-energy displacements are pronounced, various types of partial-Fourier related artifacts (e.g., signal loss; artificial signal elevation; banding artifact: see Figure 4) may exist in the MUSE-produced images. Although these partial-Fourier related artifacts have been discussed for single-shot EPI (15,16), their impact on interleaved EPI has not been previously investigated. Here we not only systematically investigated the partial-Fourier artifacts in interleaved EPI, but also further developed a new adaptive Homodyne-MUSE algorithm to reliably enable high-resolution and high-quality DWI even in the presence of pronounced k-space energy peak displacements in partial-Fourier EPI data. Our numerical simulation and experimental data demonstrate that the new adaptive Homodyne-MUSE can produce images with sharper PSF and lower aliasing artifact level in comparison to non-adaptive Homodyne-MUSE, in the presence of k-space energy peak displacements.

The simultaneous multi-band imaging is incorporated into our interleaved EPI pulse sequence so that the imaging throughput can be significantly improved for high-resolution DTI. In the implemented 2-band 2-shot and 2-band 4-shot interleaved EPI pulse sequences (Figure 4) the polarity of the second excitation RF pulse changes from shot to shot using the CAIPIRINHA scheme (13), shifting the FOV for one of the two excited slices along the phase-encoding direction and thus improving the matrix inversion conditioning when unfolding the overlapping signals with the MUSE algorithm. It has been shown previously that if the FOVs corresponding to the simultaneously excited slices are shifted differently, then the parallel MRI reconstruction of simultaneous multi-band imaging is less susceptible to noise amplification for two reasons. First, the number of overlapping voxels from multiple slices is smaller with FOV shifting; Second, the coil sensitivity profiles for the overlapping voxels of FOV-shifted images are less similar, resulting in improved matrix inversion conditioning (9,13). It should be pointed out that instead of using two sequential RF pulses (e.g., in Figure 4), one may apply a cosine modulation to a single excitation RF pulse to simultaneously excite multiple distant slices for multi-band imaging. A major advantage of the cosine modulation based simultaneous excitation is that a shorter echo time can be achieved, as compared with consecutive excitation.

To our knowledge, here we report the first integration of CAIPIRINHA multi-band imaging and iDWEPI, in which the aliasing artifacts in both slice- and phase-encoding directions can be simultaneously and effectively eliminated using the adaptive multi-band Homodyne-MUSE algorithm. In our study, we chose to incorporate the original CAIPIRINHA scheme rather than the blipped-CAIPI (9), because the CAIPIRINHA is better suitable for spin-warp imaging and interleaved EPI while the blipped-CAIPI is designed for single-shot EPI.

In our human MRI studies we demonstrated the feasibility of achieving high in-plane resolution with the multi-band MUSE technique (0.5 mm × 0.5 mm), while choosing a thick slice (6 mm). We would like to emphasize that the developed technique can be applied to a variety of DWI protocols, where voxel size and geometry may be chosen based on the targeted applications. For example, our chosen voxel geometry (0.5 mm × 0.5 mm × 6 mm) is useful for clinical DWI of detecting stroke or subtle lesions, where it is beneficial to match the voxel geometry of DWI and T2-FLAIR (typically ~ 0.5 mm × 0.5 mm × 6 mm). On the other hand, for neuroscience research that utilizes DTI and fiber tracking, it would be preferable to choose an isotropic voxel (e.g., 1.15 mm × 1.15 mm × 1.15 mm, which has the same voxel size and SNR as our chosen 0.5 mm × 0.5 mm × 6 mm voxel).

There are a few limitations in our implemented interleaved DWI technique. First, the number of EPI segments needs to be smaller than the number of RF coil elements, otherwise the phase variations between shots may not be estimated with the conventional SENSE method. Second, the positions of eyeballs may change significantly during interleaved EPI scans, potentially resulting in residual artifacts in MUSE-produced images. Residual aliasing artifacts related to eyeball movement can be eliminated by placing a spatial saturation band to suppress eyeball signals during acquisition (25).

In conclusion, the new adaptive Homodyne-MUSE partial-Fourier reconstruction can reliably produce high-quality and high-resolution diffusion-weighted images, even in the presence of 1) motion-induced k-space energy peak displacement and 2) fast phase variations originating from local susceptibility field gradients. Furthermore, our generalized MUSE algorithm is compatible with simultaneous multi-band imaging and can effectively eliminate both in-plane and through-plane aliasing artifacts in multi-band multi-shot DWI data. The integration of adaptive partial-Fourier reconstruction and multi-band MUSE thereby enables high-resolution interleaved DWI of high image quality and throughput.