Abstract
Microfluidic devices allow for the production of physiologically relevant cellular microenvironments by including biomimetic hydrogels and generating controlled chemical gradients. During transport, the biomolecules interact in distinct ways with the fibrillar networks: as purely diffusive factors in the soluble fluid or bound to the matrix proteins. These two main mechanisms may regulate distinct cell responses in order to guide their directional migration: caused by the substrate-bound chemoattractant gradient (haptotaxis) or by the gradient established within the soluble fluid (chemotaxis). In this work 3D diffusion experiments, in combination with ELISA assays, are performed using microfluidic platforms in order to quantify the distribution of PDGF-BB and TGF-β1 across collagen and fibrin gels. Furthermore, to gain a deeper understanding of the fundamental processes, the experiments are reproduced by computer simulations based on a reaction-diffusion transport model. This model yields an accurate prediction of the experimental results, confirming that diffusion and binding phenomena are established within the microdevice.
I. INTRODUCTION
Viability of organisms is sustained by the contribution of diverse constituents that compose tissues and organs. Particularly, the extracellular matrix (ECM) performs major functions such as tissue morphogenesis, differentiation and homeostasis, rendering as architectural scaffolding and establishing biomechanical and biochemical cues.1–3 Indeed, cells require complex signalling frameworks comprised of specialized molecules, such as growth factors (GFs), for intercellular communication and to carry out physiological processes.1,2
During biomolecule transport across the ECM, diverse processes take place leading to a heterogeneous and varied biochemical scenario by means of paracrine and autocrine signalling; actually, the yielding biochemical environment has great effect on major cell responses, such as proliferation, differentiation and migration.4–10 While diffusion through the matrix pores in form of soluble molecules take place, the ECM also serves as reservoir by offering binding sites to the GFs and, therefore, leading to a solid-state availability of them.11–14 In addition, GFs also interact with other molecules resulting in their degradation.15
Particularly, distinct directional single cell migrations (comprised of chemosensing, polarization and locomotion) are distinguished in function of their specific cause.16 Migration towards a soluble chemoattractant is usually defined as chemotaxis; otherwise, when the bound GF influence cell motility, by guiding cell adhesion, is denominated haptotaxis.9,17,18 Both mechanisms are crucial to cell migration and, therefore, strongly impact on developmental and regenerative processes. Thus, a deeper knowledge of the diffusion behavior of GFs within the ECM, and the related adhesion and degradation processes, is critical in order to elucidate and predict the different chemotactic and haptotactic gradients of the biomolecules, which directly affect cellular behavior.
Numerous studies have identified several GFs that play an important role by mediating a wide range of biological processes.19–22 These studies have been performed using two-dimensional (2D) substrates. However, the in vivo microenvironment mostly corresponds to a three-dimensional (3D) structure. Actually, significant differences in the behavior and effect of GFs have been identified by comparing 2D and 3D models, with 3D models mimicking more closely the in vivo behavior.23–25
Furthermore, in the last years microfluidic approaches have emerged to recreate cellular niches.26–31 These platforms allow for a controlled 3D microenvironment by including hydrogels (mimicking the ECM of tissues) and the generation of chemical gradients of diverse factors in a systematic way.27,32–39 Such a microenvironment gives rise to more reliable information about the effect of GFs during in vitro assays in order to address biological questions.
Among the many different GFs, platelet-derived growth factor-BB (PDGF-BB) and transforming growth factor-β1 (TGF-β1) have received increasing attention due to their diverse biological effects. PDGF-BB is a pro-migratory factor that plays a key role in the early stage of wound healing by enhancing proliferation and the recruitment of the fibroblasts to the wound site for ECM deposition.40,41 On the other hand, TGF-β1 stimulates fibroblasts differentiation into contractile myofibroblasts, which are responsible for matrix deposition and remodeling.41 Furthermore, it has also been reported the capability of these GFs to bind to different extracellular components exerting their biological activity.1,11,13,38,42–44 This fact points to an important regulatory mechanism in physiological and pathological processes. In fact, their interaction with collagen and fibrin ECM-proteins is of high physiological relevance.
Collagen I is one of the major components of the connective tissue, accounting for up to 30% of the total protein in the human body.2,45,46 Fibrin is an essential constituent of healing or angiogenic processes.47–49 Under physiological conditions, both can also be assembled in vitro leading to the conformation of hydrogels in which cells are cultured and grown, thereby recreating biomimetic 3D physicochemical environments.
In order to design physiologically relevant in vitro models, gradients of GFs are established across the hydrogels which are installed into the microfluidic devices. The ability to control cell behavior by regulating the availability of GFs provides a powerful tool to study and manipulate a wide array of developmental and regenerative processes that are important in biology, biomedicine and bioengineering.50 Therefore, knowing the actual character of the distribution and gradients of GFs, becomes essential in order to interpret and quantify cell response of in vitro assays. In this work, we present a characterization of the transport of PDGF-BB and TGF-β1 through two different hydrogels, collagen and fibrin, included in a microfluidic platform. The spatio-temporal distribution of each GF, together with their degradation process, is determined by combining experimental and computational approaches. Moreover, this versatile tool can be applied to further quantify the nature of other GFs or hydrogels allowing for a deep insight into the in vitro conditions.
II. MATERIALS AND METHODS
A. Microfluidic device fabrication
The geometry of the microfluidic devices is shown in Fig. 1: it contained a central channel, in which the hydrogel was located, and two media channels (addition and opposite channels) at both sides of the central channel in direct connection with the gel in order to ensure diffusion and hydration. The microfluidic devices were made of polydimethylsiloxane (PDMS-Dow Corning GmbH Sylgard 184, Dow Chemical, Germany) at a ratio of 10:1 polymer to cross-linker, using SU8-silicon wafers (Stanford University, CA) obtained by soft lithography as previously described.51 PDMS microdevices were autoclaved and dried at 80 °C overnight. Finally, they were plasma-bonded and treated with poly-D-lysine (PDL) solution (Sigma-Aldrich, Germany).
FIG. 1.
Geometry of the microfluidic device. A general view of the microdevice is shown in picture (a). The central area is demonstrated as a top view in picture (b), in which the geometry and nomenclature of the compartments are detailed: the channel (1) and the hydrogel (2) compartments. The hydrogel is injected into the central cavity (pink), whose dimensions are 2.5 × 1.3 mm; the main channels (green and blue) are filled with culture media or PBS. When a GF or dextran is added in order to establish a chemical gradient, it is included in the addition channel (green) and diffuses through the hydrogel towards the opposite channel (blue).
B. Hydrogel preparation
Two types of physiologically relevant hydrogels were assayed in this study, collagen and fibrin, in order to evaluate two different biomimetic scaffolds with regard to their chemical composition and physical properties.
Collagen I gel solution (BD Biosciences, Spain) was prepared at 2 mg·ml−1 and pH 7.4,51 while for fibrin hydrogel human fibrinogen (American Diagnostica GmbH, Germany) was diluted in the buffer indicated by the manufacturer (50 mM Tris, 100 mM NaCl, and 5 mM EDTA) at pH 7.4, and mixed with human factor XIII (American Diagnostica GmbH, Germany), human α-thrombin (American Diagnostica GmbH, Germany), CaCl2 (Sigma-Aldrich, Germany), and cell culture media FGM-2 BulletKit (Lonza, Belgium).
Hydrogels were then pipetted into the devices followed by gelation for 20 min in the incubator and hydrated right afterwards. The gels were kept in the incubator for 24 h prior to any subsequent experiment. The media channels were then filled with PBS containing 20 kDa-dextran or FGM-2 media with the GFs, PDFG-BB or TGF-β1, as described in following sections.
C. Characterization of dextran diffusion
To characterize the transport of biomolecules in both hydrogels and determine the chemical gradients generated through the device, 20 kDa-fluorescein isothiocyanate-dextran (Sigma-Aldrich, Germany) was prepared in PBS at 15 μg·ml−1 (Lonza, Belgium) and added in one of the media channels (addition channel), while PBS was added in the opposite media channel (see scheme in Fig. 1). The diffusion phenomenon was imaged by confocal imaging using a Nikon D-Eclipse C1 Confocal Microscope employing a CFI Plan Apo Lambda 2X objective. Time-lapses were acquired each 30 min for a total of 4 h.
D. Experimental quantification of GF concentration and degradation
The study of degradation and transport processes in microfluidic platforms was performed by the addition of 50 ng·ml–1 PDGF-BB (Abcam, UK) or 10 ng · ml−1 TGF-β1 (BD Biosciences, Spain) in the addition channel and the determination of their concentrations by enzyme-linked immunosorbent assays (ELISA) in both, addition and opposite, channels (see Fig. 1).
The degradation assays were performed without any hydrogel in the central chamber of the device in order to evaluate the reduction in the concentrations of the GFs without the influence of the gel; hence, avoiding the interference of diffusion and binding mechanisms. Control samples (without GFs) were also assayed. In spite of this, for the experimental quantification of the GFs concentration pattern, the hydrogels were included within the microfluidic platforms. As far as the sample obtaining is concerned, the media (GF-containing or not) from the lateral channels in direct contact to the hydrogel was extracted and processed as sample.
To determine the PDGF-BB concentration, the PDGF-BB Human ELISA Kit (Abcam, UK) was used according to manufacturer instructions. Standards (0–50 pg · ml−1) were prepared from the stock solution. All standards and samples (1:1000) were run in triplicate. After immobilization and antibody binding, and following streptavidin-HRP solution addition, incubation for 30 min with the TMB One-Step Substrate Reagent was performed. Afterwards, the stop solution was added and the absorbance of the reaction was read at 450 nm in a Synergy HT Multi-Mode Microplate Reader (BioTek Instruments, VT).
TGF-β1 concentration was quantified by the TGF-β1 ELISA Kit (Invitrogen, UK). First, samples were centrifuged (1000 g for 10 min). Similarly, standards (0–75 pg·ml−1) were obtained from the stock solution added to the microfluidic devices and quantified in triplicate as well as samples (1:100). Then, the immunoassay was carried out by the immobilization of TGF-β1 and further antibody reaction, followed by the addition of streptavidin-HRP and the stabilized chromogen. After incubation of 20 min at room temperature in the dark, the stop solution was added and the absorbance was read at 450 nm in a Synergy HT Multi-Mode Microplate Reader (BioTek Instruments, VT).
E. Modeling the GF transport within the hydrogels
In order to simulate the transport of factors through the hydrogels, as shown in Fig. 1, two compartments of the device were distinguished in our model: the channel compartment (1), where the factor is mixed with the media fluid, and the hydrogel compartment (2), that is the cavity in which the hydrogel is installed into the microdevice. Although the same equation was used for both compartments, the parameters varied depending on them, since different phenomena occurred in these domains.
We proposed a reaction-diffusion transport model, where the transport equation is derived from the law of conservation of mass and a suitable constitutive equation for the flux of the chemical factor (Fick's law),
| (1) |
where index refers to the compartment, is the concentration of the factor, is the effective diffusion coefficient, and represents the mass reduction due to both phenomena, the degradation in the channel compartment or the binding to the matrix in the hydrogel compartment. The reaction term can be written as a function of the specific compartment,
| (2) |
where and are the degradation and binding rates, respectively.
The reaction-diffusion process in the domain, as depicted in Fig. 1, is essentially planar. Therefore, we employed a 2D Finite Element simulation based on linear triangle elements and a Euler backward time integration scheme.52 The mesh contained approximately 3000 elements with characteristic element sizes between 0.1 and 0.4 μm. The total time of 24 h was subdivided into 864 steps, with a step size of 100 s each. On all boundaries of the domain, zero flux boundary conditions were applied.
F. Diffusion coefficient estimation
The standard diffusion coefficient of an element of radius within a continuous fluid, can be calculated by the Stokes-Einstein equation as53
| (3) |
where is the Boltzmann constant, the absolute temperature, and the viscosity of the fluid. The values of the standard diffusion coefficient obtained for each chemical factor, together with their radius, are shown in Table I. Actually, the values of the radii for dextran, PDGF-BB, and TGF-β1 are similar. Likewise, the variation of the diffusion coefficient is very small; moreover, the diffusivity of dextran is in the order with those previously published by Galgoczy et al.54
TABLE I.
Parameters of the chemical factors (the standard and specific diffusion coefficients particularized for each chemical factor, together with the corresponding assumed radius, are shown. For dextran, its radius has been indicated from the provider; the value for PDGF-BB has been estimated from the Protein Data Bank; and the one of TGF-β1 has been taken from a previous work.55).
| Dextran | PDGF-BB | TGF-β1 | |
|---|---|---|---|
| (10−9·m) | 3.24 | 4.50 | 3.80 |
| (10−11·m2·s−1) | 1.75 | 1.26 | 1.49 |
| (10−11·m2·s−1) | 1.09 | 0.77 | 0.92 |
| (10−11·m2·s−1) | 1.17 | 0.83 | 0.99 |
However, the diffusivity is altered when these molecules diffuse through a fibrous matrix (for instance, the hydrogel) instead of in a continuous fluid medium. Therefore, an effective diffusion coefficient was defined, which does not depend only on the molecular size but also depends on the void ratio of the porous medium in which the factor is moving. Ogston et al. (1973) and Kim and Tarbell (1994) defined an effective diffusion coefficient as follows:56,57
| (4) |
where is the void ratio of the matrix, the radius of the molecule, and is the fiber radius.
These parameters, which are gathered in Table II, were quantified for both collagen and fibrin gels by means of measurements implemented on Scanning Electron Microscope and Confocal Reflection images.58 Hence, in function on the matrix through which molecule transport occurred, the assumed effective diffusion coefficients in the hydrogel compartment are shown in Table I.
TABLE II.
Geometrical features of the hydrogels (the parameters of the model related to the microstructure of both collagen and fibrin hydrogels: fiber radius and void ratio. The data in this table are reported as mean ± SEM.).
| Collagen | Fibrin | |
|---|---|---|
| Fiber radius (nm) | 79.51 ± 33.16 | 66.53 ± 13.57 |
| Void ratio (%) | 80.15 ± 1.82 | 71.46 ± 1.00 |
| Pore size (nm) | 2.84 ± 0.94 | 1.69 ± 0.33 |
G. Microstructural study
A biophysical characterization of the hydrogels was performed in order to quantify the microstructural data required for the numerical model. Images were acquired by Confocal Reflection Imaging and Scanning Electron Microscopy (SEM).58 In fact, a Nikon D-Eclipse C1 Confocal Microscope equipped with a Plan Apo VC 60XH objective was employed to visualize the 3D networks by reflection. For SEM, following fixation and dehydration of hydrogels, they were freeze-fractured in liquid nitrogen and critical point dried (Baltec CPD030). Then, they were sputter-coated and visualized using high resolution imaging with a Merlin Field Emission Scanning Electron Microscope (FESEM) from Zeiss, working at 1 kV beam voltage and 3 kX magnification. Finally, the fiber radius, void ratio and pore size were measured by means of the free software ImageJ (http://rsb.info.nih.gov/ij).
H. Cell migration assays
The collagen gels with embedded Normal Human Dermal Fibroblasts (NHDF, Lonza) were allowed to polymerize within the microfluidic platforms. We generated chemical gradients of PDGF-BB (5 ng · ml−1) and TGF-β1 (10 ng·ml−1) across collagen gels in order to assess its effect on migration experiments. To do so, time-lapse imaging was carried out by acquiring phase contrast images every 20 min for 24 h and cells were tracked using a hand coded matlab script. Polar histograms, which take into account all the turning angles, were employed to show the directionality of the migratory cells. Additionally, in order to facilitate the interpretation of the results, zone 1 (closer to the source) and zone 2 were distinguished in the gels, as it is shown in Fig. 8. Hence, the euclidean cell speed in each zone was quantified for control and condition samples. The data are shown as mean ± standard deviation (SD) and the differences between the mean values were analyzed using two-tailed Student's t-test, considering significant p-value < 0.05.
FIG. 8.
Directed cell migration. Picture (a) is the last frame of the corresponding time-lapse acquisition (refer to SM2 in the supplementary material to watch the full movie).58 The dotted line delimits zone 1 from zone 2. The quantification shown in (b) corresponds to migratory tracks in control samples, as well as in those with generated chemical gradients by PDGF-BB and TGF-β1. The mean and SD values are gathered in Table SI of the supplementary material.58 Statistically significant: p-value < 0.05 (*: p < 0.05; **: p < 0.01; ***: p < 0.001). The polar histograms plotted for control (c), PDGF-BB (d) and TGF-β1 (e) samples indicate the directionality of the migratory cells by means of turn angles.
III. RESULTS
In order to characterize the spatio-temporal distribution of the GFs, experimental assays were performed as well as computational simulations. All the studies were carried out using PDGF-BB and TGF-β1 as GFs, and establishing chemical gradients across collagen and fibrin hydrogels.
At first, the computational model was validated by characterizing the transport of dextran. Afterwards, in order to elucidate the events occurring during GF transport in the porous-gel media, different aspects were considered: degradation measurements and assessment of the distribution of GF concentration. Next, finite element simulations of GF transport were carried out in order to replicate the in vitro experiments, allowing to improve the understanding of the biochemical environmental cues that are induced.
A. Characterization of dextran transport dynamics
The distribution of the diffusing 20 kDa-fluorescein isothiocyanate-dextran was imaged and simulated in both collagen and fibrin gels. As demonstrated in Fig. 2, the purely diffusive pattern was spread all over the microfluidic device and the evolution of the leading edge of dextran by means of speed was quantified based on both experimental and numerical results.59 In fact, it confirmed the suitability of our model to predict such processes, since the dye concentration profile deriving from both methods matched accurately. Hence, the computational simulation of the experiment for a diffusion coefficient of 1.75 × 10−11 m2·s−1, as indicated by the provider, based on the Fick's Law (without any presence of binding) was able to predict the transport of dextran through the scaffold.
FIG. 2.
Diffusive gradient of dextran. In vitro and in silico images, respectively, resulting from dextran diffusion in collagen [(a),(c)] and fibrin [(b),(d)] hydrogels, after 4 h since addition. The development in time of the leading edge of dextran in terms of speed for collagen (e) and fibrin (f) is shown in the graphs.
B. Experimental measurements of GF degradation
For the assessment of GF degradation in the devices, the concentration of PDGF-BB and TGF-β1 were evaluated 24 h after factor addition. Employing the devices without any hydrogel allowed for an accurate quantification of the decrease in their concentrations by degradation. The samples collected from the media channels were evaluated by ELISA and the concentration values obtained were plotted with respect to the initial concentrations, 100% being 50 ng·ml−1 of PDGF-BB or 10 ng·ml−1 of TGF-β1.
After 24 h, the concentration values for PDGF-BB and TGF-β1 were 45% and 70%, respectively, as shown in Fig. 3. Hence, the reductions in the concentration of the factors were approximately 55% and 30%, yielding a lower decrease in the concentration of TGF-β1 than exhibited by PDGF-BB. These results highlighted the differences in the degradation processes of PDGF-BB and TGF-β1 in the devices, and showed TGF-β1 to be significantly more stable in our experimental analysis.
FIG. 3.
Degradation of the GFs within the microfluidic device. Experimental data as percentage of initial PDGF-BB and TGF-β1 concentrations (50 ng · ml−1 and 10 ng · ml−1 are 100%, respectively) obtained from media channels of the device without any hydrogel 24 h after addition.
C. Experimental quantification of GF concentration
ELISA assays were performed to quantify the transport of the studied GFs across the hydrogels held in the microfluidic devices. 50 ng·ml−1 of PDGF-BB or 10 ng·ml−1 of TGF-β1 were added to one media channel (the addition channel) and the samples were obtained after 24 h from both media channels (the addition channel and the opposite one).
The GFs, PDGF-BB and TGF-β1, showed a similar distribution for both hydrogels as displayed in Figs. 4 and 5. Regarding PDGF-BB, for collagen hydrogels, the GF concentration detected in the addition channel compared to the initial state (50 ng · ml−1 = 100%) decreased down to 40%, while the concentration obtained in the opposite channel reached 4%. In fibrin hydrogels, percentages of approximately 45% and 8% were obtained in the addition channel and in the opposite one, respectively, when PDGF-BB was added.
FIG. 4.
PDGF-BB concentration pattern within collagen and fibrin hydrogels. Experimental ▪ and computational (corresponding to Case 4) ▪ data as percentage of the initial PDGF-BB concentration (50 ng · ml−1 = 100%) obtained from both media channels 24 h after addition.
FIG. 5.
TGF-β1 concentration pattern within collagen and fibrin hydrogels. Experimental ▪ and computational (corresponding to Case 4) ▪ data as percentage of the initial TGF-β1 concentration (10 ng·ml−1 = 100%) obtained from both media channels 24 h after addition.
For the other GF, TGF-β1, transported through collagen gels, the concentration percentage obtained from the addition channel was 30%, whereas the concentration in the opposite channel was 5%. For fibrin gels, the percentages of TGF-β1 from the addition and opposite channels were 30% and 4%, respectively. In summary, the results of this subsection precisely show the chemical gradients across the hydrogel in each considered GF-ECM combination.
D. Numerical predictions of GF transport
The model detailed in Sec. II allowed to describe the transport of GFs through hydrogels by means of three main parameters: the effective diffusion coefficient, which strongly depends on the molecular size of the factor and the geometry of the porous scaffold; the degradation rate of each specific element; and the binding factor, which quantifies the ability of the molecule to bind to the matrix.
As a main assumption, we considered that the theoretical estimation of the effective diffusion coefficients in a porous matrix (presented in Sec. II) was an accurate approach to model diffusion; indeed, other works also use a similar approach.60,61 Here, the degradation and binding rates were obtained by minimizing the difference with respect to the GF concentrations that were observed experimentally. To this end, four distinct cases were studied in order to assess these parameters: (Case 1) the values obtained in the degradation experiments were assumed as degradation rates and binding was omitted; (Case 2) the degradation rates were taken from the degradation experiments and binding rates were fitted to reduce the average difference in both channels; (Case 3) binding was omitted and the degradation rates were fitted to reduce the average difference in both channels; (Case 4) both degradation and binding rates were fitted to reduce the average difference in both channels.
The parameters estimated for each type of gel and GF are detailed in Tables III and IV. The degradation and binding rates, as well as the corresponding differences with respect to the experimental values are shown. These differences are displayed as separated differences for the addition and opposite channels, and also as the average of both differences, which was minimized by the parameter adjustment. Indeed, the average difference was reduced when both binding and degradation rates were adjusted, which corresponded to the denominated Case 4. Figs. 4 and 5 compare and visualize those optimized differences between experimental data and the numerical predictions for PDGF-BB and TGF-β1 in both hydrogels.
TABLE III.
Computational characterization of PDGF-BB transport (parameter estimation and difference computation with regard to experimental values for collagen and fibrin hydrogels considering four different conditions: (Case 1) the values obtained in the degradation experiments are assumed as degradation rates and binding is neglected; (Case 2) the degradation rates are accepted from the degradation experiments and binding ratios are fitted to reduce the average difference in both channels; (Case 3) binding is neglected and the degradation rates are fitted to reduce the average difference in both channels; (Case 4) both degradation and binding rates are fitted to reduce the average difference in both channels).
| Collagen | Fibrin | |||||||
|---|---|---|---|---|---|---|---|---|
| Case1 | Case2 | Case3 | Case4 | Case1 | Case2 | Case3 | Case4 | |
| Degradation rate, (10−6·s−1) | 9.97 | 9.97 | 4.00 | 3.00 | 9.97 | 9.97 | 1.00 | 3.00 |
| Binding rate, (10−6·s−1) | 0.00 | 0.00 | 0.00 | 10.00 | 0.00 | 0.00 | 0.00 | 0.10 |
| Addition channel difference (%) | 14.40 | 14.40 | 0.61 | 1.89 | 17.90 | 17.90 | 6.52 | 0.54 |
| Opposite channel difference (%) | 1.49 | 1.49 | 2.97 | 0.95 | 3.00 | 3.00 | 0.92 | 1.49 |
| Average difference (%) | 7.96 | 7.96 | 1.79 | 1.42 | 10.40 | 10.40 | 3.72 | 1.02 |
TABLE IV.
Computational characterization of TGF-β1 transport (refer to caption of Table III).
| Collagen | Fibrin | |||||||
|---|---|---|---|---|---|---|---|---|
| Case1 | Case2 | Case3 | Case4 | Case1 | Case2 | Case3 | Case4 | |
| Degradation rate, (10−6·s−1) | 4.68 | 4.68 | 7.00 | 5.00 | 4.68 | 4.68 | 8.00 | 4.50 |
| Binding rate, (10−6·s−1) | 0.00 | 10.00 | 0.00 | 10.00 | 0.00 | 20.00 | 0.00 | 20.00 |
| Addition channel difference (%) | 4.98 | 0.72 | 0.38 | 0.06 | 6.78 | 0.42 | 0.89 | 0.02 |
| Opposite channel difference (%) | 3.59 | 0.91 | 2.78 | 0.83 | 3.87 | 0.13 | 2.87 | 0.10 |
| Average difference (%) | 4.29 | 0.82 | 1.58 | 0.42 | 5.32 | 0.28 | 1.88 | 0.06 |
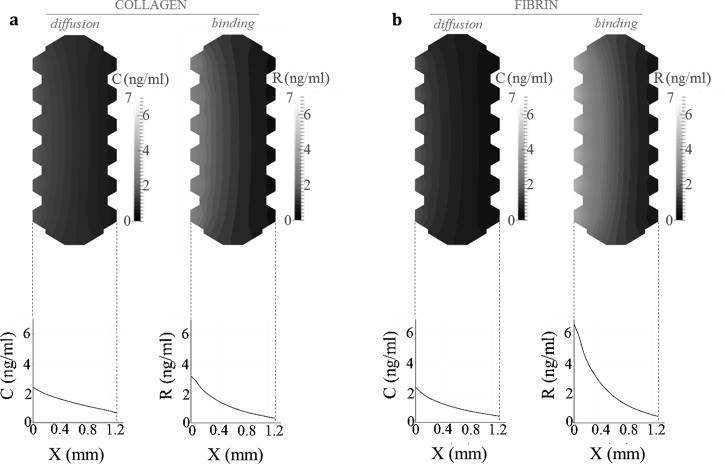
Predicting the transport mechanisms by the numerical simulations led to a deeper knowledge of the GF transport and spatio-temporal distribution of the chemical factor. Taking advantage of the adjusted models, we simulated the generated chemotactic and haptotactic cue patterns when gradients of PDGF-BB and TGF-β1 were established. The distributions of both GFs obtained from the simulations (corresponding to the Case 4) are plotted and illustrated in Figs. 6 and 7, which show the concentration pattern set across collagen and fibrin hydrogels for PDGF-BB and TGF-β1, respectively.
FIG. 6.
Numerical simulation of the spatio-temporal distribution of PDGF-BB inside the microfluidic system. The computational model predicts the spatial distribution of PDGF-BB in collagen (a) and fibrin (b) hydrogels, with respect to Case 4. The simulation figures show diffusion and binding patterns resulting after 24 h since factor addition, being the added initial concentration of 50 ng · ml−1 (source in the left side of the device). The graphs depict the evolution—over the gel width—of diffusion and binding concentration profiles, denoted as C and R, respectively. In collagen gels, both diffusion and binding processes occur simultaneously. Conversely, binding is not relevant in the case of fibrin.
FIG. 7.
Numerical simulation of the spatio-temporal distribution of TGF-β1 inside the microfluidic system. The computational model predicts the spatial distribution of TGF-β1 in collagen (a) and fibrin (b) hydrogels, with respect to Case 4. The simulation figures show diffusion and binding patterns resulting after 24 h since factor addition, being the added initial concentration of 10 ng·ml−1 (source in the left side of the device). The graphs depict the evolution—over the gel width—of diffusion and binding concentration profiles, denoted as C and R, respectively. Diffusion in both hydrogels follows a similar fashion. However, the bound factor presents enhanced activity in fibrin comparing to collagen.
E. Multiple taxis phenomena direct cell migration
Seeking to assess experimentally the impact of the beforehand quantified GF distributions, migration experiments in collagen gels were carried out and cell speed was quantified, as shown in Fig. 8. Cells in control samples were not highly migratory. Additionally, when we compared the migratory response of the cells in control samples to those within TGF-β1 gradient-generated, we did not found significant differences.58 Conversely, cells within PDGF-BB gradient-induced devices increased their cell speed and biased migration, which showed significant differences with respect to those in control samples. Besides, all the cells within the PDGF-BB gradient-generated platforms, did not behave equally. Indeed, significant differences were observed between zone 1 and 2: cell speed presented 6-fold increase for zone 1, whereas 2-fold increase was measured in zone 2.
IV. DISCUSSION
Directional cell migration is key to several physiological processes such as metastasis, morphogenesis and wound healing.62–64 Particularly, the application of controlled chemical gradients of in vitro assays is fundamental to interpret and quantify the cellular response to different biochemical conditions. Microfluidic devices show the unique feature of mimicking real cellular niches together with well-controlled chemical gradients. For this reason, a huge effort has been dedicated to their development by the scientific community.26,27,51,62,65,66
In 2D, chemical gradients are employed for a wide range of different applications.31,35,36,67,68 Nevertheless, 3D systems allow for stable chemical gradients across chips containing hydrogel scaffolds, which better recreate the real ECM, and provide physiologically more relevant models. Indeed, several works are directed to the characterization and application of chemical gradients in 3D microsystems in order to address distinct biological issues.4,34,37,39,66,69
Most of these works consider diffusion and degradation of GFs as the main mechanisms during biomolecule transport. However, there are accumulating data showing the specific binding of GFs to the ECM-proteins in vivo as well as in vitro.1,11,13,38,43,44 This leads to a heterogeneous spatial distribution of matrix-bound (or solid state) chemical factors that regulates the transport of GFs inside the ECM. For example, Martino et al. have proposed the nature to act as a GF reservoir as the main physiological function of fibrin,13 highlighting its direct and important role during wound healing. Indeed, the high physiological relevance of haptotaxis has been pointed out. In this interpretation, several works indicate the distinct impact exerted by both taxis phenomena on the cellular migration patterns, in contrast to those that consider chemotaxis as a process including haptotaxis.8,18,70 Since it is very difficult to decouple both taxis phenomena in 3D experiments, this issue remains challenging for future studies. Hence, it is potentially relevant to take into account that two distinct cues are induced in our microfluidic systems: chemotactic (soluble factors regulated by diffusion within the interstitial soluble fluid) and haptotactic (solid state factors determined by binding to the ECM) stimuli.
Our work suggests diffusion, binding and degradation mechanisms as main phenomena arising from the 3D transport of biomolecules when chemical gradients are established in microfluidic platforms that contain hydrogels. To this end, our aim was to combine microfluidic experiments with ELISAs and numerical simulations. This approach was applied to two different GFs, PDGF-BB and TGF-β1, whose chemical gradients were established in microdevices that hold two different hydrogels, collagen or fibrin. Therefore, the chemical response of the physiologically relevant biomimetic interactions between the studied GF and ECM were elucidated.
The combination of both methodologies allowed the characterization of the chemical cues (chemotactic and haptotactic) induced within the microfluidic platforms. So, on the one hand, the microfluidic experiments, combined with ELISA assays, led to the quantification of the temporal evolution of GF concentration in each compartment. On the other hand, the numerical simulations provided estimations of the spatio-temporal distribution of each GF within the scaffold gel. The quantitative comparison of both experimental and numerical results allowed for calibrating the parameters of the numerical model, as well as to validate the main assumptions in which the mathematical model is based on. Therefore, it was fundamental to set the main simplifications of our model and their implications on our results. The mathematical model here proposed assumed that three phenomena regulate the transport and conservation of GF within the scaffold gel: diffusion within the soluble fluid, temporal degradation and binding to the gel-scaffold.
First, we assumed that the diffusion coefficient of the GF in the interstitial soluble fluid is dominated by the equation of Stokes-Einstein,71 corrected by means of the Ogston approximation,56 that takes into account the complex pore space between the fibers defining the scaffold hydrogel microstructure. Actually, the Ogston approximation is one of the most used techniques to quantify the effective diffusive transport properties of molecules within collagen hydrogels.61 In order to apply these approximations, microstructural features were quantified by means of Confocal Reflectance and Scanning Electron Microscopy (SEM) imaging analysis. However, in the protocol for SEM sample preparation, the lattices are processed by dehydration, fracture and critical point drying. Therefore, at some point the networks could suffer small modifications with respect to their nature in vitro. Nevertheless, since the operation method is widely employed in the literature,72,73 we considered that measured characteristics were valid for this study.
On the other hand, we assumed the degradation rate of the GFs to be a linear function of the concentration. For each specific experiment we estimated the degradation rate parameter in order to minimize the differences between in vitro and in silico experiments. We also considered that the GF not diffusing within the fluid and not degrading was going to be bound to the matrix. Although we were not able to measure it, this assumption is not new and many different authors have considered a similar hypothesis; for example, Zhang et al. analyzed the role of diffusible binding patterns in modulating the transport and concentration of proteins in cartilage.44 In addition, there are also other experimental works that report the binding of PDGF-BB and TGF-β1 to fibrinogen and collagen I as a crucial phenomenon in their transport.13,14,43 Moreover, since GF concentrations are very low and biomimetic matrices are usually rich in proteins, it is considered that enough binding points in the hydrogel are always available and these are never saturated.
Despite these simplifications, this work clearly showed the ability of the model to predict the results obtained from the in vitro experiments by incorporating the effective diffusion, binding, and degradation phenomena. Actually, by means of computational simulations, both degradation and binding rates were fitted to predict the numerical results representing more similarly those experimentally measured, which correspond to Case 4 shown in Sec. III. Nevertheless, there are significant differences in the concentration pattern depending on the hydrogel and the GF of interest. Regarding the transport of PDGF-BB in the hydrogels, the binding rate is much more significant for collagen than in the case of fibrin gels, where the effects of degradation and diffusion processes are more relevant. Indeed, Somasundaram and Schuppan confirm the specific binding between PDGF-BB and collagen I: approximately 40% of the added factor was the bound portion in their experiments.43 In contrast, the promiscuity of PDGF-BB to bind fibrin is published to be of very short term, since Martino et al. measured that in 24 h 75% of the fibrin-bound PDGF-BB was released to the ECM.13 This fact explains the insignificant binding activity measured in this case. However, it could not explain whether the factor continues to be active or inactive once it is released, which could elucidate the possible existence of a shift among the bound and soluble factor proportions.
Concerning the transport behavior of TGF-β1, although the binding phenomenon is significant for both collagen and fibrin gels, it is 2-fold higher in the case of fibrin. Regarding the binding capability of TGF-β1, it is known to bind fibronectin and collagen type IV; however, to our knowledge, there is no evidence to bind collagen I. Hence, although our predictions are consistent with the experimental approach, conscious by the existence of bound TGF-β1 in collagen hydrogels, this event should be further cleared up. In contrast, the data obtained for fibrin hydrogels are compatible with those demonstrated by Martino et al.,13 since 24 h after addition they still found 55% of the initial amount of bound TGF-β1.
In these results, our work proposes a simplified but in vivo-like characterization of the heterogeneous distribution of the biochemical environment for in vitro representation. However, as far as the cellular contribution to the GF distribution is concerned, it is accepted that they may act as geometrical obstacles upon the chemical compounds perturbing, hence, the 3D spatio-temporal distribution of the GFs.54 In this regard, Shkilnyy et al. stated that diffusion coefficients for rhodamine B remain more or less constant up to 0.5 × 106 cell · ml−1 in case of HUVECs.74 However, they also noted that higher cell density of the same cell type resulted in a decrease of the diffusion coefficient. All this together points to that depending on the cell density, as well as cell type, the effective diffusion coefficient and reduced interstitial space may require to be adjusted.54
Adopting the reductionist simplification of omitting the effect coming from the cells, we have also performed migration assays under PDGF-BB and TGF-β1 gradients. By showing significant differences in the cellular response, depending on the applied GF gradient, we have shown cell viability of the microsystems for this type of in vitro applications. In addition, upon PDGF-BB gradient, regarding the cell speed enhancement induced by both chemotactic and haptotactic cues, we quantified to be 6-fold for zone 1 (close to the source) and 2-fold in zone 2 (further from the source). Although our concentration distribution model hypothesizes the coexistence of diffusion and binding transport mechanisms, it becomes a potential compelling challenge to decouple the effects of both taxis phenomena.
V. CONCLUSIONS
Microfluidic platforms are potential means to create 3D in vitro models, since this versatile technology allows for biomimetic microenvironments by including hydrogels and generating chemical gradients that direct cellular processes such as single cell migration. In this work, it is demonstrated that establishing chemical gradients in microdevices with biomimetic hydrogels is not straightforward, but different phenomena have to be considered, such as, effective diffusion, degradation and binding to the matrix. For such in vitro assays, therefore, two main regulatory mechanisms determine the cues that cells may sense in these physiological microenvironments: the chemotactic and haptotactic stimuli.
ACKNOWLEDGMENTS
This study was supported by the European Research Council (ERC) through project ERC-2012-StG 306751 and the Spanish Ministry of Economy and Competitiveness (DPI2012-38090-C03-01). The authors also acknowledge Dr. Roger Kamm and his group for technical assistance with the microfluidic devices.
References
- 1.Taipale J. and Keski-Oja J., FASEB J. 11, 51 (1997). [DOI] [PubMed] [Google Scholar]
- 2.Frantz C., Stewart K. M., and Weaver V. M., J. Cell Sci. 123, 4195 (2010). 10.1242/jcs.023820 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Plant A. L., Bhadriraju K., Spurlin T. A., and Elliott J. T., Biochim. Biophys. Acta 1793, 893 (2009). 10.1016/j.bbamcr.2008.10.012 [DOI] [PubMed] [Google Scholar]
- 4.Pujic Z. and Goodhill G. J., J. Neurosci. Methods 215, 53 (2013). 10.1016/j.jneumeth.2013.02.008 [DOI] [PubMed] [Google Scholar]
- 5.Roca-Cusachs P., Sunyer R., and Trepat X., Curr. Opin. Cell Biol. 25, 543 (2013). 10.1016/j.ceb.2013.04.010 [DOI] [PubMed] [Google Scholar]
- 6.Perrimon N., Pitsouli C., and Shilo B.-Z., Cold Spring Harbour Perspect. Biol. 4, a005975 (2012). 10.1101/cshperspect.a005975 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lázár-Molnár E., Hegyesi H., Tóth S., and Falus A., Cytokine 12, 547 (2000). 10.1006/cyto.1999.0614 [DOI] [PubMed] [Google Scholar]
- 8.Daub J. T. and Merks R. M. H., Bull. Math. Biol. 75, 1377 (2013). 10.1007/s11538-013-9826-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Petrie R. J., Doyle A. D., and Yamada K. M., Nat. Rev. Mol. Cell Biol. 10, 538 (2009). 10.1038/nrm2729 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Polacheck W. J., Zervantonakis I. K., and Kamm R. D., Cell. Mol. Life Sci. 70, 1335 (2013). 10.1007/s00018-012-1115-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Brizzi M. F., Tarone G., and Defilippi P., Curr. Opin. Cell Biol. 24, 645 (2012). 10.1016/j.ceb.2012.07.001 [DOI] [PubMed] [Google Scholar]
- 12.Ferrara N., Mol. Biol. Cell 21, 687 (2010). 10.1091/mbc.E09-07-0590 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Martino M. M., Briquez P. S., Ranga A., Lutolf M. P., and Hubbell J. A., Proc. Natl. Acad. Sci. U.S.A. 110, 4563 (2013). 10.1073/pnas.1221602110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Martino M. M., Briquez P. S., Güç E., Tortelli F., Kilarski W. W., Metzger S., Rice J. J., Kuhn G. A., Müller R., Swartz M. A., and Hubbell J. A., Science 343, 885 (2014). 10.1126/science.1247663 [DOI] [PubMed] [Google Scholar]
- 15.Kihara T., Ito J., and Miyake J., PLoS One 8, e82382 (2013). 10.1371/journal.pone.0082382 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Roussos E. T., Condeelis J. S., and Patsialou A., Nat. Rev. Cancer 11, 573 (2011). 10.1038/nrc3078 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Aznavoorian S., Stracke M. L., Krutzsch H., Schiffmann E., and Liotta L. A., J. Cell Biol. 110, 1427 (1990). 10.1083/jcb.110.4.1427 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Li S., Huang N. F., and Hsu S., J. Cell. Biochem. 96, 1110 (2005). 10.1002/jcb.20614 [DOI] [PubMed] [Google Scholar]
- 19.Garrett Q., Khaw P. T., Blalock T. D., Schultz G. S., Grotendorst G. R., and Daniels J. T., Invest. Ophthalmol. Vis. Sci. 45, 1109 (2004). 10.1167/iovs.03-0660 [DOI] [PubMed] [Google Scholar]
- 20.Jester J. V. and Ho-Chang J., Exp. Eye Res. 77, 581 (2003). 10.1016/S0014-4835(03)00188-X [DOI] [PubMed] [Google Scholar]
- 21.Long C. J., Roth M. R., Tasheva E. S., Funderburgh M., Smit R., Conrad G. W., and Funderburgh J. L., J. Biol. Chem. 275, 13918 (2000). 10.1074/jbc.275.18.13918 [DOI] [PubMed] [Google Scholar]
- 22.Tuli S. S., Liu R., Chen C., Blalock T. D., Goldstein M., and Schultz G. S., Curr. Eye Res. 31, 709 (2006). 10.1080/02713680600837390 [DOI] [PubMed] [Google Scholar]
- 23.Kraning-Rush C. M., Carey S. P., Califano J. P., Smith B. N., and Reinhart-King C. A., Phys. Biol. 8, 015009 (2011). 10.1088/1478-3975/8/1/015009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chen X. and Thibeault S. L., Tissue Eng. Part A 18, 2528 (2012). 10.1089/ten.tea.2012.0094 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sun T., Jackson S., Haycock J. W., and MacNeil S., J. Biotechnol. 122, 372 (2006). 10.1016/j.jbiotec.2005.12.021 [DOI] [PubMed] [Google Scholar]
- 26.Yeo L. Y., Chang H.-C., Chan P. P. Y., and Friend J. R., Small 7, 12 (2011). 10.1002/smll.201000946 [DOI] [PubMed] [Google Scholar]
- 27.Wu J., Wu X., and Lin F., Lab Chip 13, 2484 (2013). 10.1039/c3lc50415h [DOI] [PubMed] [Google Scholar]
- 28.Hee C. K., Dines J. S., Solchaga L. A., Shah V. R., and Hollinger J. O., Tissue Eng. Part B 18, 225 (2012). 10.1089/ten.TEB.2011.0603 [DOI] [PubMed] [Google Scholar]
- 29.Li X., Ballerini D. R., and Shen W., Biomicrofluidics 6, 11301 (2012). 10.1063/1.3687398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lee J.-H., Gu Y., Wang H., and Lee W. Y., Biomaterials 33, 999 (2012). 10.1016/j.biomaterials.2011.10.036 [DOI] [PubMed] [Google Scholar]
- 31.Li J., Zhu L., Zhang M., and Lin F., Biomicrofluidics 6, 24121 (2012). 10.1063/1.4718721 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kothapalli C. R., van Veen E., de Valence S., Chung S., Zervantonakis I. K., Gertler F. B., and Kamm R. D., Lab Chip 11, 497 (2011). 10.1039/c0lc00240b [DOI] [PubMed] [Google Scholar]
- 33.Chung S., Sudo R., Vickerman V., Zervantonakis I. K., and Kamm R. D., Ann. Biomed. Eng. 38, 1164 (2010). 10.1007/s10439-010-9899-3 [DOI] [PubMed] [Google Scholar]
- 34.Zervantonakis I. K., Hughes-Alford S. K., Charest J. L., Condeelis J. S., Gertler F. B., and Kamm R. D., Proc. Natl. Acad. Sci. U.S.A. 109, 13515 (2012). 10.1073/pnas.1210182109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Xu H. and Heilshorn S. C., Small 9, 585 (2013). 10.1002/smll.201202208 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Atencia J., Morrow J., and Locascio L. E., Lab Chip 9, 2707 (2009). 10.1039/b902113b [DOI] [PubMed] [Google Scholar]
- 37.Jeong G. S., Han S., Shin Y., Kwon G. H., Kamm R. D., Lee S.-H., and Chung S., Anal. Chem. 83, 8454 (2011). 10.1021/ac202170e [DOI] [PubMed] [Google Scholar]
- 38.Helm C.-L. E., Fleury M. E., Zisch A. H., Boschetti F., and Swartz M. A., Proc. Natl. Acad. Sci. U.S.A. 102, 15779 (2005). 10.1073/pnas.0503681102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pagano G., Ventre M., Iannone M., Greco F., Maffettone P. L., and Netti P. A., Biomicrofluidics 8, 046503 (2014). 10.1063/1.4893913 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Grinnell F., Trends Cell Biol. 10, 362 (2000). 10.1016/S0962-8924(00)01802-X [DOI] [PubMed] [Google Scholar]
- 41.Tomasek J. J., Gabbiani G., Hinz B., Chaponnier C., and Brown R. A., Nat. Rev. Mol. Cell Biol. 3, 349 (2002). 10.1038/nrm809 [DOI] [PubMed] [Google Scholar]
- 42.Paralkar V. M., Vukicevic S., and Reddi A. H., Dev. Biol. 143, 303 (1991). 10.1016/0012-1606(91)90081-D [DOI] [PubMed] [Google Scholar]
- 43.Somasundaram R. and Schuppan D., J. Biol. Chem. 271, 26884 (1996). 10.1074/jbc.271.43.26884 [DOI] [PubMed] [Google Scholar]
- 44.Zhang L., Gardiner B. S., Smith D. W., Pivonka P., and Grodzinsky A. J., J. Theor. Biol. 263, 20 (2010). 10.1016/j.jtbi.2009.11.023 [DOI] [PubMed] [Google Scholar]
- 45.Diegelmann R. F. and Evans M. C., Front. Biosci. 9, 283 (2004). 10.2741/1184 [DOI] [PubMed] [Google Scholar]
- 46.Timmons J., Wound Essentials 1, 8 (2006). [Google Scholar]
- 47.van Hinsbergh V. W., Collen A., and Koolwijk P., Ann. NY Acad. Sci. 936, 426 (2001). 10.1111/j.1749-6632.2001.tb03526.x [DOI] [PubMed] [Google Scholar]
- 48.Weisel J. W., Biophys. Chem. 112, 267 (2004). 10.1016/j.bpc.2004.07.029 [DOI] [PubMed] [Google Scholar]
- 49.Sidelmann J. J., Gram J., Jespersen J., and Kluft C., Semin. Thromb. Hemost. 26, 605 (2000). 10.1055/s-2000-13216 [DOI] [PubMed] [Google Scholar]
- 50.Richardson T. P., Peters M. C., Ennett A. B., and Mooney D. J., Nat. Biotechnol. 19, 1029 (2001). 10.1038/nbt1101-1029 [DOI] [PubMed] [Google Scholar]
- 51.Shin Y., Han S., Jeon J. S., Yamamoto K., Zervantonakis I. K., Sudo R., Kamm R. D., and Chung S., Nat. Prot. 7, 1247 (2012). 10.1038/nprot.2012.051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ern A. and Guermond J. L., in edited by Antman S. S., Marsden J. E., and Sirovich L., Theory and Practice of Finite Elements (Springer, New York, 2004). [Google Scholar]
- 53.Einstein A., Ann. Phys. (N.Y). 322, 891 (1905). 10.1002/andp.19053221004 [DOI] [Google Scholar]
- 54.Galgoczy R., Pastor I., Colom A., Giménez A., Mas F., and Alcaraz J., Colloids Surf. B. Biointerfaces 120, 200 (2014). 10.1016/j.colsurfb.2014.05.017 [DOI] [PubMed] [Google Scholar]
- 55.Sáez P., Ph.D. dissertation ( University of Zaragoza, 2013). [Google Scholar]
- 56.Ogston A. G., Preston B. N., and Wells J. D., Proc. R. Soc. A Math. Phys. Eng. Sci. 333, 297 (1973). 10.1098/rspa.1973.0064 [DOI] [Google Scholar]
- 57.Kim W. S. and Tarbell J. M., J. Biomech. Eng. 116, 156 (1994). 10.1115/1.2895714 [DOI] [PubMed] [Google Scholar]
- 58.See supplementary material at http://dx.doi.org/10.1063/1.4903948E-BIOMGB-8-028406 for hydrogel microstructure images, mean ± SD values from the migration quantification and migration movies.
- 59.Sudo R., Chung S., Zervantonakis I. K., Vickerman V., Toshimitsu Y., Griffith L. G., and Kamm R. D., FASEB J. 23, 2155 (2009). 10.1096/fj.08-122820 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Flury M. and Gimmi T. F., in Methods Soil Analysis: Part 4–Physical Methods, edited by Dane J. H. and Topp G. C. (Soil Science Society of America (SSSA), Madison, 2002). [Google Scholar]
- 61.Jiao Y. and Torquato S., Phys. Biol. 9, 036009 (2012). 10.1088/1478-3975/9/3/036009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Li J. and Lin F., Trends Cell Biol. 21, 489 (2011). 10.1016/j.tcb.2011.05.002 [DOI] [PubMed] [Google Scholar]
- 63.Knapp D. M., Helou E. F., and Tranquillo R. T., Exp. Cell Res. 247, 543 (1999). 10.1006/excr.1998.4364 [DOI] [PubMed] [Google Scholar]
- 64.Schneider L., Cammer M., Lehman J., Sonja K., Guerra C. F., Veland I. R., Stock C., Hoffmann K., Yoder B. K., Schwab A., Satir P., and Christensen S. T., Cell. Physiol. Biochem. 25, 279 (2010). 10.1159/000276562 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Polacheck W. J., Li R., Uzel S. G. M., and Kamm R. D., Lab Chip 13, 2252 (2013). 10.1039/c3lc41393d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Kim S., Kim H. J., and Jeon N. L., Integr. Biol. 2, 584 (2010). 10.1039/c0ib00055h [DOI] [PubMed] [Google Scholar]
- 67.Wang S. J., Saadi W., Lin F., Minh-Canh Nguyen C., and Li Jeon N., Exp. Cell Res. 300, 180 (2004). 10.1016/j.yexcr.2004.06.030 [DOI] [PubMed] [Google Scholar]
- 68.van der Meer A. D., Vermeul K., Poot A. A., Feijen J., and Vermes I., Am. J. Physiol. Heart Circ. Physiol. 298, H719 (2010). 10.1152/ajpheart.00933.2009 [DOI] [PubMed] [Google Scholar]
- 69.Farahat W. A., Wood L. B., Zervantonakis I. K., Schor A., Ong S., Neal D., Kamm R. D., and Asada H. H., PLoS One 7, e37333 (2012). 10.1371/journal.pone.0037333 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Lu J., Zhou S., Siech M., Habisch H., Seufferlein T., and Bachem M. G., Br. J. Cancer 110, 409 (2014). 10.1038/bjc.2013.706 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Jost W., Diffusion in Solids, Liquids, Gases ( Academic Press, New York, 1952). [Google Scholar]
- 72.Lai V. K., Lake S. P., Frey C. R., Tranquillo R. T., and Barocas V. H., J. Biomech. Eng. 134, 011004 (2012). 10.1115/1.4005544 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.a Ulrich T., Jain A., Tanner K., MacKay J. L., and Kumar S., Biomaterials 31, 1875 (2010). 10.1016/j.biomaterials.2009.10.047 [DOI] [PubMed] [Google Scholar]
- 74.Shkilnyy A., Proulx P., Sharp J., Lepage M., and Vermette P., Colloids Surf. B: Biointerfaces 93, 202 (2012). 10.1016/j.colsurfb.2012.01.005 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1063/1.4903948E-BIOMGB-8-028406 for hydrogel microstructure images, mean ± SD values from the migration quantification and migration movies.