Abstract
Protein conformation and orientation in the lipid membrane plays a key role in many cellular processes. Here we use molecular dynamics simulation to investigate the relaxation and C-terminus diffusion of a model helical peptide: beta-amyloid (Aβ) in a lipid membrane. We observed that after the helical peptide was initially half-embedded in the extracelluar leaflet of phosphatidylcholine (PC) or PC/cholesterol (PC/CHOL) membrane, the C-terminus diffused across the membrane and anchored to PC headgroups of the cytofacial lipid leaflet. In some cases, the membrane insertion domain of the Aβ was observed to partially unfold. Applying a sigmoidal fit to the process, we found that the characteristic velocity of the C-terminus, as it moved to its anchor site, scaled with θu−4/3, where θu is the fraction of the original helix that was lost during a helix to coil transition. Comparing this scaling with that of bead-spring models of polymer relaxation suggests that the C-terminus velocity is highly regulated by the peptide helical content, but that it is independent of the amino acid type. The Aβ was stabilized by the attachment of the positive Lys28 side chain to the negative phosphate of PC or 3β oxygen of CHOL in the extracellular lipid leaflet and of the C-terminus to its anchor site in the cytofacial lipid leaflet.
I. INTRODUCTION
Protein interactions with cell membranes play a vital role in a multitude of natural, pathogenic, and therapeutic processes including signal transduction, protein-misfolding disorders, and drug delivery.1–3 Beta-amyloid (Aβ) is an excellent model protein to study protein/membrane interactions. Aβ is a 39–42 residue amphipathic peptide released by the concerted proteolytic cleavage of the amyloid precursor protein by beta and gamma secretases in neurons.4 The distinctive lipid insertion domain (LID) of Aβ is a short transmembrane (TM) segment containing 11–13 non-polar residues bounded, at physiological pH, by a charged lysine and the charged C-terminus.5,6 The LID contains the essential elements of protein membrane translocation: (i) a charged terminus that can bind to a lipid target on the trans-side of the membrane, (ii) a charged residue that can anchor the protein by binding to the cytosolic side of the membrane, and (iii) a loosely folded insertion structure.7–9 We find that the negatively charged, deprotonated C-terminus, Ala40 or Val42, can descend and anchor to the phosphate of the polar headgroup region of the cytofacial leaflet of the lipid bilayer. However, unlike protein translocation, the binding and folding behavior of Aβ protein is mediated by purely physical peptide/lipid interactions, rather than by interactions with chaperone or carrier proteins.10,11 Also, since it is an important class of amyloidogenic peptide, Aβ interactions with neurons12,13 are important molecular events for understanding pathogenic amyloid cascade pathways.14–20 Using atomistic molecular dynamics (MD) simulation, we explored the atomic and nanosecond-scale mechanisms that regulate protein unfolding, protein relaxation and stability of membrane inserted-state of Aβ. The time-scale of protein conformational changes resulting from diffusion and relaxation kinetics in the bilayer is important because it provides (1) a key time-scale for membrane events, (2) insight on peptide residue/membrane interactions, and (3) a means of assessing the effect of membrane order on protein/lipid interactions.
We modeled the laterally heterogeneous cholesterol-enriched region of the cell membrane using palmitoyloleoyl phosphatidylcholine (PC) lipid bilayers with 40 mole% cholesterol (CHOL) and cholesterol-depleted regions using PC with no CHOL.21
While the inserted state of Aβ has been experimentally verified,18,22,23 the pathway to this state is not addressed here. Our initial protein/lipid structure was one in which the helix of 40- or 42-residue Aβ, denoted Aβ40 or Aβ42, was half-inserted in the extracellular leaflet of the bilayer, modeling a protein that has a non-polar helix or LID and a polar helix immediately after it enters the cis-side of the membrane.
We performed replicated 200 ns simulations on four protein/lipid complexes: Aβ40 or Aβ42 in PC and Aβ40 or Aβ42 in PC/CHOL. Protein conformational kinetics of Aβ and the dynamics of the protein residue/lipid polar headgroup separation distance were analyzed. Folded or unfolded translation of the Aβ C-terminus across a lipid bilayer was observed in several replicates.
Because of the pathophysiological importance of Aβ40 and Aβ42, there have been a number of recent simulations of these peptides in or on model membranes.24–29 Simulation of aggregation and release processes26,30,31 are particularly relevant to the work presented here because they can compete with unfolding, penetration, and binding phenomena.
II. METHODS
A. Aβ primary structures
The first 40 residues of Aβ40 and Aβ42 and the extra two residues of Aβ424 are: Asp-Ala-Glu-Phe-Arg-His-Asp-Ser-Gly-Tyr-Glu-Val-His-His-Gln-Lys-Leu-Val-Phe-Phe-Ala-Glu-Asp-Val-Gly-Ser-Asn-Lys28-Gly-Ala-Ile-Ile-Gly-Leu-Met-Val-Gly-Gly-Val-Val40-(-Ile-Ala42)-OH. At neutral pH, each peptide carries a net −3 charge. The peptide segment bounded by Lys28 and Val40 for Aβ40 or Ala42 for Aβ42 denotes the LID, and the rest (Asp1 to Asn27) the non-LID.
B. Atomistic molecular dynamics simulations of Aβ in lipid bilayers
The work presented here is part of a larger-scale work in which we focused on four protein/membrane systems: Aβ40 in PC (A series), Aβ42 in PC (B series), Aβ40 in PC/CHOL (C series), and Aβ42 in PC/CHOL (D series), in the presence of water and counter ions. In each case the PC was 1-palmitoyl-2-oleoyl-PC, which has a saturated sn-1 (16:0) chain and an unsaturated sn-2 (18:1) chain. For each series there were independent simulation replicates, each with identical initial spatial arrangement of the lipid and protein atoms but with a different initial velocity distribution. A number, one to four, denotes each replicate of a given series. In total, 16 simulations were undertaken: A1–A4, B1–B4, C1–C4, and D1–D4, four replicates each of four systems. Here we study conformational changes that occurred within the first 50 ns of these simulations. The longer time-scale behavior seen in these simulations, including membrane disruption and the effect of CHOL has been previously published.6
The starting structure was Aβ40 or Aβ42 half-embedded into the extracellular leaflet of a lipid bilayer. Initial structures of lipid bilayers were constructed by tiling four identical periodic images of equilibrated PC and PC/CHOL bilayers from previous work.32 The initial atomic coordinates of Aβ40 were obtained from the NMR solution structure of the protein in a micelle-water environment.5 The initial structure of Aβ42 was created from that of Aβ40 by appending Ile41 and Ala42 to the C-terminus and relaxed in water through short MD simulations.6
For the A and B series, two PC lipids in the extracellular leaflet were removed from the PC bilayer to provide an insertion point. One protein molecule, Aβ40 for the A series or Aβ42 for the B series, was then inserted into the lipid layer void. This new protein/lipid structure underwent energy minimization in vacuum to remove energetically unfavorable close contacts among the protein and lipid atoms. The energy-minimized structure was subsequently solvated in a water box, then underwent additional energy minimization. This was followed by a position-restrained simulation of 100 ps during which each atom of the protein or lipid molecules was restrained to its current position by coupling to an isotropic potential with a spring constant of 5000 kJ nm−2 mol−1. The C and D series were prepared similarly except that two PC and one CHOL lipids were removed for protein insertion. The structures after this preparation, were taken as the initial (0 ns) condition for the 200 ns production runs. The initial size of the simulation box was ∼13 × 15 × 13 nm3 for the A and B series with 574 PC and ∼14 × 16 × 14 nm3 for the C and D series with 574 PC and 383 CHOL in explicit solvent and counter ions.
Molecular dynamics simulations were performed under constant number, pressure, and temperature conditions using Gromacs 4.033–36 with Berger et al.37 and Holtje et al.38 lipid parameters and a modified GROMOS87 force field.39,40 The effect of force field on system behavior is a topic of active discussion and there have been comparative studies of membranes.41,42 For properties important in this study: POPC mobility as characterized by the diffusion constant,41 lipid order as characterized by the deuterium order parameters,41 and lipid with partially inserted protein,43 the Berger parameters perform well compared to other force fields. Importantly, this force field combination allowed consistent parameterization of all the components of interest: PC, CHOL, peptide, and water.6,31,32 Implications of using GROMOS87 and the Berger parameters are outlined in Sec. IV.
Periodic boundary conditions along the x, y, and z directions were applied. A simple point charge water model44 was used for solvent. Electrostatic interactions were estimated by Particle-Mesh-Ewald method with the direct space cutoff set to 1.0 nm.36,45,46 Pairwise van der Waals force between non-bonded atoms was derived from a twin-range cutoff Lennard-Jones potential; the interactions for pairs within 1.0 nm were evaluated every step and for pairs between 1.0 and 1.5 nm evaluated every 10 steps. Bond lengths were constrained by LINCS, a linear constraint solver algorithm.47 A leap-frog integrator with a 2 fs time step was used to integrate the motion of the systems. Temperature baths of 300 K were coupled to water, lipids, and protein separately, using a v-rescale thermostat48 with a coupling time of 0.05 ps. A Berendsen barostat49 with a coupling time of 1 ps kept the systems at an isotropic pressure of 1 atm.
C. Calculations of relaxation kinetics of Aβ
The time evolution of the distance of the C-terminus to its binding site on the cytofacial lipid leaflet exhibited a one- or two-step sigmoidal decay behavior. The time decay data provided a measure of the Aβ C-terminus movement across the lipid cytofacial leaflet. One-step or two-step logistic functions were employed to model the complex sigmoidal decay behavior of dmin.
| (1) |
| (2) |
Here, dmin is the minimum distance of the C-terminus to its target in the polar region of the cytofacial leaflet. For one-step sigmoidal decay (Eq. (1)), hi and hf are the initial and final C-terminus position in the membrane, τ is a measure of the characteristic time of the motion; it is the time at which dmin is the midpoint of hi and hf, and k is a rate constant. For two-step sigmoidal decay (Eq. (2)), the first term represents the first sigmoidal decay from hi to an intermediate position h′ and the second term the sigmoidal decay from of h′ to hf. The parameters (τ1, τ2) and (k1, k2) refer to the characteristic times and rate constants for the first and second decays, respectively.
III. RESULTS
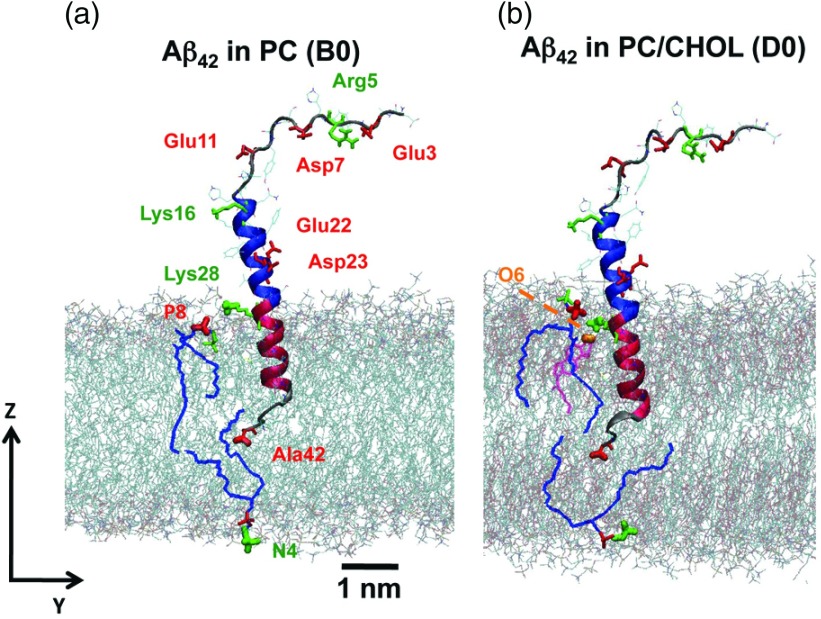
As described in Sec. II, the LID is the 13 or 15 residue-long section of the beta-amyloid starting from the positively charged Lys28 and ending with the negatively charged C-terminus (Val40 or Ala42) for the Aβ40 or Aβ42. The Lys28 of the LID was initially placed near the lipid/water interface while the C-terminus was in the middle of the bilayer. This arrangement can be seen in Figure 1, which illustrates the initial configurations of Aβ42 in PC and PC/CHOL bilayers. The 27 residue-long non-LID region (Asp1 to Asn27) of Aβ40 or Aβ42 was in the aqueous phase in our initial configurations. The polar non-LID contains charged residues, while the residues 29–39 or 29–41 of the LID, bounded by Lys28 and C-terminus, are hydrophobic.
FIG. 1.
Initial configurations of Aβ42 in PC and PC/CHOL bilayers. The blue and red ribbons represent the α-helix structures of the non-LID and LID of Aβ42 with negative (red) and positive (green) residues labeled. The PC and CHOL lipids that interact electrostatically with peptide residues are highlighted dark lines, blue, and purple, respectively. Charged lipid polar groups are highlighted: negative phosphate −PO4− of PC (red), positive trimethylammonium −N(CH3)3+ of PC (green), and negative 3β oxygen of CHOL (orange). Water is not shown. The z-direction defines the normal of the 2D planar lipid bilayer.
Of 16 simulation replicates, nine replicates, A1, B1 and B2, C1 and C2 and D1–D4, showed C-terminus diffusion across the cytofacial leaflet within the first 25 ns of simulation, as shown in Table I. Representative configurations of Aβ42 before, during and after the C-terminus anchoring in the PC and PC/CHOL cytofacial leaflet are illustrated in Figures 2–5.
Table I.
Protein kinetics parameters of the minimum distance between the C-terminus of Aβ to the N4 group of PC for Aβ40 and Aβ42 in PC or PC/CHOL bilayers.
| Aβ in lipid | Replicate | hi (nm) | hf (nm) | τ (ns) | k (ns−1) | VMAX (nm/ns) |
|---|---|---|---|---|---|---|
| Aβ40 in PC | A1 | 1.85 ± 0.06 | 0.36 ± 0.06 | 0.20 ± 0.01 | 12.0 ± 0.78 | 4.46 ± 0.34 |
| Aβ42 in PC | B1 | 1.36 ± 0.03 | 0.35 ± 0.01 | 0.17 ± 0.01 | 28.2 ± 2.58 | 7.13 ± 0.68 |
| B2a | 1.15 ± 0.01 | 0.38 ± 0.01 | 9.76 ± 0.08 | 0.47 ± 0.01 | 0.08 ± 0.01 | |
| Aβ40 in PC/CHOL | C1 | 1.63 ± 0.01 | 0.39 ± 0.01 | 3.49 ± 0.01 | 5.37 ± 0.26 | 1.67 ± 0.08 |
| C2 | 1.61 ± 0.01 | 0.34 ± 0.01 | 7.57 ± 0.03 | 0.91 ± 0.02 | 0.29 ± 0.01 | |
| Aβ42 in PC/CHOL | D1a | 1.41 ± 0.01 | 0.35 ± 0.01 | 4.89 ± 0.01 | 43.0 ± 5.04 | 11.4 ± 1.34 |
| D2 | 1.59 ± 0.02 | 0.33 ± 0.01 | 1.90 ± 0.02 | 2.20 ± 0.11 | 0.69 ± 0.04 | |
| D3 | 1.91 ± 0.01 | 0.36 ± 0.01 | 17.9 ± 0.02 | 0.64 ± 0.01 | 0.25 ± 0.01 | |
| D4 | 1.25 ± 0.01 | 0.41 ± 0.01 | 1.04 ± 0.01 | 14.8 ± 0.90 | 3.11 ± 0.19 |
The protein kinetic parameters of the second component of a 2-step sigmoidal fit. The uncertainties of fitted kinetics parameters from the nonlinear regression of are shown.
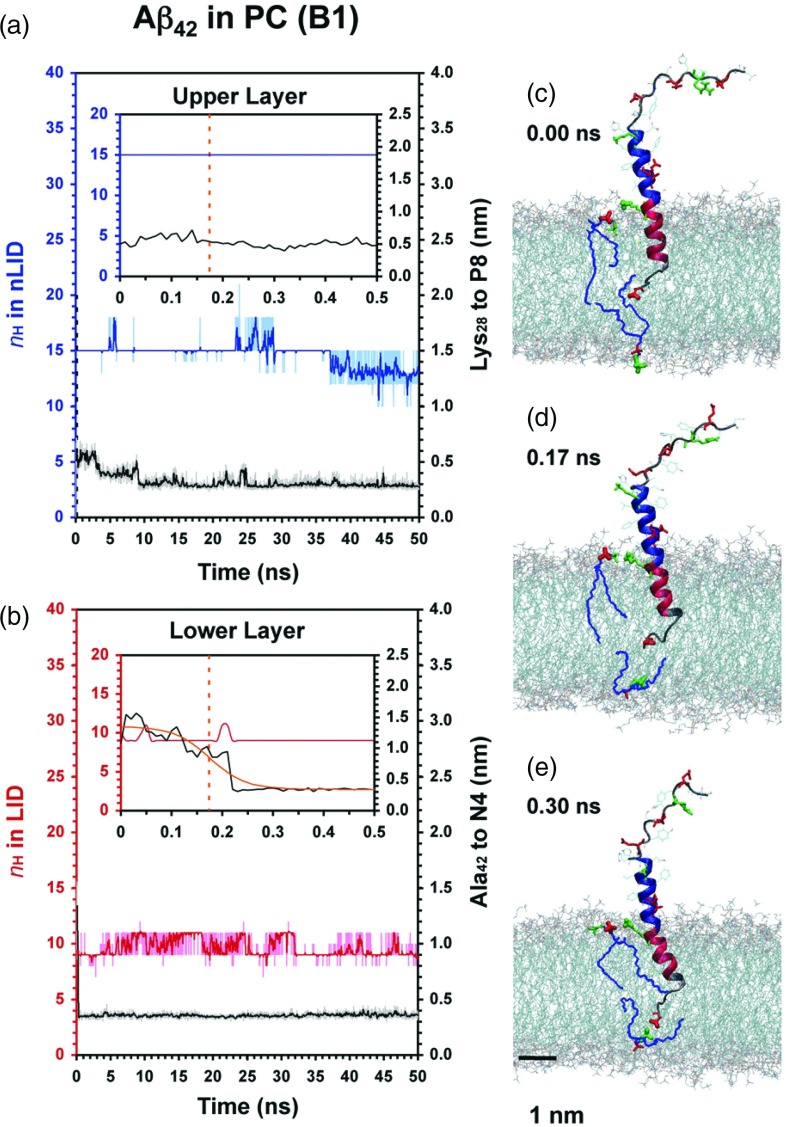
FIG. 2.
Protein conformational and protein-lipid dynamics for the folded anchoring of Aβ42 in PC. The time evolution of nH of the non-LID (blue) and LID (red), and the minimum distance between Lys28 of Aβ42 to P8 of PC (black) in the extracellular lipid leaflet (a) and that of Ala42 of Aβ42 to N4 of PC (black) in the cytofacial lipid leaflet (b) are shown. Insets show enlarged views. A 10-point running average (thick line) highlights the trend of the kinetic data. The protein conformation and the closest pairs of Lys28-P8 and Ala42-N4 are highlighted before (c), midway (d), and after (e) C-terminus diffusion to its anchor site. The sigmoidal fit of the Ala42-N4 kinetics (orange curve) and the midpoint distance at τ (orange dotted line) are shown.
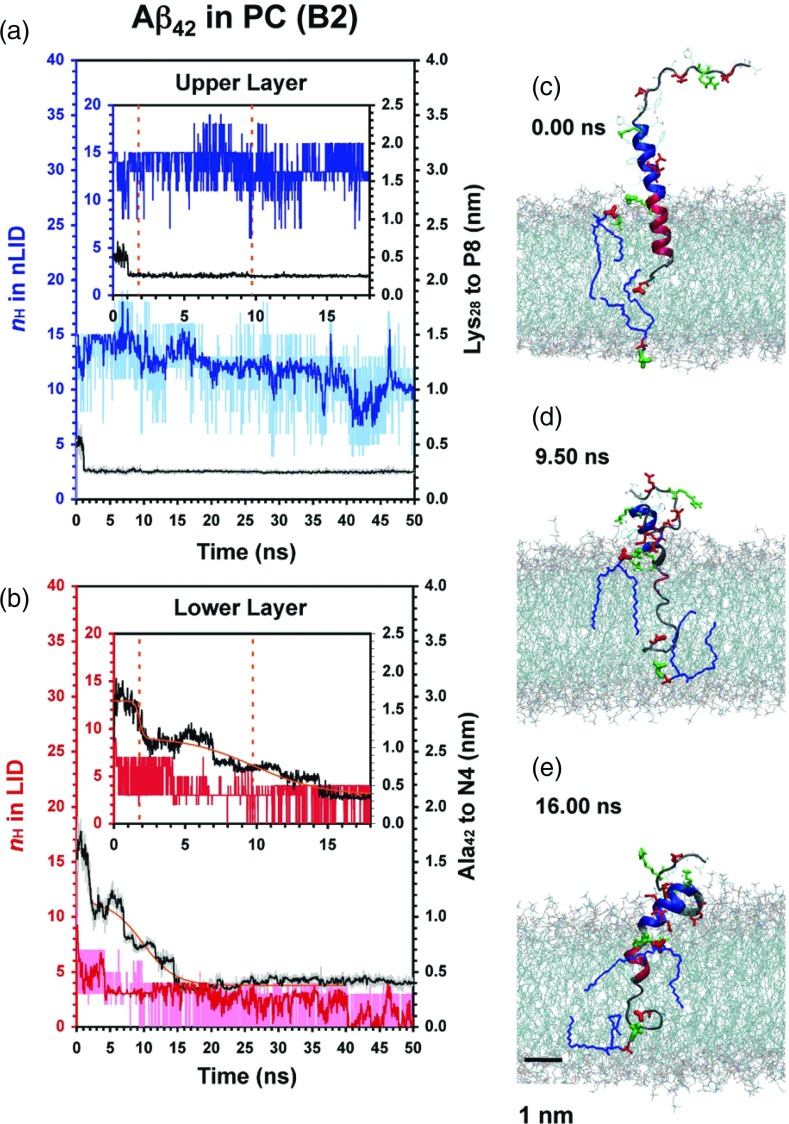
FIG. 3.
Protein conformational and site-specific protein-lipid dynamics for the relaxation of Aβ42 in PC. Similar to Figure 2 except the C-terminus motion is modeled by a 2-step sigmoidal function, Eq. (2).
FIG. 4.
Protein conformational and site-specific protein-lipid dynamics for folded Aβ42 in PC/CHOL. The minimum distance between Lys28 of Aβ42 to O6 of CHOL (green) in the extracellular lipid leaflet and the 2-step sigmoidal (Eq. (2)) fit of the Ala42-N4 kinetics are shown.
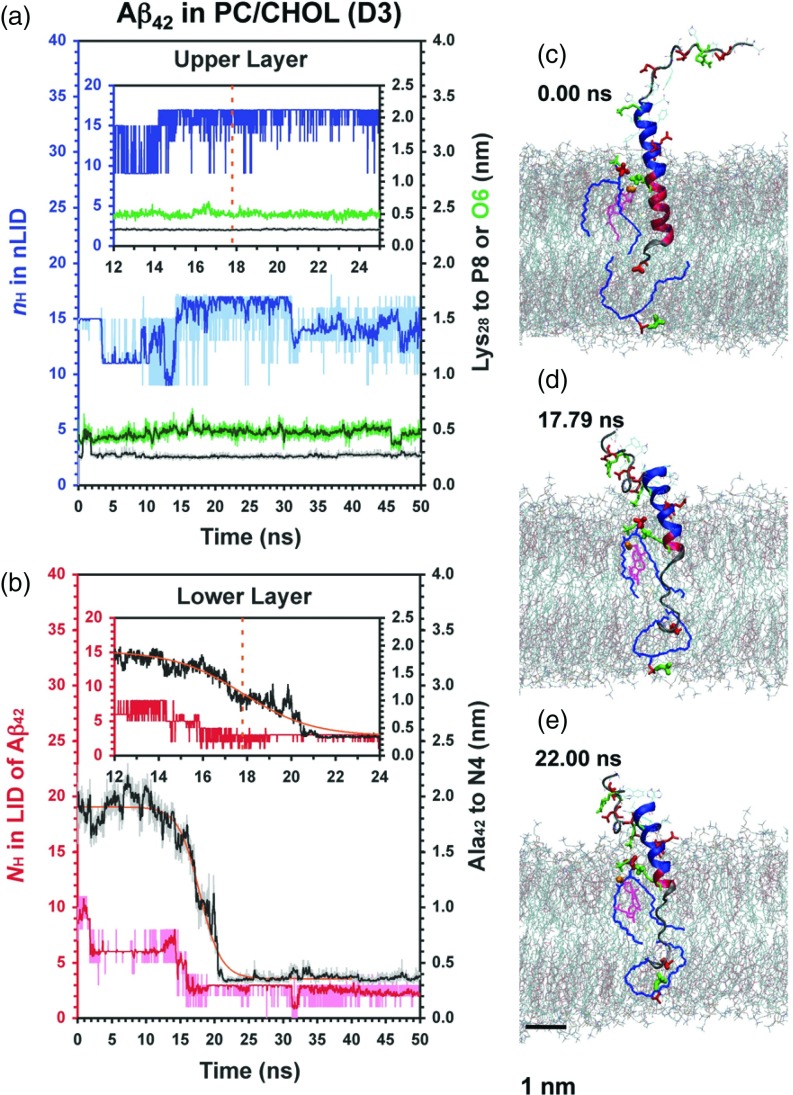
FIG. 5.
Protein conformational and site-specific protein-lipid dynamics for the unfolded relaxation of Aβ42 in PC/CHOL. The minimum distance between Lys28 of Aβ42 to O6 of CHOL (green) in the extracellular lipid leaflet and the 1-step sigmoidal (Eq. (1)) fit of the Ala42-N4 kinetics are shown.
As seen in Figures 2–5, it is clear that the entire hydrophobic LID of Aβ42 spanned the hydrophobic acyl chain region of the lipid bilayer, whereas some of the non-LID descended from the water phase and embedded to the polar region of the extracellular lipid leaflet. Interestingly, α-helix unfolding to various extents in the LID and non-LID was observed, although the non-LID remained essentially folded. For instance in B1 and B2 the LID substantially unfolded in B2 but remained largely folded in B1 (Figures 2 and 3). Similar observations for folded or unfolded peptides were found in other replicates as demonstrated in Figures S1 and S2 in the supplementary material.66
A. Residue-specific peptide interaction dynamics with the lipid headgroup
The 200 ns simulations contain rich temporal and structural information for both protein and lipid at 10 ps resolution. For the nine systems that underwent diffusion and anchoring of the C-terminus of Aβ across the lipid membrane, the process was complete within the first 50 ns and remained stable for the remaining 150 ns simulation. Consequently, only the first 50 ns of the 200 ns simulation are shown. The entire 200 ns trajectory is shown in the supplementary material.66 We extracted site-specific protein residue-to-lipid headgroup dynamics, focusing primarily on the LID of Aβ40 or Aβ42. During and after C-terminus diffusion, we observed that the negatively charged, deprotonated C-terminus, Ala40 or Val42, descended and anchored to the polar headgroup region of the cytofacial leaflet of the lipid bilayer, while the positively charged Lys28 side chain remained in close proximity to the polar headgroup region of the extracellular leaflet of the lipid bilayer (Figures 2–5). Once attached, the two charged LID terminal residues, Lys28 and C-terminus, remained attached to the extracellular and cytofacial leaflets of the lipid bilayer, respectively, throughout the entire 200 ns simulations.
The polar headgroups of PC and CHOL contain charged groups. At pH 7, the PC headgroup has a positive trimethyl-ammonium (N(CH3)3+) with an N4 nitrogen and a negative phosphate (PO4−) with a P8 phosphorous. In the lipid force field representation,38 the 3β O6 oxygen of cholesterol has a partial negative charge. Would the electrostatic interaction between the charged protein residues in the LID, Lys28, and C-terminus, and the opposite charged lipid headgroups promote anchoring and stabilize the transmembrane configuration of Aβ? To address this question, we examined the time evolution of the minimum distance (dmin) between the positively charged group of Lys28 or C-terminus residue of the LID of Aβ and the opposite charged lipid headgroup. Specifically, we measured the dmin of three charged pairs: Lys28-P8 in the extracellular lipid leaflet, Lys28-O6 in the extracellular lipid leaflet, and Val40/Ala42-N4 in the cytofacial leaflet. Representative results of replicates B1, B2, D1, and D3 are shown in Figures 2–5. The results for other replicates are given in Figures S1 and S2 in the supplementary material.66
In PC bilayers, Aβ42 exhibited fast motion with dmin of C-terminus to N4 decreasing from ∼1.7 to 0.35 nm in less than 0.5 ns for replicate B1 (Figure 2). In contrast, it took longer than 15 ns for replicate B2 (Figure 3). Similarly, in PC/CHOL bilayers, fast (replicate D1) and slow (replicate D3) diffusion of the Aβ42 C-terminus were observed, as illustrated in Figures 4 and 5, respectively. However, time lags of ∼5 and 15 ns occurred in replicate D1 and D3. A time lag was also observed in the replicates D2 and D4 as shown in Figure S2 in the supplementary material.66 Aβ40 showed identical behavior without a time lag in PC bilayer (replicate A1) and with a time lag in PC/CHOL bilayers (replicates C1 and C2), as shown in Figures S1 and S2 in the supplementary material.66
B. C-terminus kinetics of Aβ
The time evolution of dmin between the C-terminus and N4 exhibited one- or two-step sigmoidal decay behavior, as shown in Figures 2–5. Eqs. (1) and (2) were used to fit the dmin of the C-terminus to N4 for all 9 replicates, with the parameters, (hi, hf, τ, and k) and (hi, h′, hf, τ1, τ2, k1, and k2) determined by using nonlinear regression. For replicates B2 and D1, the two-step sigmoidal decay fit Eq. (2) provided a significant improvement over the one-step sigmoidal fit. The other replicates were better described by the one-step sigmoidal fit Eq. (1). Detailed description of the data fitting and the resulting parameters for B2 and D1 are given in the supplementary material.66
A useful residue-specific protein-lipid interaction parameter can be determined from the fit: VMAX, defined as the maximum velocity of the C-terminus. VMAX is determined from the time derivatives of Eq. (1) or (2). For the one-step sigmoidal decay,
| (3) |
For a general two-step sigmoidal decay, expressions for determining the two maximum velocities, V1,MAX and V2,MAX, are complicated. However, for the case where the two sigmoidal decays are well separated, as they were here, these two velocities simplify to approximately (hi – h′)k1/4 and (h′ − hf)k2/4, respectively. The maximum velocity is associated with the diffusion of the C-terminus through the lipid acyl chain region. A summary of the fitted parameters is given in Table I. It is interesting to note that the values of VMAX varied over three orders of magnitude: from 0.08 nm/ns for replicate B2 to 11.4 nm/ns for replicate D1.
C. Conformational transitions in LID and non-LID
The conformational transition kinetics of Aβ in two different domains, LID and non-LID, as quantified by nH, were determined as a function of time. There were determined for the first 25 ns for each of the 9 replicates that exhibited C-terminus anchoring in the cytofacial leaflet. Figures 2–5 show representative nH vs. time plots for Aβ42 in PC and PC/CHOL, in both LID and non-LID domains of the protein. The nH kinetics of other replicates are given in the supplementary material.66
As shown in Figures 2–5 and Figures S1 and S2 in the supplementary material,66 a striking feature of the protein conformation plots is that for the replicates exhibiting fast C-terminus motion, nH of the LID was significantly larger than those exhibiting slower motion. For example, in Figures 2 and 3, compare the predominantly helical B1 replicate with the predominantly unfolded B2 replicate. To quantify these differences, we define a dimensionless measure of the conformation, the mean fractional helical content, θH(τ) = nH(τ)/nH(0); the number of helices at time τ divided by the mean number of helices over the first 100 ps. This quantity was determined for each replicate. For example, θH(τ) (mean ± standard error of the mean) of was 0.98 ± 0.01 for D1 but 0.27 ± 0.01 for D3 as shown in Table II. On the other hand, the θH(τ) of the non-LID domain was largely unaffected. Fluctuations in the non-LID nH were smaller for the replicates exhibiting fast C-terminus motion than for those exhibiting slow motion, as shown in Table II.
Table II.
Protein secondary structure at τ for Aβ40 and Aβ42 in PC or PC/CHOL bilayers.
| Aβ in lipid | Replicate | τa (ns) | nH(τ) in the non-LIDb | θH(τ) in the non-LIDc | nH(τ) in the LIDb | θH(τ) in the LIDc |
|---|---|---|---|---|---|---|
| Aβ40 in PC | A0 | 13 | 1 | 9 | 1 | |
| A1 | 0.20 | 13.0 ± 0.00 | 1.00 ± 0.00 | 8.09 ± 0.16 | 0.89 ± 0.02 | |
| Aβ42 in PC | B0 | 15 | 1 | 10 | 1 | |
| B1 | 0.17 | 15.0 ± 0.00 | 1.00 ± 0.00 | 9.36 ± 0.24 | 0.94 ± 0.02 | |
| B2 | 9.76 | 12.5 ± 0.39 | 0.83 ± 0.03 | 2.25 ± 0.39 | 0.26 ± 0.04 | |
| Aβ40 in PC/CHOL | C0 | 13 | 1 | 9 | 1 | |
| C1 | 3.49 | 11.5 ± 0.37 | 0.88 ± 0.03 | 6.73 ± 0.33 | 0.75 ± 0.04 | |
| C2 | 7.57 | 12.7 ± 0.27 | 0.98 ± 0.02 | 5.91 ± 0.16 | 0.66 ± 0.02 | |
| Aβ42 in PC/CHOL | D0 | 15 | 1 | 10 | 1 | |
| D1 | 4.89 | 14.8 ± 0.12 | 0.99 ± 0.01 | 9.82 ± 0.12 | 0.98 ± 0.01 | |
| D2 | 1.90 | 12.0 ± 0.47 | 0.80 ± 0.03 | 6.50 ± 0.37 | 0.65 ± 0.04 | |
| D3 | 17.8 | 16.8 ± 0.18 | 1.12 ± 0.01 | 2.73 ± 0.14 | 0.27 ± 0.01 | |
| D4 | 1.04 | 15.0 ± 0.07 | 1.00 ± 0.01 | 8.67 ± 0.29 | 0.87 ± 0.03 |
τ, the half-time for the C-terminus to diffuse from its initial location to its anchor site is found from Aβ from the sigmoidal fit (Eq. (1) or Eq. (2)).
Number of helices (nH(τ)) in the non-LID (Asp-1 to Asn-27) or LID region (Lys-28 to C-terminus) of Aβ at τ.
Fractional helical content (θH(τ) = nH(τ)/ nH(0)) in the non-LID or LID region of Aβ at τ. Here nH(0) is the initial number of helices before the simulations as given by the number listed in the A0-D0 row. All nH calculations (mean ± SE) were from the DSSP analysis averaged over the 100 ps centered at τ.
D. Correlation between the C-terminus velocity and protein conformation
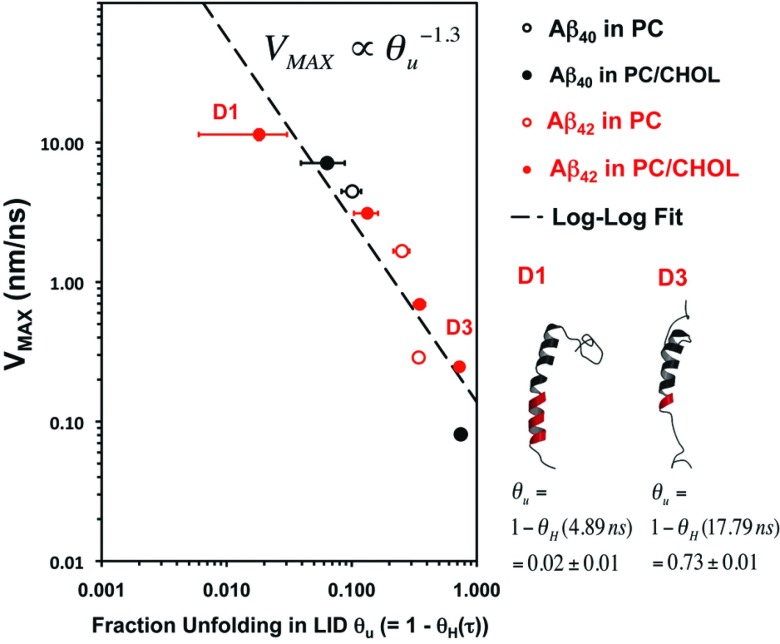
As shown in Figure 6, fast C-terminus motion only occurred when the LID conformation was primarily helical, with minimal unwinding of the LID. As the helical content θH(τ) decreased, so did the VMAX, maximum C-terminus velocity. No correlation was found between the helical content of the non-LID and VMAX. Our data, therefore, suggest that helix to coil transition of residues near the C-terminus decreases VMAX. To further quantify this relationship, we plotted VMAX against the fraction of the LID unfolding (θu), where θu is defined as (1 − θH(τ)). This relationship is plotted in log-log form in Figure 6. Results from the nine replicates in which C-terminus translation was appreciable are shown in this plot. A linear correlation was observed that suggested that VMAX scales with θu−1.3. Separate log-log plots for Aβ in PC and PC/CHOL (Figure S4 in the supplementary material66) suggest a scaling of θu −2.0 and θu −1.3, respectively. However, only three measurements for PC are available as compared to six for PC/CHOL.
FIG. 6.
Maximum velocity of the C-terminus vs. fraction unfolding in the LID of Aβ. The VMAX vs. θu plot for Aβ40 (black) and Aβ42 (red) in PC (open circles) and PC/CHOL (filled circles) bilayers are shown. θu is defined as (1 − θH(τ)), as shown in Table II. The horizontal bar indicates the standard error of the mean over 100 ps at τ. The secondary structures of the non-LID (black ribbon) and LID (red ribbon) of two simulation replicates D1 and D3 are also illustrated.
The scaling suggested above may not apply to other cholesterol concentrations. In the present case few measurements of CHOL free membranes were collected, therefore there is statistical uncertainty in the scaling parameters. Furthermore, the physical properties of cholesterol containing lipid membranes can show abrupt changes at specific cholesterol concentration,50,51 therefore it is possible that scaling could exhibit discrete values and nonlinear behavior with cholesterol concentration. The significance of the difference in the scaling index between CHOL containing and pure POPC, shown in the supplementary material,66 needs further verification, not only in the number of measurements but also in the CHOL content of the membrane and the simulation time scale. Despite the insight provided by the scaling interpretation, the effect of cholesterol on membrane peptide dynamics is still unknown.
IV. DISCUSSION
Protein conformational transition (nH versus time) and C-terminus characteristic velocity (VMAX) revealed VMAX varied more than three orders of magnitude in VMAX. Unfolded Aβ exhibits lower VMAX. We suggest this behavior is caused by unfolded peptide side-chains and backbone interacting with the surrounding non-polar lipid matrix. To better understand this process we compared the C-terminus velocity to that expected for the relaxation of a bead-spring oligomer; we consider the resistance of peptide units translation in the lipid membrane to be similar to the frictional drag on the beads of a diffusing bead-spring model polymer. This interpretation was suggested by VMAX scaling with θu−1.3, which is suggestive of polymer bead-chain relaxation.
The α-helix content of the non-LID remained relatively constant throughout the relaxation process and did not affect the conformation of the LID. The distance moved by the C-terminus (hi-hf) in Table I is relatively constant so we can consider 1/VMAX as a measure of the fastest relaxation time, τ, of the unfolding polymeric peptide chain. Since the length L of the unfolded chain is characterized by θu, the C-terminus velocity scales like τ ∝ L1.3. For a Zimm bead-spring model of a relaxing single polymer, Quake52 showed that the lowest order (effectively two beads connected by a spring) relaxation mode for a short polymer follows Zimm scaling, τ ∝ L3/2. The unfolded peptide chain in our case shows slightly less length dependence, possibly because the chain is short. However, Zimm-like behavior suggests that during the fast part of the motion, the peptide-lipid interaction is confined to hydrodynamic friction on the peptide subunits rather than stronger specific electrostatic interactions.
If we consider the PC and PC/CHOL data separately (see the supplementary material66) we find that PC has a larger scaling coefficient of θu−2. This scaling suggests Rouse-like relaxation for which the polymer chain relaxes as τ ∝ L2.
The difference in the dynamics of the Rouse and Zimm models52,53 is in the description of the friction between the bead and the surrounding fluid. In the Rouse model, each bead interacts with the surrounding fluid independently, unaffected by hydrodynamic interactions with other beads; in the Zimm model the hydrodynamic interaction of one bead affects the friction of the surrounding beads.
An analogous process occurs for protein unfolding. In the disordered tail group region of the PC membrane memory of the passage of a residue is quickly erased by highly mobile, conforming lipid tails. The friction experienced by a residue of the chain is unaffected by the motion of its neighboring residues. However, in the ordered PC/CHOL environment, the ability of a PC tail to conform to a residue is reduced by interactions with the relatively stiff cholesterol molecule. As a result, the tail-group region retains a longer “memory” of the passage of a residue, so the motion of the previous residue affects the motion of each residue. Unfortunately, we lack a significant number of observations (n = 3) in the disordered PC (see the supplementary material66). More work is needed to confirm possible cholesterol regulation. However, the implication of bead-spring models describing protein motion is that the residue-lipid interaction is dominated by hydrodynamic friction, rather than by residue-specific chemical interactions.
The propensity of a helix to unfold and the strength of lipid-peptide interactions depend on force-field parameters. While the GROMOS force fields have undergone a number of revisions since the development of the modified GROMOS87/Berger lipids used here, comparative studies suggest the behavior seen here is reasonable. However, it should be noted that the lipid-peptide interactions are likely too strong. Kukol54 compared the behavior of several lipid force fields and found that the secondary structure and integrity of a transmembrane protein was similar for both the GROMOS87/Berger force field and the GROMOS96 53A6 field often used for recent lipid/protein field in common use. After 7 ns of simulation, the protein in the GROMOS87/Berger field did show greater root mean square deviation, suggesting the structure was somewhat less stable. Tieleman et al.55 found that the strength of lipid-protein interaction was overestimated by the combination of the modified GROMOS87/Berger field. The versions and the evolution of the GROMOS force field and its use for biological membranes have been discussed in several publications.42,55,56
Overestimating the lipid-protein interaction strength could affect the present study in two ways. First, increased interaction strength would increase the magnitude of the hydrodynamic friction. While this would affect the time scale of events, it would not affect the scaling relationship or the molecular interpretation of helix relaxation/lipid interactions. The second effect is that the helix could be less stable, which would increase the probability of the unfolded state. Unfolding and the unfolded state are discussed detail below. While the proportion of replicates experiencing unfolding, Table II, may be large, the degree to which a peptide in a given replicate unfolds does not appear unrealistic compared with the results of studies using other force fields.24–26,57,58 With respect to the scaling relationship, an increased population of unfolded states provides better sampling.
Protein unfolding sets a time-scale for membrane processes. The Aβ contains linked GxxxG motifs and Aβ42 contains an additional terminal GxxxA motif. These motifs are important in helix-helix association in the lipid membrane59,60 and their presence suggests a strong tendency for multiple proteins to associate in the membrane. If the unfolding is faster than association, then association will be less favorable and may be inhibited entirely.
Is unfolding energetically favorable? Some studies of model membrane-active peptides have indicated that unfolding of an alpha helix can be enthalpically unfavorably with an energy cost of ∼4–6 kcal/mol per each unfolded residue,61,62 resulting primarily from disruption of hydrogen bonding in the low dielectric membrane environment. However, other work has suggested the energy cost of unfolding may be much lower.63 The cost may also be offset by hydrogen bonding with water and lipid phosphates,64 such as that shown in Fig. 1. In this study we observed unfolded C-terminus diffusion to an anchor site in 5 of 9 replicates consisting of Aβ of different lengths and PC with and without cholesterol (Table I). We found there could be substantial unfolding of the LID of Aβ, with an average θH as low as 0.26 for replicate B2. This is equivalent to an average of 6.75 unfolded residues.
Unfolding can still be thermodynamically favorable. For the Aβ peptide the insertion domain, except for the C-terminus, is composed of amino acids that do not H-bond (GAILMV). Once Aβ is in the membrane the enthalpy cost of the peptide bond H-bond loss has been paid, and there is little additional energy cost of unfolding, since no additional bonds are lost. Furthermore, there can be a large entropy gain achieved in the process. The enthalpy cost could be compensated by the entropy increase resulting from protein unfolding and the subsequent rearrangement of the lipid around the disordered protein has been estimated from 1.25 kcal/mol to >6.25 kcal/mol per peptide bond.61,65 Unfolded penetration of the similar model protein WALP-16 into a lipid bilayer, and the calculation of the enthalpic and entropic contributions to the free energy of the system, have been demonstrated.65
After unfolding, residue-specific protein/lipid interactions are crucial for maintaining the inserted state of the protein. The molecular mechanisms that stabilize the unfolded Aβ penetration can be inferred from the residue-specific lipid/protein interaction kinetics in this work. A “binding” pattern was observed for Lys28-to-P8 and Lys28-to-O6 in the extracellular lipid leaflet and for C-terminus-to-N4 in the cytofacial leaflet. It appears that the molecular mechanism for the stabilization of the inserted Aβ is associated with lysine snorkeling with the long arm of Lys28 attached to the P8 of PC or the O6 of cholesterol in the extracellular lipid leaflet and a C-terminus anchoring to the N4 of PC in the cytofacial lipid leaflet. We conclude that this dual attachment mechanism involving both lipid leaflets stabilized the inserted Aβ throughout the entire 200 ns of all the nine folded and unfolded penetration events found in this work. While lysine snorkeling helps stabilize the inserted state it might not be required to promote penetration.
The anchoring of the Aß C-terminus to the cytofacial membrane interface has been seen in some simulations24,26 but other conformations are common. Simulations addressing inserted Aß as the initial state show a wide range of behavior from anchoring to the extracellular membrane interface,24,27,28 to ejection from the membrane.26,31 However, few simulations26 have addressed Aß interactions with membranes composed of CHOL and unsaturated lipids. Indeed, we see anchoring in only 3 of 8 cases for membranes that do not contain CHOL. Lack of observation of anchoring may be the result of sampling statistics, the effect of membrane lipid composition, or the position of initial state.
Some fast, folded penetration events like the A1 and B1 showed no lysine snorkeling until tens of nanoseconds after anchoring was completed.66 A stable membrane inserted state would keep the protein in a vertical orientation and prohibit it from migrating to the surface in a parallel orientation, membrane surface state.
ACKNOWLEDGMENTS
This work was supported by the Robert A. Welch Research Foundation grant (D-1158), NIH (Grant No. GM090897-02), and Williams Endowment of Trinity University.
REFERENCES
- 1.Cohen F. E. and Kelly J. W., Nature (London) 426, 905 (2003). 10.1038/nature02265 [DOI] [PubMed] [Google Scholar]
- 2.Groves J. T. and Kuriyan J., Nat. Struct. Mol. Biol. 17, 659 (2010). 10.1038/nsmb.1844 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Peetla C., Stine A., and Labhasetwar V., Mol. Pharm. 6, 1264 (2009). 10.1021/mp9000662 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Selkoe D. J., Neuron 6, 487 (1991). 10.1016/0896-6273(91)90052-2 [DOI] [PubMed] [Google Scholar]
- 5.Coles M., Bicknell W., Watson A. A., Fairlie D. P., and Craik D. J., Biochemistry 37, 11064 (1998). 10.1021/bi972979f [DOI] [PubMed] [Google Scholar]
- 6.Qiu L., Buie C., Reay A., Vaughn M. W., and Cheng K. H., J. Phys. Chem. B 115, 9795 (2011). 10.1021/jp2012842 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ulmschneider J. P., Smith J. C., White S. H., and Ulmschneider M. B., J. Am. Chem. Soc. 133, 15487 (2011). 10.1021/ja204042f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wickner W. and Schekman R., Science 310, 1452 (2005). 10.1126/science.1113752 [DOI] [PubMed] [Google Scholar]
- 9.Schatz G. and Dobberstein B., Science 271, 1519 (1996). 10.1126/science.271.5255.1519 [DOI] [PubMed] [Google Scholar]
- 10.Bechtluft P., van Leeuwen R. G., Tyreman M., Tomkiewicz D., Nouwen N., Tepper H. L., Driessen A. J., and Tans S. J., Science 318, 1458 (2007). 10.1126/science.1144972 [DOI] [PubMed] [Google Scholar]
- 11.White S. H. and von Heijne G., Annu. Rev. Biophys. 37, 23 (2008). 10.1146/annurev.biophys.37.032807.125904 [DOI] [PubMed] [Google Scholar]
- 12.Butterfield S. M. and Lashuel H. A., Angew. Chem., Int. Ed. Engl. 49, 5628 (2010). 10.1002/anie.200906670 [DOI] [PubMed] [Google Scholar]
- 13.Williams T. L. and Serpell L. C., FEBS J. 278, 3905 (2011). 10.1111/j.1742-4658.2011.08228.x [DOI] [PubMed] [Google Scholar]
- 14.Gadad B. S., Britton G. B., and Rao K. S., J. Alzheimers Dis. 24, 223 (2011). 10.3233/JAO-2011-110182 [DOI] [PubMed] [Google Scholar]
- 15.Haass C. and Selkoe D. J., Nat. Rev. Mol. Cell Biol. 8, 101 (2007). 10.1038/nrm2101 [DOI] [PubMed] [Google Scholar]
- 16.Kayed R., Head E., Thompson J. L., McIntire T. M., Milton S. C., Cotman C. W., and Glabe C. G., Science 300, 486 (2003). 10.1126/science.1079469 [DOI] [PubMed] [Google Scholar]
- 17.Urbanc B., Betnel M., Cruz L., Bitan G., and Teplow D. B., J. Am. Chem. Soc. 132, 4266 (2010). 10.1021/ja9096303 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Marchesi V. T., Proc. Natl. Acad. Sci. U.S.A. 102, 9093 (2005). 10.1073/pnas.0503181102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bucciantini M., Giannoni E., Chiti F., Baroni F., Formigli L., Zurdo J., Taddei N., Ramponi G., Dobson C. M., and Stefani M., Nature (London) 416, 507 (2002). 10.1038/416507a [DOI] [PubMed] [Google Scholar]
- 20.Ross C. A. and Poirier M. A., Nat. Med. 10(Suppl), S10 (2004). 10.1038/nm1066 [DOI] [PubMed] [Google Scholar]
- 21.Lingwood D. and Simons K., Science 327, 46 (2010). 10.1126/science.1174621 [DOI] [PubMed] [Google Scholar]
- 22.Ji S. R., Wu Y., and Sui S. F., J. Biol. Chem. 277, 6273 (2002). 10.1074/jbc.M104146200 [DOI] [PubMed] [Google Scholar]
- 23.Okada T., Wakabayashi M., Ikeda K., and Matsuzaki K., J. Mol. Biol. 371, 481 (2007). 10.1016/j.jmb.2007.05.069 [DOI] [PubMed] [Google Scholar]
- 24.Lemkul J. A. and Bevan D. R., Arch. Biochem. Biophys. 470, 54 (2008). 10.1016/j.abb.2007.11.004 [DOI] [PubMed] [Google Scholar]
- 25.Lemkul J. A. and Bevan D. R., FEBS J. 276, 3060 (2009). 10.1111/j.1742-4658.2009.07024.x [DOI] [PubMed] [Google Scholar]
- 26.Lemkul J. A. and Bevan D. R., Protein Sci. 20, 1530 (2011). 10.1002/pro.678 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Davis C. H. and Berkowitz M. L., J. Phys. Chem. B 113, 14480 (2009). 10.1021/jp905889z [DOI] [PubMed] [Google Scholar]
- 28.Davis C. H. and Berkowitz M. L., Biophys. J. 96, 785 (2009). 10.1016/j.bpj.2008.09.053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Davis C. H. and Berkowitz M. L., Proteins 78, 2533 (2010). 10.1002/prot.22763 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhou X. and Xu J., PLoS One 7, e46245 (2012). 10.1371/journal.pone.0046245 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Xu Y., Shen J., Luo X., Zhu W., Chen K., Ma J., and Jiang H., Proc. Natl. Acad. Sci. U.S.A. 102, 5403 (2005). 10.1073/pnas.0501218102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zhu Q., Cheng K. H., and Vaughn M. W., J. Phys. Chem. B 111, 11021 (2007). 10.1021/jp070487z [DOI] [PubMed] [Google Scholar]
- 33.Bekker H., Berendsen H. J. C., Dijkstra E. J., Achterop S., van Drunen R., van der Spoel D., Sijbers A., Keegstra H., Reitsma B., and Renardus M. K. R., in Physics Computing 92 (World Scientific, Singapore, 1993). [Google Scholar]
- 34.Berendsen H. D., van der Spoel D., and van Drunen R., Comput. Phys. Commun. 91, 43 (1995). 10.1016/0010-4655(95)00042-E [DOI] [Google Scholar]
- 35.Lindahl E., Hess B., and van der Spoel D., J. Mol. Model. 7, 306 (2001). 10.1007/s008940100045 [DOI] [Google Scholar]
- 36.Van Der Spoel D., Lindahl E., Hess B., Groenhof G., Mark A. E., and Berendsen H. J., J. Comput. Chem. 26, 1701 (2005). 10.1002/jcc.20291 [DOI] [PubMed] [Google Scholar]
- 37.Berger O., Edholm O., and Jahnig F., Biophys. J. 72, 2002 (1997). 10.1016/S0006-3495(97)78845-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Holtje M., Forster T., Brandt B., Engels T., von Rybinski W., and Holtje H. D., Biochim. Biophys. Acta 1511, 156 (2001). 10.1016/S0005-2736(01)00270-X [DOI] [PubMed] [Google Scholar]
- 39.van Buuren A. R., Marrink S. J., and Berendsen H. J. C., J. Phys. Chem. 97, 9206 (1993). 10.1021/j100138a023 [DOI] [Google Scholar]
- 40.van der Spoel D., van Buuren A. R., Tieleman D. P., and Berendsen H. J. C., J. Biomol. NMR 8, 229 (1996). 10.1007/BF00410322 [DOI] [PubMed] [Google Scholar]
- 41.Piggot T. J., Piñeiro A., and Khalid S., J. Chem. Theory Comput. 8, 4593 (2012). 10.1021/ct3003157 [DOI] [PubMed] [Google Scholar]
- 42.Poger D. and Mark A. E., J. Chem. Theory Comput. 8, 4807 (2012). 10.1021/ct300675z [DOI] [PubMed] [Google Scholar]
- 43.Pan J., Tieleman D. P., Nagle J. F., Kucerka N., and Tristam-Nagle S., Biochem. Biophys. Acta 1788, 1387 (2009). 10.1016/j.bbamem.2009.02.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Berendsen H. J. C., Postma J. P. M., van Gunsteren W. F., and Hermans J., in Intermolecular Forces, edited by Pullman B. (Reidel, Dordrecht, The Netherlands, 1981), p. 331. [Google Scholar]
- 45.Darden T., York D., and Pedersen L., J. Chem. Phys. 98, 10089 (1993). 10.1063/1.464397 [DOI] [Google Scholar]
- 46.Essmann U., Perera L., Berkowitz M. L., Darden T., Lee H., and Pedersen L., J. Chem. Phys. 103, 8577 (1995). 10.1063/1.470117 [DOI] [Google Scholar]
- 47.Hess B., Bekke H., Berendsen H. J. C., and Fraaije J. G. E. M., J. Comput. Chem. 13, 1463 (1997). [Google Scholar]
- 48.Bussi G., Donadio D., and Parrinello M., J. Chem. Phys. 126, 014101 (2007). 10.1063/1.2408420 [DOI] [PubMed] [Google Scholar]
- 49.Berendsen H. J. C., Postma J. P. M., van Gunsteren W. F., DiNola A., and Haak J. R., J. Chem. Phys. 81, 3684 (1984). 10.1063/1.448118 [DOI] [Google Scholar]
- 50.Qiu L., Lewis A., Como J., Vaughn M. W., Huang J., Somerharju P., Virtanen J., and Cheng K. H., Biophys. J. 96, 4299 (2009). 10.1016/j.bpj.2009.02.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Somerharju P., Virtanen J. A., Cheng K. H., and Hermansson M., Biochim. Biophys. Acta 1788, 12 (2009). 10.1016/j.bbamem.2008.10.004 [DOI] [PubMed] [Google Scholar]
- 52.Quake S. R., J. Chem. Phys. 101, 4307 (1994). 10.1063/1.467480 [DOI] [Google Scholar]
- 53.Lisy V., Tothova J., and Zatovsky A. V., J. Chem. Phys. 121, 10699 (2004). 10.1063/1.1809587 [DOI] [PubMed] [Google Scholar]
- 54.Kukol A., J. Chem. Theory Comput. 5, 615 (2009). 10.1021/ct8003468 [DOI] [PubMed] [Google Scholar]
- 55.Tieleman D. P., Justin L. M., Walter L. A., Christian K., Zhitao X., and Luca M., J. Phys.: Condens. Matter 18, 1221 (2006). 10.1088/0953-8984/18/28/S07 [DOI] [Google Scholar]
- 56.Poger D., van Gunsteren W. F., and Mark A. E., J. Comput. Chem. 31, 1117 (2010). 10.1002/jcc.21396 [DOI] [PubMed] [Google Scholar]
- 57.Pannuzzo M., Milardi D., Raudino A., Karttunen M., and La Rosa C., Phys. Chem. Chem. Phys. 15, 8940 (2013). 10.1039/c3cp44539a [DOI] [PubMed] [Google Scholar]
- 58.Poojari C., Kukol A., and Strodel B., Biochim. Biophys. Acta 1828, 327 (2013). 10.1016/j.bbamem.2012.09.001 [DOI] [PubMed] [Google Scholar]
- 59.Russ W. P. and Engelman D. M., J. Mol. Biol. 296, 911 (2000). 10.1006/jmbi.1999.3489 [DOI] [PubMed] [Google Scholar]
- 60.Curran A. R. and Engelman D. M., Curr. Opin. Struct. Biol. 13, 412 (2003). 10.1016/S0959-440X(03)00102-7 [DOI] [PubMed] [Google Scholar]
- 61.Engelman D. M., Steitz T. A., and Goldman A., Annu. Rev. Biophys. Biophys. Chem. 15, 321 (1986). 10.1146/annurev.bb.15.060186.001541 [DOI] [PubMed] [Google Scholar]
- 62.White S. H. and Wimley W. C., Annu. Rev. Biophys. Biomol. Struct. 28, 319 (1999). 10.1146/annurev.biophys.28.1.319 [DOI] [PubMed] [Google Scholar]
- 63.Joh N. H., Min A., Faham S., Whitelegge J. P., Yang D., Woods V. L., and Bowie J. U., Nature (London) 453, 1266 (2008). 10.1038/nature06977 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Jaud S., Fernandez-Vidal M., Nilsson I., Meindl-Beinker N. M., Hubner N. C., Tobias D. J., von Heijne G., and White S. H., Proc. Natl. Acad. Sci. U.S.A. 106, 11588 (2009). 10.1073/pnas.0900638106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Nymeyer H., Woolf T. B., and Garcia A. E., Proteins 59, 783 (2005). 10.1002/prot.20460 [DOI] [PubMed] [Google Scholar]
- 66. See supplementary material at http://dx.doi.org/10.1063/1.4902229E-JCPSA6-141-016445 for protein conformation and site-specific protein-lipid interaction dynamics for the folded and unfolded interactions from other five simulation replicates (A1, C1, C2, D2, and D4), a demonstration of the 1- and 2-step sigmoidal fits for replicates B2 and D1, and separate log-log plots of relaxation data.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1063/1.4902229E-JCPSA6-141-016445 for protein conformation and site-specific protein-lipid interaction dynamics for the folded and unfolded interactions from other five simulation replicates (A1, C1, C2, D2, and D4), a demonstration of the 1- and 2-step sigmoidal fits for replicates B2 and D1, and separate log-log plots of relaxation data.