Abstract
Most work on the dynamic response of red blood cells (RBCs) to hydrodynamic stress has focused on linear velocity profiles. Relatively little experimental work has examined how individual RBCs respond to pressure driven flow in more complex geometries, such as the flow at the entrance of a capillary. Here, we establish the mechanical behaviors of healthy RBCs undergoing a sudden increase in shear stress at the entrance of a narrow constriction. We pumped RBCs through a constriction in a microfluidic device and used high speed video to visualize and track the flow behavior of more than 4400 RBCs. We show that approximately 85% of RBCs undergo one of four distinct modes of motion: stretching, twisting, tumbling, or rolling. Intriguingly, a plurality of cells (∼30%) exhibited twisting (rotation around the major axis parallel to the flow direction), a mechanical behavior that is not typically observed in linear velocity profiles. We present detailed statistical analyses on the dynamics of each motion and demonstrate that the behavior is highly sensitive to the location of the RBC within the channel. We further demonstrate that the observed tumbling, twisting, and rolling rotations can be rationalized qualitatively in terms of rigid body mechanics. The detailed experimental statistics presented here should serve as a useful resource for modeling of RBC behavior under physiologically important flow conditions.
I. INTRODUCTION
The proper circulation of blood, and its effectiveness in gas exchange and nutrient delivery, are strongly affected by hemorheological properties within the intricate microvascular network. At the length scales of capillaries (∼2–10 μm), the multiphase nature of blood plays a significant role in determining its fluidity and behavior.1,2 Accordingly, many investigators have examined red blood cells (RBCs) in simple shear flow and have reported a rich spectrum of RBC motions including stretching,3,4 tumbling,4 tank treading (TT),3 and swinging.5 The observed motions are largely dependent on the cell mechanical properties and the orientation and magnitude of the applied forces. Early experiments by Goldsmith and co-workers4,6–9 focused on the ratio (λ) of the intracellular viscosity to the viscosity of suspending fluid as the physical parameter dictating RBC behavior.3,4 At low λ, RBCs exhibited end-over-end rotation and tumbling; at high λ, the RBCs behaved more like a fluid drop and exhibited tank treading, with the membrane rotating around the center of mass of the cell. The analytical model by Keller and Skalak (KS model)10 was based on these observations, treating the RBC as a viscous ellipsoid capsule to capture both tumbling and tank treading behaviors. More recent experiments have revealed new modes of RBC motion that are not captured by the KS model. For example, RBCs have been shown to display shape memory11 and exhibit motions such as swinging5 and rolling.12–14 These motions have been interpreted in terms of the elasticity and stored energy in the membrane,12,15 and modifications to the KS model by Abkarian, Faivre, and Viallat5 and Skotheim and Secomb16 (the AFV-SS model) now recognize an elastic component that contributes to mode transition. While the model takes into account both the viscous and elastic components, recent work by Dupire et al.12 suggests that the shear elasticity is a key determinant of RBC deformation, motion, and orientation.
Notably, all of the above experimental work focused on simple linear velocity profiles, but RBCs in vivo frequently undergo many reversible deformations and encounter drastic variations in hydrodynamic shear stress.17 Of particular importance is flow into a contraction, which occurs physiologically during passage into capillaries and occurs pathologically in cases such as stenoses and aneurysms. In this geometry, the RBCs are exposed to a sudden increase in applied shear, and RBCs are now acknowledged to sense and respond to changes in hydrodynamic shear stress.18–20 A large body of work indicates that RBCs release adenosine 5′-triphosphate (ATP) into the extracellular space in response to changes in decreased dissolved oxygen or increased shear stress. The ATP acts as a signaling molecule to induce vasodilation of the nearby smooth muscle cells, thereby increasing the capillary diameter and corresponding blood flow rate.18–20 Wan et al.21 used a microfluidic constriction to examine the dynamics of ATP mechanotransduction; a high speed camera visualized the RBC motions, while a photoluminescent assay yielded ATP concentration as a function of position downstream from the constriction. Their work strongly suggested that ATP mechanotransduction is triggered by the subsequent relaxation of the RBC membrane rather than the initial deformation. Since then, RBC behavior in constricting channels has been investigated by several other groups21–28 and motions such as stretching,21–28 relaxing,21,22 flipping and rolling24 have been observed experimentally in healthy cells upon entering a constriction. Forsyth et al.22 further examined the contributions of intracellular viscosity to RBC dynamic motion entering a constriction by treating cells with chemical stiffening agents. They reported motions such as stretching, tumbling, and recoiling. Notably, they found that stiffening the cytosol (i.e., increasing the intracellular viscosity) strongly altered the frequency of occurrence of each motion, while stiffening only the membrane had little effect. More recent work by Forsyth et al.29 in simple linear shear conditions suggests that ATP release occurs in deformation dependent and deformation independent regimes. Specifically, their results suggest that tumbling (associated with minimal cellular deformation) and stretching motions elicited ATP release, while tank treading did not have an appreciable effect.
A key limitation of these previous studies is that the measured RBC motions were limited to small sample populations of cells, with analysis restricted to RBCs that happened to pass exactly down the center of the channel. For example, Wan et al.21 correlated visual observations of approximately 20 cells at the center of the channel to the photoluminescent ATP signal obtained from many thousands of cells. It is unclear if the small subset of cells is truly representative of the majority of RBCs; nor it is clear what fraction of the cells pass down the center of the channel.21,22 Goldsmith and previous researchers4,6–9 focused on RBCs in either tube flow or linear velocity profiles, and the behavior of cells entering constrictions is not well understood. In addition, the dynamics of these behaviors, which have time scales on the order of a few milliseconds, must be examined. Likewise, the relative fractions of RBCs exhibiting distinct behaviors and the corresponding contributions of each behavior type to the cumulative ATP release have not been established to date.
Here, we present experimental observations of the dynamic mechanical response of RBCs upon entering a narrow constriction in a microfluidic device. In contrast to previous work, we used high speed video to visualize and track the motion of RBCs across the entire channel cross-section, ultimately tracking over 4400 individual RBCs obtained from five healthy individuals. A custom image analysis program automatically extracted quantitative measurements for each cell to characterize the velocity, deformation, rotation, and type of motion. We report, for healthy RBCs, that the four main behaviors are stretching, twisting, tumbling, and rolling. The most prominent behavior exhibited was twisting, i.e., rotation about the axis parallel to flow. This motion was observed in approximately 30% of the RBCs, but is not typically seen in simple linear shear or microfluidic experiments. We present detailed quantitative measurements for each behavior and analyze how the dynamics are affected by channel region and linear velocity. Finally, we examine the mechanical origin of the observed rotations using, as a limiting case, the equations of motion for rigid ellipsoids, and we demonstrate that the rotating motions are qualitatively consistent with rigid body theory. Our experimental results and detailed statistics should prove useful for testing simulation efforts in more complex but physiologically relevant geometries, and ultimately provide insight on shear-induced ATP mechanotransduction from RBCs.
II. MATERIALS AND METHODS
A. RBC and solution preparation
Human RBCs were extracted from individual healthy donors volunteering for research studies at the Western Health Nutrition Research Center (WHNRC) located on campus at U.C. Davis. The blood was drawn by collaborators at WHNRC under pre-approved Institutional Review Board (IRB) plans that allow excess RBCs to be used for secondary use. The RBCs were separated from plasma by centrifuging 5 ml of blood at 1200 rpm at 20 °C for 4 min. The supernatant and buffy coats were removed by aspiration, and the packed RBCs were subsequently washed three times in physiological salt solution (PSS) buffer. The PSS solution was prepared according to the standard protocol by Price et al.:30 4.7 mM KCl, 2.0 mM CaCl2, 1.2 mM MgSO4, 140.5 mM NaCl, 21.0 mM tris(hydroxymethyl)amino-methane, and 11.1 mM dextrose; the pH was adjusted to 7.4 using 1 M HCl. The RBCs were then diluted to obtain a 0.5% Hct solution by adding PSS buffer. The low Hct of RBCs was necessary for observations of individual cells in the microchannel. The re-suspended RBC solution was kept at room temperature (∼25 °C) for at least 30 min to ensure constant temperature between samples. All measurements were taken within 12 h of the blood draw to prevent reduced deformation associated with storage.31
B. Microfluidic platform: Fabrication and operation
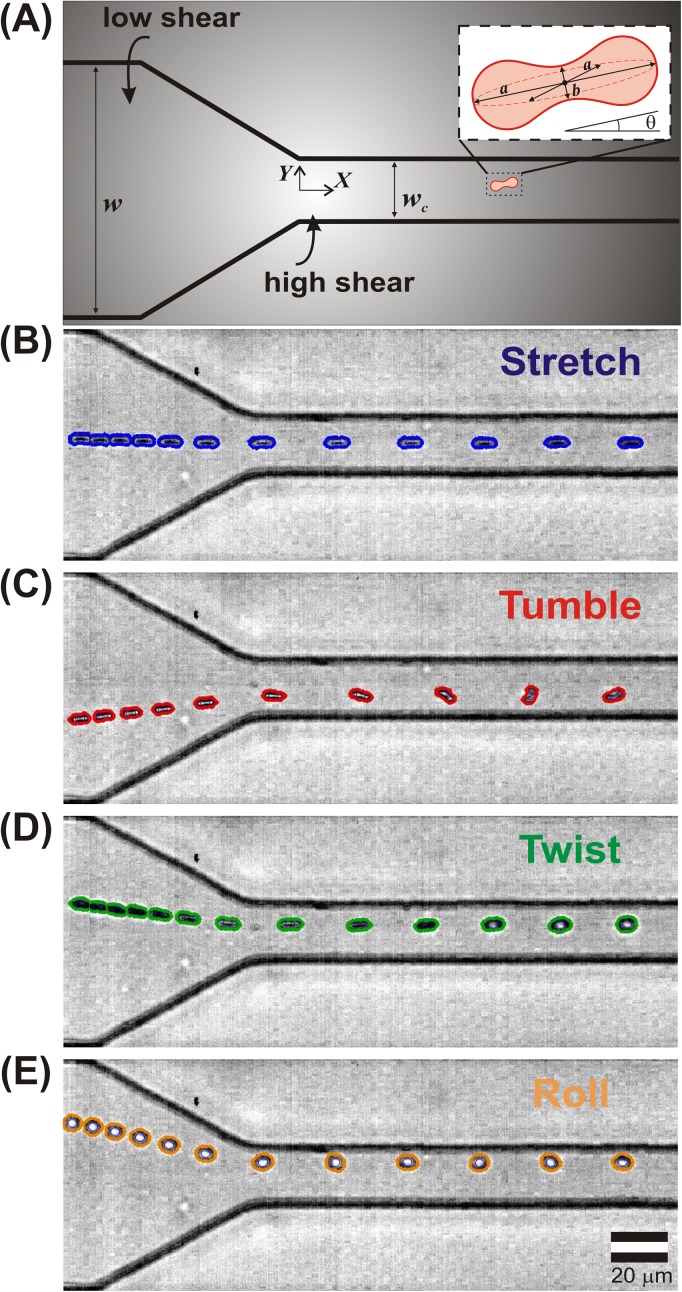
Our experimental setup utilized a microfluidic device similar to that developed by Wan et al.,21 which imposes a precisely defined change in shear stress on the RBCs via a rapid reduction in channel width. We utilized standard soft photolithographic techniques developed by Duffy et al.32 to fabricate microchannels in polydimethylsiloxane (PDMS). The microfluidic channel is sketched in Fig. 1(a). The wide sections of the microchannel, before and after the constriction, had a uniform width w = 100 μm, while the constriction itself had a width wc = 20 μm and a length of lc = 800 μm. The channel had a total length of l = 1.1 cm and height of h = 40 μm. We emphasize that in this work, the streamwise direction is denoted as the X-direction, while the crossflow direction (in the plane of the schematic) is denoted as the Y-direction (cf. Fig. 1(a)). The other crossflow direction, oriented out of the page, is denoted as the Z-direction. Note that the origin is centered at the end of the tapered region.
FIG. 1.
Schematic of the microfluidic device. (a) Dilute RBCs are pumped from a region of low shear (a wide channel, at left) to a region of high shear (the constriction, at right). Note that the origin is located at the center of the entrance of the constriction. (b)–(e) Representative superimposed series of time-lapse images extracted from high speed video each showing an individual RBC entering a constriction. RBCs are shown undergoing (b) stretching, (c) tumbling, (d) twisting, and (e) rolling motions. Each superimposed image represents the distance traveled in a 0.33 ms time interval.
To begin an experiment, a suspension of cells was loaded in a 1 ml syringe. Any visible gas bubbles were then purged and the syringe was connected to a syringe pump to control the flow rate (model number PHD 2000, Harvard Apparatus). Polyethylene tubes (0.58 mm inner diameter) were used to connect the syringe needle to the inlet and outlet holes in the device, and the RBC suspension was pumped through the channel at 5 μl/min. Since the data collection time was short (<2 min), sedimentation effects were limited. As a safeguard, the syringe was turned every 30 s and fresh tubing was used for each sample. Since the microchannel cross-sectional area was 4.0 10−3 mm2 (8.0 10−4 mm2 within the constriction), the average flow velocity was approximately 2 cm/s (10 cm/s in the constriction). The corresponding average shear rate in the wide channel is estimated as = 520 s−1. Likewise, the average shear rate in the constriction, using the constriction width (wc) as the shortest characteristic length scale is 5200 s−1. Using the entrance length of 70 μm as the characteristic X distance, the velocity gradient in the flow direction , also known as the extension rate, is estimated as 1143 s−1 in the tapered region of the channel (cf. Fig. 1(a)) and the corresponding gradient in the shear rate is 30 μm−1 s−1. We note that these shear rates are similar to those physiologically in arterioles of tens of microns in diameter.33
C. High speed video and image analysis
The RBCs were visualized with a 63× large working distance objective on an optical microscope (Leica). High-speed video of RBC deformations was acquired with a Phantom V7 camera at 12 000 frames per second, with 10–20 μs of exposure time per frame. Example movies are shown in the supplementary movies.34 In our microscopy setup, we were able to see all of the cells concurrently across the entire depth of the channel. There was no population of cells badly out of focus; cells moving at the entire range of different speeds appeared visually similar despite being located at appreciably different heights. Changes in focal plane were observed only as a very slight blurring and change in intensity; close examination of the supplementary movies shows this effect.34 Although the blurring slightly affects the image analysis (e.g., the absolute size of the RBC), note that all statistics reported here are dimensionless (e.g., L/L0) so any difference in observed absolute size due to location in different focal planes is effectively cancelled. The resulting movies were analyzed using custom image analysis routines in Matlab to extract the position, velocity, size, and orientation of individual cells. In particular, the algorithms calculated the lengths of the major and minor axes of the best fit ellipsoid to the detected boundaries of the blood cell (denoted as a and b, respectively, cf. Fig. 1(a)). Cells that came in apparent contact with other cells (i.e., the projected area of the ellipsoids overlapped) were omitted in order to remove the influence of cell-cell interactions. Details of the image analysis procedure can be found in the supplementary material (Table S.I).34
Representative sequences of time lapse images of individual RBCs passing through the microchannel constriction are shown in Figs. 1(b)–1(e). (See also supplementary movies 2–5.34) The original images were recorded in grayscale; here the RBC boundaries (as detected via our image analysis software) are superimposed in color. The images within each time lapse sequence are spaced evenly in time (0.33 ms), so the distance between any two sequential images of a blood cell reflects the distance travelled during that interval. This manner of presenting the video data highlights the acceleration experienced by the cells as they enter the constriction due to time invariant volumetric flow rate: note that the cells move slowly in the wide part of the channel (where the cell images are crowded together), but they suddenly accelerate and move quickly upon entering the constriction (where the cell images are spaced further apart).
III. RESULTS AND DISCUSSION
A. RBC behavior characterization and velocimetry
As demonstrated in Fig. 1, individual RBCs respond differently to the same flow profile. Our observations suggest that the mechanical response of the RBCs can be classified into 4 specific categories: stretching, tumbling, twisting, and rolling. In addition, we observed RBCs undergoing other motions not described by our classification scheme. We therefore defined a fifth category as “complex” to represent RBCs that went through motions described by more than one category, or motion not defined by the first four categories. The five behaviors are defined as follows:
Stretching: elongation in the direction of flow, without rotation
Tumbling: rotation around the major axis perpendicular to the direction of flow
Twisting: rotation around the major axis parallel to the flow direction
Rolling: rotation around the minor axis perpendicular to the direction of flow
Complex: all other motions, e.g., multiple motion types
The first four behaviors are illustrated more closely in Figure S.1 of the supplementary material with time lapsed images of individual RBCs traversing the channel, and corresponding representative plots of the instantaneous aspect ratio (a/b) and orientation with respect to the direction of flow are shown versus X (downstream) position in the channel constriction. (See Table S.I for details on the characterization scheme34). The other RBCs exhibited more complex motions that typically involved combinations of, or transitions between, twisting, rolling, or tumbling. Several representative complex motions are shown in Fig. S.2.
While TT motion has been previously reported in experiments in simple shear, we point out that we did not observe TT. The time scale for an individual cell to undergo a complete TT revolution has been reported previously to occur on the time scale of many seconds to minutes.5 We stress that in our experiments, the RBCs were only in the field of view for approximately 10 ms, and therefore no measureable TT was observed.
A key advantage of our automated approach is that it allowed for characterization of RBCs in the entire microchannel, instead of focusing specifically on the channel center as done previously.21,22 Based on quantitative measurements of RBC position, major axis length, minor axis length, and orientation, we were able to characterize the mechanical response of RBCs precisely as functions of cross-channel position and velocity. We conducted studies on five blood samples from five different donors, with detailed examinations of 4433 individual RBCs (n1 = 1262, n2 = 876, n3 = 1168, n4 = 779, n5 = 348).
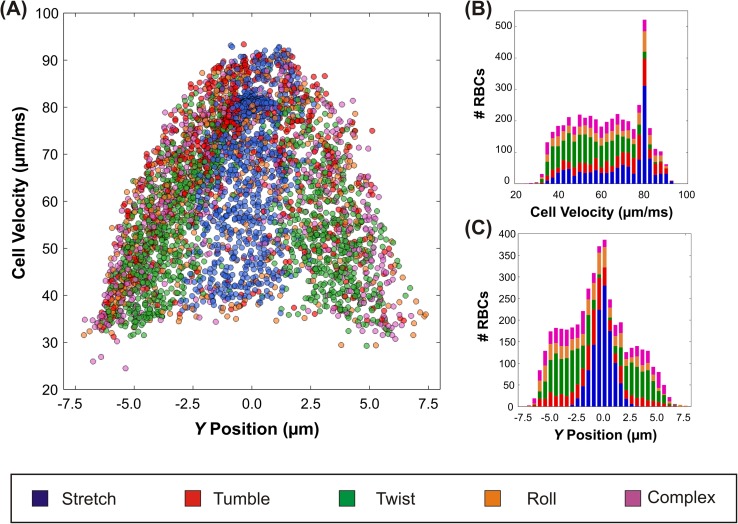
The relative fraction of RBCs exhibiting each distinct mechanical behavior upon entering the constriction is shown as a box plot in Fig. 2. Each box represents the distribution observed for each of the five distinct behaviors; note that the sum of the mean percentages for all five behaviors is 100. Note that we although we acquired blood from five different donors, we performed experiments in triplicate. The channel became irreversibly clogged in one of the experiments, but in all we had 14 unique trial replicates, identified by marker shape for each blood donor. As seen in Fig. 2, the most prominent behavior was twisting, which was exhibited on average by 30% the cells. In addition, stretching was displayed by 26% of the cells, while tumbling, rolling, and complex made up an average of about 15% each. Previous work has paid little attention to twisting, but Fig. 2 demonstrates that arguably a plurality of cells actually perform twisting upon entering a microfluidic constriction. While stretching, tumbling, and rolling motions have been reported previously in linear velocity profiles, twisting is rarely (if ever) observed. This observation suggests that the converging streamlines in the tapered part of the constriction play a key role in twisting; this idea is discussed in more detail below.
FIG. 2.
Box plot showing the fraction of RBCs exhibiting different mechanical responses upon entering a constriction. The top and bottom of the lightly shaded rectangles indicate the 25th and 75th quartiles, respectively, the thick black bars indicate the median, the dark square markers indicate the mean, and the whiskers represent the maximum and minimum values observed. The distributions are based on fourteen separate trials using five different blood donors. We ran 3 trials for each donor and show the individual data points adjacent to the box plot. Each marker shape represents a separate donor. The total number of cells observed per trial was n1 = 1262, n2 = 876, n3 = 1168, n4 = 779, and n5 = 348.
While Fig. 2 presents the overall distribution of RBC behaviors, our analysis indicates that the behavior of individual RBCs is very sensitive to location within the channel. To provide context for this position dependence, we plot the linear velocity of the RBCs in the constriction vs. Y position in Fig. 3(a). The Y position and velocity are based on the average value in the constriction (X= 20–70 μm). We found that Y position and velocity did not vary much in this range of X, unlike in the tapered region of the channel. The markers are color coded based on the observed behaviors, utilizing the same color scheme as the previous figures (stretching cells: blue; tumbling cells: red; twisting cells: green; rolling cells: orange; and complex cells: purple). RBCs traveled with velocity values ranging 25–90 μm/ms in a parabolic profile, which is consistent with the pressure-driven (Poiseuille) flow used here. The fluid near the walls is stationary (due to the no slip condition) and RBCs moving in these regions have low velocity, while near the channel center, the fluid moves fastest and RBCs in these regions have correspondingly high linear velocities. Note, however, that there is a large variation in observed RBC velocities for any particular value of Y. This range in velocities at each Y-position is due to variation in the Z-position; the video images represent the projected view of a three dimensional space with finite focal depth that precluded accurate identification of the precise RBC Z-coordinate. Therefore, for a given Y position, variation in the cell's location in the Z plane (i.e., near the top or bottom walls or at the center) also contributes to the observed variation in linear velocity.
FIG. 3.
(a) The observed downstream RBC velocity in the constriction vs. Y position. The markers are color coded based on the observed behaviors (stretching-blue, tumbling-red, twisting-green, rolling-orange, and complex-purple). Alongside, histograms of (b) the linear velocity and (c) Y position. The bars of the histograms are partitioned into color segments utilizing the same color scheme as (a) to show the relative fraction for each of the different behaviors.
The frequency distribution of cells traveling downstream at specific velocity (Fig. 3(b)) and Y position (Fig. 3(c)) are shown alongside as histograms. The peak in velocity at approximately 80 μm/ms is consistent with the increased number of cells in the center of the channel, which are associated with higher velocity. Fig. 3(c) illustrates that the majority of stretching took place at the center of the channel (Y between +/−2.5 μm), while twisting and complex motions were concentrated closer to the channel edges. Because the fluid in the center of the channel travels faster than near the edges, one would expect that for a uniformly well mixed suspension, the number of cells flowing through the center region would be largest. Indeed, simple conservation arguments indicate that the frequency distribution should be parabolic. As can be seen in Fig. 3, each type of motion was observed across a wide range of velocities at each horizontal position, i.e., the specific behavior was not significantly correlated with absolute vertical (Z) position. The only exception is that that more stretching occurred at higher velocities (near 80 μm/ms). The actual behavior distribution, we observed in Figure 2 is significant because it represents the important limiting case where no special measures were taken to alter the incoming cell spatial distribution. As shown in Fig. 3(c), the spatial distribution is not uniform: relatively more cells enter near the channel center than the edges. The large number of cells observed at the center of the channel (Fig. 3(b)) might be attributed to the Fahraeus Lindqvist effect.35 In vessels of small diameter, RBCs migrate laterally towards the vessel center in response to hydrodynamic forces and result in a cell free layer at the vessel wall, which lowers the effective viscosity. The large concentration of RBCs that we observed in the channel center, specifically of RBCs exhibiting stretching motion (indicated by the large blue subdivision), are consistent with this hypothesis.17
The results shown in Figs. 2 and 3 highlight the overall behavior of the RBCs, by identifying their specific mechanical response as functions of velocity and position. We emphasize that for each identified behavior; however, there was tremendous variation in the detailed dynamics of each behavior. For example, how far did each stretching cell stretch? How fast did tumbling cells rotate? We now turn our attention to analyzing the detailed dynamics. From the image analysis procedure, we were able to obtain comprehensive information about each cell to compile statistics on the effect of the sudden increase of shear stress on RBC mechanical dynamics. We present observations and quantitative measurements on the dynamics of each of the distinct observed behaviors. In addition, we examine the mechanical basis for the observed rotational motions by using the equations of motion for rigid ellipsoids, to assess whether our experimental results are broadly consistent with the imposed hydrodynamic torques.
B. RBC stretching
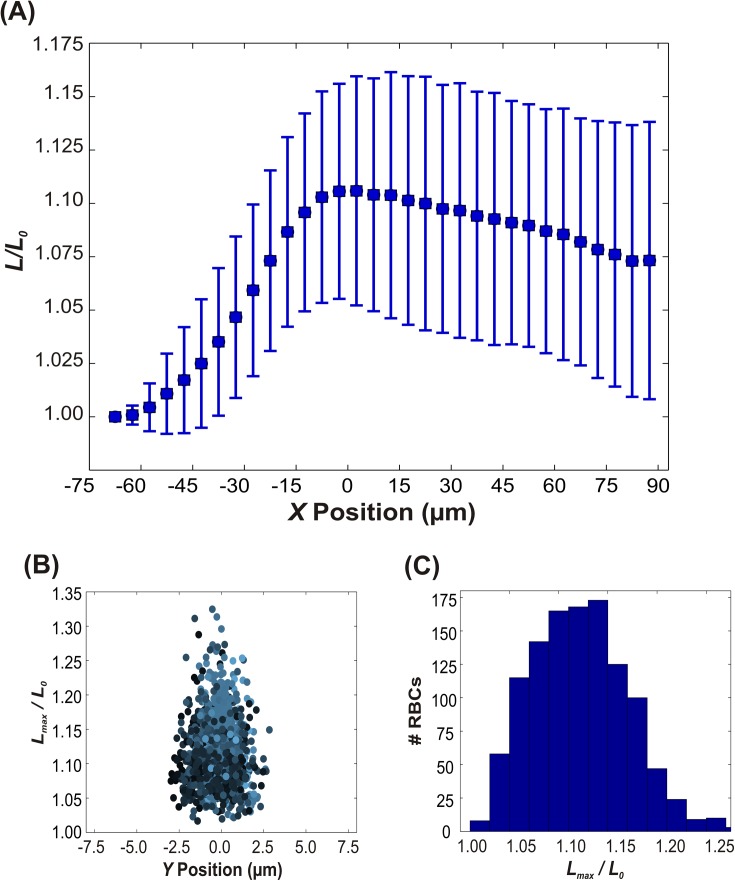
The dynamics of stretching motion are illustrated in Fig. 4(a), as a plot of the ratio of cell length (L) to initial length (L0) versus X position, averaged over all 1156 observed stretching cells. As the RBCs move through the converging region (tapering) of the channel (indicated by negative X values), they continuously elongate until they reach their maximum length (an average of approximately 10% greater than the initial length) at the entrance of the constriction (X = 0). After stretching to the maximum length, the cells decreased in length gradually, or relaxed, with some cells relaxing to their initial length. The stretching and relaxing phenomena are consistent with the geometry of the tapered region of the channel. In this region, the fluid streamlines converge and the front of the cell experiences a higher velocity than the back of the cell, which causes elongation of the RBC. For a given Y position, the extensional forces are inversely proportional to the cross sectional area due to conservation of mass in an incompressible flow; this interpretation is consistent with the observed peak in L/L0 at X = 0. As the cell moves out of the tapered region and into the constriction, the velocity at the front becomes equivalent to that of the back of the cell (i.e., the gradient in extensional force across the cell length is zero), and the cell slowly retracts. The time for relaxation is based partially on the isotropic elasticity (resistance to change in surface area) of the membrane, which returns the cell to its initial shape.
FIG. 4.
Dynamics of stretching RBCs. (a) The normalized length as a function of X position in the channel, where X = 0 corresponds to the entrance of the constriction (cf. Fig. 1(a)). Note that the RBCs stretch to their maximum length near X = 0, and then gradually relax. The error bars indicate plus or minus one standard deviation. (b) The maximum normalized length versus Y position in the channel and (c) corresponding frequency distribution. The color of each data point in (b) is weighted based on the normalized linear velocity. Lighter color corresponds to a higher velocity while darker color indicates lower velocity.
The magnitude of stretching and subsequent relaxation that we observed are broadly consistent with those previously reported for microfluidic devices with a constriction.21,22 Wan et al.21 observed cellular elongation on average of about 15%, and the relaxation was about 10% over about 4 ms. Although the average relaxation within our field of view was only 2%–3%, the average relaxation rate was approximately equivalent. We did not, however, see evidence of the “recoiling” behavior reported by Forsyth et al.22 In addition, the magnitude of stretching that we observed is similar to previous work examining the deformability index of RBCs in hyperbolic converging flows.26–28 For reference, we have included plots of the DI versus position in the supplementary material (Fig. S.4).34 Our results are consistent with those of Lee et al.,26 Yaginuma et al.,27 and Zhao et al.28 that show that the DI for RBCs in hyperbolic converging channels ranges between 0.2 and 0.25 for shear rates similar to ours.
A key feature in Fig. 4(a) is the large variability in L/L0, with standard deviations on the order of 5%. This large variation of L/L0 is probably due to two key factors. First, the exact magnitude of the extensional forces experienced by an individual RBC depends on its position in the Z plane, which we did not visualize. Second, recall that the RBCs do not all have the same viscoelastic properties. The mature erythrocyte is devoid of a nucleus and is therefore unable to synthesize proteins. During its time of 100–120 days in the circulation, an RBC must undergo numerous reversible deformations in the microcirculation in order to provide adequate tissue perfusion, and as a result, it experiences many mechanical and chemical stresses. These stresses gradually denature the functional proteins in the RBC, which are involved with many cellular functions such as membrane elasticity, cell volume, metabolic regulation, and solute transport.36,37 Furthermore, they play a key role in determining RBC internal viscosity, the surface area-to-volume ratio and the viscoelastic properties of the membrane, all known determinants of RBC deformability.38,39 The circulating RBCs, therefore, have a range viscoelasticities based on their age and the amount of protein degradation, which can be used as an indicator of the health state of the individual;40,41 older cells are typically more rigid.39 Fig. 4 shows the data collected from 1156 total stretching cells, all of which vary in age. The mechanical properties of the RBCs presumably impact the dynamics of stretching and relaxation and contribute to the variation in the absolute magnitude of L/L0.
The ratio of the maximum observed length (Lmax) to the initial length (L0) versus Y is shown in Figs. 4(b) and 4(c). The extensional forces in our microchannel were sufficient to cause RBC deformations as large as 30%, but as made clear in the histogram (Fig. 4(b)) the distribution of maximum deformations is centered around 10% to 12%. One interesting finding is that the maximum extent of deformation is not correlated with the absolute linear velocity of the cell. The color of the markers in Fig. 4(b) is weighted based on the normalized linear velocity (vRBC /vmax), with RBCs moving the fastest shown as light blue, and RBCs moving slowly shown as dark blue-black. Light blue markers (RBCs with high velocity) appear more frequently at the center of the channel and darker markers occur closer to the edges of the channel for both figures, consistent with Poiseuille flow. The darker markers that are located at the center of the channel are presumably due to variation in the cell's location in the Z direction. As seen in Fig. 4(b), RBCs exhibited the greatest degree of elongation (highest ) at the center of the channel (Y = 0), which can be attributed to the surrounding streamlines of fluid moving at high velocity. No clear correlations, however, were observed between and linear velocity (data not shown). This finding is consistent with the notion that the downstream velocity gradient , or extension rate, rather than the absolute velocity, controls the extent of deformation.
C. RBC rotations
1. Rigid body theory
We now turn our attention to the observed rotational motions, which have not previously been elucidated for RBCs in this flow geometry. A key consistency check is to determine whether the motions are qualitatively consistent with the applied shear stresses. Although the motion of RBCs has been the subject of extensive simulation and computational efforts,42–46 little work has examined the motion of RBCs entering a constriction as tested here. In the absence of detailed predictions, we instead examine the limiting case of perfectly rigid ellipsoids. We emphasize that we do not claim that RBCs behave as rigid bodies; we only wish to assess whether the observed magnitudes of angular velocity are consistent with this important limiting case.
For an arbitrary Stokesian flow field , Faxen's second law47 describes the net torque on a rigid sphere, to leading order, as
| (1) |
where is the sphere radius, is the viscosity of the suspending fluid, and is the angular velocity of the sphere; the subscript o denotes evaluation at the sphere center. In essence, Eq. (1) describes the consequence of a non-uniform flow velocity around the particle: if the top of a particle “feels” a larger velocity than the bottom of the particle, then the particle will rotate. In the absence of any induced torque, i.e., for a freely suspended particle with , then the particle angular velocity is simply one half of the local flow vorticity.46 Note, however, that Eq. (1) is only valid for spheres, and a more complicated torque balance applies to other shapes. Here, we approximate RBCs as ellipsoids with semi-axes a, b, and c and described by
| (2) |
We apply the generalized form of Faxen's second law derived by Brenner for ellipsoidal coordinates48
| (3) |
Here, is the symmetric dyadic and is the rotation dyadic. is the differential operator, and is the vector differential operator. Full details are provided in the supplementary material.34
2. Tumbling RBCs
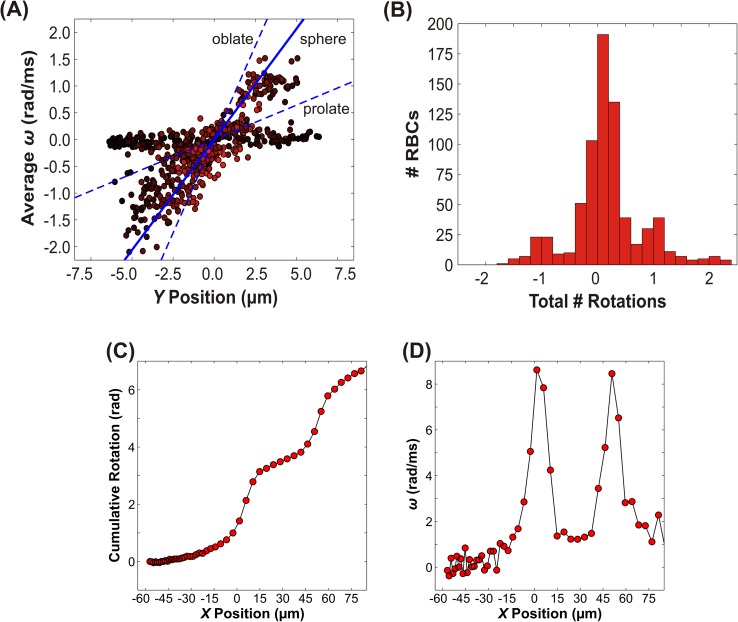
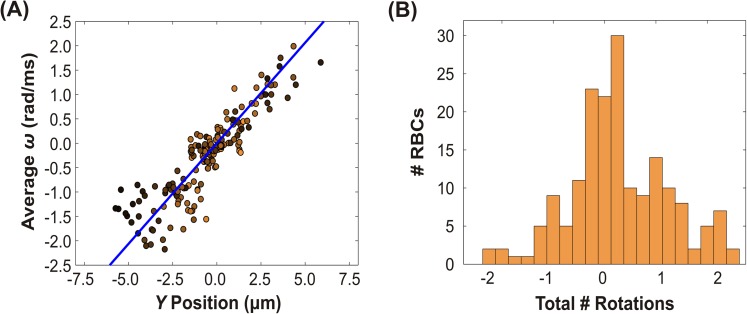
Turning our attention first to tumbling cells, Fig. 5 shows the average angular velocity (ω) and the maximum number of rotations observed in the field of view (including the tapered region and the constriction), averaged over 723 observed tumbling cells. The average angular velocity is plotted as a function of Y position in Fig. 5(a). The Y positions are based on the average value of the centroid of the best fit ellipsoid in the constriction (X= 20–70 μm). Here, positive values signify clockwise rotation, while negative values represent counterclockwise rotations (with respect to the observed field of view, cf. Fig. 1). One key observation from this plot is that there are two distinct populations, one with low linear velocity (approximately 30–55 μm/ms, shown with dark red-black markers) and low angular velocity. The angular velocities of these cells were roughly independent of Y position, but were consistently small (ω < |0.2| rad/ms). These cells tumbled slightly, but did not complete a full rotation while in the field of view. The other subpopulation consists of cells moving at intermediate to high velocity (approximately 55–95 μm/ms), with average angular velocities that vary linearly with Y position. In contrast to the slower moving cohort, most of these cells typically made one or more complete rotations while in the field of view. The bifurcation in tumbling behavior may be due to the Z position of the cells. Cells that are at the top or bottom of the channel would be expected to have low linear velocity, as seen by the darker markers that are distributed throughout all values of Y. Despite the apparent presence of two separate populations of cells, the correlation coefficient for tumbling angular velocity vs. Y was found to be +0.59; the corresponding p values was infinitesimal (p = 10−68).
FIG. 5.
Dynamics of tumbling RBCs. (a) The average angular velocity versus Y position in the microchannel. The color of each data point is weighted based on the normalized linear velocity. Lighter color corresponds to a higher velocity while darker color indicates lower velocity. Positive values of rotation and angular velocity correspond to clockwise rotations, while negative values correspond to counterclockwise rotations. The dashed lines indicate the predicted angular velocity for an oblate and prolate ellipsoid using rigid body theory; the solid line is for a sphere (cf. Eqs. (1) and (5)). (b) Histogram of the total number of rotations observed within the field of view. Each rotation of 180° was counted as 1 full rotation. Note that the maximum number of rotations occurs most frequently at integer values. (c) The cumulative rotation and (d) the corresponding instantaneous angular velocity vs. X position for an individual representative tumbling cell. Solid lines are guides for the eye. Note that the angular velocity peaks when the cell is oriented transverse to the flow direction (i.e., oblate).
In order to conduct rigid body analysis of tumbling motion, i.e., rotation around the Z-axis orthogonal to the flow direction (cf. Fig. 1(c), we focus on motion in a parallel plate channel. As an approximation, we examine the velocity profile for pressure driven flow in a parallel plate channel using
| (4) |
where is the average magnitude of the parabolic (Poiseuille) fluid velocity within the narrow part of the constriction. Substitution of this velocity profile into Eq. (3) yields a predicted angular velocity
| (5) |
A key point is that the angular velocity is predicted to vary linearly with position across the channel, qualitatively consistent with the trend observed for tumbling RBCs in Fig. 5. The exact magnitude of the angular velocity depends on whether the ellipsoid is aligned prolate (with the flow, or aligned oblate (against the flow, . Insertion of the characteristic RBC dimensions (3 μm wide, 7 μm long)49 and appropriate values for the fluid velocity and channel width yields quantitative predictions for the RBC angular velocity. These predictions are shown as dashed lines in Fig. 5; for comparison we also include the predicted angular velocity for a sphere ( 7 μm). The experimentally observed angular velocities clearly fall within the range of the two limiting cases for oblate and prolate ellipsoids. Intriguingly, the predicted angular velocity for a sphere is in excellent accord with the observed velocities, at least for the cohort of RBCs which accomplished at least one rotation. This trend might exist because the spherical case essentially serves as an “average” of the oblate and prolate orientations.
An alternative way of examining the tumbling behavior is shown in Fig. 5(b), which shows a histogram of the number of fractional rotations that occurred while the RBC was in the field of view. Each rotation of 180° was counted as 1 rotation and the sign indicates the direction of rotation, with fractional values indicating partial rotations; for example, a fractional rotation of 0.5 corresponds to a rotation of 90° or 1.57 rad. Notably, the most frequently occurring numbers of rotations are integer values, indicating that it is energetically unfavorable for RBCs to be in orientations where their axes are misaligned with flow. In fact, plots of the cumulative rotation and angular velocity as functions of X position (Figs. 5(c) and 5(d)) show that ω is not constant. When the RBC axes are aligned with flow, ω increases very slowly, and the cell does not visibly rotate. As the RBC begins to rotate, the amount of surface area exposed to the shear gradient increases until it reaches a maximum in the vertical (with respect to X) position, which also corresponds to a maximum in |ω|.
3. Rolling RBCs
Quantitative data for the angular velocity of rolling cells was more difficult to acquire because the major axis and minor axis are not as easily differentiable when the aspect ratio is near unity. Therefore, tracking the major axis and orientation to extract the number of rotations typically underestimated the observed value. We therefore selected the subset of the rolling cell population with angular velocities that we could visually corroborate via manual observations. Quantitative data for 88 cells are shown in Fig. 6(a), which show the average rolling angular velocity plotted as a function of Y position. Similar to the subset of tumbling cells with moderate to high linear velocity, the maximum number of rotations for rolling cells shows a strong linear trend with Y position that is symmetric about the origin. This trend is corroborated by the correlation coefficient of +0.91 and the corresponding p value of 10−34. The average angular velocity in rolling cells did not exhibit a clear dependence on linear velocity, as indicated by the dark colored markers distributed throughout all of the Y positions.
FIG. 6.
Dynamics of rolling RBCs. (a) The average angular velocity versus Y position in the microchannel. The color of each data point is weighted based on the normalized linear velocity. Lighter color corresponds to a higher velocity while darker color indicates lower velocity. Positive values of rotation and angular velocity correspond to clockwise rotations, while negative values correspond to counterclockwise rotations. The solid line indicates the predicted angular velocity using rigid body equations. (cf. Eq. (1)) (b) Histogram of the total number of rotations observed in the field of view. Each rotation of 180° was counted as 1 full rotation. Note that the maximum number of rotations occurs more frequently at integer values.
To test whether this behavior is consistent with the rigid body limited case, we again use the velocity profile from Eq. (4). Rolling cells, like tumbling cells, also rotate around the Z-axis orthogonal to the flow direction, but are oriented such that with no distinction between oblate and prolate. The predicted angular velocity for rolling follows from (5), and the results are plotted as a solid line in Fig. 6(a). Again, the rigid body prediction is in excellent accord with the experimental observations.
Like tumbling cells, the histogram (Fig. 6(b)) for the maximum number of rotations for rolling cells shows a clear preference for integer numbers of rotations. Rolling has been shown previously to correspond to a minimum in membrane shear strain energy, allowing the red blood cell to avoid energetically costly deformations.12 The mechanism driving the preference for an integral number of rotations, however, is unclear since nothing breaks the symmetry of the system (as opposed to the difference between oblate and prolate orientation for tumbling cells).
4. Twisting RBCs
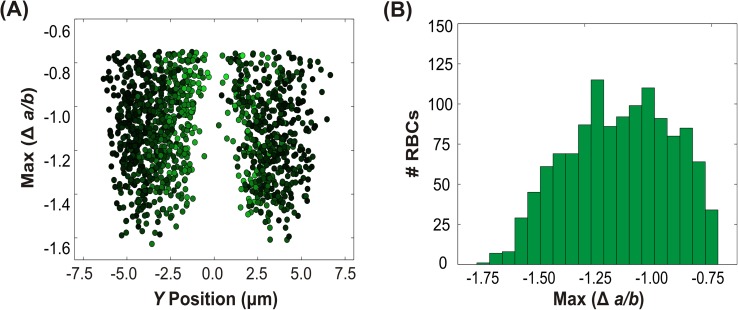
The final rotational motion we observed was twisting, which was the behavior most frequently exhibited by the RBCs: roughly a third of the cells displayed this behavior. Because we did not visualize cells from the X-direction, we were unable to obtain quantitative measurements of the twisting angular velocity. In the absence of these measurements, we therefore used what we did have available: the relative magnitude of rotation as characterized by , which represents the change in the projected aspect ratio, ). Here, the term denotes the minimum observed aspect ratio within the constriction, and denotes the maximum observed aspect ratio in the wide part of the channel. Although this metric does not provide a measure of angular velocity, it does serve as a gauge of the absolute extent of rotation as an individual RBC twists during its passage through the field of view; RBCs that had higher had larger extent of rotation. Note that it is impossible to specify whether the direction of rotation is positive or negative: when looking from above, twisting in either direction will present simply as changes in the observed aspect ratio. Fig. 7(a) shows plotted as a function of Y position, while Fig. 7(b) shows the corresponding histogram. The figures reveal several trends. First, twisting cells exhibited ranging between −1.75 and −0.75, with an average of approximately −1.10. Only “thickening” twisting (rotation from high aspect ratio to low aspect ratio) was observed, suggesting that rotation in the opposite direction (“thinning”) is not preferred. We emphasize, however, that this result partially stems from our classification scheme: cells with too small a change in aspect ratio were not classified as twisting cells. Nonetheless, “thinning” twisting (from a low aspect ratio to high aspect ratio) was rarely observed.
FIG. 7.
Dynamics of twisting RBCs. (a) The maximum change in aspect ratio versus Y position in the channel. (b) Histogram of the maximum change in aspect ratio. Note the negative scale.
More importantly, the most pronounced feature of Fig. 7(a) is the striking dependence of twisting on Y position, with the majority of twisting occurring at intermediate values of Y. Specifically, the maximum extents of deformation occurred near , where 2 is the width of the narrow constriction. No twisting was observed near The normalized linear velocity (shown again by the color weight) is highest at the center and lowest at the edges, as expected for Poiseuille flow. Again, no dependence on the linear velocity was observed (data not shown).
Our analysis of rigid body twisting focuses on the rotation about the axis parallel to the direction of flow, i.e., the X direction. A unidirectional flow in the X-direction will not induce rotation around the X-axis, since non-zero velocity components in the orthogonal directions are necessary to “push” the particle to rotate around the X-axis. In our system, there was no flow in the Z direction, i.e., everywhere in our channel. The Y velocity (), however, was non-zero in the tapered region, due to the convergence of the flow. For this tapered region, the velocity profile is readily estimated using lubrication theory47
| (6) |
Full details of the calculation are in the supplementary material;34 the key result is that the twisting angular velocity is estimated as
| (7) |
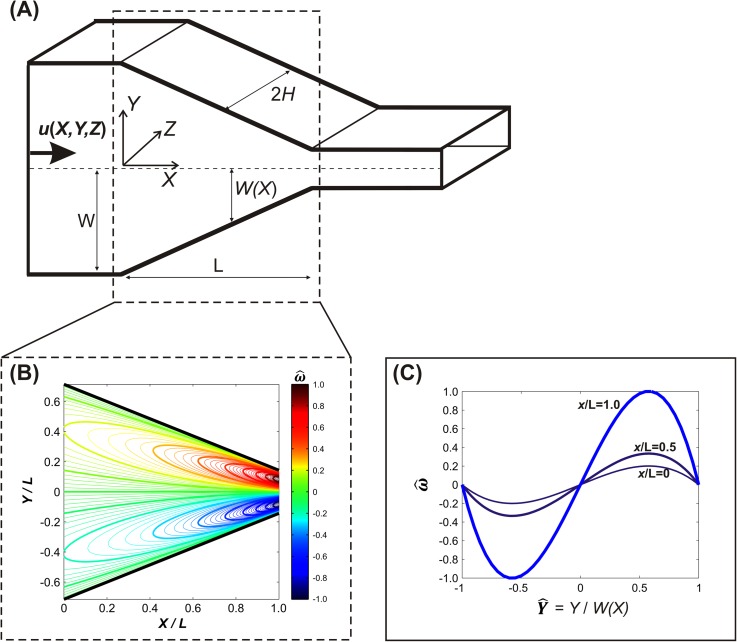
where q is the volumetric flow rate and describes the position of the tapering walls. (For simplicity, in Eq. (7) X = 0 is defined as the beginning of the taper, in contrast to end of the taper as defined previously.) The crucial aspect of Eq. (7) is that the twisting angular velocity is predicted to vary cubically across the channel cross-section, with zero magnitude in the center (Y = 0). The predicted twisting angular velocity is plotted in Fig. 8(b) versus position, where the dimensionless angular velocity is normalized as , with ωmax defined as the maximum angular velocity calculated at X/L = 1. Note that the maximal twisting velocities occur at . In our experimental setup, we were unable to visualize RBCs from the X direction and therefore could not obtain quantitative measurements of . Furthermore, although we were able to determine that a cell had twisted by virtue of its large change in observed aspect ratio, we were unable to differentiate the direction of rotation (i.e., clockwise or counterclockwise rotation around the X-axis). We can, however, compare the observed spatial distributions of twisting cells. As clearly shown in Fig. 7(a), effectively no RBCs were observed to twist down the channel center (Y = 0), with the histogram peaks occurring at near . These trends are both qualitatively consistent with the rigid body predictions (cf. Fig. 8), strongly suggesting that the observed twisting is indeed due to torque exerted by the converging flow within the tapered part of the constriction.
FIG. 8.
(a) Illustration of the tapered region of the microchannel. (b) Contour plot of the dimensionless angular velocity about the axis parallel to X for a rigid prolate ellipsoid. (c) Plot of the dimensionless angular velocity vs. at constant values of X/L = 0, 0.5, and 1.0.
IV. SUMMARY AND CONCLUSIONS
Our quantitative measurements of 4400 RBCs demonstrate that RBCs undergo one of five distinct classes of behavior in constriction flow in a microchannel: stretching, tumbling, twisting, rolling, or complex. A key finding of the present work is that the predominant motion for RBCs entering a constriction is twisting, with about one third of RBCs exhibiting this behavior. Previous studies have paid little attention to twisting, but with such a large fraction of RBCs exhibiting twisting, a renewed focus on this class of motion seems prudent. Twisting allows the red blood cell to realign with the flow in such a way the that the shear strain on the membrane is minimized; in this process, however, the viscous dissipation increases as the cell rotates between shear planes. Further work is necessary to elucidate the implications of twisting on bulk hemorheology.
Another key result presented here involves the extensive measurements of cell stretching, with cells stretching on average by about 10%. Previous work on stretching RBCs in this geometry examined relatively small sample sizes (of order 20), but our examination of more than 1000 stretching RBCs indicates that there is a tremendous amount of variability in the extent of deformation. The observed variation is presumably due to differences in the vertical position of the RBC, as well as age based variation in cell rigidity. Future studies should take care to measure sufficiently large sample sizes; a particular danger lies in the possibility of selection bias if researchers only measure the deformation of cells that “look like” they stretch sufficiently far to be worth measuring.
The final key result presented here involves the detailed measurements of rotational motion exhibited by the RBCs. The vast majority of cells exhibited rotation around various axes: together, twisting, tumbling, rolling, and complex (most of which exhibited some sort of rotation) accounted for about 75% of the RBCs. Perhaps surprisingly, the angular velocities and spatial distributions of tumbling, rolling, and twisting cells are well approximated simply using rigid body theory. This result suggests a useful limiting case for comparison with more advanced computational simulations of RBCs flowing through constrictions.
While most of the cells could be categorized into the four categories of stretching, tumbling, twisting, and rolling, a small percentage of cells (<15%) displayed complex behavior. Many of the cells characterized as complex transitioned between twisting, tumbling, and/or rolling. More work understanding the physical basis of these transitions is necessary to elucidate the full dynamics of RBCs entering a constriction. More generally, much work remains in examining how the balance of viscous dissipation and elastic strain contribute to RBC behavior upon entering a constriction, in particular, as a function of cross-flow position. Since stretching and twisting were highly sensitive to position in the channel and together account for over 50% of the RBCs behaviors, the locations of these motions may be significant factors in determining whole blood rheology in healthy individuals.
This work focused on RBCs obtained from ostensibly healthy donors, so the observed distribution of RBC behaviors should serve as a baseline for comparison with disease states known to affect RBC deformability. The distribution of behaviors for blood from healthy individuals is therefore an important first step in understanding how changes in RBC mechanical properties contribute to disease states. Further work examining the influence of the flow rate (and corresponding strain rate) on the observed behaviors is important to understand RBC response to applied shear. In addition, many questions remain as to how RBC mechanical dynamics affect ATP release and RBC mechanotransduction. Further work should examine the ATP release that is evoked by each of the different motions to assess how they impact RBC vasodilatory signaling. The present work will serve as a framework for examining these more complicated questions.
ACKNOWLEDGMENTS
Primary support for this research was provided by NSF Grant No. 1201245 (Biomechanics and Mechanobiology, CMMI). Partial support for this research was provided by Grant No. T32-GM008799 from NIGMS-NIH. We thank J. Wan and A. Forsyth for experimental advice.
References
- 1.Baskurt O. K. and Meiselman H. J., Semin. Thromb. Hemostasis 29, 435 (2003). 10.1055/s-2003-44551 [DOI] [PubMed] [Google Scholar]
- 2.Marossy A., Svorc P., Kron I., and Gresova S., Clin. Hemorheol. Microcirc. 42, 239 (2009). [DOI] [PubMed] [Google Scholar]
- 3.Fischer T., Stohrliesen M., and Schmidschobein H., Science 202, 894 (1978). 10.1126/science.715448 [DOI] [PubMed] [Google Scholar]
- 4.Goldsmith H. L. and Marlow J., Proc. R. Soc. B 182, 351 (1972). 10.1098/rspb.1972.0084 [DOI] [Google Scholar]
- 5.Abkarian M., Faivre M., and Viallat A., Phys. Rev. Lett. 98, 188302 (2007). 10.1103/PhysRevLett.98.188302 [DOI] [PubMed] [Google Scholar]
- 6.Goldsmith H., Fed. Proc. 30(5), 1578 (1971). [PubMed] [Google Scholar]
- 7.Goldsmith H., Biorheology 7, 235 (1971). [DOI] [PubMed] [Google Scholar]
- 8.Goldsmith H. and Karino T., Ann. N. Y. Acad. Sci. 283, 241 (1977). 10.1111/j.1749-6632.1977.tb41770.x [DOI] [Google Scholar]
- 9.Goldsmith H. and Marlow J., J. Colloid Interface Sci. 71(2), 383 (1979). 10.1016/0021-9797(79)90248-0 [DOI] [Google Scholar]
- 10.Keller S. R. and Skalak R., J. Fluid Mech. 120, 27 (1982). 10.1017/S0022112082002651 [DOI] [Google Scholar]
- 11.Fischer T. M., Biophys. J. 86, 3304 (2004). 10.1016/S0006-3495(04)74378-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dupire J., Socol M., and Viallat A., Proc. Natl. Acad. Sci. U. S. A. 109, 20808 (2012). 10.1073/pnas.1210236109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bitbol M., Biophys. J. 49, 1055 (1986). 10.1016/S0006-3495(86)83734-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Watanabe N., Kataoka H., Yasuda T., and Takatani S., Biophys. J. 91, 1984 (2006). 10.1529/biophysj.105.060236 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dupont C., Salsac A. V., and Barthès-Biesel D., J. Fluid Mech. 721, 180 (2013). 10.1017/jfm.2013.62 [DOI] [Google Scholar]
- 16.Skotheim J. M. and Secomb T. W., Phys. Rev. Lett. 98, 078301 (2007). 10.1103/PhysRevLett.98.078301 [DOI] [PubMed] [Google Scholar]
- 17.Chien S., Annu. Rev. Physiol. 49, 177 (1987). 10.1146/annurev.ph.49.030187.001141 [DOI] [PubMed] [Google Scholar]
- 18.Sprague R., Ellsworth M., Stephenson A., and Lonigro A., Am. J. Physiol.: Heart Circ. Physiol. 271, H2717 (1996). [DOI] [PubMed] [Google Scholar]
- 19.Sprung R., Sprague R., and Spence D., Anal. Chem. 74, 2274 (2002). 10.1021/ac011144e [DOI] [PubMed] [Google Scholar]
- 20.Sprague R. S., Bowles E. A., Achilleus D., and Ellsworth M. L., Acta Physiol. (Oxf) 202, 285 (2011). 10.1111/j.1748-1716.2010.02182.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wan J., Ristenpart W. D., and Stone H. A., Proc. Natl. Acad. Sci. U. S. A. 105, 16432 (2008). 10.1073/pnas.0805779105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Forsyth A. M., Wan J., Ristenpart W. D., and Stone H. A., Microvasc. Res. 80, 37 (2010). 10.1016/j.mvr.2010.03.008 [DOI] [PubMed] [Google Scholar]
- 23.Quinn D. J., Pivkin I., Wong S. Y., Chiam K. H., Dao M., Karniadakis G. E., and Suresh S., Ann. Biomed. Eng. 39, 1041 (2011). 10.1007/s10439-010-0232-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chen B., Guo F., and Xiang H., J. Biol. Phys. 37, 429 (2011). 10.1007/s10867-011-9224-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tomaiuolo G., Barra M., Preziosi V., Cassinese A., Rotoli B., and Guido S., Lab Chip 11, 449 (2011). 10.1039/c0lc00348d [DOI] [PubMed] [Google Scholar]
- 26.Lee S. S., Yim Y., Ahn K. H., and Lee S. J., Biomed. Microdevices 11, 1021 (2009). 10.1007/s10544-009-9319-3 [DOI] [PubMed] [Google Scholar]
- 27.Yaginuma T., Oliveira M. S. N., Lima R., Ishikawa T., and Yamaguchi T., Biomicrofluidics 7, 054110 (2013). 10.1063/1.4820414 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zhao R., Antaki J. F., Naik T., Bachman T. N., Kameneva M. V., and Wu Z. J., Biorheology 43(6), 747 (2006). [PubMed] [Google Scholar]
- 29.Forsyth A. M., Wan J., Owrutsky P. D., Abkarian M., and Stone H. A., Proc. Natl. Acad. Sci. U. S. A. 108, 10986 (2011). 10.1073/pnas.1101315108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Price A. K., Fischer D. J., Martin R. S., and Spence D. M., Anal. Chem. 76, 4849 (2004). 10.1021/ac0495992 [DOI] [PubMed] [Google Scholar]
- 31.Uyuklu M., Cengiz M., Ulker P., Hever T., Tripette J., Connes P., Nemeth N., Meiselman H. J., and Baskurt O. K., Clin. Hemorheol. Microcirc. 41, 269 (2009). [DOI] [PubMed] [Google Scholar]
- 32.Duffy D., McDonald J., Schueller O., and Whitesides G., Anal. Chem. 70, 4974 (1998). 10.1021/ac980656z [DOI] [PubMed] [Google Scholar]
- 33.Tangelder G. J., Slaaf D. W., Arts T., and Reneman R. S., Am. J. Physiol. 254, H1059 (1988). [DOI] [PubMed] [Google Scholar]
- 34.See supplementary material at http://dx.doi.org/10.1063/1.4904058E-BIOMGB-8-030406, for example, high speed videos, details of image analysis and behavior classification, additional experimental measurements, and details of the rigid body mechanics analysis.
- 35.Popel A. S. and Johnson P. C., Annu. Rev. Fluid Mech. 37, 43 (2005). 10.1146/annurev.fluid.37.042604.133933 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bartosz G., Soszynski M., and Wasilewski A., Mech. Ageing and Dev. 19, 45 (1982). 10.1016/0047-6374(82)90049-5 [DOI] [PubMed] [Google Scholar]
- 37.Pantaleo A., De Franceschi L., Ferru E., Vono R., and Turrini F., J. Proteomics 73, 445 (2010). 10.1016/j.jprot.2009.08.011 [DOI] [PubMed] [Google Scholar]
- 38.Mohandas N., Clark M. R., Jacobs M. S., and Shohet S. B., J. Clin. Invest. 66, 563 (1980). 10.1172/JCI109888 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mohandas N. and Chasis J., Semin. Hematol. 30, 171 (1993). [PubMed] [Google Scholar]
- 40.Bosch F. H., Werre J. M., Schipper L., Roerdinkholderstoelwinder B., Huls T., Willekens F. L. A., Wichers G., and Halie M. R., Eur. J. Haematol. 52, 35 (1994). 10.1111/j.1600-0609.1994.tb01282.x [DOI] [PubMed] [Google Scholar]
- 41.Mokken F. C., Kedaria M., Henny C. P., Hardeman M. R., and Gelb A. W., Ann. Hematol. 64, 113 (1992). 10.1007/BF01697397 [DOI] [PubMed] [Google Scholar]
- 42.Sui, Y. , Chew Y. T., Roy P., Cheng Y. P., and Low H. T., Phys. Fluids 20, 112106 (2008). 10.1063/1.3026569 [DOI] [Google Scholar]
- 43.Fedosov D. A., Pan W., Caswell B., Gompper G., and Karniadakis G. E., Proc. Natl. Acad. Sci. U. S. A. 108, 11772 (2011). 10.1073/pnas.1101210108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bagchi P. and Yazdani A. Z., Eur. Phys. J. E: Soft Matter 35, 103 (2012). 10.1140/epje/i2012-12103-1 [DOI] [PubMed] [Google Scholar]
- 45.Peng Z. L., Mashayekh A., and Zhu Q., J. Fluid Mech. 742, 96–118 (2014). 10.1017/jfm.2014.14 [DOI] [Google Scholar]
- 46.Cordasco D., Yazdani A., and Bagchi P., Phys. Fluids 26, 041902 (2014). 10.1063/1.4871300 [DOI] [Google Scholar]
- 47.Deen W. M., Analysis of Transport Phenomena ( Oxford University Press, New York, 1998). [Google Scholar]
- 48.Brenner H., Chem. Eng. Sci. 19, 703 (1964). 10.1016/0009-2509(64)85084-3 [DOI] [Google Scholar]
- 49.Canham P. B. and Burton A. C., Circ. Res. 22, 405 (1968). 10.1161/01.RES.22.3.405 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1063/1.4904058E-BIOMGB-8-030406, for example, high speed videos, details of image analysis and behavior classification, additional experimental measurements, and details of the rigid body mechanics analysis.