Abstract
Experimental data for the density, viscosity, refractive index and surface tension of four sulfonium- and ammonium-based Ionic Liquids (ILs) with the common bis(trifluoromethylsulfonyl)imide anion were measured in the temperature range between 288.15 and 353.15 K and at atmospheric pressure. The ILs considered include butyltrimethylammonium bis(trifluoromethylsulfonyl)imide, [N4111][NTf2], tributylmethylammonium bis(trifluoromethylsulfonyl)imide, [N4441][NTf2], diethylmethylsulfonium bis(trifluoromethylsulfonyl)imide, [S221][NTf2], and triethylsulfonium bis(trifluoromethylsulfonyl)imide, [S222][NTf2]. Based on the gathered results and on data taken from literature, the impact of the cation isomerism and of the size of the aliphatic tails, as well as the effect resulting from the substitution of a nitrogen by a sulfur atom as the cation central atom, on the thermophysical properties of sulfonium- and ammonium-based ILs is here discussed. Remarkably, more symmetric cations present a lower viscosity for the same, and sometimes even for higher, alkyl chain lengths at the cation. Additional derivative properties, such as the isobaric thermal expansion coefficient, the surface thermodynamic properties and the critical temperature for the investigated ILs were also estimated and are presented and discussed.
Keywords: Ionic liquids, Density, Viscosity, Refractive index, Surface tension
1. Introduction
Ionic liquids (ILs) are a class of neoteric solvents [1] composed of large organic cations and organic/inorganic anions that cannot easily form an ordered crystal and thus remain liquid at or near room temperature. These unique solvents are alluring interest as greener alternatives to customary organic solvents with the aim of supporting more environmentally friendly processes. Room temperature ILs are often referred to as ‘designer solvents’ due to the possibility of tuning their physical and chemical properties through a wise combination of cations, anions and/or the introduction of functional groups [1].
Novel applications of ILs continue to be regularly projected based on their excellent properties, such as negligible vapor pressure [2,3], non-flammability [4], high ionic conductivity, high solvation capacity, stability at high temperatures [5], wide liquid electrochemical windows [6], and wide liquid temperature ranges [7]. Based on these interesting properties, ILs are therefore a possible alternative for conventional solvents in separation, engineering and biotechnological processes [8–13], in electrochemistry [14,15], and as catalysts [16], thermo-fluids [17] or sensors [18].
Amongst different ILs, bis(trifluoromethylsulfonyl)imide-based ILs, [NTf2]-based ILs, have been reported to be convenient for various practical applications, such as in lithium ion batteries [19,20], dye-sensitized solar cells (DSSC) [21–23] and electric double layer capacitors [24,25]. The weakly coordinating [NTf2] anion induces a substantial depression in the melting point of the corresponding ILs, partially due to the charge delocalization that extends from the central nitrogen atom to the neighboring sulfur atoms, and, to a less extent, to the oxygen atoms. This adds a shielding effect by the oxygen atoms and the terminal –CF3 groups and reduces the columbic interactions, while increasing the ion mobility. [NTf2]-based ILs are also appropriate alternatives for apolar organic molecular liquids [26] because of their high hydrophobicity and chemical stability against moisture [27].
To fully optimize the wide range of applications for [NTf2]-based ILs, the knowledge of their thermophysical properties, viz. density, viscosity, refractive index, surface tension, conductivity and critical temperature, are of high importance, especially for any industrial design or lab application. Several studies reporting thermophysical properties for - and sulfonium-based ILs are available in literature [23,28–47]. In particular, sulfonium-based ILs are generating substantial interest as potential alternatives for their ammonium counterparts due to practical benefits including higher chemical and electrochemical stabilities [48,49]. Matsumoto et al. [45] investigated the differences upon densities, viscosities, conductivities, and thermal stability between ammonium- and sulfonium-based ILs. In contrast to most neutral molecular liquids, where the substitution of a constituent atom by a heavier one leads to a viscosity increase, the authors [45] reported lower viscosities and higher conductivities for the sulfonium-based ILs when compared to ammonium-based compounds. Similar observations were made by Lee et al. [23] on the physical and electro-chemical properties of sulfonium- and ammonium-based cations combined with the [NTf2] anion. The authors [23] reported that the sulfonium-based ILs present better performances for DSSCs than those with ammonium-based electrolytes. Another report [50] indicated that trialkylsulfonium salts based on the dicyanamide anion have lower viscosities in comparison with many other ILs, from 20 to 60 mPa·s at 293.15 K, which renders sulfonium-based ILs as highly useful for low temperature applications.
This work aims at understanding, using the data here measured and other retrieved from literature, the impact of isomerization, as well as the effect resulting from the substitution of a nitrogen by a sulfur atom as the cation’s central atom on the ILs thermophysical properties. To this end, density, viscosity, refractive index and surface tension data of four sulfonium- and ammonium-based ILs with the [NTf2] anion were measured in the temperature range between 283.15 and 353.15 K and at atmospheric pressure. Additional derivative properties, such as the isobaric thermal expansion coefficient, the surface thermodynamic properties and critical temperature of all ILs studied were also estimated. For the density, viscosity and refractive index experimental data, further comparisons with the results given by the Gardas and Coutinho group contribution methods [51,52] were carried out and new parameters are here proposed.
2. Materials and methods
2.1. Materials
Four ILs were studied in this work, namely butyltrimethylammonium bis(trifluoromethylsulfonyl)imide, [N4111][NTf2], tributylmethylammonium bis(trifluoromethylsulfonyl)imide, [N4441][NTf2], diethylmethylsulfonium bis(trifluoromethylsulfonyl)imide, [S221][NTf2], and triethylsulfonium bis(trifluoromethylsulfonyl)imide, [S222][NTf2]. The ionic structures of the studied ILs and corresponding designations are presented in Table 1. The ILs were acquired from IoLiTec with mass fraction purities higher than 99%.
Table 1.
Ionic structure, compound description, molecular weight, water content and purity of the studied ILs.
| IL | Ionic structure |
|---|---|
| butyltrimethylammonium bis(trifluoromethylsulfonyl)imide [N4111][NTf2] (396.37 g·mol−1; water wt% = 0.0253; 99%) |

|
| tributylmethylammonium bis(trifluoromethylsulfonyl)imide [N4441][NTf2] (480.53 g·mol−1; water wt% = 0.0875; 99%) |

|
| diethylmethylsulfonium bis(trifluoromethylsulfonyl)imide [S221][NTf2] (385.37 g·mol−1; water wt% = 0.0510; 99%) |

|
| triethylsulfonium bis(trifluoromethylsulfonyl)imide [S222][NTf2] (399.39 g·mol−1; water wt% = 0.0463; 99%) |

|
The water content plays an important role in the IL properties, such as surface tension and viscosity [33,53–55], and significant deviations can be found due to small amounts of water. In order to remove traces of water and volatile compounds from the ILs, individual samples of each fluid were dried at moderate temperature (≈ 313 K), vacuum (≈ 1 Pa) and under continuous stirring, for a minimum period of 48 h. After this purification procedure, and after the thermophysical properties measurements, the purity of each IL was checked by 1H, 19F and 13C NMR to assure that no degradation occurred. The final IL water content, after the drying step and immediately before the measurements, was determined with a Metrohm 831 Karl Fischer coulometer (using the Hydranal - Coulomat AG from Riedel-de Haën as analyte). The average water content and the molecular weight of each IL are presented in Table 1.
2.2. Experimental Section
2.2.1 Density and Viscosity
Density (ρ) and dynamic viscosity (η) measurements were carried out using an automated SVM3000 Anton Paar rotational Stabinger viscometer-densimeter in the temperature range from 283.15 to 353.15 K and at atmospheric pressure (≈ 0.1 MPa). The absolute uncertainty in density is ±5 × 10−4 g·cm−3, and the relative uncertainty in dynamic viscosity is ±1%. The relative uncertainty in temperature is within ±0.02 K. Further details about the use of the equipment and methodologies for the determination of densities and viscosities can be found elsewhere [53,56].
2.2.2. Refractive Index
Measurements of refractive index (nD) were performed at 589.3 nm using an automated Abbemat 500 Anton Paar refractometer, able to measure either liquid or solid samples. Refractive index measurements were carried out in the temperature range from 283.15 to 353.15 K and at atmospheric pressure. The Abbemat 500 Anton Paar refractometer uses reflected light to measure the refractive index, where the sample on the top of the measuring prism is irradiated from different angles by a light-emitting diode (LED). The maximum deviation in temperature is ±0.01 K, and the maximum uncertainty in the refractive index measurements is ±2·10−5 nD. The validity of the equipment to determine accurate refractive indices of IL samples is supported by the previously measured data for other ILs published elsewhere [57–59].
2.2.3. Surface Tension
The surface tensions of each IL were determined through the analysis of the shape of a pendant drop using a Data physics contact angle system, OCA-20 (Data Physics Instruments GmbH, Germany). Pendant drops were created using a Hamilton DS 500/GT syringe connected to a Teflon coated needle placed inside an aluminium air chamber capable of maintaining the temperature within ±0.1 K. The temperature was attained by circulating water in the double jacketed aluminium cell by means of a Julabo F-25 water bath. The temperature inside the aluminium chamber was measured with a Pt100 within ±0.1 K which is at a distance of approximately 2 cm of the drop. The surface tension measurements were performed in the temperature range from 293 to 344 K and at atmospheric pressure. After reaching a specific temperature, the measurements were carried out after 30 min to guarantee the thermal equilibrium. Silica gel was kept inside the air chamber to avoid the absorption of moisture. For the surface tension determination, at each temperature and for each IL, at least three drops were formed and analyzed. For each drop, an average of 100 images was additionally captured. The analysis of the drop shape was achieved with the software modules SCA 20. The required density data which are used in the surface tensions measurements were those determined in this work. The equipment was previously validated through the measurement of the surface tension of ultra-pure water, decane and dodecane, as well as with a large variety of ILs [59,60].
3. Results and discussions
3.1. Density
The density measurements for the studied ILs were carried out in the temperature range from (283.15 to 353.15) K, at atmospheric pressure, and the respective values are reported in Table 2 and illustrated in Fig. 1. Similar to what is observed for other tretraalkylammonium [23,28,31,33–35,41] and trialkylsulfonium [23,42,46,47] ILs, the density decreases with the cation alkyl chain length increase and, to a lower extent, with the temperature increase (at least on the temperature range evaluated), as shown in Fig. 1. Furthermore, despite the lower number of alkyl chains, the higher density of the central atom of the sulfonium-based ILs, compared to the ammonium ones, lead to higher densities.
Table 2.
Densities, ρ (kg·m−3), molar volumes, Vm (m3·mol−1), viscosities, η (mPa·s), and refractive index, nD, of the studied ILs as a function of temperature and at atmospheric pressure.
| [N4111][NTf2] | [N4441][NTf2] | [S221][NTf2] | [S222][NTf2] | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||
| T (K) | ρ | 106 Vm | η | n D | ρ | 106 Vm | η | n D | ρ | 106 Vm | η | n D | ρ | 106 Vm | η | n D |
| 283.15 | 1407.8 | 281.6 | 254.2 | 1.41220 | 1276.0 | 376.6 | 2049.8 | 1.43080 | 1517.3 | 254.0 | 78.3 | 1.42745 | 1477.0 | 270.4 | 64.4 | 1.43056 |
| 288.15 | 1403.2 | 282.5 | 184.6 | 1.41083 | 1271.7 | 377.9 | 1264.0 | 1.42933 | 1512.2 | 254.8 | 62.1 | 1.42597 | 1472.0 | 271.3 | 51.1 | 1.42906 |
| 293.15 | 1398.7 | 283.4 | 137.7 | 1.40945 | 1267.3 | 379.2 | 819.2 | 1.42787 | 1507.2 | 255.7 | 49.9 | 1.42452 | 1467.1 | 272.2 | 41.1 | 1.42765 |
| 298.15 | 1394.2 | 284.3 | 105.2 | 1.40818 | 1262.8 | 380.5 | 538.9 | 1.42643 | 1502.3 | 256.5 | 41.1 | 1.42325 | 1462.1 | 273.2 | 33.9 | 1.42632 |
| 303.15 | 1389.8 | 285.2 | 82.0 | 1.40676 | 1258.4 | 381.9 | 369.3 | 1.42491 | 1497.3 | 257.4 | 34.1 | 1.42168 | 1457.3 | 274.1 | 28.2 | 1.42472 |
| 308.15 | 1385.4 | 286.1 | 65.2 | 1.40538 | 1254.1 | 383.2 | 260.4 | 1.42338 | 1492.4 | 258.2 | 28.7 | 1.42026 | 1452.4 | 275.0 | 23.8 | 1.42325 |
| 313.15 | 1381.0 | 287.0 | 52.7 | 1.40405 | 1249.9 | 384.5 | 189.5 | 1.42194 | 1487.6 | 259.1 | 24.4 | 1.41886 | 1447.6 | 275.9 | 20.3 | 1.42185 |
| 318.15 | 1376.6 | 287.9 | 43.2 | 1.40273 | 1245.8 | 385.7 | 139.6 | 1.42047 | 1482.8 | 259.9 | 21.0 | 1.41744 | 1442.8 | 276.8 | 17.5 | 1.42044 |
| 323.15 | 1372.3 | 288.8 | 35.9 | 1.40142 | 1241.7 | 387.0 | 105.6 | 1.41902 | 1478.0 | 260.7 | 18.2 | 1.41606 | 1438.1 | 277.7 | 15.2 | 1.41906 |
| 328.15 | 1368.0 | 289.7 | 30.2 | 1.40006 | 1237.6 | 388.3 | 81.5 | 1.41758 | 1473.2 | 261.6 | 15.9 | 1.41468 | 1433.4 | 278.6 | 13.4 | 1.41767 |
| 333.15 | 1363.7 | 290.7 | 25.7 | 1.39877 | 1233.6 | 389.5 | 64.1 | 1.41613 | 1468.5 | 262.4 | 14.0 | 1.41331 | 1428.7 | 279.5 | 11.8 | 1.41629 |
| 338.15 | 1359.5 | 291.6 | 22.0 | 1.39747 | 1229.5 | 390.8 | 51.1 | 1.41468 | 1463.8 | 263.3 | 12.5 | 1.41195 | 1424.0 | 280.5 | 10.5 | 1.41490 |
| 343.15 | 1355.2 | 292.5 | 19.1 | 1.39616 | 1225.5 | 392.1 | 41.4 | 1.41324 | 1459.1 | 264.1 | 11.1 | 1.41058 | 1419.4 | 281.4 | 9.4 | 1.41353 |
| 348.15 | 1351.0 | 293.4 | 16.7 | 1.39486 | 1221.5 | 393.4 | 34.0 | 1.41180 | 1454.5 | 265.0 | 10.0 | 1.40925 | 1414.8 | 282.3 | 8.5 | 1.41215 |
| 353.15 | 1346.8 | 294.3 | 14.7 | 1.39358 | 1217.5 | 394.7 | 28.3 | 1.41040 | 1449.8 | 265.8 | 9.0 | 1.40793 | 1410.2 | 283.2 | 7.7 | 1.41077 |
Standard temperature uncertainty is u (T) = ±0.02 K and the combined expanded uncertainties, Uc, are Uc (ρ) = ±0.5 kg·m−3; Uc (η) = 0.35% ; Uc (nD) = 2 × 10−5 with an approximately 95% level of confidence.
Fig. 1.
Density as a function of temperature (left) and relative deviations (right) between the experimental data from this work and those available in the literature [23,28,32–35,37,39,40,42,46,47]. The solid lines represent the Gardas and Coutinho [51] group contribution method.
The relative deviations between the density data measured in this work and those available in the literature [23,28,32–35,37,39,40,42,46,47] are displayed in Fig. 1. Experimental data for [N4111][NTf2] and [N4441][NTf2] are in good agreement with the available literature values, with absolute average relative deviations ranging from (0.0018 to 1.4)% [28,32–35,37,39,40]. The absolute average relative deviations towards [N4111][NTf2] reported by Kilaru et al. [28], Tokuda et al. [32], Jacquemin et al. [33], Wandschneider et al. [34], Deng et al. [35] and Jacquemin et al. [40] are 1.4%, 0.11%, 0.21%, 0.024%, 0.16% and 0.0018%, respectively. The data from Kilaru et al. [28] present the higher deviations found, that seem to be related with the high amount of water present in the authors’ sample (1080 ppm). The absolute average relative deviations towards the [N4441][NTf2] previously measured by Chen et al. [37] and Anthony et al. [39] are 0.41% and 0.78%, respectively. On the other hand, the experimental data for [S221][NTf2] and [S222][NTf2] are scarce [23,42,46,47]. The only data available have been reported at a single temperature and were measured using an experimental technique (pycnometer) that inherently carries out higher uncertainties. Absolute relative deviations of 5.4% and 3.6% for [S221][NTf2] were found against the data of Fang et al. [46] and Han et al. [47], respectively. Absolute relative deviations of 1.9%, 0.14% and 5.3% were observed towards the data reported for [S222][NTf2] by Lee et al. [23], Matsumoto et al. [42] and Han et al. [47], respectively.
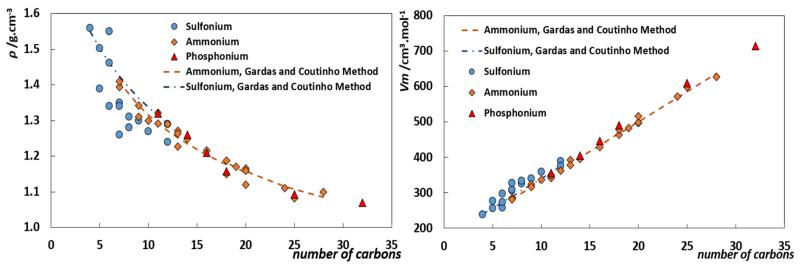
The molar volumes of the studied ILs, Vm, reported in Table 2, increase with the effective cation size in the order: [S221]+ < [S222]+ < [N4111]+ < [N4441]+. As depicted in Fig. 2, the ILs evaluated here follow the well-established concept that the density of ILs is an additive property with ion-independent molar volume increments of circa to 17.1 cm3·mol−1 per methylene addition to the IL cation [61–67].
Fig. 2.
Density and molar volume as a function of the number of carbons at the cation, for sulfonium-, ammonium- and phosphonium-based ILs with the common NTf2 anion, at 298.15 K [8,23,28,30,31,33–35,41,42,46,47,51,68–73].
The density data for the sulfonium-based ILs, with the common [NTf2] anion, present some discrepancies among different literature sources, as depicted in Fig. 2. Nonetheless, the overall trend observed suggests that the sulfonium-based ILs follow the same trend commonly reported for other ILs families, like imidazolium-, phosphonium- and ammonium-based ILs [31,57,68,69], with the above mentioned ion independent molar volume increments per –CH2 group.
Gardas and Coutinho [51] extended the Ye and Shreeve [74] approach to the estimation of IL densities for a wide range of temperatures, from 288.15 to 353.15 K, pressures, from (0.10 to 100) MPa, and several ILs families according to the following equation,
| (1) |
where ρ is the density in kg·m−3; M the molecular weight in kg·mol−1; N the Avogadro constant; V the molecular volume in Å3, T the temperature in K; and p the pressure in MPa. The universal coefficients a, b and c are 0.8005 ± 0.0002, 6.652 × 10−4 ± 0.007 × 10−4 K−1 and −5.919 × 10−4 ± 0.024 × 10−4 MPa−1, respectively, at a 95% confidence level.
Molecular volumes for the new cations were fitted to the measured density data and the values obtained are in good agreement with the experimental data, as shown in Fig. 1, with an absolute average relative deviation of 0.52% for [N4111][NTf2], 0.80% for [N4441][NTf2], 0.13% for [S221][NTf2] and 0.17% for [S222][NTf2]. The estimated cation volumes for the studied ILs, reported in Table 3, were also fitted against experimental data taken from literature for ammonium- and sulfonium-based ILs, with the common [NTf2] anion [51,66]. For the tetraalkylammonium ILs, the cation molar volume was fitted against experimental data reported by 11 literature sources [8,23,28,30,31,33–35,41,70,71]. For the trialkylsulfonium ILs, due to the discrepancies observed for the available experimental data, the cation’s molar volume was determined by fitting Eq. (1) only against the data from Matsumoto et al. [42], Fang et al. [46] and the data here reported. The molar volumes proposed for the new groups are able to provide predictions for the density of tetraalkylammonium- and trialkylsulfonium-based ILs with an absolute average relative deviation of 1.3% and 5.20%, respectively, and as depicted in Fig. 1.
Table 3.
Ionic Volumes, V, determined using the Gardas and Coutinho Group Contribution Model [51] for the studied ILs.
Thermal Expansion Coefficient
The isobaric thermal expansion coefficients, αp, of the studied ILs, which reflect the ILs volumetric changes with temperature, were calculated from the density dependency with temperature with the following equation,
| (2) |
where ρ is the density in kg·m−3, T the temperature in K, and p a fixed pressure.
The values of αp are presented in Table 4. The values obtained vary between 6.3 and 6.7 × 10−4 K−1 and are in the same order of magnitude, (5 to 7) × 10−4 K−1, of those reported for other ILs families, like ammonium-, imidazolium-, pyridinium- and pyrrolidinium-based ILs [31,57,59,75–78]. These values are considerably lower than those of molecular organic solvents and higher than those of classical molten salts [79]. Although the isobaric thermal expansion coefficients are very similar, their increase in the following IL cation orders [N4441]+ > [N4111]+ and [S222]+ > [S221]+, indicate that the increase of the effective alkyl chains size leads to a thermal expansion increase. The isothermal expansion increase with the increase in the alkyl chains length denotes, similar to other ILs [57,80], important entropic effects. Nonetheless, the results show that the alkyl side chain length presents a lower impact on the thermal expansion coefficient than that observed for the anion replacement and as discussed elsewhere [57,77,78,81].
Table 4.
Coefficients of thermal expansion, αp, for the studied ILs.
| IL | 104·(αp ± σ)a (K−1) |
|---|---|
| [N4111][NTf2] | 6.32 ± 0.09 |
| [N4441][NTf2] | 6.70 ± 0.10 |
| [S221][NTf2] | 6.49 ± 0.09 |
| [S222][NTf2] | 6.61 ± 0.10 |
Expanded uncertainty with an approximately 95% level of confidence.
3.2. Viscosity
Viscosity is an important property of ILs as it impacts ionic conductivity and mass transport phenomena, thereby tuning their suitability for particular applications and thus stands as a key point on efficient processes development. The experimental viscosity data for the studied ILs is reported in Table 2 and depicted in Fig. 3.
Fig. 3.
Viscosity data for the studied ILs. The solid lines represent the Vogel-Tammann-Fulcher (VTF) group contribution correlation [52].
As commonly observed, viscosity markedly decreases with the temperature increase. The viscosity decreases in the [NTf2]-based ILs in the following order: [N4441]+ >> [N4111]+ >>> [S221]+ > [S222]+. Furthermore, the sulfonium-based ILs present viscosities at least one order of magnitude lower than those of the ammonium ILs, as previously observed in literature [23,30].
The relative deviations between the data measured in this work and those reported in literature [23,32,33,35–37,42,44,46,47] are depicted in Fig. 4. Viscosity measurements are highly sensitive to the presence of impurities (particularly water) and therefore larger deviations from the literature data are observed. Experimental data for [N4111][NTf2] and [N4441][NTf2] are in good agreement with those reported in literature [32,33,35–37], with absolute average relative deviations ranging from (2.8 to 6.0)%. Experimental data for [S221][NTf2] and [S222][NTf2], on the other hand, present important discrepancies with literature data [23,42,44,46,47]. Apart from viscosities reported by Lee et al. [23] and Okoturo et al. [44], for [S222][NTf2], with deviations of 4.2% and 7.4%, respectively, the remaining experimental data present deviations of 13.0% for [S222][NTf2], reported by Matsumoto et al. [42], and 17.4% and 71.0% for [S221][NTf2] reported by Fang et al. [46] and Han et al. [47], respectively. Nonetheless, these deviations seem related to either the purity of the samples, temperature control or the measurement method used.
Fig. 4.
Relative deviations between the experimental viscosity data of this work and those available in the literature [23,32,33,35–37,42,44,46,47].
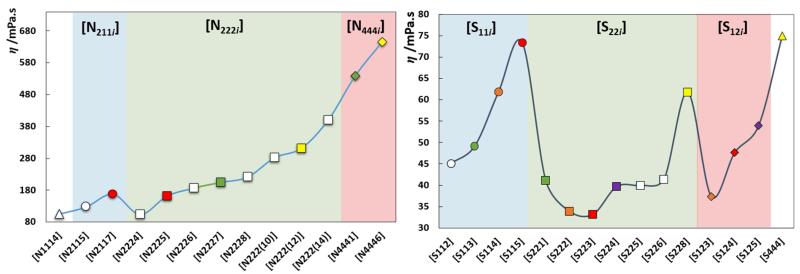
Even though the experimental data present large discrepancies among different literature sources, as depicted in Fig. 4, one can assume that the trend depicted in Fig. 5 for ammonium- and sulfonium-based ILs with the [NTf2] anion, at 298.15 K, represents correctly the viscosity dependency on the length of the cation’s alkyl chains. Similar to what was observed previously for imidazolium-based ILs [82], the symmetric sulfonium-ILs present lower viscosities than their asymmetric counterparts. Furthermore, this symmetric/asymmetric effect on the viscosity is observed not only within the same sulfonium series, like [S22i][NTf2], but also for isomers (symbols with the same color in Fig. 5) with viscosities decreasing as the cation’s symmetry increases.
Fig. 5.
Viscosity as function of the IL cation for ammonium and sulfonium-based ILs with the [NTf2] anion, at 298.15 K. Symbols with the same colour represent isomers, the remaining compounds are presented as white symbols.
To the best of our knowledge no viscosity data are available for symmetric ammonium ILs. Nonetheless, the experimental data available reveal an increase of the viscosity (higher energy barriers arising from the increase of shear stress) with the alkyl side chain length increase and that can be related to the increase of the conformational entropy and possibility of alkyl chain folding. This behavior is similar to that observed for the long alkyl chain imidazolium derivatives previously reported [83,84].
The description of viscosities for the ILs studied was carried out using the group contribution method, based on the Vogel-Tammann-Fulcher (VTF) correlation, proposed by Gardas and Coutinho [52] and represented by,
| (3) |
where η is the dynamic viscosity in mPa·s; T the temperature in K; and Aη , Bη and T0η are adjustable parameters.
As mentioned before, viscosity data are particularly sensitive to impurities and, therefore, important discrepancies among different literature sources are observed. Furthermore, the viscosities for the ammonium- and sulfonium-based ILs series present an important dependence with the number of alkyl chains and their length in contrast with the cation’s total number of carbons, as depicted in Fig. 5, which prevents the determination of a set of additive parameters. Thus, the parameters Aη , Bη and T0η were determined, for each IL, by fitting the VTF method against our experimental data and are presented in Table 5. The fitting of the data against the experimental results is depicted in Fig. 3 and average absolute relative deviations of 0.10% for [N4111][NTf2], 0.56% for [N4441][NTf2], 0.14% for [S221][NTf2] and 0.21% for [S222][NTf2] were obtained.
Table 5.
Vogel-Fulcher-Tammann correlation parameters, Aη, Bη and T0η, for the viscosity of the studied ILs.
| IL | Aη | Bη (K) | T0η (K) |
|---|---|---|---|
| [N4111][NTf2] | −1.7331 | 789.4235 | 174.58 |
| [N4441][NTf2] | −2.8227 | 1045.168 | 183.49 |
| [S221][NTf2] | −1.7099 | 771.3218 | 155.93 |
| [S222][NTf2] | −1.7345 | 733.9335 | 158.50 |
3.3. Refractive index
The refractive index specifies the dielectric response to an electrical field induced by electromagnetic waves (light) and is thus an optical property of materials. The experimental refractive index data of the investigated ILs are shown in Fig. 6 and reported in Table 2 for the ammonium- and sulfonium-based ILs. The refractive indices were measured upward and downward on temperature, with no hysteresis effects observed, and within the temperature range from 283.15 to 353.15 K. To the best of our knowledge no refractive index data are available for the studied ILs. As commonly observed, the refractive index decreases with the temperature increase. The refractive index values for the [NTf2]-based ILs decrease in the follow cationic sequence: [N4441]+ ≈ [S222]+ > [S221]+ > [N4111]+.
Fig. 6.
Refractive index data for the studied ILs. The solid lines represent the Gardas and Coutinho group contribution method [52].
The refractive index for the ILs studied was also fitted with the group contribution method proposed by Gardas and Coutinho [52], which results are depicted in Fig. 6, and that follow a linear function of the form,
| (4) |
| (5) |
| (6) |
where ni is the number of groups of type i and k is the total number of different groups in the molecule. The estimated parameters ai,nD and bi,nD for the cations of the studied ILs are given in Table 6 along with the anionic volume previously reported [52]. The average absolute relative deviation between the experimental and the fitting data are 0.0037% for [N4111][NTf2], 0.0028% for [N4441][NTf2], 0.0051% for [S221][NTf2] and 0.0051% for [S222][NTf2].
Table 6.
Group contribution parameters, ai,nD and bi,nD, determined using the Gardas and Coutinho group contribution method [52] for the refractive index.
| Ionic Species | a i,nD | bi,nD (× 10−4 K−1) |
|---|---|---|
| Cation | ||
|
| ||
| [N4111]+ | 1.4246 | 1.909 |
| [N4441]+ | 1.4510 | 2.180 |
| [S221]+ | 1.4434 | 2.037 |
| [S222]+ | 1.4476 | 2.074 |
|
| ||
| Anion | ||
|
| ||
| [NTf2]− [52] | 0.0628 | 0.775 |
The derived molar refractions, Rm, free volumes, fm, and polarizabilities were additionally determined as follows [85–87]:
| (7) |
| (8) |
| (9) |
where α0 is the electronic polarizability, ε0 the vacuum permittivity, ρ the compound’s density, M the molecular weight and NA the Avogadro number.
The free volumes and molar refraction of ammonium-based ILs are higher than those verified for the sulfonium-based ILs, as summarized in Table 7. Furthermore, similar to the molar volumes, the molar refraction and free volume increase with the effective cation size in the order: [S221]+ < [S222]+ < [N4111]+ < [N4441]+.
Table 7.
Refractive indices, isotropic polarizabilities, derived molar refractions, Rm, and free volumes, fm, at 298.15 K and atmospheric pressure.
| IL | n D | Polarizability (bohr3) | Rm (cm3·mol−1) | fm (cm3·mol−1) |
|---|---|---|---|---|
| [N4111][NTf2] | 1.40818 | 187.70 | 70.16 | 214.14 |
| [N4441][NTf2] | 1.42643 | 261.06 | 97.59 | 282.94 |
| [S221][NTf2] | 1.42325 | 174.84 | 65.36 | 191.16 |
| [S222][NTf2] | 1.42632 | 187.36 | 70.04 | 203.13 |
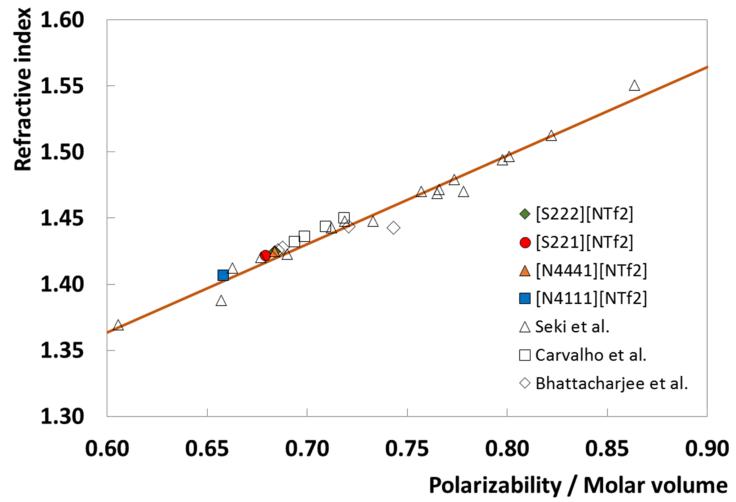
Based on the suggestion that refractive indices are an indication of the dielectric response to an electrical field, induced by electromagnetic waves, and that refractive indices can be deliberated as the first order approximation response to electronic polarization within an instantaneous time scale, Seki et al. [88] evaluated the refractive indices of 17 ILs, as a function of temperature, against theoretical polarizabilities obtained through ab initio calculations. The authors [88] proposed a correlation between the refractive index and the polarizability normalized in terms of the molecular volume. Following the work of Seki et al. [88] the correlation was extended, previously [59,69] for ammonium-, phosphonium-, piperidinium- and pyridinium-based ILs and now to the ILs studied here, showing that the proposed correlation is able to predict the refractive index of different ILs from polarizability and vice-versa, within the uncertainty of the correlation, and as depicted in Fig. 7.
Fig. 7.
Relationship between the refractive index and polarizability/molecular volume for different ILs at 303.15 K. The unfilled triangles and the solid line represent the experimental data and the correlation of Seki et al. [88]. The unfilled squares and diamonds represent the experimental data reported in previous works [59,69].
3.4. Surface tension
The experimental surface tension data measured for all the studied ILs are presented in Table 8 and depicted in Fig. 8. The surface tension values for the [NTf2]-based ammonium ILs decrease in the following cationic sequence: [N4111]+ > [N4441]+. For the sulfonium-based ILs the surface tension decreases according to: [S221]+ > [S222]+. Overall, the surface tension decreases in the following order: [S221]+ > [S222]+ > [N4111]+ > [N4441]+. The smaller trialkylsulfonium ILs present higher surface tension than the more voluminous tetraalkylammonium ILs, indicating thus a better structural organization of the IL at the air-liquid interface and a higher surface free energy and stronger intermolecular interactions. In addition, an increase in the cation alkyl side chain length leads to a decrease on the surface tension. It is well-established that the surface tension is intrinsically related with the part of the molecule that is present at the interface and, in the case of ILs, the cation has an important role [89,90]. The decrease of the surface tension with the increase of the alkyl chains length, within an IL cation family, indicates the influence of the chain length on the surface arrangement, intermolecular interactions and, thus, on the surface energy. This behavior, previously reported for other ILs families [90–94] is also observed here for the studied ammonium and sulfonium-based ILs.
Table 8.
Surface tension, γ, for the studied ILs as a function of temperature and at atmospheric pressure.
| [N4111][NTf2] | [N4441][NTf2] | [S221][NTf2] | [S222][NTf2] | ||||
|---|---|---|---|---|---|---|---|
|
| |||||||
| T (K) | γ (mN·m−1) | T (K) | γ (mN·m−1) | T (K) | γ (mN·m−1) | T (K) | γ (mN·m−1) |
| 293.2 | 33.4 | 293.3 | 30.8 | 293.2 | 35.7 | 293.3 | 35.5 |
| 298.2 | 33.2 | 298.2 | 30.6 | 298.2 | 35.5 | 298.2 | 35.2 |
| 303.2 | 33.0 | 303.2 | 30.2 | 303.2 | 35.3 | 303.2 | 35.0 |
| 313.1 | 32.5 | 313.2 | 29.7 | 313.1 | 34.8 | 313.1 | 34.4 |
| 323.1 | 32.0 | 323.2 | 29.1 | 323.1 | 34.4 | 323.0 | 34.0 |
| 333.1 | 31.5 | 333.1 | 33.9 | 333.1 | 33.4 | ||
| 343.1 | 33.4 | 343.1 | 32.9 | ||||
Standard temperature uncertainty is u (T) = ±0.1 K and the surface tension expanded uncertainty is Uc (γ) = 0.1 mN·m−1, with an approximately 95% level of confidence.
Fig. 8.
Surface tension data for the studied ILs as a function of temperature (left) and relative deviations between this work experimental surface tension data and that available in the literature (right).
Surface tension values for [N4111][NTf2] have already been reported in literature by Kilaru et al. [28], using the Du Noüy ring method, and by Wandschneider et al. [34], using the pendant drop method. Average relative deviations between our data and those published by Kilaru et al. [28] and by Wandschneider et al. [34] of −13.0% and 2.8%, respectively, were found. To the best of our knowledge, surface tension data for the remaining ILs are here reported for the first time.
Surface thermodynamic properties
The surface thermodynamic properties, namely, the surface entropy and the surface enthalpy, were derived using the quasi linear dependence of the surface tension with temperature. The surface entropy, Sγ, can be calculated according to the following equation [95,96],
| (10) |
while the surface enthalpy, Hγ, according to [95,96],
| (11) |
where γ stands for the surface tension and T for the temperature.
The values of the thermodynamic functions for all of the ILs studied and the respective expanded uncertainties, derived from the slope of the curve γ = f(T) in combination with the law of propagation of uncertainties, are presented in Table 9 [97].
Table 9.
Surface thermodynamic functions of the studied ILs and estimated critical temperatures, using both Eötvös (Eot) [99] and Guggenheim (Gug) [100] empirical equations.
| IL | (Sγ ± σ)a (× 10−5 J·m−2·K−1) | (Hγ ± σ)a (× 10−2 J·m−2) | (Tc)Eot (K) | (Tc)Gug (K) |
|---|---|---|---|---|
| [N4111][NTf2] | 4.83 ± 0.02 | 4.76 ± 0.01 | 1252 ± 7 | 1134 ± 4 |
| [N4441][NTf2] | 5.68 ± 0.12 | 4.75 ± 0.04 | 1002 ± 18 | 953 ± 14 |
| [S221][NTf2] | 4.69 ± 0.07 | 4.95 ± 0.02 | 1403 ± 27 | 1219 ± 13 |
| [S222][NTf2] | 5.08 ± 0.03 | 5.04 ± 0.01 | 1277 ± 5 | 1141 ± 4 |
Expanded uncertainty at a 95% level of confidence.
The studied ILs reveal a remarkably low surface entropy when compared with molecular organic compounds which is in agreement to the surface enthalpy and entropy results previously reported for other ILs [59,89,90,93], including imidazolium, pryidinium, pyrrolodinium and piperidinium cation cores, with the surface entropy decreasing with the increase of the alkyl chain length. These values of low surface entropies are an indication of a high surface organization as well as a highly structured liquid phase. Moreover, the results of similar surface entropy and surface enthalpy observed, for the different IL families, are an effect of similar dependency of the surface tension with the temperature.
Estimated critical temperatures
The critical temperature of fluids is a relevant thermophysical property commonly used in corresponding state correlations involving equilibrium and transport properties [98]. However, taking into account the inherent nature of ILs together with negligible vapor pressures and relatively low decomposition temperatures, the direct determination of the critical temperatures of ILs is not feasible. Rebelo et al. [2] proposed the use of the Eötvös [99] and Guggenheim [100] equations to estimate the hypothetical critical temperature of ILs, as described below,
| (12) |
| (13) |
where Tc is the critical temperature, M the molecular weight, ρ the density, and K a fitted parameter. Both equations reveal the fact that the surface tension becomes null at the critical point and although an overestimation of the critical temperature is expected, since at the critical point the pressure becomes the critical pressure, these equations provide reasonable estimations [98,101]. The critical temperature values estimated from the surface tension data are summarized in Table 9 and present similar critical temperatures to other ILs.
4. Conclusions
Experimental data on density, viscosity, refractive index and surface tension for four ILs (two ammonium- and two sulfonium-based) with the common [NTf2] anion were measured in the temperature range between (283.15 and 353.15) K and at atmospheric pressure. The group contribution methods proposed by Gardas and Coutinho were used to fit the density and refractive index of the investigated ILs. Using the reported experimental data along with other taken from literature, the impact of the ILs isomerism and of the substitution of a nitrogen central atom by a sulfur one with variable chain lengths were analysed. All the properties are dependent on the cation alkyl chain length and on the central atom composing the IL cation. In general, the density and surface tension decrease with an increase of the size of the aliphatic moieties. The results reported also highlight the effect of the cation symmetry on viscosity, with the more symmetric cations presenting a lower viscosity for the same, and sometimes even for higher, chain lengths. The refractive indices are a quantitative measure of the prominence of the dispersive forces in the IL medium and hence the ILs with longer aliphatic moieties display higher refractive index values.
From the temperature dependence of the several properties, derivative properties, such as the isobaric thermal expansion coefficient, the surface thermodynamic properties, and the critical temperature of all ILs were further estimated and presented.
Acknowledgements
The authors acknowledge FEDER funds through the COMPETE operational program and Fundação para a Ciência e Tecnologia – FCT through the projects PTDC/QUI-QUI/121520/2010 and PEst-C/CTM/LA0011/2013. P.J.C. and A.B. also acknowledge FCT for their post-doctoral grants SFRH/BPD/82264/2011 and SFRH/BPD/77858/2011, respectively. M. G. Freire acknowledges the European Research Council (ERC) for the Starting Grant ERC-2013-StG-337753.
References
- [1].Welton T. Chem. Rev. 1999;99:2071–2084. doi: 10.1021/cr980032t. [DOI] [PubMed] [Google Scholar]
- [2].Rebelo LPN, Canongia Lopes JN, Esperança JMSS, Filipe E. J. Phys. Chem. B. 2005;109:6040–6043. doi: 10.1021/jp050430h. [DOI] [PubMed] [Google Scholar]
- [3].Seddon KR. J. Chem. Technol. Biotechnol. 1997;68:351–356. [Google Scholar]
- [4].Smiglak M, Reichert WM, Holbrey JD, Wilkes JS, Sun L, Thrasher JS, Kirichenko K, Singh S, Katritzky AR, Rogers RD. Chem. Commun. 2006:2554–2556. doi: 10.1039/b602086k. [DOI] [PubMed] [Google Scholar]
- [5].Baranyai KJ, Deacon GB, MacFarlane DR, Pringle JM, Scott JL. Aust. J. Chem. 2004;57:145–147. [Google Scholar]
- [6].Matsumoto K, Hagiwara R, Ito Y. Electrochem. Solid-State Lett. 2004;7:E41–E44. [Google Scholar]
- [7].Marsh K, Boxall J, Lichtenthaler R. Fluid Phase Equilib. 2004;219:93–98. [Google Scholar]
- [8].Berthod A, Ruiz-Angel MJ, Carda-Broch S. J. Chromatogr. A. 2008;1184:6–18. doi: 10.1016/j.chroma.2007.11.109. [DOI] [PubMed] [Google Scholar]
- [9].Kubota F, Goto M. Solvent Extr. Res. Dev. 2006;13:23–36. [Google Scholar]
- [10].Zhao H. Chem. Eng. Commun. 2006;193:1660–1677. [Google Scholar]
- [11].Greaves TL, Weerawardena A, Fong C, Krodkiewska I, Drummond CJ. J. Phys. Chem. B. 2006;110:22479–22487. doi: 10.1021/jp0634048. [DOI] [PubMed] [Google Scholar]
- [12].Schneider S, Hawkins T, Rosander M, Vaghjiani G, Chambreau S, Drake G. Energy & Fuels. 2008;22:2871–2872. [Google Scholar]
- [13].van Rantwijk F, Sheldon RA. Chem. Rev. 2007;107:2757–2785. doi: 10.1021/cr050946x. [DOI] [PubMed] [Google Scholar]
- [14].Hagiwara R, Lee J. Electrochemistry. 2007;75:23–34. [Google Scholar]
- [15].Xiang HF, Yin B, Wang H, Lin HW, Ge XW, Xie S, Chen CH. Electrochim. Acta. 2010;55:5204–5209. [Google Scholar]
- [16].Shen J, Wang H, Liu H, Sun Y, Liu Z. J. Mol. Catal. A Chem. 2008;280:24–28. [Google Scholar]
- [17].Crosthwaite JM, Aki SNVK, Maginn EJ, Brennecke JF. J. Phys. Chem. B. 2004;108:5113–5119. [Google Scholar]
- [18].Shvedene NV, Chernyshov DV, Pletnev IV. Russ. J. Gen. Chem. 2009;78:2507–2520. [Google Scholar]
- [19].Sakaebe H, Matsumoto H, Tatsumi K. J. Power Sources. 2005;146:693–697. [Google Scholar]
- [20].Matsumoto H, Sakaebe H, Tatsumi K, Kikuta M, Ishiko E, Kono M. J. Power Sources. 2006;160:1308–1313. [Google Scholar]
- [21].Kawano R, Matsui H, Matsuyama C, Sato A, Susan MABH, Tanabe N, Watanabe M. J. Photochem. Photobiol. A Chem. 2004;164:87–92. [Google Scholar]
- [22].Mikoshiba S, Murai S, Sumino H, Kado T, Kosugi D, Hayase S. Curr. Appl. Phys. 2005;5:152–158. [Google Scholar]
- [23].Lee CP, De Peng J, Velayutham D, Chang J, Chen PW, Suryanarayanan V, Ho K-C. Electrochim. Acta. 2013;114:303–308. [Google Scholar]
- [24].Ue M, Takeda M, Toriumi A, Kominato A, Hagiwara R, Ito Y. J. Electrochem. Soc. 2003;150:A499–A502. [Google Scholar]
- [25].Sato T, Masuda G, Takagi K. Electrochim. Acta. 2004;49:3603–3611. [Google Scholar]
- [26].Bonhôte P, Dias A-P, Papageorgiou N, Kalyanasundaram K, Grätzel M. Inorg. Chem. 1996;35:1168–1178. doi: 10.1021/ic951325x. [DOI] [PubMed] [Google Scholar]
- [27].Freire MG, Neves CMSS, Marrucho IM, Coutinho JAP, Fernandes AM. J. Phys. Chem. A. 2010;114:3744–3749. doi: 10.1021/jp903292n. [DOI] [PubMed] [Google Scholar]
- [28].Kilaru P, Baker GA, Scovazzo P. J. Chem. Eng. Data. 2007;52:2306–2314. [Google Scholar]
- [29].Kilaru PK, Scovazzo P. Ind. Eng. Chem. Res. 2008;47:910–919. [Google Scholar]
- [30].Sun J, Forsyth M, MacFarlane DR. J. Phys. Chem. B. 1998;102:8858–8864. [Google Scholar]
- [31].Machanová K, Boisset A, Sedláková Z, Anouti M, Bendová M, Jacquemin J. J. Chem. Eng. Data. 2012;57:2227–2235. [Google Scholar]
- [32].Tokuda H, Tsuzuki S, Susan MABH, Hayamizu K, Watanabe M. J. Phys. Chem. B. 2006;110:19593–19600. doi: 10.1021/jp064159v. [DOI] [PubMed] [Google Scholar]
- [33].Jacquemin J, Husson P, Padua a. a. H., Majer V. Green Chem. 2006;8:172–180. [Google Scholar]
- [34].Wandschneider A, Lehmann JK, Heintz A. J. Chem. Eng. Data. 2008;53:596–599. [Google Scholar]
- [35].Deng Y, Husson P, Delort A-M, Besse-Hoggan P, Sancelme M, Costa Gomes MF. J. Chem. Eng. Data. 2011;56:4194–4202. [Google Scholar]
- [36].Funston AM, Fadeeva TA, Wishart JF, Castner EW. J. Phys. Chem. B. 2007;111:4963–4977. doi: 10.1021/jp068298o. [DOI] [PubMed] [Google Scholar]
- [37].Chen PY, Hussey CL. Electrochim. Acta. 2004;49:5125–5138. [Google Scholar]
- [38].Matsumoto H, Yanagida M, Tanimoto K, Nomura M, Kitagawa Y, Miyazaki Y. Chem. Lett. 2000;2000:922–923. [Google Scholar]
- [39].Anthony JL, Anderson JL, Maginn EJ, Brennecke JF. J. Phys. Chem. B. 2005;109:6366–6374. doi: 10.1021/jp046404l. [DOI] [PubMed] [Google Scholar]
- [40].Jacquemin J, Husson P, Majer V, Costa Gomes MF. J. Solution Chem. 2007;36:967–979. [Google Scholar]
- [41].Ghatee MH, Bahrami M, Khanjari N. J. Chem. Thermodyn. 2013;65:42–52. [Google Scholar]
- [42].Matsumoto H, Matsuda T, Miyazaki Y. Chem. Lett. 2000;29:1430–1431. [Google Scholar]
- [43].Couadou E, Jacquemin J, Galiano H, Hardacre C, Anouti M. J. Phys. Chem. B. 2013;117:1389–1402. doi: 10.1021/jp308139r. [DOI] [PubMed] [Google Scholar]
- [44].Okoturo OO, VanderNoot TJ. J. Electroanal. Chem. 2004;568:167–181. [Google Scholar]
- [45].Matsumoto H, Sakaebe H, Tatsumi K. J. Power Sources. 2005;146:45–50. [Google Scholar]
- [46].Fang S, Yang L, Wei C, Peng C, Tachibana K, Kamijima K. Electrochem. Commun. 2007;9:2696–2702. [Google Scholar]
- [47].Han HB, Nie J, Liu K, Li WK, Feng WF, Armand M, Matsumoto H, Bin Zhou Z. Electrochim. Acta. 2010;55:1221–1226. [Google Scholar]
- [48].Paulsson H, Berggrund M, Svantesson E, Hagfeldt A, Kloo L. Sol. Energy Mater. Sol. Cells. 2004;82:345–360. [Google Scholar]
- [49].Wang P, Wenger B, Humphry-Baker R, Moser JE, Teuscher J, Kantlehner W, Mezger J, Stoyanov EV, Zakeeruddin SM, Grätzel M. J. Am. Chem. Soc. 2005;127:6850–6. doi: 10.1021/ja042232u. [DOI] [PubMed] [Google Scholar]
- [50].Gerhard D, Alpaslan SC, Gores HJ, Uerdingen M, Wasserscheid P. Chem. Commun. 2005:5080–5082. doi: 10.1039/b510736a. [DOI] [PubMed] [Google Scholar]
- [51].Gardas RL, Coutinho JAP. Fluid Phase Equilib. 2008;263:26–32. [Google Scholar]
- [52].Gardas RL, Coutinho JAP. AIChE J. 2009;55:1274–1290. [Google Scholar]
- [53].Carvalho PJ, Regueira T, Santos LMNBF, Fernandez J, Coutinho JAP. J. Chem. Eng. Data. 2010;55:645–652. [Google Scholar]
- [54].Tian GC, Feng HK, Zhang JL. Adv. Mater. Res. 2012;549:152–156. [Google Scholar]
- [55].Grishina EP, Ramenskaya LM, Gruzdev MS, Kraeva OV. J. Mol. Liq. 2013;177:267–272. [Google Scholar]
- [56].Neves CMSS, Batista MLS, Cláudio AFM, Santos LMNBF, Marrucho IM, Freire MG, Coutinho JAP. J. Chem. Eng. Data. 2010;55:5065–5073. [Google Scholar]
- [57].Neves CMSS, Kurnia KA, Coutinho JAP, Marrucho IM, Lopes JNC, Freire MG, Rebelo LPN. J. Phys. Chem. B. 2013;117:10271–83. doi: 10.1021/jp405913b. [DOI] [PubMed] [Google Scholar]
- [58].Almeida HFD, Passos H, Lopes-da-Silva JA, Fernandes AM, Freire MG, Coutinho JAP. J. Chem. Eng. Data. 2012;57:3005–3013. [Google Scholar]
- [59].Bhattacharjee A, Carvalho PJ, Coutinho JAP. Fluid Phase Equilib. 2014;375:80–88. doi: 10.1016/j.fluid.2014.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Almeida HFD, Teles ARR, Lopes-da-Silva JA, Freire MG, Coutinho JAP. J. Chem. Thermodyn. 2012;54:49–54. [Google Scholar]
- [61].Rebelo LPN, Lopes JNC, Esperança JMSS, Guedes HJR, Łachwa J, Najdanovic-Visak V, Visak ZP. Acc. Chem. Res. 2007;40:1114–1121. doi: 10.1021/ar7000556. [DOI] [PubMed] [Google Scholar]
- [62].Gomes de Azevedo R, Esperança JMSS, Najdanovic-Visak V, Visak ZP, Guedes HJR, Nunes da Ponte M, Rebelo LPN. J. Chem. Eng. Data. 2005;50:997–1008. [Google Scholar]
- [63].Gomes de Azevedo R, Esperança JMSS, Szydlowski J, Visak ZP, Pires PF, Guedes HJR, Rebelo LPN. J. Chem. Thermodyn. 2005;37:888–899. [Google Scholar]
- [64].Esperança JMSS, Visak ZP, Plechkova NV, Seddon KR, Guedes HJR, Rebelo LPN. J. Chem. Eng. Data. 2006;51:2009–2015. [Google Scholar]
- [65].Esperança JMSS, Guedes HJR, Blesic M, Rebelo LPN. J. Chem. Eng. Data. 2006;51:237–242. [Google Scholar]
- [66].Gardas RL, Costa HF, Freire MG, Carvalho PJ, Marrucho IM, Fonseca IMA, Ferreira AGM, Coutinho JAP. J. Chem. Eng. Data. 2008;53:805–811. [Google Scholar]
- [67].Gardas RL, Freire MG, Carvalho PJ, Marrucho IM, Fonseca IMA, Ferreira AGM, Coutinho JAP. J. Chem. Eng. Data. 2007;52:80–88. [Google Scholar]
- [68].Tsunashima K, Sugiya M. Electrochem. Commun. 2007;9:2353–2358. [Google Scholar]
- [69].Carvalho PJ, Ventura SPM, Batista MLS, Schröder B, Gonçalves F, Esperança J, Mutelet F, Coutinho JAP. J. Chem. Phys. 2014;140:064505. doi: 10.1063/1.4864182. [DOI] [PubMed] [Google Scholar]
- [70].McFarlane DR, Sun J, Golding J, Meakin P, Forsyth M. Electrochim. Acta. 2000;45:1271–1278. [Google Scholar]
- [71].Makino T, Kanakubo M, Umecky T, Suzuki A. J. Chem. Eng. Data. 2013;58:370–376. [Google Scholar]
- [72].Shirota H, Fukazawa H, Fujisawa T, Wishart JF. J. Phys. Chem. B. 2010;114:9400–9412. doi: 10.1021/jp1021104. [DOI] [PubMed] [Google Scholar]
- [73].Jacquemin J, Ge R, Nancarrow P, Rooney DW, Costa Gomes MF, Pádua AAH, Hardacre C. J. Chem. Eng. Data. 2008;53:716–726. [Google Scholar]
- [74].Ye C, Shreeve JM. J. Phys. Chem. A. 2007;111:1456–1461. doi: 10.1021/jp066202k. [DOI] [PubMed] [Google Scholar]
- [75].Pereiro AB, Deive FJ, Esperança JMSS, Rodríguez A. Fluid Phase Equilib. 2010;294:49–53. [Google Scholar]
- [76].Jacquemin J, Husson P, Mayer V, Cibulka I. J. Chem. Eng. Data. 2007;52:2204–2211. [Google Scholar]
- [77].Jacquemin J, Husson P, Majer V, Padua AAH, Gomes MFC. Green Chem. 2008;10:944–950. [Google Scholar]
- [78].Gu Z, Brennecke JF. J. Chem. Eng. Data. 2002;47:339–345. [Google Scholar]
- [79].Linstrom PJ, Mallard WG, editors. NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology; Gaithersburg MD, 20899: http://webbook.nist.gov retrieved May 28, 2014. [Google Scholar]
- [80].Rocha MAA, Ribeiro FMS, Ferreira AIMCL, Coutinho JAP, Santos LMNBF. J. Mol. Liq. 2013;188:196–202. [Google Scholar]
- [81].Freire MG, Teles ARR, Rocha MAA, Schröder B, Neves CMSS, Carvalho PJ, Evtuguin DV, Santos LMNBF, Coutinho JAP. J. Chem. Eng. Data. 2011;56:4813–4822. [Google Scholar]
- [82].Rocha MAA, Neves CMSS, Freire MG, Russina O, Triolo A, Coutinho JAP, Santos LMNBF. J. Phys. Chem. B. 2013;117:10889–10897. doi: 10.1021/jp406374a. [DOI] [PubMed] [Google Scholar]
- [83].Queimada AJ, Stenby EH, Marrucho IM, Coutinho JAP. Fluid Phase Equilib. 2003;212:303–314. [Google Scholar]
- [84].Queimada AJ, Quiñones-Cisneros SE, Marrucho IM, Coutinho JAP, Stenby EH. Int. J. Thermophys. 2003;24:1221–1239. [Google Scholar]
- [85].Israelachvili JN. Intermolecular and Surface Forces. Academic Press; San Diego: 2011. [Google Scholar]
- [86].Goodwin ARH, Marsh KN, Wakeham WA. Measurement of the Thermodynamic Properties of Single Phases , IUPAC Experimental Thermodynamics. VI. Elsevier; Amsterdam: 2003. [Google Scholar]
- [87].Brocos P, Pineiro A, Bravo R, Amigo A. Phys. Chem. Chem. Phys. 2003;5:550–557. [Google Scholar]
- [88].Seki S, Tsuzuki S, Hayamizu K, Umebayashi Y, Serizawa N, Takei K, Miyashiro H. J. Chem. Eng. Data. 2012;57:2211–2216. [Google Scholar]
- [89].Carvalho PJ, Freire MG, Marrucho IM, Queimada AJ, Coutinho JAP. J. Chem. Eng. Data. 2008;53:1346–1350. [Google Scholar]
- [90].Freire MG, Carvalho PJ, Fernandes AM, Marrucho IM, Queimada AJ, Coutinho JAP. J. Colloid Interface Sci. 2007;314:621–630. doi: 10.1016/j.jcis.2007.06.003. [DOI] [PubMed] [Google Scholar]
- [91].Law G, Watson PR. Langmuir. 2001;17:6138–6141. [Google Scholar]
- [92].Dzyuba SV, Bartsch RA. ChemPhysChem. 2002;3:161–166. doi: 10.1002/1439-7641(20020215)3:2<161::AID-CPHC161>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
- [93].Carvalho PJ, Neves CMSS, Coutinho JAP. J. Chem. Eng. Data. 2010;55:3807–3812. [Google Scholar]
- [94].Sánchez LG, Espel JR, Onink F, Meindersma GW, de Haan AB. J. Chem. Eng. Data. 2009;54:2803–2812. [Google Scholar]
- [95].Adamson AW, Gast AP. Physical Chemistry of Surfaces. John Wiley; New York: 1997. [Google Scholar]
- [96].McNaught AD, Wikinson A. Compendium of Chemical Therminology, IUPAC Recommendations. Blackwell Science; Cambridge, U.K.: 1997. [Google Scholar]
- [97].Miller JC, Miller JN. Statistics for Analytical Chemistry. PTR Prentice Hall; Chichester, NY: 1993. [Google Scholar]
- [98].Poling BE, Prausnitz JM, O’Connell JP. The Properties of Gases and Liquids. McGraw-Hill; New York: 2001. [Google Scholar]
- [99].Shereshefsky JL. J. Phys. Chem. 1930;35:1712–1720. [Google Scholar]
- [100].Guggenheim EA. J. Chem. Phys. 1945;13:253–261. [Google Scholar]
- [101].Birdi KS, editor. Handbook of Surface and Colloid Chemistry. CRC Press; Boca Raton, FL: 1997. [Google Scholar]