SELEX-seq, a method for characterizing the complete repertoire of binding site preferences for transcription factor complexes

Summary

The closely related members of the Hox family of homeodomain transcription factors have similar DNA-binding preferences as monomers, yet carry out distinct functions in vivo. Transcription factors often bind DNA as multiprotein complexes, raising the possibility that complex formation might modify their DNA binding specificities. To test this hypothesis we developed a new experimental and computational platform, termed SELEX-seq, to characterize DNA binding specificities of Hox-based multiprotein complexes. We found that complex formation with the same cofactor reveals latent specificities that are not observed for monomeric Hox factors. The findings from this in vitro platform are consistent with in vivo data, and the ‘latent specificity’ concept serves as a precedent for how the specificities of similar transcription factors might be distinguished in vivo. Importantly, the SELEX-seq platform is flexible and can be used to determine the relative affinities to any DNA sequence for any transcription factor or multiprotein complex.

1. Introduction

Members of the homeodomain-containing Hox family of transcription factors (TFs) play integral roles in many aspects of metazoan development, from anterior-posterior patterning during embryogenesis to organogenesis and stem cell maintenance (1–3). As with most TFs, the DNA binding activity of Hox proteins is integral to their function - at least with regard to their control of developmental processes (4). Still, one of the more puzzling aspects of the Hox factors is that they direct exquisitely specific functions in vivo yet have very little specificity when binding to DNA in vitro (4). Importantly, this quandary is not limited to the Hox family of TFs; a similar disconnect between DNA binding specificity in vitro and functional specificity in vivo is observed for many TF families, including those encompassing the T-box, Ets, and bHLH factors (5–7). Given the importance of TF-DNA interactions in gene regulation, understanding the DNA binding specificities is one of the critical steps in deciphering the function of non-coding, regulatory DNA, and it is clear that monomeric DNA binding properties cannot fully explain the specific in vivo functions of many TFs.

For the Hox proteins, one potential solution to this specificity paradox lies in the finding that Hox proteins can bind DNA in vivo in conjunction with cofactors. The most critical cofactors known to perform this function are the PBC (pre-B cell) homeodomain TFs: Exd (Extradenticle) in Drosophila and Pbx (pre-B cell leukemia homeobox) in vertebrates. Both Exd and Pbx bind in a highly cooperative manner with Hox proteins to composite Hox-Exd binding sites (4). Importantly, beyond increasing Hox DNA binding affinities, PBC proteins enhance the DNA binding specificities of Hox proteins. That is, PBC-Hox heterodimers are more selective in their DNA binding preferences than Hox monomers. For the Drosophila Hox TF Scr (Sex combs reduced), structural studies demonstrated that interaction with Exd allows the Scr protein to recognize the unique minor groove structure of an Exd-Scr-specific DNA motif (8). Thus, in this case, interaction with the PBC protein Exd reveals a latent specificity that is intrinsic to the Hox protein Scr. This latent specificity example, combined with the fact that PBC proteins can heterodimerize with all Hox family members, suggested that the formation of Hox-PBC complexes might have a widespread impact on Hox DNA binding specificity (8).

The Homothorax (Hth)-Meis family of homedomain proteins can also influence PBC-Hox DNA binding (4). Interaction with Hth-Meis family members stabilizes PBC proteins and can promote nuclear localization of PBC proteins. Further, Hth-Meis factors also promote cooperative PBC-Hox binding on certain sequences. In Drosophila, an Hth isoform that lacks a DNA binding domain but contains the Exd interacting domain – the “Hth-Meis” (HM) domain – is sufficient for Exd nuclear localization and stability, and can carry out most Hox-related functions of hth (9,4).

We recently described a novel high-throughput method, termed SELEX-seq, that we used to systematically characterize the DNA binding specificities of all Drosophila Hox-Exd-HM complexes (hereafter referred to as Hox-Exd complexes for simplicity) (10). This approach combines the classical method of SELEX (Systematic Evolution of Ligands by Exponential Enrichment; also known as in vitro selection) (11,12) with the power of next-generation sequencing technology, and is ideally suited for exploring the DNA binding preferences of multiprotein complexes. As with traditional SELEX, an oligonucleotide containing a randomized region that is flanked by defined primer docking sites is used to bind the Hox-Exd complex of interest. DNA bound by the complex is then separated from unbound DNA, in this case using EMSA (electrophoretic mobility shift assay), though immunopurification-based assays can also be employed, and the bound DNA is then amplified by PCR and used for subsequent rounds of DNA binding and selection.

SELEX-seq differs from traditional SELEX in two respects: the number of selected (bound) DNA oligos characterized and the number of rounds of selection performed. Unlike traditional SELEX, where on the order of 10² selected DNA oligos are identified at the very end of the reiterative selection process, SELEX-seq leverages the depth of next generation sequencing to characterize 10⁷ or more selected DNA molecules at each round of selection. Additionally, whereas traditional SELEX requires many rounds of selection, the greater sequencing depth of SELEX-seq allows for identification of relevant binding sites after only one to two rounds of selection. Using a biophysical model of the SELEX procedure, relative affinities for selected sequences are then obtained by comparing the sequence composition of later rounds to that of the unselected DNA library. The combined impact of these improvements – greater coverage of selected DNA, fewer rounds of selection, and the biophysical sequence-to-affinity model – is that SELEX-seq captures more than just high affinity binding sites, and thus provides a more complete view of the binding preferences for a TF or TF-complex. And because moderate affinity binding sites are just as likely to be relevant in vivo, techniques that reveal the entire binding site repertoire for a TF or TF-complex are essential.

Applying the SELEX-seq strategy to all eight Drosophila Hox-Exd heterodimers demonstrated that complex formation with the same cofactor reveals latent specificities that are not observed for monomeric Hox factors (10), and the findings from SELEX-seq are consistent with in vivo data (13). Thus, the latent specificity phenomenon extends well beyond the Hox protein Scr, and serves as a precedent for how the specificities of other transcription factor families might be distinguished in vivo. Therefore, SELEX-seq now serves as a platform for studying numerous TFs and multiprotein TF-complexes (14). In this Chapter, we describe the detailed procedures for all of the wet lab and computational steps for executing SELEX-seq.

2. Materials

2.1 Preparation of SELEX Library and Control EMSA Probe

1. Oligonucleotides for SELEX library (see Note 1).

   SELEX_16mer_Multiplex1: 5’GTTCAGAGTTCTACAGTCCGACGATCTGG-[N₁₆]-CCAgcTgTCGTATGCCGTCTTCTGCTTG3'

   SELEX_16mer_Multiplex2: 5’GTTCAGAGTTCTACAGTCCGACGATCTGG-[N₁₆]-CCAcgTcTCGTATGCCGTCTTCTGCTTG3’

   SELEX_SR1: 5’ CAAGCAGAAGACGGCATACGA 3’

2. Oligonucleotides for Control EMSA Probe (see Note 2).

   fkhCON_Tracking_Fwd: 5’GCTATACTGTGCTATCCACAGTTCAGAGTCGTCAAGATTTATGGCCTGCTGG TCACTGGTCGTTTCCCTCTT3’

   fkhCON_Tracking_Rev: 5’AAGAGGGAAACGACCAGTGACCAGCAGGCCATAAATCTTGACGACTCTGAA CTGTGGATAGCACAGTATAGC3’

3. 10x STE Buffer: 10 mM Tris pH 8, 1M NaCl, 1mM EDTA pH8

4. DNA Polymerase I, Large (Klenow) Fragment and 10x NEB Buffer 2 (New England BioLabs)

5. T4 Polynucleotide Kinase and 10x Polynucleotide Kinase Reaction Buffer

6. 10 mM dNTP mix

7. ATP [γ- ³²P] (6000Ci/mmol 10mCi/ml; PerkinElmer) (see Note 3)

8. TE Stop Buffer: 10 mM Tris pH 8, 6.6 mM EDTA pH8

9. MinElute PCR Purification Kit (Qiagen)

10. 5% TBE Acrylamide Gel (BioRad) and 5x TBE

2.2 DNA Binding Reaction and EMSA

1. Purified DNA binding protein of interest (see Note 4)

2. 5x Binding Buffer: 50 mM Tris pH 7.5, 250 mM NaCl, 5 mM MgCl2, 20% glycerol, 2.5 mM DTT, 2.5 mM EDTA pH8, 250 µg/ml polydI-dC, 1mg/ml BSA

3. 80% Glycerol

4. 40% Acrylamide solution

5. 30% Acrylamide/bis-acrylamide solution, 37.5:1 (BioRad)

6. 10% Ammonium persulfate

7. TEMED (Tetramethylethylenediamine)

8. 5x TBE

9. Gel dryer and phosphorimager cassette

2.3 Isolation and Elution of Bound DNA

1. Elution Buffer: 0.5M NH₄OAc, 1mM EDTA, 0.1% SDS

2. Phenol:Chloroform:Isoamyl Alcohol (25:24:1, v/v) (Invitrogen/Life Technologies)

3. Ethanol

4. 3M Sodium acetate, pH 5.2

5. TE: 10 mM Tris-Cl pH 8, 1 mM EDTA pH8

2.4 DNA Amplification and Preparation of Sequencing Library

1. Oligonucleotides for amplification of SELEX library.

   SELEX_SR0: 5’GTTCAGAGTTCTACAGTCCGA3’

   SELEX_SR1: 5’CAAGCAGAAGACGGCATACGA3’

2. Oligonucleotides for preparation of sequencing library.

   SELEX_SR1: 5’CAAGCAGAAGACGGCATACGA3’

   SELEX_SR2: 5’AATGATACGGCGACCACCGACAGGTTCAGAGTTCTACAGTCCGA3'

3. Taq DNA Polymerase and 10x Taq Reaction Buffer (New England BioLabs)

4. Phusion High-Fidelity DNA Polymerase and 5x Phusion HF Buffer (New England BioLabs)

5. 10 mM dNTP mix

6. MinElute PCR Purification Kit (Qiagen)

7. 5% TBE Acrylamide Gel (BioRad) and 5x TBE

8. 10x NEB Buffer 2 (New England BioLabs)

9. Corning Costar Spin-X centrifuge tube filters (Sigma)

10. Ethanol

11. 3M Sodium acetate, pH5.2

12. 20 mg/ml Glycogen (Roche)

2.5 Computational Analysis of the Data

1. A personal computer, or an account on a shared computer system (a minimum of 1GB random access memory and 100 MB hard drive storage recommended, but more may be required depending on data and analysis options)

2. SELEX-seq software (available for download at bussemakerlab.org/software/SELEX-seq/)

3. Linux or UNIX operating system with bash shell version 4.1.5 or newer

4. R version 2.14.0 or newer

5. Perl version 5 or newer

6. Java version 1.6.0 or newer

3. Methods

3.1 Preparation of SELEX Library and Control EMSA Probe

The success of a SELEX-seq experiment is primarily driven by two components: the DNA-binding protein(s) of interest and the randomized DNA SELEX library. We have had much success using bacterially expressed (E. coli), purified His-tagged Hox and HM-Exd proteins, and the methods described here assume access to purified protein preparations. However, there is much flexibility in the methods of protein expression and purification that are suitable for SELEX-seq (10,14), so this facet of the experimental design must be optimized on a case-by-case basis.

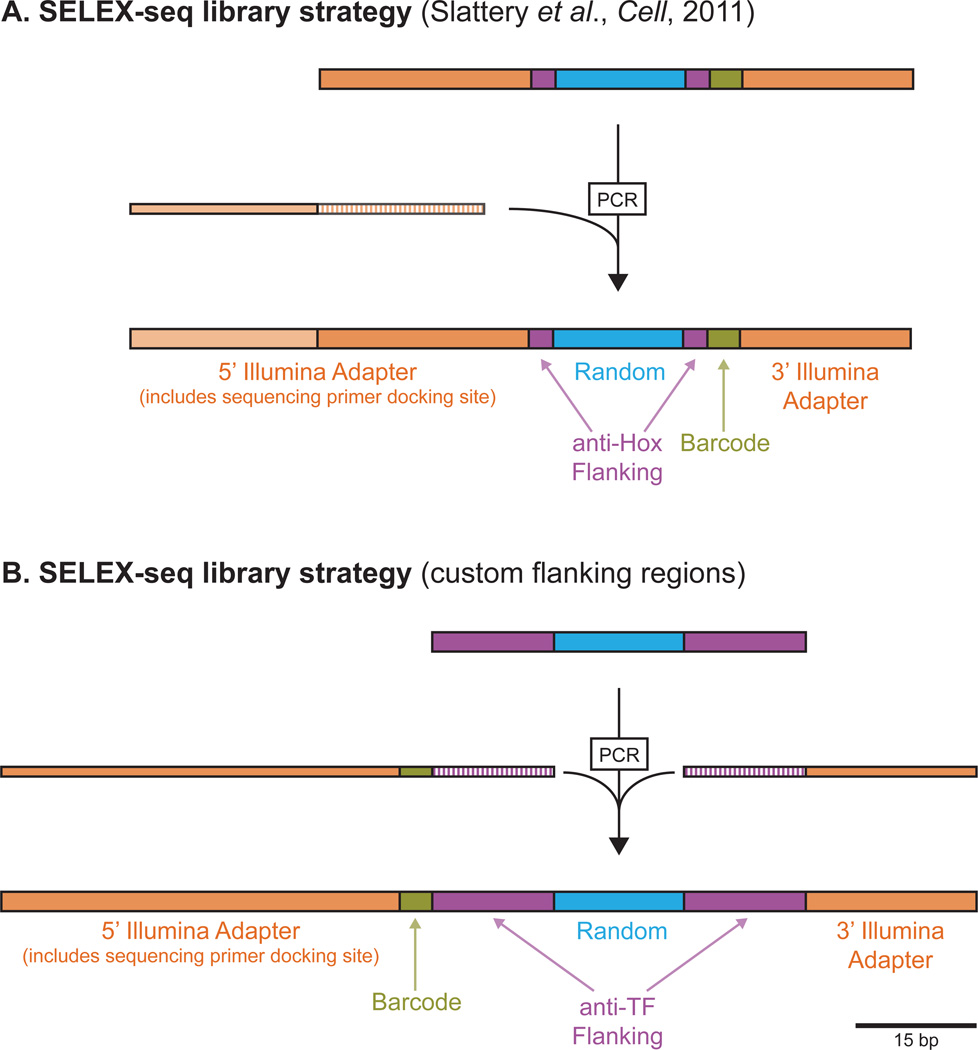
Beyond protein preparation, multiple variables must be considered when it comes to generation of the randomized SELEX library. The randomized region must be large enough to encompass the expected core DNA binding motif and also allow for capturing information regarding sequences immediately flanking the core motif; for our exploration of Hox-Exd binding we used a 16 bp randomized region because all previously characterized Hox-Exd binding sites were 10–11 bp long. In addition to the randomized region, the SELEX library must eventually carry adapter sequences that are compatible with Illumina sequencing. Sequence information for various Illumina-compatible adapters can be accessed via Illumina’s website (www.illumina.com) and the oligonucleotides used for characterizing Hox-Exd binding are shown in Fig. 1. In this case, the adapter regions are exact matches to the sequences used for the Illumina small RNA sequencing library, with the exception of the TGG/CCA sequences immediately flanking the random region (TGG[N₁₆]CCA) and the 4bp barcode region (gcTg) just 3’ of the CCA (Fig. 1). The TGG/CCA sequences flanking the randomized oligonucleotides act as “anti-Hox” flanking regions, meant to discourage Hox-Exd binding that overlaps the constant region. The 4bp barcode region allows for multiplexing of multiple SELEX-seq libraries in the same Illumina sequencing lane; two multiplex barcoded libraries (“SELEX_16mer_Multiplex1” and “SELEX_16mer_Multiplex2”) are described here, though additional barcodes can be used to increase multiplexing depth (i.e., running >2 samples per sequencing lane). The 5’ and 3’ adapter regions used for Illumina sequencing differ significantly in length (Fig. 1), so the SELEX library is designed to be near symmetrical in length – 29 and 28 bp constant regions flanking the randomized region – with the additional 5’ adapter added via PCR immediately before sequencing (Fig. 1 and 2A).

Figure 1. SELEX-seq oligonucleotide sequences.

Sequences of oligonucleotides used for SELEX library generation, DNA amplification, and Illumina sequencing.

Figure 2. Strategies for SELEX-seq library design.

(A) SELEX-seq library strategy used for the Hox-Exd study described here and in Slattery et al. (B) SELEX-seq strategy in which Illumina adapters are not added until after selection.

As described above, the “anti-Hox” sequences were sufficient to prevent Hox-Exd binding to the constant adapter sequences. This is important because TF binding within or overlapping the constant regions can significantly skew SELEX-seq results (unpublished data). Still, for some TFs there may be sequences integral to the Illumina adapter regions that also match the TF’s DNA binding motif. In cases such as this the SELEX library can be designed with custom flanking regions and Illumina-compatible adapters can be added by PCR, after the SELEX step and immediately before sequencing (Fig. 2B). Barcodes can also be added at this stage, rather than included in the initial library (Fig. 2B). Currently, Illumina sequencing is performed in 50- or 100-cycles, so the full randomized region must fall within 50 or 100 bp of the sequencing primer (of course 100 cycles of sequencing costs approximately twice as much as 50 cycles).

Finally, one of the key features of SELEX-seq is that it allows for calculation of motif enrichment after selection relative to the initial SELEX library (Round 0, or R0), which in turn allows for estimation of relative binding affinities. Because this requires sequencing data from R0, it is best to make enough double-stranded SELEX library for an entire experiment, especially if different TFs or combinations of TFs are going to be tested. If a new batch of the double-stranded SELEX library is generated in the middle of an experiment, re-sequencing of R0 may be necessary for accurate calculation of enrichment and estimation of relative affinities.

1. Anneal SELEX library template (SELEX_16mer_Multiplex1 or SELEX_16mer_Multiplex2) and SELEX_SR1. Standard annealing mix consists of 3µl of 100µM SELEX_16mer_Multiplex1 or _Multplex2 template, 6 µl 100 µM SELEX_SR1, 3 µl of 10x STE buffer, and 18 µl of water. Boil the mixture for 5 min and allow to cool slowly back to room temperature; this is most easily performed by floating the tube for 5 min in 500–700 ml boiling water in a 1 l beaker, then removing the whole beaker from heat and letting it cool down to room temperature overnight. 30 µl of 10 µM annealed product will be generated.

2. Extend the primer to generate the double-stranded SELEX library. The reaction described here makes use of one-third of the annealed product from Step 1, but can be scaled up to use all 30 µl of the annealed solution, if necessary. Mix 10 µl of annealed product from Step 1 with 8 µl water, 2.5 µl 10x NEB Buffer 2, 2 µl 10mM dNTPs, and 2.5 µl DNA Polymerase I, Large (Klenow) Fragment. Allow extension reaction to proceed for at least 30 min at room temperature, and add 1 µl of 0.5 M EDTA to stop the reaction.

3. Purify the double-stranded SELEX library (hereafter referred to as “SELEX library”) using the MinElute PCR purification kit, using the standard protocol provided by Qiagen. Measure the concentration of the SELEX library using a NanoDrop spectrophotometer and adjust to a convenient concentration for SELEX (3 µM will be used for the protocol described here). Also check that the purified SELEX library is primarily a single band of the expected size by gel electrophoresis on a 5% TBE Acrylamide Gel (BioRad). SELEX library can be stored at −20°C.

4. Generation of a control EMSA probe – which is used for tracking protein-DNA complexes – does not require a Klenow extension reaction. Full sense and antisense oligonucleotides can be used (because control probes do not have a random region). Anneal 2 µl of 50 µM fkhCON_Tracking_Fwd and 2 µl of 50 µM fkhCON_Tracking_Rev in 86 µl water and 10 µl 10x STE buffer. Anneal by boiling for 5 min and slowly cooling to room temperature as described above in Step 1. The annealed control probe can then be labeled with ³²P in the following reaction: 3.5 µl annealed probe (~1 µM, from annealing reaction), 3.5 µl water, 1 µl 10x Polynucleotide Kinase Reaction Buffer, 1 µl T4 Polynucleotide Kinase, and 1 µl ATP [γ- ³²P]. Allow reaction to proceed for 10 min at 37°C, then stop the reaction by adding 90 µl TE Stop Buffer, for a final ³²P-labeled probe concentration of 35 nM.

3.2 DNA Binding Reaction and EMSA

When running the SELEX EMSA the control binding lanes serve as tracking lanes to monitor the mobility of the protein-DNA complex. It is best to set up two tracking lanes, run on each side of the SELEX lane, to facilitate accurate tracking and isolation of the appropriate region in the SELEX lane. In addition to the tracking lanes, a “no protein” lane containing the radiolabeled control probe and no TF(s) should also be included to monitor the mobility of the free probe; this lane should also include a loading dye such as bromophenol blue for monitoring progression of the gel. When working with a multiprotein complex one should also setup lanes containing individual proteins to monitor the mobility of monomeric protein-DNA binding. For simplicity, only the SELEX and control/tracking lanes are described here.

1. Prepare a gel for EMSA by adding 3.5 ml 5x TBE, 3.1 ml 30% acrylamide/bis-acrylamide solution (37.5:1), 2.33 ml 40% acrylamide solution, and 1.1 ml 80% glycerol to 24.25 ml water. Mix well, without generating bubbles, and then add 262.5 µl 10% ammonium persulfate and 17.5 µl TEMED to catalyze polymerization. Mix briefly, pour gel, and allow gel to solidify for 1 h. After gel has solidified, be sure to flush the wells with 0.5x TBE to remove unpolymerized acrylamide and pre-run gel for 20–30 min (150 volts) in 0.5x TBE buffer. Run gel in cold room at 4°C (see Note 4).

2. Setup the 30 µl control binding reactions as follows: 1 µl of 35nM labeled control probe, 6 µl 5x Binding Buffer, 6 µl of 500 nM Exd-HM, 6 µl of 1 µM Hox, 11 µl of water (see Note 5).

3. Setup the 30 µl SELEX binding reaction as follows: 2 µl of 3 µM SELEX library, 6 µl 5x Binding Buffer, 1 µl 1 µM Exd-HM, 2 µl of 1 µM Hox, 19 µl water (see Note 5).

4. Assemble control and SELEX binding reactions on ice (or in 4°C cold room), then incubate reactions for 20 min at room temperature. The EMSA gel from step 1 should be pre-running while binding reactions are taking place. After the 20 minute incubation stop pre-running gel, load samples into lanes, and run the gel for approximately 2 h at 150 volts (4°C).

5. After running the gel, remove it from glass plates, vacuum dry on Whatman paper, wrap the dried gel in Saran wrap, and tape the gel down in a phospohorimager cassette. Expose the gel at 4°C. Short exposure times (1–2 h) should be sufficient for tracking the protein-DNA complex, but overnight exposure is also acceptable. After exposure, when scanning the phosphorscreen, adjust the phosphorimager to capture the entire gel (including extra space beyond all 4 gel borders).

3.3 Isolation and Elution of Bound DNA

1. To cut the appropriate SELEX ‘band’ from the gel, print a 1:1 copy of the phosphorimager scan. Before printing, adjust the brightness and contrast of the scan to see all gel borders. Use scissors to cut exactly around gel borders of printed scan, and cut out a window from the print corresponding to the SELEX region to be isolated (window based on the actual band in tracking lanes). Align the gel cutout with the gel taped down in phosphorimager cassette; the free DNA probe from the ‘no protein’ lane should align approximately with bromophenol blue band for probes described here. Use marker to outline the SELEX band to be cut, remove the gel from cassette, and cut SELEX band out of gel using a new razor blade.

2. Remove Saran wrap from isolated band, and remove excess Whatman paper (though some carryover of Whatman paper into elution step is acceptable). Cut the isolated band into 3–4 pieces and place all pieces in a 1.5 ml tube. Add 1 ml of Elution Buffer to tube carrying the isolated gel pieces.

3. Elute at 37°C overnight. Collect Elution Buffer from elution and add another 750 µl Elution Buffer to gel pieces. Elute for 2 h at 37°C, then remove buffer and combine with buffer from first elution.

4. Add an equal volume of phenol:chloroform to the eluted DNA solution in a 15 ml polypropylene Falcon tube. Vortex the mixture for 30 seconds, then centrifuge for 3 min at 3000g. Carefully remove the aqueous layer to a new tube (avoid interface).

5. Before ethanol precipitation of DNA, the aqueous layer should be split evenly among multiple 1.5 ml tubes because the current volume is too large for precipitation in a 1.5 ml tube (which is optimal for viewing DNA pellet). To precipitate DNA, add 2 volumes of 100% ethanol to each tube and store at −80°C (or on dry ice) for at least 30 min. After 30 min, spin tubes at max speed (>15000g) for 20 min (4°C), then wash pellet with 70% ethanol. Remove all ethanol and dry pellets (do not over-dry).

6. Dissolve precipitated DNA in 200 µl TE pH 8. 200 µl is the total volume across all tubes, so if 4 tubes were used dissolve each pellet in 50 µl TE. Once pellets are dissolved in TE, pool all in one tube (200 µl final volume). Add 25 µl of 3M Sodium acetate pH 5.2, mix well, then add 450 µl 100% ethanol. Again, precipitate at −80°C for at least 30 min, then spin tubes at max speed (>15000g) for 20 min (4°C). Wash pellet with 70% ethanol, dry pellet, and dissolve DNA in 20 µl TE pH 8.

7. Store DNA at −20°C. Half of this eluted DNA will be amplified and used for the next round of selection and sequencing, and the other half will be stored as backup.

3.4 DNA Amplification and Preparation of Sequencing Library

1. A total of 10 µl eluted DNA will be amplified for an additional round of selection. This should be setup in 5 parallel 50 µl PCR reactions, each consisting of the following: 2 µl template DNA, 39.5 µl water, 5 µl of 10x Taq Reaction Buffer, 1 µl of 20 µM SELEX_SR0, 1 µl of 20 µM SELEX_SR1, 1 µl of 10 mM dNTPs, 0.5 µl Taq polymerase. A master mix can be used to setup the 5 reactions. The PCR conditions are as follows: 2 min at 94°C, then 15 cycles of 15 seconds at 94°C, 15 seconds at 55°C, and 30 seconds at 72°C, followed by 1 minute at 72°C, and a hold at 4°C (see Note 6).

2. After PCR, pool 5 reactions back to approximately 250 µl and purify using Qiagen’s MinElute PCR Purification Kit. Follow standard Qiagen protocol, though note that 5 volumes of Buffer PB in this case amounts to 1.25 ml, so the sample plus PB volume will be approximately 1.5 ml. Because the MinElute column capacity is ~700 µl, the entire sample cannot be put through the column at once; instead apply sample to the same column in 3 successive stages, approximately 500 µl each time, being sure to discard flow through after each spin. Once all sample has been added to column, proceed as per Qiagen’s instructions. At the final step elute DNA in 13 µl Buffer EB. Estimate DNA concentration using a NanoDrop spectrophotometer. Again, as described above with the initial library, adjust to a convenient concentration for SELEX (3 µM in this case), and check that the library is primarily a single band by acrylamide gel electrophoresis. This amplified library from round 1 (R1) of selection can be stored at −20°C until round 2 of selection (R2, see Note 7) or generation of the sequencing library.

3. The amplified DNA from the previous step is then prepared for Illumina sequencing using limited cycle PCR to add the final adapter sequence (see Fig. 1 and 2A). The PCR is setup in 5 parallel 50 µl PCR reactions, each consisting of the following: 0.8 µl of 500 nM DNA template, 33.2 µl water, 10 µl of 5x Phusion HF Buffer, 2 µl of 20 µM SELEX_SR1, 2 µl of 20 µM SELEX_SR2, 1.5 µl of 10 mM dNTPs, and 0.5 µl of Phusion High-Fidelity DNA Polymerase. A master mix can be used to setup reactions. The PCR conditions are as follows: 30 seconds at 98°C, then 3 cycles of 10 seconds at 98°C, 30 seconds at 60°C, and 15 seconds at 72°C, followed by 10 min at 72°C, and a hold at 4°C.

4. Pool all 5 reactions and purify using the MinElute PCR Purification Kit (Qiagen) as described above in Step 2 of this section (elute in 10 µl Buffer EB). Run the product on a 5% TBE Acrylamide Gel (BioRad, see Note 8) with a 10 bp DNA ladder. Pre-run the gel for 10 min at 100 volts, then load sample and ladder lanes. When gel is complete (be careful not to run the product off of gel), stain the gel with ethidum bromide for 5–10 min. Visualize the PCR product on UV transilluminator. Two products will likely be visible: one higher mobility band corresponding to the selected DNA that has not acquired the full sequencing adapter (the DNA added by primer SELEX_SR2) and a lower mobility product containing the selected DNA plus all necessary Illumina adapter sequence. Cut out the band corresponding to the latter product.

5. Puncture the bottom of a 0.5 ml microfuge tube 5 times with a 21 gauge needle and stack the punctured tube in a 2 ml microfuge tube. Place the isolated gel slice from the previous step (Step 4) in the 0.5 ml tube. Centrifuge the stacked tubes for 2 min at maximum speed on a benchtop centrifuge (room temperature); gel debris will be collected in the 2 ml microfuge tube. Discard the 0.5 ml tube, and add 200 µl of 1x NEB Buffer 2 to the gel debris in the 2 ml microfuge tube. Elute DNA by rocking the 2 ml tube for 2 h at room temperature.

6. Transfer the eluate and gel debris to a Spin-X filter and centrifuge for 2 min at maximum speed on a benchtop centrifuge (room temperature). Discard the filter and gel debris, and transfer the eluate to a clean 1.5 ml microfuge tube. Add 1 µl of 20 mg/ml glycogen and 20 µl 3M sodium acetate pH 5.2, mix well, then add 650 µl cold (-20°C) 100% ethanol and vortex. Immediately centrifuge at 15000g for 20 min at 4°C.

7. After centrifugation, remove and discard supernatant, leaving pellet intact. Wash the pellet with 1 ml of room temperature 70% ethanol, remove and discard supernatant, and dry pellet. Measure DNA concentration using a NanoDrop spectrophotometer. The sample is now ready for Illumina sequencing (see Note 9).

3.5 Modeling the Biases in the Initial Pool using a Markov Model

In the remaining sections, we provide a conceptual overview of our computational analysis pipeline; detailed instructions on how to run it are provided in the online documentation that comes with the software.

Typically, there are significant sequence biases in the initial pool of random dsDNA oligonucleotides. These sequence biases are introduced during the synthesis of the ssDNA, double stranding, and/or PCR amplification steps. To account for these, we train Markov Models using our custom software and assess their predictive accuracy.

1. First, we determine the largest K-mer length (K_max) for which the relative sample error (SE) in the observed count in the initial pool (R0) is smaller than 10% for any K-mer. Since the relative sample error in a count N equals $\frac{1}{\sqrt{N}}$, this condition is satisfied when all the K-mers of a given length have counts ≥ 100. Given the significant biases in the R0 pool, this K-mer length has to be determined empirically through analysis of the R0 sequencing data, using our software. For the R0 data of Slattery et al. (2011), the longest K-mer length that satisfied this condition was K_max=8 (Table 1).

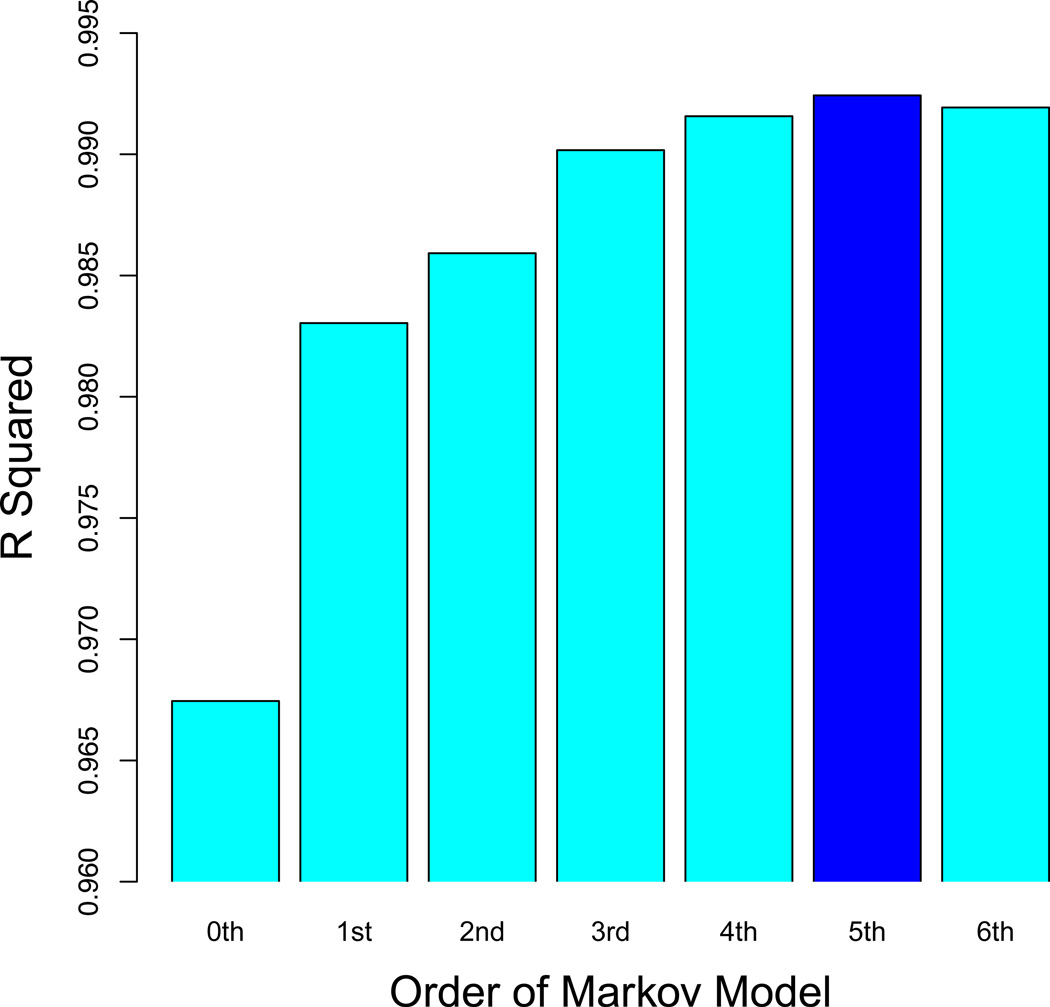
2. Next, we train Markov Models (MM) of order zero through K_max – 1. Each of these models can be used to predict an expected count for all K_max-mers (Table 1). For each order, we compute the fraction explained (R²) of the variance in the observed counts of K_max-mers in one of the multiplexes of R0 by a MM built from the other R0 multiplex (cross-validation). This MM is subsequently used to accurately estimate the frequencies of all K-mers (for K ≥ K_max) in the initial pool. In Slattery et al. (2011), we found that a 5^th-order MM attained the highest level of cross-validation predictive accuracy (R² = 0.992; Fig. 3).

Table 1.

Validation of the Markov model used to quantify the significant biases in the initial pool (R0). Shown are the most and least frequent octamers (8-mers) in R0, in descending order. We chose 8-mers because they are the longest subsequences that all have an observed count greater than 100, so that the relative sample error (SE) in the observed count is never larger than 10%. Also shown is the expected 8-mer count as predicted by a 5^th-order Markov model trained on an independent replicate. The best agreement between the observed and expected counts is obtained using 5^th-order Markov models.

8-mer	Observed Count in R0	Expected Count in R0
TTTTTTTT	6414	6366.4
ATTTTTTT	5081	5014.3
GTTTTTTT	5049	4978.2
TATTTTTT	4922	4859.7
TTTTTTTG	4885	4876.9
TTTTTTGT	4809	4821.2
TTATTTTT	4793	4760.1
TTTTTGTT	4788	4741.4
TTTGTTTT	4772	4695.6
:	:	:
CCCGCCCC	194	184.6
ACCCCCCC	190	189.7
CCCCCCCT	190	222.0
CCCGACCC	190	217.1
CCCCCCCG	189	191.1
CGCCCCCC	186	179.4
CCCCACCC	184	185.2
GCCCCCCC	179	188.1
CACCCCCC	174	189.9
CCCACCCC	165	186.0

Figure 3. Markov model optimization.

To determine the optimal order for the Markov model of the initial pool, we quantified how a Markov model trained on one replicate of R0 predicted 8-mer counts in another replicate in terms of a coefficient of determination (R²). Using the data from Slattery et al. (2011), we found that a fifth-order model has the best cross-validation performance. At lower order, the biases in R0 are not sufficiently captured; at higher order, the predictions degrade due to over-fitting.

3.6 Determining the Effective Length of the DNA Binding Site

For the particular TF or TF-complex assayed, the number of base pair positions in the protein-DNA binding site that contributes to the binding specificity is not known a priori, and their influence can extend beyond the protein-DNA interface over which direct contacts are made (e.g. through shape-mediated effects), so even a high-resolution co-crystal structure would not fully provide this information. Therefore, we use an information-theoretical approach that makes minimal assumptions to determine this effective length of the binding site. First, we apply our software to construct K-mer count tables for different lengths K up to the size of the variable region from the sequencing reads after one or more rounds of affinity-based selection (we will assume R2 in what follows). A representative example for Exd-Lab and K=12 is shown in Table 2. For each K, we convert the count table to a probability distribution by dividing by the sum over all K-mers (Table 2); in this process, all K-mers with a count <100 are lumped together into a single “background” category. Next, we compute the course-grained Kullback-Leibler divergence (D_CGKL) between the R2 distribution thus estimated and the Markov Model constructed from R0:

$$D_{\mathit{\text{CGKL}}}(K)==\sum _{i\in S_{100}(K)}(P_2(w_i)\text{log}\frac{P_2(w_i)}{P_{\mathit{\text{MM}}}(w_i)})+[1-\sum _{i\in S_{100}(K)}{P}_2(w_i)]\text{log}\left(\frac{1-{\sum }_{i\in S_{100}(K)}{P}_2(w_i)}{1-{\sum }_{i\in S_{100}(K)}{P}_{\mathit{\text{MM}}}(w_i)}\right)$$

Table 2.

A representative example illustrating our procedure for estimating relative affinities, using data for Exd-Lab binding from Slattery et al. (2011). Shown are the observed counts of all 12-mers in R2, the corresponding fraction in R2 (obtained by dividing by the total observed count), the expected frequency in the initial pool R0 (obtained using the 5^th-order Markov model), the fold-enrichment, the initial estimate of the relative affinity obtained by rescaling the fold-enrichment and taking the square root, and the standard error for the relative affinity estimate.

12-mer	Observed Count in R2	Observed Frequency in R2 (x10−3)	Estimated Frequency in R0 (x 10−7)	Fold- Enrichment from R0 to R2	Estimated Relative Affinity	Standard Error
GTAATCAATCAT	114136	1.6892	0.8735	19338.2	1.0000	0.0042
ATGATTGATTAC	135714	2.0086	1.1675	17203.7	0.9432	0.0036
AATGATTGATTA	145612	2.1551	1.3900	15504.2	0.8954	0.0033
TAATCAATCATT	99927	1.4789	1.0299	14359.6	0.8617	0.0039
GATGATTGATTA	116529	1.7247	1.3581	12699.3	0.8104	0.0034
GTCATCAATCAT	61953	0.9169	0.7348	12479.3	0.8033	0.0046
AATGATTGATGA	81746	1.2099	0.9830	12307.8	0.7978	0.0039
ATGATTGATGAC	67902	1.0050	0.8511	11808.3	0.7814	0.0042
ATGATTGATGAG	77316	1.1443	0.9984	11460.8	0.7698	0.0039
:	:	:	:	:	:	:
TTTTTGATATAT	102	0.0015	3.4059	4.4324	0.0151	0.0021
ATTGATATTTTT	103	0.0015	3.4431	4.4275	0.0151	0.0021
ATTATTTATTAT	103	0.0015	3.5303	4.3181	0.0149	0.0021
GTTTTGTTTGAT	100	0.0015	3.4723	4.2623	0.0148	0.0021
TTTTTGATTGTT	117	0.0017	4.1203	4.2026	0.0147	0.0019
TTTTTTTGATTA	116	0.0017	4.2856	4.0060	0.0144	0.0019
ATTTATTATTTT	121	0.0018	4.5488	3.9369	0.0143	0.0018
TTTGTTTGATTT	113	0.0017	4.2748	3.9123	0.0142	0.0019
TTTTTTGATTTA	103	0.0015	4.2609	3.5777	0.0136	0.0019
TTTGTTTGTTTA	103	0.0015	4.5958	3.3170	0.0131	0.0018

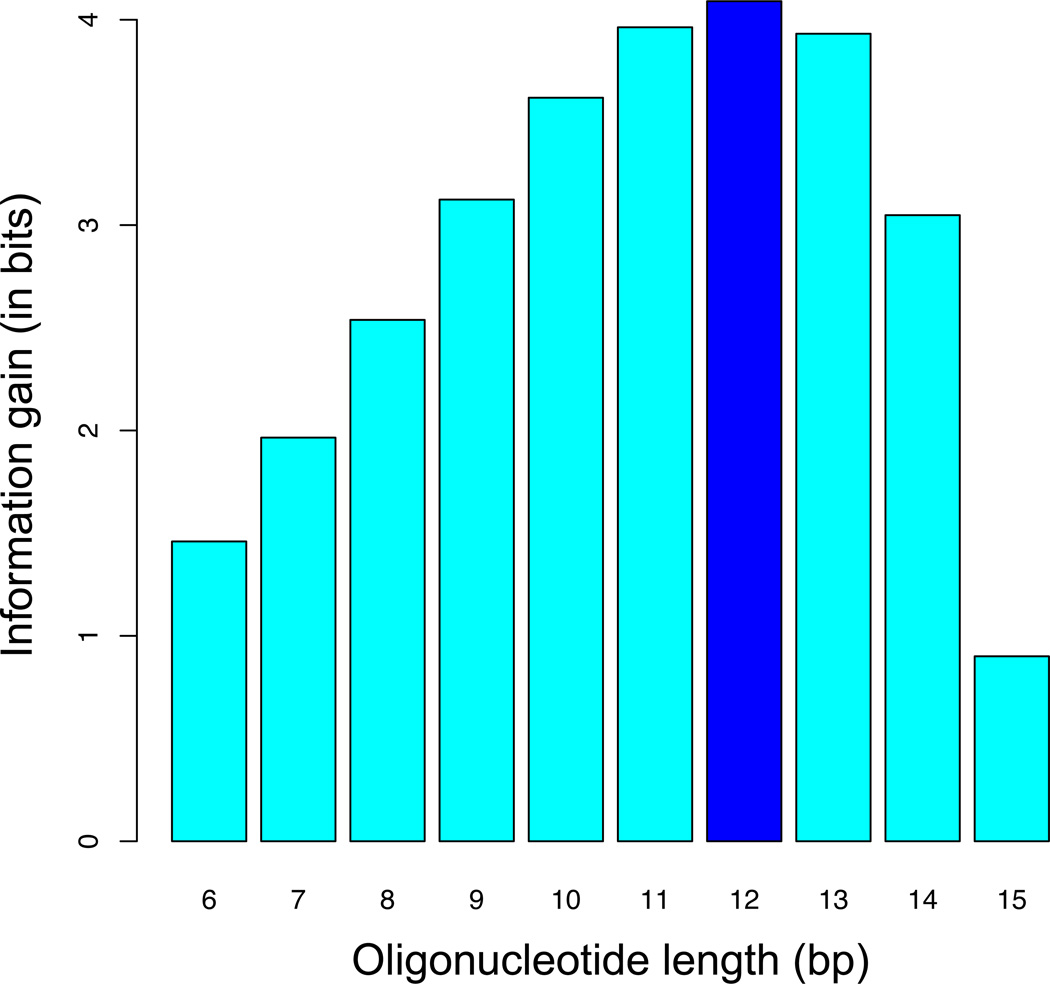
Here, S₁₀₀(K) denotes the set of K-mers or “words” w_i with counts ≥ 100 in R2, and P₂(w_i) the frequency of w_i in R2. P_MM(w_i) by contrast denotes the expected frequency of w_i in R0 as predicted using the Markov Model; see Table 2 for an example. The intuitive interpretation of D_CGKL(K) is that of the information gain associated with the transition from R0 to R2: How many more bits of information does it take to define the probability distribution in R2 after it has become more “structured” due to the affinity-based selection procedure? If K is chosen larger than optimal, the K-mer probabilities in R2 will not capture any additional sequence specificity; in fact, over-fitting to sampling errors will cause D_CGKL to decrease. Thus, the optimal value of D_CGKL provides a good estimate of the effective binding site length (K_opt). For the Hox monomer data in Slattery et al. (2011), the largest information gain was achieved using 9-mers, while for Exd-Hox dimers a 12-mer table was found to be optimal (Fig. 4).

Figure 4. Oligonucleotide length (K-mer) optimization.

To determine the optimal number of base pairs over which to quantify relative affinity, we computed the information gain (Kullback-Leibler divergence) associated with two rounds of affinity-based selection (from R0 to R2). Using the Exd-Ubx data from Slattery et al. (2011), we found that by counting 12-mers in the later round, we optimally capture the DNA binding specificity of this complex.

3.7 Calculating Relative Affinities through Relative Enrichment of Motifs

1. Our ultimate goal will be to construct a table of relative affinities for all K-mers (of length K_opt) whose underlying counts are high enough to allow for their estimation (e.g., count at least 100 for a relative sample error <10%). To this end, we use an equilibrium thermodynamics description of what happens during a single round of SELEX (15). Our model considers simultaneous competing binding reactions between a protein or protein complex P on the one hand, and a mixture of DNA molecules on the other. For each type of DNA molecule, with sequence S_i, the formation of the complex P:S_i has forward and backward rates k_on(S_i) and k_off(S_i) respectively:

   $$P+S_i\underset{k_{\text{off}}(s_i)}{\overset{k_{\text{on}}(s_i)}{\rightleftarrows }}P{S}_i$$
   The strength of binding between the protein P and a DNA molecule of type S_i is quantified by the equilibrium association constant K_a(S_i) (or, equivalently, the dissociation constant K_d(S_i)):

   $$K_a(S_i)=\frac{1}{K_d(S_i)}=\frac{\left[{\mathit{\text{PS}}}_i\right]}{\left[P\right]\left[S_i\right]}=\frac{k_{\text{on}}(s_i)}{k_{\text{off}}(s_i)}$$
2. The fractional occupancy N(S_i), defined as the probability that S_i is bound, is then given by ([P] denotes the free protein concentration):

   $$N(S_i)=\frac{\left[{\mathit{\text{PS}}}_i\right]}{\left[{\mathit{\text{PS}}}_i\right]+\left[S_i\right]}=\frac{\left[P\right]K_a(S_i)}{1+\left[P\right]K_a(S_i)}=\frac{\left[P\right]}{K_d(S_i)+\left[P\right]}$$
   If F_i and $F_i^{\prime }$ denote the frequency of oligomer S_i in the dsDNA pool before and after a given round of affinity-based selection, respectively, then for any pair of sequence S_i and a reference sequence S_ref we have:

   $$\frac{F_i^{\prime }}{F_{\mathit{\text{ref}}}^{\prime }}=\frac{N(S_i)\cdot F_i}{N(S_{\mathit{\text{ref}}})\cdot F_{\mathit{\text{ref}}}}=\left(\frac{K_d(S_{\mathit{\text{ref}}})+[P]}{K_d(S_i)+[P]}\right)\left(\frac{F_i}{F_{\mathit{\text{ref}}}}\right)$$
3. Now, if we make the assumption that the free protein concentration is much lower than the dissociation constant (i.e. the low concentration regime where [P] ≪ K_d(S_i)), then the relative affinity between the two sequences has a surprisingly simple relationship to the pre- and post-selection frequencies:

   $$\frac{K_a(S_i)}{K_a(S_{\mathit{\text{ref}}})}=\frac{\left(\raisebox{1ex}{$F_i^{\prime }$}\!\left/ \!\raisebox{-1ex}{$F_{\mathit{\text{ref}}}^{\prime }$}\right.\right)}{\left(\raisebox{1ex}{$F_i$}\!\left/ \!\raisebox{-1ex}{$F_{\mathit{\text{ref}}}$}\right.\right)}$$
   In other words, the relative affinity equals the relative enrichment in the pool. It is easy to see that after r rounds of SELEX starting from the initial pool (making the same no-saturation assumption) we have:

   $$\frac{K_a(S_i)}{K_a(S_{\mathit{\text{ref}}})}={\left(\frac{\left(\raisebox{1ex}{$F_i^{(r)}$}\!\left/ \!\raisebox{-1ex}{$F_{\mathit{\text{ref}}}^{(r)}$}\right.\right)}{\left(\raisebox{1ex}{$F_i^{(0)}$}\!\left/ \!\raisebox{-1ex}{$F_{\mathit{\text{ref}}}^{(0)}$}\right.\right)}\right)}^{\frac{1}{r}}$$
   Without loss of generality, we can choose S_ref to be highest-affinity sequence. All relative affinities will then have a value between zero and one. The frequency ratios in a later round r (where the medium-to-high affinity DNA molecules are typically sequenced thousands of times) can be estimated from the unique-sequence counts as follows:

   $$\frac{F_i^{(r)}}{F_{\mathit{\text{ref}}}^{(r)}}\approx \frac{N_i^{(r)}}{N_{\mathit{\text{ref}}}^{(r)}}$$
   The same estimator cannot be used in round zero, as the counts for the same sequences would be too low to allow for reliable statistics. Fortunately, we can use the Markov Model that was discussed above to predict the frequency ratios in round R0:

   $$\frac{F_i^{(0)}}{F_{\mathit{\text{ref}}}^{(0)}}\approx \frac{P_{\mathit{\text{MM}}}(S_i)}{P_{\mathit{\text{MM}}}(S_{\mathit{\text{ref}}})}$$

4. Our goal is to infer relative affinities $\frac{K_a(S_i)}{K_a(S_{\mathit{\text{opt}}})}$ for all K-mers S_i of a length K that typically is smaller than the length of the DNA molecules in the protein binding reaction. Strictly speaking, this requires a deconvolution, as the K-mer binding site can occur at different offsets and directions within the DNA molecule. A systematic approach to this problem will be presented elsewhere (Riley et al., unpublished). However, an approximate solution − which assumes that a single K-mer dominates the rate at which each DNA molecule is selected − is to use the above equation at the level of K-mer subsequences. In what follows, we will therefore consider F_i to denote the frequency of DNA molecules containing a specific K-mer S_i.

5. It is important to know the standard error of the relative affinity estimate. As above, P_MM(S_i) denotes the expected frequency of S_i in R0 as computed using a Markov Model. The error in the estimate of $\frac{K_a(S_i)}{K_a(S_{\mathit{\text{opt}}})}$ is dominated by the sample error in the count N(S_i)^(r) in the later round. The error in the Markov-Model estimate is expected to be much smaller; however, to be conservative, we assume it to be of the same order. This yields the following equation for the standard error (SE) in the relative affinity estimate:

   $$\mathit{\text{SE}}\left(\frac{K_a(S_i)}{K_a(S_{\mathit{\text{opt}}})}\right)=\frac{K_a(S_i)}{K_a(S_{\mathit{\text{opt}}})}\cdot \sqrt{\frac{2}{N{(S_i)}^{(r)}}}$$

6. Using the theory, statistics, and approximations described so far, we are ready to compute the relative enrichment from R0 to the later round for each K-mer, and then use it to generate an estimate of the relative affinity, and the error in this estimate. Table 2 shows the result based on the comparison of R0 and R2 for Exd-Lab, using the data from Slattery et al. (2011).

3.8 Refinement of Affinity Estimates

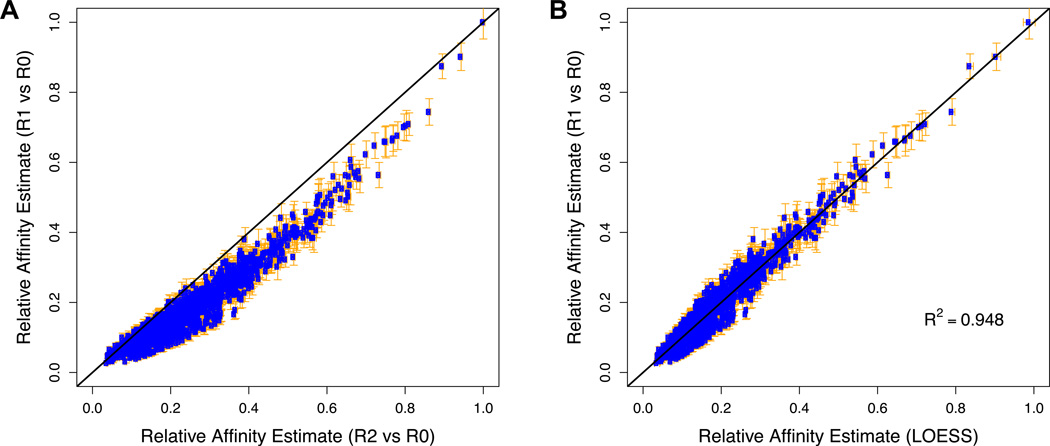
To validate consistent enrichment across the SELEX rounds, it is important to compare the fold-enrichment from R0 to R1 with the r^th-root of the fold-enrichment from R0 to Rr for all K-mers. Typically, a consistent deviation from the straight line will be observed which is presumably due to a combination of binding saturation and PCR bias (Fig. 5A). We typically find that these effects are less severe in the earlier rounds, and therefore R1/R0 is the most accurate predictor of relative affinity (i.e., closest to the true value if there would be no random error). However, since counts are lower in R1 than in subsequent rounds, the value of R1/R0 is also less precise (i.e., has a larger error). To combine the respective advantages of the more accurate counts from R1 and the more precise counts from the later round, we integrate information from multiple rounds of selection using local (LOESS) regression. The idea is to use the ranking of K-mers in terms of their enrichment in the later round to which K-mers are expected to have similar affinity, and average over the noisy affinity estimates in the earlier round. The procedure results in estimates of relative affinity that are both accurate and precise (Fig. 5B).

1. LOESS regression requires the specification of certain parameters. To determine these, we compared the LOESS-corrected relative affinities to affinities determined using EMSA gel shifts for small number of sequences in Slattery et al. (2011). An optimal fit was obtained using a 2^nd order polynomial with a smoothing span of 0.2 (see Fig. 2). We therefore used these parameter values in all our subsequent analyses.

2. We found that our results are improved when we use the relative affinities themselves as weights in the polynomial fit. The reason for this improvement is that the density of the data points is higher for lower-affinity sites (i.e, there are more ways to make a typical low-affinity site than a high-affinity one). Our weighting scheme compensates for this.

3. In theory, the binding affinity for any K-mer and its reverse complement should be identical, as they represent two equivalent ways of referring to the same double-stranded DNA molecule. However, in practice, the presence of remaining strand-specific biases and sample error will give rise to small deviations from this symmetry. To address this, we simply average the two values (see Table 3). In the rare cases where the non-symmetrized relative enrichment is negative after LOESS correction, we set the value to zero before averaging. Finally, we re-normalize the table by dividing by the maximum symmetrized value.

Figure 5. Integration of data from multiple rounds of SELEX.

To obtain relative affinity estimates that are both accurate and precise, we integrate information from multiple rounds of selection using LOESS regression. (A) Direct comparison between the normalized fold-enrichment from R0 to R1 and the normalized square root of the fold-enrichment from R0 to R2 of all 12-mers for Exd-Lab using the data from Slattery et al. (2011). The deviation from the straight line is presumably due to a combination of binding saturation and build-up of PCR bias. These effects are expected to be less severe in the earlier round, and therefore R1/R0 is a more accurate predictor of relative affinity. However, since counts are lower in R1 than in R2, the value of R1/R0 is also less precise. The error bars denote the standard error in the estimate of the relative affinity, calculated as described. (B) Comparison between the R1-based affinity estimates and LOESS-based estimates resulting from integration of R1 and R2 data.

Table 3.

Refinement of relative affinities. Estimated affinities for 12-mers, before (A) and after (B) LOESS-based refinement and symmetrization over reverse complements. Entries with “NA” have counts that are too low (i.e. <100) for accurate affinity estimation.

12-mer	Relative Affinity Estimate
	R1	R2	LOESS	Symmetrized
GTAATCAATCAT	1.0000	1.0000	1.0000	1.0000 ± 0.0140
ATGATTGATTAC	0.9014	0.9432	0.9151
AATGATTGATTA	0.8744	0.8954	0.8468	0.8601 ± 0.0082
TAATCAATCATT	0.7439	0.8617	0.8003
GTCATCAATCAT	0.7047	0.8033	0.7228	0.7402 ± 0.0051
ATGATTGATGAC	0.6761	0.7814	0.6947
GATGATTGATTA	0.7091	0.8104	0.7320	0.7369 ± 0.0051
TAATCAATCATC	0.6627	0.7692	0.6793
:	:	:	:	:
AATTAATTAATG	NA	0.0242	0.0240	0.0264 ± 0.0133
CATTAATTAATT	NA	0.0225	0.0240
TATAAGATTAAT	NA	0.0226	0.0239	0.0262 ± 0.0134
ATTAATCTTATA	NA	0.0238	0.0239
CATTAATTATAT	NA	0.0226	0.0238	0.0262 ± 0.0134
ATATAATTAATG	NA	0.0236	0.0238
AATATGATATAT	NA	0.0244	0.0236	0.0259 ± 0.0136
ATATATCATATT	NA	0.0213	0.0236
TTAATTAATAAT	NA	0.0208	0.0217	0.0242 ± 0.0147
ATTATTAATTAA	NA	0.0209	0.0217