Abstract
The spin polarization-induced nuclear Overhauser effect (SPINOE) describes the enhancement of spin polarization of solvent nuclei by the hyperpolarized spins of a solute. In this communication we demonstrate that SPINOEs can be observed between [1,4-13C2]fumarate, hyperpolarized using the dissolution dynamic nuclear polarization technique, and solvent water protons. We derive a theoretical expression for the expected enhancement and demonstrate that this fits well with experimental measurements. Although the magnitude of the effect is relatively small (around 2% measured here), the SPINOE increases at lower field strengths, so that at clinically relevant magnetic fields (1.5–3 T) it may be possible to track the passage through the circulation of a bolus containing a hyperpolarized 13C-labeled substrate through the increase in solvent water 1H signal. © 2014 The Authors. Contrast Media & Molecular Imaging published by John Wiley and Sons, Ltd.
Keywords: spin–lattice relaxation, cross-relaxation, SPINOE, signal enhancement
INTRODUCTION
Nuclear magnetic resonance (NMR) spectroscopy of nuclei other than protons has been limited by a lack of sensitivity. With the development of dissolution dynamic nuclear polarization (DNP), which increases the signal-to-noise ratio in solution-state 13C experiments more than 10 000 times 1, this limitation can to some extent be overcome. The DNP process involves transferring polarization from free radical electrons, at ˜1 K and in a high magnetic field (usually 3.35 T), to the nuclear spin of interest using microwave irradiation. The electron spins return to equilibrium and the thermodynamically coupled nuclear spin polarization is enhanced. The sample is then rapidly dissolved to physiological temperatures while retaining high levels of nuclear spin polarization (up to ˜50%) in the liquid state. However, once in the liquid state the polarization decays according to the longitudinal spin–lattice relaxation time, T1, and moreover any sampling of this polarization is destructive.
The nuclear Overhauser effect (NOE) is due to polarization transfer by cross-relaxation from one nuclear spin population to another following perturbation of one of the spins (e.g. by application of RF pulses). SPINOE (spin polarization-induced NOE) describes the enhancement of solvent spin polarization by dissolved solute spins that have been hyperpolarized previously (by DNP or other methods). The inefficient cross relaxation between solute and solvent spins, owing to the relatively low concentration of the solute spins, is overcome by their high levels of polarization. In addition, since the polarization of the solute spins is already perturbed from thermal equilibrium, it does not require the application of RF pulses. Navon et al. were the first to demonstrate transfer of hyperpolarization from optically pumped 129Xe gas to solution phase proton spins without the need for radio-frequency irradiation 2. They found that the magnitude of the SPINOE enhancement depended on the proximity and relative motion of the molecules and therefore was concentration, diffusion and field-dependent.
In this communication, we demonstrate that a SPINOE can be observed in solutions of [1,4-13C2]fumarate that have been hyperpolarized using the DNP technique. We derive a theoretical expression for the expected enhancement and demonstrate that this fits well with experimental measurements. Although the magnitude of the effect is relatively small (˜2% for 20 mm [1,4-13C2]fumarate hyperpolarized to 36%), the SPINOE is field-dependent 2, and therefore at clinically relevant field strengths (1.5–3 T) it may be possible to track the passage of a bolus of hyperpolarized 13C-fumarate in the body through the increase in 1H signal of solvent water. For example, in a 3.4 T magnet the enhancement is predicted to be ˜14%.
THEORETICAL
Intermolecular SPINOE enhancement
In a two-spin system, where the two spins S and I are in different molecules and relax owing to translational diffusion, such as a 13C-labeled molecule in water (1H), the time dependence of their magnetizations following polarization of one of the spins is given by Solomon's equations 3:
| 1 |
| 2 |
where Iz and Sz are the ensemble average longitudinal magnetizations of spins I and S, respectively; I0 and S0 are the thermal equilibrium magnetizations; ρΙ and ρS are the spin–lattice relaxation rate constants (1/ρI(S) = T1,I(S)), and σIS and σSI are the cross relaxation rate constants.
Let S be the hyperpolarized 13C nuclei, and I the protons in solvent water, and assuming that Sz(t) decays only due to ρS [because Sz − S0 > > Iz − I0] and that Iz(0) = I0, eqns 1 and 2 can be simplified to:
| 3 |
| 4 |
By definition, the SPINOE enhancement η is the change in 1H longitudinal magnetization from equilibrium 4:
| 5 |
The maximum enhancement ηmax is found when the average proton signal is in the steady state 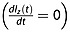 , at t = tmax. Thus,
, at t = tmax. Thus,
| 6 |
The relationship between the polarization (P) and the S magnetization at the time when the polarization is measured (tpol) is given by:
| 7 |
with the thermal equilibrium polarization of S (P0) given by the difference in state populations normalized by the total number of spins. In the high-temperature approximation for spins-1/2, this is 5:
| 8 |
where γ is the gyromagnetic ratio, ħ is the reduced Planck's constant (h/2π), κB is the Boltzmann constant, T is the temperature of the sample and B0 is the magnetic field strength.
Inserting eqns 3 and 7 into eqn 6, accounting for the exponential decay of the polarization from the moment it is measured to the time of maximum enhancement, and with hyperpolarization of the S spin (13C), Sz(tpol) > > S0, one gets the maximum enhancement in terms of independently measurable parameters:
| 9 |
where S and I are the spin quantum numbers of the nuclei. For an extended mathematical description the reader is referred to the literature 2,5,6.
Cross-relaxation owing to intermolecular dipole–dipole interactions is caused by the diffusion of solvent water and solute molecules. Since:
and
6 the cross-relaxation rate constant in the absence of molecular binding can be extended to nuclei with different spin quantum numbers as:
| 12 |
| 13 |
where DIS is the mean diffusion coefficient of the two species, d is the minimum distance between the two spins, NI and NS are the concentrations of nuclear spins in the sample and 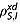 is the intermolecular contribution to the spin–lattice relaxation rate constant. Equations 12 and 13 were derived under the extreme narrowing limit,
is the intermolecular contribution to the spin–lattice relaxation rate constant. Equations 12 and 13 were derived under the extreme narrowing limit,
which is the case for water protons at room temperature and will also hold for hyperpolarized metabolites in solution 7.
Finally, setting I = S = 1/2, the SPINOE enhancement of the solvent proton spins (I) owing to hyperpolarized solute 13C spins (S) is given by:
| 15 |
The sign of the enhancement depends on the sign of γI and γS : if they are both positive (which is the case for 13C and 1H), then the sign of η(t) is opposite to that of the polarization of S 6.
Determination of 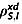 from measurable parameters
from measurable parameters
The spin–lattice relaxation time constants for the magnetically equivalent 13C1 and 13C4 in 20 mm solutions of [1,4-13C2]fumaric acid in 90% H2O and 10% 2H2O were measured (see Experimental section). The relaxation rate constant for S is influenced by intermolecular dipole–dipole interactions with solvent protons 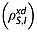 and deuterons
and deuterons 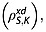 and also intramolecular interactions with fumarate protons and other relaxation mechanisms that contribute to
and also intramolecular interactions with fumarate protons and other relaxation mechanisms that contribute to 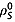 8. The spin–lattice relaxation time constants were also measured in 20 mm solutions of [1,4-13C2]fumaric acid in 100% 2H2O. In this case the relaxation of the S spins is dependent only on intermolecular relaxation with solvent deuterons
8. The spin–lattice relaxation time constants were also measured in 20 mm solutions of [1,4-13C2]fumaric acid in 100% 2H2O. In this case the relaxation of the S spins is dependent only on intermolecular relaxation with solvent deuterons 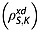 and on
and on 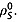
The relaxation rate constants owing to the different mechanisms add linearly, resulting in relaxation rate constants that one can measure:
| 16 |
| 17 |
Subtracting the two relaxation rate constants in eqns 16 and 17, and using eqns 12 and 13, we derive an equation dependent only on parameters that can be measured experimentally:
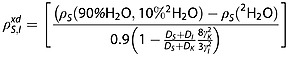 |
18 |
We make the assumptions that, in the same volume of solution, there are the same numbers of protons in 90/10% 1H2O/2H2O solution as deuterons in 100% 2H2O solution (NI = NK) and that the minimum approach distance (d) between these nuclei and the carbon spins (S) is the same, (dI = dK). For this calculation we used the ratio
obtained using the known values of the diffusion coefficients of H2O and 2H2O at 30 °C (2.6 × 10−9 and 2.1 × 10−9 m2/s, respectively) 9 and, as DS is unknown, we take the average value of the ratio in the limit when DS < < DI, DK and the limit when DS > > DI, DK. The degree of enhancement was shown to be relatively insensitive to the value used for DS, with a maximum difference of 2% in the results obtained between these two extreme cases.
Time dependence of the enhancement
Equations 4 and 5 predict that the evolution of η with time follows a biexponential function. Following the same reasoning as presented above, a time-dependent expression for η can be expressed in terms of ηmax. Here it is assumed that Sz(0) > > S0 and Sz(tmax) > > S0:
| 20 |
Equation 20 is a biexponential function of the type η(t) = A(e−Bt - e−Ct), where 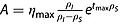 , B = ρS and C = ρI
, B = ρS and C = ρI
The time-point at which the absolute value of the enhancement is at a maximum, tmax, is dependent on the relaxation rate constants of the two species I and S:
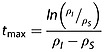 |
21 |
An exact result, obtained without making any approximations, is given by Song 6.
It can be seen from eqn 20 that, when intermolecular relaxation is not an important contributor to the relaxation of the S spin, that is, the difference in the 13C relaxation rate constants in H2O and 2H2O, |ρS(H2O) − ρS(2H2O)|, is small, then a smaller enhancement will be observed. The time to reach maximum enhancement η(tmax) also depends on T1,S: the faster the S spins relax, the earlier the maximum enhancement will be reached (Fig. 1).
Figure 1.
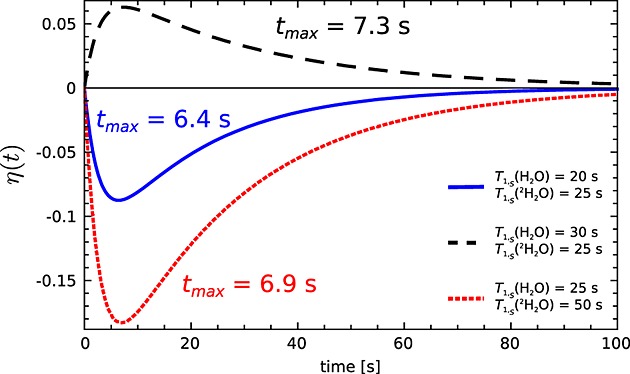
Simulation of the SPINOE enhancement of the 1H signal with 13C polarized to 50%, calculated using eqn 20. The parameters used in the simulation were T1,I = 1/ρI = 2.8 s, NI = 4.01 × 1023, NS = 1.44 × 1020, P(tmax) = 0.5, B0 = 9.4 T, T = 293 K, and different T1,S = 1/ρS as shown.
RESULTS AND DISCUSSION
Measurements of 13C spin lattice relaxation time constants (T1,S) for [1,4-13C2]fumarate showed that the 13C nuclei relaxed faster in 90/10% H2O/2H2O than in 100% 2H2O, that is, the intermolecular dipole–dipole interaction is a strong relaxation mechanism for this molecule (Table 1).
Table 1.
Measured spin–lattice relaxation times for 13C1 and 13C4 (S) in solutions of 20 mm [1,4-13C2]fumarate dissolved in 90/10% H2O/2H2O or 100% 2H2O at a magnetic field strength of 9.4 T (n = 6), 3.4 T (n = 3) and 1 mT (n = 3), and the predicted enhancement in the water signal with fumarate polarized [P(tpol)] to 0.36 ± 0.02 at tpol = 0. The spin–lattice relaxation time of the water protons (T1,I) used for calculation of the predicted enhancement was 2.83 s ± 0.02 s, which was measured at 9.4 T (n = 6). Quoted errors are the standard deviation of the mean for T1 s and the propagated errors for ηmax
| T1,S (in H2O) (s) | T1,S (in 2H2O) (s) | ηmax | B0 (T) |
|---|---|---|---|
| 27.6 ± 0.3 | 30.8 ± 0.8 | −0.020 ± 0.005 | 9.4 |
| 41.0 ± 1.3 | 66.6 ± 7.5 | −0.14 ± 0.03 | 3.4 |
| 34.3 ± 5.5 | 49.5 ± 1.2 | −450 ± 238 | 0.001 |
With these values of T1,S the maximum enhancement of the water proton signal with 20 mm [1,4-13C2]fumarate hyperpolarized to 36% and dissolved in H2O was calculated to be ˜2% at 9.4 T and >14% at lower fields [calculated using eqns 15 and 18. The water proton T1,I, used for the predicted enhancement was ˜2.8 s, which was measured at 9.4 T. Since water protons have a very short correlation time constant (˜10−11 s), their spin–lattice relaxation time is independent of the magnetic field strength 10. In tissue the T1 of water protons decreases with increasing magnetic field strength 11 and would need to be accounted for in calculation of the SPINOE. However, in an injected bolus, the T1 is expected to be approximately the same as that in pure water. Although a gadolinium chelate was used in the DNP process, the concentration of this paramagnetic ion after dissolution was too small (˜8 µm) to have an effect on the water proton T1 12,13.
The enhancement (η(t)) was determined by measuring changes in the proton signal integral following injection of a hyperpolarized sample of [1,4-13C]fumarate into H2O and was plotted as:
| 22 |
where Inon − DNP was measured in an experiment using a non-hyperpolarized solution of fumarate. Figure 2 shows the observed enhancement in water protons at 9.4 T after the addition of 20 mm [1,4-13C2]fumarate that had been hyperpolarized to 36%. The enhancement curves shown in Fig. 2 were calculated using the biexponential function [A(e−Bt - e−Ct)] defined in eqn 20 and the relaxation rate constants reported in Table 1 (dashed line) or the measured enhancements were fit to this function (solid line). There was reasonably good agreement between the water proton T1 estimated from the fit to the experimentally determined enhancement curve (3.3 ± 0.2 s) and that measured directly (2.83 ± 0.02 s; Table 1) and between the calculated maximum SPINOE value (ηamax = − 0.020 ± 0.005 s at tmax = 7 ± 1 s) and that determined from the fit to the experimental data (ηbmax = − 0.0196 ± 0.0002 s at tmax = 9 ± 1 s). However, the 13C T1 estimated from the enhancement (51.9 ± 1.2 s) curve was ˜1.7 × longer than the 13C T1 measured directly (27.6 ± 0.3 s; Table 1). This could possibly be explained by a mixing effect. The hyperpolarized [1,4-13C]fumarate was injected, via a transfer line, into a water-containing 10 mm-diameter NMR tube, that had already been placed in the magnet. Progressive mixing in the seconds after injection could have led to increasing contact of the bulk of the water protons with the 13C in the injected bolus of hyperpolarized [1,4-13C]fumarate, leading to an increased SPINOE at later time points, which would have been modulated by the decay of the 13C polarization.
Figure 2.
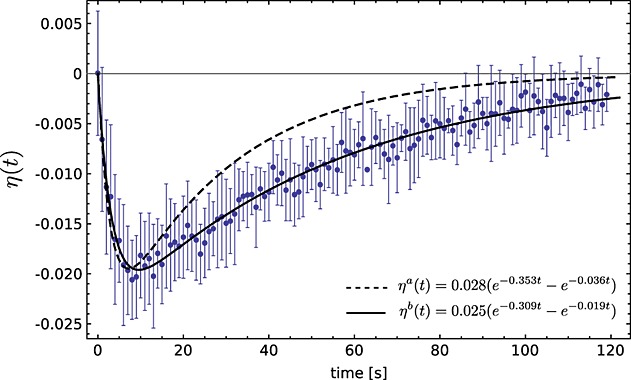
Measured SPINOE effect curve for solvent protons (water) at 9.4 T following the addition of 20 mm [1,4-13C2]fumarate that had been hyperpolarized to 36% at the time of injection (n = 2). Error bars are the standard deviation on the mean. ηa(t) was calculated using eqn 20 and the experimental values shown in Table 1 (dashed line). ηb(t) is the best fit to the experimental data (solid line).
CONCLUSION
We have shown, both experimentally and theoretically, that the magnitude of the SPINOE effect measured with 20 mm fumarate hyperpolarized to 36% at 9.4 T is ˜2%. This depends on the ratio of the longitudinal relaxation time constant of solvent protons to the cross-relaxation contribution to the relaxation of 13C-nuclei in the solute, which in turn depends on the magnetic field strength. In the case of fumarate, SPINOE increases at lower field strengths, the calculated effect reaching ˜14% at 3.4 T, which is close to the field strengths used in the clinic (1.5–3 T). The effect will be even higher at lower magnetic field strengths (Table 1). The SPINOE effect offers the possibility of following the progress of a bolus of hyperpolarized 13C-labeled material in the bloodstream by acquiring signal from solvent protons, rather than from the 13C itself. This avoids the loss of hyperpolarization that would result from 13C signal acquisition, saving the hyperpolarization until it has reached the tissue of interest, when the chemical specificity of spectroscopy can then be exploited, through direct detection of the hyperpolarized 13C label, to monitor subsequent metabolism of the labeled compound. Detection of the enhancement in signal from solvent water protons in effect turns the inevitable loss of 13C polarization, owing to relaxation, into a detectable and potentially useful 1H signal that could be used for bolus tracking.
EXPERIMENTAL
T1 measurements
All chemicals were acquired from Sigma, unless stated otherwise. Samples of [1,4-13C2]fumaric acid (99% 13C, Cambridge Isotope Laboratories) were prepared in 40 mm phosphate buffer, pH 7.4, containing 50 mm NaCl, 40 mm NaOH, 100 mg/L EDTA and 4 mm sodium 3-trimethylsilylpropionate d4 (TSP), as a chemical shift and intensity standard. The buffer was made with either 90/10% H2O/2H2O or 100% 2H2O. 13C T1 (ρS), and 1H T1 (ρI) values were measured at room temperature using an inversion-recovery pulse sequence in a vertical 9.4 T magnet. Additional 13C T1 measurements were carried out (a) in a vertical 3.4 T magnet using an inversion-recovery pulse sequence, and (b) in the stray field of the magnet room (˜1 mT). For the latter measurement, 0.5 ml of hyperpolarized sample, dissolved in buffer made with either 90/10% H2O/2H2O or 100% 2H2O, was injected into eight 10 mm NMR tubes containing 2 ml of buffer made with either 90/10% H2O/2H2O or 100% 2H2O, respectively, that were maintained in the NMR laboratory background field of ˜1 mT at room temperature and then inserted sequentially into the 9.4 T spectrometer magnet at intervals of ˜30 s. The first spectrum of each tube was acquired using a flip angle of 6°. The area under the fumarate peak (from both the 13C1 and 13C4 resonances) was integrated and fitted to a mono-exponential decay function to determine T1. The stray field of the magnet room was measured with a transverse Hall probe attached to a hand-held gaussmeter, HIRST GM04 (Magnetic Instruments Ltd). The T1 values were then substituted into eqn 18 for prediction of enhancement values in solvent water protons using eqn 15. Propagation of errors,
was used to determine the error in the prediction, taking into account the error on each of the parameters employed in eqn 15.
Hyperpolarization of [1,4-13C2]fumaric acid and observation of the SPINOE
13C-labeled fumaric acid was hyperpolarized as described previously 14. Briefly, [1,4-13C2]fumaric acid (3.23 mmol) was dissolved in 8.74 mmol dimethyl sulfoxide containing 11.48 µmol of a trityl radical (˜18.5 mm; AH111501; GE Healthcare, Amersham, UK) and 0.48 µmol of a gadolinium chelate [˜0.8 mm; Gd-3 15; GE Healthcare, Amersham, UK]. The solution was sonicated and centrifuged, and a 40 mg aliquot was hyperpolarized at 3.35 T and ˜1.2 K, with sample irradiation with a 94 GHz microwave source operating at 100 mW for 1 h. For some samples no microwave irradiation was used as a control. The solid sample was then rapidly dissolved in 6 ml of the buffer described above, which had been pressurized to 10 bar at 180 °C. Half of the sample was injected into a 10 mm diameter NMR tube inside the magnet via a transfer line. The other half was used to determine the level of the polarization, at the time of injection, with a polarimeter. Proton signal was acquired with 6° flip-angle pulses every second. The zero time point was taken to be the moment of injection of the material into the NMR tube.
Acknowledgments
The author I.M.-R acknowledges the solid-state NMR laboratory, Radboud University (Nijmegen, The Netherlands), for measurement time on a 3.4 T spectrometer during a Short Term Scientific Mission (COST Action TD1103) and the European Union Seventh Framework Programme (FP7/2007-2013) for support under the Marie Curie Initial Training Network METAFLUX (project number 264780). This work was supported by a CRUK Programme Grant to KMB and is a contribution from the Cambridge–Manchester Cancer Imaging Centre.
REFERENCES
- 1.Ardenkjaer-Larsen JH, Fridlund B, Gram A, Hansson G, Hansson L, Lerche MH, Servin R, Thaning M, Golman K. Increase in signal-to-noise ratio of > 10,000 times in liquid-state NMR. Proc Natl Acad Sci USA. 2003;100(18) doi: 10.1073/pnas.1733835100. ): 10158–. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Navon G, Song Y-Q, Rõõm T, Appelt S, Taylor RE, Pines A. Enhancement of solution NMR and MRI with laser-polarized xenon. Science. 1996;271:1848–1851. [Google Scholar]
- 3.Solomon I. Relaxation processes in a system of two spins. Phys Rev. 1955;99(1):559–565. [Google Scholar]
- 4.MacNamara E, Rice CV, Smith J, Smith LJ, Raftery D. Cross-relaxation dynamics between laser-polarized xenon and surface species using a simple three-spin model. Chem Phys Lett. 2000;317(2000):165–173. [Google Scholar]
- 5.Abragam A, Goldman M. Principles of dynamic nuclear polarization. Rep Progr Phys. 1978;41:70. [Google Scholar]
- 6.Song Y-Q. Spin polarization-induced nuclear Overhauser effect: an application of spin-polarized xenon and helium. Concept Magnetic Res. 2000;12(1):6–20. [Google Scholar]
- 7.Kowalewski J, Maler L. Nuclear Spin Relaxation in Liquids: Theory, Experiments, and Applications. New York: Taylor & Francis; 2006. [Google Scholar]
- 8.Fitzgerald RJ, Sauer KL, Happer W. Cross-relaxation in laser-polarized liquid xenon. Chem Phys Lett. 1998;284(1998):87–92. [Google Scholar]
- 9.Yoshida K, Wakai C, Matubayasi N, Nakahara M. A new high-temperature multinuclear-magnetic-resonance probe and the self-diffusion of light and heavy water in sub- and supercritical conditions. J Chem Phys. 2005;123(16) doi: 10.1063/1.2056542. ): 164506. [DOI] [PubMed] [Google Scholar]
- 10.Gore JC, Kennan RP, Stark DDB. Magnetic Resonance Imaging. Vol. 1. St Louis, MO: Mosby; 1999. Physical and physiological basis of magnetic relaxation; pp. 33–42. (ed.), Vol. [Google Scholar]
- 11.de Graaf RA, Brown PB, McIntyre S, Nixon TW, Behar KL, Rothman DL. High magnetic field water and metabolite proton T1 and T2 relaxation in rat brain in vivo. Magn Reson Med. 2006;56(2):386–394. doi: 10.1002/mrm.20946. [DOI] [PubMed] [Google Scholar]
- 12.Tayler MCD, Levitt MH. Paramagnetic relaxation of nuclear singlet states. Phys Chem Chem Phys. 2011;13(20):9128–9130. doi: 10.1039/c1cp20471h. [DOI] [PubMed] [Google Scholar]
- 13.Friesen-Waldner L, Chen A, Mander W, Scholl TJ, McKenzie CA. Optimisation of dynamic nuclear polarisation of [1-13C] pyruvate by addition of gadolinium-based contrast agents. J Magn Reson. 2012;223:85–89. doi: 10.1016/j.jmr.2012.07.010. [DOI] [PubMed] [Google Scholar]
- 14.Gallagher FA, Kettunen MI, Hu D-E, Jensen PR, in’tZandt R, Karlsson M, Gisselsson A, Nelson SK, Witney TH, Bohndiek SE, Hansson G, Peitersen T, Lerche MH, Brindle KM. Production of hyperpolarized [1,4-13C2]malate from [1,4-13C2]fumarate is a marker of cell necrosis and treatment response in tumors. Proc Natl Acad Sci USA. 2009;106(47) doi: 10.1073/pnas.0911447106. ): 19801–. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gallagher F, Kettunen M, Day S, Hu D-E, Ardenkjær-Larsen J, in ‘t Zandt R, Jensen P, Karlsson M, Golman K, Lerche M, Brindle K. Magnetic resonance imaging of pH in vivo using hyperpolarized 13C-labeled bicarbonate. Nature. 2008;453:940–943. doi: 10.1038/nature07017. [DOI] [PubMed] [Google Scholar]


