Improving the design of the agarose spot assay for eukaryotic cell chemotaxis

Abstract

Migration of cells along gradients of effector molecules, i.e., chemotaxis, is necessary in immune response and is involved in development and cancer metastasis. The experimental assessment of chemotaxis thus is of high interest. The agarose spot assay is a simple tissue culture system used to analyze chemotaxis. Although direction sensing requires gradients to be sufficiently steep, how the chemical gradients developed in this assay change over time, and thus, under what conditions chemotaxis is plausible, has not yet been determined. Here, we use numerical solution of the diffusion equation to determine the chemoattractant gradient produced in the assay. Our analysis shows that, for the usual spot size, the lifetime of the assay is optimized if the chemoattractant concentration in the spot is initially 30 times the dissociation constant of the chemoattractant-receptor bond. This result holds regardless of the properties of the chemoattractant. With this initial concentration, the chemoattractant gradient falls to the minimum threshold for directional sensing at the same time that the concentration drops to the optimal level for detecting gradient direction. If a higher initial chemoattractant concentration is used, the useful lifetime of the assay is likely to be shortened because receptor saturation may decrease the cells’ sensitivity to the gradient; lower initial concentrations would result in too little chemoattractant for the cells to detect. Moreover, chemoattractants with higher diffusion coefficients would sustain gradients for less time. Based on previous measurements of the diffusion coefficients of the chemoattractants EGF and CXCL12, we estimate that the assay will produce gradients that cells can sense for a duration of 10 h for EGF and 5 h for CXCL12. These gradient durations are comparable to what can be achieved with the Boyden chamber assay. The analysis presented in this work facilitates determination of suitable parameters for the assay, and can be used to assess whether observed cell motility is likely due to chemotaxis or chemokinesis.

1 Introduction

Chemotaxis is the directed motion of a cell induced by a chemical gradient.¹ This process is used by white blood cells to combat infections, by embryonic cells to form tissue patterns, and by cancer cells during metastasis.² A major challenge in studying chemotaxis in vitro is generating a well-controlled chemoattractant gradient for the cells to sense. Traditional methods include the delivery of a chemoattractant from a micropipette,³ diffusion of chemoattractant across a filter separating two chambers,⁴ and diffusion across a narrow bridge linking two reservoirs.⁵ More recently, chemoattractant-releasing microspheres have been used to model chemoattractant secretion from biological cells.⁶ Microfluidic devices can generate precisely controlled chemoattractant gradients and, in principle, sustain them indefinitely.⁷ Assays using agarose gels as a medium for diffusion of chemoattractants include the under-agarose assay,⁸ the agarose drop explant method,⁹ and the agarose-in-plug method.¹⁰

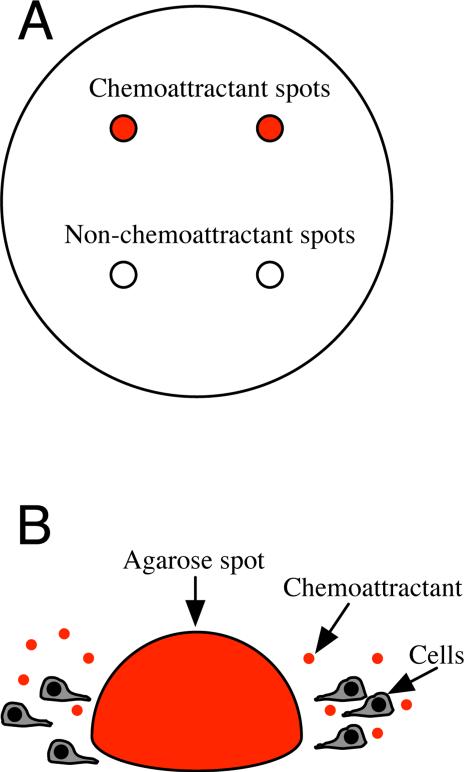
The “agarose spot assay” for the study of chemotaxis has recently been described by Wiggins and Rappoport.¹¹ In this technique, a chemoattractant is suspended in warm agarose solution that is then spotted into a cell culture dish (Figure 1). Four spots are placed, two containing chemoattractant and two serving as controls. Cells suspended in medium are plated into the dish and crawl underneath the spots containing the chemoattractant. After overnight incubation, the cells that migrated under the agarose drops are imaged and counted, and the numbers of cells that migrated under the chemoattractant and control spots are compared. This assay is inexpensive, simple to set up, and amenable to multiplexing, making it a valuable complement to more expensive and laborious methods such as microfluidic assays. The assay has been used to study cancer cell signaling and motility,^12–14 effects of Vitamin D3 on macrophage chemotaxis,¹⁵ dental pulp cell migration in wound healing,¹⁶ and neural crest cell movement during development.¹⁷ A disadvantage to the assay is that it can only sustain gradients that cells can sense for a limited duration. Additionally, the concentration profile is non-linear and varies over time. Quantitative analysis of the agarose spot assay can bring clarity to what gradients the cells would sense in the assay and for what duration, but this analysis, until now, has not been performed.

Figure 1.

Schematic of agarose spot assay. (A) Four spots of agarose gel are pipetted onto a cell culture dish. Two spots contain chemoattractant and two control spots do not. (B) Cells in medium are plated into the dish. Chemoattractant diffuses out of a spot, inducing cells to crawl under it.

Here, we calculate how the chemoattractant distribution varies over time. We then use these results to examine whether previous observations of cell motility in the agarose spot assay are best explained as chemotaxis or chemokinesis. We also discuss how the assay might be further developed and how best to tailor the method for

2 Methods

2.1 Model

We assume that the shape of an agarose spot is close to hemispherical, and that the volume of the dish is 200 times larger than the volume of the spot. These characteristics, which mimic those realized in practice, make it reasonable to represent the evolution of the chemoattractant distribution by the diffusion equation in spherical coordinates,

$$\frac{\partial c}{\partial t}=D\frac{1}{r^2}\frac{\partial }{\partial r}\left[r^2\frac{\partial c}{\partial r}\right],$$ (1)

where c is the chemoattractant concentration at a distance r from the center of the spot and t is the time since the medium was added to the dish; D is the diffusion coefficient of the chemoattractant in the medium. The spot initially has a uniform chemoattractant concentration. This approach gives accurate results for the chemoattractant distribution in and near the spot. Although the assay typically uses two spots containing chemoattractant, diffusion of chemoattractant out of a single spot is considered here; the effect of one spot on the other is minimal, and considering only a single spot simplifies the analysis without causing significant error.

2.2 Parameters used in analysis

Previously measured values of the diffusion coefficients and dissociation constants for EGF and CXCL12 are used to apply model results to the particular cases of MDAMB-231 breast cancer cells migrating in gradients of EGF (as in the study by Wiggins and Rappoport¹¹) and CXCL12 (as in the study by Vinader et al.¹⁴). Additionally, the gradients generated in the assay are compared with the gradients needed to induce chemotaxis in MDA-MB-231 cells, as estimated from experimental results.

The role of agarose in this assay is less to hinder diffusion than to prevent advection: for example, as the medium is added over the spot, the agarose keeps the chemoattractant from being dispersed rapidly. The diffusion coefficient for EGF has been measured previously, both in 0.3% agarose¹⁸ and in Hanks’ balanced salt solution,¹⁹ and is roughly 1 × 10⁻⁶cm²/s in both cases; therefore, the agarose does not appreciably hinder the diffusion of EGF. The diffusion coefficient of CXCL12 in water is 1.74 × 10⁻⁶ cm²/s.²⁰ The pore size of 0.5% agarose is ~ 1μm, much larger than the size of EGF or CXCL12, and thus, in the absence of short-range (e.g., electrostatic) interactions between the solute molecules and the agarose matrix, agarose should not be expected to hinder EGF or CXCL12 diffusion.

The K_d for EGF binding with EGF receptor (EGFR) is on the order of 1 nM.²¹ The reported K_d for CXCL12 interacting with its receptor, CXCR4, is 19 nM.²²

A major determinant of chemotactic response is the relative gradient—the steepness of the chemoattractant gradient normalized by the local chemoattractant concentration.²³ For a cell to sense a chemoattractant gradient, the gradient must be above a threshold value, which varies with the chemoattractant concentration and depends on the specific chemoattractant and the properties of the cell. Cells are most sensitive to gradients when the chemoattractant concentration is at the K_d of the chemoattractant-receptor bond, because at this concentration the difference in number of occupied receptors at the front and rear of the cell is greatest.⁵ Systematic testing of cells in various gradients and concentrations has revealed that neutrophils require a relative chemoattractant gradient of at least 1%,⁵ as do Dictyostelium discoideum.²⁴ Dendritic cells require relative gradients of 1–2.5%, depending on the chemoattractant used.²⁵ Few other types of chemotactic cells have been characterized with this level of rigor. Neuron growth cones have been observed to turn in a relative chemoattractant gradient of 10%, but at a concentration orders of magnitude higher than K_d.²⁶

The sensitivity of cancer cells to chemoattractant gradients is likely to be different for each type of cell. MDA-MB-231 breast cancer cells have been observed to crawl directionally under an EGF relative gradient of 10%.²⁷ These cells have also exhibited direction sensing in an 11 nM/mm gradient of CXCL12 at a low concentration relative to K_d,²⁸ which would have induced a difference in fractional receptor occupancy equivalent to that of a 4% relative gradient. Given the dearth of reproducible measurements of MDA-MB-231 gradient sensitivity, we primarily analyze the agarose spot assay assuming that these cells require a relative gradient of 1% to detect both EGF and CXCL12 gradients, but also describe how cell response would be different if cells actually require steeper gradients.

2.3 Numerical methods

For the conditions considered here, Eq. 1 does not have an exact solution. Hence, numerical methods were used to calculate an approximation of the chemoattractant distribution. The diffusion equation in spherical coordinates, Eq. 1, was solved by using finite differences to calculate the Laplacian,

$$\frac{1}{r^2}\frac{\partial }{\partial r}\left[r^2\frac{\partial c}{\partial r}\right],$$ (2)

the boundary conditions being ¶c/¶r|_r=₀ = 0 and c|_r = 10, where r_s is the radius of the spot. Timestepping was done with Adams predictor-corrector methods, using the odeint function in Scipy,²⁹ which is an interface for the LSODE solver from ODEPACK.³⁰ The spacing between nodes was 0.004r_s. Timesteps were $0.001r_s^{2}D$. Second-order convergence is expected for these methods and was observed when the finite difference grid was refined. Although the exact solution to Eq. 1 with the above-chosen boundary conditions is not known, the maximum difference between the calculated and the exact solution can be established. The calculated solution is less accurate for the first 30 min of the simulation because, initially, the chemoattractant profile has a discontinuity at the interface between the spot and the medium. In practice, this is not a problem when interpreting experimental results because this interval is small compared to the 6–24 hours during which the cells are typically allowed to crawl. The solution for the chemoattractant concentration at the interface between the spot and the medium is accurate to within 0.5% of the exact solution for times greater than 30 min.

3 Results

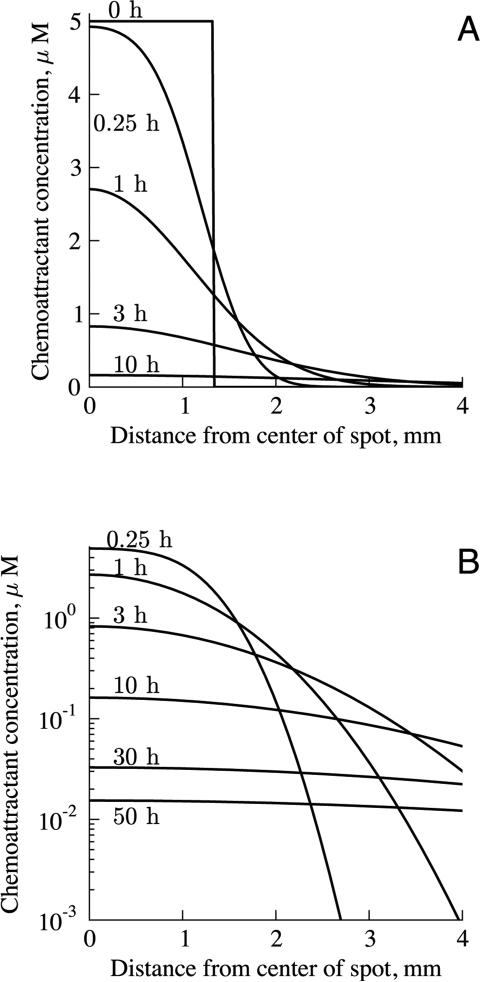
The solution is generalizable for different chemoattractants and initial concentrations, but for concreteness, we focus here on cases matching the conditions used in the studies carried out by Wiggins and Rappoport¹¹ and by Vinader et al.¹⁴ The significant experimental parameters that were different between the two studies were the type and concentration of chemoattractant used. Wiggins and Rappoport used 5 μM EGF; Vinader et al. used 125 nM CXCL12. Calculated chemoattractant distributions are shown in Figure 2. The gradient is initially steep at the interface between the spot and the medium, and flattens over time. With 5 μM of chemoattractant initially in the spot, cells located several millimeters away from the spot would be exposed to chemoattractant concentrations of tens of nanomolar, even after 50 hours.

Figure 2.

Chemoattractant distribution inside and outside of the spot over time, with 5 μM EGF in the spot initially, on (A) linear and (B) logarithmic scales. The edge of the spot is at 1.3 mm. Initially, the chemoattractant distribution curve is sharp at the interface between the spot and the medium. Over time, the chemoattractant diffuses and the gradient flattens.

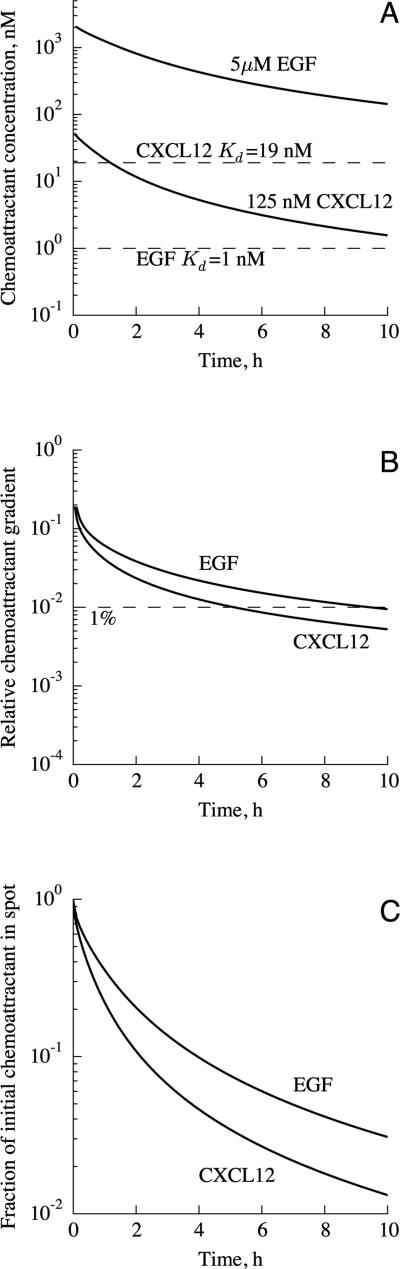
By considering when the chemoattractant concentration is close to K_d and when the gradient is sharp enough to be sensed, we can determine at what times cells at the interface between the medium and the spot would respond to the gradient. We follow the approach used by Lauffenburger and Zigmond, who analyzed several assays by focusing on the decay of the relative chemoattractant gradient over time.³¹ The time variation of chemoattractant concentration at the boundary is shown in Figure 3A. In the 5 μM EGF case the concentration of chemoattractant in and near the spot is still orders of magnitude higher than K_d even after 10 h, while in the 125 nM CXCL12 case the chemoattractant concentration drops below K_d after 1.2 h, and is an order of magnitude below K_d after 8.6 h.

Figure 3.

Variation of (A) chemoattractant concentration and (B) gradient at the in terface between the spot and medium, and (C) fraction of chemoattractant remaining in the spot. Results are shown for two cases: 5 μM EGF in the spot initially, as in Wiggins and Rappoport,¹¹ and 125 nM CXCL12 as in Vinader et al.¹⁴ In (A), the lower dashed line indicates the K_d for EGF-EGFR, and the upper dashed line is that for CXCL12-CXCR4. With an initial concentration of 5 μM, the EGF concentration would be orders of magnitude higher than K_d for the duration of the assay. In (B), the relative chemoattractant gradient, that is, the fractional change in chemoattractant concentration across the length of a cell, is shown. A threshold for gradient sensing of 1% is shown as a dashed line. The relative chemoattractant concentration does not vary with initial chemoattractant concentration.

The other major factor determining whether the chemoattractant gradient is suitable for inducing chemotaxis is whether the gradient is sufficiently steep. The threshold for gradient sensing is described in terms of the relative chemoattractant gradient, $\frac{\ell }{c}dcdx$, where λ is the length of the cell and c is the chemoattractant concentration; that is, the relative gradient is the change in chemoattractant concentration across the length of the cell divided by the average chemoattractant concentration at the cell. Calculated values of the relative chemoattractant gradient are shown, as a function of time, in Figure 3B. The relative gradient is not affected by the initial chemoattractant concentration because it is a fractional, not absolute, change in chemoattractant concentration. At the interface between the spot and the medium, the relative gradient drops below the 1% threshold at about 10 h for EGF, and 5 h for CXCL12. The higher diffusion coefficient of CXCL12 causes its relative gradient to drop more rapidly than the EGF gradient. In comparison, the under-agarose assay can sustain gradients for a longer duration, up to 22 h for a 1% gradient of EGF, and 4 h for a 5% gradient. As discussed in section 2.2, the thresholds for gradient sensing by MDA-MB-231 cells, and by cancer cells in general, have not been measured rigorously. If the thresholds are higher than 1%, the duration for which cells could sense the gradient would be shorter. For example, if cells require a 5% relative gradient, they could sense the direction of the spot for only 1 h for EGF, and 30 min for CXCL12. Given the low speeds at which these cells crawl, these short durations would render the agarose spot assay unsuitable for studying true chemotaxis of these cell types. This concern is equally applicable to the Boyden chamber⁴ assay, which sustains sharp gradients for similarly brief intervals.³¹ Moreover, the greater ease of imaging with the agarose spot assay may help it find use in applications currently served by the Boyden chamber.

This analysis can be validated by using fluorescently-labeled chemoattractant, measuring the decay of fluorescence intensity in the spot, and comparing the calculated and measured fractions of chemoattractant remaining in the spot (see Figure 3C). Also, this method could be used to calibrate the assay for different chemoattractants. We predict that 90% of the chemoattractant would leave the spot after 4 h for EGF, and 2 h for CXCL12.

4 Discussion

4.1 Interpretation of experimental results previously obtained with the agarose spot assay

In the agarose spot assay, the number of cells that migrate under spots containing chemoattractant, compared with the number under control spots, is used as a measure of chemotaxis. If more cells are found under chemoattractant spots it is assumed that cells have undergone chemotaxis. However, it is ambiguous whether this result indicates direction sensing or increased cell motility, as exhibited in chemokinesis.

The analysis described here facilitates predicting and determining whether chemo-taxis rather than chemokinesis is likely to be observed under particular experimental conditions. Specifically, our results suggest that chemotaxis was observed in the study by Vinader et al.¹⁴ because the chemoattractant concentration was close to the K_d for CXCL12-CXCR4. Conversely, as the chemoattractant concentration near the spot was much higher than the K_d for EGF-EGFR, it is unlikely that true chemotaxis was observed by Wiggins and Rappoport.¹¹ Instead, it appears that EGF might have generally increased the motility of the cells or attachment of the cells to the substrate, thereby facilitating chemokinetic movement under the agarose spot.

Additional controls would be needed to confirm that the assay is detecting chemo-taxis rather than chemokinesis. For example, addition of chemoattractant to the medium would help to determine to what extent cells crawl under a spot under chemokinetic stimulation in the absence of a gradient: separate tests with the chemoattractant concentration in the medium set equal to the initial or steady-state concentration in the spot would indicate the range of chemokinetic behavior of cells over the course of the experiment. Moreover, if fewer cells were to crawl under spots in this control, as compared with cells crawling under chemoattractant spots in the regular setup, one would conclude that motile cells are undergoing directed movement. A control with cells in a dish lacking chemoattractant would help determine the basal level of activity and clarify whether this accounts for the presence of cells under the control spots.

4.2 Improvement of the agarose spot assay

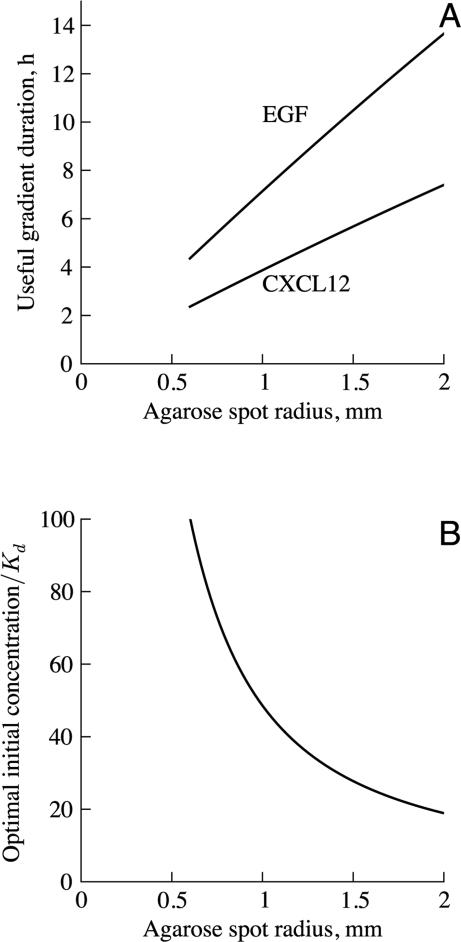
The decreasing relative chemoattractant gradient is the primary factor limiting the useful lifetime of the assay. Figure 4A shows that a larger chemoattractant spot radius provides a longer duration for which the gradient can be sensed by cells. The duration for which the gradient direction can be sensed is optimized if the chemoattractant gradient falls to the minimum threshold for directional sensing at the same time that the concentration drops to the optimal level for detecting the gradient direction, that is, a concentration equal to K_d. Figure 4B shows that, for the usual spot radius of 1.3 mm (i.e., a volume of 10 μl), the optimal chemoattractant concentration is 32K_d. A larger spot could maintain gradients for a longer period of time. Our calculations show that larger spots should have lower initial chemoattractant concentrations so that the concentration is equal to K_d when the gradient drops to the threshold for directional sensing. Spots cannot be arbitrarily large, though, as size is limited by surface tension. Spots of greater volume would be flatter than hemispherical. This is disadvantageous for the assay because the low surface area to volume ratio of hemispheres limits the rate of diffusion of chemoattractant out of the spot and it is more difficult to determine the chemoattractant profile generated by non-hemispherical spots. Regardless, experiments using larger spots should be attempted. Systematic variation of assay properties, e.g., type of agarose and the temperature at which spots are formed, could yield methodological improvements.

Figure 4.

Effect of spot size on assay characteristics. (A) Duration for which the gradient is above the threshold for direction sensing. Larger spots maintain suitable gradients for a longer duration. Assay lifetime varies inversely with the diffusion co efficient. (B) Optimal initial chemoattractant concentration, such that the chemoattrac tant concentration drops to the K_d of chemoattractant-receptor binding at the same time that the gradient falls below the threshold for sensing. A lower initial chemoattractant concentration is better for larger spots. The optimal chemoattractant concentration is proportional to K_d but does not vary with diffusion coefficient.

Inhibiting the diffusion of the chemoattractant would keep the chemoattractant gradient sharp for a longer time. Measurements of EGF diffusion indicate that 0.5% agarose does little to inhibit its movement.¹⁸ Increasing the volume fraction of agarose decreases diffusion coefficients, up to 30% for lysozyme and 50% for BSA in 4% agarose.³² EGF and CXCL12 are both smaller than lysozyme, which is smaller than BSA, so we would expect even high volume fractions of agarose to have only limited effect on their diffusion. Increasing the volume fraction of agarose would increase the stiffness of the gel, which would be undesirable if the agarose becomes too rigid for cells to crawl under.

This physical analysis of the agarose spot assay uses the assumption that the fluid in the dish is stationary. However, when the dish is moved, mixing would occur in the medium, leading to disruption of the gradient. Moreover, in some studies,^11,14 cells are plated and allowed to adhere for 4 h in 10% FCS, after which the medium is changed to 0.1% FCS to enhance direction sensing and reduce proliferation. If the medium is changed at 4 h after plating the cells, the chemoattractant concentration is subsequently about 10% of what it would be otherwise (data not shown). After the medium is changed, the concentration outside the spot is close to zero, leading to a steep gradient at the interface between the spot and the medium. Changing the medium at 4 h postpones the time at which the relative gradient drops below 1% essentially by an equal time. This could be compensated for by using a higher initial chemoattractant concentration. Moving the dish and changing the medium make it harder to know the exact gradient in the dish. Changing the medium as early as possible after plating will help to minimize the long-term effects of this disruption. Avoiding replacement of the medium would be preferable. To this effect, culture conditions that promote cell adhesion, such as coating the substrate with collagen or fibronectin,¹³ may facilitate plating cells directly into the desired assay medium.

In summary, our analysis of the agarose spot assay shows that, for the usual spot size (10 μl), the assay lifetime is optimized if the initial chemoattractant concentration is approximately 30 times the dissociation constant for the chemoattractant from its receptor. For chemoattractants with sufficiently low diffusion coefficients, the assay can sustain a gradient for several hours. Demonstrating that cell motion is chemotactic, not merely chemokinetic, is difficult. To that end, the analysis here suggests conditions where chemotactic behaviors are likely to be observed. We also propose controls to confirm chemotaxis in practice. For cells to sense the direction of a gradient in an assay, the gradient must be above a threshold and the concentration must be close to K_d, especially for shallow gradients. Lauffenburger and Zigmond previously analyzed chemotaxis assays by determining how long a relative gradient can be maintained above a given threshold.³¹ This work extends that analytic method by identifying how to select an initial chemoattractant concentration so that cells are exposed to suitable gradients and concentrations for the longest duration possible. The analysis here can be adapted to determine a suitable initial chemoattractant concentration in the under agarose assay.⁸