Single-Particle Spectroscopy Reveals Heterogeneity in Electrochemical Tuning of the Localized Surface Plasmon

Abstract

A hyperspectral imaging method was developed that allowed the identification of heterogeneous plasmon response from 50 nm diameter gold colloidal particles on a conducting substrate in a transparent three-electrode spectroelectrochemical cell under non-Faradaic conditions. At cathodic potentials, we identified three distinct behaviors from different nanoparticles within the same sample: irreversible chemical reactions, reversible chemical reactions, and reversible charge density tuning. The irreversible reactions in particular would be difficult to discern in alternate methodologies. Additional heterogeneity was observed when single nanoparticles demonstrating reversible charge density tuning in the cathodic regime were measured dynamically in anodic potential ranges. Some nanoparticles that showed charge density tuning in the cathodic range also showed signs of an additional chemical tuning mechanism in the anodic range. The expected changes in nanoparticle free-electron density were modeled using a charge density-modified Drude dielectric function and Mie theory, a commonly used model in colloidal spectroelectrochemistry. Inconsistencies between experimental results and predictions of this common physical model were identified and highlighted. The broad range of responses on even a simple sample highlights the rich experimental and theoretical playgrounds that hyperspectral single-particle electrochemistry opens.

Introduction

With the growing focus on charge transfer and storage applications using nanostructures,¹⁻⁸ a fundamental understanding of the physical and chemical processes governing charge transfer at the nanoscale is of paramount importance.⁹ Because the catalytic properties of nanoparticles are derived from their ability to store and transfer charge,¹⁰⁻¹³ nanoelectrodes prepared by attaching metal nanoparticles at submonolayer coverage on conductive substrates can be used to experimentally test the catalytic properties of nanoparticles. Electrochemical methods afford unrivaled control of surface chemistry at metal electrodes but are classically built upon bulk electrochemical current, potential, and charge relationships.¹² Changes in surface charge density of gold nanoparticles can also be detected through changes in the surface plasmon resonance energy.¹⁴⁻¹⁷ The use of these spectral characteristics to infer electrochemical processes is the subject of nanoparticle plasmon spectroelectrochemistry.

Nanoparticle size and morphology have proven to be critical in the design and engineering of efficient nanocatalysts.¹⁸⁻²⁹ Chemically prepared nanoparticles are inherently heterogeneous in size and shape even under identical growth conditions, leading to heterogeneity in catalytic and electrochemical activity within nanoparticle populations.^3,7,8,30,31 Additionally, surface defect sites have been shown to increase nanocatalyst activity.^32,33 The synthesis of nanocatalysts has historically relied heavily on iterative trial and error optimization schemes.³⁴ Several groups have recently taken advantage of theoretically predicted shape-dependent activity in their quest to make better catalysts.^18,34,35 If scientists and engineers could resolve heterogeneous activity within populations of nanoparticles, the study of highly active subpopulations could then be used to inform design principles and further optimize catalytic properties of entire populations, increasing total activity and yield.

Single-particle surface plasmon sensing of catalytic and electrochemical charging was first demonstrated by the Mulvaney group^15,16,36 and later reported by the Klar group³⁷ with a focus on the ability to tune the plasmon resonance of single nanoparticles with static potential control. A related technique utilizing the surface plasmon resonance of thin films has also been used to study electrocatalytic behavior of adsorbed single nanoparticles and the metal film itself.^38,39 Hill and Pan recently demonstrated the use of single-particle dark-field spectroscopy in tracking the synthesis of single silver nanoparticles via electrodeposition.⁴⁰ Without the deleterious effects of inhomogeneous spectral broadening due to sample inhomogeneity as in ensemble measurements, surface plasmon resonance and homogeneous line width responses directly probe changes in free electron density and plasmon damping due to surface chemistry.^15,16,37 According to the charge density tuning model, changes in charge density affect the bulk plasma frequency of the metal, resulting in shifts of the surface plasmon resonance.^{14−17,36,41} However, recent ensemble spectroelectrochemical studies suggest that chemical mechanisms might play an equal or more important role in electrochemical tuning of the surface plasmon resonance.^6,42 We hypothesize that because nanoparticle size and surface heterogeneity are important in charge transfer and storage at nanoparticle interfaces, disparities between the charge density and chemical tuning interpretations can be addressed by resolving nanoparticle heterogeneity.⁴³ Ideally, one would want to statistically sample the overall nanoparticle population but also have the ability to study subpopulations at the single-particle level if multiple mechanisms are identified.

We have developed a methodology and complementary techniques to study electrochemical heterogeneity both of a statistical distribution and within subpopulations of chemically prepared single gold nanoparticles. By combining dark-field hyperspectral imaging and short exposure single-particle spectroscopy under electrochemical control, we probed electrochemical processes of single 50 nm gold colloidal particles over a broad range of time scales and over two distinct potential ranges. Previous studies have focused on a few selected single nanoparticles measured serially and are thus blind to heterogeneous behavior across nanoparticle populations, particularly with regard to irreversible processes. Because our methodology measures many nanoparticles in parallel, we identify and illuminate the heterogeneous nature of electrochemical plasmon resonance tuning that has not been shown in existing literature.^16,37 We identified three different subpopulations of nanoparticles in the cathodic potential range on the basis of their spectral response and concluded that previous studies involving single-particle spectroelectrochemistry focused on the least populous group. By extending our dynamic spectroelectrochemical investigation of these nanoparticles into the anodic potential range, we observed multiple nanoparticle-dependent spectral tuning mechanisms. In light of the multiple mechanisms and processes identified in this system, we report on both the classification of the broader processes present and further study of electrochemically reversible processes. The process-specific activity of individual nanoparticles shown clearly in this work demonstrates the value of the methodology and technique, and findings herein pave the way toward further understanding of nanoparticle electrochemistry critical for guiding the design of nanoparticle electrodes and catalysts.

Experimental Methods

Gold spheres were purchased from BB International (nominal size: 50 nm; independent transmission electron microscopy characterization: 51 ± 7 nm)⁴⁴ and deposited on an indium tin oxide (ITO) coated glass coverslip (Fisher Scientific). A sealed spectroelectrochemical cell for transmission dark-field microscopy was constructed in-house using the ITO/gold nanoparticle working electrode, silver wire quasi-reference electrode, and silver wire auxiliary electrode. Further cell details can be found in Section 1.1 of the Supporting Information. Single-particle scattering spectra were collected with a custom instrument comprised of an inverted dark-field microscope (Zeiss AxioObserver m1, with oil immersion dark-field condenser NA = 0.7–1.4), an electrochemical workstation (CH Instruments, model 630D), and an imaging spectrograph (Princeton Instruments, Acton SpectraPro 2150i with Pixis 400 thermoelectrically cooled back-illuminated CCD) mounted atop a programmatically controlled linear translation stage (Newport Linear Actuator model LTA-HL). The potential of the nanoparticles relative to the silver quasi-reference electrode in 100 mM NaCl electrolyte was controlled using a three-electrode potentiostat synchronized with the spectrograph by means of custom software (Labview, 2011). All electrolyte solutions were prepared using Millipore-filtered deionized water. The scattered light was collected by an oil immersion objective (Zeiss, Plan-Achromat 63x, NA 0.7–1.4) and directed to an imaging spectrograph to record scattering spectra of single gold nanoparticles during cyclic voltammetry and chronocoulometry. Using a nonlinear least-squares fitting algorithm (Matlab, 2013a), scattering spectra were fit with single Lorentzian curves, from which the plasmon resonance energy and the full width at half-maximum were found.

Results and Discussion

Our custom setup allows hyperspectral imaging of many nanoparticles and single-particle cyclic coulometry with specified potentials, realized for both cathodic and anodic conditions (Figure 1). A sealed optically transparent thin-layer electrochemical cell with 50 nm gold nanoparticles dispersed on the working electrode forms a three-electrode cell with a 100 mM sodium chloride (NaCl) electrolyte (Figure 1a). Silver wires were used as an auxiliary electrode and a quasi-reference electrode. A three-electrode potentiostat controlled the potential difference at the interface of the electrolyte and the gold nanoparticle/indium tin oxide (ITO) working electrode. Detailed information on the construction of the electrochemical cell and experimental details can be found in Section 1.1 of the Supporting Information. The electronic free charge densities of the gold nanoparticles changed to establish each prescribed potential difference and were manifested as shifts in the localized surface plasmon resonance. Resonantly scattered light from individual nanoparticles was resolved with a 63× oil-immersion objective and directed to a thermoelectrically cooled back-illuminated CCD imaging spectrograph.¹⁴⁻¹⁷ By using a very thin spectroelectrochemical cell (total thickness: 1 mm) with nanoparticles directly adjacent to the collection optics, out of focus light was minimized, leading to high signal-to-noise ratios (SNRs ∼ 425) of the dark-field scattering signal. In combination with Lorentzian fitting, our instrumentation and experimental geometry allowed us to measure shifts in single-particle plasmon resonances as small as 1 meV within a few seconds. The spectrograph was mounted atop a linear translation stage, and both the spectrograph and stage were programmatically controlled and synchronized to construct hyperspectral images of sample regions containing many nanoparticles (instrument details are provided in the Supporting Information Sections 1.3 and 1.4). Using a pushbroom hyperspectral imaging scheme,^45,46 tens to hundreds of single-particle spectra were acquired in parallel under potential control. In Figure 1b, a representative 50 × 50 pixel RGB image of ITO-supported gold nanospheres is shown. The RGB image was reconstructed from a hyperspectral data cube, shown in cartoon form behind the image. Details for RGB construction from hyperspectral data can be found in Section 1.5 of the Supporting Information. Collection of a hyperspectral image at a fixed electrochemical potential took 108 s (2 s/pixel row, 54 × 284 pixel image) with an additional 60 s of equilibration time between scans at two different static potentials. In this manner, potential-dependent spectral traces from each nanoparticle were collected as a series of hyperspectral data cubes, each at a prescribed electrochemical potential. Two example potential controlled spectra from a single nanoparticle are shown in the right panel of Figure 1b.

Figure 1.

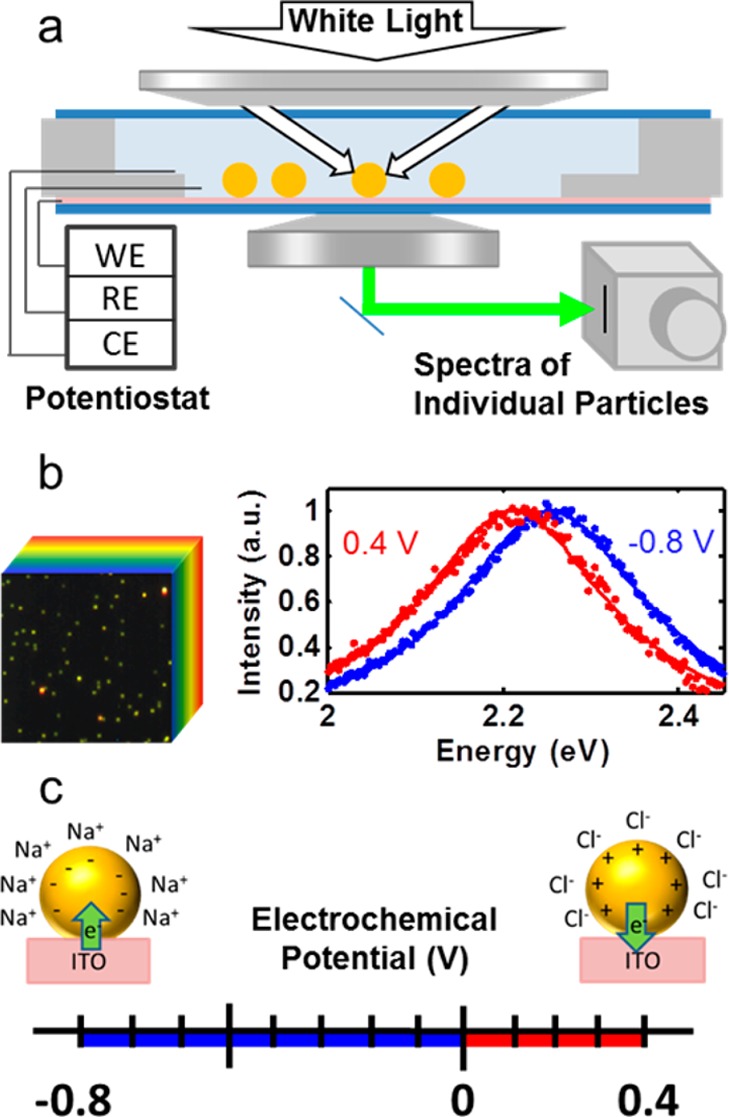
Cathodic and anodic spectroelectrochemistry of single gold nanoparticles. (a) Optically transparent thin electrochemical cell for dark-field spectroscopy of single 50 nm gold spheres on an ITO working electrode (WE) under electrochemical potential with auxiliary and reference electrodes (AE, RE) composed of silver wires. (b, left) Steady-state hyperspectral imaging of many single nanoparticles under potential control (32 × 32 μm). (b, right) Normalized spectra at potential vertices for a single nanoparticle along with Lorentzian fits. (c) Non-Faradaic cathodic (blue) and anodic (red) potential ranges with predicted charging mechanisms shown schematically.

Using the above setup, single-particle spectra were collected under two potential ranges (Figure 1c). In the cathodic range (U < 0 V, shown in blue in Figure 1c and throughout this work), electrons were injected into each nanoparticle from the conductive ITO substrate.¹⁶ The nanoparticles had a net negative charge, corresponding to a higher free electron density than a neutral nanoparticle. According to the Grahame model for electrode/electrolyte contact, a positively charged Stern layer composed primarily of hydrated cations forms at the surface of the nanoparticles as well as at the surface of the ITO (Figure 1c).⁴⁷ In the anodic range (U > 0 V, shown in red in Figure 1c and throughout this work), electrons are extracted from the nanoparticles by the potentiostat circuit, yielding lower free electron densities and net positively charged nanoparticles. To screen the positively charged gold surface, hydrated chloride anions form a negatively charged Stern layer.⁴⁷ The two potential ranges were arbitrarily defined with 0 V (vs Ag/AgCl quasi-reference electrode) as a common vertex as a matter of convention set by seminal work.¹⁶

In the cathodic potential range investigated (0 to −800 mV), the only known Faradaic process for gold electrodes in a NaCl solution is the overpotential deposition of hydrogen cations and subsequent hydrogen evolution reaction (HER). These coupled reactions are unavoidable at cathodic overpotentials and have been shown to rely heavily on crystal lattice structure and the presence of defects.^43,48 Protonation of the gold surface is electrochemically reversible, whereas HER is electrochemically and chemically irreversible. As such, we expect nanoparticle heterogeneity to result in a variety of observed spectral tuning behaviors in the cathodic potential range. However, existing literature reports only on nanoparticles following the charge density tuning model.^16,37 In the anodic potential range (U > 0 V), multiple reactions occur at gold electrodes in NaCl solutions.⁴⁸ With a pH-neutral NaCl solution, the lowest potential anodic oxidation reaction is that of chloride ions, which occurs at ∼530 mV (vs Ag/AgCl reference electrode), as detected in ensemble spectroelectrochemical measurements.⁶ In an attempt to avoid this reaction and target charge-density-related surface plasmon resonance shifts, we limited our upper potential vertex to +400 mV. Because of the above-mentioned (and other possible) coupled reactions, we examined the cathodic and anodic regimes separately. We began with cathodic potentials to explore heterogeneous nanoparticle responses under potential control.

Potential-dependent hyperspectral imaging gave us the means to observe heterogeneity within a nanoparticle population (Figure 2). Hyperspectral images at each potential were used to identify the steady-state potential induced plasmon resonance shift. Figure 2a shows an example spectral image compiled at open-circuit potential, with circled nanoparticles noting subsets identified by their potential-dependent spectral behavior. Each scattering center in the series was located and fit with a single Lorentzian function. Single gold nanoparticles were distinguished from clusters by imposing a coefficient of determination cutoff, R² > 0.95. Because we achieved a large signal-to-noise ratio, spectra were well fit. This allowed us to reliably and repeatedly detect spectral shifts as small as 1 meV.

Figure 2.

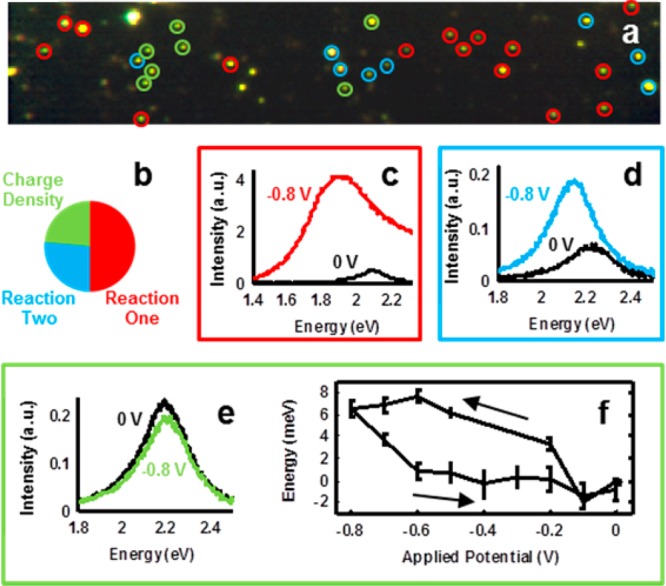
Cathodic hyperspectral steady-state electrochemical tuning of gold nanoparticles on ITO support. (a) Real-color RGB image of 50 nm gold nanoparticles at open-circuit potential. Nanoparticles that did not exhibit a Lorentzian scattering spectrum were not classified. Image size: 90 × 17 μm. (b) Classification of single-particle behavior based on the reversibility of potential-dependent spectral changes. (c) Scattering spectra at potential vertices for a single nanoparticle from subgroup Reaction One. (d) Spectra for a nanoparticle from subgroup Reaction Two. (e) Spectra for a nanoparticle showing charge density tuning of the plasmon resonance. (f) Mean peak resonance shift and associated standard error for seven nanoparticles exhibiting charge density tuning, shown as a function of applied potential. Arrows indicate applied potential scan directions.

By investigating many nanoparticles under potential control in this cathodic range (0 to −800 mV), we found that the majority of nanoparticles demonstrated behavior not predicted by charge density tuning, as shown in Figure 2b. We expected the plasmon resonance of all gold nanoparticles to blue shift linearly upon application of negative electrochemical potentials,^14,16,17,37 due to an increase in free electron density that results from electrons flowing from the potentiostat circuit into the nanoparticles and substrate in establishing the electrical potential difference between the bulk electrolyte and the nanoelectrodes. Upon exposure to cathodic potentials, spectra for half of the single gold nanoparticles that met the selection criteria (R² > 0.95) showed significant irreversible changes in their scattering spectra including significant resonance broadening, large increases in scattering intensity, and the loss of their original Lorentzian response. These nanoparticles are highlighted with red circles in Figure 2a, and representative spectra at the potential vertices are shown in Figure 2c. We attribute this to an electrochemically irreversible reaction (Reaction One).

Further identified in Figures 2a and 2b, one-fourth of the nanoparticles also showed large increases in intensity, spectral broadening, and plasmon resonance red shifts not predicted by the charge density tuning model. In contrast to nanoparticles undergoing Reaction One, the scattering spectra of nanoparticles in this subset maintained their Lorentzian line shape throughout the entire experiment, but their scattering spectra only returned to initial conditions after the application of a sufficient positive potential. These nanoparticles are highlighted by cyan circles in Figure 2a, and example spectra are shown from a single nanoparticle in Figure 2d. An example of this apparent reaction, referred to as Reaction Two, is shown in Section 2.1 of the Supporting Information. Further investigations are required to elucidate the mechanisms and potentially complex behaviors that we refer to collectively as Reactions 1 and 2.

Finally, just under a quarter of the single gold nanoparticles followed the predicted charge density tuning model. These nanoparticles are indicated by green circles in Figure 2a, and example spectra from a nanoparticle in this subset are shown in Figure 2e. Nanoparticles in this subset were well-fit throughout the experiment (R² > 0.95), show small changes in fwhm (ΔΓ < 20 meV), and demonstrated completely reversible plasmon resonance shifts. The change in peak resonance energy as a function of potential for this subset of nanoparticles is shown in Figure 2f as a mean resonance shift with associated standard error for all nanoparticles in this subpopulation. The return to initial resonance energy is a strong indicator that the spectral tuning mechanism for this subset of nanoparticles is electrochemically reversible, fitting the charge density tuning model. By design, this experiment observed the initial response of particles to electrochemical modulation. The relatively large populations of particles demonstrating potential-dependent spectral responses other than those predicted by the charge density tuning model indicate that future work will be necessary to model and fully understand the irreversible and semi-irreversible spectral tuning observed here in the cathodic potential range. Previous studies of single-particle spectroelectrochemical tuning under static potential control have only reported on the behavior of this particular subset of nanoparticles.^16,37

The most valuable electrochemical techniques are not steady-state techniques but rather are dynamic in nature.¹² The ability to precisely and quickly vary the potential at an electrode surface allows researchers to characterize electrodes, investigate fine potential structure, and determine reaction kinetics. For the same purpose, in this work we developed dynamic single-particle spectroelectrochemistry. By measuring single-particle spectra under dynamic potential control, we recorded spectral changes on the order of seconds rather than minutes as with steady-state experiments. While the value of hyperspectral potential-controlled imaging experiments lies in studying many nanoparticles simultaneously, the strengths of dynamic measurements are 3-fold: (1) Fast collection times allow many potential cycles to be measured, allowing us to probe the repeatability and reversibility of potential-dependent spectral shifts. (2) By investigating the potential scan-rate dependence of spectral response, the time scale of reaction kinetics can be interrogated. (3) Reactions with partial chemical reversibility can be probed by limiting the amount of time spent with significant electrochemical overpotentials. From a practical standpoint, recording spectra on the time scale of seconds vs minutes allows greater potential resolution to be achieved in a realistic time frame. Therefore, dynamic measurements illuminate fine potential/resonance structure not possible using static measurement techniques.

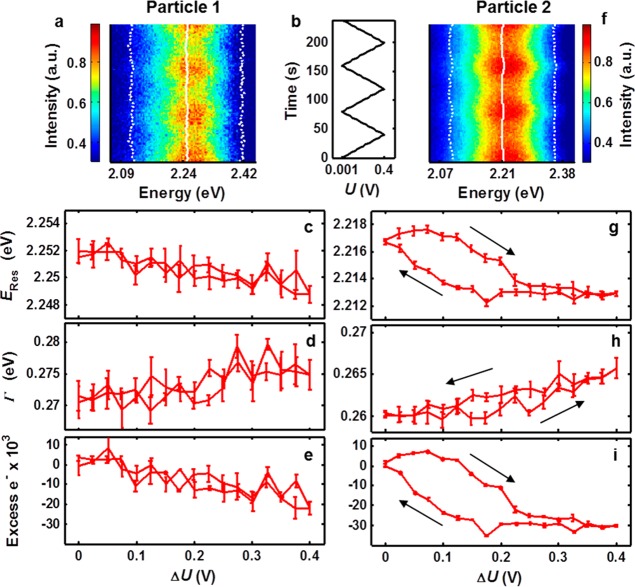
Investigations under dynamic potential control in the cathodic potential range showed that the subset of nanoparticles described in Figure 2e and 2f also demonstrated reversible spectral tuning, consistent with the charge density tuning model (Figure 3). In this experiment, the potential was swept in a sawtooth pattern at 10 mV/s between 0 and −800 mV, as shown in Figure 3a. Scattered light from a single nanoparticle was directed to the spectrograph, and spectra were recorded every 2.5 s. Each spectrum was independently fit with a single Lorentzian, and the parameters of the fit determined the resonance energy, E_Res, and full width at half-maximum, Γ. E_Res and Γ are shown in Figure 3b as solid and dashed white lines, respectively.

Figure 3.

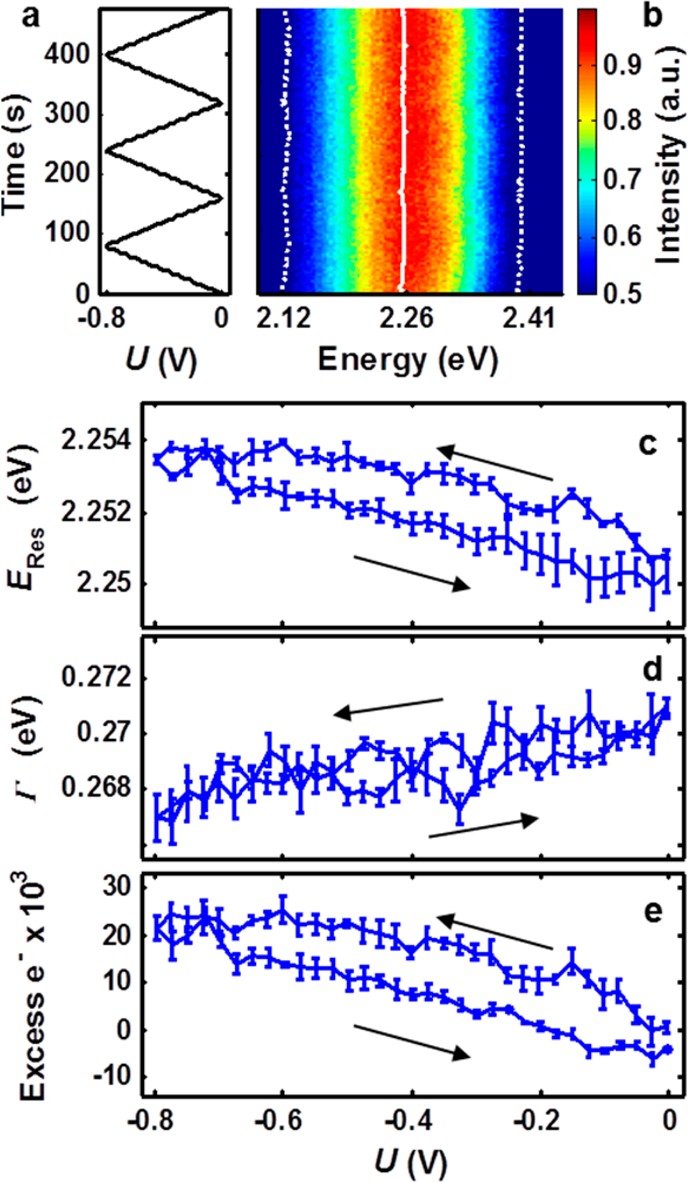
Single-particle measurement of dynamic electrochemical tuning in the cathodic range (0 to −800 mV). (a) Electrochemical potential of the working electrode relative to the reference electrode as a function of time. Sweep rate: 10 mV/s. (b) Scattering spectra under dynamic potential control. The fitted resonance energy, E_Res (solid white line), and full width at half-maximum, Γ (dotted white lines), are superimposed. (c) Reversible, cyclic E_Res response as a function of potential U shown as mean with standard error for three consecutive cycles. (d) Average Γ over three cycles as a function of potential. (e) Mie–Drude model simulations, and the number of electrons transferred from the conductive substrate to the nanoparticle is calculated. Error bars indicate propagated standard error in E_Res. Arrows indicate the scanning directions of the applied potential.

The mean and standard error for E_Res and Γ for three consecutive potential cycles after initial stabilization are shown as a function of applied electrochemical potential in Figures 3c and 3d, respectively. E_Res blue-shifted linearly with increasingly negative potentials and returned to the initial resonance as the potential U was swept back to 0 V (dE_Res/dU = −3.9 meV/V). A small but measurable potential-independent hysteresis is also apparent. To test whether this hysteresis was related to double-layer formation kinetics, the scan rate was varied (experimental data for 5, 10, and 20 mV/s is given in Section 2.2 of the Supporting Information), but no effects due to changes in scan rate were observed. We conclude that because no scan rate dependence was found for these values transient cell and double-layer dynamics occurred faster than the rate of potential changes, as expected from theory.⁴⁹ By corollary, observed spectral shifts for these nanoparticles in this potential range probed changes in equilibrium charge densities. These results are in good qualitative agreement with the charge density tuning model.

Using the charge-density-modified Drude dielectric function model along with Mie scattering theory (Mie–Drude model¹⁷), we calculated the excess charge on the nanoparticle from E_Res throughout the potential range applied in our study (Figure 3e).¹⁶ In these calculations, a model Drude dielectric function was modified to reflect changes in the nanoparticle free electron density and then used to simulate the plasmonic response as a function of applied electrochemical potential. Details and derivation of the full Mie–Drude model are found in Section 3 of the Supporting Information. At negative potentials, the nanoparticle was negatively charged and therefore had a higher free electron density, as shown in Figure 3e. Over this potential range the number of excess electrons fluctuated by ∼20 000 electrons, which is still less than 0.5% of the total conduction electrons in the nanoparticle but corresponded to a surface capacitance of ∼510 μF/cm². Figure 3d shows that Γ decreased linearly with applied potential, with dΓ/dU = 3.2 meV/V. However, the trends in Γ and scattering intensity predicted by the Mie–Drude model scattering simulations were completely opposite from the experimental results (for more details see Section 3 of the Supporting Information). For this reason, we suggest that significant theoretical work is still needed to unravel the dependence of resonance width and intensity on applied potential. In the calculation of free charge density fluctuation, each nanoparticle was assumed to be electrically neutral at the open-circuit potential of the working electrode. The actual point of zero charge for each nanoparticle is unknown and likely varies slightly from nanoparticle to nanoparticle. It should be noted that previous studies have confirmed that changes in refractive index do not play a significant role in electrochemically induced plasmon resonance tuning by varying the cationic species and observing no change in cathodic charge density tuning response.⁶ From a survey of 13 nanoparticles in this potential range obeying the charge density tuning model, we found that the response was linear but dE_Res/dU varied greatly among nanoparticles from −2 to −16 meV/V, indicating that the nanoparticles’ ability to store charge varied or that heterogeneity between the conducting substrate and metal nanoparticles played a limiting role in overall charging. For these nanoparticles, dΓ/dU also varied from 0.2 to 12 meV/V.

When the nanoparticles found to undergo charge density tuning at cathodic conditions were examined within the anodic range with dynamic potential control, a heterogeneous spectral response was observed (Figure 4), indicative of multiple processes occurring. In the anodic potential range of 0 to +400 mV, well below the chloridation onset potential expected from ensemble measurements (∼530 mV vs Ag/AgCl),⁴² some nanoparticles exhibited nonlinear spectral tuning, inconsistent with the charge density tuning model. Figure 4a illustrates a series of spectra as a function of time varying potential for two separate nanoparticles demonstrating the two observed behaviors. Particle 1 showed apparent charge density tuning in the anodic potential range. E_Res and Γ are shown as solid and dotted lines, respectively. The electrochemical potential was again swept at 10 mV/s between 0 and 400 mV as shown in Figure 4b. Take note that large modulations of the scattering intensity with potential produce an illusion of resonance narrowing at higher potentials, when in fact the opposite is true—Γ increases with increasing potential. Figure 4c plots the plasmon resonance energy as a function of potential averaged over three consecutive cycles. The resonance energy decreased linearly with increasing potential as predicted by the charge density tuning model (dE_Res/dU = −7.3 meV/V). Again, in Figure 4d, Γ increases linearly in contrast to predictions by the Mie–Drude model scattering simulation for charge density depletion (dΓ/dU = 10.6 meV/V). Using this model and applying it to the change in resonance energy (Figure 4c), the nanoparticle’s net electron flux is reported as a function of potential in Figure 4e but needs to be treated with care for the reasons already given. From the 13 nanoparticles investigated in the anodic potential range, all of them underwent reversible plasmon resonance shifts, but only 8 nanoparticles displayed linear resonance shifts and broadening with potentials like Particle 1. For these nanoparticles dE_Res/dU varied from −0.5 to −8.7 meV/V. dΓ/dU for these nanoparticles varied from 2 to 32 meV/V, nearly 3 times larger than seen in the cathodic range. We attribute this increase in resonance broadening to interface damping, resulting from the much higher polarizability of chloride ions compared to sodium ions.⁵⁰ The other 5 nanoparticles showed a nonlinear plasmonic response to the applied electrochemical potential (Particle 2 shown in Figure 4) and will be discussed next.

Figure 4.

Two distinct plasmonic responses to anodic charging. (a,f) Scattering spectra collected during dynamic potential control shown with E_Res and Γ superimposed with solid and dashed white lines, respectively. (b) Electrochemical potential of the working electrode as a function of time. Sweep rate: 10 mV/s. (c,g) Average E_Res over three consecutive cycles shown as a function of potential. (d,h) Average Γ is shown as a function of potential. (e,i) The number of electrons transferred from the nanoparticle to the substrate is shown as a function of potential, calculated using the Mie–Drude model scattering simulations and E_Res. Error bars indicate propagated standard error in E_Res.

Scattering spectra for Particle 2 are shown in Figure 4f under the potential modulation given in Figure 4b. E_Res and Γ are indicated with solid and dotted white lines, respectively. Figure 4g illustrates the mean and standard error for E_Res as a function of potential over three consecutive cycles after initial stabilization. In contrast to Particle 1, E_Res for Particle 2 decreased nonlinearly with increasing potential in the anodic range and exhibited two distinct resonance vs potential slopes. From 100 to 220 mV, dE_Res/dU = −23.2 meV/V, nearly six times larger than the linear shift observed for the nanoparticle in the cathodic potential range (Figure 3) and more than two times larger than that of Particle 1. After this initial shift, E_Res settled and shows less than 1 meV shift with increasing potential. Following the reversal of the potential sweep direction at 400 mV, almost no change in the resonance peak position occurred until a critical potential was met, below which E_Res returned to its initial value (dE_Res/dU = −24.8 meV/V). Most importantly, the nonlinearity and hysteresis were segmented in potential, indicating that the change points for dE_Res/dU have differing electrochemical potentials depending on scan direction. This behavior indicates that the mechanism responsible for these more drastic resonance shifts is likely chemical in nature, and the resonance shift change points correspond to single-particle onset potentials. In addition to potential-dependent hysteresis and tuning rates for E_Res, Γ shows similar trends in Figure 4h. From 0 to 250 mV, nearly no change in plasmon resonance width occurs (dΓ/dU = 2 meV/V). From 250 to 400 mV, broadening increases nearly linearly with dΓ/dU = 23.8 meV/V. The plasmon resonance remained broadened until roughly 200 mV on the reverse potential scan, at which point Γ decreases with a slope close to its initial value (dΓ/dU = 14.4 meV/V). These change points roughly correspond to the observed change points for E_Res.

The consistent bimodal dE_Res/dU and dΓ/dU behavior shown in Figures 4g and 4h indicates that at least one additional process along with charge depletion is occurring. Non-Faradaic charge density tuning on this nanoparticle resulted in relatively small resonance shifts and was overshadowed by the additional process that, we propose, was chemical in nature rather than physical. In a single-particle steady-state experiment involving nanorods in 100 mM NaCl on ITO, Dondapati et al. also observed larger shifts in the plasmon resonance at small positive potentials compared to expected shifts based on the Mie–Drude model. They attributed this effect to adsorbate damping due to hydration of the gold surface and excluded reactions between gold and chloride ions from their treatment.³⁷ In their experiment, they covered a very large potential range (−1 to +2 V, no reference electrode), preventing them from observing the type of hysteresis seen here in the more limited potential range. Unfortunately, their use of a two-electrode electrochemical cell precludes the direct comparison between reported applied potentials and other literature values or the present study due to unknown interfacial potential differences and considerable iR drop across the low concentration electrolyte.³⁷ In a series of dynamic ensemble spectroelectrochemical studies of many gold nanoparticles on ITO support in NaCl, Sannomiya and Dahlin et al. investigated the formation of a gold chloride surface complex.^5,6,51 By measuring the ensemble absorption spectrum of thousands of nanoparticles in parallel, they accessed scan rates as high as 1 V/s. They concluded, by observing strong scan rate dependence even below +600 mV, that metal-halide formation dominated the plasmonic response almost entirely. Because the ensemble absorption spectra were comprised of the collective absorption of many thousands of nanoparticles, it is unreasonable to expect a clearly defined onset potential for this chloridation process based on our own observations. In considering these explanations, we note that both tuning models attribute resonance shifts at small anodic potentials to a process other than charge density tuning. However, the adsorbate damping model attributes resonance shifts and spectral broadening to a physical effect, whereas metal halide formation obviously is a chemical process that then results in damping due to a layer of gold chloride. For comparison, we performed an otherwise identical experiment using a more inert electrolyte, aqueous sodium phosphate. In the cathodic and anodic potential ranges, we observed only linear changes in E_Res and Γ. Experiment details and sample control experiment data are shown in Section 2.3 of the Supporting Information. The effect of refractive index modulation of the ITO substrate as a result of electrochemically gated charge carrier concentration changes was considered through simulations. The Drude–Lorentz model was used to find the carrier concentration-dependent refractive index of ITO. This result was then used for the embedding dielectric medium in Mie scattering simulations of a 50 nm Au sphere. Even in the limiting case of a sphere completely embedded in ITO, we found that the measured resonance energy shifts would require charge carrier concentration modulation over 6 orders of magnitude larger than those reported in the relevant electrochemical ITO gating literature.⁵² We concluded that potential-dependent refractive index changes of the substrate are insignificant in our system. Additional details and calculation results are shown in Section 4 of the Supporting Information.

Our experiments showed that even at limited positive potentials some nanoparticles showed clear onset potential behavior, while others showed only linear plasmon shifts consistent with the charge density tuning model. Although we cannot exclude interface damping as a tuning mechanism, the heterogeneous onset potentials shown in some nanoparticles (e.g., Particle 2) suggest that at least one mechanism is chemical in nature, possibly metal-halide formation.⁶ In terms of this working model, we postulate that the onset potential for Particle 2 was within the potential range, while the onset potential for Particle 1 was likely above the upper potential vertex (+400 mV). We conclude that even within a very narrow subset of nanoparticles chosen based on behavior in the cathodic potential range further heterogeneity is apparent in the limited anodic potential range investigated. In light of these results, disagreement between previous single-particle and ensemble spectroelectrochemical measurements is inevitable. More importantly, however, our results show that electrochemically induced changes to nanoparticle plasmons and the associated physical and chemical mechanisms differ greatly within populations of nanoparticles.

Conclusions

This study shows that spectroelectrochemical tuning of the plasmon resonance is the result of multiple mechanisms and that the presence and distribution of mechanisms varies from nanoparticle to nanoparticle. Under steady-state cathodic potentials, the majority of nanoparticles demonstrated behavior inexplicable within the charge density plasmon resonance tuning model. Fewer than 25% of the nanoparticles observed obeyed this model. These nanoparticles were investigated under dynamic potential control, and their plasmonic response to an applied electrochemical potential was found to be completely reversible. For positive potentials, some of these nanoparticles showed signs of an additional tuning mechanism, likely chemical rather than physical in nature. This result suggests that some combination of nanoparticle or nanoparticle/substrate properties of these nanoelectrodes dictates their charge transfer or charge storage capability. The methodology and techniques developed herein allow the quantitative study of catalytic and electrochemical activity of single nanoparticles, both statistically and dynamically. We hope that this proof of principle study of heterogeneous single-particle electrochemistry will inspire future investigations and serve as a tool in informing design principles for the engineering of specific electrochemical and catalytic nanoparticles and nanostructures. Ongoing work focuses on in-depth study of the multiple mechanisms first reported here by measuring the effects of other electrolytes, ion concentrations, nanoparticle morphology and size, potential ranges, and electrode materials.

Supporting Information Available

Details for: experimental methods, electrochemical cell preparation, instrumentation, spectral processing, data analysis, hyperspectral to RGB conversion, scan rate dependence data, the semireversibility of Reaction Two shown in Figure 2, description of the charge-density-modified Drude dielectric function model and Mie Theory simulations, and simulations of refractive index changes of ITO with charge carrier concentration. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States