Abstract
Background
The aim of this study was to contrast the collapse values of the postoperative weight-bearing areas of different tantalum rod implant positions, fibula implantation, and core decompression model and to investigate the advantages and disadvantages of tantalum rod implantation in different ranges of osteonecrosis in comparison with other methods.
Material/Methods
The 3D finite element method was used to establish the 3D finite element model of normal upper femur, 3D finite element model after tantalum rod implantation into different positions of the upper femur in different osteonecrosis ranges, and other 3D finite element models for simulating fibula implant and core decompression.
Results
The collapse values in the weight-bearing area of the femoral head of the tantalum rod implant model inside the osteonecrosis area, implant model in the middle of the osteonecrosis area, fibula implant model, and shortening implant model exhibited no statistically significant differences (p>0.05) when the osteonecrosis range was small (60°). The stress values on the artificial bone surface for the tantalum rod implant model inside the osteonecrosis area and the shortening implant model exhibited statistical significance (p<0.01).
Conclusions
Tantalum rod implantation into the osteonecrosis area can reduce the collapse values in the weight-bearing area when osteonecrosis of the femoral head (ONFH) was in a certain range, thereby obtaining better clinical effects. When ONFH was in a large range (120°), the tantalum rod implantation inside the osteonecrosis area, shortening implant or fibula implant can reduce the collapse values of the femoral head, as assessed by other methods.
MeSH Keywords: Femoral Neoplasms, Finite Element Analysis, Tantalum
Background
Osteonecrosis of the femoral head (ONFH) is a degenerative disease that severely affects people’s lives. ONFH commonly occurs in individuals aged 20 to 50 years old, with a male-to-female ratio of about 4:1. Given its diverse pathological mechanisms, this disease shows local blood circulation disorder of the femoral head, resulting in avascular necrosis of bone cells, bone trabecula fracture, femoral head collapse, and even osteoarthritis. The surgical treatment for early osteonecrosis (ARCOI or Grade II) includes core decompression, free vascularized fibula transplant [1], and porous tantalum rod implantation.
Porous tantalum rod implantation has more advantages than pure core decompression and free vascularized fibula transplant. This treatment can provide an effective support for subcartilaginous osseous lamella by reestablishing bone defect at the weight-bearing site of the femoral head after internal decompression of the femoral head. Tantalum rod implantation is relatively simple, with a small surgical wound; thus, this treatment method is readily accepted by doctors and patients [2,3]. However, reports on the clinical efficacy and postoperative follow-up of tantalum rod implantation, as well as understanding of the operation, vary. Porous tantalum rod has many advantages in clinical application for early ONFH, but poor clinical effects have also been reported [4]. Treatment failure and complications occur because of poor tantalum rod implant position or incorrect understanding of the indications for surgery. Therefore, selection of tantalum rod implant position, displacement after implantation into the relative position, and stress evaluation are very important.
In this study, the 3D finite element method was used to establish a finite element model of the normal upper femur, 3D finite element model after tantalum rod implantation into different positions of the upper femur in different osteonecrosis areas, and fibula implant and core decompression. A total of 22 3D finite element models were established. Analysis of the displacement and investigation of the biological stress were also carried out. This study would provide a theoretical basis for the clinical application of porous tantalum rod implantation for ONFH and the collapse reduction of the femoral head after osteonecrosis.
Material and Methods
Establishment of 3D finite element model of the normal upper femur
A 40-year-old healthy adult male, 174 cm tall and weighing 60 kg, was selected for this study. The volunteer disclaimed any disease history, trauma surgery, pain history, abnormal movement history, or genetic history of small back, double hip joint, or bilateral lower extremities. The femoral disease was excluded after obtaining the frontal image of the pelvis, full-length image of the bilateral lower extremities, and CT thin scanning. The volunteer was placed in a supine position and instructed to avoid any movement. The scanning bed was adjusted to center the scanning area. The scanning data were saved on a CD in a DICOM format.
Simpleware software was used to establish the triangular mesh model and mesh division. ScanFE was employed to automatically and rapidly divide the stereo model to mesh using the Solid45 tetrahedron element, and show the number of elements and nodes. A total of 360 881 nodes and 908 685 elements were found in the 3D finite element model of the normal upper femur; among which, 185 193 nodes and 526 303 elements were found in the cortical bone, whereas 175 688 nodes and 382 382 elements were found in the cancellous bone.
Based on other studies, we assumed that all materials were isotropic, uniform, and continuously linear, with direct assignment of the modulus of elasticity and Poisson ratio [5–8]. The modulus of elasticity and the Poisson ratio of the cortical bone were 16 800 MPa and 0.2, respectively; whereas those of the cancellous bone were 700 MPa and 0.4, respectively. These data were loaded in the hypermesh software. Finally, the 3D finite element model was completed by importing to Abaqus software [9–12] (Figure 1A).
Figure 1.
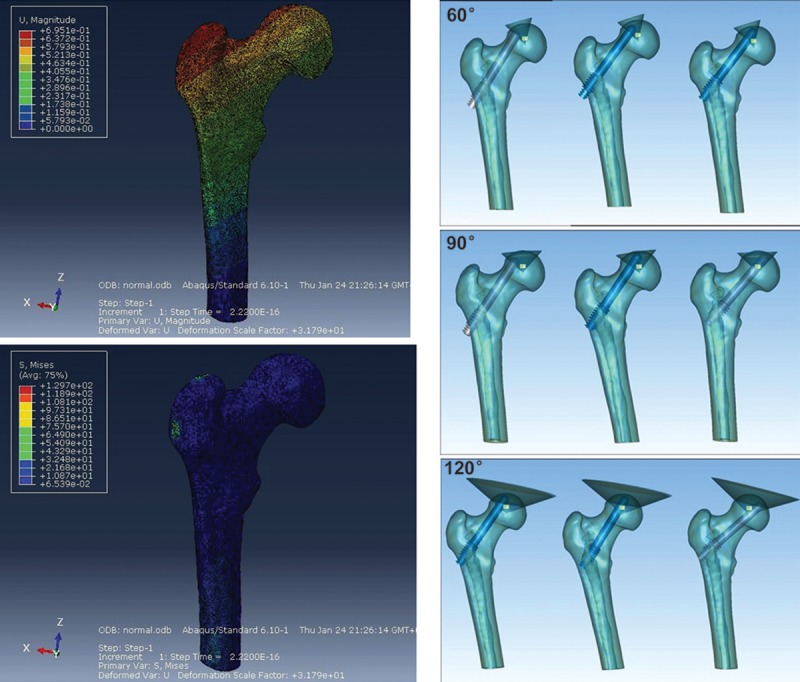
3D finite element model of the upper femur. (A) Frontal and rear images of the 3D finite element model in the Abaqus software. Upper: Displacement cloud map; Lower: Stress cloud map. (B) Schematic of tantalum rod implantation into the different positions of the osteonecrosis area (from left to right: outside, middle, and inside) for ONFH in the cone-shaped range of 60°, 90°, and 120°.
Establishment of the finite element model of tantalum rod implantation into the femoral system
Based on the 3D finite element model of the normal upper femur established in the first section, the osteonecrosis area of the femoral head was simulated to be the cone. The top point of the cone was located in the femoral head core. The opening angle of the cone was used to confirm the ONFH range, which was divided into 3 groups – 60°, 90°, and 120°. Cancellous bone was set as osteonecrosis. In ascending order, simulation and generalization of the actual ONFH in different positions and ranges are clinically expected. Three models were established.
Based on the 3F finite element model of ONFH, tantalum rod implantation was simulated to implant a tantalum rod into the upper femur. The tantalum rod was implanted inside, in the middle, and outside the osteonecrosis area based on the model in 60°, 90°, and 120° of osteonecrosis. The distance from the top of the tantalum rod to the cortical bone of the femoral head was 5 mm. The remaining space in the osteonecrosis range was filled with artificial bone. Nine models were established (Figure 1B). The same method was used to design the 3D finite element model of the core decompression for ONFH, the 3D finite element model of the fibula implant for ONFH, and the 5-mm shortening implant for ONFH. A total of 21 different 3D finite element models of the upper femur were established. Validation of the 3D finite element model was verified [13–16].
The tantalum rod (Zimmer Company) was measured by use of a ZLDS200 laser scanner. SolidWorks2012 software was used to establish the 3D finite element model of the tantalum rod and the 3D digital model. Geomagic Studio10 was employed to determine the osteonecrosis area and the tantalum rod position, and the assembly was completed (Figure 2). The same method was performed to complete the design assembly of the 3D finite element model of core decompression for ONFH, 3D finite element model of fibula implant for ONFH, and 3D finite element model of 5-mm shortening tantalum rod for ONFH.
Figure 2.
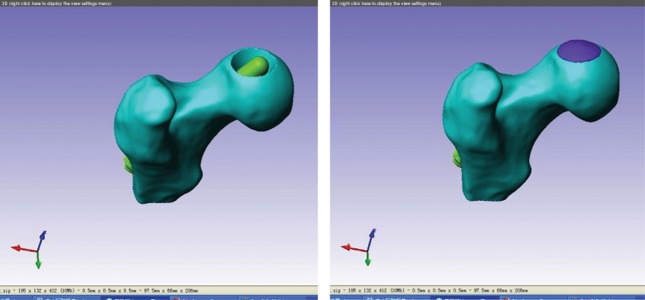
Tantalum rod assembly model for ONFH in the range of 60°. (A) Cancellous bone and tantalum rod assembly model for ONFH in the range of 60° (B) Cancellous bone, tantalum rod, and artificial bone assembly model for ONFH in the 60° range.
The assembled femur model was imported into ScanCAD. The friction coefficient between the tantalum rod and the cancellous bone was 0.88. Given the very high friction coefficient, we simulated and set the tantalum rod and the cancellous bone as a whole (common node) and simulated the cortical bone as 2 mm. Based on ScanFE, the tetrahedron Solid45 element was used to rapidly and automatically divide the 3D model into mesh, showing the number of elements and nodes.
Deformation and stress analysis of 3D finite element model with tantalum rod implant
Abaqus 6.10 software was used to load a total of 22 different 3D finite element models of the upper femur in ODB format. To digitize the points in the weight-bearing area of the femoral head for the 22 3D finite element models of the upper femur, 20 points were evenly digitized in the weight-bearing area of each 3D finite element model according to the unified approach. The displacement value of each element was recorded.
To digitize the points on the surface of the artificial bone implant region in the weight-bearing area of the femoral head of the 15 3D finite element models of the upper femur, 20 points were evenly digitized in the range of artificial bone implantation of the weight-bearing area of the femoral head of each 3D finite element model according to the unified approach. The von Mises stress value of each element was recorded.
Statistical analysis
The SPSS16.0 software package was used to carry out one-factor ANOVA for the obtained data, t test for independent samples, and other process analyses. Statistical results were recorded and analyzed and are presented in the Discussion section.
Results
Displacement in the weight-bearing area of the femoral head of the 3D finite element model
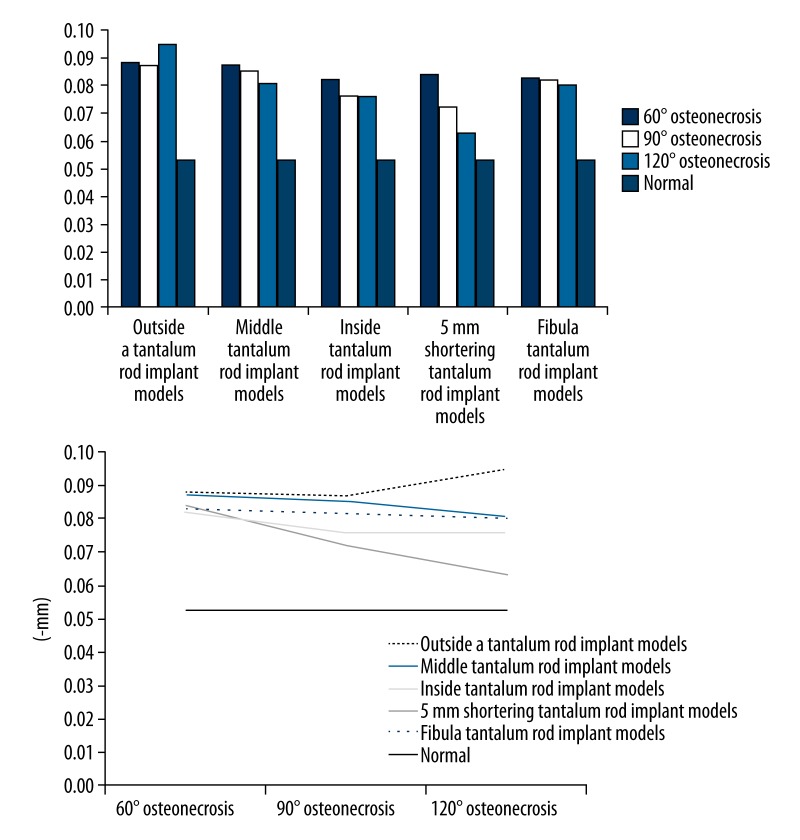
Abaqus 6.10 software was used to analyze the relative data model. In the 3D finite element model of the upper femur, displacements in the weight-bearing area of the femoral head of the 3D finite element model are shown in Table 1 and Figure 3.
Statistical analysis was performed using SPSS 16.0 software, and the results are as follows (in mm):
Table 1.
Mean displacement in the weight-bearing area of the femoral head of the 3D finite element model (mm).
| 60° | 90° | 120° | Normal | |
|---|---|---|---|---|
| Without treatment | 0.870 | 1.109 | 1.547 | 0.053 |
| Simple core decompression | 1.896 | 1.926 | 1.995 | |
| Tantalum rod implantation inside of the osteonecrosis area | 0.082 | 0.076 | 0.076 | |
| Tantalum rod implantation in the middle of the osteonecrosis area | 0.087 | 0.085 | 0.081 | |
| Tantalum rod implantation outside of the osteonecrosis area | 0.088 | 0.087 | 0.095 | |
| 5-mm shortening implant | 0.084 | 0.072 | 0.063 | |
| Fibula implant | 0.083 | 0.082 | 0.080 |
Figure 3.
Collapse values in the weight-bearing area of the femoral head of the different osteonecrosis ranges of finite element models and different tantalum rod positions.
a. When the osteonecrosis area was 60° cone
Single-factor ANOVA was carried out for the collapse values in the weight-bearing area of the femoral head after tantalum rod implantation inside, in the middle, and outside the osteonecrosis area to compare the differences among the 3 groups. The pairwise comparison found that the collapse value in the weight-bearing area of the femoral head of the tantalum rod implant model inside the osteonecrosis area was significantly lower than that outside the osteonecrosis area (M=0.082±0.009, M=0.088±0.010, p<0.05). Comparison between the inside and the middle implant models, as well as between the middle and the outside implant models, showed no significant difference (p>0.05).
When the osteonecrosis area was 60° cone, the tantalum rod implant model inside the osteonecrosis area was compared with the 60° osteonecrosis, 60° core decompression, 60° fibula implant, and 60° tantalum rod shortening 5-mm implant models; t test for independent samples was performed. Differences among the 60° inside implant model, the 60° osteonecrosis model, and the core decompression model were statistically significant (M=0.082±0.009, M=0.87±0.185, M=1.896±0.234, p<0.05).
b. When the osteonecrosis area was 90° cone
A pairwise comparison was carried out for the 3 models. The result showed that the collapse value in the weight-bearing area of the tantalum rod implant model inside the osteonecrosis area was significantly lower than that in the middle of the osteonecrosis area (M=0.076±0.005, M=0.085±0.009, p<0.05). The collapse value in the weight-bearing area of the femoral head of the inside implant model was significantly lower than that of the outside implant model (M=0.076±0.005, M=0.087±0.007, p<0.05). Comparison of the middle with the outside implant models showed that the mean collapse value in the weight-bearing area of the femoral head of the latter was lower, but was not significantly different (p>0.05).
When the osteonecrosis area was 90° cone, the tantalum rod implant model in the middle of the osteonecrosis area was compared with 90° osteonecrosis, 90° core decompression, 90° fibula implant, and 90° tantalum rod shortening 5-mm implant models; t test for independent samples was performed. The comparison result with fibula implantation had no significant difference; however, significant differences (p<0.05) were observed among other groups.
c. When osteonecrosis area was 120°cone
Similarly, a pairwise comparison was performed for the 3 models. The result showed that the collapse value in the weight-bearing area of the tantalum rod implant model inside the osteonecrosis area was significantly lower than that outside the osteonecrosis area. The mean collapse value in the weight-bearing area of the femoral head of the inside implant model was lower than that of the middle implant model, without significant difference. When the middle implant model was compared with the outside implant model, its collapse value in the weight-bearing area of the femoral head was significantly lower than that of the outside implant model.
When the osteonecrosis area was 120° cone, the tantalum rod implant model outside of the osteonecrosis area was compared with 120° osteonecrosis, 120° core decompression, 120° fibula implant, and 120° tantalum rod shortening 5-mm implant models; t test for independent samples was performed. The comparison of the 120° tantalum rod implant model with the other models showed that the collapse value in the weight-bearing area of the femoral head of the tantalum rod implant model was significantly lower than that of the osteonecrosis model (M=0.095±0.011, M=1.547±0.243, p<0.05) and the core decompression model (M=0.095±0.011, M=1.995±0.263, p<0.05); significantly higher than that of the fibula implant model (M=0.095±0.011, M=0.080±0.012, p<0.05) and the tantalum rod shortening 5-mm implant model (M=0.095±0.011, M=0.063±0.013, p<0.05).
Von Mises stress distribution on the surface of the artificial bone implant area of the 3D finite element model
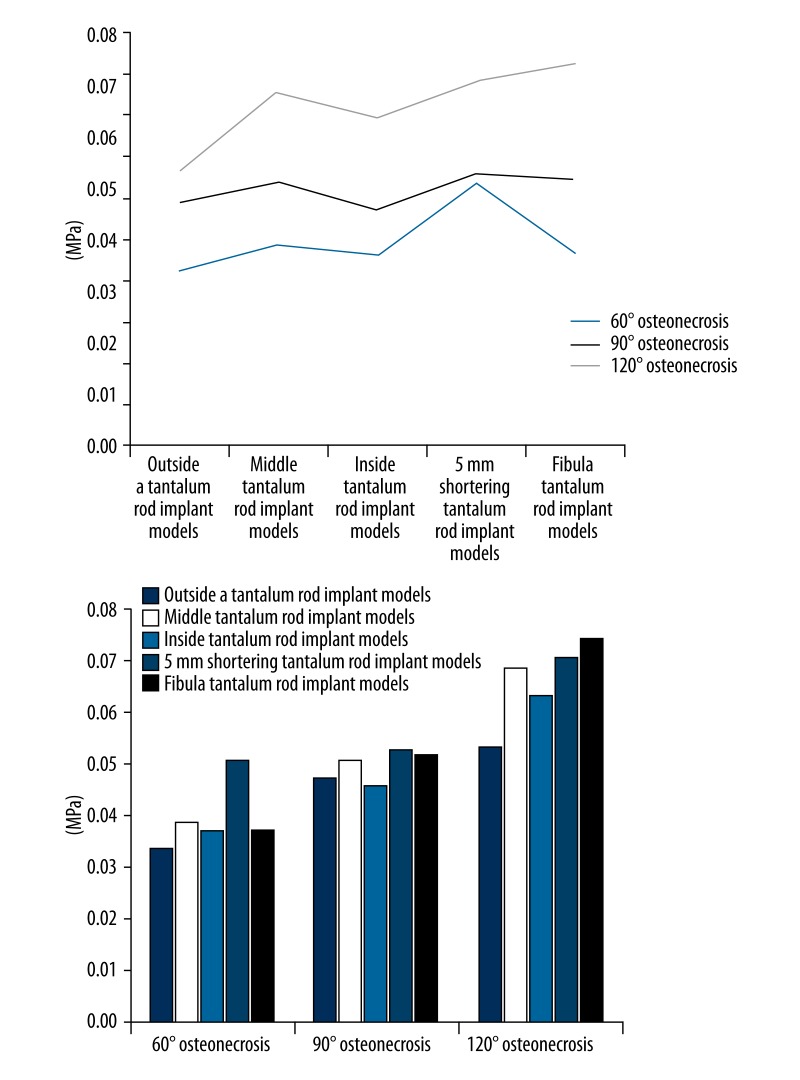
Abaqus 6.10 software was used to obtain the overall stress condition of a certain element on the surface of the artificial bone implant area under the cortical bone in the weight-bearing area of the femoral head (Table 2 and Figure 4).
SPSS16.0 software was used for the statistical analysis of the data, and the results were as follows:
Table 2.
Von Mises stress mean on the implant surface of artificial 3D finite element model (MPa).
| 60°osteonecrosis | 90°osteonecrosis | 120°osteonecrosis | |
|---|---|---|---|
| Tantalum rod implant inside of the osteonecrosis area | 0.336 | 0.471 | 0.532 |
| Tantalum rod implant in the middle of the osteonecrosis area | 0.390 | 0.509 | 0.684 |
| Tantalum rod implant outside of the osteonecrosis area | 0.372 | 0.457 | 0.634 |
| Tantalum rod shortening 5-mm implant | 0.509 | 0.527 | 0.706 |
| Fibula implant | 0.372 | 0.517 | 0.741 |
Figure 4.
Stress on the surface of artificial bone implant area of the 3D finite element model and stress on the surface of artificial bone implant area in different positions.
a. When osteonecrosis area was 60° cone
Single-factor ANOVA was carried out for Von Mises stress distribution on the artificial bone surface in the weight-bearing area of the femoral head after tantalum rod implantation inside, in the middle, and outside of the osteonecrosis area to compare the differences among the 3 groups; a pairwise comparison was also performed. The results showed that the stress on the artificial bone surface of the tantalum rod implant model inside the osteonecrosis area was significantly lower than that in the middle of the osteonecrosis area (M=0.336±0.060, M=0.390±0.080, p<0.05). The inside implant model was compared with the outside implant model; the mean stress on the artificial bone surface was lower than that of the outside implant model, without significant difference (p>0.05). The mean stress on the artificial bone surface of the middle implant model was higher than that of the outside implant model, without significant difference (p>0.05).
When the osteonecrosis area was 60° cone, the tantalum rod implant model inside the osteonecrosis area was compared with 60° fibula implant model and 60° tantalum rod shortening 5-mm implant model; t test for independent samples was conducted. The result showed that the stress on the artificial bone surface of the 60° tantalum rod implant model was significantly lower than that of the tantalum rod shortening 5-mm implant model (M=0.336±0.060, M=0.509±0.145, p<0.05). No significant difference was found in the other groups (p>0.05).
b. When the osteonecrosis area was 90° cone
Similarly, a pairwise comparison was performed among the 3 groups of models in 90°. The result showed that the mean stress on the artificial bone surface of the tantalum rod implant model inside the osteonecrosis area was lower than that in the middle of the osteonecrosis area, without significant difference (p>0.05). The mean stress on the artificial bone surface of the inside implant model was higher than that of the outside model, without significant difference (p>0.05). The stress on the artificial bone surface of the middle implant model was significantly higher than the outside implant model (M=0.509±0.068, M=0.457±0.063, p<0.05).
When the osteonecrosis area was 90° cone, the tantalum rod implant model in the middle of the osteonecrosis area was compared with the 90° fibula implant model and the 90° tantalum rod shortening 5-mm implant model; t test for independent samples was carried out. The results of the 2 groups showed no significant differences (p>0.05).
c. When the osteonecrosis area was 120° cone
Similarly, a pairwise comparison was performed among the 3 groups of models in 120°. The result showed that the stress on artificial bone surface of the tantalum rod implant model inside the osteonecrosis area was significantly lower than that in the middle of the osteonecrosis area (M=0.532±0.048, M=0.684±0.055, p<0.05). The stress on the artificial bone surface of the inside implant model was significantly lower than that of the outside implant model (M=0.532±0.048, M=0.634±0.059, p<0.05). The stress on the artificial bone surface of the middle implant model was significantly higher than that of the outside implant model (M=0.684±0.055, M=0.634±0.059, p<0.05).
When the osteonecrosis area was 120° cone, the tantalum rod implant model outside of the osteonecrosis area was compared with the 120° fibula implant model and the 120° tantalum rod shortening 5-mm implant model; t test for independent samples was performed. Significant differences between the 2 groups were observed. The stress on the artificial bone surface of the 120° tantalum rod implant model was significantly lower than that of the 120° fibula implant model (M=0.634±0.059, M=0.741±0.057, p<0.05) and the 120° tantalum rod shortening 5-mm implant model (M=0.634±0.059, M=0.706±0.061, p<0.05).
Discussion
Tantalum rod implantation has been widely applied to early ONFH clinically; however, studies on the correct tantalum rod implantation for ONFH are not available to date [17–20]. This paper aimed to establish the 3D finite element model imitating tantalum rod implantation in different positions and to analyze the deformation force conditions of the femoral head and the best location of tantalum rod implantation to provide a theoretical basis for investigating the clinical application of porous tantalum rod implantation for ONFH and collapse reduction after osteonecrosis. This study further verified the advantages of tantalum rod implantation for early ONFH by comparing the core decompression and the fibula implantation models.
Results showed that the different tantalum rod implantations have less effect on the collapse value in the weight-bearing area of the femoral head when the osteonecrosis range is small. However, the collapse values in the weight-bearing area of the tantalum rod implant model in the range of osteonecrosis, implant model in the middle of osteonecrosis area, fibula implantation model, and shortening implant model exhibited no statistical significance when the osteonecrosis range was up to 60° (P>0.05). Thus, necrotic morphology is not only cone-shaped when the osteonecrosis range is small; the small range of osteonecrosis is clinically diversified. Given the limited range of osteonecrosis, the tantalum rod implantation position had no significant effect on the postoperative collapse of the femoral head. Therefore, an exclusive drive for tantalum rod implant position can be ignored by making tantalum rod implantation for a small range of osteonecrosis. No significant difference was observed between the fibula implantation and tantalum rod implantation for small osteonecrosis range. Considering the damage to the donor site, fibula implantation was not effective compared with tantalum rod implantation when the osteonecrosis range is small [21,22].
With the increase in osteonecrosis range, the different positions of tantalum rod implantation will have increasing effect on the collapse value. When the osteonecrosis range is up to 120°, the collapse values in the weight-bearing area of the tantalum rod implant model in the osteonecrosis range, implant model outside of osteonecrosis area, fibula implantation model, and shortening implant model exhibits a statistical significance (P<0.01). Therefore, tantalum rod implant position should be close to the inside of the osteonecrosis area to reduce postoperative collapse value when the osteonecrosis range is large. Tantalum rod implantation is more effective than fibula implantation when the tantalum rod implant position is proper for large osteonecrosis range.
When the osteonecrosis range was small, the surface contact stress of artificial bone under the cortical bone was small after tantalum rod implantation; thus, the tantalum rod implant position showed no great effect on stress. When the osteonecrosis range was up to 60°, a statistical significance was observed for stress on the artificial bone surface between the tantalum rod implant model inside the osteonecrosis and the shortening implant model (p<0.01); no statistical significance was found among the other groups. This result is consistent with the aforementioned conclusion obtained from the collapse value. We speculate that, when tantalum rod implant operation is conducted in a small osteonecrosis area, an exclusive drive for tantalum rod implant position is unnecessary with the increase in osteonecrosis area, and the effect of tantalum rod implant position on stress is continuously increased. When the osteonecrosis range is up to 120°, statistically significant differences are observed in the stress on the artificial bone surface among the tantalum rod implant model inside of the osteonecrosis area, tantalum rod implant model outside of the osteonecrosis area, fibula implant model, and shortening implant model (p<0.01). The stress of the inside implant model is significantly lower than the other implant positions. Therefore, the tantalum rod implant inside the osteonecrosis area can reduce postoperative collapse value in the weight-bearing area, as well as the stress value on the artificial bone surface, to decrease the effect of the operation on the support effect of the femoral head.
The results showed that the collapse value in the weight-bearing area of the untreated and simply core decompressed ONFH increases with the increase in osteonecrosis area. However, the collapse value is reduced with the increase in osteonecrosis area using implant treatment methods. These findings are not completely consistent with those of Zhang et al. [23]. The inconsistency may be due to the large effect of the support implantation in a large-scale ONFH on stress, causing stress distribution to change, which needs to be further studied and verified.
For the tantalum rod applied to early ONFH, the implant rod was closer to the inside of the osteonecrosis area when the osteonecrosis area was the same, and the collapse value in the weight-bearing area of the femoral head was relatively lower. Therefore, implanting a tantalum rod inside the osteonecrosis area is better when performing surgery and filling artificial bone into the remaining space. When the osteonecrosis area is larger (120°) compared with the tantalum rod implant outside of the osteonecrosis area, the tantalum rod implant inside the osteonecrosis area, tantalum rod shortening implant, or fibula implant can reduce the collapse value of the femoral head (p<0.05).
Conclusions
Inconsistencies exist in the understanding of the effects and follow-up of the tantalum rod implant method applied to early ONFH [24,25]. At present, no acknowledged surgical technique or relevant studies that can clearly reduce postoperative collapse of the femoral head are available [26]. No relevant study has been conducted on the relationship between tantalum rod implant position and postoperative collapse of femoral head because of the different ranges and diverse shapes of osteonecrosis. We summarized the 3 different osteonecrosis ranges of the femoral head and the diverse shapes of the osteonecrosis area, and established a 3D finite element analog for each tantalum rod implant in different positions and angles. We also carried out an analysis and comparison with fibula implant based on the obtained displacement and stress, providing a theoretical basis for the application of porous tantalum rod in early osteonecrosis of the femoral head in clinical practice. Thus, the application of a tantalum rod in different ranges and shapes of osteonecrosis is evidence-based. A relatively optimal position can be selected to implant a tantalum rod for different early osteonecrosis patients to reduce postoperative collapse of and stress on the artificial bone in the femoral head. The limitations of this study are that statistical analysis on data groups in different angles was not performed, and the experimental result analyzed using finite element cannot be directly used in clinical treatment. Therefore, future studies should carry out large-scale and large-sample clinical experiments according to the requirements of evidence-based medicine to transform the research results into clinical treatment.
Acknowledgement
The authors appreciate receiving support from the Research Fund of Science and Technology Commission of Shanghai Municipality: multicenter clinical trial of osteonecrosis of the femoral head protection (11411950401).
Footnotes
Source of support: Research Fund of Science and Technology Commission of Shanghai Municipality: multicenter clinical trial of osteonecrosis of the femoral head protection (11411950401)
References
- 1.Mont MA, Jones LC, Hungerford DS. Nontraumatic osteonecrosis of the femoral head: ten years later. J Bone Joint Surg Am. 2006;88:1117–32. doi: 10.2106/JBJS.E.01041. [DOI] [PubMed] [Google Scholar]
- 2.Varitimidis SE, Dimitroulias AP, Karachalios TS, et al. Outcome after tantalum rod implantation for treatment of femoral head osteonecrosis: 26 hips followed for an average of 3 years. Acta Orthop. 2009;80:20–25. doi: 10.1080/17453670902804877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lieberman JR, Berry DJ, Mont MA, et al. Osteonecrosis of the hip: management in the 21st century. Instr Course Lect. 2003;52:337–55. [PubMed] [Google Scholar]
- 4.Floerkemeier T, Thorey F, Daentzer D, et al. Clinical and radiological outcome of the treatment of osteonecrosis of the femoral head using the osteonecrosis intervention implant. Int Orthop. 2011;35:489–95. doi: 10.1007/s00264-009-0940-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Peng J, Wang AY, Sun MX, et al. Three-dimensional analysis of spatial structure of cancellous bone sample of femeral head. The Orthopedic Journal of China. 2005;13:924–26. [Google Scholar]
- 6.Tsao AK, Roberson JR, Christie MJ, et al. Biomechanical and clinical evaluations of a porous tantalum implant for the treatment of early-stage osteonecrosis. J Bone Joint Surg Am. 2005;87(Suppl 2):22–27. doi: 10.2106/JBJS.E.00490. [DOI] [PubMed] [Google Scholar]
- 7.Mason R, Tennekes H, Sánchez-Bayo F, Jepsen PU. Immune Suppression by Neonicotinoid Insecticides at the Root of Global Wildlife Declines. J Environ Immunol Toxicol. 2013;1:3–12. [Google Scholar]
- 8.Petroianu GA, Lorke DE, Athauda G, et al. Pralidoxime and Obidoxime: Phosphylationinduced Changes in logP (partition coefficient) J Environ Immunol Toxicol. 2013;1:35–40. [Google Scholar]
- 9.Schildhauer TA, Robie B, Muhr G, et al. Bacterial adherence to tantalum versus commonly used orthopedic metallic implant materials. J Orthop Trauma. 2006;20:476–84. doi: 10.1097/00005131-200608000-00005. [DOI] [PubMed] [Google Scholar]
- 10.Bobyn JD, Stackpool GJ, Hacking SA, et al. Characteristics of bone ingrowth and interface mechanics of a new porous tantalum biomaterial. J Bone Joint Surg Br. 1999;81:907–14. doi: 10.1302/0301-620x.81b5.9283. [DOI] [PubMed] [Google Scholar]
- 11.Kong XJ, Liu XW, Li JY, Yang YJ. Advances in Pharmacological Research of Eugenol. Curr Opin Complement Alternat Med. 2014;1:e00003. [Google Scholar]
- 12.Liu YM, Li ZY, Li XM, Pan RL. Review on the Toxic Effects of Radix Bupleuri. Curr Opin Complement Alternat Med. 2014;1:e00002. [Google Scholar]
- 13.Wirtz DC, Schiffers N, Pandorf T, et al. Critical evaluation of known bone material properties to realize anisotropic FE-simulation of the proximal femur. J Biomech. 2000;33:1325–30. doi: 10.1016/s0021-9290(00)00069-5. [DOI] [PubMed] [Google Scholar]
- 14.Shuler MS, Rooks MD, Roberson JR. Porous tantalum implant in early osteonecrosis of the hip: preliminary report on operative, survival, and outcomes results. J Arthroplasty. 2007;22:26–31. doi: 10.1016/j.arth.2006.03.007. [DOI] [PubMed] [Google Scholar]
- 15.Gerada J, DeGaetano J, Sebire NJ, et al. Mucosal Inflammation as a Component of Tufting Enteropathy. Immunogastroenterology. 2013;2:62–67. [Google Scholar]
- 16.Lv XY, Luo WZ, Wang YQ, et al. Bilateral thoracotomy for removal of uncommon postmediastinal multi-schwannomas. Thoracic Cancer. 2010;3:130–32. doi: 10.1111/j.1759-7714.2010.00022.x. [DOI] [PubMed] [Google Scholar]
- 17.Liu G, Wang J, Yang S, et al. Effect of a porous tantalum rod on early and intermediate stages of necrosis of the femoral head. Biomed Mater. 2010;5(6):65003. doi: 10.1088/1748-6041/5/6/065003. [DOI] [PubMed] [Google Scholar]
- 18.Malizos KN, Papasoulis E, Dailiana ZH, et al. Early results of a novel technique using multiple small tantalum pegs for the treatment of osteonecrosis of the femoral head: a case series involving 26 hips. J Bone Joint Surg Br. 2012;94:173–78. doi: 10.1302/0301-620X.94B2.27287. [DOI] [PubMed] [Google Scholar]
- 19.Hernández JR, Barlés GN, Eudaldo M, et al. Fistula to the native esophagus after pharyngogastrostomy for malignant disease: A rare phenomenon in esophageal surgery. Thoracic Cancer. 2013;4:71–74. doi: 10.1111/j.1759-7714.2012.00112.x. [DOI] [PubMed] [Google Scholar]
- 20.Casillas-Ramírez A, Elias-Miró M, Jiménez-Castro MB, et al. AICAR and Trimetazidine in University of Wisconsin Solution are Effective to Increase Survival in Recipients Transplanted with Steatotic Livers. Immunogastroenterology. 2012;1:58–68. [Google Scholar]
- 21.Bawany MZ, Rafiq E, Thotakura R, et al. Successful management of recurrent biliary colic caused by pancreatic stent migration after Whipple procedure. J Interv Gastroenterol. 2012;2:97–98. doi: 10.4161/jig.22209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Reddy SB, Lee JG, Chang KJ, Muthusamy V. The impact of diphenhydramine and promethazine in patients undergoing advanced upper endoscopic procedures. J Interv Gastroenterol. 2013;3:122–27. [Google Scholar]
- 23.Yiyuan Z, Eryou F, Riqi C, et al. Analysis on biomechanics and three-dimensional finite element of porous tantalum block implant for chemic necrosis of the femeral head. The Orthopedic Journal of China. 2012;20:1113–16. [Google Scholar]
- 24.Luo HY, Chen CW. [Treatment of adult early femur head necrosis with the tantalum screw]. Zhongguo Gu Shang. 2011;24:482–85. [PubMed] [Google Scholar]
- 25.Varitimidis SE, Dimitroulias AP, Karachalios TS, et al. Outcome after tantalum rod implantation for treatment of femoral head osteonecrosis: 26 hips followed for an average of 3 years. Acta Orthop. 2009;80:20–25. doi: 10.1080/17453670902804877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Aldegheri R, Taglialavoro G, Berizzi A. The tantalum screw for treating femoral head necrosis: rationale and results. Strategies Trauma Limb Reconstr. 2007;2:63–68. doi: 10.1007/s11751-007-0021-9. [DOI] [PMC free article] [PubMed] [Google Scholar]