Time-reversed adapted-perturbation (TRAP) optical focusing onto dynamic objects inside scattering media

Abstract

The ability to steer and focus light inside scattering media has long been sought for a multitude of applications. To form optical foci inside scattering media, the only feasible strategy at present is to guide photons by using either implanted¹ or virtual^2–4 guide stars, which can be inconvenient and limits potential applications. Here, we report a scheme for focusing light inside scattering media by employing intrinsic dynamics as guide stars. By time-reversing the perturbed component of the scattered light adaptively, we show that it is possible to focus light to the origin of the perturbation. Using the approach, we demonstrate non-invasive dynamic light focusing onto moving targets and imaging of a time-variant object obscured by highly scattering media. Anticipated applications include imaging and photoablation of angiogenic vessels in tumours as well as other biomedical uses.

To focus light deep into scattering media such as biological tissues, conventional manipulation of its phase is infeasible due to random scattering. As the propagation distance increases, the number of unscattered photons decays exponentially and becomes negligible beyond one transport mean free path (l_t′)⁵ ; therefore, control of light is limited to a superficial depth of l_t′. Obviously, it is highly desirable to break through this optical diffusion limit.

One can tune the scattered light in phase to maximize the spatial⁶ or spatiotemporal⁷ energy density at a desired location. By means of iterative wavefront shaping^6–8, a large number of spatial modes are controlled to focus through⁶, or into^1,9,10, a scattering medium at the target location, where a guide star is placed to generate feedback. However, these methods work by sequentially probing the input modes, an approach which remains impractically slow when the controlled degrees of freedom are many. A faster approach is to time-reverse (by phase-conjugating monochromatic light¹¹) the scattered photons from a guide star back to their origin. To this end, nonlinear nanoparticles¹² and fluorescent beads¹³ have served as implanted guide stars, and focused ultrasound^2–4,14 has functioned as a virtual one. However, physical implantation is invasive and inflexible, and the virtual alternative requires physical contact for acoustic coupling and low loss at a sufficiently high acoustic frequency; they are unfavourable or infeasible for many scattering media.

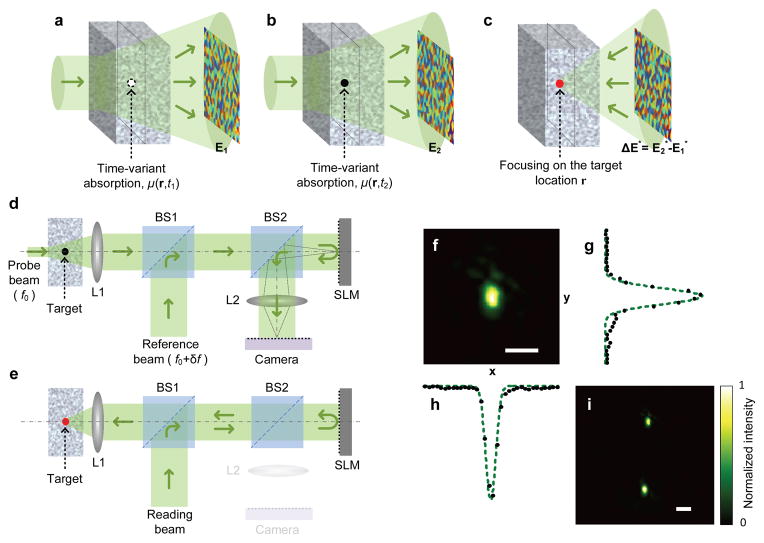
Here, we explore the feasibility and potential applications of a new technology, named time-reversed adapted-perturbation (TRAP) optical focusing, which offers a strategy for passively guiding light inside scattering media without invasive implantation or physical contact. It works by remotely probing the scattering medium and employing spontaneous motions or intrinsic permittivity variations of the target as the guide stars. Although our analysis centres on absorption, generalization to the full permittivity tensor is straightforward (see Supplementary Discussion). The TRAP process comprises two steps. In step 1, the scattered light field distributions E₁ and E₂, defined at a location exterior to the scattering region, are probed at instants t₁ and t₂ while the target absorption changes from μ(r, t₁) to μ(r, t₂), as depicted in Fig. 1a,b, and the rest of the medium stays unchanged. The process is written mathematically as ${\mathbf{E}}_1={\mathbf{TE}}_1^t,{\mathbf{E}}_2={\mathbf{TE}}_2^t$, where ${\mathbf{E}}_i^t(i=1,2)$ denotes the field distribution on the target plane at instant t_i, and T is a transmission matrix characterizing the medium^8,9. Subtracting the above equations yields the field perturbation ΔE = E₂ − E₁ = TΔE^t. Because E₁ and E₂ are recorded interferometrically at two instants, instability of the two arms of the interferometer can lead to an overall random phase offset. If the phase of E₁ is adapted by minimizing the norm ||ΔE|| (see Supplementary Methods), ΔE^t is null anywhere except at the target location r. In step 2, as shown in Fig. 1c, focusing on the target position is subsequently achieved when the phase-adapted perturbation ΔE is phase-conjugated: T^TΔE^* = (T^†ΔE)^* ≈ (ΔE^t)^*, where the superscripts “T” and “†” denote transpose and conjugate transpose, respectively, and T^†T ≈ I (I is the identity matrix) is assumed¹⁴. In the special case of a moving target inside the scattering region, the perturbation satisfies δμ(r₁)= −δμ(r₂) ≠ 0, where δ denotes the change from t₁ to t₂. Under such circumstances, phase-conjugating ΔE focuses light simultaneously on the old and the new target locations r₁ and r₂ (see Supplementary Movie 1 for details).

Figure 1. Principle and schematic of TRAP focusing.

a–c, Focusing to a single absorber. The exterior fields at instant t₁ (a) and t₂ (b) are measured to calculate ΔE. ΔE^* is produced to promote TRAP focusing (c). d, e, Principle of DOPC. The light paths follow the solid arrows. In the probing mode (d), the exterior fields are measured interferometrically to obtain the TRAP phase map. In the focusing mode (e), the SLM displays the synthesized phase map, and the reading beam is turned into a phase-conjugated beam to form a focus. See Methods for details. f, Light intensity distribution measured on the focal plane when a single focus is formed. g, h, Focal intensity profiles sampled along y and x directions in f. Dashed lines are Gaussian fits. i, Focal intensity distribution showing focusing at two points due to a moving target. L, lens; BS, beamsplitter. Scale bars, 50 μm.

To guarantee high energy gain, digital optical phase conjugation (DOPC)^3,4 is employed in TRAP focusing. The focusing process is schematically shown in Fig. 1d, e, and explained in detail in Methods. Speckle-scale focusing between two optical diffusers is demonstrated by perturbing the medium using a target particle, as shown in Fig. 1f (the cross-sectional intensity distributions along y and x are shown in Fig. 1g, h, respectively), and a moving particle induces focusing at two points, as shown in Fig. 1i (see Supplementary Methods for details).

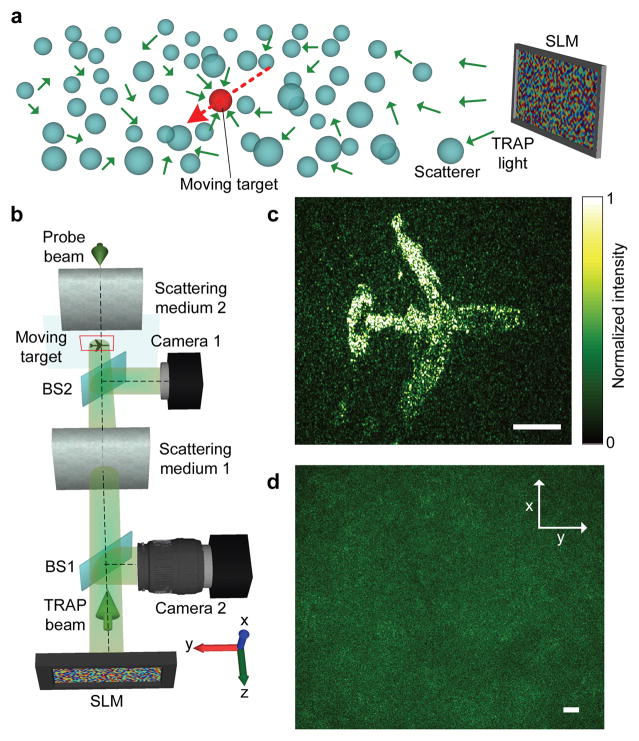
An attractive feature of TRAP focusing is the ability to dynamically focus light onto a moving target hidden inside a scattering medium. As the target moves, a remote sensor keeps taking snapshots of the scattered electromagnetic field E_i (index i denotes the current target location) and generating phase maps from $\mathrm{\Delta }{\mathbf{E}}_i^{\ast }={\mathbf{E}}_i^{\ast }-{\mathbf{E}}_0^{\ast }$, where E₀ is obtained when the target is absent. Repetitively reading the newly updated phase map ensures focusing onto the target, given an adequately short time lag between phase conjugation and the latest snapshot. The concept is demonstrated in Fig. 2, where light focuses dynamically from an SLM onto a moving target inside a scattering medium (Fig. 2a). In the experiment shown in Fig. 2b, an absorptive airplane pattern, printed on a transparency, was continuously translated between two optical diffusers. Meanwhile, the intensity distribution on the target was projected onto a camera by a beamsplitter to monitor the TRAP focus in real time. The light distribution outside the scattering medium, as measured on the SLM surface, manifested a random speckle pattern (Fig. 2d), indicating complete loss of the wavefront information. In salient contrast, as shown in Fig. 2c, light was dynamically focused onto the moving target as if scattering were totally suppressed (see Supplementary Methods for the experimental details and Supplementary Movie 2 for the dynamic focusing process). The demonstration, in which the scattering medium is static or quasi-static, does not bear full resemblance to a real situation. In reality, if the scattering medium changes too fast, the focusing will fail because the subtraction can no longer completely cancel the background. Consequently, for TRAP focusing to adapt to medium changes, the electronic processing time and the light round trip time have to be shorter than the medium correlation time; the maximum working distance is ultimately defined by the light round trip time.

Figure 2. Dynamic light focusing onto a moving target hidden inside a scattering medium.

a, Illustration of the concept. Light from an SLM is focused onto a moving target inside a scattering medium. b, Experimental arrangement. c, Focal light intensity distribution. d, Speckle pattern observed on the SLM surface during the probing process. BS: beamsplitter. Scale bars, 500 μm.

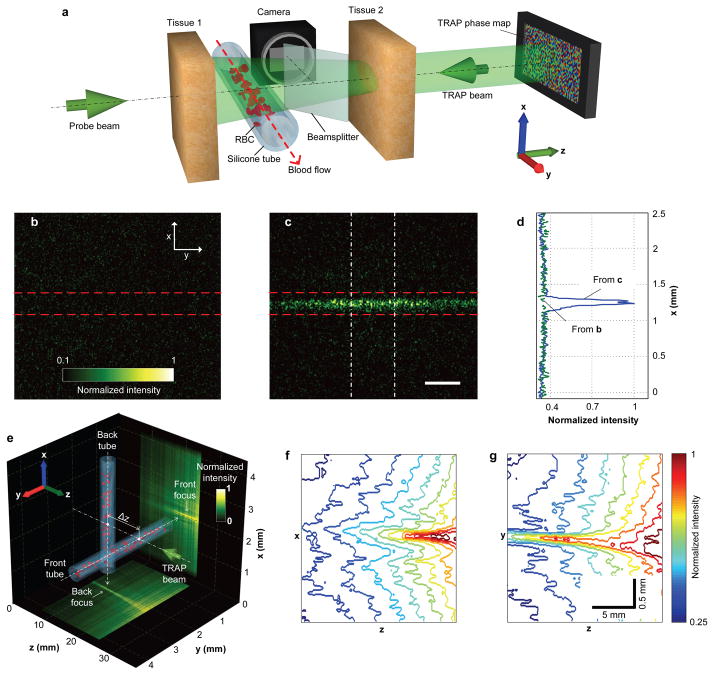
In deep tissue imaging, TRAP focusing can enhance the signal and contrast by redistributing and concentrating light on the targets, hence extending the imaging depth. For example, red blood cells (RBCs) are extensively employed as endogenous contrast agents. They provide important physiological information, such as metabolism¹⁵. At shallow (<1 mm) depths, light scattering by moving RBCs provides a contrast mechanism for mapping blood perfusion¹⁶; such motion contrast creates intrinsic guide stars for time-reversed deep focusing. At two instants t₁ and t₂, RBCs form two sets of spatial patterns within blood vessels. S_i denotes a set of RBC positions at instant i (i = 1, 2). If Δt = |t₁ − t₂| is selected to be between τ_RBC and τ_tissue (the field decorrelation times associated with the RBC and tissue movements, respectively), TRAP focusing generates optical foci at both S₁ and S₂, and thus concentrates energy on the RBCs. The concept was demonstrated by the set-up shown in Fig. 3a, where a blood-filled translucent silicone tube (300 μm inner diameter) was buried between two pieces of ex vivo chicken breast tissue samples, each 2.5 mm thick (~ 2.5 l_t′ ⁴, see Supplementary Methods for sample preparation). During the TRAP procedure, S₁ and S₂ were realized by flowing diluted bovine blood (see Supplementary Methods for sample preparation) in the tube. The comparative focal light intensity distributions shown in Fig. 3b, c demonstrate that TRAP focusing achieved significant energy enhancement at the target region. The enhancement factor, according to Fig. 3d, was approximately 300%, limited by experimental constraints (see Supplementary Methods). Furthermore, when the vessels formed a three-dimensional (3D) pattern, TRAP focusing faithfully shaped light onto the corresponding structure, as shown in Fig. 3e–g (see Supplementary Methods and Supplementary Movie 3 for a 3D visualization).

Figure 3. Focusing light onto flowing targets inside biological tissue.

a, Experimental configuration. Light is focused onto the tube through tissue 2. The focal intensity is monitored by a CMOS camera. b, c, Focal light intensity distribution due to an incorrect (b, phase map shifted by 3 pixels) and a correct (c) phase map. Dashed lines highlight the tube boundaries. d, Intensity distributions across the tube obtained by integrating horizontally within the region enclosed by the dashed-dot lines in c. The baseline is obtained by applying the same integration procedure to b. e, Two vessels are arranged perpendicularly to each other, separated by Δz = 1 cm in the axial (z) direction. The measured light distribution is projected along the x and y directions to the bottom and right surfaces of the cube, respectively. f, g, Intensity contours of the front (f) and back (g) foci. Scale bar in c, 500 μm.

Compared to schemes employing ultrasonic tagging^2–4, the major advantage of TRAP focusing is efficiency. Ultrasound fundamentally lacks specificity. For targeted light delivery (such as in photodynamic therapy), an image has to be acquired before the region of interest is determined. Moreover, the ultrasonic tagging approach concentrates light only at the ultrasonic beam, whereas TRAP focusing simultaneously enhances energy deposition onto the perturbed target in the entire field of view. Such a unique capability can be extremely useful in many applications, such as phototherapy of port wine stains and photoacoustic computed tomography of blood vessels¹⁵.

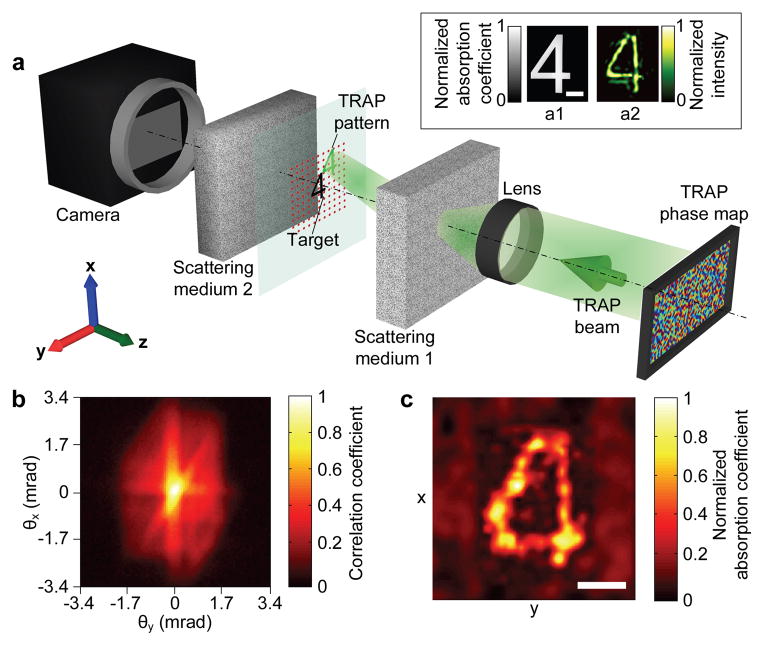
A time-varying object can also be optically imaged by TRAP focusing. In the experiment shown in Fig. 4a, an absorptive target (the number “4”) hidden between two optical diffusers was completely invisible externally. When the target moved into the scattering region being probed, its TRAP pattern copied and spatially overlapped itself. We employed the speckle scanning technique, originally invented by Bertolotti et al.¹⁷ and recently implemented in biological samples by Yang et al.¹⁸, to scan the TRAP pattern across the target laterally (in x and y) by stepping through different phase gradients on the SLM while the transmitted light was monitored by a camera located outside the scattering region. The autocorrelation of the object, shown in Fig. 4b, was assessed after mathematical manipulations (see Supplementary Methods), and the shape of the object was readily obtained by an iterative algorithm¹⁹, as depicted in Fig. 4c. In comparison to previous approaches based on the memory effect for imaging through or inside scattering media^12,17, TRAP focusing images only the perturbed regions, a feature especially useful in observing dynamic targets hidden in a relatively static background. This scheme will find ready applications in imaging angiogenic vessels in tumours. A limitation of the speckle scanning mechanism is the decrease of the speckle correlation angle with the medium thickness. Because the scanning has to cover the entire target, the imaging field of view, as well as the maximum target size, is reduced at greater depths¹⁸.

Figure 4. Imaging a hidden time-variant object.

a, Experimental arrangement. The SLM surface is imaged by a lens onto the surface of scattering medium 1 for memory scanning. The energy transmitted through scattering medium 2 is measured by a CMOS camera. Inset: the target and TRAP patterns. a1, Photograph of the target (plotted in absorption to reverse the contrast). a2, Intensity distribution of the TRAP pattern. b, The target’s autocorrelation coefficient measured as a function of incident angle. c, The reconstructed object plotted in normalized absorption coefficient. Scale bars, 100 μm.

TRAP focusing uses subtraction to convert the embedded novelties to guide stars. In the past, differentiation has been widely applied to novelty detection. Optical novelty filters were invented to image changing parts in a scene by temporarily unbalancing an interferometer or perturbing a two-beam coupling device comprising a slow photorefractive crystal^20,21. Holographic interferometry reveals differential information of an object by reconstructing superimposed holograms²². Recently, digital subtraction was used to enhance laser speckle imaging²³ and assist optical particle tracking²⁴. A microwave imaging scheme was proposed for tracking moving targets in clutter by subtracting multistatic data matrices and performing subsequent time reversal²⁵. Among these endeavours, TRAP focusing is the first demonstration of scattering compensation using visible light by integrating optical time reversal with novelty detection.

Apart from permittivity change and translational movement, rotation and tumbling of an object can equivalently exert perturbation and promote focusing. This can be understood by projecting the finite-sized object to a basis formed by the input modes, thus translating the movement of the object to the perturbation of the original projection. Under the same framework, multiple objects can be generalized as a spatially disconnected object and treated similarly. An alternative TRAP model is given in the Supplementary Discussion. The upper bound for the target size is ultimately limited by the focus peak to background ratio^3,4, whereas the smallest size is determined by the signal to noise ratio (γ) of the detection system. To resolve a single spatial mode in the presence of M input modes, 2N_sγ² ≫ M is required, where N_s is the number of holograms used for the phase map calculation, and M equals the space-bandwidth product on the target plane (see Supplementary Discussion).

TRAP focusing (and time reversal in general) is sensitive to medium displacement and decorrelation (see Supplementary Discussion), which suggests that the whole procedure (including phase map measurements, electronic processing, and phase conjugation) must be accomplished sufficiently fast to adapt to the dynamics of the scattering medium. The speed of the current system can be dramatically improved once faster SLMs and cameras are available. An amplitude-only holographic configuration can further speed up the process (see Supplementary Discussion). The energy enhancement ratio at the target locations can also be dramatically increased if more spatial modes are phase conjugated (enabled by large pixel count SLMs and cameras²⁶). We performed light focusing and imaging between two scattering media, where open access to the “inside” of the combined scattering medium enables convenient validation. This arrangement is, in principle, equivalent to focusing into a scattering medium¹⁴.

We emphasize that TRAP focusing does not necessarily rely solely on endogenous contrast agents. Its capability could be further extended by introducing exogenous agents with controlled motions or absorptions, such as magnetomotive particles²⁷, voltage-sensitive dyes²⁸ and photo-switchable dyes and proteins^29,30. By incorporating such labelling strategies, TRAP focusing could be made even more versatile and powerful.

In summary, the TRAP focusing technology is envisioned to have profound impacts in a wide range of applications where the scattering effect needs to be suppressed, including optical tracking and trapping, photoacoustic tomography, optogenetics, photothermal therapy, and photodynamic therapy. Other wave-related fields can also potentially benefit from the same concept.

Methods

Experimental set-up

The experimental set-up used to generate and acquire the experimental data is shown in Supplementary Fig. S1. The source used was a Q-switched frequency-doubled Nd:YAG laser (Elforlight Inc., UK) centred at 532 nm with pulse duration of 10 ns and coherence length of 7 mm. The repetition rate of the laser was tuneable between 50 Hz and 200 Hz, and the full pulse energy was 0.6 mJ. Before entering the Mach-Zehnder interferometer, the light beam was collimated to a diameter of 2 mm by a beam expander. The power injected into the system was adjustable via a half-wave plate (HWP) paired with a polarizing beamsplitter (PBS), and further attenuated through a neutral density filter. Light was split into a probe beam and a reference beam by another PBS, the ratio between the two beams was controlled by a HWP. The polarization of the reference beam was rotated by 90° before passing through an acousto-optic modulator (AOM) which up-shifted its frequency by δf. The reference beam was further expanded by an afocal lens pair to a diameter of 25 mm and spatially filtered by a pinhole. The probe beam entered a scattering cell composed of two optical diffusers (DG10-600, Thorlabs, USA) or two pieces of ex vivo chicken breast tissue. The reference beam was combined with the scattered light from the probe by a 50:50 beamsplitter (BS1). The path lengths of the reference and probe beams were balanced for strongest interference using two tuneable delay lines. The combined beams then entered the DOPC module. Inside the DOPC, the beams were retro-reflected by the surface of a phase-only SLM (vis-PLUTO, Holoeye, Germany). The beams were further reflected by a 90:10 (90% transmission) beamsplitter (BS2) to form a speckle pattern on an sCMOS camera (pco. Edge, PCO AG, Germany). The pixels of the camera and the SLM were digitally aligned with ≤1 (pixel) alignment error for optimal phase conjugation quality. Once the scattered fields were measured at two instants, a TRAP phase map was calculated and displayed on the SLM. In the hologram reading mode, the probe beam was blocked. The reference beam passed through BS1 and BS2 and impinged on the SLM. Reflection by the SLM generated the phase-conjugated beam, which was delivered to the scattering medium after passing through BS2 and BS1. The light intensity distribution on the focal plane inside the two scattering media was monitored either by replacing the target with a CMOS camera (Firefly MV, Point Grey Research, Canada), or by using a BS to reflect the focal pattern onto the camera.

TRAP phase map measurement

The frequency difference between the probe and reference beams was set by the AOM modulation frequency, which was δf = 50.0000125 MHz. The AOM was triggered by a function generator (DG4000, RIGOL Technologies, China) with a sinusoidal waveform at δf. A delay generator (DG645, Stanford Research Systems, USA), sharing a global time-base with the function generator, produced two channels of pulse sequences at f_s = 50 Hz with a proper relative delay to externally trigger and synchronize the laser and the camera. The reference beam, when undersampled at f_s by the camera, cycled through four phases—0, π/2, π, 3π/2—corresponding to four interferograms P_i (i = 1, 2, 3, 4). During the measurement, the SLM was blanked by displaying a constant phase map (phase value = 0). The complex amplitude of the field was obtained by E = (P₁ − P₃) + i(P₂ − P₄). After the two complex amplitudes were acquired, they were subtracted to get ΔE, and the TRAP phase map was calculated by Φ = −arg [Im (ΔE)/Re(ΔE)] (arg[·] denotes taking the argument).

For applications requiring higher measurement accuracy (e.g., the experiment shown in Fig. 1f–i, where the perturbation was weak), a different signal acquisition scheme was used. The AOM was driven at δf = 50.0000001 MHz, and the delay generator triggered the laser and the camera at 200 Hz and 4 Hz, respectively. The sampling frequency of f_s = 4 Hz ensured a phase difference of π/2 between neighbouring frames. The exposure time of the camera was set to 51 ms, during which 10 laser shots were averaged to reduce the noise caused by laser shot-to-shot intensity fluctuations.

TRAP focusing based on DOPC

In the probing mode (Fig. 1d), the scattered electromagnetic field distribution on a phase-only spatial light modulator (SLM) was measured via digital phase-shifting holography. The virtual difference field ΔE was synthesized by subtracting the fields acquired before and after the perturbation and then optimizing the phase offset. A phase map Φ was then extracted from ΔE and subsequently conjugated to yield the TRAP phase map (−Φ). In the focusing mode (Fig. 1e), an intense planar reading beam was transformed into a time-reversed beam after reflecting off the SLM, and converged onto the target.