Wealth and Health Behavior: Testing the Concept of a Health Cost

Abstract

Wealthier individuals engage in healthier behavior. This paper seeks to explain this phenomenon by exploiting both inheritances and lottery winnings to test a theory of health behavior. We distinguish between the direct monetary cost and the indirect health cost (value of health lost) of unhealthy consumption. The health cost increases with wealth and the degree of unhealthiness, leading wealthier individuals to consume more healthy and moderately unhealthy, but fewer severely unhealthy goods. The empirical evidence presented suggests that differences in health costs may indeed partially explain behavioral differences, and ultimately health outcomes, between wealth groups.

1 Introduction

Unhealthy lifestyles and unhealthy consumption are more prevalent among the poor, and account for a large fraction of the substantial socioeconomic disparities in health (Contoyannis and Jones 2004; Cutler et al. 2011). More affluent individuals are less likely to smoke, drink heavily, be overweight, and use illegal drugs, and are more likely to exercise and engage in preventive care (e.g., Cutler and Lleras-Muney 2010; Cutler et al. 2011; Cawley and Ruhm, 2012). A phenomenon of particular interest is that richer people tend to engage more in some unhealthy behaviors, such as drinking moderately,¹ but less in other unhealthy behaviors, such as smoking and excessive alcohol consumption (Cutler and Lleras-Muney 2010; Cawley and Ruhm 2012; see also Table 1).² What explains these differences in health behaviors across wealth groups remains largely unclear (Cutler et al. 2011).

Table 1.

Descriptive statistics of the dependent and independent variables, for the full sample and for subgroups

Outcome	Full sample	Most Healthy Most Wealthy	Most Healthy Least Wealthy	Least Healthy Most Wealthy	Least Healthy Least Wealthy
HRS
Log Household Wealth	12.71	13.46	11.88	12.88	10.84
Log Amount Inherited	10.59	10.91	10.22	10.62	9.93
Relative Amount Inherited (%)	11.97	7.77	18.90	10.42	40.25
Log Food Expenditures	4.64	4.86	4.62	4.70	4.37
Smoking (%)	15.84	10.61	17.60	13.79	21.61
Log Number of Cigarettes	2.18	2.16	2.19	2.18	2.17
Drinking (%)	49.60	66.97	51.38	48.26	31.57
Log Number of Drinks	1.04	1.17	1.01	0.97	0.88
Heavy Drinking (%)	14.14	10.18	13.84	12.29	17.56
Physical Activity	3.65	3.91	3.76	3.57	3.34
Number of observations	153,024	38,272	37,173	39,968	37,611
BHPS
Log Imputed Household Wealth	10.78	11.88	9.97	11.06	8.64
Log Household Income	10.13	10.45	9.88	10.23	9.63
Log Amount Won	3.70	3.73	3.73	3.60	3.66
Log Amount Won (Big Win)	7.33	7.39	7.30	7.26	7.26
Relative Amount Won (%)	0.08	0.03	0.20	0.06	0.69
Relative Amount Won (Big Win, %)	2.07	0.86	5.08	1.08	27.80
Log Food Expenditures	3.20	3.58	3.09	3.19	2.51
Smoking (%)	26.07	16.31	31.22	24.33	40.81
Log Number of Cigarettes	2.39	2.20	2.42	2.37	2.57
Drinking Out	3.21	3.43	3.24	3.09	2.76
Sports	3.78	4.14	3.84	3.58	3.01
Number of observations	165,488	60,912	55,945	23,710	24,281

Notes: Author’s calculations on basis of the 1992–2010 HRS and 1997–2008 BHPS. Note that Log Household Wealth and Log Household Income are calculated on basis of the sample of inheritance recipients (HRS) or lottery winners (BHPS). Relative amounts are calculated by the ratio of exp(log amount won)/exp(log household wealth).

Theoretical models of consumption and saving have difficulty explaining differences in unhealthy consumption across wealth groups. In these models, wealth enables more consumption, and the quantity purchased is governed by the monetary price of the good, permanent income and wealth, as well as preferences. Unless preferences differ substantially, these models would predict that wealthier individuals would engage more, not less, in unhealthy consumption.

In this paper we empirically evaluate a theory of health behavior (Galama and van Kippersluis, 2010) that provides a potential explanation for the observed differences in consumption patterns across wealth groups. The theory highlights the importance of a “health cost” of unhealthy behavior in explaining differences in health behavior between groups. To test the theory, we generate theoretical predictions of the effect of wealth shocks on health behavior, exploit both inheritance receipts and lottery winnings as plausibly exogenous variation in wealth, investigate heterogeneity in the effects of wealth shocks on health behavior across wealth and health groups, and employ the theory to interpret the empirical results. The paper contributes to three literatures: the literature on health behaviors, the literature on health disparities, and the literature relating to the value of life.

We present a theory based upon Galama and van Kippersluis (2010).³ The model builds on the human capital theory of the demand for health investment (Grossman 1972) with two important extensions. First, we use a health production process that is subject to diminishing returns to scale. This addresses the degeneracy of the solutions for investment and health (see Ehrlich and Chuma 1990; Galama 2011) that characterizes commonly employed linear investment models.⁴ It is further attractive in that the health investment process is generally thought of as being subject to diminishing returns (Wagstaff 1986). Second, we explicitly model the effect of consumption on health through its effect on the health deterioration rate. We distinguish healthy consumption (such as the consumption of healthy foods, sports and exercise) from unhealthy consumption (such as smoking, excessive alcohol consumption). Healthy consumption provides utility and is associated with health benefits in that it lowers the health deterioration rate. Unhealthy consumption provides utility but increases the health deterioration rate.⁵ The decision to engage in unhealthy consumption is governed by the monetary cost (i.e. the price of a pack of cigarettes) as well as a health cost (i.e. the value of health lost).

The theoretical contribution of this work, compared to Galama and Van Kippersluis (2010), consists of performing comparative dynamic, as opposed to static, analyses to derive predictions regarding the effect of wealth shocks on health behavior. Comparative dynamic analyses take into account all possible dynamic adjustments over the life cycle, and allow investigating the full dynamic response to wealth shocks. The model predicts that wealth has two effects. First, there is the familiar direct effect: wealth allows individuals to purchase more (unhealthy) consumption goods. But there is also an indirect effect: the health cost is higher for wealthier individuals, as well as for less healthy individuals, and for a higher degree of unhealthiness of the good (the extent to which it increases the aging rate). The direct and the indirect wealth effect compete and while the net effect is ambiguous, we predict that: 1) wealthy individuals are likely to engage more in moderately (direct wealth effect dominates) and less in severely unhealthy consumption (indirect health cost effect dominates), and 2) the strength of the response to an unexpected wealth shock is smallest for the most wealthy, least healthy, and for a high degree of unhealthiness of the consumption good. Differences in health cost can thus provide a possible explanation for the observed positive association between wealth and moderately unhealthy consumption and the negative association with severely unhealthy consumption.

While the concept of a trade-off between utility from unhealthy consumption, the price of consumption and its health consequences is certainly not new, the theory is the first to successfully produce the observed differences in consumption patterns between wealth groups discussed above. The Grossman (1972) model emphasizes health investments (associated with a health benefit) but does not allow for disinvestments (such as unhealthy behavior, associated with a health cost). To the best of our knowledge, only Forster (2001) and Case and Deaton (2005) have previously modeled unhealthy consumption as a choice variable affecting health deterioration. These papers however do not allow for an effect of wealth on unhealthy behavior.⁶ Even the seminal theory of rational addiction (Becker and Murphy, 1988), while arguing conceptually for an effect of unhealthy addictive consumption on health, does not explicitly model this effect. None of these theories therefore are able to produce the observed positive association between wealth and moderately unhealthy consumption and the negative association with severely unhealthy consumption. These models also do not predict differences in the strength of the consumption response to an unexpected wealth shock between wealth and health groups, for which we find empirical evidence.

In the second part of the paper we employ plausibly exogenous variation in wealth to test the two theoretical predictions. In particular, we investigate differences in responses to wealth shocks across consumption goods that vary in the degree of unhealthiness, and between wealth and health groups, to test the empirical relevance of our concept of the health cost of unhealthy consumption. To the best of our knowledge, this is the first attempt at explicitly modeling and empirically evaluating the predictions of a theory that considers the full marginal cost of unhealthy consumption, involving both a monetary cost and a health cost.

A relatively small empirical literature has investigated the effect of wealth on health behaviors, exploiting the unemployment rate, work experience, parental background, and spousal characteristics as instrumental variables (Ettner 1996), cohort-level variation in income (Adda et al. 2009), the Earned Income Tax Credit (EITC, Kenkel et al. 2011), inheritance receipt (Kim and Ruhm 2012), and lottery winnings (Apouey and Clark 2014).⁷ These studies generally suggest a positive effect of wealth shocks on unhealthy behaviors such as alcohol consumption and smoking.

In contrast to this literature, and motivated by our theory, we focus on an investigation of differences in the effect of wealth on health behavior between wealth and health groups. We find evidence for heterogeneity in responses to wealth shocks, something the empirical literature has not explored thus far. Another contribution we make to the empirical literature is our use of a more conservative and robust empirical approach by including individual-specific fixed effects, by estimating various different specifications, and exploiting both inheritances and lottery winnings as plausibly exogenous variation in wealth.⁸ Last, while previous empirical studies lack a proper theoretical foundation, and results were interpreted on a rather ad-hoc basis, our model provides a framework for an economic interpretation of the effect of wealth on health behavior and health.

The empirical evidence presented in this paper is in line with our two main theoretical predictions and hence provides support for the empirical relevance of a health cost of unhealthy consumption. The theory, and in particular the concept of a “health cost”, helps in understanding our empirical findings: wealth effects are found to be larger for drinking than for smoking because of differences in the health-detriment of their consumption, and the most healthy least wealthy respond stronger to wealth shocks than do the least healthy most wealthy, as they value health less (small health cost). These results have implications for three distinct literatures.

Regarding the literature on health behaviors, on average we find a positive effect of wealth shocks on unhealthy consumption, which implies that income transfers may have the unintended consequence of increasing unhealthy consumption among the individuals receiving the transfer (see also Kenkel et al. 2011). Yet importantly, and in line with the theory, we provide novel empirical evidence that shows that in response to a sudden increase in wealth, unhealthy individuals do not increase their unhealthy consumption while healthy individuals do. Unhealthy individuals appear to care more about the next marginal unit of health. This suggests that there may be adverse population health effects of wealth redistribution for healthy, but less so for unhealthy, disadvantaged segments of society.

Regarding the literature on health disparities, our results suggest that health costs play an important role in generating differences in health behavior. Such differences in unhealthy lifestyles and unhealthy consumption contribute substantially to the health gradient (e.g. Cutler et al., 2011), with some arguing that in developed countries, it is personal lifestyles that cause the greatest variation (Fuchs, 1986). Our results may also provide an explanation for the empirical regularity that, despite a strong and well-established positive association between wealth and health (Cutler et al. 2011), scholars have failed to identify a positive causal effect of wealth and income variations on health (Adams et al. 2003; Snyder and Evans, 2006). Our findings suggest that the often-cited benefits of additional income in providing access to health care, technology, and healthy food, are partially offset by an increase in unhealthy behavior, potentially explaining the lack of a causal effect. Since a positive association between wealth and health is observed, selection is likely to play an important role, in which factors such as, e.g., education, cognitive abilities and discount rates correlate positively with both wealth and health.

Last, the evidence we present on the importance of the health cost of unhealthy consumption adds to the literature on the value of a statistical life (VSL, see Viscusi and Aldy, 2003, for a review). Assessments of the VSL generally involve investigating the risk of death and injury that people are willing to take (usually in a setting of hazardous work) and how much they should be paid for taking these risks. In our theory, individuals make a similar trade-off. They are willing to engage in a certain amount of unhealthy consumption for the instantaneous utility it provides, as long as this benefit outweighs the associated health cost: the reduction in life-time utility due to health loss associated with unhealthy consumption. Thus, the VSL and our concept of a health cost are closely related and insight in the VSL might be gained from studies such as ours employing risky health behaviors. For example, our research suggests there are important differences in health costs between health and wealth groups, which in turn suggest potential heterogeneity in the VSL in terms of these same dimensions.

The paper is organized as follows. Section 2 formulates a theory of wealth, health and consumption patterns, and discusses predictions. Section 3 presents the data and empirical methodology. Section 4 presents the results and robustness checks, and Section 5 provides a summary and discussion.

2 A theory of wealth, health, and unhealthy consumption

2.1 Theoretical formulation

Individuals maximize the life-time utility function

$${\int }_0^{T}U[C_h(t),C_u(t),H(t)]e^{-\mathrm{\beta }t}dt,$$ (1)

where T denotes the life span, assumed exogenous for simplicity,⁹ β is a subjective discount factor and individuals derive utility from healthy consumption C_h(t), unhealthy consumption C_u(t) and from health H(t). Time t is measured from the time an individual has completed her education and joined the labor force. Utility increases with healthy consumption ∂U/∂C_h > 0, unhealthy consumption ∂U/∂C_u > 0, and with health ∂U/∂H > 0, but at a decreasing rate ${\partial }^{2}U/\partial C_h^2<0,{\partial }^{2}U/\partial C_u^2<0$, and ∂²U/∂H² < 0.

The objective function (1) is maximized subject to the following dynamic equations,

$$Ḣ(t)={\mu }_I(t)I{(t)}^{\mathrm{\alpha }}-d[t,C_h(t),C_u(t),H(t);\mathrm{\xi }(t)],$$ (2)

$$Ȧ(t)=\mathrm{\delta }A(t)+Y[H(t)]-p_{C_h}(t)C_h(t)-p_{C_u}(t)C_u(t)-p_I(t)I(t),$$ (3)

and we have initial and end conditions: H(0), H(T), A(0) and A(T) are given.

Ḣ(t) and Ȧ(t) in equations (2) and (3) denote time derivatives of health H(t) and assets A(t). Health (equation 2) can be improved through investment in health I(t), and deteriorates at the health deterioration rate d(t). The health-production function μ_I(t)I(t)^α has an efficiency μ_I(t), and exhibits diminishing returns to scale (DRTS; 0 < α < 1). The health deterioration rate d(t) depends endogenously on healthy consumption C_h(t) and unhealthy consumption C_u(t), on the health stock, H(t), and on a vector of exogenous variables ξ(t) (e.g., environmental conditions). Consumption can be healthy (∂d/∂C_h ≤ 0) or unhealthy (∂d/∂C_u > 0). Health deterioration is a general function of health (d[H(t)]), as opposed to the standard assumption that it is proportional to the health stock (d[H(t)] ∝ H(t)) as in Grossman (1972) and most of the subsequent health-capital literature (for an exception, see Dalgaard and Strulik, 2014).

Assets A(t) (equation 3) provide a return δ (the return to capital), increase with income Y(t) and decrease with purchases of healthy consumption goods C_h(t), unhealthy consumption goods C_u(t), and health investment I(t), at prices p_Ch (t), p_Cu (t), and p_I(t), respectively. Income Y(t) is assumed to be an increasing and concave function of health H(t) (∂Y/∂H > 0, and ∂²Y/∂H² < 0). Last, we assume that individuals face no borrowing constraints.

Thus, we have the following optimal control problem: the objective function (1) is maximized with respect to the control functions C_h(t), C_u(t), and I(t), subject to the constraints (2) and (3). The Hamiltonian (see, e.g., Seierstad and Sydsaeter 1987) of this problem is:

$$\Im =U(t)e^{-\mathrm{\beta }t}+q_H(t)Ḣ(t)+q_A(t)Ȧ(t),$$ (4)

where q_H(t) is the marginal value of health H(t) (in utils per unit of health) and q_A(t) is the marginal value of assets A(t) (in utils per monetary unit).

2.2 First-order conditions

Derivations of the first-order conditions can be found in appendix A. The first-order condition for health investment is

$$q_{h/a}(t)={\mathrm{\pi }}_I(t),$$ (5)

where q_h/a(t) is the ratio of the marginal value (or shadow price) of health and the marginal value (or shadow price) of wealth, q_h/a(t) = q_H(t)/q_A(t), which we will denote as the “relative value of health”. The relative value of health represents the marginal benefit of health investment, and its evolution is determined by the co-state equation

$$\frac{\mathrm{\partial }{q}_{h/a}}{\mathrm{\partial }t}=q_{h/a}(t)[\frac{\mathrm{\partial }d}{\mathrm{\partial }H}+\mathrm{\delta }]-[\frac{1}{q_A(0)}\frac{\mathrm{\partial }U}{\mathrm{\partial }H}{e}^{-(\mathrm{\beta }-\mathrm{\delta })t}+\frac{\mathrm{\partial }Y}{\mathrm{\partial }H}],$$ (6)

where q_A(0) is the marginal value (or shadow price) of initial wealth.

The RHS of equation (5), π_I(t), is the marginal cost of health investment I(t)

$${\mathrm{\pi }}_I(t)\equiv \frac{p_I(t)I{(t)}^{1-\mathrm{\alpha }}}{\mathrm{\alpha }{\mu }_I(t)}.$$ (7)

The marginal cost of health investment increases with the price of investment goods and services p_I(t) and with the level of investment I(t), due to DRTS in the health production process μ_I(t)I(t)^α (0 < α < 1; see equation 2).

The first-order condition for healthy consumption is

$$\frac{\mathrm{\partial }U}{\mathrm{\partial }{C}_h}=q_A(0)[p_{C_h}(t)-{\mathrm{\phi }}_{d{C}_h}(t)]e^{(\mathrm{\beta }-\mathrm{\delta })t},$$ (8)

where p_Ch (t) is the price of healthy consumption C_h(t), representing the direct monetary cost of consumption, and φ_dCh (t) is the marginal health benefit of healthy consumption

$${\mathrm{\phi }}_{d{C}_h}(t)\equiv -q_{h/a}(t)\frac{\mathrm{\partial }d}{\mathrm{\partial }{C}_h}.$$ (9)

The marginal health benefit of healthy consumption φ_dCh (t) represents the marginal value of health saved: it is the product of the relative value of health q_h/a(t) and the amount of health “saved” [∂d(t)/∂C_h(t)].¹⁰ Compared to a model in which consumption has no health consequences, the “full” price (marginal cost) of healthy consumption is lower because of its health benefit (see 8).

Similarly, the first-order condition for unhealthy consumption is

$$\frac{\mathrm{\partial }U}{\mathrm{\partial }{C}_u}=q_A(0)[p_{C_u}(t)+{\mathrm{\pi }}_{d{C}_u}(t)]e^{(\mathrm{\beta }-\mathrm{\delta })t},$$ (11)

where p_Cu (t) is the price of unhealthy consumption C_u(t) (direct monetary cost) and π_dCu (t) is the marginal health cost of unhealthy consumption

$${\mathrm{\pi }}_{d{C}_u}(t)\equiv q_{h/a}(t)\frac{\mathrm{\partial }d}{\mathrm{\partial }{C}_u}.$$ (12)

Compared to a model in which consumption has no health consequences, the “full” price (marginal cost) of unhealthy consumption is higher because of its health cost (see 11).

2.3 Predictions

In order to predict the effect of an unanticipated wealth shock we compute the comparative dynamic effect of an infinitesimally small change in initial wealth A₀. The comparative dynamic effect is obtained by taking the derivative of the first-order conditions (5), (8), and (11), the dynamic co-state equation (6), and the health transition equation (2) with respect to A₀.

Assuming first-order effects dominate higher-order effects,¹¹ the comparative dynamic effect of initial wealth on healthy consumption can be summarized as (see Appendix B for detail):

$$\frac{\mathrm{\partial }{C}_h}{\mathrm{\partial }{A}_0}={\mathrm{\lambda }}_{C_h}(t)\times [\frac{U_{C_h}}{q_A(0)}\frac{\mathrm{\partial }{q}_A(0)}{\mathrm{\partial }{A}_0}+\frac{\mathrm{\partial }d}{\mathrm{\partial }{C}_h}\frac{\mathrm{\partial }{q}_{h/a}}{\mathrm{\partial }{A}_0}],$$ (13)

where λ_Ch (t) = [U_ChCh − q_H(t)d_ChChe^βt]⁻¹ is negative under the plausible assumptions of diminishing marginal utility of healthy consumption (U_ChCh < 0) and diminishing marginal health benefit of healthy consumption (d_ChCh > 0), and U_x = ∂U/∂x, U_xx = ∂²U/∂x², d_xx = ∂²d/∂x².

Thus, the impact of wealth on healthy consumption can be decomposed into the impact of wealth on (i) the marginal value of lifetime wealth q_A(0), and (ii) the relative value of health q_h/a(t). The first term between brackets on the RHS of equation (13) represents the direct wealth effect, which is positive under the assumption of diminishing returns to wealth (∂q_A(0)/∂A₀ < 0)¹²: an increase in wealth allows more healthy consumption. Yet, wealth also has an indirect effect through the second term between brackets on the RHS. In appendix B we show that an increase in wealth leads to a higher relative value of health q_h/a(t), at least initially. Intuitively, given diminishing returns to wealth and consumption, a marginal increase in wealth leads individuals to place a higher relative value on health compared to wealth, thereby increasing their health investment and the health stock.¹³ Given that λ_Ch (t) < 0, ∂q_A(0)/∂A₀ < 0 and ∂d/∂C_h < 0, both the direct and indirect effect operate in the same direction, and the initial response to an increase in wealth is to increase demand for healthy consumption: ∂C_h/∂A₀ > 0.

The comparative dynamic effect of initial wealth on unhealthy consumption can be summarized as (see Appendix B for detail):

$$\frac{\mathrm{\partial }{C}_u}{\mathrm{\partial }{A}_0}={\mathrm{\lambda }}_{C_u}(t)\times [\frac{U_{C_u}}{q_A(0)}\frac{\mathrm{\partial }{q}_A(0)}{\mathrm{\partial }{A}_0}+\frac{\mathrm{\partial }d}{\mathrm{\partial }{C}_u}\frac{\mathrm{\partial }{q}_{h/a}}{\mathrm{\partial }{A}_0}],$$ (14)

where λ_Cu (t) = [U_CuCu − q_H(t)d_CuCue^βt]⁻¹ is plausibly negative.¹⁴ Similar to healthy consumption, additional wealth enables purchases of more unhealthy consumption goods – the direct wealth effect (first term on the RHS of 14). Yet, additional wealth also increases the relative value of health q_h/a(t) and thus the marginal health cost of unhealthy consumption π_dCu (t) (the indirect wealth effect; second term between the brackets on the RHS of 14): the indirect wealth effect competes with the direct wealth effect.

While we cannot a priori sign the relation between unhealthy consumption and wealth, the two competing effects predict an interesting pattern of behavior. The importance of the indirect wealth effect, that is the importance of the health cost, is proportional to ∂d/∂C_u (the degree of “unhealthiness” of the consumption good). This implies that an increase in wealth may lead to increased demand for moderately unhealthy consumption goods (direct effect dominates) and reduced demand for severely unhealthy consumption goods (indirect effect dominates).

Formally, what constitutes moderately and severely unhealthy goods is determined by a threshold above which the indirect health cost effect dominates the direct wealth effect, and can be derived from (14). An unanticipated increase in wealth leads to a decrease in unhealthy consumption if

$$\frac{\mathrm{\partial }d}{\mathrm{\partial }{C}_u}>\frac{-\frac{U_{C_u}}{q_A(0)}\frac{\mathrm{\partial }{q}_A(0)}{\mathrm{\partial }{A}_0}}{q_A(0)\frac{\mathrm{\partial }{q}_{h/a}}{\mathrm{\partial }{A}_0}}.$$ (15)

and will lead to an increase in unhealthy consumption otherwise. Note that this threshold is not universal. It differs by socioeconomic status (e.g., wealth) and by health. In practice, we study different types of unhealthy consumption with varying degrees of unhealthiness to investigate whether their consumption increases or decreases in response to an unanticipated increase in wealth (permanent income) for certain groups defined by wealth and health status.

Apart from differential responses depending on the unhealthiness of the good, we also expect the impact of a wealth shock on unhealthy consumption to be smaller among wealthier individuals for two reasons. First, the direct effect of a given absolute wealth shock is smaller among wealthier individuals (diminishing returns to wealth). Second, wealthier individuals place a higher relative value on health compared to wealth, and as a result have a higher health cost for a given degree of “un-healthiness” of the good. The larger the health cost compared to the monetary cost, the smaller the behavioral response is toward a wealth shock. This is because the direct wealth effect operates primarily through the marginal value of wealth q_A(t) in the expression for the monetary cost q_A(t)p_Cu (t), which is a first-order effect (i.e., responsive to changes in wealth), while the indirect health cost effect operates primarily through the marginal value of health q_H(t) in the expression for the health cost q_H(t)(∂d/∂C_u), which is a second-order (indirect) effect (i.e., less responsive to wealth; see 11). A large (unresponsive) health cost therefore dampens the direct wealth effect.

While the relative value of health q_h/a(t) plausibly increases with wealth due to diminishing returns (∂q_A(t)/∂A(t) < 0; as discussed earlier), it plausibly decreases with health for the same reason: due to diminishing returns to health (∂q_H(t)/∂H(t) < 0).¹⁵ Hence, less wealthy and more healthy individuals face a smaller health cost, and the indirect wealth effect is smaller for them.

In sum, the theory provides us with the following two main predictions:

1. An unexpected wealth shock leads to increased demand for healthy and moderately unhealthy consumption goods, but decreased demand for severely unhealthy goods.

2. For unhealthy consumption goods, the strength of the response to an unexpected wealth shock is smallest for the most wealthy, least healthy, and for a high degree of unhealthiness of the consumption good.

2.4 Towards an empirical specification

The first-order conditions for healthy consumption (8) and unhealthy consumption (11) guide our empirical analysis. While we do not have direct measurements of all relevant variables of the first order conditions, if we approximate q_A(0), and q_h/a(t) by including controls for life-time wealth (permanent income), education, and health status, and under invertibility of the utility function, a first-order linear approximation would be

$$\text{ln}{C}_{i,t}=\mathrm{\alpha }+{\mathrm{\beta }}_1\text{ln}{W}_i+{\mathrm{\beta }}_2\text{ln}{H}_{i,t-1}+{\mathrm{\beta }}_3\text{ln}{E}_i+\mathrm{\gamma }{Z}_{i,t-1}+({\mathrm{\tau }}_t\times {\mathrm{\theta }}_r)+{\mathrm{\epsilon }}_{i,t},$$ (16)

where i denotes the individual and t the wave, C_i,t is the consumption outcome, W_i is life-time wealth, H_i,t−1 is lagged health status, E_i is education, and Z_i,t−1 covers time-varying socio-demographic factors influencing both life-time wealth and health behaviors, such as age and employment status. To account for differences in the price of unhealthy consumption goods and medical services, and for region-specific policies affecting the outcomes, we include region-wave interactions, where τ_t denotes wave dummies, and θ_r are regional dummies. ε_i,t is an error term. The coefficients β can be interpreted as (combinations of) the structural parameters of the model, but these are not our main interest in this study. Their estimation would require functional form assumptions, and our aim here is primarily to test the theoretical predictions.

Life-time wealth (permanent income) W_i is unobserved, and difficult to construct from a limited number of repeated observations for a given individual. We include individual fixed effects α_i to account for this permanent component of wealth, and to capture all other time-invariant model parameters such as discount rates and other preference parameters thought to influence both wealth and health behaviors.

We exploit exogenous variation in wealth deriving from inheritances and lottery winnings to test how variation in life-time wealth (permanent income) W_i affects consumption decisions. The use of inheritances and lottery winnings as variation in life-time wealth W_i is justified as Friedman (1957; Chapter 3, p. 23) and Keeler et al. (1985) argue that windfall gains represent an increase in permanent income, and individuals smooth consumption with the marginal propensity to consume equaling the annuity value of the windfall gain (Meghir, 2004; Jappelli and Pistaferri, 2010).¹⁶

Importantly, the permanent income hypothesis suggests that in order to affect consumption decisions, the shock to wealth should be unanticipated (Friedman, 1957; Jappelli and Pistaferri, 2010), otherwise it would already be included in the value of q_A(0) and consumption would be unaffected. Whether the shock is of a transitory (as is the case for unanticipated inheritances and lottery winnings) or of a more permanent nature (e.g., an unanticipated and permanent raise in salary) is not important, according to the permanent income hypothesis. As long as the annuitized value of the shock is the same (so that the change in q_A(0) is identical), the response to transitory and permanent shocks should be identical, leading to a permanent increase in the level of consumption (consumption smoothing).¹⁷ The most relevant validation of our approach therefore is establishing that the shocks are unanticipated. We present evidence in section 3.2 and 4.3, supporting the notion that the timing and size of both inheritances and lottery winnings is largely unanticipated.

3 Data and Methodology

We extract inheritance receipt from the US Health and Retirement Study (HRS), and lottery winnings from the British Household Panel Survey (BHPS).We discuss the data sources and empirical strategies below.

3.1 HRS Data and Descriptive Statistics

To exploit exogenous variation in wealth deriving from inheritances we use the US Health and Retirement Study (HRS) for the years 1992–2010. For most of the variables we use the RAND version of the HRS, which is a user-friendly, harmonized version of the data. The information regarding inheritance receipt and expectations, the number of cigarettes smoked per day, and food expenditures are taken from the original HRS files. The initial HRS cohort consists of around 13,500 individuals born between 1931 and 1941. It has been appended by additional cohorts of different birth years. The total sample size consists of 153,024 person-year observations for 27,900 distinct individuals. The first column of the top panel of Table 1 presents averages of the dependent and independent variables defined below, and Table 8 in appendix C lists all HRS variables and their unit of analysis employed in this work.

Dependent variables

Our first dependent variable in the HRS is Food Expenditures,¹⁸ which is not interpreted as either healthy or unhealthy but serves to verify if wealth shocks have an effect on overall consumption. Measures of unhealthy consumption are Smoking, “Do you smoke cigarettes now?”; Number of Cigarettes,¹⁹ “About how many cigarettes or packs do you usually smoke in a day now?”; Drinking, “Do you ever drink any alcoholic beverages, such as beer, wine, or liquor?”; Number of Drinks, which is the product of the answers to the questions “In the last three months, on average, how many days per week have you had any alcohol to drink?” and “In the last three months, on the days you drink, about how many drinks do you have?” (this definition is also used by Kim and Ruhm 2012); and Heavy Drinking, a binary indicator of whether the individual drinks 3 or more glasses on an occasion when drinking (this definition is also used by, e.g., Arcidiacono et al. 2007). Our measure of healthy consumption is Physical Activity, which is defined as the highest frequency of performing any light, moderate or vigorous physical activity. The questions are “How often do you take part in sports or activities that are mildly energetic/moderately energetic/vigorous?”, respectively, and are measured in five categories.

For the number of cigarettes smoked per day the question wording changed considerably from wave 1994 to 1996. Therefore, in the analyses of cigarettes per day we restrict our analysis to wave 1996 and beyond. Frequency of drinking is only available from 1996 on, and food expenditures are only available from 2000 on. Physical activity is used since 2004 due to a major change in the question wording. All monetary values are measured in natural logarithms,²⁰ and converted to 2005 US dollars using the Consumer Price Index (CPI).

Independent variables

Household Wealth is defined as the sum of all wealth components less all debt.²¹ Information on Inheritance receipt is obtained from the question “In the past two years, have you (or your partner) received money or property in the form of an inheritance, a trust fund, or an insurance settlement?”, where we disregard trust funds and insurance settlements. If answered affirmative, the respondents are asked “About how much did you receive from the inheritance?”. The answer to this question defines Amount Inherited. Individuals not providing exact amounts were requested to answer whether the value was less than, about, or more than 50,000 US dollars, which we converted to 17,276, 50,000, and 186,509 US dollars, respectively, given the sample averages in those categories (taken from Kim and Ruhm 2012).²² We drop individuals who report having received an inheritance before the first wave (1992), as we don’t know the exact timing of the receipt, and this could bias the estimates.

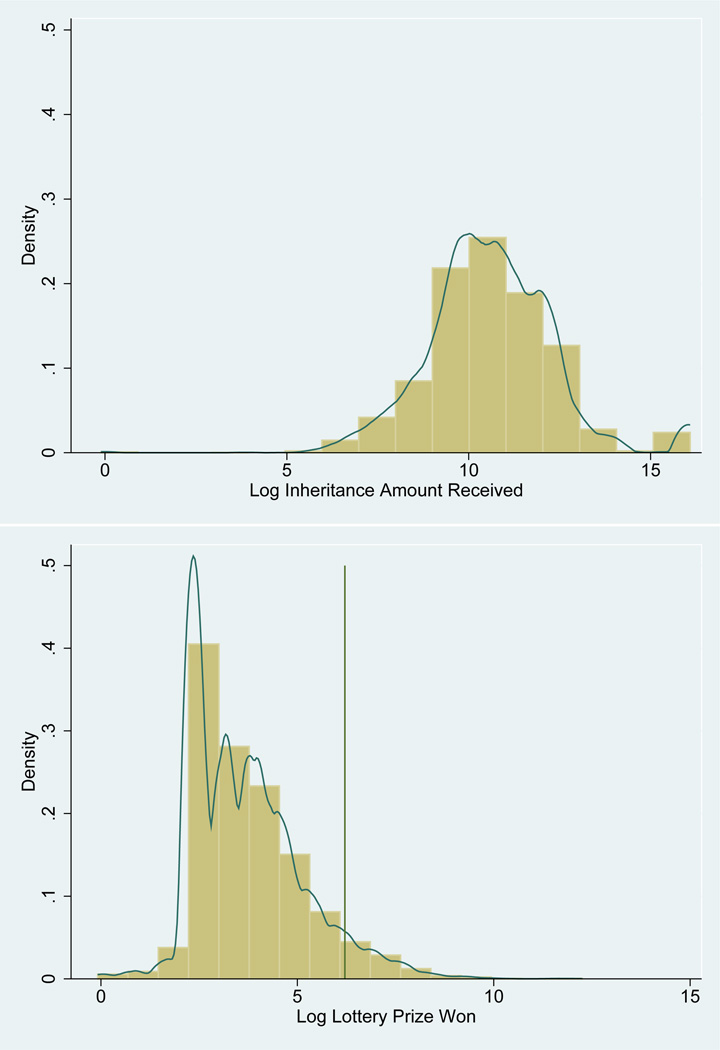
Between 2.7 and 6.9% of the sample received an inheritance over the waves. Figure 1 (top panel) and Table 1 show that the mean of the log of inheritance is substantial: corresponding to around 40,000 US dollars,²³ or 12% of current wealth.

Figure 1.

Distribution of the logarithm of inheritance amounts in US dollars in the HRS (top) and of lottery prizes won in British pounds in the BHPS (bottom). The bar graphs show the data binned in 16 discrete units of the amount inherited and the log of the prize won, and the solid curves are Epanechnikov kernel densities. The vertical bar in the bottom Figure corresponds to 500 British pounds, above which lottery winnings are defined as big.

Control variables

the first lag of Household Wealth, the first lag of Household Income, Age and its square Age², Sex, Race, the first lag of Census Region (five regions), the first lag of Household Size, the first lag of the Number of Children, Years of Education, the first lag of Health Status (five categories), the first lag of Marital Status (eight categories), the first lag of Employment Status (binary), Ever Smoked, and the first lag of Health Insurance. Additionally we include controls for whether Mother Died, Father Died, Mother in Law Died, or Father in Law Died since the last wave, and whether the individual got Widowed since the last wave. All control variables are defined in Table 8 in Appendix C. They are selected on the basis of the theoretical considerations discussed in Section 2.4, and to account for time-varying factors potentially influencing inheritance receipt and health behaviors. Interactions between time dummies and region dummies are used to capture regional differences over time.

Table 2 presents the averages of the control variables by inheritance receipt status. Inheritance recipients are statistically significantly different in nearly every single domain from non-recipients (compare columns 2 and 3). White, wealthy, working, higher educated, and high-income individuals are more likely to receive an inheritance. As one would expect, the fraction for which a parent or parent in law died is considerably higher in the inheritance recipients group.

Table 2.

Descriptive statistics of the control variables by inheritance receipt in the HRS

Variable	No Inheritance	Inheritance	Small Inheritance	Big Inheritance
Log Household Wealth	11.31	12.71***	12.03	12.86***
Log Household Income	10.43	11.29***	10.83	11.40***
Age	65.81	62.12***	61.54	62.25**
Sex	0.42	0.46***	0.45	0.46
Race
White/Caucasian	0.81	0.95***	0.92	0.95***
Black/African American	0.14	0.03***	0.05	0.03***
Other	0.04	0.02***	0.02	0.02
Census Region
Northeast	0.16	0.14***	0.14	0.13
Midwest	0.25	0.31***	0.32	0.31
South	0.41	0.34***	0.36	0.33*
West	0.17	0.21***	0.18	0.22***
Other	0.00	0.00	0.00	0.00
Household Size	2.29	2.27***	2.36	2.25***
Number of Children	3.27	2.93***	3.09	2.90***
Years of Education	12.18	13.86***	13.29	13.99***
Health Status
Excellent	0.13	0.19***	0.17	0.20*
Very Good	0.29	0.36***	0.34	0.37*
Good	0.31	0.29***	0.30	0.29
Fair	0.19	0.12***	0.14	0.11**
Poor	0.09	0.04***	0.05	0.04*
Marital Status
Married, Married spouse absent	0.66	0.78***	0.75	0.79***
Partnered	0.03	0.03	0.03	0.03
Separated/Divorced (categories 4 to 6)	0.10	0.08***	0.10	0.07**
Widow	0.18	0.09***	0.10	0.08**
Never Married	0.03	0.02**	0.02	0.02
Employment Status	0.41	0.53***	0.53	0.53
Ever Smoked	0.58	0.57	0.60	0.56***
Health Insurance	0.83	0.79***	0.77	0.80**
Mother died	0.02	0.13***	0.11	0.13*
Father died	0.01	0.05***	0.05	0.06*
Mother in law died	0.02	0.10***	0.08	0.11***
Father in law died	0.01	0.04***	0.03	0.04*
Widowed	0.03	0.02***	0.02	0.02
Observations	146,165	6,859	1,233	5,626

^*p-value < 0.1,

^**p-value < 0.05,

^***p-value < 0.01

Notes: Author’s calculations on basis of the 1992–2010 HRS. Small Inheritance recipients are those that received an inheritance below 10,000 US dollars, and Big Inheritance recipients received amounts above that threshold. The asterisks denote whether the difference in means between non-recipients (column 2) and recipients (column 3) and between small (column 4) and big recipients (column 5) are statistically significant. Marital status is grouped into 5 categories for exposition reasons (see Table 8 for definitions of categories).

3.2 HRS Methodology

The receipt of an inheritance has been shown to represent useful and important variation in wealth (see Meer et al. 2003; Michaud and Van Soest 2008; Kim and Ruhm 2012; Carman 2013), although questions have been raised regarding its exogeneity and whether inheritances are unanticipated.

We seek to address the potential endogeneity of the receipt and size of an inheritance using two empirical strategies.

First specification: FE Inheritance

Our first approach is to include an individual-specific fixed effect to account for the fact that inheritance recipients are intrinsically different from non-recipients. The fixed effect controls for all time-invariant personal characteristics likely to influence both inheritance receipt and health behaviors, such as life-time wealth (or permanent income), education, risk aversion, cognitive and non-cognitive abilities, and time preference. Additionally, we include control variables to account for possible time-varying variables influencing both inheritance receipt and health behaviors. A parsimonious version of equation (16) can be written as

$$\text{ln}{C}_{i,t}={\mathrm{\alpha }}_i+\mathrm{\beta }{I}_{i,t}+\mathrm{\gamma }\prime X_{i,t-1}+({\mathrm{\tau }}_t\times {\mathrm{\theta }}_r)+{\mathrm{\epsilon }}_{i,t},$$ (17)

where C_i,t is the outcome measure for individual i at time t, α_i represents the individual-specific fixed effect, I_i,t is a binary indicator of whether one received an inheritance, X_i,t−1 is a matrix of plausibly exogenous control variables including lagged health, and (τ_t × θ_r) are the interactions between time dummies and region dummies capturing regional differences over time regarding the business cycle, inflation, and other changes affecting the outcome and inheritance receipt that differ between regions over time.

Second specification: FE Log Amount Inherited

While specification (17) provides useful estimates of the average impact of an inheritance, larger inheritances may represent larger increases in wealth and may affect the outcomes stronger. Our second approach is therefore to exploit information on the actual amount inherited by including the logarithm of the amount won, A_i,t, directly in the specification. Since the size of an inheritance may still be correlated with individual characteristics (compare columns 4 and 5 of Table 2), we include individual-specific fixed effects and time-varying control variables, which defines our second specification:

$$\text{ln}{C}_{i,t}={\mathrm{\alpha }}_i+\mathrm{\beta }\text{ln}{A}_{i,t}+\mathrm{\gamma }\prime X_{i,t-1}+({\mathrm{\tau }}_t\times {\mathrm{\theta }}_r)+{\mathrm{\epsilon }}_{i,t}.$$ (18)

An alternative approach is to employ inheritance receipt as an instrumental variable (IV) for wealth. Inheritances represent important shocks to household wealth. The effect of an inheritance on log household wealth is highly significant at the 1% level, and estimated to be 0.1600 (0.0172) using the FE Inheritance specification in (17), and 0.0165 (0.0016) using the FE Log Amount Inherited specification in (18). Hence, an inheritance on average increases annual household wealth by 16%, and a 10% increase in the inheritance amount increases wealth by around 0.2%. These coefficients can be used as the first stage of an IV estimation. Given the strong first-stage (the corresponding F-statistics are 86.65 and 107.24, respectively), IV results are qualitatively the same in terms of sign and significance as the reduced form coefficients presented in Section 4.1, so employing IV would not change any of our conclusions. One would simply divide the reduced-form coefficients presented in Table 4 by 0.1600 in the FE Inheritance specification and by 0.0165 in the FE Log Amount Inherited specification to obtain IV estimates. However, the impact of inheritances on wealth does not provide a viable first stage. Since part of the inheritance will be spent on consumption, it will not be included in reported wealth in the survey. This would lead to underestimating the effect of inheritance receipt on wealth, and hence overestimating any impact of wealth on the consumption outcomes. For this reason we do not present IV estimates.

Table 4.

Estimates of the effect of inheritance receipt – HRS

Outcome	FE Inheritance	FE Log Amount Inherited
Full sample (panel 1)
Log Food Expenditures	0.0487*	0.0051**
N = 77,720	(0.0256)	(0.0025)
Smoking	0.0095***	0.0009***
N = 118,604	(0.0029)	(0.0003)
– Among Smokers	0.0232	0.0021
N = 18,693	(0.0157)	(0.0015)
– Among Non-Smokers	0.0021	0.0002
N = 99,600	(0.0016)	(0.0001)
Log Number of Cigarettes	0.1044*	0.0094*
N = 16,034	(0.0533)	(0.0051)
Drinking	0.0137***	0.0012**
N = 118,604	(0.0052)	(0.0005)
Log Number of Drinks	0.0107	0.0006
N = 54,126	(0.0148)	(0.0013)
Heavy Drinking	0.0054	0.0006
N = 54,126	(0.0058)	(0.0005)
Physical Activity	0.0016	− 0.0003
N = 57,633	(0.0191)	(0.0017)
Most Healthy and Most Wealthy (panel 2)
Log Food Expenditures	0.0105	0.0023
N = 20,554	(0.0385)	(0.0036)
Smoking	0.0105***	0.0009***
N = 31,278	(0.0038)	(0.0003)
– Among Smokers	0.0199	0.0016
N = 3,395	(0.0281)	(0.0026)
– Among Non-Smokers	0.0039*	0.0004**
N = 27,789	(0.0021)	(0.0002)
Log Number of Cigarettes	0.0498	0.0049
N = 2,901	(0.0890)	(0.0080)
Drinking	0.0179**	0.0014**
N = 31,278	(0.0075)	(0.0007)
Log Number of Drinks	0.0167	0.0006
N = 19,073	(0.0188)	(0.0017)
Heavy Drinking	0.0065	0.0005
N = 19,073	(0.0079)	(0.0007)
Physical Activity	− 0.0356	− 0.0035
N = 15,498	(0.0265)	(0.0024)
Most Healthy and Least Wealthy (panel 3)
Log Food Expenditures	0.0458	0.0042
N = 19,295	(0.0453)	(0.0043)
Smoking	0.0225***	0.0021***
N = 29,215	(0.0069)	(0.0006)
– Among Smokers	0.0689**	0.0061**
N = 5,152	(0.0304)	(0.0030)
– Among Non-Smokers	0.0012	0.0001
N = 24,004	(0.0034)	(0.0003)
Log Number of Cigarettes	0.2429**	0.0225**
N = 4,423	(0.1033)	(0.0101)
Drinking	0.0285***	0.0030***
N = 29,215	(0.0108)	(0.0010)
Log Number of Drinks	0.0272	0.0028
N = 13,587	(0.0311)	(0.0030)
Heavy Drinking	− 0.0045	− 0.0003
N = 13,587	(0.0118)	(0.0012)
Physical Activity	− 0.0361	− 0.0034
N = 14,319	(0.0390)	(0.0037)
Least Healthy and Most Wealthy (panel 4)
Log Food Expenditures	0.0979**	0.0096**
N = 20,475	(0.0471)	(0.0045)
Smoking	− 0.0015	− 0.0000
N = 31,058	(0.0055)	(0.0005)
– Among Smokers	0.0008	0.0008
N = 4,379	(0.0311)	(0.0030)
– Among Non-Smokers	0.0001	0.0001
N = 26,586	(0.0032)	(0.0003)
Log Number of Cigarettes	0.1246	0.0122
N = 3,737	(0.1066)	(0.0101)
Drinking	− 0.0001	− 0.0002
N = 31,058	(0.0102)	(0.0009)
Log Number of Drinks	− 0.0161	− 0.0014
N = 13,836	(0.0304)	(0.0027)
Heavy Drinking	0.0010	0.0003
N = 13,836	(0.0125)	(0.0011)
Physical Activity	0.1198***	0.0102***
N = 15,012	(0.0399)	(0.0036)
Least Healthy and Least Wealthy (panel 5)
Log Food Expenditures	0.1035	0.0096
N = 17,396	(0.0750)	(0.0073)
Smoking	0.0045	0.0002
N = 27,053	(0.0107)	(0.0011)
– Among Smokers	0.0072	0.0002
N = 5,767	(0.0387)	(0.0041)
– Among Non-Smokers	0.0021	0.0002
N = 21,221	(0.0065)	(0.0006)
Log Number of Cigarettes	0.0421	0.0020
N = 4,973	(0.1331)	(0.0135)
Drinking	− 0.0029	− 0.0003
N = 27,053	(0.0174)	(0.0016)
Log Number of Drinks	− 0.0149	− 0.0014
N = 7,630	(0.0647)	(0.0063)
Heavy Drinking	0.0464	0.0051*
N = 7,630	(0.0285)	(0.0027)
Physical Activity	− 0.0294	− 0.0045
N = 12,804	(0.0799)	(0.0076)

^*p-value < 0.1,

^**p-value < 0.05,

^***p-value < 0.01

Notes: Author’s calculations on basis of the 1992–2010 HRS. “FE Inheritance” refers to model (17), and “FE Log Amount Inherited” to model (18). Note that all models include the same set of control variables as in Table 8. “Most Healthy” are those in “Excellent” or “Very Good” self-reported health at first observation in the panel, and “Least Healthy” are those in “Good”, “Fair”, or “Poor” self-reported health at first observation. “Most Wealthy” and “Least Wealthy” include individuals that at first observation are, respectively, above and below the age-wave-specific median household wealth.

To gauge the severity of the anticipation effect, we followed Goodstein (2008) and experimented with controlling for the lagged subjective probability of receiving an inheritance, obtained from information in the HRS on expectations about inheritances available in waves 1994 to 2006.²⁴ The results were very similar to our baseline specifications (and are available upon request). Further, inheritance expectations are available only for the period 1994 to 2006, and are subject to large item non-response. Besides, anticipation of inheritances would only lead to underestimation of any wealth effect on consumption. For these reasons, we do not use expectation information in our baseline specifications.

Finally, since the receipt of an inheritance may be associated with a bereavement effect due to the loss of a beloved one that may independently affect health behavior, we control for whether Mother Died, Father Died, Mother in Law Died, or Father in Law Died since the last wave, and whether the individual got Widowed since the last wave (Brown et al. 2010).²⁵

3.3 BHPS Data and Descriptive Statistics

The BHPS is a multi-purpose panel survey among households in Great Britain covering all individuals aged 15 and above in the household. The panel runs since 1991, and in 1999 samples from Scotland and Wales were added. The BHPS provides information on a wide variety of demographic, socioeconomic and health outcomes for around 15,000 individuals each year. We use waves 7 to corresponding to the years 1997 to 2008, as relevant information on lottery winnings is not available before 1997. The total sample size is 165,488 person-year observations for 26,462 distinct individuals. The first column of the bottom panel of Table 1 presents averages for the dependent and independent variables defined below, and Table 9 in appendix C lists all BHPS variables and their unit of analysis employed in this work.

Dependent variables

Our first dependent variable is Food Expenditures,²⁶ “How much do you personally spend in an average month on eating out at, or buying takeaway food from, a restaurant, pub or cafe, including school meals or meals at work?”, which again is not interpreted as either healthy or unhealthy but serves to verify whether lottery winnings have any effect on consumption. Our measures of unhealthy consumption are Smoking, “Do you smoke cigarettes?”; Number of Cigarettes, “Approximately how many cigarettes a day do you usually smoke, including those you roll yourself?”; and Drinking Out, “How often do you go out for a drink at a pub or club?” in five categories.²⁷ Our measure for healthy consumption is Sports, “How often do you play sport/go walking/swimming?” in the same five categories as for drinking. The Drinking Out and Sports variables are only available every other year.²⁸ All monetary values are measured in natural logarithms,²⁹ and converted to year 2005 British pounds using the Consumer Price Index (CPI).

Independent variables

Accurate wealth information is only available in 2000 and 2005. We follow Banks et al. (2003) and compute Household Wealth by adding the net value of vehicles, savings accounts, investments, home and all other property, and subtracting the total of mortgages and other debts. Lottery Winnings are based on the answer to the question “Have you personally received any payments, or payment in kind, from a win on the football pools, national lottery or other form of gambling since previous year?”. If answered positively, the answer to the next question “About how much in total did you receive (was this worth)?” defines Amount Lottery Won in British pounds. Big Win is defined as amounts won of 500 British pounds or more.

Lottery winnings (see Table 1) are fairly common, ranging from 7 to 19% of the sample in each year. Over the course of the panel 7,113, or 27%, out of a total of 26,462 distinct individuals won the lottery at least once. The distribution of log lottery winnings is shown in the bottom panel of Figure 1. Most lottery winnings are small, and the average of the log amount corresponds to around 40 British pounds,³⁰ which is less than 1% of total household wealth. Between 3 and 8% of lottery winners in any year win a big amount of over 500 British pounds (indicated by the vertical line in Figure 1). The average of the log amount won for big wins corresponds to 1,500 British pounds, representing 2% of household wealth and 6% of annual household income.

Control variables:

the first lag of Household Income, Age and its square Age², Sex, the first lag of Region (19 regions), the first lag of Household Size, the first lag of the Number of Children, Level of Education, the first lag of Health Status (five categories), the first lag of Marital Status (seven categories), the first lag of Employment Status (ten categories), and interactions between time dummies and region dummies. These control variables are defined in Table 9 in appendix C. Table 3 provides descriptive statistics by lottery winning status, which shows that lottery winners are significantly different in many characteristics from non-winners, e.g. more often male, married and college educated.

Table 3.

Descriptive statistics of control variables by lottery winning status, BHPS

Variable	Non-winners	Winners	Small Win	Big Win
Log Household Wealth	10.44	10.78***	10.75	11.21
Log Household Income	10.03	10.13***	10.13	10.18
Age	45.90	45.48***	45.44	46.17
Sex	0.44	0.57***	0.56	0.61***
Region
Greater London (regions 1 and 2)	0.05	0.06***	0.06	0.06
South (regions 3 and 4)	0.17	0.24***	0.24	0.22
East (regions 5 and 6)	0.08	0.11***	0.11	0.09*
West (regions 7 and 8)	0.06	0.06***	0.06	0.07
North (regions 9 to 16)	0.16	0.21***	0.21	0.21
Wales (region 17)	0.16	0.11***	0.11	0.10
Scotland (region 18)	0.17	0.18	0.18	0.18
Northern-Ireland (region 19)	0.14	0.03***	0.03	0.07***
Household Size	2.86	2.77***	2.78	2.76
Number of Children	0.52	0.45***	0.45	0.54***
Level of Education
Post-secondary Education (levels 1 to 5)	0.44	0.48***	0.48	0.43***
Completed Secondary Education (levels 6 and 7)	0.26	0.27***	0.27	0.29
Less than Secondary Education (levels 8 to 13)	0.29	0.25***	0.25	0.28*
Health Status
Excellent	0.23	0.22***	0.22	0.25**
Good	0.46	0.49***	0.49	0.46
Fair	0.21	0.20***	0.20	0.19
Poor	0.08	0.07***	0.07	0.08
Very poor	0.02	0.02	0.02	0.02
Marital Status
Married, Civil partnership	0.53	0.57***	0.57	0.52***
Widowed	0.08	0.06***	0.05	0.07**
Never Married	0.29	0.28	0.28	0.28
Separated, Divorced, Dissolved civil partnership	0.10	0.09***	0.09	0.13***
Employment Status
Self-employed	0.07	0.07***	0.07	0.15***
Employed, Maternity leave	0.50	0.58***	0.58	0.55*
Disabled	0.05	0.04***	0.04	0.03
Unemployed, Government training schemes	0.04	0.02***	0.02	0.02
Retired	0.22	0.19***	0.19	0.19
Full-time student, Family care, Other	0.14	0.09***	0.09	0.06***
Number of observations	149,333	16,155	15,274	881

^*p-value < 0.1,

^**p-value < 0.05,

^***p-value < 0.01

Notes: Author’s calculations based on the 1997–2008 BHPS. Small Win refers to an amount won under 500 British pounds, and Big Win to an amount won above 500 British pounds. The asterisks denote whether the difference in means between non-winners (column 2) and winners (column 3) and between small winners (column 4) and big winners (column 5) are statistically significant. For ease of exposition, the 19 regions are subdivided into eight sub regions, the 13 educational categories into three, marital status into four and employment status into six categories (see Table 9 for definitions of the 19 regions, 13 education levels, 7 marital status and 10 employment status categories).

3.4 BHPS Methodology

Even though winning the lottery likely represents an unanticipated shock to wealth (Imbens et al. 2001; Gardner and Oswald 2007; Apouey and Clark 2014), it is not randomly distributed across the population – not everyone plays the lottery, and lottery winners differ in various characteristics from non-winners (see Table 3). Moreover, the group of non-winners includes individuals that did not play the lottery, and individuals that did play but did not win. These too may be very different groups. A limitation of the BHPS is that we cannot distinguish between non-winners who played and nonplayers, and hence lottery winnings are endogenous. Once more we use two different strategies to overcome the endogeneity issue.

Third specification: FE Big Lottery Won

This approach is based on Imbens et al. (2001) and distinguishes between “small” and “big” lottery winnings. With many small lottery winnings, this offers two advantages over a specification that only includes a binary indicator for having won the lottery or not. First, below a certain threshold, lottery winnings are unlikely to influence behavior and including them will attenuate the coefficient estimates. Given an average amount won of 32 British pounds, a large fraction of lottery winners is not expected to change behavior. Second, since individuals who win small amounts plausibly share characteristics with individuals who win big amounts, they can act as a natural control group for the big winners. Under the assumption that, conditional on winning the lottery, the amount won is unrelated to personal characteristics, big lottery winnings represent the effect of a wealth shock. The drawback of this approach is that one needs to determine a threshold above which lottery winnings are considered big, which is essentially arbitrary.

In order to make this process least arbitrary we tested the assumption for different threshold levels. On the basis of these analyses,³¹ a threshold of 500 British pounds was deemed most appropriate. Using this threshold, statistically significant differences between small and big winners are fewest. Table 3 presents the differences in the covariates’ means across small and big lottery winners (results are very similar for the 250 and 1,000 British pounds thresholds). Although differences in average characteristics between small and big winners are smaller than between non-winners and lottery winners, important differences remain, e.g., males are overrepresented in the “Big Win” group, and this group is less educated, less often married, and more often self-employed. Plausibly this residual heterogeneity stems from the fact that we do not observe the number of lottery tickets bought, which could be related to individual characteristics such as sex, income, and unobserved characteristics. To account for this residual heterogeneity within the group of lottery winners, we add an individual-specific fixed effect. The corresponding equation, our third specification to be estimated, can be summarized as

$$\text{ln}{C}_{i,t}={\mathrm{\alpha }}_i+{\mathrm{\beta }}_1{I}_{i,t}+{\mathrm{\beta }}_{2}I[A_{i,t}>c]+\mathrm{\gamma }\prime X_{i,t-1}+({\mathrm{\tau }}_t\times {\mathrm{\theta }}_r)+{\mathrm{\epsilon }}_{i,t},$$ (19)

where I_i,t is a binary indicator of whether one won the lottery or not, A_i,t denotes the amount won, c represents the threshold for big lottery winnings, here taken as 500 British pounds, I [·] is the indicator function (1 when true, 0 if false), and (τ_t × θ_r) are the interactions between time dummies and region dummies capturing regional differences in monetary prices, excise taxes, and other changes affecting the outcome and lottery play that differ between regions over time. β₂ measures the effect of a wealth shock (big lottery win) on the relevant outcome.

Our Fourth specification

FE Log Amount Lottery Won consists of replacing the amount received through an inheritance by the amount won in the lottery in equation (18) (Section 3.2). The approach is again based on the assumption that conditional on winning the lottery, whether you win a big or small amount is random. An advantage of this approach is that it does not require setting an arbitrary threshold.

In the BHPS it is not possible to estimate the first stage effect of lottery winnings on wealth, since wealth is only available in 2000 and 2005. The large number of years between the two waves and the fact that only 18% of the individuals in our sample report wealth in both 2000 and 2005 prevents us from estimating the FE Big Lottery Won and FE Log Amount Lottery Won specifications for wealth.³² This prevents us from using an Instrumental Variable approach. However, as we discussed before (see Section 3.2) IV approaches would lead to similar results but overestimate effects sizes. The effect of lottery winnings on food expenditures (for which we have data for all years of the panel) is 0.0959 (0.0388) in the FE Big Lottery Won specification and 0.0069 (0.0030) in the FE Log Amount Lottery Won specification, both of which are statistically significant at the 5% level (see Table 4). This suggests large lottery winnings provide exogenous and important variation in wealth and builds confidence in our FE Big Lottery Won and FE Log Amount Lottery Won specifications.

4 Results

In Section 4.1 we present the results for the HRS and in Section 4.2 we present results for the BHPS.

4.1 The effect of inheritances

We first estimate the two specifications (17) and (18) for the full HRS sample to verify theoretical prediction 1 of Section 2.3 using inheritances. Then we estimate the two specifications for subgroups defined by wealth and health to verify theoretical prediction 2 of Section 2.3. We estimate the impact of inheritance receipt on smoking separately for those who smoked in the previous wave and those who did not smoke, as the decision to quit or initiate smoking is very different (e.g., Gilman et al. 2003). For cigarette consumption, we restrict to those that smoked in the last wave, and we restrict to those that drank in the previous wave, to estimate the effect on the number of drinks and the indicator for heavy drinking. In all models we use robust standard errors clustered at the household level, as the sample includes both respondents and their spouses.

Full sample

Panel 1 of Table 4 presents the reduced-form coefficients of estimating models FE Inheritance (17) and FE Log Amount Inherited (18). The first line presents evidence that the receipt of an inheritance increases food expenditures. Individuals spend on average about 100 US dollars on food per week (exp(4.64); see Table 1), and the receipt of an inheritance increases this by 4.9% (see under FE Inheritance in Panel 1 of Table 4), suggesting that receipt of an inheritance of 40,000 US dollars on average increases food expenditures per week by around 5 US dollars (or about 260 US dollars per year).³³

A sudden wealth increase in the form of an inheritance receipt increases the prevalence of smoking by around one percentage point (see under FE Inheritance in Panel 1 of Table 4), or 6.0% (see Table 1). Although not statistically significant, the point estimates are larger for those who previously smoked, suggesting that what drives the effect on smoking prevalence is smokers not quitting rather than non-smokers initiating.^34,35 On the intensive margin, smokers increase the number of cigarettes they smoke per day by around 10% on average. A sample average of 8.8 (exp(2.18)) cigarettes per day among smokers suggests that inheritance recipients receiving an amount of 40,000 US dollars, or 12% of household wealth, on average, smoke about 0.9 cigarettes more per day.

The prevalence of drinking also increases following the receipt of an inheritance by 1.37 percentage points, or 2.76%. There is no evidence of a change in the number of drinks consumed per week or in the prevalence of heavy drinking. Physical activity is also not affected by the receipt of an inheritance.

Subgroup analyses

We analyze the responses in four subgroups: (a) most healthy most wealthy, (b) most healthy least wealthy, (c) least healthy most wealthy and (d) least healthy least wealthy.

According to our theory, responses to a change in wealth are a function of wealth W and health H (see equation 16). We stratify the sample by initial wealth and initial self-reported health, and define four groups of roughly similar size. We use wealth and self-reported health at first observation since these measures are not contaminated by possible inheritance receipt during our observation period. We first divide the sample on the basis of initial self-reported health, where “Excellent” and “Very Good” health form the “Most Healthy” group, and “Good”, “Fair” or “Poor” health form the “Least Healthy” group. Then within those groups we stratify by wealth, where the “Most Wealthy” group is defined as individuals whose wealth at first observation is greater than the age-wave-specific median wealth.³⁶ The remainder constitutes the “Least Wealthy” group. The bottom half of Table 1 shows that for all subgroups an inheritance represents a substantial wealth shock. For the most healthy most wealthy, an inheritance represents 8% of household wealth on average, and this increases to 40% for the least healthy least wealthy.

Panels two to five of Table 4 show the effect of inheritance receipt among the four subgroups. The most striking observation is that virtually all results seem to be driven by the healthier part of the population (panels 2 and 3). The fact that virtually no response is seen among the least healthy shows that, despite the larger relative size of the wealth shock among the least healthy, the most healthy respond more to a change in wealth, in line with our theoretical prediction. This suggests that the direct wealth effect alone cannot explain the observed behavioral responses, and suggests that health costs may be important and larger for unhealthy individuals.

Within the healthy group of individuals, the prevalence of smoking and drinking increases upon receipt of an inheritance, with larger effect sizes for the least wealthy compared to the most wealthy: the most healthy most wealthy increase smoking by around 1.1 percentage point (or 10%) and drinking by 1.8 percentage points (or 2.7%), while the most healthy least wealthy increase their prevalence of smoking by 2.3 percentage points (or 13%) and drinking by 2.9 percentage points (or 5.6%).

Interestingly, for the most healthy and least wealthy a positive effect is found in the number of cigarettes consumed but not for other subgroups. This finding is in line with the theoretical prediction (cf. prediction 2 in Section 2.3) that the response to a wealth shock is stronger for individuals with low health costs, i.e. for the least wealthy most healthy. Given the average number of cigarettes smoked per day in this group is 8.9 (exp(2.19)), the point estimate suggests an increase of 24.3%, or around 2.2 cigarettes per day.

The results for exercise, our measure of healthy consumption, are in line with the theory. Among the least healthy and most wealthy (panel 4) we find a large and significant positive response, whereas for the most healthy least wealthy we do not find a significant effect (panel 3). This is as expected, given that health benefits are highest for the least healthy most wealthy and lowest for the most healthy least wealthy. Since health benefits reduce the effective price, the prediction from the theory is that the least healthy most wealthy would respond the most to healthy consumption and the most healthy least wealthy would respond the least to healthy consumption.³⁷ The data is consistent with this pattern.

4.2 The effect of lottery winnings

We estimate the two fixed effects specifications (19) and (18) for the full BHPS sample to verify theoretical prediction 1 of Section 2.3, and estimate the same regressions for subgroups defined by an imputed wealth measure and health status to verify theoretical prediction 2 of Section 2.3.

We estimate the impact of lottery winnings on smoking separately for those who smoked in the previous wave and for those who did not. For the number of cigarettes consumed, we restrict the analyses to those who smoked in the last wave. In all models we use robust standard errors clustered at the individual level.

Full sample

Table 5 presents the results of estimating the models FE Big Lottery Win (19) and FE Log Amount Won (18). Panel 1 of Table 5 shows a positive effect of lottery winnings on food expenditures. The size of the coefficient in the FE Big Lottery Won specification is 0.096, and statistically significant, suggesting that food expenditures increase by around 10% following a big lottery win. The baseline amount spent on food is around 25 British pounds (exp(3.20); see Table 1), suggesting that individuals spend 2.5 British pounds more per month on food after a win of 1,500 British pounds, on average.

Table 5.

Estimates of the effect of lottery winnings – BHPS

Outcome	FE Big Lottery Won	FE Log Amount Lottery Won
Full sample (panel 1)
Log Food Expenditures	0.0959**	0.0069**
N = 134,829	(0.0388)	(0.0030)
Smoking	− 0.0047	0.0002
N = 134,829	(0.0091)	(0.0006)
– Among Smokers	0.0115	− 0.0005
N = 34,678	(0.0237)	(0.0015)
– Among Non-Smokers	− 0.0014	− 0.0003
N = 100,151	(0.0053)	(0.0004)
Log Number of Cigarettes	0.0480	− 0.0014
N = 34,678	(0.0601)	(0.0042)
Drinking Out	0.1076*	0.0145***
N = 74,142	(0.0566)	(0.0036)
Sports	− 0.0424	0.0114**
N = 61,848	(0.0842)	(0.0054)
Most Healthy and Most Wealthy (panel 2)
Log Food Expenditures	0.0089	0.0057
N = 49,252	(0.0478)	(0.0041)
Smoking	− 0.0002	0.0004
N = 49,252	(0.0106)	(0.0008)
– Among Smokers	0.0272	0.0041
N = 7,838	(0.0393)	(0.0031)
– Among Non-Smokers	0.0025	− 0.0006
N = 41,414	(0.0036)	(0.0005)
Log Number of Cigarettes	0.0568	0.0077
N = 7,838	(0.1070)	(0.0089)
Drinking Out	0.1730*	0.0105**
N = 27,132	(0.0922)	(0.0053)
Sports	− 0.0748	− 0.0023
N = 22,303	(0.1264)	(0.0074)
Most Healthy and Least Wealthy (panel 3)
Log Food Expenditures	0.0529	0.0073
N = 44,414	(0.0748)	(0.0057)
Smoking	0.0087	0.0020*
N = 44,414	(0.0193)	(0.0012)
– Among Smokers	0.0711*	0.0006
N = 13,831	(0.0391)	(0.0026)
– Among Non-Smokers	− 0.0027	0.0001
N = 30,583	(0.0150)	(0.0007)
Log Number of Cigarettes	0.1451	− 0.0017
N = 13,831	(0.0970)	(0.0068)
Drinking Out	0.0821	0.0156**
N = 24,441	(0.0943)	(0.0066)
Sports	0.0147	0.0181*
N = 20,383	(0.1668)	(0.0110)
Least Healthy and Most Wealthy (panel 4)
Log Food Expenditures	0.1572	0.0137*
N = 18,996	(0.1343)	(0.0077)
Smoking	− 0.0494*	− 0.0026
N = 18,996	(0.0298)	(0.0017)
– Among Smokers	− 0.1230*	− 0.0043
N = 4,563	(0.0736)	(0.0042)
– Among Non-Smokers	− 0.0130	− 0.0007
N = 14,433	(0.0135)	(0.0011)
Log Number of Cigarettes	− 0.2287	− 0.0034
N = 4,563	(0.1812)	(0.0113)
Drinking Out	0.0969	0.0160
N = 10,468	(0.1600)	(0.0100)
Sports	0.1319	0.0232
N = 8,842	(0.2169)	(0.0142)
Least Healthy and Least Wealthy (panel 5)
Log Food Expenditures	0.3200**	− 0.0006
N = 19,104	(0.1257)	(0.0105)
Smoking	− 0.0024	− 0.0012
N = 19,104	(0.0216)	(0.0017)
– Among Smokers	0.0197	− 0.0017
N = 7,819	(0.0450)	(0.0029)
– Among Non-Smokers	− 0.0202	− 0.0008
N = 11,285	(0.0129)	(0.0012)
Log Number of Cigarettes	0.1140	− 0.0039
N = 7,819	(0.1323)	(0.0090)
Drinking Out	0.1803	0.0312***
N = 10,509	(0.1657)	(0.0118)
Sports	− 0.3022	0.0229
N = 8,904	(0.2337)	(0.0181)

^*p-value < 0.1,

^**p-value < 0.05,

^***p-value < 0.01

Notes: “FE Big Lottery Won” refers to (19) and “FE Log Amount Lottery Won” to (18). All models include the control variables in Table 9. “Most Healthy” are those initially in “Excellent” or “Good” health, and “Least Healthy” are those initially in “Fair”, “Poor”, or “Very Poor” health. “Most Wealthy” and “Least Wealthy” include individuals that at first observation are, respectively, above and below the age-wave-specific median imputed household wealth.

The top panel of Table 5 shows no effect on either smoking and the number of cigarettes smoked. Using the FE Big Lottery Won specification, we can rule out with 95% confidence prevalence changes larger than 1.4 percentage points (or 5.2%), and prevalence changes in the number of cigarettes smoked larger than 16.8% (or more than 1.8 cigarettes; see also Table 1).

We find strong and robust evidence that lottery winnings increase the frequency of drinking out in a pub or club. The effect is statistically significant in both models estimated. To get an idea of the size of this effect, we used the probability of drinking out at least once a month as the dependent variable in our specifications (not shown). In our FE Big Lottery Won specification the coefficient is 0.0466 and is statistically significant at the 5% level. Hence, upon winning an amount of 1,500 British Pounds in the lottery, the probability of drinking out at least once a month increases by around five percentage points, or 10% given a baseline prevalence of around 50%. The frequency of engaging in sports shows a positive response to lottery winnings in the FE Log Amount Lottery Won model only.

Subgroup analyses

As for the HRS, we analyze the responses in four subgroups: (a) most healthy most wealthy, (b) most healthy least wealthy, (c) least healthy most wealthy and (d) least healthy least wealthy. First, we split the sample according to whether one’s initial health (at panel entrance) is “Excellent” or “Good” on the one hand, or “Fair”, “Poor” or “Very Poor” on the other. Then, within those subsamples we stratify according to whether the initial imputed wealth (at panel entrance) is above or below the age-wave-specific median imputed wealth.³⁸ Unfortunately, house-hold wealth is only available in two waves and even then it is often missing, hence we use an imputed measure of household wealth to divide the sample into wealth subgroups. We obtain Imputed House-hold Wealth as follows. In the years 2000 and 2005, where we observe actual household wealth, we regress it on the set of control variables, particularly household income, health, age, age-squared, and the level of education. We use this model to predict household wealth for all individuals and years.³⁹

The top half of Table 1 shows that a “Big Win” of over 500 British pounds represents 5% and 28% of household wealth, for the most healthy least wealthy and the least healthy most wealthy, respectively. For wealthier individuals the wealth shock is around 1% of household wealth.

Panels two to five of Table 5 show how the different groups respond to exogenous variation in wealth in the form of lottery wins. The results suggest that larger lottery winnings increase food expenditures in all groups, as point estimates are all positive (with one exception) but not always statistically significant. Consistent with the results for the full sample, for none of the wealth-health subgroups we observe an effect on smoking or on the number of cigarettes consumed. The point estimates for drinking out are positive in all subgroups, although they are not always statistically significant.

4.3 Robustness Checks

Our main specification includes individual-specific fixed effects and time-varying control variables. The fixed effects purge the wealth effects from time-invariant unobserved factors, while the lags of time-varying control variables such as age, household income, self-reported health, and employment proxy for time-varying factors influencing both wealth shocks and health behavior. In order to gauge the relative importance of the fixed effects and the time-varying control variables, Tables 10 to 13 in the Appendix present the results of both OLS and fixed effects models, gradually including additional control variables. Tables 10 and 11 present variations of the “FE Inheritance” and “FE Log Amount Inherited” specifications for the HRS, and Tables 12 and 13 show variations of the “FE Big Lottery Won” and “FE Log Amount Won” specifications for the BHPS. In all tables, we present 6 specifications: (OLS 1) OLS without any controls, (FE 1) FE without any controls, (OLS 2) OLS with controls but excluding potentially endogenous controls such as employment, marriage, etc., (FE 2) FE with controls but excluding endogenous controls, (OLS 3) OLS including full controls, and (FE 3) FE including full controls. Column (FE 3) presents the final results that are used in the paper.

We find that (i) including individual fixed effects strongly affects the results, with substantial deviations from the OLS coefficients (compare OLS with FE columns), (ii) adding (time-varying) control variables leads to some decrease in the OLS coefficients (compare OLS 1 with OLS 2 and with OLS 3), but does not change fixed effects coefficients (compare FE 1 with FE 2 and with FE 3), and (iii) excluding potentially endogenous controls does not change the OLS or fixed effect results (compare OLS 2 with OLS 3, and FE 2 with FE 3). This suggests that the inclusion of individual fixed effects is essential to overcoming omitted variables bias, and that our fixed-effect results are not sensitive to the inclusion of (potentially endogenous) time-varying controls, limiting the scope for proxy variables bias. For these reasons, the paper focuses on our preferred specification FE 3.

While the limited influence of excluding the time-varying control variables is encouraging, an additional way of gauging bias from potential time-varying omitted variables is presented in Tables 14 and 15 in the Appendix. Here, we investigated whether the lags of time-varying factors included in our analyses were correlated with receiving an inheritance (Table 14) or with winning the lottery (Table 15). Virtually all factors, including among others childbirth, household size, region, and employment status were insignificant. For inheritance receipt, apart from age, only family income, self-reported health being “good”, and being separated/divorced are related to inheritance receipt. For lottery winnings, apart from age-squared, none of the variables are statistically significant. Taken together, these results build confidence that the wealth shocks induced by inheritances and lottery winnings can be considered exogenous, conditional on including individual fixed effects and our set of time-varying control variables, although we cannot rule out that we have omitted some specific unobserved time-varying factors.

Apart from the inclusion of subjective probabilities of inheritance receipt discussed in section 3.2, a further check for the potential effect of anticipation of inheritances on our results is to include the lead of inheritance receipt in our preferred specification (FE 3). If the lead of inheritance receipt (i.e. inheritances received in the next wave) were to affect the relevant outcomes in the current period, this would be a sign of anticipation. Only for smoking the lead of inheritance receipt has a positive and statistically significant coefficient. For heavy drinking the coefficient is negative, somewhat surprisingly, and in all other cases the lead is statistically insignificant. Reassuringly, in all cases the inclusion of the lead of inheritance receipt does not affect our estimates. For lottery winnings it is less likely that there is anticipation, and indeed we find no evidence of anticipation when including the lead of lottery winnings in our specifications. None of the leads are significant, and the coefficients of current period lottery winnings are not affected by the inclusion of future lottery winnings (this result as well as results for the remainder of the robustness checks are available upon request).

We also experimented with using lottery winnings and inheritances one period lagged to allow for some time delay in the response. This exercise produced similar results for lottery winnings in the BHPS, while the point estimates using inheritances in the HRS were much smaller and mostly insignificant. This suggests that the largest effect of inheritances in the elderly HRS population is immediate, and that most of the windfall gains are spend quickly. This interpretation is corroborated by the fact that two waves after the receipt of an inheritance the wealth of inheritance recipients is barely higher than for non-inheritance recipients. Further, there are no significant differences in food expenditures between recipients and non-recipients one wave after receipt of an inheritance.

We employed specifications comparing “Big Inheritances” with “Small Inheritances” in the HRS, as for example in Kim and Ruhm (2012). We chose not to use these specifications for two reasons. First, very few inheritance amounts can plausibly be considered small (see Figure 1): less than one percent of the inheritance recipients receives an inheritance below 500 US dollar, and the tenth percentile is already above 5,000 US dollars. Hence, the assumption of no effect on small recipients is unlikely to be valid given the high threshold required to generate a sufficiently large control group of small recipients. A second reason is that while distinguishing between small and big inheritances, point estimates and their statistical significance were very sensitive to the chosen cut-off. For example, we followed Kim and Ruhm (2012) and defined “Big Inheritance” as amounts received greater than 10,000 US dollars, but found that results varied substantially when using other arbitrary thresholds such as 1,000, 5,000 or 15,000 US dollars. Additionally, using the specification with a threshold at 10,000 US dollars we find no evidence of an increase in food expenditures for big inheritance recipients. This is likely because the working hypothesis that inheritances below 10,000 US dollars are small enough not to impact behavior is invalid, and this would lead to underestimation of effect sizes.

We exploited state-level variation in house prices as an instrument for individual wealth gains, but could not reject a positive effect of housing wealth on the aggregate consumption of renters, casting doubts about the exogeneity of house price increases (see also Browning et al. 2013). We also experimented with variations in stock market wealth, relying on changes in the Standard & Poors Index as in Schwandt (2011). However, our analyses could not establish an effect of increases in stock market wealth on aggregate consumption, casting doubt on its usefulness as an instrument for variation in wealth.

Relative rather than absolute changes in wealth may matter in consumption decisions. We experimented with replacing the logarithm of the amount won or inheritance received A_i,t by the logarithm of the ratio of the amount won or received over total current household income (BHPS) or total current household wealth (HRS). Results were very similar.

We used a static selection procedure to define subgroups by initial health and initial wealth. This has the advantage that the individuals selected into one of the four subgroups remain in that subgroup over the course of the panel study. Alternatively, one might consider a dynamic selection procedure in which one stratifies individuals dynamically on the basis of the previous’ wave wealth and health. This has the advantage that the information is more up-to-date, but we no longer follow the same subgroup of individuals. We also used this dynamic selection procedure and found that differences were minimal.

We replaced our imputed wealth measure by education for the purpose of defining subgroups of lifetime full wealth, distinguishing in the BHPS between three education levels on the basis of the OECD International Classification (ISCED – OECD 1996). For the HRS we also distinguished between three educational levels on the basis of years of education. Results were very similar.

We investigated differential responses by gender and age, and while the effects on females and older individuals are typically slightly larger than for males and younger individuals, we could not reject the null hypothesis that effects are similar across genders and age.

Apart from physical activity, the HRS also includes preventive care measures (every other wave respondents are asked whether they had a blood test for cholesterol, a flu shot, monthly self-checks for breast lumps, a mammogram, a pap smear, and a check for prostate cancer), and out-of-pocket (OOP) medical expenditures. We do not present results for the preventive care measures in our main analysis since preventive care is not an accurate measure of healthy consumption. Unlike healthy consumption, preventive care does not have an instantaneous effect on health deterioration (it is associated with better future health or future reduced health deterioration) and hence does not provide an instantaneous health benefit. Second, it is hard to imagine that engaging in preventive care provides direct utility, such that a direct wealth effect may be absent. Nonetheless, we estimated the effect of inheritance receipt for preventive care measures and find that none of these measures respond to inheritance receipt (only among the least healthy and most healthy we observe a decrease in the use of a mammogram and a reduction in checks for prostate cancer, marginally statistically significant at the 10% level in both specifications). As for preventive care, OOP medical expenditures are not easily interpretable as a measure of healthy consumption as OOP has both preventive and curative aspects, and is a strong function of health shocks, of health insurance status and of the generosity of health insurance. No effect on OOP was found (except for a positive coefficient that is marginally significant at the 10% level in the FE Log Amount Inherited specification only).

While the models (17), (18), and (19) are specified in linear form, we also estimated logit models for the binary indicators, and negative-binomial count models for the variables concerning the number of cigarettes and the number of drinks. The results were very similar.

As in most panels, there is considerable attrition in the BHPS and the HRS: 30 and 36% of the sample, respectively, is lost by the final wave. We repeated the analyses using inverse probability weights to correct for sample attrition due to observables (Jones et al. 2006), and find very similar point estimates. Hence attrition bias is not likely to alter any of our main conclusions.⁴⁰

5 Discussion

This paper presents a theory of health behavior, in which the marginal cost of unhealthy consumption consists not only of the direct monetary outlays, as in standard life cycle models, but also of a health cost (value of health lost). As a result, wealth has two competing effects: (i) a direct wealth effect increasing demand for unhealthy consumption, and (ii) an indirect health cost effect decreasing the demand for unhealthy consumption goods. Which of the two effects dominates is theoretically ambiguous, but, according to our theory, the indirect health cost effect is larger for more wealthy individuals, less healthy individuals, and for a higher degree of unhealthiness of the good.

A first prediction (prediction 1) of the theory is therefore that a wealth shock leads to increased demand for healthy and moderately unhealthy consumption goods, but decreased demand for severely unhealthy goods. This may provide an economic rationale for why wealthier individuals are more likely to drink moderately, but less likely to smoke and drink heavily (see Table 1, and Cawley and Ruhm, 2012). A second prediction (prediction 2) is that the strength of the response to an unexpected wealth shock is smallest for the wealthy, least healthy, and for a high degree of unhealthiness of the consumption good.

We employ inheritances and lottery winnings as plausible exogenous and unanticipated variation in wealth to test the theory’s predictions. Tables 6 and 7 provide a high-level overview of the key findings (distilled from Tables 4 and 5). A + indicates a positive response and a − indicates a negative response.⁴¹ We find strong and robust evidence that wealth shocks increase the prevalence of drinking alcohol, but the number of drinks and heavy drinking are not affected (Table 6). This suggests that it is mostly modest, occasional drinking that increases following a wealth shock. Apparently, for moderate drinking the direct wealth effect dominates the indirect health cost effect, which is in line with what the theory predicts (cf. hypothesis 1). Heavy drinking is plausibly more detrimental to health than drinking moderately and the absence of an effect on heavy drinking would be consistent with the theoretical prediction that in such cases the health cost effect dampens the direct wealth effect.

Table 6.

Summary of full sample effects

Outcome	HRS	BHPS
Smoking	+
# Cigarettes	+
Drinking	+	+
# Drinks		N/A
Heavy Drinking		N/A
Exercise		+

Notes: Summary for the full sample, obtained from panel 1 of Table 4 and 5. A + indicates a positive response and a − a negative response. Effects are included if at least one effect size is recorded at a p-value < 0.05 or in two specifications at a p-value of < 0.1.

Table 7.

Summary of wealth by health subgroup effects

		Most Wealthy		Least Wealthy
	Outcome	HRS	BHPS	HRS	BHPS
Most Healthy	Smoking	+		+
	# Cigarettes			+
	Drinking	+	+	+	+
	# Drinks		N/A		N/A
	Heavy Drinking		N/A		N/A
	Exercise
Least Healthy	Smoking
	# Cigs.
	Drinking				+
	# Drinks		N/A		N/A
	Heavy Drinking		N/A		N/A
	Exercise	+

Notes: Results for wealth by health subgroups of the HRS and BHPS panels, obtained from panels 2 to 5 of Table 4 and 5. Rest as in Table 6.

While inheritance receipt in the HRS does increase the prevalence of smoking and the number of cigarettes smoked, a lottery win in the BHPS does not. These results are however not necessarily inconsistent with one another as the absence of an effect in the BHPS does not rule out the effect sizes estimated in the HRS.⁴² In light of the theory, our findings suggest that the direct wealth effect still outweighs the indirect health cost effect for smoking. The moderate increases in smoking are consistent with the notion that smoking is more unhealthy than drinking but not sufficiently unhealthy that individuals reduce smoking in response to a wealth shock.

Comparing our empirical results to the literature, we confirm the finding of Kim and Ruhm (2012) of a limited effect of receiving an inheritance on physical activity,⁴³ the finding of Ettner (1996) and Apouey and Clark (2014) that alcohol consumption increases with income, and the finding of Kenkel et al. (2011) that smoking and income are positively related in the US. Our findings challenge some other conclusions of Kim and Ruhm (2012): they reported an effect of a big inheritance receipt on both the prevalence and intensity of drinking, but not on smoking or on the number of cigarettes smoked. Given the differences in characteristics across small and big inheritance recipients, the estimates of Kim and Ruhm (2012) may be biased by unobserved heterogeneity. Indeed we find marked differences across models that do (as in our work) and that do not (as in Kim and Ruhm, 2012) include individual fixed effects (see Tables 10 to 13 in the Appendix).

In contrast to the empirical literature, and motivated by our theory, we focus on an investigation of differences in the effect of wealth on health behavior between wealth and health groups. We find evidence for essential heterogeneity in responses to wealth shocks, something the empirical literature has not explored thus far. Table 7 summarizes the results. The most striking pattern is that the least healthy (bottom left and right quadrant) do not appear to change behavior in response to positive wealth shocks, with the exception of the most wealthy least healthy engaging more in exercise and the least wealthy least healthy more in social drinking. The result that the least healthy do not change their behavior is in line with our prediction that the least healthy have greater health costs, which dampens the behavioral response to a wealth shock.

We also confirm the theoretical prediction that the most wealthy, least healthy (high health cost) do not change their unhealthy behaviors while the least wealthy most healthy (low health cost) increase their unhealthy behaviors, in response to a positive wealth shock. The most healthy least wealthy respond stronger: the effect on smoking and drinking is generally larger, and the effect on cigarette consumption is only apparent among the most healthy least wealthy (compare panel 2 with panel 3 in Tables 4 and 5).

The results for exercise, our only measure of healthy consumption, show a large and significant positive response among the least healthy most wealthy (high health benefit), whereas for the most healthy least wealthy (low health benefit) we do not find a significant effect. Because the predicted pattern for healthy consumption is the opposite of unhealthy consumption (see discussion in Section 4.1), this is in line with the theory.

Our empirical findings support the notion that the response to a wealth shock decreases in wealth, increases in health, and decreases in the unhealthiness of the good, and provide support for our theoretical concept of a health cost. These empirical findings cannot be explained by conventional lifecycle models. Even though such models would also predict smaller wealth effects among wealthier individuals, these models do not systematically predict smaller responses for less healthy individuals and for more unhealthy consumption goods. Moreover, in a behavioral economic setting with hyperbolic discounting (e.g., O’Donoghue and Rabin, 1999) one might expect a “naive” individual to under save and over indulge, they would be poor and unhealthy and presumably respond strongly to a positive wealth shock, whereas a “sophisticate” would be wealthy and healthy and respond moderately, to a positive wealth shock. This would predict a stronger response to wealth for unhealthy individuals, the opposite of our prediction and of our empirical finding.

Our findings have implications for the literature on health behaviors, health disparities, and the value of a statistical life (VSL), as discussed in the introduction. Regarding the literature on health behaviors, we find there may be adverse population health effects in terms of increased unhealthy behavior of wealth redistribution for healthy, but less so for unhealthy, disadvantaged segments of society. Regarding the literature on health disparities, our results suggest that analyses of the health benefits and health costs of health behaviors are important to understanding the formation and evolution of health disparities. Last, the VSL and our concept of a health cost are closely related and insight in the VSL might be gained from studies such as ours employing risky health behaviors.

While our results suggest that health costs play a role in explaining health behaviors, our empirical estimates also suggest health costs cannot fully explain why wealthy individuals engage less in severely unhealthy behaviors such as smoking and heavy drinking (Table 1). Health costs do operate in the right direction: the effect of a positive wealth shock on smoking and heavy drinking is smaller than for other, plausibly less unhealthy, goods, and the response is strongest for the least wealthy most healthy. Yet, the estimated wealth effects for smoking and heavy drinking are generally non-negative, and in the case of smoking even positive. Thus in order to explain the negative association between wealth and severely unhealthy behavior, there must be, in addition to a causal effect of wealth, a strong negative selection effect, in which factors such as education, cognitive abilities and discount rates correlate positively with wealth, and negatively with severely unhealthy behaviors.

Our theory is classical in the sense that it approximates human behavior by assuming individuals are rational and forward looking. In addition we have not modeled uncertainty such as health shocks. As a result, our theory predicts that individuals smooth consumption, following the wealth shocks they receive. Yet, empirically we found evidence that most of the wealth is spent within a few years following a wealth shock. This suggests that the observed responses are only representative of short-term effects of wealth shocks, more in line with a model in which individuals are credit constrained, or a behavioral model in which individuals spend most of their windfall immediately. Future theoretical work would benefit from modeling the role of credit constraints, and/or myopic behavior by, e.g., introducing hyperbolic discounting, in addition to our novel concept of a health cost. A more comprehensive theory may also wish to incorporate the extent to which a good is addictive (e.g., Becker and Murphy 1988).