Advantages and Challenges of Relaxor-PbTiO₃ Ferroelectric Crystals for Electroacoustic Transducers- A Review

Abstract

Relaxor-PbTiO₃ (PT) based ferroelectric crystals with the perovskite structure have been investigated over the last few decades due to their ultrahigh piezoelectric coefficients (d₃₃ > 1500 pC/N) and electromechanical coupling factors (k₃₃ > 90%), far outperforming state-of-the-art ferroelectric polycrystalline Pb(Zr,Ti)O₃ ceramics, and are at the forefront of advanced electroacoustic applications. In this review, the performance merits of relaxor-PT crystals in various electroacoustic devices are presented from a piezoelectric material viewpoint. Opportunities come from not only the ultrahigh properties, specifically coupling and piezoelectric coefficients, but through novel vibration modes and crystallographic/domain engineering. Figure of merits (FOMs) of crystals with various compositions and phases were established for various applications, including medical ultrasonic transducers, underwater transducers, acoustic sensors and tweezers. For each device application, recent developments in relaxor-PT ferroelectric crystals were surveyed and compared with state-of-the-art polycrystalline piezoelectrics, with an emphasis on their strong anisotropic features and crystallographic uniqueness, including engineered domain - property relationships. This review starts with an introduction on electroacoustic transducers and the history of piezoelectric materials. The development of the high performance relaxor-PT single crystals, with a focus on their uniqueness in transducer applications, is then discussed. In the third part, various FOMs of piezoelectric materials for a wide range of ultrasound applications, including diagnostic ultrasound, therapeutic ultrasound, underwater acoustic and passive sensors, tactile sensors and acoustic tweezers, are evaluated to provide a thorough understanding of the materials’ behavior under operational conditions. Structure-property-performance relationships are then established. Finally, the impacts and challenges of relaxor-PT crystals are summarized to guide on-going and future research in the development of relaxor-PT crystals for the next generation electroacoustic transducers.

I. Introduction

1.1 General information on electroacoustic transducers

An electroacoustic transducer is a type of device that transforms an electrical signal into acoustic waves or converts an acoustic wave to an electrical signal, or, in many cases, operates in both directions. Electroacoustic transducers are versatile and include magnetostrictive, electrostatic and piezoelectric devices, among which piezoelectric transducers are the most commonly used in a diverse range of applications, such as industrial nondestructive evaluations, underwater acoustics, medical ultrasonics for diagnostics and therapy, ultrasonic cleaning, and material processing, to name a few [1–9]. The operational frequency range varies greatly depending on the applications. For example, common frequencies of 2 to 10 MHz are used in nondestructive testing and evaluation to locate flaws in materials, but lower frequencies can also be used to inspect low density materials. Medical diagnostic transducers generally operate in the frequency range of 2 to 18 MHz, though frequencies up to 50–100 MHz have been used for intravascular, ophthalmic, skin imaging and small animal imaging. The useful spectrum of underwater acoustic extends from sub-audible and audible frequencies allowing for great distances (one to several kilometers) to ultrasonic frequencies (up to > 1 MHz) where echo distances are shorter and increase accuracy of distance measurements is desirable [3,7]. Applications over this wide frequency range require numerous transducer designs. A number of geometries have been demonstrated, resulting in effective underwater acoustic transducers [10]. Each design offers a number of advantages and disadvantages associated with the geometry of the transducer. Common transducer designs include but are not limited to the following: flextensional “cymbal” transducers, where the piezoelectric active material is sandwiched between two mechanical end caps, and the primary axis of mechanical motion is perpendicular to the primary axis of acoustic radiation [10–13]; 1–3 (or 2-2) composite transducers, where a series of piezoelectric pillars (or sheets) are arranged with a predetermined lateral spacing and filled with a mechanically lossy polymer matrix, which operates in an effective longitudinal (or sliver) mode, thus offering greater bandwidth and improved acoustic impedance matching with water or tissue [10,14–20]; and tonpilz transducers (Langevin transducers), where stacked piezoelectric rings are connected with a head and a tail mass resulting in longitudinal operational mode [3,10,21–22]. These underwater acoustic devices are useful in ocean engineering in many ways. For example, the precise location of specific points or objects is often critical when drilling for oil and gas in the deep ocean or laying underwater cables or pipelines, while the combination of underwater and seismic acoustics is needed for finding deposits of oil or gas under the oceans [3].

The first attempt to use ultrasound transducer for medical diagnosis was based on a transmission technique by the Dussik brothers in 1937, working in Austria [8,9]. Research into medical applications of ultrasound is usually said to have started with the work of Wood and Loomis [23], who made a comprehensive study of both the physical and biological effects of ultrasound on biological media. An extensive literature list soon started to develop, particularly after 1954, when the first compound B-scan imaging system was reported. Ultrasonics has since found usage in numerous aspects of medical procedures, including diagnostic (low power), therapeutic (intermediate power), and surgical (high power in several forms, such as heat and mechanical) applications [2]. Ultrasonic wave propagation in body tissue is, in large measure, controlled by the acoustic impedance contrast at boundaries and various scattering mechanisms presented at the different scales within tissue, such as velocity and attenuation factors. These are the basic factors that determine the effectiveness of both diagnostic and therapeutic applications of ultrasound [2].

Recent decades have seen a second revolution in electroacoustic transducers, which benefit from modern electronics as well as with increasing digitization and computer-based data processing, imaging capability to deliver in-situ processing and advanced display/visualization capabilities [2]. These advances have been combined to facilitate new applications at both low and high powers using modern instrumentation and analysis capabilities, leading to major growth and diversification of electroacoustic applications, which in turn drive the developments of new transducer materials [2–4].

1.2 History of piezoelectric materials for transducers

Piezoelectric materials are the heart of piezoelectric transducers and sensors [24–34]. Fig. 1 gives a general milestone map for piezoelectric transducer material development as a function of their respective piezoelectric performance. The piezoelectric effect was first found in 1880 by Pierre and Jacques Curie [35]. They discovered that a stress applied to crystals, such as quartz, produced an electric charge on the surface (direct effect). Conversely, an electric field applied to the surfaces produced a change in the dimensions, and hence an alternating voltage applied to a crystal produced acoustic waves in the surrounding medium. Quartz piezoelectric crystal was used as a transducer material in 1917 by Langevin, who designed the first electroacoustic transducer by sandwiching quartz between steel plates [2,3]. Rochelle salt (sodium potassium tartrate tetrahydrate) crystal was first synthesized in 1655, but its ferroelectricity and subsequent piezoelectric were demonstrated later by Valasek in 1921 [36–38], showing a stronger piezoelectric effect than quartz, and also became available in the form of synthetic crystal to provide an alternate for the electroacoustic transducers [38]. However, Rochelle salt was found to be not stable against dehydration either in vacuum or in dry air. In addition, Rochelle salt is one of few ferroelectric crystals with limited ferroelectric range and two clear Curie points [38–39]. Motivation of exploring new man-made transduction materials lead to the discovery and development of potassium dihydrogen phosphate (KDP) [40] and ammonium dihydrogen phosphate (ADP) [41] crystals in 1935 and the early 1940’s, in which the structural arrangement of phosphate tetrahedral is linked by hydrogen bonding at the corners, showing relatively strong piezoelectric activity. It was generally accepted that ferroelectricity was highly correlated with the hydrogen bonds in the early Rochelle salt and KDP/ADP periods [6,38,42–43]. The ADP crystals were then established as extremely useful for high power acoustic transducers, replacing Rochelle salt [43]. Up to 1945, the principal ultrasonic transducer materials were natural quartz and ADP crystals [3].

Fig. 1.

General milestone map for piezoelectric transducer material development. KDP/ADP: KH₂PO₄/(NH₄)H₂PO₄; BT: BaTiO₃; LN: LiNbO₃; PZT: Pb(Zr,Ti)O₃; PN: PbNb₂O₆; PMN: Pb(Mg_1/3Nb_2/3)O₃; PMN-PT: Pb(Mg_1/3Nb_2/3)O₃-PbTiO₃.

In the early 1940’s, a breakthrough was achieved by the use of ferroelectrics that can be obtained in polycrystalline ceramic form. The first of these ferroelectrics, barium titanate (BaTiO₃), with the perovskite structure based upon corner linking of oxygen octahedra, was discovered independently by Von Hippel [44] and Goldman [45]. The first working piezoelectric ceramic transducer can be credited to Gray in 1945, who had the first clear understanding of the importance of electrical poling in establishing a remnant polar domain configuration in the ceramics and corresponding strong piezoelectric response [46]. By the early 1950s, ceramic piezoelectric transducers based on BaTiO₃ (BT) were well established in a number of both civil and military applications [38,47]. However, due to the concerns about the stability against depoling - accompanied by multi polymorphic phase transitions (PPTs) in pure BT - and the low field stability (low coercive field E_C) [38, 48–50], it was necessary to explore other ferroelectric perovskite compounds with enhanced performance [51–53]. Some of the very early basic work on pure PbTiO₃ and PbZrO₃-PbTiO₃ (PZT) solid solution systems led to the useful outline of its phase diagram [54–56]. The milestone studies, which established the PZT system as exceptionally suitable piezoelectric material formulations, were carried out by Jaffe et al., who discovered that the nearly temperature-independent morphotropic phase boundary (MPB) in PZT was of vital importance for transducer applications, due to the abnormally high piezoelectric and electromechanical properties near the MPB compositions [57–62]. The leading position of PZT compositions was due to their strong piezoelectric effect and relatively high Curie temperature. PZTs also allowed a wide variation in chemical modification to obtain a wide range of operating parameters without serious reduction of the piezoelectric effect, where the chemical dopants included isovalent substitutes of the lead cation by base earth elements and acceptor or donor dopants on the A or B sites [61–62]. Most effects of acceptor or donor doping were attributed to the type of lattice vacancies that arose, where oxygen vacancies induced by acceptor dopants inhibited domain wall motion, while lead vacancies induced by donor dopant made the domain wall motion easier, leading to different “hard” and “soft” characteristics, respectively [63–68]. A series of formulation-labeled PZT (PZT4, PZT5A, PZT5H, PZT8, etc.) have been established to emphasize various properties. Table I summarizes several commercially available PZT ceramics which have been extensively used for more than 60 years [69–71]. It can be seen that different compositions are outstanding with regard to different characteristics and thus beneficial to different applications. The high electromechanical coupling and piezoelectric coefficient of PZT5H have led to its use in medical imaging transducers, while PZT5A is a better choice for sensing applications due to its high piezoelectric voltage coefficient and higher Curie temperature. Meanwhile, the high resistivity of the donor doped PZTs at elevated temperatures allows usage to very low frequencies (the low limit frequency of the materials is inversely proportional to the time constant RC=ε₀Kρ, where ε₀ is the vacuum permittivity, K, the dielectric constant and ρ, the resistivity). On the contrary, the low mechanical and dielectric losses of PZT4 and PZT8 compositions benefits applications in high power transducers and ultrasonic motors requiring high drive fields. Other formulations, such as PZT6 and PZT7, also found usage in specific applications, where high temperature/time stability and low permittivity are desired, respectively [38, 69–71].

Table I.

Principal properties of various PZT based polycrystalline ceramics, compared to BaTiO₃ (BT), PbNb₂O₆ (PN) ceramics and LiNbO₃ (LN) crystals. T_C (°C); d (pC/N); s (pm²/N) [70–71]

	TC	$K_{33}^T$	$K_{11}^T$	d33	d15	k33	k15	kt	$s_{33}^E$	$s_{55}^E$	Qm
PZT2	370	450	990	152	440	0.63	0.70	0.51	14.8	45	680
PZT4	328	1300	1475	289	496	0.70	0.71	0.51	15.5	39	500
PZT5A	365	1700	1730	374	584	0.705	0.685	0.49	18.8	47.5	75
PZT5H	193	3400	3130	593	741	0.75	0.675	0.505	20.7	43.5	65
PZT6B	350	460	475	71	130	0.375	0.377	0.30	9.35	28.2	1300
PZT7A	350	425	840	150	362	0.66	0.67	0.50	13.9	39.5	600
PZT8	300	1000	1290	225	330	0.64	0.55	0.48	13.5	31.9	1000
BT	115	1700	1450	190	260	0.50	0.48	0.38	9.5	22.8	300
PN	570	225	/	85	/	0.38	/	/	25.4	/	15
LN	1150	30	84	6	68	0.16	0.61	0.16	5.02	17	3000

Undoubtedly, the PZT family is, by far, the most important and versatile compositional base for piezoelectric elements. In addition to PZTs, other developments in ferroelectric materials are also of major interest. In 1952, studies by Goodman uncovered the interesting and strong ferroelectric properties in lead metaniobate (PbNb₂O₆: PN) with a tungsten bronze structure [38,72]. It exhibits unusual properties not generally present in other piezoelectric materials and has been the subject of considerable research because of its high hydrostatic sensitivity (due to its large anisotropy, allowing a better response under hydrostatic pressures), low mechanical Q_m (being only ≪ 20, benefiting the fabrication of wide bandwidth transducers for high frequency pulse echo measurements that require a short pulse and critical resolution) and negligible aging in a wide temperature range due to its high Curie temperature [38,73–75]. The metaniobate is a problematic ceramic to process, but easily forms solid solution with other end members such as BaNb₂O₆ with decreased Curie temperature [76], and thus has been specialized for industrial nondestructive evaluation/testing (NDE/NDT) applications. Another development in piezoelectric materials is crystal growth of LiNbO₃ (LN) and LiTaO₃ (LT) [77–79], which were synthesized for the first time in Bell laboratories and their ferroelectric properties revealed by Matthias and Remeika [80]. Both crystals have an ilmenite structure [81]. The detailed structure and properties were reviewed by Smith et al. [82] and Weis et al.[83]. Both LN and LT are well known for their low acoustic losses and are thus excellent materials for surface acoustic wave (SAW) devices [77–78]. LN, possessing relatively large electromechanical coupling factors and very high Curie temperature of 1150 °C, has been actively studied for high temperature acoustic transducer [84–86]. In addition, it has been studied for high frequency (>20MHz), broad bandwidth single-element transducer applications due to its very high acoustic velocity and low dielectric constant [87–88]. LN possesses a number of useful orientation-controlled crystal cuts, which are now extensively used in transducer applications, including compression 36° rotated y-cut and shear 163° rotated y-cut.

In the 1970s, it was deemed that further improvements in the performance of established piezoelectrics were not forthcoming. Thus, various piezoelectric composites were introduced by Newnham in 1978, through the concept of “engineered biphasic connectivity” [14]. The particular significance of piezoelectric composites is that the structurally and compositionally homogeneous ceramics or single crystals can be combined with a passive polymer material to form composites, increasing material flexibility and improving acoustic impedance matching between the active material and the medium in which the acoustic wave travels. By structurally combining a piezoelectric ceramic and a polymer with certain connectivity, the resulting composite material can successfully integrate the advantages of both materials. Several interesting connectivity patterns were developed, including 0–3, 1–3 and 2-2 structures, and are now being widely employed in transducer applications [13–20,89–110].

Another very important transduction material category is relaxor based ferroelectrics [111–117], with a partially disordered structure and polar nanoregion (PNR), leading to extremely large dielectric constant. One such material is lead magnesium niobate (PMN), first reported in 1961 [118]. The large dielectric constant benefits the electric field induced strain level through the electrostrictive coefficient, with the advantage of very low strain hysteresis, causing PMN to be actively studied for medical and underwater transducer applications [119–125]. Analogous to PZT system, the relaxor components can form solid solutions with classic ferroelectric PT, possessing MPB regions and ultrahigh dielectric and piezoelectric properties [126–136]. Of particular importance is that some of the relaxor-PT ferroelectric solid solutions can be grown into single crystals, such as Pb(Mg_1/3Nb_2/3)O₃-PbTiO₃ (PMN-PT) and Pb(Zn_1/3Nb_2/3)O₃-PT (PZN-PT). The first attempt on the crystal growth started in the early 1980s [137–138], but extensive studies on the relaxor-PT crystals have occurred since the late 1990s. The crystals were found to exhibit high electric field induced strains (~1.7%) and high electromechanical couplings (~0.9) [139–140], demonstrating the potential for improvement over PZT in electroacoustic transducer applications, which are the target piezoelectric materials in this review article.

1.3 Scope of Review

Relaxor-PT single crystals have attracted significant attention and have been actively studied over the last 20 years. Focus on the fundamental understanding of the origin of ultrahigh piezoelectricity and their merits in practical electromechanical applications, showing uniqueness and advantages of the crystals over state-of-the-art polycrystalline ceramics. Several review articles have been written on the crystal growth, property characterizations, piezoelectric mechanisms and related applications [141–154]. However, there have been no review articles surveying the “figure of merits” of relaxor-PT single crystals for various electroacoustic applications, which is very important for the material and device scientists to understand the material behavior under practically operational conditions. This review article provides an understanding of the material structure-property-device performance relationships of relaxor-PT crystals and corresponding applications, which may help the readers to better understand the materials from an application viewpoint and the acoustic devices from a functional material aspect.

II. The development of Relaxor-PT single crystals

2.1 Background

Single crystal PMN was initially reported in the early 1960s, and it was not until the early 1970s that another relaxor ferroelectric material, lead zinc niobate PZN, was reported. It was found that single crystals in the PZN-PT system could be readily grown from high temperature PbO flux [137–138]. Following studies on PZN-PT single crystals in the early 1990s [155–156], systematic studies on the piezoelectric properties of Relaxor-PT crystals poled along different crystallographic directions were reported in late 1990s and early 2000s. They showed ultrahigh piezoelectric coefficients and electromechanical coupling factors on the order of >1500 pC/N and > 0.9 respectively, far outperforming state-of-the-art ferroelectric PZT ceramics and triggering interest in crystals for various applications [157–237]. Today, relaxor ferroelectric PMN-PT crystals continue to be an exciting research area that promises even further discoveries, and have been commercialized with the help of the mature Bridgman crystal growth method [187,207,210,229,230]. However, issues of PMN-PT crystals include their low Curie temperature and ferroelectric phase transition temperatures, low coercive field and mechanical quality factor (for high power applications). The Curie temperature T_C, rhombohedral-to-tetragonal ferroelectric phase transition temperature T_RT and coercive field E_C determine the temperature and field stabilities, which are major concerns for many electroacoustic applications. In addition, low T_C, T_RT and low E_C bring up the issues of polarization stability under various maintenance storage and driving conditions [141]. Therefore, a dc bias electric field may be required to maintain the polarization and the performance of the devices [18]. Loss in sensitivity, however, occurs when applying a dc bias, which also adds complexity and cost to the driving electronics [171]. Furthermore, though having low dielectric loss (~0.002, similar to hard PZTs), the low mechanical quality factors Q_m of PMN-PT crystals, ~100, have been limiting factors in high power transducers and resonance based acoustic devices [166,195,196]. Owing to the above issues observed in PMN-PT crystals, it is desired to develop new single crystal systems with broadened temperature usage range and improved reliability under thermal/electric field, and mechanical stress [141–142].

Over the last ten years, extensive effort has been focused on new crystal systems, including binary [238–268] and ternary [269–315] relaxor-PT crystal systems, in which Pb(Mg_1/3Nb_2/3)O₃-PbZrO₃-PbTiO₃ (PMN-PZT) [269–275] and Pb(In_0.5Nb_0.5)O₃-Pb(Mg_1/3Nb_2/3)O₃-PbTiO₃ (PIN-PMN-PT) [278–289] have been actively studied due to the potential growth ability of large size and high quality crystals. With new developments in the relaxor-PT single crystals in 2010, the concept of various generation crystals was proposed by Smith [141,316]. The first generation crystals exhibit high electromechanical coupling and piezoelectric coefficients that produce transducers with larger bandwidth (×2) and higher sensitivity (+10 dB) when compared with the state-of-the-art polycrystalline ceramic technology, which already have been commercialized in medical ultrasonic imaging [139–140]. Second generation crystals extend the high electromechanical properties to a broader range of temperature, electric field and mechanical stress, expanding their design envelope by reducing the need for heat shunts and applied dc fields. Crystals with higher ferroelectric phase transition temperatures and higher coercive fields are in this category [141,153,275,278], where the potential commercialization of the ternary PIN-PMN-PT and PMN-PZT is expected. Third generation crystals include the addition of small amount of dopants to tailor the crystal’s electromechanical parameters in order to meet specific device requirements. For example, Mn-doped relaxor-PT crystals have been developed, with greatly increased mechanical quality factors and high piezoelectric properties [273,296,298], which will benefit resonance based devices, such as ultrasonic transducers and motors. The detailed comparison of the three generations of crystal systems are given in Table II [161,273,278,290,304,317]. It was observed that the 2^nd and 3^rd generation crystals possess comparable piezoelectric and electromechanical properties to those of 1^st generation crystals, but with higher ferroelectric phase transition temperatures (~30°C higher) and higher coercive fields (double the value of 1^st Gen), allowing for broader temperature usage and higher drive fields /increased signal intensities. In addition, the mechanical quality factor of 3^rd generation crystals is about 5–10 times higher than those of 1^st and 2^nd generation crystals, offering the possibility for high power transducer applications.

Table II.

Property comparison of the three generations relaxor-PT crystals.

Crystal	TC (°C)	TRT (°C)	EC (kV/cm)	Eint (kV/cm)	$K_{33}^T$	d33 (pC/N)	k33	Qm
PMN-PT29 (Gen I)	135	96	2.3	0	5400	1700	0.91	150
PMN-PT (MPB) (Gen I)	155	65	2.8	0	8200	2800	0.95	100
PIN-PMN-PT (Gen II)	191	125	5.0	0	4400	1500	0.92	180
PIN-PMN-PT (MPB) (Gen II)	197	96	5.5	0	7200	2700	0.95	120
Mn:PIN-PMN-PT (Gen III)	193	119	6.0	1.0	3700	1100	0.90	800
Mn:PMN-PZT (Gen III)	203	141	6.3	1.6	3400	1100	0.92	1050

2.2 General observations of relaxor-PT single crystals: Properties vs T_C and T_RT

Generally, the Curie temperature and ferroelectric phase transition temperature (polymorphic phase transition: PPT) are important parameters to evaluate the performance of ferroelectric materials, due to the fact that these temperatures not only relate to the material structures, but also determine the temperature usage range and temperature stability of the material properties. In polycrystalline ferroelectric materials, knowledge of the Curie temperature shows a strong relationship of dielectric and piezoelectric properties with T_C [157,318]. For relaxor-PT single crystals, however, both T_C and PPT (T_RT) must be considered, due to the strongly curved MPB. Thus, it is desirable to understand the general relationships, if any, for relaxor-PT single crystal systems.

Fig. 2 shows the room temperature electromechanical coupling factor (k₃₃) and piezoelectric coefficient (d₃₃) of [001]-oriented relaxor-PT-based ferroelectric single crystals as a function of Curie temperature T_C and/or rhombohedral–tetragonal phase transition temperature T_RT [242,252,279,305,318–328]. Fig. 2(a) depicts the electromechanical coupling k₃₃ as a function of Curie temperature for various crystals with compositions near their respective MPBs, where k₃₃ values were found to be on the order of 0.9 for all [001] domain-engineered rhombohedral relaxor-PT crystals, regardless of their phase transition temperatures (T_C or T_RT). From Fig. 2(b), however, the levels of piezoelectric coefficients (d₃₃) were found to decrease with increasing T_RT, other than T_C as observed for polycrystalline ceramics [167]. Thus, relaxor-PT single crystals possessing MPB compositions exhibit higher dielectric and piezoelectric properties, but lower ferroelectric phase transition temperatures and deteriorated thermal stability of the properties when compared to the rhombohedral compositions far away from MPB. The general trend of coercive field of [001]-oriented ferroelectric single crystals as a function of Curie temperature is shown in Fig. 3, where E_C was found to increase with increasing T_C [163,318]. It is of interest to note that for the same crystal system, tetragonal compositions were found to possess significantly higher coercive fields when compared with their rhombohedral counterparts, not just higher T_C. The 90° ferroelastic domain walls and high c/a ratio (c and a are the crystal lattice parameters) make the main contributions to the enhanced coercive field [373].

Fig. 2.

(a) Electromechanical coupling of relaxor-PT crystals as a function of Curie temperature; (b) Piezoelectric coefficient of relaxor-PT crystals as a function of T_RT. BSPT: BiScO₃-PbTiO₃; PYNT: Pb(Yb_0.5Nb_0.5)O₃-PbTiO₃. (Reprinted with permission from S. J. Zhang and T. R. Shrout, IEEE Transactions on Ultrasonics Ferroelectrectrics Frequency Control 57, 2138 (2010). Copyright© 2010, IEEE) [318]

Fig. 3.

Coercive field as a function of Curie temperature for perovskite relaxor-PT crystals. (Reprinted with permission from S. J. Zhang and T. R. Shrout, IEEE Transactions on Ultrasonics Ferroelectrectrics Frequency Control 57, 2138 (2010). Copyright© 2010, IEEE) [318].

2.3 The uniqueness of relaxor-PT single crystals

Relaxor-PT based ferroelectric single crystals offering high performance with ultra-high electromechanical coupling and piezoelectric coefficient far out-perform state-of-the-art piezoelectric PZTs, attracting extensive attention to these crystal systems in last 20 years. In addition, the crystals exhibit several unique properties inherently associated with the engineered domain configurations, which are not existent in polycrystalline ceramics. In this section, the uniqueness of relaxor-PT crystals, including crystallographic anisotropy, high intrinsic piezoelectric, high cryogenic properties and newly developed shear vibration modes, will be discussed.

2.3.1 Crystallographic Anisotropic Characteristics

Polycrystalline ceramics such as PZT are in ∞∞m symmetry with inversion center in their unpoled status, transfer to ∞m symmetry after poling, exhibiting piezoelectric activity. Contrary to ceramics, relaxor-PT single crystals are in macroscopic 4mm, mm2 and 3m symmetries when poled along their crystallographic [001], [011] and [111] directions respectively, leading to strong anisotropic characteristics in their functionalities. Prior to the discussions of anisotropic behavior exhibited in relaxor-PT single crystals, engineered domain configuration [139,143,145,151,176,180,181], which is a very important concept for ferroelectric crystals, will be introduced first. A domain engineered ferroelectric crystal is one which has been poled by the application of a sufficiently large field along one of the possible polar axes of the crystal other than the zero-field polar axis, creating a set of domains in which the polarization vectors are oriented so that their angles to the poling direction are minimized [331]. In R, O and T phases, different engineered domain configurations and single domain states with different macroscopic symmetries can be achieved by poling along specific crystallographic directions, as listed in Table III.

Table III.

The relationship between the engineered domain configurations and crystal phase/poling directions. The standard coordinate for [111] poled crystals is X:[11̄0]/Y:[112̄]/Z:[111], while they are X:[01̄1]/Y:[100]/Z:[011] and X:[100]/Y:[010]/Z:[001] for [011] and [111] poled crystals (after [176]).

^*Single domain crystals mean that the crystals are poled along the direction parallel to their respective spontaneous polarization directions, where almost all domains are aligned along poling directions, the electromechanical properties of crystals can be treated as that of single domain. It should be noted that ideal single domain state is hard to be achieved in perovskite crystals, since it possesses very high levels of electrical and mechanical energies, and is not stable.

Fig. 4 shows a Relaxor-PT single crystal boule grown by the Bridgman method, which can be separated into three different composition phases, including R phase, O/M (monoclinic) phase and T phase along the growth direction, due to the large segregation coefficient of Ti⁴⁺ [153,187,207]. It was observed that the crystals exhibit 4mm macroscopic symmetry when the crystals were poled along [001] directions, with engineered domain configurations 4R and 4O in R and O phase crystals respectively, while single domain state 1T is presented in T phase crystals. Meanwhile, the crystals are in mm2 and 3m symmetries when poled along [011] and [111] directions, corresponding to engineered domain configurations 2R, 2T and 3O, 3T respectively, with single domain states 1O and 1R obtained in O and R crystals owing to their spontaneous polarization directions being along [011] and [111]. In the notations, the numbers ‘1’, ‘2’ and ‘4’ mean that there are one, two and four degenerate polarization directions in the poled crystals. The letters ‘T’, ‘R’ and ‘O’ indicate the crystals are in tetragonal, rhombohedral and orthorhombic ferroelectric phases, respectively.

Fig. 4.

As grown relaxor-PT crystal (middle), domain observation under polarized light for unpoled crystal wafer with R, O and T phases (left), where there is no clear domain wall observed in R crystals, while cloudy and clear domain walls being observed in O and T crystals, respectively. The relevant macroscopic symmetries when poled along different crystallographic directions and the desirable properties corresponding to different domain configurations are listed in the figure (right).

2.3.1.1 Anisotropy in rhombohedral relaxor-PT crystals

About fifty percent of the as-grown PMN-PT crystal boule is in rhombohedral phase, being in 4R, 2R and 1R domain configurations when poled along its crystallographic directions [001], [011] and [111] respectively. The high longitudinal piezoelectric coefficients d₃₃ are obtained in [001] and [011] poled rhombohedral crystals [305], while thickness shear piezoelectric coefficients d₁₅ exhibit superior values in [011] and [111] poled crystals [172,293,297,306].

Of particular significance is that the 2R domain configuration, which exists in the [011] poled rhombohedral crystals, exhibits high longitudinal, thickness shear and transverse piezoelectric activities simultaneously [282,300,302]. In 2R domain configuration, there are two independent thickness shear piezoelectric coefficients, d₁₅ and d₂₄, and two transverse piezoelectric coefficients, d₃₁ and d₃₂, where d₁₅ »d₂₄ and –d₃₂ »d₃₁, due to the fact that the contribution of the polarization rotation to the shear deformation S₄ and extensional deformation S₁ in 71° domains will negate one another [302]. Furthermore, a new face shear (contour shear) vibration mode with high piezoelectric coefficient d₃₆ can also be achieved in rotated 2R crystals (ZXt45° cut) [332–333], leading to a unique feature of relaxor-PT crystals, which will be discussed in 2.3.1.4. In addition to the piezoelectric properties, mechanical quality factor Q_m also shows anisotropic behavior, where the longitudinal Q₃₃ for 4R domain configuration is on the order of 100, while the value is above 1000 in single domain state 1R due to the absence of domain wall. Of interest is that both high piezoelectric coefficient d₃₃ and mechanical Q₃₃ were observed in 2R engineered domain configuration due to the fact that only 71° domains remained after polarization [334–335], which will benefit the high power applications at resonance frequency.

In order to clearly demonstrate the anisotropic behavior in R crystals, the principal properties and anisotropic ratios are given in Table IV. It can be observed that single domain rhombohedral PMN-PT crystals possess high anisotropic ratio with ultra-high transverse dielectric, shear elastic and shear piezoelectric constants, contributing to the high longitudinal piezoelectric coefficient in engineered domain configurations. For comparison, the PMN-PT ceramic counterpart was found to possess much lower anisotropic characteristics.

Table IV.

Property anisotropic ratio for rhombohedral PMN-PT crystals with different domain configurations, and compare to PMN-PT ceramic counterpart, d_ij: pC/N, the values in this table are small due to the fact that the listed compositions are in deep rhombohedral phase. [128,233]

PMN-PT Crystal		Piezoelectric property					Mechanical Qm		Anisotropic ratio
Poling direction	Domain Configuration	d33/ d33*	d31 /d31*	d32/d32*	d15/d15*	d24/d24*	Q33	Q15	ε11/ε33	s55/s33	d15/d33
[001]	4R	1180	−570	−570	122	122	140	30	/	/	/
[011]	2R	860	450	−1150	2160	160	750	40	/	/	/
[111]	1R	97	−43	−43	2380	2380	2000	25	8.4	21.9	24.5
PMN-PT ceramic		800	−395	−395	1090	1090	75	15	0.81	2.7	1.36

2.3.1.2 Anisotropy in tetragonal and orthorhombic relaxor-PT crystals

In contrast to rhombohedral crystals with 1R single domain state, the [001] poled tetragonal crystals show higher coercive field and higher T_C, along with the absence of ferroelectric phase transition T_RT/T_OT above room temperature and high mechanical Q₃₃, making them potentially useful for high power transducer applications [293,336]. Table V lists the principal properties and the anisotropic ratios for PIN-PMN-PT with single domain states 1O and 1T. Similar to 1R single domain state, large property anisotropic ratios were observed, with very high transverse dielectric and shear piezoelectric constants, leading to high longitudinal piezoelectric properties in engineered domain configurations.

Table V.

Property anisotropic ratio for orthorhombic and tetragonal PIN-PMN-PT crystals with single domain states, d_ij: pC/N. [293, 306].

PIN-PMN-PT Crystal		Piezoelectric property					Mechanical Q		Anisotropic ratio
Poling direction	Domain Configuration	d33	d31	d32	d15	d24	Qm33	Qm15	ε11/ε33	s55/s33	d15/d33
[011]	1O	350	153	−346	4550	4100	1500	30	5.38	18.8	13.0
[001]	1T	530	−200	−200	2350	2350	1800	30	13.8	1.34	4.43

For tetragonal crystals with engineered domain configurations 2T and 3T, on the other hand, high domain wall density can be achieved when the special poling procedure is employed, so-called domain size/wall engineering, leading to high dielectric constant of >10,000 and electromechanical coupling of 0.75~0.78, essential for the electrical impedance matching in high frequency 2D array medical imaging transducers [337–338].

Of particular importance in orthorhombic 1O crystals is the piezoelectric coefficient d₂₄, with high temperature stability and values of ~2000 pC/N due to the vertical R-O phase boundary in the phase diagram [339–340]. Correspondingly, in engineered domain configuration 3O, the longitudinal coefficient d₃₃ is on the order of >800 pC/N with minimal temperature variation (<6 %) due to the fact that the value of d₃₃ in 3O configuration is mainly contributed by the large d₂₄ value in 1O single domain state, taking advantage of the anisotropic piezoelectric properties [139]. This will be discussed in detail in section 3.3.3.1.

2.3.1.3 Orientation dependence of piezoelectric coefficients

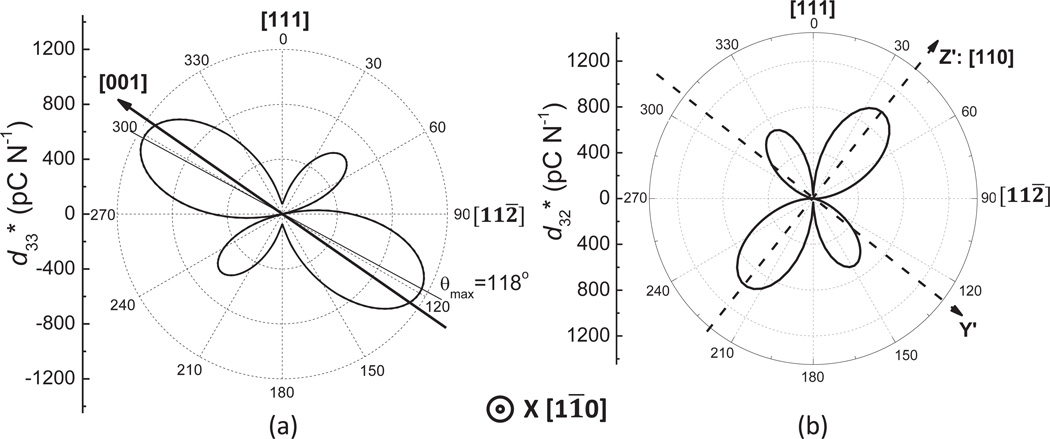
In relaxor-PT crystals, the maximum longitudinal and transverse piezoelectric coefficients do not exist in single domain crystals based on their standard coordinates. As shown in Fig. 5, the highest longitudinal coefficient d₃₃* was observed in the coordinate system with the Z’ axis rotated to the [001] direction, while the highest coefficient d₃₂* was achieved in the coordinate system with Z’, Y’ and X’ axes along [110], [001̄] and [11̄0] directions, respectively. Therefore, in practical applications, rhombohedral relaxor-PT crystals are poled along [001] (4R domain configuration) and [011] directions (2R domain configuration) to obtain optimum piezoelectric coefficient d₃₃* and d₃₂*, respectively. This phenomenon is due to the high level of shear coefficient d₁₅ in the single domain state (d₁₅>>d₃₃) [178,180,206,292,297,327,328]. It should be noted that the data used in Fig. 5 is from the rhombohedral PIN-PMN-PT crystals with a composition away from the MPB [292]. The anisotropic properties of relaxor-PT crystals with MPB compositions are similar to Fig. 5, but with much higher d₃₃* and d₃₂* values being on the order of ~2000 pC/N [290,341].

Fig. 5.

Orientation dependence of the piezoelectric coefficient (left) d₃₃* and (right) d₃₂* for single domain PIN-PMN-PT crystals. For plotting the figures, the X axis is fixed along [11̄0] direction, the Z and Y axis are rotated around X axis. It can be seen from figure (a) and (b) that the maximum piezoelectric coefficients of rhombohedral PIN-PMM-PT crystal are not presented in the standard coordinate system of 3m point group (X, Y, and Z axis are along [11̄0], [11̄2] and [111] direction, respectively). For d₃₃*, the maximum value is observed when the Z’ axis is rotated to [001] direction. For d₃₂*, the maximum value is presented in the coordinate system with Z’ and Y’ axis being along [110] and [001̄] directions, respectively.

2.3.1.4 Origin of the piezoelectric anisotropy

In order to further understand the piezoelectric anisotropy of relaxor-PT ferroelectric crystals [176,179,228,233,342], the dielectric permittivity, spontaneous polarization and electrostrictive coefficients, which contribute to the piezoelectricity of ferroelectric materials, were investigated as a function of orientations. Fig. 6 shows the orientation dependence of the piezoelectric coefficient, dielectric constant (relative dielectric permittivity), polarization and electrostrictive coefficient for tetragonal relaxor-PT crystals. The maximum d₃₃* is achieved along the direction of 48° rotation from the [001] axis [293]. The anisotropy of piezoelectric activity is determined by the orientation dependences of polarization, dielectric constant and electrostrictive coefficient. The maximum polarization is along the polar direction of the single domain crystals and decreases to zero when the direction is perpendicular to the polar axis, as given in Fig. 6(a). For the dielectric constant, on the contrary, the anisotropic characteristic depends on various factors, e.g., temperature, composition, phase transition, etc. For ferroelectric materials, the maximum dielectric constant ε₃₃* is generally along the directions perpendicular to the polar axis when the material is on the proximity of the ferroelectric-ferroelectric phase transition, as revealed in Fig. 6(b). Meanwhile, the maximum ε₃₃* will be along the polar direction if the ferroelectric material approaches the ferroelectric-paraelectric phase transition [178,179,343]. The anisotropy of electrostrictive coefficient Q₃₃* is dominated by the crystal structure. For all perovskite-type materials, the orientation dependence of electrostrictive coefficient Q₃₃* is similar, as given in Fig. 6(c), where the maximum and minimum values are along the <100> and <111> directions, respectively [344,345]. It can be seen that the polarization and electrostrictive coefficient possess stable anisotropic properties in perovskite-ferroelectrics, while the anisotropy of the dielectric constant is very sensitive to the temperature, composition, stress, etc. Thus, differences in piezoelectric anisotropy among different perovskite-ferroelectrics are dominated by the dielectric anisotropy.

Fig. 6.

The orientation dependence of the spontaneous polarization P₃*, dielectric permittivity ε₃₃*, electrostrictive coefficient Q₃₃* and piezoelectric coefficient d₃₃* for tetragonal PIN-PMN-PT crystals. Based on the equation d∝PεQ, the orientation dependence of d₃₃* is determined by orientation dependence of spontaneous polarization P₃*, dielectric permittivity ε₃₃ and electrostrictive coefficient Q₃₃*. To obtain the coefficient value (Q₃₃*, d₃₃*, or ε₃₃*) of one direction, a line along this direction should be plotted from the origin to surface of 3D figure. An intersection point can be found between the line and surface of 3D figure. The distance between this intersection point and the origin indicates the coefficient value along the direction of this line. (input data from ref. [293])

2.3.2 Intrinsic and Extrinsic Contributions

Another uniqueness of relaxor-PT crystals is that the intrinsic contribution (lattice deformation), which dominates their high longitudinal piezoelectric coefficients, are on the order of ~90–95 % due to the high stability of the engineered domain configurations [133]. As a comparison, the intrinsic contribution of their polycrystalline counterparts was reported to be only 50–75 %, revealing the domain wall extrinsic contribution in ceramics is >25 % [343]. The extrinsic contribution in the ferroelectric materials can be quantitatively evaluated by Rayleigh analysis and high electric field measurements [346–356]. Calculated from the Rayleigh analysis, the ratios of extrinsic contribution to the total piezoelectric response for PMN-PT crystals as a function of composition are given in Fig. 7(a), where the error bars were calculated from three samples for each composition [354]. The error bars were relatively high for compositions near the phase boundaries, demonstrating that the extrinsic contribution for the compositions on the proximity of the MPBs was not stable when compared to that of the compositions far away from the MPB, where the extrinsic contribution ratios for PMN-0.31PT and PMN-0.35PT crystals were found to be on the order of 10 %. The ratio was 7 % for tetragonal PMN-0.37PT crystal, while it was less than 5 % for all other compositions [354]. A similar trend was also observed in PIN-PMN-PT crystals, as given in Fig. 7(b) [305], where the extrinsic contribution is generally less than 5 % for rhombohedral crystals, while the values go up to 12 % for compositions in proximity of the MPB. This phenomenon was also observed in other domain engineered configurations, such as [011] poled PIN-PMN-PT:Mn crystals with 2R domain configuration, where the extrinsic contribution is only on the order of < 2 % [357–358]. This is due to the fact that Mn dopants in the crystals behave as acceptors, inducing oxygen vacancies and forming defect dipoles, clamping the extrinsic domain wall motion [141,334].

Fig. 7.

The level of extrinsic contribution to piezoelectric response at 1kV/cm for (a) (1-x)PMN-xPT crystals with various compositions [Reprinted with permission from F. Li et al., Journal of Applied Physics 108, 034106 (2010). Copyright © 2010, the American Institute of Physics.]; (b) PIN-PMN-PT crystals, where the increase of T_C represents the PT content increasing in PIN-PMN-PT crystals. Reprinted with permission from F. Li et al., Journal of Applied Physics 109, 014108 (2011). Copyright © 2011, the American Institute of Physics.

2.3.3 Piezoelectric properties at cryogenic temperatures

As discussed above, the intrinsic contribution dominates the piezoelectricity in relaxor-PT crystals, making them suitable for cryogenic temperature applications [359–368] since the extrinsic domain wall motion is greatly affected by temperature [174,179,197,340,369–372]. For example, the piezoelectric coefficients were reported to be on the order of > 900 pC/N for PIN-PMN-PT crystals at 120 K, much higher than the room temperature piezoelectric activity of polycrystalline ceramics (~750 pC/N for PZT-5H) [363].

The temperature-dependent intrinsic and extrinsic contributions of PIN-PMN-PT crystals and PMN-PT ceramics are summarized in Fig. 8(a) [363]. As expected, both intrinsic and extrinsic contributions decreased with decreasing temperature for all compositions. Based on thermodynamic analysis, the shear piezoelectric response (d₁₅) of the rhombohedral/monoclinic single domain state will decrease as temperature moves away from the polymorphic phase transition temperature (PPT) [158,178]. The reduction of shear piezoelectric response corresponds to an effective “hardening” of the polarization rotation process [180], leading to the decrease of intrinsic piezoelectricity. For PMN-PT ceramics, not only intrinsic piezoelectricity, but also the extrinsic contribution α (α is an indicative parameter for extrinsic piezoelectric contribution) drastically decreased from 280 to 40 cm/kV as the temperature decreased from 300 to 120 K, attributed to the clamping of domain wall motion [369–370]. Fig. 8(b) shows the relative variation in piezoelectric response as a function of temperature for PIN-PMN-PT crystals and compared to PMN-PT ceramics. At 120 K, the piezoelectric response was found to decrease by 27 % and 40 % for PIN-PMN-PT crystals with R and MPB compositions, respectively. The PMN-PT ceramic exhibited the largest decrease: ~75 % of the original value.

Fig. 8.

(a) The temperature dependent Rayleigh parameters, (b) Variation of d₃₃ as a function of temperature for [001] poled PIN-PMN-PT crystals and PMN-PT ceramics. (data from ref. [363])

Fig. 9(a) depicts the variation of the d₃₃ coefficient and value of K₃₃P_r versus temperature for PMN-28PT crystals. The two curves exhibit similar variation, in good agreement with the fact that, for piezoelectric material, d₃₃ is proportional to Q₃₃P_rε_r (ε_r: relative dielectric permittivity), where Q₃₃ and P_r are electrostrictive coefficient and remnant polarization, respectively. Assuming that Q₃₃P_r is almost temperature independent in the cryogenic temperature range, the d₃₃ curve should present a similar trend with the dielectric behavior. By extrapolation of the curves, the d₃₃ value at 0 K was estimated to be 150 pC/N, similar to that of PZT ceramics. Fig. 9(b) depicts the variation of the electromechanical coupling k₃₃ and elastic constant $s_{33}^E$. To discuss the cryogenic electromechanical properties, Fig. 9 can be divided into three temperature regions: region I (T=10–100 K), region II (T=100–250 K) and region III (T=250–300 K) [372]. In region II, the piezoelectric, dielectric, elastic and electromechanical coupling coefficients were found to exhibit high stability with respect to temperature when compared with regions I and III. In regions I and III, the piezoelectric, dielectric and elastic coefficients were found to drastically decrease with decreasing temperature, while the coupling factor only showed decreasing tendency in region I. In region III, the crystal deviates from the R-T phase transition point, leading to the decrease of d₃₃, ε₃₃ and $s_{33}^E$, while in region I, the degradation of d₃₃, ε₃₃ and $s_{33}^E$ cannot be explained by the same mechanism. Based on the thermodynamic analysis, the tangent of d₃₃-T curves will decrease as the crystal deviates from the phase transition point, indicating that the variation of d₃₃ will decrease with the crystal deviating from the phase transition point. However, the tangent of d₃₃-T curves in region I was found to be much higher than that in region III, so the large divergence of d₃₃ in region I cannot be explained based on the thermodynamic theory of traditional ferroelectrics. In addition, no abnormal reduction of piezoelectric coefficients at cryogenic temperature was observed in PZT ceramics [369]. It was proposed that the decreased d₃₃ was related to the influence of temperature on the compositional fluctuation-induced random electric fields, polarization and point defects, which give rise to combinatory pinning effects on the macro domain walls motions [372]. The drastic decrease of d₃₃, ε₃₃ and $s_{33}^E$ of relaxor-PT crystals in temperature region I was thought to be associated with the nature of the relaxor: disordered B-site cations and polar nanoregions. With decreasing temperature, the size of polar nanoregions will increase and PNRs will transform to ferroelectric state, thus the thermal fluctuations induced by polar nanoregions (in relaxor state) may die away, leading to a decrease of piezoelectric response [368]. It is worth noting that although the piezoelectric response decreases in both regions I and III, the electromechanical coupling factor only decrease in region I, demonstrating that the phonons associated with the nature of relaxor may dominate the level of electromechanical coupling factor.

Fig. 9.

Temperature dependence of d₃₃ and K₃₃P_r; (b) Temperature dependence of k₃₃ and $s_{33}^E$ for PMN-0.28PT crystals. (Reprinted with permission from F. Martin et al., Journal of Applied Physics 111, 104108 (2012). Copyright © 2012, the American Institute of Physics. [365]

2.3.4 The development of new shear vibration modes

2.3.4.1 Thickness shear vibration modes

Table VI summarizes the thickness shear properties for various crystals with different domain configurations and compares them to commercial PZT5 and PZT8 polycrystalline ceramics [374,375]. It is evident that high shear piezoelectric coefficients and elastic compliances can be easily achieved in crystals with single domain states, such as “1R” and “1O” [162,278,292], which will benefit the broad bandwidth transducer applications (high electromechanical coupling) at low operational frequency range (large elastic compliance). In addition, the high shear elastic compliance (low frequency constant) of single crystals results in small parts for the same frequency compared to polycrystalline ceramics, allowing miniaturization of the transducers or sensors [374].

Table VI.

Comparison of the shear vibration modes in various domain configurations, and compared to PZT5 and PZT8 ceramics [340,375]. [hkl]/(hkl)=poling direction/electrode face.

Poling/ electrode	Engineered domain	Crystal	Ec (kV/cm)	Eint (kV/cm)	KT	d15 (pC/N)	k15	N15 (Hz.m)	Qm15
111/11̄0	1R	Pure PIN	5.0	0	6000	3030	0.93	470	30
110/1̄10	2R	Pure PIN	5.0	0	6500	2800	0.92	570	20
		PIN-Mn	7.3	1.2	4600	2200	0.91	520	30
110/1̄10	1O	Pure PIN	5.5	0	5600	3400	0.95	380	20
		PIN-Mn	9.0	0.6	5800	3500	0.95	360	25
001/100	1T	Pure PIN	12.0	0	15000	2200	0.85	850	20
		PIN-Mn	11.5	1.5	8000	1200	0.77	950	30
PZT5 (Ceramic)			17	0	1730	584	0.685	830	15
PZT8 (Ceramic)			15	8	1290	330	0.55	1010	150

However, issues exist for the usage of shear vibration modes, including temperature instability of dielectric and piezoelectric properties, low allowable drive field stability (due to the working direction, i.e. applied electric field, is normal to the poling direction in the thickness shear mode) [375], low mechanical quality factor (which is very important for high power application) and cross-talk effect, etc. [141]. Although large shear properties have been observed in crystals with single domain state, the single domain crystal is subject to cracking from the large electric field induced strain/stress during the poling process [330]. Fig. 10 shows the strain versus electric field curves for rhombohedral PMN-PT crystals along [001] and [111] directions [42], where very high negative strain was observed in [111] poled crystals (this value is about −0.7 % for [001] poled tetragonal crystals [330]). This is due to the fact that the non-180° ferroelastic domains are not equivalent to [111] direction, as shown in Fig. 10(b), thus leading to a very large negative strain during ferroelastic domain switching. The electric field induced strain will lead to cracks during poling, which can be avoided in multi domain state, as shown in Fig. 10(c). The [111] spontaneous strains are equivalent to [001] direction, thus the very low negative strain in crystals with 4R engineered domain configuration is associated with the piezoelectric coefficient other than ferroelastic domain switching. Of particular interest is that large shear d₁₅ and low frequent constant, being on the order of ~2800 pC/N and 570 Hz·m respectively, were also obtained in engineered domain configuration “2R”, with the advantage of no-cracking during the poling process [302], as listed in Table VI.

Fig. 10.

(a) Strain versus electric field curves for PMN-0.29PT crystals measured along [001] and [111] directions at room temperature. (b) Schematic illustration of the domain switching for rhombohedral crystal. (b) [111] oriented crystal. At the coercive, which is antiparallel to the [111] direction, [111] domain could transform to the [1̄11], [11̄1], [1̄1̄1], [111̄], [1̄11̄], and [11̄1] domains, (c) [001] oriented crystal. At the coercive, which is antiparallel to the [001] direction, [111], [1̄11], [11̄1] and [1̄1̄1] domains transform to the [111̄], [1̄11̄], [11̄1̄], and [1̄1̄1̄] domains). Reprinted with permission from L. Jin et al. Journal of the American Ceramics Society 97, 1 (2014) Copyright © 2014, The American Ceramic Society. [42]

2.3.4.2 Face (contour) shear vibration mode

Though thickness shear exhibits ultrahigh piezoelectric coefficients, coupling factors and elastic compliances, the low field stability inherently associated with the 90° polarization rotation angle (the working direction is normal to the poling direction) will restrict their applications at high drive field condition (will be discussed in section 3.3.3.2) [141,374]. Recently, it was reported that [011] poled rhombohedral crystals possessed high face shear properties when the sample was rotated along poling direction of about 45°. That is, Zt±45° cut samples, which incorporate two extensional lateral modes [332–335], exhibit promising properties different from their thickness shear counterparts. Ultralow frequency transducers were projected based on the face shear (or d₃₆) mode in PMN-PT crystals due to their ultralow frequency constant and high piezoelectric coefficients [376,377]. In addition, due to the uniqueness of the face shear vibration in combination with high coupling and high mechanical Q₃₆, face shear crystals have been studied for tactile sensing and ultrasound motor applications [378–382]. In contrast to conventional thickness shear d₁₅, the face shear vibration mode can be repolarized; i.e., the poling electrode is the same as the active electrode [141,340,374]. The ac driving field level and mechanical quality factor Q₃₆ of the face shear mode were reported to be significantly higher compared to thickness shear vibration modes, owing to the fact that the applied electric field in face shear vibration is along polarization direction [141,374].

The principal properties related to the face shear vibration mode for relaxor-PT crystals are reported in Table VII and compared to conventional thickness shear properties [300,333,383]. The dielectric constant for the studied crystals was found to be in the range from 4500 to 5200, while the dielectric loss was in the range of 0.1–0.2%. The elastic compliance $s_{66}^E$ and piezoelectric coefficient d₃₆ were found to be on the order of 160–200 pm²/N and 2000–2500 pC/N respectively, with electromechanical coupling factor k₃₆ being 0.80–0.83. It should be noted that the property variations observed in all shear vibration modes are closely related to the crystal composition, following the general trend of relaxor-PT crystals [318]. The value of ~500 Hz∙m for the ultra-low face shear frequency constant N₃₆ was obtained, which is similar to the values of thickness shear modes, ~350–600 Hz·m [333]. Fig. 11 shows the comparison of the piezoelectric deformation of thickness shear and face shear vibrations. For the case of face shear mode, the frequency constant refers to the large dimension (length) of the samples, allowing for design of ultralow frequency and broad bandwidth transducers with minimized dimension [374,383]. In addition, it is important to note that the mechanical quality factor Q₃₆ obtained for the face shear crystals are on the order of 150–180 (higher Q₃₆ >350 was observed for 3^rd generation relaxor-PT crystals), significantly higher than those of the thickness shear modes, ~20–30. The low mechanical Q₁₅ is believed to relate to the ease of polarization rotation in corresponding thickness shear cuts, while the enhanced Q₃₆ in face shear is due to the polarization rotation angle of 35.5° in [011] poled rhombohedral crystals [141,357]. Meanwhile, the field stability ratio of the face shear vibration mode, on the order of 100% of its respective coercive field, greatly expands the usage range for high power application, which is due to the fact that the working direction is along the poling direction in face shear vibration [335]. Above the coercive field, the crystals will be depolarized due to the micro cracks induced by the large anisotropy of the transverse strains [298].

Table VII.

The comparison of thickness shear and face shear in [011] poled rhombohedral PIN-PMN-PT and PIN-PMN-PT:Mn crystals with “2R” engineered domain configuration. [300,333,383] N_r: Resonance frequency constant, where N₁₅ is not necessarily related to the $s_{55}^E$, while $N_{36}=\raisebox{1ex}{$F$}\!\left/ \!\raisebox{-1ex}{$\sqrt{4\rho s_{66}^E}$}\right.$ [333]

Crystal	Vibration mode	KT	tanδ	deff (pC/N)	keff	sE (pm2/N)	Nr (Hz·m)	Qm	Drive stability ratio
PIN	Face shear	4500	0.004	2000	0.81	170	550	180	100%
PIN:Mn	Face shear	3790	0.002	1800	0.80	170	550	350	100%
PIN	Thickness shear	6500	0.015	2800	0.92	161	570	20	40%

Fig. 11.

(a) Schematic figure of thickness shear piezoelectric deformation, (b) Schematic figure of face shear piezoelectric deformation. P is the poling direction. It should be noted that the resonance frequency is controlled by the thickness of the piezoelectric element in thickness shear deformation, while it is controlled by the edge length of the element in face shear deformation. Reprinted with permission S.J. Zhang et al. IEEE Transactions on Ultrasonics Ferroelectrectrics Frequency Control 60, 1572 (2013) Copyright © 2013, IEEE. [374]

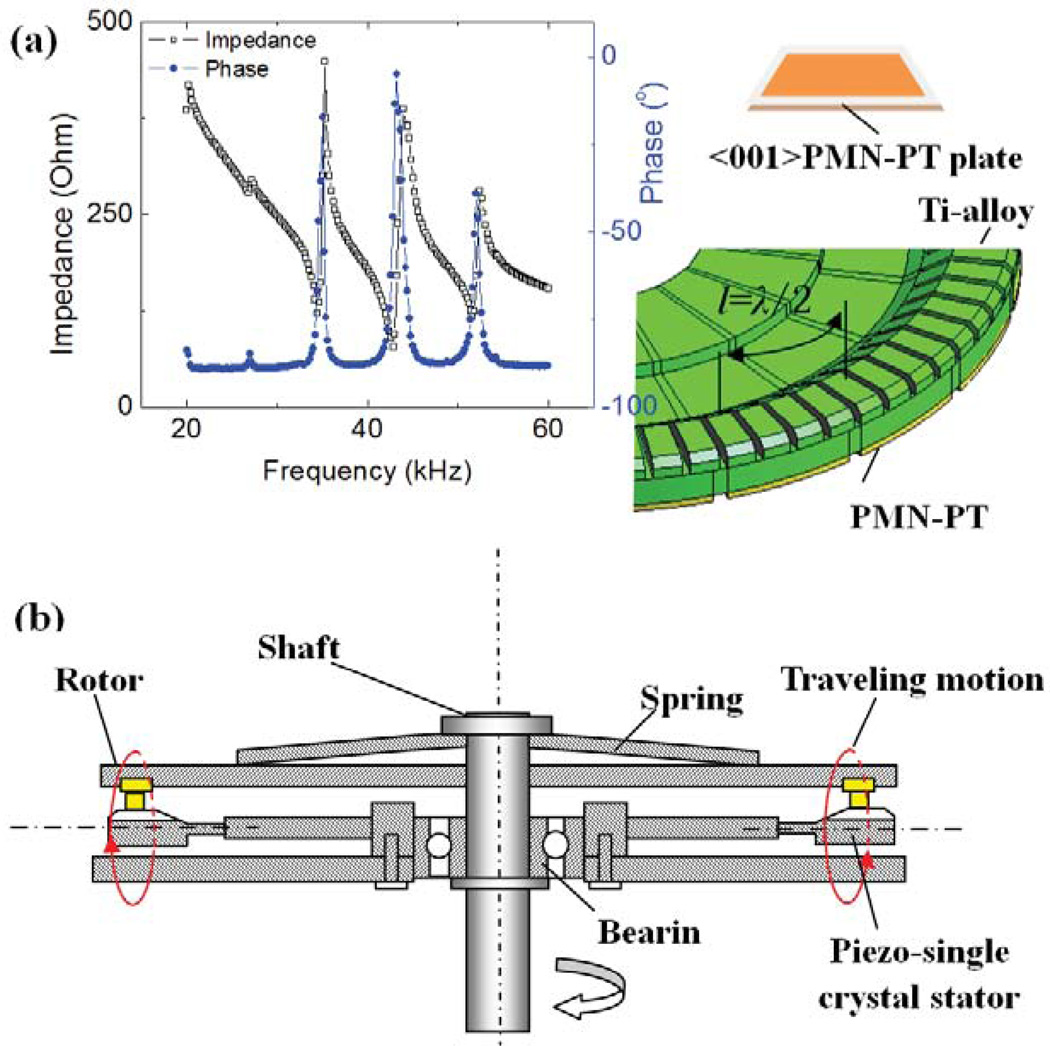
Other uniqueness of the relaxor-PT single crystals include high coupling and low mechanical loss, leading to high figure of merit (FOM) of k²Q_m for high power transducer applications [318], and simultaneous high piezoelectric and low strain hysteresis for high precision actuator applications [139]. These will be discussed in the following section III.

III. Figure of merits (FOM) of piezoelectric materials for various electroacoustic applications

A figure of merit is a number employed to characterize the performance or efficiency/effectiveness of a device or material, albeit the definition of FOM is difficult. It is extremely valuable to the device design process because it compels the designer to think critically about what parameters are the most meaningful to a successful design outcome.

3.1 Medical Diagnostic Ultrasound

3.1.1 Piezoelectric materials for ultrasound imaging (diagnostic)

There are many different medical imaging modalities, such as radiography, magnetic resonance imaging (MRI), computed tomography (CT), elastography, photoacoustic imaging, and ultrasound, to name a few. Among these, medical ultrasound uses high frequency broadband transducers, with advantages of real time monitoring of moving structures and no ionizing radiation, etc. [384]. Ultrasonic transducers convert electrical energy into mechanical form when generating an acoustic wave (transmitter) and convert mechanical energy into an electrical signal when detecting the echo (receiver) [2]. In general, broadband transducers should be used for medical ultrasonic imaging. The broad bandwidth response corresponds to a short pulse length, resulting in a better axial resolution which is dominated by the high electromechanical coupling factor, acoustic impedance and electrical impedance matching [385]. Fig. 12 gives a schematic view of the obstetric ultrasound imaging for a developing fetus, with a three-port network ultrasonic imaging transducer and the operational mechanism. The transducer consists of two mechanical components including the matching and backing layers, and one electrical component, the piezoelectric element, which is the heart of the transducer. It can be seen from the figure that both transmission efficiency and reception sensitivity parameters (TP and RP, respectively) are closely associated with the thickness electromechanical coupling k_t, clamped dielectric constant ${\epsilon }_{33}^s$ and elastic stiffness $c_{33}^D$ of the piezoelectric element [385]. Meanwhile, the bandwidth (e.g. −6dB fractional bandwidth) is also related to the coupling factor, where broad bandwidth can be achieved in materials possessing high coupling factor. Since the acoustic impedance of the piezoelectric materials is about ~30–37 MRayl, much higher than those of water or human tissues (~1.5–5 MRayl), a substantial part of the emitted acoustic energy will be lost, leading to a poor resolution and sensitivity. Thus single or multi matching layer(s) with lower acoustic impedance(s) are required to further improve the front acoustic matching of the transducer. The backing material is added to the rear of the transducer in order to damp the acoustic backwave and to reduce the pulse duration [385]. In addition, the electrical impedance of the transducer needs to be matched to the resistance of the coaxial cable and electrical circuit, which is generally 50 Ohm. The electrical impedance is inversely associated with the capacitance of the transducer, thus determined by the clamped dielectric constant and dimension of the piezoelectric element [24].

Fig. 12.

Schematic view of the medical imaging system and the operational mechanism. The equations are from references [3,385]. k: coupling; ${\epsilon }_{33}^S$: clamped dielectric, $c_{33}^D$: elastic stiffness, ρ: density, v: sound velocity, R: electrical impedance, C: capacitance, Z: acoustic impedance.

Based on the above discussion, the figure of merit (FOM) of the piezoelectric element for imaging transducers is the electromechanical coupling, which accounts for the high resolution, high power efficiency and broad bandwidth [385]. The thickness coupling factor for piezoelectric materials, including the relaxor-PT single crystals and PZT ceramics, is generally on the order of 0.5–0.6 [70–71]. In order to take advantage of the ultrahigh longitudinal coupling of relaxor-PT crystals, 1–3 and 2-2 crystal/epoxy composites have been extensively studied and commercialized in various transducer applications [11–20, 386–387]. Fig. 13 gives the geometries of monolithic samples, 2-2 and 1–3 composites, with their corresponding coupling factors, which are thickness mode, sliver mode and longitudinal mode, respectively. The coupling factors of longitudinal k₃₃ and sliver k₃₃’ modes are found to be >0.9 and ~0.8 respectively, both much higher than that of thickness mode k_t ~0.6, greatly benefitting transducer applications [374,388]. Furthermore, the composites are found to possess the advantage of lower acoustic impedance associated with the passive epoxy phase, about 12–20 MRayl, much smaller than those of single crystals (~30–37 MRayl), thus improving acoustic matching of transducers to the human body [2,385]. Table VIII lists the principal properties of relaxor-PT single crystals as compared to the state-of-the-art PZT-5H polycrystalline ceramics. The relaxor-PT crystals are found to exhibit higher electromechanical coupling factors, higher piezoelectric coefficients and higher elastic compliance when compared to PZT5H ceramics, which will benefit greater bandwidth, higher sensitivity and reduced device dimension for ultrasound transducer applications. Meanwhile, the lower dielectric loss will suppress internal heat generation, thus reducing the operating temperature rise. It should be noted that the clamped dielectric constants of relaxor-PT crystals are lower than those of ceramics, alberit their high free dielectric constants, this will impair the electrical impedance matching for array transducer applications. In addition, the lower coercive field of crystals will deteriorate the drive stability.

Fig. 13.

The comparison of various vibration modes of relaxor-PT crystals and their corresponding electromechanical coupling values.

Table VIII.

Comparison of 1^st generation crystals and PZT5H ceramics for medical imaging transducers. T: °C; E_C: kV/cm; d: pC/N; s: pm²/N.

	TC	TRT	EC	$K_{33}^T$	tanδ	$K_{33}^S$	k33	d33	$k_{33}^{\prime }$	kt	$s_{33}^E$
PMNT	135	96	2.2	5400	0.004	910	0.91	1540	0.82	0.60	60.0
PZT5H	193	/	7.0	3400	0.02	1470	0.75	593	0.67	0.505	20.7

3.1.2 High frequency ultrasonic imaging and the challenges of piezoelectric crystals

The medical community has increasingly looked to other ultrasonic capabilities for the potential insights that can be given to biomedical systems through improving current diagnostic ultrasonic frequency ranges, e.g. the 2–10 MHz range, and in some cases up to about 20 MHz [2]. High-frequency imaging beyond 30 MHz was reviewed by Lockwood et al. [389], including the ophthalmic ultrasound at 60 MHz, intravascular and intra-articular imaging up to 60MHz, skin imaging at 100 MHz, and some early works at 40–60 MHz investigating mouse embryonic development. Other studies used the acoustic microscope as a tool to determine tissue properties, such as those in fresh tissue at 100 MHz, which were measured by Scherba et al. [390]. Fig. 14 lists transducer operational frequencies and the corresponding imaging human tissues, with the frequency ranges from 2.5 MHz to 100 MHz [2]. Generally, higher operational frequency gives rise to higher resolution (smaller wavelength), but with less penetration. For a piezoelectric transducer, the frequency is closely related to the elastic constant (sound velocity or frequency constant) and the thickness of the piezoelectric materials, where a smaller thickness usually corresponds to a higher frequency for the same material [391–392]. Lithium niobate single crystals have been studied for high frequency transducer applications by employing 36° rotated Y-cut sample with coupling factor k_t of 0.48, clamped dielectric constant of ~40 and high elastic stiffness (high sound velocity of 7340 m/s), which makes the high frequency piezoelectric element easier [87–88, 393]. However, the coupling factor is far inferior to that of relaxor-PT crystals.

Fig. 14.

Medical imaging transducer operational frequency and the corresponding imaging human tissues. The equations are from [391]. C: capacitance; A: sample area; t: sample thickness; f_a: antiresonance frequency; c^D: elastic stiffness; v: sound velocity; λ: wavelength; f: frequency.

As given in Fig. 14, it should be noted that the capacitance of the piezoelectric element is inversely proportional to its thickness; in order to match the electrical impedance, it is desirable to use low dielectric constant monolithic crystals for high frequency applications. It was reported that the tetragonal monolithic PMN-PT single crystals, with coupling factors k_t of 0.6 and clamped dielectric constant of ~200–300, showed promising properties for single element transducers with operational frequency range of >40 MHz [394–395]. As discussed in section 3.1.1, the FOM for medical imaging is the coupling factor. Thus, in order to further increase the electromechanical coupling factor, 1–3 crystal/epoxy composites have been actively studied, taking advantage of the high longitudinal coupling k₃₃ of relaxor-PT crystals (as shown in Fig. 13). Traditionally, the dice-and-fill method is employed to develop low- frequency (<10 MHz) 1–3 composite transducers. However, due to the physical limitation of blade and brittleness of the active materials, the traditional method cannot be used to develop high- frequency (>30 MHz) composite transducers [90–93]. With the increasing demand of high-frequency ultrasonic applications, etch-and-fill technique and facile method have been developed recently [396–397]. Using the ICP (Inductively Coupled Plasma) -RIE (Reactive Ion Etching) dry etching technique, PMN-PT single crystals can be etched to a periodic pillar pattern with a sidewall angle of >85° [398–404]. However, recent experimental data for PMNT crystal/epoxy 1–3 composites (piezoelectric composite- micromachined ultrasound transducer PC-MUT) operating at high frequencies >20 MHz exhibited a relatively large decrease in electromechanical coupling, with values being less than 0.75, showing a strong scaling effect and leading to the question of the origin of property degradation at high frequencies [141,374,405–406].

Fig. 15 shows the electromechanical properties of relaxor-PT crystal/epoxy 1–3 composites as a function of sample thickness. For comparison, the longitudinal coupling factors (k₃₃) of the monolithic relaxor-PT crystals were calculated by the equation $k_{33}=\sqrt{1-\left(\raisebox{1ex}{${\epsilon }_{33}^S$}\!\left/ \!\raisebox{-1ex}{${\epsilon }_{33}^T$}\right.\right)}$ and plotted as a function of sample thickness. Note that the corresponding resonance frequencies on the top X-axis of Fig. 15 were calculated from the frequency constants by assuming ~1000 Hz·m for both monolithic and 1–3 composites samples. As shown in Fig. 15, the monolithic PMN-PT crystals were found to exhibit a decrease trend in coupling (k₃₃) with decreasing the thickness of crystal, due to the degradation of the free dielectric constant [405–406]. The 20 MHz PIN-PMN-PT/epoxy 1–3 composites were found to maintain higher electromechanical coupling factors on the order of 0.80, compared to 20 MHz PMN-PT composites with coupling of only 0.74. It should be noted that all 1–3 composites have the same volume fraction and ratio of post height to width. The observed scaling effect is reported to be associated with the ferroelectric domain size, where the large domains will be clamped by the surface boundary when the physical size of samples becomes of the same order as the domain size, inhibiting the domain wall motion and restricting the polarization rotation. This can be confirmed by the domain observations, where the domain size of PMN-PT crystals was found to be on the order of 10–20 µm, while it is only about 1 µm for PIN-PMN-PT crystals, showing the advantage of the ternary system [405–406]. Similar phenomena were also reported for BT and KT single crystals, where fine domain size accounted for the enhanced piezoelectric properties [407–409]. Furthermore, in polycrystalline PMN-PT ceramics, the fine grain ceramics were found to possess improved properties [121] and scaling effect when compared to their coarse grain size counterparts, due to their smaller domain size (domain size is proportional to $\sqrt{\mathit{\text{grain size}}}$) [410–412]. Admittedly, the surface damage layer induced by the dicing process and the stiffness of the epoxy filler also contribute to the coupling degradation; these can be alleviated by RIE dry etching and employing soft epoxy.

Fig. 15.

Electromechanical coupling factor for monolithic and crystal/epoxy 1–3 composites as a function of sample thickness and corresponding ultrasound frequency. Reprinted with permission from H. J. Lee et al., Journal of Applied Physics 107, 124107 (2010). Copyright © 2010, the American Institute of Physics. [405]

In order to confirm the role of domain size on the piezoelectric properties in ultrathin samples, a field-cool poling approach was applied to PMN-PT crystals with 100 µm thicknesses, where significantly smaller domain sizes on the order of ~5 µm were achieved [198]. Consequently, the piezoelectric coefficient was greatly improved from 1300 pm/V (coarse domain sample ~20 µm) to 2200 pm/V, as shown in Fig. 16(a), due to the fact that the domain size of field-cool poled crystals is much smaller than the thickness of the samples, leading to less impact on the polarization rotation and domain wall motion from the boundary clamping [198]. The stability of the engineered domain wall was further investigated by domain observation and strain behavior measurement as a function of pulse-field and number of cycles on the thin PMN-PT crystals. With increasing the pulse electric field magnitude and cycling number, the piezoelectric coefficients were found to decrease from 2000 pm/V to 1300 pm/V, as given in Fig. 16 (b), corresponding to the enlarged domain size from 5 µm to 30 µm with applied field from 3 kV/cm to 6 kV/cm (~3E_C) after 1.5×10⁶ pulses, demonstrating the inferior field stability of the finer domains [198].

Fig. 16.

Left: Unipolar strain as a function of electric field for room temperature poled (a) and field cooling poled (b) [001] oriented PMN-PT crystals (with thickness of 100 µm); Right: the unipolar strain behavior after pulse tests (a) 3 kV/cm, 7 × 10⁵ cycles, (b) 3 kV/cm, 7 × 10⁷ cycles, (c) 6 kV/cm, 7 × 10⁵ cycles, (d) 6 kV/cm, 1.5 × 10⁶ cycles. Reprinted with permission from D. B. Lin et al. Scripta Materialia 64, 1149 (2011), Copyright © 2011, Acta Materialia Inc. [198]

3.2 Therapeutic and Surgical Ultrasound

3.2.1 Piezoelectric materials for therapeutic ultrasound and surgical applications

Low intensity ultrasound, which leads to minimal biological effects and no tissue damage, is typically used for medical diagnostic imaging. As acoustic intensity increase, other effects can also occur, specifically heating and cavitation. Therefore, ultrasound can be used as a therapeutic agent that can deliver heat and also cause non-thermal cell stimulating effects [413]. As the power increases, there is a continuum of interaction which changes from “therapy,” where there are beneficial effects on tissue, to “surgery” in which tissue is destroyed. The transition to surgery from therapy occurs simply through either increased duration of treatment or increase in the power used. The various destructive interactions can be considered in several categories [2, 413–419], including (1) high intensity focused ultrasound (HIFU), which uses a heating mechanism; (2) lithotripsy/histotripsy, which uses focused shock waves to break up hard/soft subjects, such as kidney stones or tumor tissue; and (3) a number of other high power-low frequency interactions, all using a horn or tip in contact with tissue to cause disruption. Fig. 17 gives the operational mechanisms for HIFU (a), histotripsy and its related usage for drug delivery (b). It can be seen that the acoustic pressure generated by HIFU creates tissue movement (dilatation and contraction) whose amplitude is directly related to the pressure level, as the tissue response is not perfectly elastic. Thus energy is lost and converted into heat, exceeding a threshold thermal dose equivalent to 56 °C for 1 s, producing tissue coagulative necrosis and cell death [2]. The operational frequency range for HIFU is generally in the range of 0.8 ~2 MHz with acoustic pressure up to 70 MPa. On the contrary, the mechanism of histotripsy is controlled acoustic cavitation, where the ultrasound pressure changes (compressive and rarefactive pressures) induced microbubbles in the human body. The formation, oscillation and collapse of microbubbles create localized stresses and pressures at the cellular and subcellular level resulting in cellular destruction [1–5,9,392–394,414–418].

Fig. 17.

The basic principles of HIFU producing tissue necrosis (a), Operational mechanism for drug delivery using ultrasound waves (b).

The use of ultrasound to promote drug delivery was first reported by Fellinger and Schmid, who developed a successful treatment for polyarthritis by using ultrasound to drive hydrocortisone ointment into the inflamed tissues [420]. The technique of driving drug molecules across the percutaneous barrier to the target area using ultrasonic perturbation is termed “sonophoresis” or “phonophoresis” [421]. Since then, a wide variety of drug/ultrasound combinations have been implemented for sonophoresis. Most recently, ultrasound application has been used to promote delivery of high molecular weight proteins through intact skin. In addition to sonophoresis research, ultrasound has been shown to enhance the effects of several therapeutic drug classes, including chemotherapeutic, thrombolytic, and gene-based drugs, where the drugs are only released at the site of the tumor, while the patient’s total body exposure to the drugs would be limited. This, for certain types of cancer, could help reduce the unpleasant side effects of the chemotherapy [415,422]. Furthermore, ultrasound contrast agents, which were originally developed for diagnostic ultrasound, have been shown to augment the delivery and effectiveness of certain drugs. These ultrasound contrast agents can also be used as drug carriers for responsive and targeted drug delivery in the presence of ultrasound insonation. Meanwhile, the presence of microbubbles will enormously enhance delivery of genetic material, proteins and smaller chemical agents/drugs [416]. The operational frequency for lithotripsy/histotripsy is relatively low, being in the range of 0.25~0.5 MHz, with intensity up to 30 MPa, frequency range up to 2 MHz for drug delivery application, and acoustic pressure of 0.2~8 MPa [423].

The Langevin type transducer is generally accepted for medical surgical applications, such as Harmonic scalpel which is cutting instrument used during surgical procedures to simultaneously cut and coagulate tissue, and ultrasonic surgical handpieces for neurosurgery and orthopedic surgery, etc. All these surgery ultrasounds are operated at low frequency range and resonance mode, with a “horn” type of displacement amplification mechanism. Fig. 18 shows this type medical surgical ultrasound device, such as ultrasonic scissors and scalpel, and the original steel portion of the Langevin transducer can be modified with a “horn” concept to increase the displacement amplitude. By tapering the metal tip portion, the displacement level can be significantly amplified, which can be used for ultrasonic cutters and cavitation [419]. For these applications, in order to achieve high intensity, the ultrasound transducer is driven by tone bursts at resonance frequency with low duty cycle (~20 %).

Fig. 18.

Langevin transducer with a horn for medical surgery applications. Equations are from [3,10,388]. P_disp: dissipated power; ω: angular frequency; Y_r: Young’s modulus; S: strain; Q_m: mechanical quality factor; k: electromechanical coupling; d: piezoelectric coefficient; v₀: vibration velocity at the horn tip; P: acoustic power; ε: dielectric permittivity; E: electric field.

3.2.2 Advantages and Challenges of Relaxor-PT Crystals

From a material viewpoint, the medical therapy and surgery require operation at resonance frequency; thus, a high mechanical quality factor Q_m is preferable because of the high-power output without heat generation. Meanwhile, other properties, such as high electromechanical coupling factor (relates to the bandwidth and efficiency/sensitivity of the transducer) and high piezoelectric coefficient (relates to the output acoustic power), are desirable for therapeutic/surgical applications. It is also notable that the actual mechanical vibration amplitude at the resonance frequency is directly proportional to Q_m value (i.e., displacement amplification factor), while the power dissipation (heat generation) from the piezoelectric elements in ultrasonic transducer operated at resonance frequency is inversely proportional to the mechanical Q_m [3,10,296,388]. Thus, the FOM of materials for high power therapeutic/surgical applications is the product of dQ_m and/or k₂Q_m [424]. In ferroelectrics, the Q_m is mainly affected by the existence of domain wall motion and polarization rotation, where the polarization rotation angle was found to play an important role in the determination of Q_m value in relaxor-PT crystals because of the inherent anisotropic characteristics [141,334,346]. Table IX gives the loss and quality factors for relaxor-PT crystals as a function of polarization rotation angle. With increasing the polarization rotation angle from 0 to 90°, the piezoelectric coefficients were found to greatly increase with mechanical quality factors going down (or losses increase), resulting in the high piezoelectric d and loss for thickness shear vibration mode and low piezoelectric d and loss for longitudinal vibration mode in single domain states [141,334]. Of particular significance is that the [011] poled relaxor-PT crystals with 2R engineered domain configuration exhibit high piezoelectric coefficients, yet possess low mechanical loss due to the smaller polarization rotation angle on the order of 35.5° [334]. Table X lists the principal properties of 2^nd generation and 3^rd generation relaxor-PT crystals along various crystallographic directions, compared to state-of-the-art “hard” PZT8 polycrystalline ceramics. It can be observed that single crystals exhibit ultrahigh piezoelectric and electromechanical couplings, leading to high FOM when compared to PZT8 ceramics. Of particular interest is that [011] poled PIN-PMN-PT:Mn crystals were found to possess d · Q_m of five times that of PZT8 ceramics. Furthermore, the high elastic compliance (three times higher than that of PZT8) allows lower operational frequency or smaller device dimensions when compared to PZT8. It should be noted that single crystals exhibit low phase transition temperature and low coercive field (and internal bias), which will deteriorate the thermal stability (temperature usage range) and field stability (power limitation). These are the issues need to be addressed.

Table IX.

Mechanical Q_m as a function of polarization rotation angle for relaxor-PT single crystals with different engineered domain configurations (the angle between the direction of applied electric field and spontaneous polarization vectors). [141]

Domain configuration	Vibration mode	Polarization rotation angle	Mechanical quality factor	Dielectric loss	Piezoelectric coefficient (pC/N)
4R	longitudinal	54.7°	100~200	0.2~1%	>1500
4O/M	longitudinal	≤ 45°	200~400	0.2~1%	>1500
2R	longitudinal	35.3°	500~800	0.2~0.5%	1000~1500
1T/1R	longitudinal	0°	>1000	0.2%	60~500
1T/1R	shear	90°	<30	1~2%	>2000

Table X.

Comparison of hard PZT ceramics and single crystals for high power applications [278,300,345].

	TC (°C)	TFF (°C)	EC (kV/cm)	Eint (kV/cm)	d33 (pC/N)	k33	tanδ	Qm	$s_{33}^E$ (pm2/N)	d · Qm (pC/N)	k2 · Qm
PIN [001]	191	125	5.0	0	1510	0.92	0.002	150	68.4	226k	127
PIN [011]	192	93/118	5.5	0	1360	0.92	0.002	500	56.8	680k	423
PIN:Mn [001]	192	125	5.0	0.2	1340	0.92	0.002	700	62.4	938k	592
PIN:Mn [011]	197	106/121	5.9	0.3	1050	0.90	0.002	1000	43.8	1050k	810
PZT4	328	/	12	5	289	0.70	0.004	500	15.5	145k	245
PZT8	300	/	15	8	225	0.64	0.004	1000	13.5	225k	410

For polycrystalline ceramics, a consequence of high Q_m is the sacrifice of electromechanical couplings. As shown in Fig. 19, the coupling k₃₃ is found to decrease with increasing mechanical Q_m values. Thus, both high Q_m and high coupling cannot be simultaneously achieved in polycrystalline ceramics [425]. Of particular significance is that for domain engineered relaxor-PT crystal systems, in contrast to ceramics, the mechanical Q_m values can be improved without sacrificing the electromechanical coupling [318]. As shown in Fig. 19, the modified crystal systems exhibit different levels of Q_m, in the range of 70–2000, while maintaining ultrahigh electromechanical coupling on the order of >0.85, demonstrating the 3^rd generation relaxor-PT crystals to be unique piezoelectrics and potential materials for high power electromechanical applications [273,296,304,336, 357,358,426,427].

Fig. 19.

The relationship between mechanical Q_m and electromechanical coupling factor for different polycrystalline and single crystal systems. Reprinted with permission from S. J. Zhang and T. R. Shrout, IEEE Transactions on Ultrasonics Ferroelectrectrics Frequency Control 57, 2138 (2010). Copyright© 2010, IEEE [318]

3.3 Underwater acoustics

As underwater acoustic technology matured it began to have significant commercial applications such as depth sounding to provide detailed ocean bottom mapping [3]. Bottom mapping techniques can be readily extended to the exploration of the underwater oil/gas or mineral mining, underwater cable or pipeline inspections and oceanographic research. In addition, it also has commercial importance in the fishing industry where transducers have been developed specifically for locating schools of fish [1–3]. The underwater acoustic transducer can be categorized into active and passive types, where active transducer uses a sound transmitter and a receiver, while passive transducer listens without transmitting.

3.3.1 Piezoelectric materials for underwater active transducer applications

Fig. 20 shows the sketch for underwater electroacoustic transducers used to locate a large school of fish. In addition to the FOM of materials for high power transducer applications, other factors also need to be considered for underwater acoustic transducers. For example, it is desirable that the underwater transducers operate at the low frequency range with miniaturized dimensions, high drive fields and high duty cycles [6–7]. Furthermore, as with other electroacoustic transducers, a prestress is required for the underwater transducer package, thus affecting the piezoelectric behavior.

Fig. 20.

Schematic figure for underwater electroacoustic transducer applications, locating a large school of fish. Equations are from [3]. R_r: radiation resistance; R: internal mechanical resistance; v₀: vibration velocity at transducer surface; η_ea: electroacoustic efficiency; k_eff: electromechanical coupling; Q_m: mechanical quality factor; s: elastic compliance; c: elastic stiffness; ρ: density; N: frequency constant; V: voltage; d: piezoelectric coefficient.

The FOM of the piezoelectric materials for underwater acoustic applications is dQ_m relating to the acoustic velocity and/or k₂Q_m being associated with the electroacoustic efficiency [388]. In addition, it can be observed from the acoustic efficiency equation that dielectric loss also plays an important role for the performance of underwater transducers [3]. However, due to the nonlinear characteristics of ferroelectrics, such as domain wall motion and phase transition, the measured losses strongly depend on the amplitude of the drive field [10,200,216,296,428–433], which is closely related to the practical transducer applications. These measured values are referred to as large signal losses, to be separated from the small signal losses (measured at V_rms≤1V). Fig. 21 shows the mechanical loss and dielectric loss as a function of drive field. The longitudinal mechanical loss was measured at driving resonance frequency for different crystal systems and phases, as given in Fig. 21 (a). All the mechanical losses were found to increase with increasing the drive field, and were saturated when the fields were above 0.15 kV/cm [141,296]. Of particular interest is that the saturated loss for [001] poled tetragonal PIN-PMN-PT crystals was found to be much lower than those of rhombohedral crystals, due to the absence of domain wall (single domain state), while the ternary crystals were found to possess lower loss when compared to their binary counterparts, being related to the higher Curie temperature and coercive field [336]. The dielectric loss was measured as a function of drive field at 1 kHz frequency, as shown in Fig. 21 (b), exhibiting similar trend for different crystal systems [429]. The compositions far away from MPB show lower dielectric loss, while the acceptor doped PIN-PMN-PT crystals possess much lower loss when compared to the undoped counterparts, due to the stabilization of the domain wall motion by internal bias [429].

Fig. 21.

(a) Mechanical loss factor (inverse of mechanical Q_m) of various relaxor-PT crystals as a function of drive field at resonance frequency. Reprinted with permission from S. J. Zhang and F. Li, Journal of Applied Physics 111, 031301 (2012). Copyright © 2012, the American Institute of Physics. [141] (b) Dielectric loss of various relaxor-PT crystals as a function of drive field at 1Hz. Reprinted with permission from N. Sherlock, L. Garten, S. Zhang, T. Shrout and R. Meyer, Journal of Applied Physics 112, 124108 (2012). Copyright © 2012, the American Institute of Physics. [429].

Transducers operating at low frequency with high output power require large displacement of the radiating surfaces [10]. Some geometries of underwater transducers are given in Fig. 22. As first demonstrated by Langevin, the addition of end (tail) mass to a piezoelectric stack lowers the resonance frequency of the tonpilz, allowing for low frequency operations without requiring prohibitive stack lengths [3,6,10]. An electric field is generally applied along the polarization of the piezoelectric stack via the sandwiched electrodes, resulting in a 33-mode operation. Actuation from the piezoelectric stack causes the head mass to radiate acoustic energy into the surrounding water, while the tail mass is not in contact with the surrounding water. The head and tail masses offer additional parameters to the stack length when determining the fundamental resonance frequency, and this design can be scaled from 1–100 kHz frequency [10]. The presence of the stress bolt and compressive stress bias reduces the dependence on high quality surface preparation of the piezoelectric elements [10]. It can be observed that different piezoelectric vibrations can be employed in the underwater acoustic transducers, including the above mentioned longitudinal 33 mode, which gives the high electromechanical coupling of >0.9 and piezoelectric coefficient of >1500 pC/N. The transverse vibration 32 mode can be used to generate large displacement taking advantage of the length dimension, with electromechanical coupling of ~0.9 and piezoelectric coefficient of −1500 pC/N, which was reported to allow lower drive and bias voltages while simplifying the construction with minimal impact on transducer effective coupling, size and bandwidth [321,434–438]. More recently, single crystals with shear vibration modes drew attentions for low frequency acoustic transducer applications, due to the ultrahigh elastic compliance, piezoelectric coefficient and coupling factor. The schematics of the designed transducers using thickness shear and face shear vibrations are presented in Fig. 22 (b), where the parallelepiped shaped piezoelectric elements disposed between and attached to the tail mass and the head mass through the elongated shaft extending from the head and within the cavity of the tail mass [376]. In this way, the piezoelectric deformation of the shear vibration modes (including the thickness shear and face shear) will generate large displacement of the head mass at low frequency range.

Fig. 22.

Schematic figures of acoustic transducers with various geometries. The piezoelectric elements with different vibration mechanisms used in these transducers are given at the bottom, P: poling direction; ■: Electrodes on piezoelectric elements. (Figures adapted from ref. [10, 376])

All these designs will allow the low driving electric field to have large displacements, closely associated with the piezoelectric coefficients, the displacement amplification factor (Q_m) and the dimension of the piezoelectric elements. Table XI lists the principal properties of the shear vibrations modes and compared to longitudinal and transverse vibration modes. The thickness shear vibration mode was found to exhibit ultrahigh piezoelectric and electromechanical properties, but with very low mechanical quality factor, due to the fact that the polarization rotation angle is 90° in thickness shear, thus giving rise to high dielectric, piezoelectric and loss. Of particular significance is that the high elastic compliance leads to very low frequency constants, benefit the low operating frequency or miniaturization of the devices, which will be discussed in section 3.3.3.

Table XI.

Comparison of the shear vibration modes with the longitudinal and transverse modes for PIN-PMN-PT crystals. [278,300,340]

		KT	deff (pC/N)	keff	sE (pm2/N)	Qm	dQm (pC/N)
Thickness shear	1R	6000	3030	0.93	200	30	105k
Face shear	2R	4500	2000	0.82	170	180	360k
Longitudinal	4R	4400	1510	0.92	68	150	226k
Transverse	2R	4360	1780	0.92	101	150	267k

3.3.2 Piezoelectric materials for passive sensor (hydrophone) applications

Hydrophones are one important category of piezoelectric sensors, which detect the acoustic pressure signals and noise in water while producing an output voltage proportional to pressure [3,17,440]. Fig. 23 gives schematic of the hydrophone operational mechanism. Acoustic pressure is considered to be effectively hydrostatic as the wavelengths of sounds in low frequency range are much larger than the sensor dimensions [3]. The voltage produced under hydrostatic pressure is used to measure the sensitivity of a hydrophone. In this regard, a useful parameter to evaluate piezoelectric materials for use in hydrophones is the voltage coefficient g_h, which relates output voltage to the hydrostatic stress. Another parameter is the hydrostatic charge coefficient d_h, which describes polarization resulting from a change in stress, with d_h = d₃₃+d₃₁+d₃₂ (for poled polycrystalline ceramics, d₃₁=d₃₂). A useful figure of merit (FOM) for hydrophone materials is the product of the voltage and charge coefficients, d_h×g_h [3,102,342,441]. A basic limitation on hydrophone performance is the electrical noise generated internally, which must not exceed the total sea noise, including the noise from ships, fish, waves, etc., as shown in Fig. 23 [3]. At far below the resonance frequency, the energy dissipation is mainly dominated by the dielectric loss. Thus the alternative FOM has been proposed to take into account the dielectric loss of the sensors, which is given by (d_h×g_h/tanδ) [3,442–443]. Other desirable properties for hydrophone sensors include, but are not limited to, low density for good acoustic impedance matching with water; and minimal variation of d_h and g_h with pressure, temperature, and/or frequency [17,444–445].

Fig. 23.

Schematic of hydrophone operational mechanism. Equations are from [3,10]. P_disp: dissipated power; tanδ: dielectric loss; ω: angular frequency; E: electric field; ε: dielectric constant; d_h: hydrostatic piezoelectric charge coefficient; g_h: hydrostatic piezoelectric voltage coefficient;V₀: volume of the sensing material.

PZT ceramics and relaxor-PT single crystals have been widely used for medical transducer applications; however, they have limited utility in transducers under hydrostatic conditions because of their relatively low hydrostatic piezoelectric coefficients, due to d₃₃ about twice the magnitude and opposite in sign from d₃₁, thus leading to a relatively low d_h which is generally on the order of 40–70 pC/N for perovskite ferroelectric ceramics [342]. In addition, the high permittivity results in low g_h coefficients. There has been a longtime interest in developing piezoelectric composites for underwater hydrophone applications because of their high hydrostatic sensitivity, good acoustic impedance matching to water, and high-pressure tolerance [15,92–93,97–102,107–110]. Piezocomposite hydrophones are dominated by 1–3 type connectivity in which the arrangement of piezoelectric material and polymer will reduce the influence of the 31 and 32 transverse extensional modes and produce a significant improvement in hydrostatic voltage sensitivity, with a high FOM. Other engineered connectivities, such as parallel-connected 2-2 composites, which are stacks of piezoelectric ceramic sheets separated by passive polymer layers, have also been investigated [97–99,101,105]. Recently, 2-2 lamellar composites consisted of relaxor-PT single crystals have been theoretically studied, giving a promising FOM of 16 pm²/N for a crystal volume of 25 % [107–109]. The 2-2 composite takes advantage of the strong anisotropic behavior of [011]_C poled single crystals, with macroscopic mm2 symmetry, in which the d₃₃ and d₃₁ are both positive while d₃₂ is negative. The contribution of d₃₂ to the hydrostatic d_h value is greatly reduced when the polymer layers are perpendicular to the 2 direction (Y axis, as shown in Fig. 24, where the [011]_C direction is along Z axis, and [01̄1]_C [100]_C are the X and Y axes, respectively), with minimal reduction of the d₃₃ and d₃₁ values. Thus, the hydrostatic piezoelectric d_h is significantly improved [99,141]. In addition, the dielectric constant of 2-2 composite is much lower than that of the crystal phase due to the ultralow dielectric of the passive epoxy phase, leading to a higher piezoelectric voltage coefficient g_h.

Fig. 24.

Schematic diagram of 2-2 crystal/epoxy composite comprised of [011] poled relaxor-PT single crystals, with layers parallel to X axis. (Figure adapted from ref. [99])

Table XII gives comparison of the hydrostatic properties for various piezoelectric materials, including polymer, ceramics, crystals and composites. The lead metaniobate was found to possess high FOM value, but with relatively low dielectric constant [72]. Of particular interest is that the 2-2 crystal/epoxy composites comprised of [011] poled relaxor-PT crystals, with the lamellar direction parallel to X axes, show increased hydrostatic properties, due to the fact that the large negative d₃₂ coefficients are greatly eliminated in this structure [99]. The hydrostatic properties of the 2-2 composites were found to be significantly enhanced by adding stiff faceplate, decreasing the Young’s modulus and Poisson’s ratio of the epoxy matrix. The highest FOM value, being on the order of 92 pm²/N, was achieved in O-soft+bubbles 2-2 composites (where O means orthorhombic crystal, soft means epoxy with low Young’s modulus and bubbles means micro bubbles being added in the epoxy to further decrease the Poisson’s ratio of the epoxy), with $\raisebox{1ex}{$a_1$}\!\left/ \!\raisebox{-1ex}{$d_h$}\right.$ (normalized pressure coefficient of the hydrostatic piezoelectric variation) being on the order of 0.031 ppm/Pa, while R-soft+bubbles 2-2 composite was found to possess FOM value of 11 pm²/N, with much higher pressure stability [99]. The hydrostatic piezoelectric properties, together with further optimizing the structural design, will make the 2-2 lamellar composites comprised of [011] poled relaxor-PT single crystals promising for hydrostatic transducer applications [99].

Table XII.

Comparison of hydrostatic properties for various materials [99]. For R -soft+bubbles, R means rhombohedral crystal, soft means epoxy with low Young’s modulus and bubbles means micro bubbles being added in the epoxy to further decrease the Poisson’s ratio of the epoxy.

Material	KT	dh (pC/N)	gh (mVm/N)	dh · gh (pm2/N)	tanδ
PVDF polymer	13	6	53	0.32	0.02
PbNb2O6 ceramic	225	67	34	2.3	0.01
PZT5 ceramic	1800	40	2.5	0.10	0.02
[100] PMN-PT crystal	4436	80	2	0.16	0.004
[011] PIN-PMN-PT “2R”	3000	87	3	0.29	0.002
[011] PIN-PMN-PT “1O”	1500	110	8	0.91	0.002
PZT 0–3 composite	43	7	17	0.11	0.01
PZT 1–3 composite	54	27	56	1.5	0.01
[011] R composite	1500	160	12	1.9	<0.01
[011] O composite	470	100	24	2.4	<0.01
[011] R -soft+bubbles	1500	390	29	11	<0.01
[011] O -soft+bubbles	400	570	161	92	<0.01

3.3.3 External Field Stability of Piezoelectric Properties

3.3.3.1 Thermal stability of the piezoelectric properties

The thermal stability of dielectric and piezoelectric properties is very important for most electromechanical applications, such as medical imaging and underwater acoustic. In general, the dielectric and piezoelectric responses of relaxor-PT ferroelectric crystals exhibit relatively large temperature variation, owing to the multiple polymorphic phase transitions (PPTs) lying in or near the temperature range of −50 −100°C [18,141,318]. Based on thermodynamic analysis of perovskite single crystals, the temperature dependence of the transverse dielectric permittivity is strongly related to the ferroelectric phase transitions. Fig. 25 (a) shows the temperature dependent piezoelectric variation of 1O single domain state crystals, where the shear piezoelectric coefficient d₂₄ was found to maintain similar value till T_OT transition temperature, with variation being less than 6 %, much less than that of d₁₅ in the same temperature range, which was found to be on the order of ~200 % [339]. This phenomenon can be explained by the fact that the piezoelectric coefficients follow the same trend as the dielectric permittivity as a function of temperature, where the permittivity is greatly enhanced when approaching the MPB [339–340,446–448]. As given in Fig. 26, in 1O single domain state, two independent thickness shear vibrations exist, including d₁₅ and d₂₄. When the sample is poled along [011]_C and electrode on (01̄1)_C face, the applied electric field E₁ is along [01̄1]_C direction, leading to the piezoelectric shear deformation d₁₅, where the polarization will rotate from [011]_C to [001]_C direction, which is the spontaneous polarization of tetragonal phase. Thus, the temperature dependent d₁₅ is related to the strongly curved O-T phase boundary, accounting for the strong temperature dependent behavior. On the contrary, for piezoelectric shear d₂₄ deformation, the sample is poled along [011]_C direction and electrode on (100)_C face, the applied field E₂ is along [100]_C direction, where the polarization will rotate from [011]_C to [111]_C direction, which is associated with the spontaneous polarization of rhombohedral phase; thus the temperature dependent thickness shear d₂₄ corresponds to the vertical O-R phase boundary [339–340,449], exhibiting high thermal stability. As expected, the longitudinal coefficient d₃₃ along [111]_C direction for crystals with 3O engineered domain configuration, which is dominated by the value of d₂₄ in 1O single domain state, was found to show temperature independent behavior (with variation of <6 % in the studied temperature range), yet with high value of ~900 pC/N, as given in Fig. 26 (b) [141,139,374].

Fig. 25.

(a) Temperature dependent shear piezoelectric coefficients for PIN-PMN-PT crystals with “1O” single domain state (data from [339–340]), (b) Temperature dependent longitudinal piezoelectric coefficient for PIN-PMN-PT crystals with “3O” engineered domain configuration (data from [141]).

Fig. 26.

Two independent shear piezoelectric responses (15- and 24-mode) and related polarization rotation path in orthorhombic crystals, where the solid and dotted blue arrows represent the polarization rotation process under perpendicular electric field. The coordinate system of orthorhombic crystal is presented on the left. The principal axis of orthorhombic phase are notated as [001]_O, [010]_O and [100]_O, being equal to [011]_C, [0–11]_C and [100]_C cubic axis, respectively (adapted from [339]). The related phase diagram exhibiting strongly curved O-T MPB and vertical R-O MPB were given at the bottom of the figure.

3.3.3.2 Drive field stability

Ferroelectrics exhibit nonlinear properties under high drive field, owing to the interfaces (domain wall and/or phase boundary) motion [346,354]. The piezoelectric and dielectric responses of relaxor-PT single crystals generally increase with increasing drive field up to a threshold value, above which the samples will be depolarized and lose the piezoelectric activity [171,450]. The threshold value is closely related to the respective coercive field of ferroelectrics, which is on the order of 2–10 kV/cm for relaxor-PT crystals, depending on the phase and composition. For the longitudinal vibration mode, the allowable drive field level can generally go up to three times of their respective coercive fields when the transducer is driven by a pulse field, as shown in Figure 14 [198]. In the case of thickness shear vibrations, however, it is a totally different scenario, due to the fact that the working direction of thickness shear is perpendicular to the poling direction, where the allowable drive field is much lower than the respective coercive field [374,375]. As listed in Table XIII, the field stability ratios (allowable drive field level divided by coercive field) of pure relaxor-PT single crystals were found to be on the order of ~40% for thickness shear modes, less than half of the coercive field, regardless of crystal systems, whereas the 2^nd generation crystals, such as PIN-PMN-PT, offer the advantage of higher allowable drive fields owing to their higher coercive fields, being double the value of PMN-PT binary counterparts [141,375]. Of particular significance is that for the acceptor (Mn) modified relaxor-PT single crystals (3^rd generation crystals), internal bias was found to be on the order of 0.6–1.2kV/cm [143,273,298], leading to the enhanced allowable drive field, with field stability ratio increasing to >65 %, which is much higher than those of pure counterparts [375]. Furthermore, it should be noted that the drive field stability of relaxor-PT crystals can also be enhanced by applying the uniaxial stress to crystals [451], which will be discussed in the following section.

Table XIII.

Thickness shear properties comparison for [011] poled rhombohedral relaxor-PT crystals (in 2R engineered domain configuration) [233,300,358,375].

Poling/ electrode	Crystal	Ec (kV/cm)	Einit (kV/cm)	$K_{11}^T$	d15 (pC/N)	k15	$s_{55}^E$ (pm2/N)	Allowable field level (kV/cm)	Field Stability Ratio
1st Generation	PMNT	2.2	0	4240	2160	0.92	147	1.0	45%
2nd Generation	Pure PIN	5.0	0	6500	2800	0.92	161	2.0	40%
3rd Generation	PIN-Mn	5.9	0.3	4900	2030	0.90	117	4.0	68%

3.3.3.3 Uniaxial prestress

Electroacoustic transducers with tonpilz structures (widely used for underwater acoustic, ultrasonic medical surgery, NDT/NDE, ultrasonic cleaning, to name a few) includes the piezoelectric elements, tail mass and head mass, and the stress bolt connecting the head and tail masses by running through the piezoelectric elements. When tightened, this bolt generates a compressive stress bias through the piezoelectric elements. These piezoelectric materials tend to fail under relatively small tensile stress (often 10–20 MPa without special surface preparation), but can survive very high compressive stress [10]. With no stress bolt present, actuation of the piezoelectric elements would result in equal operation under tension and compression, but the compressive stress bias prevents operating in tension and allows the transducer to operate at much higher drive levels [10]. Thus, it is desirable to understand the piezoelectric behavior under uniaxial prestress.

Fig. 27 shows the strain-electric field (S-E) loops measured at 5 kV/cm bipolar electric field and 0–20 MPa prestress for 3^rd generation crystals (PIN-PMN-PT:Mn). As shown in Fig. 27 (a), when the bipolar electric field is below 5 kV/cm (coercive field is about 7 kV/cm) [298], the crystal sample showed linear strain-field relationship with no concern of depoling, and the piezoelectric coefficient was calculated from the slope of S-E loop and found to be 1700 pm/V. With an increasing prestress, domain reversal occurs, as demonstrated by the typical butterfly strain loops, with greatly decreased coercive field (from ~7 kV/cm to 1.5 kV/cm) and negative strain level (from 0.9 ‰ to 0.13 ‰). Meanwhile, the piezoelectric coefficient was found to increase to 2500 pm/V at prestress of 10MPa, and then slightly decreased to 2000 pm/V at 20 MPa, and the negative strain was found to be zero when the prestress was further increased to 40 MPa (not shown here), revealing the loss of piezoelectricity [452]. This phenomenon can be explained by the stress induced phase transition and depolarization, as shown in Fig. 28. In crystals with a 4R engineered domain configuration, 71° and 109° ferroelastic domains exist, with polarization vectors pointing to [111], [1̄11], $[\overline{11}1]$ and [11̄1] directions [181,340]. As the compressive stress is applied along [001] direction, the polar vectors of [001] oriented rhombohedral crystals will rotate from <111> to <011> directions, as shown in Fig. 28 (a)–(b). It is proper to believe that the compressive stress induces the rhombohedral crystals approaching R-O phase transition, and is responsible for the increase of piezoelectric coefficient at prestress of 10 MPa. With further increasing the compressive stress, the crystals may transform to the O phase or be depolarized by the stress as shown in Fig. 28 (c)–(d). Thus, the piezoelectric coefficient was found to decrease at prestress of 20 MPa and disappear at prestress of 40 MPa.

Fig. 27.

Strain electric field loops for PIN-PMN-PT:Mn (a) as a function of applied compressive prestress, (b) measured at 10MPa prestress and as a function of dc bias. (data from [452])

Fig. 28.

Schematic of domain variation for [001] poled rhombohedral relaxor-PT crystal under uniaxial stress. (a) original state for [001] poled rhombohedral relaxor-PT crystal, where the solid arrows represent the possible domain directions. (b) under a moderate uniaxial stress. (c) and (d) show the two possible conditions of domain variation under a strong stress. For (c), the rhombohedral domains are transformed to orthorhombic domains by applying a stress. For condition (d), rhombohedral crystal is depolarized by the stress, where the blue arrows represent the new domain directions.

In order to maintain the linear strain behavior and avoid the depolarization under prestress, dc bias is generally applied to the piezoelectric materials [10,18,325]. Fig. 27 (b) shows the bipolar strain behavior at 10 MPa uniaxial prestress and applied ac field of 5 kV/cm, as a function of dc bias. The S-E loop measured at 10 MPa and zero dc bias exhibits a typical butterfly shape, with negative strain being on the order of 0.13 ‰, indicating that domain switch will occur if the crystal is driven by ac field under certain prestress, which will induce strain nonlinearity and deteriorate the drive field stability. It is interesting to note when a positive dc bias field was applied to the crystal, the center of the electric field was shifted toward the positive side. As a result of the increased amplitude of the positive dc bias field, the field-induced strain was extended as well on the negative side of the ac field, leading to a negative strain of 1.3 ‰. It is quite obvious that the driving electric field range, in which the crystal exhibits a linear strain response, is expanded to ±4 kV/cm or ±6 kV/cm respectively when a 2 kV/cm or 4 kV/cm dc bias is applied, indicating that the reduced linear range of the strain response for PIN-PMN-PT:Mn crystals under an uniaxial prestress could be recovered by application of a positive dc bias to the crystal [452]. Of particular interest is that the strain loops show similar slopes, leading to a similar piezoelectric coefficient of ~2400–2500 pm/V, demonstrating that the dc bias field being on the order of < 4 kV/cm has minimal effect on the piezoelectricity.

Fig. 29 shows the bipolar strain behavior of transverse vibration for PIN-PMN-PT:Mn crystals at 5 kV/cm ac field and various transverse prestress levels, with measurements on pure crystals given in the small inset for comparison. It was found that all the strain curves for doped crystals are linear and non-hysteretic, demonstrating no domain reversal occurs at 5 kV/cm under different prestress conditions; however, large hysteresis was observed for pure crystals, revealing that an ac field (~5 kV/cm) induces domain wall motion and leads to depolarization in pure crystals. This can be explained by the enhanced coercive field (~7 kV/cm) and existence of internal bias (~0.6 kV/cm) of manganese modified crystals [298], which will clamp domain wall motion and stabilize the domains. The corresponding piezoelectric coefficient d₃₂ as a function of prestress for doped and pure crystals are given in Fig. 29 (b), where one can see that the piezoelectric coefficient of PIN-PMN-PT:Mn crystals is about −1450 pm/V at 0 MPa and decreased to ~ −1000 pm/V at 21 MPa [453]. Of particular significance is that the piezoelectric coefficients measured with decompression sweep are similar to the values with loading sweep, indicating the ac driving field at 5 kV/cm has minimal effect on the piezoelectric properties of manganese modified crystals. On the contrary, it was found that the piezoelectric coefficients for pure PIN-PMN-PT crystals with both deep rhombohedral and MPB compositions decreased greatly under the combination of ac electric field and prestress, being on the order of 400 pm/V at 21 MPa, maintaining the same values during decompression sweep, indicative of the occurrence of depolarization [453].

Fig. 29.

(a) Bipolar strain behavior for PIN-PMN-PT:Mn crystals under various prestress levels (small inset shows strain behavior of pure PIN-PMN-PT for comparison), (b) Piezoelectric coefficient d₃₂ as a function of prestress for PIN-PMN-PT:Mn and compared to its pure counterparts Reprinted with permission from S. J. Zhang et al., Applied Physics Letters 102, 172902 (2013). Copyright © 2013, the American Institute of Physics [453].

In order to understand the piezoelectric properties under the combination of ac electric field and transverse stress, schematic of [011]_C poled rhombohedral relaxor-PT single crystal is given in Fig. 30. For [011]_C poled R crystals, 180° ferroelectric domains and 109° ferroelastic domains reversed with applying electric field along [011]_C direction. Only 71° ferroelastic domains remain with polarization vectors pointing at [11̄1]_C and [1̄1̄1]_C directions, exhibiting “2R” engineered domain configuration [181]. The polarization rotates from <111>_C directions to [011]_C direction via Cm monoclinic (01̄1)_C plane under an applied electric field along [011]_C direction, while the transverse compressive stress along [100]_C direction will move the polarization vectors away from the stress field direction and favor the poling state along [011]_C. Apparently, [100]_C transverse preload tends to increase the transverse extensional piezoelectric d₃₂ values under [011]_C electric field, via the MPB shift with the mechanical stress. The R-O MPB was thought to shift to lower PT content with increasing compressive stress, indicating that the studied R crystal is approaching the R-O phase boundary with increasing stress, thus leading to higher piezoelectric properties [324,454–455], analogue to the [001] prestress on [001] poled R crystals (shown in Fig. 28). However, if the composition of the studied crystal is on the proximity of MPB region, both the electric field and preload stress are cooperative driving forces for the R to O phase transformation [226]. This leads to a dramatic drop in the strain level along [100]_C direction due to the field/stress induced orthorhombic single domain state, accounting for the significantly decreased d₃₂ [453]. On the other hand, the ac bipolar drive field with magnitude of respective coercive field will induce domain reversal and lead to depolarization under transverse stress, even for the composition away from the MPB. In addition, the ac field will induce microcracks in the crystals under transverse compression due to the large anisotropic characteristics in [011] poled crystals with mm2 macroscopic symmetry, where the depolarization is unrecoverable during the decompression sweep, as in the case of pure PIN-PMN-PT crystals. The manganese modified crystals, however, show depolarization-resistant behavior. This is due to the fact that the enhanced coercive field and existence of internal bias favor the poling state as a result of clamped domain wall motion and reduced polarization rotation, demonstrating that the 3^rd generation crystals (for example, PIN-PMN-PT:Mn) are promising for acoustic transducer applications [453].

Fig. 30.

Polarization rotation for [011] poled crystals under applied transverse compressive stress σ² and electric field E₃. Reprinted with permission from S. J. Zhang et al., Applied Physics Letters 102, 172902 (2013). Copyright © 2013, the American Institute of Physics [453].

Fig. 31 shows the P-E curves as a function of compressive uniaxial prestress for thickness shear-mode PIN-PMN-PT crystals with 1T and 2R domain structures, respectively [451]. It should be noted that P-E loops were used for the thickness shear vibrations, instead of strain curves, due to the limitation of the measurement fixture. It was reported that the allowable drive field for thickness shear vibration is about ~40 % of its respective coercive field [375]. Thus, the P-E loops exhibit large hysteresis at the drive field of 4kV/cm (> ½E_C), under zero uniaxial stress for both 1T and 2R domain configurations due to the irreversible domain wall motion, leading to the depolarization of the samples. Of particular significance is that the hysteretic properties of both 1T and 2R crystals were greatly reduced by applying compressive stress to the crystals, owing to the stabilized domains by the compression prestress, as shown in Fig. 32. Therefore, the allowable electric fields can be enhanced by applying uniaxial compressive stress perpendicular to the poling direction, which were found to increase to 4.5 kV/cm and 4 kV/cm for 1T crystals at compressive stress of 25 MPa and 2R crystals at 55 MPa, respectively [451]. With applying compressive stress, though the shear piezoelectric response decreased due to the decreased dielectric permittivity [340,456–458], as confirmed by the decreased slope of the P-E loops, the level of allowable drive field increased. Therefore, the improvement in maximum shear-strain is expected by applying compressive stress. The S_max of 1T crystals was increased by 38 % under compressive stress of 25 MPa (from 0.5 % to 0.7 %), while the S_max of 2R crystals was increased by 50 % under compressive stress of 55 MPa (from 0.7 % to 1.0 %). In addition, the dielectric loss factors can be evaluated by the hysteresis area of the P-E loops [141,459]. The values are on the order of 20 % and 50 % for 2R and 1T crystals, respectively, at electric field of 4 kV/cm without applying stress, being reduced to the order of 4 % by applying compressive stresses of 55 MPa and 25 MPa for 2R and 1T crystals, respectively, which will benefit the general transducer applications (reduced heat generation). Thus, the results indicated that the allowable drive electric field of the thickness shear-mode crystals can be enhanced by applying compressive stress perpendicular to the polar direction (the same direction of the applied ac field) and lead to increased shear strain [451].

Fig. 31.

P-E loops at various uniaxial compressive stress for PIN-PMN-PT crystals with “1T” (a) and “2R” (b) domain states (measured at 1Hz). Reprinted with permission from F. Li et al., Applied Physics Letters 100, 192901 (2012). Copyright © 2012, the American Institute of Physics. [451].

Fig. 32.

Schematic of polar vectors for (a) [001] poled tetragonal crystal and (b) [011] poled rhombohedral crystal under perpendicular uniaxial stress. (Figures adapted from ref. [451])

3.3.4 Cross-talk associated with shear modes

Cross-talk is a complex phenomenon in electromechanical applications, electrically or mechanically, which will produce an error in the measured output signal for sensing applications and lead to a high noise level, or introduce extra displacement other than the required; thus, it is important to understand the piezoelectric cross-talk and the approach to eliminate the effect [460]. For example, the thickness shear piezoelectric d₁₆, on the order of −1700 pC/N, was observed in crystals with [111] poled rhombohedral relaxor-PT crystals (1R single domain state) and strongly cross-talks with piezoelectric d₁₅ [332]. Under this condition, the [111]/(11̄0) samples will generate an electric signal E₁ under both S₅/T₅ and S₆/T₆ strain/stress, as shown in Fig. 33, which hinders the detection of signal S₅/T₅ and S₆/T₆ independently. Thus, it is desirable to reduce or eliminate the cross-talk effect in practical applications. It was reported that d₁₆ can be eliminated by rotating the sample around X-axis with angle of $\alpha =\mathit{\text{arctan}}\left(\frac{-d_{16}}{d_{15}}\right)$ [332,461,462]. Another approach to obtain thickness shear samples without cross-talk includes the utilization of domain configurations other than 1R single domain state, such as 1T and 1O/2R with macroscopic symmetries of 4mm and mm2, respectively, where the d₁₆ value is zero [321,374]. It should be noted that for face shear vibration, cross-talk from extensional vibrations d₃₁ or d₃₂ can be eliminated by rotating the sample along Z-axis with angle of $\alpha =\mathit{\text{arctan}}\left(\frac{d_{31}}{-d_{32}}\right)$ or $\alpha =\mathit{\text{arctan}}\left(\frac{-d_{32}}{d_{31}}\right)$, respectively, without sacrificing the large d₃₆ [374,463] as shown in Fig. 34 (a), however, the other d₃₂ or d₃₁ mode yet presents. This is due to the fact that for Ztθ cut plate with mm2 symmetry, there exist $s_{16}^{\text{'}}=s_{26}^{\text{'}}\ne 0$ and $d_{31}^{\text{'}}=d_{32}^{\text{'}}\ne 0$. Thus, the face shear is always coupled to face longitudinal mode [464–465].

Fig. 33.

Piezoelectric coefficient matrix and cross-talk of piezoelectric 15- and 16-mode in 1R relaxor-PT crystals. The arrows represent the polarization of 1R relaxor-PT crystal. The coordinate systems for piezoelectric coefficient matrix and the shear sample are given on right.

Fig. 34.

Schematic of Ztθ cut sample (a) and ZXlt θ/ψ cut sample (b).

It is known that elastic matrix of 4mm crystals, such as [001]_C poled relaxor-PT crystals is the same as that of 4̄2, which only possesses face shear piezoelectric coefficients d₁₄ and d₃₆. However, the face shear mode cannot be excited through piezoelectric effect if d₃₆ is zero in 4mm symmetry. It is observed that when Euler rotation is made for 4mm plate, face shear d₃₆ exists under the rotated coordinate:

$$d_{36}^{\text{'}}=\frac{1}{2}\text{sin}\theta \text{sin}2\theta \text{sin}2\psi (d_{33}-d_{31}-d_{15})$$

Here θ and ψ are the second and third Euler angles. It is seen from the equation that is $d_{36}^{\text{'}}$ independent of the first Euler angle ϕ (i.e the rotation about Z-axis). When one of θ and ψ is zero, $d_{36}^{\text{'}}=0$. Thus, different from mm2 symmetry, any single-rotated 4mm plate, such as Ztθ cut, cannot support face shear mode. The non-vanished d₃₆ can appear for the double-rotated ZXlt θ/ψ cut plate as shown in Fig. 34 (b), where the thickness and other two edges of the plate are along Z-, Y- X- axes, respectively. To get such a plate, the coordinate is rotated first about X-axis by θ, then rotated about new Z-axis (Z’) by ψ. It is seen from the equation that when $\theta ={\text{cos}}^{-1}(\sqrt{\frac{1}{3}})$ and $\psi =\frac{\pi }{4},d_{36}^{\text{'}}$ reaches its maximum and ${(d_{36}^{\text{'}})}_{\text{max}}=0.385(d_{33}-d_{31}-d_{15})$. For the double-rotated cut, there exist $s_{16}^{\text{'}}=s_{26}^{\text{'}}\ne 0,d_{31}^{\text{'}}=d_{32}^{\text{'}}\ne 0$, which are similar to Zt 45° rotated mm2 plate. The calculated results are listed in Table XIV and compared to those of Zt 45° rotated mm2 plate. For the double-rotated 4mm plate, the electromechanical coupling factor k₃₆ is much less than Zt 45° mm2 plate, but with similar value of d₃₆, being on the order of >1500 pC/N. Of particular significance is that the transverse piezoelectrics are much less than those of the face shear piezoelectric $d_{31}^{\text{'}}=d_{32}^{\text{'}}\ll d_{36}^{\text{'}}$, promising for sensing applications demanding no crosstalks.

Table XIV.

Piezoelectric properties of Zt45° cut [011] poled and ZXlt 54.7°/45° cut [001] poled relaxor-PT crystals, s_ij: pm²/N; d_ij: pC/N.

Crystal cut	Domain configuration	Symmetry	$s_{11}^{*}=s_{22}^{*}$	$s_{16}^{*}=s_{26}^{*}$	$s_{66}^{*}$	$d_{31}^{*}=d_{32}^{*}$	$d_{36}^{*}$	$k_{36}^{*}$	KT
ZXt45°	2R	mm2	11.0	21.9	120	364	1650	0.83	3800
ZXlt 54.7°/45°	4R	4mm	10.3	−14.9	190	2.7	1540	0.61	3800

It should be noted that the piezoelectric cross-talk can also be reduced or eliminated by specifically designed sensor/transducer structures. To illustrate this idea, we give an example of a sensor design by using 24 shear mode of 1R relaxor-PT crystals. From piezoelectric coefficient matrix (Fig. 33), it is known that the piezoelectric coefficients d₂₁ and d₂₂ play as cross-talks for shear mode d₂₄ in 1R relaxor-PT crystals. Figure 35 gives the special design to eliminate the impact of piezoelectric coefficients d₂₁ and d₂₂. By this design, the electric signal induced by stress T₁ and T₂ can be eliminated, while the electric signal induced by shear stress T₄ is doubled. Compared to the 15-mode, the particular merit of 24-mode in 1R domain configuration is that the crystal doesn’t need to be rotated by a special angle and cut again after poling for eliminating the cross-talk effect, meanwhile, keep the same properties as 15-mode [466].

Fig. 35.

The design of 24-mode sensor by using 1R relaxor-PT crystal. In this figure, the blue arrows represent the polarization of 1R crystal. By this design, the cross-talks from d₂₁ and d₂₂ piezoelectric effects can be eliminated. (Figures adapted from ref. [466])

3.4 Piezoelectric tactile sensors

Tactile sensor is a device that is able to detect a given property, such as pressure, force, temperature, elasticity, etc., of a contact event in a predetermined area and subsequent pre-processing of the signals [467,468]. Tactile sensors have been broadly applied in automotive, electronics, intelligent machinery, defense and biomedical industry.

3.4.1 Piezoelectric materials and FOM for tactile sensors

Among numerous types of tactile sensors including piezoresistive, capacitive, piezoelectric, optical, and ultrasonic wave types (as given in Fig. 36), piezoelectric type is cost effective, simple, and highly sensitive to dynamic contact deformation [468]. However, the piezoelectric sensor based on direct piezoelectricity (or direct piezoelectric sensing) requires additional electrical circuitry for a quasi-static tactile sensing [469]. On the other hand, piezoelectric resonators including bulk acoustic wave (BAW) and surface acoustic wave (SAW) resonators are capable of both dynamic and static measurements. This type of piezoelectric sensing is also called resonant piezoelectric sensing or acoustic wave sensing. In contrast to direct piezoelectric sensors, the sensing performance of these resonant piezoelectric tactile/bio sensors is heavily dependent on the resonance properties of piezoelectric materials [470,471].

Fig. 36.

Schematic of tactile sensing techniques.

In the medical field, piezoelectric tactile sensors have been developed for measuring the elastic stiffness of tissues [472–475]. Examples include the endoscopic sensor in minimally invasive surgery (MIS) [476–477], the smart skin used in diagnosing the breast tumor or prostate gland disease, and also sensors for the intraocular pressure (IOP) in the human eye [478]. Typical resonator sensors measure changes in the resonant frequency caused by interaction between piezoelectric resonator and target materials. The change in the resonant frequency is directly proportional to the applied force by the Sauerbrey equation [479]. The local distribution of the applied mechanical stress can be detected by measuring the fundamental frequency shift of the resonator array. A relatively new tactile sensing technique, which uses the relationship between electrical impedance of the piezoelectric resonator and acoustic load impedance of the front load, has been developed for the fingerprinting application [480]. The electrical impedance of piezoelectric elements at particular frequency is changed when an object is applied to the front surface of a sensor. This change is related to the acoustic impedance of the applied objects. As a result, the distribution of the acoustic load impedance of the object can be mapped by measuring the electrical impedance of each element of the array in a rapid fashion. This device can be highly sensitive as a biometric sensor compared to capacitive and thermal tactile sensors since the contrast ratio of acoustic impedance between air and tissue is 4000:1, while that of thermal conductivity is about 8:1 and dielectric permittivity is 32:1 [481]. For these reasons, this acoustic impedance sensing is promising for applications in the biomedical industry (artificial skin sensor) and service robotics (touch screen and fingerprint reader).

The most known material of direct piezoelectric tactile sensor is PVDF piezoelectric polymer. Although piezoelectric ceramics and single crystals have much higher piezoelectricity, the piezoelectric polymers are preferred in non-resonant tactile sensing application due to their high piezoelectric voltage g coefficients, excellent flexibility and biocompatibility [482–483]. On the other hand, acceptor doped ceramics and quartz crystals with high mechanical quality factors were adopted in the resonance-based tactile sensors, where the variation of resonant frequency and impedance at resonance are sensing parameters [484–485]. The key material properties of the conventional piezoelectric materials for the tactile sensing applications are presented in Table XV. Therefore, the FOM of the piezoelectric materials for the non-resonant type piezoelectric tactile sensor can be defined as piezoelectric voltage coefficient (g_ij=d_ij/ε), while the FOM of resonant type tactile sensor can be dQ_m or k₂Q_m, which is similar to the high power ultrasound transducer applications.

Table XV.

Properties of piezoelectric materials for tactile sensors [486–488].

Type	Material	kt	d33 (pC/N)	${\epsilon }_{33}^T/{\epsilon }_0$	Qm
Non-resonant	PVDF	0.146	−32.5	7.6	8.5
Resonant	PZT-8	0.48	225	1000	1,000
	Quartz (X cut)	0.10	2.3	4.6	~27,000

3.4.2 Advantages and Challenges of Relaxor-PT Crystals

The FOM of dQ_m or k₂Q_m among various relaxor-PT crystals is shown in Table X and XI, which suggests that Mn-doped PIN-PMN-PT crystals exhibit the highest dQ_m of 1050×10³ pC/N, being much higher than quartz and acceptor doped ceramics. Of interest is that the face-shear mode relaxor-PT crystals have drawn research attention due to their high piezoelectric coefficients (e.g. d₃₆ of 1600–2800 pC/N) and ultrahigh elastic compliances $(s_{66}^E>120\mathrm{p}{\mathrm{m}}^2/\mathrm{N})$. More importantly, unlike thickness shear mode, the face shear mode was found to possess much higher mechanical quality factor Q_m (>120, compared to ~30 for thickness shear mode) and can be easily repolarized since the poling electrodes are the same as the active electrodes [335]. These unique properties suggest the need of further study on face shear mode single crystals for potential advanced applications.

By using the face-shear mode PMN-PT single crystal resonators, a new type of tactile sensor has been developed [378–380]. In this reported sensor configuration, the thin polymer layer (silicone rubber) was used as a sensing layer and attached to the large surface of a face shear mode resonator. The electrical impedance amplitude changes induced by the applied surface loads were measured. The sensitivity or the ratio of electrical impedance change to the surface load variations was calculated and compared among thickness mode, thickness-shear mode and face-shear mode single crystal piezoelectric resonators. Fig. 37 presents the results of measured electrical impedance changing with acoustic load impedance in three different modes at resonant frequency. One can observe that for the face-shear mode resonator, the electrical impedance increased rapidly with the increasing acoustic impedances of surface loads at the resonant frequency. This is in stark contrast to the findings from thickness and thickness-shear mode resonators with similar sizes. Specifically, the ratio of electrical impedance shift to the applied acoustic impedance of the face-shear mode resonator was found to be at least 20 times and 90 times higher than those of thickness-shear mode and thickness mode resonators, respectively.

Fig. 37.

Measured electrical impedance at the resonant frequency; impedance change in relation to (a) material properties of sensing layer and (b) applied force. Reprinted with permission from K. Kim et al., Applied Physics Letters 100, 253501 (2012). Copyright © 2012, the American Institute of Physics. [379].

In addition to the single element acoustic load sensor, face shear mode tactile sensor array was developed by Kim et al [378]. The 8×8 tactile sensor array is composed of aforementioned sensors. The face shear mode PMN-PT single crystal plates (820×820×300 µm³) were also used as an active material. One difference of the sensing element is that polydimethylsiloxane (PDMS) was used as the sensing layer instead of the silicone rubber. This is because PDMS is transparent, flexible and has low acoustic impedance. Based on the sensing element design, the array exhibited the spatial resolution of 1.1 mm, which is high enough as a tactile sensor application. The fabricated array was tested with different liquids such as water and isopropyl alcohol (IPA) due to their different acoustic impedance: 1.5 MRayl (water) and 0.9 MRayl (IPA), respectively. The electrical impedance change due to the applied liquid drop was measured using impedance analyzer. The sensor array with a water drop and corresponding mapped image is shown in Fig. 38. The dark elements in the mapped image show larger electric impedance shift due to the water drop. On the other hand the bright area indicated small impedance shift at the resonant frequency. The electrical impedance shift variation is caused by surface force distribution on the sensing array and the droplet thickness variation. Going forward, the challenge of current piezoelectric tactile sensing technology by both resonant and non-resonant types is temperature dependency [483,489], and this is also the limitation of relaxor-PT crystals. Thus, temperature-independent properties of domain-engineered crystals can be considered together with aforementioned FOM for tactile sensor applications.

Fig. 38.

(a) Sensor array with an applied water drop; (b) Mapped image for water drop. Reprinted with permission from K. Kim et al., IEEE IUS 2012, 1059 (2012). Copyright © 2012, IEEE. [378].

3.5 Acoustic Tweezers

Acoustic tweezers is a device that can remotely capture and manipulate target particles using acoustic waves. Acoustic tweezers has been widely researched for medical, biological, and chemical applications [490,491]. Optical tweezers has been the most well-known and widely used contact-free method due to its high precision, but it is also known to have several drawbacks. First, optical tweezers works only for optically transparent and shallow media. Second, the target particles can be damaged due to the high intensity of a focused laser. Third, it is difficult to be miniaturized since the required apparatus are bulky, expensive, and complicated [492,493]. These problems can be relieved to some degree by using acoustic tweezers because of its relative simplicity, independence to the targets’ material properties, and non-invasiveness to biological objects. Thus, acoustic tweezers has been actively researched over the last two decades.

3.5.1 Piezoelectric materials for acoustic tweezers

Based on the numerous reported acoustic tweezing methods, the operation mode can be categorized into (a) standing bulk acoustic wave (SBAW), (b) standing surface acoustic wave (SSAW), and (c) single beam mode (Fig. 39).

Fig. 39.

Schematic of acoustic tweezers.

(a) Standing bulk acoustic wave: In order to superpose two or more beams, multiple ultrasonic transducers or one transducer with a reflector are used for the SBAW mode manipulation [494]. In the standing wave field, the stationary points of the zero acoustic pressure amplitude (pressure node) coincide with the maximum velocity (velocity anti-node) [495]. The gradient of the acoustic pressure (Bernoulli pressure) leads to a steady-state acoustic radiation force. Thus, the particles are typically trapped in the pressure node (velocity anti-node) of the standing wave field [496,497], and then the trapped particles are manipulated by changing the frequency of the acoustic waves [494]. In this mode, the general operating frequency range was from 1 to 15 MHz, and PZT4 piezoelectric ceramic transducers were used in the reported studies because of their relatively high Q_m [498,499]. (b) Standing surface acoustic wave mode: For the integration of a manipulation system with microfluidics, particle manipulations using SSAW was developed [500]. SSAW tweezers is composed of two equal inter-digital transducers (IDTs) and a microfluidic channel. The most of IDTs for SSAW tweezers are made of Y+128° X-propagation lithium niobate (LiNbO₃) due to its high coupling factor in SAW generation [500,501]. The interference of two SAWs at the fluid in the microchannel generates a standing wave field. Therefore, the microparticles are aligned and patterned inside the microchannel [502]. In comparison with SBAW, SSAW has several advantages. First, the frequency can be easily increased up to hundreds of megahertz for highly precise manipulations. Second, SSAW tweezers can be easily integrated into a microsystem, because the reflector is not necessary, whereas SBAW requires almost perfect acoustic reflection from the microchannel, but microchannels are usually made of PDMS, which has a poor acoustic reflection in fluid [502]. (c) Single beam acoustic wave: The single beam acoustic trapping can manipulate a single particle by using a single acoustic beam, while the standing wave approach only works for trapping a group of particles [503,504]. For the single beam tweezing, highly focused ultrasound beam is necessary because it generates a negative radiation force that pulls the particle towards the focal point. A sharp acoustic intensity variation along the lateral direction of the acoustic beam is the requirement for the single beam tweezers [505]. It was reported that tightly focused beams at 96 MHz and 200 MHz are able to capture lipid particles with a size of 50 µm and 10 µm in diameter, respectively [504,506]. Large aperture and thin thickness of the piezoelectric component is usually desired for very high frequency (> 100 MHz) focused ultrasound with a sharp focus. Therefore, zinc oxide (ZnO) film and LiNbO₃ single crystals have been broadly utilized for high frequency focused ultrasound transducers due to their low dielectric permittivity and acceptable electro-mechanical couplings [504,507].

3.5.2 Advantages and Challenges of Relaxor-PT Crystals

Although the LiNbO₃ single crystal is the dominant piezoelectric material for SSAW and single beam tweezers, the superior piezoelectric and dielectric properties of relaxor-PT single crystals have also been studied for particle manipulations using microfluidic devices [508,509] and needle transducers [510]. The common motivation to use PMN-PT single crystals is the miniaturization of the ultrasound transducer with an acceptable radiation force. For miniaturized transducers, high dielectric constant of active material is desirable because the transducer can maintain acceptable electrical impedance [510]. In addition, high piezoelectricity and electro-mechanical coupling are always a plus in focused ultrasound. Therefore, it is fair to say that relaxor-PT single crystal is a promising candidate for acoustic tweezers due to its superior piezoelectric, dielectric, and couplings compared to PZT, ZnO, and LiNbO₃.

The Needle transducers for ultrasonic imaging and tweezing made of PMN-PT single crystals were developed by Hsu et al. (Fig. 40) [510]. At the resonant frequency, the maximum displacement of the target particle was measured to determine the distance through which the target particle can be pulled by the trapping force. This result showed that the PMN-PT single beam tweezers can manipulate a microparticle (15 µm) with the size smaller than the wavelength of the ultrasound wave (24 µm) [510]. The microfluidic device for standing BAW tweezing was developed using PMN-33%PT single crystals (Fig. 41) [508]. The polystyrene particles were trapped at the center of the cavity within 200 ms after the electric field was applied at resonant frequency [508]. This result shows that the PMN-33%PT single crystals can be promising to generate enough amplitude of the standing wave field in miniaturized tweezers.

Fig. 40.

Design cross section of a self-focused needle transducer. Reprinted with permission from H. Hsu et al., Applied Physics Letters 101, 024105 (2012). Copyright © 2012, the American Institute of Physics. [512].

Fig. 41.

(a) Schematic and (b) photograph of the microfluidic device for ultrasonic trapping of microparticles. Reprinted with permission from S. Guo et al., Applied Physics Letters 92, 213901 (2008). Copyright © 2008, the American Institute of Physics. [508].

FOM of piezoelectric materials for acoustic tweezers can then be determined on the basis of the acoustic tweezers types. For SBAW and SSAW acoustic tweezers, mechanical Q_m and piezoelectricity of piezoelectric materials are the key parameters to consider. In the aspect of SAW based tweezers, the PMN-PT crystal has more promising points than LiNbO₃, which is the most-used piezo-substrate for SAW. PMN-PT crystals with MPB composition showed lower surface acoustic velocity, higher coupling factor, and lower power flow angle (PFA) than those of LiNbO₃ [511]. The low acoustic wave velocity is required for high manipulation resolution at miniaturized dimension, and low power flow angle is advantageous for reduced acoustic attenuation and improve electromechanical performance of SAW devices. The maximum coupling factor, minimum velocity, and minimum PFA of Y-cut PMN-PT single crystal are 0.35, 1156 m/s, and 1.5°, respectively, whereas the LiNbO₃ substrate has those parameters of 0.2, 3300 m/s, and 7°, respectively [511]. Therefore, the PMN-PT crystals have great merits for miniaturized SSAW tweezers. On the other hand, the single beam tweezers showed more promising performance for the precise manipulation of a single microparticle compared to SBAW or SSAW tweezers. For the single beam tweezers, high acoustic power at the resonant frequency is required. The operation frequency is not usually modulated during a particle manipulation. Therefore, the FOM of piezoelectric materials for the single beam acoustic tweezers can be similar to high power therapeutic applications (dQ_m and/or k² Q_m). Thus, the Mn-doped PIN-PMN-PT can show better performance than PMN-PT crystal in single beam tweezing application, because the Mn:PIN-PMN-PT has much higher dQ_m (1050×10³) than PMN-PT crystals (~420×10³). Although high resonance performance may be most important for the single beam tweezers, the miniaturized transducer for imaging and tweezing, as in [510], need to be designed aiming both high power and wide bandwidth. Moreover, desirable dielectric property for miniaturized transducers also conflicts with the large aperture and high frequency (>100 MHz) design. Therefore, one may design a SBAW, a SSAW or a single beam acoustic tweezers using respective piezoelectric materials to meet the specific application requirements.

3.6 Ultrasonic Motors

Ultrasonic motor (USM) is a motor operated by the ultrasonic vibration. The applied electrical signal is converted to the elastic waves in active material attached to a stator, and then the friction tip on the stator can excite the rotor by ultrasonic vibration. Miniaturized motors have been in great demand in various electromechanical systems such as camera modules, deformable mirrors, precision positioning adaptive structures in aerospace applications and biomedical instruments [513].

3.6.1 Piezoelectric Materials for Ultrasonic Motors

The USMs are known to have high efficiency and accuracy in millimeter or micrometer scale, whereas the conventional electromagnetic (EM) motors are suggested with very low power density and poor efficiency, accuracy, and reliability [514]. Thus, numerous designs of USMs have been developed such as travelling wave motors, wobbling mode motors, shear mode disk rotary motor, and hybrid mode linear motors [367,513,515]. All these piezoelectric ultrasonic motors operating in friction drive mechanism at resonance exhibit quick response, high resolution in positioning, low profile, and high power density [513,516,517]. These motors usually adopt piezoelectric materials in the driving components, and operate at resonance for the maximum electric-to-mechanical energy conversion [382,518].

Hard piezoelectric materials with a high mechanical quality factor Q_m are considered proper driving materials in order to minimize heat generation and maximize the displacement at resonance [518]. For example, PZT4 and PZT8 ceramics that have Q_m of 500 and 1000, respectively, have been often used in piezo-motor applications [513,515]. Other piezoelectric material properties such as piezoelectric coefficients, electromechanical couplings, dielectric constants, etc. are also important parameters to be considered in USMs for high energy density. As an example, the energy density (U) in a USM under a lateral mode resonance driving can be simplified as the following equation [519].

$$U=\frac{1}{2}{Q}_{m31}^2{k}_{31}^2{\epsilon }_{33}{E}^2=\frac{1}{2s_{11}^E}{Q}_{m31}^2{d}_{31}^2{E}^2$$

where k₃₁ is the electromechanical coupling factor, ε₃₃ is the dielectric constant, E is the electric field, d₃₁ is the piezoelectric coefficient, and $s_{11}^E$ is the elastic compliance of a piezoelectric material. This equation shows that high mechanical quality factor, electromechanical coupling factor, and dielectric constant are advantageous for high energy density of USMs [520].

Therefore, the FOM can be closely related to the energy density shown in the above equation and can be determined as $Q_m^2{k}_{ijkl}^2{\epsilon }_{ij}$ (i, j, k, l = 1, 2, 3). This FOM is similar to that of materials for the therapeutic and surgical high power ultrasound. The advantages and challenges for this application are also similar to the high power ultrasound applications described in section 3.2.2. The difference is that the piezo-motors usually operate in more than two modes including a lateral mode (31 mode), thickness mode, and shear mode, whereas the high power ultrasound usually only involves one vibration mode.

3.6.2 Advantages and Challengers of Relaxor-PT Single Crystals

Generally, in spite of their high piezoelectric and dielectric properties, relaxor-PT single crystals are not optimal driving materials for piezo-motors due to their relatively low Q_m. However, for miniaturized USM designs working in non-continuous mode, the heat generation by the loss is not an issue, and hence relaxor-PT crystals can be used as a driving material because of their high dielectric constants and electromechanical couplings. Ci et al. developed a standing wave PMN-PT single crystal ultrasonic linear motor operating in high-order face shear modes (FS-2 and FS-3 modes) and compared with a larger size piezo-ceramic motor [382]. Fig. 42 schematically shows the USM with motion trajectories of the two non-isomorphic in-plane face-shear vibration modes [382]. Face shear mode of the PMN-PT crystal was utilized for the USM design due to its prominent electromechanical coupling (0.77–0.83) and higher Q_m (100–450). The prototyped face shear mode motor exhibited large generating force (e.g. 1.0 N) at a relatively low driving voltage (50 V_pp), which is really impressive compared to even larger size PZT motors [382,521].

Fig. 42.

Vibration amplitude properties of FS-2 and FS-3 modes, (a) and (c) measured displacement amplitudes (colored contours) and simulated deformation shapes (red contours), corresponding to T/4 and 3 T/4 cycle, (b) and (d) measured motion trajectories of the Corners (A) and (B). Reprinted with permission from P. H. Ci et al., Applied Physics Letters 104, 242911 (2014). Copyright © 2014, the American Institute of Physics [382]

In addition to the high Q_m and high coupling, the high coercive field E_c is also advantageous to USMs operating at their resonance frequency since higher driving field can be applied to improve the energy density, according to the above equation. Therefore, the second generation crystals, PIN-PMN-PT, were adopted to develop a double-mode piezoelectric rectangular plate actuator due to the higher E_c (~5 kV/cm), which is one of the simplest designs of piezoelectric motors [514]. The first longitudinal (L1) and the second bending (B2) mode were excited to generate an elliptical motion of the frictional tip (Fig. 43) [522]. The displacement of the developed motor along the longitudinal direction was ~0.11 µm under 5 V input voltage, which is comparable to the performance of the multilayer piezo-ceramic motors [514].

Fig. 43.

Schematic drawings of piezoelectric single-crystal PIN-PMN-PT L1-B2 double-mode micro-motor. Reprinted with permission from T. Hemsel and J. Wallaschek, Ultrasonics 38, 37–40 (2000). Copyright © Elsevier B.V. (2000) [522].

Considering the fact that the mechanical quality factor and coupling factors equally affect the energy density, the 3^rd generation relaxor-PT crystals can be a promising driving material due to their even higher Q_m. For example, [001]_C poled Mn:PIN-PMN-PT crystal shows k₃₁ of 0.49, Q₃₁ of 500, and ${\epsilon }_{33}^T/{\epsilon }_0$ of 3810 [304], and then the FOM is 229×10⁶, which is much larger than those of conventional hard piezo-ceramics including PZT8 and PZT4 ceramics, with FOM of 90×10⁶ and 35×10⁶, respectively (Table XVI).

Table XVI.

Comparison of hard ceramics and relaxor-PT crystals for USM application [278,317,304].

Piezo Materials	k31	d31 (pC/N)	${\epsilon }_{33}^T/{\epsilon }_0$	Qm31	$Q_{m31}^2{k}_{31}^2{\epsilon }_{33}(\times {10}^6)$
PMN-PT29 (Gen I)	0.44	−699	5400	120	15
PMN-PT (MPB) (Gen I)	0.59	−1330	8200	80	18
PIN-PMN-PT (Gen II)	0.50	−712	4400	150	25
PIN-PMN-PT (MPB) (Gen II)	0.65	−1337	7240	100	31
Mn:PIN-PMN-PT (Gen III)	0.49	−609	3810	500	229
Mn:PMN-PZT (Gen III)	0.45	−531	3410	600	249
PZT4	0.33	−123	1300	500*	35
PZT8	0.30	−97	1000	1000*	90

^*The mechanical Q_m31 for polycrystalline ceramics is assumed to be the same value of Q_m33.

3.6.3 Relaxor-PT Single Crystal Cryogenic Motors

In addition to the high energy density of relaxor-PT single crystal USMs, excellent cryogenic properties of relaxor-PT crystals, as described in section 2.3.3, are also attractive characteristics of relaxor-PT single crystal USMs. PMN-PT single crystal wobbling mode linear piezo-motor and PMN-PT single crystal traveling wave linear and rotary motors were developed recently for cryogenic actuation applications [367].

Fig. 44 shows a PMN-PT single crystal piezomotor based on wobbling mode with center coupling [359]. Two PMN-PT single crystal ring stacks were fabricated with segmented electrodes to apply one pair of voltage signals with a π/2 phase difference such that a “wobbling motion” at the center part of the stator was excited with high efficiency. The motor was driven at 41.5 kHz, and operated successfully from room temperature down to −200 °C [359]. Fig 45 shows the design of a single crystal traveling wave USM [366]. The motor was made of nine PMN-PT single crystal isosceles trapezoids, which were bonded on a titanium-alloy ring forming uni-morph structures and operated on a nine wavelengths (9λ) flexure traveling wave principle. The measured maximum torque output of this PMN-PT traveling wave motor was 1.5 kg·cm, the minimum step resolution was 0.072°/step, and the power consumption at a 25 % duty cycle was 2 W. This motor successfully operated in a liquid-nitrogen environment of 77 K under a load.

Fig. 44.

Wobbling mode piezomotor. Left: schematic view of a wobbling motor; Middle: photograph of an assembled stator with two single crystal stacks; Right: assembled single crystal linear motor. Reprinted with permission from S. X. Dong et al., Applied Physics Letters 86, 053501 (2005). Copyright © 2005, the American Institute of Physics [359]

Fig. 45.

PMN-PT single crystal/Ti-alloy 9λ traveling wave motor: (a) PMN-PT/Ti-alloy stator and its impedance spectrum; and (b) motor configuration. Reprinted with permission from S. X. Dong et al., Applied Physics Letters 92, 153504 (2008). Copyright © 2008, the American Institute of Physics [366]

The cryogenic performance of the 2^nd generation crystal motor was also reported. The wobbling mode linear motor using PIN-PMN-PT was developed and the cryogenic performance was characterized by Li et al. [523]. The measured cryogenic performance was prominent in comparison with that of the previously reported PZT ceramic based motor. The maximum linear speed of 75 mm/s at room temperature was decreased to 45 mm/s at the cryogenic temperature of −175 °C. Although there was 50% decrement of the speed at the cryogenic temperature, this performance still shows great merits of the 2^nd generation crystal in comparison for the cryogenic motor application in comparison with the conventional PZT ceramic based motor, which could work well at temperatures above −80 °C, and stopped working completely at −100 °C [523].

The published work suggests that PMN-PT single crystal motors have a significant torque improvement relative to PZT ones, under relatively low voltages in cryogenic environments. The second generation and third generation relaxor-PT single crystals may be even more promising for cryogenic motors due to their increased quality factor Q_m and coercive field E_c.

IV. Summary

4.1 Impact and Significance of Relaxor-PT Crystals

Relaxor-PT single crystals have been some of the most important materials among the piezoelectric families, due to their ultrahigh piezoelectric coefficients and electromechanical coupling factors on the order of >1500 pC/N and >0.9 (k₃₃), respectively, far outperforming state-of-the-art ferroelectric PZT ceramics. PMN-PT, as the first generation relaxor-PT crystals, have been successfully commercialized in medical diagnostic transducers, showing great advantages compared to their PZT ceramic counterparts. In addition to the ultrahigh piezoelectric properties, relaxor-PT crystals show strong anisotropic characteristics as well, resulting in some new piezoelectric modes which do not exist in ceramic counterparts, such as independent giant thickness shear piezoelectric coefficients d₁₅/d₂₄ in [011] poled orthorhombic crystals with mm2 macroscopic symmetry and face shear d₃₆ mode in [011] poled rotated rhombohedral crystals. These properties can be unique in designing new and high performance piezoelectric devices for specific applications including miniaturized underwater transducer and biomedical sensing.

4.2 Challenges

Relaxor-PT crystals possess great advantages over conventional polycrystalline ceramics, being successfully employed for commercial medical imaging. Lots of challenges, however, are still present for the growth and utilization of relaxor-PT crystals, specifically for applications with operations over wide temperature range and at high power conditions, such as high power therapeutic transducers and underwater transducers. These challenges include, but are not limited to: how to achieve large crystals with homogeneous composition (related to crystal cost and property variation), how to enhance the coercive field (related to the input power), how to increase ferroelectric phase transition temperature T_RT (related to the temperature usage range), how to achieve temperature independent dielectric and piezoelectric properties (related to reliability and stability) and how to improve the mechanical quality factor (related to the output power). With respect to materials design, some improvements have been achieved in the second and third generation crystals, where the coercive field, T_RT and mechanical quality factor have been enhanced to some extents. In addition to materials design, researches on device design and modeling are also being challenged for better utilization of relaxor-PT crystals in new applications. By proper design, it is expected that the shortcomings of relaxor-PT crystals can be avoided in practical applications.

4.3 Future Research

PMN-PT and PIN-PMN-PT crystals have been successfully grown along <001> crystallographic direction, with 50–100 mm in diameter and 100–200 mm in length, by using the modified Bridgman method. However, the chemical inhomogeneity of the as-grown relaxor-PT crystals yet persists, albeit much improvement has been achieved by continuous top-feeding growth method. It is desirable to focus the research on the chemical homogeneity along the axial and radial directions of the crystals with efforts on the modified growth technique.

In addition, it is well accepted that relaxor-PT crystals show great advantages in piezoelectric devices, however, the applications have been mainly focused on some traditional areas, where PZT ceramics have been maturely utilized. In these areas, relaxor-PT crystal devices are generally designed following the techniques of PZT-ceramic devices. Although the devices may exhibit much improved performance when PZT ceramics are replaced by relaxor-PT crystals, new functionalities weren’t achieved in these devices. In the future, designing devices with specific functionalities by utilizing relaxor-PT crystals is important and worthy of more research attention. As discussed in this review, relaxor-PT crystals exhibit lots of novel properties which do not exist in PZT ceramics. Thus, new devices for specific applications can be designed by considering these novel properties. For example, by using the piezoelectric face shear mode, relaxor-PT crystals have shown great potential for underwater acoustic and tactile sensing applications.

With the advancements of material and device developments, it is expected in the near future that various new electroacoustic transducers based on relaxor-PT crystals could play an increasingly important role in the respects of bio-detection, human health, security and life science.

Nomenclature

d_ijk

piezoelectric coefficient measured in the stardard coordinate system, pC/N

d_ijk*

piezoelectric coefficient measured/calculated in the rotated coordinate system, pC/N

d_h

hydrostatic piezoelectric charge coefficient, pC/N

g_h

hydrostatic piezoelectric voltage coefficient, Vm/N

$K_{ij}^T$

dielectric constant under constant strain

$K_{ij}^S$

dielectric constant under constant stress

k_iμ/k

electromechanical coupling factor

k_t

electromechanical coupling factor for thickness mode

$s_{ii}^E$

elastic compliance, m²/N

Q_m

mechanical quality factor

T_C

Curie temperature, °C

T_RT

rhombohedral-tetragonal phase transition temperature, °C

T_OT

orthorhombic-tetragonal phase transition temperature, °C

E_C

coercive field, kV/cm

E_int

internal bias field, kV/cm

Q_λμ

electrostrictive coefficient, m⁴/C²

${\epsilon }_{33}^S$

dielectric permittivity under constant strain, F/m

${\epsilon }_{33}^T$

dielectric permittivity under constant stress, F/m

$c_{33}^D$

elastic stiffness under constant electric displacement, N/m²

ρ

density, g/cm³

c

elastic stiffness, N/m²

v

vibration velocity of transducer surface, m/s

tanδ

dielectric loss

P_disp

dissipated power

ω

angular frequency

Y_r

Young’s modulus

S

strain

P

acoustic power

R_r

radiation resistance

R

internal mechanical resistance

η_ea

electroacoustic efficiency

V_rms

the amplitude of measurement voltage

N_ij

frequency constant

NDT/NDE

non-destructive testing/evaluation

LN

LiNbO₃

LT

LiTaO₃

BT

BaTiO₃

SAW

surface acoustic wave

BAW

bulk acoustic wave

SBAW

standing bulk acoustic wave

SSAW

standing surface acoustic wave

PNR

polar nanoregion

PMN

lead magnesium niobate

PMN-PT

Pb(Mg_1/3Nb_2/3)O₃-PbTiO₃

PZN-PT

Pb(Zn_1/3Nb_2/3)O₃-PbTiO₃

FOM

figure of merits

PZT

PbZrO₃-PbTiO₃

PZT4, PZT5A, PZT5H, PZT8, etc.

impurities-labeled PZT

PIN-PMN-PT

Pb(In_0.5Nb_0.5)O₃-Pb(Mg_1/3Nb_2/3)O₃-PbTiO₃

PMN-PZ-PT

Pb(Mg_1/3Nb_2/3)O₃- PbZrO₃-PbTiO₃

PYNT

Pb(Yb_0.5Nb_0.5)O₃-PbTiO₃

BSPT

BiScO₃-PbTiO₃

PC-MUT

piezoelectric composite- micromachined ultrasound transducer

HIFU

high intensity focused ultrasound

MPB

morphtropic phase boundary

PPT

polymorphic phase transition

IOP

intraocular pressure

PDMS

polydimethylsiloxane

IPA

isopropyl alcohol

IDT

inter-digital transducers

V_pp

peak-to-peak voltage

1O, 3O, 4O, 1T, 2T, 3T, 1R, 2R, 4R

various domain configurations for relaxor-PT crystals