Optimal resource allocation in cellular sensing systems

Significance

Cells continually have to sense their environments to make decisions—to stay put or move, to differentiate or proliferate, or even to live or die. However, they are thwarted by noise at the cellular scale. Cells use signaling networks to filter this noise as much as possible and sense accurately. To operate these networks, resources are required: time, protein copies, and energy. We present a theory for the optimal design of cellular sensing systems that maximize sensing precision given these resources. It reveals a new design principle, namely that of optimal resource allocation. It describes how these resources must be allocated so that none are wasted. We show that the chemotaxis network of Escherichia coli obeys this principle.

Abstract

Living cells deploy many resources to sense their environments, including receptors, downstream signaling molecules, time, and fuel. However, it is not known which resources fundamentally limit the precision of sensing, like weak links in a chain, and which can compensate each other, leading to trade-offs between them. We present a theory for the optimal design of the large class of sensing systems in which a receptor drives a push–pull network. The theory identifies three classes of resources that are required for sensing: receptors and their integration time, readout molecules, and energy (fuel turnover). Each resource class sets a fundamental sensing limit, which means that the sensing precision is bounded by the limiting resource class and cannot be enhanced by increasing another class—the different classes cannot compensate each other. This result yields a previously unidentified design principle, namely that of optimal resource allocation in cellular sensing. It states that, in an optimally designed sensing system, each class of resources is equally limiting so that no resource is wasted. We apply our theory to what is arguably the best-characterized sensing system in biology, the chemotaxis network of Escherichia coli. Our analysis reveals that this system obeys the principle of optimal resource allocation, indicating a selective pressure for the efficient design of cellular sensing systems.

Biochemical networks are the information-processing devices of life. Like any device, they require resources to be built and run. Components are needed to construct the network, space is required to accommodate the components, time is needed to process the information, and energy is required to make the components and operate the network. These resources constrain the design and performance of any biochemical network. However, it is not clear which resources are indispensable, thus fundamentally limiting the performance of the network, and which resources might trade-off against each other. Here, we consider the interplay among cellular resources, network design, and performance in a canonical biochemical function, namely sensing the environment.

Living cells can measure chemical concentrations with extraordinary precision (1–3), raising the question what sets the fundamental limit to the accuracy of chemical sensing (1). Cells measure chemical concentrations via receptors on their surface. These measurements are inevitably corrupted by noise that arises from the stochastic arrival of ligand molecules by diffusion and from the stochastic binding of the ligand to the receptor. Berg and Purcell pointed out that the sensing error is fundamentally bounded by this noise extrinsic to the cell, but that cells can reduce the error by taking multiple independent measurements (1). One way to increase the number of measurements is to add more receptors (1, 4). Another is to take more measurements per receptor over time; here, the cell infers the concentration not from the instantaneous number of ligand-bound receptors, but rather from the average receptor occupancy over an integration time T (1, 4–11).

This time integration has to be performed by the signaling networks that transmit the information from the surface of the cell to its interior (10). Although the work of Berg and Purcell and subsequent studies identify time and the number of receptors as resources that limit the accuracy of sensing, the fundamental limits that have emerged ignore the cost of making and operating the signaling network. Making proteins is costly; producing proteins that confer no benefit to the cell can slow down bacterial growth (12). Moreover, many networks are driven out of thermodynamic equilibrium by the continuous turnover of fuel molecules such as ATP, leading to the dissipation of heat (13–17). In fact, one can estimate that the fuel needed to operate a sensory network is comparable to that to make new components after cell division (SI Text).

In this manuscript, we present a theory for the optimal design of sensing systems, which maximizes sensing precision given the available cellular resources. The theory applies to the large class of sensing systems in which a receptor drives a Goldbeter–Koshland push–pull network (18). These systems are ubiquitous in prokaryotic and eukaryotic cell signaling (19): examples include GTPase cycles, as in the Ras system, phosphorylation cycles, as in MAPK cascades, and two-component systems like the chemotaxis system of Escherichia coli.

We derive for this class of systems how the sensing accuracy depends on not only the number of receptors and their integration time, but also on the resources required to build and operate the downstream signaling network: the copies of signaling molecules and fuel. This allows us to address the following questions: How do the sensing limits set by the latter resources compare with the canonical limit of Berg and Purcell, which is set by the resources time and the number of receptors? How does the limit set by one resource depend on the levels of the other resources? Can resources compensate each other to achieve a desired sensing precision, leading to trade-offs between them, or are the limits set by the respective resources fundamental, i.e., independent of the levels of the other resources? In addition, what do these relationships imply for the optimal design of a system that maximizes sensing precision?

We find that the resource limitations of these systems emerge naturally when the signaling networks are viewed as devices that discretely, rather than continuously, sample the receptor state via collisions of the signaling molecules with the receptor proteins. This analysis reveals that three classes of resources are required: (i) receptors and their integration time, (ii) copies of downstream molecules, and (iii) energy (fuel). Indeed, these classes cannot compensate each other: each imposes a sensing limit, and it is the limiting class that imposes the fundamental limit on the accuracy of sensing. However, there can be trade-offs within each class of resources. Receptors and integration time trade-off against each other in achieving a desired sensing accuracy, and power and response time trade-off against each other to meet the energy requirement for taking a measurement.

Our theory makes a strong prediction for the optimal design of sensing systems. Because the fundamental resource classes cannot compensate each other in achieving a desired sensing precision, any class that is not limiting the sensing precision is in excess and thus wasted. This naturally leads to a previously unidentified design principle, namely that of optimal resource allocation. It states that in an optimally designed sensing system each fundamental class of resources is equally limiting so that no resource is wasted. We test this prediction for the chemotaxis system of Escherichia coli, which is a specific example of the class of push–pull sensing systems (Fig. 1). Our analysis reveals that this network obeys the principle of optimal resource allocation. This indicates that there is a selective pressure on not only the topology of sensing networks that enhances robustness of adaptation (20–22), but also on the efficient allocation of cellular resources for precise sensing.

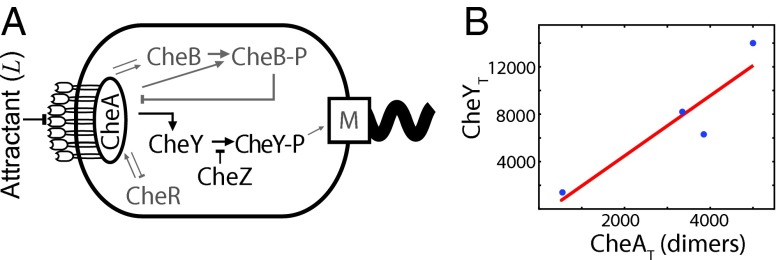
Fig. 1.

The chemotaxis network of E. coli obeys the principle of optimal resource allocation, which states that in an optimally designed system each cellular resource is equally limiting. (A) Cartoon of the sensing system. The receptor is via the adaptor protein CheW associated with the kinase CheA. This complex, coarse-grained as R in our model, can bind extracellular ligand L and activate the intracellular messenger protein CheY (x in our model) by phosphorylating it; phosphorylated CheY controls the rotation direction of the motor. Deactivation, i.e., dephosphorylation, of CheY is catalyzed by the phosphatase CheZ; the effect of CheZ is coarse-grained into the deactivation rate. The proteins CheR and CheB, which implement adaptation, have been omitted, because we are interested in the lower bound on the accuracy of sensing in static environments. (B) The principle of optimal resource allocation, Eq. 5, predicts that the number of CheY proteins, $X_T$, scales linearly with the number of receptor–CheA complexes, $R_T$, with a slope given by the relaxation time of the signaling network, ${\tau }_r$, over the correlation time of the receptor ligand-binding state, ${\tau }_c$. Plotted are data from ref. 23 for two E. coli strains under two different growth conditions; the number of CheA dimers is a proxy for the number of receptor–CheA complexes. The line is a best fit to the data, having a slope of $\approx 3$. The resource allocation principle, Eq. 5, thus predicts that ${\tau }_r/{\tau }_c\approx 3$. This is on the same order of magnitude as that given by the relaxation time, ${\tau }_r\approx 100\hspace{0.17em}\text{ms}$ (24), and correlation time ${\tau }_c\approx 10\hspace{0.17em}\text{ms}$, estimated from the measured receptor–ligand dissociation constant (25) and association rate (26).

Results

Sensing at the Molecular Level.

We consider a cell with $R_T$ receptor proteins that independently bind ligand L, $R+L\rightleftharpoons RL$ (Fig. 2A). The receptor drives a push–pull network, which is a canonical nonequilibrium motif in prokaryotic and eukaryotic cell signaling (19). In these systems, the receptor itself or the enzyme associated with it, such as CheA in E. coli (Fig. 1), catalyzes the chemical modification of a readout protein x, such as CheY. Active readout molecules $x^{\ast }$ can decay spontaneously or be deactivated by an enzyme, like the phosphatase CheZ in E. coli.

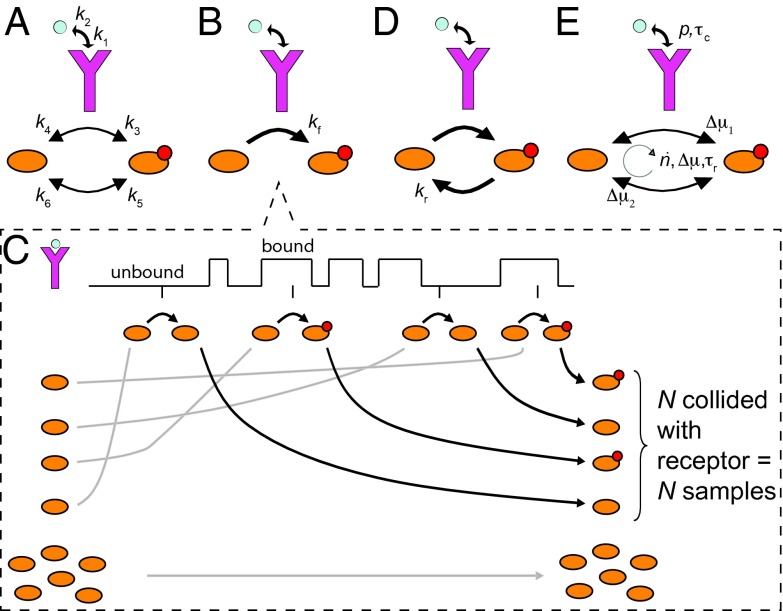
Fig. 2.

Sensing at the molecular level. The sensing precision in terms of the rate constants $\left\{k_i\right\}$ (A) does not reveal the resource requirements (Eq. S8). To reveal these, the signaling network is viewed as a device that discretely samples the ligand-binding state of the receptor. The accuracy of sensing depends on how the samples are taken (B and C), erased (D), and on how reliable they are (E). (B) The ligand-bound receptor drives the modification of a downstream readout (i.e., the push–pull network $RL+x\to RL+x^{\ast }$). (C) The signaling network in B discretely samples the receptor state, illustrated for one receptor. The states of the receptor over time are encoded in the states of the N molecules that collided with it: the readout is modified if the receptor is bound; otherwise, it is unmodified. Molecules that collide with the unbound receptor are indistinguishable from those that have never collided, leading to an additional error. (D) Active molecules can be degraded, erasing samples. (E) All reactions are in principle reversible, compromising the encoding of the receptor state into the readout. The sensing error is determined by collective variables that reveal the resource requirements for sensing: the probability p that the receptor is bound to ligand, the receptor–ligand correlation time ${\tau }_c$, the flux $\dot{n}$, the relaxation time ${\tau }_r$, and the free-energy drops $\mathrm{\Delta }{\mu }_1$ and $\mathrm{\Delta }{\mu }_2$ across the activation and deactivation reactions of the readout, respectively.

The cell infers the ligand concentration c from the instantaneous concentration of the output $x^{\ast }$, by inverting the mean input–output relation $\overline{x^{\ast }}\left(c\right)$. Linearizing $\overline{x^{\ast }}\left(c\right)$ and using error propagation, the expected fractional error in the concentration estimate is then as follows (1, 5, 11):

$${\left(\frac{\delta c}{c}\right)}^2=\frac{1}{c^2}\frac{{\sigma }_{x^{\ast }}^2}{{\left(\frac{d\overline{x^{\ast }}}{dc}\right)}^2}.$$ [1]

The error is low if the readout responds sensitively to changes in ligand concentration, as measured by the gain $d\overline{x^{\ast }}/dc$, but is not noisy, as quantified by the variance ${\sigma }_{x^{\ast }}^2$.

We can compute ${\sigma }_{x^{\ast }}^2$ from the linear-noise approximation (SI Text), and using Eq. 1, this yields Eq. S8 for the sensing error. It is a complicated expression in terms of the eight fundamental variables in the system: the six rate constants describing the forward and reverse rates of the three reactions (including ligand–receptor binding), and the total copy numbers $X_T$ and $R_T$ (Fig. 2A).

Inspired by the analysis of a simpler system, we can arrive at a much more illuminating expression for the sensing error, by viewing the signaling network as a device that samples the receptor state (SI Text). The general principle is that the activation reaction, $x+RL\stackrel{k_{\text{f}}}{\to }{x}^{\ast }+RL$ generates samples of the ligand-binding state of the receptor by storing the receptor state in the stable modification states of the readout molecules (Fig. 2 B and C). Readout molecules that collide with a ligand-bound receptor are activated, whereas those that collide with an unbound receptor remain inactive. In this way, each readout molecule that has interacted with the receptor provides a memory or sample of the ligand-occupation state of that receptor molecule; collectively, the readout molecules encode the history of the receptor states. Intuitively, we expect that if there are N receptor–readout interactions, then the cell has N samples of the receptor state and the error in the concentration estimate, $\delta c/c$, is reduced by a factor of $\sqrt{N}$, or less if the samples are not independent. To derive the effective number of independent samples, we need to consider not only the creation of samples, but also the erasure of samples and the quality of the samples (Fig. 2 D and E). The decay of the readout, $x^{\ast }\stackrel{k_{\text{r}}}{\to }x$ (Fig. 2D), is equivalent to discarding or erasing samples. Additionally, reactions are microscopically reversible, which means that readout activation can occur independently of the receptor, $x\stackrel{k_{-\text{r}}}{\to }{x}^{\ast }$, and receptor-mediated modifications can occur in the wrong direction, $x^{\ast }+RL\stackrel{k_{-\text{f}}}{\to }x+RL$ (Fig. 2E). These reverse reactions compromise the encoding of the receptor state into the readout: an active $x^{\ast }$ molecule no longer encodes the ligand-bound state of the receptor at a previous time with 100% fidelity, because it could have been activated independently of the receptor; similarly, x, rather than $x^{\ast }$, may reflect a modification by a ligand-bound receptor. These reverse reactions thus reduce the reliability of a receptor sample. Energy is needed to break time reversibility and to protect the coding.

How receptor samples are taken (Fig. 2 B and C), erased (Fig. 2D), and how they are stored in the readout x (Fig. 2E), determine the number of receptor samples, their independence, and their accuracy, which together set the sensing precision (SI Text):

$${\left(\frac{\delta c}{c}\right)}^2=\frac{1}{p\left(1-p\right)}\frac{1}{{\overline{N}}_I}+\frac{1}{{\left(1-p\right)}^2}\frac{1}{\overline{N}}.$$ [2]

Here, p is the probability that a receptor is bound to ligand, and $1/\left(p\left(1-p\right)\right)$ is the “instantaneous error,” i.e., the sensing error based on a single concentration estimate via a single receptor. The quantity ${\overline{N}}_I$, discussed below, is the average number of samples that are independent. The second term, with $\overline{N}$ the total number of samples, accounts for the fact that the cell cannot distinguish between those molecules x that have collided with an unbound receptor (and hence provide information on the receptor occupancy), and those that have not collided with the receptor at all (Fig. 2C; SI Text). However, when p is small and/or $\overline{N}$ is large, the second term is small compared with the first. Eq. 2 then shows that the sensing error has a form that one would expect for a sampling protocol: the sensing error is that of an estimate based on a single concentration measurement, $1/\left(p\left(1-p\right)\right)$, divided by the average number of independent measurements, ${\overline{N}}_I$.

The number of independent measurements ${\overline{N}}_I$ can be expressed in terms of collective variables that, as we will show, describe the resource limitations of the cell (Fig. 2E):

$${\overline{N}}_I=\underset{f_I}{\underbrace{\frac{1}{\left(1+2{\tau }_c/\mathrm{\Delta }\right)}}}\underset{{\overline{N}}_{\text{eff}}}{\underbrace{\stackrel{q}{\overbrace{\frac{\left(e^{\mathrm{\Delta }{\mu }_1}-1\right)\left(e^{\mathrm{\Delta }{\mu }_2}-1\right)}{e^{\mathrm{\Delta }\mu }-1}}}\stackrel{\overline{N}}{\overbrace{\frac{\dot{n}{\tau }_r}{p}}}}}.$$ [3]

This expression has a clear interpretation. Cells count only those samples created less than a relaxation time ${\tau }_r$ in the past; nothing that happened earlier can influence the current state, including its ability to sense. Hence, ${\tau }_r$ is the effective integration time. The quantity $\dot{n}$ is the flux of x across the cycle of activation by the receptor and deactivation; it is given by $\dot{n}=k_{\text{f}}\overline{x}{R}_{T}p-k_{-\text{f}}\overline{x^{\ast }}{R}_{T}p$, where $\overline{x}$ and $\overline{x^{\ast }}$ are the average number of x and $x^{\ast }$ in steady state. The product $\dot{n}{\tau }_r$ is thus the number of cycles of readout molecules involving collisions with ligand-bound receptor molecules during the system’s relaxation time ${\tau }_r$. The quantity $\dot{n}{\tau }_r/p$ is the total number of readout cycles involving collisions with receptor molecules, be they ligand bound or not. It is thus the total number of receptor samples taken during ${\tau }_r$, $\overline{N}$.

Not all of these samples are reliable. The effective number of samples taken during ${\tau }_r$ is ${\overline{N}}_{\text{eff}}=q\overline{N}$, where $0\le q\le 1$ measures the quality of each sample. Here, $\mathrm{\Delta }{\mu }_1$ and $\mathrm{\Delta }{\mu }_2$ are the average free-energy drops across the activation and deactivation pathway respectively, in units of ${\mathit{k}}_{\mathit{B}}\mathit{T}$ (Fig. 2E); $\mathrm{\Delta }\mu =\mathrm{\Delta }{\mu }_1+\mathrm{\Delta }{\mu }_2$ is the total free-energy drop across the cycle. When $\mathrm{\Delta }\mu =\mathrm{\Delta }{\mu }_1=\mathrm{\Delta }{\mu }_2=0$, an active readout molecule is as likely to be created by the ligand-bound receptor as it is created spontaneously and there is no coding and no sensing; indeed, in this limit, $q=0$ and ${\overline{N}}_{\text{eff}}=0$. In contrast, when $\mathrm{\Delta }{\mu }_1,\mathrm{\Delta }{\mu }_2\to \mathrm{\infty }$, $q\to 1$ and ${\overline{N}}_{\text{eff}}\to \overline{N}$.

The factor $f_I$ denotes the fraction of samples that are independent. It depends on the correlation time ${\tau }_c$ of receptor–ligand binding and on the time interval $\mathrm{\Delta }=2{\tau }_r/\left({\overline{N}}_{\text{eff}}/R_T\right)$ between samples of the same receptor. Samples farther apart are more independent.

Fundamental Resources and Trade-Offs.

We can use Eqs. 2 and 3 to understand how cellular resources limit the precision of sensing. A resource or combination of resources that fundamentally limits sensing is a (collective) variable $Q_i$ that, when fixed, puts a nonzero lower bound on the sensing error, no matter how the other variables are varied. A fundamental resource class $Q_i$ is thus mathematically defined by the following: ${\text{MIN}}_{Q_i=\text{const}}{\left(\delta c/c\right)}^2=f\left(\text{const}\right)>0$. To find these classes, we numerically or analytically minimized the sensing error, constraining (combinations of) variables yet optimizing over the other variables. As we show in SI Text, when only $R_T{\tau }_r/{\tau }_c$ is constrained, ${\left(\delta c/c\right)}^2\ge 4/\left(R_T{\tau }_r/{\tau }_c\right)$; when only $X_T$ is fixed, ${\left(\delta c/c\right)}^2\ge 4/X_T$; when only $\dot{w}{\tau }_r$ is limiting, ${\left(\delta c/c\right)}^2\ge 4/\left(\dot{w}{\tau }_r\right)$. When all resources are present in finite amounts, the minimum sensing error is set by the highest lower bound:

$${\left(\frac{\delta c}{c}\right)}^2\ge \text{MAX}\left(\frac{4}{R_T{\tau }_r/{\tau }_c},\frac{4}{X_T},\frac{4}{\dot{w}{\tau }_r}\right).$$ [4]

Fig. 3 A–C shows that the resource classes $R_T{\tau }_r/{\tau }_c$, $X_T$, and $\dot{w}{\tau }_r$ are indeed fundamental: the minimum sensing error is bounded by the limiting class and cannot be reduced by increasing another resource. Clearly, increasing a single resource, e.g., $X_T$, cannot reduce the sensing error indefinitely. The sensing error will eventually plateau, namely when it becomes limited by another resource, e.g., $R_T{\tau }_r/{\tau }_c$. These fundamental resource classes thus cannot compensate for each other in achieving a required sensing precision and hence do not trade-off against each other. However, within these classes, trade-offs are possible. We now elucidate why the fundamental classes cannot compensate each other, whereas resources within a given class can, leading to trade-offs between them.

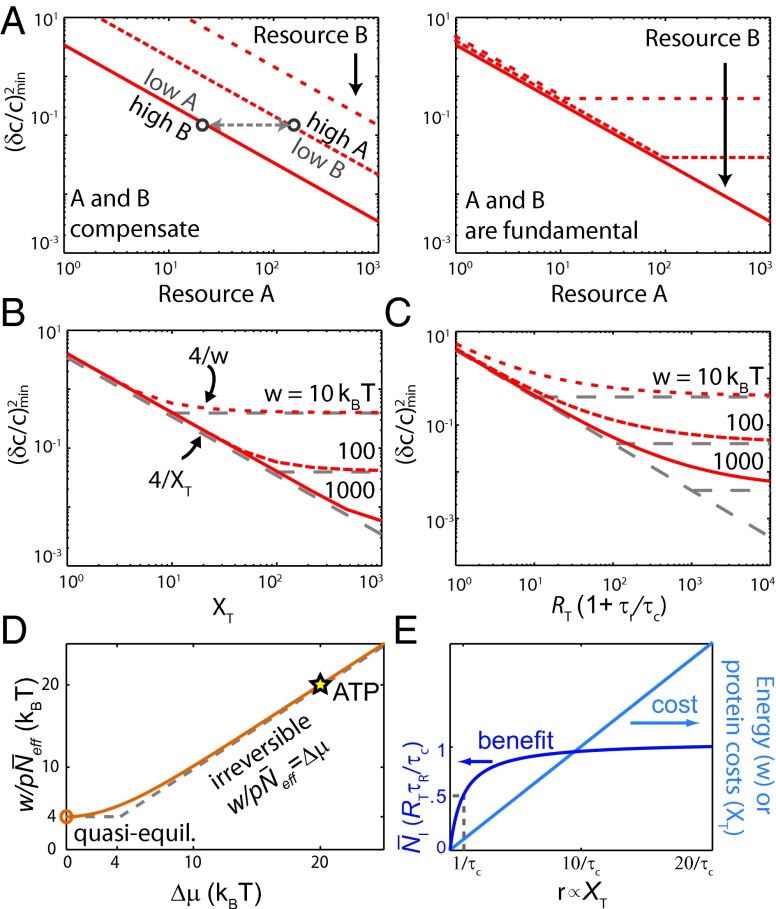
Fig. 3.

Trade-offs in nonequilibrium sensing. (A) When two resources A and B compensate each other, one resource can always be decreased without affecting the sensing error, by increasing the other resource; concomitantly, increasing a resource will always reduce the sensing error. When both resources are instead fundamental, the sensing error is bounded by the limiting resource and cannot be reduced by increasing the other. (B and C) The three classes time/receptor copies, copies of downstream molecules, and energy are all required for sensing, with no trade-offs among them (Fig. 4). The minimum sensing error obtained by minimizing Eq. 2 is plotted for different combinations of (B) $X_T$ and w, and (C) $R_T\left(1+{\tau }_r/{\tau }_c\right)$ and w (SI Text). The curves track the bound for the limiting resource indicated by the gray lines, showing that the resources do not compensate each other. The plot for the minimum sensing error as a function of $R_T\left(1+{\tau }_r/{\tau }_c\right)$ and $X_T$ is identical to that of (C) with w replaced by $X_T$. (D) The energy requirements for sensing. In the irreversible regime $\left(\mathrm{\Delta }\mu \to \mathrm{\infty }\right)$, the work to take one sample of a ligand-bound receptor, $w/\left(p{\overline{N}}_{\text{eff}}\right)$, equals $\mathrm{\Delta }\mu$, because each sample requires the turnover of one fuel molecule, consuming $\mathrm{\Delta }\mu$ of energy. In the quasiequilibrium regime $\left(\mathrm{\Delta }\mu \to 0\right)$, each effective sample of the bound receptor requires $4{\mathit{k}}_{\mathit{B}}\mathit{T}$, which defines the fundamental lower bound on the energy requirement for taking a sample. When $\mathrm{\Delta }\mu =0$, the network is in equilibrium and both w and ${\overline{N}}_{\text{eff}}$ are 0. ATP hydrolysis provides $20{\mathit{k}}_{\mathit{B}}\mathit{T}$, showing that phosphorylation of readout molecules makes it possible to store the receptor state reliably. The results are obtained from Eq. 3 with $\mathrm{\Delta }{\mu }_1=\mathrm{\Delta }{\mu }_2=\mathrm{\Delta }\mu /2$. (E) Sampling more than once per correlation time requires more resources, although the benefit is marginal. As the sampling rate is increased by increasing the readout copy number $X_T$, the number of independent measurements ${\overline{N}}_I$ saturates at the Berg–Purcell limit $R_T{\tau }_r/{\tau }_c$, but the energy consumption and protein cost $\left(\propto X_T\right)$ continue to rise.

Time/Receptor Copy Numbers, $R_T{\tau }_r/{\tau }_c$.

An independent sample of the same receptor can be taken roughly every $2{\tau }_c$. Naturally, samples can be taken more frequently. In fact, cells can time-integrate as in the theory of Berg and Purcell (1): if $X_T\to \mathrm{\infty }$, the receptors are sampled infinitely fast and $\mathrm{\Delta }\to 0$ and ${\overline{N}}_{\text{eff}}\to \mathrm{\infty }$. However, increasing $X_T$ cannot reduce the sensing error ad infinitum, because the number of receptor samples that are independent will saturate at the Berg–Purcell factor, $R_T{\tau }_r/{\tau }_c$, and the sensing error ${\left(\delta c/c\right)}^2$ will plateau at $4/\left(R_T{\tau }_r/{\tau }_c\right)$. Indeed, $R_T{\tau }_r/{\tau }_c$ is the maximum number of independent concentration measurements—the total number of receptors $R_T$ times the maximum number of independent measurements per receptor ${\tau }_r/{\tau }_c$. This shows that there is no fundamental relationship between sensing and receptor copy number: the latter can be traded against time to reach a desired sensing precision. Essentially, the error is determined by the total number of samples and it does not matter, as long as the samples are independent, whether these samples are from the same receptor over time or from many receptors at the same time.

Downstream Readout Molecules, $X_T$.

The concentration measurements need to be stored in the readout molecules. Each readout molecule provides at most one sample, because at any given time it exists in only one modification state, regardless of how many times it has collided with the receptor or how long the integration time ${\tau }_r$ is. There is no mechanistic sense in which a single molecule “integrates” the receptor state. As a consequence, no matter how the network is designed, how much time or energy it uses, or how many receptors it has, cells are fundamentally limited by the pool of readout molecules: the sensing error ${\left(\delta c/c\right)}^2\ge 4/X_T$.

Energy, $\dot{w}{\tau }_r$.

The free-energy drop across a cycle, $\mathrm{\Delta }\mu$, must be provided by a fuel molecule such as ATP. The power, the rate at which the fuel molecules do work, is $\dot{w}=\dot{n}\mathrm{\Delta }\mu$, and the total work performed during ${\tau }_r$ is $w\equiv \dot{w}{\tau }_r$. This work is spent on taking samples of receptor molecules that are bound to ligand, because only they can modify downstream readout molecules. Hence, the work needed to take one effective sample of a ligand-bound receptor is $w/\left(p{\overline{N}}_{\text{eff}}\right)$, with ${\overline{N}}_{\text{eff}}$ given by Eq. 3. Fig. 3D shows this quantity as a function of $\mathrm{\Delta }\mu$. While $w/\left(p{\overline{N}}_{\text{eff}}\right)=\mathrm{\Delta }\mu /q$ increases continuously with $\mathrm{\Delta }\mu$, two limiting regimes can be observed.

When $\mathrm{\Delta }\mu >4{\mathit{k}}_{\mathit{B}}\mathit{T}$, the work to take one effective sample of a ligand-bound receptor becomes simply $w/\left(p{\overline{N}}_{\text{eff}}\right)=\mathrm{\Delta }\mu$. In this regime, the readout reactions are essentially irreversible, $q\to 1$, and each sample requires the turnover of one fuel molecule, using $\mathrm{\Delta }\mu$ of energy. Energy limits the accuracy of sensing, not because it limits the reliability q of each sample, but because it limits the total number of samples ${\overline{N}}_{\text{eff}}=\dot{n}{\tau }_r/p$ by limiting the receptor sampling frequency $\dot{n}$: ${\left(\delta c/c\right)}^2\ge 1/(\dot{n}{\tau }_r)=\mathrm{\Delta }\mu /(\dot{w}{\tau }_r)$. Intriguingly, this bound suggests that for a fixed amount of energy, $w=\dot{w}{\tau }_r$, spent during the relaxation time ${\tau }_r$, the sensing error can be reduced to zero by reducing $\mathrm{\Delta }\mu$ to zero. However, this lower bound only applies when $q\to 1$, i.e., when $\mathrm{\Delta }\mu >4{\mathit{k}}_{\mathit{B}}\mathit{T}$.

When $\mathrm{\Delta }\mu <4{\mathit{k}}_{\mathit{B}}\mathit{T}$, the system transitions to a quasiequilibrium regime in which each fuel molecule provides a small but nonzero amount of energy. In this regime, the system can still consume significant amounts of energy when the fuel molecules are consumed at a rapid rate $\dot{n}$ by many distinct readout molecules. In the limit that $\dot{n}\to \mathrm{\infty }$ and $\mathrm{\Delta }\mu \to 0$ at fixed $\dot{w}=\dot{n}\mathrm{\Delta }\mu$, the effective number of samples given by Eq. 3 reduces to ${\overline{N}}_{\text{eff}}\to \dot{w}{\tau }_r/\left(4p\right)$. Each readout–receptor interaction corresponds to an increasingly noisy measurement of the receptor state $\left(q\to 0\right)$, but many noisy measurements $\left(\overline{N}=\dot{n}{\tau }_r/p\to \mathrm{\infty }\right)$ contain the same information as 1 perfect measurement—provided that collectively at least $4{\mathit{k}}_{\mathit{B}}\mathit{T}$ was spent on them. Indeed, as Fig. 3D shows, $4{\mathit{k}}_{\mathit{B}}\mathit{T}$ is the fundamental lower bound on the work needed to take one accurate sample of a ligand-bound receptor. It puts another bound on the sensing error: ${\left(\delta c/c\right)}^2\ge 4/(\dot{w}{\tau }_r)$. The bound can be reached when $R_T{\tau }_r/{\tau }_c$ and $X_T$ are not limiting, and $\mathrm{\Delta }\mu \to 0$.

Eq. 4 shows that the sensing precision depends on the work done in the past relaxation time, $w=\dot{w}{\tau }_r$, setting up a trade-off among speed, power, and accuracy, as found in adaptation (13). When the response needs to be rapid, ${\tau }_r$ needs to be small and the power demand is high: the samples, which require energy, must be taken close together in time. However, when the cell can wait a long time ${\tau }_r$ before responding, the power $\dot{w}$ required to make w large can be infinitesimal: the samples can be created far apart in time. There is no minimum power requirement for sensing.

Optimal Resource Allocation.

Because the fundamental resource classes cannot compensate each other in achieving a desired sensing precision, any class that is in excess of the minimum amount necessary to achieve that precision is wasted. For example, the benefit of sampling the receptor faster by increasing $X_T$ in reducing the sensing error saturates, whereas the total protein and energetic costs continue to rise with $X_T$ (Fig. 3E). To the extent that all resources affect growth, evolutionary pressure should tend to drive systems so that no resource is wasted, which occurs when all are equally limiting. Resource-optimal systems sample the receptor about once per correlation time and use just enough fuel and downstream molecules to do so. Quantitatively, from Eq. 4, all resources are equally limiting when

$$R_T{\tau }_r/{\tau }_c\approx X_T\approx w.$$ [5]

In an optimal sensing system, the number of independent concentration measurements $R_T{\tau }_r/{\tau }_c$ equals the number of readout molecules $X_T$ that store these measurements and equals the work (in units of ${\mathit{k}}_{\mathit{B}}\mathit{T}$) to create the samples.

Comparison with Experiment.

Eq. 5 makes a strong prediction for the optimal design of the large class of sensing systems that are based on the push–pull motif. We can test this prediction for the chemotaxis system of E. coli (Fig. 1), which has been well characterized experimentally. In this system, the receptor forms a complex with the kinase CheA. This complex, which is coarse-grained into R, can bind the ligand L and activate the intracellular messenger protein CheY (x) by phosphorylating it. Deactivation of CheY is catalyzed by CheZ, the effect of which is coarse-grained into the deactivation rate (SI Text).

The number of chemotaxis proteins depends on the growth rate: the number of receptors and CheY proteins varies as much as 10-fold as a function of strain and growth medium (23). Interestingly, however, these variations occur in concert for all components and thus hardly change their relative amounts (23). This is the scaling behavior predicted by Eq. 5, assuming that ${\tau }_r$ is robust to variations in the growth rate.

Not only the scaling of the number of CheY proteins, $X_T$, with the number of receptor–CheA complexes, $R_T$, can be tested, but also the magnitude of their ratio. A fit of the data of Li and Hazelbauer, shown in Fig. 1B, shows that $X_T/R_T\approx 3$ for different strains and growth media (23). Eq. 5 thus predicts that ${\tau }_r/{\tau }_c\approx 3$. The relaxation rate ${\tau }_r^{-1}$ is $\approx 2 {\text{s}}^{-1}$ for the attractant response and $\approx 20 {\text{s}}^{-1}$ for the repellent response (24), yielding ${\tau }_r\approx 100 \text{ms}$. Hence, Eq. 5 predicts that ${\tau }_c\approx 30 \text{ms}$. This prediction can be tested, assuming that the correlation time ${\tau }_c$ of the receptor–CheA complex is that of receptor–ligand binding. Specifically, we can estimate ${\tau }_c$ from the receptor–ligand dissociation rate $k_{\text{off}}$ as ${\tau }_c\simeq 1/\left(2k_{\text{off}}\right)$, $\left(p\approx 0.5\right)$. The dissociation constant of Tar-aspartate (receptor–ligand) binding $K_D\approx 0.1\hspace{0.17em}\mu \text{M}$ (25), and with an association rate $k_{\text{on}}\approx {10}^9{\text{M}}^{-1}\mathrm{\cdot }{\text{s}}^{-1}$ (26), this yields $k_{\text{off}}\approx 100 {\text{s}}^{-1}$ and an estimated correlation time ${\tau }_c\approx 10 \text{ms}$, in line with the prediction of Eq. 5.

Eq. 5 also predicts that the total number of CheY molecules $X_T$ equals the chemical work $w=\dot{n}\mathrm{\Delta }\mu {\tau }_r$ (in units of ${\mathit{k}}_{\mathit{B}}\mathit{T}$) to phosphorylate CheY during ${\tau }_r$. In steady state, the flux $\dot{n}$ of CheY phosphorylation balances the flux of CheYp dephosphorylation. The latter equals the inverse lifetime ${\tau }_l^{-1}\approx {\tau }_r^{-1}$ times the number of CheYp molecules in steady state, $\alpha X_T$, where α is the fraction of CheY that is phosphorylated. This yields $w\approx \alpha \mathrm{\Delta }\mu X_T$. The fraction $\alpha \approx 0.16$ (24). CheY phosphorylation is driven by ATP hydrolysis, which means that $\mathrm{\Delta }\mu =20{\mathit{k}}_{\mathit{B}}\mathit{T}$. Hence $w\approx 3X_T$, thus on the order of $X_T$, as Eq. 5 predicts. We thus argue that in the chemotaxis system of E. coli, the resources are optimally allocated, i.e., according to Eq. 5.

Discussion

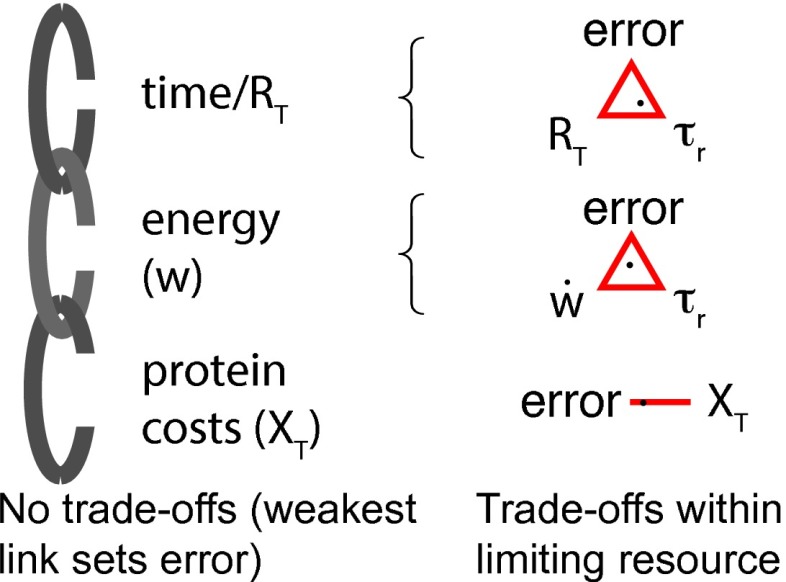
Fig. 4 summarizes our analysis. The sensing precision is limited by three classes of resources. The resource class time/receptors $R_T{\tau }_r/{\tau }_c$ determines the maximum total number of independent concentration measurements that can be taken. However, these measurements need to be stored in downstream molecules. Moreover, energy is needed to store the samples reliably and to protect the coding. These three classes of resources are indeed fundamental. The sensing error is bounded by the limiting class like the weakest link in a chain, and other classes cannot compensate for it. For example, adding receptors and readout molecules does not improve sensing if not enough energy is used to take the samples (Fig. 3B); similarly, waiting more time to take another sample is not beneficial if the cell has no more readout molecules left to write the sample to, or cannot expend energy fast enough to accomplish the writing (Fig. 3C). However, within the fundamental resource classes, trade-offs are possible: time can be traded against the number of receptors to reach a required number of measurements, whereas power can be traded against speed to meet the energy requirement for a desired sensing accuracy. These design principles are in marked contrast to those of equilibrium sensing systems, which are not driven out of equilibrium via fuel turnover: the sensing precision of these systems is limited by the number of receptors; downstream networks can never improve the accuracy of sensing (27).

Fig. 4.

The relationship between resources and the precision of biochemical sensing. The sensing precision is fundamentally limited by time and receptor copies, energy, and copies of downstream readouts. These three classes of resources cannot compensate each other, and it is the limiting resource that sets the fundamental limit to the precision of sensing. Within each class, however, trade-offs are possible: Power can be traded against speed to meet the energy requirement for reaching a desired sensing accuracy, whereas time can be traded against the number of receptors.

We find that at least $4{\mathit{k}}_{\mathit{B}}\mathit{T}$ is needed for reliably encoding a measurement. One of the most widely used coding strategies is phosphorylation, which requires ATP. In vivo, ATP hydrolysis provides about $20{\mathit{k}}_{\mathit{B}}\mathit{T}$. This is sufficient to take one receptor sample essentially irreversibly (Fig. 3D), which means that q reaches unity. Readout phosphorylation thus makes it possible to store the receptor state reliably.

Nonequilibrium networks can exhibit more complicated features than those of the simple push–pull motif, as in the MAPK cascade. The molecular picture for time integration suggests that our results hold generally, even in these more complicated systems. Indeed, we find the same or more severe resource limitations in signaling cascades and in networks with simple negative or positive feedback (SI Text). Although cascades can increase the response time (10), which increases information transfer, they do not make sensing more efficient in terms of energy or readout molecules.

In an optimally designed system, each fundamental resource is equally limiting. This leads to a specific prediction for the design of an optimal sensing system: the integration time, energy, and copy numbers of receptor and readout should satisfy Eq. 5. Importantly, this design principle of optimal resource allocation is independent of the resource costs. This is because the sensing precision is bounded by the limiting resource class; resources that are in excess cannot improve sensing and are thus wasted, no matter how cheap they are. Fig. 3 C and D show that, even close to the optimum where all resources are equally limiting, the minimum error closely follows the lower bound of Eq. 4 (SI Text), supporting the idea that Eq. 5 is indeed fairly insensitive to the resource costs. It explains perhaps why Eq. 5 so successfully predicts the design of the E. coli chemotaxis system.

The optimal trade-off between nonfundamental resources within the fundamental resource classes will depend on their fitness costs and benefits. For example, how receptors are traded against time in reaching a desired sensing precision will depend on the benefit of a fast response time and the cost of making the receptor proteins.

To understand how E. coli moves in a concentration gradient, we have to understand not only how the sensing system filters high-frequency ligand-binding noise by time averaging the receptor state—the topic of this study—but also how, on much longer timescales, the adaptation system computes the change in the concentration and filters low-frequency noise induced by the cell’s random motion in the concentration gradient (28). Recently, Lan et al. (13) found a trade-off between the speed, power, and accuracy of adaptation, which mirrors the trade-off between power, speed, and precision of sensing observed here. Interestingly, the adaptation and sensing system share the receptor. In fact, the adaptation system continually performs work to keep the receptor activity close to 0.5. There is thus an energetic adaptation cost associated with the receptors, in addition to the energetic cost of synthesizing them. This adaptation cost will affect the trade-off between the nonfundamental resources receptors and time. It will not, however, affect the design principle of optimal resource allocation, which is based on the fundamental resource classes and hence insensitive to resource costs.

Whether other sensing systems satisfy the design principle of Eq. 5 remains an interesting question. Two-component systems are ideal for testing this once kinetic data and protein expression levels become available (29). Eq. 5 not only makes predictions for individual systems but also predicts that the fundamental resources should vary proportionally to each other across different systems. For example, the relation predicts that the lifetime ${\tau }_r$ of the modified readout should increase, ceteris parabus, with its expression level $X_T$. The design principle of Eq. 5 can also be used to construct optimal synthetic networks that minimize resource consumption.

Finally, the process of sampling a time series, like the receptor state over time, defines a specific, familiar computation that could be conducted by any machine; it is instantiated in the biochemical system by the readout–receptor pair. We find that the free-energy drops across the “measurement” and “erasure” steps, $\mathrm{\Delta }{\mu }_1$ and $\mathrm{\Delta }{\mu }_2$, should be identical to minimize the energetic cost, even though the fuel molecule need only be involved in one of the reactions, preparing a nonequilibrium state that relaxes via the other. This allocation of energy differs from that typically considered in the computational literature, in which only the erasure step requires energy (30). In the cellular system, both steps are computational erasures: although only the erasure step erases memory of the receptor state, both steps erase the state of the molecule involved in the collision. Interestingly, when $p=0.5$, the average work to measure the state of the receptor is $2{\mathit{k}}_{\mathit{B}}\mathit{T}$, which is perhaps surprisingly close to the Landauer bound, ${\mathit{k}}_{\mathit{B}}\mathit{T}\ln \left(2\right)$ (30).