Electric fingerprint of voltage sensor domains

Significance

A central paradigm in the subject of cellular excitability is whether or not a dynamic membrane voltage field contributes to the operation of voltage sensor proteins. This issue has challenged an entire generation of scientists because static and dynamic contributions of the field cannot be discriminated from electrophysiology measurements. The dilemma imposes that structure-based calculations are required to solve the issue. By following this approach, we report that reshaping or dynamics of the field does not impact significantly the domain energetics or operation. As such, the functional diversity of voltage sensors observed in nature originates from variations in the detailed atom–atom interactions of the domain (chemical free energy) rather than in its coupling with the membrane voltage.

Abstract

A dynamic transmembrane voltage field has been suggested as an intrinsic element in voltage sensor (VS) domains. Here, the dynamic field contribution to the VS energetics was analyzed via electrostatic calculations applied to a number of atomistic structures made available recently. We find that the field is largely static along with the molecular motions of the domain, and more importantly, it is minimally modified across VS variants. This finding implies that sensor domains transfer approximately the same amount of gating charges when moving the electrically charged S4 helix between fixed microscopic configurations. Remarkably, the result means that the observed operational diversity of the domain, including the extension, rate, and voltage dependence of the S4 motion, as dictated by the free energy landscape theory, must be rationalized in terms of dominant variations of its chemical free energy.

Voltage sensor (VS) domains are electrically charged membrane proteins made of four packed helices (1). The fourth segment (S4) contains four highly conserved positively charged amino acids, R₁ through R₄. By interchanging its conformation between two main states (resting and activated) in response to voltage variations, VS domains displace the S4 charges across the membrane capacitance, giving rise to $\Delta Q$, the so-called gating charge (2). As a result of their function of converting voltage variations into molecular motions, VS domains are ubiquitous in a number of electrically mediated processes, either as domain components of phosphatases (2) or proton (3) and ion channels (4–8).

Despite the conservation of S4 sequences, nature has designed a variety of constructs (2) that present a wide range of voltage dependence and absolute rates of activation. For instance, the VS kinetics is markedly distinct between voltage-gated Na⁺ and K⁺ channels (9), a feature that complies with their respective role in the fast and slow phases of the action potential. Drastic kinetic shifts can even be observed in VS differing by point mutations (10, 11). In all of these constructs, the S4 operation results from the fine balance between the chemical and the electrical components of the relative free energy of the segment. Whereas the former depends on the S4 energy in the absence of an electrical driving force, the latter arises essentially from $\varphi \left(\mathit{r}\right)$ (12), a dimensionless scalar field that reports the fraction of the membrane voltage coupled to every S4 charge $q_i$. As mostly embodied in the transporter model (13), the reshaping of $\varphi \left(\mathit{r}\right)$ along with S4 displacements appears as one potential mechanism impacting the sensing process. Facing the VS diversity, it has been unknown to which extent the field reshaping may impact the S4 operation in distinct constructs and account for its energetic differences.

Here, by benefiting from an increasing number of atomistic structures of VS-containing channels or enzymes made available recently, we use all-atom molecular dynamics (MD) simulations (14–16) in combination with electrostatic calculations (17, 18) to investigate voltage-coupling properties of sensor domains. Anticipating our results, we find that, although primarily conformation independent, $\varphi \left(\mathit{r}\right)$ is minimally modified over the VS variants. This finding points to marginal dynamic contributions of the membrane voltage field to the energetics and diversity of VS proteins.

Theory and Methods

Energetics of Voltage-Sensor Domains.

Given its critical role in the sensing mechanism, we focus our analysis on a reduced thermodynamic system formed by S4. We consider the helix embedded along with the other VS segments in an impermeable membrane bathed by salt solutions and in presence of an external voltage $V$ (Fig. 1). Under these conditions, the free energy of S4 in a fixed microscopic configuration $\mathit{X}$ can be expressed as (19)

$$F\left(\mathit{X},V\right)=F\left(\mathit{X},0\right)+\Delta F\left(\mathit{X},V\right)$$ [1]

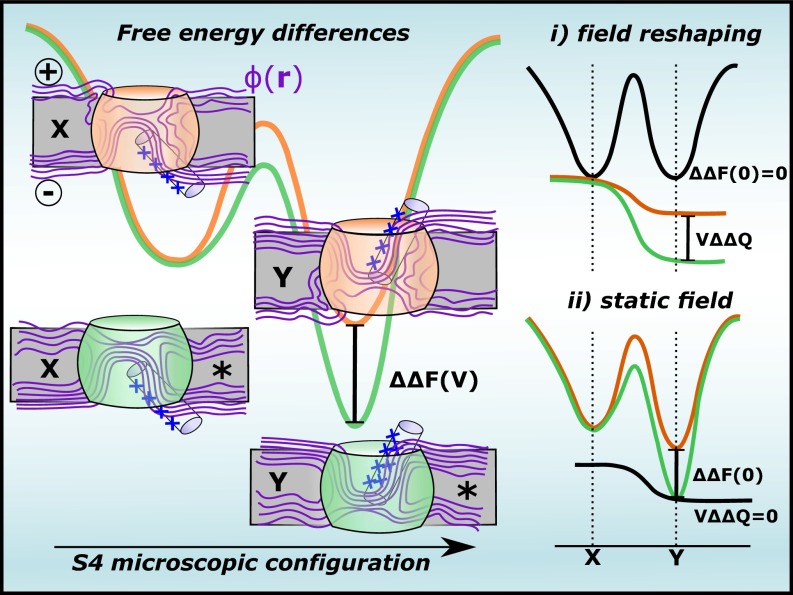
Fig. 1.

Hypothetical free energy landscapes showing the S4 energetics in distinct VSs. For fixed $\mathit{X}$ and $\mathit{Y}$ microscopic configurations of S4 under voltage $V$, $\Delta \Delta F\left(V\right)=\Delta \Delta F\left(\text{0}\right)+V\Delta \Delta Q$ is the variation of the helix energy upon perturbation (*) of the protein-membrane surroundings, where $\Delta \Delta F\left(\text{0}\right)$ and $\Delta \Delta Q$ are, respectively, perturbation-induced changes of the chemical free energy and the gating charge. In two contrasting scenarios, $\Delta \Delta F\left(V\right)$ may arise from (i) reshaping of the membrane-voltage field $\varphi \left(\mathit{r}\right)$ that accounts for energetic differences via $V\Delta \Delta Q$ and/or (ii) chemical free energy modifications that account for $\Delta \Delta F\left(\text{0}\right)$.

where $F\left(\mathit{X},\text{0}\right)$ denotes the chemical free energy of the helix that depends on the system energy in the absence of an electrical driving force ($V=\text{0}$), and $\Delta F\left(\mathit{X},V\right)$ denotes its excess free energy when coupled to an external voltage. Here, $\mathit{X}\equiv \text{{}{\mathit{r}}_{\mathbf{1}},\mathrm{...},{\mathit{r}}_N\text{}}$ maps specifically the Cartesian coordinates of all atoms of S4.

The voltage-independent term accounts for the microscopic potential energy of S4 and its (polar and nonpolar) solvation energy in the protein-membrane environment (20). Differently

$$\Delta F\left(\mathit{X},V\right)=VQ\left(\mathit{X}\right),$$ [2]

depends on $V$ and on the effective charge $Q\left(\mathit{X}\right)$ of S4

$$Q\left(\mathit{X}\right)={\displaystyle \sum _i{q}_i}{\varphi }_{\mathit{X}}\left({\mathit{r}}_i\right),$$ [3]

in which $q_i$ is the ith S4 atom charge, and ${\varphi }_{\mathit{X}}\left({\mathit{r}}_i\right)$ is a dimensionless scalar field (12); it varies between 0 (intracellular side) and 1 (extracellular side). Note that $\varphi \left(\mathit{r}\right)$ depends on the intradomain dielectric for the fixed configuration of S4 (Eq. 11), justifying its dependence with $\mathit{X}$ made explicit in Eq. 3; that is, we use the subscript $\mathit{X}$ for that purpose.

As discussed in ref. 19, the meaning of $\varphi \left(\mathit{r}\right)$ runs deeper than the definition of the effective charge of S4 as it transduces the molecular motions of the segment into the gating charge $\Delta Q$. To make this explicit, let us consider any set of atomic displacements $\Delta \mathit{X}\equiv \text{{}\Delta {\mathit{r}}_{\mathbf{1},}\mathrm{...},\Delta {\mathit{r}}_N\text{}}$ leading S4 to a new configuration $\mathit{Y}\equiv \text{{}{\mathit{r}}_{\mathbf{1}}+\Delta {\mathit{r}}_{\mathbf{1},}\mathrm{...},{\mathit{r}}_N+\Delta {\mathit{r}}_N\text{}}$ relative to its protein-membrane surroundings. From Eq. 1, the voltage-dependent free energy difference associated with the configuration change of the helix writes as

$$F\left(\mathit{Y},V\right)-F\left(\mathit{X},V\right)=F\left(\mathit{Y},\text{0}\right)-F\left(\mathit{X},\text{0}\right)+V\left[Q\left(\mathit{Y}\right)-Q\left(\mathit{X}\right)\right],$$ [4]

in which $F\left(\mathit{Y},\text{0}\right)-F\left(\mathit{X},\text{0}\right)$ is the voltage-independent chemical free energy change, and $V\left[Q\left(\mathit{Y}\right)-Q\left(\mathit{X}\right)\right]$ is the electrical energy related to the transfer of the gating charge $\Delta Q=Q\left(\mathit{Y}\right)-Q\left(\mathit{X}\right)$ in the process. Thus, from Eq. 3,

$$\Delta Q={\displaystyle \sum _i{q}_i}\left[{\varphi }_{\mathit{Y}}\left({\mathit{r}}_i+\Delta {\mathit{r}}_i\right)-{\varphi }_{\mathit{X}}\left({\mathit{r}}_i\right)\right],$$ [5]

is the direct link of $\Delta Q$ with the microscopic displacement of S4 via the voltage-coupling variation of the segment.

Eq. 5 shows that $\Delta Q$ does not measure the physical displacements of S4 charges but rather the fraction of the membrane potential each charge traverses. As such, gating charges could arise (i) from displacements of $q_i$ relative to a static voltage field across the membrane or (ii) from the field reshaping itself, induced by changes in the environment of a rather static $q_i$, or any combination of (i) and (ii). Here, we make this notion explicit as

$$\Delta Q={\displaystyle \sum _i{q}_i}\left[{\varphi }_{\mathit{X}}\left({\mathit{r}}_i+\Delta {\mathit{r}}_i\right)-{\varphi }_{\mathit{X}}\left({\mathit{r}}_i\right)+{\delta }_{\mathit{X}\mathit{Y}}^i\right],$$ [6]

with

$${\delta }_{\mathit{X}\mathit{Y}}^i={\varphi }_{\mathit{Y}}\left({\mathit{r}}_i+\Delta {\mathit{r}}_i\right)-{\varphi }_{\mathit{X}}\left({\mathit{r}}_i+\Delta {\mathit{r}}_i\right),$$

denoting the dynamic field contribution to $\Delta Q$ (the mathematical notation ${\delta }_{\mathit{X}\mathit{Y}}$ reads as the field reshaping between configurations $\mathit{X}$ and $\mathit{Y}$ at the fixed space position $\mathit{r}+\Delta \mathit{r}$; Fig. 2). Eq. 6 suggests the reshaping of $\varphi \left(\mathit{r}\right)$ as one potential mechanism that impacts the free energy landscape of S4. Indeed, reshaping is one key feature of the so-called transporter model trying to rationalize $\Delta Q$ in terms of molecular motions of S4 (13).

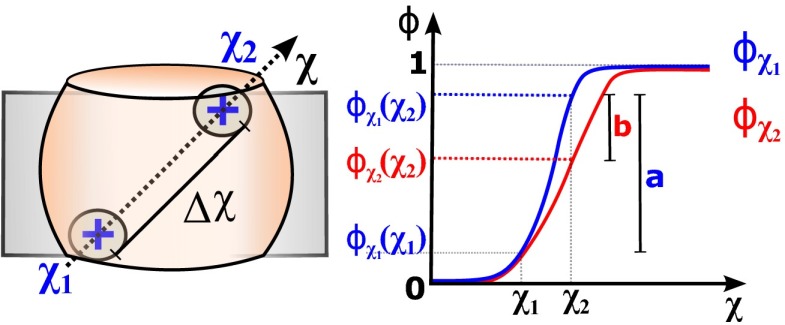
Fig. 2.

Voltage coupling variation $\Delta \varphi =\left[{\varphi }_{{\mathbf{\chi }}_2}\left({\mathbf{\chi }}_2\right)-{\varphi }_{{\mathbf{\chi }}_1}\left({\mathbf{\chi }}_1\right)\right]$ of the charge $q_i$ when displacing $\Delta \mathbf{\chi }$ along a given path $\mathbf{\chi }$ within the sensor domain. By assuming that ${\varphi }_{\mathbf{\chi }}\left(\mathbf{\chi }\right)$ reshapes as the particle moves along $\mathbf{\chi }$, $\Delta \varphi$ can be decomposed into static (a) and dynamic (b) contributions.

One direct consequence is that reshaping may also underlie the energetic variations in distinct sensor constructs. To show this clearly, we generalize Eq. 4 to include the energetics of S4 conditioned to an alchemical perturbation (*) of its adjacent protein-membrane components induced by protein mutations. By plugging Eq. 4 into a thermodynamic cycle analysis, the variation of the S4 energetics $\Delta \Delta F\left(V\right)$ due to the perturbation is written accordingly to

$$\Delta \Delta F\left(V\right)=\Delta \Delta F\left(\text{0}\right)+V\Delta \Delta Q,$$ [7]

where

$$\Delta \Delta F\left(\text{0}\right)=\left[F^{*}\left(\mathit{Y},\text{0}\right)-F^{*}\left(\mathit{X},\text{0}\right)\right]-\left[F\left(\mathit{Y},\text{0}\right)-F\left(\mathit{X},\text{0}\right)\right],$$

and

$$\Delta \Delta Q=\left[Q^{*}\left(\mathit{Y}\right)-Q^{*}\left(\mathit{X}\right)\right]-\left[Q\left(\mathit{Y}\right)-Q\left(\mathit{X}\right)\right],$$

are, respectively, the perturbation-induced variations of the relative chemical free energy of the helix and of its gating charge. From Eq. 5, it follows that

$$\Delta \Delta Q={\displaystyle \sum _i{q}_i}\left[{\delta }_{\mathit{Y}\mathit{Y}*}^i-{\delta }_{\mathit{X}\mathit{X}*}^i\right],$$ [8]

with

$${\delta }_{\mathit{X}\mathit{X}*}^i={\varphi }_{\mathit{X}}^{*}\left({\mathit{r}}_i\right)-{\varphi }_{\mathit{X}}\left({\mathit{r}}_i\right),$$

and

$${\delta }_{\mathit{Y}\mathit{Y}*}^i={\varphi }_{\mathit{Y}}^{*}\left({\mathit{r}}_i+\Delta {\mathit{r}}_i\right)-{\varphi }_{\mathit{Y}}\left({\mathit{r}}_i+\Delta {\mathit{r}}_i\right),$$

describing, respectively, the perturbation-induced variations of $\varphi \left(\mathit{r}\right)$ for the fixed $\mathit{X}$ and $\mathit{Y}$ configurations of S4. Both of these terms denote dynamic contributions of the voltage field to $\Delta \Delta Q$, thereby clarifying how such quantities may account for energetic differences in distinct sensor domains.

Voltage Coupling $\mathrm{\varphi }\left(\mathit{r}\right)$.

In terms of a continuum electrostatic treatment for the ionic solution that bathes the protein and membrane components, the function $\varphi \left(\mathit{r}\right)$ can be defined from a linearized Poisson-Boltzmann (PB-V) equation that accounts for the effect of the transmembrane (TM) electrostatic potential (12)

$$\nabla \cdot \left[\in \left(\mathit{r}\right)\nabla \mathrm{\varphi }\left(\mathit{r}\right)\right]-{\overline{\mathrm{\kappa }}}^2\left(\mathit{r}\right)\left[\mathrm{\varphi }\left(\mathit{r}\right)-V\mathrm{\Theta }\left(\mathit{r}\right)\right]=0$$ [9]

where, $\mathrm{\in }\left(\mathit{r}\right)$ and $\overline{\mathit{\kappa }}$ are, respectively, the space-dependent dielectric constant and Debye-Huckel ionic screening factor, and $\Theta \left(\mathit{r}\right)$ is a Heaviside step function equal to 0 on one side of the membrane and 1 on the other side. Eq. 9 shows that $\varphi \left(\mathit{r}\right)$ is independent of any charge densities $\rho \left(\mathit{r}\right)$ provided by S4 and its adjacent protein-membrane medium. However, it depends on the dielectric and accessibility maps for the fixed configuration of S4 within the surroundings.

Alternatively, $\varphi \left(\mathit{r}\right)$ can be further expressed via an explicit all-atom formulation, the so-called electrical distance (21, 22)

$$\varphi \left(\mathit{r}\right)\equiv \frac{\partial }{\partial V}\Phi \left(\mathit{r},V\right){|}_{V=\text{0}},$$ [10]

in which $\Phi \left(\mathit{r},V\right)$ is the electrostatic potential defined from Poisson's equation (18) that relates the potential with the local charge density ${\rho }_i\left(\mathit{r},V\right)$, the sum running over all atoms of S4, and the surroundings (protein + membrane + solution). As previously demonstrated, this formulation is a linear-response approximation (19). Because the charge-density contributions to $\Phi \left(\mathit{r},V\right)$ cancel out in Eq. 10, the electrical distance definition also embodies the unique dependency of the coupling parameter with the dielectric morphology of the system as described in Eq. 9.

Within the gating charge equation, these voltage coupling definitions have been extensively used to make concrete connections between microscopic models and experiments (23–28).

Computational Methods.

Table S1 presents the set of VSs considered in the study. Each of these structures was obtained from MD simulations based on the available X-ray crystal structures (2–7, 29). Their detailed description can be found in the original papers (25, 27, 28, 30–32). It is important to clarify that, besides the structure by Delemotte et al. (8), other resting state models were proposed for Kv1.2 (33–35). Given that these structures were proven to provide with a consensus model for the resting state of the channel (36), we focus our investigation on the former model. Here, the dataset was first characterized as a variant set of sequences and conformations through sequence/structural analysis. Then, each of the structures was embedded in a lipid bilayer for MD simulation and subsequent computation of the voltage-coupling map $\varphi \left(\mathit{r}\right)$. Specifically, $\varphi \left(\mathit{r}\right)$ was independently determined via solution of the PB-V equation and the electrical distance definition to evaluate the dependence of the results with both formulations (continuum vs. all-atom). Whereas the PB-V route is based on continuum electrostatics, the electrical distance is in contrast computed directly from MD simulations, thereby taking into account the solvent explicitly. A detailed description of the calculations is provided as SI Text.

Results and Discussion

Dataset of VS Structures.

Over the years, X-ray crystal structures of distinct voltage-gated channels have been determined, including KvAP (4), Kv1.2 (5), Kv1.2/Kv2.1 (6), NavAb (7), and NavRh (8); all of them feature sensor domains in the activated state. Following characterization of their structural details in a lipid bilayer (24, 25, 28, 30, 32), atomistic models of the resting state (27, 28, 31, 32), explaining most of the experimental data, have been further proposed for these channels, except for NavRh, as described in recent reviews (1). Besides the voltage-sensitive channels, the resolved X-ray structures of the phosphatase domain Ci-VSP (2) (activated and resting) and the proton channel mHv1cc (3) (resting) have provided additional exemplars of the construct.

The structures reveal that VSs have an hourglass-like construction, featuring water crevices disconnected by an occluding hydrophobic site within the domain that provides a gating pore for the S4 arginines (Fig. 3). The activation involves the S4 charges moving across the occluding site while forming conformation-dependent salt bridges with VS acidic residues (1). Despite such common features, primary sequence variations within the gating pore suggest functional differences, as amino acid replacements in this region profoundly impact the domain energetics (9–11). From the multiple sequence alignment presented in Fig. S1, the pairwise sequence similarities within the gating pore region are spread between 60% and 99%. By graphing every pairwise similarity, we find that the sensor domains Kv1.2/Kv1.2 and mHv1cc are, for instance, minimally and maximally distant from Kv1.2. Careful inspection of the VS structures suggests that the sequence variability is reflected in the resting and activated states of the S4 helix, which are fairly heterogeneous across the domains (Fig. 3). This conclusion is supported by the quantification of structural distances via a contact matrix mapping the microscopic configuration of S4 within the protein (see SI Text for details). Fig. S2 shows structural distances that amount to ∼10 Å between resting configurations of distinct VS domains; these differences are attributed in part to a variable transmembrane (TM) positioning (∼2–10 Å) and twist (∼10°–100°) of S4. Similar estimates are reported for the activated configuration of S4. The present results reflect that the extensions of the conformational changes taking place in each VS domain separately are variable, thus reinforcing the notion of functional differences among them (i.e., different free energy landscapes).

Fig. 3.

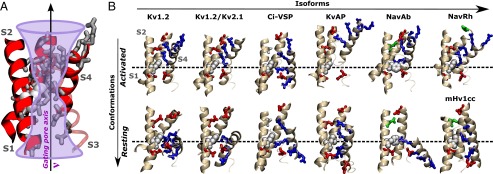
Dataset of VS structures. (A) General hourglass-like construction of sensor domains. Shown is the gating pore along which the S4 charges travel during activation. A highly conserved phenyl group (white) plugs the most constricted hydrophobic region along the gating pore and disconnects internally and externally open water crevices. (B) Molecular views of the VS structures. Highlighted is the conformation-dependent position of the S4 basic residues (blue sticks) and the salt-bridges/hydrogen-bonds they form with the acidic/polar residues (red/green sticks) of other VS segments (see Table S2 for details). Only segments S1, S2, and S4 are shown for clarity.

Taken together, the available dataset provides us with a variant set of sequences and conformations of the VS that is particularly useful for comparative analysis of electrical properties of the domain.

Voltage Coupling Analysis and Field Reshaping.

Eqs. 6 and 8 indicate how any given dependence of the voltage coupling with sequence (${\delta }_{\mathit{X}{\mathit{X}}^{\mathbf{\ast }}}^i$ or ${\delta }_{\mathit{Y}{\mathit{Y}}^{\mathbf{\ast }}}^i$) and structure (${\delta }_{\mathit{X}\mathit{Y}}^i$) might affect the energetics of S4. In the following, we exploit these equations to investigate $\varphi \left(\mathit{r}\right)$ across the VS structures. For that purpose, the domain isoforms are seen as alchemically perturbed versions of each other, featuring amino acid replacements outside S4, and their activated and resting conformations as distinct $\mathit{X}$ and $\mathit{Y}$ configurations of the segment within its surroundings. Because each of these conformational states are heterogeneous across the domain variants, the definitions of $\mathit{X}$ and $\mathit{Y}$ are loose when analyzing the set of structures through Eq. 8.

Accordingly, the variations ${\delta }_{\mathit{X}\mathit{Y}}^i$, ${\delta }_{\mathit{X}{\mathit{X}}^{\mathbf{\ast }}}^i$, and ${\delta }_{\mathit{Y}{\mathit{Y}}^{\mathbf{\ast }}}^i$ are estimated here in the form of the ${\mu }_{kl}$ parameter, which reports the field reshaping between two VS structures $k$ and $l$. Specifically, ${\mu }_{kl}$ is defined as the line integral of $\Delta {\varphi }_{kl}$ along the gating pore axis $\mathbf{\nu }$

$${\mu }_{kl}\mathrm{=}\frac{1}{|z_{\text{out}}-z_{\text{in}}|}{\displaystyle \underset{z_{\mathrm{in}}}{\overset{z_{out}}{\int }}\left[{\mathrm{\varphi }}_{\mathit{k}}\left(\mathbf{\nu }\left(z\right)\right)\mathrm{-}{\mathrm{\varphi }}_{\mathit{l}}\left(\mathbf{\nu }\left(z\right)\right)\right]\left|\dot{\mathbf{\nu }}\left(z\right)\right|dz},$$ [11]

in which $\mathbf{\nu }\left(z\right)=a\widehat{\mathit{i}}+b\widehat{\mathit{j}}+z\widehat{\mathit{k}}$ is the axis in parametric form, with $\mathbf{\nu }\left(z_{\text{in}}\right)$ and $\mathbf{\nu }\left(z_{\text{out}}\right)$ denoting the pore edges along the transmembrane direction $z$ (see the graphical representation of $\mathbf{\nu }$ in Fig. 3A). The gating pore supplies the immediate environment for the S4 charges during activation, justifying our choice of evaluating the field reshaping along this path. In Eq. 11, $\varphi \left[\mathbf{\nu }\left(z\right)\right]$ reads as the voltage coupling profile along the gating pore of the VS, which is extracted directly from the 3D voltage-coupling map $\varphi \left(\mathit{r}\right)$. Fig. 4A shows the profiles calculated over the entire dataset of VS structures. Thus, the computation of ${\mu }_{kl}$ is reduced in practice to the integration of the differences between two coupling profiles, normalized by the transmembrane length of the gating pore. Within this framework, the ${\mu }_{kl}$ parameter has the following meanings to our ultimate goal: (i) when computed between the activated and resting conformations of the same domain isoform, ${\mu }_{kl}$ provides an estimate for the average field reshaping impacting the S4 charge $i$ on the helical motion (that is, ${\delta }_{\mathit{X}\mathit{Y}}^i$); (ii) when determined between resting or activated conformations of two distinct domain isoforms, it reports the average field reshaping under perturbation of the protein-membrane environment of S4 (that is, ${\delta }_{\mathit{X}{\mathit{X}}^{\ast }}^i$ or ${\delta }_{\mathit{Y}{\mathit{Y}}^{\ast }}^i$). We denote each of these estimates as ${\mu }_{kl}^{\mathit{X}\mathit{Y}}$, ${\mu }_{kl}^{\mathit{X}{\mathit{X}}^{\ast }}$, and ${\mu }_{kl}^{\mathit{Y}{\mathit{Y}}^{\ast }}$. By replacing them back into Eqs. 6 and 8, $\Delta Q_{kl}=+4e_{\text{0}}{\mu }_{kl}^{\mathit{X}\mathit{Y}}$ and $\Delta \Delta Q_{kl}=+4e_{\text{0}}\left[{\mu }_{kl}^{\mathit{Y}{\mathit{Y}}^{\ast }}-{\mu }_{kl}^{\mathit{X}{\mathit{X}}^{\ast }}\right]$ report the dynamic contribution of the voltage field to $\Delta Q$ and $\Delta \Delta Q$, assuming voltage coupling with four gating residues.

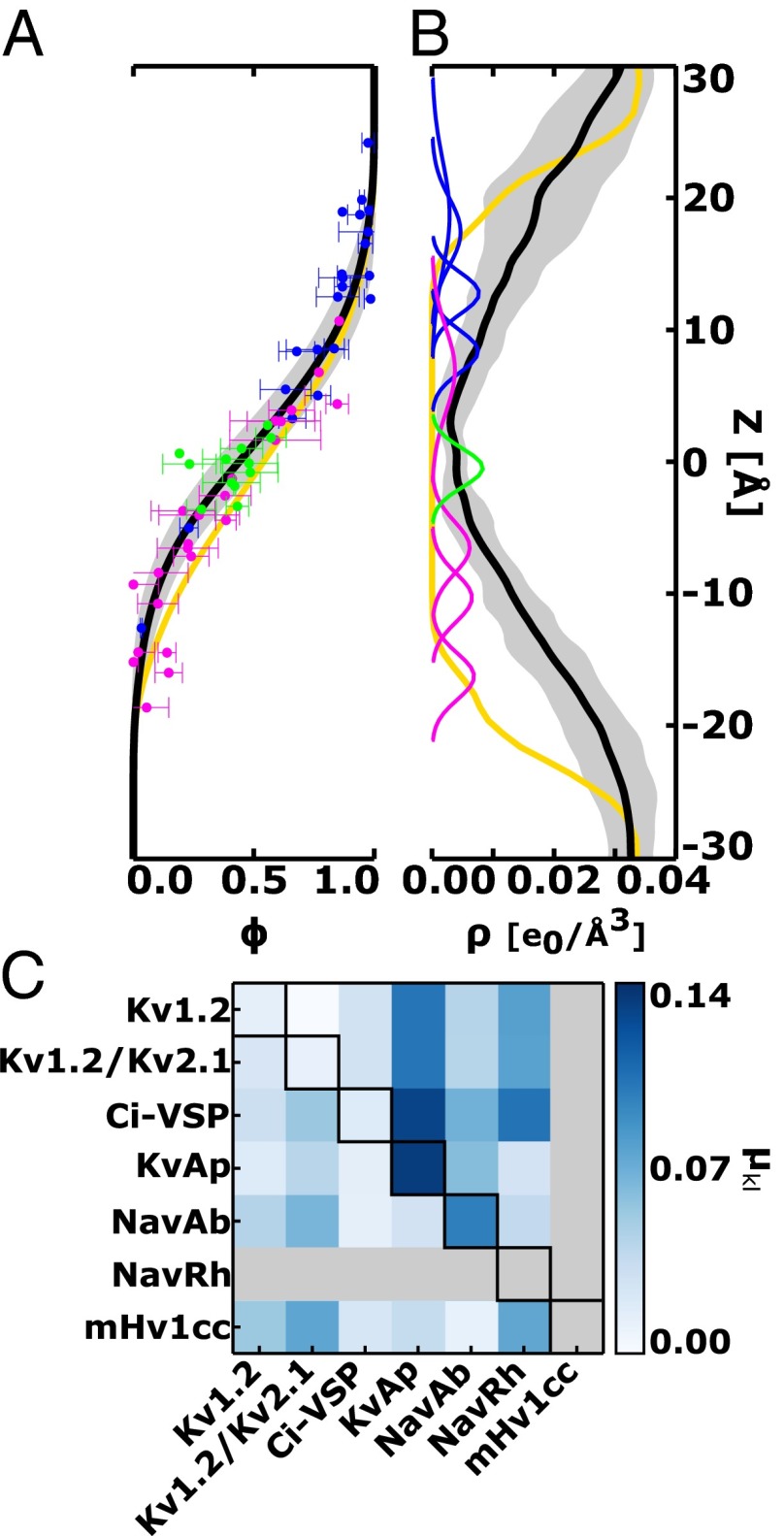
Fig. 4.

Voltage-coupling analysis and field reshaping. (A) Voltage coupling $\varphi \left(z\right)$ and (B) water density $\rho \left(z\right)$ profiles along the TM direction $z$ of the gating pore. For clarity, the entire dataset is presented as an average curve (black) with associated error bars (gray shading). Also shown are coupling and density values for the phenyl center (green) and the S4 basic amino acids in their activated (dark blue) and resting (pink) positions. Note that the average coupling profile (black) is fundamentally distinct from that of a bare lipid bilayer (yellow). The steepest part of $\varphi$ at the phenyl center implies the existence of a focused voltage gradient across the domain compared with the lipid bilayer. (C) Field reshaping ${\mu }_{kl}$ between voltage-sensor structures $k$ and $l$. Diagonal values report the ${\mu }_{kl}^{\mathit{X}\mathit{Y}}$ estimates between conformations of a fixed domain isoform, whereas lower and upper triangular regions of the matrix representation present, respectively, the ${\mu }_{kl}^{\mathit{X}{\mathit{X}}^{*}}$ and ${\mu }_{kl}^{\mathit{Y}{\mathit{Y}}^{*}}$ estimates for a fixed conformation over distinct isoforms. In the computation of ${\mu }_{kl}$, each of the profiles ${\varphi }_k\left(z\right)$ and ${\varphi }_l\left(z\right)$ corresponds to an average over four independent domain subunits. Here, the voltage coupling was determined via an all-atom formulation through the electrical distance definition (Figs. S3 and S4). Independent estimates based on continuum electrostatic calculations are presented in Fig. S5.

Fig. 4C presents, in matrix representation, the ${\mu }_{kl}$ estimates computed over the dataset of sensor structures. The on-diagonal entries show the ${\mu }_{kl}^{\mathit{X}\mathit{Y}}$ values between conformations of the same domain. Note that ${\mu }_{kl}^{\mathit{X}\mathit{Y}}$ cannot be evaluated for mHv1cc and NavRh as only one conformational state of the VS is known for these channels (Table S1). In contrast, the off-diagonal entries in the lower triangular region of the matrix show the field reshaping between the resting conformation of distinct domains (${\mu }_{kl}^{\mathit{X}{\mathit{X}}^{\ast }}$), whereas those in the upper triangular region are the same estimates for the activated conformation (${\mu }_{kl}^{\mathit{Y}{\mathit{Y}}^{\ast }}$). The most significant variations ${\mu }_{kl}^{\mathit{X}\mathit{Y}}=\text{0}.14$, ${\mu }_{kl}^{\mathit{X}{\mathit{X}}^{\ast }}=\text{0}.08$, and ${\mu }_{kl}^{\mathit{Y}{\mathit{Y}}^{\ast }}=\text{0}.14$ are, respectively, found for KvAP/KvAP, mHv1cc/NavRh, and Ci-VSP/KvAP, indicating that the field reshaping is worth at most 0.15 across the entire dataset. As such, the ${\mu }_{kl}$ estimates calculated here correspond to marginal values of $\Delta Q_{kl}$ and $\Delta \Delta Q_{kl}$, in the order of 0.6 e₀. In terms of electrical energies, the contributions $V\Delta Q_{kl}$ and $V\Delta \Delta Q_{kl}$ are ∼2.5 kT for the physiologically relevant voltage of 100 mV (3.86 kT/e₀).

The conclusion emerging from this analysis is that the estimates fall into the range of thermal energy, thereby pointing to a weak dependence of the voltage-coupling map with sequence and structure across the dataset. Not only for Kv1.2 (27) or Kv1.2/Kv2.1 (28) as previously suggested, our result supports that the voltage field intrinsic to sensor domains is primarily static or conformation independent. More importantly, it reveals the conservation of the voltage field over distinct constructs. This conservation is a remarkable finding that contrasts with their operational differences, including the extension of the S4 activation motion (Fig. 3) and $\Delta Q$ values (Table S1). It is worth mentioning that the results in Fig. 4 were obtained following calculations of $\varphi$ via the electrical distance definition (Eq. 10). As shown in Fig. S5, the same analysis was independently reproduced through calculations of $\varphi$ via solution of the PB-V equation (Eq. 9). Despite the intrinsic differences between the PB-V and the electrical distance (continuum vs. all-atom), the estimates agree in both formulations, thus strengthening our conclusions.

Energetic Implications.

Because $\varphi \left(\mathit{r}\right)$drops substantially across the occluding hydrophobic site within the domain (Fig. 4A), the static nature of the field ensures that most of the electrical energy $V\Delta Q$ arises from the physical displacement of S4 charges across that region. Specifically, up to 72% of the total gating charge potentially transported by one of the S4 basic amino acids across the entire membrane results from its displacement over a narrower (20 Å) region nearby the occluded site. This result is consistent with previous measurements (37) and calculations (24, 27) showing the existence of a focused electrical field within the domain.

The corroboration here that the voltage field is static in distinct constructs is of particular interest, given the long-lasting controversy concerning the activation mechanism of VSs. Until now, three competing models have been proposed: transporter, paddle, and sliding-helix (1). The transporter proposes that hydration of S4 focuses the electric field within the domain and activation involves reshaping this intensely focused field around the helix rather than extensively displacing it across the membrane. In contrast, the sliding-helix devises that S4 goes through a large piston-like motion on activation, forming conformation-dependent salt bridges while crossing a focused, motionless field. Finally, the paddle states that S4 and the C-terminal region of S3 form a “voltage-sensor paddle” that would move a large distance within the membrane during activation (a revised model was recently proposed based on the X-ray structure of Kv1.2-Kv2.1) (6). Currently, although not refuting key features of the paddle or transporter models, i.e., the S3-S4 forming paddle, hydration of the domain and field focalization, the emerging picture from the VS structures and their manifold studies (including the presented one) depicts major characteristics of the sliding-helix.

The consequence of the voltage field being conserved across distinct constructs relies on marginal contributions of $V\Delta \Delta Q$ to their energetic differences, i.e., distinct sensor domains transfer about the same amount of gating charges when moving their S4 helices between fixed microscopic configurations. The latter is one critical result meaning that their diversity, including the extension, rate, and voltage dependence of the S4 motion or $\Delta Q$ as dictated by the free energy landscape, must be rationalized in terms of dominant modifications of their chemical free-energies $\Delta \Delta F\left(\text{0}\right)$ (scenario ii in Fig. 1). Consistent with this notion, one recent computational study shows that gating pore mutations in Kv1.2 destabilizes, in ∼4 kcal/mol, the chemical free energy associated with the transfer of a single S4 charge across the domain hydrophobic core (38). This estimate, that represents a lower boundary for $\Delta \Delta F\left(\text{0}\right)$ involving sequential transfer of four S4 charges, is substantially larger than the estimates of $V\Delta \Delta Q$ computed herein. Given that the electrical energy depends further on the S4 charges, the present conclusion must hold for every perturbations not resulting into charge neutralization of the helix. In practice, the statement above can be understood in terms of ensemble average gating charge displacement vs. voltage measurements, which is familiar to most experimentalists in the form of $\langle Q\rangle \left(V\right)$ curves. Hence, rightward or leftward shifts between the $\langle Q\rangle \left(V\right)$ curves of distinct VS domains read as differences in the chemical free energy stability of their resting or activated states. This concept is illustrated in Fig. S6 for a minimalist continuum electrostatic model of the VS. The rational would also apply for kinetic measurements of the gating charge [i.e., variations of the activation time ($\tau$) in distinct VSs would derive from differences in the chemical free energy barrier for activation].

The intradomain dielectric $\mathrm{\in }\left(\mathit{r}\right)$ imposed by the distribution of protein atoms, lipids, and waters (Fig. 4B) reflects deep structure-function relationships in the construct. At the origin of the solvation energies of S4 (23), $\mathrm{\in }\left(\mathit{r}\right)$ seems to be optimum for the stability of the segment within the protein-membrane environment, suggesting that significant modifications would come at the expenses of structural defects. At the origin of $\varphi \left(\mathit{r}\right)$ the dielectric also appears to be optimum for the VS sensitivity within physiological (millivolt) ranges of the membrane potential by ensuring the focalization of the voltage field within the domain (37). This hypothesis raises the idea that sensor domains were subjected to evolutionary pressure while restrained by $\mathrm{\in }\left(\mathit{r}\right)$, thereby rationalizing the conservation of $\varphi \left(\mathit{r}\right)$ over the domain sequence itself.

Concluding Remarks.

The present work deals with a central paradigm in the subject of excitable systems in biology, namely dynamic contributions of the membrane voltage field to VS energetics. Far from being trivial, this issue has challenged an entire generation of scientists because static and dynamic contributions of the voltage field cannot be discriminated from measurements of $\Delta Q$, as reflected in the competing models trying to rationalize the VS function. As described above, the issue emerges because $\Delta Q$ reports electrical displacements of S4. As such, gating charges could arise from displacements of S4 relative to a static field or from the field reshaping itself. The dilemma imposes that structure-based calculations are required to solve the issue. Here, we followed this approach by quantifying the field reshaping $\mu$ across a number of VS structures. In light of barely modifiable coupling properties, our conclusion is that the diversity in the extension, rate, and voltage dependence of the S4 motion observed in nature must be rationalized in terms of chemical free energy differences (i.e., differences in the detailed atom-atom interactions of the domain rather than in its electrical coupling properties). In typical gating charge vs. voltage measurements, variations in the amount of $\Delta Q$ transported by distinct VSs at a fixed voltage arise from modifications in their chemical free-energies.

We believe the results are of broad interest as they provide an important clarification about the energetics of sensor domains and are synchronous with recent advances in theoretical and experimental fronts dealing with the VS structure and operation. Structure-based calculations (38) or recently devised median-voltage methods (39) have just started to be applied for determination of chemical free energy variations of the domain. The present study reinforces the referred methods as powerful strategies to assess VS perturbations.