Significance
The endoplasmic reticulum (ER) is an important membrane-bound organelle in all eukaryotic cells. Depending on cell type and functional state, the ER membrane can adopt different morphologies, including a network of interconnected tubules, and sheets that can contain fenestrations or be stacked on top of each other. How these different morphologies are generated is unclear. Here, we present a comprehensive theoretical model that explains the formation and interconversion of virtually all known ER morphologies. The model is based on two types of membrane-shaping proteins, exemplified by the reticulons and lunapark, which both stabilize the high membrane curvature in cross-sections of tubules and sheet edges, but favor straight or concave sheet edges, respectively. The predictions of the model are experimentally verified.
Keywords: endoplasmic reticulum, reticulon, lunapark, morphology, model
Abstract
The peripheral endoplasmic reticulum (ER) forms different morphologies composed of tubules and sheets. Proteins such as the reticulons shape the ER by stabilizing the high membrane curvature in cross-sections of tubules and sheet edges. Here, we show that membrane curvature along the edge lines is also critical for ER shaping. We describe a theoretical model that explains virtually all observed ER morphologies. The model is based on two types of curvature-stabilizing proteins that generate either straight or negatively curved edge lines (R- and S-type proteins). Dependent on the concentrations of R- and S-type proteins, membrane morphologies can be generated that consist of tubules, sheets, sheet fenestrations, and sheet stacks with helicoidal connections. We propose that reticulons 4a/b are representatives of R-type proteins that favor tubules and outer edges of sheets. Lunapark is an example of S-type proteins that promote junctions between tubules and sheets. In a tubular ER network, lunapark stabilizes three-way junctions, i.e., small triangular sheets with concave edges. The model agrees with experimental observations and explains how curvature-stabilizing proteins determine ER morphology.
How the characteristic shapes of subcellular organelles are generated is a fundamental question in biology. The morphology of the endoplasmic reticulum (ER) is particularly intriguing because it consists of domains of different shapes, varies in structure among different cell types, and is extensively remodeled during the cell cycle and changes of the metabolic state. In all eukaryotic cells, the ER is a continuous membrane system with a common luminal space, comprising the nuclear envelope and the peripheral ER. The peripheral ER includes a network of membrane tubules and interspersed sheets (1–3). Tubules have high membrane curvature in cross-section, with a radius in the range of 15 to 25 nm (4). Sheets consist of two extended membrane surfaces that lie parallel to one another and are connected by curved surfaces of sheet edges. In a cross-section perpendicular to the sheet plane, the curvature of the edge surface is comparable to that of tubules (5). Tubules often emanate from the edges of sheets, but can also be connected with each other by junctions. In many cell types, peripheral ER sheets contain holes (fenestrations), the rims of which form internal edges of the sheets (2, 5, 6). Finally, ER sheets can be stacked on top of each other. Although sheet stacking is seen in all cells, it is most prominent in “professional” secretory cells, such as pancreatic or salivary gland cells, which secrete most of their synthesized proteins (7). Recent work has shown that stacked sheets adopt a “parking garage” structure, in which the different levels are connected by helical ramps (8).
The structure of the ER not only differs among cell types, but also can change over the course of the cell cycle and during differentiation (9). For example, in Xenopus egg extracts, Caenorhabditis elegans, and some tissue culture cells, ER tubules convert into sheets during mitosis (10–13), and ER sheets accumulate and form stacks during the maturation of B cells into plasma cells. The different morphologies of the peripheral ER relate to distinct functions of the membrane domains (9). Sheets generally accommodate membrane-bound polysomes engaged in the synthesis of secretory and membrane proteins. Tubules, however, may specialize in lipid synthesis, Ca2+ signaling, and contact with other organelles.
We are interested in the fundamental question of how the different morphologies of the peripheral ER—tubules, sheets, fenestrated sheets, and helicoidal membrane stacks—are generated and interconverted. Previous work has identified two integral membrane protein families involved in shaping ER tubules: the reticulons and DP1 (deleted in polyposis 1)/Yop1p (4, 14, 15). Members of both families are highly expressed in all eukaryotic cells. These proteins stabilize the high curvature of tubules in cross-section; they most likely generate high membrane curvature by forming wedges in the cytoplasmic leaflet of the lipid bilayer and by oligomerizing into arc-like scaffolds around the tubules (1, 14, 15). Because the reticulons and DP1/Yop1p localize not only to tubules, but also to sheet edges, they can also stabilize the high cross-sectional curvature of these edges, keeping the two sheet surfaces closely apposed (5). These proteins therefore generate not only tubules, but also sheets, and their abundance determines the balance between the two morphologies, with a higher concentration of the proteins generating more tubules at the expense of sheets (4, 5). We have also proposed that some members of the reticulon and DP1/Yop1p families promote the generation of helicoidal connections between membrane sheets (8). A recently discovered player in ER morphology is the lunapark protein (16). Although its function remains unclear, it is a ubiquitous membrane protein that localizes to three-way junctions in yeast and mammalian cells (16, 17).
Previous theoretical models for how the reticulons and DP1/Yop1p shape the ER were based on the assumption that they stabilize the high membrane curvature in cross-sections of tubules and sheet edges (4, 5). These models can explain the generation of tubules and sheets, as well as their interconversion, but they cannot explain the experimentally observed shapes of ER sheets, junctions between sheets and tubules, sheet fenestrations, or the generation of helicoidal sheet connections. To explain helicoidal connections, we have postulated that some members of the reticulons or DP1/Yop1p families not only stabilize the positive curvature of the sheet edge perpendicular to the membrane surface, but also the negative curvature along the helical edge line (8). We now show that the specific favored curvature of the edge line is generally crucial for shaping the ER. We describe a theoretical model that explains the formation of virtually all observed ER morphologies on the basis of just two types of curvature-generating proteins. Both types stabilize the high curvature in cross-section of tubules and sheet edges, but one favors straight edges and the other negatively curved edges. We suggest that reticulons 4a/b are representatives of proteins that favor straight edge lines, whereas lunapark is an example of proteins that favor negatively curved edge lines. In a tubular ER network, lunapark stabilizes three-way junctions, i.e., small triangular sheets with concave edges. Our model is supported by experimental observations and can explain how the ER is remodeled simply by changes in the expression or activity levels of the curvature-stabilizing proteins.
Results
A Theoretical Model for ER Morphologies.
Qualitative description of the model.
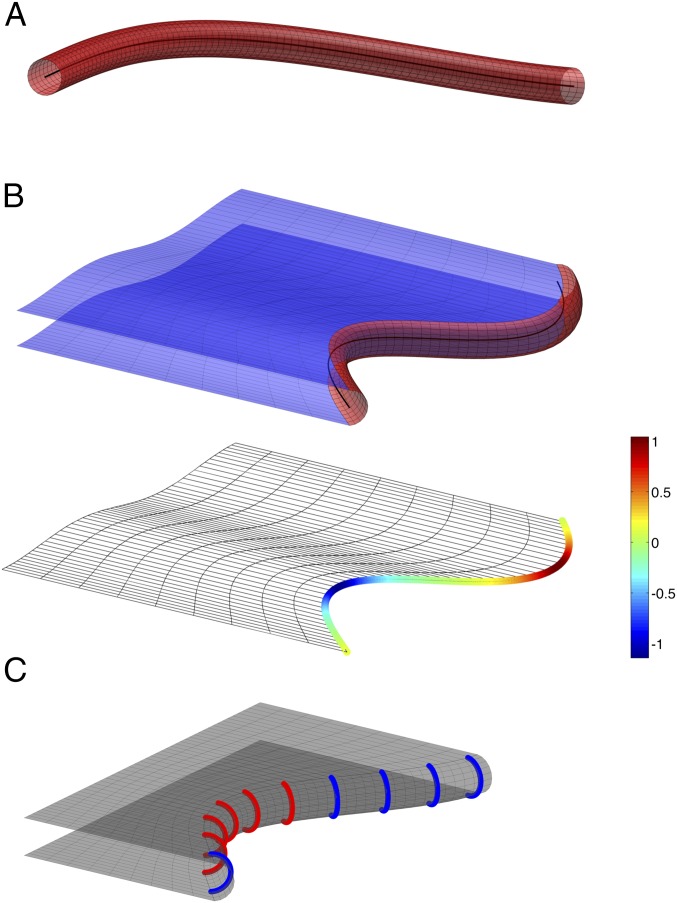
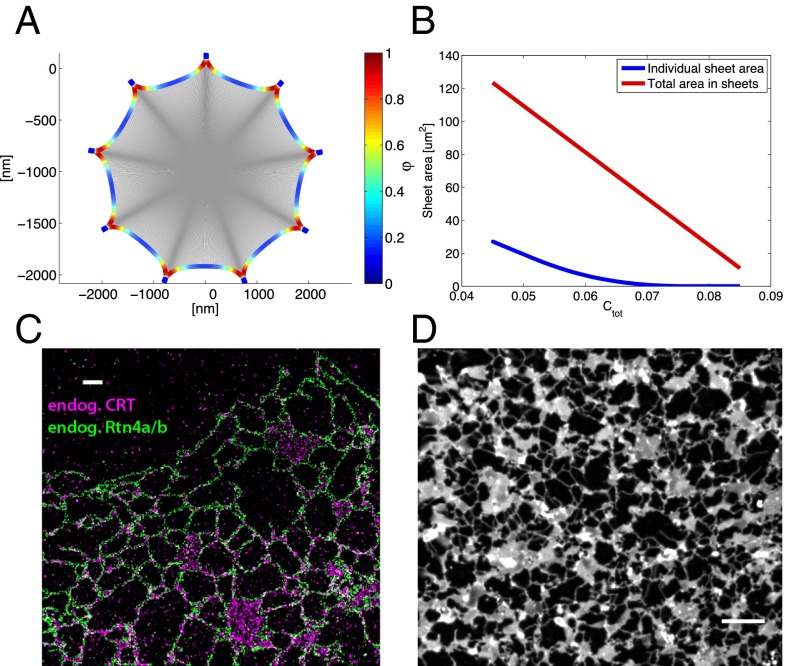
Our goal is to develop a comprehensive model that can explain essentially all observed ER morphologies. Our strategy is to determine the equilibrium state of the system by searching for the ER morphology that is associated with the minimal system energy. Such considerations have been used to model tubules, sheets, and stacked sheets of the ER (4, 5, 8), and to determine the cellular shape of erythrocytes (18). We consider four types of basic membrane structures: tubules, sheets, fenestrated sheets, and helicoidal connections between stacked sheets. A tubule is considered to be a cylinder, the axis of which can bend in space (Fig. 1A). We represent a tubule by its axis line. A sheet is considered to consist of two membrane surfaces that are parallel to each other and are connected by an edge membrane (Fig. 1B). The shape of the edge membrane can be approximated by a half-cylinder whose axis bends along the sheet rim (Fig. 1B and Fig. S1). We model a sheet by a single representative surface lying in the middle between the two membrane surfaces. The representative surface is bordered by an edge line, which is the curved axis of the hemicylindrical edge membrane (Fig. 1B). The edge line can be straight, bulge away from the sheet plane (have a positive curvature), or indent into the sheet (have a negative curvature). Tubules can emerge from sheet edges, in which case the tubule axis branches off from the edge line.
Fig. 1.
Representation of ER tubules and sheets in a theoretical model. (A) A tubule is considered to be a cylinder, the axis of which is curved in space (black line). (B) A sheet consists of two parallel membrane surfaces (Upper, in blue). The sheet edge is considered to be a half-cylinder (in red), the axis of which curves in the plane of the sheet (black line). The sheet is represented by a single surface between the two membrane surfaces (Lower), which is bounded by an edge line that can adopt positive or negative curvature. The curvature is color-coded (scale on the right, arbitrary units [1/length]). See also Fig. S1. (C) A scheme depicting edge-promoting proteins as arcs along a sheet edge. Edge promoters favoring a negatively curved edge line (type S) are colored in red, and promoters of straight edge lines (type R) are colored blue.
We assume that there are two types of proteins that form tubules and sheet edges, called R and S. As in previous models, we consider these proteins to form arc-like scaffolds that are separated by a constant, optimal distance along tubules or edges (45 nm; Fig. 1C) (4, 5). Both types, R and S, stabilize the positive membrane curvature of tubules and sheet edges in cross-sections perpendicular to their axes, but favor different curvatures of the edge line, and , respectively. In the following, we will refer to and as the line spontaneous curvatures of R and S proteins, respectively. We assume that the R protein have zero line spontaneous curvature, , meaning that the edge generated by R-protein molecules tends to be straight. The S protein is assumed to generate a negatively curved edge line, meaning that its line spontaneous curvature is negative, . The relative abundance of the R and S proteins at each point of the edge will determine the local curvature of the edge line, and vice versa, the curvature of the edge line will influence the localization of the proteins (Fig. 1C).
System energy.
We determine the equilibrium ER morphology by minimizing the total energy of the system. The model considers several contributions to the system energy (described in detail in SI Text):
-
i)
The elastic bending energy of sheet surfaces, which is the energy required to bend the two membranes of a sheet away from their preferred flat shape (18, 19). This energy includes contributions from the membrane curvature per se (mean curvature), as well as from the Gaussian curvature of the sheet membranes. The mean curvature energy accounts for changes of membrane shape, whereas the energy of the Gaussian curvature is associated only with topological changes, such as variations in the number of sheets, formation of sheet fenestrations, or of helicoidal connections between stacked sheets.
-
ii)
The elastic bending energy of the sheet edges, which describes the energy required for bending the edge line away from its preferred spontaneous curvature (8). The effective spontaneous curvature of the edge line depends on the line spontaneous curvatures of the R and S proteins, and , as well as on the relative abundance of R and S proteins in the edge. This energy also includes a contribution from the Gaussian curvature.
-
iii)
The line tension of the sheet edges, representing the energy cost (per unit length of the edge line) of transition of a cylindrical tubule to the hemicylindrical sheet edge. This energy takes into account that the curvature-stabilizing proteins can adopt more positions on a tubule compared with a sheet edge, as they have twice the surface area available (cylinder vs. half-cylinder). The increase in the entropic contribution to the free energy associated with moving proteins from tubules into sheet edges is proportional to the length of the edge line. Another contribution to the line tension, which is not explicitly taken into account by our estimation, can originate from the membrane deformations related to connecting a hemicylindrical edge surface with two planar membrane surfaces (SI Text).
-
iv)
The entropic contribution to the free energy associated with the uneven distribution of the two types of curvature-stabilizing proteins R and S along the edge line. This contribution to the system energy resists the partitioning of the two types of curvature-stabilizing proteins into separate domains along the edge line, a segregation favored by the difference in their spontaneous curvatures.
Another possible contribution to the energy arises from the network entropy, which is related to the number of configurations the system can adopt in each morphology (20). This contribution would tend to break up a network and would disfavor junctions with multiple connections. However, this energy term is relevant only when the system is very dilute (21), i.e., in the case of long tubules with few junctions, and is therefore not included in our calculations.
Energy minimization.
We seek the equilibrium morphology of the system corresponding to any given concentration of the R and S proteins. We define concentrations, [R] and [S], as the fraction of the total membrane area that is covered by these proteins (each R or S protein occupies ∼300 nm2) (4). Instead of [R] and [S], we use as variables the total protein concentration Ctot = [R] + [S] and the fraction of S proteins Φ = [S]/([R] + [S]). To find the equilibrium morphologies, we minimize the total energy of the system for different Ctot and Φ. We performed the calculations for different line spontaneous curvatures of S proteins, , and different relative contributions to the energy of the mean and Gaussian curvatures of the ER membrane, because these parameters may vary among different cells.
Because the curvature-stabilizing proteins generate both the sheet edges and the tubules emerging from these edges, the total concentration of the R- and S-type proteins, Ctot, determines the total edge length (the sum of the lengths of all tubules and sheet edges in the system). An increase of Ctot results in membrane being moved from planar sheet surfaces into sheet edges and tubules. Variation of the fraction of S proteins, Φ, affects the overall morphology of the system by changing the ratio between the lengths of negatively curved and straight edges.
In summary, the energy-minimization procedure determines how, for a given Ctot and Φ, the total surface area and edge length are distributed into individual sheets and connecting tubules; it also calculates the optimal shape of these sheets, the most favorable number of tubules emanating from a sheet, and the number of junctions. Finally, the model determines the optimal distribution of the curvature-stabilizing proteins R and L along the edge line.
Modeling Results and Comparison with Experiments.
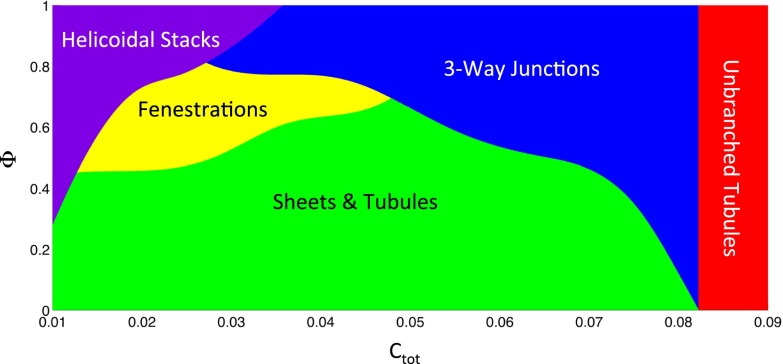
The results of our calculations, presented as a morphology diagram (Fig. 2), show that different ER morphologies are energetically favored at different ranges of the total concentration of the curvature-inducing proteins, Ctot, and different values of the fraction of S proteins, Φ. Calculations using different values of the estimated Gaussian bending modulus of the membrane and the spontaneous curvature of the edge line induced by S-type proteins do not result in qualitatively different morphologies. In the following, we will discuss the different regimes of this morphology diagram.
Fig. 2.
Morphology diagram. The energetically favored ER morphology was calculated for different values Ctot of the total concentration of curvature-stabilizing proteins and different fractions Φ of the S-type proteins that favor a negatively curved edge line. A three-way junction is defined as a triangular sheet with an area below 0.1 μm2. A fenestration is defined as a sheet connected by tubules that are shorter than the distance between adjacent tubules emerging from a sheet.
Tubules and three-way junctions.
Our model predicts that at high concentrations of the curvature-stabilizing proteins, Ctot, all membranes are found in long, nonbranched tubules (red area in Fig. 2). As estimated previously (4), complete conversion into tubules is achieved with ∼8.8% surface coverage by these proteins (saturation level). The complete conversion into tubules at high Ctot happens irrespective of the fraction of S proteins, Φ, and corresponds to a situation in which all membranes are completely converted into curved edges. Beyond the saturation level, any further increase of the S- or R-protein concentration would only serve to reduce the distance between the arc-like scaffolds along the tubules below the optimal separation, with no further effect on membrane morphology. The almost complete conversion of sheets into tubules has indeed been observed upon overexpression of several of the curvature-stabilizing proteins in tissue culture and yeast cells (5, 14). As shown below, this is also true for overexpression of lunapark, the prototype of an S-type protein.
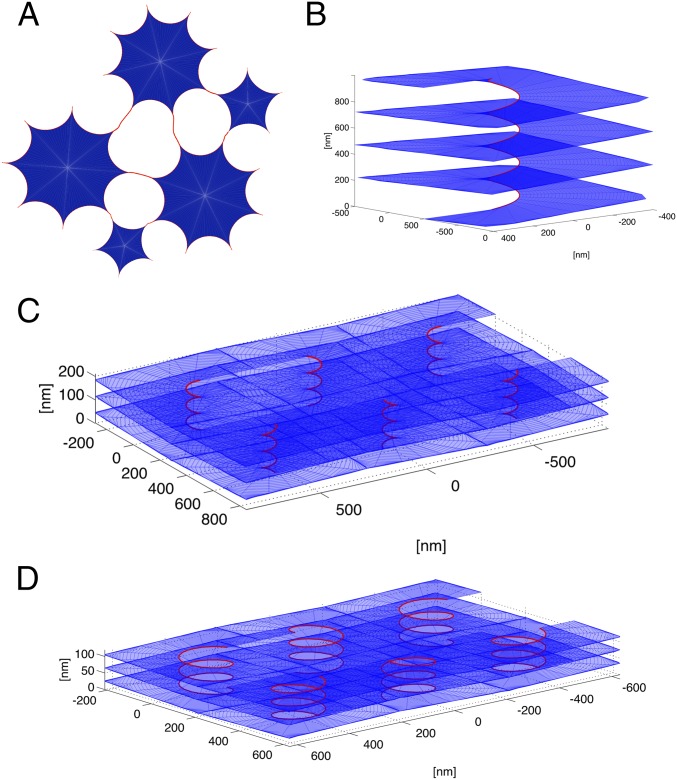
The next prominent area in the morphology diagram corresponds to somewhat lower concentrations of the curvature-stabilizing proteins, Ctot, at which the membranes are not completely converted into curved edges (blue area in Fig. 2). In this case, the model predicts the formation of a tubular network in which tubules are connected by small, equilateral, triangular sheets (Fig. 3A). These sheets have a size comparable to the tubule diameter, so that they can be considered to be three-way junctions of tubules; indeed, they would be seen as three-way junctions experimentally, because the area of the sheets (<0.1 μm2) is below the resolution of ordinary light microscopy. The edge lines of the small sheets have a high negative curvature, with S proteins concentrated at the most negatively curved parts (see color-coded edge distribution in Fig. 3A). The distance between three-way junctions varies, becoming large with Ctot approaching the saturation level (boundary between the blue and red regions of the morphology diagram in Fig. 2). Our model predicts that in a tubular ER network, symmetrical three-way junctions are the only connections between tubules.
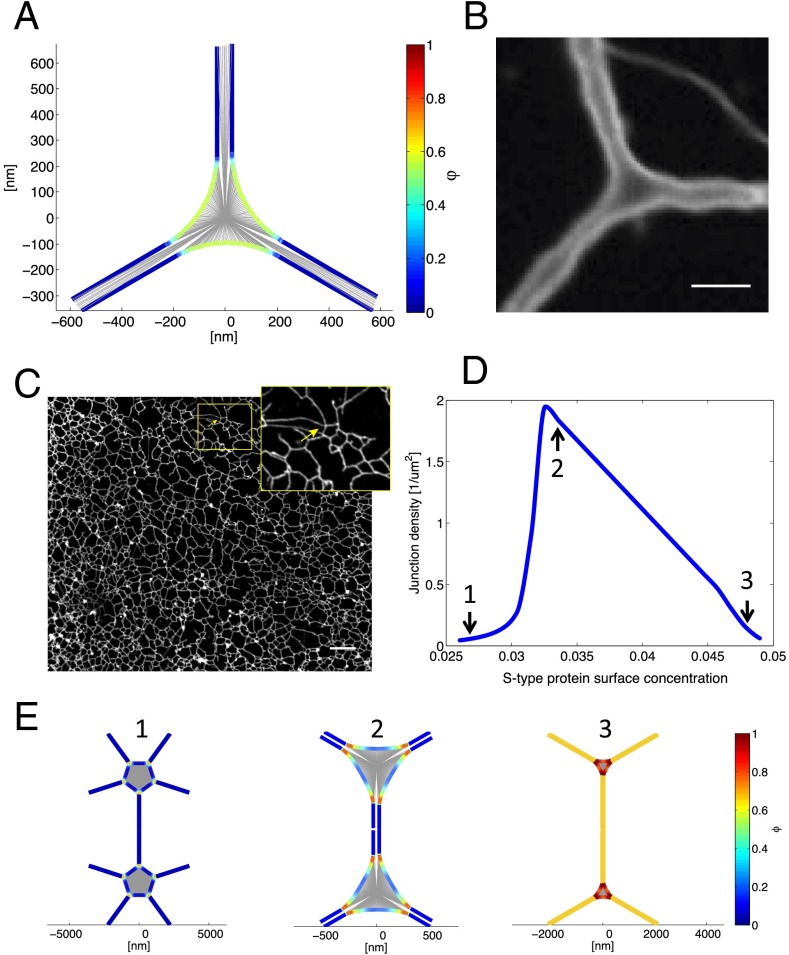
Fig. 3.
Three-way tubular junctions. (A) Top view of a theoretical three-way junction between tubules. The central area is a flat sheet with concave edges. The concentration of the S-type protein, Φ, is color-coded (scale on the right); it is higher in the three-way junction than in the emerging tubules. (B) Three-way junction between dilated ER tubules formed with Xenopus egg membranes. An ER network was formed in the absence of cytosol with a light membrane fraction isolated from Xenopus extracts. The membranes were prelabeled with the hydrophobic dye DiOC18 and visualized by confocal fluorescence microscopy after incubation for 2 h, at which point the diameter of the membrane tubules is greatly increased. (Scale bar: 3 µm.) See also Movie S1. (C) Tubular ER network in interphase Xenopus egg extracts. A crude meiotic (CSF) extract was driven into interphase by addition of Ca2+ ions for 30 min. The image shows that three-way junctions are the predominant connectors. (Scale bar: 10 µm.) (Inset) Magnification of a rare example of a four-way junction. (D) Theoretical prediction of the density of tubular junctions (number of sheets per membrane surface) as a function of the concentration of S-type proteins. The concentration of the R-type proteins was kept constant at 0.04 surface coverage. The shape of the junctions at the indicated points (arrows) is shown in E. (E) For three points in D, the shape of the junctions and the concentration of the S-type protein along the edge line are shown. The concentration is color-coded (scale on the right).
Some experimental justification for treating three-way tubular junctions as small sheets comes from observing ER networks generated with Xenopus egg membranes after an extended incubation period (Fig. 3B). Under these conditions, the tubules have a drastically increased diameter, so that their membrane can be distinguished from their lumen. The images show three tubules emanating from small, flat, triangular sheets with concave edges (Fig. 3B). Optical sectioning and 3D reconstruction confirm that the junctions consist of flat, parallel membranes (Movie S1). Although it is unclear why the tubules dilate after long incubation times, it seems likely that the junctions scale accordingly. The triangular shape of three-way junctions can also be seen in 3D reconstructions of electron tomographs of the tubular ER network in tissue culture cells (22).
Our model predicts that three-way junctions are the predominant connections in a tubular network. Indeed, three-way junctions are often seen in light microscopy images of tissue culture cells, but quantification is difficult because the network is very dense and contains many interspersed larger sheets. We therefore analyzed the ER network in an interphase extract of Xenopus eggs, which consists almost entirely of tubules (Fig. 3C). An ER network was generated with a crude extract and stained with a hydrophobic fluorescent dye (10). Using an automated image-processing algorithm, we determined that the network consists almost exclusively of tubules connected by three-way junctions (99.5% and 0.5% of all junctions contain three and four connections, respectively; no junctions of higher connectivity were detected).
Our model predicts that S-type edge proteins localize predominantly to the three-way junctions (Fig. 3A). A recently discovered protein, lunapark, indeed localizes to three-way junctions both in Saccharomyces cerevisiae and, after moderate overexpression, in mammalian tissue culture cells (16). We confirmed this localization for endogenous lunapark in mammalian COS cells (Fig. 4A). Not all three-way junctions contain detectable levels of lunapark, raising the possibility that other junction proteins also favor a negative curvature of the edge line, or that there are junctions that consist of tethered, rather than fused, tubules. Nevertheless, lunapark seems to be an excellent candidate to be an S-type curvature-stabilizing protein that favors a negatively curved edge line.
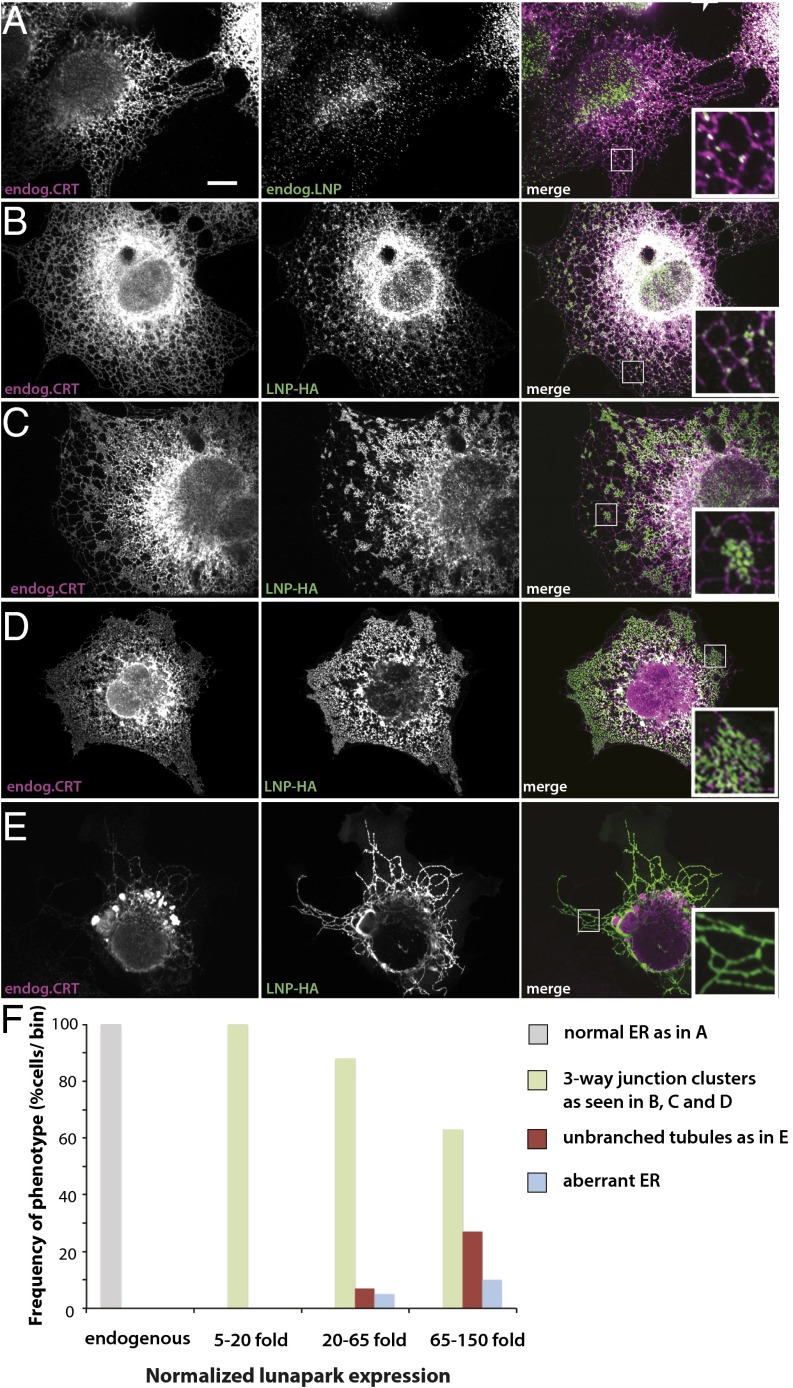
Fig. 4.
Transient expression of lunapark in COS cells. (A) The localization of endogenous lunapark (Lnp) and calreticulin (CRT) was determined by immunostaining with specific antibodies. The samples were analyzed by confocal microscopy. (Right) Merged image. (B) An HA-tagged version of lunapark (Lnp-HA) was transiently expressed in COS cells, and its localization compared with that of endogenous CRT. The samples were analyzed by fluorescence microscopy using HA and CRT antibodies. Shown is a cell that expresses Lnp-HA at a low level. (C–E) As in B, but with progressively higher expression levels of Lnp-HA. (Scale bar: 10 µm.) See also Fig. S2. (F) COS cells were transiently transfected with Lnp-HA as in B–E, but the Lnp protein was stained with a specific antibody as in A. The cell area was segmented manually, and the mean expression level of lunapark was quantified for every cell using ImageJ. At different expression levels of lunapark, the number of cells that showed normal ER as in A, three-way junction clusters as in B–D, unbranched tubules as in E, or aberrant ER was determined. The cells were binned into groups of similar expression levels (normalized relative to the mean Lnp level in untransfected cells), and for each bin the number of cells with a given ER morphology was plotted as percentage of the total number of cells (n = 90 cells).
We further investigated whether lunapark behaves like an S-type protein by comparing the theoretical and experimental ER morphologies at different lunapark levels. Our model predicts that the number of junctions per membrane surface has a maximum at a certain fraction of the S proteins (Fig. 3D). As the level of S proteins increases, the junctions change from large sheets with multiple tubular connections, to three-way junctions with short connecting tubules, to three-way junctions that are separated by long tubules (Fig. 3E). The S proteins are predicted to localize to the regions where tubules emanate from sheets, and to distribute throughout the tubules at high concentrations (Fig. 3E).
To experimentally test these predictions, we first increased the levels of lunapark by transiently expressing a HA-tagged version (Lnp-HA) in COS cells. The localization of Lnp-HA was compared with that of endogenous calreticulin (Fig. 4), a general ER marker, or reticulon (Rtn) 4a/b (Fig. S2), a marker for ER tubules and sheet edges. When Lnp-HA was expressed at low levels in COS cells, the protein localized similarly to the endogenous protein, mostly to three-way junctions (compare Fig. 4B with Fig. 4A and Fig. S2A with Fig. S2B). Some of the punctae also localize to tubules, particularly to kinks. In cells expressing Lnp-HA at higher levels, the protein was found in clusters of densely branched tubules (Fig. 4 C and D and Fig. S2 C and D). These areas seem to have an extremely high number of three-way junctions per membrane surface. Finally, at very high expression levels, Lnp-HA localized to long, nonbranched tubules. The resulting ER structure was largely devoid of three-way junctions. The recently published lunapark transfection experiments likely correspond to this high expression level (23). The unbranched tubules contain Rtn4a/b (Fig. S2E), but seem to be depleted of calreticulin (Fig. 4E); this is similar to what has been observed upon overexpression of reticulons or DP1 (4), suggesting that the tubules become so narrow that luminal proteins are squeezed out. These results show that, as predicted, the number of junctions initially increases and eventually decreases with increasing lunapark concentration. The eventual distribution of lunapark throughout the tubules is also in agreement with the model (Fig. 3E). Similar results were obtained with COS cells stably expressing lunapark as a fusion with the fluorescent mCherry protein (Fig. S3): an increase in the expression of lunapark led to clusters of three-way junctions and eventually to unbranched tubules. Again, calreticulin was depleted from the unbranched tubules.
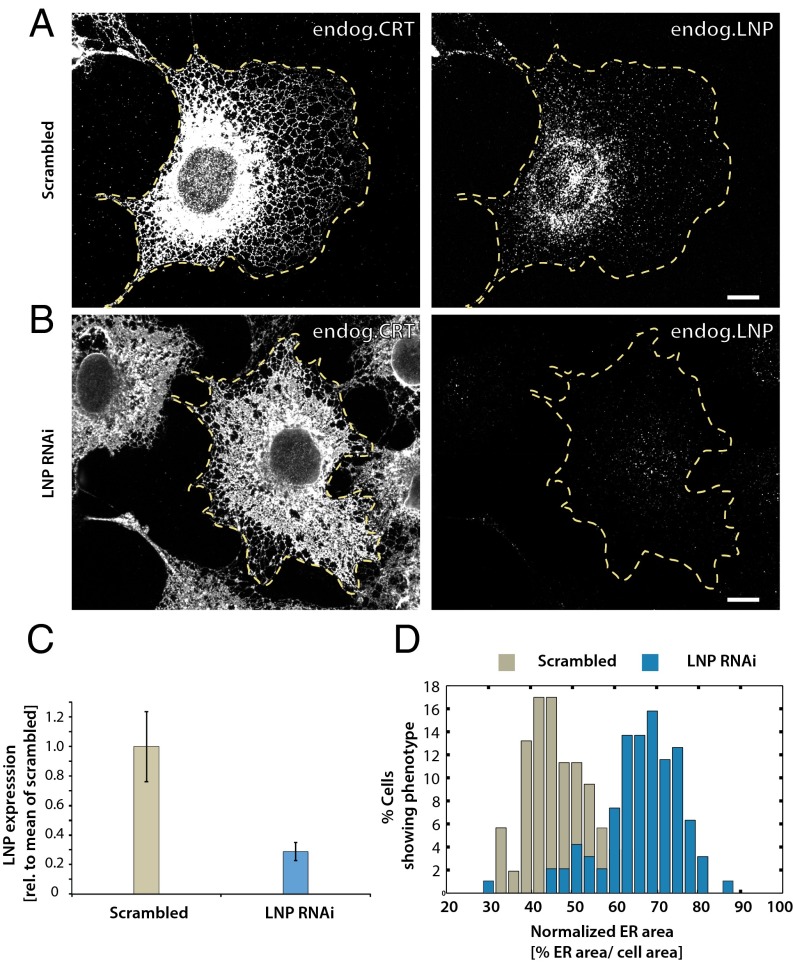
Our theory predicts that, at very low concentrations of lunapark, three-way junctions should disappear and be converted into large sheets with multiple tubule connections, because such structures need fewer S-type proteins to stabilize their negatively curved segments of edge lines (Fig. 3E). We tested this prediction by depleting lunapark from COS cells by RNAi. The cells were analyzed for endogenous calreticulin and Rtn4a/b by immunofluorescence microscopy. Indeed, in cells depleted of lunapark, many three-way junctions were transformed into large sheets (Fig. 5B vs. Fig. 5A; quantification shown in Fig. 5 C and D). Taken together, the experimental data support the theoretical model and indicate that lunapark is a curvature-stabilizing protein that prefers a negatively curved edge line. The localization of Rtn4a/b throughout the tubules and sheets edges indicates that these curvature-stabilizing proteins favor a less negatively curved edge line. Rtn4a/b might therefore be examples of R-type proteins that promote straight edge lines.
Fig. 5.
ER morphology changes upon depletion of lunapark in COS cells. (A) COS cells were transfected with control scrambled RNAi oligonucleotides for 72 h and analyzed for endogenous CRT and endogenous lunapark (LNP) by immunofluorescence microscopy. The cells were segmented manually (yellow dotted line) and lunapark expression level was determined after correction for mean background (Fig. 5C). (B) As in A, except that lunapark was depleted with RNAi oligonucleotides for 72 h. (C) To quantify the depletion of lunapark after treatment with RNAi, the cells were segmented manually and the mean lunapark fluorescence level was determined for every cell (n = 95 cells). The mean fluorescence level is displayed normalized to the mean fluorescence in control cells treated with scrambled oligonucleotide (n = 53 cells; ±SD). (D) To quantify the increase of the peripheral ER area after depletion of lunapark, the cellular area and the peripheral ER area were segmented. The cells were segmented manually and the CRT signal marking the ER area was segmented using the trainable WEKA segmentation plug-in in ImageJ. The total area covered by the peripheral ER was determined as the fraction of the total cell area. The cells were binned according to the fractional cell area covered by the peripheral ER, and the frequency of the phenotype in the cells was plotted as a histogram (n = 95 cells treated with Lnp RNAi, and n = 53 cells treated with scrambled control siRNA). (Scale bars: 10 µm.)
Large sheets with multiple tubule connections.
Our model predicts that, at intermediate and low concentrations of the curvature-stabilizing proteins, Ctot, and low fraction of S proteins, Φ, the sheets become larger and are connected to multiple tubules (Fig. 2, green area; Fig. 6A). The edges are most negatively curved at the regions where the tubules emerge from the sheets, and S-type proteins preferentially localize to these regions (Fig. 6A). When Ctot increases at a given Φ value, both the individual sheet size and the total sheet surface decrease (Fig. 6B).
Fig. 6.
Model prediction and experimental verification of large ER sheets with multiple tubule connections. (A) Predicted large sheet with multiple tubule connections. The calculations were performed for Ctot = 0.04 surface coverage and Φ = 0.2. The concentration of the S-type protein along the edge line,, is color-coded (scale on the right). (B) Calculated total and individual sheet areas as a function of Ctot (red and blue lines, respectively). The individual sheet areas were calculated for Φ = 0.2. (C) Endogenous calreticulin (endog. CRT) and reticulon 4a/b (endog. Rtn4a/b) were visualized in COS cells by STORM using specific antibodies followed by secondary antibodies labeled with fluorescent dyes. (D) ER network in a mitotic Xenopus egg extract. Cyclin BΔ90 was added to a crude interphase extract and the ER network was stained with the hydrophobic dye DiIC18; it was visualized by spinning-disk confocal microscopy. (Scale bar: 10 µm.)
The predictions of our model are consistent with images obtained for tissue culture cells by superresolution light microscopy (STORM). For these experiments we visualized in COS cells endogenous calreticulin and Rtn4a/b with specific antibodies followed by incubation with fluorescently labeled secondary antibodies (Fig. 6C). The images show that larger sheets are often connected with multiple tubules (Fig. 6C). In addition, the localization of endogenous Rtn4a/b throughout all tubules and sheet edges provides the strongest evidence yet that these proteins are general curvature-stabilizing proteins, rather than specific tubule-promoting proteins. This localization of the reticulons is also consistent with their proposed role as R-type proteins. To analyze the relationship between sheets and tubules in Xenopus egg extracts, we added nondegradable cyclin B (cyclin BΔ90) to an interphase extract, converting it into a mitotic state in which sheets are much more prominent than in interphase (10) (Fig. 6D). Again, larger sheets have more tubules emanating from them. Our model suggests that the ER morphology in tissue culture cells and mitotic Xenopus egg extracts corresponds to a situation in which Ctot and Φ dictate the formation of both sheets and tubules (green area in Fig. 2). The experimental data show that there is significant heterogeneity in sheet sizes and numbers of tubules emerging from individual sheets; this is consistent with our calculations, which indicate that the energy differences between states become small for larger sheets with multiple tubular connections (SI Text). Thus, thermal fluctuations may explain the observed heterogeneity.
Sheet fenestrations.
Our calculations show that, for all parameter values chosen, fenestrations with highly curved edge lines (radii in the order of ∼100 nm or smaller) are not energetically favored over sheet stacks with helicoidal connections (see below). Although the existence of such small fenestrations has been proposed (6, 24), our model predicts that fenestrations between large sheets are more prominent. We define such fenestrated states as a situation in which the length of tubules between neighboring sheets is shorter than the distance between adjacent tubules along the sheet edge (Fig. 7A). A fenestrated state is then predicted for intermediate values of Ctot and Φ (Fig. 2, yellow area). The edge length of the fenestrations is on the order of microns, consistent with experimental observations in both mammalian tissue culture cells and yeast cells (2, 5, 6).
Fig. 7.
Model prediction of fenestrations and helicoidal membrane stacks. (A) Scheme showing how large sheets connected by short tubules generate fenestrations between sheets. Sheets of different sizes and tubule connections are shown. (B) Shown is a helicoid connecting stacked sheets. The calculations were performed for Ctot = 0.02 and Φ = 0.9. (C) A rectangular array of helicoidal connections. The calculations were performed for Ctot = 0.015 and Φ = 0.8. The pitch of the helical edge is 80 nm, the internal radius is 30 nm, and the distance between neighboring helicoids is 500 nm. (D) A rectangular array of helicoidal connections. The calculations were performed for Ctot = 0.03 and Φ = 0.8. The pitch distance of the helical edge is 40 nm, the internal radius is 80 nm, and the distance between neighboring helicoids is 400 nm.
Sheet stacks with helicoidal connections.
Finally, our model predicts that at low Ctot and high Φ values, membrane stacks with helicoidal connections are energetically favored (Fig. 2, purple area). These stacks consist of membrane sheets that are connected by membrane surfaces with helical edges (Fig. 7B). The negatively curved internal edges of these surfaces are stabilized by S-type proteins. The energetic cost of the Gaussian curvature makes helicoids favorable over small fenestrations. However, the difference in energy depends on the exact value of the membrane modulus of Gaussian curvature and on other factors, such as the number of sheets in a stack. Therefore, the border between the yellow and purple areas in the morphology diagram may vary between different cells. Although not included in the model, forces that would resist the lateral expansion of sheets would also favor helicoids over fenestrations (8), whereas stretching forces would have the opposite effect. Throughout most of the purple area in Fig. 2, the distance between the helicoids is large (on the order of microns), which may correspond to the observed low density of helicoids in salivary glands (8). However, at increasing values of Ctot, this distance decreases (Fig. 7 C and D). We calculated the optimal pitch of the helical edge of helicoids at several points in the morphology diagram. The results indicate that the pitch decreases with increasing values of Ctot, resulting in a shorter vertical separation between the stacked sheets. Our model thus predicts that the densely packed membrane sheets with helicoidal connections seen in secretory cells require a low total concentration of curvature-stabilizing proteins, Ctot, with a high percentage of them favoring a negatively curved edge line (high Φ).
Discussion
We have developed a comprehensive theoretical model that accounts for essentially all observed ER morphologies. The model is based on the crucial insight that curvature-stabilizing proteins not only promote the high membrane curvature in cross-sections of tubules and sheet edges, as previously proposed, but also determine the preferred curvature of the edge line. All ER shapes can then be explained by assuming just two types of curvature-stabilizing proteins: one that favors the formation of a straight edge line (R-type proteins), and another that favors a negatively curved edge line (S-type proteins). The two types of proteins together determine the total length, the preferred shape, and the elastic properties of the sheet edges. By varying the concentrations of these two proteins, the model can explain the formation of tubules, sheets, fenestrations, and stacked sheets with helicoidal connections. The two types of proteins have distinct roles in generating morphology. R-type proteins generate tubules and outer boundaries of sheets, as these have low or positive curvature of the edge line. S-type proteins, however, generate structures that contain negatively curved edge lines. These include three-way junctions between tubules, junctions between tubules and sheets, holes in sheets, and helicoidal sheet connections.
Our simple model can describe a number of different experiments. For example, long, nonbranched tubules are predicted to be prominent at high total concentrations of curvature-stabilizing proteins, a prediction confirmed by overexpression experiments (5, 14). The model predicts that, at nonphysiologically high concentrations, S-type proteins also generate long, nonbranched tubules, which we confirmed for lunapark (Fig. 4; Figs. S2 and S3). Conversely, at low concentrations of the curvature-stabilizing proteins, the formation of large sheets is predicted, as observed in cells lacking or depleted of these proteins (14, 25). Changes in the expression level of lunapark also produced the predicted effects on the shape and size of sheets and tubular junctions (Figs. 4 and 5; Figs. S2 and S3). The model predicts three-way junctions to be essentially the only connections between tubules, which again is confirmed by experimental observations (Fig. 3C). Finally, we provide an explanation for the observation that an ER network with interspersed sheets is rather heterogeneous with respect to sheet size and number of tubules emerging from the sheets. According to our model, the energetic differences between these structures are rather small, so that they may coexist due to thermal fluctuations. In summary, although the model is conceptually simple, it can explain a large number of experimental observations.
Our work suggests that lunapark is a representative of S-type proteins, i.e., curvature-stabilizing proteins that favor a negatively curved edge line. Our overexpression data show that lunapark stabilizes the positive membrane curvature seen in cross-sections of tubules and sheet edges. Lunapark localization to three-way junctions, which we show are actually small triangular sheets with concave edges, suggests that it stabilizes the negative curvature of edge lines. The qualitative agreement between model predictions and overexpression data further supports the assumption that lunapark is an S-type protein. We therefore suggest that lunapark plays an important role in generating and stabilizing three-way tubular junctions; this differs from a previous proposal, according to which lunapark is involved in abolishing three-way junctions (16). The previous proposal was based on the ER morphology observed in S. cerevisiae cells lacking Lnp1p, the lunapark homolog. The authors suggested that the ER was highly reticulated, i.e., contained more three-way junctions. However, owing to the low resolution of the light microscopy images and the lack of serial sections in the electron microscopy images, one cannot exclude the possibility that the structure actually consists of sheets with fenestrations between them. This interpretation would be consistent with our overexpression data in mammalian cells. Though it is difficult to envision a molecular mechanism by which lunapark would actively abolish three-way junctions, our model can easily explain how the absence of lunapark would decrease the number of three-way junctions and promote sheet formation. Inactivation of lunapark may also be a mechanism by which tubule-to-sheet conversion takes place in Xenopus egg extracts during the transition from interphase to mitosis, because the number of three-way junctions is drastically reduced (10).
The localization of reticulon 4a/b throughout tubules and sheet edges indicates that these proteins favor a less negatively curved edge line than does lunapark. Although we do not know the exact magnitude of the spontaneous curvature of the edge that they promote, they are good candidates to be R-type proteins, which favor an edge line with little curvature. It is interesting that the reticulon 4a/b isoforms are abundant in many tissue culture cells and in Xenopus extracts (14), explaining why tubular networks or networks with interspersed sheets are generally prominent (9), whereas helicoidal sheet stacks seem to be restricted to specialized cell types (7).
Our model makes the simplifying assumption that there are only two types of edge-promoting proteins. However, in reality, there may be more of these proteins, each promoting a distinct edge curvature. In addition, different proteins might be expressed in different cell types, which might explain why there are so many different isoforms of the reticulons and DP1 expressed in a cell-specific manner (26). For example, lunapark may be the major S-type protein for cells with a prominent tubular network, but it is of low abundance in pancreatic cells, which have prominent stacked ER sheets. Thus, a different S-type protein likely stabilizes the negatively curved helical edges of sheet connections. One candidate for an S-type protein in these cells is DP1, which is only slightly less abundant in the ER of pancreatic cells than the sheet-promoting proteins Climp-63 and p180 (5). The curvature-stabilizing proteins DP1 and Rtn3 are also up-regulated in differentiating B cells under conditions of sheet proliferation (27). These proteins may thus be required to stabilize the negative curvature of the helical edge lines of intersheet connections. More generally, we suggest that the expression levels of different curvature-generating proteins determine the specific ER morphology in different cells. In addition, it is conceivable that some curvature-stabilizing proteins are inactivated by modification, e.g., phosphorylation, which could explain ER morphology changes during mitosis.
Our model suggests that many observed sheet fenestrations are empty spaces between sheets connected by short tubules, rather than small holes in a sheet. This conclusion seems to be in agreement with light and electron microscopy results (5, 8, 14), but it disagrees with observations made in some cells after labeling the ER lumen with a horseradish peroxidase-generated precipitate (6, 24). However, it is unclear why this technique detected similarly small holes with heterogeneous diameters in the nuclear envelope (24). In addition, the existence of small fenestrations has been challenged by experiments that used a different fixation method and stained the membrane (12). If small fenestrations indeed exist, they might be explained by factors that shift the energetic difference between helicoids and microfenestrations in favor of the latter. Perhaps, in some cells certain ER membrane proteins can change the modulus of Gaussian curvature of sheets, or the cytoskeleton may pull on the sheets, thereby favoring fenestrations over helicoids. Finally, it is also conceivable that microfenestrations are a kinetic intermediate in the formation of helicoidal connections.
Our model considers equilibrium states, in which each morphology corresponds to a global minimum in the energy landscape. The model does not consider the kinetic pathways by which different morphologies are generated or the energy barrier between these states. Specifically, our model does not include membrane fusion of ER tubules or the disappearance of polygons in an ER network (called ring closure) (28). These processes could generate a steady state of ER morphologies, rather than a static equilibrium. For example, the fusion of ER tubules may be followed by the accumulation of lunapark in the newly formed three-way junctions, whereas ring closure may cause the redistribution of lunapark into the tubules. Although it is known that membrane-bound GTPases, the atlastins in vertebrates and Sey1p and its homologs in yeast and plants (29, 30), mediate ER membrane fusion, their inclusion in a theoretical model will require the consideration of ER dynamics and a better understanding of their functional interaction with curvature-stabilizing proteins. Specifically, it will be important to understand the mechanistic basis for the observed opposing effects of lunapark and Sey1p on yeast ER morphology (16).
We also did not include in the current model the effects of sheet-promoting proteins, such as Climp-63, p180, and kinectin (5), or the association of ER membranes with the cytoskeleton (31, 32). Sheet-promoting proteins would effectively reduce the concentration of the curvature-stabilizing proteins, i.e., lower Ctot in our morphology diagram (Fig. 2), thereby favoring tubule-to-sheet transitions. Force generation by cytoskeleton dynamics or molecular motors seems to affect primarily the spatial distribution of ER membranes in cells, rather than the generation of ER morphology per se (33). Nevertheless, such forces could change the boundaries in the morphology diagram and, when acting locally, could account for the coexistence of different ER morphologies in a single cell. Finally, because the bending modulus and the modulus of Gaussian curvature are only known approximately for ER membranes, the exact boundaries in the morphology diagram could vary among different cells and conditions. Considering the complexity of cells and the many factors that can affect ER morphology, it is remarkable that our simple model can go a long way to explain how the ER is shaped.
Experimental Procedures
Theory.
The model is described in detail in SI Text.
Mammalian Cell Culture Experiments and Microscopy.
HA-tagged human lunapark was expressed in COS-7 cells. The cells were analyzed by immunofluorescence microscopy using antibodies to HA and antibodies to either calreticulin or Rtn4a/b. After incubation with fluorophore-labeled secondary antibodies, the samples were analyzed with a spinning-disk confocal microscope. For depletion of lunapark by RNAi, COS7 cells were transfected with siRNA oligonucleotides and incubated for 72 h before analysis by immunofluorescence microscopy with antibodies against calreticulin and Rtn4a/b. Superresolution (STORM) experiments were performed on fixed COS-7 cells with calreticulin and Rtn antibodies, followed by staining with Alexa 647 and Cy3B labeled secondary antibodies. STORM images were acquired as previously described (34, 35).
For stable expression of lunapark, the HA tag in Lnp-HA was replaced by mCherry and inserted into the pHAGE2 vector. Lentivirus was produced in 293T cells and used to infect COS7 cells. Cells were subsequently selected with blasticidin. Cells were fixed and stained for calreticulin as previously described (15). Images were acquired using a spinning-disk confocal microscope.
In Vitro Experiments with Xenopus laevis Egg Extracts.
Interphase and meiotic ER networks were generated with crude Xenopus egg extracts or isolated membranes, as previously described (10). ER membranes were stained with fluorescent hydrophobic dyes and visualized with a spinning confocal microscope. Quantification of the connectivity of ER tubules was performed with a custom ImageJ script. The 3D representations of three-way junctions were constructed using confocal slices of the ER network and the 3D visualization software bioView3D (36).
Details of the experimental procedures are given in SI Text.
Supplementary Material
Acknowledgments
We thank Yoko Shibata and Nicholas Bodnar for critical reading of the manuscript; L. Ding and the Nikon Imaging Center at Harvard Medical School for assistance with the image analysis and microscopy; and M. Kirschner and R. Ward for generous help in supporting T.S. Support for this work is provided by the Israel Science Foundation (M.M.K.) and National Institutes of Health Grant GM05586 (to T.A.R.). J.V. gratefully acknowledges support from a Burroughs-Wellcome Career Award at the Scientific Interface. X.Z. and T.A.R. are Howard Hughes Medical Institute Investigators.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1419997111/-/DCSupplemental.
References
- 1.Shibata Y, Hu J, Kozlov MM, Rapoport TA. Mechanisms shaping the membranes of cellular organelles. Annu Rev Cell Dev Biol. 2009;25:329–354. doi: 10.1146/annurev.cellbio.042308.113324. [DOI] [PubMed] [Google Scholar]
- 2.Friedman JR, Voeltz GK. The ER in 3D: A multifunctional dynamic membrane network. Trends Cell Biol. 2011;21(12):709–717. doi: 10.1016/j.tcb.2011.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Goyal U, Blackstone C. Untangling the web: Mechanisms underlying ER network formation. Biochim Biophys Acta. 2013;1833(11):2492–2498. doi: 10.1016/j.bbamcr.2013.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hu J, et al. Membrane proteins of the endoplasmic reticulum induce high-curvature tubules. Science. 2008;319(5867):1247–1250. doi: 10.1126/science.1153634. [DOI] [PubMed] [Google Scholar]
- 5.Shibata Y, et al. Mechanisms determining the morphology of the peripheral ER. Cell. 2010;143(5):774–788. doi: 10.1016/j.cell.2010.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Puhka M, Joensuu M, Vihinen H, Belevich I, Jokitalo E. Progressive sheet-to-tubule transformation is a general mechanism for endoplasmic reticulum partitioning in dividing mammalian cells. Mol Biol Cell. 2012;23(13):2424–2432. doi: 10.1091/mbc.E10-12-0950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fawcett DW. The Cell. Saunders; Philadelphia: 1981. [Google Scholar]
- 8.Terasaki M, et al. Stacked endoplasmic reticulum sheets are connected by helicoidal membrane motifs. Cell. 2013;154(2):285–296. doi: 10.1016/j.cell.2013.06.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shibata Y, Voeltz GK, Rapoport TA. Rough sheets and smooth tubules. Cell. 2006;126(3):435–439. doi: 10.1016/j.cell.2006.07.019. [DOI] [PubMed] [Google Scholar]
- 10.Wang S, Romano FB, Field CM, Mitchison TJ, Rapoport TA. Multiple mechanisms determine ER network morphology during the cell cycle in Xenopus egg extracts. J Cell Biol. 2013;203(5):801–814. doi: 10.1083/jcb.201308001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Poteryaev D, Squirrell JM, Campbell JM, White JG, Spang A. Involvement of the actin cytoskeleton and homotypic membrane fusion in ER dynamics in Caenorhabditis elegans. Mol Biol Cell. 2005;16(5):2139–2153. doi: 10.1091/mbc.E04-08-0726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lu L, Ladinsky MS, Kirchhausen T. Cisternal organization of the endoplasmic reticulum during mitosis. Mol Biol Cell. 2009;20(15):3471–3480. doi: 10.1091/mbc.E09-04-0327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lu L, Ladinsky MS, Kirchhausen T. Formation of the postmitotic nuclear envelope from extended ER cisternae precedes nuclear pore assembly. J Cell Biol. 2011;194(3):425–440. doi: 10.1083/jcb.201012063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Voeltz GK, Prinz WA, Shibata Y, Rist JM, Rapoport TA. A class of membrane proteins shaping the tubular endoplasmic reticulum. Cell. 2006;124(3):573–586. doi: 10.1016/j.cell.2005.11.047. [DOI] [PubMed] [Google Scholar]
- 15.Shibata Y, et al. The reticulon and DP1/Yop1p proteins form immobile oligomers in the tubular endoplasmic reticulum. J Biol Chem. 2008;283(27):18892–18904. doi: 10.1074/jbc.M800986200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chen S, Novick P, Ferro-Novick S. ER network formation requires a balance of the dynamin-like GTPase Sey1p and the Lunapark family member Lnp1p. Nat Cell Biol. 2012;14(7):707–716. doi: 10.1038/ncb2523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chen S, Novick P, Ferro-Novick S. ER structure and function. Curr Opin Cell Biol. 2013;25(4):428–433. doi: 10.1016/j.ceb.2013.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Markin VS. Lateral organization of membranes and cell shapes. Biophys J. 1981;36(1):1–19. doi: 10.1016/S0006-3495(81)84713-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Helfrich W. Elastic properties of lipid bilayers: Theory and possible experiments. Z Naturforsch C. 1973;28(11):693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 20.Tlusty T, Safran SA. Entropic networks in colloidal self-assembly. Phil Trans R Soc A. 2001;359(1782):879–881. [Google Scholar]
- 21.Tlusty T, Safran SA. Microemulsion networks: The onset of bicontinuity. J Phys Condens Matter. 2000;12:A253–A262. [Google Scholar]
- 22.Puhka M, Vihinen H, Joensuu M, Jokitalo E. Endoplasmic reticulum remains continuous and undergoes sheet-to-tubule transformation during cell division in mammalian cells. J Cell Biol. 2007;179(5):895–909. doi: 10.1083/jcb.200705112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Moriya K, et al. Protein N-myristoylation plays a critical role in the endoplasmic reticulum morphological change induced by overexpression of protein Lunapark, an integral membrane protein of the endoplasmic reticulum. PLoS ONE. 2013;8(11):e78235. doi: 10.1371/journal.pone.0078235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Joensuu M, et al. ER sheet persistence is coupled to myosin 1c-regulated dynamic actin filament arrays. Mol Biol Cell. 2014;25(7):1111–1126. doi: 10.1091/mbc.E13-12-0712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Anderson DJ, Hetzer MW. Reshaping of the endoplasmic reticulum limits the rate for nuclear envelope formation. J Cell Biol. 2008;182(5):911–924. doi: 10.1083/jcb.200805140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Oertle T, Schwab ME. Nogo and its paRTNers. Trends Cell Biol. 2003;13(4):187–194. doi: 10.1016/s0962-8924(03)00035-7. [DOI] [PubMed] [Google Scholar]
- 27.Luckey CJ, et al. Memory T and memory B cells share a transcriptional program of self-renewal with long-term hematopoietic stem cells. Proc Natl Acad Sci USA. 2006;103(9):3304–3309. doi: 10.1073/pnas.0511137103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lee C, Chen LB. Dynamic behavior of endoplasmic reticulum in living cells. Cell. 1988;54(1):37–46. doi: 10.1016/0092-8674(88)90177-8. [DOI] [PubMed] [Google Scholar]
- 29.Orso G, et al. Homotypic fusion of ER membranes requires the dynamin-like GTPase atlastin. Nature. 2009;460(7258):978–983. doi: 10.1038/nature08280. [DOI] [PubMed] [Google Scholar]
- 30.Hu J, et al. A class of dynamin-like GTPases involved in the generation of the tubular ER network. Cell. 2009;138(3):549–561. doi: 10.1016/j.cell.2009.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Du Y, Ferro-Novick S, Novick P. Dynamics and inheritance of the endoplasmic reticulum. J Cell Sci. 2004;117(Pt 14):2871–2878. doi: 10.1242/jcs.01286. [DOI] [PubMed] [Google Scholar]
- 32.Friedman JR, Webster BM, Mastronarde DN, Verhey KJ, Voeltz GK. ER sliding dynamics and ER-mitochondrial contacts occur on acetylated microtubules. J Cell Biol. 2010;190(3):363–375. doi: 10.1083/jcb.200911024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Prinz WA, et al. Mutants affecting the structure of the cortical endoplasmic reticulum in Saccharomyces cerevisiae. J Cell Biol. 2000;150(3):461–474. doi: 10.1083/jcb.150.3.461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Vaughan JC, Dempsey GT, Sun E, Zhuang X. Phosphine quenching of cyanine dyes as a versatile tool for fluorescence microscopy. J Am Chem Soc. 2013;135(4):1197–1200. doi: 10.1021/ja3105279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Huang B, Wang W, Bates M, Zhuang X. Three-dimensional super-resolution imaging by stochastic optical reconstruction microscopy. Science. 2008;319(5864):810–813. doi: 10.1126/science.1153529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kvilekval K, Fedorov D, Obara B, Singh A, Manjunath BS. Bisque: A platform for bioimage analysis and management. Bioinformatics. 2010;26(4):544–552. doi: 10.1093/bioinformatics/btp699. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.