Propensity Score Method for Partially Matched Omics Studies

Abstract

This paper focuses on the problem of partially matched samples in the presence of confounders. We propose using propensity score matching to adjust for confounding factors for the subset of data with incomplete pairs, followed by integrating the P-values computed from the complete and incomplete paired samples, respectively. Several simulations and a case study on DNA methylation are considered to evaluate the operating characteristics of the proposed method.

Introduction

The advancement in biotechnologies has revolutionized numerous disciplines including biology and medicine. Several high-throughput platforms including whole genome arrays and the next-generation sequencing instruments are available for profiling large-scale omics data. These cutting edge biotechnologies have spurred rapid biomarker discovery and personalized medicine approach in multiple diseases, in particular, cancer research. In recent years, genomewide profiling utilizing these technologies has been carried out to identify biomarkers associated with cancer development and progression. In this paper, we consider the matched pairs samples for identifying differentially expressed biomarkers between two groups. Matched/paired study design is commonly used in omics/biomarkers profiling because it automatically accounts for confounding factors. Examples of matched/paired designs include profiling n (1) tumor and adjacent normal lesions, (2) pre- and post-drug treatment samples, or (3) one-to-one matching of patients by demographic covariates (eg, age, gender, race, etc.) from the two groups of interest. We will use the tumor versus normal samples hereafter for expository purpose.

Ideally, one expects a total of 2n samples from such matched/paired design. However, in practice, circumstances such as RNA degradation, array failure, or insufficient resources could result in a subset of patients missing in either the tumor or matched normal biomarker profiles. For example, n₁(<n) patients have both the tumor and matched normal profiles, whereas n₂ and n₃ patients have only tumor and normal samples, respectively. Such incomplete or missing paired samples are also known as partially matched samples.

Several methods have been developed to analyze partially matched data generated from the Gaussian distribution.^1–4 Recently, Kuan and Huang⁵ and Yu et al.⁶ extended the approach to non-parametric setting, which does not require the Gaussian assumption. Specifically in Kuan and Huang,⁵ we introduced a simple and robust method for analyzing partially matched samples based on the weighted Z-test to combine the P-values computed using (1) paired sample tests (eg, paired t-test or Wilcoxon sign rank test) on the n₁ matched pairs and (2) two-sample tests (eg, two-sample t-test or Mann–Whitney test) on the incomplete n₂ and n₃ pairs. The P-value pooling approach has been shown to achieve good operating characteristics compared to existing methods.

As alluded earlier, matched/paired design is an appealing approach to avoid confounding. However, when a subset of samples has incomplete pairs in partially matched samples scenarios, this can result in unbalanced covariates between the tumor and normal groups. Nonetheless, the above-mentioned methods assume that the confounding factors among the n₂ and n₃ incomplete matched pairs are absent or negligible. If this assumption does not hold, the conclusions drawn from these methods are no longer valid. In this paper, we introduce an approach to adjust for potential confounders based on propensity score matching method in partially matched samples. Our paper is organized into five sections. In Section 2, we describe the proposed method, followed by Sections 3 and 4, which demonstrate the operating characteristics of the proposed approach in simulations and case study, respectively. We conclude with a discussion in Section 5.

Method

Let (X_i, Y_i) be a matched pair for subject i, i = 1, …, n, where X_i and Y_i are the tumor and normal measurements, respectively. Without loss of generality, we assume that (X_i, Y_i) are complete matched pairs for i = 1, …, n₁; Y_i’s are missing for i = n₁ + 1, …, n₁ + n₂, and X_i’s are missing for i = n₁ + n₂ + 1, …, n₁ + n₂ + n₃. That is, n₁ patients have both the tumor and matched normal profiles, whereas n₂ and n₃ patients have only tumor or normal samples, respectively. Let Z_i = (Z_1i, …, Z_pi) denote the p covariates for subject i, for instance, Z_1i = age, Z_2i = gender, etc. The first step is to create pseudo-pairs between the n₂ and n₃ incomplete pairs by matching the covariate information. We will use propensity score method to accomplish this step. To simplify the notation, we introduce subscript j to denote sample j, j = 1, …, n₂ + n₃ among the incomplete pairs, and let Z_j denote the corresponding covariate information. Let O_j denote the measurement for subject j. Note that O_j = X_j for j = 1, …, n₂ and O_j = Y_j for j = n₂ + 1, …, n₂ + n₃. We also let G_j denote the group indicator for sample j, ie, G_j = 1 and 2 for normal and tumor samples, respectively.

Propensity score method

The propensity score method, introduced by Rosenbaum and Rubin,⁷ is a popular approach in observational studies to create balance in multiple confounding covariates between the two groups. The propensity score is defined as

$$e_j=P(G_j=2|Z_j)$$

There are several approaches for estimating e_j, including logistic regression and machine learning techniques such as boosted regression,⁸ classification trees (CART), and random forests. A comparison of these methods is provided in Lee et al.⁹

There are four main methods for removing confounding effects based on e_j, namely (1) propensity score matching, (2) stratification on propensity score, (3) covariate adjustment using propensity score, and (4) inverse probability weighting by propensity score. We refer the readers to Austin¹⁰ for a review on these different approaches. In this paper, we consider two approaches based on propensity scores to account for confounding effects. The first approach is covariate adjustment using propensity score via a linear model

$$O_j={\beta }_0+{\beta }_G{G}_j+{\beta }_e{e}_j+{\epsilon }_j$$ (1)

where ε_j ~ N(0, 1) if the biomarker measurements are approximately Gaussian distributed after appropriate normalization and transformation. Otherwise, one can use the generalized linear model¹¹ with appropriate link function for non-Gaussian data. One can then evaluate if the expression of tumor is significantly different from normal by testing the hypothesis H₀: β_G = 0.

The second approach is based on Mahalanobis distance on covariate ranks with propensity score caliper¹² for matching the covariates between the n₂ tumor and n₃ normal samples from incomplete pairs. Let r_j be the vectors of covariate ranks for sample j. The Mahalanobis distance between sample j in the tumor group and sample k in the normal group is defined as

$$d_{jk}=(r_j-r_k)\prime {\sum ^{⌢}}^{-1}(r_j-r_k)$$

where $\sum ^{⌢}$ is the estimated pooled covariance matrix for the ranks. On the other hand, the propensity score caliper c is defined as the maximum propensity score distance between sample j and k allowed within a match. In other words,

$$d_{jk}=\{\begin{array}{ll}(r_j-r_k)\prime {\sum ^{⌢}}^{-1}(r_j-r_k)\hfill & \text{if }D(e_j,e_k)\le c\hfill \\ \infty \hfill & \text{otherwise}\hfill \end{array}$$

The choice of caliper width is related to bias–variance trade-off where small caliper width results in bias reduction but at the expense of increasing variance, and vice versa.¹³ A few studies have been conducted to investigate the optimal caliper width in propensity score matching, including the work of Austin¹³ and Wang et al.¹⁴ Based on these works and our own experience in propensity score matching, we recommend using caliper width equal to 0.2 of the standard deviation of the logit of the propensity score, which tends to have better performance, ie,

$$D(e_j,e_k)=\frac{|\log \mathrm{it}(e_j)-\log \mathrm{it}(e_k)|}{\sqrt{\left({\gamma }_1^2+{\gamma }_2^2\right)}/2}\text{and}c=0.2$$

where ${\gamma }_G^2$ is the variance of logit of the propensity score in the Gth group. The samples are matched using the optimal full matching algorithm.^15–17 Matching algorithm aims to group tumor and normal samples that have similar covariates, ie, small d_jk. Optimal full matching subdivides the samples into collection of matched sets S, where each set consists of a tumor with any number of normal samples or a normal sample with any number of tumors by minimizing the net discrepancy Σ_j,k∈Sd_jk ^15,17 The Olsen’s algorithm is used to create optimal matching (see Hansen¹⁵ and Hansen and Klopfer¹⁶ for details).

Test statistics for matched set

The tumor and normal samples within each matched set tend to be correlated since they have comparable baseline covariates.^7,18 For one-to-one pairing, one usually uses paired sample t-test or Wilcoxon signed-rank test to test if the expression level of tumors is significantly different from the normal samples. However, in the full matching scenario, each tumor is paired with several normal samples and vice versa; thus, the paired sample t-test or Wilcoxon signed-rank test needs to be generalized to such one-to-many pairing. In this paper, we consider a generalization of the paired sample t-test under the scenario that the biomarker measurements are approximately Gaussian distributed. Following Rosner,¹⁹ a generalized paired sample t-test can be derived based on a one-way random effects ANOVA model given by

$$d_s={\overline{X}}_s-{\overline{Y}}_s=\alpha +{\delta }_s+{\epsilon }_s,s=1,\dots ,S$$

where α is the overall within-pair mean difference between tumor and normal samples, ${\delta }_s~N(0,{\sigma }_D^2)$ is the random effect for the sth pairing, ${\epsilon }_s~N(0,{\sigma }_s^2)$ is the random error, and S is the total number of matched sets. In addition, σ_s = σ² (1/m_1s + 1/m_2s) where m_1s and m_2s are the number of tumors and normals in matched set s, respectively. The hypothesis for testing if the expression of tumor is different from normal samples translates into testing α = 0. The test statistic is given by

$$\widehat{t}=\widehat{\alpha }/{(V_{11})}^{1/2}$$

where

$$V_{11}=\frac{\left\{{\displaystyle {\sum }_{s=1}^S{w}_s^3}{(d_s-\widehat{\alpha })}^2-{\displaystyle {\sum }_{s=1}^S{w}_s^2}/2\right\}}{\left[\left({\displaystyle {\sum }_{s=1}^S{w}_s}\right)\left\{{\displaystyle {\sum }_{s=1}^S{w}_s^3}{(d_s-\widehat{\alpha })}^2-{\displaystyle {\sum }_{s=1}^S{w}_s^2}/2\right\}-{\left\{{\displaystyle {\sum }_{s=1}^S{w}_s^2}(d_s-\widehat{\alpha })\right\}}^2\right]}$$

and

$$w_s=\frac{1}{{\widehat{\sigma }}_D^2+{\widehat{\sigma }}_s^2}$$

σ² is estimated using the usual unbiased estimator, whereas α and ${\sigma }_D^2$ are estimated using numerical methods (see Rosner¹⁹ for details). For large samples, the P-value of $\widehat{t}$ can be obtained from the asymptotic distribution N(0, 1). For small samples, the P-value can be computed from the permutation test, by permuting the labels of tumor and normal samples within each matched set. Suppose there are m_1s tumors and a total of N_s samples in matched set s, then the total number of possible permutations is ${\prod }_{s=1}^S\left({}_{m_{1s}}^{N_s}\right)$.

On the other hand, the generalized non-parametric test for one-to-many pairing can be carried out via the aligned rank test of Hodges and Lehmann²⁰ if the data are non-Gaussian. We refer the readers to Hodges and Lehmann,²⁰ and Heller et al.²¹ for additional details on implementing the aligned rank test.

P-values pooling

We follow the idea of our earlier work in Kuan and Huang⁵ to test if the biomarker is significantly up or down regulated in tumor compared to normal samples by pooling the P-values from the n₁ complete and (n₂, n₃) incomplete pairs. The P-value for the n₁ complete matched pairs is computed using either the paired sample t-test or Wilcoxon signed-rank test, denoted as p₁. On the other hand, the P-value for the incomplete pairs p₂ is computed based on the linear model using propensity score as covariate (equation (1) of Section 2.1), the generalized t-test, or aligned signed rank test (Section 2.2). The next step is to pool the two P-values by borrowing the idea of meta-analysis. Several methods are available for pooling P-values including the inverse normal and Fisher’s methods. In Kuan and Huang,⁵ we showed that pooling P-values based on weighted Z-test has good operating characteristics compared to other methods. The weighted Z-test for combining the P-values is based on transforming the P-values into Z-score Z_a = Φ⁻¹(1 − p_k), k = 1, 2. The combined P-value by the weighted Z-test^5,22 is given by

$$p_c=1-\Phi \left(\frac{w_1{Z}_1+w_2{Z}_2}{\sqrt{w_1^2+w_2^2}}\right)$$ (2)

where w_k’s are the corresponding weights. Although different choices of weights have been proposed in the literature, Kuan and Huang,⁵ Zaykin²³ showed that setting the weights as the square root of the sample sizes works well in practice. Thus, we set $w_1=\sqrt{2n_1}$ and $w_2=\sqrt{n_2+n_3}$. In addition, pooling P-values is only meaningful if p₁ and p₂ are computed from one-sided hypothesis tests to avoid directional conflict. One can obtain a two-sided combined P-value as follows. Let p₁ and p₂ be the one-sided P-value for the same alternative (eg, “greater”) hypothesis, and p_c be the combined one-sided P-value from equation (2). The two-sided P-value is given by

$$p_c^{*}=\{\begin{array}{ll}2p_c\hfill & \text{if }{p}_c<1/2\hfill \\ 2(1-p_c)\hfill & \text{otherwise}\hfill \end{array}$$

Simulation

We carry out simulation to evaluate the performance of propensity score method to adjust for potential confounders in partially matched samples. n paired sample measurements (X_ij, Y_ij) of a biomarker i for the tumor and matched normal group are generated from bivariate Gaussian distribution,

$$\left(\begin{array}{c}{X}_{ij}\\ Y_{ij}\end{array}\right)~N\left(\left(\begin{array}{c}{\mu }_X+\beta Z_1-\beta \log (Z_2)\\ {\mu }_Y+\beta Z_1-\beta \log (Z_2)\end{array}\right)\right),\left(\begin{array}{cc}{\sigma }_X^2& \rho {\sigma }_X{\sigma }_Y\\ \rho {\sigma }_X{\sigma }_Y& {\sigma }_Y^2\end{array}\right)$$

where Z₁ and Z₂ are confounders, and μ_X and μ_Y are the true mean expressions for tumor and normal groups, respectively. We consider (n₁, n₂, n₃) = (70, 15, 15), (50, 25, 25), and (30, 35, 35) and set σ_X = σ_Y = 1, whereas ρ ~ U(0, 1) to capture various degrees of correlation between tumor and normal matched pairs. In addition, we set μ_Y = 0 and μ_X = 0, 0.1, 0.2, …, 0.5 for different effect sizes, and β = 0, 0.5, 1, and 2 for zero, moderate, strong, and very strong confounding effects. To simulate unbalanced confounders arising from incomplete matched pairs, we generate Z₁, Z₂ ~ N(0, 1) for i = 1, …, n₁, Z₁ ~ N(−0.2, 1), Z₂ ~ N(0.2, 1) for i = n₁ + 1, …, n₁ + n₂, and Z₁ ~ (0.2, 1), Z₂ ~ N(−0.2, 1) for i = n₁ + n₂ + 1, …, n₁ + n₂ + n₃.

We compare the performance of the following methods in our simulation studies:

1. Gold standard (Gold-std): The P-value was computed from paired sample t-test on n₁ + n₂ + n₃ original matched pairs assuming complete data set. This is the reference test.

2. Paired only: The P-value was computed from paired sample t-test on the n₁ complete matched pairs only, and discarding the n₂ and n₃ incomplete pairs.

3. Two sample: Combining the P-value from paired sample t-test on the complete n₁ matched pairs and the P-value from two-sample t-test on the incomplete n₂ and n₃ samples using the weighted Z-test approach.⁵

4. Propensity score with full matching (FM-PS): Combining the P-value from paired sample t-test on the complete n₁ matched pairs and the P-value from generalized t-test on full matched data by Mahalanobis distance with propensity score caliper c = 0.2 on the incomplete n₂ and n₃ samples.

5. Propensity score with regression adjustment (Reg-PS): Combining the P-value from paired sample t-test on the complete n₁ matched pairs and the P-value from linear regression model using propensity score as covariate on the incomplete n₂ and n₃ samples.

Single biomarker

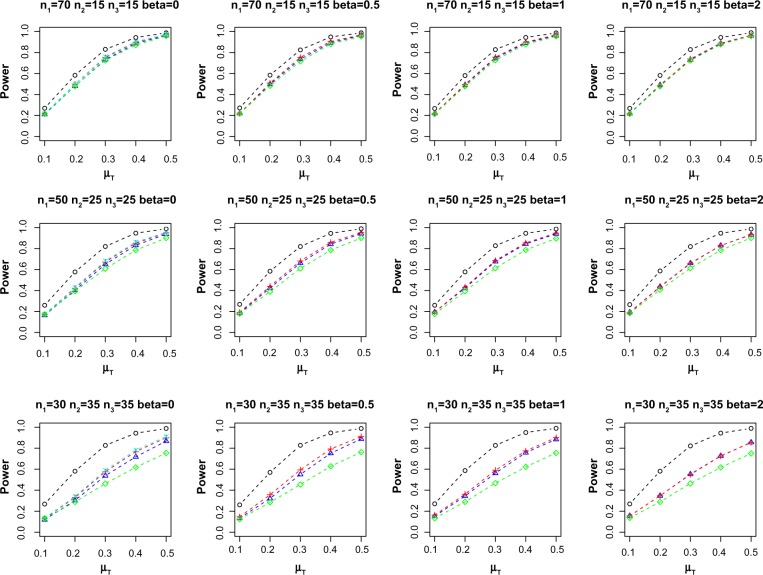
We first evaluate the performance of propensity score methods in adjusting for unbalanced covariates in single biomarker setting. Table 1 reports the average empirical Type I error at nominal α = 0.05 over 10,000 replications. When there is no confounding effect, ie, β = 0, all the methods control the Type I error. However, for β ≠ 0, the two-sample method exhibits the largest Type I error inflation. On the other hand, paired only, FM-PS, and Reg-PS methods control the Type I error under all the scenarios considered in the simulation. Figure 1 shows the average power for different combinations of n₁, n₂, n₃, and β for methods that control the Type I error (empirical Type I error ≤ 0.055). As expected, missing samples in incomplete matched pairs reduce the power compared to complete data set (Gold-std). However, incorporating the incomplete matched pairs with proper adjustment for confounders via FM-PS or Reg-PS methods exhibit increased statistical power compared to using only the n₁ paired samples when n₂ and n₃ are substantially large. When n₂ and n₃ are small relative to n₁, using only the n₁ paired samples is comparable to methods that incorporate n₂ and n₃. Both FM-PS and Reg-PS methods show comparable performance in this simulation study.

Table 1.

Average empirical Type I error at nominal α = 0.05. Italicized values indicate that the empirical Type I error is greater than 0.055.

METHOD	β= 0	β= 0.5	β= 1	β= 2
n1 = 70, n2 = 15, n3 = 15
Gold-std	0.0455	0.0473	0.0503	0.0501
Paired only	0.0479	0.0494	0.0490	0.0518
Two-sample	0.0475	0.0643	0.0794	0.0922
FM-PS	0.0462	0.0485	0.0469	0.0476
Reg-PS	0.0480	0.0502	0.0441	0.0442
n1 = 50, n2 = 25, n3 = 25
Gold-std	0.0527	0.0541	0.0495	0.0541
Paired only	0.0486	0.0536	0.0534	0.0531
Two-sample	0.0476	0.1044	0.1460	0.1809
FM-PS	0.0483	0.0467	0.0465	0.0485
Reg-PS	0.0494	0.0476	0.0443	0.0416
n1 = 30, n2 = 35, n3 = 35
Gold-std	0.0522	0.0543	0.0483	0.0489
Paired only	0.0507	0.0494	0.0499	0.0465
Two-sample	0.0522	0.1712	0.2805	0.3663
FM-PS	0.0449	0.0454	0.0422	0.0460
Reg-PS	0.0524	0.0479	0.0452	0.0446

Figure 1.

Average power at nominal α = 0.05. Sample size (n₁, n₂, n₃) and effect of confounding β are indicated in the header of each plot. Power curves for methods that did not control Type I error (ie, empirical Type I error > 0.055) are not shown.

Notes: ○: Gold-std, ∆: FM-PS, +: Reg-PS, ×: two-sample, and ⋄: paired only.

Multiple biomarkers

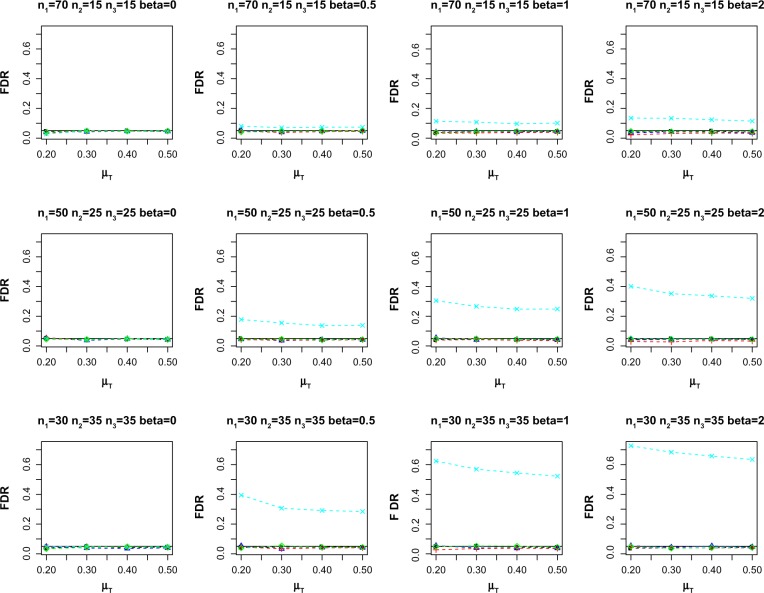
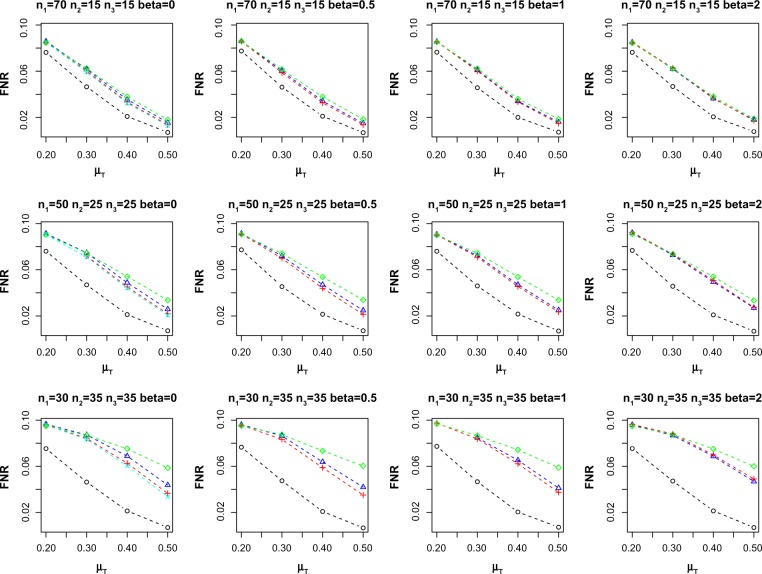
As omics data involve testing multiple biomarkers simultaneously (within a multiple hypothesis testing framework), we also simulate the observations from multiple biomarkers setting. We consider 1000 biomarkers and repeat each simulation setting over 100 replications. We use the false discovery rate (FDR) procedure of Benjamini and Hochberg²⁴ to adjust for multiple hypothesis testing. Figure 2 reports the average empirical FDR for the different methods at nominal FDR = 0.05. Similar to the single biomarker case, two-sample method exhibits the largest inflated empirical FDR for β ≠ 0. On the other hand, FM-PS, Reg-PS, and paired only methods control the FDR across the different scenarios. Figure 3 shows the empirical false nondiscovery rate (FNR) for the methods under comparison. FNR is an analog of Type II error in multiple hypothesis testing settings, and is defined as the proportion of false negatives among the total number of non-rejection. Empirical FNR is large when the number of incomplete matched pairs is large. On the other hand, both FM-PS and Reg-PS methods result in lower FNR compared to paired only method.

Figure 2.

Average empirical FDR at nominal FDR = 0.05. Sample size (n₁, n₂, n₃) and effect of confounding β are indicated in the header of each plot.

Notes: ○: Gold-std, ∆: FM-PS, +: Reg-PS, ×: two-sample, and ⋄: paired only.

Figure 3.

Average empirical FNR at nominal FDR = 0.05. Sample size (n₁, n₂, n₃) and effect of confounding β are indicated in the header of each plot. FNR values for methods that did not control FDR (ie, empirical FDR > 0.055) are not shown.

Notes: ○: Gold-std, ∆: FM-PS, +: Reg-PS, ×: two-sample, and ⋄: paired only.

Case Study

We illustrate the proposed propensity score adjustment for partially matched samples on a publicly available DNA methylation data from Selamat et al.²⁵ (downloaded from Gene Expression Omnibus (GEO) under accession number GSE32861). The data set consists of 58 matched pairs of lung adenocarcinoma and adjacent non-tumor lung tissue after removing paired sample 3023_T/N.²⁵ Methylation for these samples was profiled using the Illumina HumanMethylation27 BeadChip, which covers 27,578 CpGs. We use a subset of baseline covariates measured for each sample (ie, age, smoking status, stage, recurrence, KRAS mutation, EGFR mutation, and LKB1 mutation) to illustrate the performance of the different methods. Age and stage are continuous and ordinal variables, respectively, whereas the other covariates are binary variables.

We randomly choose n₁ out of 58 matched pairs to be complete matched pairs. Next, we generate 58 − n₁ indicator variables, ie, δ_k, k = 1, …, 58 − n₁, where

$$P({\delta }_k=1)=\frac{\exp ({\beta }^t{Z}_k)}{1+\exp ({\beta }^t{Z}_k)}$$

and

$${\beta }^t{Z}_k={\text{Age}}_k-{\text{Smoke}}_k+{\text{Stage}}_k-{\text{Recur}}_k+KRA{S}_k-{\text{EGFR}}_k+{\text{LKB1}}_k$$

after standardizing each covariate. This function generates approximately equal number of 0s and 1s on average. Among the remaining 58 – n₁ pairs, we set n₂ pairs to be missing in non-tumor lung tissue corresponding to those with δ_k = 1, and the remaining to be missing in lung adenocarcinoma. We consider n₁ = 10, 20, 30, 40, and for each n₁, the process is repeated 50 times.

We apply FM-PS, Reg-PS, two-sample, and paired only methods on the logit-transformed methylation β-values, ie, log(β/(1 − β))^26,27 of each CpG. Since CpGs that are truly differentially methylated between lung adenocarcinoma and non-tumor lung tissues are unknown in the case study, we use the results from paired sample t-test on the full 58 matched pairs as Gold-std. We define the true positive CpGs as the subset of CpGs that are significant at the Benjamini and Hochberg²⁴ FDR of 0.05 for the Gold-std method. We compare the list of significant CpGs identified by FM-PS, Reg-PS, two-sample, and paired only methods at FDR = 0.05 to the true positive CpGs. In Table 2, we report the average empirical FDR, FNR, and average true positive (ATP) CpGs identified by each method. The ATP CpG is also the number of overlapping CpGs identified by each method and the Gold-std method. Two-sample method declares a larger number of false positives as indicated by the inflated empirical FDR. In this case study, the effect of confounding is moderate; thus, FM-PS, Reg-PS, and paired only methods are able to control the FDR. However, both FM-PS and Reg-PS methods have lower FNR and larger ATP compared to paired only method. This shows that the propensity score method for partially matched samples is able to adjust for confounders and improve the power of detecting differentially methylated CpGs.

Table 2.

Average empirical FDR, FNR, and ATP at nominal FDR = 0.05.

METHOD	PAIRED ONLY	TWO-SAMPLE	FM-PS	Reg-PS
n1 = 10, n2 = 24, n3 = 24
FDR	0.0304	0.0822	0.0285	0.0256
FNR	0.5439	0.2121	0.4649	0.4478
ATP	3457	13722	6908	7527
n1 = 20, n2 = 19, n3 = 19
FDR	0.0322	0.0625	0.0256	0.0247
FNR	0.4443	0.1897	0.4053	0.3810
ATP	7690	14014	8941	9568
n1 = 30, n2 = 14, n3 = 14
FDR	0.0352	0.0537	0.0393	0.0333
FNR	0.3512	0.1632	0.3241	0.2948
ATP	10422	14395	11183	11715
n1 = 40, n2 = 9, n3 = 9
FDR	0.0354	0.0648	0.0404	0.0534
FNR	0.2404	0.1193	0.2269	0.1803
ATP	12955	15028	13201	13973

We carry out a gene ontology (GO) analysis to provide biological insights into the list of significant CpGs at FDR = 0.05 identified from the Gold-std method using the Bioconductor package topGO.²⁸ We consider both the elim Fisher’s exact test (elim.Fisher) and elim Kolmogorov–Smirnov test (elim.KS) implemented in topGO based on Alexa et al.²⁹ The elim method has been shown to improve interpretation of the GO analysis by integrating GO graph topology and iteratively removing genes that map to significant GO terms from a higher level GO terms.²⁹ The P-values from each of the test are adjusted via the Benjamini–Hochberg method.²⁴ Tables 3–5 report the GO terms corresponding to biological process (BP), molecular function (MF), and cellular component (CC) that exhibit adjusted P-values <0.05 by both the elim.Fisher and elim.KS test, respectively. For example, the BP GO analysis identifies a GO term related to positive regulation of ERK1 and ERK2 cascade, which has been shown to be implicated in lung adenocarcinomas.^30,31

Table 3.

Significant BP GO terms for the CpGs identified by the Gold-std method in the lung adenocarcinoma case study. The reported P-values are adjusted via the Benjamini–Hochberg FDR control.²⁴

BIOLOGICAL PROCESS
GO ID	TERM	ANNOTATED	SIGNIFICANT	EXPECTED	elim.Fisher	elim.KS
GO:0007268	Synaptic transmission	1153	803	685.54	2.18e-07	2.54e-17
GO:0048704	Embryonic skeletal system morphogenesis	159	120	94.54	0.0122	1.94e-ll
GO:0031424	Keratinization	58	53	34.49	0.00019	2.97e-ll
GO:0007155	Cell adhesion	1577	1067	937.64	0.0122	7.27e-08
GO:0048265	Response to pain	54	46	32.11	0.0139	9.22e-08
GO:0009952	Anterior/posterior pattern specification	350	246	208.1	0.0283	1.21e-07
GO:0007156	Homophilic cell adhesion	177	133	105.24	0.0102	1.29e-07
GO:0007186	G-protein coupled receptor signaling pat.	1035	721	615.38	0.000349	6.24e-06
GO:0007193	Adenylate cyclase-inhibiting G-protein c.	91	73	54.11	0.0122	6.24e-06
GO:0007267	Cell-cell signaling	1923	1319	1143.36	0.0122	6.24e-06
GO:0070374	Positive regulation of ERK1 and ERK2 cas.	0.174	128	103.46	0.0201	3.26e-05
GO:0050911	Detection of chemical stimulus involved.	19	19	11.3	0.0161	4.15e-05
GO:0001755	Neural crest cell migration	80	65	47.57	0.0122	4.15e-05
GO:0023019	Signal transduction involved in regulati.	33	30	19.62	0.0201	4.15e-05
GO:0007204	Elevation of cytosolic calcium ion conce.	326	240	193.83	0.0322	9.08e-05
GO:0048484	Enteric nervous system development	30	28	17.84	0.0139	9.73e-05
GO:0030198	Eextracellular matrix organization	537	375	319.28	0.0102	9.73e-05
GO:0021527	Spinal cord association neuron different.	27	25	16.05	0.0322	0.000155
GO:0042742	Defense response to bacterium	209	150	124.27	0.0313	0.000266
GO:0006954	Inflammatory response	845	564	502.41	0.0217	0.000556
GO:0030855	Epithelial cell differentiation	905	611	538.09	0.0139	0.00112
GO:0045666	Positive regulation of neuron differenti.	112	86	66.59	0.0217	0.00185
GO:0030335	Positive regulation of cell migration	428	294	254.48	0.0139	0.00265
GO:0019233	Sensory perception of pain	137	105	81.46	0.0122	0.00301
GO:0048485	Sympathetic nervous system development	45	40	26.76	0.0122	0.00496
GO:0045165	Cell fate commitment	417	299	247.94	0.034	0.00999
GO:0007215	Glutamate receptor signaling pathway	88	75	52.32	0.0122	0.0181
GO:0021846	Cell proliferation in forebrain	43	38	25.57	0.0139	0.0194
GO:0007631	Feeding behavior	155	117	92.16	0.0122	0.0273

Table 5.

Significant CC GO terms for the CpGs identified by the Gold-std method in the lung adenocarcinoma case study. The reported P-values are adjusted via the Benjamini–Hochberg FDR control.²⁴

CELLULAR COMPONENT
GO ID	TERM	ANNOTATED	SIGNIFICANT	EXPECTED	elim.Fisher	elim.KS
GO:0005887	Integral to plasma membrane	2079	1443	1242.77	3.14e-14	3.64e-35
GO:0005576	Extracellular region	3134	2161	1873.41	1.35e-09	1.82e-27
GO:0005615	Extracellular space	1398	964	835.68	5.49e-ll	4.19e-25
GO:0005886	Plasma membrane	6289	4079	3759.38	2.08e-05	2.84e-14
GO:0005578	Proteinaceous extracellular matrix	547	402	326.98	1.32e-07	1.39e-13
GO:0016021	Integral to membrane	6898	4421	4123.42	0.000363	1.86e-ll
GO:0 04 5211	Postsynaptic membrane	294	209	175.74	0.00296	4.46e-10
GO:0008076	Voltage-gated potassium channel complex	117	92	69.94	0.0012	7.64e-10
GO:0030054	Cell junction	11 9 7	776	715.53	0.0105	2.57e-06
GO:0034774	Secretory granule lumen	105	79	62.77	0.0 419	0.00149

Discussion

Partially matched samples could give rise to unbalanced covariate distribution among the incomplete matched pairs in large-scale matched pair omics studies. This paper extends the P-value pooling method of Kuan and Huang⁵ to a framework based on propensity score for adjusting unbalanced covariate distribution among the incomplete matched pairs. We consider two approaches using propensity score, namely, (1) full matching followed by generalized t-test (FM-PS) and (2) propensity score as covariate in regression model (Reg-PS). Both methods are able to reduce the number of false positives by accounting for the confounders. Currently, we use the full matching approach based on Mahalanobis distance with propensity score calipers^15–17 and the one-way random effects ANOVA model¹⁹ for deriving the generalized paired t-test. One can also use other matching algorithms based on propensity score.¹⁰

In this paper, we assume that the biomarker measurements are properly transformed such that they are approximately Gaussian distributed. If Gaussian assumption is violated, one can replace the generalized paired t-test with the generalized non-parametric aligned rank test of Hodges and Lehmann²⁰ and Heller et al.²¹ in FM-PS method, and replace regular linear regression with generalized linear models.¹¹ For instance, in our case study on DNA methylation, the analysis is carried out on the logit transformed beta values (also known as M values). An alternative approach is to analyze the untransformed beta values using beta regression in the Reg-PS method. The choice of analyzing DNA methylation data on either beta values or M values is an ongoing active research.^32,33

Both the FM-PS and Reg-PS methods exhibit comparable performance in both our simulations and case study. In this paper, we assume a linear propensity score–outcome relationship that enables us to apply direct adjustment with a linear propensity score term in Reg-PS. In such cases, Reg-PS method is computationally more efficient and easier to implement compared to FM-PS method. However, if the propensity score–outcome relationship is non-linear, one will need to consider more complicated models, for instance, the generalized additive model (GAM) as proposed in Myers and Louis.³⁴ In such cases, the FM-PS method may be a better alternative as this approach does not require specification of the propensity score–outcome relationship. Thus, we recommend that the users compare the results from both Reg-PS and FM-PS methods in practice.

Table 4.

Significant MF GO terms for the CpGs identified by the Gold-std method in the lung adenocarcinoma case study. The reported P-values are adjusted via the Benjamini–Hochberg FDR control.²⁴

MOLECULAR FUNCTION
GO ID	TERM	ANNOTATED	SIGNIFICANT	EXPECTED	elim.Fisher	elim.KS
GO:0004930	G-protein coupled receptor activity	741	566	440.86	2.51e-10	1.67e-22
GO:0004984	Olfactory receptor activity	67	62	39.86	7.72e-07	2.26e-15
GO:0005509	Calcium ion binding	977	654	581.27	0.000243	1.29e-13
GO:0043565	Sequence-specific DNA binding	1129	735	671.71	0.00888	5.34e-12
GO:0005201	Extracellular matrix structural constitu.	123	95	73.18	0.00634	1.81e-08
GO:0005234	Extracellular-glutamate-gated ion channe.	29	26	17.25	0.0283	6.5e-07
GO:0005125	Cytokine activity	332	234	197.53	0.00604	1.33e-05
GO:0005230	Extracellular ligand-gated ion channel a.	122	99	72.58	0.0147	3.79e-05
GO:0004890	GABA-A receptor activity	33	29	19.63	0.0283	6e-05
GO:0015269	Calcium-activated potassium channel acti.	27	25	16.06	0.0192	0.000132
GO:0004888	Transmembrane signaling receptor activit.	1333	979	793.08	0.0363	0.000591
GO:0005540	Hyaluronic acid binding	32	29	19.04	0.0179	0.00185
GO:0015293	Symporter activity	213	152	126.73	0.0216	0.00232
GO:0020037	Heme binding	201	144	119.59	0.0216	0.00558
GO:0005506	Iron ion binding	238	169	141.6	0.0192	0.00558
GO:0016918	Retinal binding	28	25	16.66	0.0363	0.0104
GO:0005242	Inward rectifier potassium channel activ.	37	32	22.01	0.0283	0.0126
GO:0015279	Store-operated calcium channel activity	16	16	9.52	0.0229	0.0212
GO:0008227	G-protein coupled amine receptor activit.	67	58	39.86	0.0216	0.0315