The Effect of Fertility Reduction on Economic Growth

Abstract

We assess quantitatively the effect of exogenous reductions in fertility on output per capita. Our simulation model allows for effects that run through schooling, the size and age structure of the population, capital accumulation, parental time input into child-rearing, and crowding of fixed natural resources. The model is parameterized using a combination of microeconomic estimates, data on demographics and natural resource income in developing countries, and standard components of quantitative macroeconomic theory. We apply the model to examine the effect of a change in fertility from the UN medium-variant to the UN low-variant projection, using Nigerian vital rates as a baseline. For a base case set of parameters, we find that such a change would raise output per capita by 5.6 percent at a horizon of 20 years, and by 11.9 percent at a horizon of 50 years.

1 Introduction

How does population growth affect economic growth? More concretely, in the context of a high-fertility developing country, how much higher would income per capita be if the fertility rate were to fall by a specified amount? This is an old question in economics, going back at least to Malthus (1798). Over the last half century, the consensus view has shifted from fertility declines having strong effects, to their not being very important, and recently back toward assigning them some significance (Sindig 2009; Das Gupta, Bongaarts, and Cleland 2011).

For an issue that has been studied for so long, and with such potential import, the base of evidence regarding the economic effects of fertility (or population growth more generally) is rather weak. In some ways, this should not be a surprise. Population growth changes endogenously as a country develops. Further, factors that impact population, such as changes in institutions or culture, are also likely to affect economic growth directly, and they are poorly observed as well. Finally, the lags at which fertility changes affect economic outcomes may be fairly long. Thus, at the macroeconomic level, it is very hard to sort out the direct effects of population growth from those of other factors. Much of the current thinking about the aggregate effects of fertility decline relies on results from cross-country regressions in which the dependent variable is growth of GDP per capita and the independent variables include measures of fertility and mortality, or else measures of the age structure of the population. However, as discussed in Section 2, there are severe econometric problems with this approach.

Our goal in this paper is to quantitatively analyze the economic effects of reductions in fertility in a developing country where initial fertility is high. We ask how economic measures such as GDP per capita would compare in the case where some exogenous change reduces fertility to the case where no such exogenous change takes place. The answer to this question will be very different from simply observing the natural coevolution of fertility and economic development, because in our thought experiment we hold constant all the unobserved factors that in reality affect both fertility and economic growth.

To address our research question, we construct an demographic-economic simulation model in which fertility can be exogenously varied.¹ We trace out the paths of economic development under two scenarios: a “baseline,” in which fertility follows a specified time path, and an “alternative” in which fertility is lower. Because we want to realistically model high-fertility developing countries in which fertility will likely be falling over the next several decades, both our baseline and alternative scenarios involve falling paths of fertility; the difference is that fertility falls faster in the alternative scenario. We use the United Nations (UN 2010) medium-fertility population projection as our baseline, and the UN low-fertility population projection as our alternative scenario.²

The model we build takes proper account of general equilibrium effects, the dynamic evolution of population age structure, accumulation of physical and human capital, and resource congestion. It is parameterized using a combination of microeconomic evidence and economic theory. Throughout the paper, our focus is on giving a quantitative analysis of changes in fertility, so that we can estimate how much extra output a given fertility change will produce over a specific time period. The simulation approach also permits an analysis of the strength of the various mechanisms at work. We hope that, by showing how behavioral effects that are often studied in isolation can be integrated to answer macroeconomic questions, we can reorient the academic discussion of population and development along more quantitative and practical lines.

The methodology we employ is not conceptually new. Rather, we are proceeding in the tradition of Coale and Hoover (1958) and many others discussed below. However, we improve on existing work in several dimensions. First, we trace out the effects of changes in the population through many more potential channels than were addressed in previous literature.³ Second, we ground our estimates of the magnitudes of effects in well-identified microeconomic studies of individual behavior. In much of the previous literature, key magnitudes were chosen either in an ad hoc fashion or solely based on theory. Third, we are able to measure the magnitude of the different channels that are analyzed. This makes the simulation rather less of a black box. Finally, the structure of our simulation is both transparent and flexible. The paper itself includes a good deal of robustness testing, and our full computer model is available and easily altered by anyone wishing to conduct further testing. The simulation model that we build is general, but it has characteristics that can be tailored to the situation of particular countries. In addition to country-specific demographic characteristics (vital rates, initial age structure), the model can incorporate country-specific measures of the role of natural resources in aggregate production and the openness of the capital market.

To reiterate a point made above, our goal in this paper is not to build the best possible forecast of the actual path of GDP per capita in a particular country. Rather, our interest is in asking how the forecast path of GDP would change in response to a change in fertility. That is, we compare the paths of GDP in two otherwise identical scenarios that differ only in terms of fertility. Such an exercise necessitates a baseline scenario from which to work. We use a very straightforward baseline in which, for example, productivity growth is constant. While one could consider a different baseline, it is important to note that errors in the baseline forecast that we use will only have second-order effects on our estimate of the difference between the baseline and alternative scenarios.

Our finding is that a reduction in fertility raises income per capita by an amount that some would consider economically significant, although the effect is small relative to the vast gaps in income between developed and developing countries. In the version of our model parameterized to match the economic and demographic situation of Nigeria, we find that shifting from the UN medium-fertility population projection to the UN low-fertility population projection raises income per capita by 5.6 percent at a horizon of 20 years, and by 11.9 percent at a horizon of 50 years. The simple dependency effect (fewer dependent children relative to working adults) is the dominant channel for the first several decades. At longer horizons, the effects of congestion of fixed resources (à la Malthus) and capital shallowing (à la Solow) become more significant than dependency, although the latter remains important. The fourth most important channel in the long run is the increase in human capital that follows from reduced fertility.

Whether the overall effect of fertility on economic outcomes that we find in our model is large or small is mostly in the eye of the beholder – a point to which we return in the paper's conclusion. It is also important to note the hurdles that stand between a finding that reductions in fertility would raise output per capita by an economically significant amount (if that is how one interprets the magnitude of our finding) and a conclusion that some policy intervention that achieved such a reduction in fertility would be a good thing. First, our analysis says nothing at all about the methods, costs, or welfare implications of such interventions. Second, GDP per capita is not necessarily the correct welfare criterion. The question of how a social planner should treat the welfare of people who may not be born as a result of some policy is cult (Razin and Sadka 1995; Golosov, Jones, and Tertilt 2007).

The rest of this paper is structured as follows. Section 2 discusses how our work relates to the previous literature. Section 3 discusses the baseline and alternative fertility scenarios we consider and shows how the dynamic paths of population size and age structure differ between them. Section 4 presents the economic model and discusses our choice of base case parameters. Section 5 presents simulation results for the base case model, discusses the sensitivity of results to altering our parameter assumptions, and presents a decomposition of the effects of fertility on output via different channels. Section 6 looks more deeply at different choices regarding the investment rate and how they interact with demographic change. Section 7 similarly goes into greater depth regarding assumptions about the role of the fixed factor in production. Section 8 concludes.

2 Relationship to previous literature

Attempts to assess the effect of fertility changes on economic outcomes can be classified among three categories: aggregate (macroeconomic) statistical analyses, microeconomic studies, and simulation modeling. In this section, we briefly review these three approaches, and we also discuss a number of studies that have presented broad syntheses of research on the topic. Of course, the existing literature is vast in all of these areas, and so our summary is by necessity highly selective. We conclude the section by discussing how the approach we take in the rest of the paper compares to what has come before.

2.1 Macroeconomic analyses

The best known early aggregate analysis of the relationship between population growth and development is Kuznets (1967). His study found a positive correlation between growth rates of population and income per capita within broad country groupings, which he interpreted as evidence of a lack of a negative causal effect of population growth on income growth, contrary to the prevailing view at the time.

A number of studies followed in the line of Kuznets (1967) in examining the relationship between population growth and different factors that were viewed as being determinants of income growth. For example, Kelley (1988) found no correlation between population growth and growth of income per capita, and similarly no relationship between population growth and saving rates. Summarizing many other studies, he concluded that the evidence documenting a negative effect of population growth on economic development was “weak or nonexistent.”

Since the early 1990s, many analyses of the effect of population on economic outcomes have followed the “growth regression” model popularized by Barro (1991) and Mankiw, Romer, and Weil (1992). In these regressions, terms representing population growth, labor force growth, or dependency ratios are included as right hand side variables. For example, Kelley and Schmidt (2005) regress the growth rate of income per capita on the growth rates of total population and the working-age population, incorporating both Solow effects (dilution of the capital stock by rapid growth in the number of workers) and dependency effects. They find that the demographic terms are quantitatively important. More specifically, their regression explains approximately 20 percent of the growth of income per capita on average over the period 1960–1995. Bloom and Canning (2008) regress the growth rate of income per capita on the growth rate of the working-age fraction of the population (along with standard controls), finding a positive and significant coefficient. Since high growth of the working-age fraction follows mechanically from fertility reductions, they see this as showing the economic benefits of reduced fertility.

Unfortunately, very little of the literature taking an aggregate approach to the effects of population on economic outcomes deals adequately with the issue of identification. The determinants of population growth, most notably fertility, are endogenous variables. Changes in fertility are not only themselves affected by economic outcomes, but they are also affected by unobserved variables that may also have direct effects on the economy. These could include human capital, health, characteristics of institutions, cultural outlook, and so on. Because of these issues of omitted variables and reverse causation, the ability to draw inferences from the conditional correlations in growth regressions is very weak.⁴ The fact that changes in economic outcomes are sometimes regressed on lagged changes in fertility (as represented, for example, by population age structure) is only a slight improvement, since there is bound to be serial correlation in the unobserved factors that affect both fertility and economic outcomes.

A small number of studies have attempted to circumvent the identification problem in the macroeconomic context using instrumental variables. Acemoglu and Johnson (2007), using worldwide health improvements during the international epidemiological transition to instrument for country-specific reductions in mortality, conclude that higher population growth has a significant negative effect on GDP per capita at a horizon of several decades. Li and Zhang (2007) use shares of non-Han populations (which were not subject to the one-child policy) across Chinese provinces to instrument for population growth, finding a negative effect on the growth of GDP per capita. Bloom et al. (2009), using abortion legislation as an instrument, find a negative impact of fertility on female labor force participation. They conclude that the extra labor supply would be a significant channel through which lower fertility would raise income growth, although they mention that saving and human capital accumulation are expected to be important channels as well.

2.2 Microeconomic analyses

A second approach to examining the relationship between population and economic outcomes has been to look to a finer level of analysis: households, rather than countries. Examination of household data often allows for proper identification to be achieved in a way in which it cannot be done using macro data. Joshi and Schultz (2007) and Schultz (2009) study the long run effects of a randomized trial of contraception provision in provision in Matlab, Bangladesh. They find that reduced fertility produced persistent and significant positive effects on the health, earnings, and household assets of women, and on the health and earnings of children. Miller (2010) uses variations in the timing of the introduction of the Profamilia program in Colombia to identify both the effect of contraceptive availability on fertility and the effect of fertility on social and economic outcomes. He finds that ability to postpone first births leads to higher education as well as independence for women. For those treated at a young age, Profamilia reduced fertility by 11-12 percent and raised education by 0.08 years. Rosenzweig and Zhang (2009), examining data from China and using twins as a source of exogenous variation in the number of children, find that higher fertility reduces educational attainment. For rural areas, the elasticity of schooling progress with respect to family size is estimated at between -9 and -26 percent. On the other hand, Angrist, Lavy, and Schlosser (2006) in Israeli data, and Black, Devereux, and Salvanes (2005) in Norwegian data, using twins as well as sex-mix preference as instruments for the number of children, find no effect of the number of children on child quality.

While cross-country regressions suffer from severe econometric problems, they do have the advantage – if one is interested in studying the aggregate effects of fertility decline – of focusing on the right dependent variable. By contrast, a good many microeconomic studies examine the link between fertility at the household level and various outcomes for individuals in that household (wages, labor force participation, education, etc.). These studies cannot directly answer the question of how fertility reduction affects the aggregate economy for three reasons. First, many of the effects of such reduction run through channels external to the household – either via externalities in the classic economic sense (for example, environmental degradation) or through changes in market prices, such as wages, land rents, and returns to capital (Acemoglu 2010). Second, even if one ignores the issue of external effects, aggregating the different channels by which fertility affects economic outcomes is not trivial. Finally, as in the macroeconomic literature, the long time horizon over which the effects of fertility change will affect the economy limits the ability of a single study to capture them.

2.3 Simulation models

In principle, if one knows the magnitude of the different structural channels that relate economic and demographic variables, these can be combined into a single simulation that will effectively deal with the issues of aggregation and general equilibrium. In practice, however, simulation models are only as credible as their individual components – that is, both the structural channels that they incorporate and the manner in which these structural relationships are parameterized.

The intellectual ancestor of modern economic-demographic models is Coale and Hoover (1958), who set out to study the effect of fertility change in India. They start by making alternative population forecasts for India under three exogenous fertility scenarios: high (constant at its 1951 level), medium (declining 50 percent over the period 1966–1981), and low (declining 50 percent over the period 1956–1981). Total population in 1986 in their model is 22 percent higher in the high-fertility than the medium-fertility scenario, and 7 percent lower in the low-fertility than the medium-fertility scenario. In terms of production, the authors assume that there is an exogenous incremental capital-output ratio that is invariant to investment and population (there is no human capital or land in the production function). Their finding is that, at a time horizon of 30 years, income per capita is 15 percent higher in the low-fertility scenario and 23 percent lower in the high-fertility scenario as compared to the medium-fertility scenario. The primary mechanism driving their results is capital accumulation: with high population growth, a high dependency ratio negatively impacts the saving rate and thus investment and growth. Of particular note, the model treats spending on child health and education as consumption rather than investment.

A recognizably more modern production model is incorporated into Denton and Spencer (1973). They use a neoclassical production function that allows the marginal products of capital and labor to vary with the capital-labor ratio. Fertility and mortality rates are taken as exogenous. The model includes capital accumulation (with saving being a fixed fraction of disposable income) and age-specific labor supply. The model is fit to data from Canada and is used to analyze the aggregate effects of changes in the fertility path. Enke (1971) applies a somewhat similar model to a stylized developing country. He compares paths of income per capita under two scenarios: a high-fertility scenario, in which the gross reproduction rate (GRR) stays constant at 3.025 from 1970 through 2000, and a low-fertility scenario in which the GRR falls from 3.025 in 1970 to 2.09 in 1985 and 1.48 in 2000. Total population in 2000 is 37 percent higher in the high-fertility than in the low-fertility scenario. The underlying economic model uses capital and labor as inputs in a Cobb-Douglas production function.⁵ Population is divided into 5-year intervals, with varying age-specific labor force participation. The effects that he finds are quite large: income per capita in the low-fertility scenario is 13 percent larger than in the high-fertility scenario in 1985, and it is 43 percent larger in 2000. Much of the force driving his results comes from a higher saving rate in the low-fertility scenario that is, in turn, due to a Keynesian consumption function in which the average propensity to consume falls as disposable income rises, and in which the level of consumption is partially proportional to population size.

Simon's (1976) model is similar in many respects to that of Enke (1971), but with several alterations that reverse key results. In Simon (1976), social overhead capital rises with population size to allow for economies of scale in production (specifically, better road networks that facilitate more efficient production). Similarly, technological change in the industrial sector is a function of the overall size of the population. Unlike Enke (1971), the model also features an explicit labor-leisure choice as well as separate agricultural and industrial sectors. Taking fertility as exogenous, Simon (1976) finds that, for the first 60 years of the simulation, constant population size leads to higher income per capita than growing population, although the difference is quite small. For longer time horizons, growing population (at a moderate rate) is better than constant population.

Simulation models that developed further in this line included multiple productive sectors (agriculture, industrial, and service), a government sector, and urbanization. Several also included an endogenous response of fertility. In reviewing a number of these models, Ahlburg (1987) argues that they “vary considerably in their complexity… The cost of the models' increased complexity is that it is often very difficult to uncover the underlying assumptions and, particularly, since few carry out sensitivity analysis, the key assumptions.” His summary of the concrete findings of these simulation models is that fertility decline would have modest positive effects on income per capita, although much smaller than predicted by population pessimists such as Enke (1971).

In a similar vein, Kelley (1988) cites many obstacles to constructing a credible model to address the issue of how rapid population growth impacts development in the Third World. Among these obstacles are general equilibrium feedbacks, the difficulty of constructing credible long-range demographic forecasts, potential changes in policy or institutions that may occur over the forecast interval, and the lack of available data to specify and validate such a model. He concludes, “Clearly, providing a quantitative, net-economic-impact answer to the population-counterfactual question is at best a remote possibility.”.

Later simulation models have stressed the importance of human capital increases that accompany fertility reductions. Lee and Mason (2010) incorporate a “quality-quantity” trade-off in a model that does not include physical capital or land. The elasticity of human capital investment per child with respect to the total number of children is close to negative one, implying that total spending on human capital of children is invariant to the number of children. A reduction in fertility of 10 percent will therefore raise schooling per child by 10 percent. Their model has a simple 3-period age structure with a working-age generation as well as dependent children and elderly. Examining cross-country data, they derive an estimated semi-elasticity of human capital with respect to years of education of 7 percent. Their simulation considers a developing country in which there has already been a rapid rise in the net reproduction rate (NRR) due to falling child mortality. In the baseline scenario of their simulation, there is continuing decline in mortality and an even more rapid fall in fertility that temporarily overshoots the replacement level. The authors then consider deviations from this baseline scenario, involving the decline in fertility being faster or slower. An alternative scenario with slowly falling fertility has consumption per equivalent adult roughly 12 percent lower than the baseline scenario for the first two generations of the simulation.⁶

Although simulation models waned in popularity in academic circles after the 1980s, they remained popular as didactic tools and for more policy-oriented analyses. The RAPID model (Abel 1999) allows for a variety of user-input demographic scenarios.⁷ However, the path of total GDP in the simulation is completely invariant to population, thus delivering the result that reduced population growth has very large effects on income per capita. The SEDIM model (Sanderson 2004) takes a more serious approach to general equilibrium. There is an aggregate production function that uses capital, labor, and human capital (but not land). Wages, savings, education, and fertility are all taken as endogenous. Population is broken into single-year age groups. The model is first calibrated to historical data and then used to simulate alternative scenarios.

In many of the models discussed above, one of the crucial channels through which demographic change affects economic outcomes is saving and capital accumulation. An issue that any such model must deal with is whether and how the consumption/saving decisions made by households are affected by their expectations of future demographic and economic developments. In modern macroeconomic models, the standard assumption is of rational or model-consistent expectations, although application of this assumption in the case of long-run demographic change can be quite complex. Auerbach and Kotlikoff's (1987) 55-period overlapping generations model represents a methodology for solving for the rational expectations equilibrium in such a case, although their emphasis is on developed-country issues, in particular government funded transfer programs.

Recent work by macroeconomists interested in long-run growth has extended the approach of Auerbach and Kotlikoff (1987) to create fully “micro-founded” computable general equilibrium models to analyze the interaction of population and economic outcomes (for example, Doepke, Hazan, and Maoz 2007). In such work, utility maximizing households are modeled as continuously reoptimizing their decisions (fertility, child education, consumption, labor supply) in response to changes in forecast paths of aggregate variables. The approach requires explicitly modeling household utility functions, including preferences over child quality and quantity, as well as budget constraints and credit market constraints faced by households and firms.

2.4 Broad syntheses

Two of the most important syntheses of contemporary thinking on the subject of how fertility affects development in poor countries are those by the National Academy of Sciences (NAS 1971) and the National Research Council (NRC 1986). NAS (1971) presents nuanced discussions of many of the potential channels through which rapid population growth can affect economic outcomes, including resource depletion, capital dilution due to rapid labor force growth, urbanization, and reductions in the saving rate caused by a large dependent population. In contrast to much of the literature up to the time, there is a strong emphasis on the role of human capital, and the increase in the fraction of national income that must be devoted to education when fertility is high. The authors are circumspect regarding the difficulties of long-range forecasting. They mostly limit themselves to a horizon of 2-3 decades, during which the dominant effects of fertility changes will be on the numbers of dependent children, and comment on the lack of credible models with which to make longer-term assessments. Although they firmly eschew the idea of a “population crisis” that was popular at the time, they nevertheless conclude that lower population growth in developing countries would significantly increase income per capita, and that reduced fertility should be a policy goal for most developing nations. Specifically, they urge countries with high population growth to reduce their rates of natural increase to less than 15 per 1,000 over the following two decades.

NRC (1986) is most notable for crystallizing a perspective skeptical of theorized negative effects of population growth, based both on available empirical evidence and principles of economic theory. The report also stresses the economic mechanisms that work to reduce negative effects of population growth, in particular the ability of markets and institutions to adjust to increased population. Much of the intellectual heft of the report is directed at the question of whether interventions in fertility decisions of households are warranted. The authors focus in particular on the questions of externalities and imperfect information on the part of households. To the extent that couples take into account the effect of their fertility decisions on the health and economic success of their children (including, for example, the effect of lower fertility on education and land per capita), the authors do not see a role for government. To an even greater extent than NAS (1971), the authors of NRC (1986) are reluctant to take a quantitative approach to discussing the effects of fertility change on long-term economic outcomes.⁸

NRC (1986) is often identified as the standard-bearer of the “revisionist” view that fertility change has a relatively small effect on economic development. Over the last decade, however, the pendulum has swung somewhat back in the other direction. Kohler (2012) starts by pointing out that although the majority of the world's population now lives in countries where fertility has fallen below the replacement rate, there are substantial areas of the world in which fertility remains quite high – specifically, with an NRR above 1.5 and a growth rate of population above 2.5 percent per year. Regarding these areas, he assesses the degree to which continued high fertility or stalled fertility declines constitute threats to economic development (as part of a broader cost-benefit evaluation of policies targeted at reducing population growth). He pays particular attention to the views of a new generation of population pessimists, typified by Campbell et al. (2007). Kohler's (2012) review of the different channels by which population affects economic outcomes includes resource scarcity, the “demographic dividend” from changes in population age structure, and effects of population size on innovation. His admittedly very rough and ready conclusion is that in current high-fertility countries a reduction of one percent per year in population growth would yield an increase of one percent per year in growth of income per capita. Another recent synthesis of current research (Das Gupta, Bongaarts, and Cleland 2011) concludes “At bottom, there is little fundamental disagreement on the issue. There is broad consensus that policy settings that support growth are the key drivers of economic growth, while population size and structure play an important secondary role in facilitating or hindering economic growth.” Sindig (2009) also reviews the current literature, identifying an emerging consensus that fertility reduction, while not a sufficient condition for economic growth, may well be a necessary one.

2.5 Structure of our model

In its basic structure, our model is clearly in the tradition of the simulation studies discussed above. We construct a general equilibrium model in which fertility and mortality (and thus population size and age structure) are exogenous. The endogenous variables in the model include physical and human capital, labor force participation, and wages. Output is produced in a neoclassical production function that takes physical capital, land, and a human capital aggregate (embodying education and experience) as inputs. Population is divided into 5-year age groups, and the time interval is 5 years.

An important way in which our model differs from previous work is that we focus not only on the overall effect of fertility change, but on the different channels by which fertility impacts the economy. This focus on channels allows for a more nuanced discussion of how our results compare to the predictions of different theories. Existing literature has discussed a number of channels that lead from demographic change to economic outcomes. At the risk of some intellectual straight-jacketing, we classify these effects as follows. The most basic effect of population on output per capita is through the congestion of fixed factors, such as land. We call this the Malthus effect. A second channel is the capital shallowing that results from higher growth in the labor force. We call this the Solow effect. Four channels run through the age structure of the population, which is a function of past fertility and mortality rates. First, in a high-fertility environment, a reduction in fertility leads, at least temporarily, to a higher ratio of working-age adults to dependents. Holding income per worker constant, this mechanically raises income per capita. We call this the dependency effect. Second, a concentration of population in their working years may raise national saving, feeding through to higher capital accumulation and higher output. We call this the life-cycle saving effect. Work by Bloom and Williamson (1998) on the demographic dividend has stressed a combination of the dependency and life-cycle saving effects. Third, slower population growth shifts the age distribution of the working-age population itself toward higher ages. In developing countries, this increase in average experience would be expected to raise productivity, even though in more developed countries the shift into late middle ages might lower productivity. We call this the experience effect. Fourth, if older workers participate in the labor market at a higher rate than workers just entering the workforce, the shifting age distribution towards higher ages will lead to higher overall labor force participation, thereby increasing income per capita. We call this the life-cycle labor supply effect. Another effect of reduced fertility is to lower the quantity of adult time that is devoted to child-rearing, freeing up more time for productive labor. We call this the childcare effect. Reductions in fertility are often associated with an increase in parental investment per child. We call this the child-quality effect. Finally, an increase in the size of the population may raise productivity directly, by allowing for economies of scale, or may induce technological or institutional change that raises income per capita.⁹ We call this the Boserup effect. In this paper, we attempt to quantify the first eight of these effects (Malthus, Solow, dependency, life-cycle saving, experience, life-cycle labor supply, childcare, and child quality).

A second significant difference between our model and previous simulations is in the parameterization of the underlying economic relations. In comparison to previous studies, we go much further in grounding our parameterization in well-identified microeconomic analyses of the types discussed above. The channels that we parameterize in this fashion include the returns to schooling and experience, the effect of fertility on education, and the effect of fertility on female labor supply. The range of existing estimates and our procedures for choosing parameters are discussed in Section 4 of the paper.

Unlike models in the tradition of Auerbach and Kotlikoff (1987), the saving and human capital investment decisions in our model do not have any forward looking component. Similarly, we do not provide a complete foundation for household decisions in terms of household optimization. Rather, we look at the applied microeconomics literature for estimates of the effects of contemporaneous variables on accumulation (such as education). In our view, economists's current understanding of household decision-making in developing countries is simply too limited to produce a quantitatively useful model that incorporates a fully optimizing micro-founded setup.

Of all the simulation models discussed above, the one that is closest in spirit to ours is the SEDIM model. The biggest difference between SEDIM and our model is in the calibration of key parameters. As discussed below, we rely on formal microeconomic estimates to supply the key parameters of our model, including the effects of education and experience on labor efficiency, the effect of fertility on education and labor supply, and so on. By contrast, the SEDIM model takes a much more ad hoc approach. A second difference is that unlike the SEDIM model, we do not allow for the endogenous evolution of fertility in response to changes in income (that result from an initial change in fertility). We are sympathetic to this approach and may pursue it in future research, but at this point we hold off for two reasons: first, there is no well-identified measure of how much fertility should respond to such a change; and second, our basic analysis shows that the response of income to fertility declines is relatively modest, and so we would expect the “second-round” effect of income on fertility to be modest as well. Finally, the SEDIM model has no land or fixed resources, and so the Malthusian effect of population increase is ignored.

Unlike Simon (1976), we take technological change as fully exogenous. His view that a higher level of population will lead to more technological progress, because there will be more people available to come up with new ideas, has been incorporated into the macro-growth literature (see, for example, Jones 1995). However, in our view, these models are better applied to the world as a whole or to the countries at the cutting edge of technology than to individual developing countries for a simple reason: the vast majority of technological progress in a typical developing country will be imported from abroad, and thus the growth rate of technology will be insensitive to the country's own population.

One way in which our approach differs significantly from that of NRC (1986) is that we explicitly focus on output per capita rather than utility. The question of how properly-considered utility would change due to a reduction in fertility is enormously complex: one must deal with externalities, household information sets, and the vexing issue of constructing a social welfare function that includes people who might not be born (Golosov, Jones, and Tertilt 2007). By contrast, the question we pose – whether reducing fertility would raise output per capita – is more easily addressed.

Following the analyses of NAS (1971), NRC (1986), and most of the simulation models discussed above, we focus on the effects of slowing population growth due to an exogenous decline in fertility. Much of our emphasis is on the channel of human capital, which was also emphasized by NRC (1986). Like Lee and Mason (2010), our analysis considers deviations of fertility from a path that is declining even in the baseline scenario. Unlike their paper, however, we use a much more realistic demographic structure.

3 Demographic scenarios

As already noted, we divide population into 5-year age groups, and each time period in our model corresponds to 5 years. Our analysis is focused on considering deviations of the path of fertility from what would occur along some baseline. Our model can be easily tailored to consider different baseline and alternative scenarios.

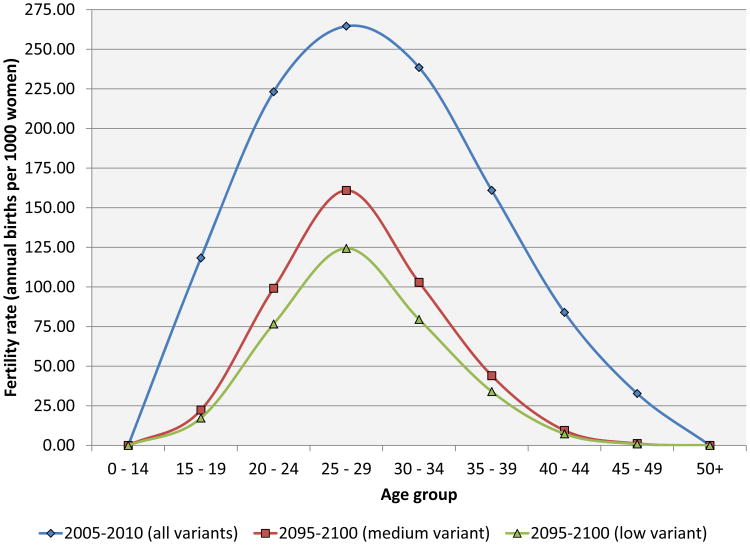
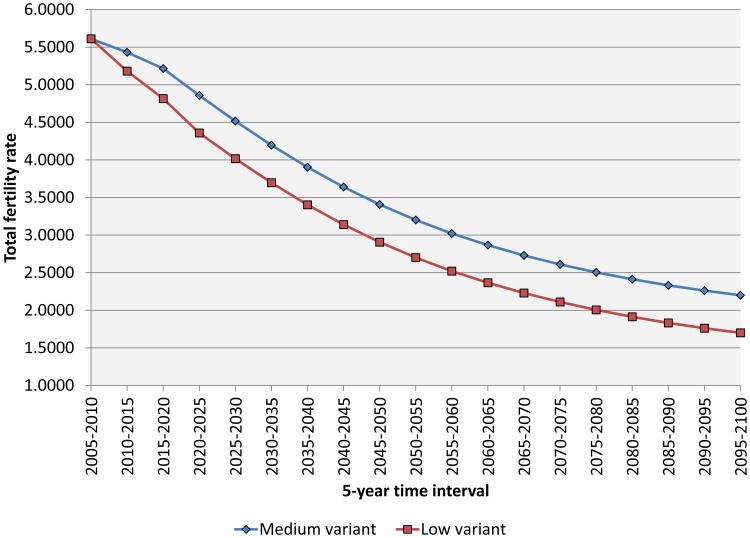
For the analysis in this paper, we tailor the model to fit Nigeria. Specifically, we take the UN (2010) medium-fertility population projection as our baseline population forecast, and the UN low-fertility variant as our alternative scenario. The UN reports population by 5-year age group for every 5-year period through 2100. The UN also reports age-specific fertility rates for every 5-year period through 2100. Figure 1 shows these age specific fertility rates for the initial period and then for the final period under the two different fertility scenarios. Figure 2 shows the paths of the total fertility rate (TFR) in the two scenarios. The medium variant has the TFR declining rapidly at first, and then with some slowdown, from 5.61 in 2005–2010 to 4.52 in 2025–2030, and 3.41 in 2045–2050. Fertility in the low variant is the same as that in the medium variant in 2005–2010, and then differs from the medium variant by a TFR of 0.25 in 2010–2015, 0.4 in 2015–2020, and by a fixed TFR of 0.5 there after. The difference between the UN high- and medium-fertility variants is the same.

Figure 1. Age-specific fertility rates by time period and demographic scenario.

Figure 2. The time paths of the total fertility rate by demographic scenario.

Unfortunately, the UN does not provide much guidance regarding how one should interpret the differences between the high-, medium-, and low-fertility projections. For example, we do not know if the TFR gap between the high and low projections incorporates most conceivable outcomes, although in our view this is unlikely. The fact that, looking at other countries, the TFR gap between the high and low projections is almost always exactly one suggests that this gap is not determined by a formal statistical procedure. This being said, we still believe that using the TFR gap between the medium and low projections – as a measure of the difference in fertility that might result from policy or other exogenous changes – is not unreasonable. To give two examples, Miller (2010) estimates that the Profamilia program in Colombia reduced fertility by half a child, and Joshi and Schultz (2007) estimate that a contraception provision program in Matlab, Bangladesh, reduced fertility by 15 percent, at a time when the TFR was slightly above 6, implying a reduction in the TFR of 0.9.

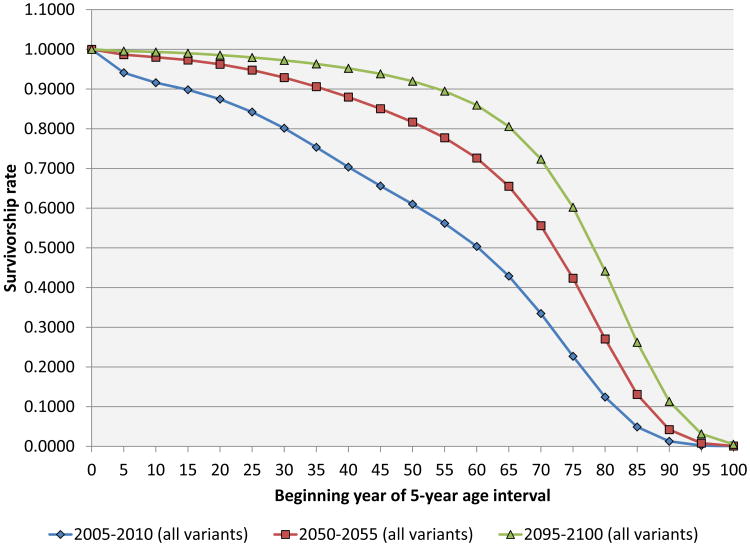
The UN does not provide explicit mortality schedules, but were are able to back these out from the other data in their forecasts.¹⁰ The two scenarios feature the same future paths of age-specific mortality. Figure 3 shows the life table survivorship function (males and females) for the first and last periods of the UN projection as well as one period in the middle. Life expectancy at birth rises from 50 in 2005–2010 to 60 in 2030–2035 and 70 in 2065–2070.

Figure 3. Age-specific survivorship rates by time period.

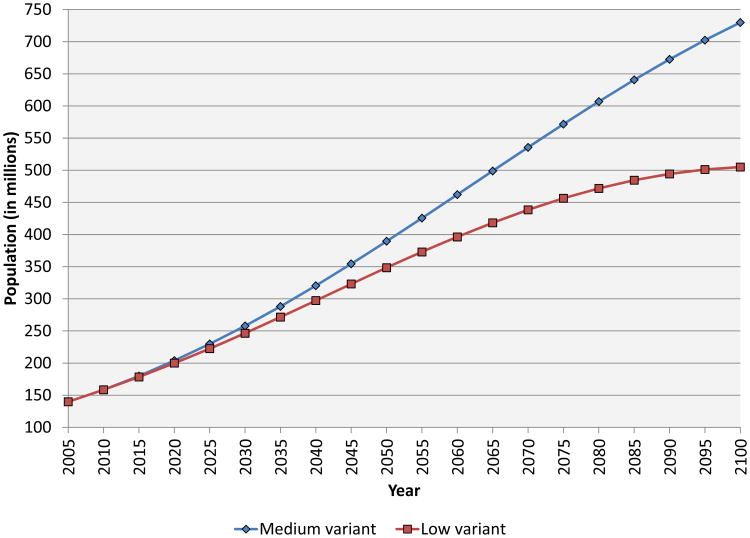
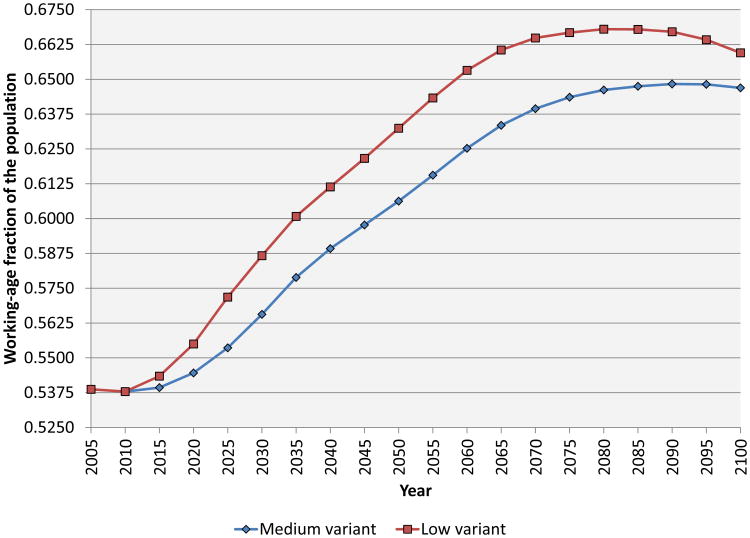
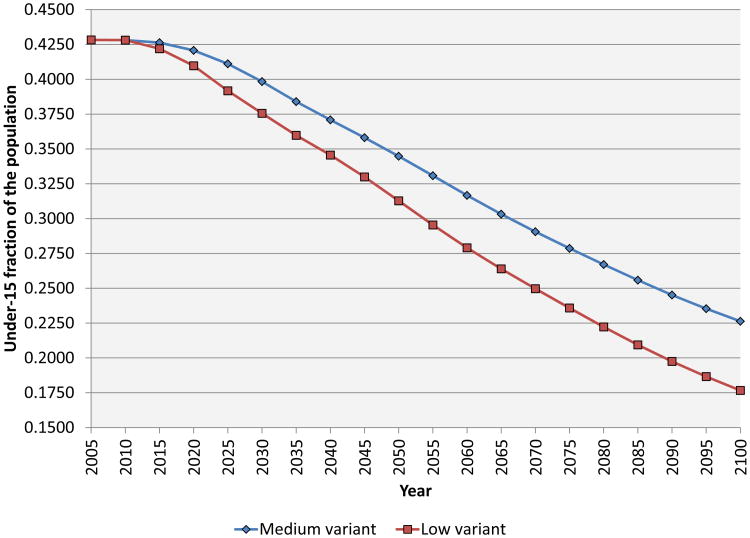
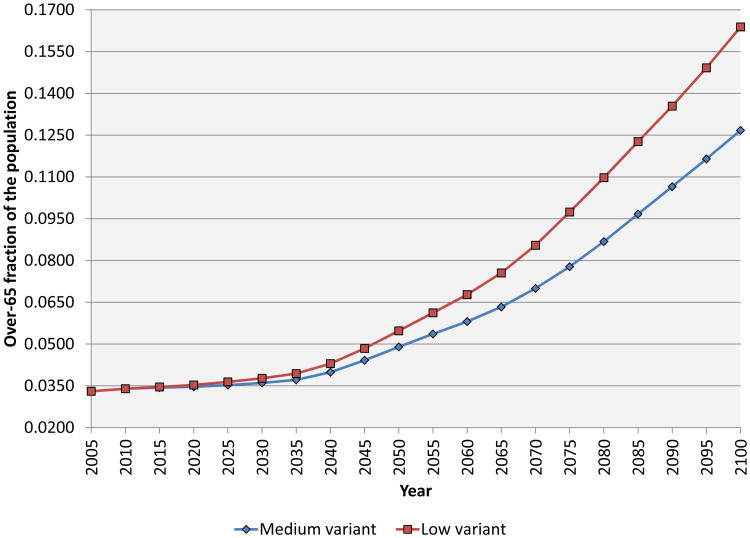
Figure 4 show the paths of total population in the two scenarios. Population in the low variant is 4.4 percent lower than the medium variant at a horizon of 2030, and 10.6 percent lower in 2050. Figures 5, 6, and 7 show, respectively, the working-age (15-64), young (under 15), and elderly (65+) fractions of the population in our baseline and alternative scenarios. Bloom and Williamson (1998) have emphasized the demographic dividend from lower dependency that results from reduced fertility. In both the scenarios we examine, there is a significant rise in the working-age fraction of the population over the next several decades, but the increase is larger in the low-fertility scenario. For example, in 2050, the working-age fraction is 60.6 percent in the medium-fertility scenario versus 63.2 percent in the low-fertility scenario (relative to 53.9 percent in 2010).

Figure 4. The time paths of population by demographic scenario.

Figure 5. The time paths of the working-age fraction of the population by demographic scenario.

Figure 6. The time paths of the under-15 fraction of the population by demographic scenario.

Figure 7. The time paths of the over-65 fraction of the population by demographic scenario.

4 Economic model and its parameterization

4.1 Production

In our base case model, aggregate production is given by a standard Cobb-Douglas production function. The factor inputs are land (which we use as a short hand for all fixed factors of production), physical capital, and effective labor, so that aggregate output in period t, Y_t, is

$$Y_t=A_t{K}_t^{\alpha }{H}_t^{\beta }{X}^{1-\alpha -\beta },$$

where α + β < 1, X is a fixed arbitrary stock of land, and A_t is productivity.

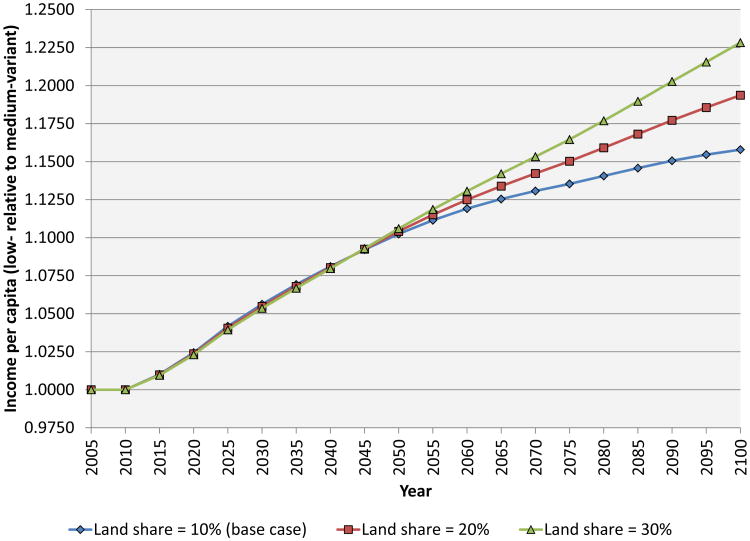
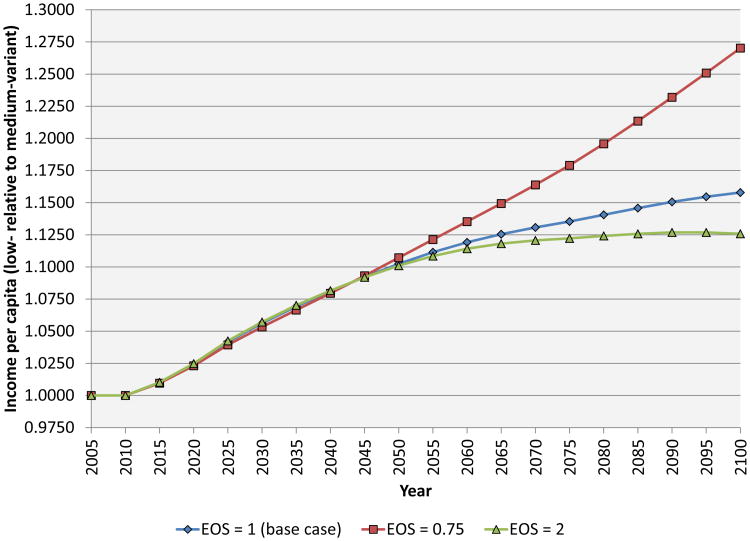
We assume fairly standard values for factor shares: we set α = 0:3 and β = 0:6, meaning that the implied share of land is 10 percent. In Section 7, we revisit the role of fixed factors of production. We consider the sensitivity of our results to both the share of land in national income and the elasticity of substitution between land and other factors of production. We also examine data on natural resource shares of national income. For convenience, we set the growth rate of productivity in the model to zero. The speed of productivity growth is obviously of paramount importance to the growth of income per capita, but reasonable variations in this parameter have only trivial effects on the quantity on which we focus – the ratio of income in the alternative scenario to income in the baseline scenario.

4.2 Physical capital accumulation

In our base case setup, we handle capital accumulation extremely simply, by following Solow (1956) in assuming that a fixed share of national income is saved in each period.¹¹ Specifically, the stock of capital in period t, K_t, evolves over time according to

$$K_{t+1}=s{Y}_t+(1-\delta )K_t,$$

where s and δ are the fixed saving and depreciation rates, respectively. We assume that the annual saving rate is 8.55 percent, which corresponds to the investment share of real GDP reported by Heston, Summers, and Aten (2009) for Nigeria in 2005. We assign a standard value of 5 percent to the depreciation rate.

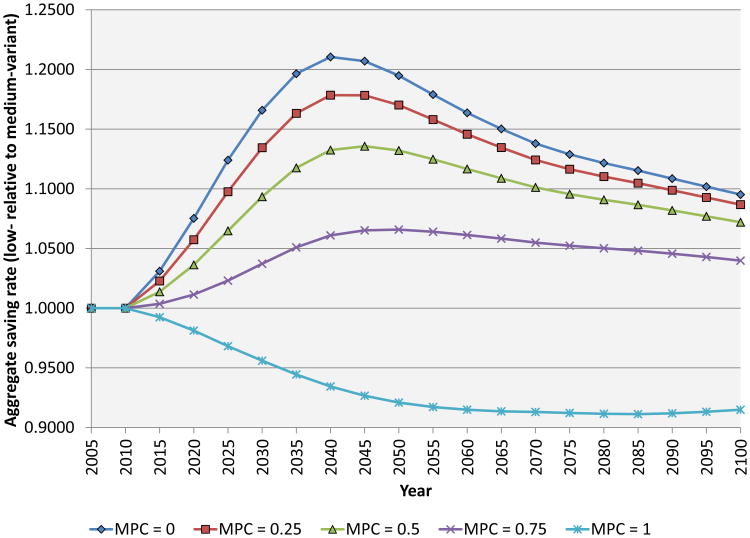
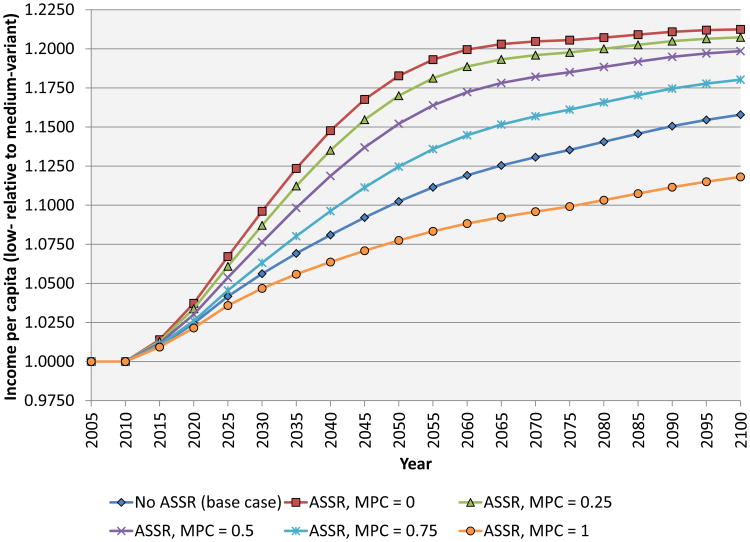
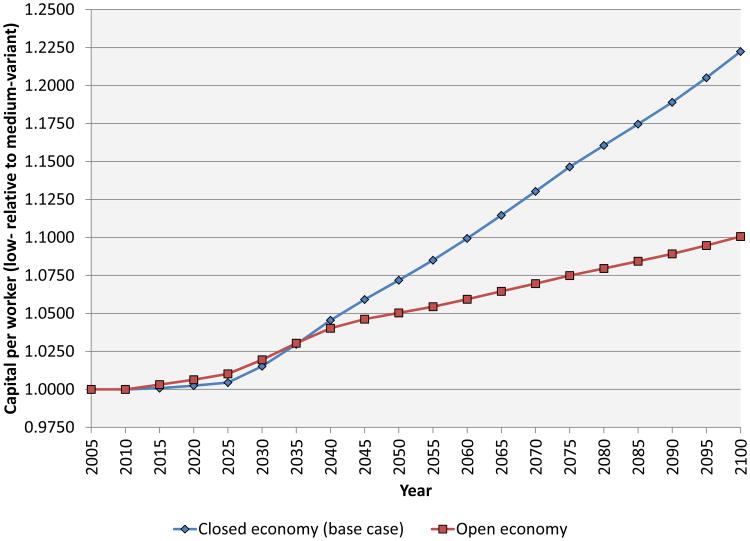
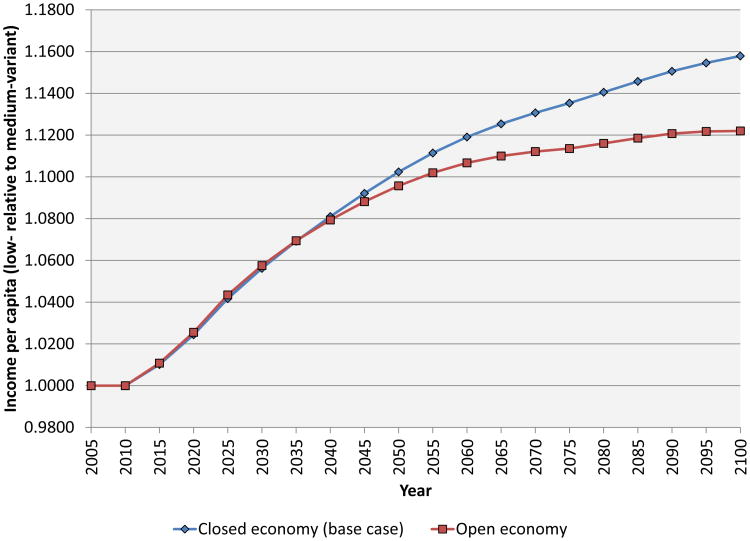
In Section 6, we consider two alternative models of investment. First, we allow for variable age-specific saving rates, with workers in their prime earning years having higher saving rates. This introduces an additional channel though which demographic change affects growth. ¹² Second, we consider the case of an economy that is fully open to international capital flows. This shuts off the Solow channel whereby slower growth of the labor force raises the level of capital per worker.

4.3 Effective labor

We model an individual's effective labor as a function of his or her age-specific labor force participation rate and level of human capital. Human capital, in turn, is a function of his or her schooling and experience. We assume that human capital inputs of individuals with different characteristics are perfectly substitutable. Thus, the stock of effective labor in period t, H_t, is

$$H_t=\sum _{15\le i<65}(h_{i,t}^s\times h_{i,t}^e\times {\mathit{\text{LFPR}}}_{i,t})N_{i,t},$$

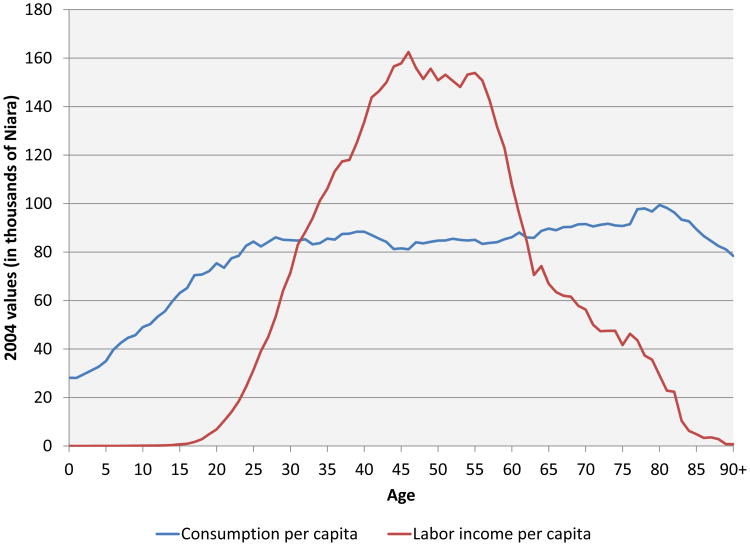
where N_i,t is the number of individuals of age i in the population in period t, LFPR_i,t is their labor force participation rate, and $h_{i,t}^s$ and $h_{i,t}^e$ are, respectively, their levels of human capital from schooling and experience. We assume that children enter the labor force at 15 and workers leave the labor force at 65.

In our simulations, we use labor force participation rates reported by the International Labour Organization (2011) for Nigeria in 2005. Specifically, we employ gender- and age-specific labor force participation rates to construct total labor force participation rates by age, using the fraction of males and females in each age group as population weights. Since our baseline and alternative scenarios both feature forecast paths with declining fertility, we modify the female labor force participation rates in each future period to reflect the effect of a decrease in time devoted to child-rearing on total labor supply. This procedure is explained in Section 4.4.

4.3.1 Returns to schooling

Years of schooling are aggregated into human capital from schooling using a log-linear specification,

$$h_{i,t}^s=exp[\theta S],$$

where θ is the return to an additional year of schooling. The return to schooling will be relevant for the exercises we conduct because reductions in fertility will raise the average level of schooling.

Estimating the returns to schooling has a long history in economics, going back to at least Mincer (1974) but beginning as early as the 1950s for the United States. The seminal works in estimating the Mincerian returns to schooling across different countries in the world are Psacharopoulos (1973; 1985; 1994) and Psacharopoulos and Patrinos (2004), who find in the most recent iteration of their results that the returns to schooling in Sub-Saharan Africa range from 4.1 to 20.1 percent, with an average return of 11.7 percent. These results, however, have been criticized for being driven by data of poor quality. Banerjee and Duflo (2005) improve on the quality of these estimates and find a range of 3.3 to 19.1 percent, with an average return of 9.75 percent.

One concern with these estimates is that they measure the average return to education in a country. If the change in fertility occurs mostly among low education workers, and the returns to education differ with the level of education, using the average return to schooling for all workers may be misleading. Psacharopoulos and Patrinos (2004) do estimate the returns to education by education level, and they find that the returns fall as the level of education rises. However, the higher quality estimates from Schultz (2004) indicate the opposite. He finds that in Nigeria, the return to primary education is approximately 2.5 percent per year, while the return to university education is in the 10-12 percent range. Moreover, the returns to primary education vary between 2 and 17 percent over a sample of six African countries, with an average of approximately 8 percent.

Another concern with these estimates is that they are obtained by running OLS regressions, and therefore the standard econometric concerns of endogeneity and omitted variables are not addressed. Duflo (2001) exploits a quasi-natural experiment involving a school building program in Indonesia, and she estimates the returns to education to be between 6.8 and 10.6 percent. Oyelere (2010) uses a similar research design, exploiting the provision and then revocation of free primary education in certain regions of Nigeria, to estimate the returns to education. She finds a return of only 2.8 percent, consistently with Schultz (2004).

For our base case model, we choose a value of θ = 10 percent, which is the standard value applied in much of the growth literature and represents a rough average of the estimates discussed above. In testing for robustness, we examine both Oyelere's (2010) estimate of 2.8 percent, which has the advantages of being well identified, primary education specific, and based on data for Nigeria, as well as 20 percent, which is the upper bound of estimates from Banerjee and Duflo (2005) for Sub-Saharan African countries.

4.3.2 Returns to experience

Human capital from on-the-job experience for a worker of age i in period t, $h_{i,t}^e$, is computed as

$$h_{i,t}^e=exp[\varphi (i-15)+\psi {(i-15)}^2].$$

Experience will play a role in our simulations because declines in mortality and fertility will lead to a population with higher average age and thus higher average experience.

As with the literature on the returns to education, labor economists have been estimating the returns to experience in the United States since the 1950s. Internationally, there are a large number of studies with somewhat conflicting results. Estimates of the Mincerian returns to experience in African nations are highly unreliable due to poor data quality. The seminal work remains Psacharopoulos (1994), who implicitly estimates the returns to experience across a set of 45 different countries, in addition to estimating the returns to education. Unfortunately, Psacharopoulos (1994) does not directly report these estimates. Bils and Klenow (2000) take the estimates from Psacharopoulos (1994), add seven additional countries, and report them all in Appendix B of their paper. For our base case setup, we use values of 0.052 for ϕ and 0.0009875 for ψ, corresponding to the average of the estimates for each of these coefficients across the four Sub-Saharan African countries (Botswana, Côte d'Ivoire, Kenya, and Tanzania) in Bils and Klenow (2000).¹³

4.3.3 Effect of fertility on education

We expect that lower fertility will raise the average level of schooling. Models of the fertility transition stress the movement of households along a quality-quantity frontier in which investment per child in health and education rises as the number of children falls. It does not follow from this observation, however, that the change in schooling that would result from an exogenous change in fertility is the same as the change that would accompany declining fertility when both measures are evolving endogenously.

A large literature analyzes the theoretical relationship between the number of siblings and educational attainment. However, there are few empirical studies from developing countries that use natural experiments to establish causal estimates of the effect of fertility on years of schooling. Using data from India, Rosenzweig and Wolpin (1980) and Rosenzweig and Schultz (1987) find that an exogenous increase in fertility due to the birth of twins decreases the level of schooling for all children in a household. Unfortunately, they do not provide estimates in a form that can be imported into our model. In addition, this work has faced criticisms due to the imprecision of estimates arising from a small sample size and methodological problems such as not controlling for birth order. Lee (2008), using the gender of the first child as an instrument for fertility, finds that higher fertility decreases educational investment per child in Korean data, but the effect is somewhat small. Using Norwegian data, Black, Devereux, and Salvanes (2005) find a negative effect of family size (using twins as a natural experiment) on educational attainment, but the effect disappears once birth order is controlled for.

To assess the change in fertility in which we are interested, we use results from Joshi and Schultz (2007), who analyzed a randomized intervention in Matlab, Bangladesh. They found that a TFR reduction of 15 percent, resulting from the intervention, led to an increase of 0.52 years of schooling for males aged 9-14.¹⁴

To give an example of how this finding is incorporated into our model, notice that in the UN medium-fertility variant, the TFR falls from 5.61 in 2005-2010 to 5.43 in 2010-2015, a reduction of 0.18. Since this corresponds to a reduction of 3.2 percent in the TFR for Nigeria in 2005, the relevant increase in schooling over this period is $0.52\times \frac{3.2}{15.0}=0.11$ years 15.0 of schooling. In the UN low-fertility variant, however, the TFR falls to 5.18 in 2010-2015, or a reduction by 0.43 in the TFR. Using a similar calculation, the increase in years of schooling under the low-fertility variant is 0.27. As fertility continues to fall over time in the two scenarios, years of schooling increases, with the increase being larger for the UN low-fertility scenario because it features a larger decline in fertility.

4.4 Childcare effects on labor supply

Raising children requires a good deal of labor. That labor is spread over many years and is divided among many individuals, but the largest piece usually comes from the child's mother. Reduced fertility should thus potentially increase the labor supply of women. A large literature has examined the effect of fertility on female labor supply in developed countries. Generally, these studies find a moderate to large negative effect.¹⁵ However, surprisingly little research has been done to assess the effect of fertility on female labor supply outside of Europe and the United States. Among studies focusing on non-Western countries, Chun and Oh (2002) use sex of the first child as an instrument for fertility in Korean data, and they find that having an additional child reduces labor force participation by 40 percent. Bloom et al. (2009) use exogenous changes in abortion laws at the country level as an instrument for fertility, finding that an additional birth reduces lifetime labor supply by about two years. However, neither of these papers estimate the effect of fertility on female labor force participation strictly in a developing country, where one would expect the effect of fertility on female labor force participation to be lower since child-rearing is often combined with productive activities. A handful of studies focusing on developing countries are currently underway, but this literature is still in its infancy.¹⁶

Beyond the general lack of research in this area, assigning a quantitative magnitude to the effect of fertility on female labor supply is difficult for several reasons.

• There are obviously strong economies of scale in child-rearing – the time cost associated with the first child is far higher than the marginal time cost of subsequent children. For example, Tiefenthaler (1997), examining data from Cebu, Philippines, finds that 14 months after birth, female labor market hours had declined by 39 percent in the case of first births, but by only 10 percent if there were already children aged 0-5 in the household. If there were both children aged 0-5 and children aged 6-17 in the household, female labor market hours were actually slightly higher at 14 months following a birth.

• Not all time spent on children is subtracted from production. A good part of time devoted to child-rearing may be at the expense of leisure or, in the case of siblings, human capital investment (which is not counted as part of national income).

• Child-rearing is often combined with productive activities, especially in developing countries. For example, a woman may carry a baby in a sling or watch children out of the corner of her eye while she works at a productive task. In this case, the cost of child-rearing in terms of productive labor would only be the decrement in productivity that results from such multitasking.

Despite these caveats, the time cost of child-rearing may still be a significant component in the economic response to fertility decline. We measure the effect of fertility change on labor supply through the childcare channel by specifying a parameter we call the labor market time cost of a marginal child. Summarizing all these considerations in a single parameter is obviously too simplistic but, in doing so, we at least have a concrete measure that can be implemented in our model. Specifying the time cost of the marginal child might also be considered problematic because the marginal cost would be expected to fall with the number of children. However, Holmes and Tiefenthaler (1997) conclude the that the marginal time cost of children is roughly constant for the third and higher children, and for the experiments we are considering, the TFR generally remains above two.¹⁷

Mechanically, we implement the childcare effect by increasing female labor force participation in each year by the hypothesized change in age-specific fertility multiplied by the labor market time cost (in years) of a marginal child. For example, if in our experiment, age-specific fertility of women aged 25-29 drops from 0.2646 to 0.2179 (as it does in the UN medium-fertility scenario between 2005–2010 and 2045–2050), and if the labor market time cost of a marginal child is one year, then labor force participation for women in this age group would rise by 4.67 percentage points.¹⁸

There only remains the question of choosing the base case parameter value for the time cost of children. In the Cebu data used by Tiefenthaler (1997), weekly labor market hours fall from 10.4 prenatally to 5.0 at two months, 6.6 at six months, and 9.5 at 14 months for women who have other children aged 0-5 in the household; and from 13.1 prenatally to 7.6 at two months, 11.3 at six months, and 13.8 at 14 months for those with children aged both 0-5 and 6-17 in the household. Crudely interpolating these data, and allowing for an almost total cessation of labor market activity in the first month after delivery, hours averaged over the first year are reduced roughly 5 per week in the first group and 3 per week for the second group. Weekly labor market hours for men in the same households do not change much in response to a birth, and are equal to roughly 40. So, in this data, women in these two groups lose 0.125 or 0.075 years of full-time equivalent labor market input in the first year after the birth of a marginal child. The complete or nearly complete recovery of labor hours by 14 months after delivery suggests that the decrement in subsequent years should be very small. On the other hand, there are a good number of these years. Further, we have data on neither the efficiency loss by women with small children who are working, nor any long-term health consequences of multiple pregnancies that might impede labor input for many years. As a rough guess for our base case parameterization, we specify a labor market time cost of 0.5 years per marginal child.¹⁹

Table 1 shows the age-specific labor force participation rate (LFPR) for Nigerian women in 2005 and the implied levels of the LFPR if the TFR were reduced by one (assuming a constant percentage reduction in each age-specific fertility rate), using our base case value of 0.5 for the time cost of a marginal child. For comparison, we also show the age-specific LFPR for men. The actual labor supply effect will depend on the actual projected change in the age specific fertility rate, which varies over time and between variants. The effect is linear in the size of the TFR change, and for a TFR change of one, it is very small.

Table 1. The labor supply response to a drop in the total fertility rate by one.

Age group	Male LFPR	Female LFPR	Female LFPR	Female LFPR
	Nigeria 2005	Nigeria 2005	with TFR drop	increase factor
15-19	35.0%	31.5%	32.5%	1.034
20-24	44.1%	37.7%	39.7%	1.053
25-29	61.4%	44.5%	46.8%	1.053
30-34	77.1%	50.8%	52.9%	1.042
35-39	80.1%	55.7%	57.1%	1.026
40-44	81.0%	57.0%	57.8%	1.013
45-49	83.1%	63.5%	63.8%	1.005
50-54	79.6%	65.8%	65.8%	1.000
55-59	81.2%	66.2%	66.2%	1.000
60-64	75.2%	64.0%	64.0%	1.000

4.5 Other channels not covered

A simulation study such as ours is useful only to the extent that it covers all of the quantitatively important channels through which a change in fertility affects the macroeconomy. We have tried to keep our framework transparent and open, so that we (or someone else) can add other channels if there is an appropriate basis. Here, we discuss some potential channels that we have not included, either because we think that they are of secondary quantitative importance or because we did not have a basis for quantifying them.

4.5.1 Boserup effects

There are several channels through which higher population density could positively affect the level of income per capita. In the context of agriculture, Boserup (1965) stressed that, as population rose, farmers were induced to switch to more intensive methods, which meant that the land constraint did not end up lowering income per worker. A more generalized version of this effect would be that higher population would induce technological progress more generally, that is outside of agriculture, either out of “necessity,” or because more people raises the likelihood of someone having a productive idea (Jones 1995). A completely different channel by which population growth could raise output would be by allowing for better trade and economies of scale in production. In the African context, it is often noted that long distances and poor roads lead to an extremely high cost of trade.

We do not include any of these channels in our analysis for several reasons. Regarding agriculture, some of the possibilities for intensification and substitution of other inputs for land are already included in our production function approach. In particular, Section 7 (and the literature on which it draws) discusses evidence on the substitutability of other inputs for land. The intensity of cultivation varies enormously in Sub-Saharan Africa, but the Boserupian description in which fertile land can easily be shifted from fallow to continuous cultivation seems inappropriate for most countries. Indeed, data show that over the last decades cultivation in Africa has increasingly expanded onto marginally suitable land (Weil 2008a).

Regarding gains from scale as population rises, we are of two minds. On the one hand, we agree that costly transport raises trade costs and leads to an inefficient scale of production in many African countries (Gollin and Rogerson 2009). However, it is not clear that population growth over the next several decades will lead to increases in rural population density that would facilitate trade. Rather, Africa is rapidly urbanizing, implying that much of the growth of population in the next decades will end up in already large cities (Weil 2008a). It is hard to believe that mega cities such as Lagos do not already have sufficient size to achieve economies of scale in production.

On a more prosaic level, we were not able to find quantitative estimates of the size of Boserup effects that we could incorporate into our model.

4.5.2 Effects through health improvements

Another channel through which fertility declines could possibly affect output is through improvements in health. These could result from the same quality-quantity shift that we model in the case of education. Ashraf, Lester, and Weil (2008) discuss how improvements in health can be translated quantitatively into productive human capital. However, Joshi and Schultz (2007) find no effect of the fertility intervention in Matlab, Bangladesh on child health.

5 Basic results

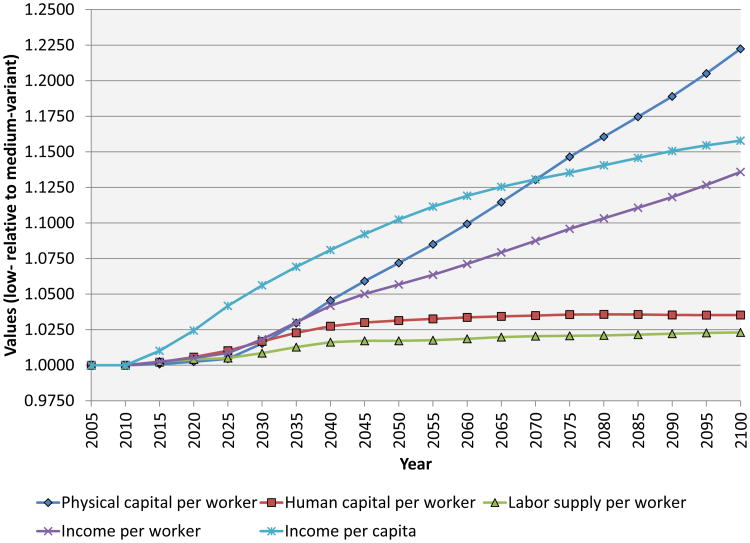
Figure 8 shows the paths of physical capital per worker, human capital per worker, labor input per worker, income per worker, and income per capita in our simulation, using the base case parameters discussed above. The path of output per worker reflects the dynamics of human and physical capital per worker, labor input per worker, and land per worker (which we do not show, but which can be inferred from Figure 8). As in all the figures that follow, we show the ratio of outcomes in the alternative scenario to outcomes in the baseline scenario. Further, in discussing our simulation results below, we refer to the year 2010 (that is, the last year before fertility in the baseline and alternative scenarios begin to diverge) as the start of our simulation, so references to time horizons in our simulation should be interpreted with respect to this year.

Figure 8. The base case economic projection.

Figure 8 shows that, in our base case setup, the long-run effect of reducing fertility from the UN medium variant to the low variant is to raise output per capita by 11.9 percent at a horizon of 50 years. At a 20-year horizon, the increase in income per capita is 5.6 percent.²⁰ Because fertility in the alternative scenario is lower than in the baseline scenario for the entire period we examine, income in the two scenarios continues to diverge.

Before going further, it is of interest to compare the findings of our simulation model with results from other studies. We focus on Bloom and Canning (2008), a well-cited cross-country regression study that appeared in this Review. In that paper, the independent variable of interest is the growth rate of the working-age fraction of the population, and the dependent variable is the growth rate of income per capita. The relevant coefficient is estimated at 0.996 using a simple OLS regression, and at 1.394 when the authors use lagged endogenous variables as instruments.

To compare the Bloom and Canning (2008) findings to our results, we first look at the growth rate of the working-age fraction of the population in our baseline and alternative scenarios. In both scenarios, the working-age fraction is 0.5379 in 2010, the first year of our simulation. Under the medium-fertility scenario, the fraction rises to 0.6252 in the year 2060, but it rises to 0.6532 under the low-fertility scenario. The implied annual growth rates of the working-age fraction are 0.301 percent per year in the medium-fertility variant and 0.389 percent per year in the low-fertility variant. To get the effect of lower fertility on income growth, we multiply the difference between these two growth rates (that is, 0.088 percent per year) by the Bloom and Canning (2008) coefficient. This yields an income growth differential (between the two scenarios) of 0.088 percent per year using their OLS estimate and 0.123 percent per year using their IV estimate. By contrast, in our simulation, the change in fertility from the medium to the low variant leads to income per capita rising by 11.9 percent over the first 50 years of the simulation, implying an increment to growth of 0.225 percent per year. In other words, the effect that we find in our simulation is roughly twice as large as theirs.

5.1 Component channels

As discussed above, demographic change affects economic outcomes through a number of channels, which may operate at different relative intensities at different time horizons. It is of interest to decompose the overall effect of fertility reduction into the parts that run through these different channels. Some caution is necessary, however, because there are clearly interactions among the different effects. In particular, the effect of fertility through any one channel will depend on which other channels are operative. For example, the effect of increased labor force participation of working-age adults will be larger or smaller, depending on the fraction of the population made up of such adults. To address this problem, we do all of our analysis of the effects of fertility through each of the different channels under the assumption that all the other channels are operative – that is, we consider the results in our full simulation relative to the case where one channel is “deleted” (an alternative would be to assume that no other channels were operative).

We begin by looking at several channels individually. This allows us to perform an analysis of the sensitivity of our results to assumptions about key parameters. We then do a full decomposition, showing the relative importance of the different channels at different time horizons.

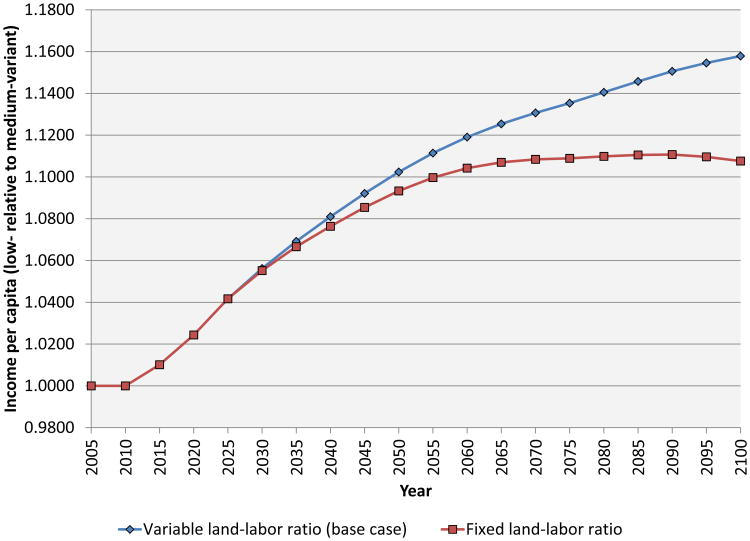
To gauge the importance of non-reproducible factors, we conduct a simulation in which the level of land per worker in the alternative scenario follows the same path as it does in the baseline scenario. In other words, we ignore the effect of lower fertility in preventing the land-labor ratio from falling, while allowing for all the other economic effects of fertility decline. Figure 9 compares the path of output per capita in this case to the base case. The figure illustrates the extent to which the classic Malthusian channel operates only over relatively long time horizons. For the first 35 years of the simulation, the path of income per capita when the Malthus effect is suppressed looks only slightly different than when the effect is present (for the first 15 of these years, this is mechanically true because the ratio of land to labor is the same across the baseline and alternative scenarios). In the longer run, however, the effect of reduced congestion of the fixed factor becomes prominent – at an 80-year horizon, income per capita is only 11.1 percent above baseline with the effect suppressed, versus 15.1 percent above baseline with the effect present.

Figure 9. The effect of the land-labor ratio on income per capita.

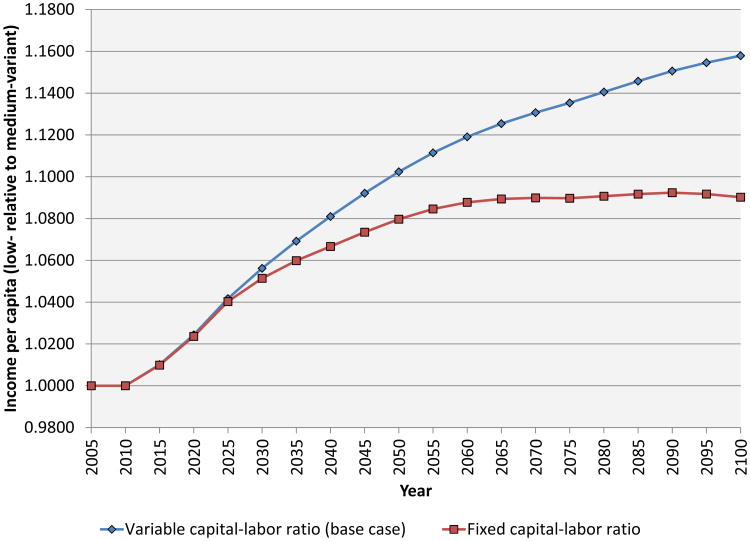
We conduct a similar exercise to look at the importance of the capital-shallowing channel. Specifically, we examine the case in which the level of physical capital per worker is the same in the alternative scenario as it is in the baseline scenario. The result is shown in Figure 10. As with the Malthus effect, for the first 15 years of the simulation, suppressing the Solow effect makes no difference to the level of income per capita because the number of workers does not differ between the baseline and alternative scenarios. At year 50, output per capita is 8.8 percent above baseline when the Solow effect is suppressed, compared to 11.9 percent above baseline when the Solow effect is present.

Figure 10. The effect of the capital-labor ratio on income per capita.

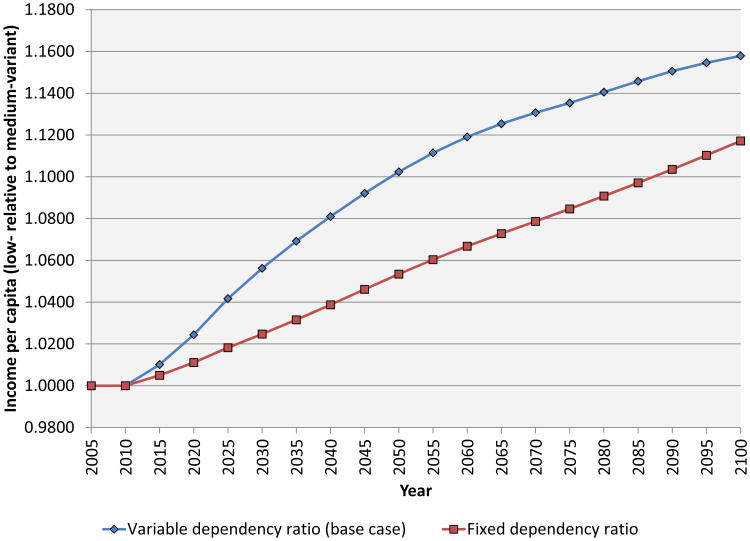
Figure 11 shows the dependency effect, comparing the base case to the case where the dependency ratio in the alternative scenario is fixed to remain the same as in the baseline scenario. Here, not surprisingly, the phase-in of the effect is almost immediate. Fifteen years after the beginning of the simulation, income per capita is only 1.8 percent above baseline when the dependency effect is suppressed, versus 4.2 percent above baseline when the effect is present. By year 50, the increase in income per capita is 5.2 percentage points higher in the base case than in the case where the dependency effect is suppressed. From this point onward, the difference between the two paths appears roughly constant.

Figure 11. The effect of the dependency ratio on income per capita.

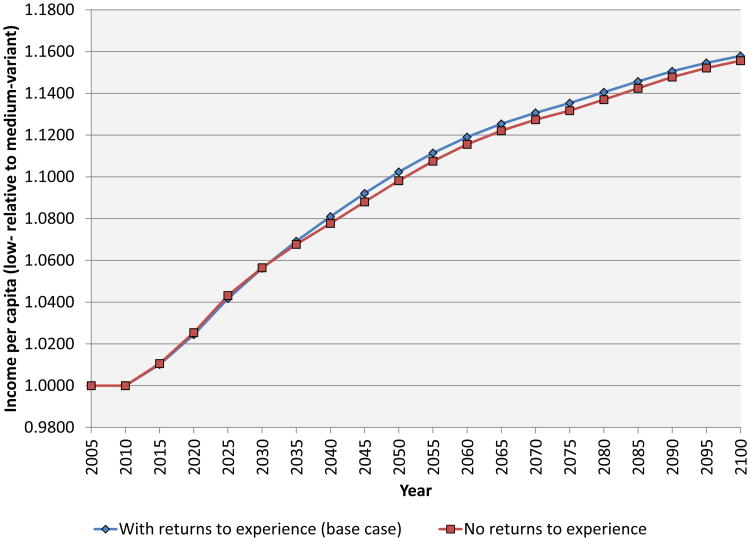
Figure 12 looks at the experience channel. We compare the base case to the case where the experience effect is shut down (by assuming that the return to experience is zero). As the figure shows, the experience effect is not of great import. For example, at a 50 year horizon, the increase in output per capita is 0.4 percentage points lower when the experience effect is suppressed than in the base case. The reason this effect is so small may be that, in the alternative scenario in our simulation, the labor force continues to remains relatively young despite the faster reduction in fertility over time. Simulations that looked at more slowly growing populations might find a bigger effect. It is also interesting to note that, in the early periods of the simulation, output per capita is actually slightly higher in the case where there is no experience effect than in the base case. This is because the increase in effective labor (that results from lower fertility in the alternative scenario relative to baseline) is primarily concentrated among young, inexperienced workers.

Figure 12. The effect of returns to experience on income per capita.

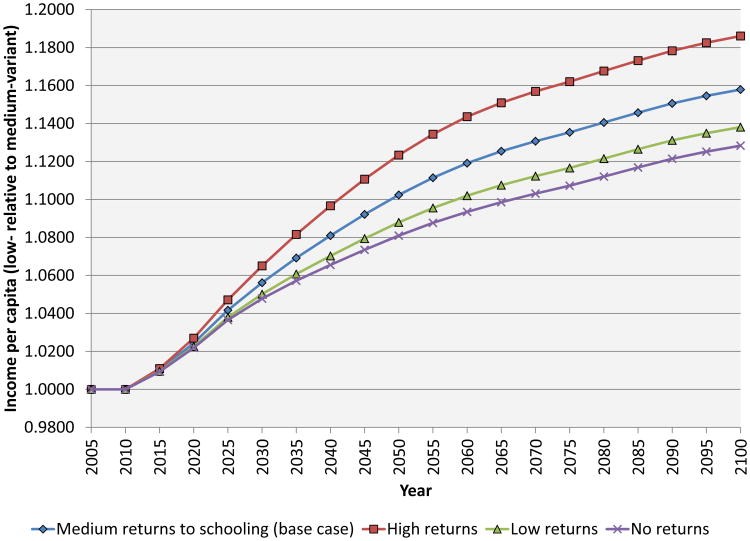
In Figure 13, we vary the amount of extra human capital that is produced by an additional year of schooling. As discussed above, our base case assumption is that the return to education is 10 percent per year of schooling, which is consistent with standard estimates. In the figure, we show alternative projections under three different levels of the return to education: 20 percent and 2.8 percent, which are consistent with the upper bound of estimates from Banerjee and Duflo (2005) and the estimate of Oyelere (2010), respectively, as well as a return of zero, which shuts down this particular channel completely. The figure shows that schooling plays an appreciable role in determining the economic effects from reduced fertility. At a horizon of 50 years, for example, output per capita is 9.4 percent above baseline in the case where the return to schooling is zero (which is the same as if there were no increase in schooling), versus 11.9 percent higher in the base case. Thus, roughly speaking, schooling accounts for one quarter of the income gain (from lower fertility in the alternative scenario relative to baseline) at this time horizon.

Figure 13. The effect of returns to schooling on income per capita.

As would be expected, the effect of higher schooling due to lower fertility phases in as the cohorts that received the additional schooling enter the labor force and replace those that did not. Thus, for the first 15 years of the simulation this channel contributes little to higher income.

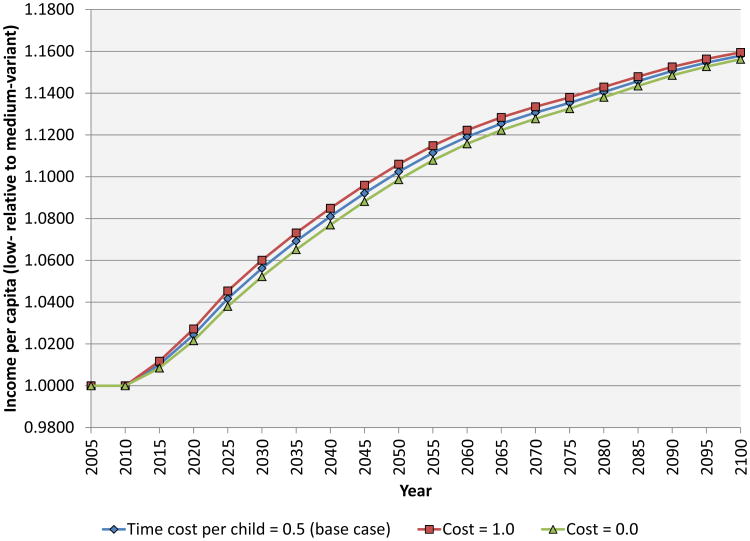
Figure 14 examines the childcare channel. We consider variations in the parameter reflecting the time cost of a marginal child. Specifically, we compare the path of income per capita using our base case assumption of a cost per marginal child of 0.5 years (of labor market input) to alternatives of one and zero. The channel turns out to be rather weak. At a horizon of 15 years, for example, income per capita is 4.2 percent above baseline when the marginal cost of a child is at its base case value of 0.5, versus 4.5 percent above baseline when the marginal cost of a child is one, and 3.8 percent above baseline when the marginal cost of a child is zero.

Figure 14. The effect of reduced childcare on income per capita.

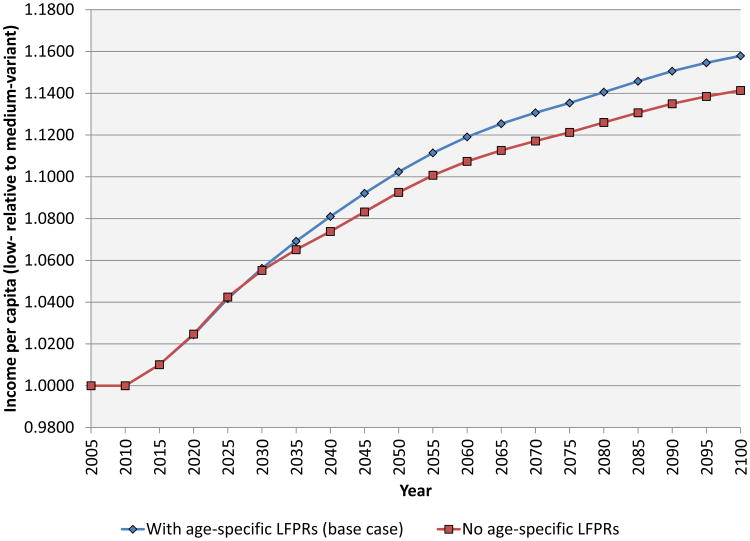
Finally, Figure 15 shows the life-cycle labor supply effect. We compare the base case parameterization of our model to the case where labor force participation rates are constant across age groups. Like the experience channel, the life-cycle labor supply channel has a relatively modest effect on income per capita. After a horizon of 50 years, income per capita is only 1.2 percentage points lower without the life-cycle labor supply effect than in the base case. This channel is also similar to the experience channel in that, in the short run, output per capita is slightly higher without the life-cycle labor supply effect. Again, this is because the increase in labor supply (from lower fertility in the alternative scenario relative to baseline) is initially concentrated among younger workers with lower labor force participation rates.

Figure 15. The effect of age-specific labor force participation on income per capita.

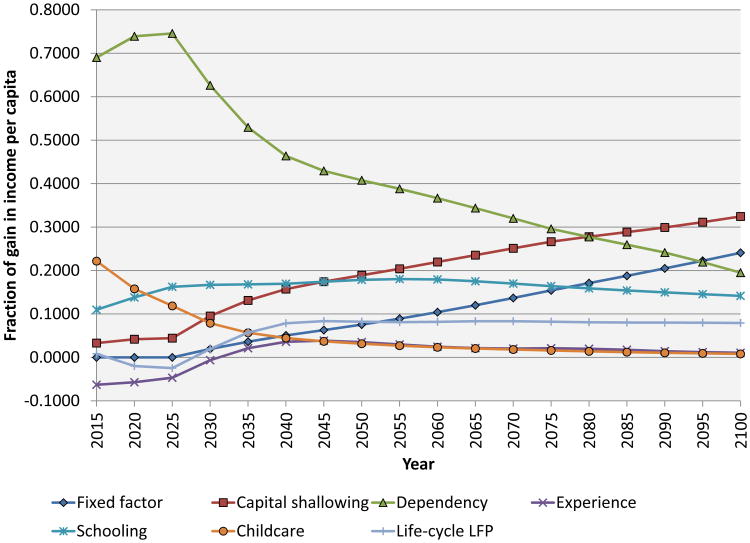
5.2 Decomposition of channels

Figure 16 presents a full decomposition of the fraction of the gain in income per capita at each point in time that is due to the different channels we study. Because of interactions among the different channels, the individual channel effects that we study above do not sum to the total effect of a decline in fertility on income per capita. To do a decomposition of the fraction of the gain in income per capita that is due to each channel, we thus proceed as follows. As above, we calculate the importance of individual channels by comparing the level of income per capita in each year in our base case projection to the level of income per capita when the channel is suppressed. For each year, we then add up these individual effects to get a proxy for the total effect that ignores interactions. Finally, we divide the individual effects by the proxy (for the total) to produce a share of the total income gain due to each effect at each time horizon.

Figure 16. Decomposition of the gain in income per capita by channel.

The figure shows that the dependency effect is by far the dominant channel in the short run, explaining roughly 70 percent of the income gain in the first 15 years of the simulation, and only falling below 40 percent of the total after 45 years. The childcare effect, which is conceptually very similar to the dependency effect, has a somewhat comparable trajectory, although at a much lower level. At a horizon of 50 years, the four dominant effects are dependency (36.7 percent of the total gain), Solow (22.0 percent), schooling (18.0 percent), and Malthus (10.4 percent). At a horizon of 90 years, the same four effects are dominant, but in a different order: Solow (32.4 percent), Malthus (24.1 percent), dependency (19.5 percent), and schooling (14.2 percent).

6 Alternative models of investment

6.1 Age-specific saving rates

Discussions of the demographic dividend from reduced population growth, such as Bloom and Williamson (1998), have often stressed the benefits to national saving from having a large fraction of the population in its working years. In addition to raising income directly by lowering the dependency ratio, the capital accumulation from this extra saving can result in an increase in output per worker. In this section, we explore incorporating such effects into our model.

One way to incorporate a demographic effect on national savings would be to combine data on age-specific saving rates with the evolving age structure of the population in each demographic scenario we examine. Poterba (1994) presents data on age-specific saving rates in a number of developed countries. However, such data are generally not available for developing countries, and the data that do exist show little to no evidence of life-cycle saving behavior. For example, Deaton (1992) calculates household consumption and income over the life cycle in Côte d'Ivoire, finding no clear relationship between age and saving, consumption, or even income. Beyond this lack of data, there is a theoretical problem in looking at age-specific saving rates. Weil (1994) points out that data on age-specific saving does not take into account the externality effects across generations via support of children and the aged, bequests, and other transfers. As the age structure of the population changes, so do these intergenerational flows. To give a simple example, consider a reduction in the number of children aged 0-4 in a population, holding fixed the numbers of people in all other age groups. Holding age-specific saving rates constant (for all age groups that have non-zero income) would then imply that this reduction in the number of children does not have any effect at all on the aggregate saving rate. But in reality, such a reduction would reduce the dependency burden facing working-age adults, resulting in higher consumption, saving, or more likely, both.

An alternative to looking at age-specific saving rates is to look at age-specific income and consumption. Based on data from Soyibo, Olaniyan, and Lawanson (2011), Figure 17 shows the life-cycle patterns of consumption and labor income for Nigeria in 2004. The gap between consumption and labor income at any age is accounted for by transfers from other age groups (either through family or institutions), non-labor income (such as rent on land or capital), and additions to or subtractions from savings. The construction of data like these for a large number of countries has been the goal of the National Transfer Accounts project (Lee and Mason 2011).

Figure 17. The economic life cycle in Nigeria, 2004.

It is apparent from Figure 17 that a change in the population age structure that puts a higher fraction of the population in the mid-life years, where labor income exceeds consumption, will expand society's budget constraint. Under such conditions, it will be possible for there to be a higher level of consumption on average or for savings to rise, if not both. However, it is not immediately clear which of these should happen, or in what proportion.

The piece of data missing from Figure 17 is non-labor income. To calculate this, we start with data on the aggregate national saving rate in Nigeria in 2005, from Heston, Summers, and Aten (2009), which was 8.55 percent. We impute total non-labor income such that, given the consumption and labor income profiles, as well as the age structure of the population, we exactly match this saving rate. That is, defining x₂₀₀₅ as non-labor income per capita in 2005, and c_i and w_i as consumption per capita and labor income per capita, respectively, at age i,

$$0.0855=1-\left[\sum _{i=0}^{100}{N}_{i,2005}{c}_i\right]/[x_{2005}\sum _{i=0}^{100}{N}_{i,2005}+\sum _{i=0}^{100}{N}_{i,2005}{w}_i]$$

In the Nigerian data that we use as a benchmark, the level of x₂₀₀₅ is 30,586 Niara per capita. This implies that non-labor income is 44 percent of total income, which is not inconsistent with our model in which production is Cobb-Douglas and labor's share of national income is 60 percent, capital's share is 30 percent, and land's share is 10 percent.

We can now look more explicitly at how changes in demographic structure affect consumption possibilities. When the age structure of the population changes, labor income per capita shifts, because people at different ages have different levels of labor income. In addition, however, the consumption “needs” of the population also change. Although we do not model this explicitly, we assume that the varying pattern of consumption by age reflects both changing biological needs for consumption over the course of the life cycle and the arrangements by which consumption is divided up among different groups in society. For simplicity, we assume that these relative levels of consumption do not change as the age structure of the population changes, and we call them consumption needs, even though this is not very good terminology. Slower population growth, by reducing the fraction of the population made up of children, puts more people in ages that have higher relative consumption – this effect undoes some of the benefit of having more people earning labor income.

Putting together the change in labor income and the change in consumption needs, we can calculate the demographically-induced increase in available demographically-adjusted income less demographically-adjusted consumption needs relative to a base year of 2005.²¹ We call this term the change in disposable income (ΔDI_t), which is again a slight abuse of terminology.²² That is,

$$\mathrm{\Delta }D{I}_t=[x_t\sum _{i=0}^{100}{N}_{i,t}+\sum _{i=0}^{100}{N}_{i,t}{w}_i-\sum _{i=0}^{100}{N}_{i,t}{c}_i]-[x_{2005}\sum _{i=0}^{100}{N}_{i,2005}+\sum _{i=0}^{100}{N}_{i,2005}{w}_i-\sum _{i=0}^{100}{N}_{i,2005}{c}_i].$$

The final question is how this extra disposable income will be divided between saving and consumption. In a naïve model, one might assume that needs-adjusted consumption remains constant while the additional disposable income all goes into savings. This would indeed give a very large demographic dividend in terms of capital accumulation, but we don't see it as being very sensible because it ignores one of the major reasons why people in their prime working years have consumption lower than earnings, which is that they are transferring resources to people in other age groups. When there are fewer such dependents, there is less need for such transfers, and so working-age adults can afford to consume more. The change in demographics slackens the household budget constraint in a fashion similar to the slackening that would result from higher income. Thus, in our view, rather than assuming fixed age-specific consumption in the face of demographic change, a more reasonable course is to invoke the idea of a marginal propensity to consume (MPC), a standard component of many macroeconomic models.²³

For such a commonly discussed parameter, there are very few available estimates of the MPC. Using time series data for the United States, Feldstein (2009) estimates the MPC out of real disposable income to be 0.70. In the Federal Reserve Board model for the United States in the mid 1990s, the MPC out of labor income was 0.51 (Brayton and Tinsley 1996). Paxson (1992) looks at income variations caused by weather variability among farmers in Thailand. She finds an MPC ranging between 0.17 and 0.27. Kan, Peng, and Wang (2011) look at the consumption response to a voucher program in Taiwan, and they calculate an MPC of 0.33. In considering these estimates, it should be noted that they are all concerned with the MPC out of short-run variation in income. The usual presumption is that the MPC to consume out of short-run income is lower than the propensity to consume out of longer- term changes in income. The demographic changes that we are considering are relatively long-term in nature, and so a higher MPC is presumably appropriate. Indeed, if we are considering a long run of a decade or more, the right assumption might be that the MPC is equal to the average propensity to consume, that is, one minus the saving rate. This is the assumption that is used in the previous part of the paper in which the saving rate is constant.

Given that we have very little idea what the right value of the MPC to use is, we simply present our estimates for the full range of values, all the way from zero to one. Figure 18 shows the impact of the shifting age structure on the aggregate saving rate under different values for the MPC. Saving is shown in the low-fertility relative to the medium-fertility scenario. In the case where the MPC is zero, the saving rate is 21.1 percent higher in the alternative scenario than in the baseline 30 years after the beginning of the simulation. Even an MPC of 0.5 leads to saving being 13.3 percent higher in the alternative than in the baseline scenario at a horizon of 30 years.²⁴ It is interesting to note in the figure that, unlike the analysis of Bloom and Williamson (1998), the demographic window of high savings does not shut down after a few decades. The reason is that, in the demographic experiment we are considering, fertility starts at such a high level that the faster decline in fertility in the alternative scenario results in only a very minor increase in old-age dependency relative to the baseline scenario.

Figure 18. The effect of age-specific saving on the aggregate saving rate.

Figure 19 looks at the time paths of income per capita under the same set of assumptions about the MPC. In the case where the MPC is equal to zero, income per capita in the low-fertility scenario is 9.6 percent higher at a horizon of 20 years and 20.0 percent higher at a horizon of 50 years than in the baseline. By contrast, in our base case parameterization with a fixed saving rate, output is 5.6 percent higher (relative to baseline) at 20 years and 11.9 percent higher at 50 years. In other words, for this extreme parameterization, there is an enormous effect of saving on income. If the MPC is one (which also strikes us as unreasonable), income rises by 4.7 percent (relative to baseline) after 20 years, and by 8.8 percent after 50 years – that is, by less than in our base case of a constant saving rate. The increase in income generated by the life-cycle saving effect is roughly linear in the MPC. Overall, our analysis of age-specific savings does not produce very concrete answers, but we are hopeful that the framework we have set up here will be helpful in clarifying future analyses of this issue.

Figure 19. The effect of age-specific saving on income per capita.

6.2 International capital flows

An important part of our results is driven by the assumption of Solovian saving. It is possible to adjust this assumption in a straightforward way even without building a life-cycle savings model, simply by assuming that the economy is open to international capital flows that equalize the return to capital around the world, at least up to a country fixed effect.²⁵

Figures 20 (capital per worker) and 21 (income per capita) show that allowing for capital flows (assuming a fixed world interest rate) has relatively little effect on the behavior of income, although it does have a larger effect on the capital stock.²⁶ With an open economy, the capital stock initially rises somewhat faster (in response to lower fertility in the alternative scenario relative to baseline) because of the increase in labor supply from reduced childcare, as well as the increase in human capital from schooling as school-age cohorts at the time of the fertility decline start joining the labor force, both of which produce a nascent rise in the marginal product of capital. By contrast, in the base case, capital initially accumulates rather slowly as income rises. Thus, capital per worker is higher in the open economy case than in the base case for the first 25 years. In the long run, however, capital per worker is higher in the base case than in the open economy case because slower labor force growth drives down the marginal product of capital, which in the open economy leads to a capital outflow. The difference in output per capita between the base case of Solow savings and the case with perfectly open capital markets is surprisingly small – never more than a couple of percentage points in the first 50 years of the simulation.

Figure 20. The effect of international capital flows on capital per worker.

Figure 21. The effect of international capital flows on income per capita.

7 The role of land in the production function

Our base case treatment of land involved assuming both a particular functional form (Cobb-Douglas, in other words, unit elasticity of substitution) and a particular exponent on land in the production function. In this section, we relax both of these assumptions. We adopt a CES production function in which we can specify an elasticity of substitution between a capital-labor-technology composite factor, on the one hand, and the fixed factor on the other,

$$Y_t={[(1-a){(A_t{K}_t^{\alpha }{H}_t^{1-\alpha })}^{\frac{\sigma -1}{\sigma }}+a{X}^{\frac{\sigma -1}{\sigma }}]}^{\frac{\sigma }{\sigma -1}},$$

where σ is the elasticity of substitution. If the fixed factor is paid its marginal product, then its share of national income at time t, ϕ_t, will be

$${\varphi }_t=\frac{a{X}^{\frac{\sigma -1}{\sigma }}}{(1-a){(A_t{K}_t^{\alpha }{H}_t^{1-\alpha })}^{\frac{\sigma -1}{\sigma }}+a{X}^{\frac{\sigma -1}{\sigma }}}.$$

If the elasticity of substitution is not unity, the fixed factor's share of national income will vary as physical capital and effective labor are accumulated, population grows, and technology improves. For example, if σ > 1, so that other factors can more easily substitute for the fixed factor, then the fixed factor's share of income will decline over time. Thus, one should be able to learn something about the elasticity of substitution, at least in a gross sense, by observing how the income share of the fixed factor changes over time, as A, K, and H accumulate.

Figure 22 shows data for doing such an analysis. The horizontal axis measures output per worker. The data on the vertical axis is an estimate of the income share of non-reproducible factors of production, from Caselli and Feyrer (2007).²⁷ The Caselli and Feyrer (2007) estimates are in turn built on data from the World Bank (2005) on the values of physical capital, crop land, pasture land, and subsoil resources. As the figure shows, the share of natural resources in total income in many developing countries is often in excess of 25 percent.

Figure 22. Fixed-factor income share and output per worker across countries.

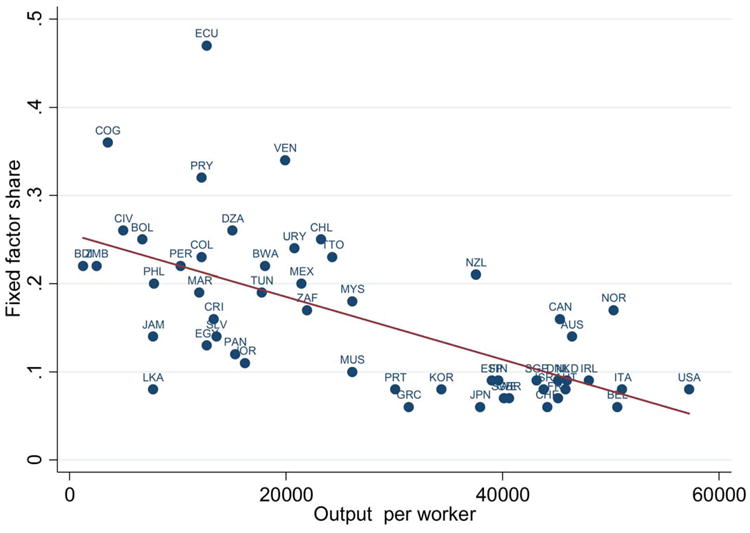
Using data like this, Weil and Wilde (2009) present estimates of the elasticity of substitution between natural resources and other inputs into production. Their estimate is in the neighborhood of two, which is consistent with the earlier estimate of Nordhaus and Tobin (1972) that is based on US data. However, all of these estimates are fairly imprecise. In addition, the elasticity of substitution will vary with the resource in question. For example, in developing countries with a large natural resource sector that is effectively detached from the rest of the economy (for example, offshore oil wells), the elasticity of substitution between natural resources and other inputs is infinity.

The CES production function can be re-written to show how total output compares at two points in time, as the quantities of physical capital and effective labor change along with the level of productivity. Specifically,

$$\frac{Y_s}{Y_t}={[(1-{\varphi }_t){\left(\frac{A_s{K}_s^{\alpha }{H}_s^{1-\alpha }}{A_t{K}_t^{\alpha }{H}_t^{1-\alpha }}\right)}^{\frac{\sigma -1}{\sigma }}+{\varphi }_t]}^{\frac{\sigma }{\sigma -1}}$$

To do this comparison, one does not need to know the quantity of the fixed factor X or the parameter a, but only the income share of the fixed factor at a point in time, the elasticity of substitution, and the growth of the inputs into production, all of which we were already measuring. We use a value of $\alpha =\frac{1}{3}$ which is consistent with our earlier parameterization of giving capital an exponent of 0.3 when the land share is 10 percent.

Figure 23 shows how the results of the model are altered when the income share of land is increased from 10 percent to 20 and 30 percent. There are significant differences between the three simulations in GDP per capita at long horizons. In the long run, as expected, a higher land share means that the gains from reduced population growth are larger. Surprisingly, however, for the first 50 years of the simulation, there is little difference in the income gain in simulations using different land shares. The explanation is that there is an offsetting factor: the larger is the land share, the less valuable are the initial gains in human capital and labor supply (due to increased schooling and reduced childcare) that result from slower population growth.

Figure 23. The effect of land share on income per capita.

Figure 24 shows how varying the elasticity parameter σ influences our findings by comparing our base case projection with results obtained under σ = 0:75, where land is more complementary than in the Cobb-Douglas case, and under σ = 2, where land is more substitutable. Intuitively, the greater this substitutability, the less severe will be the consequences of increased population pressure on the fixed factor, and thus the smaller will be the income gains from lower fertility. At very long time horizons, this prediction is borne out, but as in the experiment where we vary the land share, differences among the projections in the first 50 years of the simulation are minimal.

Figure 24. The effect of land substitutability on income per capita.

8 Conclusion

For more than half a century, economists and demographers have wrestled with the question of how much reducing fertility in a developing country would raise income per capita. Unfortunately, there is little agreement on the answer. A fair segment of the scholarly community views reduced fertility as an important factor contributing to economic development. Some go further and argue that reduced population growth is a necessary condition for achieving other development aims, such as the Millennium Development Goals. However, there is another reasonably large contingent of scholars who view fertility reduction as a consequence, rather than a cause, of other underlying changes that produce development. Under this view, a reduction in fertility would not, by itself, contribute significantly to economic growth. Beyond this disagreement, we detect a general cynicism regarding the ability of social scientists to say anything useful about the economic effects of fertility – the issue is viewed as political rather than scientific, and conclusions from empirical analyses are often assumed to reflect the pre-existing views of authors.

In this paper, we have tried to re-boot the discussion of how fertility affects growth along more pragmatic and quantitative lines. We have done our best to avoid both the methodological failings and opacity that we see in much of the previous literature. In particular, we argue that the currently fashionable approach of looking econometrically at aggregate data on fertility and economic outcomes (for example, in a cross-country regression) is fatally flawed in its ability to identify causal relationships. Fertility is an endogenous variable, so describing how it covaries with economic development is very different than being able to say what the causal link between the two is. Instead, our chosen tool is a simulation model, an approach that goes all the way back to the beginning of this literature. In the simulation approach, the different channels by which changes in fertility affect economic outcomes can be individually specified, and identification can be achieved by looking at microeconomic evidence. In addition to this microeconomic evidence, we bring to bear data on demographic structure, measures of the natural resource share in national income, and standard components of quantitative macroeconomic theory. Our simulation exercise is not meant to deliver the best possible forecast of future GDP, but rather (as is true in any experimental approach) it takes a ceteris paribus approach, comparing the outcomes in a country that follows a low fertility path with an otherwise identical country following a higher fertility path.

We have shown that a simulation model need not be a black box, in which the authors' prejudices can be comfortably hidden. We deal with the problem of opacity by fully laying out the model's structure, and showing robustness to changes in parameters or elimination of different channels. Further, to a far greater extent than previous authors, we have grounded the different structural channels in our model on a base of well-specified microeconomic studies. In this sense, we have incorporated a good deal of literature that is relevant to the issue of how fertility affects economic growth but does not address that question directly. Finally, we arm the reader with the ultimate tool for penetrating the black box by providing a fully working version of our model, in which the user can shut down channels, change parameters, and alter the demographic scenarios with ease.

An additional advantage of our methodological approach is that we are able to look not only at the aggregate effect of fertility reduction on income, but also at the different channels through which this effect operates. This allows us to link our result back to the underlying theoretical channels that are discussed in the literature. To be specific, we examine eight different channels: congestion of fixed factors (Malthus effect), capital shallowing (Solow effect), changes in the ratio of workers to dependents (dependency effect), changes in the average experience of the population (experience effect), changes in the saving rate (life-cycle saving effect), changes in the labor supply of working-age adults (life-cycle labor supply and childcare effects), and changes in the average level of schooling (child-quality effect). Each channel is separately modeled and parameterized.

A final advantage of our approach is that we have posed the question of how fertility affects growth in the context of examining the difference between outcomes resulting from two fully-specified demographic scenarios. One of the many issues that cloud the current discussion of the economic effects of fertility reduction is that different authors focus on different fertility reductions. This makes it hard to see the extent to which their predictions conform with one another. In this paper, we have shown how the findings of our simulation model could be compared directly to the estimates from a cross-country regression study. We think that this sort of approach should always be taken in evaluating regression coefficients; and similarly that simulation models should be compared by using the same demographic scenarios.

We apply our simulation model to data from Nigeria. The reduction in fertility that we consider is the difference between the medium- and low-fertility variants of the UN's (2010) population forecasts. This is a difference in the TFR of 0.5, phased in over a period of 15 years, relative to a baseline of declining fertility. This particular reduction seems reasonable as something that could result from some exogenous intervention. For a base case set of parameters, we find that this reduction in fertility will raise output per capita by 5.6 percent at a horizon of 20 years, and by 11.9 percent at a horizon of 50 years. The effects that we find are roughly linear in the size of the fertility reduction considered – a reduction in the TFR by one leads to roughly twice as big an increase in output per capita. The dependency effect, and to a lesser extent the labor supply effects, are the dominant channels by which reduced fertility affects income per capita in the short run (in the first quarter century after a fertility reduction). At a horizon of 50 years, the four dominant effects are dependency (36.7 percent of the total), Solow (22.0 percent), schooling (18 percent) and Malthus (10.4 percent). In the very long run, the Malthus effect becomes the dominant channel, followed in importance by the Solow effect.

Is the effect of fertility reduction that we find large? To some extent, the answer to this question depends on what benchmark one is using. NRC (1986) frames the question as whether a reduction in fertility would be to “vault a typical country into the ranks of the developed,” and concludes that the answer is definitely “no.” The results presented here are certainly consistent with this view. But the belief that fertility reduction alone could be the key to development probably has few adherents today anyway. Authors such as Das Gupta, Bongaarts, and Cleland (2011) and Sindig (2009) use terms like “important secondary role” and “necessary condition” in referring to the effect of slowing population growth on development. Although they do not quantify these terms, our sense is that the results we find are smaller than what these authors believe. For example, the effect on GDP per capita that we find, 11.9 percent over 50 years resulting from a TFR reduction of 0.5, amounts to a change in the growth rate of only about a quarter of a percent per year. By contrast, between 1990 and 2009, GDP per capita in Nigeria grew at 2.9 percent per year (although during the two decades prior to that it actually fell slightly).

Another useful benchmark against which one can compare our results is the findings of cross-country regressions in which the growth rate of income per capita is the dependent variable and measures of demographic change (such as the growth rate of the working-age fraction of the population) are on the right hand side. Regressions like these are widely used in policy-oriented discussions of the effects of demographic change. In Section 5 of this paper, we go through the exercise of applying the findings in one such study, Bloom and Canning (2008), to the demographic scenarios that we analyze. We find that our estimate of the economic impact of fertility reduction is roughly twice as large as theirs.

Yet another way to benchmark our results is to look directly at poverty. This seems natural, given that we are focusing our analysis on poor countries, most of which will likely still be poor several decades hence. In 2010, the poverty rate in Nigeria was 68 percent. The World Bank (2000) estimates the elasticity of poverty rates with respect to average income to be in the neighborhood of two. Thus, the increase of 5.6 percent in income per capita would reduce the poverty rate by approximately 7.5 percentage points. This seems to us to be a significant magnitude. Of course, as we have stressed repeatedly, concluding that a given fertility reduction would have an economically significant effect on income per capita is very different from concluding that engineering such a fertility reduction would be a good thing. To address the latter question, one would have to know the costs, both financial and in terms of welfare, of lowering fertility, and one would also have to have some way of assessing the utility consequences of children not being born.

Finally, in discussing the magnitude of the results that we present, we want to return to the issue of methodology. We think that a key advantage of the simulation model we have presented is its transparency. If one believes that the effects of population on economic development are larger than what we have estimated, then there has to be a way to alter our model to produce that larger effect, either by changing the parameters or by introducing new channels that we have left out. We think that conducting the debate in terms of specific parameters and channels is likely to be far more enlightening than debating the overall effect of fertility changes.