Using propensity scores in difference-in-differences models to estimate the effects of a policy change

Abstract

Difference-in-difference (DD) methods are a common strategy for evaluating the effects of policies or programs that are instituted at a particular point in time, such as the implementation of a new law. The DD method compares changes over time in a group unaffected by the policy intervention to the changes over time in a group affected by the policy intervention, and attributes the “difference-in-differences” to the effect of the policy. DD methods provide unbiased effect estimates if the trend over time would have been the same between the intervention and comparison groups in the absence of the intervention. However, a concern with DD models is that the program and intervention groups may differ in ways that would affect their trends over time, or their compositions may change over time. Propensity score methods are commonly used to handle this type of confounding in other non-experimental studies, but the particular considerations when using them in the context of a DD model have not been well investigated. In this paper, we describe the use of propensity scores in conjunction with DD models, in particular investigating a propensity score weighting strategy that weights the four groups (defined by time and intervention status) to be balanced on a set of characteristics. We discuss the conceptual issues associated with this approach, including the need for caution when selecting variables to include in the propensity score model, particularly given the multiple time point nature of the analysis. We illustrate the ideas and method with an application estimating the effects of a new payment and delivery system innovation (an accountable care organization model called the “Alternative Quality Contract” (AQC) implemented by Blue Cross Blue Shield of Massachusetts) on health plan enrollee out-of-pocket mental health service expenditures. We find no evidence that the AQC affected out-of-pocket mental health service expenditures of enrollees.

Policymakers and program administrators are often interested in the effects of interventions such as new provider payment mechanisms, policies such as mental health parity, and clinical interventions such as new disease screening tools. In many health services settings, randomization to these programs or policies is unfeasible, and researchers and policymakers are left with the need to use non-experimental studies to estimate the effects of those programs or policies. The fundamental challenge in such non-experimental studies is selection bias -- the individuals or groups experiencing the program or policy of interest may be different from those not exposed to it. For example, physician practices that choose to participate in a new payment system may be quite different (and serve patients quite different) from those that do not participate.

A common non-experimental design used to estimate the effects of policies or programs instituted at a particular point in time is a “difference in differences” (DD) model. DD models compare changes over time in a group unaffected by the policy change to changes over time in a group affected by the policy change, and attributes the “difference-in-differences” to the effect of the policy. DD methods provide unbiased effect estimates if the trend over time would have been the same between the treatment (intervention) and comparison groups in the absence of the intervention. Because of the existence of information on temporal trends from the comparison group, DD methods are sometimes preferred over interrupted time series designs that do not necessarily have a comparison group. However, a concern with DD models is that the program and intervention groups may differ in ways that are related to their trends over time, or their compositions may change over time. Propensity score methods are another non-experimental study design that is commonly used to handle this type of confounding in other non-experimental studies. However, the particular considerations when using propensity scores in the context of a DD model have not been well investigated. As detailed below, a particular complication in applying propensity score methods in the context of DD models is that there are no longer just two groups (treatment and comparison); there are essentially now four groups: treatment pre, treatment post, comparison pre, and comparison post. This paper illustrates the use of propensity score weighting to ensure the comparability of all four of these groups. The method is particularly relevant for DD settings where the composition of each group may change over time, such as if the patient population served by physician practices changes systematically across time, or if the composition of physician groups changes differentially over time due to turnover or consolidation.

This work is motivated by an evaluation of a new payment and delivery system innovation, in particular an accountable care organization model called the “Alternative Quality Contract” (AQC) implemented by Blue Cross Blue Shield of Massachusetts (BCBSMA) in 2009. The AQC was an initiative aimed at reducing spending and improving quality by paying providers a global budget and bonuses for meeting quality benchmarks; participation in the AQC was voluntary. Song et al. (2012) found that the AQC led to lower medical spending and improved performance on quality measures in the first two years of implementation. The current paper is concerned with the effects of the AQC on mental health care spending, and in particular, out-of-pocket mental health expenditures. Companion papers detail the substantive results (work in progress); the current paper is meant to illustrate the DD and propensity score methods, not to provide effect estimates of the AQC. We first describe the details of the approach and proposed method, followed by a simulation study to illustrate the ideas, and finally application of the methods to estimating the effects of the AQC.

Details of the approach

Estimand of interest

We first introduce some notation and clarify the estimand of interest. Informally, we are interested in the effect of an intervention or program, the “treatment” (in our motivating case study, the AQC), on an outcome (in the AQC example, out-of-pocket mental health spending) in a “post” period (following implementation of the intervention of interest), comparing the (potential) outcome if a group of individuals were subject to the AQC to the (potential) outcomes we would see if that same group of individuals were not subject to the AQC.

Formally, adapting notation from Abadie (2005), denote the potential outcome under treatment (exposure E) for individual i at time p (pre vs. post) as Y^E(i, p), with p=0,1 and E=0,1. To be specific, Y⁰(i,1) denotes the outcome that would be observed for individual i at time 1 (“post”) if she does not receive the treatment (exposure); Y¹(i,1) denotes her outcome at time 1 if she does receive the treatment. Since at time p=0 no treatment has yet been applied, Y⁰(i, 0) and Y¹(i, 0) are essentially pre-treatment covariates and generally one would assume that Y⁰(i, 0)=Y¹(i, 0); that an individual’s pre-treatment “outcome” is not affected by their subsequent treatment assignment. We use the outcome (Y) notation for these values to reflect their status as a “special” covariate that reflects the baseline (pre-period) value of the outcome of interest, and because of convention in the DD literature. Moving forward, for simplicity, we drop the individual argument i and write the potential outcomes as Y^E(p). Causal inference is interested in comparing outcomes under the treatment and comparison conditions, such as Y¹(1)−Y⁰(1). We refine this further below, but for now assume that interest is in estimating the average treatment effect: Δ=E[Y¹(1)−Y⁰(1)]. What has been called “the fundamental problem of causal inference” (Holland, 1986) is that we only observe one of these two potential outcomes for each individual. For people with E_i=1 we observe their potential outcome under treatment; for people with E_i=0 we observe their potential outcome under control.

Standard Difference-in-Differences Designs

In its simplest form, the DD design can be illustrated in a 2×2 table, with the observed data illustrated in Table I. The DD estimate is the quantity in the lower right hand box, which can be thought of either as the change in the difference between groups across time, or the change across time in the difference between groups. The intuition for the DD estimate can be explained by thinking of the pre-post difference in outcomes for the program group as including both the effect of the AQC (what we want) but also any secular time trends from pre to post (what we don’t want). However, the pre-post difference in the comparison (non-AQC) group gives us an estimate of those secular trends, which we can subtract off from the time trend observed in the treatment group comparison to isolate the effect of the AQC, removing (subtracting) the secular time trend. Shadish, Cook, and Campbell (2002) provide a nice introduction to the DD design and its properties. Classic examples employing a DD design include Card and Krueger (1994) and Card (1990).

Table I.

Illustrative DD design (observed data)

	Treatment Group (AQC)	Comparison Group (non-AQC)	Difference
Pre	ӯ1,pre	ӯ0,pre	ӯ1,pre−ӯ0,pre
Post	ӯ1,post	ӯ0,post	ӯ1,post−ӯ0,post
Change	ӯ1,post−ӯ1,pre	ӯ0,post−ӯ0,pre	Δ̂ = (ӯ1,post−ӯ1,pre)−(ӯ0,post−ӯ0,pre) = (ӯ1,pre−ӯ0,pre)−(ӯ1,post−ӯ0,post)

For clarity later, define a variable, Group, as follows, which relates to the four cells in Table I:

$$\mathit{\text{Group}}=\{\begin{array}{c}1\mathit{\text{if}}E=1\mathit{\text{and}}P=0\hfill \\ 2\mathit{\text{if}}E=1\mathit{\text{and}}P=1\hfill \\ 3\mathit{\text{if}}E=0\mathit{\text{and}}P=0\hfill \\ 4\mathit{\text{if}}E=0\mathit{\text{and}}P=1\hfill \end{array}$$

To obtain standard errors and significance levels for the DD estimate, a parametric model is usually fit using a “long” dataset with each observation reflecting a person at a particular time point, with the model of the general form:

$$\mathrm{f}({\mathrm{Y}}_{\text{it}})=\mathrm{\alpha }+\mathrm{\beta }{\mathrm{E}}_{\mathrm{i}}+\mathrm{\gamma }{\mathrm{P}}_{\mathrm{t}}+\mathrm{\delta }{\mathrm{E}}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{t}}+{\mathrm{\epsilon }}_{\text{it}}$$ (1)

where Y_it is the value of the outcome observed for person i at time t, E_i is an indicator of person i being in the Exposed (treatment) group (vs. comparison group) and P reflects the time period (pre (0) vs. post (1)). The parameter δ is the DD estimator; the point estimate of δ from this model is equivalent to a non-parametric approach that takes the difference in the changes over time between the two groups (the change in differences in Table I, Δ̂). This model can be adapted for non-continuous outcomes or correlated error terms; for illustration purposes we focus on the simple continuous case here.

In its basic form, the DD model relies on an assumption that in the absence of the program or policy of interest, the treatment and comparison groups would have had the same trends across time. In other words, that the comparison group serves as a valid reflection of the trends over time that the treatment group would have experienced had they not been exposed to the program of interest. Using the potential outcome notation from above this assumption can be expressed as:

$$\mathrm{E}[{\mathrm{Y}}^0(1)-{\mathrm{Y}}^0(0)|\mathrm{E}=1]=\mathrm{E}[{\mathrm{Y}}^0(1)-{\mathrm{Y}}^0(0)|\mathrm{E}=0]$$ (A-1)

As stated above, Y⁰(0) is the pre-treatment value of the outcome (i.e., it is a baseline covariate that happens to be the same measure as the outcome of interest, just measured at the earlier time point), and thus its value is observed for everyone: those in the treatment group and in the control group (E=0 and E=1). In addition, Y⁰(1) is observed for the control group. In contrast, however, Y⁰(1) is an unobserved counterfactual for individuals in the treatment group (E=1). This assumption represented by Equation (2) is thus not testable. However, as discussed below, the assumption can be made more reasonable through careful selection of the comparison group, and appropriate adjustment for covariates.

There are two types of selection bias that are of concern in DD studies: across time and across group. Selection bias across time occurs when the groups themselves change in composition across time. In fact, standard DD estimation as well as a newer non-parametric method called “changes-in-changes” (Athey & Imbens, 2006) rely on the group composition not systematically changing. However, changes in group composition are common with data that comes from repeated cross sections rather than longitudinal data on individuals. For example, in the AQC study, the patients being served by a particular physician practice may change, patients may switch physicians and thereby between treatment and control groups, or individuals may enroll or disenroll from their BCBSMA health plan entirely. Selection bias across group occurs when the groups themselves differ, for example, if the types of providers that choose to enter the AQC are different from and/or serve different patients than providers who do not. Selection bias across groups can also occur if providers consolidate across time, both potentially changing practice patterns as well as price negotiation leverage with providers. In DD contexts, the crucial aspect is if the groups differ with respect to variables that are also related to their trends across time (Abadie, 2005; Imbens & Wooldridge, 2009). That is, it is okay if the groups differ in their levels of the outcomes in the pre period (e.g., if the AQC and non-AQC groups have different levels of mental health out-of-pocket spending in the pre period). A problem would arise if their spending trends over time – in the absence of the AQC – were different, as this would violate Assumption A-1.

Current approaches for minimizing these selection biases in DD models are somewhat limited. Straightforward adjustment for covariates in the DD regression model does not generally work, although some approaches have been proposed (e.g., Abadie, 2005). To limit the potential for selection bias across groups, researchers try to be clever about selecting a comparison group that is likely to reflect the unobserved trends that the program group would have experienced, but this selection is often ad hoc. In the interrupted time series setting (which can be thought of as a DD model but with more time points), an approach has been developed that weights the comparison group to make the baseline trends similar in the program group and the (weighted) comparison group (Linden & Adams, 2011). However, that approach is not feasible in the standard DD setting with only one pre-period time point, and does not account for changes in group composition over time.

To limit selection bias due to changes in group composition across time, researchers can sometimes restrict the sample in a way that avoids this type of selection bias. In the motivating example, the sample could be restricted to individuals who are continuously enrolled for two years, i.e., present in both the “pre” and “post” years. This is not always feasible, however, and may result in large power losses or a loss of generalizability if there is high turnover from year to year. This is true in particular in studies of rare outcomes or when interest is in the effects of a program on a small subgroup of individuals, such as individuals receiving substance abuse treatment or those with serious mental illness. Another example where restriction to continuously enrolled individuals is problematic is when studying treatments or interventions that change substantially across different ages, such as studying services for children with autism. Restricting to, say a four-year continuously enrolled sample would mean, for example, that if the children were on average 10 years old at the beginning of the study period, they would be 14 years old on average at the end. This change in the age distribution over time may lead to difficulties in interpreting any changes in services received over that same time period as being due to any policy change versus simply due to the aging of the sample.

Propensity score methods

Propensity score methods are commonly used to minimize selection bias in non-experimental studies. First introduced by Rosenbaum and Rubin (1983), propensity scores are used to “balance” program and comparison groups on a set of baseline characteristics; i.e., to make the groups as similar as possible with respect to those observed baseline characteristics. The propensity score itself is defined as the probability of receiving the program of interest as a function of those covariates, and is commonly estimated using logistic regression. Common ways of using the propensity score to balance the groups include matching, weighting, and subclassification (Stuart, 2010). There are arguably three main benefits of using the propensity score. First, using these propensity score approaches reduces extrapolation and subsequent dependence on the outcome model specification (Ho et al., 2007), leading to more robust inferences. Second, the propensity scores condense the full set of covariates (potentially a large number) into a scalar summary, making those balancing approaches more feasible. And finally, the propensity score process is done without use of the outcome variable, thereby separating the “design” of the study from the “analysis,” and thus reducing the potential for bias (Rosenbaum, 2010; Rubin, 2007).

Propensity score methods have traditionally been used with two treatment groups, but there has been some work extending to multiple groups. Imai and van Dyk (2004) and Imbens (2000) formalized the “generalized propensity score” for multilevel treatments and McCaffrey et al. (2013) extended weighting methods to multiple treatment groups.

Integration of propensity scores and DD models

We propose the use of multiple group propensity score weighting in the context of parametric DD models. In particular, we propose the use of weighted regression models, where the estimated effects are obtained using a parametric model such as in Equation (1), but with a weighted regression, where observations are weighted to ensure similarity on some observed characteristics. This is similar to Inverse Probability of Treatment Weighting (IPTW) and its extension to multiple treatments in McCaffrey et al. (2013), but in the DD context the “groups” to be weighted reflect both treatment status as well as time (pre vs. post). Given concern about potential changes in group composition over time, we first refine the estimand of interest, clarifying that we are interested in the effect of the program on the individuals in Group 1: those who are untreated at time 0 but subsequently become treated at time 1. Denoting “Group” by G, we can denote this estimand as Δ_G=1=E_X|G=1E[Y¹(1)−Y⁰(1)|X=x].

In particular, we propose a weighting strategy that will weight the 4 groups (treatment pre, treatment post, comparison pre, comparison post) to be similar on a set of key characteristics; this can be thought of as weighting each of the four cells in Table I to reflect the covariate distribution in the treatment group during the pre period, thus removing biases due to differences in covariate distributions between the four groups in Table I. Importantly, this approach does not require longitudinal data on individuals; rather, it can be implemented with data from repeated cross-sections.

In this setting, the propensity score is defined as the probability of being in Group 1 (versus Groups 2, 3, or 4). To estimate the propensity scores, fit a multinomial logistic regression predicting Group as a function of a set of observed covariates X. Each individual will have four resulting propensity scores, e_k(X_i): the probability of being in Group k, for k=1 to 4. (Note that these four will sum to one for each individual). The weights are then created in such a way that each of the four groups is weighted to be similar to Group 1, the treatment group in the pre period. This is accomplished using the following weight for individual i:

$${\mathrm{w}}_{\mathrm{i}}={\mathrm{e}}_1({\mathrm{X}}_{\mathrm{i}})/{\mathrm{e}}_{\mathrm{g}}({\mathrm{X}}_{\mathrm{i}})$$ (2)

where g refers to the group that individual i was actually in. Thus, individuals in Group 1 will receive a weight of 1, while individuals in other groups receive a weight that is proportional to the probability of their being in Group 1 relative to the probability of their being in the group they were actually in.

To think through how this approach works, we can decompose the estimand of interest, using the assumptions detailed below, and denoting the observed outcome as Y:

$${\mathrm{\Delta }}_{\mathrm{G}=1}={\mathrm{E}}_{\mathrm{X}|\mathrm{G}=1}\mathrm{E}[{\mathrm{Y}}^1(1)-{\mathrm{Y}}^0(1)|\mathrm{X}=\mathrm{x}]={\mathrm{E}}_{\mathrm{X}|\mathrm{G}=1}\mathrm{E}[{\mathrm{Y}}^1(1)|\mathrm{X}=\mathrm{x},\mathrm{E}=1]-{\mathrm{E}}_{\mathrm{X}|\mathrm{G}=1}\mathrm{E}[{\mathrm{Y}}^0(0)|\mathrm{X}=\mathrm{x},\mathrm{E}=1]-({\mathrm{E}}_{\mathrm{X}|\mathrm{G}=1}\mathrm{E}[{\mathrm{Y}}^0(1)|\mathrm{X}=\mathrm{x},\mathrm{E}=0]-{\mathrm{E}}_{\mathrm{X}|\mathrm{G}=1}\mathrm{E}[{\mathrm{Y}}^0(0)|\mathrm{X}=\mathrm{x},\mathrm{E}=0])$$

The second of these terms is observed (from Group 1); the other 3 can be estimated from the observed data, by reweighting Groups 2 (the first term), 3 (the fourth term), and 4 (the third term) to reflect the covariate distribution of Group 1. In particular, using the weights w_i defined in Equation (2), standard propensity score theorems (Rosenbaum & Rubin, 1983), and the assumptions detailed below a consistent estimate of each of the four terms can be obtained using:

$${\mathrm{\mu ̂}\prime }_g=\frac{\sum _{i=1}^{n}I(G_i=g)Y_i{w}_i}{\sum _{i=1}^{n}I(G_i=g)w_i}$$ (3)

Thus, by fitting a weighted parametric model such as Equation (1) but using weights defined in Equation (2), we can obtain a consistent estimate of the treatment effect of interest, even in the presence of selection bias due to observed covariates across the four groups. See McCaffrey et al. (2013) for a similar idea applied in a somewhat different context and Appendix A.1 of Lechner (2011) for a formal proof.

This approach relies on three primary assumptions:

Propensity score overlap (common support/positivity):

$$0<p(G_i=g|X_i)<1\text{ for all }\mathrm{g}=1:4\text{ and all }\mathrm{X}$$ (A-2)

$$\text{Unconfoundedness}:\mathrm{E}[{\mathrm{Y}}^0(1)-{\mathrm{Y}}^0(0)|\mathrm{E},\mathrm{X}]=\mathrm{E}[{\mathrm{Y}}^0(1)-{\mathrm{Y}}^0(0)|\mathrm{X}]$$ (A-3)

$$\text{Exogeneity}:{\mathrm{X}}^1={\mathrm{X}}^0=\mathrm{X}.$$ (A-4)

Assumption (A-2) assumes that all individuals have a positive probability of being in each of the four groups. Assumption (A-3) can be thought of as a slight relaxation of Assumption (A-1) above; it assumes that membership in the treatment group is not related to the trend over time that would be observed under the control condition, conditional on the observed covariates X. Assumption (A-4) formalizes the premise that the covariates X are truly covariates, in that they are not affected by the treatment (Lechner, 2011). A final assumption is the standard causal inference assumption of the Stable Unit Treatment Value Assumption (SUTVA; Rubin, 1977), which assumes that each individual’s potential outcomes are not affected by the treatment assignments of any other subjects, and that there is only one “version” of the treatment and one “version” of the control.

To provide additional intuition for these weights, individuals who look very similar to those in Group 1, and very different from the individuals in their own group, will receive higher weights; those who look dissimilar from those in Group 1, and more similar to individuals in their own group, will receive lower weights since they are somewhat over-represented when trying to represent Group 1. These weights are very similar in spirit to Inverse Probability of Treatment Weights (IPTW), which weight each individual by the inverse probability of being in the group they are in (one over the probability of being treated for the treatment group; one over the probability of being control for the control group; Lunceford and Davidian, 2004). The difference is that IPTW weights weight each sample (treatment and control) up to the combined sample of treated and control groups, whereas in our application we weight each group to Group 1.

As illustrated further below in the simulation study, another strategy could be to estimate separate propensity score models at each time point, weighting the treatment group to the control group at each time point. While this accounts for differences between treatment groups at each time point, it does not account for changes that may happen in each group (treatment and control) over time; the four-group weighting adjusts for those temporal changes in case-mix within each group in addition to the differences between groups.

There are two important points to make here about the four-group weighting. First, to avoid “post treatment bias” (Rosenbaum, 1984), it is important not to balance on (weight by) any variables that may have been affected by the program. For example, if the program leads physician practices to change their patient pool pre to post, for example, by enrolling healthier patients only, then balancing on health status would condition away part of the treatment effect. It is important to only balance characteristics that are likely not affected by the program of interest. In the AQC example, where limited covariates are available in any case, we balance on age, sex, co-occurring substance abuse, and a risk score, under the assumption that practices were unlikely to change their patient pool as a result of the AQC (and based on empirical evidence that there was little change in the risk score over time; Song et al., 2012). Another way to think about this in the context of the AQC evaluation is that we do not want patient case mix changes to be part of the “AQC effect” on spending or quality. The goal of the AQC is to lower costs and improve quality by changing the way care is delivered and financed, not by a physician group simply attracting healthier enrollees. So by adjusting for these variables associated with case mix, we can essentially “net out” case mix changes from impact estimates, in the absence of the ability to use a continuously enrolled sample.

Second, the choice of group to weight to is not necessarily straightforward. In the procedure detailed above, we chose to weight to the treatment “pre” group. In the AQC example this asks the question “What is the effect of the AQC on mental health out-of-pocket costs as compared to usual practice, among those individuals who were in physician’s practices in the year before those practices entered the AQC?” Another possibility would have been to weight to the combined AQC and non-AQC groups in the pre period, which would ask a slightly different question: “What is the effect of the AQC on mental health out-of-pocket spending as compared to usual practice, among all individuals served by this health plan in the pre period?” This could be done by modifying the weights such that the numerator would be the probability of being in Group 1 or 2; see McCaffrey et al. (2013) for a discussion of a similar strategy in an analogous setting with multiple treatment groups.

Simulation study

We now present a small motivating simulation study to illustrate the setting and approach. Consider a setting with 500 individuals in each group (treatment and comparison, pre and post) and a single normally distributed covariate X. (Of course the real benefits of propensity scores come in with multiple covariates but to illustrate concepts we use a single covariate here). We do not assume longitudinal measures on the same individuals; rather we have repeated cross-sections from the treatment and control groups.

Assume the following simple model for the “outcome” Y (which includes pre-treatment measures of the outcome variable), expressed as a function of Treatment (exposure) E, Pre/Post status P, and the covariate X:

$$Y=\alpha +{\beta }_{E}E+{\beta }_{P}P+{\beta }_{X}X+{\beta }_{EP}EP+{\beta }_{EX}EX+{\beta }_{PX}PX+{\beta }_{EPX}EPX+u,u~N(0,1)$$ (4)

We compare six methods of estimating the effect of the treatment on the outcome Y, among the individuals in the treatment group in the pre period (Δ_G=1; the estimand of interest defined above):

1. A simple naïve DD model: Y = α + β_EE + β_PP + β_EPEP + u,u ~ N(0,1), where the estimate of β_EP is taken as the DD estimate.

2. A DD model that also includes the covariate X: Y = α + β_EE + β_PP + β_EPEP + β_XX + u,u ~ N(0,1), where the estimate of β_EP is again taken as the DD estimate

3. A weighted version of the outcome regression model in Approach (1), with propensity score weights estimated separately at each time point.

4. A weighted version of the outcome regression model in Approach (2), with propensity score weights estimated separately at each time point.

5. A weighted version of the outcome regression model in Approach (1), with the four group propensity score-based weights defined in the previous section.

6. A weighted version of the outcome regression model in Approach (2), with the four group propensity score-based weights defined in the previous section.

For each method we calculate the bias in estimating Δ_G=1, as well as the actual confidence interval coverage of nominal 95% confidence intervals. Note that the outcome DD models themselves are inherently misspecified, in particular leaving out some interaction terms. However, they reflect the common models that would be run, without knowledge of the true model specified in Equation (4). If the outcome model (the DD model) were correctly specified then it would yield unbiased effect estimates, without need for the propensity score approach.

We consider four simulation settings that vary in how the four groups differ in the covariate X: one where the groups differ at baseline but do not change in composition over time, one where they do not differ at baseline but change in composition in different ways, and two with both complications. The size of these differences are described in Table II, and are on the order of .2–.3 standard deviations, which reflect moderate-size covariate imbalances across groups (Stuart, 2010). The other parameters are set at β_E = .3,β_P = .1,β_X = .2,β_EP = .1,β_EX = .1,β_PX = .2,β_EPX = .15, although their particular values do not especially matter for the general conclusions presented here.

Table II.

Simulation settings

Setting	Label	Covariate difference at baseline	Change in × in control group	Change in ×in treatment group
1	No Diff	0	0	0
2	Group Diff	0.3	0	0
3	Group and Time Diff	0.3	0.2	0.2
4	Group by Time Diff	0.3	0.1	−0.2

Table III presents the simulation results for bias and confidence interval coverage, respectively. In Setting 1 all six models work well, because there is no selection bias across groups or across time. However, with any type of selection bias (across group or across time) the performance of the naïve method degrades. The naïve DD models lead to higher bias and lower confidence interval coverage than the propensity score weighted models, particularly when the groups change in composition over time. Approaches (3) and (4), which fit separate propensity score models at each time point, thus equating treatment and control at each time point (but not across time), perform relatively well in terms of confidence interval coverage across all four settings, but have higher bias than the four group weighting approach when the treatment and control group composition changes over time (Settings 3 and 4), and even when there is just a difference at baseline (Setting 2). The four group propensity score weighting eliminates the covariate differences across the four groups in all four settings (details not shown, but the covariate means are in fact equal across groups after weighting) and thus leads to accurate effect estimates in all settings considered. With different values for the regression coefficients in Model (4) the exact size of the bias and under-coverage of the naïve DD models varies, however the story remains the same—that simple regression adjustment for X does not suffice, while the four-group propensity score weighting approach we consider yields unbiased effect estimates with good coverage rates.

Table III.

Bias and Nominal 95% Confidence Interval Coverage rates of treatment effect estimation using 6 DD models

Setting	Bias
	(1): Naïve DD	(2): DD with X	(3): (1) with separate wts	(4): (2) with separate wts	(5): (1) with 4 group weighting	(6): (2) with 4 group weighting
1	−0.0047	−0.0048	−0.0047	−0.0047	−0.0048	−0.0048
2	0.060	0.060	−0.023	−0.023	−0.00043	−0.00064
3	0.112	0.111	0.029	0.029	0.0017	0.0018
4	0.204	0.089	−0.034	−0.035	0.00026	0.00024
	Confidence interval coverage (Nominal=.95)
	(1): Naïve DD	(2): DD with X	(3): (1) with separate wts	(4): (2) with separate wts	(5): (1) with 4 group weighting	(6): (2) with 4 group weighting
1	.94	.95	.97	.95	.96	.95
2	.91	.90	.96	.94	.96	.94
3	.79	.76	.95	.93	.96	.95
4	.44	.83	.94	.92	.95	.93

Application to the Alternative Quality Contract

Payment and delivery system reforms are being considered by many payers to address longstanding concerns about health care spending growth and to improve the efficiency and quality of care. Global budget contracts, which compensate providers through a risk-adjusted prospective payment for all primary and specialty care for a defined population in a set period, gives providers flexibility in allocating resources. When combined with performance incentives (such as quality metrics), global payment holds providers accountable for both the quality and the costs of care. The Alternative Quality Contract (AQC) was one such initiative launched by Blue Cross Blue Shield of Massachusetts (BCBSMA) in 2009. The AQC combines global payment with performance incentives in a way that resembles the Pioneer accountable care organization (ACO) models authorized under the Affordable Care Act, although the two programs also differ on several dimensions. Implementation of the AQC model was associated with lower medical spending as measured by claims submitted by providers (driven primarily by shifting outpatient facility care to providers with lower fees, but also by lower utilization starting in year 2) and improved ambulatory care quality in its initial phase, particularly among organizations that had previously been paid only by fee-for-service (FFS; Song et al., 2012). However, no information is available on how this model affected care for mental illnesses, which often go undetected or undertreated in primary care and for which care across the primary and specialty care sectors is often poorly coordinated under existing financing approaches (Edlund et al., 2004).

By 2011, 12 provider organizations caring for approximately 430,000 enrollees were covered under the AQC contract. AQC enrollees are largely BCBSMA health maintenance organization (HMO) members, all of whom designated a primary care physician (PCP) affiliated with an AQC provider organization. AQC provider organizations include large physician-hospital organizations and umbrella organizations combining smaller independent practices.

In this paper we are interested in estimating the effects of the AQC on mental health care spending, and in particular the out-of-pocket expenditures borne by patients. This paper focuses on the enrollees who were served by physician groups that entered the AQC in the second year (2010); companion papers will consider multiple AQC cohorts. The sample consists of individuals 18 – 64 years old who were enrolled in BCBSMA for all 12 months of either 2009 or 2010, and who received at least one mental health service. An enrollee is considered to be in the Treatment (AQC) group if her primary care provider belongs to an organization that entered the AQC in 2010. In fact, there were two types of AQC organizations: those that did bear risk for mental health and substance abuse treatment spending in their risk contracts with BCBSMA, and those that did not. For the illustrative study here, we combine the two into one “AQC” group. The comparison group consists of patients served by primary care providers whose organizations did not enter the AQC by the end of 2010. We observe a “pre” (2009) and “post” (2010) time point for both the treatment and comparison groups, thus making this a typical DD design. The total sample sizes in each group, as well as basic descriptive statistics, are presented in Table IV.

Table IV.

Characteristics of AQC and non-AQC enrollees in pre and post periods. Standardized difference in means defined as the difference in means divided by the standard deviation.

Covariate	Group 1: AQC pre	Group 2: AQC Post	Group 3: non-AQC pre	Group 4: non-AQC post	Unweighted standardized difference in means			Weighted standardized difference in means
					2 vs. 1	3 vs. 1	4 vs. 1	2 vs. 1	3 vs. 1	4 vs. 1
Age 18–24 (%)	12	14	14	18	.06	.05	.17	0	0	0
Age 25–34 (%)	13	13	12	11	−.01	−.04	−.08	0	0	0
Age 35–64 (%)	56	54	48	45	−.03	−.14	−.22	0	0	0
Male (%)	40	40	42	42	.00	.04	.05	0	0	0
Risk score	1.83	1.80	1.72	1.64	−.01	−.05	−.09	0	0	0
Substance abuse (%)	6	6	6	5	.00	−.03	−.04	0	0	0
N	12,025	12.061	106,485	100,981

A challenge in estimating the effects of the AQC is that patient panels change over time due to changes in insurance coverage or changes in affiliations of primary care providers. Thus, the treatment and comparison groups are defined as the groups of patients served by AQC or non-AQC providers in a given year; those individual patients may change, and we do not necessarily have two-year longitudinal data on individuals. As discussed above, one alternative would be to restrict attention to individuals who are continuously enrolled over the two-year time frame. However, that approach becomes less feasible when there is interest in small subgroups (such as individuals with more severe mental health conditions or those with mental health and co-occurring substance use disorders) or in longer time periods (e.g., if interest is in the longer-term effects of the AQC). We thus use the four-group propensity score weighting approach described above to adjust for differences both across the types of patients served by AQC and non-AQC providers as well as for possible case-mix changes in both groups over time (from 2009 to 2010). In part due to limited characteristics available in the data, but also because of the concerns described above about not adjusting for “post-treatment” variables, in the propensity score models we adjust for age group, sex, co-morbid substance abuse disorder, and a risk score calculated by BCBSMA from current-year diagnoses, claims and demographic information using the diagnostic-cost-group (DxCG) scoring system (Verisk Health), which is similar to the Medicare Advantage plan risk adjustment approach (Pope et al., 2004). It was thought unlikely that the case mix of enrollees served by providers with respect to these characteristics would change as a result of the AQC and thus it would be safe to include them in the propensity score adjustment. Empirical analyses also indicated little change in the risk score as a result of the AQC (Song et al., 2012).

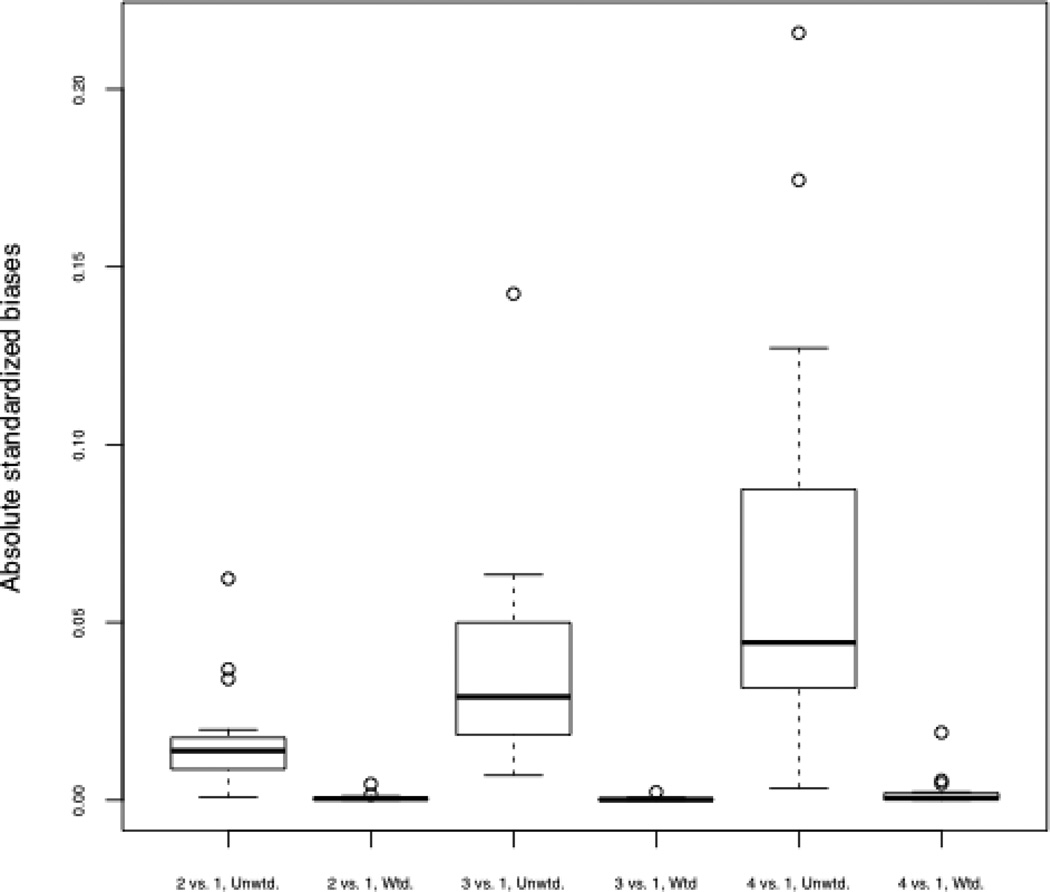
Table IV presents descriptive statistics on the four groups of interest. We see that the enrollees in AQC organizations had slightly higher risk scores than non-AQC enrollees and were slightly younger. There were also some changes in group composition across time, with more younger enrollees in both groups (AQC and non-AQC), and particularly in the non-AQC group. A common metric indicating group similarity is the standardized difference in means, defined as the difference in means of the covariate divided by the (unweighted) standard deviation (Stuart, 2010). Columns 5–7 and 8–10 show the unweighted and weighted standardized differences in means, respectively, for each covariate when comparing each of the groups to Group 1 (the AQC enrollees in the pre period; our target population). A common standard in the propensity score literature more generally is that a standardized difference in means greater than 0.1 or 0.2 represents a substantial difference between groups, such that standard regression adjustment for that covariate may be unreliable (Stuart, 2010). A few of the unweighted standardized differences in means rise to this level, particularly when comparing the non-AQC group in the post period to the AQC group in the pre period. However, the weighting was fully successful in removing these covariate differences, as indicated by the weighted standardized differences in means equal to 0. Figure 1 shows boxplots of the standardized differences in means for each of the covariates as well as all of the two-way interactions between covariates, and indicates that excellent balance (very small standardized differences in means) on all of these variables and interactions was obtained for all three comparisons (2 vs. 1, 3 vs. 1, and 4 vs. 1) following the weighting. Although extreme weights can be a problem with inverse weighting approaches, the distribution of weights is reasonable in this data, without extreme outliers, and with minimum and maximum weights across all groups of 0.03 and 2.64, respectively.

Figure 1.

Boxplots of absolute standardized differences in means of each covariate and all two-way interactions between covariates, for the three comparisons of interest. “Unwtd.” reflects standardized differences before propensity score weighting; “Wtd.” reflects standardized differences after the four-group propensity score weighting.

The effects of the AQC on out of pocket expenditures are shown in Table V, for both unweighted and propensity score-weighted models. Because approximately 25% of individuals had no out of pocket costs we fit a two-part model that first models the probability of having any out-of-pocket costs, and then, conditional on costs being greater than 0, models log(costs) (Buntin & Zaslavsky, 2004). (The log transformation is used to make the distribution of costs more normally distributed). As seen by the coefficients on the AQC by post interaction term, there is no evidence that the AQC increased the probability of having out-of-pocket costs whether or not an individual had some nor the level of those costs on average if an individual had some, in either the unweighted or weighted models. We chose to examine out-of-pocket spending as an illustrative outcome; in practice, we would expect the ACQ to affect total spending among enrollees with mental health conditions but not enrollee out-of-pocket spending since the intent of this innovation is to lower spending by changing how providers practice medicine rather than by simply shifting costs from the health plan to consumers. Comparing the standard errors and confidence intervals there is a slight price paid in variance from using the propensity score weights: looking at the coefficient on the AQC by post interaction, the standard errors when using the weights are 35% and 67% larger than the standard errors from unweighted models for any OOP costs and log(costs), respectively. However, as illustrated in the simulations, the bias should be lower in the weighted models, thus indicating a bias-variance tradeoff.

Table V.

Effects of the AQC on out of pocket (OOP) costs. 95% confidence interval in square brackets. Standard error in parentheses.

	Intercept	AQC	Post	AQC*Post
Unweighted
Any OOP costs	1.10 *** [1.08, 1.11] (0.0071)	0.38 *** [0.33, 0.43] (0.025)	−0.17 *** [−0.19,−0.15] (0.010)	0.043 [−0.025, 0.111] (0.034)
log(costs) if costs > 0	4.40 *** [4.39,4.41] (0.0046)	−0.012 [−0.040,0.016] (0.014)	0.070 *** [0.057,0.083] (0.0066)	0.024 [−0.016,0.064] (0.020)
Weighted
Any OOP costs	1.38 *** [1.33,1.43] (0.023)	0.098 *** [0.03,0.16] (0.033)	−0.057 * [−0.12,0.01] (0.032)	−0.019 [−0.10,0.07] (0.046)
log(costs) if costs > 0	4.42 *** [4.41,4.43] (0.0062)	−0.027 *** [−0.044,−0.0096] (0.0087)	0.083 *** [0.065,0.101] (0.0088)	0.014 [−0.010,0.038] (0.012)

^*/**/***p-value < .05/.01/.001

Conclusions

This paper has introduced the use of four group propensity score weighting in DD models as a way to control for confounding due to observed covariates that differ either across groups in the pre period, or even over time due to changes in group composition. The method weights each of the four groups to be similar to some common group, such as the treatment group in the pre period. Using simulation we saw that the four group weighting approach can accurately recover treatment effects, and in an applied example it successfully balanced the four groups with respect to observed baseline characteristics. Although in our motivating example the unweighted and weighted outcome regression models yielded similar conclusions, this would not necessarily always be the case.

A key assumption underlying the four group propensity score weighting is that the changes in group composition over time are not affected by the program of interest. In the motivating example care was taken to only balance on covariates believed to be unaffected by the AQC. A second key assumption is that, given the observed covariates, the trends across time seen in the control group reflect the trends the treatment group would have experienced in the absence of the treatment. The propensity score reweighting proposed here allows for adjustment due to observed covariates, but cannot account for potential unobserved differences that would lead to different trends. In addition, a potential drawback of the proposed weighting approach is increased standard errors; this is the common bias-variance trade-off, where the goal is to obtain less biased effect estimates, but it may be at the cost of increased variance. This is a particular concern if there are extreme weights, and thus the distribution of weights should be checked for outliers.

Future work should further investigate these methods and alternative approaches. For example, Werner et al. (2009) used a propensity score matching approach to adjust for changing case mix in a DD-type model, but where the matching was done across time (matching pre to post), separately within the treatment and control groups. Similarly, Song et al. (2012) fit separate propensity score models for each time point, equating the treatment and control groups at each time point. That strategy may be particularly appealing when in a difference-indifference type framework with a treatment group and a comparison group, but where there are more than two time periods available (also known as a comparative interrupted time series design). The approach proposed in this paper has the advantage of simultaneously adjusting both across time and group, equating the four groups. However, future work should further investigate the benefits and drawbacks of this four group weighting in comparison to other approaches, including in more general settings.

In conclusion, both DD models and propensity scores are seen as strong non-experimental study design options when randomization is not feasible. However, by combining them we may be able to make even more robust inferences, taking advantage of the important study design elements of both.