Arithmetic memory networks established in childhood are changed by experience in adulthood

Abstract

Adult bilinguals show stronger access to multiplication tables when using the language in which they learned arithmetic during childhood (LA+) than the other language (LA−), implying language-specific encoding of math facts. However, most bilinguals use LA+ throughout their life, confounding the impact of encoding and use. We tested if using arithmetic facts in LA− could reduce this LA− disadvantage. We measured event related brain potentials while bilingual teachers judged the correctness of multiplication problems in each of their languages. Critically, each teacher taught arithmetic in either LA+ or LA−. Earlier N400 peak latency was observed in both groups for the teaching than non-teaching language, showing more efficient access to these facts with use. LA+ teachers maintained an LA+ advantage, while LA− teachers showed equivalent N400 congruency effects (for incorrect versus correct solutions) in both languages. LA− teachers also showed a late positive component that may reflect conflict monitoring between their LA+ and a strong LA−. Thus, the LA− disadvantage for exact arithmetic established in early bilingual education can be mitigated by later use of LA−.

Introduction

Verbally rehearsing arithmetic facts, like multiplication tables, leads to encoding and retrieving these facts as language representations [6]. How well these facts are represented in verbal memory predicts long-term mathematical competence [10]. For bilinguals, the language in which they learned arithmetic (LA+) often shows better access to arithmetic facts than their other language (LA−) [6, 9, 18, 26, 28]. This advantage for the LA+ persists into adulthood, seemingly uninfluenced by language proficiency [26]. By implication, bilinguals may be at a disadvantage when performing arithmetic in their LA− (e.g., taking standardized tests in LA−), creating a dilemma for parents and educators of bilingual children. Twenty percent of U.S. children speak English as a second language, making it critical to determine how this LA− disadvantage can be mitigated. Here, we tested if frequent use of LA−, in adult bilinguals who naturally use one language for simple arithmetic more than the other, could reduce or eliminate the LA− disadvantage for multiplication facts.

Memory networks for single digit multiplication (e.g., 2 X 3 = 6) are formed in childhood, when these concepts are learned through rote memorization, linking operands with their solutions and other arithmetic concepts within the network [4]. Time to solve a problem or judge the correctness of a multiplication solution acts as a measure of the connectivity between facts in the network [2, 4, 24]. Bilinguals typically learn arithmetic in one language, and often report preferring to use this language for retrieving arithmetic facts [18]. Moreover, these facts appear to be accessed preferentially in the language of learning [e.g., 9, 26, 28]. For example, Spelke and Tsivkin [28] taught bilingual adults new arithmetic facts in one language, and observed that these facts were retrieved more accurately in the training language than their other language [28]. Similarly, Bernardo [3] showed that bilingual high-school students performed better on arithmetic in their language of schooling even though it was not their native language. Salillas and Wicha [26] reported that this LA+ advantage persists into adulthood, independent of general language proficiency in LA−. That is, LA+ seemed to have an advantage over LA− even when LA− was the more proficient language.

These findings suggest format-, or language-, specific encoding of arithmetic facts that influences processing across the lifespan. Moreover, although reading fluency and vocabulary size influence math achievement [see review 1], arithmetic fact retrieval may be insensitive to these factors. However, these studies potentially confounded the impact of encoding and use, given that most bilinguals continue to use LA+ throughout their life. In fact, Salillas and Wicha [26] observed that bilinguals who used LA− more often showed better access to multiplication facts in LA−. Thus, encoding may not be the only factor driving the LA+ advantage.

Experience, loosely defined here as frequent use of information to perform a task, is known to cause neuronal reorganization and changes in behavioral patterns in bilinguals [7, 19, 20]. Here, we tested if experience using LA− for arithmetic, without explicit training of multiplications in LA−, can reduce or eliminate the LA− disadvantage. We measured performance on simple multiplications in LA+ and LA− in bilinguals who naturally used these facts more in one language than the other, namely, bilingual elementary school teachers. This population allowed us to tease apart frequency of use and initial learning, since half of the sample taught primarily in LA+ and the other half in LA−. We hypothesized that if the LA− disadvantage were irreversible, then the disadvantage would be observed in both groups, independent of teaching experience. If, however, experience using LA− mitigates the disadvantage, then LA− would be disadvantaged only in the LA+ teaching group.

The current study was adapted from Salillas and Wicha [26]. Simple multiplication problems were presented one operand at a time, with a solution that was either correct or not (3×2=6 versus 3×2=7). Each number was presented as a word in English (e.g., three two six) or Spanish (e.g., tres dos seis). While the teachers judged the correctness of each multiplication, we recorded accuracy, delayed response time and event related potentials (ERPs) to solution onset.

ERPs are a direct measure of electrical brain activity that has been used to study arithmetic fact retrieval [11, 23–26]. We focused on the N400, a negative-going wave that peaks around 400 ms post-stimulus onset, and a subsequent positive-going wave, the late positive component (LPC). The N400, first observed to language stimuli [16], is modulated by the predictability or semantic fit of a word in its preceding context (e.g., a sentence) [reviewed by 15]. The worse the semantic fit is the larger the N400 amplitude is relative to a more contextually probable target [e.g., He spread the warm bread with socks; 16]. That is, smaller N400 amplitude reflects easier access to the information in memory. An equivalent N400 effect has been observed for simple arithmetic problems [11, 23, 25, 26], with striking similarity in timing and morphology to the linguistic N400 [8, 23, 24]. The arithmetic N400 shows increased negative amplitude for incorrect than correct solutions, reflecting automatic spread of activation in the memory network from operand to solution [24, 26]. Subsequent to the N400, a positive deflection has been observed in some cases with larger positive amplitude for incorrect than correct multiplication solutions [23, 26]. A late positive component (LPC), called a P600 when it is related to processing linguistic structure [14, see also 27 for arithmetic structure P600], has been observed to a variety of linguistic stimuli, from language translations to unexpected endings on jokes [5, 20]. Less well understood than the N400, the LPC may reflect more controlled processing or reprocessing of information [14]. In arithmetic, the LPC is likely related to cognitive load or conflict in processing a problem. Conflict in resolving incorrect solutions may occur between the strong encoded LA+ and LA− in stages of controlled processing (LPC), especially for individuals with a stronger representation of LA− [29].

We predicted that teaching would strengthen access to arithmetic facts in that language, which would be indexed by larger N400 effects compared to the other language. The difference between N400 amplitude to correct and incorrect solutions should be larger for LA+ than LA− for LA+ teachers (learn = teach), but equivalent across languages for LA− teachers (learn ≠ teach). In addition, the LPC should be larger for LA− than LA+ teachers, because competition will be greater between the learned language (LA+) and teaching language (LA−) when LA− is used more frequently.

Material and Methods

Participants

Participants were 14 (11 female) healthy elementary school teachers (mean age 37.43 years, range 27–48 years)¹. All participants’ first language (L1) was also their language of learning arithmetic (LA+). All participants actively taught or had extensive recent experience teaching arithmetic (mean 9.21 years; range 1–12 years). Half of the participants taught primarily in LA+ (learn = teach) and half in LA− (learn ≠ teach). Critically, the years of teaching in LA− were significantly different between groups (t=4.408, p<0.001).

All participants were fluent in English and Spanish, with 9.07 years as the mean age of exposure (AOE) to the second language (L2) (range 0–27 years²; L2 was Spanish for 2 participants³ and English for all others). Language proficiency was assessed using the Boston Naming Test [BNT; 12], sections of the Woodcock Language Proficiency Test (i.e., Picture Vocabulary, Oral Vocabulary, and Verbal Analogies) in English and Spanish [32], and an adapted LEAP-Q questionnaire [17]. A percentile score (RPI) was obtained for the Woodcock data using the BVAT [22] scoring system. The groups differed in percent language use for both LA+ (t=−2.93, p=0.013) and LA− (t=2.93, p=0.013), consistent with increased daily use of the teaching language. The groups were equivalent on all other measures: BNT LA+ (t=−2.05, p=0.063; mean: LA+ teachers=50.43, LA− teachers=42.29); BNT LA− (t=0.87, p=0.404; mean: LA+ teachers=41.71, LA− teachers=45.29); BVAT LA+ (t=−2.02, p=0.066; mean RPI: LA+ teachers=89.29, LA− teachers=73.00); BVAT LA− (t=−1.61, p=0.133; mean RPI: LA+ teachers=81.43, LA− teachers=61.71).

Stimuli and Procedure

Each problem consisted of 3 sequential number words presented with no symbols, as follows: a fixation mark “*” (800 ms duration), first operand (350 ms duration; 250 ms blank ISI), second operand (350 ms duration; 150 blank ISI), solution (350 ms duration; 650 ms ISI) and delayed⁴ response prompt “?” (1000 ms ITI). At the prompt, participants pressed a key on a keyboard (right hand index and middle fingers, counterbalanced across participants) to judge if the problem was correct (e.g., * two three six ?) or incorrect (e.g., * two three thirteen ?). Number words were displayed in lower-case letters in Spanish and English⁵, with maximum solution size of 20. Twenty-four experimental trials appeared 8 times each, twice with a correct solution and twice with an incorrect solution in each language, for 192 total trials. Twelve similar trials were used only for practice. Pseudo-randomization ensured no more than 3 consecutive correct or incorrect items and no consecutive presentations of the same problem. Responses to filler multi-format trails (e.g., 2 × 3 = six), which reduced proximate redundancy of critical trails, were not analyzed. ERPSystem (Holcomb Lab) was used for stimulus presentation and data acquisition and processing.

Continuous electroencephalograms (EEG) were recorded from 26 tin scalp electrodes in geodesic array through analog bioamplifiers (SA Instrumentation, Inc.) with a .01 Hz (RC; −6 dB/oct) to 100 Hz (Butterworth; −12 dB/oct) band pass filter. EEGs were referenced online to the left mastoid with impedances maintained below 5kΩ, and sampled at 250 Hz then re-referenced offline to the average of left and right mastoids. Electrodes below and at the outer canthi of each eye were used to discard trials offline containing blinks (polarity inversion) or horizontal movements (square wave onset). Trials with amplifier blocking (flat line) and excessive movement (maximum amplitude) were also removed with roughly equal loss across conditions (M=17%; range: 2–29%). Test thresholds were tailored to maximize signal-to-noise ratios per subject. Data was filtered (.1–30.0 Hz, 3^rd order Butterworth) prior to analysis in SPSS.

Results

Greenhouse-Geisser correction is reported for comparisons with more than 1 degree of freedom; significance is reported at p<0.05.

Behavioral Findings

Accuracy and delayed response times (dRT) were subjected to separate mixed repeated measures ANOVAs with group (LA+ teachers, learn = teach; LA− teachers, learn ≠ teach) as a between-subject factor, and congruency (correct, incorrect) and language (teaching language, non-teaching language) as within-subject factors. Mean accuracy for correct identification of correct and incorrect problems was 97.81% (range 96.62–98.56%). dRTs were analyzed for accurate responses only (trials were eliminated for incorrect judgments and responses before the cue, past a 2000 ms cut-off, or two standard deviations from the mean). There were no effects of congruency for either accuracy or dRT, and no differences in either measure across groups or languages.

ERP Findings

ERPs were extracted from the continuous EEG from solution onset and averaged by condition. On average, 19% of trials (range: 4–29%) were lost to performance errors, and ocular or muscle artifacts. Mean amplitude relative to a 100 ms pre-stimulus baseline and peak latency of the congruency effect (incorrect minus correct solutions) for trials with correct identification of correct and incorrect problems were subjected to separate omnibus ANOVAs with group (LA+ teachers, LA− teachers) as a between-subject factor and congruency (correct, incorrect), language (teaching language, non-teaching language), and electrode (26) as within-subject factors. Scalp distribution was examined for interactions with electrode using a 16-electrode subset (LLPf, LLFr, LLTe, LLOc, LMPf, LMFr, LMCe, LMOc, RLPf, RLFr, RLTe, RLOc, RMPf, RMFr, RMCe, RMOc [as per 31], Figure 1A), which were divided into 4 equal quadrants by hemisphere (left, right), laterality (lateral, medial), and anteriority (prefrontal, frontal, temporal/central, and occipital).

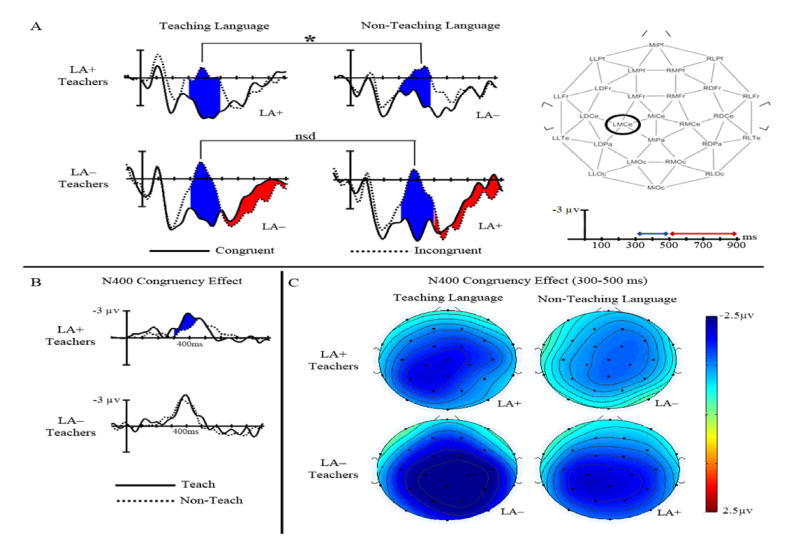
Figure 1.

Congruency Effects by Language and Group. Negative microvolts are plotted up on the Y-axis and milliseconds on the X-axis. (A) Group grand average ERPs at the Left Medial Central electrode (LMCe) for correct and incorrect solutions in each language; * indexes significant effects. Blue and red bars on timescale indicate analysis windows for N400 and LPC, respectively, and shading on ERPs indexes significant effects. Head diagram shows electrode distribution and position of LMCe. (B) Congruency effect as difference ERPs (incorrect minus correct) at LMCe. (C) Isovoltage scalp topography (26 electrodes) for the N400 congruency effects (incorrect minus correct); figures created using ERPSYSTEM and EEGLAB.

Peak Latency

The N400 congruency effect (incorrect minus correct solutions) peaked ~20 ms earlier for the teaching language (387.06 ms) than the non-teaching language (407.87 ms) (congruency difference wave, Teaching Language: F_(1,12)=12.26 p=0.004 η²=0.49; Group X Teaching Language: F_(1,12)=1.21, p=0.293 η²=0.09), indexing faster access to multiplication facts in the teaching language, regardless of whether it was the LA+ or LA−. There were no significant LPC peak latency differences across the teaching and non-teaching languages in either group (mean peak latency: teaching 702.48 ms; non-teaching 656.53 ms). ERP windows were selected from 300–500 and 500–900 ms to encompass N400 and LPC mean amplitude, respectively⁶.

N400 (300–500 ms)

N400 mean amplitude analyses revealed a main effect of Congruency (F_(1,12)=65.19, p<0.001 η²=0.85), with larger negativity for incorrect than correct solutions (Figure 1A). This widespread effect was largest over medial-posterior electrodes (Congruency x Laterality x Anteriority: F_(3,36)=7.96, p=0.002 η²=0.40). LA+ teachers and LA− teachers showed equivalent N400 congruency effects (Group x Congruency: F_(1,12)=0.092, p=0.767 η²=0.17). The congruency effect was also equivalent for the teaching and non-teaching languages (Congruency x Language: F_(1,12)=0.09, p=0.773 η²=0.01).

The critical comparison of the congruency effect between languages in each group reached significance as an interaction by hemisphere (Group x Congruency x Teaching Language x Hemisphere: F_(1,12)=6.32, p=0.027 η²=0.35). LA+ teachers showed a larger N400 congruency effect in the teaching than non-teaching language, which was largest over the left but present over both hemispheres (Figure 1C). In contrast, LA− teachers showed no difference across the teaching and non-teaching languages. No other effects reached significance.

Linear regressions were conducted with all 14 participants to determine if individual factors accounted for the variance in mean amplitude of the N400 congruency effect [7, 20, 21]. There were no significant relationships (teaching language N400 effect and: total teaching years r=0.328, p=0.252; AOE r= 0.264, p=0.362; LA− use r=0.412, p=0.144; BNT r=0.100, p=0.734; BVAT r=0.029, p=0.921; non-teaching language N400 effect and: AOE r=0.266, p=0.358; LA− use r=0.203, p=0.486; BNT r=0.071, p=0.810; BVAT r=0.010, p=0.973).

LPC (500–900 ms)

Mean LPC amplitude was not different between the teaching and non-teaching languages in either group. There was a localized interaction between Group and Congruency and Laterality (F_(1,12)=5.14, p=0.043 η²=0.30). Post-hoc region of interest analyses with 7 medial-central electrodes in a narrower window (450–850ms) revealed larger LPC amplitude for incorrect than correct trials for LA− teachers (p=0.030), but no difference for LA+ teachers (p=0.798) (red highlight, Figure 1A). No other theoretically relevant effects reached significance.

Discussion

Spanish-English bilingual elementary school teachers judged the correctness of simple multiplication problems, presented as number words in each of their languages. The critical manipulation was that half taught primarily in their language of learning arithmetic, or LA+, and half in their other language, LA−. We recorded accuracy, delayed response times and event related potentials to the solutions.

The behavioral results showed no effects of congruency, teaching language or group, perhaps because of the very fast and accurate responses in this population (i.e., floor/ceiling effects, respectively). In contrast, ERPs revealed a subtle difference in brain activity between the groups. A main effect of congruency showed larger negative amplitude for incorrect than correct solutions in the N400 window, consistent with several studies showing an Arithmetic N400 in monolinguals and bilinguals [11, 23–26]. This N400 effect (incorrect minus correct trials) was present for both LA+ teachers and LA− teachers, and in both the teaching and non-teaching languages. However, it was modulated differently across languages and groups in 2 ways.

First, the N400 congruency effect peaked earlier for the teaching than non-teaching language in both groups. Second, amplitude of the effect was larger for the teaching than non-teaching language only for LA+ teachers, where LA+ continued to be the most frequently used language for arithmetic. For LA− teachers, where LA− was used more frequently for arithmetic on a daily basis, equivalent N400 effects were observed for the teaching and non-teaching languages. Finally, a focal LPC congruency effect was observed only for LA− teachers, where larger positive amplitude was observed for incorrect than correct solutions.

The lack of behavioral effects may reflect the extensive experience that elementary school teachers have with multiplication tables. This experience is what made bilingual teachers an ideal sample for testing the malleability of the bilingual arithmetic system. Bilingual teachers are a diverse population [unlike 3] that can use arithmetic in their LA− in a naturalistic setting, without explicit relearning [unlike 28]. The sample was limited, however, even for the extensive bilingual community in San Antonio, Texas. A future multi-city study with teachers, and analysis of performance in other populations like bilingual children, will speak to the generalizability of our findings. Nevertheless, our findings support malleability of multiplication fact representation and use.

We hypothesized that teaching in LA− would strengthen access to arithmetic facts in LA−, as indexed by the amplitude of the N400 congruency effect. Our findings revealed a larger effect in the teaching than non-teaching language only for LA+ teachers. That is, the language of learning arithmetic (LA+) remained the more efficient language for processing simple arithmetic when the LA+ was also the more frequently used language for arithmetic facts. In contrast, equivalent N400 congruency effects were observed in the teaching and non-teaching languages for LA− teachers, indicating that experience using LA− for math facts can eliminate the LA− disadvantage. These findings implicate more efficient access to math facts in the language that is most frequently used for these facts regardless of which language the facts were learned in during childhood. Given that these changes occurred in adulthood indicates that the memory network for arithmetic facts is more flexible than can be inferred from prior research [26].

In both groups, the N400 congruency effect peaked ~20 ms earlier for the teaching than non-teaching language. LA+ teachers and LA− teachers differed significantly in their frequency of using each of their languages, because of the amount of time they spent teaching in one language. The groups did not differ in language proficiency in either language. This lends support to the hypothesis that it is experience using math facts in a language that increases efficiency of access to these facts, and not other factors like proficiency. However, frequency of use did not modulate the LA+ N400 congruency effect. This may indicate that LA+ has reached a maximum level of efficiency for accessing math facts in these individuals, or it may indicate that LA+ is less malleable than the LA−. Perhaps during early learning of math facts the LA+ might be more influenced by frequency of use. Additional research is needed to determine the limits of this LA− malleability with experience, and which, if any, factors can modulate LA+.

We also hypothesized that a late positive component (LPC) would occur subsequent to the N400, especially in LA− teachers who would experience more conflict between their languages in later stages of controlled processing. Incorrect solutions elicited larger positivity at the LPC than correct solutions only in LA− teachers (Figure 1A). There was no LPC effect for LA+ teachers (Figure 1A). Thus, although LA− teachers show evidence of equivalent efficiency of access to multiplication facts in both languages, as indexed by the N400, conflict between the languages induced a processing cost, as indexed by the LPC. The degree of conflict between the LA+ and LA− was greater for LA− teachers than LA+ teachers, because LA− had been strengthened through experience. There is accumulating evidence that bilinguals activate both languages, and that the stronger language causes greater interference, even when only one language is in use [13, 33]. The verbal memory networks for multiplication facts may also be simultaneously active for both languages in these bilinguals, with a stronger LA− causing greater interference for LA− than LA+ teachers. These findings are also in line with the conflict monitoring response hypothesis [29, 30], which argues that a P600, which has similar timing and morphology to the LPC, arises when there is competition between words (e.g., an unexpected plausible word) or when there is conflict between accepting and rejecting a word (e.g., a semantically correct, misspelled word). Equivalent LA+ and LA− representations of arithmetic facts in verbal memory may create competition when judging the correctness of the solutions.

In brief, these ERP results suggest that it is possible to alter the organization of and access to multiplication facts in the LA−, mitigating the LA− disadvantage in bilinguals.

Conclusion

The current findings provide evidence that the adult bilingual arithmetic memory network is sensitive to the effects of experience. With experience, access to bilingual arithmetic facts in LA− can be strengthened resulting in comparable processing as in LA+. Therefore, bilinguals are capable of restructuring simple arithmetic associations, indicating that both early learning and later use of arithmetic facts affect the efficiency of accessing these facts from memory. With bilingualism continuing to grow and bilingual education becoming ever more popular, this finding has fundamental implications for the long-term effects of teaching the increasing number of children in the US who are bilingual.

Highlights.

• A bilingual’s language of learning (LA+) shows an advantage for arithmetic facts.

• N400 congruity effect was measured for simple multiplication in bilingual teachers.

• LA+ teachers maintained an LA+ advantage over their other language (LA−).

• Teaching in LA− results in similar brain activity for LA+ and LA−.

• Experience in adulthood can diminish the LA− disadvantage. Abstract