A computational method for computing an Alzheimer’s Disease Progression Score; experiments and validation with the ADNI dataset

Abstract

Understanding the time-dependent changes of biomarkers related to Alzheimer’s disease (AD) is a key to assessing disease progression and to measuring the outcomes of disease-modifying therapies. In this paper, we validate an Alzheimer’s disease progression score model which uses multiple biomarkers to quantify the AD progression of subjects following three assumptions: (1) there is a unique disease progression for all subjects, (2) each subject has a different age of onset and rate of progression, and (3) each biomarker is sigmoidal as a function of disease progression. Fitting the parameters of this model is a challenging problem which we approach using an alternating least squares optimization algorithm. In order to validate this optimization scheme under realistic conditions, we use the Alzheimer’s Disease Neuroimaging Initiative (ADNI) cohort. With the help of Monte Carlo simulations, we show that most of the global parameters of the model are tightly estimated, thus enabling an ordering of the biomarkers that fit the model well, ordered as: the Rey auditory verbal learning test with 30 minutes delay, the sum of the two lateral hippocampal volumes divided by the intra-cranial volume, followed by (the clinical dementia rating sum of boxes score and the mini mental state examination score) in no particular order and lastly the Alzheimer’s disease assessment scale-cognitive subscale.

1. Introduction

The ability to precisely identify the stage of disease, predict the rate of disease progression, and accurately measure the outcomes of potential therapies [8, 11] is critical to the successful management of Alzheimer’s disease (AD). The classical characterization of late-onset Alzheimer’s disease progression is a time-ordered succession of three stages: normal (N), mild cognitive impairment (MCI), and AD. Physical measurements of disease progression, i.e., biomarkers, are used to classify patients into these three stages, but it has been challenging to reliably define finer stages of the disease. In [5], we have proposed a method for computing an Alzheimer’s Disease Progression Score (ADPS) by computationally combining seven biomarkers of AD. A bi-product of this study was a temporal ordering of the biomarkers. Experiments conducted on the combined AD Neuroimaging Initiative (ADNI) I, GO, and II datasets provided an ordering of the biomarkers which was consistent with [4] except for a cognitive test, the Rey Auditory Verbal Learning Test, 30 minutes recall (RAVLT30), which was found to become dynamic very early in the development of the disease. The statistical validation of this ordering was performed by resampling from the collection of subjects. Since the statistical model used is a regression, it can be argued that an additional validation would be obtained by sampling from the residuals.

In this paper we validate the methodology presented in [5] using the technique of sampling from the residuals. We adopt the model-based bootstrap that is widely employed in regression analysis (see, [14, 7], and references therein) and time series ([1, 12]) and has become increasingly popular for inference of longitudinal processes ([15, 10]). The benefit of the proposed approach is that it enables us to quantify estimation uncertainty and impute missing values [3]. The rest of this paper is organized as follows: in Section 2.1 we present the statistical model. The optimization algorithm used for fitting the parameters is presented in Section 2.2. The ADNI dataset and the selection of the biomarkers is presented in Sections 2.3 and 2.4 respectively. Section 2.5 motivates and then describes the sampling method. The results are presented in Section 3 followed by a discussion of our findings in Section 4. Concluding remarks are presented in Section 5.

2. Method

Our research first describes then evaluates an algorithm for computing an Alzheimer’s disease progression score (ADPS), which assigns a time dependent score to each subject.

2.1. Statistical Model

The method we use is based on three assumptions:

1. All subjects follow a common disease progression but differ in their age of onset and rate of progression;

2. As the disease progresses, each biomarker changes continuously and monotonically following a sigmoid shaped curve; and

3. In the longitudinal period over which biomarkers are observed, the rate of progression for a given subject is constant.

The proposed computation positions the longitudinal measurements of each subject on a common disease progression scale. Since it is considered to be a common scale, all subjects are expected to undergo the same biological and cognitive changes when they reach the same value (or score) on this scale. Thus, individuals are generally mapped to different positions on this scale and they progress at different rates regardless of their age of disease onset.

The age t of subject i is to be transformed into the ADPS s_i as

$$s_i(t)={\alpha }_{i}t+{\beta }_i$$ (1)

after estimation of the subject dependent parameters α_i and β_i, which indicate rate and onset of disease, respectively. A linear transformation is justified because the interval over which longitudinal observations of the ADNI subjects occur is short relative to the overall disease duration. Our objective is to compute a score for all I subjects in the ADNI database by estimating α = (α₁, …, α_I) and β = (β₁, …, β_I). The subject dependent parameters α and β are deliberately modeled as fixed effects, not random effects, as the ADPS may ultimately be used as a covariate.

The longitudinal dynamic of each biomarker is assumed to be the same across the population and can be represented as a sigmoidal function f of ADPS s. Using θ_k = (a_k, b_k, c_k, d_k) to represent the vector of sigmoid function parameters for the k-th biomarker, we can write the form of the the k-th biomarker as

$$f(s;{\theta }_k)=a_k{(1+e^{-b_k(s-c_k)})}^{-1}+d_k.$$ (2)

The minimum and maximum values of the sigmoid function are d_k and d_k + a_k, and the value of s for which the biomarker is the most dynamic, having maximum slope a_kb_k/4 corresponding to its inflection point, is c_k. Sigmoids offer a parsimonious parametric model which is often a better fit than linear models for biomarkers [2, 13]. They are also similar in form to the conceptual evolution of biomarkers envisioned by Jack et al. [4] (Fig. 1). A comparison of different shapes (linear, sigmoid, quadratic, splines) of various biomarkers as function of ADAS-COG is presented in [9]

Figure 1.

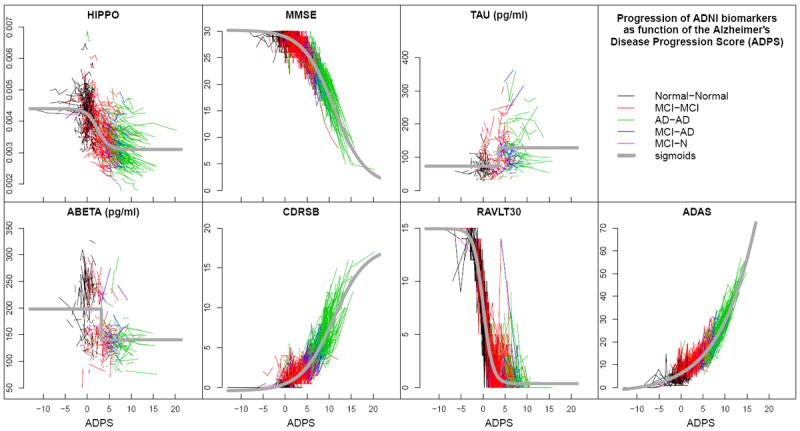
The values of seven biomarkers, measured at all visits of all ADNI subjects, are plotted on the normalized ADPS. Each connected polyline represents the consecutive visits of a single subject, and each line segment is colored according to the subject’s clinical diagnoses between visits (see legend). The gray curves are the sigmoid functions representing the fitted behavior of each biomarker in the normalized space. (Reproduced from [5])

The ADNI database contains measurements y_ijk of biomarker k for subject i at visit j. Since there are irregularities in data collection, we use I to denote the set of triples (i, j, k) for which measurements are available. Each biomarker observation can be written as

$$y_{\mathit{ijk}}=f({\alpha }_i{t}_{\mathit{ij}}+{\beta }_i;{\theta }_k)+{\sigma }_k{\epsilon }_{\mathit{ijk}},\left(i,j,k\right)\in I,$$ (3)

where t_ij is the age of subject i at visit j. Observation noise in each biomarker is modeled for simplicity by the product of ε_ijk, which are independent random variables with zero mean and unit variance, and σ_k, which is the standard deviation of biomarker k. The collection of standard deviations σ = (σ₁, …, σ_K) comprise another unknown that must be estimated.

The unknowns in this problem are α, β, θ, and σ and the least squares problem associated with the observation model in (3) is

$$\begin{array}{l}l\left(\alpha ,\beta ,\theta ,\sigma \right)\\ =\sum _{\left(i,j,k\right)\in I}\log {\sigma }_k+\frac{1}{2{\sigma }_k^2}{(y_{\mathit{ijk}}-f({\alpha }_i{t}_{\mathit{ij}}+{\beta }_i;{\theta }_k))}^2.\end{array}$$ (4)

Necessary conditions on the available data I for guaranteeing the identifiability of the parameters are as follows:

1. For each biomarker, there is at least one subject i with α_i ≠ 0 and with at least four distinct time-points in I.

2. For each subject, there is at least one biomarker which is available at two time points in I

In practice, a sufficient number of data points per parameter is needed in order to obtain tight estimators. Examining first the case with no missing data, the number of equations in (3) is IJK where I is the number of subjects, J is the number of time-points and K is the number of biomarkers. The number of parameters is 2I + 5K, counting two parameters per subject, and five per biomarker (four for the sigmoid and one for the standard deviation). In applications where I is large compared to K, the number of data points per parameter is close to JK/2. Note that longitudinal data (J > 1) is critical for such modeling. However, a small number J of time-points together with a small number K of biomarkers is in principle acceptable. The subset of ADNI presented in Section 2.4 has numerous missing data points. We will use simulations to study the quality of the estimation of the parameter c for each biomarker. This parameter is critical for ordering the biomarkers.

2.2. Parameter Fitting

Parameter fitting is performed using alternating least squares wherein the parameters θ, α, β, and σ are optimized iteratively starting from the values computed in the previous step. The details of the fitting algorithm are shown in Alg. 1. The initial values (Line 1) are α⁽⁰⁾ ≡ 1 and β⁽⁰⁾ ≡ 0. Because of the additive form of (4), optimization over θ is done serially over each of the K biomarkers while keeping (α and β fixed). Similarly, optimization over (α, β) is performed serially over each of the I subjects while keeping θ fixed. Fitting of θ, α, and β requires optimization of continuously differentiable nonconvex functions, which is carried out using the Levenberg-Marquardt algorithm [6] (Lines 4 and 8). I_k (line 4) is the number of subjects and visits available for biomarker k. The denominator in the equation of Line 5 is the number of degrees of freedom. A canonical way to parameterize sigmoid functions is to constrain the parameter b_k in (2) to be non-negative. This is enforced with the loop over biomarkers (Lines 12–16), which does not modify the objective function in (4). Our experiments confirm that successful fitting is accomplished in 30 iterations; i.e., L = 30 on Line 2.

Algorithm 1.

Algorithm for the fitting of the parameters

1: Inititialize α(0), β(0)

2: for l = 1 to L do

3:  for k = 1 to K do

4:    ${\theta }_k^{(1)}=\arg {\min }_{{\theta }_k}{\sum }_{(i,j)\in I_k}{(y_{\mathit{ijk}}-f({\alpha }_i^{(0)}{t}_{\mathit{ij}}+{\beta }_i^{(0)};{\theta }_k))}^2$

5:    ${\sigma }_k^{{(1)}^2}=\frac{1}{|I_k-2I-4|}{\sum }_{(i,j)\in I_k}{(y_{\mathit{ijk}}-f({\alpha }_i^{(0)}{t}_{\mathit{ij}}+{\beta }_i^{(0)};{\theta }_k^{(1)}))}^2$

6:  end for

7:  for i = 1 to I do

8:    $({\alpha }_i^{(1)},{\beta }_i^{(1)})=\arg {\min }_{{\alpha }_i,{\beta }_i}{\sum }_{(j,k)\in I_i}\frac{1}{{\sigma }_k^{{(1)}^2}}{(y_{\mathit{ijk}}-f({\alpha }_i{t}_{\mathit{ij}}+{\beta }_i;{\theta }_k^{(1)}))}^2$

9:  end for

10:  α(0) = α(1); β(0) = β(1)

11: end for

12: for k = 1 to K do

13:  if bk < 0 then

14:    $a_k^{(1)}=-a_k^{(1)},b_k^{(1)}=-b_k^{(1)},d_k^{(1)}=d_k^{(1)}+a_k^{(1)}$

15:  end if

16: end for

17: for i = 1 to I do

18:   ${\alpha }_i^{(1)}=\frac{{\alpha }_i^{(1)}}{{\sigma }_N},{\beta }_i^{(1)}=\frac{{\beta }_i^{(1)}-m_N}{{\sigma }_N}$

19: end for

The units of ADPS are arbitrarily defined, which implies that we must choose two specific numerical values in order to fully specify the ADPS. This situation is analogous to the selection of a scale for temperature, where the numerical values of the freezing and boiling points of water determine the scale. In our experiments we chose to fix the ADPS such that after computation over the entire population, the computed ADPS for all visits of subjects with normal clinical assessment had a trimmed mean value (m_N) and a trimmed standard deviation (σ_N) which are set respectively to zero and one. This is accomplished in Lines 17–19.

2.3. The Alzheimer’s Disease Neuroimaging Initiative cohort

Data used in the preparation of this article were obtained from the Alzheimers Disease Neuroimaging Initiative (ADNI) database (http://adni.loni.ucla.edu/). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public private partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimers disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California San Francisco. ADNI is the result of efforts of many coinvestigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 adults, ages 55 to 90, to participate in the research, approximately 200 cognitively normal older individuals to be followed for 3 years, 400 people with MCI to be followed for 3 years and 200 people with early AD to be followed for 2 years. For up-to-date information, see www.adni-info.org.

2.4. Biomarker selection

The available data in ADNI are measurements in elderly humans of multiple biomarkers associated with Alzheimer’s disease. Hundreds of subjects, categorized into N, MCI, and AD, were examined at baseline and with repeat visits every 6 to 12 months for a period of up to 60 months.

The following seven biomarkers were selected for use based on their relevance in assessing the progression of AD.

1. the sum of the two lateral hippocampal volumes¹ normalized by dividing by the intra-cranial volume (HIPPO);

2. the Alzheimer’s Disease Assessment Scale-cognitive subscale (ADAS);

3. the Mini-Mental State Examination score (MMSE);

4. the Aβ₄₂ protein level measured from the cerebrospinal fluid (ABETA);

5. the Tau protein level measured from the cerebrospinal fluid (TAU);

6. the Clinical Dementia Rating Sum of Boxes score (CDRSB);

7. the Rey Auditory Verbal Learning Test, 30 minutes recall (RAVLT30)

A detailed description of the ADNI population, protocols and biomarkers is provided at http://adni.loni.ucla.edu/.

The ADNI, ADNI GO, and ADNI 2 biomarker datasets were downloaded from the ADNI server (http://adni.loni.ucla.edu/) on November 24, 2011. All visits without date information were removed. Subjects not having at least two measurements for at least one of the seven biomarkers were also removed. Subjects not having at least two measurements of the HIPPO biomarker were removed. The total number of subjects remaining was 687, where 389 were male, 275 were female, and 23 had unknown sex. The total number of visits was 3658, and the clinical diagnoses at these visits were 1103 normal, 1513 MCI, and 1010 AD² Of the seven biomarkers considered, only ADAS and RAVLT30 were available at the time of download from the ADNI 2/GO dataset. The protocol for these biomarkers is the same in ADNI, ADNI 2, and ADNI GO.

2.5. Sampling from the residuals

The analysis of a longitudinal, simultaneously acquired collection of biomarkers of ADNI dataset is a complex task for several reasons. First, for each biomarker, the sequences of measurements obtained across time point are correlated. Table 1 shows the correlation between measurements taken at baseline and at one year after baseline. The correlation is larger than 0.7 for all the biomarkers and is as high as 0.98 in case of the volume of the hippocampus over all subjects.

Table 1.

Correlation coefficient for each biomarker between the measurements at baseline and 1 year after baseline

Biomarker	Correlation coef.	Biomarker	Correlation coef.
HIPPO	0.98	ADAS	0.83
MMSE	0.74	TAU	0.93
ABETA	0.94	CDRSB	0.85
RAVLT30	0.8

Secondly, the structure of the missing data in ADNI is complex. The schedule of visits depends on the status (N, MCI, AD) at baseline and is different for different biomarkers³. Moreover, the subjects are recruited over a relatively long period; hence the number of available measurements at an earlier visit (e.g. baseline) is significantly larger than at a later one (e.g. baseline plus 36 months). Table 2 shows the proportion of available measurements relative to the total number of subjects for each of the 7 selected biomarkers and each time-point.

Table 2.

Proportion in % of available data for each biomarker and each time point. The denominator is the number of subjects with ADAS measurement at baseline. Note that only MCI subjects have a visit at 18 month after baseline which explains why the numbers are lower for all the biomarkers at the 18 months visit.

Time-point	HIPPO	ADAS	MMSE	TAU	ABETA	CDRSB	RAVLT30
baseline	99	100	100	53	53	100	99
+6 months	97	99	99	0	0	99	99
+12 months	96	99	99	45	45	98	98
+18 months	40	45	45	0	0	45	45
+24 months	73	88	88	13	13	87	86
+36 months	20	62	64	3	3	62	63

We now describe the sampling from the residual algorithm which we employ. The key idea is to construct a bootstrap distribution of y_ijk while taking into account its dependence structure, which then can be employed for inference and imputation purposes. In particular, the residuals ε_ijk are ideally independent and identically distributed (i.i.d.). However, since measurements are taken consecutively over time, this is not the case, as Table 1 indicates. Thus, we can attempt to filter out temporal dependence among ε_ijk by applying an appropriate filter (e.g., an autoregressive model), and the resulting new filtered residuals η_ijk should be close to the i.i.d. assumption. Hence, given conditional independence of η_ijk, we can employ the classical bootstrap and sample new realizations of ${\eta }_{\mathit{ijk}}^{\ast }$ from the estimated empirical probability distribution of η_ijk. Substituting in the sampled ${\eta }_{\mathit{ijk}}^{\ast }$ into the filter yields new bootstrap residuals, ${\epsilon }_{\mathit{ijk}}^{\ast }$ which in turn can be plugged-in into the estimated model (3) and the new proxy bootstrap values $y_{\mathit{ijk}}^{\ast }$ are thus obtained. The resulting bootstrap distribution of $y_{\mathit{ijk}}^{\ast }$ serves as a proxy to the unknown distribution of y_ijk, and can be employed to assess errors in parameter estimation and imputation of missing values as described in the Algorithm 2 below.

Algorithm 2.

Algorithm for sampling from the residuals

1: Sample ηijk independently from a standard Normal distribution, assuming no missing data;

2: Compute εijk using the AR(1) model, imputing the values ηijk as residuals;

3: Compute yijk using the model (3), imputing εijk as residuals;

4: Determine the missing data for each biomarker with the following sampling procedure: Sample from a 2 state (not available (NA), not NA) non-homogeneous Markov chain indexed by the successive visits. The transition matrix was estimated separately for each status at baseline (N, MCI and AD) and before hand.

5: Estimate all the parameters from the simulated dataset with missing data obtained at the last step using Alg. 1. Notate $c_k^{(m)}$ the estimated parameter c for biomarker k at iteration m.

In order to assess the quality of the parameter fitting algorithm presented in Alg. 1, we generated a large number (M = 40, 000) of simulated datasets by sampling from the residuals as follows. First, we estimated all of the parameters in the model using Alg. 1 and the ADNI dataset. Second, we computed the residuals ε_ijk from (3). Since these residuals showed correlation over time for each biomarker, we fit an autoregressive AR(1) model for the residuals of each biomarker. We then repeated the procedure described in Alg. 2 M = 40, 000 times.

3. Results

3.1. ADPS computed for ADNI subjects

The ADPS was computed for all subject visits in the combined ADNI, ADNI 2, and ADNI GO data sets (with minimal exclusions as described in Section 2.4). Results are presented in Fig. 1. Overall, Normal subjects (black) have the smallest ADPS, MCI subjects (red) have moderate ADPS, and AD subjects (green) have the largest ADPS. Lower ADPS are therefore consistent with the normal population and higher ADPS are indicative of increased presence of dementia. Those subjects whose clinical status changes from MCI to AD (blue) are found mostly between the red and green colors. The estimated sigmoidal behaviors of each biomarker are shown in gray.

3.2. Assesment of the quality of the estimation of the inflection point of each biomarker curve

The estimator of the parameter c_k for biomarker k using the ADNI dataset is denoted $c_k^T$, where “T” stands for “Target”. Each sampling from the residuals, indexed by m, produces a simulated dataset from which an estimator of c_k is computed using Alg. 1 and is notated $c_k^{(m)}$. The histograms for the data ${\{c_k^{(m)}-c_k^T\}}_{m\in \{1;\dots ;40,000\}}$ for each biomarker k are presented in Fig 2. In comparing k these histograms, be advised that the scale of the horizontal axis is not the same for each biomarker. Recall that the parameter c_k, the inflection point of each sigmoid, records the moment in the disease progression where the biomarker k changes the most (is the most dynamic). First, consider the biomarkers HIPPO, TAU, ABETA, and RAVLT30. The mean square error for these estimators is small. Indeed, the histograms obtained by sampling from the residuals are centered close to the origin with a small standard deviation. These results give validity to the choices and the settings of the optimization algorithm. Second, in the case of MMSE and CDRSB, some bias is observed and the standard deviation is moderated. Finally, in the case of ADAS, the bias as well as the standard deviation are larger. Note that the fitted sigmoids for these three biomarkers do not level off in the later stages of the disease (see Fig 1), which might explain why the fit is less stable (large bootstrap standard deviation). One remedy to stabilize the estimation could be to constrain the extremal values, d_k and d_k + a_k. For example, the maximum value for ADAS is 70 which could be enforced during the optimization process.

Figure 2.

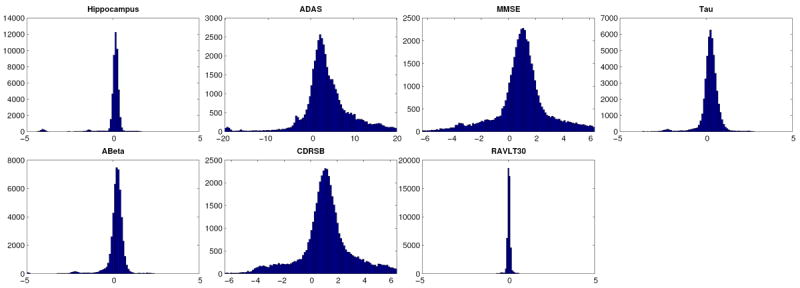
Distribution of the errors in estimating the parameter c of the sigmoid (see (2)) as function of the progression time-line of the disease.

3.3. Ordering of the biomarkers

For each simulation, the parameter c_k, i.e. the inflection point of the sigmoid fitted to biomarker k, was obtained and the summary of the ordering of the c_k values for each of the 40,000 simulations is presented in Table 3. Clearly, the ordering the most prevalent is as follows: RAVLT30, HIPPO, ABETA, TAU, then (CDRSB, MMSE) in no particular order and then ADAS. This result is consistent with our results obtained in [5] where the statistical method used to assess this ordering, i.e., resampling from the subjects, was different than the method used here, i.e, sampling from the residuals. Care should be taken in interpreting this result in term of the ordering of the biomarkers. In particular, ABETA and TAU biomarkers are not well explained by the model, see Fig. 1. One can visually see that there is a large residual variance in the case of these two biomarkers by comparing the spread of the data points around the sigmoid curves in grey. As a consequence, we prefer to eliminate these biomarkers from our analysis and propose the following ordering of the biomarkers: RAVLT30, HIPPO, then (CDRSB and MMSE) in no particular order then ADAS.

Table 3.

Ordering of the biomarkers according to the location of the inflection point. For each biomarker (line), the value recorded in column j is the number of times, in percent, this biomarker has an inflection point which is the j^th smallest out of the seven biomarkers. This was computed using 40,000 independent samples. The results are truncated to the nearest tenth of a percent.

	#1	#2	#3	#4	#5	#6	#7
RAVLT30	99.7	0.3	0	0	0	0	0
HIPPO	0	99.4	0.4	0.1	0	0.1	0
ABETA	0.1	0.2	95.9	3.7	0	0	0
TAU	0.1	0.1	3.8	96	0	0	0
CDRSB	0	0	0	0.1	65.4	33.5	1
MMSE	0	0	0	0	32.3	66	1.7
ADAS	0	0	0	0	2.2	0.4	97.3

4. Discussion

Amyloid concentration in the brain is known to change very early in the disease process [17, 18]. Why is it then that we do not detect an early change of ABETA? There are several non-exclusive possible explanations. One is that ABETA is a noisy measurement of the amyloid burden, eventually contaminated by one or several physiological covariates. A complementary explanation is that there are several paths to disease within the ADNI subjects. For example, there might be MCI or even AD subjects who are impaired for reasons unrelated to Alzheimer’s (depression, tau only pathologies, vascular dementia). Recall that the first assumption in our model is that there is a unique disease progression for all the subjects. A violation of this hypothesis would result in a lack of fit for some of the biomarkers and could also modify our conclusions about the ordering of the biomarkers.

The fact that the RAVLT30 biomarker is dynamic early in the disease process is an interesting result which deserves further investigations in ADNI. Using data from the Canadian Study of Health and Aging, it was found in [16] that the RAVLT was predictive of neurodegenerative changes up to 10 years prior to diagnosis Also, early changes in the hippocampus volume might occur very early in the disease process while being too subtle to be detected with the current protocol and that progress in the acquisition and/or image processing technology might reveal these subtleties. Finally, the reader is reminded that the results were obtained for the ADNI dataset as of November 4th 2011 and do not necessarily extrapolate to a larger or different population.

5. Conclusion

We have presented a validation of a multi-biomarker, data-driven approach to assess time-dependent changes of biomarkers in AD and to localize subjects on a common scale of disease progression over the entire range of progression represented in the ADNI cohort. The sampling from the residuals analysis show that the inflection point of the biomarker sigmoid curves are well estimated for most biomarkers. Our presented model and subsequent validation argue that the following ordering of the biomarkers should be considered: RAVLT30, HIPPO, then (CDRSB and MMSE) in no particular order and lastly ADAS.