Accelerated MRI Thermometry by Direct Estimation of Temperature from Undersampled k-Space Data

Abstract

Purpose

Acceleration of MR thermometry is desirable for several applications of MR-guided focused ultrasound, such as those requiring greater volume coverage, higher spatial resolution, or higher frame rates.

Theory and Methods

We propose and validate a constrained reconstruction method that estimates focal temperature changes directly from k-space without spatial or temporal regularization. A model comprising fully-sampled baseline images is fit to undersampled k-space data, which removes aliased temperature maps from the solution space. Reconstructed temperature maps are compared to maps reconstructed using parallel imaging (SPIRiT) and conventional hybrid thermometry, and temporally-constrained reconstruction (TCR) thermometry.

Results

Temporal step response simulations demonstrate finer temporal resolution and lower error in 4×-undersampled radial k-space reconstructions compared to TCR. Simulations show that the k-space method can achieve higher accelerations with multiple receive coils. Phantom heating experiments further demonstrate the algorithm’s advantage over reconstructions relying on parallel imaging alone to overcome undersampling artifacts. In vivo model error comparisons show the algorithm achieves low temperature error at higher acceleration factors (up to 32× with a radial trajectory) than compared reconstructions.

Conclusion

High acceleration factors can be achieved using the proposed temperature reconstruction algorithm, without sacrificing temporal resolution or accuracy.

Introduction

Recent technological developments have combined thermal therapies with MRI for targeting, temperature monitoring and assessment of thermal dose in the brain and body [1]. In particular, MRI-guided focused ultrasound (MRgFUS) is increasingly being applied to treat uterine fibroids and cancer [2–5], relieve pain from bone metastases [6, 7], and stimulate deep brain tissue to treat neurological conditions [8, 9]. Additionally, animal studies have demonstrated that MRgFUS can induce gene expression [10] and also facilitate drug delivery [11], even across the blood-brain barrier [12, 13].

In MRgFUS, ultrasound energy is generated outside the body and delivered noninvasively to a specific location within the tissue, ideally without affecting any tissues outside the targeted volume. The primary role of MRI in the procedures is to provide images with soft tissue contrast for targeting, and to provide real-time temperature measurements to monitor thermal dose to the targeted tissue, where temperature measurements are conventionally based on the proton resonance frequency shift with temperature. While acoustic energy is nominally focused to a single point in the body, there is an ever-present risk that dangerous heating may occur in other regions in the near-and far-fields of the transducer, so it is desirable to measure temperature rises with as high a frame rate as possible throughout the tissue to ensure patient safety. However, MRgFUS procedures are currently limited to 2D temperature imaging of a handful of slices in real-time. For example, typical thermometry protocols for closed-loop ablation of uterine fibroids use spoiled gradient echo or multishot echo-planar imaging (EPI) to image up to six slices [14, 15] approximately every three seconds. However, due to their limited volume coverage those scans can miss dangerous heating that can occur outside the target volume, particularly near tissue interfaces and bones [16]. Some form of scan acceleration is required to simultaneously achieve large volume coverage and a high frame rate in thermometry, using either pulse sequences that acquire k-space data faster [17] or temperature reconstructions that do not require full k-space data.

Temperature reconstruction-based approaches to accelerating MR thermometry can be loosely grouped into three categories: parallel imaging, compressed sensing, and temporal regularization-based approaches. Parallel imaging with multiple receive coils is commonly used to accelerate anatomical and functional MR imaging [18, 19], and has been applied to thermometry [20–24]. However, to achieve high accelerations, parallel imaging requires many coils in close proximity with the body, which is often impossible in MRgFUS since the FUS apparatus is large and must be in direct contact with the body. Because of these limitations, the development of MRgFUS-compatible coil arrays is an active area of research, and state-of-the-art arrays still comprise many fewer coils than are typically used in conventional parallel imaging [25–27].

Compressed sensing [28] has also been applied to MR thermometry [29, 30]. However, these techniques rely on compressibility of image magnitude to constrain the solution space, and errors can arise when the phase component of the image contains high spatial frequency variations such as those caused by heating [31]. Furthermore, compressed sensing must typically be combined with parallel imaging to achieve high accelerations. Compressed sensing reconstructions that incorporate phase regularization have been proposed for thermometry [31, 32], but to date no such method has been described that robustly enables high acceleration factors in a wide variety of acquisition scenarios.

Temporal regularization-based approaches [24, 33–35] assume that images or temperature change slowly during treatment. For example, the temporally constrained reconstruction (TCR) method [33] jointly reconstructs treatment images using a temporal roughness penalty. This enables acceleration when the k-space undersampling pattern is alternated in time so that aliasing artifacts move between consecutive images and are filtered out by the penalty. Other temporal regularization-based approaches have leveraged the bioheat equation and/or Kalman filtering, either to similarly suppress rapidly-changing aliasing artifacts while preserving slower temperature changes, or to interpolate between fully-sampled temperature images acquired at a lower frame rate [34, 35]. While all these approaches are capable of producing temperature maps at any desired frame rate, due to regularization their true temporal resolution lies somewhere between the accelerated and fully-sampled frame rates. Furthermore, the alternating k-space sampling patterns required by some methods may lead to increased eddy current distortions, and generally limit pulse sequence design.

This work introduces an approach to accelerated temperature imaging that is based on fitting a constrained treatment image model directly to undersampled k-space data. Because the treatment image model comprises fully-sampled pretreatment/baseline images, aliased temperature maps are removed from the solution space, without temporal regularization. The method is compatible with parallel imaging and can be used with any readout trajectory. Simulations will demonstrate improvements in temporal resolution compared to TCR, that the method is compatible with and benefits from multicoil receive, and that it is robust to motion and rapidly-varying background anatomical phase. Experiments will investigate in vivo model error as a function of acceleration, and compare the method to conventional parallel imaging reconstructions. Aspects of this work have been previously reported elsewhere [36, 37].

Theory

Signal Model and Problem Formulation

The proposed method estimates temperature maps from undersampled k-space data by fitting a constrained image model directly to the data, without an explicit image reconstruction step. The hybrid multibaseline and referenceless treatment image model is used [38], which comprises a weighted combination of fully-sampled baseline images acquired prior to heating, a polynomial phase shift to model center frequency drift and other bulk phase shifts unrelated to heating, and a spatially-sparse heating-induced phase shift. When applied to estimate temperature maps from fully-sampled images, hybrid thermometry has been shown to produce accurate temperature measurements in the human brain and porcine liver with FUS heating [39, 40], and in the human heart and liver with motion [38].

The k-space signal model is the discrete Fourier transform (DFT) of the hybrid image model:

$$y_i=\sum _{j=1}^{N_s}{e}^{i{\overrightarrow{k}}_i·{\overrightarrow{x}}_j}\left(\sum _{l=1}^{N_b}{b}_{l,j}{w}_l\right)e^{i\left({\{\mathit{Ac}\}}_j+{\theta }_j\right)}+{\epsilon }_i,$$ (1)

where y_i is one k-space data sample, i = 1, …, N_k indexes the N_k acquired samples, N_s is the number of image voxels, k⃗_i is the k-space location of sample i, the ${\{{\mathit{b}}_l\}}_{l=1}^{N_b}$ are complex baseline library images reconstructed from fully-sampled k-space data acquired prior to treatment, the w_l are baseline image weights, A is a matrix of smooth (e.g., low-order polynomial) basis functions, c is a polynomial coefficient vector, θ is a heating-induced phase shift, which is negative for a temperature increase [41] and is assumed to contain mostly zero entries, and ε is complex Gaussian noise. The role of the baseline library images ${\{{\mathit{b}}_l\}}_{l=1}^{N_b}$ is to capture physiological and anatomical amplitude and phase variations across respiratory and cardiac cycles. The role of the polynomial phase shift Ac is to model phase changes induced by smooth magnetic field shifts, such as center frequency drift and those caused by respiration and bowel filling. The phase shift θ that results from targeted heating is modeled as a focal shift separate from these other phase components. Sparsity of θ is exploited by the algorithm to separate it from the polynomial phase shift, and reflects the fact that in a targeted thermal therapy like MRgFUS, temperature rises will occur in a minority of image voxels. To estimate θ, the signal model in Eq. 1 is fit to acquired k-space data ỹ by solving the constrained minimization problem:

$$\begin{array}{ll}\text{minimize}\hfill & \frac{1}{2}{\Vert \stackrel{\sim }{\mathit{y}}-\mathit{y}(\mathit{w},\mathit{c},\mathit{\theta })\Vert }^2+\lambda {\Vert \mathit{\theta }\Vert }_1,\hfill \\ \text{subject}\text{to}\hfill & \mathit{\theta }\underset{\_}{\prec }0\hfill \\ \hfill & {\sum }_{l=1}^{N_b}{w}_l=1\hfill \\ \hfill & \mathit{w}\underset{\_}{\succ }0,\hfill \end{array}$$ (2)

where the first term in the objective function is proportional to the negative log-likelihood of the data (when neglecting noise in the baseline images), ||θ||₁ is the ℓ₁ norm of θ, and λ is a regularization parameter that controls the sparsity of θ.

This method can reconstruct artifact-free temperature maps from undersampled k-space data because the fully-sampled baseline image component of the model removes images (and corresponding temperature maps) from the solution space that contain aliasing artifacts in their magnitude. Solutions containing aliasing artifacts in their phase that cannot be modeled by some combination of the baseline images, a polynomial phase shift and a sparse phase shift are also eliminated from the solution space.

Algorithm

A solution to the problem in Eq. 2 is found using the following alternating minimization algorithm, given initial estimates of w, c, and θ:

1. repeat

2. Update w: A quadratic programming problem,

   $$\begin{array}{ll}\text{minimize}\hfill & \frac{1}{2}{\Vert \stackrel{\sim }{\mathit{y}}-\mathit{G}\text{diag}\left\{e^{i\left({\{\mathit{Ac}\}}_j+{\theta }_j\right)}\right\}\mathit{Bw}\Vert }^2\hfill \\ \text{subject}\text{to}\hfill & {\sum }_{l=1}^{N_b}{w}_l=1\hfill \\ \hfill & \mathit{w}\underset{\_}{\succ }0,\hfill \end{array}$$ (3)

   is solved, where G is a (possibly non-uniform) DFT matrix, and B is a matrix whose columns are the baseline images.

3. Update θ: The following constrained minimization problem is solved using the nonlinear conjugate gradient (NLCG) algorithm described in the Appendix (J A Fessler, Image reconstruction: Algorithms and Analysis, to be published.):

   $$\begin{array}{ll}\text{minimize}\hfill & \frac{1}{2}{\Vert \stackrel{\sim }{\mathit{y}}-\mathit{G}\text{diag}\left\{e^{i{\theta }_j}\right\}\mathit{f}\Vert }^2-\lambda {\sum }_{j=1}^{N_s}{\theta }_j\hfill \\ \text{subject}\text{to}\hfill & \mathit{\theta }\underset{\_}{\prec }0,\hfill \end{array}$$ (4)

   where f_j ≜ e^i{Ac}_j {Bw}_j.

4. Update c: The update for c is similar to the θ update, except that the gradient, and consequently the NLCG search direction, incorporate the basis matrix A,

   $${\nabla }_{\mathit{c}}\mathrm{\Psi }={\mathit{A}}^{\prime }{\nabla }_{\theta }\mathrm{\Psi },$$ (5)

   and there are no nonpositivity constraints.

5. until Stopping criterion met

6. To eliminate temperature bias due to the ℓ₁ norm, steps 1–5 are repeated with λ = 0, and θ is only updated in voxel locations that were more negative than a threshold value after Step 5.

Parallel Imaging

When imaging with more than one receive coil, (w, c, θ) are simultaneously fit to all coils’ data. Because the baseline images are weighted by the coil sensitivities, the algorithm implicitly performs a SENSE reconstruction [18, 42], without requiring a separate sensitivity map measurement. It will be demonstrated in simulations that the algorithm is able to exploit multiple receive coils to improve temperature map accuracy at higher accelerations, compared to a single receive coil.

Methods

Algorithm Implementation

The proposed algorithm was implemented in MATLAB R2013a (Mathworks, Natick, MA, USA) on a workstation with a 3.4 GHz E31270 Intel Xeon CPU (Intel Corporation, Santa Clara, CA, USA) and 16 GB of RAM¹. The DFT matrix G was evaluated using non-uniform fast Fourier transforms [43]. Baseline images were reconstructed from fully-sampled k-space data using a conjugate gradient algorithm [44]. When more than one baseline image was used, the baseline image weights w were solved for using MATLAB’s quadprog function. The polynomial phase coefficient vector c and temperature phase shift vector θ were initialized to zeros. Updates for c and θ used 5 iterations. Voxels where θ was more negative than −0.01 radians were corrected for temperature bias due to the ℓ₁ norm as described in Step 6 of the algorithm. In this stage, c and θ updates contained 5 and 10 iterations, respectively. The algorithm stopped when the relative change in the objective function was less than 0.1% between consecutive iterations.

In the following simulations and experiments, the k-space thermometry algorithm is compared with TCR [33] and temperature maps estimated after image reconstruction by either conjugate gradient (CG) or SPIRiT [45], using a hybrid thermometry image model. SPIRiT kernels were calibrated using the (fully-sampled) baseline image and reconstructions used a 5 × 5 kernel and a 30 × 30 calibration region, and the SPIRiT regularization parameter was set to the median of the absolute value of the k-space data. Given a reconstructed image m from CG or SPIRiT, temperature phase shifts were estimated as:

$${\theta }_j=\angle (m_j{f}_j^{\ast }),$$ (6)

for each voxel j, where f is the baseline image with polynomial phase shift estimated by the k-space algorithm.

Temporal step response simulation

To investigate the temporal step response of reconstructed temperature maps and compare it to TCR, k-space data of a simulated circular phantom and an instantaneous on-off Gaussian-shaped (FWHM of 0.8 pixels) heat-induced phase shift were generated for a golden angle (GA) radial trajectory with FOV = 20 cm, matrix size = 64×64, TE = 16 ms, and 101 radial lines for full sampling. The peak phase shift of 1.7 radians corresponded to 13 °C heating at 3 T. The median absolute value of the k-space data was 4.37. Temperature change maps were reconstructed at 4× acceleration (25 lines, 91 samples per line) using TCR and the k-space method. TCR reconstructions used a weighting factor α = 100 and 100 iterations. The k-space method used λ = 10⁻⁴, one baseline image, and a zeroth-order polynomial fit.

Multicoil receive simulation

The same circular object and Gaussian-shaped phase shift were generated with the same settings as the temporal step response simulation for a single receive coil with uniform sensitivity, and for a simulated 8-channel 3 T receive coil array [46]. k-Space data were synthesized using GA radial and 2DFT readout trajectories. Temperature maps were reconstructed by the k-space method and by Eq. 6 from images reconstructed by SPIRiT from the 8-channel data. Reconstructions were performed across a range of acceleration factors, with 64 (2DFT) and 91 (GA radial) k-space samples per line. The k-space method again used λ = 10⁻⁴, one baseline image, and a zeroth-order polynomial fit.

Motion simulation

A simulation was performed to validate the algorithm’s robustness to motion and its ability to regress rapidly-varying background anatomical phase, in the same manner as was done in Ref. [38] for the image domain hybrid algorithm. 64 × 64 images of a rectangular object were generated with background phase comprising a weighted sum of low frequency Fourier components. A library of 50 baseline images were generated across a range of vertical organ positions, representative of motion that could be observed in the liver as part of a normal breathing cycle. 100 uniformly-distributed random positions within this range were chosen and used to synthesize treatment images with Gaussian-shaped phase shifts to simulate focal heating (peak magnitude corresponding to a 23 °C heat rise at 3 T) and sixth-order random polynomial phase shifts. k-Space data were generated from the treatment images using an 8×-accelerated radial trajectory (12 lines, 91 samples per line) with one receive coil and FOV = 20 cm, matrix size = 64×64, and TE = 16 ms. The k-space temperature reconstruction algorithm was applied using the generated baseline library, a sixth-order polynomial fit, and λ = 0.2. A second order finite differencing spatial roughness penalty (with regularization parameter β = 1) was added to the θ cost function following the method described in Ref. [47]. The median k-space data amplitude was 0.75.

Phantom heating experiments

To evaluate the method model experimentally, a tissue-mimicking gel phantom was sonicated using a Philips Sonalleve MR-HIFU system (Philips Healthcare, Vantaa, Finland) operated at 1.2 MHz and 100 Watts for 36 seconds, and targeting a 12 mm diameter treatment cell. The system was installed on a 3 T scanner (Philips Achieva, Philips Healthcare, Best, Netherlands). Gradient echo imaging was performed for temperature monitoring with 2DFT and GA radial readout trajectories and five receive coils. Parameters for the 2DFT and GA radial sequences were: FOV = 40 cm; matrix size = 192×192; slice thickness = 7 mm; TR = 32 ms; TE = 16 ms. The multicoil data were compressed to three coils by thresholding the singular values of the data matrix at five percent of the largest singular value. The median k-space data amplitude was 8.58 for 2DFT and 15.65 for GA radial scans. In addition to the k-space domain reconstructions, temperature maps were estimated using Eq. 6 and images reconstructed by CG and SPIRiT. Temperature maps were reconstructed to a 96 × 96 matrix with 20 cm FOV. Reconstructions used one baseline image, a zeroth-order polynomial fit, λ = 0.016 (2DFT) and 0.0075 (GA radial), and β = 2⁻¹¹ (2DFT) and 2⁻¹² (GA radial). 2DFT reconstructions were performed after taking every fifth line of the original 192×192 matrix in either the x- or y-direction, corresponding to 2.5× acceleration relative to the 20 cm reconstructed FOV (39 lines; 96 samples per line after averaging adjacent samples in the original matrix). GA radial data were undersampled by 16× relative to the 20 cm reconstructed FOV (9 lines; 192 samples per line).

In vivo model validation

To validate the k-space signal model in vivo in the absence of heat, sagittal brain images were collected in a healthy volunteer using an 8-channel receive array and GA radial readout trajectory at 3 T (Philips Achieva, Philips Healthcare, Best, Netherlands) under approval of the Institutional Review Board at Vanderbilt University with: FOV = 25.6 cm; matrix size = 128×128; slice thickness = 3 mm; TR = 100 ms; TE = 10 ms; 256 k-space samples per line. Multicoil data were compressed to four coils using singular value thresholding as in the phantom heating experiments. Temperature maps were estimated using k-space reconstructions and Eq. 6 with CG- and SPIRiT-reconstructed images. To evaluate temperature errors that could arise in the k-space reconstructions, the algorithm was executed without the θ updates (Step 3 was skipped and θ was fixed at 0) so that only the baseline image weights and background phase shift were estimated, using seven baseline images and a first order polynomial matrix. Then, keeping those baseline image and polynomial phase estimates fixed by skipping Steps 2 and 4, the algorithm was repeated to fit θ with λ = 0. Temperature maps were reconstructed with no acceleration (256 lines; 97 maps), 2× acceleration (128 lines; 109 maps), 4× acceleration (64 lines; 116 maps), 8× acceleration (32 lines; 119 maps), 16× acceleration (16 lines; 121 maps), and 32× acceleration (8 lines; 121 maps). Errors were averaged over dynamic frames to determine the mean errors for each acceleration factor. The median k-space data amplitude was 85.04.

Results

Temporal step response simulation

The fully-sampled and undersampled k-space trajectories and corresponding magnitude image and baseline subtraction temperature map reconstructions of the simulated data are shown in Fig. 1a. Undersampling results in a noisy appearance of the magnitude image, and coherent streaking artifacts in the temperature maps. The temperature in the center voxel is plotted for the true and reconstructed maps in Fig. 1b. The k-space method better tracks the instantaneous temperature changes, achieving finer temporal resolution than TCR. Figure 1c shows temperature maps at 5 seconds, immediately after a transition. The k-space reconstruction has small truncation errors around the hot spot, but overall much lower error and no visible aliasing artifacts. With TCR, aliasing artifacts could be reduced by increasing temporal regularization, but this would further degrade temporal resolution.

Figure 1.

Temporal step response simulation. (a) Illustration of fully-sampled and 4x-undersampled radial trajectories and corresponding image and baseline subtraction temperature map reconstructions. Undersampling results in noisy-looking magnitude images and streaking in temperature maps. (b) Temperature in the center of the hot spot versus time. The proposed k-space-based reconstruction achieves finer temporal resolution than TCR since it does not depend on temporal regularization to suppress aliasing artifacts. (c) Just after the step temperature rise at 5 seconds (circle on x-axis in (b)), aliasing artifacts are visible in the TCR estimate, but not in the k-space method’s estimate.

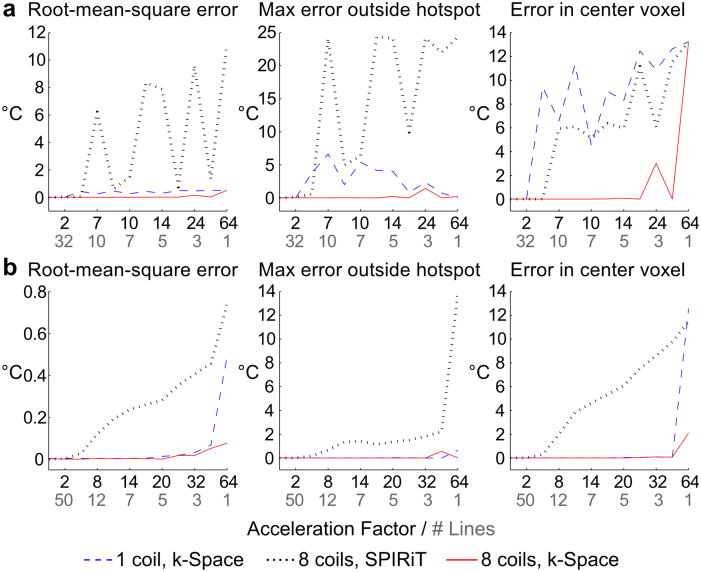
Multicoil receive simulation

Multicoil receive simulation results are shown in Fig. 2. Root-mean-square error within the object, maximum error within the object excluding the temperature hotspot, and error in the center voxel of the reconstructed temperature maps were calculated for the 2DFT and GA radial reconstructions. The changing interference of coherent aliases at different acceleration factors results in oscillation in the 2DFT SPIRiT errors. Similar patterns are observed to a lesser degree in the single-coil k-space reconstructions at higher acceleration factors. However, the multicoil k-space reconstructions are free from these artifacts and produce temperature estimates with low error using as few as four readout lines, indicating that the accuracy of the k-space method’s reconstructions improves with multiple receive coils. GA radial reconstructions using the k-space-based method do not exhibit significant aliasing artifacts in either single- or multi-coil cases. Error remains low for single-coil k-space estimates even when only two radial lines are used for temperature reconstruction. In contrast, the SPIRiT reconstructions are increasingly affected by undersampling artifacts with increasing acceleration factor.

Figure 2.

Multicoil receive simulation. Root-mean-square error, maximum error outside the hotspot, and error in the center voxel are plotted for (a) 2DFT and (b) GA radial trajectories. Black labels along the x-axis indicate acceleration factor, and gray labels indicate the corresponding number of readout lines used in the reconstruction. k-Space reconstruction errors are generally lower than SPIRiT errors, and multi-coil k-space estimates have lower error than single-coil estimates.

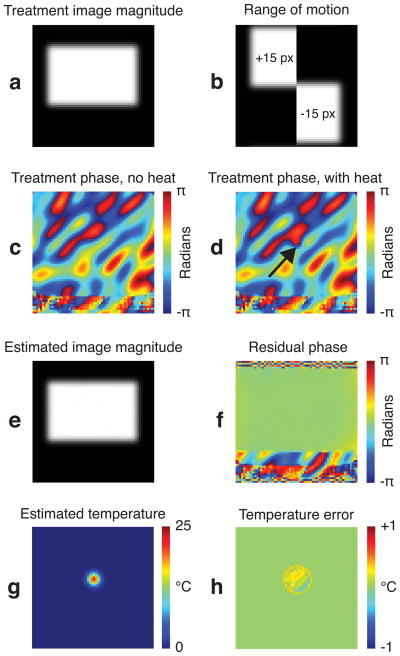
Motion simulation

Results from one of the object positions are shown in Fig. 3. Figure 3f shows the residual phase after k-space thermometry, which was calculated by subtracting the fitted hybrid image model phase from the synthesized treatment image phase. No large residual phase errors are present within the object. The RMS and maximum temperature errors corresponding to the residual phase errors across all the random positions were 0.16 and 1.19 °C, respectively. The temperature maps were also accurately estimated (Figs. 3(g,h)). The RMS and maximum temperature map errors were 0.10 and 1.47 °C, respectively. These results indicate that the hybrid signal model was able to account for all sources of phase, and that the k-space thermometry algorithm was able to determine the parameters of that model.

Figure 3.

Motion simulation. (a) The treatment magnitude image, containing the moving rectangular object. (b) The first and last images in the baseline library, indicating the range of object motion. (c) A treatment image phase, with no heat present, contains polynomial and low frequency Fourier components. (d) The same phase in (c), with the Gaussian hot spot. (e) The estimated image magnitude, derived from the weighted baseline images. (f) Residual phase difference between the images in (e) and (a). (g) The estimated Gaussian-shaped temperature shift. (h) Temperature map error.

Phantom heating experiments

Figure 4 shows the 2DFT phantom experiment results. Image-domain temperature reconstructions were highly sensitive to the relative orientation of the coil array (which encoded primarily along x) and the undersampled dimension, and aliasing artifacts in the images were lower when data was undersampled along the x-direction. Compared to the CG reconstruction, the SPIRiT algorithm was able to reduce but not fully remove artifacts from undersampling, likely due to the low number of receive channels (three, after coil compression) relative to the acceleration factor (2.5×). The k-space temperature reconstructions were free from artifacts, regardless of the undersampled dimension. Figure 4c shows that the k-space temperature maps were free from artifacts over the entire course of the experiment, and closely matched the fully-sampled reconstructions. Temperature changes were overestimated in the SPIRiT temperature maps throughout the experiment.

Figure 4.

2DFT experiment. (a) Magnitude images reconstructed with full sampling (left) and 2.5x undersampling in the x- or y-dimensions. (b) Temperature maps reconstructed at peak from data undersampled in either the x or y dimensions using CG, SPIRiT, and k-space-based methods. (c) Temperature maps reconstructed along the timecourse of the heating experiment using CG and full sampling (top), SPIRiT-reconstructed images and 2.5x undersampling along the x-direction (middle), and the k-space method and 2.5x undersampling along the x-direction (bottom). Plot of temperature evolution in the central voxel as a function of time for fully-sampled (CG) and 2.5x-undersampled (SPIRiT and k-space-domain) temperature maps. Circles along the x-axis indicate times of the displayed temperature maps.

Results from the GA radial scan are shown in Fig. 5. As in the 2DFT case, large aliasing artifacts are present in CG and SPIRiT reconstructions, but not in k-space-based reconstructions. At 16× acceleration, SPIRiT-based temperature estimates are consistently lower than the heating estimated from fully-sampled data. The k-space temperature reconstruction algorithm produces heating estimates that closely match the fully-sampled results throughout the experiment.

Figure 5.

Golden angle radial experiment. (a) Magnitude images reconstructed with full sampling (left) and 16x undersampling with CG (middle) and SPIRiT reconstructions (right). (b) Temperature maps reconstructed at peak heat using fully-sampled CG and 16x-undersampled CG, SPIRiT, and k-space-based models. (c) Top: Temperature maps reconstructed along the timecourse of the heating experiment with full sampling using CG (top), 16x-undersampling using SPIRiT-reconstructed images (middle), and 16x-undersampling using k-space reconstruction (bottom). Bottom: Plot of temperature evolution in the central voxel as a function of time for fully-sampled (CG) and 16x-undersampled (SPIRiT and k-space-domain) temperature maps. Circles along the x-axis indicate times of the displayed temperature maps.

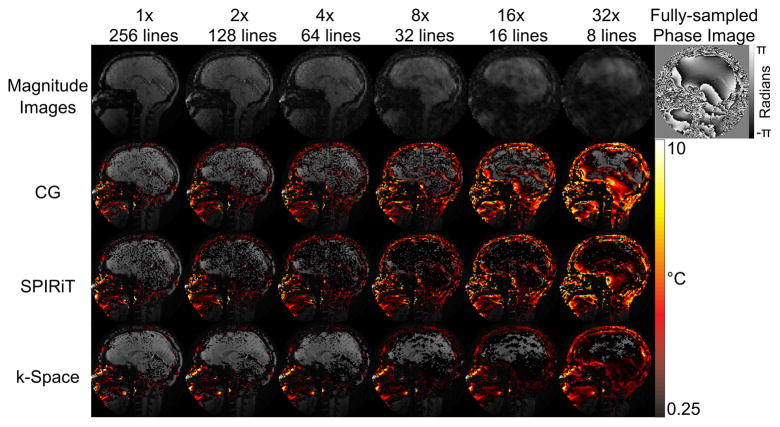
In vivo model validation

Figure 6 shows the in vivo model validation results. As expected, temperature errors increased with acceleration factor for all reconstruction methods. At high acceleration factors, the CG-reconstructed temperature maps have large errors, which are reduced but not removed by using SPIRiT. The k-space method’s maps reflect a globally increased temperature uncertainty resulting from lower SNR, but no significant aliasing artifacts within the brain up to 32× acceleration.

Figure 6.

In vivo model validation (no heating). Top Row: Magnitude images reconstructed at different acceleration factors. The phase of one fully sampled image is shown at the top right. Bottom Three Rows: Comparison of mean positive temperature errors over 0.25C for CG, SPIRiT, and k-space temperature reconstructions. Moderate acceleration leads to large temperature errors in the CG and SPIRiT reconstructions, but the k-space reconstructions suffer only an apparent loss in SNR in the brain up to 32x acceleration.

Computation time

Table 1 shows the computation times for the proposed algorithm, averaged over 10 repeated reconstructions, for one temperature map from simulated and phantom heating data. 2DFT reconstructions used approximately twice as many k-space samples per map as GA radial reconstructions, and required almost twice as much time (15 seconds vs 8 seconds for the same number of iterations). Reconstruction times were significantly longer for simulated data, which was likely due to the lack of noise in the simulations, and a lack of spatial roughness regularization.

Table 1.

Computation Time and Iteration Count

Dataset, acceleration factor	Time (s)	Number of iterations
Simulated phantom, 4×	74.1	Steps 1–5: 6; step 6: 3
2DFT gel phantom, 2.5×	14.6	Steps 1–5: 3; step 6: 3
GA radial gel phantom, 16×	8.2	Steps 1–5: 3; step 6: 3

Discussion

The proposed k-space-based temperature reconstruction approach was demonstrated in simulations and experiments to produce accurate temperature maps from undersampled k-space data. Temporal step response function simulations demonstrated that the method reconstructs 4×-undersampled temperature maps with finer temporal resolution than the TCR method, which uses temporal regularization to suppress undersampling artifacts. Small errors were observed around the edges of the hotspot due to thresholding (RMS error: 0.0047 °C; max error: 0.074 °C), but undersampling artifacts were not present in the k-space-based temperature reconstructions. Due to their broader temporal point spread function, TCR maps had large errors during rapid temperature changes, with a streaking pattern typical of radial undersampling (RMS error: 0.23 °C; max error: 2.98 °C). Although increased temporal regularization could have reduced TCR aliasing artifacts, this would have further decreased its effective temporal resolution. We note that this simulation was designed to compare the response of the two algorithms to large instantaneous temperature rises, which do not occur in practice. However, frame rates of one volume every few seconds are common in thermometry, especially with the desire to increase volumetric coverage. This leads to the possibility that large temperature changes can occur within one to two time frames, and in such cases it is preferable that the reconstructed temperature maps have a temporal resolution that is no more coarse than the data frame rate. Future work will apply the proposed algorithm to enable expanded volumetric coverage in MR thermometry, without sacrificing temporal resolution.

Multicoil receive simulations demonstrated that the k-space algorithm benefits from multicoil reception. For 2DFT and GA radial trajectories, k-space temperature estimates from multicoil data had lower error within and outside the hotspot using as few as four (2DFT) and two (GA radial) readout lines. The results suggest that using multiple receive coils may be more advantageous for Cartesian trajectories, although additional experiments will be needed to evaluate this. In both Cartesian and non-Cartesian simulations, low-error temperature reconstructions were achieved at higher levels of acceleration using the k-space method compared to using parallel imaging alone.

A similar pattern was observed in phantom heating experiments. 2DFT and GA radial data were undersampled at 2.5× and 16×, respectively. Results showed that undersampled k-space temperature reconstructions closely matched the fully-sampled temperature maps, and in both experiments the k-space reconstructions were free from aliasing artifacts. In comparison, SPIRiT-based temperature maps suffered from aliasing artifacts and degraded accuracy across the timecourse of the experiments. Unlike the SPIRiT-based temperature reconstructions, the accuracy of the k-space reconstructions was not significantly affected by the relative orientation of the undersampling and coil array dimensions, though it may be more sensitive to relative orientation at higher acceleration factors.

To validate the hybrid k-space signal model and investigate possible temperature errors that could arise in the method, data from a healthy volunteer were collected without heating. Above moderate acceleration factors, large errors became apparent in CG temperature reconstructions. SPIRiT maps also had high error at these factors, although they appeared diminished compared to CG results. Error maps from k-space reconstructions were affected by decreasing SNR, but no significant artifacts appeared until the data was accelerated at 32×. These results suggest that the hybrid k-space signal model accurately captures anatomic phase variations and smooth phase shifts, over a wide range of acceleration factors in vivo. The results of the motion simulation further demonstrated the algorithm’s ability to regress background anatomical phase in the presence of motion.

Compared to temporal regularization-based approaches such as TCR, the k-space-based algorithm makes no assumptions on the temporal dynamics of temperature, and was shown in simulations to provide superior temporal resolution to TCR. The k-space algorithm also does not require k-space undersampling patterns to change between consecutive acquisitions, as was demonstrated by the 2DFT phantom reconstructions, where the accelerated sampling pattern was held fixed for the entire duration of the experiment. However, higher accelerations may be possible with the proposed method if temporal regularization is added to the objective function in Eq. 2 and an alternating k-space sampling pattern is used.

While the proposed algorithm expands on the capabilities of hybrid multibaseline and ref-erenceless thermometry [38], it also inherits some of its limitations. One is that the algorithm requires the assumption of focal heating to separate heat-induced phase shift from the polynomial phase shifts. Thus, in its current form the algorithm may not be suitable for imaging more diffuse heating patterns such as heating caused by RF electric fields generated by the MRI scanner (SAR), which may be well-modeled by polynomials. An extension to those cases would require development of new approaches to the background and heating phase separation problem, which could then be incorporated with the algorithm. If tissue motion occurs in a direction not captured by the baseline library, the method will also become inaccurate. However, if registration information is available to track this motion, it may be possible to reuse previously-acquired baseline images in the new orientation, since smooth phase shifts caused by reorientation of the tissue in the magnet could be captured by the polynomial phase shift. Finally, like the original hybrid thermometry method the proposed algorithm does not account for the presence of fat in heated voxels. Because fat experiences a negligible frequency shift with temperature, its signal degrades the accuracy of temperature estimates when it is present in a voxel but not accounted for. While it is common to suppress fat in PRF-shift thermometry acquisitions using spectral-spatial excitations [48], its signal can be used for thermometry based on changes in longitudinal or transverse relaxation rates, or as a temperature-independent phase or frequency reference for PRF-shift thermometry. In those scenarios multi-echo acquisitions can enable separation of water and fat signals. To apply the proposed k-space algorithm to such acquisitions, a multi-echo signal model would need to be developed that comprises both water and fat components, and that solves for a heat-induced frequency shift (rather than a phase shift) in water. Such a model would incorporate previously-acquired and separated water and fat baseline images. Extensions of the original hybrid method have been developed that estimate heat-induced frequency changes from multi-echo acquisitions [49], and that use fat images as a phase reference for PRF thermometry [50].

For the current implementation of the algorithm, the measured compute times for one frame were on the order of 8–15 seconds. While not compatible with real-time clinical use, these times are feasible for retrospective reconstructions that would be useful for preclinical studies [51]. Furthermore, the current implementation used only one CPU core, and a multi-threaded or GPU-based implementation of the algorithm may yield compute times compatible with real-time use [52]. The presented reconstructions also used a non-uniform Fast Fourier Transform algorithm to evaluate multiplications with the G matrix, which includes a computationally-expensive gridding step [43]. This step could be eliminated for Cartesian-sampled data (2DFT and EPI), which are the most commonly-used k-space trajectories in thermometry. Finally, initializing the algorithm with a previous solution for the temperature map, baseline weights and polynomial coefficients could help accelerate convergence, particularly when little or no motion is present. As for any reconstruction approach, multi-slice temperature reconstructions could be parallelized across slices, so the in-plane acceleration enabled by a real-time-compatible extension of the proposed algorithm could be leveraged to increase the number of acquired slices, without sacrificing temporal resolution. Further development of the algorithm to achieve real-time compute times will be the focus of future research efforts.

Conclusions

Accelerated temperature imaging is important to support current and enable future MRI-guided thermal interventions. We have presented an algorithm for temperature reconstruction by fitting a constrained model directly to k-space data. The proposed algorithm is capable of estimating focal temperature changes from k-space data with high temporal resolution and accuracy, even at high acceleration factors.

Appendix

NLCG algorithm for θ updates

The steps of the nonlinear conjugate gradient algorithm (J A Fessler, Image reconstruction: Algorithms and Analysis, to be published.) used to update the heating-induced phase shift θ in Step 3 of the algorithm are:

1. repeat

2. Calculate search direction p: A column vector g = ∇_θΨ of the first derivatives of the objective function Ψ(θ) in Eq. 4 with respect to the elements of θ is first calculated as:

   $${\mathit{g}}^n={\nabla }_{\mathit{\theta }}\mathrm{\Psi }=\mathfrak{R}\left\{i\text{diag}\left\{f_j^{\ast }{e}^{-i{\theta }_j^n}\right\}{\mathit{G}}^{\prime }\left(\stackrel{\sim }{\mathit{y}}-\mathit{G}\text{diag}\left\{e^{i{\theta }_j^n}\right\}\mathit{f}\right)\right\},$$ (7)
   where G is a (non-uniform) DFT matrix. Using the Polack-Ribière conjugate gradient formula, the search direction at iteration n is given by:

   $${\mathit{p}}^n=\{\begin{array}{ll}-{\mathit{g}}^n,\hfill & n=0\hfill \\ -{\mathit{g}}^n+\frac{\langle {\mathit{g}}^n-{\mathit{g}}^{n-1},{\mathit{g}}^n\rangle }{{\Vert {\mathit{g}}^{n-1}\Vert }^2}{\mathit{p}}^{n-1},\hfill & n\ge 1\hfill \end{array}$$ (8)
3. Calculate step size α: α is evaluated subject to non-positivity constraints as follows: If ${\theta }_j^n>\epsilon$ for some threshold ε (ε = π/1000 was used in the present work) and $p_j^n>0$, then set $p_j^n=0$ since the search direction will lead to violation of the non-positivity constraint at that location, for any α. Then solve

   $${\alpha }_n=\underset{\alpha }{\text{argmin}}\mathrm{\Psi }({\mathit{\theta }}^{\mathit{n}}+\alpha {\mathit{p}}^n)$$ (9)
   using a backtracking line search. Next, determine if the α returned by the line search causes violation of the non-positivity constraint. Let zⁿ = θⁿ + α_npⁿ. If [zⁿ]₋ ≠ zⁿ, then set

   $${\mathit{p}}^n={[{\mathit{z}}^n]}_{-}-{\mathit{\theta }}^n$$ (10)
   and perform another backtracking line search with the updated pⁿ:

   $${\alpha }_n=\underset{\alpha \in [0,1]}{\text{argmin}}\mathrm{\Psi }({\mathit{\theta }}^{\mathit{n}}+\alpha {\mathit{p}}^n)$$ (11)

4. Update θ: θⁿ⁺¹ = θ ⁿ + αpⁿ

5. until The desired number of iterations is reached.