Abstract
There is an on-going debate about whether fixation durations during reading are only influenced by the processing difficulty of the words being fixated (i.e., the serial-attention hypothesis) or whether they are also influenced by the processing difficulty of the previous and/or upcoming words (i.e., the attention-gradient hypothesis). This article reports the results of three simulations that examine how systematic and random error in the measurement of fixation locations can generate two phenomena that support the attention-gradient hypothesis—parafoveal-on-foveal effects and large spillover effects. These simulations demonstrate how measurement error can produce these effects within the context of a computational model of eye-movement control during reading (E-Z Reader; Reichle, 2011) that instantiates strictly serial allocation of attention, thus demonstrating that these effects do not necessarily provide strong evidence against the serial-attention hypothesis.
All measurements are estimates of the value of the thing being measured. As such, all measurements introduce two types of error—a systematic error that consistently causes the estimated values to be either too big or small across repeated measurements, and a random error that causes the estimated values to fluctuate from one measurement to the next. Given this, it should not be surprising that measurements of an eye’s spatial location at any given point in time is also subject to both systematic and random error (Holmqvist, Nystöm, & Mulvey, 2012; Reingold, 2014). However, to date, we believe that there has been too little consideration of the theoretical implications of measurement error, or to how it might contribute to our understanding of eye-movement control in visual-cognitive tasks. In the remainder of this article, we will focus on one specific example from within our research area—the debate about how attention is allocated during reading.
The question about how attention is allocated during reading is a contentious one (cf., Radach & Kennedy, 2013; Reichle, Liversedge, Pollatsek, & Rayner, 2009) that was “brought to a head” during the last decade with the development of computational models of eye-movement control during reading that actually instantiate the two possible theoretical stances on this question. According to the first stance, attention is allocated in a strictly serial manner during reading, with the “spotlight” of attention first being focused on one word until it has been identified and then shifting to the next word. Although the E-Z Reader model (Reichle, Pollatsek, Fisher, & Rayner, 1998; Reichle, Pollatsek, & Rayner, 2012) probably best exemplifies this position, other models have also included the assumption that words are attended to and identified in a strictly serial manner (e.g., EMMA; Salvucci, 2001). However, according to the second theoretical stance, attention is allocated as a distributed gradient that normally encompasses 3-4 words at any given time, with the gradient moving down a line of text as the words within the gradient are identified. Although the SWIFT model (Engbert, Nuthmann, Richter, & Kliegl, 2005; Schad & Engbert, 2012) probably best exemplifies this position, other models have also included the assumption that attention is allocated in a manner that supports the concurrent lexical processing of multiple words (e.g., Glenmore; Reilly & Radach, 2006). Because the strengths and weaknesses of specific models and the more general debate about attention allocation during reading have been discussed at length elsewhere1, we will not rehash those issues here, but will instead focus on two empirical findings that have informed the debate—parafoveal-on-foveal effects and (large) spillover effects. Both of these effects are related to the more basic question of whether the time spent looking at a particular word during reading is primarily influenced by the lexical processing of that word (and thus its lexical properties), or whether the looking time on a word is instead also affected by the lexical processing (and thus the lexical properties of) the spatially adjacent words (for reviews, see Drieghe, 2011; Schotter, Angele, & Rayner, 2012). In other words, the debate is about the extent to which fixation durations on a word reflect strictly local lexical processing of that word, or whether it instead typically reflects some degree of distributed lexical processing of a few spatially adjacent words2.
With that background, parafoveal-on-foveal effects refer to the finding that lexical properties of a word in the parafovea somehow affect the time spent looking at the word that is currently being fixated (i.e., the word in the fovea). For example, the time spent fixating wordn may be modulated by the frequency of occurrence of wordn+1. Such a finding is naturally compatible with attention-gradient models of eye-movement control (e.g., SWIFT) because the “decision” about when to move the eyes from a given word is dependent upon the lexical processing rates of all of the words within the attention gradient. Importantly, such a finding appears to be at odds with serial-attention models (e.g., E-Z Reader) because of their assumption that the “decision” about when to move the eyes from a word is only dependent on the lexical processing rate of that word. Therefore, one might hope that clear evidence of parafoveal-on-foveal effects would provide a “fatal bullet” against serial-attention models (and thereby provide evidence supporting attention-gradient models), but unfortunately this has not happened because the existence of these effects remains equivocal. For example, although several studies examining the effects of word frequency have reported evidence of lexical parafoveal-on-foveal effects during reading (Kennedy & Pynte, 2005; Kliegl, Nuthmann, & Engbert, 2006; Risse & Kliegl, 2012), a large number of studies have not (Carpenter & Just, 1983; Drieghe, Rayner, & Pollatsek, 2008; Henderson & Ferreira, 1993; Kennison & Clifton, 1995; Rayner, Fischer, & Pollatsek, 1998). And although one might discount the latter set of null findings because “absence of evidence” is not “evidence of absence,” it is important to know why the effects—if they do exist—are so ephemeral, sometimes both appearing and not appearing across different experiments within the same study (cf., Experiments 2 vs. 4, Hyönä & Bertram, 2004).
In a converse manner, spillover effects refer to the finding that the lexical properties of a word that was just fixated (and that is therefore now in the parafovea) somehow affect the time spent looking at the word that is currently being fixated. For example, the time spent fixating wordn may be modulated by the frequency of wordn-1. Although the existence of lexical spillover effects during reading is not controversial because they have been reported in a large number of studies, their expected size is contentious. Returning to our example, most reported spillover effects are fairly small in magnitude, typically being some fraction of the size of the frequency effect that is observed on the previously fixated word (Rayner & Duffy, 1986; Rayner, Ashby, Pollatsek, & Reichle, 2004); however, there have also been reports of more substantial spillover effects, being approximately of the same magnitude as the frequency effects on the previously fixated word (Kliegl et al., 2006). These large spillover effects are more naturally accounted for by parallel-attention models (e.g., SWIFT) because of their assumption that “decisions” about when to move the eyes are modulated by lexical processing of whatever words happen to be within their attention gradient. However, because serial-attention models (e.g., E-Z Reader) account for spillover effects by positing that processing difficulty of the fixated word affords less time for parafoveal processing of the upcoming words (thereby inflating the fixations on those words when they are fixated), these models can only explain small spillover effects.
Apart from the fact that evidence for parafoveal-on-foveal and large spillover effects is not reliable across studies, advocates of the serial-attention position have argued that the “evidence” for distributed lexical processing may be due to some combination of artifacts that can contribute to a decoupling between a reader’s intended and actual points of regard (Drieghe, 2011; Rayner, White, Kambe, Miller, & Liversedge, 2003). Two of these sources of error are intrinsic to readers themselves—imperfect binocular convergence of the eyes (Liversedge, White, Findlay, & Rayner, 2006) and the oculomotor error associated with executing saccades (McConkie, Kerr, Raddix, & Zola, 1988). To understand how these two sources of error might give rise to “evidence” of a parafoveal-on-foveal effect with the theoretical framework of serial-attention allocation, imagine a situation in which the reader has just identified wordn and now intends to move his/her attention and eyes to wordn+1 so that it can be processed and identified. Now imagine that attention shifts to wordn+1 and its processing begins, but because of imperfect convergence, the reader’s left eye moves to wordn+1 but the right eye (which is the one whose location is typically being measured) only moves to the end of wordn. Or imagine that, because of oculomotor error, both of the reader’s eyes fall short of their intended target and land on the end of wordn. If one assumes that the time required to identify wordn+1 then determines when the reader moves his/her eyes forward, then both of these described situations will result in apparent parafoveal-on-foveal effects because the lexical properties (e.g., frequency) of wordn+1 will affect when the eyes move from wordn.
The third possible artifact that might contribute to “evidence” for distributed lexical processing will be the focus of the remainder of this article—the measurement error that is actually intrinsic to eye-tracking technology. Although current generations of eye trackers typically allow for spatial accuracy of ~0.5° if properly calibrated (Reingold, 2014), a variety of factors are known to influence the quality of calibration and hence the accuracy of the resulting measurements, including differences between participants (e.g., eye shape, attentiveness, etc.), skill differences of the persons operating the eye trackers, and the type of eye tracker, to name just a few (Holmqvist et al., 2012). Although one can take precautions to minimize the amount of measurement error in an eye-tracking experiment (e.g., frequently recalibrating the eye tracker), it is impossible to either know the exact amount of measurement error or to eliminate it completely. That being said, we believe that it is important to consider how the inclusion of some amount of measurement error might affect the outcomes of experiments that have provided “evidence” of distributed lexical processing. The crux of our argument is schematically illustrated in Figure 1, which shows four hypothetical situations involving three spatially adjacent words and a frequency manipulation of the middle word (i.e., wordn).
Figure 1.
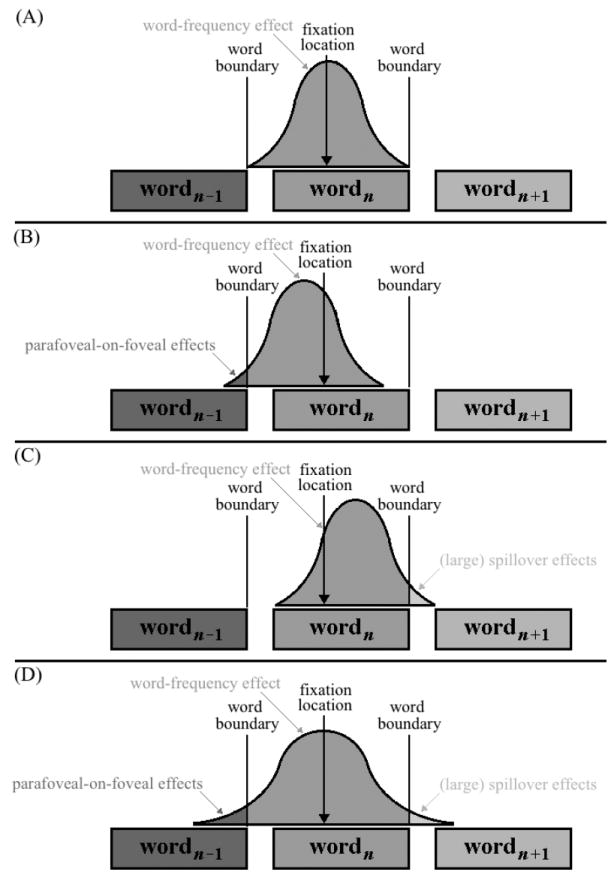
A schematic diagram showing three spatially adjacent words, the locations of the boundaries that are (by convention) used to assign fixations to specific words, the location of an actual fixation, and the distribution of possible locations at which the fixation might be recorded as having occurred with the introduction of some amount of measurement error. Panel A shows the hypothetical situation in which the distribution of possible recorded fixation locations on wordn (as indicated by the distribution of possible fixation locations between the left edge of the blank space immediately before wordn and the right edge of that word); in this situation, serial-attention models (e.g., E-Z Reader; Reichle et al., 2012) predict that any manipulation of wordn’s frequency will only affect fixation durations on that word, giving rise to a standard word-frequency effect. Panel B shows a situation in which some amount of negative systematic bias shifts the distribution of possible fixation locations to the left, so that some fixations on wordn are recorded as having been on wordn-1; in this situation, any manipulation of wordn’s frequency will affect some of the fixation durations on wordn-1, causing an apparent parafoveal-on-foveal effect. Panel C shows the opposite situation in which positive systematic bias causes some fixations on wordn to be recorded as having been on wordn+1, thereby inflating the apparent size of the spillover effect. Finally, Panel D shows what happens when the random component of measurement error increases, increasing the variability of the distribution of possible fixation locations so that some fixations on wordn are recorded as having been on both wordn-1 and wordn+1; this final situation contributes to both parafoveal-on-foveal and spillover effects.
Panel A shows a situation in which the eyes are fixated near the center of wordn and, although there is a fair amount of systematic and random measurement error associated with estimating the precise location of that fixation (as represented by the Gaussian distribution of possible fixation locations that is shifted slightly to the left of wordn’s center), the distribution of that error is completely between the boundaries that are used to “score” fixations as having occurred on wordn. Because the fixation is accurately scored as having been on wordn and because the duration of that fixation will be primarily influenced by the lexical properties (e.g., frequency) of that word, the situation that is depicted in Panel A will result in a standard word-frequency effect.
However, we believe that the situations shown in Panels B-D are more representative of what actually happens in most eye-movement experiments. Panel B shows a situation in which some non-negligible amount of negative systematic error causes some fixations on wordn to be erroneously scored as having occurred on wordn-1; because all of the fixation durations are presumably influenced by the frequency of wordn but some of those fixations are erroneously scored as having been on wordn-1, the situation depicted in Panel B will result in a parafoveal-on-foveal effect. In a similar manner, Panel C shows a situation in which positive systematic error causes some of the fixations on wordn to be erroneously scored as having occurred on wordn+1, inflating the size of the spillover on that word. Finally, Panel D shows a situation in which the overall variability in the random measurement error increases, causing some of the fixations on wordn to be scored as having been on wordn-1 and wordn+1 and thereby resulting in both parafoveal-on-foveal effects and inflated spillover effects.
Finally, it is important to emphasize that, although repeated measurements are prescribed to reduce the size of the random component of measurement error (because the expected value of the random error for an infinite number of measurements is 0), this precaution is completely ineffective because the random error will not “average out” in the situations depicted in Figure 1. The reason is because individual measurements are not being added together to estimate a single fixation location; rather, individual measurements are being assigned to specific values (i.e., words) depending on whether they fall to the left or right of the boundaries that are used to demarcate individual words. That being said, the situations depicted in Figure 1 will not be remedied by simply increasing the number of observations. In the next section of this article, we report simulations to test this and other predictions about measurement error and its influence on parafoveal-on-foveal and spillover effects.
Simulations
To test our hypotheses about the possible role of measurement error in parafoveal-on-foveal and spillover effects, three simulations were completed to determine how these effects might be modulated by both systematic and random measurement error. These simulations used the standard version of E-Z Reader with its default parameter values (Reichle et al., 2012) and 1,000 statistical subjects per condition. Our decision to use E-Z Reader is that was motivated by both its architecture (i.e., it is a serial-attention model) and because it is a serious candidate model of eye-movement control during reading (i.e., it has been used to simulate the various “benchmark” findings that have been used to evaluate other such models). As with previous simulations (e.g., see Reichle, 2011), the 48 sentences that were originally used by Schilling, Rayner, and Chumbley (1998) to examine frequency effects were used as “frames” to examine the consequences of manipulating the lexical properties of two spatially adjacent words, with “wordn” being arbitrary assigned to the within-sentence ordinal positions of the target words used by Shilling et al. so that the lexical properties of those words and the preceding or following words could be manipulated. The specific details of how this was actually done will be described next.
Simulation 1
Because the simulation was intended to examine parafoveal-on-foveal effects, the question of interest was whether the frequency of wordn would affect looking times on wordn-1. Therefore, the lengths of both words were set equal to 5 letters and their cloze predictabilities were set equal to 0. The frequency of wordn-1 was then set equal to 1 per million and the frequency of wordn was manipulated, being set equal to 1 versus 10,000. Although these values are largely arbitrary, the frequency values were selected to maximize the size of the simulated frequency effect, thereby allowing us to determine how this manipulation, in combination with some amount of measurement error, might produce eye-movement patterns that are indicative of parafoveal-on-foveal effects. Measurement error was also manipulated in two ways: First, by introducing a range of negative versus positive bias (±4 character spaces, in half-character increments); and second, by increasing the standard deviation of the random measurement error (also (±4 character spaces, in half-character increments). To introduce systematic error, the recorded locations of all fixations were shifted to the left or right by some fixed amount; to introduce random error, the recorded locations of individual fixation were shifted by an amount that was sampled from a Gaussian distribution. Our rationale for using the specific indicated values was that it allows individual readers of this article to evaluate both the consequences and plausibility of different amounts of measurement error. However, we would argue that, because 3 character spaces corresponds to approximately 1° of visual angle, this amount of measurement error in not implausible given common conventions of calibrating eye-trackers so that the mean error is ~0.5° of visual angle (Reingold, 2014). Finally, the effects of these manipulations were assessed using two standard dependent measures: (1) first-fixation duration, or the time spent looking at a word when it is initially fixated during the first pass through a sentence; and (2) gaze durations, or sum of all first-pass fixations on a word. Figure 2 shows how the frequency of wordn differentially affected these two measures on both wordn (i.e., word-frequency effects) and wordn-1 (i.e., parafoveal-on-foveal effects), with Panels A and B respectively showing how these effects were modulated by systematic versus random error.
Figure 2.

Simulation 1: Mean simulated word-frequency effects as measured using first-fixation duration (FFD) and gaze duration (GD) on wordn-1 and wordn as a function of the frequency of wordn. Panel A and B respectively show how the frequency effects are modulated by systematic and random measurement error.
Panel A indicates that, without measurement error, the frequency of wordn modulated first-fixation (M = 33 ms) and gaze durations (M = 41 ms) on that word, but produced no parafoveal-on-foveal effects on wordn-1 (M = -1 ms and M = 1 ms for first-fixation and gaze durations, respectively). However, as Rayner et al. (2003) surmised, moderate negative measurement bias (e.g., -3 characters) produced modest parafoveal-on-foveal effects in first-fixation durations (M = 3 ms) and comparatively large effects in gaze durations (M = 11 ms). Furthermore, the introduction of moderate positive bias (e.g., +3 characters) markedly reduced the frequency effects in first-fixation (M = 4 ms) and gaze durations (M = 14 ms) and eliminated the parafoveal-on-foveal effects in both measures (M = -1 ms and M = -2 ms, respectively). Finally, as Panel B indicates, increasing the standard deviation of the random measurement error moderately (e.g., +3 characters) also decreased the frequency effect in both first-fixation (M = 25 ms) and gaze durations (M = 34 ms), but produced small parafoveal-on-foveal effects in the gaze durations (M = 6 ms). Thus, to summarize, the introduction of negative measurement bias produced large parafoveal-on-foveal effects in both first-fixation and gaze durations, while increasing random measurement error produced modest parafoveal-on-foveal effects in the gaze durations.
Simulation 2
One important implication of the preceding demonstration was actually anticipated by Rayner et al. (2003) in their re-analysis of data from an eye-movement experiment reported by Rayner (1975). In this experiment, a boundary paradigm either permitted or prevented readers from viewing specific target words prior to actually fixating those words so that the processing cost associated with not having a valid parafoveal preview of the target word can be ascertained. These costs are typically 40-50 ms (Hyönä, Bertram, & Pollatsek, 2004) and indicate that a parafoveal word normally undergoes considerable visual and lexical processing prior to being fixated (see Reingold, Reichle, Glaholt, & Sheridan, 2012). Perhaps surprisingly, the re-analysis of the Rayner (1975) data indicated that a small cost was incurred on the pre-boundary word, but only for fixations located near the ends of the pre-boundary word. Rayner et al. (2003) suggested that this evidence for a parafoveal-on-foveal effect might instead reflect mis-located fixations, or instances when the reader was attending and intending to fixate the post-boundary word, but because of saccadic error fixated the pre-boundary word. However, another non-mutually exclusive interpretation of this finding is that it reflects measurement error, as suggested by the results of the first simulation.
To examine this possibility, a second simulation was completed to examine how the cost associated with the prevention of parafoveal preview might be modulated by systematic and random measurement error. This simulation was very similar to the first except that, rather than manipulating the frequency of wordn, parafoveal processing of wordn was manipulated (i.e., allowed vs. prevented) prior to fixating on or to the right of the blank space preceding the word. The lengths, frequencies, and predictabilities of both wordn-1 and wordn were therefore set equal to 5 letters, 1 per million, and 0, respectively. Also, intermediate values of systematic and random measurement error (±4 character spaces, in half-character increments) were used to more precisely examine the consequences of such error.
Figure 3 shows the mean preview effects, or the differences in first-fixation and gaze durations on wordn-1 and wordn as a function of whether or not parafoveal processing of wordn was permitted, and of the amount of systematic (Panel A) and random (Panel B) measurement error. Two key results are evident in Figure 3. The first can be seen in Panel A, which shows that a cost associated with the prevention of parafoveal processing of wordn is not evident on wordn-1 except in the conditions involving negative bias. For example, the mean costs associated with a bias of -3 character spaces are 5 ms for first-fixation durations and 19 ms gaze durations. The second key result can be seen in Panel B, which shows that preventing parafoveal processing of wordn causes a small cost on wordn-1 (M = 6 ms for gaze durations) when the standard deviation of the random measurement error is increased to +3 or more characters. Together, these results show that modest systematic or random measurement error may—at least in part—explain findings that might otherwise be interpreted as evidence for parafoveal-on-foveal effects (see Drieghe, 2011).
Figure 3.

Simulation 2: Mean simulated parafoveal preview effects as measured using first-fixation duration (FFD) and gaze duration (GD) on pre-boundary (wordn-1) and post-boundary (wordn) words during a simulated boundary paradigm, as a function of systematic measurement bias (Panel A) and random measurement error (Panel B).
Simulation 3
The final simulation examined how systematic and random error might modulate the size of spillover effects, which as discussed in the beginning of this article, remain contentious (cf., Kliegl et al., 2006; Rayner, Pollatsek, Drieghe, Slattery, & Reichle, 2007; see also Kliegl, 2007). More precisely, the simulation was intended to illustrate how the frequency of wordn affects the looking times on wordn+1, and how these spillover effects might in turn be modulated by measurement error. The simulation was therefore identical to the first except that the frequency of wordn was manipulated (1 vs. 10,000) to determine how measurement error affected first-fixation and gaze durations on wordn+1. (The other lexical properties of wordn and wordn+1 were identical to those of the words used in the first two simulations.)
Figure 4 shows how the frequency of wordn differentially affected these measures on both wordn (i.e., word-frequency effects) and wordn+1 (i.e., spillover effects), with Panels A and B respectively showing how these effects were modulated by systematic versus random error. As Panel A shows, without measurement bias, there are large frequency effects in both first-fixation (M = 29 ms) and gaze durations (M = 40 ms), and modest spillover effects on both measures (M = 4 ms for both measures). However, the most theoretically important finding is that, although moderate positive measurement bias (e.g., +3 characters) reduced the frequency effects (M = 5 ms and M = 11 ms for firstfixation and gaze durations, respectively), it actually increased the size of the spillover effect for both first-fixation (M = 27 ms) and gaze durations (M = 33 ms). Finally, as Panel B shows, increasing the standard deviation of the random measurement error (e.g., +3 characters) had a similar effect, reducing frequency effects (M = 23 ms and M = 33 ms for first-fixation and gaze durations, respectively) and enhancing spillover effects (M = 10 ms and M = 13 ms for first-fixation and gaze durations, respectively). These results therefore collectively show that positive bias and/or increased variability in random measurement error can contribute to the observation that a word’s frequency can modulate the looking times on the next word more than on the word itself.
Figure 4.

Simulation 3: Mean simulated word-frequency effects as measured using firstfixation duration (FFD) and gaze duration (GD) on wordn and wordn+1 as a function of the frequency of wordn. Panel A and B respectively show how the frequency effects are modulated by systematic and random measurement error.
Discussion
As indicated in the Introduction, we contend that the significance of systematic and random measurement error and the specific roles that they can play in contributing to important but contentious empirical phenomena have often not been fully appreciated. The simulations reported in this article represent an attempt to redress this oversight by showing how measurement error might produce experimental results that purportedly provide evidence for the existence of two such phenomena—parafoveal-on-foveal effects and (large) spillover effects. Our simulations collectively show that measurement error can produce effects that closely resemble these effects but that cannot be taken as evidence for parallel lexical processing because they were generated by a model (E-Z Reader; Reichle, 2011) whose architecture specifically precludes such effects. That being said, however, it is important not to misconstrue the implications of these results or what we are claiming.
For example, we are not claiming that all eye-tracking experiments are compromised by large amounts of measurement error; if that were true, then one might expect reports of, for example, parafoveal-on-foveal effects during reading to be routine, when in fact they are not (e.g., see Carpenter & Just, 1983; Drieghe et al., 2008; Henderson & Ferreira, 1993; Hyönä & Bertram, 2004; Kennison & Clifton, 1995; Rayner et al., 1998). Our simulations instead suggest why these effects are sometimes observed and sometime not; why studies with relatively few re-calibrations (e.g., because the participant needs to read large amounts of text) or with older, less accurate eye-trackers should be more prone to measurement error and thus more likely to provide evidence of these effects. For example, consider a study by Kennedy and Pynte (2005) that claimed to provide strong evidence of parafoveal-of-foveal effects. Subsequent analyses of those data (Kennedy, 2008) indicated that these effects were observed even when the fixations on the fixated word were quite distant (e.g., up to 7 character spaces to the left of) the parafoveal word, thus suggesting that these effects were unlikely to be due to mis-located fixations (or measurement error). However, additional analyses of those same data also indicated the absence of the highly reliable spillover effect (Kennedy, Pynte, Murray, & Paul, 2013). This finding of parafoveal-on-foveal effects in the absence of spillover is exactly what might be predicted on the basis of our simulations if the measurement error associated with the Kennedy and Pynte study included a large negative bias (e.g., see Figs. 2A & 4A). Although it is not possible to directly confirm this hypothesis, it is consistent with the methodology of that study; although Kennedy and Pynte report that the “effective resolution” of their eye-tracking system was “considerably better than one character position” (p. 157), the text was displayed across 40 5-line screens and the eye tracker “was calibrated prior to the presentation of each set of three screens” (p. 156)— conditions that we suspect are likely to foster large measurement error.
Finally, it is important to note that we are not claiming that measurement error is the only factor that contributes to patterns of data that have been interpreted as providing evidence for distributed lexical processing, or that measurement error can necessarily explain the results of all experiments that provide evidence for distributed lexical processing. For example, as already mentioned, it is well established that the oculomotor system is intrinsically prone to error (Liversedge et al., 2006; McConkie et al., 1988). Furthermore, it is difficult to know precisely how these different sources of error might contribute to the more complex configurations of results in which, for example, the same experiment provides evidence for both parafoveal-on-foveal effects and large spillover effects (Kliegl, 2007; Kliegl et al., 2006; cf., Rayner et al., 2006). Further empirical and computational research on this topic is clearly necessary.
Acknowledgments
The work reported in this article was completed while the first author was a Leverhulme Visiting Professor (VP1-2011-009) at the University of Southampton, UK. The work was also supported by grant HD053639 from the National Institutes of Health awarded to the first author.
Footnotes
For an overview of these models of eye-movement control in reading, see the 2006 special issue of Cognitive Systems Research.
Although the finding of inflated fixation duration prior to skipping might also be considered as being consistent with distributed lexical processing, this finding can be explained by serial- and parallel-attention accounts and thus will not be discussed in this article (see Reichle & Drieghe, 2013).
References
- Carpenter PA, Just MA. What your eyes do while your mind is reading. In: Rayner K, editor. Eye movements in reading: Perceptual and language processes. New York, NY: Academic Press; 1983. pp. 275–307. [Google Scholar]
- Drieghe D. Parafoveal-on-foveal effects on eye movements during reading. In: Liversedge SP, Gilchrist ID, Everling S, editors. Oxford Handbook on Eye Movements. Oxford, England: Oxford University Press; 2011. pp. 839–855. [Google Scholar]
- Drieghe D, Rayner K, Pollatsek A. Mislocated fixation can account for the parafoveal-on-foveal effects in eye movements during reading. Quarterly Journal of Experimental Psychology. 2008;61:1236–1349. doi: 10.1080/17470210701467953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engbert R, Nuthmann A, Richter E, Kliegl R. SWIFT: A dynamical model of saccade generation during reading. Psychological Review. 2005;112:777–813. doi: 10.1037/0033-295X.112.4.777. [DOI] [PubMed] [Google Scholar]
- Henderson JM, Ferreira F. Eye movement control during reading: Fixation measures reflect foveal but not parafoveal processing difficulty. Canadian Journal of Experimental Psychology. 1993;47:201–221. doi: 10.1037/h0078814. [DOI] [PubMed] [Google Scholar]
- Holmqvist K, Nyström, Mulvey F. Eye tracker data quality: What it is and how to measure it. Proceedings of the Symposium on Eye Tracking Research and Applications. 2012:45–52. [Google Scholar]
- Hyönä J, Bertram R. Do frequency characteristics of nonfixated words influence the processing of fixated words during reading? European Journal of Cognitive Psychology. 2004;16:104–127. [Google Scholar]
- Hyönä J, Bertram R, Pollatsek A. Do frequency characteristics of nonfixated words influence the processing of fixated words during reading? European Journal of Cognitive Psychology. 2004;16:104–127. [Google Scholar]
- Kennedy A. Parafoveal-on-feveal effects are not an artifact of mis-located saccades. Journal of Eye Movement Research. 2008;2:1–10. [Google Scholar]
- Kennedy A, Pynte J. Parafoveal-on-foveal effects in normal reading. Vision Research. 2005;45:153–168. doi: 10.1016/j.visres.2004.07.037. [DOI] [PubMed] [Google Scholar]
- Kennedy A, Pynte J, Murray WS, Paul S-A. Frequency and predictability effects in the Dundee corpus: An eye movement analysis. Quarterly Journal of Experimental Psychology. 2013;66:601–618. doi: 10.1080/17470218.2012.676054. [DOI] [PubMed] [Google Scholar]
- Kennison SM, Clifton C. Determinants of parafoveal preview benefit in high and low working memory capacity readers: Implications for eye movement control. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1995;21:68–81. doi: 10.1037//0278-7393.21.1.68. [DOI] [PubMed] [Google Scholar]
- Kliegl R. Toward a perceptual-span theory of distributed processing in reading: A reply to Rayner, Pollastsek, Drieghe, Slattery, and Reichle (2007) Journal of Experimental Psychology: General. 2007;136:530–537. doi: 10.1037/0096-3445.136.3.520. [DOI] [PubMed] [Google Scholar]
- Kliegl R, Nuthmann A, Engbert R. Tracking the mind during reading: The influence of past, present, and future words on fixation durations. Journal of Experimental Psychology: General. 2006;135:12–35. doi: 10.1037/0096-3445.135.1.12. [DOI] [PubMed] [Google Scholar]
- Liversedge SP, White SJ, Findlay JM, Rayner K. Binocular coordination of eye movements during reading. Vision Research. 2006;46:2363–2374. doi: 10.1016/j.visres.2006.01.013. [DOI] [PubMed] [Google Scholar]
- McConkie GW, Kerr PW, Reddix MD, Zola D. Eye movement control during reading: I. The location of initial fixations on words. Vision Research. 1988;28:1107–1118. doi: 10.1016/0042-6989(88)90137-x. [DOI] [PubMed] [Google Scholar]
- Radach R, Kennedy A. Eye movements in reading: Some theoretical context. The Quarterly Journal of Experimental Psychology. 2013;66:429–452. doi: 10.1080/17470218.2012.750676. [DOI] [PubMed] [Google Scholar]
- Rayner K. The perceptual span and peripheral cues in reading. Cognitive Psychology. 1975;7:65–81. [Google Scholar]
- Rayner K, Ashby J, Pollatsek A, Reichle ED. The effects of frequency and predictability on eye fixations in reading: Implications for the E-Z Reader model. Journal of Experimental Psychology: Human Perception and Performance. 2004;30:720–732. doi: 10.1037/0096-1523.30.4.720. [DOI] [PubMed] [Google Scholar]
- Rayner K, Duffy SA. Lexical complexity and fixation times in reading: Effects of word frequency, verb complexity, and lexical ambiguity. Memroy & Cognition. 1986;14:191–201. doi: 10.3758/bf03197692. [DOI] [PubMed] [Google Scholar]
- Rayner K, Fischer MH, Pollatsek A. Unspaced text interferes with both word identification and eye movement control. Vision Research. 1998;38:1129–1144. doi: 10.1016/s0042-6989(97)00274-5. [DOI] [PubMed] [Google Scholar]
- Rayner K, Pollatsek A, Drieghe D, Slattery TJ, Reichle ED. Tracking the mind during reading via eye movements: Comments on Kliegl, Nuthmann, and Engbert (2006) Journal of Experimental Psychology: General. 2007;136:520–529. doi: 10.1037/0096-3445.136.3.520. [DOI] [PubMed] [Google Scholar]
- Rayner K, White SJ, Kambe G, Miller B, Liversedge SP. On the processing of meaning from parafoveal vision during eye fixations in reading. In: Hyönä J, Radach R, Deubel H, editors. The mind’s eye: Cognitive and applied aspects of eye movement research. Oxford, England: Elsevier; 2003. pp. 213–234. [Google Scholar]
- Reichle ED. Serial attention models of reading. In: Liversedge SP, Gilchrist ID, Everling S, editors. Oxford Handbook on Eye Movements. Oxford, England: Oxford University Press; 2011. pp. 767–786. [Google Scholar]
- Reichle ED, Drieghe D. Using E-Z Reader to examine word skipping during reading. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2013;39:1311–1320. doi: 10.1037/a0030910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reichle ED, Liversedge SP, Pollatsek A, Rayner K. Encoding multiple words simultaneously in reading is implausible. Trends in Cognitive Sciences. 2009;13:115–119. doi: 10.1016/j.tics.2008.12.002. [DOI] [PubMed] [Google Scholar]
- Reichle ED, Pollatsek A, Fisher DL, Rayner K. Toward a model of eye movement control in reading. Psychological Review. 1998;105:125–157. doi: 10.1037/0033-295x.105.1.125. [DOI] [PubMed] [Google Scholar]
- Reichle ED, Pollatsek A, Rayner K. Using E-Z Reader to simulate eye movements in non-reading tasks: A unified framework for understanding the eyemind link. Psychological Review. 2012;119:155–185. doi: 10.1037/a0026473. [DOI] [PubMed] [Google Scholar]
- Reilly R, Radach R. Some empirical tests of an interactive activation model of eye movement control in reading. Cognitive Systems Research. 2006;7:34–55. [Google Scholar]
- Reingold EM. Visual Cognition. Manuscript in press; 2014. Eye tracking research and technology: Toward objective measurement of data quality. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reingold EM, Reichle ED, Glaholt MG, Sheridan H. Direct lexical control of eye movements in reading: Evidence from survival analysis of fixation durations. Cognitive Psychology. 2012;65:177–206. doi: 10.1016/j.cogpsych.2012.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risse S, Kliegl R. Evidence for delayed parafoveal-on-foveal effects from word n+2 in reading. Journal of Experimental Psychology: Human Perception and Performance. 2012;38:1026–1042. doi: 10.1037/a0027735. [DOI] [PubMed] [Google Scholar]
- Salvucci DD. An integrated model of eye movements and visual encoding. Cognitive Systems Research. 2001;1:201–220. [Google Scholar]
- Schad DJ, Engbert R. The zoom lens of attention: Simulating shuffled versus normal text reading using the SWIFT model. Visual Cognition. 2012;20:391–421. doi: 10.1080/13506285.2012.670143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schilling HEH, Rayner K, Chumbley JI. Comparing naming, lexical decision, and eye fixation times: Word frequency effects and individual differences. Memory & Cognition. 1998;26:1270–1281. doi: 10.3758/bf03201199. [DOI] [PubMed] [Google Scholar]
- Schotter ER, Angele B, Rayner K. Parafoveal processing in reading. Attention, Perception, & Psychophysics. 2012;74:5–35. doi: 10.3758/s13414-011-0219-2. [DOI] [PubMed] [Google Scholar]


