Integrated Cortical Structural Marker for Alzheimer’s Disease

Abstract

In this paper we propose an approach to integrate cortical morphology measures for improving the discrimination of individuals with and without very mild AD. FreeSurfer was applied to scans collected from 83 participants with very mild AD and 124 cognitively normal individuals. We generated cortex thickness, white matter convexity (aka “sulcal depth”) and white matter surface metric distortion measures on a normalized surface atlas in this first study to integrate high resolution gray matter thickness and white matter surface geometric measures in identifying very mild AD. Principal component analysis (PCA) was applied to each individual structural measure to generate eigenvectors. Discrimination power based on individual and combined measures are compared, based on stepwise logistic regression and 10-fold cross-validation. Global AD likelihood index and surface-based likelihood maps were also generated. Our results show complementary patterns on the cortical surface between thickness, which reflects gray matter atrophy, convexity, which reflects white matter sulcal depth changes; and metric distortion, which reflects white matter surface area changes. The classifier integrating all three types of surface measures significantly improved classification performance compared to classification based on single measures. The PCA-based approach provides a framework for achieving high discrimination power by integrating high-dimensional data, and this method could be very powerful in future studies for early diagnosis of diseases that are known to be associated with abnormal gyral and sulcal patterns.

Introduction

Progressive gray matter atrophy that spreads from the medial temporal lobe to the parietal and prefrontal cortices is a prominent characteristic of the neurodegeneration that accompanies Alzheimer disease (AD) (Braak and Braak, 1991). Disruption of white matter integrity and decreases in white matter volume have also been observed around the temporal lobe, corpus callosum, and inferior longitudinal fasciculus in AD patients (Guo et al., 2010), and around bilateral parahippocampal and temporal gyri in individuals with mild cognitive impairment (MCI) (Stoub et al., 2006; Xie et al., 2006). Moreover, a recent study found white matter integrity degradation in cognitively normal individuals at risk for amnestic MCI, while gray matter structures were relatively preserved in these individuals (Zhuang et al., 2012). These results indicate that white matter changes may be induced by different pathological origin compared to gray matter atrophy. And these local white matter volume and integrity changes are likely associated with geometric distortion to the white matter surface. Taken together, cortical geometric features, which represent white matter atrophy, and cortical gray matter thickness may provide complementary information on AD progress. Therefore, integrating these features may increase predictive power for identifying patients with AD at an early stage.

Recent developments of surface-based modeling (SBM) in magnetic resonance imaging (MRI) (Apostolova and Thompson, 2008; Dickerson et al., 2011) have enabled us to capture subtle changes of geometric features of the cortical mantle. As an alternative to widely used Region of Interest (ROI) analysis (Jack et al., 1999) and Voxel Based Morphometry (VBM) (Hamalainen et al., 2007), these surface-based methods model the cortical gray matter mantle and its interfaces with the white matter and cerebrospinal fluid (CSF) as geometrical mesh structures. SBM achieves inter-subject registration of individual cortical mantle surfaces to a template based on high-dimensional diffeomorphic maps (Apostolova and Thompson, 2008; Fischl et al., 1999; Miller, 2004), providing gray matter thickness measures sensitive to sub-millimeter changes in neuropsychiatric diseases (Im et al., 2008).

Several studies have shown that combined multivariate or multimodal data – structural MRI including cortical thickness, volume, and tensor-based morphemotry, functional MRI, FDG-PET, and non-imaging data including CSF biomarker and neurocognition – could improve diagnostic power (Desikan et al., 2009; Fan et al., 2008; Hinrichs et al., 2011; Kim and Lee, 2012; Park et al., 2012; Zhang et al., 2011), and combining cortical gray matter thickness and white matter surface measures could increase prediction accuracy in autism (Ecker et al., 2010). In this paper, we present the first study to integrate cortical white matter surface geometric and cortical thickness measures on the cortical surface vertices to discriminate very mild AD from cognitively normal controls. SBM was used to generate the following three cortical measures: 1) thickness, which reflects gray matter atrophy; 2) convexity, which reflects white matter sulcal depth changes; 3) metric distortion, which reflects white matter surface area changes. The surface geometric measures (i.e., convexity and metric distortion) reflect the widening and shallowing of the cortical folding pattern. As these cortical measures represent related but different aspects of neuropathological changes, we hypothesized that integrating surface geometric measures along with cortical thickness would increase the power of discriminating individuals with very mild AD from age-matched healthy subjects.

Methods

Participants

Participants from the Knight Alzheimer Disease Research Center at Washington University School of Medicine were included this study. All participants were administered the Clinical Dementia Rating scale (CDR) (Morris, 1993) and diagnosis and staging of dementia of the Alzheimer type (DAT) (McKhann et al., 1984). Within our sample, 124 individuals received a CDR of 0 (i.e., controls), and 83 received a CDR of 0.5 with a concurrent diagnosis of DAT (i.e., very mild AD). Demographic data are reported in Table 1.

Table 1.

Demographic data of all subjects.

	Cognitively normal control (CDR 0) N=124	Very mild AD (CDR 0.5) N=83	Comparison (p value)
Gender (M/F)	42/82	40/43	χ2 =4.26, p=0.039
Age (Mean/Std)	74.7 ±10.2	75.0 ± 8.6	t=−0.23, p=0.82

MRI Acquisition and Image Processing

All MR scans were collected on a 1.5-Tesla Siemens VISION system. The MR scanning protocol included the collection of 2–4 3D MPRAGE volumes (TR=9.7 ms, TE=4.0 ms, flip angle=10°, voxel resolution 1×1×1.25 mm³, acquisition time=6.5 min per scan). The MPRAGE scans for each subject were aligned with the first and averaged to create a low-noise image volume.

All MR images were processed using FreeSurfer (FS) v4.0.2. Manual quality assurance procedures were carried out by a trained rater to correct geometric inaccuracies or topological defects. Although on average 30–60 minutes were required to complete the QA procedure per scan, we did not record the exact time or type of correction and the rater was blinded as to the CDR of the subjects. It would have been valuable to know whether more clinically severe cases required more correction.

In this study, the following three cortical measures were provided by FS:

1. Cortical thickness (thk), calculated as the shortest distance between the pial surface and white surface at each vertex.

2. Average convexity(sulc), calculated as the integral movement distance of each white surface vertex during spherical inflation. It captures large-scale geometric features and in the meantime is insensitive to small-scale local noise (Fischl et al., 1999).

3. Local metric distortion (Jacobian), calculated as the ratio of a triangle on the registered sphere and the triangle on the white surface (before spherical inflation), normalized for the total area of the white surface. (Wisco et al., 2007).

These parameters capture complementary information of the cortical surface (i.e., cortical mantle thickness, white surface folding depth and surface area distortion) for each participant. They were registered and re-indexed into FS’s template “fsaverage” surface during the spherical surface inflation and registration process, followed by 20-mm FWHM smoothing kernel. We chose a relatively small smoothing kernel size (as opposed to 35 mm) to allow for good localization and sensitivity while reducing the impact of registration misalignment due to the relatively large sample size (Lerch and Evans, 2005).

Statistical Analysis

Multiple surface-based cortical measures suffer from dimensionality problems, with 163,842 vertices for each hemisphere. This over-sampling problem (i.e., the number of variables being far larger than the number of observations) can lead to unreliable classifier performance (Duin, 2000; Park et al., 2012; Ramirez et al., 2010). Several machining learning methods, such as partial least squares (Andersen et al., 2012; Ramirez et al., 2010; Thiele et al., 2013; Westman et al., 2012; Westman et al., 2011) and support vector machine (Davatzikos et al., 2008; Fan et al., 2008; Kloppel et al., 2008; Lerch et al., 2008; Magnin et al., 2009; O’Dwyer et al., 2012; Plant et al., 2010; Wee et al., 2011), which can extract feature variables based on subjects’ label structure, have demonstrated to be effective in data dimensionality reduction while achieving good classification performance. These learning methods have been developed into a variety of algorithms that have been applied to both structural and functional MR data in studies of AD and MCI patients.

The more traditional but effective way to reduce data dimensionality while preserving topographical distribution is to use manifold-learning method, such as principal component analysis (PCA). The PCA procedure on surfaces has been described in detail in (Joshi et al., 1997; Wang et al., 2001) and applied extensively by our group for analysis of deformation-based subcortical structural shape (Csernansky et al., 2004a; Goldman et al., 2011; Mamah et al., 2012; Wang et al., 2007; Wang et al., 2001; Wang et al., 2003). Here we applied this method to the analysis of cortical thickness and geometric measures, indexed on the “fsaverage” template surface where all subjects’ vertices were in correspondence via above-mentioned registration and re-indexing procedure. Because the computation of eigenvectors (EV) involved an integral (Joshi et al., 1997) over the tessellated “fsaverage” surface, all surface measures were first weighted by the area of the elemental triangles of the template surface, giving rise to matrices, X_mn^thk, X_mn^sulc, X_mn^Jacobian, where m=number of subjects and n=number of surface vertices. These matrices were then subject to singular value decomposition (SVD), resulting in coefficients associated with the EVs for each parameter matrix of each hemisphere. EVs that accounted for 80% of the total variance (i.e., dominant EVs) were used as dependent measures for subsequent statistical analyses in SAS (SAS Institute Inc., 2004). We chose 80% as variance threshold based on previous experience on analyzing surface data. We note that using the same 80% threshold across the different measures did not necessarily lead to the same number of EVs in the final outcome (for example, see Table 2).

Table 2.

MANOVA results of eigenvector coefficients in both hemispheres.

PCs accounting for 80% variance	F	df	p
LH cortical thickness (first 35 EVs)	2.42	35	<0.0001
RH cortical thickness (first 37 EVs)	2.73	37	<0.0001
LH cortical convexity (first 56 EVs)	1.50	56	0.027
RH cortical convexity (first 56 EVs)	1.61	56	0.013
LH metric distortion (first 41 EVs)	1.54	41	0.031
RH metric distortion (first 41 EVs)	1.50	41	0.041

It has been shown previously that multivariate surface PCA output eigenvector coefficients follow an F-distribution are suitable for general linear model (GLM) statistical analysis, irrespective of whether groups are balanced or not (Csernansky et al., 2004b). Therefore, multivariate analysis of variance (MANOVA) was used to test for group differences on dominant EV coefficients in each individual cortical parameter model (i.e., thickness, convexity and metric distortion) in each hemisphere. Because gender distribution was significantly different between groups (see Table 1), it was included as a covariate.

For each individual cortical parameter model, if the MANOVA test was significant, a stepwise logistic regression was then used to select the subset of EVs that could optimally discriminate the subject groups. This procedure was similarly applied to models that were pooled from combinations of two measures as well as to an overall model that was pooled from all three measures. We did not impose constraints on the number of model fitting EVs that optimally discriminated groups. In all regression procedures, gender was included as a dependent variable. The SAS procedure provided Receiver Operating Characteristics (ROC) curves for each model and provided comparisons of the areas under the curve (AUC) across different models. In order to further validate the predictive power of selected optimal EV subsets, we also conducted 10-fold cross validation logistic regression models based on selected EV subsets of each model and generated ROC curves for all models. In order to decide if these selected EVs were dependent on the particular subjects used to generate the eigenvectors, we repeated the stepwise logistic regression procedure 10 times, each time randomly excluding 10% subjects (without replacement). And the frequencies of selected EVs of the optimal model across the 10 experiments were calculated to verify the stability of the EV models.

Integrated AD Likelihood Map and Global Index

In order to visualize brain regions showing the most salient effects of combined structural abnormalities associated with AD, we generated an integrated likelihood value at each surface index. To achieve this, the most discriminating subset of EVs for cortical thickness, convexity and metric distortion, selected by stepwise logistic regression, were first used to represent subject i in group g as

$$U_i^g(x)=[{\displaystyle {\sum }_j^{N_1}{\alpha }_{\mathit{ij}}^{\mathit{thk}}{\phi }_j^{\mathit{thk}}(x),{\displaystyle {\sum }_j^{N_2}{\alpha }_{\mathit{ij}}^{\mathit{sulc}}{\phi }_j^{\mathit{sulc}}(x)}},{\displaystyle {\sum }_j^{N_3}{\alpha }_{\mathit{ij}}^{\mathit{Jacobian}}{\phi }_{\mathit{j}}^{\mathit{Jacobian}}(x)]},$$

where x is the vertex, N₁, N₂, N₃ are the total numbers of selected EVs, ${\phi }_j^{\mathit{measure}}$ is the j^th selected EV for each parameter of cortical thickness, convexity and metric distortion, and $a_{\mathit{ij}}^{\mathit{measure}}$ is the coefficient of ${\phi }_j^{\mathit{measure}}$ for subject i. A likelihood ratio map (indicating likelihood for AD, >0) was calculated for each subject at surface vertex x in terms of Mahalanobis distance from $U_i(x)\text{to }{\widehat{\overline{U}}}^{\mathit{AD}}(x)$ – Mahalanobis distance from $U_i(x)\text{to }{\widehat{\overline{U}}}^{\mathit{ctrl}}(x)$:

$$\text{exp}\left(\wedge (x)\right)=\text{exp}\left({[U_i(x)-{\widehat{\overline{U}}}^{AD}(x)]}^T{\widehat{\sum }}^{-1}(x)[U_i(x)-{\widehat{\overline{U}}}^{AD}(x)]-{[U_i(x)-{\widehat{\overline{U}}}^{\mathit{ctrl}}(x)]}^T{\widehat{\sum }}^{-1}(x)[U_i(x)-{\widehat{\overline{U}}}^{\mathit{ctrl}}(x)]\right)$$

where ${\widehat{\overline{U}}}^g$ and $\widehat{\sum }$, are the sample mean of group g (i.e., AD or control) and the pooled sample covariance. Visualized on the white surface, the likelihood ratio map describes which brain regions are more likely affected by AD through the combined effect of cortical thinning and changes in the white surface convexity and metric distortion.

Similarly, a global index of AD associated with the same subset of EVs for cortical thickness, convexity and metric distortion was calculated as follows. For each hemisphere, we first defined a coefficient vector Z_i for subject i as

$${\mathrm{Z}}_i=[({\alpha }_{i1}^{\mathit{thk}},\dots ,{\alpha }_{i{N}_1}^{\mathit{thk}}),({\alpha }_{i1}^{\mathit{sulc}},\dots ,{\alpha }_{i{N}_2}^{\mathit{sulc}}),({\alpha }_{i1}^{\mathit{jacobian}},\dots ,{\alpha }_{i{N}_3}^{\mathit{jacobian}})].$$

Then the global index of AD was defined as

$${\wedge }_i={(Z_i-{\widehat{\overline{Z}}}^{AD})}^T{\widehat{\sum }}^{-1}(Z_i-{\widehat{\overline{Z}}}^{AD})-{(Z_i-{\widehat{\overline{Z}}}^{\mathit{ctrl}})}^T{\widehat{\sum }}^{-1}(Z_i-{\widehat{\overline{Z}}}^{\mathit{ctrl}}),$$

where ${\widehat{\overline{Z}}}^g$ and $\widehat{\sum }$ are the sample means of each group and the pooled sample covariance. Here Λ_i is a log-likelihood ratio centered around 0 and related to a given reconstruction using the same discriminating subset of EVs as above.

Both the likelihood map (surface vertex-wise) and the global index integrate information from all three cortical parameters. While the global index reflects the overall probability that a subject belongs to the AD group, the surface vertex-wise map visualizes this probability in a region specific manner. Therefore, for confirmation purposes, group comparison of each of the raw cortical measures (i.e., cortical thickness, convexity and metric distortion) is performed using general linear models (GLM) at each vertex, with False Discovery Rate (FDR) at a value of q=0.05. The likelihood map should visually reflect a combination of the 3 raw maps.

Results

MANOVA and group discrimination

Group effects were significant across hemispheres for cortical thickness, convexity and metric distortion (see Table 2). Results of stepwise logistic regression procedures for individual cortical measure models as well as combined model are listed in Table 3.

Table 3.

Stepwise logistic regression EV selection results for all models.

Model name	Number of selected EVs (percentage of variance covered)
1. LH thickness	7 EVs (40.5%)
2. RH thickness	7 EVs (35.8.5%)
3. LH convecxity	8 EVs (12.9%)
4. RH convecxity	9 EVs (9.5%)
5. LH metric distortion	5 EVs (11.2%)
6. RH metric distortion	3 EVs (10.2%)
7. LH thickness + convecxity	2 thickness EVs(33.4%) + 6 convecxity EVs(9.6%)
8. RH thickness + convecxity	6 thickness EVs(35.0%) + 7 convecxity EVs(7.1%)
9. LH thickness + metric distortion	6 thickness EVs(39.1%) + 4 metric distortion EVs(10.5%)
10. RH thickness + metric distortion	8 thickness EVs(36.5%) + 2 metric distortion Evs(2.7%)
11. LH convecxity + metric distortion	4 convexity EVs (7.3%) + 6 metric distortion EVs (14.5%)
12. RH convecxity + metric distortion	10 convexity EV (9.5%) + 6 metric distortion EVs (11.4%)
13. LH three measure combined	7 thickness EVs (40.0%) + 6 convexity EVs (8.6%) + 4 metric distortion EVs (6.7%)
14. RH three measure combined	7 thickness EVs (34.9%) + 9 convexity EVs (10.8%) + 5 metric distortion EVs (7.8%)

We note that the cortical thickness EVs that were selected as optimal discriminators accounted for over 35% of total thickness variance (40.9% for LH and 35.8% for RH). In contrast, for convexity and metric distortion, the selected eigenvectors accounted for just about 10% of total convexity variance and total metric distortion variance respectively(12.9% for convexity in LH and 9.46% in RH; 11.2% for metric distortion in LH and 10.2% in RH). This suggests that AD related changes in cortical thickness are more diffused than the changes in cortical convexity and metric distortion. Indeed this can be observed by comparing cortical maps (see Figure 2, first 3 columns) across the 3 measures.

Figure 2.

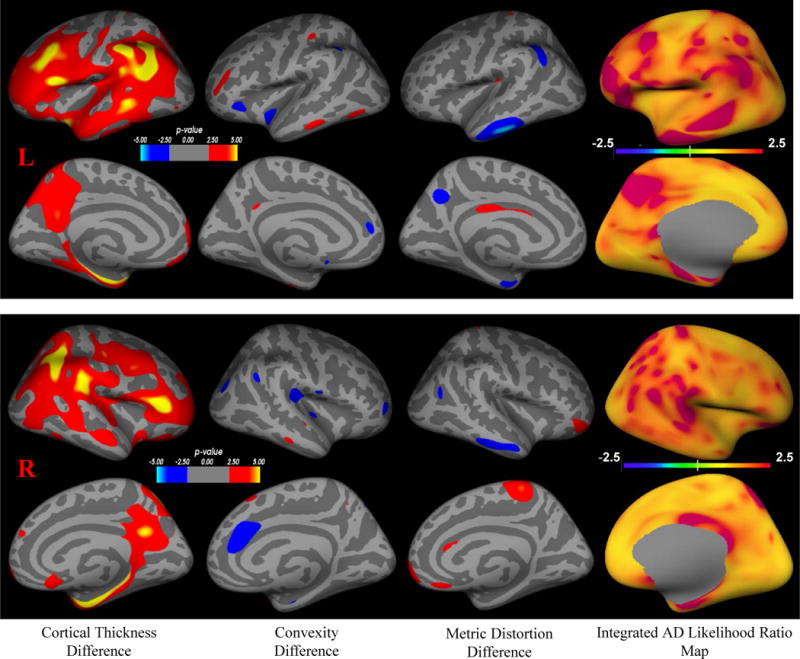
Integrated AD likelihood ratio map based on integrated cortical thickness, convexity and metric distortion. Column from left to right: 1) cortical thickness difference with FDR, 2) convexity difference with FDR, 3) metric distortion difference with FDR between the cognitively normal aging group (control, CDR=0) and the very mild AD group (patient, CDR=0.5), 4) Integrated AD likelihood ratio map based on discrimination function analysis using combined cortical thickness, convexity and metric distortion measures. The two upper rows are likelihood ratio map for the left hemisphere, showing lateral and medial surface views. The lower two rows are likelihood ratio map for the right hemisphere, showing lateral and medial surface views.

ROC curves generated from10-fold Cross Validation for each parameter model are shown in Figure 1, and accuracy, sensitivity, specificity, as well as AUC are reported in 4. In each hemisphere, cortical thickness showed higher discrimination power than convexity and metric distortion (SAS AUC comparison, all p<0.01). We note that the best classification accuracy achieved across the 3 measures were in comparable range from 73% to 79%. The integrated model in the right hemisphere showed the best discrimination power, significantly larger than any single- or two-parameter models (AUC comparison, all p<0.0001).

Figure 1.

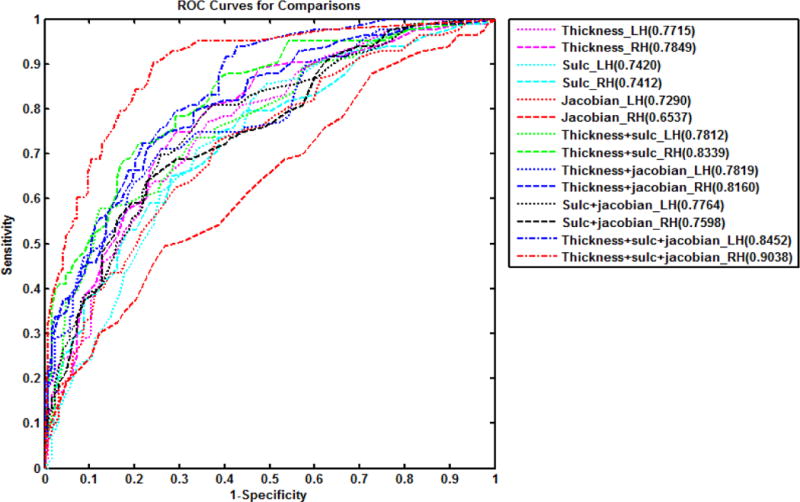
Discrimination for the logistic regression models. The numbers in the legend indicate the Area Under Curve (AUC) for each model.

In order to verify the stability of the selected eigenvectors for the optimal integrated model (Model 14), we performed 10 different stepwise logistic regression procedures, each with 10% subjects excluded (without replacement). The average frequency of the selected EVs among these experiments is 7.2 out of 10 (Thickness_EV1: 10; Thickness_EV8: 10; Thickness_EV15: 8; Thickness_EV16: 2; Thickness_EV31:10; Thickness_EV34: 9; Thickness_EV37: 4; Sulc_EV14: 7; Sulc_EV15: 1; Sulc_EV21: 6; Sulc_EV25: 10; Sulc_EV26: 5; Sulc_EV30: 9; Sulc_EV31: 8; Sulc_EV45: 9; Sulc_EV50: 7; Jacobian_EV8: 7; Jacobian_EV20: 10; Jacobian_EV29: 9; Jacobian_EV40: 3).

Integrated AD Likelihood Map

Using the selected subsets of eigenvectors, we calculated the likelihood ratio (e^Λ(x)) at each surface vertex x for each subject. The likelihood ratio represents the possibility of being drawn from the AD patient distribution versus the control distribution. We visualize the mean likelihood ratio index map for AD patients in Figure 2, column 4. In the reddish regions the likelihood ratio index is larger than 2.5, and this is interpreted as having a likelihood of this node fitting the AD condition at least 2.5 times higher than the likelihood of this node fitting the control condition, which means these nodes are highly possible to be impacted by AD. In Figure 2 we also visualize group differences (surface-based GLM) in cortical thickness (column 1), convexity (column 2) and metric distortion (column 3). In Figure 3 we plot the global index of AD.

Figure 3.

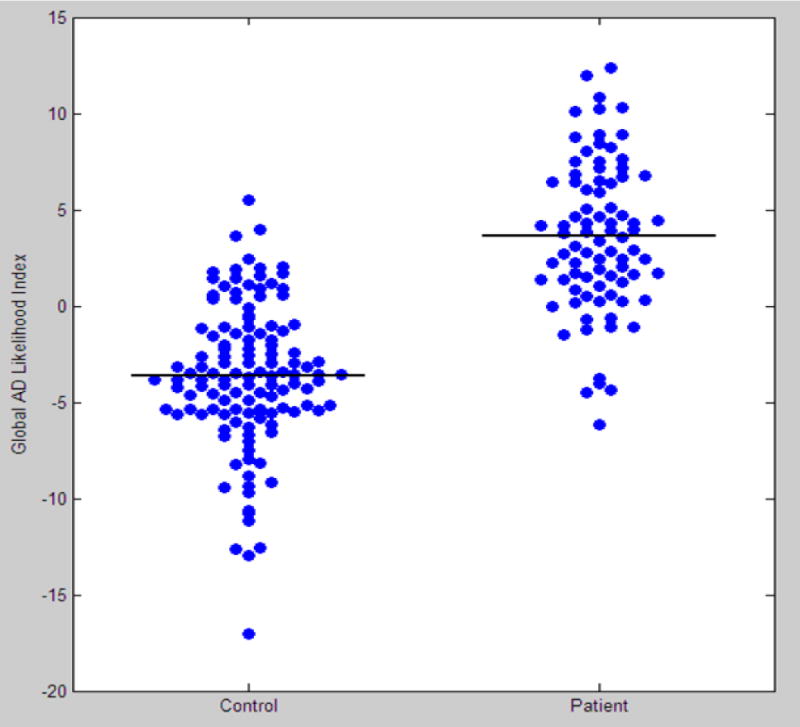
The Global AD likelihood Index for cognitively normal aging group (control, CDR=0) and very mild AD group (patient, CDR=0.5).

Discussion

We developed an innovative approach to distinguish individuals with very mild AD from cognitively normal elderly individuals using multi-dimensional cortical structural data. Our approach integrates information from multiple sources of information to generate a global index of AD (see Figure 3) and indicates the most relevant diseased-related regions as shown in the integrated AD likelihood map (see Figure 2, column 4). The combined measures showed improvement in the diagnostic power.

We observed extensive cortical thinning among patients with very mild AD in cortical regions including prefrontal, supramarginal, enthorinal, precuneus, posterior cingulate cortices and parahippacampus cortex, which are consistent with regions reported in the literature (Dickerson et al., 2011; Frisoni et al., 2010). Regions showing convexity and metric distortion differences were mostly overlapping with regions showing cortical thinning, but to a much smaller extent. There were also several non-overlapping regions for these measures, especially along the cingulate cortex. Our results are consistent with asymmetric patterns of gray matter and white matter changes in association with AD or MCI (Stoub et al., 2006; Zhuang et al., 2012; Zhuang et al., 2013), as well as findings of white matter atrophy around corpus callosum as reported by Guo, et al (2010).

Surface geometric measures of convexity and metric distortion reflect the widening and shallowing of the cortical folding pattern due to regional white matter atrophy. Wide-spread decreases in white matter fractional anisotropy has been reported in patients with AD and MCI (Bozzali et al., 2002; Guo et al., 2010; Im et al., 2008; Rogalski et al., 2009; Rose et al., 2006; Stoub et al., 2006). A recent study found white matter integrity degradation in cognitively normal individuals at risk for amnestic MCI while gray matter structure in these individuals were relatively preserved (Zhuang et al., 2012). Our findings of non-overlapping and complementary patterns between gray matter and white matter changes lend further evidence that these changes in AD may be induced by different pathophysiological origins. We are currently replicating these findings in the Alzheimer Disease Neuroimaging Initiative (ADNI) database.

While the AD literature is abundant with studies focusing on cortical thickness and volume change, there have been very few studies that investigated cortical geometric change. Two such studies have shown significant sulcal depth change in AD patients (Im et al., 2008; Park et al., 2012), and Park, et al (2012) demonstrated sulcal depth had comparable discrimination power as cortical thickness; however, integrating these two measures did not result in improved discrimination power. This perhaps is due to the fact that these studies calculated sulcal depth based on the pial surface, and its change may therefore reflect the combined effect from gray matter atrophy and white matter changes. In our study, the geometric measures were calculated based on the white surface, and when integrated with cortical thickness, the classification accuracy improved from 72% to 81%.

In our study, we observed that only about 10% of the total variance in convexity and metric distortion was discriminative and that the regions associated with these 10% variance were a small portion of the overall white surface. This pattern would have presented significant challenges to traditional ROI approaches that other studies have employed. However, our surface-based PCA method was able to take advantage of these subtle changes because specific subsets EVs were able to provide needed classification power. It is therefore not surprising that the three individual measures demonstrated comparable discrimination power with each other despite differences in the extent of cortical coverage. A detailed comparison between our approach and ROI-based approaches for measuring convexity and metric distortion across ROIs (such as one using FreeSurfer cortical parcellation schemes (Desikan et al., 2006)) is underway.

In our integrated analysis, we performed PCA within each individual parameter set first, followed by discriminant function analysis on the combined sets of EVs. An alternative would be to concatenate all the three types of measurements (cortical thickness, convexity, and metric distortion) at each vertex and apply PCA to the concatenated matrix. Then the discriminant function analysis would select a combined discriminative eigenvector. This approach may result in fewer dependent variables for subsequent discriminant function analysis to further alleviate over-fitting issues. However, this method would bias towards measures that accounted for larger proportion of the total variance. For example, the subset of EVs account for about 40% of the variance from cortical thickness was discriminating but the subset of EVs account for only 10% variance from convexity and metric distortion was discriminating. As we have shown in our results, when PCA was applied to individual measures, EVs accounting for various levels of variance were selected for discrimination (i.e. more lower-order EVs for cortical thickness, and more higher-order EVs for the average convexity). However, when we applied the alternative approach using concatenated PCA, the discrimination power was significantly reduced (not shown).

One of the limitations of this study is that the EVs were drawn from all subjects during cross-validation. This may result in an overly optimistic performance. However, we chose this cross-validation procedure for visualization and evaluation of the distribution of the selected EVs, and for comparison of classifier performance among different models instead of generating an absolute classifier accuracy. Nonetheless, in a true leave-n-out validation scheme, PCA decomposition should be performed on a new training set for each new testing set with subsequent logistic regression. However, this would have prevented us from comparing or evaluating the different EVs set, because they would have been drawn from the different subject sets. A study focused on verifying the EV variability and the integrated model is currently under way.

In addition, PCA maximizes the coverage of total variance that includes both inter-group and intra-group variance among the data. However, for improving classification power, we should aim to maximize inter-group variance. Therefore, machine learning methods such as partial least squares that can capture inter-group variance while reducing data dimensionality may be more suitable. Future studies will use these methods to extract features from multimodality data and compare with performance achieved by PCA.

In conclusion, to the best of our knowledge, this is the first study to report findings in white matter surface geometric measures of convexity and metric distortion in very mild AD, and changes in these measures can be partially attributable to white matter changes associated with AD. Our surface-based statistical framework demonstrates that cortical white matter surface convexity, metric distortion and cortical thickness can provide complementary information, and when combined they can increase our ability to discriminate individuals with very mild AD from cognitively healthy controls. In addition, the proposed statistical framework of performing data reduction and integrated discrimination analysis could also be used for multimodality data, for example, to integrate structural, functional and metabolic imaging data into the same framework.

Table 4.

Accuracy, sensitivity, specificity, and AUC based on 10-fold cross-validation procedures. Selections of eigenvectors are listed above.

Model	accuracy	sensitivity	specificity	AUC
1	69.6%	66.3%	71.8%	0.771
2	72.5%	73.5%	71.8%	0.785
3	68.1%	65.1%	70.2%	0.742
4	67.2%	66.3%	67.7%	0.741
5	65.2%	67.5%	63.7%	0.729
6	58.5%	54.2%	61.3%	0.654
7	69.6%	69.9%	69.4%	0.781
8	73.4%	74.7%	72.6%	0.834
9	73.0%	71.1%	74.2%	0.782
10	73.9%	73.5%	74.2%	0.816
11	71.5%	69.9%	72.6%	0.776
12	68.1%	68.7%	67.7%	0.760
13	74.9%	74.7%	75.0%	0.845
14	81.2%	79.5%	82.3%	0.904