Abstract
Introduction
The first peak of the knee adduction moment curve during walking has been shown to be a good clinical surrogate measure of medial tibiofemoral joint loading and osteoarthritis. Defining the relative contributions of the variables that dictate the knee adduction moment, such as center of mass, center of pressure, vertical ground reaction force, and knee adduction angle (i.e. lower limb alignment), has not been formally investigated within the same cohort of individuals.
Purpose
Therefore, the goal of this study was to determine which of these variables is the biggest determinant of the first peak of knee adduction moment curve.
Methods
Instrumented gait analysis was collected for 30 individuals. Variables significantly correlated with the peak knee adduction moment were input into a stepwise multi-variable linear regression model.
Results
The knee adduction angle predicted 58% of the variance in the first peak knee adduction moment and the vertical ground reaction force magnitude predicted the second most variance (20%).
Conclusions
The most effective way to modify the peak knee adduction moment may be to change the knee adduction angle (e.g. offloader brace), followed by changing the vertical magnitude of the ground reaction force (e.g. cane use).
Introduction
Medial tibiofemoral osteoarthritis (OA) is a multifactorial problem of which abnormal loading of the medial aspect of the joint is regarded as an important contributing factor [1, 2]. Since direct measurements of tibiofemoral contact stress are difficult to measure in vivo, the external knee adduction moment (KAM) has been shown to be a good clinical surrogate measure of medial tibiofemoral joint loading [3]. The peak knee adduction moment has been shown to predict the severity of OA [4] and presence of symptoms [5]. Also, patients with medial compartment OA tend to have a higher first peak KAM [6]. This has led to plethora of treatment options that attempt to lower the peak KAM.
Numerous potential gait modifications have been proposed to reduce the KAM. These alterations include decreased walking speed, increased stance width, toe-out, medial thrust gait, trunk sway, high mobility shoes, variable stiffness shoes, wedge insoles, offloader braces, and canes [7]. These interventions aim to alter four variables associated with the KAM: ab-adduction of the knee, magnitude of the ground reaction force (GRF), the location of the body’s center of mass (COM), and the location of the center of pressure (COP). However, the contribution of each of these four variables to the KAM remains largely unknown. Identification of which variable(s) most closely predict the KAM would then help clinicians develop more specific and efficacious interventions.
There have been a few investigations into the factors associated with the knee adduction moment. For example, Hunt et al. examined the correlation of the KAM to the frontal plane moment arm and the magnitude of frontal plane GRF in patients with OA. They found the magnitude of the knee adduction moment to be most associated with the magnitude of the moment arm (r = 0.57), which was inferred to be more dependent on knee adduction, followed by the magnitude of the frontal plane GRF (r = 0.25) [8]. In a follow up study, Hunt et al. examined the correlation between knee adduction moment and knee adduction, WOMAC pain score, gait speed, toe-out angle, and lateral trunk lean in patients with OA. They concluded that knee ab-adduction (r = 0.51 and r = 0.61), followed by trunk lean (r = −0.39 and r = −0.33), most correlated with the first and second knee adduction moment peaks [9]. While these studies have addressed two factors, dynamic knee adduction and COM translation as measured by the trunk angle, they have not considered other variables that have been modified to alter the KAM. In addition, while studies have reported on the effect specific gait modification strategies have on the KAM (e.g. lateral wedge insoles[10]), the contribution of each factor cannot be elucidated since each strategy may have altered more than one variable at a time. Also, previous reports have used symptomatic patient populations which makes it difficult to assess how much of the observed mechanics are related to altering the KAM versus a reaction to pain. Indeed, pain has been correlated with the KAM[11]. While the current literature is informative as to the potential individual contributions of these modifiable factors to peak KAM, a study considering all four possible factors in the same cohort of healthy pain free controls is lacking. Identifying these features in a healthy population first would be an important step towards the further development of injury prevention and treatment programs.
Defining how modifiable factors such as COP, COM, ab-adduction knee angle, and GRF magnitude are predictive of the first peak of the KAM is needed to provide clinicians with clearer insights into which variables to manipulate when prescribing a treatment to reduce abnormally high KAM. The literature has found knee adduction, trunk lean, and the magnitude of the GRF to explain 32–37% [8, 9], 11–15% [9], and 6% [8] of the variance in the KAM, respectively. This leaves 42% unaccounted for, which may be due to COP location. Therefore, the goal of this study was to determine which variable is the biggest determinant of the knee adduction moment: the location of the center of pressure, the location of the body’s center of mass, knee adduction angle, or the magnitude of the ground reaction force. We hypothesized that the COP location would predict the most amount of the KAM variance, followed by the knee adduction angle, the COM location, and the vertical and medial GRF.
Methods
Data Collection
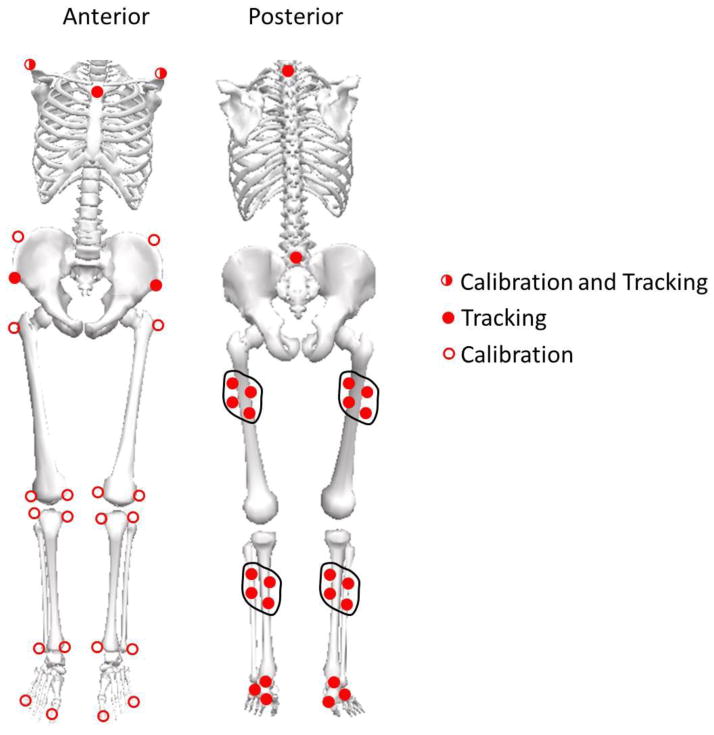
Following a protocol approved by an institutional review board, subjects were recruited from the local community via word of mouth. After providing informed consent, motion capture data was collected for 30 subjects (mean age:24 SD:3 yrs, mean height: 1.66 SD: 0.05 m, mean mass: 59.6 SD: 7.0 kg) walking on a treadmill (mean self-selected speed of 1.31 SD: 0.11 m/s). Forty-nine retroreflective markers were placed on the subject using a previously established configuration (Figure 1) [12]: anatomic markers on the L4–5 junction, bilateral iliac crests, anterior superior iliac spines, greater trochanters, medial and lateral femoral epicondyles, tibial plateaus, malleoli, and the first and fifth metatarsal heads. Tracking markers were placed on rigid shells on the thighs, shanks, and posterior aspects of the shoes. Three-dimensional marker trajectories were measured during walking by sampling at 200 Hz with a 15 camera motion analysis system (Motion Analysis Corp, Santa Rosa, USA) while simultaneously collecting force data at 1200 Hz using an instrumented Bertec treadmill (Bertec, Columbus, OH).
Figure 1.
Forty-nine retroreflective markers were placed on the body: 20 for calibration of the model, 27 for tracking, and 2 for both tracking and calibration.
Knee Kinematics and Kinetics Calculations
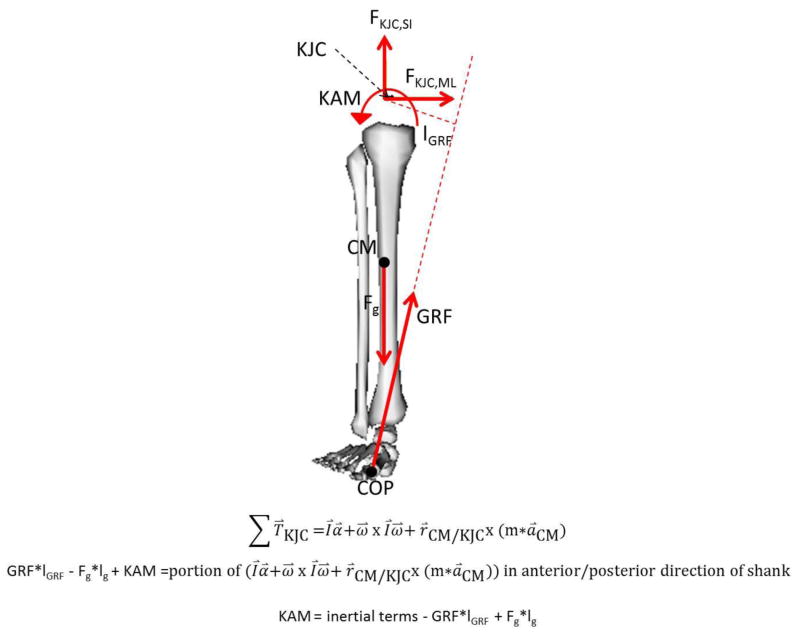
Visual 3D (C-motion, Germantown, MD, USA) was used to filter the data, calculate a functional hip joint center [13], perform inverse kinematics, and perform inverse dynamics. Marker data was filtered at 8 Hz and force data filtered at 35 Hz using a fourth-order low-pass zero-lag Butterworth filter. A residual analysis was performed on the data and used to choose these cutoff frequencies (Winter, 2009). Using a previously established biomechanical model [14], joint angles and moments were calculated according to successive body fixed rotations using the order of flexion-extension, ab-adduction, followed by internal-external rotation [15]. The mass properties of the segments were modeled as conical frustums [16]. The knee adduction moment (Figure 2), a result of inverse dynamics, was resolved into the coordinate system of the tibia. Custom Matlab code (MathWorks Inc., Natick, MA) was used to extract the first peak knee adduction moment as well as kinematic variables at the same instant in time as the peak knee adduction moment: the adduction angle of the tibiofemoral joint, the location of the center of pressure relative to the foot origin (centered between the malleoli), the magnitude of the ground reaction force in the vertical and medial-lateral directions, and the global position of the body’s center of mass. The body COM did not include the head or arms. Data was collected from 5 trials for each subject and then averaged. Knee adduction moment was normalized to body mass times height [17] and ground reaction force by body weight squared [18]. These variables affect the KAM through either the moment arm of the ground reaction force (knee adduction angle, location of center of pressure, and location of center of mass) or the ground reaction force directly.
Figure 2.
Free body diagram of the lower limb with the equation (Newton’s equation of motion) used to calculate the knee adduction moment. TKJC = torque about the knee joint center (vector), I = inertia of lower limb (matrix), α = angular acceleration of lower limb (vector), ω = angular velocity of lower limb (vector), rCM/KJC = position vector from center of mass of the lower segment to the knee joint center, m = mass of lower limb (scalar), aCM = acceleration of lower limb (vector), GRF = magnitude of ground reaction force in frontal plane (scalar), lGRF = moment arm of frontal plane GRF (scalar), Fg = weight of lower limb (scalar), lg = moment arm of weight in frontal plane (scalar), KAM = knee adduction moment (scalar).
Statistical Analysis
Using SPSS (SPSS Inc., Chicago, IL), variables were checked for normality using the Kolmogorov-Smirnov test with a Lilliefors significance correction. Subsequently, Pearson’s correlations coefficients were calculated and those variables significantly correlated with the peak knee adduction moment were input into a forward stepwise multi-variable linear regression model (Pin=0.05, Pout=0.1) to determine the amount of variance in KAM explained by the kinematic variables. Effects due to multicollinearity were limited by ensuring the Pearson’s correlation coefficients between variables input in the regression model were less than 0.8 [19]. Model fit to the data was examined using the Durbin-Watson value [19]. The assumption of homogeneity of variance and linearity was verified by qualitative inspection of the regression of standardized residual versus regression of standardized predicted value plot. Since previous work has found trunk lean (i.e. COM location) to be a predictor of KAM [9], the correlations of COP (i.e. GRF location) and GRF magnitude with COM location were also investigated as a secondary analysis to better understand the mechanism behind how COM may affect KAM.
Results
The superior-inferior location of the COP with respect to foot origin (r = −.450, p = 0.013), vertical magnitude of the GRF (r = 0.676, p < 0.001), and the knee adduction angle (r = 0.762, p < 0.001) were significantly correlated with the knee adduction moment (Table 1) and thus input in the multi-variable linear regression model. There was no collinearity found between these variables (Table 1). The knee adduction angle and vertical magnitude of the GRF were significant predictors of the first peak KAM (Table 2), explaining 58% and 20% of the variance, respectively (Figure 3). The Durbin-Watson value of the linear regression model was 1.865. A higher first peak KAM was associated with increased knee adduction angle and vertical magnitude of the GRF. Even though the superior-inferior location of the COP was correlated with the KAM, it was not a significant predictor in the regression model (explained <2% of the variance when forced into the linear regression model, Table 2). There was no correlation found between the knee adduction moment and the medial-lateral location of the COP, the location of the body COM, or the medial-lateral magnitude of the GRF.
Table 1.
Correlations between variables of interest.
| Peak knee adduction moment | Medial-lateral location of COP | Superior-inferior location of COP | Medial-lateral location of body COM | Superior-inferior location of body COM | Medial-lateral magnitude of GRF | Vertical magnitude of GRF | Knee adduction angle | ||
|---|---|---|---|---|---|---|---|---|---|
| Peak knee adduction moment | Pearson Correlation | 1 | |||||||
| Sig. (2-tailed) | |||||||||
| N | 30 | ||||||||
| Medial-lateral location of COP | Pearson Correlation | −.094 | 1 | ||||||
| Sig. (2-tailed) | .621 | ||||||||
| N | 30 | 30 | |||||||
| Superior-inferior location of COP | Pearson Correlation | −.450* | −.285 | 1 | |||||
| Sig. (2-tailed) | .013 | .126 | |||||||
| N | 30 | 30 | 30 | ||||||
| Medial-lateral location of body COM | Pearson Correlation | .220 | −.420* | .184 | 1 | ||||
| Sig. (2-tailed) | .261 | .026 | .349 | ||||||
| N | 28 | 28 | 28 | 28 | |||||
| Superior-inferior location of body COM | Pearson Correlation | −.025 | −.458* | .087 | .359 | 1 | |||
| Sig. (2-tailed) | .900 | .014 | .659 | .061 | |||||
| N | 28 | 28 | 28 | 28 | 28 | ||||
| Medial-lateral magnitude of GRF | Pearson Correlation | .275 | .264 | −.206 | −.311 | −.302 | 1 | ||
| Sig. (2-tailed) | .142 | .158 | .274 | .107 | .119 | ||||
| N | 30 | 30 | 30 | 28 | 28 | 30 | |||
| Vertical magnitude of GRF | Pearson Correlation | .676** | .005 | −.179 | −.033 | −.087 | .308 | 1 | |
| Sig. (2-tailed) | .000 | .981 | .343 | .869 | .659 | .097 | |||
| N | 30 | 30 | 30 | 28 | 28 | 30 | 30 | ||
| Knee adduction angle | Pearson Correlation | .762** | −.128 | −.399* | .334 | .100 | .073 | .328 | 1 |
| Sig. (2-tailed) | .000 | .500 | .029 | .082 | .614 | .700 | .076 | ||
| N | 30 | 30 | 30 | 28 | 28 | 30 | 30 | 30 |
Correlation is significant at the 0.05 level (2-tailed).
Correlation is significant at the 0.01 level (2-tailed).
Table 2.
Results of forward stepwise multi-variable linear regression for KAM as the dependent variable
| R | R2 | Adjusted R2 | Change in R2 | p | |
|---|---|---|---|---|---|
| Knee adduction angle | .762 | .581 | .566 | - | <0.001 |
| Knee adduction angle + vertical GRF | .885 | .783 | .767 | .203 | <0.001 |
| Knee adduction angle + vertical GRF + superior- inferior COP | .895 | .801 | .778 | .018 | >0.05 |
Figure 3.
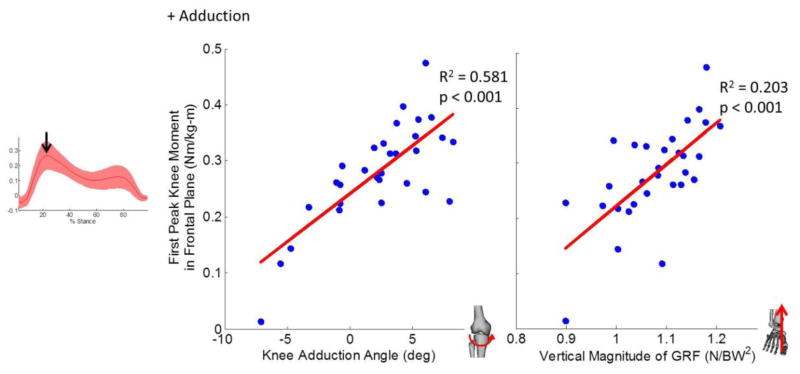
The knee adduction angle and superior-inferior magnitude of the GRF explained 58% and 20%, respectively, of the variance seen in the KAM.
The medial-lateral location of the COP was significantly correlated with the medial-lateral location (r = −0.420, p = 0.026) and superior-inferior location (r = −0.458, p = 0.014) of the COM. No correlation was found between COM location and the magnitude of the GRF in either the vertical or medial-lateral direction.
Discussion
The knee adduction moment has been used as a surrogate measure of medial tibiofemoral cartilage loading, especially in the development of non-pharmacological treatments in patients with medial compartment tibiofemoral OA. In order to develop non-surgical options to treat these patients and reduce cartilage loading, it is imperative to first define what factors affect the KAM. We investigated the association of the center of mass, center of pressure, adduction angle, and ground reaction force magnitude on the KAM, finding that the adduction angle, followed by the vertical magnitude of the GRF, are the two main predictors of the first peak KAM. This provides information on which strategies might be the most effective in altering KAM.
There was a significant association between knee adduction angle and the peak KAM, with the adduction angle predicting 58% of the variance. These results are in agreement with earlier studies where alignment has been shown to explain 25%–50% of the first peak of the KAM in osteoarthritic individuals [9, 20], a 50% reduction in KAM after a tibial osteotomy [7, 21], and a 19–50% reduction in medial thrust gait [7]. As the knee adduction angle increases, the medial compartment experiences greater compression loads in the cartilage. As this greater compression force in the medial compartment is not acting at the knee joint center, it then adds to the knee adduction moment about the knee joint center. Knee offloader braces have been designed and advocated as a potential mechanism to decrease the KAM by altering knee alignment to be in a more abducted configuration [22–24]. In addition, variable stiffness shoes have also been shown to increase knee abduction angle and decrease the first peak knee adduction moment [25–27]. The results of the current study suggest that using these types of interventions would address the largest determinant of the KAM as opposed to other potential measures and provide additional evidence of the mechanism behind which these interventions are effective.
There was also a significant correlation between the vertical magnitude of the GRF and the peak KAM, which accounted for 20% of the variance in peak KAM. This result suggests that the next effective treatment besides ab-adduction alignment is one that alters the vertical GRF (e.g. canes or walking poles, weight loss). This result is in agreement with a review [7] that cane use may reduce the peak KAM by the second largest amount. Since the KAM is mostly determined by the frontal plane magnitude of the GRF and its moment arm about the knee joint center [8], a direct reduction in GRF would also result in a decreased KAM. When a cane is used, part of the GRF is shifted to the cane and the GRF under the foot reduced, hence the decrease seen in KAM [28].
Trunk sway is thought to alter the COM and line of action of the GRF, thus effectively altering the moment arm of the GRF about the joint center to reduce the KAM [9, 29]. No correlation was found between COM and GRF magnitude in either direction, which contradicts the theory that the direction of the GRF is related to the COM position in the frontal plane [9, 29]. No data have been presented in the literature to suggest the COM and GRF direction are related in the frontal plane. In the sagittal plane, the GRF passes through a point superior to the COM rather than through the COM, due to ankle torque modulation to maintain stability during walking [30, 31]. Future work could investigate if these findings extend to the frontal plane as well. The results of the current study are in disagreement with another recent paper that found trunk sway to explain much of the variance in peak KAM [9]. One potential explanation is that there may be other variables altered by trunk sway that were not assessed in the previous study. Since the trunk COM is moving medial-laterally during trunk sway, not only could the COP move, but the magnitude of the ground reaction force may also change, as was shown by the current study’s findings that the vertical magnitude of the ground reaction force explained much of the variance in KAM. We also found a significant correlation between COM and COP. Winter suggests the COP location varies in response to imbalances in the COM location [32]. This relation of COM and COP comes about via the rotational equations of motion. A shift in the COP will in turn alter the torque of the GRF about the COM. Therefore a shift in COM may occur to maintain the desired motion or equilibrium position.
Our results suggest trunk sway may need further investigation to understand how it functions to reduce KAM. Our results may also provide insight into how other current gait modifications alter KAM. Decreased walking speed has been shown to decrease KAM by 8%, which may be due to changes in the GRF [33]. Since our results show 20% of the KAM to be attributed to the vertical GRF, there may be other factors that interact and change during walking speed to affect KAM. Increased stance width can decrease KAM by up to 9% [7, 34], toe-out by 1% [35], and lateral-wedge insoles by 9% [36], all of which are thought to be a result of alterations in medial-lateral COP. However, our results showed medial-lateral COP to not be significantly related to KAM and superior-inferior COP an insignificant predictor (1% of the variance). Therefore, these modifications may be acting through other mechanisms (i.e. GRF, knee alignment) that could be investigated in future studies. High mobility shoes can decrease KAM by 8% by altering the COP and GRF [27, 37]. Our results suggest that these shoes may not be changing the GRF as its main mechanism but rather the COP. Although our results may be used to gain some insight into the relationship between these gait modification strategies and the KAM, they also cannot fully explain the reductions in KAM, thus highlighting that these modifications are multifactorial in nature.
One important study design factor to consider in the interpretation of our results is the use of healthy subjects. In a prospective study, a higher knee adduction moment in healthy elders has been related to the later development of knee pain [38]. Our results suggest targets to reduce the KAM in healthy, asymptomatic subjects to prevent future problems. Also, individuals with symptomatic, painful osteoarthritis may make alterations in their gait, which would make mechanisms of KAM reduction hard to elucidate without this base knowledge in healthy subjects. Future work is needed to extend the results of this study and assess the strength these relationships in osteoarthritis patients.
There are some limitations to consider in this study. Due to the cross-sectional design, causality could not be explicitly established. Future studies could use biomechanical modeling to prove our suggested mechanisms of how each variable alters peak KAM. The results were able to explain 78% of the variance in the first peak knee adduction moment. Although considerable, this leaves 22% unaccounted for. Variables not considered included the inertial terms and the torque the weight of the lower limb produces about the knee joint center (Figure 2). The linear regression model used was also a limitation. A forward elimination regression model was used since this has been used in other cross-sectional studies in the literature [39, 40]. Although a forward method is more likely to miss a predictor than the backward methods, results from a backward method did not affect the interpretation of our results. Finally, the subjects walked on a treadmill rather than overground. Frontal plane moments have been shown to not vary between treadmill and overground walking [41, 42]. Therefore, we expect our results to be generalizable to overground walking.
This study determined which variables explained a majority of the variance seen in the first peak of the knee adduction moment curve during gait in terms of four modifiable variables: the location of the center of pressure, the location of the body’s center of mass, ab-adduction angle of the knee, and the magnitude of the ground reaction force. Our results show that ab-adduction angle explains most of the variance in peak KAM, thus suggesting reductions in it may be an effective treatment. Altered vertical GRF magnitude explained the second most variance, suggesting another important variable in the modification of peak KAM. These results can provide insight into critical variables that affect KAM so we can understand current treatment strategies better and develop new ones.
Highlights.
Knee adduction angle predicted 58% of the variance in peak knee adduction moment
Vertical ground reaction force magnitude predicted 20% of the variance
Offloader braces may be most effective way to modify peak knee adduction moment
Acknowledgments
We thank our collaborator Becca Williams for her input on this project. This work was partially funded by the Division of Information and Intelligent Systems of the National Science Foundation, grant 1231545 as well as by the National Institute of Arthritis and Musculoskeletal and Skin Diseases of the National Institutes of Health under award number K23AR062069.
Footnotes
There are no conflicts of interest to disclose.
The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Andriacchi TP, et al. A framework for the in vivo pathomechanics of osteoarthritis at the knee. Ann Biomed Eng. 2004;32:447–457. doi: 10.1023/b:abme.0000017541.82498.37. [DOI] [PubMed] [Google Scholar]
- 2.Vincent KR, et al. The pathophysiology of osteoarthritis: A mechanical perspective on the knee joint. PM&R. 2012;4:S3–S9. doi: 10.1016/j.pmrj.2012.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhao D, et al. Correlation between the knee adduction torque and medial contact force for a variety of gait patterns. J Orthop Res. 2007;25:789–797. doi: 10.1002/jor.20379. [DOI] [PubMed] [Google Scholar]
- 4.Sharma L, et al. Knee adduction moment, serum hyaluronan level, and disease severity in medial tibiofemoral osteoarthritis. Arthritis Rheum. 1998;41:1233–1240. doi: 10.1002/1529-0131(199807)41:7<1233::AID-ART14>3.0.CO;2-L. [DOI] [PubMed] [Google Scholar]
- 5.Thorp LE, et al. Relationship between pain and medial knee joint loading in mild radiographic knee osteoarthritis. Arthritis Rheum. 2007;57:1254–1260. doi: 10.1002/art.22991. [DOI] [PubMed] [Google Scholar]
- 6.Baliunas AJ, et al. Increased knee joint loads during walking are present in subjects with knee osteoarthritis. Osteo and Cart. 2002;10:573–579. doi: 10.1053/joca.2002.0797. [DOI] [PubMed] [Google Scholar]
- 7.Fregly BJ. Gait Modification to Treat Knee Osteoarthritis. HSSJ. 2012;8:45–48. doi: 10.1007/s11420-011-9229-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hunt MA, et al. Associations among knee adduction moment, frontal plane ground reaction force, and lever arm during walking in patients with knee osteoarthritis. J Biomech. 2006;39:2213–2220. doi: 10.1016/j.jbiomech.2005.07.002. [DOI] [PubMed] [Google Scholar]
- 9.Hunt M, et al. Lateral trunk lean explains variation in dynamic knee joint load in patients with medial compartment knee osteoarthritis. Osteo and Cart. 2008;16:591–599. doi: 10.1016/j.joca.2007.10.017. [DOI] [PubMed] [Google Scholar]
- 10.Hinman RS, et al. Lateral wedge insoles for medial knee osteoarthritis: Effects on lower limb frontal plane biomechanics. Clin Biomech. 2012;27:27–33. doi: 10.1016/j.clinbiomech.2011.07.010. [DOI] [PubMed] [Google Scholar]
- 11.Foroughi N, Smith R, Vanwanseele B. The association of external knee adduction moment with biomechanical variables in osteoarthritis: a systematic review. The Knee. 2009;16:303–309. doi: 10.1016/j.knee.2008.12.007. [DOI] [PubMed] [Google Scholar]
- 12.Noehren B, et al. The effect of pain on hip and knee kinematics during running in females with chronic patellofemoral pain. Gait & Posture. 2012;36:596–599. doi: 10.1016/j.gaitpost.2012.05.023. [DOI] [PubMed] [Google Scholar]
- 13.Schwartz MH, Rozumalski A. A new method for estimating joint parameters from motion data. J Biomech. 2005;38:107–116. doi: 10.1016/j.jbiomech.2004.03.009. [DOI] [PubMed] [Google Scholar]
- 14.Noehren B, et al. Proximal and distal kinematics in female runners with patellofemoral pain. Clin Biomech. 2012;27:366–371. doi: 10.1016/j.clinbiomech.2011.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Grood ES, Suntay WJ. A joint coordinate system for the clinical description of three-dimensional motions: application to the knee. J Biomech Engr. 1983;105:136–144. doi: 10.1115/1.3138397. [DOI] [PubMed] [Google Scholar]
- 16.Hanavan EP., Jr . A mathematical model of the human body. 1964. DTIC Document. [PubMed] [Google Scholar]
- 17.Butler RJ, et al. Frontal-Plane Gait Mechanics in People With Medial Knee Osteoarthritis Are Different From Those in People With Lateral Knee Osteoarthritis. Phys Ther. 2011;91:1235–1243. doi: 10.2522/ptj.20100324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wannop JW, Worobets JT, Stefanyshyn DJ. Normalization of ground reaction forces, joint moments and free moments in human locomotion. J Appl Biomech. 2012;28:665–676. doi: 10.1123/jab.28.6.665. [DOI] [PubMed] [Google Scholar]
- 19.Field A. Discovering statistics using SPSS. Sage publications; 2009. [Google Scholar]
- 20.Barrios JA, Royer TD, Davis IS. Dynamic versus radiographic alignment in relation to medial knee loading in symptomatic osteoarthritis. J Appl Biomech. 2012;28:551–9. doi: 10.1123/jab.28.5.551. [DOI] [PubMed] [Google Scholar]
- 21.Wada M, et al. Relationship between gait and clinical results after high tibial osteotomy. Clin Orthop Relat Res. 1998;354:180–188. doi: 10.1097/00003086-199809000-00022. [DOI] [PubMed] [Google Scholar]
- 22.Gross KD, Hillstrom HJ. Noninvasive devices targeting the mechanics of osteoarthritis. Rheum Dis Clin North Am. 2008;34:755–776. doi: 10.1016/j.rdc.2008.06.001. [DOI] [PubMed] [Google Scholar]
- 23.Ramsey DK, Russell ME. Unloader Braces for Medial Compartment Knee Osteoarthritis: Implications on Mediating Progression. Sports Health: Multidisciplinary Approach. 2009;1:416–426. doi: 10.1177/1941738109343157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kutzner I, et al. The effect of valgus braces on medial compartment load of the knee joint–in vivo load measurements in three subjects. Journal of biomechanics. 2011;44:1354–1360. doi: 10.1016/j.jbiomech.2011.01.014. [DOI] [PubMed] [Google Scholar]
- 25.Boyer KA, et al. Kinematic adaptations to a variable stiffness shoe: Mechanisms for reducing joint loading. J Biomech. 2012;45:1619–1624. doi: 10.1016/j.jbiomech.2012.04.010. [DOI] [PubMed] [Google Scholar]
- 26.Erhart JC, et al. A variable-stiffness shoe lowers the knee adduction moment in subjects with symptoms of medial compartment knee osteoarthritis. J Biomech. 2008;41:2720–2725. doi: 10.1016/j.jbiomech.2008.06.016. [DOI] [PubMed] [Google Scholar]
- 27.Jenkyn TR, Erhart JC, Andriacchi TP. An analysis of the mechanisms for reducing the knee adduction moment during walking using a variable stiffness shoe in subjects with knee osteoarthritis. Journal of biomechanics. 2011;44:1271–1276. doi: 10.1016/j.jbiomech.2011.02.013. [DOI] [PubMed] [Google Scholar]
- 28.Gross KD. Device use: walking AIDS, braces, and orthoses for symptomatic knee osteoarthritis. Clin Geriatr Med. 2010;26:479–502. doi: 10.1016/j.cger.2010.03.007. [DOI] [PubMed] [Google Scholar]
- 29.Powers CM. The influence of abnormal hip mechanics on knee injury: a biomechanical perspective. J Orthop Sports Phys Ther. 2010;40:42–51. doi: 10.2519/jospt.2010.3337. [DOI] [PubMed] [Google Scholar]
- 30.Gruben KG, Boehm WL. Mechanical interaction of center of pressure and force direction in the upright human. J Biomech. 2012;45:1661–1665. doi: 10.1016/j.jbiomech.2012.03.018. [DOI] [PubMed] [Google Scholar]
- 31.Gruben KG, Boehm WL. Force direction pattern stabilizes sagittal plane mechanics of human walking. Human Move Sci. 2012;31:649–659. doi: 10.1016/j.humov.2011.07.006. [DOI] [PubMed] [Google Scholar]
- 32.Winter DA. Biomechanics and motor control of human movement. 4. Waterloo, Ontario: Wiley; 2009. [Google Scholar]
- 33.Robbins SM, Maly MR. The effect of gait speed on the knee adduction moment depends on waveform summary measures. Gait & Posture. 2009;30:543–546. doi: 10.1016/j.gaitpost.2009.08.236. [DOI] [PubMed] [Google Scholar]
- 34.Fregly BJ, Reinbolt JA, Chmielewski TL. Evaluation of a patient-specific cost function to predict the influence of foot path on the knee adduction torque during gait. CMBBE. 2008;11:63–71. doi: 10.1080/10255840701552036. [DOI] [PubMed] [Google Scholar]
- 35.Guo M, Axe MJ, Manal K. The influence of foot progression angle on the knee adduction moment during walking and stair climbing in pain free individuals with knee osteoarthritis. Gait & Posture. 2007;26:436–441. doi: 10.1016/j.gaitpost.2006.10.008. [DOI] [PubMed] [Google Scholar]
- 36.Butler RJ, et al. The effect of a subject-specific amount of lateral wedge on knee mechanics in patients with medial knee osteoarthritis. J Orthop Res. 2007;25:1121–1127. doi: 10.1002/jor.20423. [DOI] [PubMed] [Google Scholar]
- 37.Shakoor N, et al. Effects of specialized footwear on joint loads in osteoarthritis of the knee. Arthritis Care & Research. 2008;59:1214–1220. doi: 10.1002/art.24017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Amin S, et al. Knee adduction moment and development of chronic knee pain in elders. Arthritis Care & Research. 2004;51:371–376. doi: 10.1002/art.20396. [DOI] [PubMed] [Google Scholar]
- 39.Rutherford D, et al. Foot progression angle and the knee adduction moment: a cross-sectional investigation in knee osteoarthritis. Osteo and Cart. 2008;16:883–889. doi: 10.1016/j.joca.2007.11.012. [DOI] [PubMed] [Google Scholar]
- 40.Pohl MB, et al. Biomechanical predictors of retrospective tibial stress fractures in runners. J Biomech. 2008;41:1160–1165. doi: 10.1016/j.jbiomech.2008.02.001. [DOI] [PubMed] [Google Scholar]
- 41.Lee SJ, Hidler J. Biomechanics of overground vs. treadmill walking in healthy individuals. J Appl Phys. 2008;104:747–755. doi: 10.1152/japplphysiol.01380.2006. [DOI] [PubMed] [Google Scholar]
- 42.Riley PO, et al. A kinematic and kinetic comparison of overground and treadmill walking in healthy subjects. Gait & Posture. 2007;26:17–24. doi: 10.1016/j.gaitpost.2006.07.003. [DOI] [PubMed] [Google Scholar]