Mechanistic Studies of an Autonomously Pulsing Hydrogel/Enzyme System for Rhythmic Hormone Delivery

Abstract

Numerous hormones are known to be endogenously secreted in a pulsatile manner. In particular, gonadotropin replacing hormone (GnRH) is released in rhythmic pulses, and disruption of this rhythm is associated with pathologies of reproduction and sexual development. In an effort to develop an implantable, rhythmic delivery system, a scheme has been demonstrated involving a negative feedback instability between a pH-sensitive membrane and enzymes that convert endogenous glucose to hydrogen ion. A bench prototype system based on this scheme was previously shown to produce near rhythmic oscillations in internal pH and in GnRH delivery over a period of one week. In the present work, a systematic study of conditions permitting such oscillations is presented, along with a study of factors causing period of oscillations to increase with time and ultimately cease. Membrane composition, glucose concentration, and surface area of marble (CaCO₃), which is incorporated as a reactant, were found to affect the capacity of the system to oscillate, and the pH range over which oscillations occur. Accumulation of gluconate^- and Ca²⁺ in the system over time correlated with lengthening of oscillation period, and possibly with cessation of oscillations. Enzyme degradation may also be a factor. These studies provide the groundwork for future improvements in device design.

1. Introduction

Numerous hormones are endogenously secreted in a pulsatile, episodic manner, the periodicity of which is as important as the chemical structure of the hormone [1-4]. Rhythmicity or quasirhythmicity of hormones often occurs in an ultradian fashion, i.e. several cycles per day. In some cases, periodicity of secretion is believed to be set to match the kinetics of desensitization and resensitization of target receptors [1, 5].

For example, gonadotropin releasing hormone (GnRH: aka luteinizing hormone releasing hormone, LHRH) is a decapeptide “master hormone” that is released rhythmically from the hypothalamus every 1-2 hours under neuroendocrine control [6-8]. Following portal transport to the anterior pituitary gland, GnRH stimulates hypophysial secretion of luteinizing hormone (LH) and follicle stimulating hormone (FSH). These peptide hormones travel to the gonads, where they stimulate secretion of other peptide and steroid sex hormones such as secretin, estradiol, testosterone and progesterone. Insufficient secretion of GnRH results in reproductive disorders associated with hypogonadotropic hypogonadism (HH), which occurs in both men and women, and is manifested in arrested or regressed sexual maturation and fertility [4, 9]. Treatment of hormonal disorders associated with HH warrants hormone delivery in a temporal pattern mimicking the endogenous ultradian rhythm. Studies have demonstrated the ability of pulsed GnRH to restore reproductive function in women with HH, while continuously administered GnRH and its synthetic analogs suppress reproductive function [10].

Several approaches to ultradian GnRH delivery have been proposed [11-14]. Wearable intravenous and subcutaneous pumps with rhythmic external control have an established track record for GnRH fertility therapy, but these devices carry risk of infection and other inconveniences. Transdermal iontophoretic delivery of GnRH has been investigated [15, 16], as have been the intranasal and buccal routes [17, 18]. To date, however, no adequate substitute for pumps has advanced.

The high potency and hence extremely low dose requirement of hormones such as GnRH suggests that implanted systems could provide ultradian doses over extended time periods. It has been proposed, for example, that small doses of GnRH be released from microfabricated multi-well chips, with different wells activated in sequence by electrodissolution or electrothermal destruction of sealing layers [19, 20]. Such systems require electrical power provided either by an external source with transcutaneous wires, or a co-implanted battery.

Previous work demonstrated the principle of the autonomous rhythmic hormone delivery system based on a hydrogel and enzymes [21, 22], described in Section 2. Under proper conditions, the system exhibits ultradian oscillations in internal pH and coherent pulses of released GnRH. However, it was also found that these rhythmic behaviors, when present, are not sustained indefinitely. The period of pH oscillation, and hence the interval between pulses of GnRH release, increase with time, and eventually oscillations cease.

The ability of the system to produce pH oscillations and rhythmically pulsed GnRH release depends critically on membrane chemistry and other design features, and on glucose concentration. The present study deals with effects of certain design parameters on the system's capacity to oscillate, with factors causing progressive increase in period of pH oscillations, and with factors that lead to the ultimate cessation of those oscillations. Due to the expense of working with GnRH, the hormone was not included in these studies. It is presumed that pulsatile GnRH release will correlate with pH oscillations as shown before—this assumption will have to be reconfirmed at further development stages. Since GnRH is highly potent and can be present in very low concentrations, it is not expected to perturb the system's dynamics.

Section 2 provides a brief review of the hydrogel/enzyme based oscillator and experiments that have been previously reported. Experimental methods for the present work are described in section 3. In the first part of section 4, the effects of system parameters on the capacity of the system to initiate sustained oscillations are studied. In the second part of section 4, factors contributing to lengthening of oscillation period and ultimate cessation of oscillations are investigated. Discussion, conclusions and suggestions for future work are presented in section 5.

2. General Background

The ultradian rhythmic hormone delivery system under investigation consists of an chamber containing GluOx, Cat and GluLac, plus the hormone to be released (e.g. GnRH). The chamber communicates with the external environment, which contains a constant concentration of glucose, through a poly(N-isopropylacrylamide-co-methylacrylic acid) [poly(NIPAM-co-MAA)] hydrogel membrane. This membrane exhibits a sharp transition in permeability to glucose with change in pH inside the chamber. When the membrane is in its charged and swollen state (MAA sidechains deprotonated), glucose diffuses from outside through the membrane into the chamber, where it is rapidly converted to hydrogen ions according to the reactions

$$\begin{array}{c}\text{Glucose}+{\mathrm{O}}_2+{\mathrm{H}}_2\mathrm{O}\stackrel{\mathit{\text{GluOx}}}{\to }\text{Glucose lactone}+{\mathrm{H}}_2{\mathrm{O}}_2\\ \text{Glucose lactone}\stackrel{\mathit{\text{GluLac}}}{\to }\text{Gluconic Acid}\overleftarrow{\to }\text{Gluconate}+{\mathrm{H}}^{+}\\ {\mathrm{H}}_2{\mathrm{O}}_2\stackrel{\mathit{\text{Cat}}}{\to }½{\mathrm{O}}_2+{\mathrm{H}}_2\mathrm{O}\end{array}$$ (I)

The first reaction produces gluconolactone and H₂O₂, an unwanted byproduct [23, 24]. The second reaction converts gluconolactone to gluconic acid, which rapidly dissociates to gluconate^- and H⁺ (pKa=3.76, well below the operating pH range of the oscillator), decreasing intrachamber pH. The third reaction eliminates H₂O₂ and restores half of the O₂, which is then available to participate in the first reaction. In the studies conducted here, enzymes were added in excess, so that the reactions were fast compared to other processes, even away from their optimal pH ranges.

Following reactions (I), hydrogen ions diffuse from the chamber into the membrane and neutralize the charged MAA groups, eventually leading to collapse of the membrane and attenuation of glucose influx. Consequently, hydrogen ion production inside the chamber is reduced, and intrachamber pH increases. Subsequent loss of acidic protons from the membrane into the external medium and reswelling of the membrane reestablish glucose permeability, and conditions are now in place to repeat the cycle. The cyclic changes in intrachamber pH, membrane charge, and membrane swelling underlie the rhythmic release of hormone across the membrane.

Initial studies established that poly(NIPAM-co-MAA) hydrogel membranes, exposed on one side to constant pH 7.0 but with the other side exposed to media of varying pH values, exhibit large transitions in permeability to glucose as a result of collapse and swelling of hydrogel proximal to the variable pH side [25, 26]. The collapse and swelling transitions occur at different pH values on the variable side, and the membrane's permeability therefore exhibits bistability and hysteresis in the pH range between those values. This property is very useful in promoting oscillations. Without it, the membrane would likely relax to an intermediate, stationary swelling/permeability state in which glucose influx, enzymatic conversion, and clearance of H⁺ are in exact balance, with no oscillations.

Later studies showed that the collapsed, impermeable state of the hydrogel membrane is temporally unstable. While a pH drop leads initially to collapse and near shutoff of permeation, eventually the membrane reverts to a state of intermediate permeability, which appears to arise by accumulation of lateral stress on the collapsed side, followed by phase separation into collapsed and partially permeable swollen domains [27]. The importance of this observation will become apparent below.

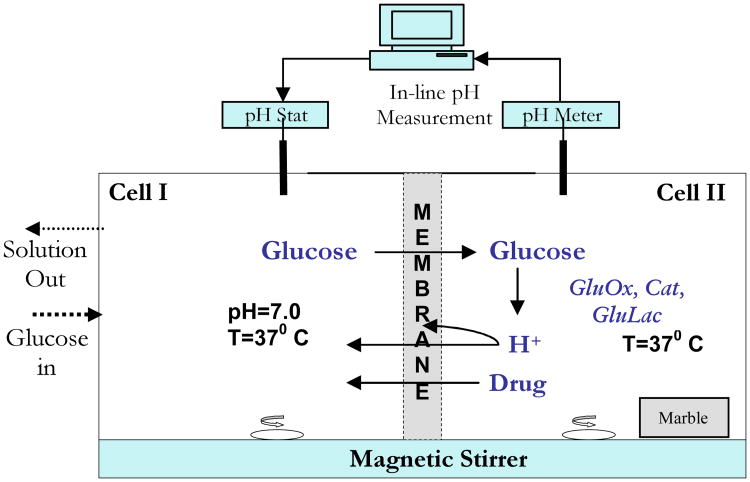
Figure 1 is a schematic of a bench prototype of the oscillating hormone delivery system. The prototype is a side-by-side diffusion apparatus, with the poly(NIPAM-co-MAA) separating two well stirred cells. Cell I corresponds to the external environment. Aqueous glucose solution flows into Cell I at a fixed rate, and waste is removed at an equal flow rate. Cell I is maintained at pH 7.0 by a pH stat. Cell II, which corresponds to the rhythmic delivery device's internal chamber, contains the enzymes. Fluctuations of pH in Cell II are monitored by an electrode. Details are provided in the section 2.

Figure 1.

Schematic of glucose driven chemomechanical oscillator.

The earliest experiments with this prototype yielded very slow, transient changes in pH in Cell II, but no sustained oscillations, probably due to the appearance of the proposed intermediate permeability state of the membrane [26]. It was hypothesized that this intermediate state is a trap into which the system can fall if pH changes are not sufficiently rapid [27]. To ensure rapid pH changes in Cell II, external glucose concentration was increased and granular marble was introduced into Cell II. Heterogeneous reaction of H⁺ with marble (CaCO₃) provides a shunt pathway for H⁺ clearance via the reactions [28]

$$\begin{array}{c}{\mathrm{H}}^{+}+{\text{CaCO}}_3(\mathrm{s})\to {\text{Ca}}^{2+}+{\text{HCO}}_3^{-}\\ {\mathrm{H}}^{+}+{\text{HCO}}_3^{-}\leftrightarrow {\text{CO}}_2+{\mathrm{H}}_2\mathrm{O}\end{array}$$ (II)

Combining the enhanced rate of H⁺ production due to increasing glucose flux across the membrane, and enhanced rate of H⁺ depletion due to the marble reaction, the up and down slew rates of pH in Cell II are increased. With proper adjustments, transitions between the high and low permeability states of the hydrogel membrane occur with sufficient rapidity that the membrane does not fall into the intermediate permeability trap. With these modifications, pH in Cell II exhibits sustained ultradian oscillations, with concomitant rhythmic pulses of GnRH release across the membrane.[22, 29] With increasing duration the oscillation period increases, however, until after one week the oscillations cease, presumably because the slew rate of pH change becomes so slow that the intermediate permeability/stationary state regime is entered.

3. Materials and Methods

Membranes

N-isopropylacrylamide (NIPAM, Polysciences), 2-methylacrylic acid (MAA, Aldrich) and ethyleneglycol dimethacrylate (EGDMA) were dissolved in 1 mL of 50:50 v/v water-methanol, along with 5 mg of ammonium persulfate (APS, Polysciences) and 20 μl of tetraethylmethylenediamine (TEMED, Aldrich). The solution was polymerized at 10 °C between glass plates separated by a 400 μm spacer. The molar feed composition of NIPAM-MAA used was either 95:5 (5 mol% MAA) or 90:10 (10 mol% MAA). The EGDMA composition was fixed at 0.5 mol % for all hydrogel membranes. The resulting hydrogels were extensively washed and conditioned in 50 mM saline media, with 0.02 wt% sodium azide (Aldrich) added as an antifungal agent.

Preparation of Marble and Characterization of Marble Reactivity

Marble tiles (Botocino Fiorito type: Marble and Tile Company, St. Paul, MN) of thickness 1 cm, were machine cut into rectangular slabs of defined dimension, either 2cm × 2cm × 1cm or 2cm × 1.5cm × 1cm. Some of the latter, smaller slabs were coated with candle wax on one 2cm × 1cm face and one 1.5cm × 1cm face, further reducing their exposed surface areas. In all experiments involving marble, one broad (2 × 2 cm² or 2 × 1.5 cm²) face was laid down flush with the bottom of the vessel in which it was placed, and the test surface areas were S = 6.5, 10, and 12 cm². Constancy of surface area was verified at the end of experiments using calipers.

A special reactor was constructed to determine the surface reactivity, κ, of the marble. Details of these experiments and analysis leading to the estimate of κ = 8.3×10^-3 cm/s are provided in the Supporting Information. This value was used in calculating the heterogeneous reaction constant, k_marble = κS/V for a given realization of the oscillator, V being the volume of Cell II (see below).

Hydrogel/Enzyme-Based pH Oscillator

The glucose driven chemomechanical oscillator, illustrated in Figure 1, was a side-by-side transport cell (Crown Glass) consisting of two 100 ml cells, each containing V=80 ml saline solution (50 mM NaCl, with 0.02 wt% sodium azide). The cells were separated by a circular poly(NIPAM-co-MAA) hydrogel membrane disk that was mounted and clamped by an O-ring, with 3.14 cm² of membrane surface exposed to each cell. Both cells were magnetically stirred (600 rpm) and water jacketed at 37 °C.

Glucose at a specified concentration in 50 mM saline flowed into Cell I at 1.4 ml/min under control of a peristaltic pump (SciLog), which also drained the contents of Cell I at equal rate. The pH in Cell I was stat-ed at 7.0 using an autotitrator (Metrohm 719 S Titrino). Cell II contained 5000 units of glucose oxidase (Sigma 190 IU/mg) and 27000 units of catalase (Sigma 13,610 IU/mg, with trace amounts of gluconolactonase). Due to their high molecular weights, the enzymes did not permeate the membrane. A cut marble slab of specified surface area, S, was placed into Cell II away from the magnetic stir bar.

In an experimental run, fresh, glucose free, pH 4.4 saline solution containing the enzymes was introduced into Cell II, without marble, while fresh pH 7.0 saline was dispensed into Cell I. Following several hours conditioning at 37 °C, with the pH gradient maintained by separate pH stats in the two cells, the marble slab was placed in Cell II and the pH stat burette in Cell II was removed. Cell I was rapidly emptied and refilled with pH 7.0 saline containing glucose of specified concentration and 0.01 wt% 2-bromo-2-nitro-1,3-propanediol as an antimicrobial. The peristaltic pump, charged with the same glucose solution, was turned on, initiating turnover of glucose solution in Cell I. pH oscillations in Cell II were continuously monitored by an electrode (Corning) and recorded on a PC.

Calcium Ion Studies

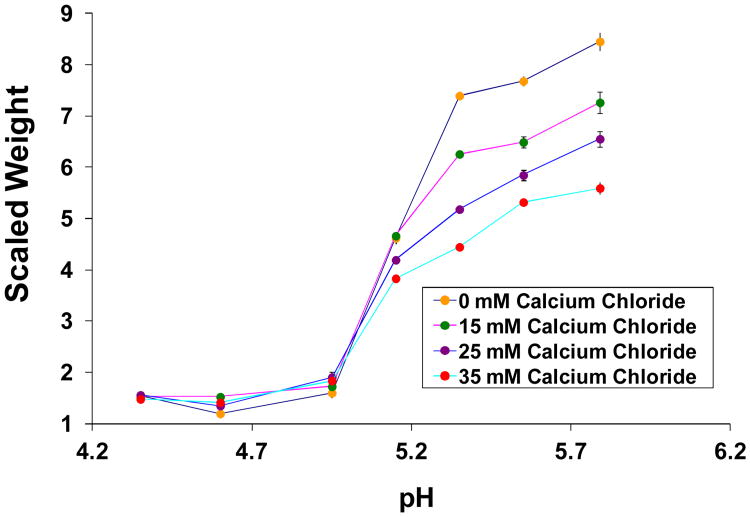
Calcium ion dependent free swelling of 10 mol% MAA hydrogels was investigated in an environment containing increasing concentrations of calcium chloride. After initial equilibration in 50 mM saline media at pH 6, hydrogels were cut into circular disks, 10 mm in diameter. Stock sodium acetate pH buffers with ionic strength 50 mM were prepared. Calcium chloride (CaCl₂) was added to these buffers at four concentrations: 0 mM, 15 mM, 25 mM and 35 mM. Small amounts of 0.1N sodium hydroxide (NaOH) or HCl were added to adjust the final buffer pH. At each pH and CaCl₂ concentration hydrogel disks, in triplicate, were equilibrated for 48 hours in test tubes, which were sealed to prevent pH change due to contact with atmospheric carbon dioxide. Temperature was fixed at 37 °C using a water bath. Upon equilibration, the disks were removed, touched with a kim wipe to remove excess surface water, and weighed on an electrobalance (Sartorius BL 60 S). Dry weights were measured on the same balance after dessicating the hydrogels for 4 days under vacuum at room temperature. Scaled weight=wet weight/dry weight was calculated at each CaCl₂ concentration and pH.

To study oscillations in the presence of CaCl₂, the same configuration was used as for the studies involving gluconate^-, except that CaCl₂ was introduced into Cell II. pH oscillations were initiated in saline without CaCl₂. After a certain time, a small aliquot of highly concentrated CaCl₂ solution was spiked into Cell II solution to bring CaCl₂ to a specified level. Later, the contents of Cell II were replaced by a calcium-free enzyme solution in saline. Effects of these sudden changes in CaCl₂ concentration on oscillatory behavior were recorded.

4. Results

4.1 Factors permitting long term oscillations

In this section we investigate the combinations of marble reactivity, glucose concentration, and membrane composition that are conducive to oscillations. Two primary hypotheses are tested. The first hypothesis is that oscillations will occur over a bounded range of feed glucose concentration, C_G. When C_G is too low, generation of H⁺ in Cell II will not be sufficient to cause membrane collapse. When C_G is too high, residual glucose permeability of the hydrogel in the collapsed state leads to generation of enough H⁺ to sustain collapse. As a corollary, increased marble reactivity in Cell II must be offset by increased feed glucose concentration, since clearance of H⁺ by marble affects the availability of acidic protons to enter the membrane.

The second hypothesis relates to the effect of membrane composition on observed pH oscillations in Cell II. By varying the amount of MAA in the hydrogel, we alter the pH values in Cell II required to induce collapse and reswelling of the proximal hydrogel skin layer. Assuming that critical concentrations of ionized MAA groups are required in the membrane for each of these transitions, we infer that with increasing MAA content, transitions will occur at higher H⁺ concentrations and hence lower pH values in Cell II. Assuming that permeabilities to glucose in both the swollen and collapsed states of the membrane are only weakly affected by MAA content, we also expect that glucose feed concentration must increase with MAA content in order to provide the lower pH values needed for oscillations.

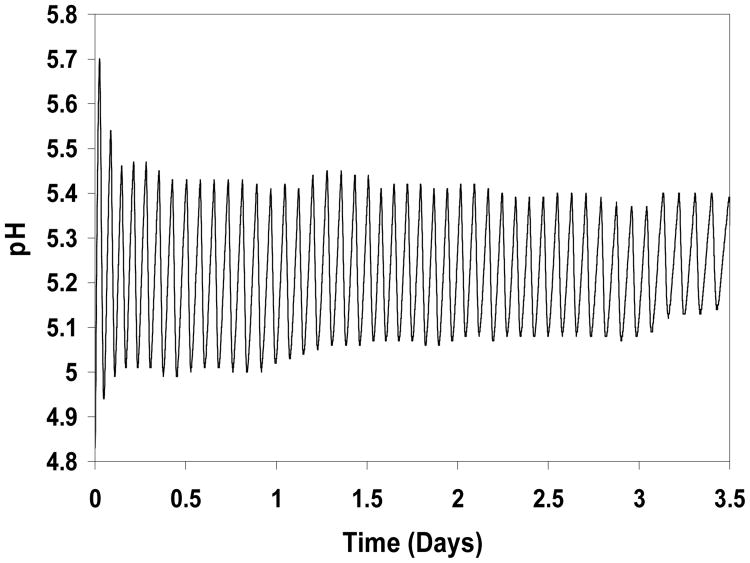
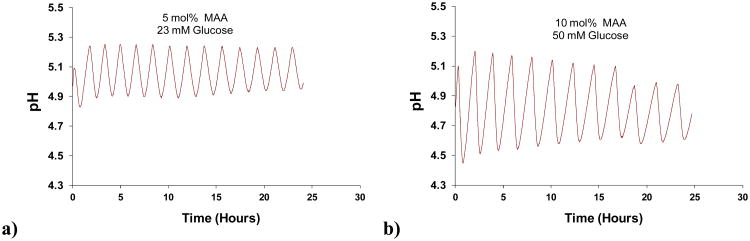
The first experiment was carried out with a 5 mol% MAA membrane, a marble slab with S=10 cm² exposed surface area in Cell II, and 25 mM glucose flowing into Cell I. As illustrated in Figure 2, sustained pH oscillations between pH 5.0-5.1 and 5.4-5.5, lasting 3.5 days, were recorded in Cell II, demonstrating the viability of the oscillator over an extended time period. These oscillations exhibited similar characteristics to those that were observed previously [20,21], namely an initial decay in amplitude and a steady increase in period. For example, fourteen peaks are observed between 0.5 and 1.5 days, but only twelve between 2.5 and 3.5 days. The small fluctuations in peak and trough locations are probably due to the discrete in time manner by which pH values were recorded.

Figure 2.

Performance of oscillator with 5 mol% MAA hydrogel and marble slab with surface area S=10 cm². Donor cell glucose concentration is 25 mM.

In subsequent experiments, membrane composition, exposed marble surface area, and glucose concentration were varied. For a given marble surface area, S, the same membrane was used for all glucose concentrations, C_G. pH transients were recorded for ∼24 hr under each condition, followed by reconditioning steps as described above. Occasionally a membrane would break and another membrane of identical composition was mounted in the cell, and the whole glucose concentration range would be run again.

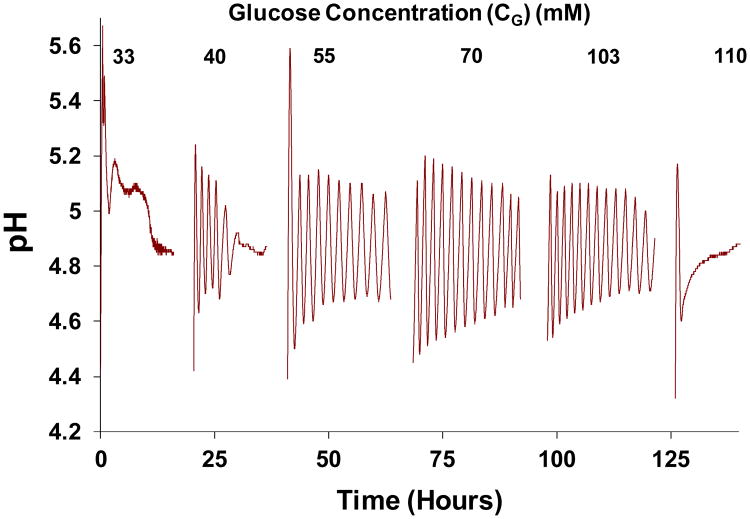
Figure 3 shows an example of a glucose concentration scan conducted with a 10 mol% MAA hydrogel membrane, and a marble slab of exposed surface area S=10 cm². The concentration of glucose fed into Cell I was increased in steps from C_G=33 to 110 mM, and the record of pH transients in Cell II is displayed. Short breaks in the record correspond to recharging of solutions in Cell I and II and membrane reconditioning. Oscillations decay rapidly at the high and low ends of C_G, but oscillations are sustained at intermediate value of C_G.

Figure 3.

pH transients observed in Cell II in response to a range of glucose concentrations (C_G, mM) introduced into Cell I, with pH in Cell I maintained at 7.0. Hydrogel membrane was synthesized with 10 mol% MAA, and exposed marble surface area was S=10 cm² so k_marble=1.25×10^-3 sec^-1. Breaks correspond to periods during which solutions in Cells I and II were changed, and membrane reconditioning occurred.

Because of the long duration of the experiments and the delicacy of the experimental setup, it was not possible to determine a sharp boundary between conditions supporting sustained oscillations and conditions in which oscillations are only transient. For the present work, visual inspection of the graphs was used and an arbitrary criterion was chosen, whereby the system was considered to exhibit sustained oscillations if oscillations persisted through 24 hours at a given glucose exposure. By this criterion, oscillations shown in Fig. 3 were considered to be sustained at glucose feed concentrations C_G = 55, 70, and 103 mM. A few oscillations were recorded for C_G = 40 mM, but the system relaxed to steady state within ∼12 hr. For C_G = 33 and 110 mM, oscillations decayed very rapidly. Similar scans for other marble surface areas, S, for both 10 mol% MAA membranes (Figures S3) and 5% MAA membranes (Figure S4) are shown in the Supporting Information.

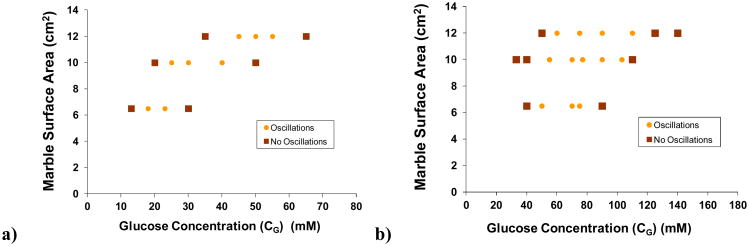
Figure 4 displays phase diagrams mapping out (C_G, S) conditions in which sustained oscillations occur, and where decay to a stationary state (before 24 hr at a given condition) occurs, with the 5 mol% MAA and the 10 mol% MAA membrane. Both cases reveal a funnel-shaped phase boundary, with the width of the oscillatory region decreasing as surface area of the marble decreases. The funnels are “tilted” such that the oscillatory regions move to lower glucose concentration ranges as S decreases. The “funnel” is shifted to higher glucose concentrations when MAA content in the hydrogel membrane is increased from 5 mol% to 10 mol%. These observations are consistent with the hypothesis that increased marble surface area, and hence reactivity, must be met with an increasing glucose concentration in order to provide conditions that are compatible with oscillatory behavior.

Figure 4.

Phase diagrams indicating dynamic behaviors, with hydrogel membranes synthesized with a) 5 mol% and b) 10 mol% MAA content. ( ) decay to a stationary pH value; ( ) sustained oscillations. Marble surface areas of 6.5, 10, and 12 cm² correspond to k_marble = 0.67×10^-3, 1.04×10^-3, and 1.28×10^-3 sec^-1, respectively.

We turn now to the second hypothesis that membrane composition, in addition to affecting the range of glucose and marble conditions that are conducive to oscillations, also will affect the pH range over which oscillations occur. Evidence that this is the case is provided by comparing Figs. 2 and 3. For the 5% MAA membrane (Fig. 2) pH oscillations display troughs between pH 5.0-5.1 and peaks between 5.4-5.5. For the 10% MAA membranes (Fig. 3), trough and peak values are pH∼4.7 and pH∼5.1, respectively. As predicted above, increased MAA incorporation in the hydrogel membrane leads to an acid shift in the oscillations. This phenomenon is also demonstrated in Figure 5, which reports an experiment in which a 10 mol% MAA membrane was first tested, followed by a 5 mol% MAA membrane. Notice here that there is a slight acid shift of both peaks and troughs for the 5 mol% MAA membrane, compared to Fig. 2. We have found that these features may depend on conditioning and mounting of the membrane. However, such variations are less than those seen between membranes of different compositions.

Figure 5.

pH oscillations with a) 5 mol% and b) 10 mol% MAA incorporated into the hydrogel membrane. Marble surface area was 6.5 cm².

These studies confirm that membrane composition, marble reactivity (as controlled by its surface area), and glucose feed concentration all affect the ability of the system to produce sustained oscillations. The reason for the tradeoff between marble reactivity and glucose concentration is clear. With increasing marble reactivity, more acidic protons generated by enzymatic conversion from glucose are removed before they can exert their effect on the membrane. To keep pH in Cell II within the range compatible with oscillations, more glucose must cross the membrane to be converted to H⁺. Hence, glucose feed must be increased. This explanation accounts for the tilted funnel-like phase boundaries in Figure 4.

The effect of membrane composition, i.e. MAA content, is explained in terms of the primary effect of molar density of ionized MAA groups on the collapse and swelling transitions of membrane proximal to Cell II. Increased MAA incorporation shifts the swelling/shrinking characteristic, and hence the range of oscillations, in the acid direction, and thus increases the concentration range of glucose feed that is needed to produce oscillations. This effect has been reported previously [21, 30], and is accounted for in the model of Dhanarajan et al [31].

4.2 Factors Causing Slowing and Cessation of Oscillations

Reactions (I) and (II) result in the production of gluconic acid, which dissociates into H⁺ and gluconate^-, plus Ca²⁺, HCO₃^- and CO₂. These species accumulate to differing extents in Cell II and are cleared through the membrane into Cell I, where they are removed in the waste stream. CO₂ may also evaporate into the head space above the aqueous media. While H⁺ is integral to the oscillation mechanism, the other products are not. Nevertheless, accumulation of the other products may affect behavior over times longer than a single oscillation. Gluconate^- and HCO₃^- are pH-buffering species, while Ca ⁺ concentration can affect the swelling and shrinking properties of the membrane. In this section we focus on long term behavior of the pH-swelling oscillations, and attempt to relate changes in period and ultimate cessation of oscillations to accumulation of these species in Cell II.

4.2.1 pH-Buffering Effects

To determine whether gluconate or bicarbonate ions affect oscillation period, it was necessary to measure their accumulation. To this end, pH oscillations where measured under a single condition but for an extended period. For this experiment, a 10 mol% MAA hydrogel membrane was used, and the steady input glucose concentration in Cell I was chosen as C_G=75 mM, and the marble surface area was S=12 cm.

Following conditioning of the membrane and initiation of oscillations, aliquots of 700 μl were taken without replacement from Cell II at selected time points corresponding to peak pH values, and were titrated with 0.009N hydrochloric acid (HCl) in a well stirred glass vial, at room temperature. As a control, an aliquot of freshly prepared saline solution containing only the enzymes (i.e. Cell II solution at the beginning of a run) was titrated. For each aliquot titrated, the change in pH with respect to the amount of HCl added was recorded. Titration curves were fit (lsqcurvefit, Matlab Optimization Toolbox) to the following equation, derived in Supporting Information, to determine the buffer concentration in each aliquot:

$${[\mathrm{A}]}_{\mathrm{T},0}=\frac{\frac{v}{V_0}{[\text{HCl}]}_{\text{in}}+{10}^{-{\text{pH}}_0}-(1+\frac{v}{V_0}){10}^{-\text{pH}}}{\frac{1}{1+{10}^{\text{pH}-\text{pKa}}}-\frac{1}{1+{10}^{{\text{pH}}_0-\text{pKa}}}}$$ (1)

where

• V₀ = Volume of aliquot in the vial (0.7 mL)

• v = Volume of 0.009 N HCl added from the autotitrator (mL)

• [HCl]_in = Concentration of HCl delivered from autotitrator (0.009 M)

• pH0 = pH of aliquot measured before titration

• pH = pH of aliquot measured during titration

• pKa = Fitted value of pKa

• [A]_T,0 = Fitted total buffer concentration (acid + base) at beginning of titration (M)

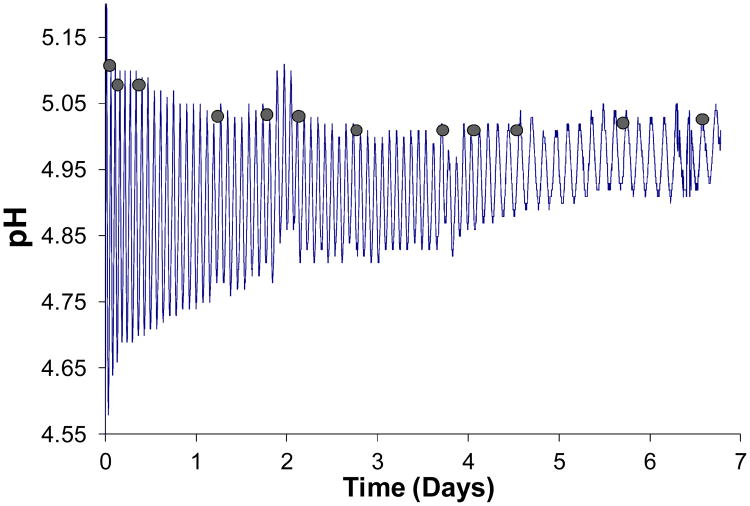
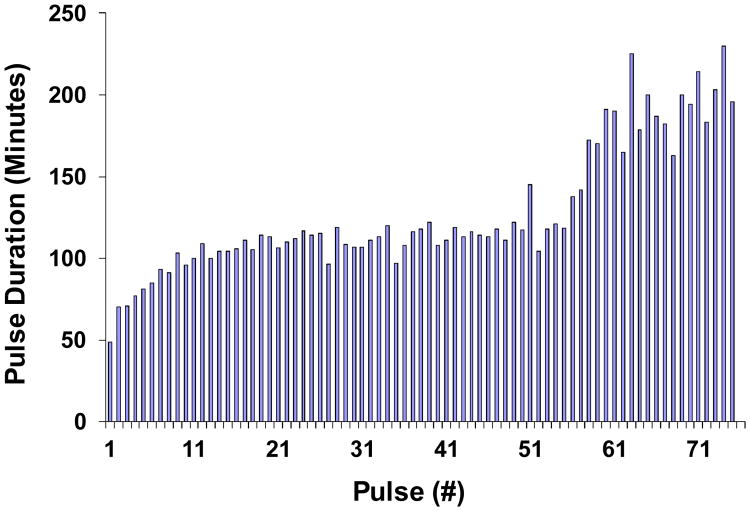
Figure 6 shows oscillations, which lasted approximately one week. After 6.77 days, the membrane fractured and no more data could be recorded. Amplitude reduction and retardation of pH dynamics are observed as time progresses. Figure 7 shows peak to peak durations, indicative of period of oscillation. Period started at about 40 min and then approached, with decaying exponential deviation, a plateau value of about 110 min. After about 3.7-3.8 days (or ∼50 peaks), however, period increased once again to an average value of about 200 min, perhaps signaling onset of an unspecified fatigue process, perhaps leading to the final break.

Figure 6.

pH oscillations in Cell II over 6.77 days. The membrane was a 10 mol% MAA-90 mol% NIPAM hydrogel. Marble surface area was S=12cm². Glucose in Cell I was C_G=75 mM. Shaded circles indicate points at which 700 μl aliquots were withdrawn to determine, by titration, the extent of buffer buildup in Cell II as a function of time.

Figure 7.

Increase in periodicity of pH oscillations in Cell II with time. Raw data from Figure 6. A discernible increase is seen after 50 periods, which corresponds to Day 3.8 in Figure 6.

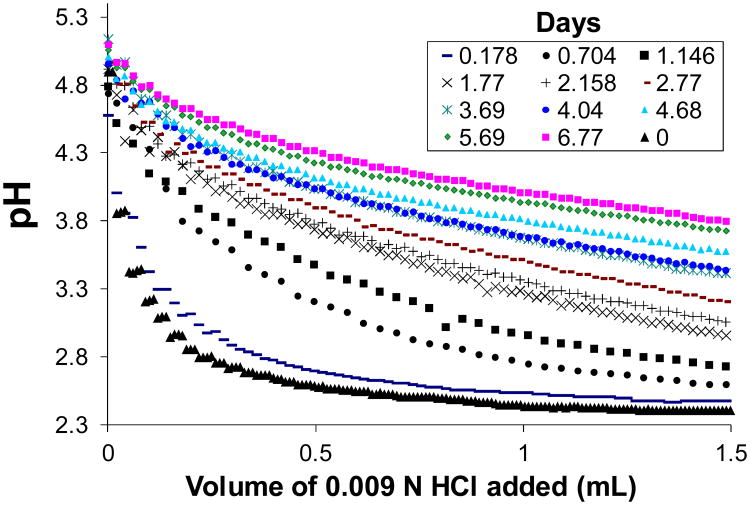
Figure 8 displays titration curves measured for the aliquots sampled at the time points designated by filled circles in Fig. 6, close to the alkaline peaks. Also included in this figure is the titration curve of the enzyme medium prior to introducing glucose. With increasing time, the titration curves shifted in the alkaline direction and became flatter as more HCl was needed to neutralize the medium. Evidently, a buffering species was accumulating over time.

Figure 8.

Increase in buffer concentration of the Cell II solution with time, for oscillations shown in Fig. 6. Curves represent titration data for aliquots withdrawn at different time points.

Figure 9 shows least-squares best fits of Eq. (1) to the experimental data, at representative time points, with [A]_T,0 and pKa estimated simultaneously. The model does not fit well for aliquots collected during the first day of the oscillation run, as evidenced by distinct regions of over- and underestimation of the data. Here the titration behavior is dominated by the enzymes in Cell II. However, fits improve markedly after Day 1, and become essentially perfect after Day 2, indicating the dominance of a single monoprotic buffer.

Figure 9.

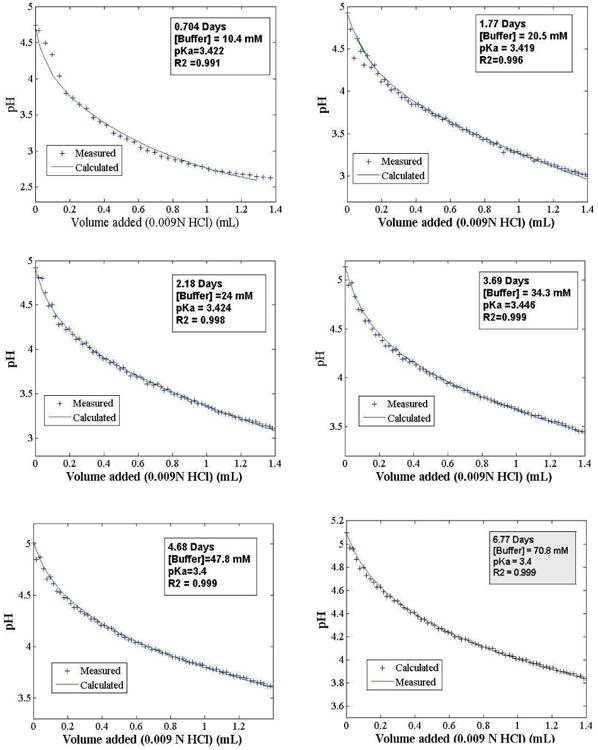
Titration curves for six time points in Figure 8 fitted to Eq. (1). Estimated gluconate/gluconic acid concentration ([A]_T0) and pKa values are indicated in each frame.

Figure 10 is a plot of the estimated values of [A]_T,0 and pK_a extracted from the fits, for all time points recorded. Assuming a single buffer species, the fitted pKa values cluster rather tightly around an average value of 3.42. Estimated buffer concentration increases steadily over time, with two stages. The first stage appears to exhibit decay in rate of accumulation of buffer until about 3.8 days, after which the slope of the accumulation curve increases, heading toward that of glucose in Cell I. Unfortunately, the experiment ended due to membrane breakage, and later accumulations of buffer could not be assessed.

Figure 10.

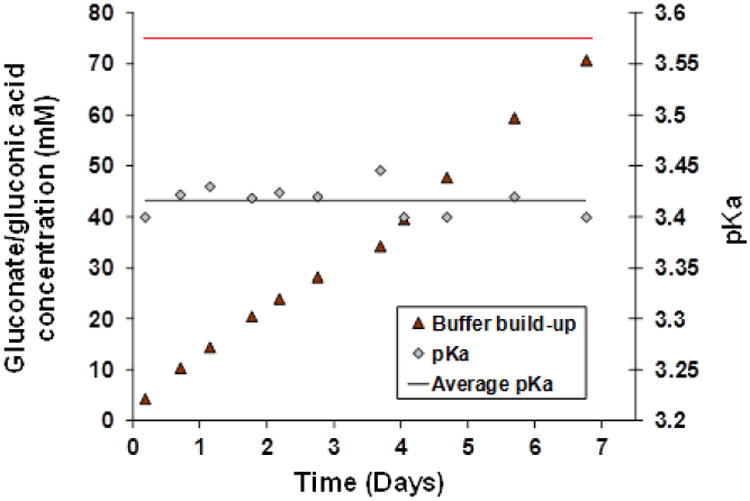
Estimated buildup of gluconic acid/gluconate buffer ([A]_T,0) with time in Cell II of the oscillator prototype. Also shown are the estimated pKa values estimated at each time point. Estimations are based on curves in Fig. 9 fitted to Eq. (1). Average pKa=3.42 (black line). Cell I glucose concentration (75 mM) is shown as a red line.

Based on these results, it is most reasonable to conclude that gluconic acid/gluconate^- is the dominant buffer species. Although the pKa of this acid/base pair in water is listed as 3.76, it is expected to be lowered in salt solution due to electrostatic screening, as predicted by Debye-Hückel theory [32]. The average fitted pKa=3.42 is consistent with this expectation. The bicarbonate buffering system is of little importance since its pKa is near 6.4, well above the pH values occurring in the present experiments. In fact, we expect that most of bicarbonate will be converted to CO₂, which should be rapidly cleared from the system.

4.2.2 Calcium Ion Effects

Accumulation of calcium ion in both Cells II and I as a result of the marble reaction (II) is expected to affect swelling, either by simply increasing ionic strength, or due to increased Donnan distribution into the membrane due to its +2 charge. Figure 11 shows the results of free swelling studies with 10 mol% MAA hydrogels at different pH values and CaCl₂ concentrations. With increasing concentration, CaCl₂ caused a decrease in swelling ratio. The effect was most significant when hydrogels were in the swollen state. Data was not gathered at high enough resolution to discern an effect of CaCl₂ concentration on the pH value at which the swelling transition was initiated.

Figure 11.

Swelling isotherms showing swelling of 10 mol% MAA hydrogels as a function of pH, at different concentrations of calcium chloride.

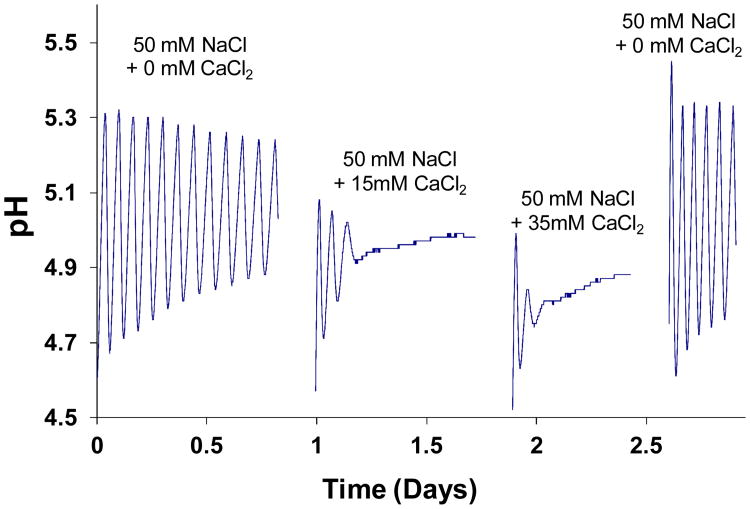
In the second study, the system was run with various initial concentrations of CaCl₂ in Cell II. The results shown in Figure 12 affirm the role of CaCl₂ as a factor that can cause oscillations to cease. Sustained oscillations were observed with 0 mM CaCl₂. However, with 15 mM and 35 mM CaCl₂, oscillations were rapidly quenched. Oscillations were reestablished when CaCl₂ was removed. Studies were run sequentially with the same hydrogel mount, but were interrupted by changes in enzyme/CaCl₂ solution charged into Cell II. With increasing CaCl₂ concentration, oscillations were quenched more rapidly, and the stationary state pH was shifted in the acid direction.

Figure 12.

Effect of calcium ion on oscillations. C_G = 75 mM.

5. Discussion

5.1 pH Oscillations

Figure 2 exhibits common features of the glucose-hydrogel-marble oscillator, namely an initial period of relatively rapid, relatively high amplitude oscillations, followed by settling of the system over time into an essentially steady amplitude but increasing period. We believe that the membrane requires a finite relaxation time to respond to pH change. Initially, with low buffer build-up, pH in Cell II changes rapidly, and response by the membrane is relatively sluggish, leading to overshoots and undershoots in the pH waveform. As buffer builds up, pH change in Cell II becomes slower, and the membrane swelling/shrinking dynamics follow pH changes more closely.

To confirm that transient over- and undershoot behavior is due to relatively slow relaxation of the membrane, a supplementary experiment was carried out, in which Cell II was initially charged with 45 mM sodium gluconate. All other conditions were the same as before. As shown in Figure S5, oscillations, once started, proceeded with essentially constant amplitude and period for the 1.4 day period of observation. The initial pH transient rise seen in this record was probably due to a startup lag in glucose transport and H⁺ production, during which marble consumed H⁺ that was already in Cell II.

5.2 Buffer Buildup

The experimental results indicate that gluconate^-/gluconic acid plays a decisive role in slowing pH oscillations. Equation (1) fits the titration data of Fig. 9 extremely well after 2 days, assuming a single buffer with pKa near 3.42. This value is close to the pKa value for gluconate/gluconic acid in water, pKa=3.76. The acid shift in pKa is expected due to stabilization of gluconate^- by the ionic atmosphere provided by added salt, Ca²⁺ from the marble (see below), and the buffer itself. The magnitude of the shift is reasonably consistent with predictions of Debye-Hückel theory, although the latter may be difficult to utilize in a quantitative manner due to the nonuniform distribution of charge on the gluconate ion and the complexity of the ion atmosphere. Buffering by bicarbonate is not reflected in Eq. (1) or its fit to the data, presumably because bicarbonate is mostly converted to CO₂ in the acidic solution contained in Cell II. Once transported to Cell I, however, CO₂ will revert to HCO₃^- in the pH 7.0 stat-ed environment.

Before Day 2, the fits using Eq. (1) are less satisfactory. We attribute the early titration curves primarily to the enzymes. While the enzyme concentrations are in the micromolar range, each enzyme molecule contained numerous titratable groups, which can contribute substantially when little gluconate had been produced, especially at t=0. An initial effort to correct for enzyme presence at early times was abandoned when it was determined that the resulting equations would be complicated and dependent on some ad hoc assumptions.

Accumulation of gluconate in Cell II, shown in Figure 10, apparently occurred in two phases. In the first phase, gluconate concentration rose steadily, but in a slightly decelerating manner. At about 3.8 days, however, there was a sudden boost of the slope of accumulation, and accumulation remained unabated as the fitted concentration of gluconate approached the external glucose concentration (75 mM). Had the membrane not ruptured, gluconate concentration in Cell II would probably have eventually exceeded glucose concentration in Cell I.

Curiously, the boost in gluconate accumulation rate coincided roughly with the time that the oscillations in Fig. 6 exhibited an apparent slowdown. These two behaviors may be related. Operation of the device involves membrane-limited diffusion of glucose to Cell II, rapid enzymatic conversion of glucose to H⁺ and gluconate^- in Cell II, and ultimate back diffusion of gluconate^- through the membrane into Cell I, with subsequent elimination through the drain line. One would expect gluconate^- concentration in Cell II to approach a level that depends on the average ratio of membrane permeabilities to glucose and gluconate^- (and relatively dilute gluconic acid) over the pH oscillation cycle. This ratio may have changed at the point where oscillations slowed down.

Being of similar size, glucose, gluconic acid and gluconate should have similar diffusivities. However, since the membrane is negatively charged, the Donnan potential partially excludes gluconate^- from the membrane, thereby reducing clearance of gluconate from Cell II. It is therefore not surprising that estimated gluconate^- concentration continued to rise steadily and could be projected to surpass the feed glucose concentration had oscillations not stopped. Further investigations of phenomena determining the extent and kinetics of accumulation of gluconate^- are warranted. In particular, the relatively sudden change in system behavior after ∼4 days (∼50 peaks) needs to be better elucidated. Both the slowing of oscillations and the acceleration in gluconate^- accumulation may be due to a change in membrane structure, the nature of which is not presently understood.

5.3 Calcium Ion Effects

In reactions (II), the production of each calcium ion by the marble reaction is matched by consumption of one or two (usually two near pH 5) hydrogen ions, each of which is produced by the enzyme-catalyzed reactions, with accompanying production of gluconate^-. Thus, approximately two gluconate^- molecules ae produced for each calcium ion, and one might expect calcium accumulation to track that of gluconate^-, within about a factor of two. However, Ca²⁺ should leave Cell II through the membrane more rapidly than gluconate^-, first because it is smaller and therefore has a larger diffusion coefficient, especially in a partially obstructed medium such as a hydrogel, and second because the membrane's Donnan potential favors Ca²⁺ partitioning but opposes gluconate^- entry. It is therefore unlikely that Ca²⁺ will accumulate as rapidly as gluconate^- in Cell II. In this regard, we cannot be sure from the present experiments whether the Ca²⁺ would quench oscillations if experiments (Figure 9) were carried out at relevant concentrations. Future studies should address accumulation of Ca²⁺ by direct chemical analysis. That said, a discussion of the observed effects of Ca²⁺ on membrane swelling and oscillations in the system is worthwhile.

The free swelling studies in Figure 10 suggest a significant decrease in swelling ratio of the hydrogel membrane as concentration of CaCl₂ increases from 0 mM to 35 mM. It is well known that the Donnan potential is more effective in causing divalent cations (such as Ca²⁺) to partition into the anionic hydrogel than it is for monovalent cations such as Na⁺. Further, divalent cations neutralize twice as many fixed anions in the gel, and therefore the overall osmotic swelling force due to Ca²⁺ is less than that due to Na⁺ [33]. In addition to these pure osmotic effects, it has been observed that Ca²⁺ has an effect on polymer/water interactions in hydrogels, as summarized by changes in the Flory c parameter [34-36].

Calcium effects on free swelling of the hydrogel are expected to have some correlation with calcium effects on pH oscillations. However, the hydrogel membrane in the pH-oscillator is clamped and exposed to gradients of solution concentrations. Because of this breakage of symmetry, other factors may be involved. Before discussing these factors, we recall from Fig. 9 that quenched oscillations are regenerated by fresh introduction of solutions to Cell II, which would not occur if membrane fatigue or rupture terminated the oscillations. Thus, irreversible changes to the hydrogel membrane, including fatigue, can be ruled out as a factor responsible for cessation of oscillations. The effect of calcium ion on the membrane swelling/deswelling is reversible, in agreement with other experimental studies.

According to Figure 12, the number of pH swings before cessation of oscillations decreased with increasing CaCl₂ concentration, and the stationary pH decreased. Because these observations are based only on two CaCl₂ concentrations, only cautious speculations can be made. Since glucose feed was the same for both 15 mM and 35 mM CaCl₂, it seems likely that permeability of the membrane to glucose was slightly higher in the latter case. It also appears that the stationary state corresponded to a swollen, relatively high permeability membrane. If increased calcium ion concentration caused the membrane to shrink somewhat in the direction of glucose transport, without significantly affecting the obstruction of glucose by the network, then permeability could be increased.

We conclude this section by arguing that a simple increase in ionic strength with addition of CaCl₂ is not sufficient to explain our results. Ionic strength is defined by $I=(1/2)\sum z_i^2{C}_i$, where z_i and C_i are the valence and concentration of the i'th ion in Cell II solution, respectively. Ionic strength has classically been taken as a sufficient parameter when it greatly exceeds the hydrogel's molar fixed charge density, ω_f, through the expression for osmotic swelling pressure [37], $\mathrm{\Delta }{\mathrm{\Pi }}_{\text{ion}}=RT{\omega }_f^2$, where RT is the thermal energy product. This condition should not hold for the present hydrogels, however, as the concentration of ionizable groups in the hydrogel is relatively high.

According to the expression for I, addition of 35 mM CaCl₂ to 50 mM NaCl solution produces a solution of ionic strength of 155 mM. In Figure S6 it is shown, however, that a solution of NaCl at the same ionic strength (equal incidentally to physiologic ionic strength) permits oscillations that are very similar to those seen in 50 mM solutions. Therefore, ionic strength in itself does not affect oscillations in the present system, and the Ca²⁺ effect must be attributed to other factors such as enhanced Donnan partitioning and reduction in hydrogel swelling.

5.4 Enzyme Activity

Both GluOx and Cat are known to degrade over time, with a rate constant that increases linearly with the concentration of H₂O₂ [23]. In addition, H₂O₂ is a competitive (product) inhibitor of the GluOx reaction [24]. The degradation kinetics of GluLac are not characterized, to our knowledge. The effects of gluconate^- on enzyme activity have only been studied at relatively low gluconate^- concentrations [23]. Similarly, the effects of accumulated Ca²⁺ are not known, nor are the effects on long term operation at low (∼5) pH. In our studies we used a strong excess of both GluOx and Cat, reasoning that H₂O₂ would be rapidly consumed and therefore have little effect on enzyme activity. It was also believed that with strong enzyme excess, the system could lose substantial enzyme activity without compromising the assumption that the enzyme catalyzed reaction is fast compared to other processes in the system. Unfortunately, enzyme activity was not determined during the course of our oscillation experiments.

Loss of Cat activity could autoaccelerate as it would lead to slower removal of H₂O₂ and hence faster degradation of Cat, and GluOx degradation rate would also increase with time However, reduction in GluOx. activity, either by degradation or by H₂O₂ product inhibition, would slow down this process since less H₂O₂ would be produced. This complex web, which also could include effects of increasing concentrations of gluconate^- and Ca²⁺, is expected to ultimately lead to slowed conversion of glucose to H⁺, which might speculatively contribute to the “second wave” of increase in period of oscillations seen after ∼4 days (Figs. 6 and 7). However, a full accounting would also require an explanation for the increase in rate of gluconate^- accumulation that occurs at that point (Fig. 10).

4. Conclusions

In this paper we have studied factors governing the oscillatory behavior of a system that is ultimately intended for rhythmic hormone delivery. This system is an early investigational prototype—its size and other factors preclude its practicality as a therapeutic system. Nevertheless, some useful design principles have emerged.

First, it is clear that the negative feedback instability principle that governs rhythmic behavior applies only over specific ranges of system parameters. This observation has been justified theoretically and it is well established with other chemical and biochemical oscillators [38, 39]. In the present system, the joint dependence of rhythmicity on glucose concentration and heterogeneous marble reactivity is attributed to the ability of those variables to “target” the system into its bistable region, while calcium concentration most likely alters the overall swelling response of the membrane, perhaps even eliminating bistability. Where tested, these effects are reversible in the sense that oscillations are restored when suitable solution conditions are refreshed.

Second, when designing a system that relies on complex physicochemical feedback, the effects of chemical factors that can vary with time must be recognized. The increase in gluconate^- concentration leads to a gradual slowing of pH oscillations due to its buffering effect. The gradual accumulation of Ca²⁺ due to the marble reaction also affects dynamics. As reported previously, slowing down of oscillations can lead to cessation, probably due to gradual stress induced phase separation of the membrane following collapse [27]. We note however, that in the present case oscillations most likely ceased due to membrane rupture following a week of testing, and that efforts are warranted to improve the long term fatigue resistance of the hydrogels [40].

Third, the accumulation of Ca²⁺ is due to marble, which was incorporated into the system as a means of speeding up pH dynamics, which in turn was needed to prevent the system from falling into a steady state trap. The need for marble might be eliminated by reducing the size of the system in such a way that the ratio of the device chamber volume to the membrane's (surface area)×(glucose permeability) product is substantially decreased, since this ratio is predicted to be proportional to the intrinsic dwell times of the system in its states of high and low glucose transference [26, 41]. With marble eliminated, there will be no need to increase the feed glucose concentration far above its normal physiological level (3-7 mM). Lowering of feed glucose concentration would have the added benefit of reducing the accumulation of gluconate^- in Cell II and its effect on periodicity of oscillations.

Fourth, the range of membrane bistability, and hence the range of pH oscillations, depends on membrane composition. This result has been demonstrated previously, by modifying both the structure and degree of incorporation of the acid membrane component [21, 30]. Further understanding of the precise effects of membrane composition on oscillatory behavior is an area for future research.

The object of the present work was to provide well controlled conditions to study oscillator behavior. Such conditions might not always be present in physiological contexts. For example, blood glucose exhibits diurnal and postprandial fluctuations even in nondiabetic individuals. These fluctuations could translate into fluctuating periodicities of pH oscillations and hormone release. Also, the experimental system was open to air, with O₂ and CO₂ exchange occurring in the head space of Cell II. This head space would not exist in an implanted system, and potential O₂ limitations of the glucose oxidase reaction (I) might need to be ameliorated by more sophisticated design [42, 43]. Finally, issues of enzyme stability need to be more carefully addressed.

To conclude, we place the present work in the context of other recently reported oscillating systems involving chemical reactions and hydrogels. In the simplest systems, a pH-sensitive hydrogel is exposed to a chemical pH-oscillator [44-49]. Oscillations in hydrogel swelling are “slaved” to those of the external reaction, and the hydrogel must be designed to respond quickly to external pH changes, either by being very thin or highly porous. In more “autonomous” systems, the oscillating reaction occurs exclusively inside the hydrogel, while the external solution's chemical composition is held constant by flow into and out of the reaction chamber, which is a continuous stirred tank reactor (CSTR). The CSTR is sometimes replaced by a batch or a semibatch reactor, in which case oscillations eventually lose their coherence or eventually die out due to changes in the external solution composition. In the most studied example, initially pioneered by Yoshida et al. but [50-53] and studied by several other groups [54-59], the hydrogel is placed in an aqueous medium supporting the Belousov-Zhabotinsky (BZ) reaction, perhaps the best known chemical oscillator, which operates by cyclic oxidation and reduction of its reactants. All BZ reactants are provided by the external solution, but a redox catalyst, essential to the reaction, is incorporated into the hydrogel as a sidechain. Thus, the reaction occurs only inside the hydrogel. Depending on dimensions of the hydrogel and the intrinsic frequency of the reaction, either the whole hydrogel oscillates in phase, or it will exhibit traveling waves of swelling and shrinking. By clever design, a rich variety of undulating, “walking,” pinwheel-like spiraling, and other “life-like” behaviors are obtained. In a second example of autonomous oscillations based on coupling between hydrogel swelling and chemical reaction, investigated by De Kepper et al. [45, 60], cylindrical or conically shaped P-MAA hydrogels are exposed to a bistable chemical reaction medium. Nonlinear, hysteretic feedback between permeation of reactants and products into and out of the hydrogel, which depends on diameter, and protonation/deprotonation of the hydrogel, which cause shrinking and reswelling, combine to create an oscillation in hydrogel diameter.

Recently, Aizenberg et al. [61] reported an elegant oscillating microfluidic system, in which a catalyst for an exothermic reaction is stamped onto tips of an array of microfins, which is mechanically coupled to a thermosensitive poly(NIPAM)-based hydrogel, both elements being anchored to the same base. The hydrogel is covered first by an inert fluid layer whose level is below the fin tips, and then a second, reactive fluid layer, which immerses the tips. Heat generated from the reaction is transferred to the hydrogel, which contracts and bends the tips into the inert layer, stopping the reaction. Subsequent cooling resets the hydrogel and fins to their initial state. The process repeats itself in a regular, oscillatory manner, which is sustained by fluid replenishment in the microfluidic channel. It is interesting to speculate that a similar system, with glucose oxidase/gluconolactonase/catalase stamped onto fins that are coupled to a pH-sensitive hydrogel [62], with a single layer of glucose solution flowing below the fin tips, might oscillate in a similar way.

A motivation behind the systems just reviewed is to mimic rhythmic pumping, motile, and homeostasis maintaining functions that are present in living systems. Unfortunately, these systems typically involve toxic reactants, intermediates, and products. The rhythmic hormone delivery system discussed in this paper is fueled by glucose and oxygen, and is facilitated by calcium carbonate in the form of marble. The first two are present in blood, whereas marble ultimately dissolves into Ca²⁺ and CO₂, which are also natural compounds. As noted above, with proper engineering marble might be eliminated. The hydrogel membrane consists of NIPAM and MAA. While hydrogels containing these components are considered biocompatible, they have not been approved for implantation in humans. Other more “natural” hydrogels such gelatin [54] or elastin-like elastomers [63], suitably modified for sharp hysteretic pH-sensitivity, might be substituted for NIPAM/MAA. Biostability of any hydrogel will also be a criterion for inclusion in a long term implantable system.