Leaf area and light use efficiency patterns of Norway spruce under different thinning regimes and age classes

Highlights

► Absorbed light was only marginally superior to predict volume increment than leaf area. ► Larger trees were consistently more efficient than smaller trees. ► Thinning increased the efficiency of an average tree.

Abstract

Silviculture focuses on establishing forest stand conditions that improve the stand increment. Knowledge about the efficiency of an individual tree is essential to be able to establish stand structures that increase tree resource use efficiency and stand level production. Efficiency is often expressed as stem growth per unit leaf area (leaf area efficiency), or per unit of light absorbed (light use efficiency). We tested the hypotheses that: (1) volume increment relates more closely with crown light absorption than leaf area, since one unit of leaf area can receive different amounts of light due to competition with neighboring trees and self-shading, (2) dominant trees use light more efficiently than suppressed trees and (3) thinning increases the efficiency of light use by residual trees, partially accounting for commonly observed increases in post-thinning growth. We investigated eight even-aged Norway spruce (Picea abies (L.) Karst.) stands at Bärnkopf, Austria, spanning three age classes (mature, immature and pole-stage) and two thinning regimes (thinned and unthinned). Individual leaf area was calculated with allometric equations and absorbed photosynthetically active radiation was estimated for each tree using the three-dimensional crown model Maestra. Absorbed photosynthetically active radiation was only a slightly better predictor of volume increment than leaf area. Light use efficiency increased with increasing tree size in all stands, supporting the second hypothesis. At a given tree size, trees from the unthinned plots were more efficient, however, due to generally larger tree sizes in the thinned stands, an average tree from the thinned treatment was superior (not congruent in all plots, thus only partly supporting the third hypothesis).

1. Introduction

In recent decades, many forest scientists have investigated resource use efficiency of trees and forests. Efficiency is defined as the ratio between some measure of biomass production and a measure of resource supply or use. The numerator could be gross primary production, net primary production or stemwood increment over a defined time period. Many different measures of resources have been used as a denominator, quantifying either light, water or nutrients. Light (or proxies for light) was found to be most closely related to wood production (Monteith, 1972), since it is the main driver for photosynthesis. Typically, an efficiency measure implementing light as the resource is referred to as radiation use efficiency (RUE) or light use efficiency (LUE).

Understanding forest or ecosystem level phenomena requires detailed information from an individual tree level. For a long time, light as a resource for individual trees was hard to determine, so proxies like leaf area (LA) or sapwood area (based on the pipe-model-theory (Shinozaki et al., 1964)) were used. Alternatively, Waring et al. (1980) introduced a measure of tree vigor as the ratio of stemwood volume increment to LA. Later, the same ratio was investigated and termed growth efficiency or leaf area efficiency (LAE) (O’Hara, 1988). Next, several models were developed to evaluate the amount of light that was absorbed by trees or canopies (see Brunner (1998) for a collection of different light models). This enabled estimates of LUE for individual trees. As stemwood volume is the predominant interest in forest production, it is now common to express LUE as stemwood volume increment per unit of absorbed photosynthetically active radiation (APAR; also known as photon flux density) (e.g. Binkley et al., 2010; Marková et al., 2011).

The ability of LA to predict stemwood volume increment is already well known (e.g. Binkley and Reid, 1984; Berrill and O’Hara, 2007). In fact, LA is often substituted as a proxy for APAR, however shade might cause deviations from that assumption. For example, one unit of LA can receive different amounts of light as a consequence of self-shading (i.e. leaves from the upper crown shade leaves in lower parts of the crown) and competition (shadecast from neighboring trees or trees at higher canopy layers).

Trying to understand stand-level resource use characteristics, Binkley (2004) hypothesized that the “decline in stand-level growth near canopy closure is driven by increasing dominance of larger trees, leading to declining efficiency of resource use by smaller trees”. This hypothesis was supported for Eucalyptus stands, finding that LUE increases with increasing tree size (Binkley et al., 2010), though the effect was too small to account for stand-level declines in growth. Dominant Eucalyptus trees not only absorbed more light, they produced more stemwood per unit of light than non-dominant trees. Similar patterns have been observed when stem growth was examined as a function of LA (e.g. O’Hara, 1988; Seymour and Kenefic, 2002; Fernández et al. 2011), but exceptions have also been reported (e.g. Maguire et al., 1998; Reid et al., 2004; Fernández and Gyenge, 2009). The differences are likely due to species-specific variation in stand structure, age, density and site.

In this study we conduct a direct comparison of leaf area efficiency and light use efficiency for Norway spruce (Picea abies (L.) Karst.). Our analysis includes different growth classes (mature, immature and pole-stage stands) and thinning variants, which are expected to influence both measures of efficiency. We estimate the absorbed light per crown with the three-dimensional crown model Maestra (Medlyn, 2004) to investigate three main hypotheses:

• -Light absorption by tree crowns should be a better predictor of stem volume increment than crown leaf area. Depending on shading (self-shading or competition) a unit of leaf area can receive different amounts of light.
• -Dominant trees should use absorbed light more efficiently than suppressed trees. If leaf area is a sufficient proxy for light, the pattern should be similar.
• -Light use efficiency, as well as leaf area efficiency should increase for residual trees after thinning.

2. Material and methods

2.1. Study areas

The study area is located at Bärnkopf in Lower Austria (N 48°23′24″, E15°00′20″, 800 m a.s.l.). We planned to establish three pairs of thinned and unthinned plots of three stand ages (mature, immature and pole-stage). One plot of each pair had not been thinned for ten years (hereafter called unthinned; UT) and the other plot had been thinned approximately five years ago (hereafter called thinned; T). We found a shortage of larger pole-stage areas, so we decided to establish two pairs of smaller pole-stage plots (pole-stage1 and pole-stage2), which led to a total of four plot pairs.

Table 1 shows the plot characteristics of these eight plots. As could be expected, the quadratic mean diameter (qmd) was always larger for the thinned treatment. The two pole-stage stands differed substantially in site index (mean height of 100 largest diameter trees at age 100) and thus were treated separately in the study.

Table 1.

Plot characteristics of eight sample plots (four plot pairs) from Bärnkopf. Dominant height is the mean of 100 largest diameter trees and stand density index was calculated according to Reineke (1933).

No.	Growth class	Area (ha)	Age (year)	Quad. mean diameter (cm)	Dominant height (m)	Stand density index	Site index (m)
1	Mature thinned	3.05	123	50.3	37.4	523	35.6
2	Mature unthinned	2.93	128	47.9	37.6	692	35.5
3	Immature thinned	1.72	78	38.8	31.2	634	34.4
4	Immature unthinned	1.24	78	35.9	30.7	843	33.8
5	Pole-stage1 thinned	0.48	43	24.2	23.7	623	39.0
6	Pole-stage1 unthinned	0.15	38	17.9	22.0	1114	39.0
7	Pole-stage2 thinned	0.30	58	23.1	24.2	683	31.7
8	Pole-stage2 unthinned	0.13	41	15.5	17.3	1000	30.5

Measurements were made during the growing season of 2008 (April to September). All trees were measured for diameter at breast height (dbh), height to base of live crown (hcb) and total height. Coordinates and 6–8 crown radii (depending on crown shape) were measured using a computer aided laser-based tool for field data collection (Field-Map Version 8 (IFER, 2008)).

Within each plot, 27 sample trees were selected to represent three different dbh-classes and within those, three different leaf area index classes. The number of sample trees of the two pole-stage pairs was pooled to one pair (n = 54).

Sample trees were carefully felled and measured in more detail to establish allometric leaf area equations. For more information about this process and the equations see Laubhann et al. (2010) and Gspaltl and Sterba (in press). These established equations were used to calculate projected LA.

2.2. Volume increment

In a first step, the annual bole volume increment (AVI) was estimated for the 162 sample trees (27 per plot). It was calculated as the direct volume difference from the beginning to the end of the 5 year investigation period (2003–2007).

Stem discs were taken from felled trees at three heights (1.3 m, 30% of the total height and at the base of the live crown) to measure diameter (without bark) and diameter increment in the laboratory. Height increment was measured with a measuring tape by counting the whorls. Bole volume at the beginning and end of the investigation period was calculated by dividing the tree in sections of different geometric forms and summing up the sections to total tree bole volume (similar to Eckmüllner et al. 2007 and Huber et al. 2009).

Considering that this procedure to estimate AVI is very data intensive, in a second step a possibility to estimate AVI on non-felled trees had to be found. According to Assmann (1970) volume increment results from the combined effects of basal area increment, height increment and also a change in the form factor. However, for Norway spruce at greater ages he found the form height (product of breast height form-factor by total tree height) to remain constant.

For the sample trees we plotted AVI versus the annual basal area increment (ABAI) on a double logarithmic scale and found a strictly linear relationship which significantly differed between the plots. Total tree height from the end of the period (h) could significantly improve this relationship. Hence we found a separate log-linear equation of the form ln (AVI) = α₀ + α₁ · ln(ABAI) + α₂ · ln(h) for every plot that explained 93.5–98.2% of the variation in ln(AVI). For the back-transformation to the non-logarithmic-form AVI = exp^α0 · ABAI^α1 · h^α2 a plotwise correction factor λ = Σ (AVI_observed)/Σ (AVI_predicted) had to be applied. Total height, height to the base of the live crown and dbh (outside bark) were measured from every tree at the end of the period. Also every tree got cored and the 5 year radial increment was measured in the laboratory. With these measurements we could calculate ABAI from every tree, however first we had to establish an equation to calculate the bark thickness (BT) for every tree, which had to be deducted twice from the dbh (outside bark). We used the data from the stem discs at 1.3 m height, where bark thickness was also measured, and fitted a nonlinear equation of the form $\sqrt{\mathit{BT}}=0.589+0.157\sqrt{\mathit{RoB}}$, with the bark thickness (BT) and the radius outside bark (RoB) (R² = 0.768).

Comparing AVI for the thinned and the unthinned treatments in each pair of plots showed no significant difference in variances for the mature and the immature stands, but significant differences for both pole-stage pairs. However, a two sample Welch t-test, which allows for unequal variances, showed significant differences for all pairs, with the thinned treatment showing a higher mean AVI than the unthinned treatment.

2.3. Maestra setup

Maestra, a three-dimensional array model which couples stomatal conductance, photosynthesis, and light absorption provided the mathematical modelling framework (Wang and Jarvis, 1990a). In this study, only photosynthetically active radiation absorbed by individual tree crowns was critical, where Maestra uses an array of tree crowns to calculate radiation absorption from leaves by considering direct beam, diffuse, and scattered beam irradiance (Norman and Welles, 1983). The radiation submodel of Maestra has been validated successfully for Sitka spruce (Picea sitchensis (Bong.) Carrière) and Monterey pine (Pinus radiata D. Don) (Wang and Jarvis, 1990b) and also applied to Picea abies in several studies (Jarvis, 1999; Medlyn et al., 2005; Ibrom et al., 2006).

In Maestra, calculations were performed separately on sunlit and shaded leaf fractions per crown grid point, where volume and LA were calculated throughout the crown at each grid points x, y, and z coordinates. Thus, we divided every individual tree crown into 12 layers and assigned 24 grid points to each layer. All APAR calculations were made for each grid point, which represents a spatial subvolume of the crown. The path length of radiation reaching each grid point was calculated from the size and shape of the tree crowns through which the radiation passed, and the distribution of LA within them. Beer’s Law was applied to each path length of either direct or diffuse radiation intercepted on a grid point. Direct and diffuse radiation were treated separately, where transmission of diffuse APAR was handled by the method developed by Norman (1979). Multiple scattering was calculated by the method of Norman and Welles (1983). Total APAR per tree crown was calculated in Maestra by summing individual APAR of the sub-volumes. Potential shading by all neighboring trees within the plot on each individual tree crown was also taken into account by Maestra. To avoid edge effects, border trees (two outermost tree rows) were included in the simulations, but not included in our evaluation of patterns of light use and tree growth.

Site specific model input consisted of (i) detailed individual tree data: xy-coordinates, crown radii, total tree height, height to crown base, dbh and LA and (ii) plot characteristics: latitude, longitude, slope and bearing. We used tree data from the end of the investigation period to avoid any bias from back-dating models.

In addition, each tree crown was parameterized for the following: the leaf area density (LAD) distribution, the foliage clumping factor, the leaf angle distribution, the average leaf incidence angle and the geometric crown shape. Except for the vertical LAD distribution, these parameters where taken from Picea abies literature (Medlyn et al., 2005; Ibrom et al., 2006) and are listed in Appendix Table A.1.

2.3.1. Leaf area density distribution

In Maestra the LAD distribution is assumed to follow a β-function in the horizontal and vertical direction. LA data from the sample trees was available from a previous study (Laubhann et al., 2010) to estimate the LAD distribution for each crown along a vertical depth profile:

$$\text{rLA}={\beta }_0·{\text{rCL}}^{{\beta }_1}·{(1-\text{rCL})}^{{\beta }_2}$$ (1)

where the relative leaf area (rLA) is the percentage of LA per crown third to the total LA of the tree and the relative crown length (rCL; 0 at the crown base and 1 at the top of the tree) (Table A.2). Parameters for the horizontal LAD distribution were taken from Ibrom et al. (2006).

2.3.2. Time-scale

Daily meteorological Maestra input data (min–max temperature and total short-wave radiation) were available for all plots from 2003 to 2007 via a climate interpolation software that was parameterized and validated for Austria (Daymet; Hasenauer et al., 2003). Initially, a test run of Maestra was carried out for one plot over the entire investigation period and daily APAR values were analyzed. For comparison, three days were chosen which had minimum, mean and maximum APAR of the total stand: a cloudy day at the end of December 2004, a very sunny day in March 2005 and a mean APAR day on the 10th of June 2007. Maestra simulations showed the very sunny day to have 40–95% more light absorption per tree than the average day, and the cloudy day had 92% less light absorption per tree than the average day. The pattern of relative differences between the trees, however, stayed constant for all comparisons, indicated by very high correlations (r = 0.99) of APAR in all stands. To test the hypotheses in this study, the inter-tree APAR pattern (relative difference) is the center of interest. We decided to calculate APAR for our hypotheses tests using the day with mean APAR to be representative of the whole investigation period.

2.3.3. Shading effects

To separate the effects of self-shading (leaves from upper crown shade leaves from lower parts of the crown) from competition (neighboring trees shade the subject tree), we ran Maestra twice while changing only one parameter at a time. First, all trees in each plot were considered in the calculations, which means that the calculated absorbed light per crown was reduced by shading of other trees, and by self-shading (APAR). And second, the effect of neighboring trees was removed, so that only self-shading reduced the absorbed light (APAR_{no_comp}).

2.4. Efficiency

Leaf area efficiency (LAE) was calculated as annual volume increment (AVI) per projected leaf area (dm³ m⁻²). To get a useful scale of light use efficiency (LUE) we used APAR from the representative day (see Section 2.3.2) and AVI (dm³ MJ⁻¹). To reach a common time-scale, LUE values have to be divided by 365 days. One tree from the thinned mature stand was identified as an outlier, because of an implausibly high efficiency, and was dropped from further analysis.

2.5. Statistical analyses

Analysis of variance (ANOVA) was used to test for differences between growth classes and treatments. Based on the allometric principle which describes the changes in shapes of plants, we use double logarithmic regressions (Eq. 2) to obtain information about general trends.

$$\ln (y)={\alpha }_0+{\alpha }_1·\ln (x)\leftrightarrow y={\exp }^{{\alpha }_0}·x^{{\alpha }_1}$$ (2)

All statistical analyses were conducted using the open source software R (R Development Core Team, 2011). For plotwise regressions we used convenient functions of the nlme-package (Pinheiro et al., 2011).

3. Results

3.1. Leaf area density distribution

The vertical distribution of LA differed substantially between plots, growth classes and dbh-classes. The thinning treatments did not alter the vertical distribution of LA. Once growth classes were considered, vertical LAD did not significantly differ between treatments (except pole-stage1) nor between dbh-classes (except immature).

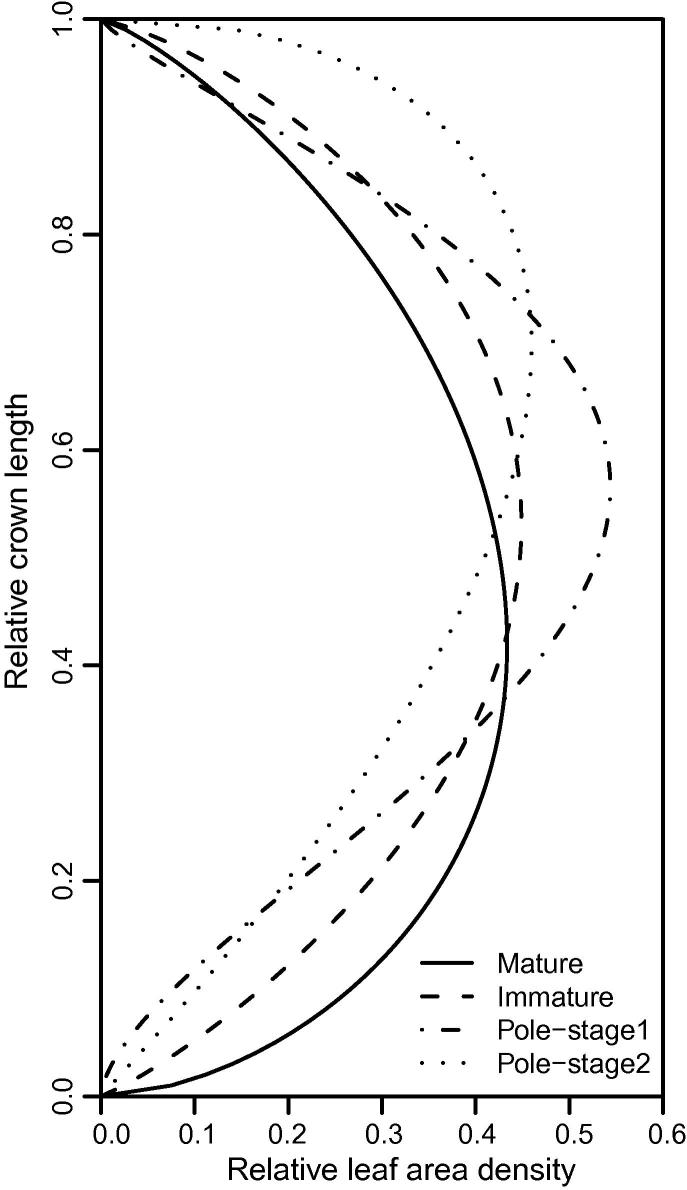
A trend could be observed (Fig. 1), where maximum LAD moved up the crown with growth classes (42.5%, 53.1%, 56.6% and 69.7% of the crown length for mature, immature, pole-stage1 and pole-stage2, respectively).

Fig. 1.

Vertical leaf area density distribution following a β-function (Eq. 1) separated for the four growth classes. Relative crown length with zero on the crown base and one at the tree top. The integral of each curve over the relative crown length equals one.

3.2. Comparison of APAR to LA

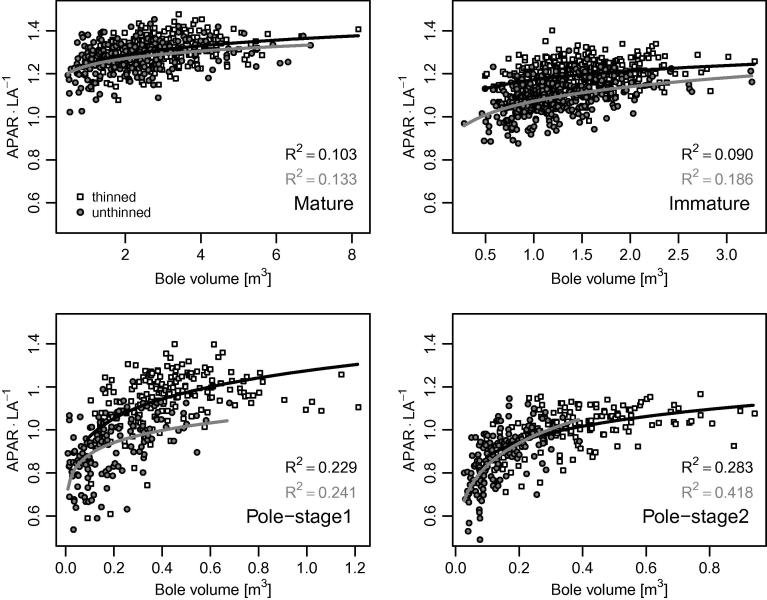
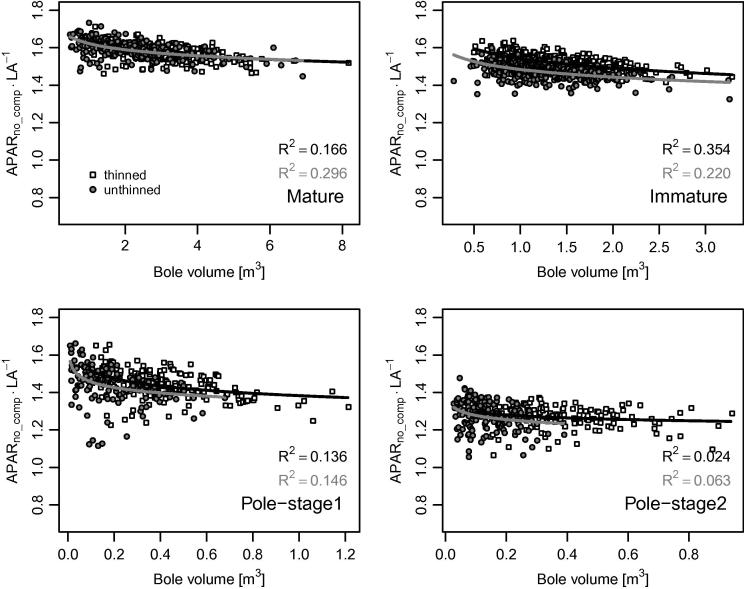
The relationship between APAR and LA was linear for all plots (R² = 0.971–0.988) and differed between growth classes and treatments. We observed steeper slopes for the thinned versus the unthinned treatments and the slopes increased as growth class increased (from pole-stage1 to pole-stage2 to immature and mature stands). In Fig. 2, APAR per LA was plotted against the bole volume. Double logarithmic regression lines were fitted, which differed significantly between the growth classes. A comparison between the treatment variants thinned and unthinned for each growth class showed a significant difference in the immature stands, differences other than the slope in the mature and pole-stage1 stands, and differences except for the intercept in the pole-stage2 stand. All parameters of the double logarithmic regressions were significant (α = 0.05), though coefficients of determination were mostly weak (especially for the mature and immature stands). APAR per LA increased with bole volume, whereas this increase was more pronounced in the two pole-stage stands, as opposed to the older growth classes (mature and immature). This pattern occurred when APAR considered self-shading and shading of neighboring trees. To differentiate those effects, the same comparison was made using APAR_{no_comp}, which excluded any effect of neighboring trees. Fig. 3, therefore, only illustrates the effect of intra-crown shading. Regression parameters of the double logarithmic regression lines were all significant (α = 0.05) and differed between growth classes and thinning variants. In between the growth classes, thinning variants did not differ in the mature stands, and only differed in their slope for the other growth classes. In all growth classes, the effect of self-shading increased with increasing bole volume, which is represented by a decreasing APAR_{no_comp} per unit of LA (Fig. 3).

Fig. 2.

Across the growth classes and thinning treatments, larger trees either showed no increase in absorbed photosynthetically active radiation (APAR) per individual tree leaf area (LA) relative to smaller trees, or an increase in APAR · LA⁻¹. No case showed lower APAR · LA⁻¹ for larger trees. Lines depict double-logarithmic regressions and their respective coefficients of determination (R²) are displayed (black for thinned and shaded for unthinned); note the different scales of the abscissa between the growth classes.

Fig. 3.

When the effect of shading from neighbors was excluded from the calculation of absorbed photosynthetically active radiation (APAR_{no_comp}) the ratio of APAR_{no_comp} to individual tree leaf area (LA) decreased with increasing bole volume. The effect of self-shading was larger for trees with higher bole volume. Lines depict double-logarithmic regressions and their respective coefficients of determination (R²) are displayed (black for thinned and shaded for unthinned); note the different scales of the abscissa between the growth classes.

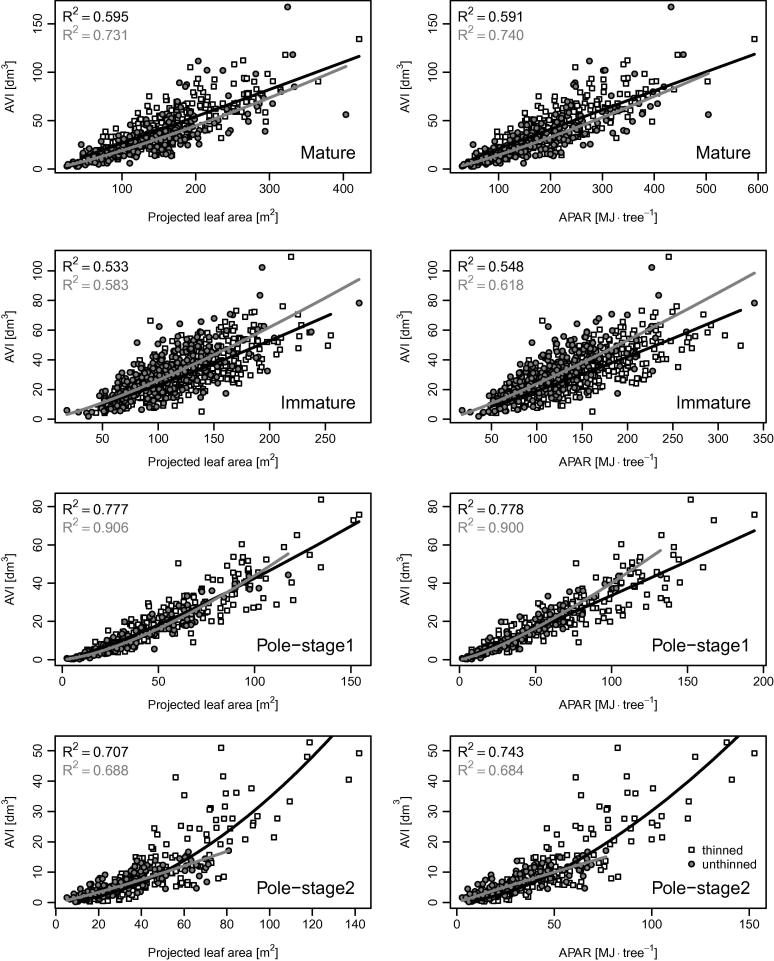
To compare the predictive power of LA and APAR estimates of AVI we fitted double-logarithmic regression lines (Fig. 4). For given growth classes, the thinning treatments differed significantly for the AVI vs. LA relationship (except the slope of the immature stand) and also for the AVI vs. APAR relationship (except the slope of the immature stand and the intercept of the pole-stage1 stand). Considering the coefficient of determination, stem growth related slightly better to APAR than LA. Both relationships (AVI vs. LA and AVI vs. APAR) showed a somewhat exponential increase in the younger stands (pole-stage1 and pole-stage2) but a more linear increase in the older stands (mature and immature).

Fig. 4.

Comparison of the predictive power to estimate annual bole volume increment (AVI) from projected leaf area (left column) and absorbed photosynthetically active radiation (APAR) (right column) per growth class and treatment. Lines depict double-logarithmic regressions and their respective coefficients of determination (R²) are displayed (black for thinned and shaded for unthinned).

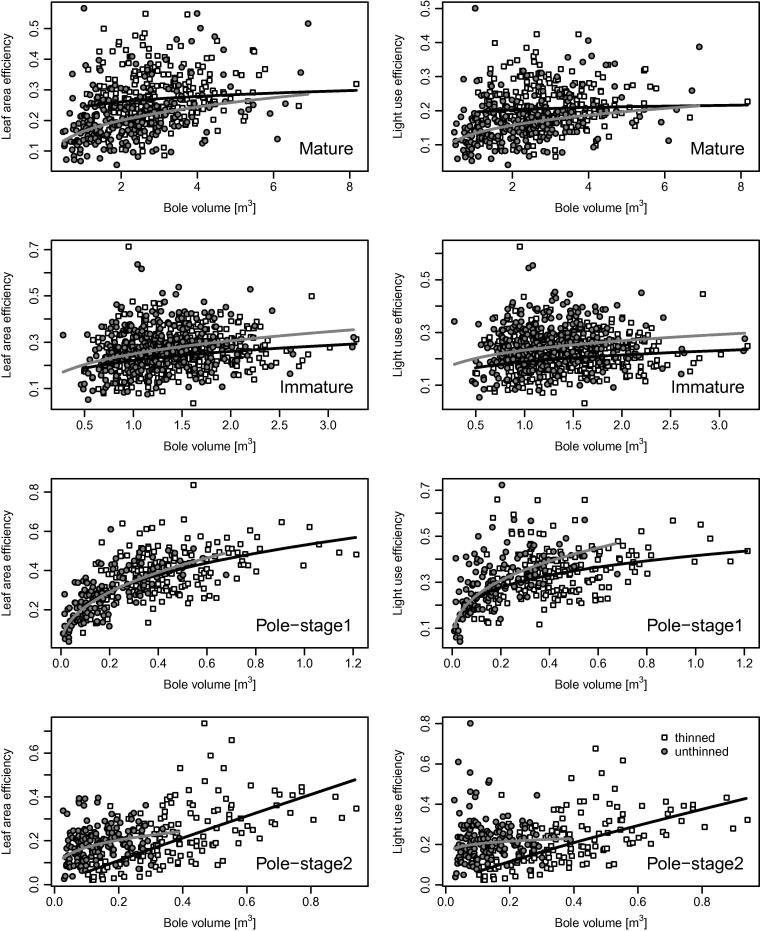
3.3. Efficiency

The analysis of the relationship between efficiency (LAE and LUE) and volume revealed significant differences between growth classes and treatments (Fig. 5). For a given growth class differences between the treatments were significant for the mature and the pole-stage2 stands (LAE and LUE). For LAE, the slope was not significantly different from zero in the immature stand, and the relationship did not differ at all for the pole-stage1 stands. Similarly for LUE, the slope did not differ between treatments for the immature and the pole-stage1 stand. Plotwise regressions were all significant, except for the thinned mature stand (both efficiency patterns) and the unthinned pole-stage2 stand (LUE). Coefficients of determination were generally weak, although higher in the pole-stage stands (except pole-stage2 UT) than in the mature and immature stands. As a general trend, both efficiencies indicate an increasing pattern over tree size (Fig. 5).

Fig. 5.

Comparison of the relationship between leaf area efficiency and bole volume (left column) to the relationship of light use efficiency to bole volume (right column). Double-logarithmic regression lines depict the overall trend (black for thinned and shaded for unthinned).

With given tree size (i.e. bole volume) both efficiencies (LAE and LUE) were higher for the unthinned variants (except for the mature stands). To identify further differences between the thinned and unthinned treatments we conducted a comparison at the stand-level. Because variances differed significantly in some cases, we applied Welch two-sample t-tests to test for differences between the means. The thinned variant always showed significantly higher LAE than the unthinned variant (except for the immature stands). LUE showed the same pattern, except that additionally no significant difference could be found between thinned and unthinned for the pole-stage2 stand. The average tree from the thinned treatment received 28.8%, 34.7%, 104.2% and 84.7% more light (for mature, immature, pole-stage1 and pole-stage2, respectively) than an average tree from the unthinned treatment.

4. Discussion

4.1. Comparison of APAR to LA

The relationship between APAR and LA was linear and differed between growth classes and thinning variants. Binkley et al. (2010) found similar patterns for Eucalyptus grandis (W. Hill es Maid.) trees and concluded that “larger trees capture just as much light per unit leaf area as mid-size trees and canopies of small trees were not substantially shaded by neighbors”. Mathematically this is only true, however if the intercept in the APAR to LA relationship is not significantly different from zero. As for the actual Picea abies plots, all intercepts were highly significant, a curvi-linear relationship of APAR per LA over tree size could be expected. To get more insight, we analyzed the amount of APAR that one unit of LA receives per tree. We found that overall growth classes and thinning variants, larger trees absorbed more light per unit LA than smaller trees (Fig. 2). There are two main reasons that could explain the difference in APAR to LA: (i) self-shading: light has to penetrate through the upper crown before it arrives at leaves in lower parts of the crown and (ii): inter-crown shading or competition: light has to penetrate through other crowns (either neighbors or upper story trees) before it hits the subject crown. To be able to differentiate those two effects, we manipulated Maestra to remove the effects of neighbors. This analysis revealed a pattern of decreasing APAR_{no_comp} per LA with increasing tree size (increasing effect of self-shading) (Fig. 3). We conclude, for Norway spruce over a variety of growth classes and thinning variants, that (i) the effect of self-shading increases with increasing tree size, (ii) competition strongly reduces the light per unit of LA for smaller trees and (iii) the effect of competition is stronger than the self-shading (i.e. for the smaller trees).

Binkley et al. (2002) also used Maestra to model absorbed light for a plot of Eucalyptus saligna trees. They found that APAR per unit of LA declined exponentially with increasing tree size (i.e. diameter) and explained the decline with greater self-shading within canopies of larger trees. The strong competition effect (shading from neighboring trees) that we found among the Picea abies trees was not apparent in Eucalyptus trees. This could be explained by the fact that the tree size variation in Picea abies stands is expected to be higher than in short rotation Eucalyptus plantations, which leads to higher interactions among the individuals. These two species also differ in their light tolerance, with Eucalyptus typically being a light demanding and Picea abies a semi-shade tolerant species. Pearcy et al. (2004) used a very detailed three-dimensional crown model and found lower self-shading effects for shade tolerant than for light demanding species.

Selaya et al. (2007, 2008) used a two-dimensional canopy model to calculate intercepted light for three tropical rain forest stands of different ages. A comparison of daily intercepted light per unit of LA between stands of different ages (6 month, 2 and 3 year), revealed only small differences between the tallest (short-lived pioneers) and the smaller (later successional) tree species in the young stand, but an increasing difference among older ages (about threefold). The short-lived pioneers start to dominate other species in these early successional stages, and show higher amounts of light per unit LA, which agrees with the overall increasing pattern found in our study.

As expected, projected tree LA was a good predictor of bole volume increment. The relationship differed among growth classes and thinning variants, whereas the older stands (mature, immature) showed linear trends and the younger stands (pole-stage1, pole-stage2) expressed a moderate exponential increase. Similarly, Berrill and O’Hara (2007) investigated Coast redwood (Sequoia sempervirens (D. Don) Endl.) trees and found a highly linear relationship between periodic annual tree volume increment and LA for trees of the overstory and the main canopy, while the relationship was non-linear (exponential) for trees of the understory. Our hypothesis, that absorbed light (i.e. APAR) would be a better estimator for bole volume increment, could not be entirely supported for Norway spruce. Although the ratio of APAR to LA varied with tree size, the predictive power of light was either as good or only marginally superior to the tree LA. Similarly, for four to five year old Loblolly (Pinus taeda L.) and Slash pine (Pinus elliotii Engelm. var. elliotti) clones, Emhart et al. (2007) found that light interception and crown volume were generally better correlated with stem volume increment than LA.

4.2. Efficiencies

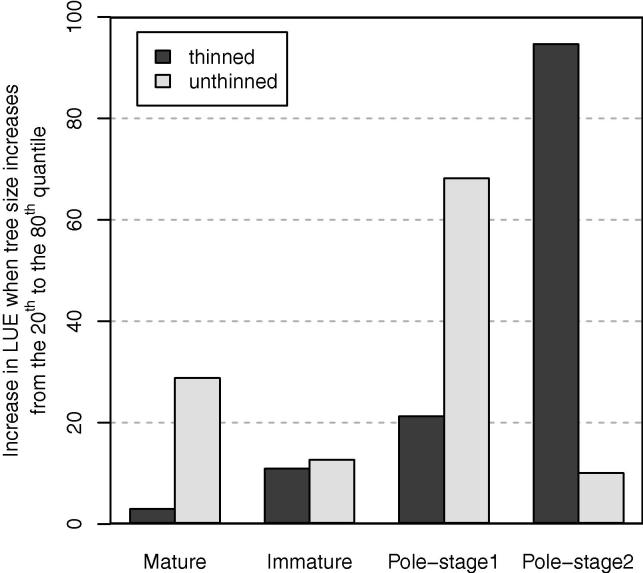
Generally, the leaf area and light use efficiency increased with increasing tree size (i.e. bole volume). Similarly, Binkley et al. (2010) found that large Eucalyptus trees not only absorbed more light than smaller trees, but that they could produce more bole volume increment per unit of light. The relative difference in LUE for the 20th and the 80th quantiles of the tree size (in this case tree rank) was 1.8-fold or 180%. For comparison we calculated the LUE for the same quantiles of tree size (i.e. bole volume) and found similar, but not so pronounced patterns (Fig. 6). The highest increase was only 0.9-fold and in most of the cases it was below 0.3-fold. The same difference was found by Campoe et al. (submitted for publication-a) who reports a slight increase in LUE of Pinus taeda under different fertilization and irrigation effects. Again, large Eucalyptus trees were found to be 2.4-fold more efficient than smaller trees (Campoe et al., submitted for publication-b). For Shining gum (Eucalyptus nitens (H. Deane & Maiden) Maiden) plantations, Forrester et al. (in review) found that LUE did not depend on any measure of tree size under different treatments (thinning, pruning, fertilization). Given that all of these studies were conducted with Maestra, we expect the distinctions among species are real and worthy of further investigation.

Fig. 6.

Percentage of relative increase in light use efficiency (LUE) when tree size (i.e. bole volume) increases from the 20th to the 80th quantile.

Alternatively, Brunner and Nigh (2000) used a different light model (Brunner, 1998) to evaluate light use efficiency of a 50-year old Douglas fir (Pseudotsuga menziesii (Mirb.) Franco) stand and found a hyperbolic decreasing pattern over weighted leaf area (i.e. projected tree leaf area weighted with the percentage of absorbed light).

Although the ratio of APAR to LA varied with tree size, the efficiency pattern did not differ substantially when bole volume increment was referred to LA or APAR. We are not aware of any study that reports a decreasing efficiency with increasing tree size in Maestra simulations, but rather several studies for a wide variety of tree species report an increasing or constant efficiency (Binkley et al., 2010; Campoe et al., submitted for publication-a, submitted for publication-b; Forrester et al., in press). However, there are other models that report a strongly decreasing trend (i.e. Brunner and Nigh, 2000). Although this might be due to differences in the model structures, the same discrepancies were observed for the LAE, which was investigated more frequently in the last decades. When analyzing light use efficiency in terms of bole volume production, the carbon allocation to different tree compartments would be expected to have an additional influence on the efficiency patterns. However, an investigation in generic biomass functions for Norway spruce in Central Europe (synthesis of data from 19 authors) indicated that the proportion of biomass allocated to the stem was unaffected by social status (Wirth et al., 2004).

These different patterns of resource use efficiency (ReUE) might be explained by the ability of a tree to acquire resources. As long as enough resources are available (i.e. canopy closure is not reached) all trees of a stand are equally efficient (Binkley et al., 2002; Binkley, 2004; Fernández and Gyenge, 2009). When inter-tree competition starts, larger trees are able to acquire enough resources, whereas smaller trees might already reach their resource compensation point (minimum resource quantity needed to produce a positive growth). That implies an increase in ReUE for larger trees but a decrease in ReUE for smaller trees-supporting the pattern in this study.

For Ponderosa pine (Pinus ponderosa C. Lawson), Fernández and Gyenge (2009) observed differences in the water use efficiency before canopy closure, indicating that differentiation in efficiency is defined in earlier stages (before canopy closure) to determine the dominant and suppressed trees.

A comparison between the thinned and the unthinned treatments revealed that (i) on a tree-level basis, with a given tree size, trees from the unthinned plots were more efficient (except the mature stands) and (ii) on the stand-level, the mean tree of the thinned stand was either more efficient (mature and pole-stage1), as efficient (pole-stage2), or less efficient (immature) than the mean tree of the unthinned plots.

Wang (1988) found that dry matter per APAR was not affected by thinning, but rather from nitrogen fertilization for plots of Sitka spruce. Forrester et al. (in press) showed that for Eucalyptus nitens plantations, LUE in terms of annual above ground biomass increased with thinning, while LUE in terms of wood mass declined. They speculate that a decline of efficiency with thinning may occur on sites that are limited by resources other than light. When analyzing light regimes, we had to assume that water and nutrient supply was ample, which may not have been the case for the immature stand (the only plot showing a decrease of efficiency with thinning).

Assuming that the trees are a representative sample for one hectare, one could roughly scale up to a hectare-level by multiplying the mean efficiency with the stems per hectare. This gives a clear pattern, proving that due to the higher stem number per hectare, the unthinned treatment is always more efficient (with 12.2%, 80.3%, 152%, 185% for mature, immature, pole-stage1 and pole-stage2, respectively). That would mean that more wood per unit light is produced in an unthinned stand. However, forestry typically focuses on producing high quality saw-log timber that cannot be obtained without thinning. Hence a trade-off has to be found between growing the most efficient trees at a low risk of damage with the amount of trees per unit area.

5. Conclusions

Light absorption by tree crowns, simulated with Maestra, was only a slightly better predictor for stem volume increment than crown leaf area. We were able to differentiate the shading effects and found that for Norway spruce the effect of neighbor competition was more pronounced than the self-shading.

Although the relationship of absorbed light to leaf area varied with tree size, we could not detect a different trend between light use efficiency and leaf area efficiency. Both indicated that trees with higher tree size not only received more light (leaf area) but also were able to produce more stem volume increment per unit of light (leaf area). We speculate that the higher efficiency in larger trees was not a result of higher productivity, but rather of a lower efficiency in smaller trees.

On an individual tree-level, we found that at a given tree size, individuals from the unthinned plots were more efficient; however at the stand-level the average tree from the thinned plots was more efficient, since the tree sizes were generally higher. Unfortunately, this trend was not consistent within all plots and does not fully agree with our third hypothesis.

Appendix A

Table A.1. Set of Maestra input parameters for Norway spruce (Picea abies (L.) Karst.).

Parameter names and units	Abbreviation	Parameter	Source
Confile
Start date	STARTDATE	10/06/07
End date	ENDDATE	10/06/07
Number of layers in the crown	NOLAY	12
Number of points per layer	PPLAY	24
Number of zenith angles	NZEN	11
Number of azimuth angles	NAZ	5
Number of shading trees	NOTREES	0 – all, 1 –subject tree
Physiological File:
Transmittance and Reflectance (PAR/NIR/IRa):
Soil reflectance (%)	ROHSOL	0.10/0.30/0.05	Ibrom et al. (2006)
Needle transitivity (%)	ATAU	0.03/0.26/0.00	Ibrom et al. (2006)
Needle reflectance (%)	ARHO	0.07/0.33/0.05	Ibrom et al. (2006)
Jmax Parameter:
Electron transport rate (μmol m−2 s−1 at 25°C)	JMAX	71.7	Ibrom et al. (2006)
Curvature of light response curve of electron transport	THETA	0.71	Medlyn et al. (2005)
Quantum yield of electron transport (mol mol−1)	AJQ	0.3	Ibrom et al. (2006)
Activation energy (J mol−1)	EAVJ	40,000	Ibrom et al. (2006)
Deactivation energy (J mol−1)	EDVJ	2,20,000	Ibrom et al. (2006)
Entropy term (J K−1 mol−1)	DELSJ	710	Ibrom et al. (2006)
Vcmax Parameter:
Carboxylation rate (μmol m−2 s−1 at 25°C)	VCMAX	43	Ibrom et al. (2006)
Activation energy (J mol−1)	EAVC	56,000	Ibrom et al. (2006)
Deactivation energy (J mol−1)	EDVC	200,000	Medlyn et al. (2005)
Foliar dark respiration:
Foliar dark respiration rate (μmol m−2 s−1 at 25°C)	RD	2.75	Ibrom et al. (2006)
Temperature (in °C) at which RD is specified	RTEMP	25	Ibrom et al. (2006)
Fraction by which dark respiration is reduced in the light	DAYRESP	0.6	Medlyn et al. (2005)
Foliage Q10 values	FOLQ10	0.0862	Stockfors and Linder (1998)
Stomatal Conductance Model (Ball-Berry):
Input parameter (mol m−2 s−1)	G0	0.0	Jarvis (1999)
Input parameter (mol m−2 s−1)	G1	5.5	Jarvis (1999)
CO2 compensation point (μmol mol−1)	GAMMA	55	Jarvis (1999)
Number of sides of the leaf with stomata	NSIDES	1	Ibrom et al. (2006)
Width of the leaf (m)	WLEAF	0.001	Ibrom et al. (2006)
Structure File:
Leaf area density distribution (vertical and horizontal)	JLEAF	2	–
Parameter of beta distribution	BPT	a, b, c, de, f	Vertical: own data horizontal: Ibrom et al. (2006)
Number of age classes	NOAGEC	1	Assumed
Foliage clumping factor	RANDOM	0.64	Medlyn et al. (2005)
Shape of the canopy	CSHAPE	CONE	Assumed
Leaf angle distribution (spherical)	ELP	1	Medlyn et al. (2005)
Number of leaf area classes	NALPHA	1	Assumed
Average leaf incidence angle	AVGANG	0	Assumed
aPhotosynthetically active radiation (PAR), near infra-red (NIR), infra-red (IR)

Table A.2. Parameters for the β-function that estimates the leaf area density distribution (Eq. 1). For the horizontal distribution, we also used parameters from Ibrom et al. (2006): d = 1.21, e = 0.38 and f = 0.94.

Plot	Vertical
	a	b	c	RMSE
Mature thinned	1.15	0.59	0.84	0.091
Mature unthinned	1.09	0.58	0.78	0.105
Immature thinned	1.67	0.95	0.91	0.103
Immature unthinned	1.18	0.81	0.64	0.094
Pole-stage1 thinned	2.69	1.43	1.02	0.089
Pole-stage1 unthinned	7.12	1.98	1.64	0.058
Pole-stage2 thinned	1.08	0.88	0.50	0.120
Pole-stage2 unthinned	1.25	1.21	0.43	0.110
Ibrom et al. (2006)	12.47	1.67	1.25