Does Proximity Matter? Distance Dependence of Adolescent Friendships

Abstract

Geographic proximity is a determinant factor of friendship. Friendship datasets that include detailed geographic information are scarce, and when this information is available, the dependence of friendship on distance is often modelled by pre-specified parametric functions or derived from theory without further empirical assessment. This paper aims to give a detailed representation of the association between distance and the likelihood of friendship existence and friendship dynamics, and how this is modified by a few basic social and individual factors. The data employed is a three-wave network of 336 adolescents living in a small Swedish town, for whom information has been collected on their household locations. The analysis is a three-step process that combines 1) nonparametric logistic regressions to unravel the overall functional form of the dependence of friendship on distance, without assuming it has a particular strength or shape; 2) parametric logistic regressions to construct suitable transformations of distance that can be employed in 3) stochastic models for longitudinal network data, to assess how distance, individual covariates, and network structure shape adolescent friendship dynamics. It was found that the log-odds of friendship existence and friendship dynamics decrease smoothly with the logarithm of distance. For adolescents in different schools the dependence is linear, and stronger than for adolescents in the same school. Living nearby accounts, in this dataset, for an aspect of friendship dynamics that is not explicitly modelled by network structure or by individual covariates. In particular, the estimated distance effect is not correlated with reciprocity or transitivity effects.

1. INTRODUCTION

Homophily is a major characteristic of friendship: individuals tend to become and remain friends with others that are similar to them (e.g., Lazarsfeld and Merton, 1954; Cohen, 1977; Kandel, 1978; McPherson et al., 2001). Geographic proximity is one of the essential causes of homophily because people that are spatially close are more likely to meet and interact, and because geographically-bounded organizations, such as neighbourhoods or schools, congregate individuals who are similar in characteristics like religion, ethnicity, income, etc. Hence, spatial propinquity fosters the creation and maintenance of relationships between people that are alike (Lieberson, 1980; Feld, 1982; Blau et al., 1984; McPherson et al., 2001).

The literature argues that the probability, contact frequency, and strength of social ties decline with distance. Wellman (1996) found that most types of relationships, especially those characterised by frequent interactions, occur more often within one mile of an individual's home than farther away. In agreement, Carrasco et al. (2008) state that after accounting for gender, age, income, use of communication technologies and degree of closeness in a relationship, individuals have to be more proactive in seeking opportunities for socialising with those who live more than 35 km away than with those living closer by.

Moreover, the development of modern transportation and communication technologies has not destroyed, but transformed and diversified, the effect that geographic proximity has on social relations (Dijst, 2006). Real friendships grow through tangible interactions, which are less expensive at shorter distances (Butts, 2002). Residential proximity is amongst the strongest predictors of how often friends get together to socialise (Verbrugge, 1983; Tsai, 2006), and relationships solely based on non face-to-face contacts (such as e-mail or telephone) usually originate and develop on pre-existing, tangible ties (Carley and Wendt, 1991).

While the general agreement is that the likelihood of social relationships decreases with distance, little is known about the relevant features of this falloff and how it changes in time and by other spatial and social factors. This is partially because longitudinal network data that includes the exact location of the actors is rather scarce (particularly if the actors are human individuals), and also because most network studies are spatially constrained, so geographic distances might not play a major role (Butts, 2002).

Many social institutions are organised in space, implying that their effects on relationships might be correlated with distance. Hence, accounting for spatial arrangements and distances amongst social actors is important when analysing social processes, institutions and contexts, as argued by White (1992) and Pattison and Robins (2002). When the distance dependence of friendship is relevant, a misspecification of its functional form may lead to erroneous conclusions about other, spatially-bounded social factors.

Some relevant studies have focused on the influence of geographic proximity on social relationships in more detail, usually employing an exponential or a power-law (e.g. Latané et al. 1995; Butts, 2002; Liben-Nowell et al. 2005; Daraganova et al., 2010). In particular, Latané et al. (1995) conclude that the average number of interactions people find noteworthy or memorable, is proportional to the inverse of the distance at which individuals live, and argue that this is in accordance with the theory of social impact (Latané, 1981), which states that social impact (in the form of spending time with, being influenced by, etc.) is a function of the inverse square of distance¹.

In many of these works, however, the functional form of the association between distance and social relationships is either modelled by pre-specified parametric functions, or by rough approximations. Further, they often assume that the ties between pairs of actors are independent, so even when pertinent individual and social characteristics are accounted for, network structure is usually not considered.

This paper aims to give a detailed representation of the dependence of friendship on distance, and how this dependence is modified by a few basic individual characteristics and social factors. First, we find the functional form of the effect of distance without making any assumptions about its relevant features. Next, we construct parametric estimates of this effect to assess how its strength and shape change in time and in the presence of basic similarity and institutional proximity measurements. Finally, we employ these results in parametric models for longitudinal social network analysis, to study how the association between friendship and distance is modified when the interdependent nature of the relationships, and the structural characteristics of a network are considered.

We employ an age-defined cohort of adolescents living in a small Swedish town for whom there is information on the distance between the houses where they live. The study design is such (see Section 3), that it is reasonable to assume the dataset represents practically all friendships with frequent contacts for adolescents of this age in the town.

The first aim of this article is data-analytic and methodological in nature. A second aim is to get substantive insights about the distance dependence of adolescent friendship. In this respect the model tests a number of hypotheses, indicated by H1-H5 below, based on the following theoretical considerations and expectations.

In general, we expect for the likelihood of friendship to decrease with distance (H1), because proximity between households leads to increasing opportunities, and decreasing costs of various kinds, for meeting and interaction (Zipf, 1949; Verbrugge, 1983). Attending the same school also yields meeting opportunities, with the added component that in school the adolescents are together for a significant part of the day, which is not necessarily the case if they live close by. Schools as well as neighbourhoods (short distances) yield foci for social contacts (Feld, 1981). Hence, we hypothesize that the effect of living nearby on the likelihood of friendship will be weaker if the adolescents go to the same schools (H2). Also, as adolescents grow older they become less dependent on their parents (Steinberg and Silverberg, 1986) and will have more resources to explore spaces further away from home, so the distance dependence of friendships should become weaker as they age (H3). In addition, we expect that estimated effects of distance on friendship will become weaker when tendencies towards transitivity and reciprocity (which may be expected to be important, cf., e.g., Hallinan, 1974) are considered, because their effects might be correlated (H4). Finally, we expect the dependence of friendship creation on distance to be stronger than that of friendship maintenance (H5), as in the latter the distance-related cost or effort necessary to establish a friendship has already been overcome (Zipf, 1949).

This study can hopefully serve a dual purpose. On the one hand, the results, although based on a data set from one town, may have some degree of generalisability to other places and can thus provide insight in the ways in which a meaningful geographic context influences friendships between adolescents. On the other hand, the methodological approach may serve as a point of departure for other studies of distance dependence.

2. METHODOLOGY

We consider longitudinal social network data that consists of repeated observations of a set of n actors (or nodes) and the relationships between them (or ties), along with the geographic location of the actors and other individual or pairwise attributes. Ties are regarded as binary (i.e., existent or non-existent) and it is assumed that the locations of the actors are constant in time.

To assess the effect of geographic proximity on the probability of friendship we would ideally employ a fully flexible model for distance together with network dependence; but a method combining these in a single analysis is yet unavailable. Therefore, we follow a three-step process. First, using logistic Generalized Additive Models (“GAM”; Hastings and Tibshirani, 1986), a descriptive approach is elaborated in which the network dependence is ignored and the n(n-1) binary tie variables are treated as if they were independent, but allowing complete generality in the functional form. This yields a detailed description of the relevant features of the effect of spatial distance on friendship. Second, the effects obtained are approximated by parsimonious parametric functions, using standard logistic regressions. This produces a small number of transformations of distance for which a linear combination gives a close representation of the effect of distance on the log-odds of friendship, under the assumption of tie independence. We do this in both a static (existence of friendships) and a dynamic (creation and maintenance of friendships) perspective. Finally, these transformations of distance are used in Stochastic Actor-Oriented Models (“SAOM”; Snijders, 2001) for network dynamics, a parametric framework that allows analysing the distance effect on friendship while fully taking into account network dependencies. The third step is carried out only for the dynamic case, because the number of analyses presented is already quite large, and because the static instance is covered by Daraganova et al., (2010).

2.1 Generalized Additive Models

Generalized Additive Models were formulated by Hastie and Tibshirani (1986) as an extension to Generalized Linear Models (GLM) that allow the inclusion of smooth functions of the explanatory variables along with the standard parametric components. They are particularly useful when the functional form of the association between a covariate and the response is not known or assumed to be complex, and it is desired to estimate it from the data without assuming it has a specific parametric form.

As in the GLM, we wish to represent how a dependent variable Y may depend on explanatory variables X₁, X₂, …, X_p. The response Y is assumed to have a distribution f_Y(y) which is a member of a so-called exponential family (see McCullagh and Nelder, 1989 for a mathematical definition); common examples are Gaussian, Bernoulli and Poisson distributions. The expected value of Y, called µ_Y, is transformed by a link function g(µ_Y) that can assume any real value.

We consider the Bernoulli distribution for tie variables, for which the expected value lies between 0 and 1. The link function mostly used for the Bernoulli distribution is the logit function, where

$$\mathit{\text{logit}}({\mu }_Y)=\mathit{\text{ln}}\left(\raisebox{1ex}{${\mu }_Y$}\!\left/ \!\raisebox{-1ex}{$(1-{\mu }_Y)$}\right.\right)$$ (1)

which ranges over all real numbers. Use of this link function effectively provides a model for the log-odds of the occurrence of a tie.

The GLM assumes a linear dependence of Y on the explanatory variables X₁,X₂, … X_p, expressed by

$$g({\mu }_Y)=\sum _{j=1}^p{\beta }_j{X}_j$$ (2)

where the linear combination $\sum _{j=1}^p{\beta }_j{X}_j$ is called the linear predictor.

Suppose that there is another covariate Z for which the functional form of the effect on the response is unknown (the model can also be defined for several of such variables). The GAM allows including this covariate in a flexible way, by replacing its regression coefficient β by a smooth, non-parametric function s (Hastie and Tibshirani, 1990) so that the dependence of Y on X₁, X₂, …, X_p, Z can be expressed by

$$g({\mu }_Y)=\sum _{j=1}^p{\beta }_j{X}_j+s(Z)$$ (3)

To estimate the smooth function S that best represents the form of the association between the covariate Z and the response Y, two requirements are combined: the smoothness of the function and the goodness of fit between observations and model. In general, these requirements go into opposite directions, as a very jagged function might give a perfect fit while a linear function (which has maximum smoothness) might give a poor fit. To understand this, suppose that there are no covariates X_j (i.e., p = 0) and that the response Y is normally distributed, so the link is the identity link (i.e., g(µ_Y) = µ_Y). The function S is found by minimising

$$\sum _i{(y_i-s(z_i))}^2+\lambda \int {(s{\text{'}}^{\text{'}}(u))}^{2}du$$ (4)

where the sum of the squared deviations between fitted and observed values controls the lack fit, while the integral is a measure of lack of smoothness. This integral is zero for a linear function, which is maximally smooth. The parameter λ is a positive number which defines the trade-off between goodness of fit and smoothness, and it should be tuned to obtain an optimal result.

It can be proved that the family of functions that minimise expression (4) are so-called cubic splines (Silverman and Green, 1994). These functions are continuous, piecewise cubic polynomials joined at the unique observed values z_i in the dataset (Hastie and Tibshirani, 1990). A good criterion for determining λ is making the difference between the fitted and the true expected values of independently obtained new data points as small as possible. A common measure is the Unbiased Risk Estimator (UBRE) for the mean squared error (Wood, 2006a). The UBRE is a measure of the cross-validated likelihood of observing the data under the proposed model and it works like a generalised Akaike Information Criterion (AIC) for the GLM, in the sense that the model with the smallest UBRE provides a good global fit for the data.

To fit the GAM we employed the R library mgcv version 1.6-2 (Wood, 2006a).

2.2 Logistic Regressions with quadratic B-splines

The GAM can provide great detail on the relevant features of the dependence of the response on the covariates; however, this model assumes that the observations are independent, which is implausible for network ties and leads to an underestimation of the uncertainty of estimates of parameters and functional form. Hence, some characteristics that might seem relevant under the GAM might not actually be significant when considering that the observations are dependent. Furthermore, the results from the GAM cannot be directly employed in parametric models for network dynamics. Thus, as an intermediate step we construct parametric estimations of the GAM using standard logistic regressions, as defined in expressions (1) and (2), which numerically evaluate the most relevant aspects of the association between distance and the likelihood of friendship.

To understand how the approximations are constructed, suppose that the GAM for the dependence of a certain binary response Y on a single covariate X shows that the logit of the probability of Y being equal to 1, decreases with a certain tendency for 0 ≤ X ≤ K, and then it keeps on decreasing but in a different fashion for X ≥ k Further, assume that both components of the overall estimated curve (before and after k) are smooth and have relatively simple shapes, such as linear or quadratic. We can represent this change in trend by a function f_k(x) defined as

$$f_k(x)={(x-k)}^2\text{for}x>k,\text{and}{f}_k(x)=0\text{for}x\le k.$$ (5)

Then we perform a logistic regression of Y on the covariates X, X² and f_k(x), which usually provides a good approximation to the results of the non-parametric regressions obtained by the GAM if the conditions stated above regarding the piece-wise smoothness and simplicity of the overall curve are roughly satisfied. The transformations f_x(x) are known as quadratic B-splines with "knot" k (Seber and Wild, 1989). It is possible for the trend to change at more than one knot, so we would have to include a quadratic B-spline for each of these points.

Employing quadratic B-splines provides advantages over polynomial transformations of the covariates applied to the whole range, because the B-splines represent functional dependence locally, whereas polynomials represent global dependence. For instance, adding a few points to a dataset in a polynomial regression can change the fitted function at values of X which are very distant from the values of the added points. Whether quadratic splines are a good approximation is an empirical question, and in our case they performed very well.

2.3 Stochastic Actor-Oriented Models for Network Dynamics

In the final stage of this study we employ Stochastic Actor-Oriented Models (SAOM) to integrate the transformations of distance found by the GAM and GLM in a more suitable framework of analysis for network evolution. A thorough, non-mathematical explanation of the SAOM can be found in Snijders et al. (2010), while a more technical treatment is provided in Snijders (2001) and Snijders (2005).

The SAOM require longitudinal network data, that is, two or more repeated observations of a network on the same set of n actors. In its most standard expression the models assume that actors are linked through binary, directed ties. The network is supposed to evolve in continuous time, but it is only observed at discrete time points. At time t we can represent the network by an n × n adjacency matrix X(t) such that X_ij(t) = 1 if at time t actor i has a tie to actor j, and X_ij(t) = 0 otherwise, for i ≠ j = 1, …, n In addition to the existing ties at each observation, most datasets include information about the actors that can affect the nature and patterns of network evolution. These covariates can be actor-bound (e.g., gender) or dyadic (e.g., spatial distance).

The SAOM are constructed on the following assumptions: network ties are states, occasionally changing in dependence on the existence of other ties. On these grounds, the network is assumed to be a continuous time Markov chain, which entails that the future of the network is probabilistically determined by its present state (without information from the past being necessary). Since the “state” of the Markov chain is the entire network, tie changes are represented as the result of a process where relationships are probabilistically formed and terminated due to the existence of other relationships. The SAOM also assume that actors control their outgoing ties, and that they have full information of the network and of the other actors. At any single moment (unobserved between the observation moments), one randomly selected actor gets the opportunity to change its personal network, and only one tie variable can change at a time. This happens for numerous moments between the observation times, together resulting in many differences between consecutive network observations.

Given that an actor i is selected to make a change, the probability distribution of the tie variable to be changed is determined by the so-called objective function f_i(β, x), which can be interpreted as a measure of the satisfaction of actor i with a given network configuration x, where

$$f_i(\beta ,x)=\sum _k{\beta }_k{s}_{ki}(x)$$ (6)

is a linear combination of network statistics s_ki(X), as perceived by i. The parameter vector β represents the weight each of these statistics has on the actor's tie changes and needs to be estimated from the data.

The network that results if actor i changes the tie variable X_ij can be denoted by x(i∼f). Formally, x(i ∼ i) denotes x itself. The probability that the new network state is x(i∼f), given that actor i is selected to make a change and the current network state is x, is assumed to be given by

$$p(x(i~j),x)=\frac{\text{exp}\left\{f_i\right(\beta ,x(i~j)\left)\right\}}{\sum _{h=1}^n\text{exp}\left\{f_i\right(\beta ,x(i~h)\left)\right\}}$$ (7)

An interpretation of the parameters β can be obtained from the following, If actor i has the opportunity to change his/her personal network, and x^[1] and x^[2] are two possible choices, then the ratio of the probability of choosing x^[1] over x^[2] is

$$\frac{p(x^{[1]},x_j\beta )}{p(x^{[2]},x_j\beta )}=\text{exp}\left\{f_i\right(\beta ,x^{[1]})-f_i(\beta ,x^{[2]}\left)\right\}$$ (8)

A catalogue of possible statistics and more complex model specifications can be found in Snijders (2005) and Snijders et al. (2010). The parameters of the SAOM were estimated using the RSiena package (Ripley and Snijders, 2010).

3. DESCRIPTION OF THE DATA

The data employed is part of the '10 to 18 Study' carried out by the University of Örebro in Sweden. The entire dataset is a panel of five waves collected annually between 2001 and 2005 in a small, geographically isolated Swedish town. At each wave all 4th to 12th-grade students (aged 10 to 18 years) were asked to identify three very important peers as well as up to ten friends with whom they spent time inside of school and up to ten peers with whom they spent time outside of school, with the possibility of nominating the same peers in more than one category. The respondents could identify these peers as friends, siblings, romantic partners or other. A detailed description of the project, as well as details on the data collection can be found in Burk et al. (2007) and Burk et al. (2008).

For this study we only consider friendship nominations, because the effect of distance could be different for friends than for siblings or romantic partners. We say that participant i considers j a friend, if i nominates j as a very important peer or as someone with whom he/she spends time with, in or out of school.

The dataset selected is composed by three network observations (2002 to 2004) of the 339 students that in 2002 were starting secondary school (seventh grade) in one of the three secondary schools in town. These 339 students are practically all the individuals in the age cohort that lived in this town between 2002 and 2004. Given the geographical isolation of the town, the majority of peers that were nominated were also likely to have participated in the study. Only friendship nominations within the cohort are considered, and self-nominations are invalid. The first and last waves (collected in 2001 and 2005) were dropped to avoid complications with passing from primary to secondary school, or from secondary to post-secondary school. For simplicity, the 2002 wave is referred to as the first wave, and the other two are named accordingly.

For each participant there are a few basic characteristics that we employ: gender, age, ethnicity, household location, and school and class membership at each wave. The household locations were obtained from geo-coding addresses, and the information used is the matrix of between-household linear distances measured in kilometres. The complete catalogue of variables is broader; it comprises other socio-demographic measurements and behavioural and psychological items that are beyond the scope of the current study. The variables considered here constitute basic measurements of proximity and similarity that account for meeting and interacting opportunities and for the most elementary notions of homophily.

3.1 Descriptive Statistics

Amongst the 339 adolescents on the selected cohort, there were three whose household locations were more than 300 km away from the town's centre, so we removed them from the analysis because they seemed to be incorrectly captured or measured. Of the remaining 336 participants, nine were absent in the first wave, one in the second and three in the last wave. The chosen group consisted of 187 males (56%) and 149 females (44%). When the first wave was collected, 75% of the adolescents were 13 years old and 24% were 14 years old; the remaining 1% was either 12 or 15 years old. The three secondary schools were attended by 74 (22%), 89 (26.5%), and 173 (51%) students respectively, and these numbers remained roughly constant through the whole period of interest. Further, 93.5% declared to be Swedish.

Table 1 displays, for each wave, a few basic structural network statistics. The mean number of friendship nominations per adolescent (average outdegree) increases from one wave to the next, indicating that the participants became more active through time. The reciprocity indices (proportion of friendships that are reciprocated per total number of friendships) of more than 60% are in line with other sociometric adolescent friendship data (e.g., Gest et al., 2007). Regarding friendship dynamics, between the first two network observations 735 friendships were created, 528 were dissolved, and 709 were maintained, while the figures for the period between the last two waves are 616, 573 and 880, respectively. This suggests that friendships became more stable as the adolescents grew older.

Table 1.

Structural network statistics at each wave

	Wave 1	Wave 2	Wave 3
Existing friendships	1,246	1,491	1,513
Average outdegree	3.71	4.44	4.50
Density	0.01	0.013	0.013
Reciprocated friendships	756	976	962
Reciprocity index	0.61	0.66	0.64

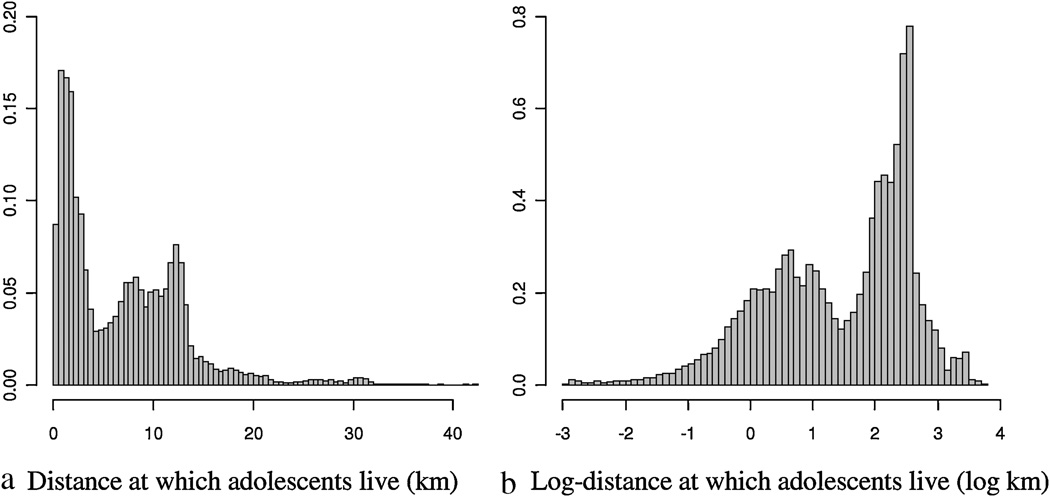
Because distance is a symmetric measurement, the distribution of the distance between households is taken between non-directed pairs of adolescents. For n = 336 individuals there are n(n-1) = 112,560 directed pairs that can be formed. Thus, the distribution of distances is considered over the $\frac{112,560}{2}=56,280$ non-directed pairs of adolescents. The distances between households ranged between 0 and 42.20 km, with mean and median values of 6.93 and 5.93 km, and standard deviation of 6.08 km. In the whole dataset there were 15 pairs living at zero distance, and 220 pairs living at a distance smaller than 50 meters. Given the low number of pairs in this situation, and to obtain more stable results, these distances were transformed to 60 meters (the smallest distance larger than 50 meters). Figure 1 displays histograms for the distribution of distance and its logarithm. The distributions are roughly bimodal: most adolescents lived at a distance between 0 and 4.5 km or at a distance between 7.5 and 14 km, which corresponds to the presence of two main population clusters in the town. A few pairs (3% of the total) lived at distances larger than 20km, somewhat large for the town's size, implying that there were a few participants whose registered address was in either a nearby town or rural area.

Figure 1.

(a) Distribution of the distance (km) at which pairs of adolescents live (b) Distribution of the logarithm of the distance at which pairs of adolescents live (log km)

To gain an initial sense on how distance affects friendships, Table 2 displays the proportion of pairs of adolescents that are friends amongst all pairs living at a certain distance range. At each wave, roughly 8% of all the pairs living between 0 and 200 meters were friends. This proportion decreases to approximately 3.5% for pairs living between 200 and 500, and to 1% for pairs living between 4 and 7 km, barely reaching 0.1% for adolescents living more than 20 km away.

Table 2.

Proportion of pairs of adolescents that are friends at each wave, amongst all pairs that live at a certain distance range

Distance range (km)	Pairs of adolescents living in the range	Proportion of adolescents that are friends
		Wave 1	Wave 2	Wave 3
0.0 – 0.2	1,190	7.6%	8.2%	7.7%
0.2 – 0.5	3,720	3.5%	3.7%	3.3%
0.5 – 1.0	9,628	2.3%	2.6%	2.5%
1.0 – 2.0	18,346	1.5%	1.6%	1.6%
2.0 – 4.0	16,774	1.2%	1.4%	1.4%
4.0 – 7.0	11,522	1.0%	1.2%	1.3%
7.0 – 12.0	29,896	0.7%	0.8%	0.9%
12.0 – 20.0	17,858	0.3%	0.5%	0.6%
≥20.0	3,626	0.1%	0.1%	0.1%

4. MODEL SPECIFICATION

4.1 GAM and GLM

To gain a comprehensive view of the effect of distance on friendship, we analyse both the static (existence) and the dynamic (creation and maintenance) perspectives. The analyses for existence of friendships are cross-sectional studies on each wave. The cases are all pairs of adolescents (i, j) for i, j = 1, …, 336, i ≠ j, where the response is a binary variable taking the value of 1 if i nominated j as a friend in a given wave, and 0 otherwise. For creation of friendships, the observations are all pairs (i, f) that are not friends in wave w = 1, 2 and the response is 1 if i nominated j as a friend in wave w + 1, and 0 otherwise. For friendship maintenance the observations are all pairs that are friends in a certain wave, and the response is 1 if they remained to be friends in the consecutive wave, and 0 if they did not.

The main covariate is the logarithm of the distance between the adolescents’ households, because distance on its raw scale exhibited extreme negative skewness (Figure 1a) and because the GAM and GLM proceeded better with log-distance. We begin by fitting models for log-distance only. Since going to the same school is the main social context that also provides meeting opportunities, like living nearby, as a next step we fit models that include a linear term for school membership, and then we test for an interaction between distance and school membership. The results of the logistic GAM are presented in plots with 95% confidence bands (dashed lines) for the estimated smooth term of the distance effect. These confidence bands are based on the Bayesian posterior covariance matrix of the smooth and parametric terms included in the model (Wood, 2006b). Their calculation assumes that the friendships between different pairs of adolescents are independent, so they are a crude estimate of uncertainty. This is acceptable in our case because the GAM have a descriptive, rather than an inferential function. For comparison purposes, all plots are in the same scale.

The results of the standard logistic regressions that approximate the GAM are shown in tables. The logarithm of distance is always included and, when this is required to approximate the functional form, also the squared log-distance and the relevant quadratic B-splines f_k defined in expression (5). In all cases one or two quadratic splines were sufficient to give a good approximation. Non-significant terms were dropped from the model, unless higher-order terms incorporating the same variable were significant. The plots of these regressions are not displayed because they are quite similar to those of the GAM, while being smoother due to dropping non-significant terms.

To adjust for the underestimation of uncertainty derived from assuming that the observations are independent, only the distance transformations that are significant at the 0.01 level or less are included. Hence, the parametric logistic regressions are somehow simplified approximations of the GAM.

For all the subsets analysed the maximum number of missing observations was 5.3%. This data was imputed when the available information from other waves allowed it, otherwise it was omitted.

4.2 SAOM

The SAOM for network evolution accounts for the interdependent nature of the observations, and thus provides better estimates of uncertainty. The analyses are performed for pairs of consecutive waves, to be consistent with the non-parametric and parametric logistic regressions, and also to avoid complications with heterogeneity of the parameters in time.

Three model specifications are employed. First we consider a basic range of structural statistics (e.g., tendency towards transitivity) and exogenous covariates (school and class membership, gender and ethnicity), but no distance effects are included. Next, we present a model that controls for reciprocity, outdegree, school membership and the distance related-effects found to be relevant by the GAM and the GLM. The final model specification combines the previous two. The details and mathematical formulae of these effects can be found in Snijders et al. (2010).

The range of possible model specifications is broader. However, the objective is not to find the best possible fit to the data but to illustrate how the information found in the logistic regressions can be incorporated into a more suitable framework of analysis for network evolution, and to assess how the distance-related effects, individual covariates, and network statistics modify each other.

5. RESULTS

In Section 5.1 we present the results for the Generalized Additive Models and logistic regressions, and in Section 5.2 we discuss the results for the Stochastic Actor-Oriented Models. Section 5.3 considers what can be concluded concerning Hypothesis H1-H5 (see Section 1)

5.1 Description of the Functional Form by Logistic Regressions

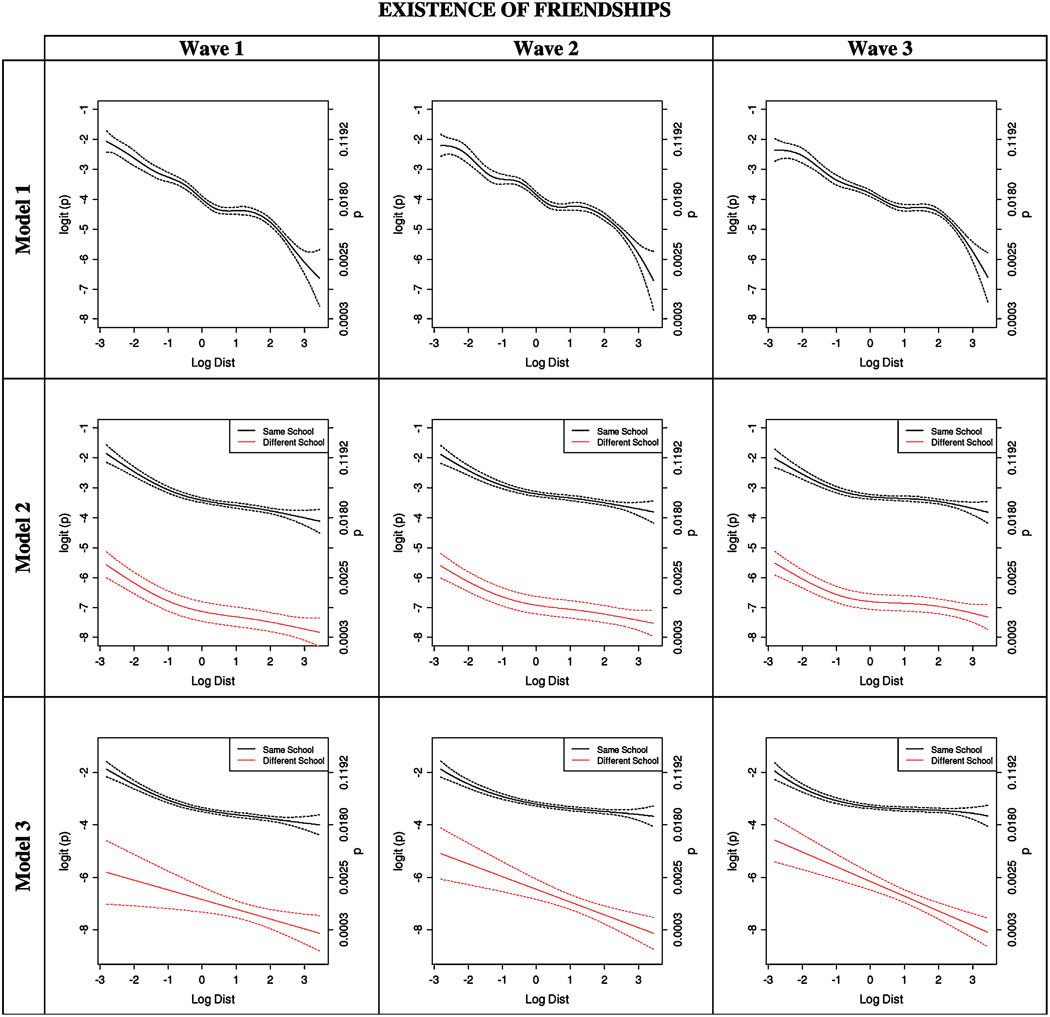
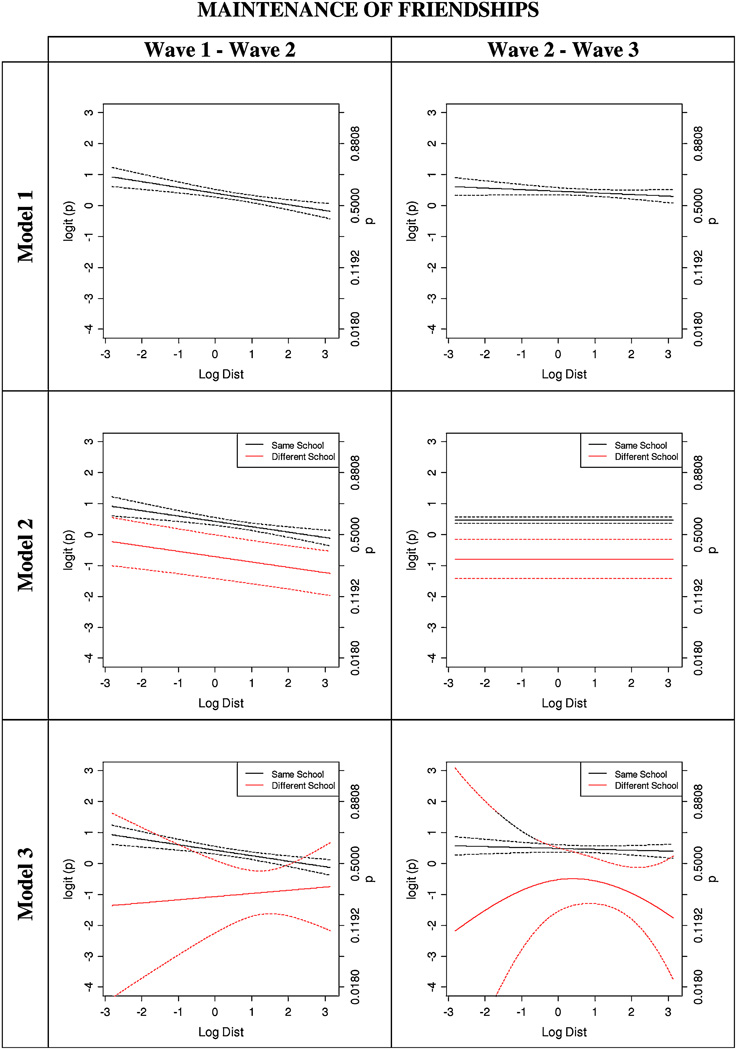
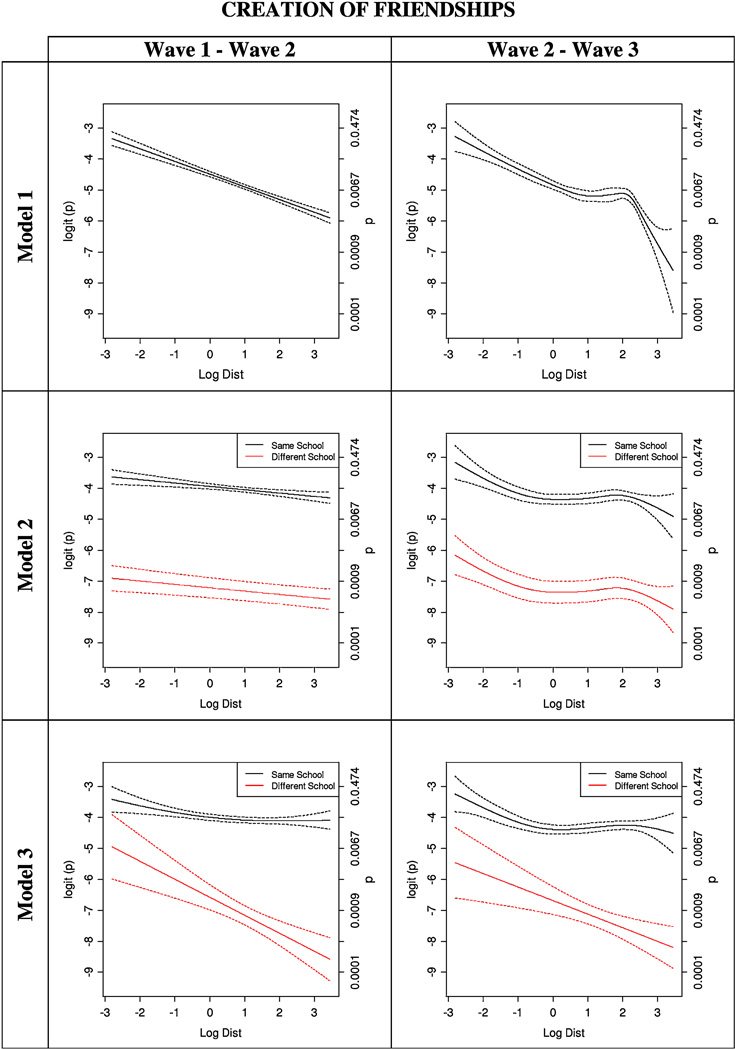
The results of the GAM are shown in Figures 2 to 4. In all plots the left vertical axis shows the logit and the right axis the probability. The results of the parametric approximations to the GAM are shown in Tables 3 to 5. We discuss distance dependence first for friendship existence, then for friendship creation, and finally for friendship maintenance.

Figure 2.

Logistic GAM for the probability of friendship existence. There were 1.2%, 1.3% and 1.4% existing friendship at waves 1, 2 and 3 respectively. In all panels the horizontal axis is the logarithm of the distance at which the adolescents live, and the left and right vertical axes are, respectively, the estimated logit of the probability and the estimated probability of friendship existence. The dashed lines represent 95% confidence bands. Model 1 includes only a smooth term on distance. Model 2 includes a parametric component for an indicator variables taking the value of 1 if the adolescent attended the same school (black lines) and −1 otherwise (red lines). Model 3 fits a smooth term on log-distance for cash level of an indicated variables Same School that takes the value of 1 if the adolescents attended the same school (black line), and −1 if they did not (red line).

Figure 4.

Logistic GAM for the probability, of friendship. Of the existing friendship at wave 1,57.3% were maintained at wave 2 while 60.6% is the prop for the period between the last two waves. In all panels the horizontal axis is the logarithm of the distance at which the adolescents live, and the left and right vertical axes are, respectively, the estimated logit of the probability and the estimated probability of friendship existence. The dashed lines represent 95% confidence bands. Model 1 includes only a smooth term on distance. Model 2 includes a parametric component for an indicator variable taking the value of 1 if the adolescents attended the same school (black lines) and −1 otherwise (red line). Model 3 fits a smooth term log-distance for cash level of an indicator variable Same School that takes the value of 1 if the adolescents attended the same school (black line), and −1 if they did not (red line).

Table 3. EXISTENCE OF FRIENDSHIPS.

Standard logistic regressions for existence of friendships at each wave. Est. means estimated coefficient and SE is estimated standard error. The terms f_k are the quadratic B-splines with knot in k in logarithmic scale.

Wave 1
	Model 1		Model 2		Model 3
	Est	SE	Est	SE	Est	SE
Intercept	−4.02	0.05***	−7.15	0.17***	−6.89	0.24***
Log-Dist	−0.87	0.11***	−0.26	0.03***	−0.50	0.13***
Log-Dist 2	−0.07	0.05	0.11	0.02***	0.06	0.01***
f0.00	0.58	0.15***
f1.00	−1.03	0.19***	−0.24	0.09*
Same School			3.71	0.16***	3.49	0.24***
School * Log-Dist					0.17	0.13

Wave 2
	Model 1		Model 2		Model 3
	Est	SE	Est	SE	Est	SE
Intercept	−3.90	0.04***	−6.94	0.15***	−6.51	0.19***
Log-Dist	−0.76	0.09***	−0.21	0.03***	−0.58	0.11***
Log-Dist 2	−0.06	0.05	0.10	0.02***	0.05	0.01***
f0.00	0.49	0.13***
f1.00	−0.87	0.17***	−0.22	0.08*
Same School			3.72	0.15***	3.32	0.19***
School * Log-Dist					0.31	0.11*

Wave 3
	Model 1		Model 2		Model 3
	Est	SE	Est	SE	Est	SE
Intercept	−3.89	0.04***	−6.81	0.13***	−6.23	0.16***
Log-Dist	−0.72	0.10***	−0.16	0.03***	−0.65	0.10***
Log-Dist 2	−0.06	0.05	0.11	0.02***	0.06	0.01***
f0.00	0.49	0.13***
f1.00	−0.87	0.16***	−0.24	0.08*
Same School			3.50	0.13***	2.95	0.16***
School * Log-Dist					0.43	0.09***

The stars indicate the level of significance at which the estimated parameter is different from zero:

^*p – val < 0.01

^**p – val < 0.001

^***p – val < 0.0001

Same School is an indicator variable taking the value of 1 if the pair of adolescents attended the same school and 0 otherwise. School * Log-Dist is an interaction between the logarithm of distance and belonging to the same school.

Table 5. MAINTENANCE OF FRIENDSHIPS.

Standard logistic regressions for maintenance of friendships between consecutive network observations. Est. means estimated coefficient and SE is estimated standard error..

Wave 1 - Wave 2
	Model 1		Model 2		Model 3
	Est	SE	Est	SE	Est	SE
Intercept	0.40	0.06***	−0.71	0.36	−1.07	0.60
Log-Dist	−0.19	0.04***	−0.17	0.04***	0.10	0.36
Same School			1.14	0.36*	1.50	0.60
School * Log-Dist					−0.28	0.36

Wave 2 - Wave 3
	Model 1		Model 2		Model 3
	Est	SE	Est	SE	Est	SE
Intercept	0.46	0.06***	−0.75	0.33	−0.61	0.49
Log-Dist	−0.05	0.04	−0.03	0.04	−0.15	0.31
Same School			1.24	0.33***	1.10	0.49
School * Log-Dist					0.12	0.31

The stars indicate the level of significance at which the estimated parameter is different from zero:

^*p – val < 0.01

^**p – val < 0.001

^***p – val < 0.0001

Same School is an indicator variable taking the value of 1 if the pair of adolescents attended the same school and 0 otherwise. School * Log-Dist is an interaction between the logarithm of distance and belonging to the same school.

Friendship Existence

Amongst all pairs of adolescents, roughly 1.3% pairs were friends at each wave. Dividing the group by school membership, around 3.5% of the pairs of adolescents that attended the same school were friends, while this proportion is 0.1% for pairs in different schools.

Figure 2 shows the estimates of the functional dependency of the log-odds of existence of friendship on log-distance, as obtained from the GAM. Model 1 includes distance only. Model 2 includes distance and an additive effect of attending the same school. Model 3 estimates separate GAM for the two subgroups of pairs attending the same school, or different schools. Approximations by quadratic splines are in Table 3. In all cases, the general tendency is for the likelihood of friendship existence to decrease with log-distance in a smooth combination of linear and quadratic falloffs. The functions are not linear, but linear approximations would not lead to a gross misrepresentation. When only distance is considered (Model 1) several points of inflection are visible, but the results from the parametric regressions in Table 3 indicate that only 0.0 (1 km) and 1.0 (2.7 km) are significant (at least at the 0.01 level). However, by controlling for whether the pairs attend the same school (Models 2 and 3), these changes in curvature gradually loose relevance. Model 2 illustrates that the logit of the probability of friendship existence is consistently much smaller for pairs in different schools. Model 3 shows that, if no assumption is made about the two curves being parallel, the decay can be well approximated by a quadratic curve for pairs of adolescents in the same school, and by a linear curve, which also is steeper than the former, for pairs in different schools. As a methodological remark, we can see that the very small proportion of friendships in different schools leads to wider confidence bands, more so in Model 3 than in Model 2, where the assumption of an additive effect is made.

Comparing the model specifications (Table 3), we see that all the included effects have approximately the same strength across waves.

Friendship Creation

Of all pairs of adolescents that were not friends at a given wave, about 0.7% pairs had become friends in the next wave. This was 1.5% for pairs in the same school and merely 0.06% for pairs in different schools.

Figure 3 shows the GAM estimates of how the log-odds of friendship creation depends on log-distance. Model 1 includes distance only; Model 2 also considers an additive effect of attending the same school, and Model 3 estimates separately for the subgroup of pairs attending the same school, and the group of pairs going to different schools. Approximations by quadratic splines are in Table 4. Almost everywhere the log-odds of friendship creation decreases with log-distance; the small parts where the log-odds seems to increase somewhat are not significant, given the width of the confidence bands. The trend is linear for the period between the first two waves, and quadratic with a point of inflection in 1.5 (4.5 km) for the period between the last two waves. As illustrated in Models 2 and 3 in Table 4, this point of inflection, represented by f _1.50, is no longer significant when we control for school membership. Model 2 shows that the likelihood of friendship creation is systematically smaller for pairs of adolescents in different schools. When we allow a difference in shape of the distance effect by school membership as in Model 3, the distance dependence for pairs in the same school is approximately quadratic, mildly decreasing at small distances but levelling off for distances larger than 1km; while for pairs in different schools it is approximately linear, and stronger than for pairs in the same school. This pattern is seen at both periods.

Figure 3.

Logistic GAM for the probability of friendship creation. There were 0.7% created friendship between the first two waves, and 0.6% between the last two waves. In all panels the horizontal axis is the logarithm of the distance at which the adolescents live, and the left and right vertical axes are, respectively, the estimated logit of the probability and the estimated probability of friendship existence. The dashed lines represent 95% confidence bands. Model 1 includes only a smooth term on distance. Model 2 includes a parametric component for a indicator variable taking the value of 1 if the adolescents attended the same school (black lines) and −1 otherwise (red lines), Model 3 fits a smooth term on log-distance for each level of an indicator variable Same School that takes the value of 1 if the adolescent attended the same school (black line), and −1 if they did not (red line).

Table 4. CREATION OF FRIENDSHIPS.

Standard logistic regressions for creation of friendships between consecutive network observations. Est. means estimated coefficient and SE is estimated standard error. The terms f_k are the quadratic B-splines with knot in k in logarithmic scale.

Wave 1 - Wave 2
	Model 1		Model 2		Model 3
	Est	SE	Est	SE	Est	SE
Intercept	−4.49	0.05***	−7.21	0.17***	−6.58	0.21***
Log-Dist	−0.41	0.03***	−0.11	0.03***	−0.58	0.13***
Log-Dist 2
f1.50
Same School			3.28	0.16***	2.62	0.21***
School * Log-Dist					0.49	0.14***

Wave 2 - Wave 3
	Model 1		Model 2		Model 3
	Est	SE	Est	SE	Est	SE
Intercept	−4.88	0.06***	−7.35	0.17***	−6.73	0.22***
Log-Dist	−0.30	0.04***	−0.09	0.04	−0.55	0.13***
Log-Dist 2	0.13	0.02***	0.13	0.03***	0.06	0.02*
f1.50	−0.85	0.18***	−0.6	0.2***
Same School			2.98	0.17***	2.42	0.23***
School * Log-Dist					0.42	0.13**

The stars indicate the level of significance at which the estimated parameter is different from zero:

^*p – val < 0.01

^**p – val < 0.001

^***p – vol < 0.0001

Same School is an indicator variable taking the value of 1 if the pair of adolescents attended the same school and 0 otherwise. School * Log-Dist is an interaction between the logarithm of distance and belonging to the same school.

Friendship Maintenance

Amongst the pairs of adolescents that were friends at a given wave, approximately 59% remained friends in the next wave. These proportions were 61% for adolescents in the same school and 30% for adolescents in different schools.

Figure 4 presents the GAM estimates of how the log-odds of friendship maintenance depends on log-distance. Here also, Model 1 includes distance only, Model 2 adds an additive effect of attending the same school, and Model 3 presents estimates for the pairs attending the same school and separately for the pairs going to different schools. Approximations by quadratic splines are in Table 5. Figure 4 shows that the log-odds of friendship maintenance decreases linearly with log-distance in all model specifications for the period between the first two waves, and that there is no dependence on distance for the second period. Belonging to different schools decreases significantly the probability of friendship maintenance (Model 2). Note that when an interaction between school membership and log-distance is included (Model 3), all terms become insignificant. This is because there are very few cases for friendship maintenance in different schools and the estimations are unreliable for this group (Figure 4, bottom row). Hence Model 2 here is more meaningful than Model 3.

5.2 Assessing the Effect of Geographic Proximity on Friendship Dynamics

Table 6 presents the results of the SAOM for analysing the dependence of friendship dynamics on the distance at which the adolescents live, for pairs of consecutive waves. The model specifications were described in Section 4.2.

Table 6.

SAOM for the effect of distance between households on friendship dynamics, for pairs of consecutive network observations. Est. means estimated coefficient and SE is its standard error.

	Wave 1 to Wave 2						Wave 2 to Wave 3
	Model 1		Model 2		Model 3		Model 1		Model 2		Model 3
	Est	SE	Est	SE	Est	SE	Est	SE	Est	SE	Est	SE
Rate	21.83	1.77	10.15	0.51	21.44	1.75	17.40	1.22	8.51	0.41	17.00	1.20
Outdegree	−1.99	0.27***	−3.49	0.08***	−2.42	0.25***	−2.22	0.19***	−3.38	0.07***	−2.57	0.27***
Reciprocity	2.42	0.10***	2.92	0.07***	2.43	0.10***	2.26	0.11***	2.66	0.07***	2.28	0.10***
Transitive Triplets	0.70	0.03***			0.68	0.03***	0.62	0.03***			0.61	0.03***
3-Cycles	−0.57	0.06***			−0.57	0.06***	−0.51	0.06***			−0.52	0.06***
Outdegree - popularity √	−0.74	0.10***			−0.66	0.09***	−0.70	0.08***			−0.62	0.09***
Outdegree - activity √	−0.32	0.06***			−0.25	0.06***	−0.15	0.04***			−0.11	0.05*
Same Sex	0.26	0.04***			0.27	0.04***	0.33	0.03***			0.34	0.04***
Same Ethnicity	0.57	0.11***			0.59	0.11***	0.22	0.09*			0.22	0.12
Same Class	0.34	0.05***			0.37	0.05***	0.57	0.06***			0.59	0.05***
Same School	0.73	0.06***	0.94	0.06***	0.75	0.07***	0.62	0.05***	0.86	0.05***	0.65	0.06***
LogDist			−0.23	0.05***	−0.29	0.05***			−0.25	0.05***	−0.29	0.05***
LogDist2			0.00	0.01	0.00	0.01			0.01	0.01	0.02	0.01
LogDist × Same School			0.15	0.04***	0.19	0.04***			0.18	0.04***	0.20	0.05***

The stars indicate the level of significance at which the estimated parameter is different from zero.

^*p – val < 0.05

^**p – val < 0.01

^***p–val < 0.001

Based on the results obtained by the logistic regressions (Section 5.1), the distance effects included are the linear and square log-distance, and the interaction between log-distance and school membership. In preliminary analyses we also included quadratic B-splines with knots in 0, 1 and 1.5 (corresponding to 1, 2.7 and 4.5 km), but none of them were found to be significant. This is consistent with the results from the parametric logistic regressions, in which the significance of the inflection points disappeared when control for school membership was introduced. As well, we tested whether the effect of distance on maintaining friendships is different than for creating them (known as the endowment effect, see Snijders et al., 2010), but this was not significant.

The rate parameter represents the average number of opportunities that actors get to change their personal networks between consecutive waves². Considering network structure and individual covariates (Models 1 and 3), the adolescents had roughly 21 opportunities to change their personal networks between the first two waves, and 17 between the last two. When only distance-related effects are taken into account (Model 2), the rates are smaller (i.e. 10 and 8.5), which happens because between consecutive waves there are fewer changes in terms of the few, distance-related effects than in terms of a wider range of statistics. The difference between periods suggests the friendships are slightly more stable when the adolescents grow older.

All model specifications confirm a few known aspects of the nature of adolescent friendships. There is a strong tendency towards reciprocity (the reciprocity parameter is positive and significant), and evidence for transitive closure and local hierarchy (because the transitive triplets parameter is positive, while the 3-cycle parameter is negative). As well, the adolescents favour relationships in their same class and school, and with others of the same gender. The preference for friendships of the same ethnicity is important in the first period but irrelevant in the second. The negative outdegree-popularity effect shows that adolescents that nominate many friends are less likely to be chosen as friends, while the negative outdegree-activity effect reflects that adolescents with higher outdegrees at a given moment are less likely to create new ties subsequently.

The reading of the log-distance effects can be done from either the second or third model specifications, because the estimated parameters are rather similar. In contrast to the GAM and the GLM results, the quadratic effect of distance is not significant. To interpret the numerical values of the parameters, it should be considered that attending the same school is represented by a centred dummy variable. Due to the centring, its values are 0.6 for attending the same school and −0.4 for attending different schools. Ignoring the non-significant and small quadratic term, the resulting effect of log-distance for those attending the same school is −0.18, and for those attending different schools −0.37. The numbers are practically the same for both periods. These negative coefficients imply that the adolescents favour relationships with others that live close to them, while the magnitude of this effect is about twice as small if the adolescents go to the same school.

To further interpret the numerical value of the estimate obtained for the effect of distance, we can calculate the probability ratio of an adolescent i choosing to create a friendship with one adolescent j that lives at a log-distance d from i, over another adolescent h that lives at d + ln(2), if j and h are equal with respect to i in all the other characteristics. Succinctly formulated, this is the effect of doubling the distance between the households on friendship creation. Using expression (8) we obtain that, at both periods, the probability of choosing to create a friendship with j is 1.13 times larger than with h if i, j and h go to the same school, and 1.30 times larger if neither j nor h attend the same school as i. Within the town, distances can be much more than a factor of 2 apart. Hence, the effect of geographic proximity between households is strong and relevant when the adolescents do not go to the same school, but rather small when they do attend the same school.

A comparison between Model 1 and Model 3 shows that most of the estimated parameters of the structural characteristics and covariates are not importantly modified by the inclusion of the distance-related effects. Thus, the proximity between households accounts for a different aspect of the friendship dynamics, which is most remarkable for the triadic effects, entailing that geographic distance has a different dimension than social distance (at least for social configurations of three actors).

Analogously, a parallel assessment of the second and third models shows that the estimated reciprocity and same school effects are attenuated when including other structural characteristics and notions of similarity between individuals. The parameter estimates for the log-distance effects are nearly the same in Models 2 and 3 at both periods, confirming that the distance between-households accounts for an aspect of friendship dynamics that cannot be explained by other basic individual characteristics and measures of network structure.

5.3 The results in the light of initial expectations

At the end of Section 1 five hypotheses, H1-H5, were presented. We discuss these in turn.

We found clear evidence for a negative effect of distance on the existence of friendship ties (Figure 2) and on the creation of friendship ties (Figure 3); for maintenance of friendship (Figure 4), there was an effect only in the first period of the study (mainly 13 going to 14 years) but not in the second period (14 going to 15). In the dynamic model (SAOM) for friendship too (Table 6), there was an evident distance effect. This supports hypothesis H1, with the exception of the case of friendship maintenance for the age range of middle adolescence (14 going to 15 years).

Going to the same school likewise had a strong effect on friendship, and this interacted with distance as expected according to hypothesis H2: for those going to different schools, living nearby is more important than for those going to the same school. Figure 2, Model 3, shows this for friendship existence, with a difference in slopes mainly for distances larger than 1 km. Figure 3, Model 3, shows this for creation of new friendships. For maintenance of friendships the effect is not significant, which may be due to the low number of friendships in different schools. The dynamic model also supported this interaction hypothesis (Table 6, Models 2 and 3).

For those attending the same school, distances have an effect mainly below 350 m (log-distance less than −1; Figures 2 and 3, Model 3). For larger distances the slope of the logit becomes negligible, and practically null after 1 km (log-distances larger than 0). This plateau suggests that having an institutional setting, in which the adolescents spend a significant part of the day, provides meeting opportunities and a social focus (Feld, 1981) comparable to living nearby. In this context, it would be interesting to assess if the same phenomenon occurs for other institutional settings, such as organised activities.

The findings with respect to the expected attenuation of distance effects as adolescents get older were ambiguous. The non-linear nature of the effect of distance make it more difficult to even formulate this as an unequivocal hypothesis for a given parameter, but it can be visually assessed by comparing the results for Wave 1–2 to those for Wave 2–3. Figures 2 and 3 suggest that over this limited age range there is little change in the effect of distance on existence or on creation of friendship ties. Table 5 (Models 1–2) shows evidence that distance is less important for maintenance of friendships in the 14–15 years age range than in the 13– 14 age range. The SAOM results gave no support for decreasing importance of distance when adolescents get older. Together, this is a very partial confirmation of hypothesis H3.

The expectation that taking into account network dependencies, such as transitive closure, would decrease the estimated effects of distance (H4), was not supported at all, as can be seen from Table 6 when comparing Models 2 and 3. The correlations between the parameter estimates for the distance effect and the parameter effects for structural network effects in the SAOM all were less in absolute value than .2. The distance effect was correlated with the effect of going to the same school, and taking distance into account reduced the effect of attending the same school by about one quarter of its initial value.

As expected, the effect of distance on friendship creation was clearly stronger than on friendship maintenance, as can be seen from comparing Figures 3 and 4. Unfortunately, we were not able to obtain converging parameter estimates when trying to test this in the SAOM.

6. DISCUSSION

The objective of this paper was to give an accurate description of the functional form of the distance dependence of friendship existence, creation, and maintenance. In addition, we aimed at proposing a methodology that can be employed when studying the distance dependence of network dynamics.

We analysed a three-wave network of 336 adolescents living in a small Swedish town. First, we used Generalized Additive Models (GAM; Hastie and Tibshirani, 1986) to assess the relevant features of the association between distance and friendship, without making rigid assumptions about its parametric form. Next, we constructed parametric approximations of these results using standard logistic regressions. A first model only considered the effect of log-distance between households on the log-odds of friendship. Then we assessed how the strength and shape of this effect were modified by school membership. Finally, we employed the logistic regression results in estimating stochastic actor-oriented models for network evolution (SAOM; Snijders, 2001), to compare how distance affects the dynamic of friendship when basic individual covariates and network structural characteristics are considered. Five hypotheses were formulated and tested.

A general descriptive result is that, as expected, there was a clear effect of distance on the existence and creation of friendship, and this could be represented very well by modelling the log-odds of friendship existence, and of friendship creation, as a smooth function of the logarithm of distance; a linear function of log-distance was in all cases at least a quite reasonable approximation, and in some cases the best representation. When in a logistic regression the estimated probabilities are small (such as for creation and existence of friendships), the logit is well approximated by the logarithm. If for these cases the log-odds of friendship depends linearly on log-distance, we obtain a power-law dependence of probabilities on distance, because

$$\text{logit}(p)={\beta }_{\downarrow }0+{\beta }_{\downarrow }1\text{log}(\text{dist})\Rightarrow p\approx {\alpha }_{\downarrow }0{\text{dist}}^{\uparrow }({\beta }_{\downarrow }1)$$ (9)

where α₀. = exp(β₀). Hence, the probability of friendship is proportional to dist^β1. We obtained estimated values of β₁ roughly in the range between −0.7 and −0.2. The proportionality to inverse distance (β₁ = −1) or inverse distance squared (β₁ = −2), proposed by some authors (e.g., Latané et al, 1995; Butts, 2002) thus is not at all supported by our results. We think that, when probability of friendship is approximately proportional to a power of distance, the precise value of this power will depend on various aspects of the context, including the range of distances under consideration, in our case up to 20 km; at larger distances different processes will play a role.

The results from the GAM and logistic regression analysis are descriptive of distance dependence of friendship and were generally supportive of our hypotheses (Section 5.3): friendships get less probable as distances increase; the importance of living nearby decreases when there are other social foci such as in our case the joint attendance of a school; the importance of distance may get weaker as adolescents get older, but in our restricted age range (13–15 years mainly) this was supported only weakly; and distance is more important for creating than for maintaining friendships. These results, although obtained here for one specific case of a medium-sized town in Sweden, are qualitatively in line with general considerations, and we think that they will retain their validity more widely for the probability of real friendships among adolescents in geographically bounded regions.

The smooth dependence of the log-odds of friendship creation on log-distance led us to using logarithmically transformed distance in a more encompassing network model (SAOM) of friendship dynamics, also representing network dependencies. The irregularities in the dependence of friendship on log-distance, presumably connected to the spatial layout of the town, already were smoothed out when controlling for attending the same school (as shown by the differences between Models 1 and 2 in Figures 2–4) and were further reduced in the SAOM, where only a linear effect of log-distance was significant. Thus, the non-parametric GAM analysis was a useful first step to suggest a transformation of distance in the parametric SAOM approach. In our case, the use of distance in the SAOM led to different estimates for effects of other foci such as school, but not to important differences in parameter estimates for triadic or degree-related structural effects.

It is debatable that the distance between households “as the crow flies” is the best way to account for real geographic proximity and accessibility. These aspects will usually depend on the availability of transportation and communication technologies, the population density, level of urbanisation, and the town's topology. In this sense, we cannot expect our findings to extend to cities or towns with very different characteristics to the one studied. Nevertheless, by using the shortest spatial distance between households we still found important and well-interpretable results. This suggests that indeed the geographic proximity between social actors is relevant for friendship networks that are relatively constrained in space, although more detailed measurements of the constraints and possibilities offered by distance may be useful to capture further important features of the effects of space and distance on social relationships.