ADDRESSING CONFOUNDING WHEN ESTIMATING THE EFFECTS OF LATENT CLASSES ON A DISTAL OUTCOME

Abstract

Confounding is widely recognized in settings where all variables are fully observed, yet recognition of and statistical methods to address confounding in the context of latent class regression are slowly emerging. In this study we focus on confounding when regressing a distal outcome on latent class; extending standard confounding methods is not straightforward when the treatment of interest is a latent variable. We describe a recent 1-step method, as well as two 3-step methods (modal and pseudoclass assignment) that incorporate propensity score weighting. Using simulated data, we compare the performance of these three adjusted methods to an unadjusted 1-step and unadjusted 3-step method. We also present an applied example regarding adolescent substance use treatment that examines the effect of treatment service class on subsequent substance use problems. Our simulations indicated that the adjusted 1-step method and both adjusted 3-step methods significantly reduced bias arising from confounding relative to the unadjusted 1-step and 3-step approaches. However, the adjusted 1-step method performed better than the adjusted 3-step methods with regard to bias and 95% CI coverage, particularly when class separation was poor. Our applied example also highlighted the importance of addressing confounding – both unadjusted methods indicated significant differences across treatment classes with respect to the outcome, yet these class differences were not significant when using any of the three adjusted methods. Potential confounding should be carefully considered when conducting latent class regression with a distal outcome; failure to do so may results in significantly biased effect estimates or incorrect inferences.

1. Introduction

Latent variable modeling is an increasingly popular statistical method in public health, health services, and social science research since many constructs of interest in these fields are not directly observable. For example, mental health conditions, such as depression, are not directly observable but rather measured through a diagnostic checklist. Standard analytic approaches would treat depression status, as measured by these diagnostic items, the same as any fully observed variable, such as gender or clinic site. On the other hand, latent variable methods appropriately account for the measurement error inherent in using a set of observed items to represent an underlying latent construct (Collins and Lanza 2010; Hagenaars and McCutcheon 2002; Lazarsfeld and Henry 1968), resulting in more appropriate statistical inferences.

One common type of latent variable modeling is latent variable regression, which models the association between a latent variable and auxiliary variables of interest (either predictors or distal outcomes). When causal inference is the objective, a common estimand is the Average Treatment Effect (ATE). Under a potential outcomes framework, the ATE is the average difference (across the population) of the outcome had an individual received the treatment condition and the outcome had he or she received the control condition (Stuart 2010). In the case of more than two treatment conditions, estimated treatment effects compare the average pairwise differences in potential outcomes for two given treatments. The validity of the estimated causal effect relies on comparable treatment groups, obtained through randomization or careful analysis of observation data. When one is interested in estimating the causal effects of a latent treatment variable on a distal outcome, one must utilize observational data, given the impossibility of randomizing a latent treatment. Estimation of causal effects using observational data requires carefully addressing potential confounding; like in settings all variables are fully observed, latent variable regression that does not account for potential confounding may conflate true treatment effects with baseline group differences.

When interested in the effect of an observed treatment on a latent outcome, traditional methods to address confounding, such as propensity scores, can be easily implemented, given the fully observed nature of the treatment (Butera et al. 2013; Lanza et al. 2013b). n this paper we focus on the converse, estimating the effect of a latent treatment on a directly observed outcome; implementing propensity score methods is less straightforward in this context since standard propensity score approaches require that each individual have an observed treatment group. One could use a classify-analyze strategy (Clogg 1995) in order to predict latent class for each individual, and then implement standard propensity score methods with regard to predicted latent class. Alternatively, one could use a recently proposed joint modeling approach that estimates the effect of an observed treatment on a distal latent outcome while adjusting for confounders (Kang and Schafer 2010). In this paper, using both a simulation study and motivating example we compare the performance of classify-analyze methods that incorporate propensity scores to a joint estimation strategy.

Our motivating example involves estimating the effect of substance use treatment services for adolescents on subsequent substance use problems. Using national evaluation data from outpatient treatment providers funded through the Substance Abuse and Mental Health Services Administration’s (SAMHSA) Center for Substance Abuse Treatment (CSAT), we identified latent classes characterized by groupings of treatment services received by youth. Given the observational nature of our data, it is important to control for baseline differences across groups when estimating the effects of treatment class on substance use outcomes. It is plausible that demographic characteristics, justice system involvement, and baseline substance use may be associated with both the types of treatment a youth receives and substance use outcomes. Failing to account for baseline differences could lead to biased effect estimates, as is the case with non-experimental studies more generally.

In this paper, we first discuss the challenges associated with addressing confounding when estimating the effects of a latent variable on a distal outcome and review current methods. We then conduct a simulation study that compares three proposed methods for addressing confounding when estimating the effects of a latent treatment, as well as two methods that do not adjust for potential confounding in order to demonstrate the potential for bias. Finally, we apply these methods to our adolescent substance treatment dataset in order to address the substantive question at hand. We highlight that the statistical inference can change markedly when confounding is not addressed.

2. Background

2.1 Latent Class Analysis

Latent class analysis (LCA) is a widely used latent variable model that assumes an underlying structure of discrete, mutually exclusive, and exhaustive latent classes. Latent class membership cannot be directly observed; instead, it is indirectly measured using a comprehensive set of indicators that span the latent construct. LCA models individuals’ latent class membership based on their observed response pattern across the indicators; each individual, by definition, belongs to exactly one latent class (Collins and Lanza 2010; Hagenaars and McCutcheon 2002; Lazarsfeld and Henry 1968).

Let C = c_k denote latent class membership in class c_k, where k = 1, 2, …, K, and let U_j denote one of the J observed latent class indicators, where j = 1, 2, …, J. The classical LCA model represents the probability of observing response pattern u as follows:

$Pr(\mathit{U}=\mathit{u})={\sum }_{k=1}^{K}Pr(C=c_k){\prod }_{j=1}^{J}Pr(U_j=u_j\mid C=c_k)$, where Pr(C = c_k) denotes the probability of belonging to class c_k and Pr(U_j = u_j | C = c_k) denotes the conditional indicator probability, namely the probability of responding to indicator U_j with value u_j, given membership in class c_k. An additional quantity of interest is the posterior class membership probability, Pr(C = c_k|U = u), namely the probability of membership in class c_k given an observed response pattern u. A fundamental assumption of classical LCA is local independence, meaning that the indicators U₁, U₂, …, U_J are assumed to be mutually independent after conditioning on latent class membership c_k. This assumption is denoted in Figure 1 by the lack of correlation arrows among the indicators U₁, U₂, …, U_J. Maximum likelihood estimation is typically used to estimate LCA parameters.

Fig. 1.

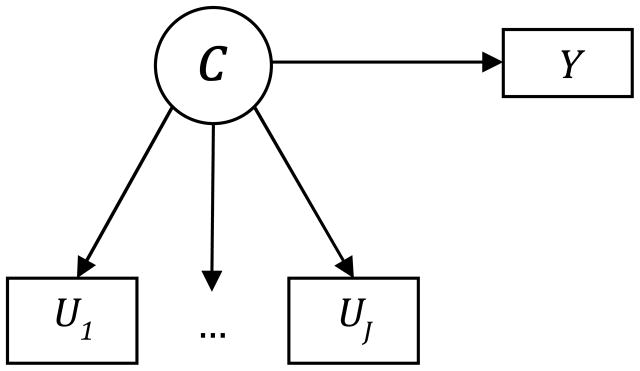
Schematic figure of latent class analysis with distal outcomes. C denotes the latent class variable, U₁, U₂, …, U_J denote the J latent class indicators, and Y denotes the distal outcome.

2.2 Latent Class Analysis with Distal Outcomes

Latent class models that regress latent classes on predictive covariates have long been used in social and behavioral research and are widely available in standard statistical software. Typically, latent class model with covariates is estimated with a binary or multinomial logistic regression model (depending on the number of classes). In contrast, methods to regress a distal outcome on latent class (see Figure 1), have been developed more recently and are the focus of this paper (Asparouhov and Muthén 2013; Kang and Schafer 2010; Lanza et al. 2013a).

In addition to the standard LCA assumption of local independence, latent class regression with a distal outcome requires an additional assumption of unconfounded measurement, which assumes that the indicators are independent of the distal outcome, given latent class (Bakk et al. 2013; Kang and Schafer 2010). This assumption is denoted by a lack of a direct effect arrow connecting the indicators U₁, U₂, …, U_J and the outcome Y in Panel B of figure 1.

LCA with distal outcomes may be conducted using either a 1-step or 3-step method. The relative merits of each approach have been previously discussed (Asparouhov and Muthén 2013, Bolck et al. 2004; Feingold et al. 2013; Vermunt 2010). In brief, 1-step methods fit a joint model that simultaneously estimates the latent class measurement model and the structural model describing the relationship between the latent classes and the auxiliary variable (i.e., the distal outcome). In general, 1-step methods yield unbiased and efficient parameter estimates, yet may not converge in some cases due to complexity of the joint likelihood and are not easily implemented for all possible analyses. Thus, 3-step methods (“classify-analyze” methods) are also commonly used, the most common of which are modal assignment and pseudoclass assignment. Three-step methods first fit a latent class model and predict latent class based on the estimated posterior class membership probabilities. Then, the association between the latent classes and the auxiliary variable is estimated through a regression model using predicted latent class membership. Under modal assignment, individuals are predicted to be in the latent class for which they have the highest posterior class membership probability (Clogg 1995; Nagin 2005). Under pseudoclass assignment, latent class membership is predicted by random draws from the multinomial distribution defined by an individual’s posterior class membership probabilities (Bandeen-Roche et al. 1997; Goodman 2007; Wang et al. 2005); pseudoclass assignment is often performed multiple times (e.g., 20), with final estimates obtained by using multiple imputation combining rules to combine results across draws (Rubin 1987).

2.3 Propensity Score Methods as a Means to Address Confounding

Propensity score methods are standard methods for addressing selection bias in an observational study (Rosenbaum and Rubin 1983; Rubin 2001; Stuart 2010). In the case of two treatment groups T = {0,1}, the propensity score is defined as the probability that an individual received the treatment (T =1), conditional on the individual’s observed covariates, and is denoted p(x_i) = Pr(T_i = 1 | X_i = x_i) where X_i represents the individual’s vector of observed covariates and i = 1, 2, …, N. The propensity score can be extended to cases in which there are more than two treatment groups; Imbens (2000) refers to this as the generalized propensity score, defined as p(t, x_i) = Pr(T_i = t | X_i = x_i), where t ∈ .

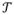In order to obtain unbiased estimates of treatment effects, one would like to compare groups that only differ with regard to treatment assignment. Randomized experiments achieve this goal through randomization, which balances groups with regard to both observed and unobserved factors; observational studies attempt to mimic randomized studies by balancing groups on a rich set of observed factors. Rosenbaum and Rubin (1983) show that groups that are matched with regard to propensity score values are also matched with regard to all of the covariates that went into estimating the propensity score, making propensity scores a parsimonious and potent analytical approach. Propensity scores can be incorporated in the final analysis through propensity score matching, subclassification, or weighting; we primarily focus on propensity score weighting in this paper – details on other methods can be found in (Stuart 2010). Propensity score weighting implements a weighted regression, in which each individual’s weight is a function of his or her propensity score. A common weighting approach is Inverse Probability of Treatment Weighting (IPTW) which weights each individual by the inverse probability of receiving the treatment he or she truly did receive; treated individuals receive a weight of 1/p(x_i) and control individuals a weight of 1/[1− p(x_i)] (Lunceford and Davidian 2004). Under IPTW, both the treatment and control groups are weighted to reflect the overall study population; thus the difference in potential outcomes between the treatment and control groups after weighting estimates the ATE. In this study, we will use an extension of IPTW for more than two treatment groups proposed by McCaffrey et al. (2013). In brief, this approach fits k binary propensity score models for k treatment groups (Class 1 vs not, Class 2 vs not, and Class k vs not); each individual’s IPTW is based on the propensity score estimated from the model corresponding to his or her observed treatment group. Each of the k treatment groups is weighted to look like the overall study population, and ATE estimates comparing pairwise differences in treatment groups can be obtained after weighting.

Propensity score methods are preferable to regression covariate adjustment for several reasons. First, propensity score methods do not necessarily rely on the parametric modeling assumptions required by regression adjustment (Ho et al. 2007). Additionally, propensity score methods avoid potential bias that arises from extrapolating beyond observed data in traditional regression models when the treatment groups have little overlap with respect to covariates (Stuart 2010). Furthermore, propensity scores are an advantageous dimension reduction technique when there are a substantial number of baseline covariates to adjust for (Rosenbaum and Rubin 1984). Finally, as advocated by Rubin, it is philosophically cleaner to separate the analytic step of controlling for confounding from the step of implementing the final structural model (Rubin 2001). Separation prevents potential bias that may arise from adjusting for covariates solely because they favorably influence the treatment effect estimates.

2.4 Confounding in Latent Variable Regression when Treatment is Latent

We now discuss extensions of LCA with distal outcomes that can account for potential confounders (see Figure 2). Complexity arises when controlling for confounding when the treatment variable of interest is a latent variable given the uncertainty regarding an individual’s true treatment status.

Fig. 2.

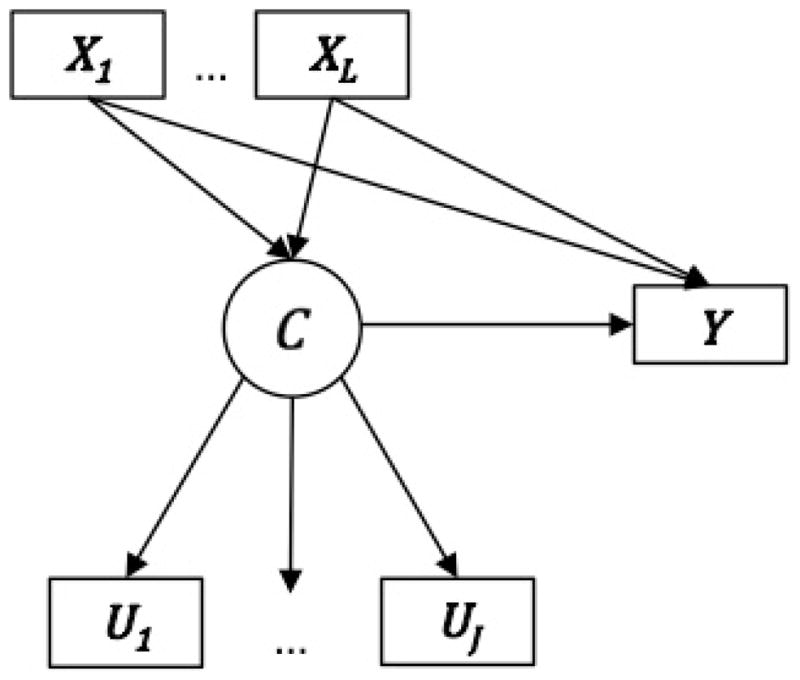
Schematic figure of latent variable regression with confounding when the treatment is a latent variable. C denotes the latent class variable, U₁, U₂, …, U_J denote the J latent class indicators, X₁, X₂, …, X_L denote the L potential confounders, and Y denotes the distal outcome.

Recently, Kang and Schafer (2010) proposed a 1-step method known as Latent Class Causal Analysis (LCCA) that jointly models the latent class indicators U, the potential confounders X, and the distal outcome Y, modeled as the vector of potential outcomes (Y_i(1), Y_i(2), …, Y_i(K)) corresponding to the K classes. Again, let (U₁, U₂, …, U_J) denote the J latent class indicators and let (X₁, X₂, …, X_L) denote the L potential confounders. One component of the LCCA model is the LCA modeling the relations between indicators and the latent classes; parameters of interest are the conditional indicator probabilities, Pr(U_j = u_j|C = c_k). LCCA models the relations between covariates X and latent class membership with a multinomial logistic regression model; the parameters of interest are denoted α, a L × K matrix of class-specific coefficients, the c_k^th column of which is denoted α_ck = (α_1,ck, α_2,ck,…, α_L,ck)^T. LCCA specifies a linear model for the potential outcome model, such that Pr(Y|X_i = x_i) ~ N(β^Tx_i, Σ), where β denotes a L × K matrix of the class-specific coefficients, the c_k^th column of which is denoted β_ck = (β_1,ck, β_2,ck,…, β_L,ck)^T, and Σ is a K × K covariance matrix for Y. Thus, the general form of the likelihood can be expressed as follows:

$$l_i(\theta )=\mathit{log}\sum _{c_k=1}^K\left\{\frac{exp({\mathit{x}}_i^T{\mathit{\alpha }}_{{\mathit{c}}_{\mathit{k}}})}{{\sum }_{c_k^{\prime }=1}^{K}exp({\mathit{x}}_{\mathit{i}}^{\mathit{T}}{\mathit{\alpha }}_{{\mathit{c}}_{\mathit{k}}^{\prime }})}\right\}\left\{\prod _{j=1}^{J}Pr(U_j=u_j\mid C=c_k)\right\}\left\{{(2\pi {\sigma }_{c_k}^2)}^{-1/2}\mathit{exp}\left\{\frac{-1}{2{\sigma }_{c_k}^2}{(y_i-{\mathit{x}}_i^T{\mathit{\beta }}_{{\mathit{c}}_{\mathit{k}}})}^2\right\}\right\}$$

where α_ck = (α_1,ck, α_2,ck,…, α_L,ck)^T, β_ck = (β_1,ck, β_2,ck,…, β_L,ck)^T, and ${\sigma }_{c_k}^2\in \mathbf{\sum }$ for c_k = 1, 2, …, K. Estimates of the ATE are then obtained from the maximum-likelihood parameter estimates via expected estimating equations (Wang et al. 2008). LCCA is implemented in the lcca package for R (Kang and Schafer 2010; Schafer and Kang 2013).

This 1-step method for latent class regression with confounders faces the same limitations previously discussed regarding 1-step methods for latent class regression. Particularly, LCCA may not converge under all conditions, given the added complexity of the joint model due to the inclusion of the confounders. Furthermore, these methods require specialized software in order to maximize the joint likelihood; although 1-step methods for latent class regression are currently available in some statistical packages (e.g., Mplus and SAS), the lcca package for R is one of the only packages that implements a 1-step method that addresses confounding. Given the implementation challenges of a 1-step approach, as well as the fact that the LCCA method uses a covariate adjustment approach, rather than propensity score methods which may be more flexible and yield better statistical performance in some settings, we investigate the incorporation of propensity score methods with two commonly used 3-step methods, namely modal and pseudoclass assignment.

Three-step methods resolve challenges of uncertainty of latent class membership by creating a predicted latent class variable, a trade-off that introduces some misclassification of individuals in order to gain tractability. A 3-step approach allows the use of standard propensity score methods, as the propensity scores are estimated with regard to the predicted latent class. The general outline for incorporating propensity scores into a 3-step approach is as follows: (1) fit a LCA model and obtain estimates of posterior class membership probabilities; (2) use modal or pseudoclass assignment to create the predicted latent class variable; (3) estimate the propensity score model by regressing predicted latent class on potential confounders; (4) calculate propensity score weights (IPTW) and assess covariate balance after weighting; (5) fit a weighted regression model for the distal outcome on predicted latent class, using propensity score weights. Under the pseudoclass approach, steps (3)–(5) are implemented multiple times; final estimates are obtained through the use of standard multiple imputation combining rules.

3. Simulation Study

3.1 Methods

First, we conducted a latent class simulation study to compare Kang and Schafer’s 1-step method to the proposed 3-step approaches, modal assignment with propensity score weighting and pseudoclass assignment with propensity score weighting. In addition to these three methods, we also considered the 1-step method without covariate adjustment and modal assignment without propensity score weighting in order to assess the impact of ignoring potential confounding.

Data were simulated in R (R Core Team, 2013) and were comprised of 15 binary latent class indicators, defining a 3-class structure, 8 independent and normally-distributed covariates, and a single continuous distal outcome. For the purpose of data generation, we created a random variable representing true treatment class T = t where t = {1,2,3}, which was generated under a multinomial distribution with equal probabilities for the three treatment groups. Based on one’s true latent class, 15 binary latent class indicators were generated as independent random Bernoulli variables. Within a given class, all indicators were generated with the same probability (conceptually, “low,” “medium,” or “high”); the more distinct these indicator probabilities were across classes, the greater the class separation. We considered the following sets of indicator probabilities for Class 1, 2, and 3: (5%, 50%, 95%), (10%, 50%, 90%), (20%, 50%, 80%), and (30%, 50%, 70%).

The covariates, representing potential confounders, were associated with both true latent class and the outcome; the strength of these associations was controlled by way of the α parameters (i.e., the coefficient vector linking the covariates and class membership) and β parameters (i.e., the coefficient vector linking the covariates and the distal outcome). We specified class-specific parameter vectors α_c = (α_1,c, α_2,c, α_3,c, α_4,c, α_5,c, α_6,c, α_7,c, α_8,c) and β_c = (β_1,c, β_2,c, β_3,c, β_4,c, β_5,c, β_6,c, β_7,c, β_8,c) where c = {1,2,3}. Each individual’s vector of covariates X = (X₁, X₂, …, X₈) was generated as the product of the vector α_c corresponding to his or her true treatment class (c = t) and a vector of independent standard normal random variables Z = (Z₁, Z₂, …, Z₈), where Z ~ N(0,1). Subsequently, the potential outcome for class c was generated as the linear combination of an individual’s covariates X and the parameters β_c, such that Y_c = β_0,c + β_1,cX₁ + β_2,cX₂ + β_3,cX₃ + β_4,cX₄ + β_5,cX₅ + β_6,cX₆ + β_7,cX₇ + β_8,cX₈. An individual’s observed outcome was taken to be the potential outcome associated with his or her true treatment class (c = t). We specified the true treatment effect size in terms of β_0,c: for all simulations (β_0,1 = 1, β_0,2 = 1.5, β_0,3 = 2).

Simulations investigated the effect of varying both class separation (i.e., entropy) and degree of confounding. By varying the magnitude of both the α parameters and β parameters, we could control the magnitude of the confounding. For simplicity, within a given class, all α parameters were equal (α₁ = α₂ = ··· = α₈) and all β parameters were equal (β₁ = β₂ = ··· = β₈). We considered the following values for the α and β vectors, where larger values of α and β indicate greater confounding: (α₁ = α₂ = α₃ = β₁ = β₂ = β₃ = 1); (α₁ = β₁ = 1; α₂ = β₂ = 1.1; α₃ = β₃ = 1.2), (α₁ = β₁ = 1; α₂ = β₂ = 1.25; α₃ = β₃ = 1.5), and (α₁ = β₁ = 1; α₂ = β₂ = 1.5; α₃ = β₃ = 2). Each simulated dataset contained 5,000 observations and 1,000 simulations were performed at each setting.

The 1-step method was implemented using the lcca function in the lcca package for R (Schafer and Kang 2013), specifying a 3-class model. In the lcca function, the user separately specifies covariates to control for with respect to the latent class indicators and with respect to the outcome; we allowed all 8 covariates to predict both the indicators and the outcome. We obtained estimates of the ATE from the lcca function. We implemented modal and pseudoclass assignment based on 3-class LCA results obtained using the lca function in the lcca package. Propensity scores, modeling modal or pseudoclass predicted class, were estimated using logistic regression; propensity score weighting for multiple groups was conducted using the method described by McCaffrey et al. (2013). We fit 3 binary propensity score models (Class 1 vs not, Class 2 vs not, and Class 3 vs not) and for each individual used the propensity score estimated from the model corresponding to his or her predicted class membership to calculate an inverse probability of treatment weight (IPTW). Weights were trimmed at the 98^th percentile to avoid extreme weights (Cole and Hernán 2008). Differences in outcomes across classes were then estimated using propensity score weighted models that regressed the distal outcome on modal or pseudoclass assignment; this was implemented using the survey package in R (Lumley 2004, 2013). IPTW also generates estimates of the ATE, making these results directly comparable to the results from LCCA. Twenty pseudoclass draws were obtained (Graham et al. 2007), which generated 20 effect estimates that were then combined using the multiple imputation combining rule (Rubin 1987; Wang et al. 2005). Unadjusted models were estimated by implementing the lcca function specifying no covariates and by implementing modal assignment without propensity score weighting. For the purposes of this simulation, all outcome and propensity score models were correctly specified.

Our primary interest was estimation of the three pairwise class effect estimates with regard to the distal outcome (namely ȳ₂ − ȳ₁, ȳ₃ − ȳ₁, and ȳ₃ − ȳ₂). We assessed statistical performance in terms of percent bias (% bias), standard error (SE), root mean squared error (RMSE), and the 95% confidence interval (CI) coverage rate (i.e., the percentage of 95% confidence intervals that contained the true difference in means). For each simulation condition investigated, performance statistics were calculated with regard each of the three pairwise class effects; the results we report represent the averages across the three class effects. Bias is reported as the standardized percent bias ((θ̂ − θ)/θ) × 100 to account for the fact that the three true treatment effects were not equal across pairwise comparisons.

3.2 Results

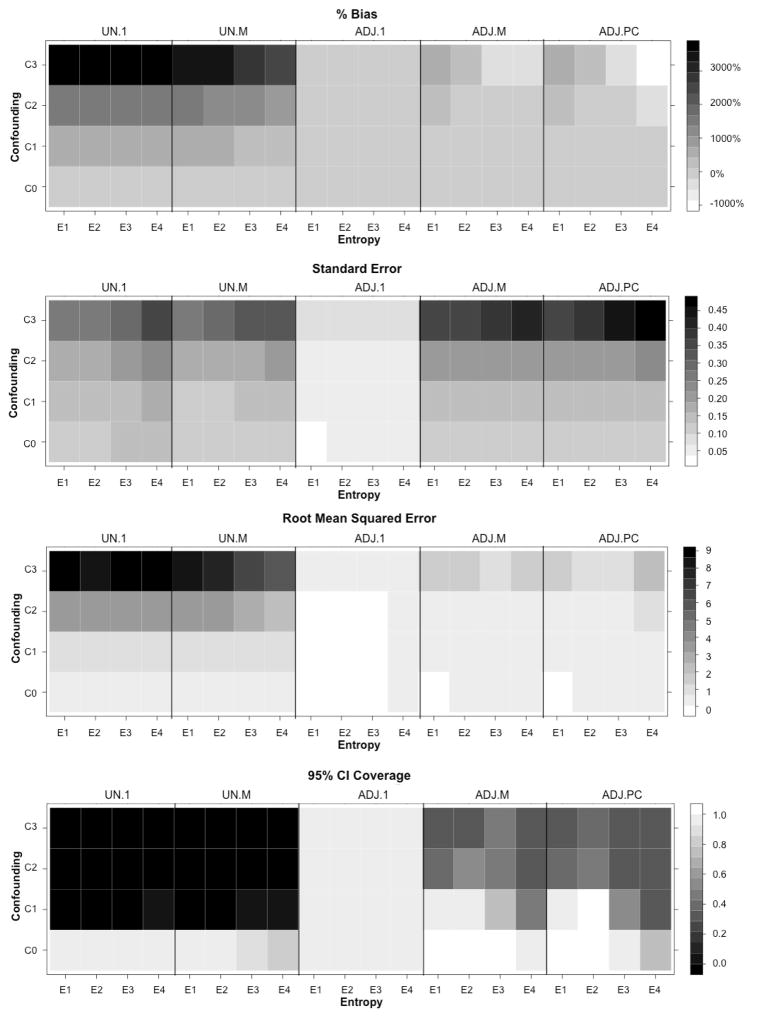
Figure 3 presents four figures depicting percent bias, SE, RMSE, and 95% CI coverage rates for each method as a function of both entropy and degree of confounding (numerical results presented in Table 1). In the absence of confounding, the percent bias for unadjusted and adjusted LCCA were similar, as was the percent bias for unadjusted and adjusted modal assignment, as expected. When confounding was present, the percent bias for both unadjusted methods were an order of magnitude larger than the percent bias of the three adjusted methods for nearly every condition. The percent bias for LCCA (unadjusted and adjusted) was primarily affected by the degree of confounding, whereas the 3-step methods (unadjusted and adjusted) were affected by both the degree of confounding and entropy. Adjusted LCCA showed very small percent bias (<10%) regardless of the degree of confounding or entropy. Modal and pseudoclass assignment with IPTW both showed notable reductions in the magnitude of percent bias compared to the unadjusted methods, yet the percent bias for these methods was consistently larger than for adjusted LCCA. Modal and pseudoclass assignment with IPTW generally performed similarly with respect to percent bias, with the exception that modal assignment performed consistently better than pseudoclass assignment for conditions with the lowest entropy (denoted E4 in Figure 3, Table 1).

Fig. 3.

Average percent bias (% bias), standard error, root mean square error, and 95% confidence interval (CI) coverage across the three pairwise class contrasts as a function of both entropy and degree of confounding.

Abbreviations: UN.1=unadjusted 1-step; UN.M=unadjusted modal assignment; ADJ.1=1-step with covariates; ADJ.M=modal assignment with IPTW; ADJ.PC = pseudoclass assignment with IPTW. Entropy: E1=0.50, E2=0.70, E3=0.90, E4=0.96. Confounding: C0=(α₁ = α₂ = α₃ = β₁ = β₂ = β₃ = 1); C1=(α₁ = β₁ = 1; α₂ = β₂ = 1.1; α₃ = β₃ = 1.2); C2=(α₁ = β₁ = 1; α₂ = β₂ = 1.25; α₃ = β₃ = 1.5); C3=(α₁ = β₁ = 1; α₂ = β₂ = 1.5; α₃ = β₃ = 2). In all figures dark shading indicates worse performance.

Table 1.

Average percent bias (% bias), standard error (SE), root mean square error (RMSE), and 95% confidence interval (CI) coverage across the three pairwise class contrasts.

	Average % Bias				Average SE
	C0E1	C0E2	C0E3	C0E4	C0E1	C0E2	C0E3	C0E4
UN.1	0.7%	−1.0%	−1.0%	−0.7%	0.106	0.110	0.128	0.152
UN.M	−4.5%	−13.1%	−36.1%	−47.3%	0.104	0.104	0.104	0.104
ADJ.1	0.1%	0.0%	0.2%	−0.1%	0.035	0.037	0.043	0.054
ADJ.M	−5.1%	−12.2%	−35.4%	−46.9%	0.104	0.104	0.105	0.104
ADJ.PC	−5.3%	−14.5%	−45.0%	−67.8%	0.104	0.104	0.105	0.105
	C1E1	C1E2	C1E3	C1E4	C1E1	C1E2	C1E3	C1E4
UN.1	526.7%	527.6%	526.4%	529.3%	0.127	0.132	0.154	0.186
UN.M	503.5%	471.6%	366.3%	318.1%	0.126	0.127	0.129	0.130
ADJ.1	0.4%	−0.3%	−0.2%	0.9%	0.037	0.038	0.043	0.050
ADJ.M	16.7%	−6.1%	−76.5%	−108.2%	0.129	0.130	0.132	0.133
ADJ.PC	16.3%	−12.5%	−103.8%	−170.4%	0.129	0.131	0.134	0.136
	C2E1	C2E2	C2E3	C2E4	C2E1	C2E2	C2E3	C2E4
UN.1	1496.0%	1495.4%	1496.8%	1496.3%	0.169	0.174	0.201	0.238
UN.M	1440.2%	1359.8%	1107.0%	984.3%	0.171	0.174	0.183	0.189
ADJ.1	0.5%	0.4%	3.6%	6.9%	0.044	0.044	0.046	0.048
ADJ.M	131.6%	67.0%	−125.9%	−204.8%	0.190	0.194	0.202	0.207
ADJ.PC	132.5%	50.2%	−193.8%	−364.2%	0.192	0.198	0.211	0.218
	C3E1	C3E2	C3E3	C3E4	C3E1	C3E2	C3E3	C3E4
UN.1	3588.0%	3583.2%	3588.5%	3588.5%	0.263	0.270	0.306	0.349
UN.M	3461.9%	3274.4%	2704.7%	2427.8%	0.275	0.286	0.314	0.330
ADJ.1	0.7%	2.2%	4.2%	2.8%	0.070	0.071	0.071	0.072
ADJ.M	621.3%	387.2%	−225.4%	−437.3%	0.341	0.362	0.394	0.405
ADJ.PC	627.5%	333.1%	−401.8%	−862.6%	0.352	0.390	0.438	0.461

	Average RMSE				Average 95% CI Coverage
	C0E1	C0E2	C0E3	C0E4	C0E1	C0E2	C0E3	C0E4
UN.1	0.104	0.109	0.123	0.146	95.1%	95.4%	95.5%	95.7%
UN.M	0.104	0.108	0.133	0.151	95.0%	93.8%	87.1%	82.1%
ADJ.1	0.029	0.031	0.038	0.048	98.4%	98.0%	97.6%	97.5%
ADJ.M	0.032	0.042	0.091	0.116	100.0%	100.0%	99.9%	97.4%
ADJ.PC	0.031	0.045	0.110	0.163	100.0%	100.0%	99.2%	74.2%
	C1E1	C1E2	C1E3	C1E4	C1E1	C1E2	C1E3	C1E4
UN.1	1.249	1.252	1.251	1.263	0.0%	0.0%	0.1%	0.7%
UN.M	1.195	1.120	0.877	0.764	0.0%	0.0%	0.9%	2.6%
ADJ.1	0.030	0.032	0.038	0.046	98.0%	97.8%	97.5%	96.6%
ADJ.M	0.115	0.108	0.207	0.275	99.2%	99.9%	76.7%	48.7%
ADJ.PC	0.116	0.111	0.263	0.413	99.0%	100.0%	50.3%	30.8%
	C2E1	C2E2	C2E3	C2E4	C2E1	C2E2	C2E3	C2E4
UN.1	3.553	3.552	3.557	3.557	0.0%	0.0%	0.0%	0.0%
UN.M	3.422	3.231	2.636	2.341	0.0%	0.0%	0.0%	0.0%
ADJ.1	0.034	0.035	0.038	0.042	98.9%	98.6%	98.3%	97.8%
ADJ.M	0.545	0.461	0.489	0.621	41.2%	51.0%	43.8%	33.7%
ADJ.PC	0.551	0.450	0.596	0.930	41.6%	48.3%	33.7%	32.2%
	C3E1	C3E2	C3E3	C3E4	C3E1	C3E2	C3E3	C3E4
UN.1	8.616	8.605	8.619	8.620	0.0%	0.0%	0.0%	0.0%
UN.M	8.316	7.862	6.493	5.807	0.0%	0.0%	0.0%	0.0%
ADJ.1	0.043	0.044	0.159	0.263	99.4%	99.7%	99.5%	99.2%
ADJ.M	1.751	1.299	0.959	1.314	33.1%	35.4%	44.6%	34.2%
ADJ.PC	1.771	1.201	1.230	2.168	33.1%	38.9%	35.5%	29.4%

Abbreviations: UN.1=unadjusted 1-step; UN.M=unadjusted modal assignment; ADJ.1=1-step with covariates; ADJ.M=modal assignment with IPTW; ADJ.PC = pseudoclass assignment with IPTW. Entropy: E1=0.50, E2=0.70, E3=0.90, E4=0.96. Confounding: C0=(α₁ = α₂ = α₃ = β₁ = β₂ = β₃ = 1); C1=(α₁ = β₁ = 1; α₂ = β₂ = 1.1; α₃ = β₃ = 1.2); C2=(α₁ = β₁ = 1; α₂ = β₂ = 1.25; α₃ = β₃ = 1.5); C3=(α₁ = β₁ = 1; α₂ = β₂ = 1.5; α₃ = β₃ = 2).

With regard to SE, adjusted LCCA consistently yielded the smallest SE estimates, while the other four methods yielded SE estimates approximately 2–6 times larger in magnitude. When there was no confounding (denoted C0) or minimal confounding (denoted C1), these four methods have similar SEs; as confounding increases (denoted C2 and C3 in our simulations), both modal and pseudoclass assignment with IPTW yield notably larger SEs than unadjusted LCCA and unadjusted modal. For all methods, SEs increase as entropy decreases; the magnitude of this increase is smallest for adjusted LCCA.

In general, the RMSE estimates for the three adjusted methods were much smaller than the RMSE estimates for the two unadjusted methods, with RMSE for adjusted LCCA being particularly small. The large RMSE for the unadjusted methods was primarily driven by the magnitude of the bias. The magnitude of RMSE for the adjusted 3-step methods reflects both notable bias and larger SE estimates, whereas the RMSE for adjusted LCCA is quite small due to both smaller bias and SE. RMSE estimates for both modal and pseudoclass assignment with IPTW were significantly smaller than the unadjusted methods, yet were often an order of magnitude larger than adjusted LCCA for the conditions with the greatest degree of confounding.

In the absence of confounding and high entropy (C0E1, C0E2), both unadjusted methods show close to nominal 95% CI coverage, yet coverage for these methods is 0% under almost all conditions that involve confounding (C1, C2, and C3). In general, the adjusted LCCA method yields conservative 95% CI coverage (greater than 97% for all conditions) and is not significantly affected by degree of confounding or entropy. Coverage rates for both modal and pseudoclass assignment with IPTW are also conservative (near 100%) when there is little or no confounding and high entropy; however, coverage notably decreases as entropy decreases and confounding increases. Both of these methods show quite poor coverage rates under the conditions with the greatest confounding (C2 and C3).

4. Motivating Example

4.1 Methods

We applied the five previously discussed methods to our substantive question of interest: what is the effect of classes of substance use treatment services that youth receive in typical outpatient treatment on substance use problems? First, we empirically identified classes of treatment services (grouped into domains of individual-focused, family-based, and case management services) that are commonly provided in outpatient treatment using LCA; we then estimated the association between class membership and subsequent substance use problems, while controlling for potential confounding associated with the nonrandomized allocation of treatment services. Data came from a national database of adolescents who received drug treatment services funded by Substance Abuse and Mental Health Services Administration’s Center for Substance Abuse Treatment (see Appendix for details). This analysis was restricted to the 5,527 youth ages 12–18 who exclusively received outpatient services (i.e., no inpatient and residential treatment services) between study baseline and 3 months (see Table 2 for youth characteristics). For study participation, parents provided written informed consent and adolescents provided assent; institutional review boards approved the study protocol at each site.

Table 2.

Descriptive statistics of the overall adolescent sample (n=5,527).

	Mean (SD) or n (%)
Demographics
Age	15.6 (1.3)
Female	1,462 (26.5%)
White	2,854 (51.6%)
Black	758 (13.7%)
Hispanic	1,217 (22.0%)
Other	697 (12.6%)
Substance Use
Prior substance use treatment	1,478 (26.8%)
Days of substance use, past 90 days	10.4 (11.7)
Substance Problem Scale, past year [Range: 0–16]	6.5 (4.4)
Substance Dependence Scale, past year [Range: 0–7]	2.4 (2.2)
Treatment Motivation Index [Range: 0–5]	1.8 (1.3)
Does not recognize substance use problems	645 (11.7%)
Legal (past 90 days)
Criminal justice system involvement	2,836 (51.3%)
Spent time in controlled environment	1,817 (32.9%)
Arrested	1,183 (21.4%)
Crime Violence Scale [Range: 0–31]	6.5 (5.3)
Mental Health (past 90 days)
Days affected by emotional problems	19.8 (16.8)
Behavior Complexity Scale [Range: 0–33]	10.1 (7.9)

All youth were assessed with the Global Appraisal of Individual Needs (GAIN; Dennis 2003), a comprehensive instrument that assesses the following domains: demographics, substance use and substance use treatment, risk behaviors, mental and physical health, legal status, environment risk factors, and education/vocation status. All data collected with the GAIN are based on youth self-report; reliability studies have found very good reliability statistics for the majority of the GAIN indices (i.e., Cronbach’s α greater than 0.85; Dennis et al. 2010). The GAIN’s Treatment Received Scale (TxRS) was used to assess the substance use treatment services that youth received from study baseline to 3 months; this 20-item scale includes subscales that measure provision of Direct (i.e., individual-focused), Family (i.e., family-based), and External (i.e., case management) services (Dennis et al. 2010). A total of 12 items, 4 from each of the subscales, were used as latent class indicators (see Table 3). In previous work, we determined that a 4-class model best described out data, based on information criteria (BIC, adjusted BIC, AIC), entropy, and class interpretability (Schuler et al. n.d; Schuler 2013). We identified the following classes: Low Service Utilization class (10.5% of youth), Individual-Focused Services class (42.3%), Individual- and Family-Focused Services class (36.5%), and Multiple Services class (10.7%).

Table 3.

Probability of endorsing the latent class indicators in the total sample and by latent class.

Latent Class Indicators	Total Sample n=5,527	Low n=579	Indiv n=2,340	Indiv & Fam n=2,016	Multiple n=592
Individual-focused services
Teach/review with you relapse prevention problems?	78.1%	14.1%	87.0%	83.4%	95.6%
Talk about different ways to solve problems?	90.8%	38.4%	97.0%	98.0%	98.6%
Talk with you about your friends?	81.5%	24.6%	86.4%	89.3%	96.8%
Require you to take urine tests?	70.4%	57.0%	70.1%	73.5%	75.0%
Family-based services
Work with you at your home?	24.5%	8.3%	5.8%	36.6%	65.4%
Meet with family members of yours more than one time?	58.5%	24.8%	20.7%	96.1%	96.5%
Work with members of your family on communication?	46.0%	11.1%	7.6%	82.9%	91.2%
Hook your family up with services?	13.0%	1.9%	3.4%	6.3%	80.4%
Case management services
Call you on the phone in between appointments?	56.8%	23.8%	51.2%	63.8%	86.2%
Talk with a counselor, teacher or other adult at school?	19.2%	15.5%	20.0%	24.3%	65.8%
Hook you up with other services?	33.3%	6.5%	11.2%	9.4%	92.6%
Provide you with transportation to appointments?	26.3%	23.9%	21.7%	37.4%	69.2%

Abbreviations: Low = Low Service Utilization class; Indiv = Individual-Focused Services class; Indiv & Fam = Individual- and Family-Focused Services class; Multiple = Multiple Services class.

Estimated class sizes are based on modal assignment.

Our objective was to estimate the causal effects of these four treatment classes on subsequent substance use problems. The distal outcome of interest is the change in the Past Month Substance Problem Scale (SPS) score from baseline to 3 months. The SPS scale is a count of 16 symptoms, including the 7 DSM-IV criteria for substance dependence, the 4 DSM-IV criteria for substance abuse, 2 items concerning substance-related health and psychological problems, and 3 items related to less severe symptoms (e.g., hiding use, people complaining about use, and weekly use; Dennis et al. 2010).

Given the observational nature of the data, it is likely that both treatment services received by youth as well as substance use outcomes are associated with baseline youth characteristics such demographics, baseline substance use, and justice system involvement. Thus, adjusted analysis controlled for the following potential confounders: demographic variables [age, sex, and race/ethnicity (self-reported as White, Black, Hispanic, and Other)]; baseline substance use variables [prior substance use treatment (lifetime), current recognition of substance problems, days of substance use (past 90 days), Substance Dependence Scale (past year), and Treatment Motivation Index]; legal status variables [any justice system involvement; any arrests; any days in a controlled environment (each with respect to past 90 days); and the Crime Violence Scale]; and mental health variables [days affected by emotional problems (past 90 days), and the Behavioral Complexity Scale].

Analyses for adjusted LCCA, modal assignment with propensity score weighting, and pseudoclass assignment with propensity score weighting included the 12 latent class indicators, the distal outcome (SPS change score), and the potential confounders. Analyses using the unadjusted LCCA model and modal assignment included only the 12 latent class indicators and the distal outcome. A 4-class model was specified for all methods. The same covariates were included in the LCCA model as were included in the propensity score models. For each method we present all 6 of the estimated pairwise differences in distal outcomes between classes; we applied a stepwise Bonferroni correction to adjust for multiple comparisons (Hochberg 1988).

4.2 Results

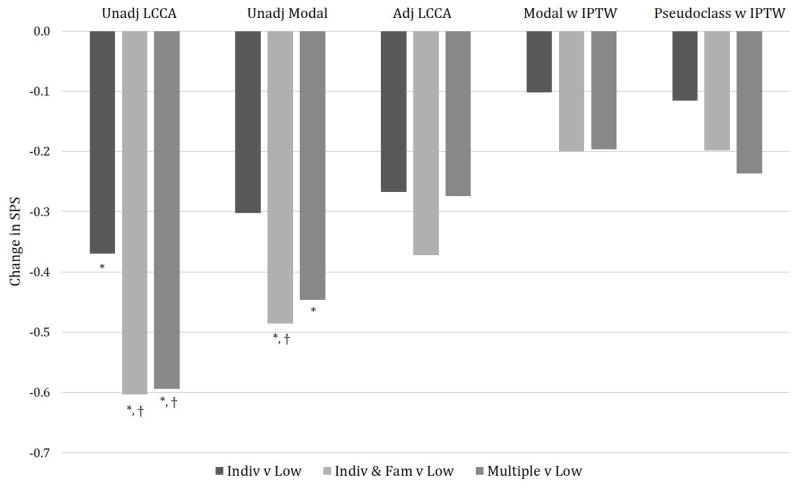
As Figure 4 and Table 4 show, unadjusted and adjusted estimates vary significantly with regard to the resulting statistical inference. The unadjusted 1-step method suggests that the Individual-Focused Services class, the Individual- and Family-Focused Services class, and the Multiple Services class each have significantly larger decreases on the Substance Problem Scale from baseline to 3 months than the Low Service Utilization class (respective estimates are −0.37, p=0.04; −0.60, p=0.001; and −0.59, p=0.01). Similarly, the unadjusted analysis based on modal assignment also suggests that the Individual- and Family-Focused Services class and the Multiple Services class each have significantly larger decreases on the SPS than the Low Service Utilization class (respective estimates are −0.49 p=0.004; and −0.45, p=0.03). When a stepwise Bonferroni correction was applied, the following contrast remained significant: Individual- and Family-Focused Services versus Low Service Utilization and Multiple Services versus Low Service Utilization (unadjusted LCCA), and Individual- and Family-Focused Services versus Low Service Utilization (unadjusted modal). However, none of the adjusted methods (LCCA, modal assignment with IPTW, or pseudoclass assignment with IPTW) show any significant differences across classes with regard to changes in SPS.

Fig 4.

Estimated class differences, relative to the Low Services Class, with respect to change in Substance Problem Scale (from baseline to 3 months), as estimated by three methods that adjust for potential confounding and two unadjusted methods.

* denotes p-values < 0.05, † denotes stepwise Bonferroni-corrected p < 0.05

Abbreviations: Low = Low Service Utilization class; Indiv = Individual-Focused Services class; Indiv & Fam = Individual- and Family-Focused Services class; Multiple = Multiple Services class

Table 4.

Estimated class differences with respect to change in Substance Problem Scale (from baseline to 3 months), as estimated by three methods that adjust for potential confounding and two unadjusted methods

	Unadjusted LCCA			Unadjusted Modal
Class Comparison	Est	SE	p-val	Est	SE	p-val
Indiv v Low	−0.37	0.18	0.04*	−0.30	0.17	0.07
(Indiv & Fam) v Low	−0.60	0.18	0.001*,†	−0.49	0.17	0.004*,†
Multiple v Low	−0.59	0.23	0.01*,†	−0.45	0.21	0.03*
(Indiv & Fam) v Indiv	−0.23	0.14	0.10	−0.18	0.11	0.09
Multiple v Indiv	−0.22	0.19	0.24	−0.14	0.16	0.38
Multiple v (Indiv & Fam)	0.01	0.21	0.97	0.04	0.17	0.81

	Adjusted LCCA			Modal with IPTW			Pseudoclass with IPTW
Class Comparison	Est	SE	p-val	Est	SE	p-val	Est	SE	p-val
Indiv v Low	−0.27	0.35	0.44	−0.10	0.18	0.58	−0.12	0.18	0.53
(Indiv & Fam) v Low	−0.37	0.29	0.20	−0.20	0.18	0.27	−0.20	0.18	0.27
Multiple v Low	−0.27	0.36	0.45	−0.20	0.24	0.41	−0.24	0.24	0.32
(Indiv & Fam) v Indiv	−0.11	0.18	0.56	−0.10	0.11	0.38	−0.08	0.12	0.47
Multiple v Indiv	−0.01	0.26	0.98	−0.09	0.19	0.62	−0.12	0.19	0.52
Multiple v (Indiv & Fam)	0.10	0.28	0.73	0.00	0.19	0.98	0.08	0.12	0.47

^*denotes p < 0.05,

^†denotes stepwise Bonferroni-corrected p < 0.05

Abbreviations: Low = Low Service Utilization class; Indiv = Individual-Focused Services class; Indiv & Fam = Individual- and Family-Focused Services class; Multiple = Multiple Services class

This example highlights that conducting LCA with distal outcomes with and without controlling for potential confounding can lead to notably different substantive interpretations. The unadjusted analyses suggest that youth in each of the three other treatment classes show significantly larger decreases on the Substance Problem Scale at 3 months compared to the Low Services class; yet, the adjusted analyses finds no significant differences in substance problems among the groups after controlling for baseline substance use, demographics, and factors such as juvenile justice involvement. These unadjusted and adjusted comparisons suggest different clinical interpretations – the unadjusted analysis indicates that the Low Services group show significantly smaller substance problems improvements relative to the other groups, indicating that youth should be provided a greater number of treatment services (in keeping with the other latent classes) in order to achieve greater reductions in substance problems. However, the adjusted analyses indicate that treatment groups are similarly effective, given baseline need, such that the services provided to youth in the Low Service class are as effective, given their baseline characteristics, as the services provided to youth in the three other classes, given their baseline characteristics. One interpretation of the adjusted results is that the similar effect sizes seen across treatment groups reflect efficient referral to, self-selection into, or tailoring of services based on youth need. Alternatively, treatment effectiveness may be relatively independent of the specific treatment services a youth receives, and instead reflect a general supervision effect; thus, the similar effect sizes may represent the magnitude of a general supervision effect, adjusting for casemix differences across classes. Given the significantly different clinical ramifications of our unadjusted and adjusted analyses, this example highlights the importance of accounting for significant baseline differences across treatment groups in order to facilitate an unbiased comparison when conducting latent class regression with distal outcomes.

5. Discussion

The results from our simulation study and our motivating example of adolescents in substance use treatment both demonstrate that effect estimates from latent class regression with distal outcomes may vary substantially whether or not potential confounding is adjusted for. Confounding in settings where all variables are fully observed is widely recognized and addressed statistically, yet recognition of and statistical methods for confounding in latent variable regression are only recently emerging. Controlling for confounding in latent variable regression presents unique challenges, particularly when the latent variable is the treatment of interest. In this paper we examine a recently proposed 1-step method, LCCA, which addresses confounding through joint modeling of the latent class indicators, confounders, and the distal outcome. Additionally, we examine methods to incorporate propensity score weighting with classical 3-step methods, namely modal and pseudoclass assignment.

In general, our results indicate that LCCA performs quite well under a range of conditions, yielding very small bias, reasonable SE, and small RMSE estimates. Confidence interval coverage rates were somewhat conservative in our simulation results. However, LCCA (or broadly, 1-step methods) may not be feasible in all settings due to implementation challenges, such as lack of model convergence. Additionally, in some cases, the latent class estimation under a 1-step method may be unduly influenced by the distal outcome. Initially, we considered an additional outcome, the Substance Frequency Scale. However, implementation of LCCA with this outcome yielded a notably different 4-class structure, with regard both to conditional indicator probabilities and estimated class prevalences, than the 4-class model presented. We were unable to present results regarding the Substance Frequency Scale given that the 1-step and 3-step results were not comparable due to differences in the estimated latent class structure. Conceptually, it is undesirable for the distal outcome to significantly influence the latent classes, particularly when the goal is to estimate the causal effect of class membership on the distal outcome; Petras and Masyn (2010) further discuss this limitation of 1-step methods for distal outcomes.

We found that modal and pseudoclass assignment combined with IPTW was able to significantly reduce the bias in the effect estimates in the presence of confounding, indicating that combining 3-step methods with propensity score methods is a promising approach. Consistent with previous studies, the 3-step methods performed much more favorably in conditions of high entropy and showed poor performance when entropy was low (0.50), since low entropy increased the rate of misclassification (Asparouhov and Muthén 2013; Bolck et al. 2004; Vermunt 2010). These methods also showed worse performance under conditions with greater degrees of confounding, indicating that the IPTW approach was not able to fully adjust for confounding. This may be due to the fact that the propensity score is calculated with respect to the predicted latent class, meaning that IPTW balances predicted latent classes, rather than true latent classes, on baseline covariates. Misclassification with regard to individual’s latent class in the propensity score model results in residual bias, since the propensity score is not able to fully adjust for the true association between latent classes and confounders. In a sense, by adding an additional estimation step (i.e., propensity score modeling) that relies on predicted latent class, these 3-step methods introduce additional bias relative to 3-step methods in contexts with no confounding. This additional bias is evident when comparing simulation results for conditions with no confounding to conditions with confounding for a given entropy level. However, this limitation is inherent to the nature of latent variables: since latent classes are unobserved, we can never estimate the propensity score or assess balance with regard to the true latent class.

For simplicity and given that corrected 3-step methods have not yet been widely adopted by applied researchers, we chose to focus only on classical 3-step methods in this study. Several methods have been proposed in recent years to correct the bias from 3-step methods for latent class regression with covariates or with distal outcomes – see Asparouhov and Muthén (2013), Bakk et al. (2013), Lanza et al. (2013a), Petersen et al. (2013), and Vermunt (2010) for details on these correction methods. In the absence of confounding, these corrected 3-step methods perform quite similarly to 1-step methods with respect to bias, SE, RMSE and 95% CI coverage, yet are often less computationally intensive. Given that classical 3-step methods combined with IPTW were found to significantly reduce confounding, future work will explore extending correction methods for use in conjunction with propensity score methods to further improve the performance of 3-step methods in the context of confounding.

Note that our simulation studies did not vary sample size, although other work has shown that sample size does affect the performance of both 1-step and 3-step methods in contexts without confounding. Thus, it is plausible that sample size would also impact performance in our context. Previous work has shown that sample size particularly impacts performance when combined with poor class separation (low entropy). As Vermunt (2010) describes, maximum likelihood estimation of LCA models often generates solutions which overestimate class differences, particularly in cases of low entropy and small sample size which yields bias in both the 1-step (typically resulting in parameter overestimation) and 3-step (typically resulting in parameter underestimation) methods, although 3-step methods are more sensitive to sample size. In the context of confounding, the addition of covariates in the 1-step model does provide additional information on class membership and improve classification, thus potentially offsetting some of the deleterious effects of small sample size.

Although our simulation results highlight the performance of the 1-step method, a 3-step approach offers greater modeling flexibility. One notable advantage is that 3-step methods allow estimation of the latent classes without influence from the distal outcome. Additionally, it is possible that a 3-step method with propensity scores would be more advantageous relative to a 1-step model in the case of model misspecification. In our simulation study, both the latent class/covariate model and the covariate/distal outcome model were correctly specified. Given the parametric constraints of the joint model specified in the lcca package, it is likely in practice that one or both of the association models will be incorrectly specified. Propensity score methods have been shown to be relatively robust to model misspecification relative to covariate adjustment; additional strategies to buffer the effects of model misspecification include non-parametric estimation of the propensity score (Lee et al. 2009; McCaffrey et al. 2004; Stuart 2010) and using doubly robust estimation (Kang and Schafer 2007). Thus, another notable advantage of a 3-step approach is that it allows the incorporation of propensity score methods, which may perform better under some conditions, particularly model misspecification, than the covariate adjustment implemented in 1-step methods.

Overall, this paper highlights that applied researchers should think critically about confounding in the context of latent variable regression; as in contexts with fully observed variables, failure to adjust for potential confounders may lead to significantly biased results and potentially misleading inferences. Although methodological development in this area has been limited so far, given the complications of latent treatment groups, we discuss three proposed methods, a 1-step approach as well as 3-step approaches that include propensity score weighting. As we discuss, each of these approaches do reduce confounding bias, the 1-step method more effectively than the 3-step methods, yet each approach has limitations. Future methodological work should focus on developing and refining methods that can address confounding for LCA with distal outcomes, and assess performance under a broader array of conditions, including model misspecification.

Appendix. Overview of the 9 CSAT-funded treatment programs that youth in the sample were enrolled in

Program Name	Program Overview	N (%)	Relevant References
Effective Adolescent Treatment	Supported Motivational Enhancement Therapy/Cognitive Behavioral Therapy (MET/CBT-5) implementation	2,494 (45.1%)	Dennis et al. 2004; Melchior et al. 2007; SAMHSA 2003
Cannabis Youth Treatment	Provided MET/CBT-5, MET/CBT-12, family education and therapy (Family Support Network), MET-CBT with the Adolescent Community Reinforcement Approach (ACRA), or Multidimensional Family Therapy	451 (8.2%)	Dennis et al. 2004; Diamond et al. 2002
Adolescent Treatment Models	Provided community-based, evidence supported treatment services for adolescents	211 (3.8%)	Dennis et al. 2003
Adolescent Residential Treatment	Provided residential treatment and community-based continuing care services	50 (0.9%)	SAMHSA 2002
Strengthening Communities for Youth	Developed and strengthen substance use screening, referral and treatment systems, particularly by building partnerships among community, school-based and juvenile justice systems	792 (14.3%)	Dennis et al. 2008
Targeted Capacity Expansion	Supported development and expansion of comprehensive and integrated substance treatment services, particularly to underserved populations	283 (5.1%)	Wilson et al. 2005
Young Offenders Reentry Program	Provided community-based treatment and supportive services to youth re-entering the community	357 (6.5%)	SAMHSA 2004
Family and Juvenile Treatment Drug Court	Provided treatment services, wrap-around services, and case management as part of drug court	345 (6.2%)	SAMHSA 2005
Assertive Adolescent and Family treatment	Provided community-based, family – centered care through the Adolescent Community Reinforcement Approach and Assertive Continuing Care	544 (9.8%)	Godley et al. 2007